Identification of Functional Substates of KRas during GTP Hydrolysis with Enhanced Sampling Simulations

Abstract

As the hub of major signaling pathways, Ras proteins are implicated in 19% of tumor-caused cancers due to perturbations in their conformational and/or catalytic properties. Despite numerous studies, the functions of the conformational substates for the most important isoform, KRas, remain elusive. In this work, we perform an extensive simulation analysis on the conformational landscape of KRas in its various chemical states during the GTP hydrolysis cycle: the reactant state KRasGTP·Mg²⁺, the intermediate state KRasGDP·Pi·Mg²⁺ and the product state KRasGDP·Mg²⁺. The results from enhanced sampling simulations reveal that State 1 of KRasGTP·Mg²⁺ has multiple stable substates in solution, one of which might account for interacting with GEFs. State 2 of KRasGTP·Mg²⁺ features two substates “Tyr32_in” and “Tyr32_out”, which are poised to interact with effectors and GAPs, respectively. For the intermediate state KRasGDP·Pi·Mg²⁺, Gln61 and Pi are found to assume a broad set of conformations, which might account for the weak oncogenic effect of Gln61 mutations in KRas in contrast to the situation in HRas and NRas. Finally, the product state KRasGDP·Mg²⁺ has more than two stable substates in solution, pointing to a conformation-selection mechanism for complexation with GEFs. Based on these results, some specific inhibition strategies for targeting the binding sites of the high-energy substates of KRas during GTP hydrolysis are discussed.

1. Introduction

Ras protein¹ participates in many vital signaling pathways that control the division, growth and proliferation of cells. It is a small GTPase with a Mg²⁺ ion at the active site and exhibits a modest level of intrinsic guanosine triphosphate (GTP) hydrolysis activity.^{2, 3} In cells, its catalytic region is anchored to the intramembrane through a hyper variable region. Ras can switch between active and inactive conformations⁴ through binding with GTP and the guanosine diphosphate (GDP), respectively. The active conformation of the complex RasGTP·Mg²⁺ can interact with effector proteins to transmit signals to kinases downstream. GTP hydrolysis in Ras is accelerated by GTPase-activating proteins and leads to an inactive conformation for the RasGDP·Mg²⁺·Pi state.⁵ Reactivation of Ras requires binding to the guanine nucleotide exchange factors (GEFs)⁶ and formation of the GEF·Ras complex. The binding to GEFs prompts the exchange of GDP with GTP at the active site, leading back to the activated conformation of Ras.

Dysregulation of Ras in cells often leads to various tumor-related cancers. In fact, almost 19% tumor-caused diseases⁷ in human are related to the three Ras isoforms: HRas, NRas and KRas (KRas4A and KRas4B). Among them, 11% and 4% cancers such as melanoma and neck squamous have been associated with NRas and HRas mutants. On the other hand, KRas mutant genes have been identified in 85% cancers such as the pancreatic ductal adenocarcinoma, colorectal adenocarcinoma and lung adenocarcinoma.⁸ In recent years, Ras has (re)emerged as a potentially promising drug target⁹ for cancer treatment, especially following Amgen’s¹⁰ development of a covalent inhibitor of the KRasG12C mutant. Numerous strategies have been proposed for inhibitor design^11–13 targeting Ras, especially for KRas,¹⁴ which include inhibiting the active conformation of RasGTP,¹⁵ stabilizing the inactive hydrolysis product RasGDP¹⁶ and hindering the GDP/GTP exchange,¹⁷ etc. Considering the conformational flexibility of Ras, to further improve the effectiveness and specificity of inhibitors,¹⁸ it is essential to establish the functionality for every specific conformational state of Ras isoforms.¹⁹

Along this line, the conformation-function relationship of Ras had been explored by a number of pioneering experimental studies. In one set of experiments, Kalbitzer and co-workers^20–25 have performed a series of ³¹P NMR investigations to elucidate the conformational dynamics of Ras in solution. They proposed that HRasGTP·Mg²⁺ had two functional states, referred to as State 1 and State 2, which interact with GEFs²⁵ and effectors,^{21, 26} respectively. State 2 of HRasGTP·Mg²⁺ was observed to be the dominant population in solution and conformational transition to State 1^27–29 occurred at the time scale of microseconds to milliseconds.^{30, 31} For States 1 of HRasGTP·Mg^{2+ 28} and HRasGDP·Mg²⁺,^{32 31}P NMR and X-ray experiments have identified more than one substates, although the functions of these substates were difficult to establish based on experiments alone.³³ Moreover, the three isoforms, KRas, HRas and NRas, exhibit different kinetic properties and diverse conformations in solution.^{34, 35} For example, the equilibrium ratio of State 2 and State 1 of the wild type HRasGTP·Mg²⁺ was reported to be nearly 12:1, but that of KRasGTP·Mg²⁺ was observed to be 1:1 in solution.^{34, 36} To further understand the functions of various conformational (sub)states and factors that regulate their equilibria, detailed atomistic simulations are required.

Motivated by such consideration, numerous molecular dynamics (MD)^37–44 and enhanced sampling simulations^{33, 45–47} have been performed to investigate conformational properties of Ras^48–50 and to dissect their biological function. Lu et al.⁵¹ observed that KRasGTP·Mg²⁺ had one active state and three inactive substates in solution. Chakrabarti et al.⁵² identified the functional difference between the two isoforms of KRas4A and KRas4B in the Switch I (SW1) region based on free energy surface constructed from MD simulations. Li et al.³³ utilized replica-exchange MD (REMD)⁵³ simulations to extensively sample the conformations of HRasGTP·Mg²⁺ and identified two substates for State 2 based on computed two-dimensional free energy landscape (2D-FEL). Furthermore, the two substates “Tyr32_in” and “Tyr32_out” have been demonstrated to interact with the effectors and GAPs, respectively, using FTIR experiments.³³ In a subsequent study, Zeng et al.⁵⁴ explored the FELs of the hydrolyzed intermediates HRasGDP·Pi·Mg²⁺, NRasGDP·Pi·Mg²⁺ and the product state HRasGDP·Mg²⁺ using REMD simulations. Their simulation results revealed that Gln61 forms strong hydrogen-bonding interactions to stabilize Pi in the intermediate state, which might explain the significant oncogenic effect of Gln61 mutations in HRas and NRas. Moreover, they characterized some specific substates of the hydrolysis product state HRasGDP·Mg²⁺ and suggested that HRas follows a conformational selection^{55, 56} mechanism to interact with GEFs.

Although a number of simulation studies of KRas have been carried out, the conformational features of various functional states during the GTP hydrolysis cycle still await to be firmly established. In particular, an intriguing question concerning KRas is that while Gln61 is the most frequently mutated residue in NRas (63%) and HRas (37%) in cancers, it is only 2% among all mutations of KRas.⁵⁷ As previous conformational studies^51,52 on the states of KRas were mainly performed by using the classical MD simulations, a comprehensive insight into the functions of the substates of KRas in the whole conformational space was, therefore, inaccessible. Previously, we have carried out a series of REMD simulations^33,54 on three key states of HRas in the GTP hydrolysis and clarified the functions of the respective substates. In this work, using REMD simulations, we conduct a systematic analysis of conformational properties of KRas in the process of GTP hydrolysis, focusing, in particular, on the substates of the reactant state KRasGTP·Mg²⁺, the intermediate state KRasGDP·Pi·Mg²⁺ and the product state KRasGDP·Mg²⁺. Our study provides a detailed elucidation of the relationship between structure and function in KRas during GTP hydrolysis. The results will help identify structure-based inhibition strategies of targeting KRas.

2. Methods

2.1. System Setup

The chain A in the crystal structure of the Q61H mutant of KRas (PDB: 3GFT)⁵⁸ was used to build the initial models for State 2 of KRasGTP·Mg²⁺ and the intermediate state KRasGDP·Pi·Mg²⁺, with the His61 residue mutated back to Gln. The substrate GppNHp molecule was substituted with the GTP molecule in State 2, and with GDP·Pi in the intermediate state. The position of Pi was determined by referring to the previously simulated structure of GAP·RasGDP·Pi.⁴¹ The initial structures of State 1 of KRasGTP·Mg²⁺ and KRasGDP·Mg²⁺ were constructed from the chain A of crystal structure (PDB: 4OBE).⁵⁹ For State 1 of KRasGTP·Mg²⁺, the GDP in 4OBE was substituted with a GTP molecule. All the crystal water molecules in 3GFT and 4OBE were removed except for the crystal water molecules coordinated to the Mg²⁺ ions and the side chain of Asp57. All titratable residues were set to their default protonation state (i.e., neutral pH condition) with the Amber14SB force fields.⁶⁰ The model of the complex GEF·KRas without the substrate GDP·Mg²⁺ was directly constructed from the crystal structure (PDB: 6EPL),⁶¹ while the model for GEF·KRasGDP·Mg²⁺ was built by fitting the simulated conformation of KRasGDP·Mg²⁺ to the backbone of KRas in 6EPL; the GDP in the resulting structure was replaced with GTP to further develop a model for GEF·KRasGTP·Mg²⁺. All experimental structures used in this paper are summarized in Table S1 in Supporting Information (SI). The protein systems were immersed in a truncated octahedron box of TIP3P⁶² water molecules and counterions Na⁺ and Cl⁻ were added to neutralize the entire systems.

2.2. MD and REMD Simulations

All simulations were carried out with the AMBER18 package⁶³ using the Amber14SB⁶⁰ force fields for proteins. The force fields of the substrates GTP, GDP and Pi were adopted from the previous study.^{64, 65} The SHAKE⁶⁶ protocol was employed to constrain the bonds involving hydrogen atoms and the integration time step was set to 2 fs. The cutoff for van der Waals and real-space electrostatic interactions was set to 8 Å. Long-range electrostatic interactions were treated using the Particle Mesh Ewald method.⁶⁷ Langevin dynamics⁶⁸ was performed with a collision frequency of 2.0 ps at the temperature of 300 K and the pressure of 1 atm. Each system was first energy-minimized and then heated to 300 K within 2 ns in the NVT ensemble. In the heating process, the backbone atoms of proteins were restrained with a force constant of 50 kcal/mol/Ų. The systems were then further equilibrated for 500 ns without restraints in the NPT ensemble. Representative structures were generated from the clustering analysis based on the final 400 ns of each trajectory.

The last snapshots in those simulation trajectories were extracted to set up REMD simulations. For each system, 64 replicas with the temperature ranging from 278 K to 429 K were used for enhanced sampling. Each structure was first pre-equilibrated at each temperature for 200 ps. Then the simulation time of each replica was extended for 350 ns in the NVT ensemble and the cumulative trajectory of each system is 22.4 μs. To maintain the proper coordination of the Mg²⁺ ion during the REMD simulations, a set of distance restraints was applied to the Mg²⁺ ion and its coordinating residues in the KRasGTP·Mg²⁺, KRasGDP·Pi·Mg²⁺ and KRasGDP·Mg²⁺ systems (see Figure S1 of SI), as was done in HRas.⁵⁴ The coordinates were saved at an interval of every 2 ps for the subsequent analysis.

2.3. Construction of 2D Free Energy Landscapes

Data analysis is performed based on the sampled 100–350 ns trajectories at 278 K to be consistent with previous NMR experiments.^{21, 36, 69} Since it has been observed in the NMR experiments that the interconversion of State 2 and State 1 occurred in the millisecond time scale, it was impossible to sufficiently sample State 2 and State 1 simultaneously in a simulation. In practice, the REMD simulations were carried out by starting from the initial structures of State 2 and State 1 to assure the sufficient samplings, respectively. The REMD simulations performed at current conditions had the moderate exchange ratios (Figure S2(a) of SI). The calculated values of the root-mean square deviation (RMSD) and radius of gyration (R_g) of every 50 ns make sure the convergence of the REMD simulation (Figure S2(b) of SI). No apparent unfolding of the secondary structures was observed to take place at high temperatures (Figure S2(c) of SI). The RMSD curves were calculated by referring to the positions of all heavy atoms in the crystal structure of 3GFT. The 2D-FEL was constructed in terms of the two coordinates of RMSD and Rg using the Weighted Histogram Analysis Method (WHAM).⁷⁰ The single linkage method with the RMSD cutoff of 1.0 Å was selected to perform the clustering analysis on the conformations extracted from the trajectories. The CPPTRAJ⁷¹ module in AMBER and in-house Python codes were used to perform all analyses; figures were produced using the Chimera software.⁷² The sitemap software was applied to predict the potential binding pockets of the sampled structures.⁷³

3. Results and Discussion

3.1. State 2 of KRasGTP·Mg²⁺

To explore the conformational space of State 2 of KRasGTP·Mg²⁺, we first performed REMD simulations based on the crystal structure of 3GFT in which the hydroxyl oxygen of the Thr35 residue is coordinated to Mg²⁺. Figure 1a shows the corresponding 2D-FEL in terms of two chosen reaction coordinates: RMSD with respect to 3GFT and R_g. At first glance, the 2D-FEL of KRasGTP·Mg²⁺ is dramatically different from that of HRasGTP·Mg²⁺ obtained in our previous study,³³ which revealed two stable free energy basins that are well separated by a high barrier locating at the RMSD of 3.3 Å. By contrast, Figure 1a displays only a single stable free energy basin, which spans RMSD values of 1.6–3.0 Å and R_g of 15.0–15.5 Å. Beyond the RMSD value of 3.0 Å, the sampled conformations distribute diffusely over a large RMSD range of 3.0-5.0 Å, which is remarkably different from State 2 of HRasGTP·Mg²⁺ characterized in our previous work.³³ The notable differences between the two 2D-FELs suggest that KRasGTP·Mg²⁺ is overall more flexible structurally than HRasGTP·Mg²⁺.

Figure 1.

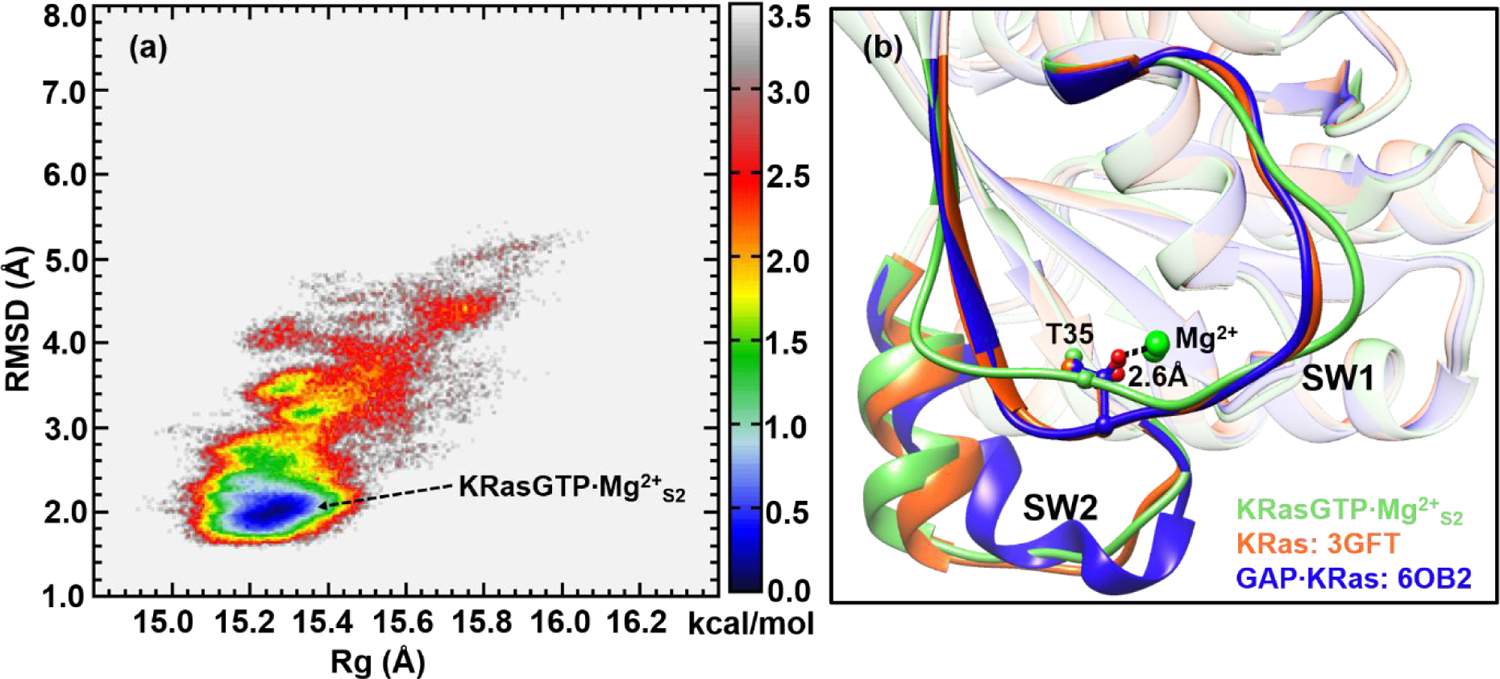
(a) Constructed 2D-FEL of KRasGTP·Mg²⁺ from REMD simulations that initiated from crystal structure 3GFT at 278 K; the reaction coordinates are the RMSD relative to the reference crystal structure (3GFT, all heavy atoms) and the Rg. The units of RMSD and R_g are in Å and the free energy is in kcal/mol. (b) Representative structure of KRasGTP·Mg²⁺_S2 is superimposed with that of the KRas Q61H mutant (PDB: 3GFT) and that in the complex GAP·KRas (PDB: 6OB2).

The free energy basin located around the RMSD of 2.0 Å is likely to represent State 2 of KRasGTP·Mg²⁺ (denoted as “KRasGTP·Mg²⁺_S2” below), since Thr35 is coordinated to the Mg²⁺ ion.⁷⁴ This is illustrated in Figure 1b by the superposition of a structure from this basin, following a clustering analysis with the crystal structure of 3GFT and KRas in the complex of GAP·KRas (PDB: 6OB2);⁷⁵ the RMSDs relative to 3GFT and 6OB2 are 1.02 and 1.47 Å respectively, indicating a high degree of structural similarity. In particular, the structure of KRasGTP·Mg²⁺_S2 features a stable coordination of Thr35 to Mg²⁺ with a distance of 2.6 Å.

3.2. Conformational Change and Function of Tyr32

As discussed in our previous work, State 2 of HRasGTP·Mg²⁺ features two adjacent low-energy regions, referred to as the “Tyr32_in” and “Tyr32_out” substates.³³ FTIR experiments³³ demonstrated that the “Tyr32_in” and “Tyr32_out” substates were involved in interacting with effectors and GAPs, respectively. By contrast, as shown in Figure 1a, the State 2 region of KRasGTP·Mg²⁺ does not appear to exhibit any notable subbasins, which begs the question of how KRas recognizes effectors and GAPs. Accordingly, we analyzed the conformational distribution of Tyr32 in the structural ensemble sampled from REMD. The inset of Figure 2a shows that the relevant dihedral angle (C-CA-CB-CG) of Tyr32 indeed exhibits two major stable basins, with the minima around 53.0 and −67.0 degrees, respectively. These two conformations correspond to the expected “Tyr32_in” and “Tyr32_out” orientations, similar to HRasGTP·Mg²⁺.³³

Figure 2.

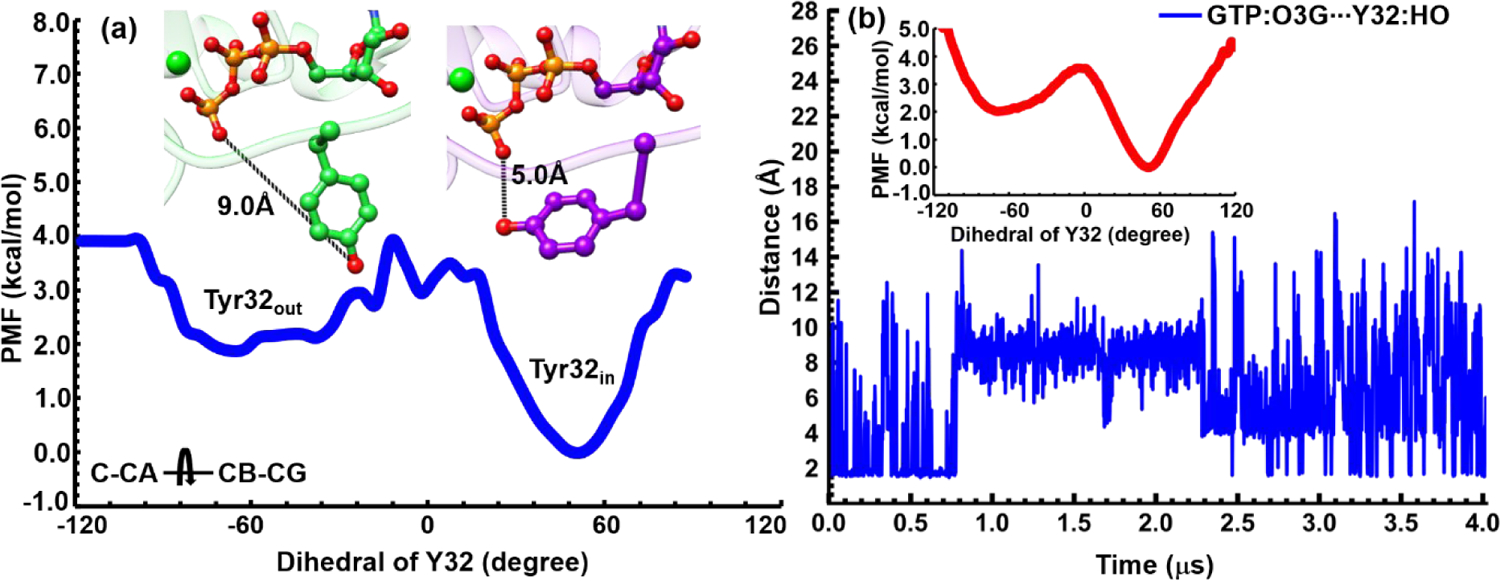
(a) Computed PMF for the sidechain isomerization of Tyr32 as characterized by the C-CA-CB-CG dihedral angle. The two minima of the PMF correspond to the “Tyr32_out” and “Tyr32_in” substates, respectively, as illustrated by the corresponding snapshots colored in green and purple, respectively. (b) The distance between the O3G oxygen of GTP and HO bond of Tyr32 during an unbiased MD trajectory of 4 μs duration. The PMF for Tyr32 isomerization computed based on this trajectory is shown as an inset.

The one-dimensional potential of mean force (PMF) in Figure 2a indicates that Tyr32_in is more stable than Tyr32_out by nearly 2.0 kcal/mol with a modest barrier. Thus, compared to the previously discussed case of HRasGTP·Mg²⁺,³³ the two substates are expected to interconvert even more rapidly in solution. This is confirmed by an independent 4 μs MD simulation of State 2 of KRas, which illustrates a rapid fluctuation of Tyr32 (see Figure 2b); the estimated PMF for Tyr32 rotation is also similar to that from REMD simulations. The rapid interconversion observed in these MD simulations is in line with the experimental observation³⁶ that the SW1 region of KRas is more flexible than that of HRas, although the qualitative two-state behaviors of Tyr32 are the same.

Thus, we expect that KRasGTP·Mg²⁺ recognizes effectors and GAPs in a way similar to HRasGTP·Mg²⁺. For example, the crystal structure of the Raf·KRas complex (PDB: 2MSE)⁷⁶ shows that Tyr32 adopts the “Tyr32_in” conformation, similar to the Raf·HRas complex (PDB: 4G0N)⁷⁷ (see Figure S3 of SI). For the interaction with GAP, the situation is less clear. For HRas, the crystal structure of the GAP·HRas complex (PDB: 1WQ1)⁷⁸ illustrates that Tyr32 adopts the “Tyr32_out” conformation (see Figure S4 of SI) since the Arg finger of GAP has to rotates into the active site to assist GTP hydrolysis,⁷⁹ as demonstrated by FTIR experiments.⁸⁰ For KRas, the crystal structure of GAP·KRas (PDB: 6OB3)⁷⁵ appears not to support such a mechanism (see Figure S5 of SI), since the Arg residue of GAP remains in the proximity of the substate rather than forming H-bonds with the substrate GppNHp. Thus, the interaction mechanism of KRas and GAP needs to be further elucidated with further experiments.

3.3. Substates of State 1 of KRasGTP·Mg²⁺

Previous NMR study⁷⁴ revealed that State 1 of the HRas T35S mutant exhibited two stable conformations in solution. To explore the relevant conformations in KRasGTP·Mg²⁺, we performed REMD simulations that started from the crystal structure of 4OBE⁵⁹ and constructed the corresponding 2D-FEL, as shown in Figure 3a. It is somewhat surprising that the obtained 2D-FEL starting from the State 1 structure 4OBE is very different from that starting from the State 2 structure 3GFT (Figure 1a), even though the same coordinates are used to project the 2D-FELs. By comparing the regions beyond RMSD of 3 Å in Figure 3a and 1a, it is evident that the regions corresponding to State 1 were poorly sampled by the REMD simulations that started from the State 2 structure 3GFT, while the regions corresponding to State 2 were poorly sampled by the REMD trajectories that started from the State 1 structure 4OBE.The discrepancies between Figures 1a and 3a highlight the challenge of adequately sampling protein conformations even with REMD simulations and projecting the free energy onto a low-dimensional space.

Figure 3.

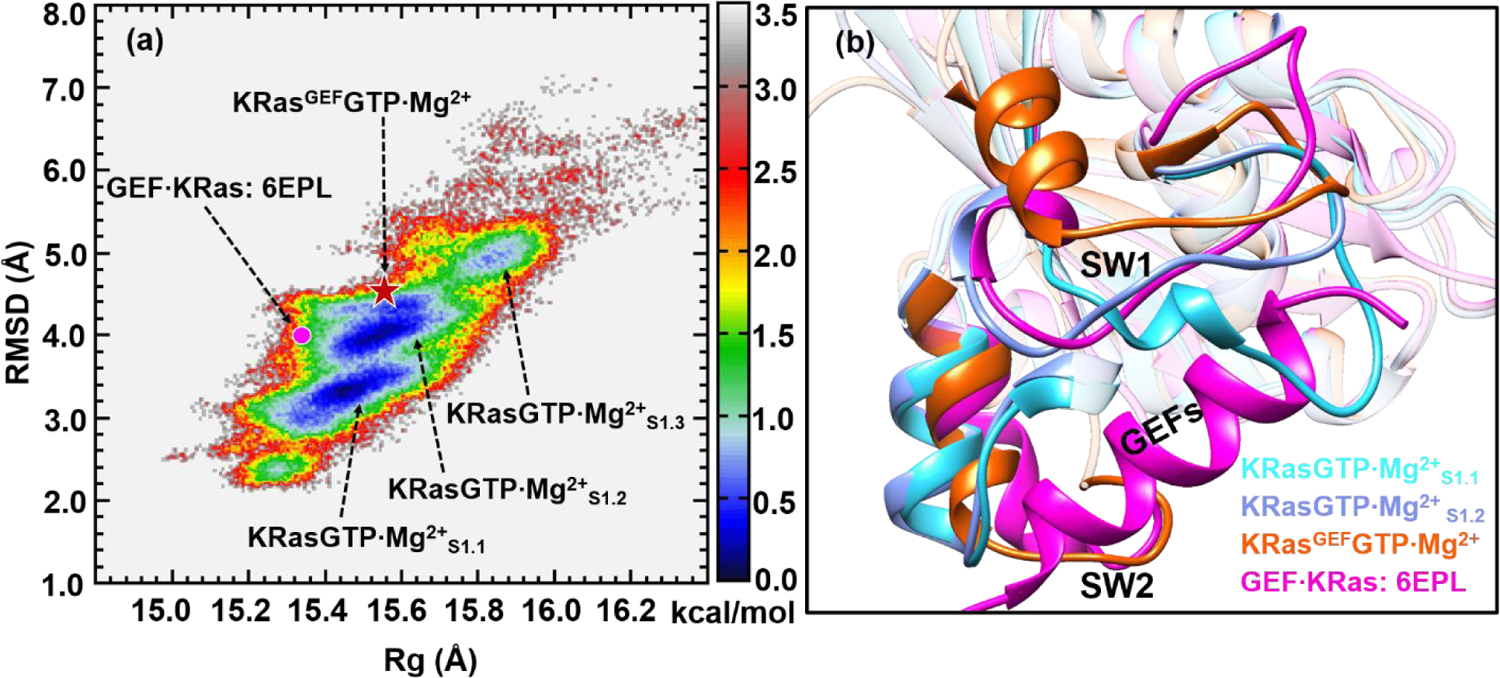
(a) Constructed 2D-FEL of KRasGTP·Mg²⁺ from REMD simulations initiated from the structure 4OBE at 278 K; the reaction coordinates are the same as those in Figure 1. The three substates are denoted as KRasGTP·Mg²⁺_S1.1, KRasGTP·Mg²⁺_S1.2 and KRasGTP·Mg²⁺_S1.3, respectively. The dot denotes the projection of KRas in the crystal structure of the complex GEF·KRas (PDB: 6EPL). The pentacle denotes the projection of the representative structure of KRas^GEFGTP·Mg²⁺ from MD simulations. The units of RMSD and R_g are in Å and the free energy is in kcal/mol. (b) The cartoon representation of the overlapped secondary structures of KRasGTP·Mg²⁺_S1.1, KRasGTP·Mg²⁺_S1.2, KRas^GEF·GTP·Mg²⁺ and KRas in the GEF·KRas complex.

Figure 3a features three separated low-free-energy regions beyond the RMSD value of 3.0 Å, herein denoted as KRasGTP·Mg²⁺_S1.1, KRasGTP·Mg²⁺_S1.2 and KRasGTP·Mg²⁺_S1.3, respectively, where the subscript “S1” highlights the lack of coordination of Thr35 to Mg²⁺ in these substates, as defined for HRas.⁵⁴ The substate KRasGTP·Mg²⁺_S1.3 has a higher free energy and thus is less populated in solution.

The multiple substates presented in Figure 3a are consistent with the multiple structures obtained for the HRasT35S mutant.²⁸ Besides, ³¹P NMR experiments have demonstrated that State 1 is responsible for interacting with GEFs.²⁵ To establish which substate of KRasGTP·Mg²⁺ interacts with GEFs, we built an all-atom model of GEF·KRas from the crystal complex structure of 6EPL and performed 500 ns classical MD simulations. Following the notations defined for the GEF·HRas complex,⁵⁴ we designate the conformation of KRas from the simulated GEF·KRas complex as KRas^GEFGTP·Mg²⁺. Projection of 6EPL and the simulated KRas^GEFGTP·Mg²⁺ structure onto the 2D-FEL in Figure 3a suggest that the relevant conformations fall into the region of KRasGTP·Mg²⁺_S1.2 with the RMSD value of ~4.0 Å.

To further identify the structural differences between KRasGTP·Mg²⁺_S1.1, KRasGTP·Mg²⁺_S1.2, KRas^GEFGTP·Mg²⁺ and KRas in the crystal complex of 6EPL, we compare their structures following clustering analyses in Figure 3b. The comparison suggests that their conformations mainly differ in the SW1 region. The SW1 loop of KRasGTP·Mg²⁺_S1.1 in cyan is less open than those of 6EPL and KRas^GEFGTP·Mg²⁺, and it overlaps with the purple α-helix of GEF, which inserts into the active site of KRas. The SW1 loop of KRasGTP·Mg²⁺_S1.2 in blue is more open than that of KRasGTP·Mg²⁺_S1.1, and it orients in a way similar to the loop of GEF·KRas.

3.4. Substates of the Intermediate State KRasGDP·Pi·Mg²⁺

The GTP molecule in KRas is hydrolyzed to yield the products GDP and Pi. The hydrolysis intermediate state is labeled as KRasGDP·Pi·Mg²⁺. As shown in Figure 4a, its 2D-FEL features three local low-free-energy basins, denoted as KRasGDP·Pi·Mg²⁺_S2, KRasGDP·Pi·Mg²⁺_S1.1 and KRasGDP·Pi·Mg²⁺_S1.2, respectively. The most stable substate KRasGDP·Pi·Mg²⁺_S2 spans the range of the RMSD values from 1.6 to 2.4 Å, which is broader than the range of 1.8–2.2 Å observed for KRasGTP·Mg²⁺_S2 in Figure 1a. The difference suggests that the GTP hydrolysis in KRas renders KRasGDP·Pi·Mg²⁺_S2 more flexible than KRasGTP·Mg²⁺_S2. The 2D-FEL of KRasGDP·Pi·Mg²⁺ is quite different from that of HRasGDP·Pi·Mg²⁺ in our previous study.⁵⁴ The latter shows that all the substates are well separated from each other, especially for the most stable substate HRasGDP·Pi·Mg²⁺_S2, which suggests a slow conversion between the different substates. The smaller differences in free energies as well as the lower barrier between KRasGDP·Pi·Mg²⁺_S2 and KRasGDP·Pi·Mg²⁺_S1.1 here suggest that their interconversion is likely more rapid than that in HRas, a conjecture that we hope further experimental analysis can verify. In this regard, the 2D-FEL of KRasGDP·Pi·Mg²⁺ is more similar to that of NRas, which also features a rather low barrier between NRasGDP·Pi·Mg²⁺_S1.1 and NRasGDP·Pi·Mg²⁺_S2 on the 2D-FEL.⁵⁴

Figure 4.

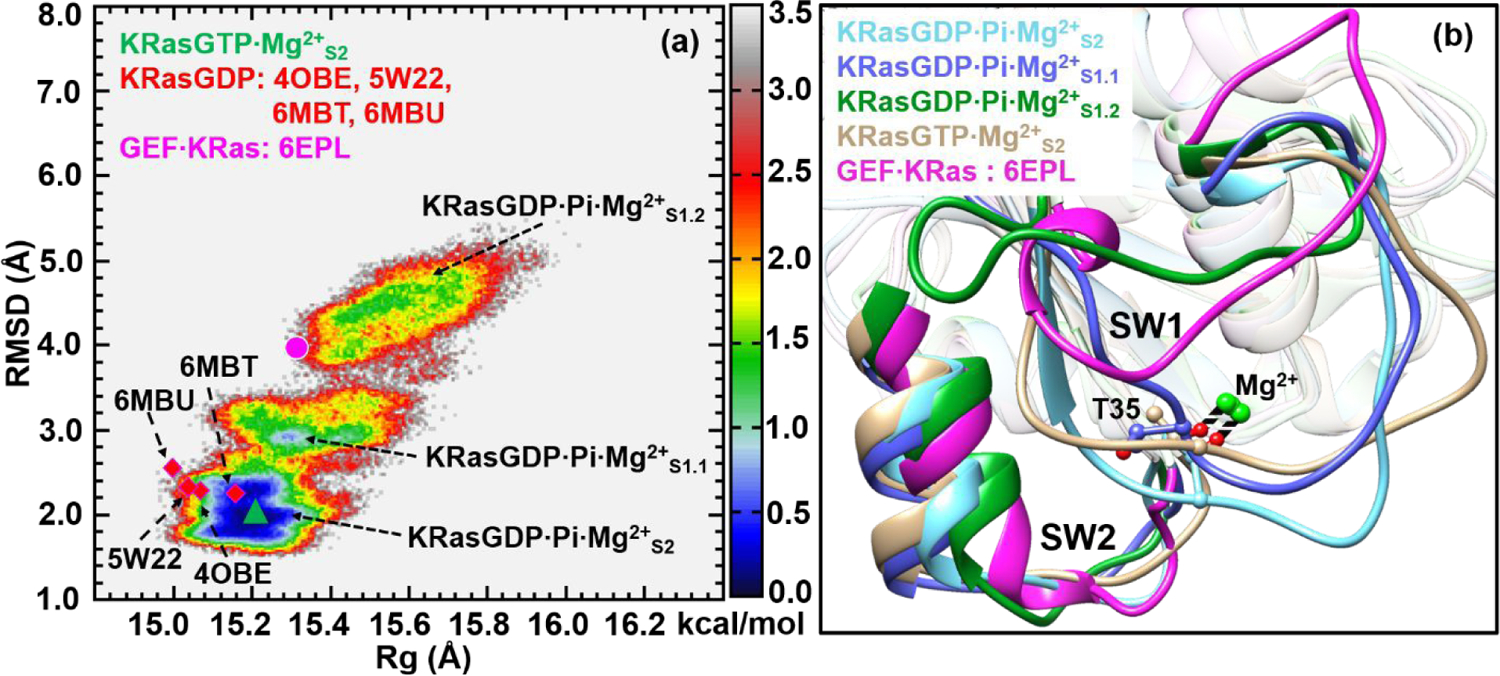
(a) Constructed 2D-FEL of the intermediate state KRasGDP·Pi·Mg²⁺ at 278 K; the reaction coordinates are identical to those in Figures 1 and 3. The three substates are denoted as KRasGDP·Pi·Mg²⁺_S2, KRasGDP·Pi·Mg²⁺_S1.1 and KRasGDP·Pi·Mg²⁺_S1.2, respectively. The purple dot and green triangle denote the projections of KRasGTP·Mg²⁺_S2 and KRas in the GEF·KRas complex. The squares denote the projections of various crystal structures of KRasGDP·Mg²⁺ with PDB codes of 4OBE, 5W22, 6MBU and 6MBT. The units of RMSD and R_g are in Å and the free energy is in kcal/mol. (b) The cartoon representation of the overlapped secondary structures of KRasGDP·Pi·Mg²⁺_S2, KRasGDP·Pi·Mg²⁺_S1.1, KRasGDP·Pi·Mg²⁺_S1.2 KRasGTP·Mg²⁺_S2 and KRas in GEF·KRas.

To characterize the structure of the intermediate state, we performed the clustering analysis on the three basins, and the corresponding representative structures are overlaid in Figure 4b. The structure of the S2 substate of KRasGDP·Pi·Mg²⁺ features a stable coordination of Thr35 to Mg²⁺, while they are broken in the S1.1 and S1.2 substates. The projection of KRasGTP·Mg²⁺_S2 falls in the basin of KRasGDP·Pi·Mg²⁺_S2 in Figure 4a, hinting at a structural similarity between them (Figure 4b). A further comparison of the Mg²⁺ coordination at their active sites (see Figure S6 of SI) indicates that they have the H-bond interaction networks similar to each other. In our previous REMD simulations of HRas,⁵⁴ it was observed that the structure of HRasGDP·Pi·Mg²⁺_S1.1 resembled the crystal structures of HRasGDP·Mg²⁺. Here, we projected the crystal structures of KRasGDP·Mg²⁺ with PDB codes of 4OBE,⁵⁹ 5W22,⁸¹ 6MBT⁸² and 6MBU⁸² onto the 2D-FEL in Figure 4a. These four structures are located below the region of KRasGDP·Pi·Mg²⁺_S1.1, revealing that the conformations in solution are more flexible than those observed in the crystalline states. The overall feature of the 2D-FEL indicates that the intermediate state of KRas features a number of different substates rather than a highly localized structural state as observed for HRas.⁵⁴

3.5. Hydrogen-Bonding Interactions in KRasGDP·Pi·Mg²⁺

Our previous REMD simulation study⁵⁴ on the hydrolysis intermediate states revealed that the key Gln61 residue formed stable hydrogen bonds with Pi in the active site of HRasGDP·Pi·Mg²⁺ and NRasGDP·Pi·Mg²⁺, and that Gln61 adopted some specific conformations with the dihedral Mg²⁺-CA_Q61-CB_Q61-OE1_Q61 distributed narrowly around 0.0 degree.⁵⁴ The hydrogen-bonding network involving Gln61 is thus expected to play an important role in stabilizing the intermediate of HRas and NRas, an observation consistent with the fact that Gln61 mutations account for 63% and 37% mutated hotspots in NRas and HRas in all cancers.⁵⁷ By contrast, Gln61 mutations account for only 2% in KRas-related cancers. To explain this striking difference, we further analyzed the conformations of KRasGDP·Pi·Mg²⁺_S2 in terms of the active site features.

Figure 5a shows the representative structure of KRasGDP·Pi·Mg²⁺_S2 following the clustering analysis. This conformation features the Pi being engaged in an extensive hydrogen bonding network, similar to the cases of HRas and NRas.⁵⁴ However, the estimated probabilities of various hydrogen-bonds formed between Pi and nearby residues are rather different from HRas and NRas, as shown in Figure 5b. For HRas and NRas, the probabilities of Pi forming hydrogen-bonds with GDP, Thr35, Gly60 and Lys16 are beyond 60%, especially with the key residue Gln61.⁵⁴ However, the populations of hydrogen bonds formed by Pi and Gln61 are low in KRas, merely around 20%, suggesting that the interaction strength is weaker than those in HRas and NRas.

Figure 5.

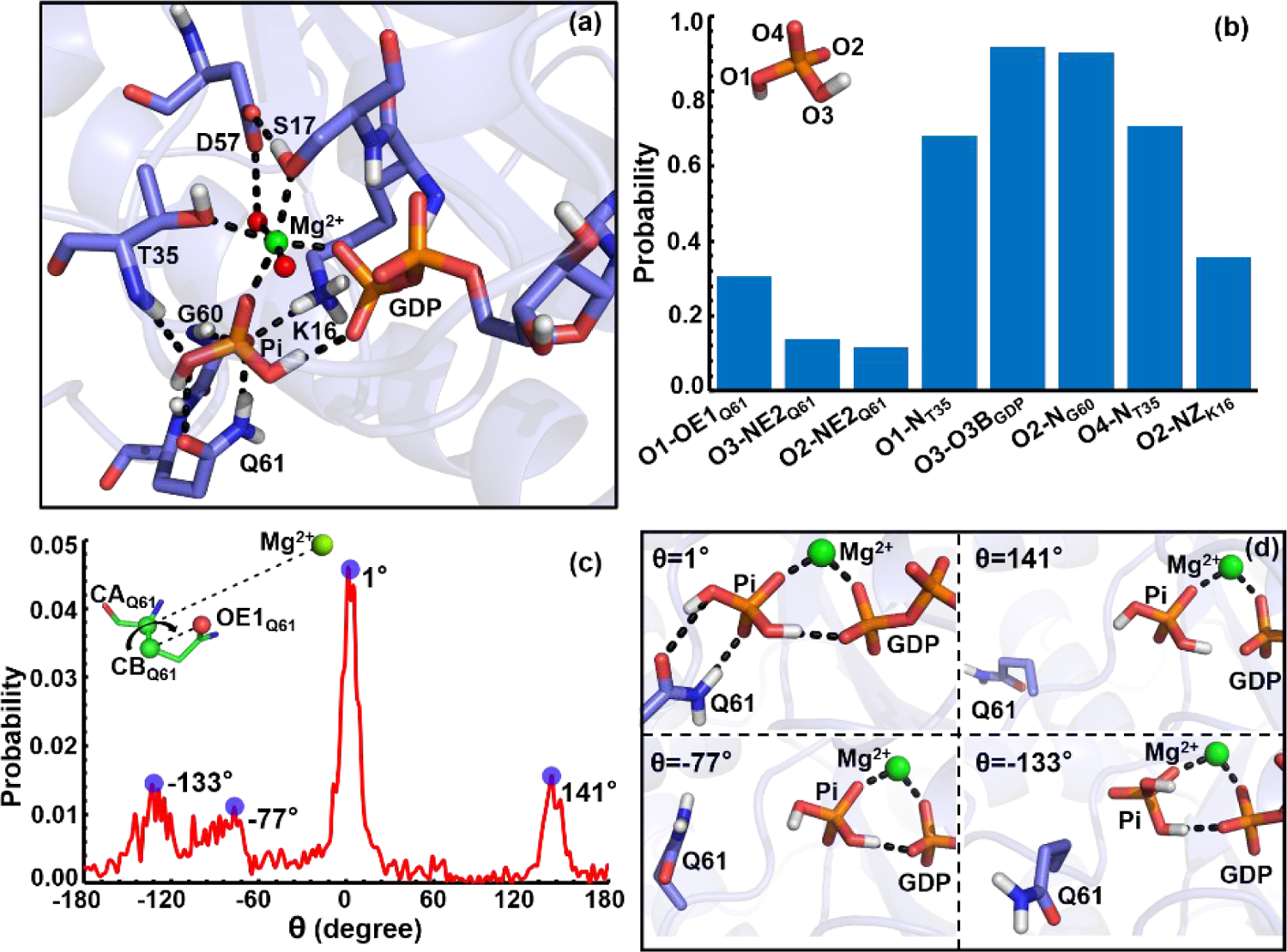
(a) The hydrogen-bonding network in the active site of a representative structure of KRasGDP·Pi_S2 from clustering analysis. The GDP, Pi, Mg²⁺ and the key residues in the hydrogen-bonding network are shown in stick models and hydrogen-bonds are indicated with dotted lines. (b) The probability of hydrogen-bond interactions between Pi with the atoms of Q61, T35, GDP and K16. (c) The distribution of the Mg-CA_Q61-CB_Q61-OE1_Q61 dihedral angle in KRasGDP·Pi_S2. The stable hydrogen-bonding conformations are highlighted on the right, which correspond to the probability peaks with the dihedrals of θ=1, 141, 77 and 133 degrees in panel (c), respectively.

Figure 5c presents the probability distribution of the key dihedral angle, Mg²⁺-CA_Q61CB_Q61-OE1_Q61, sampled from the structural ensemble. It features a broad distribution from −180.0 to 180.0 degrees, which is completely different from the narrow distributions in HRas and NRas around 0.0 degree.⁵⁴ The dihedral distribution highlights four major peaks around −133.0, −77.0, 1.0 and 141.0 degrees. Among them, the distribution around 1.0 degree has a population of 4.5%, higher than other three peaks. The distinct hydrogen-bonding patterns that correspond to the four peaks are shown in Figure 5d, and only one of them involves tight interactions between Pi and Gln61. Evidently, KRasGDP·Pi·Mg²⁺ does not feature a uniquely stable Gln61-Pi interaction, which could explain why Gln61 mutations are less implicated as cancer-inducing mutations in KRas.

3.6. Substates of KRasGDP·Mg²⁺

After Pi is released from the binding pocket, the product state KRasGDP·Mg²⁺ quickly transforms to an inactive conformation. The 2D-FEL in Figure 6a exhibits two substates with the stable basins labeled as KRasGDP·Mg²⁺_S1.1 and KRasGDP·Mg²⁺_S1.2, with their RMSD values in the ranges of 2.8–3.8 and 4.2–4.8 Å, respectively. Overall, the RMSD values of KRasGDP·Mg²⁺ span from 2.0 to 7.0 Å during the REMD simulations, indicating a much more flexible structure than the intermediate state. Compared to the previous 2D-FEL of HRasGDP·Mg²⁺,⁵⁴ in which HRasGDP·Mg²⁺_S1.2 is less stable than HRasGDP·Mg²⁺_S1.1, the stability of KRasGDP·Mg²⁺_S1.2 is comparable to KRasGDP·Mg²⁺_S1.1. The higher stability of KRasGDP·Mg²⁺_S1.2 implies that it could serve as a specific inactive substate for inhibitor design (see below).

Figure 6.

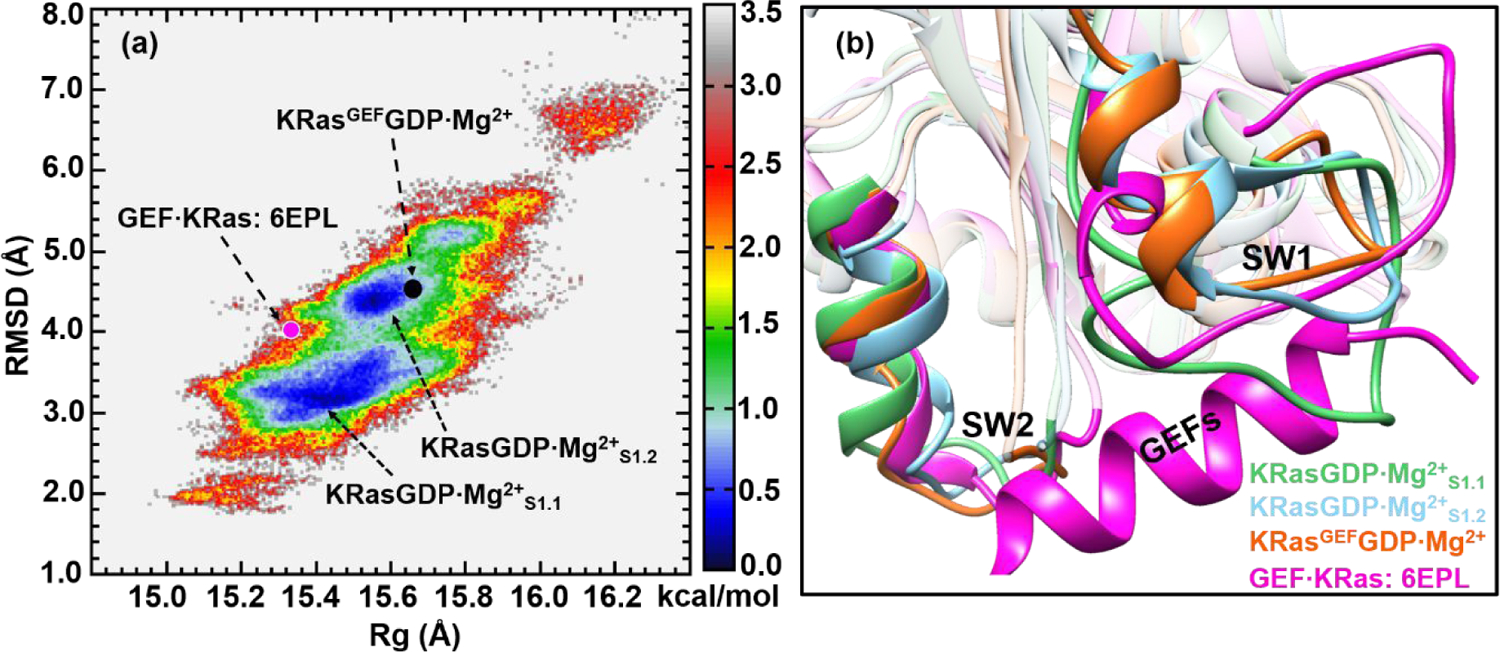
(a) Constructed 2D-FEL of KRasGDP·Mg²⁺ from REMD simulations at 278 K; the reaction coordinates are identical to those in Figures 1, 3 and 4. The two substates are denoted as KRasGDP·Mg²⁺_S1.1 and KRasGDP·Mg²⁺_S1.2, respectively. The purple and black dots denote the projections of KRas in GEF·KRas (PDB: 6EPL) and the representative structure from KRas^GEFGDP·Mg²⁺ simulations. The units of RMSD and R_g are in Å and the free energy is in kcal/mol. (b) The cartoon representation of the overlapped secondary structures of KRasGDP·Mg²⁺_S1.1, KRasGDP·Mg²⁺_S1.2, KRas^GEF·GDP·Mg²⁺ and KRas of GEF·KRas. The loop of KRasGDP·Mg²⁺_S1.1 obstructs the insertion of the α-helix of GEF.

In our previous study of HRas,⁵⁴ it was proposed that HRasGDP·Mg²⁺_S1.2 interacts with GEFs. To explore the situation for KRas, we projected the crystal structure of KRas in GEF·KRas (PDB: 6EPL) and representative structure of KRas^GEFGDP·Mg²⁺ from our simulations onto the 2D-FEL in Figure 6a. The projection of GEF·KRas is located at the edge of the KRasGDP·Mg²⁺_S1.2 basin with a RMSD around 4.0 Å, while KRas^GEFGDP·Mg²⁺ falls in the middle of the low-free-energy region. These projections indicate that the simulated KRas^GEFGDP·Mg²⁺ in GEF·KRas is similar to KRasGDP·Mg²⁺_S1.2 in solution, whereas the crystal structure of KRas appears to be more compact.

Figure 6b shows the overlaid representative structures of KRasGDP·Mg²⁺_S1.1, KRasGDP·Mg²⁺_S1.2, KRas^GEFGDP·Mg²⁺ and KRas in GEF·KRas. It is evident that the green loop of SW1 in KRasGDP·Mg²⁺_S1.1 occupies the position of the interfacing α-helix of GEFs, while the conformation of KRasGDP·Mg²⁺_S1.2 features an open loop to accommodate the latter. Thus, the hydrolysis product KRasGDP·Mg²⁺ indeed selects the conformation of the S1.2 substate rather than the most stable S1.1 to interact with GEFs, similar to the conformation-selection mechanism proposed for HRas and GEFs.⁵⁴

In addition, a comparison of the structural change of KRas in the process of exchanging GDP with GTP in GEFs is conducted. The three complexes of GEF·KRasGDP·Mg²⁺, GEF·KRas and GEF·KRasGTP·Mg²⁺ constructed with 6EPL were each simulated with 500 ns MD (see Figure S7 of SI). Figure 7 shows the overlaid representative conformations, denoted as KRas^GEFGDP·Mg²⁺_S1 and KRas^GEFGTP·Mg²⁺_S1, with a calculated RMSD of 3.0 Å. The hydrogen-bonding interaction between Asp57 and Ser17 observed in the product state KRasGDP·Mg²⁺ (PDB: 5W22)⁸¹ is broken in KRas^GEFGDP·Mg²⁺_S1, indicating an active site poised for the release of Mg²⁺ and GDP. For the simulated conformation of KRas^GEF_S1, the SW1 and Switch II (SW2) regions are loosened because of the lack of nonbonded interactions between GDP and Mg²⁺ (see Figure S8 of SI). Reloading GTP and Mg²⁺ into KRas^GEF_S1 leads to a compact structure of KRas^GEFGTP·Mg²⁺_S1, in which Asp57, Ser17, water (WAT), Mg²⁺ and GTP form stable hydrogen-bonding interactions; the SW2 region also moves toward the GTP due to the global conformational change. After detachment of GEF from KRas, the conformation of KRas^GEFGTP·Mg²⁺_S1 gradually relaxes to the substate of KRasGTP·Mg²⁺_S1.2.

Figure 7.

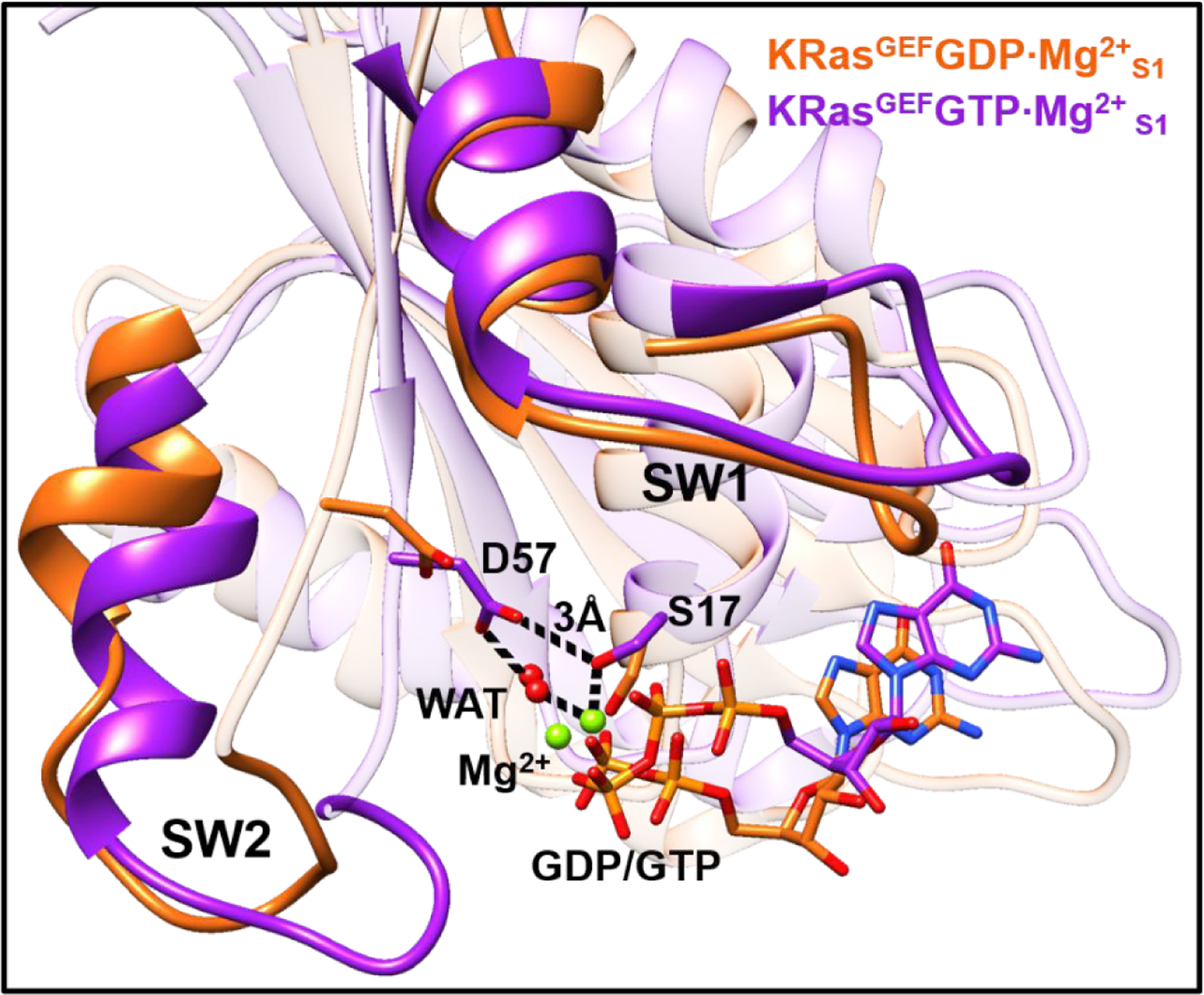
Overlap of the representative structures of the conformations of KRas^GEFGDP·Mg²⁺_S1 and KRas^GEFGTP·Mg²⁺_S1 obtained from unbiased MD simulations. The key residues Asp57, Ser17, Mg²⁺ and GDP/GTP at the active site are shown in sticks.

3.7. Binding Pockets in Substates of KRas

On the basis of known crystal structures of Ras-inhibitor complexes and MD simulations,⁸³ Gorfe and co-workers^{14, 84} highlighted four binding pockets P1, P2, P3 and P4 on the surfaces of KRas (see Figure 8). In this work, the extensive sampling of KRas conformations with REMD makes it possible to target high-energy conformations as well, which are likely to feature additional binding sites not visible in available crystal structures.

Figure 8.

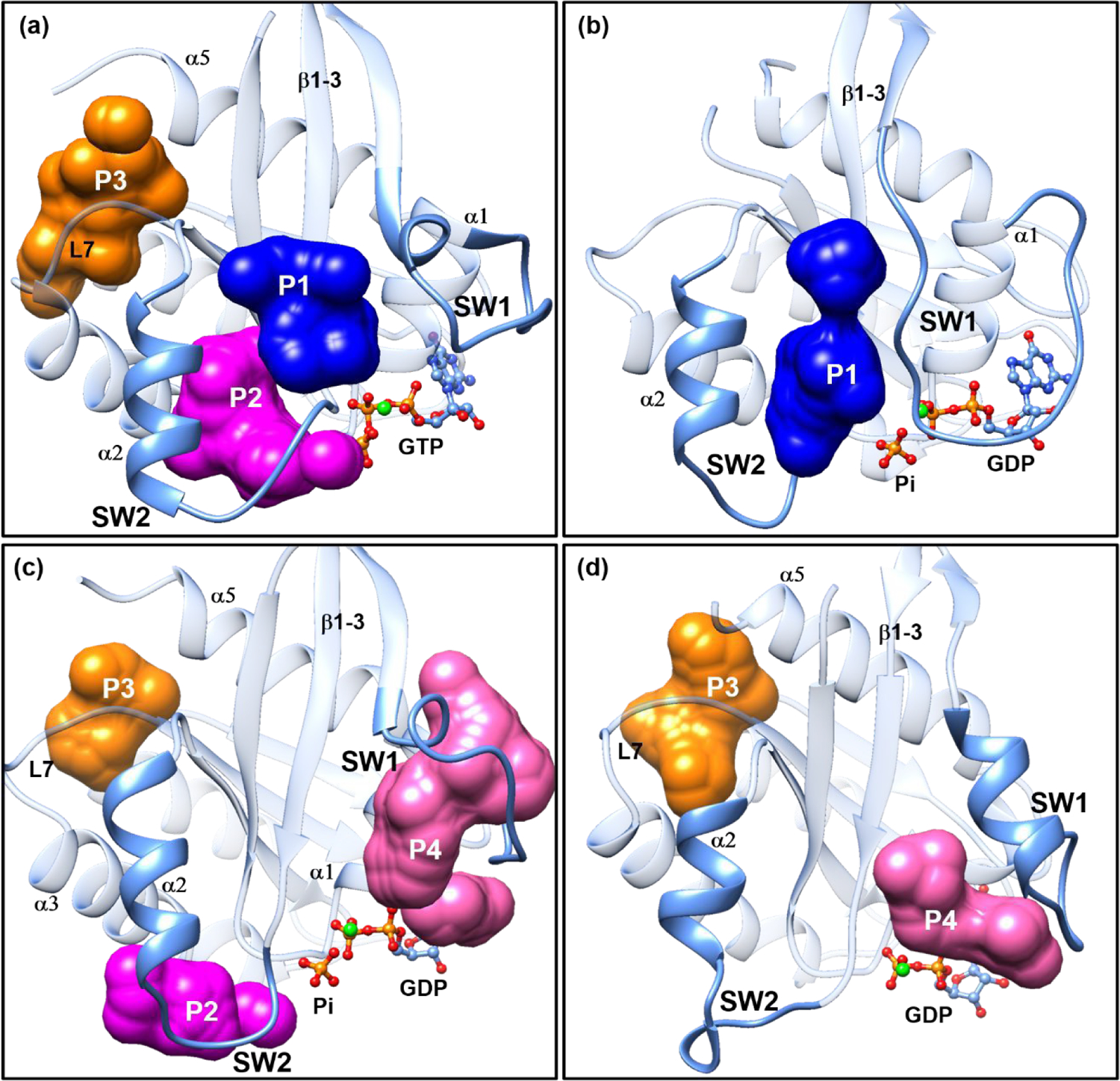
The most populated representative structures of the high-energy substates (a) KRasGTP·Mg²⁺_S1.2, (b) KRasGDP·Pi·Mg²⁺_S1.1, (c) KRasGDP·Pi·Mg²⁺_S1.2 and (d) KRasGDP·Mg²⁺_S2.2 generated from clustering analysis. The SW1 and SW2 denote the Switch I and II regions, respectively. The β1–3 denotes the β1, β2 and β3 sheets. The α1, α2, α3 and α5 denote the α-helices 1, 2, 3 and 5, respectively. L7 means loop 7 of KRas. The P1, P2, P3 and P4 refer to the binding pockets that can be targeted with small molecules identified with the sitemap module of the Schrödinger software⁹⁰.

To this end, we extracted the structures of KRasGTP·Mg²⁺_S1.2, KRasGDP·Pi·Mg²⁺_S1.1, KRasGDP·Pi·Mg²⁺_S1.2 and KRasGDP·Mg²⁺_S1.2 from the high-energy basins in the 2D-FELs and performed an additional 300 ns of MD simulation for each. The calculated RMSD values of the four systems (see Figure S9 of SI) indicate that their conformations stay in the local minima of respective substates. Then, clustering analyses were carried out and the most populated structures for each system were subjected to sitemap to find the potential binding pockets. Figures 8a–d list the identified binding pockets in the four systems, labeled with P1–P4, respectively, which are helpful for identifying novel inhibition strategies toward them as discussed below.

The KRasGTP·Mg²⁺_S1.2 substate is a high-energy one (Figure 3a), and its representative structure has three prominent binding pockets P1, P2 and P3 (Figure 8a). P1 is a cleft formed by the three β-sheets (β1–3) and the SW2 region. It is an effective inhibition site frequently identified in KRas G12D mutants.^{85, 86} The P2 site, positioning between the α-helix 2 (α2) and the α-helix 3 (α3), is preferred by covalent inhibitors targeting the KRas G12C mutant.^{10, 15, 59, 87} The P3 site is an allosteric site in the proximity of the α-helix 5 (α5) and loop 7 (L7). A small molecule binding to P3 impairs the interaction of KRas with the downstream Raf in the Raf-MEK-ERK signaling pathway.⁸⁸ In KRasGTP·Mg²⁺_S1.2, the loop of SW1 is more flexible than that in KRasGTP·Mg²⁺_S1.1 so that the P1–P3 sites are able to accommodate larger molecules. Figure 8a indicates that the pre-hydrolysis state KRasGTP·Mg²⁺ could be inhibited through stabilizing the KRasGTP·Mg²⁺_S1.1 substate by binding molecules to the P1–P3 sites. This is feasible since the population of the inactive State 1 of KRasGTP·Mg²⁺ is comparable to its active State 2 in solution.³⁶

For the intermediate state, we focus on the high-energy substates S1.1 and S1.2 of KRasGDP·Pi·Mg²⁺. Figure 8b shows that the S1.1 substate merely has one binding site P1 available for targeting and it seems to be narrower than that in Figure 8a. By contrast, the S1.2 substate in Figure 8c has three binding sites P2, P3 and P4, in which the P4 site is located in the flexible SW1 region. The SW1 region is composed of residues rich in hydrogen-bonding donors and could bind andrographolide derivatives.⁸⁹ Targeting the hydrolysis intermediate substates can shift the conformational equilibrium toward the intermediate state so that the active state KRasGTP·Mg²⁺ is inhibited.

Figure 8d shows that KRasGDP·Mg²⁺_S1.2 has two binding sites P3 and P4. Since we propose that KRasGDP·Mg²⁺ as well as HRasGDP·Mg²⁺ select the S1.2 substate to interact with GEF,⁵⁴ the P4 binding site is located at the position of the α-helix of GEFs that inserts into the active site. With small molecules bound at the P4 site, the interaction of KRas and GEFs would be interrupted.

4. Conclusion

In this work, we conduct a comprehensive REMD and MD simulations of KRas in its various chemical and conformational states during the GTP hydrolysis. The results allow us to identify the functionally specific substates of KRas that interact with specific protein partners (e.g., GAP and GEF) during the functional cycle, as summarized in Scheme 1. It is established²⁵ that the biological function of State 1 is to interact with GEF. The 2D-FEL constructed from our REMD simulations exhibits two clear substates in State 1 of KRasGTP·Mg²⁺, and the structural analysis suggests that while KRasGTP·Mg²⁺_S1.1 is better compared to the crystal structures of KRasGTP·Mg²⁺, it is KRasGTP·Mg²⁺_S1.2 that is poised to interact with GEF. KRasGTP·Mg²⁺ is also observed in our simulations to switch between State 1 and State 2 with comparable populations as observed in experiments.³⁶ The constructed 2D-FEL of State 2 of KRasGTP·Mg²⁺ does not clearly exhibit two free energy basins in the RMSD-R_g space as observed for State 2 of HRasGTP·Mg²⁺.³³ However, the two substates S2.1 and S2.2 of KRasGTP·Mg²⁺ can be defined on the basis of the calculated PMF for Tyr32 sidechain isomerization; they correspond to the “Tyr32_out” and “Tyr32_in substates defined for HRasGTP·Mg²⁺,³³ with the aromatic rings of Tyr32 pointing to the solution and GTP, respectively. The conformational interconversion between these two substates occurs more rapidly than that in HRasGTP·Mg²⁺ because the SW1 region of KRas is structurally more flexible.

Scheme 1.

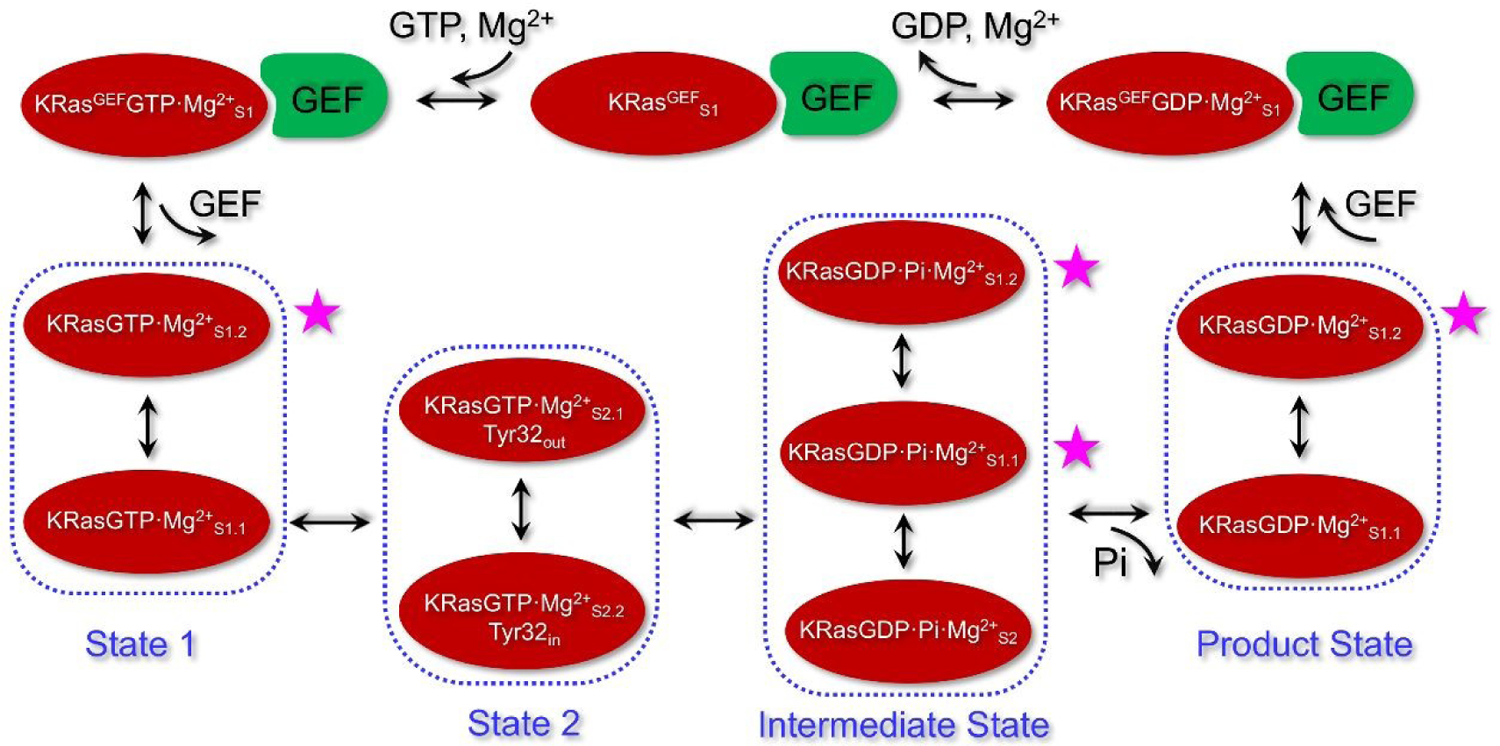
An illustration for the processes of GTP hydrolysis and exchange in KRas, including the specific substates defined based on the conformations from REMD simulations. State 1 and State 2 of KRasGTP·Mg²⁺ include substates KRasGTP·Mg²⁺_S1.1 and KRasGTP·Mg²⁺_S1.2, as well as KRasGTP·Mg²⁺_S2.1 and KRasGTP·Mg²⁺_S2.2, respectively. The intermediate state of KRasGDP·Pi·Mg²⁺ is compose of three major substates S2, S1.1 and S1.2. After Pi is released, KRasGDP·Mg²⁺_S1.1 is the most stable product substate. KRasGDP adopts the S1.2 substate to complex with GEF and forms the conformation of KRas^GEFGDP·Mg²⁺_S1. Release of GDP and Mg²⁺ leads to the KRas^GEF_S1 substate. Binding of the next GTP forms the conformation of KRas^GEFGTP·Mg²⁺_S1. Dissociation of GEF leads to State 1 of KRasGTP·Mg²⁺ in solution. The four high-energy substates, marked with the purple stars, could serve as the potential drug targets.

Following the GTP hydrolysis, KRas fluctuates among the flexible intermediate substates KRasGDP·Pi·Mg²⁺_S2 and KRasGDP·Pi·Mg²⁺_S1.1, rather than being localized in one particularly stable substate as observed for HRas. In particular, the side-chain of Gln61 adopts a broad set of conformations in the KRas intermediate substates, rather than being locked into a stable hydrogen-bonding network with Pi as identified in HRas and NRas.⁵⁴ This observation indicates that the hydrogen-bonding interaction between Gln61 and Pi is not as stable as those in other two isoforms, which might explain why Gln61 mutations are implicated in only 2% of KRas related cancer.

The release of Pi from the intermediate substates leads to KRasGDP·Mg²⁺_S1.1, which represents the most stable substate of KRasGDP·Mg²⁺ in solution. To exchange GDP through GEF, KRas has to select another more open conformation KRasGDP·Mg²⁺_S1.2 to complex with GEF. For the formation of the GEF·KRas complex, one α-helix of GEF inserts into the active site of KRas so that all interactions between Mg²⁺ and the surrounding residues including Thr35 are broken. The insertion of GEF into KRas undoubtedly decreases the affinity of GDP and Mg²⁺ with KRas, which facilitates their release and leads to KRas^GEF_S1. Then, the second GTP and Mg²⁺ are reloaded into the active site of KRas to form KRas^GEFGTP·Mg²⁺_S1. Following GEF dissociation, KRas^GEFGTP·Mg²⁺_S1 first relaxes to KRasGTP·Mg²⁺_S1.2, and then the more stable KRasGTP·Mg²⁺_S1.1.

In conclusion, the current REMD simulations have revealed a few major differences for states of HRas and KRas in the GTP hydrolysis. First, KRasGTP·Mg²⁺ has a smaller kinetic barrier between State 2 and State 1 than that of HRasGTP·Mg²⁺. Second, the intermediate state of KRasGDP·Pi·Mg²⁺ has three stable substates, while HRasGDP·Pi·Mg²⁺ has a specific substate that features the H-bond interaction of Q61 and Pi. Third, the KRasGDP·Mg²⁺ product state has two substates with comparable stabilities. The detailed characterization of various substates of KRas and their functional significance provides a deeper understanding in the structural transitions of KRas that underlie its interaction with various proteins and co-factors during the functional cycle. Moreover, based on the detailed substates in the functional cycle in Scheme 1, we also propose new strategies for targeting the high-energy substates at different stages of GTP hydrolysis, which represent new opportunities for intervening KRas-related cancers.

Supplementary Material

ESI

Table S1 summarizes the relevant crystal structures with PDB IDs. Figure S1 shows the distance restraints applied to the active sites of KRasGTP·Mg²⁺ and KRasGDP·Mg²⁺. Figure S2 presents the calculated exchange ratios, the RMSD and Rg values of every 50 ns and the distributions of helix and RMSD at different temperatures. Figure S3 shows the orientation of Tyr32 in the Raf·KRas and Raf·HRas crystal structures. Figure S4 shows the orientation of Tyr32 in the GAP·HRas and HRas crystal structures. Figure S5 shows the Arg finger in the GAP·HRas and GAP·KRas crystal structures. Figure S6 shows the H-bond networks at the active sites of KRasGTP·Mg²⁺_S2 and KRasGDP·Pi·Mg²⁺_S2. Figure S7 shows the calculated RMSDs of MD trajectories of the KRas^GEF, KRas^GEFGDP·Mg²⁺ and KRas^GEFGTP·Mg²⁺ complexes. Figure S8 shows the overlaid conformations of KRas^GEF_S1, KRas^GEFGDP·Mg²⁺_S1 and KRas^GEFGTP·Mg²⁺. Figure S9 shows the calculated RMSD curves of the high-energy structures from MD trajectories.