Wavefront engineered light needle microscopy for axially resolved rapid volumetric imaging

Abstract

Increasing the acquisition speed of three-dimensional volumetric images is important—particularly in biological imaging—to unveil the structural dynamics and functionalities of specimens in detail. In conventional laser scanning fluorescence microscopy, volumetric images are constructed from optical sectioning images sequentially acquired by changing the observation plane, limiting the acquisition speed. Here, we present a novel method to realize volumetric imaging from two-dimensional raster scanning of a light needle spot without sectioning, even in the traditional framework of laser scanning microscopy. Information from multiple axial planes is simultaneously captured using wavefront engineering for fluorescence signals, allowing us to readily survey the entire depth range while maintaining spatial resolution. This technique is applied to real-time and video-rate three-dimensional tracking of micrometer-sized particles, as well as the prompt visualization of thick fixed biological specimens, offering substantially faster volumetric imaging.

1. Introduction

The visualization of the three-dimensional (3D) structures of biological specimens is vital to examine their detailed behavior and functionality in vivo. Laser scanning microscopy has been extensively employed for this purpose owing to its optical sectioning ability accomplished by confocal detection using a small pinhole [1] or multi-photon excitation processes [2] for fluorescence specimens. However, 3D image acquisition using these point-scanning-based methods is, in principle, based on the image stacking of multiple images by changing the observation plane, which takes some time as the observation depth increases.

To overcome this limitation, various imaging techniques have been developed, which have remarkably expanded the potential of optical microscopy [3]. Scanning with multiple focal spots using a spinning disk [4–7], line scanning [8–11], light sheet illumination [12–17], and temporal focusing [18] are well-established methods that can directly improve the imaging speed. These techniques are highly effective for speeding up the capturing of optical sectioning images with a frame rate of 1 kHz by a spinning disk [4] or over 10 kHz by line scanning [9]. However, mechanical movement of the observation plane using for example a piezo scanner is still required to construct 3D volumetric images, which becomes a bottleneck to rapid 3D imaging. Some sophisticated techniques in light sheet illumination have achieved 3D imaging without the mechanical movement of a specimen or an objective lens, by utilizing an extended depth-of-field for detection [14] or the implementation based on all acousto-optic scanning systems [15]. The light sheet-based technique is one of the promising techniques for rapid whole-body imaging of living specimens [14,15,17]. However, the orthogonally arranged, characteristic optical system for illumination and detection may limit the applicability to various observation conditions using a high numerical aperture objective lens.

Recording multiple axial planes simultaneously without changing the axial position of an objective lens is another approach for the rapid visualization of 3D images. Simultaneous acquisition of multiple axial planes has been achieved in various microscope setups exploiting, for example, ingenious optical designs [19–22], computational reconstruction based on light field approaches [23–25], or remote focusing of multiplexed excitation pulses with high-speed signal processing [26,27]. Notably, an imaging technique based on inclined excitation and/or detection with respect to the optical axis [28–31] has paved the way for acquiring sectioning images along directions different from the focal plane. However, the effective aperture angle for detection is reduced by the inclined observation angle, which restricts the achievable spatial resolution [32].

Laser scanning microscopy using a focal spot with an extended focal depth—known as a Bessel beam or “light needle”—can visualize the entire volume of specimens within the focal depth from a single two-dimensional (2D) scanning process [33–35]. Although the use of a light needle spot permits rapid volumetric imaging with a high spatial resolution in the traditional frameworks of laser scanning microscopy [36,37], it only records projected images of specimens along the axial direction with no depth information. This major drawback in light needle microscopy has recently been addressed by converting emitted fluorescence signals into an Airy beam [38]. By taking advantage of the non-diffracting and self-bending properties of an Airy beam [39,40], the depth information of the fluorescence signals can be retrieved as lateral information at the detector plane. However, the bending propagation behavior of an Airy beam following a parabolic trajectory causes depth-dependent axial spatial resolution. Moreover, the detectable observation depth and signal intensity are strictly determined by the propagation property of an Airy beam, imposing a trade-off between them. Nevertheless, this technique proved the potential applicability for axially-resolved volumetric imaging in light needle microscopy by introducing spatial modulation of the wavefront—namely, the wavefront engineering of fluorescence signals. As successfully demonstrated in super-resolution localization microscopes [40–43] and sensing [44,45], wavefront engineering provides a high degree of design freedom for extracting depth information, and exploiting it will further advance the 3D acquisition capability of light needle microscopy.

Here, we propose a novel approach, based on a multiplexed computer-generated hologram (CGH), to manipulate the wavefront of fluorescence signals to laterally shift the image position depending on its axial position. The proposed method was applied to light needle scanning two-photon microscopy to demonstrate real-time and video-rate volumetric imaging. The engineered wavefront modulation enables the extraction of depth information without movement of the observation plane. Using the proposed method, 3D volumetric images can be captured at a speed equal to the frame rate of 2D raster scanning, which greatly improves the acquisition speed for 3D volumetric imaging in the framework of point-scanning-based imaging. Furthermore, this technique also enables prompt image acquisition with a limited number of raster scans even for specimens much thicker than the focal depth of a light needle without serious deterioration of image quality.

2. Theory

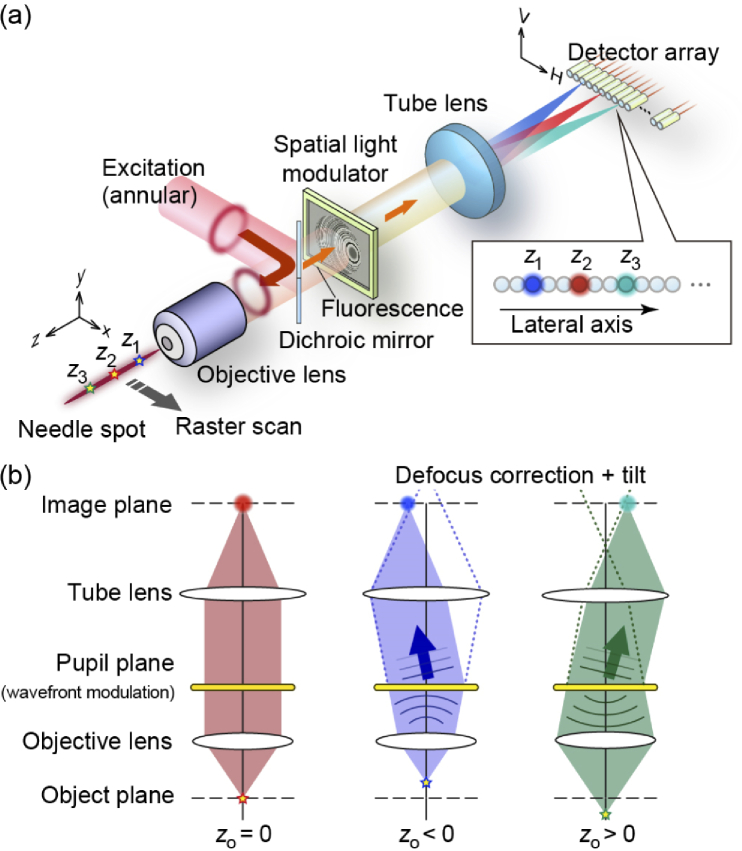
The proposed method is based on two-photon excitation imaging using needle spot excitation with an extended focal depth, achieved using a Bessel beam formed by annular beam focusing. Fluorescence specimens along the axial direction are simultaneously excited using a needle spot with an extended focal depth. Laser scanning microscopy utilizing light needle excitation provides deep-focus images, where the entire volumetric information within the focal depth can be recorded as a single image, the depth information vanishing. In general, the use of needle spot excitation merely diminishes the optical sectioning capability even in two-photon excitation imaging. By contrast, the present method can retrieve the depth information of images by applying wavefront modulation for fluorescence signals. As illustrated in Fig. 1(a), the wavefront of the fluorescence signals emitted by the excitation of a needle spot are modulated at the pupil plane of the objective lens. With this modulation, each fluorescence signal is detected at different lateral positions depending on its original axial position—that is, z₁, z₂, and z₃ in Fig. 1(a)—as described below. By placing a one-dimensional (1D) array detector at the image plane, we can acquire the depth information of samples from the 2D raster scanning of a needle spot without the need to move the observation plane. Owing to this lateral shift behavior of emission signals as well as the 1D array detection, the present method attains the optical sectioning capability in laser scanning microscopes utilizing needle spot excitation. Compared to conventional laser scanning microscopy, the acquisition speed of 3D volumetric images significantly increases with the number of detection channels under the same frame rate of raster scanning for an excitation spot.

Fig. 1.

Depth retrieval using wavefront engineering for fluorescence signals. (a) Fluorescence signals emitted from fluorophores located at different depth positions (z₁ – z₃) are detected by different lateral position at the detector plane by modulating its wavefront at the pupil plane. (b) Schematic diagram of element CGH.

To realize preferable wavefront modulation, we introduce an approach based on multiplexed CGHs [46]. The key feature required in the present method is that a point source located at z along a needle spot is imaged at a specific lateral position H on the image plane with the relationship H = αz, where α is the lateral shift coefficient. This relationship manifests the linearly varying lateral shift behavior of a point spread function (PSF) in an imaging system, converting the depth information into lateral information through wavefront modulation. Figure 1(b) explains the basic principle for realizing the laterally shifting PSF using wavefront modulation based on the multiplexed CGH, represented by coherent superposition of element CGHs, and applied at the pupil plane of an objective lens. In conventional imaging systems, a point source located at z_o can be imaged only when z_o = 0. When $z_{\text{o}}\ne 0$ , the point image is blurred by the defocus wavefront. The role of the element CGH is to correct (cancel) the defocus component of the signals from z_o and to add a wavefront tilt to laterally shift the PSF on the image plane. We can then obtain the lateral shift behavior represented as H = αz by applying the superposed element CGHs to the fluorescence emissions.

To design the required CGH pattern, we first consider the wavefront of the fluorescence emission from a point source located at z_o on the beam axis. By considering the defocus correction and the wavefront tilt to the fluorescence emission, the electric field at the pupil plane can be expressed as follows:

$$E(\xi ,\eta ;z_{\text{o}})=E_0\text{exp}[-i{\psi }_{\text{defocus}}(\xi ,\eta ;z_{\text{o}})+i{\psi }_{\text{tilt}}(\xi ,\eta ;z_{\text{o}})],$$ (1)

where (ξ, η) is the position on the pupil plane, and E₀ is the complex amplitude of the fluorescence emission. For simplicity, we assume that E₀ = 1. In the exponential term, ψ_defocus and ψ_tilt represent the defocus under high NA conditions [47,48] and the applied wavefront tilt, respectively. These terms can be expressed as follows:

$${\psi }_{\text{defocus}}(\xi ,\eta ;z_{\text{o}})=nk{z}_{\text{o}}\sqrt{1-\frac{N{A}^2}{a^2{n}^2}({\xi }^2+{\eta }^2)},$$ (2)

and

$${\psi }_{\text{tilt}}(\xi ,\eta ;z_{\text{o}})=k\xi \sin \theta ,$$ (3)

where k is the wavenumber of the fluorescence emission, n is the refractive index of the medium, NA is the numerical aperture of an objective lens with a pupil radius a, and θ represents the tilt angle of the wavefront.

By applying wavefront modulation, as represented in Eq. (1), the image of a point source at z_o is formed at the focal plane of a tube lens with a focal length f_t as $H=\sim f_{\text{t}}\theta$ for a small θ. We then consider a discrete set of an N-channeled array detector aligned along the H-axis with a pitch of δ and suppose that N point sources located along the z-axis (z_i = z₁, …, z_N) at even intervals are imaged on the specific detector channel. To satisfy this condition, we set the wavefront tilt angle for the point source at z_i to be ${\theta }_i=z_i(N-1)\delta /(f_{\text{t}}{d}_{\text{range}})$ , where d_range = z_N – z₁ is the observation depth range whose center coincides with the focus of the objective lens (z = 0). This condition ensures the linear relationship of the PSF between z_i within the observation depth range and the lateral position H_i of the i-th detector channel, as $H_i=\alpha z_i$ with $\alpha =(N-1)\delta /d_{\text{range}}$ . Based on this concept, the phase distribution $W(\xi ,\eta )$ to be applied to the fluorescence signals at the pupil plane can be expressed as the superposition of the element CGHs, as follows:

$$W(\xi ,\eta )=\arg \left\{\sum _{i=1}^N\text{exp}[-i{\psi }_{\text{defocus}}(\xi ,\eta ;z_i)+i{\psi }_{\text{tilt}}(\xi ,\eta ;z_i)+2\pi i{c}_i]\right\},$$ (4)

where c_i (from 0 to 1) is the initial phase coefficient of each CGH element.

To reproduce the lateral-shift PSFs without unfavorable interference fringes caused by phase-only modulation indicated by Eq. (4), the c_i values must be optimized in a coherent superposition. To this end, we employ a genetic algorithm to optimize the c_i values to maximize and make uniform the peak intensities of the PSFs at the designed position H_i (see Appendix A).

By applying the phase distribution represented in Eq. (4) to the fluorescence emission, we can impose linearly varying lateral shift behavior onto the PSF for a point object along the needle spot excitation. This behavior is realized by multiplexing the designed wavefronts, implying that the peak intensity of the resultant PSF decreases with multiplicity N. Nonetheless, a significant advance over Airy beam conversion [38] is that—in addition to its linearly varying lateral shift characteristic—the observation depth range d_range and the lateral shift coefficient α can be independently designed on demand. These characteristics allow us to apply the present method to broader observation conditions and various sample thicknesses by only changing the wavefront design.

3. Experimental results

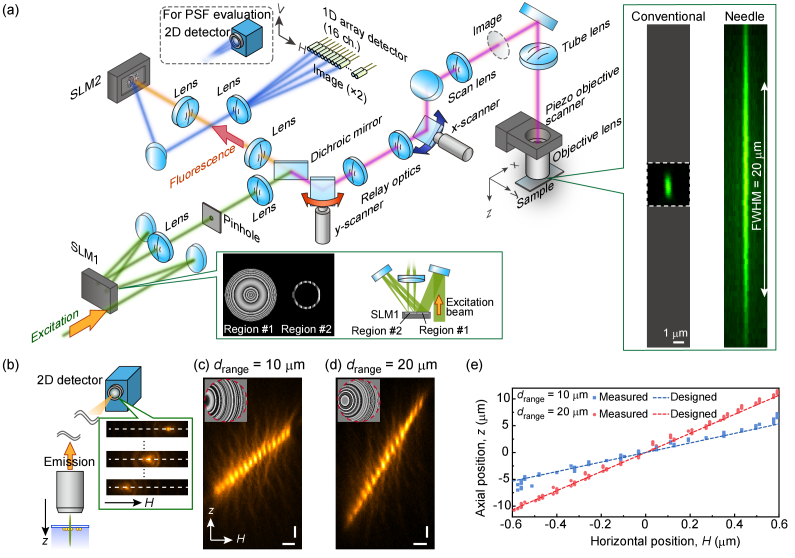
We demonstrate the proposed method using a home-built laser scanning microscope, as shown in Fig. 2(a), comprising a setup similar to that used in our previous work [38], based on a two-photon excitation microscope utilizing a 1040-nm femtosecond-pulsed laser source (femtoTRAIN 1040-5, Spectra Physics) with a repetition rate of 10 MHz and a pulse width below 200 fs. The formation of a needle spot at the focal point was achieved by converting the excitation laser beam into an annular-shaped beam using a phase-only spatial light modulator (SLM-100, Santec). The spatial light modulator—that is, SLM1 in Fig. 2(a)—was placed at the position where the pupil plane of a water-immersion objective lens (CFI Apochromat LWD Lambda S 40XC WI, Nikon) with NA = 1.15 was projected using 4f relay systems. We adopted a double-path configuration—see the bottom inset in Fig. 2(a)—to maximize the conversion efficiency of a thin-annular-shaped beam from a Gaussian beam incidence by dividing the SLM1 into two regions.

Fig. 2.

Experimental setup and the evaluation of the linearly varying lateral shift behavior of the fluorescence emission. (a) Schematic of the microscope system. (b) Illustration of the evaluation of the lateral shift behavior using a 2D detector. The intensity profiles along the white dashed lines (H axis) are exploited to reconstruct the Hz planes for observation depth ranges of (c) d_range = 10 µm and (d) d_range = 20 µm. Horizontal and vertical scale bars in (c) and (d) are 200 µm and 2 µm, respectively. Insets in (c) and (d) show the phase distribution applied to the fluorescence signals by the SLM2. Red-dashed circles in the insets indicate the pupil size of the objective lens. (e) Evaluation of the lateral shift behavior of the fluorescence emission for the observation depth ranges of 10 and 20 µm. The measured peak position along the H axis at each z position are plotted as well as the designed lateral shift variation (dashed lines).

In the first region (Region #1), the phase distribution expressing an axicon and a Fresnel lens was applied to an incident Gaussian beam to form an annular intensity distribution in the second region (Region #2). The annular beam was efficiently filtered using a thin-annular-mask with a wavefront tilt in Region #2, which separated the annularly masked region from the background by exploiting a pinhole located at its Fourier plane—the lateral and axial sizes of the needle spot depend on the inner and outer radii of the annular mask in Region #2. We designed an annular mask to form a needle spot with a focal depth of 20 µm and a lateral size of 0.36 µm, measured by its full-width and half-maximum (FWHM) sizes. It should be noted that the designed lateral size is identical to that expected by plane wave focusing under NA = 1.15 for two-photon excitation using a circularly polarized 1040-nm beam. The inner and outer radii of the annular mask were 0.680a and 0.718a, respectively, with a being the radius of the pupil (2a = 11.5 mm). The focused excitation beam was raster-scanned on the samples using two Galvano mirrors (8315KM40B, Cambridge Technology).

The inset shown on the right-hand side of Fig. 2(a) displays the measured intensity distributions of the focal spot—that is, two-photon excitation PSF—on the xz plane, obtained by imaging an isolated 200-nm orange bead using a normal detection setup equipped with a point detector [not shown in Fig. 2(a)]. By applying an annular mask, we produced a needle spot with a focal depth of 20 µm, as expected. To obtain a signal level equivalent to that of conventional imaging, an increase in laser power is required for light needle excitation because of the inverse relationship between its peak intensity and the focal depth. The laser power used in our experiment was in the range of several tens to ∼100 mW, depending on the experimental conditions. In this excitation condition, photobleaching or damage was not observed during the experiment.

The emitted fluorescence signals were separated using a dichroic mirror (NFD01-1040-25 × 36, Semrock) and the wavefront was modulated using another phase-only spatial light modulator [SLM2 in Fig. 2(a), SLM-100, Santec] at the position where the pupil of the objective lens was transferred using relay optics. The wavefront, as expressed in Eq. (4), was displayed on the SLM2. The converted fluorescence signals were then detected using a 1D array detector through a lens with an effective focal length of 400 mm in the optical system, providing a total magnification of 80. The 1D array detector was composed of a custom-made optical fiber bundle comprising 16 multi-mode fibers with a core diameter of 50 µm and aligned one-dimensionally with a pitch of 75 µm. The opposite end of each fiber was proximately coupled to a 4 × 4 arrayed multi-pixel photon counter module (C13369-3050EA-04, Hamamatsu). The output signals were recorded using a data acquisition system in synchronization with Galvano mirrors to reconstruct the 3D images. To evaluate the lateral shift characteristics of the emission PSF in detail, we placed an electron-multiplying charge-coupled device (EMCCD) camera (iXon Ultra 897, Andor) at the image plane instead of the 1D array detector, as described below.

As shown in Fig. 2(b), we first evaluated the lateral shift behavior of the converted fluorescence signals by recording the intensity distribution at the image plane using the EMCCD camera. A 20-µm needle spot was focused on a fixed position within a cluster of 200-nm orange beads thinly adhered to a coverslip, the fluorescence signal being measured while changing the focal point along the z axis using a piezo objective scanner (MIPOS 500, Piezosystem Jena). We applied wavefront modulation with design parameters N = 16, δ = 75 µm, and a fluorescence wavelength λ_em = 560 nm for d_range = 10 µm [Fig. 2(c)] and 20 µm [Fig. 2(d)] to emitted fluorescence signals (see Appendix A for the detailed design parameters including c_i). By changing the axial position of the focus with respect to the sample, the fluorescence point image (corresponding to the emission PSF) was successfully replicated 16 times with different lateral positions, as shown in Figs. 2(c) and 2(d). We estimated the peak position along the H axis of the PSF for the axial movement of the sample, as shown in Fig. 2(e). This evaluation clearly demonstrates a linearly varying lateral shift for the emission PSF. Importantly, owing to the multiplexing of a finite number of wavefronts, the point image of the converted fluorescence signals appeared only at well-defined, discrete lateral positions. Thus, each fiber channel of the 1D array detector at the image plane could efficiently detect fluorescence signals only from the specific axial position in accordance with the design.

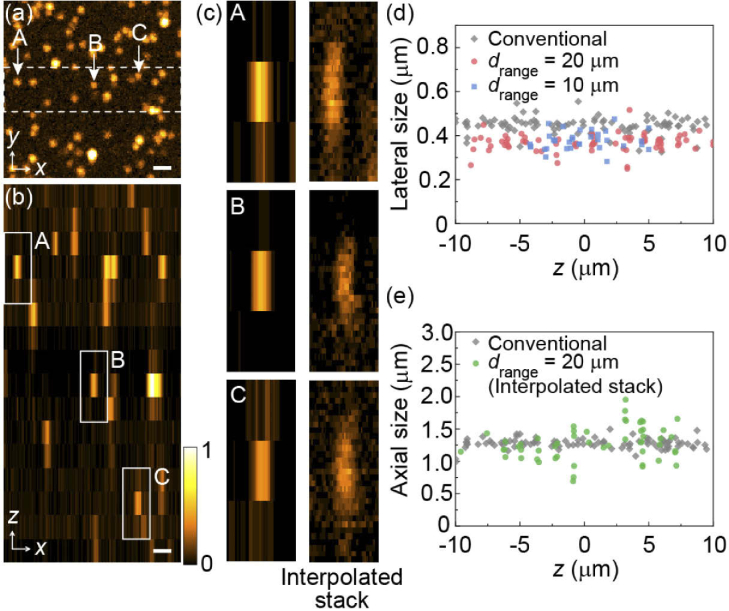
Figure 3 shows an image of 200-nm orange beads embedded in agarose gel reconstructed using single 2D scan of the 20-µm needle with the 1D array detector. Wavefront modulation with d_range = 20 µm was used for fluorescence emission. The 16 detection channels along the H axis correspond to a depth range of 20 µm with an axial pitch of 1.33 µm. As shown in Figs. 3(a) and 3(b), the individual beads were clearly resolved three dimensionally. Whereas the reconstructed axial plane [Fig. 3(b)] displays a relatively low pixel resolution owing to the limited number of detection channels, the axial position of the beads was clearly extracted. The left panel of Fig. 3(c) shows magnified views of the typical beads located at different axial positions within the observation volume. In the present setup, the fluorescence signals from such small beads were detected using a single channel only, indicating low crosstalk between adjacent detection channels. When the further reduction of crosstalk is required, a largely spaced fiber array with a pitch larger than 75 µm may be used along with an accordingly designed CGH.

Fig. 3.

Imaging of 200-nm orange fluorescence beads embedded in agarose gel, reconstructed from a single 2D scan of a light needle with the observation depth d_range = 20 µm. (a) Maximum intensity projection of the reconstructed 3D image. (b) The xz plane displayed as maximum intensity projection along the y axis within the region indicated by the white dashed rectangle in (a). The scale bars in (a) and (b) are 1 µm. The magnified views of the three representative beads (at z = 6, −0.67, and −7.33 µm) labeled A–C in (a) and (b) are shown in the left panels in (c). The right panels in (c) correspond to the images of the same beads obtained from the interpolated stack (see main text). Evaluated lateral and axial bead sizes of each bead as a function of the axial position are shown in (d) and (e), respectively.

The present setup utilizes 16 detection channels for axial positions, which limits the sampling points along the axial direction. Thus, to accurately evaluate both lateral and axial PSF sizes of the optical system, we repeated the light needle scans for the same region by finely changing the observation plane for a depth range of 1.33 µm with a pitch of 0.133 µm. This procedure provides interpolated images by rearranging the recorded frames, as shown in the right panel of Fig. 3(c), the individual beads being finely visualized. By measuring the lateral and axial sizes of these reconstructed bead images, we analyzed the spatial resolution of the proposed method.

Figure 3(d) plots the lateral spatial resolution, estimated by considering the geometric mean of the FWHM values along the x and y axes, as a function of the axial position. The average lateral sizes within the observation depth were estimated to be 0.367 ± 0.039 µm and 0.377 ± 0.042 µm for the wavefront modulation with d_range = 20 µm [red circles in Fig. 3(d)] and d_range = 10 µm [blue squares in Fig. 3(d)], respectively. These results were comparable to those obtained by the conventional two-photon excitation microscope using a Gaussian beam [gray diamonds in Fig. 3(d)], where the measured lateral spatial resolution was 0.477 ± 0.038 µm. We further evaluated the axial spatial resolution using the interpolated stack image for d_range = 20 µm with needle imaging [Fig. 3(d)]. The average axial spatial resolution was 1.276 ± 0.256 µm [green circles in Fig. 3(e)], which is almost the same as that measured for conventional imaging (1.277 ± 0.078 µm) using the Gaussian beam [gray diamonds in Fig. 3(e)]. These results proves that the high spatial resolution of the present method is nearly identical to that expected in conventional laser scanning microscopy for both the lateral and axial directions. The achieved spatial resolution was partly attributed to confocality expected by each optical fiber channel. In our configuration, the fluorescence signals modulated by the element CGH produced point images (Airy patterns) with a lateral size of 1.22λ_em M /NA = ∼48 µm, where M is the magnification of the imaging system (=80). This size is almost the same as the core diameter (50 µm) of each optical fiber, corresponding to ∼ 1 Airy unit in confocal detection. Therefore, the 1D fiber array used in our setup behaved as the array of a confocal pinhole that can contribute to improving the spatial resolution for both the lateral and axial directions. Furthermore, Figs. 3(d) and 3(e) also demonstrate the achievement of the depth-independent spatial resolution due to the linearly varying lateral shift for the converted PSFs, which differs substantially from the previous approach based on Airy beam conversion [38].

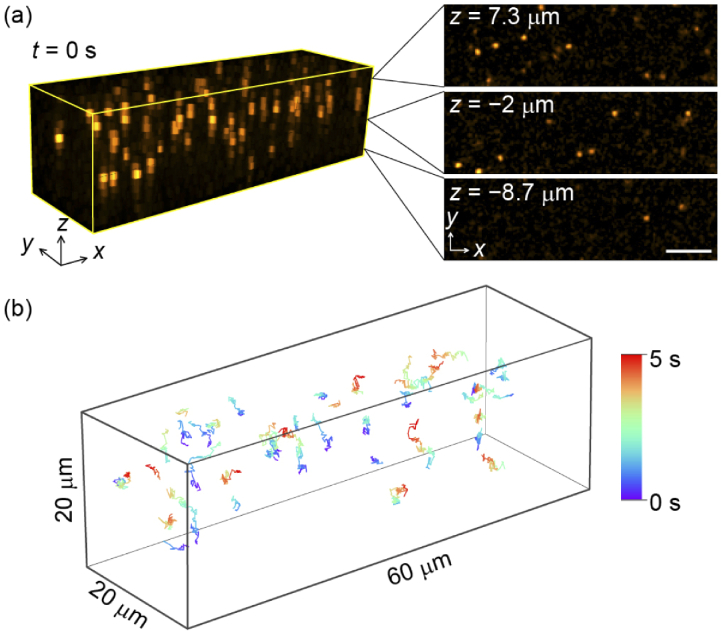
Figure 4 shows an example of rapid volumetric imaging with a 20-µm needle to continuously record the motion of 1-µm orange beads suspended in water. By continuous raster scanning of the needle for an image size of 200 × 60 pixel² using a pixel dwell time of 1.2 µs, we achieved continuous 3D imaging at a rate of 31 volumes per second (vps). Despite the limited number of axial planes (N = 16) in the present setup, the Brownian motion of the beads was successfully recorded in three dimensions [Fig. 4(a)]. The 3D positions of all observed beads were then analyzed and tracked using TrackMate [49]. During the acquisition period (five seconds), no significant drift of the optical components including the objective lens was observed, which ensured the tracking accuracy of particles. Figure 4(b) and Visualization 1 ^{(6.9MB, mp4)} demonstrate the 3D trajectories of the beads, supporting the imaging capability of video-rate capturing of the 3D dynamic motion for fluorescence specimens.

Fig. 4.

Video-rate imaging of 1-µm orange beads suspended in water with an acquisition rate of 31 vps. (a) 3D view of the image at t = 0. The rendered volume size is 60 × 17.8 × 20 µm³. The xy planes at z = 7.3, −2, and −8.7 µm are displayed on the right-hand side. The scale bar is 10 µm. (b) 3D trajectory of the Brownian motion of 44 beads recorded during 5 s. Only the beads wandering over 30 frames within the observing volume are depicted.

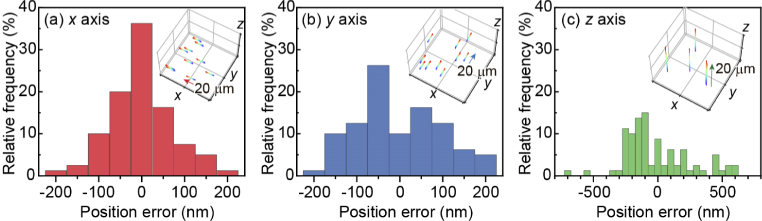
Note that, however, the localization accuracy differs between the lateral (x and y) and axial (z) directions because the voxel dimension in Fig. 4 was 0.30 µm × 0.30 µm × 1.33 µm. To estimate the localization accuracy in this imaging condition, the position of 1-µm beads fixed on a coverslip was tracked under the 1D stepwise motion with a step size of 250 nm using a nanometer precision piezo-stage (Nano-LPQ, Mad City Labs). Following the procedure reported by Louis et al. [50], we evaluated the position error for each axis by comparing the estimated step size with the real step size induced by the stage. Figure 5 shows the typical examples of the relative frequency distribution of position errors measured for a 1-µm bead under the 1D movement of 20 µm (80 track points). The localization accuracy was then calculated as the mean of the absolute error with respect to all detected beads. From this procedure, the localization accuracy in the present imaging condition was determined to be 50, 69, and 230 nm for the x, y, and z axes, respectively. The relatively low accuracy for the z axis mainly attributed to the depth pitch designed by the CGH (d_range = 20 µm). The axial localization accuracy will be improved simply by applying a multiplexed CGH with smaller d_range.

Fig. 5.

Typical examples of the relative frequency distribution of position errors measured for a 1-µm bead along the x (a), y (b), and z (c) axis. The position of the 1-µm bead was evaluated for the 1D stepwise movement of 20 µm with a step of 250 nm (see inset in each panel). In each step, a 3D image with a volume of 120 ×120 × 20 µm³ (voxel size: 0.30 µm × 0.30 µm × 1.33 µm) was taken by single 2D scanning using a pixel dwell time of 1.2 µs.

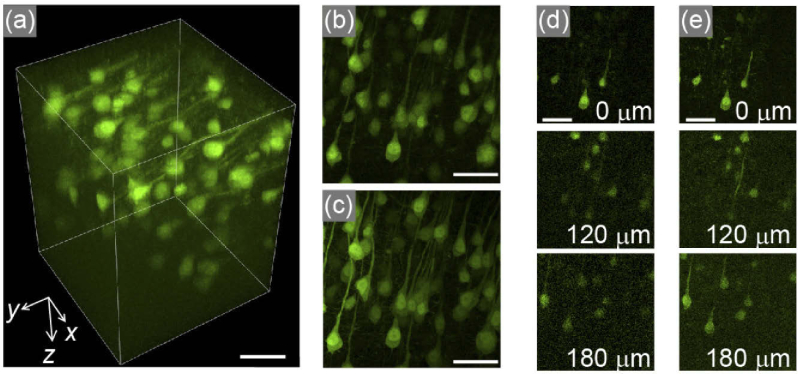
We examined another scenario in which a specimen to be observed was even thicker than the observation depth range designed using wavefront modulation. Even in this situation, the proposed method could notably increase the speed of visualizing the entire volume of the specimen, depending on the number of detection channels. Figure 6(a) and Visualization 2 ^{(7.5MB, mp4)} show the reconstructed 3D image of pyramidal neurons in a 200-µm-thick fixed brain slice of an H-line mouse (16 weeks old), acquired by stacking needle-scans 13 times with a stack pitch of 20 µm along the axial direction. The sample was treated with the optical clearing reagent, ScaleA2 [51].

Fig. 6.

Acquisition of pyramidal neurons in a fixed H-line mouse brain with an acquisition volume of 200 × 200 × 260 µm³. (a) 3D view reconstructed from 13 volumes acquired by light needle scanning with a stack pitch of 20 µm (see Visualization 2 ^{(7.5MB, mp4)} ). (b) Maximum intensity projection image along the z axis of (a). (c) The corresponding image acquired using conventional Gaussian beam stacking with a z pitch of 1.33 µm, resulting in 196 images, for the same region. (d), (e) Representative xy planes at specific z positions, noted in each panel, for (b) and (c) are shown in (d) and (e), respectively. Each scale bar is 50 µm.

In this experiment, we utilized an excitation light needle with a focal depth of 30 µm to make uniform the excitation intensity along the axial direction under the wavefront modulation of d_range = 20 µm. Stacking the images taken by the needle scans produced 196 slices with a depth pitch of 1.333 µm, corresponding to an observation depth of 260 µm. In the present setup, the acquisition of the entire volume required 23 s for raster scanning of 200 × 200 µm² by 512 × 512 pixel² with a pixel dwell time of 4 µs. This acquisition time was ∼11 times faster than that required by conventional image stacking for the identical volume using a Gaussian beam (260 s for 196 slices with the same scanning speed). As shown in Figs. 6(b)–6(e), the fluorescence images obtained using the present method were almost identical to those acquired using the conventional two-photon excitation microscope, even near the bottom of the sample. This result implies that the depth information of the fluorescence signals emitted from the deep region was correctly retrieved using wavefront modulation in our setup.

4. Discussion and conclusions

As demonstrated in this study, the proposed method enables video-rate and real-time 3D volumetric imaging achieved by scanning a light needle with an extended focal depth and wavefront modulation for fluorescence emission to retrieve the depth information. One of the significant features of this method is that it can be constructed using the traditional framework of laser scanning microscopy. This allows us to fully utilize the pupil size of an objective lens for image formation, which is distinct from the previous implementation of 3D volumetric imaging techniques based on inclined excitation and/or detection [28–31].

Thus, the present method enables 3D imaging without sacrificing the spatial resolution in both the lateral and axial directions. Additionally, the observation depth range can be readily controlled by changing only the applied phase pattern on the second SLM with neither replacement nor mechanical adjustments of the optical components. Along with this observation depth adaptability, further extension of the light needle length by modifying the annular mask design on the first SLM enables the rapid observation of much thicker specimens. Such versatility is advantageous for three dimensionally visualizing various biological specimens and their dynamic motions occurring in the subcellular to cellular range or tissue levels by exploiting the desired wavefront modulation on demand. In practice, however, chromatic dispersion of SLMs, particularly implemented by liquid crystals as employed in this study, needs to be considered when the wavefront of fluorescence signals with a broader emission spectrum is modulated. Such chromatic dispersion may blur the emission PSF on the image plane, which eventually degrades the spatial resolution and the resultant image quality. Nonetheless, no serious degradation caused by the chromatic dispersion was observed in the present experimental conditions. This attributes to the relatively narrow bandwidth of fluorescence [less than 50 nm in FWHM for the orange beads (Figs. 2–5) and the fluorescence protein (Fig. 6)]. For detection of signals with a broader emission bandwidth, the insertion of a band-path filter may be necessary, depending on experimental conditions.

In the present setup, we adopted 16 detection channels corresponding to depth information. In principle, the number of slices along the axial direction can be increased by simply adding detection channels. However, this should be accompanied by an increase in the multiplicity N of the element CGH in the wavefront modulation to assign the desired axial position to each detection channel. In this case, as noted in Section 2, one needs to consider the equipartition of the signal intensity, meaning that the signal intensity detected at each channel is, in principle, reduced by a factor of N. In fact, the mean signal intensity on the image position using the multiplexed CGH in the present setup was 5.3% (theoretical: 6.25% for N = 16) compared to the normal detection without wavefront modulation (see Appendix B). This fact indicates that, for 3D image formation, the improved acquisition speed using the N-fold detection channels is equivalent to increasing the scanning speed by a factor of N for a laser scanning microscope with a single point detector. Both cases result in a lowering of the signal-to-noise ratio, which may need to be compensated for by increasing the excitation laser power. In addition, the use of a liquid crystal-based SLM as used in this study generally leads to less light use efficiency and, in some cases, generates unfavorable higher-order diffracted signals due to the pixelated, phase-only characteristics of spatial light modulation. This will become problematics when the multiplicity of the CGHs further increases, where the local phase gradient of designed wavefront modulation exceeds the pixel resolution of the SLM. As a result, the detectable intensity of converted fluorescence signal decreases, which eventually restricts a usable pixel dwell time in the present method. The limitation of the SLMs, however, can be alleviated by introducing more advanced techniques for wavefront modulation such as multi-level diffractive optics [52]. Nevertheless, a major advantage of the proposed method is that 3D images are formed from a single raster scanning of a light needle and can be acquired at a speed equal to 2D raster scanning of an excitation laser beam. Consequently, the proposed method could further increase the acquisition speed for 3D imaging through the introduction of a faster scanner—such as a resonant scanner—with no concern for mechanical movement along the axial direction.

In summary, we have proposed a novel method to capture 3D volumetric images rapidly from 2D raster scanning of a light needle with an extended focal depth. The depth position was retrieved by employing wavefront modulation based on a multiplexed CGH technique. By using the developed system, real-time and video-rate acquisition of the 3D motion of micrometer-sized particles in water was achieved to enable 3D tracking of individual particles. Our method has also been applied to 3D image acquisition of thick fixed biological specimens, demonstrating an acquisition speed ∼10 times faster than that of conventional image stacking. The proposed method can provide spatial resolutions along the lateral and axial directions, almost equivalent to conventional laser scanning microscopy. Moreover, the observation depth and number of observation planes can be readily controlled by simply changing the modulation pattern on the SLM without any mechanical adjustments. In the future, such imaging capability and controllability offer superior versatility as a rapid 3D imaging technique that will be widely applied to visualize the dynamic motions of biological specimens, intercellular or intracellular behaviors, and functionality in vivo.

Appendix

A. Detailed procedure of the optimization of CGH

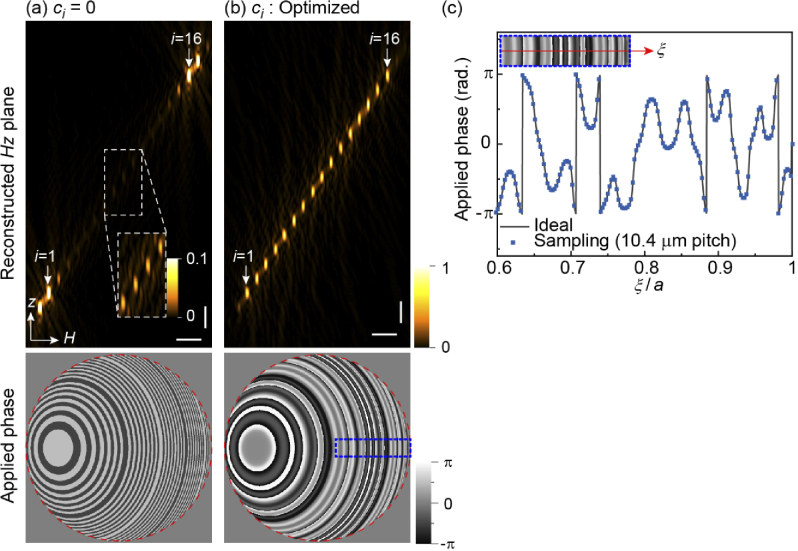
To achieve the desired lateral shift behavior by N-multiplication of the element CGHs, the initial phase coefficients c_i (i = 1 to N) in Eq. (4) must be appropriately determined—otherwise the superposition of the element CGHs results in unfavorable interference in the PSF on the image plane, as shown in Fig. 7(a), where c₁ = c₂ =… = c₁₆ (= 0) for N = 16. For the equivalent c_i value, the peak intensity at H_i (=αz_i) along the center position (V = 0) on the image plane weakens, except for i = 0 and 16, owing to the destructive interference. Such undesired interference also produces additional peaks outside the designed axial range.

Fig. 7.

Numerical simulations of the lateral shift behavior of the wavefront engineered PSF. (a) and (b) Intensity distributions of the PSF reconstructed on the Hz plane (top panel) for the movement of a point source along the z axis with the constant initial phase values (c_i = 0) (a) and the optimized phase values (b) for the design parameters d_range = 20 µm, N = 16, δ = 75 mm with a fluorescence wavelength of 560 nm. The horizontal and vertical scale bars are 0.2 mm and 2 µm, respectively. The color scale of the top panels is normalized to the maximum intensity of (b). The bottom panels show the corresponding phase distribution of the multiplexed CGHs applied to fluorescence signals. The red-dashed circle indicates the pupil size of the objective lens. (c) Wrapped phase variation along the ξ axis on the magnified area (inset) indicated by the blue-dotted rectangle in (b). Blue squares correspond to the actual sampling points of the SLM pixels used in our study.

We optimized c_i values based on a genetic algorithm (GA) using the calculated peak intensities at H_i for the resultant PSF. To evaluate the PSF and its lateral shift behavior, we simulated the image of a point source located at z_o by calculating the Fourier transform of the electric field E(ξ, η; z_o) of the emitted signal at the pupil plane after applying the multiplexed CGH, corresponding to Eq. (1) in the main text. The intensity distribution of the point image I_p at the image plane (H, V) can be written as I_p(H, V; z_o) = {FT[E(ξ, η; z_o)]}², where FT represents the Fourier transform. The aim of the optimization is to maximize and make uniform the peak intensities I_p,i = I_p(H_i, 0; z_i) for i = 1 to N under the given condition of c_i values in Eq. (4).

In our homemade optimization procedure based on GA, we set the fitness value f to be $f=Ave(I_{\text{p},i})/STD(I_{\text{p},i})$ , where Ave and STD denote the average and standard deviation of I_p,i, respectively. In the GA method, the f values were calculated for individuals containing different c_i values (genes), which were then evaluated to prepare the next iteration (generation) to maximize the f value.

Table 1 summarizes the optimized phase values for d_range = 10 µm and 20 µm with design parameters of N = 16 and δ = 75 µm for a fluorescence wavelength of 560 nm, obtained from the iteration of a few thousand generations for 30 combinations. As shown in Fig. 7(b), the multiplexed CGH with the optimized phase values produces a lateral shift PSF with an almost uniform peak intensity at the designed H_i position. The coefficient of variation (CV) of the calculated 16-multiplexed peaks was determined to be 5% for d_range = 20 µm and 8% for d_range = 10 µm. Note that the axial intensity profile of an excitation needle spot also affects the detected signal intensity. In our experiments (Figs. 2–5), we employed the needle spot with an axial FWHM size of 20 µm. Thus, for the CGH with d_range = 20 µm, for example, the detectable signal intensity at z = ±10 µm is half the intensity detected at z = 0 µm. However, we can simply improve the uniformity related to the excitation PSF by using a needle spot with a further extended focal depth as demonstrated in Fig. 6.

Table 1. Initial phase values for multiplexed CGHs.

	drange = 10 µm	drange = 20 µm
c 1	0.3527994502271875	0.768148757440062
c 2	0.5040868217457589	0.9088085670611212
c 3	0.2170186158308386	0.41791947918452543
c 4	0.39109756485535097	0.972547518580914
c 5	0.8635344417905402	0.24278484002810885
c 6	0.6546695536142608	0.29037673385362583
c 7	0.057536181138117204	0.9546187729339882
c 8	0.04079693591587086	0.6847695035463944
c 9	0.4495936174959214	0.08995452427135109
c 10	0.6302891560649588	0.5936212122117045
c 11	0.22305452246275137	0.6207776666418281
c 12	0.10362301479234948	0.688170851413293
c 13	0.3981930014882419	0.23617677607907606
c 14	0.2937439935673053	0.9208546349263655
c 15	0.07256903640133505	0.6344581785429848
c 16	0.6888160535904292	0.7292918867819143

The obtained CGH is characterized as asymmetric phase distribution about the origin of the pupil and exhibits a steep phase gradient particularly in the region indicated by the blue rectangle in the bottom panel of Fig. 7(b). Figure 7(c) plots the phase variation along the horizontal axis (ξ axis) in the magnified area as well as the sampling points corresponding to the SLM pixels used in our study. This plot indicates that the SLM with a pixel pitch of 10.4 µm can adequately display the designed CGH.

B. Evaluation of the detection efficiency

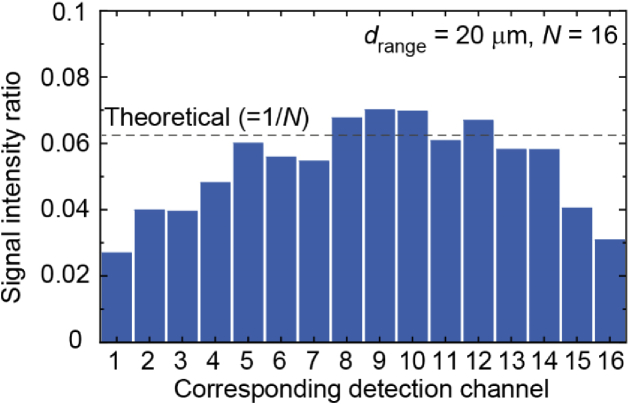
As described in Section 2, the use of the N-multiplexed CGH for fluorescence signals results in the laterally shifted N-multiplexed signals with a peak intensity reduced by a factor of N at the detector plane. Theoretically, the detectable signal intensity at each detection channel in the present setup (N = 16) is limited to 6.25% compared to that without wavefront modulation for fluorescence signals. Figure 8 shows the measured signal intensity at the detector plane for the wavefront modulation (d_range = 20 µm and N = 16), which was evaluated from the fluorescence images sequentially recorded by the EMCCD under 20-µm needle excitation fixed at a static position, in the same manner as shown in Fig. 2(b). The signal intensity was determined by averaging the center 3×3 pixels (= 48 × 48 µm², almost equivalent to the core diameter of the 1D fiber array) on the point images by changing the axial position of a thin fluorescence sample from -10 to 10 µm using the piezo objective scanner. The measured signal intensity at each detection position corresponding to the 16 detection channels was compared to that obtained without wavefront modulation, which was accomplished by applying a plain pattern on the SLM (SLM2). The signal intensity ratio averaged over the 16 channel positions was 5.3% compared to the normal detection without the wavefront modulation. The difference from the theoretical value (6.25%) was due to the inhomogeneity of the detection intensity caused by the axial intensity profile of the 20-µm needle spot as mentioned in Appendix A. Except for this inhomogeneity related to the excitation spot, the measured result shown in Fig. 8 suggests that, in the condition used in our experiment, the wavefront modulation by the SLM2 was achieved without a serious decrease in light use efficiency.

Fig. 8.

Evaluation of the signal intensity ratio at each detection point compared to normal detection without the wavefront modulation.

Funding

Precursory Research for Embryonic Science and Technology10.13039/501100009023 (JPMJPR15P8); Japan Society for the Promotion of Science10.13039/501100001691 (19H02622); Japan Agency for Medical Research and Development10.13039/100009619 (JP20dm0207078); Konica Minolta Science and Technology Foundation10.13039/100007418; Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials.

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.