Technique Comparison for Efficient Orthodontic Tooth Measurements Using Digital Models

Abstract

Objective:

To determine the best technique for measuring mesial-distal tooth widths on digital models.

Methods:

The individual mesial-distal tooth widths were measured (first molar to first molar, maxillary and mandibular) on 32 stone casts and corresponding digital models (emodels, GeoDigm, Chanhassen, Minn). The digital models were measured using five different techniques: occlusal aspect, occlusal aspect zooming in on each individual tooth, facial aspect rotating as needed, facial aspect from three standard positions (R buccal, facial, and L buccal), and qualitatively rotating the model in any position deemed necessary. Measurements were repeated three times at least 1 week apart. The operator time needed to complete each set of measurements was recorded.

Results:

Four of five digital measurement techniques (except for the facial aspect from three standard positions) showed a slight positive bias (overestimation in measured width) compared with stone cast measurements. Measuring from the occlusal aspect resulted in the greatest Pearson correlation (98.509%), the least Altman-Bland standard deviation of differences value (1.881 mm), and the second fastest measuring time (2 minutes 3 seconds). Qualitatively rotating the model had similar Pearson correlation and Altman-Bland values to the Occlusal technique but took the longest time to measure (7 minutes 1 second).

Conclusions:

The Occlusal measurement technique for digital models was the best combination of accuracy, repeatability, and speed of measurement.

INTRODUCTION

Stone casts have long been the gold standard for measuring mesial-distal tooth dimensions and calculating the Bolton Index for tooth size discrepancies, as well as for determining intra-arch space discrepancies.1,2 The Bolton Index compares the ratio of the sum of the mesial-distal maxillary tooth widths (first molar to first molar) to the sum of the mesial-distal mandibular tooth widths (first molar to first molar) using an ideal ratio to determine if there is a tooth size discrepancy.3,4 When there is a significant deviation from the ideal Bolton ratio, even if the teeth are aligned (naturally or as a result of orthodontic treatment), the occlusion of the teeth may not be ideal. For this reason, accurate measurement of the mesial-distal tooth widths and subsequent calculation of the Bolton ratio is a very helpful tool for determining if any modifications in tooth size are necessary for a favorable treatment outcome.5

There are many advantages of using digital models in place of stone casts. One is the ease of portability. Indeed, a digital model can be sent instantly via e-mail, which can be very useful when collaborating with other professionals. Physical cast replication is not necessary, therefore saving time and materials. Also, stone casts require a relatively large amount of physical storage space, whereas digital models offer an acceptable digital substitution for cast archival.6,7 Durability is a factor with stone casts; through use and examination, a stone cast can be damaged or broken. Durability is not an issue with digital models. Digital models can also be virtually manipulated (ie, cross-sectioning or virtual trimming and segmenting) without being permanently altered.

Digital models have been shown to be an acceptable substitute for stone casts.2 Some studies have shown no statistical difference between the measurements made on digital models and stone casts,7,8 whereas other studies have found some statistically significant differences, but none that are clinically significant.9,10 Importantly, diagnosis and treatment decisions are not statistically different when using digital models rather than stone casts.1,11 Measuring mesial-distal tooth widths on digital models has been shown to be faster than using a digital caliper on a stone cast.7,9

An investigation of various digital measurement techniques has not been reported. An ideal measurement technique should be accurate (ie, a clinically insignificant difference between the chosen method and measurements made on a stone cast of the same dentition), precise (ie, easily repeatable), and able to be completed in a timely manner (relative to other techniques). The purpose of this study was to determine the digital model measurement technique that yields the best combination of speed, accuracy, and precision.

MATERIALS AND METHODS

Casts/Models

In this study, 32 patients presenting for orthodontic treatment consented to be included and represented a variety of typical malocclusions. Before beginning the study, all models were de-identified. Stone casts with corresponding digital models were used. All models were fully dentate (first molar to first molar), and all teeth were fully erupted. No orthodontic treatment had previously been performed. The digital models were produced by the GeoDigm Corporation, and their software was used to take the measurements on the digital models (emodel, version 6.0, GeoDigm Corp, Chanhassen, Minn). The scanning technique used by the Geodigm Corporation is a nondestructive laser scanning process. The digital model file sizes ranged from 1141 Kb to 1366 Kb. The computer used has an Intel Xeon 3.00-GHz processor with 4 GB of RAM. The computer screen resolution was 1600 × 1200 pixels. The mouse used had 400 dots per inch precision, and the speed was set on the sliding scale at 5 out of 10. Prior to beginning the study, the primary investigator spent 2 weeks taking mesial-distal tooth measurements and calibrated both digital model and stone cast measurements with an experienced board-certified orthodontist.

Measurements

Stone casts

The individual teeth on each stone cast from first molar to first molar were measured to the nearest 0.01 mm by one operator using a digital caliper. These measurements were repeated twice more, at least 1 week apart, resulting in a total of three sets of measurements for each cast.

Digital models

The teeth on the digital models were measured to the nearest 0.01 mm using the following five techniques (Figure 1):

Figure 1.

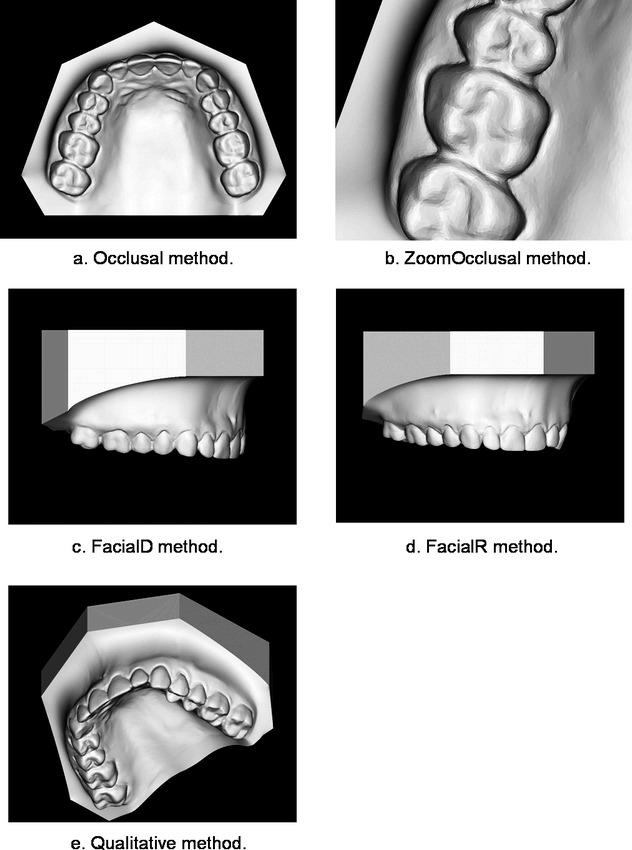
Digital methods of measurement. These images represent the five digital measurement techniques: (a) Occlusal, (b) ZoomOcclusal, (c) FacialR, (d) FacialD, and (e) Qualitative. Images reproduced from the Geodigm emodel software.

• Occlusal: All teeth were measured from the Geodigm standard occlusal aspect of the cast.

• ZoomOcclusal: All teeth were measured from the Geodigm standard occlusal aspect of the cast, but the zoom function was used to magnify each individual tooth before taking the measurement.

• FacialR: All teeth were measured from the facial aspect, rotating the cast about its axis as the operator deemed necessary to take each measurement.

• FacialD: All teeth were measured from the facial aspect using three standard positions: left buccal, facial, and right buccal.

• Qualitative: The model was rotated qualitatively in any plane the operator deemed necessary before taking each separate tooth measurement.

All measurements were repeated twice for each method, at least 1 week apart, resulting in a total of three sets of measurements for each digital method.

All measurements

For each stone cast/digital model measurement technique, the mesial-distal dimension of teeth, first molar to first molar, maxillary and mandibular, were recorded on a spreadsheet. Each set of measurements was timed to the nearest second using a stopwatch and recorded (Figure 2).

Figure 2.

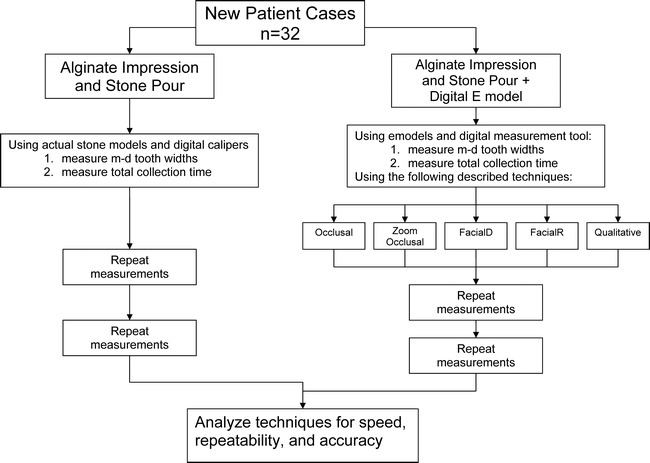
Flow chart of methods.

Statistical Analyses

Accuracy

Accuracy was defined as the agreement between a digital model and the stone cast. This agreement was estimated in two ways. The Pearson correlation was used to estimate the strength of the linear relationship between each digital model measurement and the stone cast measurements. For each measurement technique, the correlation was calculated in two ways. The first calculation consisted of comparing the sum of the tooth widths on each set of models (maxillary plus mandibular) with the sum of the tooth widths on the corresponding stone casts. The second correlation compared each individual tooth to the corresponding tooth on the stone cast.

The Altman-Bland12,13 approach was used as a way to assess the degree to which the digital model measurement techniques agree with the stone cast digital caliper measurements. For each digital model set (the sum total of the tooth widths for each dentition), the bias was computed as the average of the differences between the digital measurements and the stone cast measurements. The null hypothesis of zero bias was tested with a paired t-test. Calculation of the Altman-Bland agreement range provided 95% agreement limits for each digital model measuring technique.

Repeatability

Repeatability was tested in two different ways: tooth-for-tooth repeatability and whole-dentition repeatability. Individual tooth-for-tooth repeatability was determined by calculating the standard deviation of differences for each set of measurements (three per tooth) for each digital technique and the stone casts. Total arch repeatability was tested by calculating the standard deviation of the sum of the tooth widths for each set of measurements (three sets per dentition) for each digital technique and the stone casts.

RESULTS

Speed

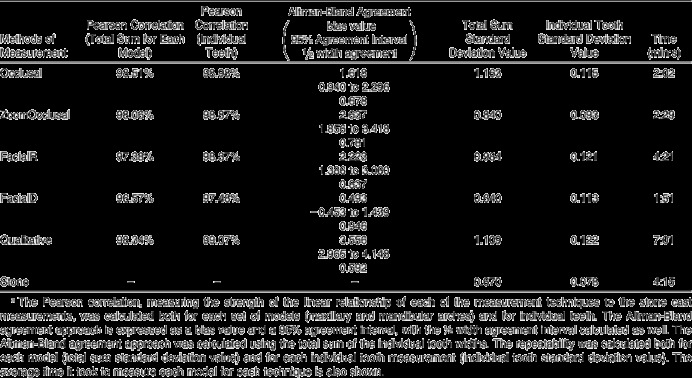
The average time it took to measure the stone casts was 4:15 (4 minutes 15 seconds). The average time it took to measure the digital models was 2:02 for the Occlusal, 2:29 for the ZoomOcclusal, 1:51 for the FacialD, 4:21 for the FacialR, and 7:01 for the Qualitative techniques (Table 1).

Table 1.

Results from the statistical interpretation^a

Accuracy

Using the Pearson correlation test for the total sum of the teeth, the Occlusal technique had the strongest linear correlation to the stone cast measurements (98.51%), followed by the Qualitative (98.34%), ZoomOcclusal (98.06%), FacialR (97.38%), and FacialD (96.57%) techniques (Table 1). Using the Pearson correlation test for individual teeth measurement, the Qualitative technique had the greatest linear correlation to the stone cast measurements (99.06%), followed by the Occlusal (98.98%), ZoomOcclusal (98.88%), FacialR (98.37%), and FacialD (97.45%) techniques (Table 1).

For the Altman-Bland t-tests, the only t-test that accepted the null hypothesis that there was zero bias was the Facial D method (P value  =  .2961). For all of the other tests, the null hypothesis was rejected, as all of their P values were P < .0001.

Using the Altman-Bland agreement approach, the FacialD technique had the least bias (0.493), followed by the Occlusal (1.618), FacialR (2.223), and Qualitative (3.556) techniques (Table 1; Figure 3). The Qualitative technique has the smallest 95% agreement interval (2.965 to 4.148, with a half-width agreement of 0.592), followed by the Occlusal (0.940 to 2.296, 0.678), ZoomOcclusal (1.856 to 3.418, 0.781), FacialR (1.386 to 3.060, 0.781), and FacialD (−0.453 to 1.439, 0.946) techniques (Table 1; Figure 3).

Figure 3.

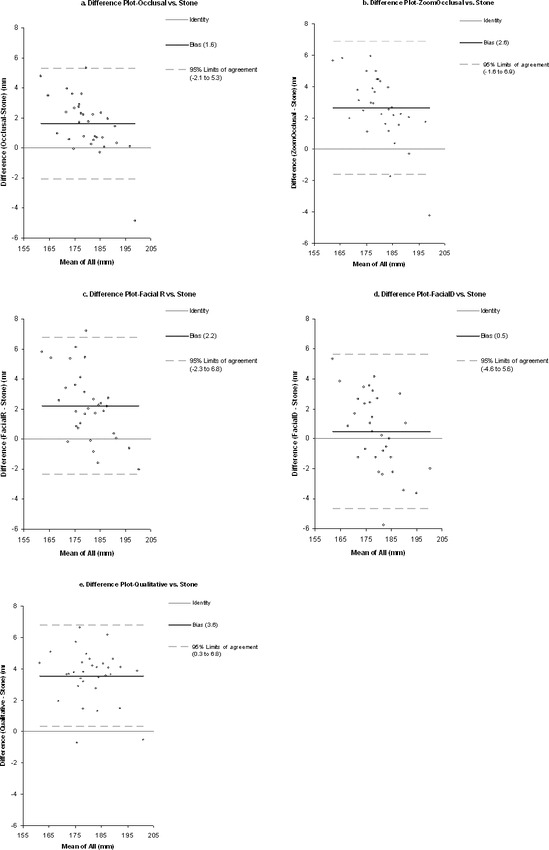
Summary of the Altman-Bland tests: difference plots. These graphs show each of the 32 casts and the average agreement difference between the digital techniques and the stone cast measurements. The overall bias of each technique is shown, along with the 95% agreement interval.

Repeatability

The tooth-for-tooth standard deviation of differences value (in mm) was smallest for the ZoomOcclusal technique (0.093), followed by the FacialD (0.113), Occlusal (0.115), FacialR (0.121), and Qualitative (0.122) techniques. The standard deviation for the stone measurements was 0.078 (Table 1).

The standard deviation of differences value (in mm) for the total sum of the teeth was the smallest for the FacialD technique (0.640), followed by the ZoomOcclusal (0.840), FacialR (0.984), Qualitative (1.109), and Occlusal (1.163) techniques. The standard deviation for the stone measurements was 0.670 (Table 1).

DISCUSSION

Overall, digital techniques tend to slightly overestimate actual stone cast measurements, indicated by their positive bias values. However, because this bias is small and because a strong correlation exists between the stone measurements and digital measurements, this bias should not restrict clinical use. In addition, when using these measurements as a ratio of the maxillary and mandibular widths (such as with the Bolton Index), any significance of the bias is further diminished.

Other studies have reported mixed results for measurement bias. Bell et al7 found a positive bias to their results but also deemed the bias to not be clinically significant. Mullen et al9 mounted 0.25-mm ball bearings on the casts to be measured before they were digitized and then subsequently measured the diameter of the ball bearings in addition to the mesial tooth widths. They found that the ball bearings were digitally measured slightly greater than their actual diameter, but when measuring the mesial-distal tooth widths on the same casts, they were found to be measured statistically smaller than the measurements made on the plaster models. Mullen et al9 also found that the second time each of the digital models were measured, the result was a significantly smaller measurement. Often studies found no statistical difference between the stone cast measurements and the digital measurements1,8 or found a statistical difference, but not one that was clinically significant.2,10

The FacialD technique had the greatest inaccuracies of the five digital techniques. This should be somewhat intuitive because two-dimensional linear measurements of nonuniformly curved surfaces (ie, the curve of the arch from three standard facial views) will almost certainly cause some mesial-distal tooth measurements to be underestimated. This is why the bias appears to be smaller in this method (0.493): the inherent positive bias of the digital models is being compensated for by the smaller measurement of some teeth in the arch. Because this undermeasurement is not uniform across all teeth, the Pearson correlation suffers, as shown by this technique's having the worst correlation for both the total dentition correlation (96.57%) and individual teeth correlation (97.48%). This technique also has the largest agreement interval, indicating that this measuring technique does not reliably measure all dentitions in the same way (ie, the curvatures of the arches are most likely influencing whether certain teeth are overestimated or underestimated using this technique). Positives of the FacialD technique, where the cast is not arbitrarily rotated, are that it has the potential to be very repeatable and fast. Even though this proved to be is a very fast technique with high precision, the inaccuracies and poor correlation to the stone cast measurements make it an undesirable technique for routine use.

The FacialR measurement technique has a somewhat better correlation to the stone measurements because views can be rotated for every tooth in the arch, rather than just having three standard views like FacialD. Because of the individual rotation for each tooth, however, the FacialR technique has lower repeatability than some of the other techniques (0.984 standard deviation for the total sum repeatability and 0.121 individual tooth standard deviation). Each time the operator measures a certain model with this technique, the arch may be rotated to a slightly different view, increasing the likelihood of obtaining a different measurement. For the ZoomOcclusal measurement technique, the concept that zooming in on each tooth would enhance the ability of the operator to make an accurate measurement was not proven true. The image on the computer screen of the digital model appeared grainy at high magnifications, decreasing the ability of the operator to accurately select interproximal points. If future digital modeling software has improved resolution at high magnifications, this measurement technique may potentially demonstrate superior results.

Both the Occlusal and Qualitative measurement techniques have positive characteristics. The Qualitative technique has the smallest Altman-Bland agreement interval (0.592), the best Pearson correlation for individual teeth measurements (99.07%), and the second best Pearson correlation when looking at the entire dentition (98.34%), but it also has the greatest bias (3.56). With the Qualitative technique, the operator can get a clear view of each tooth regardless of its alignment in the arch; this is why it has very strong linear correlation and the smallest agreement interval. The Qualitative technique, however, introduces more variability with regard to repeating measurements because the observer will not always measure each tooth from the exact same aspect every time, unlike the techniques using standard views. This flexibility does allow the observer to measure misaligned teeth from their correct mesial-distal orientation, but the technique's repeatability suffers because of this arbitrary movement. It is important to note, however, that all of the repeatability measures showed that all of the techniques are quite repeatable, with standard deviations not exceeding 1.2 mm for the entire dentition or 0.13 mm for individual teeth. The Occlusal technique also has very strong Pearson correlations, including the best total dentition correlation (98.51%) and the second best tooth-for-tooth correlation (98.98%). It also has the second smallest agreement interval (0.678), bested only by the Qualitative technique. The reason the Altman-Bland correlation is slightly lower for the Occlusal technique than for the Qualitative technique is most likely because at times, the Occlusal technique is less able to capture an accurate measurement of teeth that are severely misaligned relative to the occlusal plane. However, this effect seems to minimally affect the statistics, which suggests that this is a factor only in arches with severely misaligned teeth.

Both the Qualitative and Occlusal techniques have strong repeatability and accuracy characteristics, and both are acceptable measurement techniques. What sets the Occlusal technique apart, however, is that it takes less than one-third of the time to perform (average of 2:01 vs 7:02). For this reason, the Occlusal technique is recommended as the technique of choice for measuring mesial-distal tooth widths on digital models.

Future research may look at modifications to the Occlusal technique to improve its few shortcomings. For example, perhaps for certain teeth that are severely misaligned, a more Qualitative technique approach should be taken while still measuring the rest of the teeth from the occlusal view. Another possible area for future study could be to assess the accuracy of stone casts. While stone casts have long been considered the gold standard when measuring mesial-distal tooth widths, it is possible that the positive bias (overestimation) of the digital models is really not a bias at all but rather that the teeth are routinely measured small. It is, after all, most unlikely that a digital calipers is able to reach the exact interproximal contact point of a tooth when that tooth is in contact with other teeth. This could be tested by designing a study that incorporates the measurement of actual teeth without mesial and distal contacts in addition to the digital models and stone casts. The current study is limited to conclusions about this specific software and version; additional studies could be done to determine whether these results can be generalized to other digital model measurement software or other versions of this software.

CONCLUSIONS

• All digital methods have a slight positive bias, but this small bias should not restrict the clinical use of digital techniques for measuring mesial-distal tooth widths.

• The Occlusal technique, measuring each mesial-distal tooth width from the standard occlusal aspect, is the best combination of accuracy, repeatability, and speed of measurement and therefore the best choice for routine digital measurement of mesial-distal tooth widths in a clinical setting.