Path Integral Molecular Dynamics of Liquid Water in a Mean‐Field Particle Reservoir

Abstract

We present a simulation scheme for path integral simulation of molecular liquids where a small open region is embedded in a large reservoir of non interacting point‐particles. The scheme is based on the latest development of the adaptive resolution technique AdResS and allows for the space‐dependent change of molecular resolution from a path integral representation with 120 degrees of freedom to a point particle that does not interact with other molecules and vice versa. The method is applied to liquid water and implies a sizable gain regarding the request of computational resources compared to full path integral simulations. Given the role of water as universal solvent with a specific hydrogen bonding network, the path integral treatment of water molecules is important to describe the quantum effects of hydrogen atoms’ delocalization in space on the hydrogen bonding network. The method presented here implies feasible computational efforts compared to full path integral simulations of liquid water which, on large scales, are often prohibitive.

Path integral molecular dynamics of liquid water is performed in an open system set up where analytic boundary conditions connect the open system to a reservoir of non‐interacting point‐particles. This novel set up assures sizable computational advantages and allows for simulations which are prohibitive with standard approaches.

Introduction

Water is a universal solvent characterized by a unique hydrogen bonding network among liquids. Classical molecular dynamics over the last decades has proven to be a powerful tool of investigation for solvation processes on a large scale ^[1] while ab initio molecular dynamics has provided a deep understanding of the microscopic dynamics of hydrogen bonds of water at quantum mechanical/electronic level. ^[2] However, while classical models have the inherent limit of not taking explicitly into account the quantum nature of the hydrogen bonding, ab initio molecular dynamics is often computationally too demanding for the scale of analysis required by many systems of interest. Path integral molecular dynamics (PIMD),[ ³ , ⁴ ] using classical‐like potentials, lies in between, in terms of both: computational costs and increase of physical accuracy. It captures relevant quantum characteristics of the hydrogen bond formation by describing the spatial delocalization in space of a light atom as the hydrogen and its effects on the structural and dynamical properties of the bonding network; yet, the cost of simulations is still very high compared to classical simulations. Recently developed numerical techniques based on spatial adaptive molecular resolution (AdResS)[ ⁵ , ⁶ , ⁷ , ⁸ , ⁹ ] have allowed for the simulation of small open subsystems that exchange molecules with a larger coarse‐grained environment. ^[10] This progress paves the way towards simulations of small systems at high resolution embedded in a simplified environment. The results for structural and thermodynamic properties have the same accuracy of calculations at high resolution for large systems.[ ¹¹ , ¹² ] In this perspective, this work presents the extension to PIMD, with water as a crucial showcase, of the most advanced AdResS methodology for open systems, ^[13] where the large environment is drastically reduced to non‐interacting point‐particles (tracers) governed by a mean‐field potential derived from first principles of statistical mechanics. It must be reported that past work[ ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ ] has actually already achieved, with sufficient technical success, the inclusion of the path integral technique in adaptive resolution schemes. However the corresponding adaptive methodology used in these references was not designed, both conceptually and technically, for accurately simulating open systems embedded in a generic reservoir, resulting, above all, in a complex coding procedure not straightforwardly transferable from software to software and with sub‐optimal computational performances. Instead the latest incarnation of AdResS of Ref. [13], besides being technically highly simplified, was made also conceptually rigorous and numerically more accurate compared to the previous methodology.[ ¹⁹ , ²⁰ ] The successful implementation of the path integral procedure into the model of Ref. [13] represents a relevant conceptual and technical step forward in the field. In fact the encouraging results open interesting scenarios for the inclusion of quantum effects of hydrogen delocalization in water‐mediated interactions for a large variety of solutes, that is a direct extension of studies where the standard classical AdResS technique of Ref. [13] has already been successfully used;[ ²¹ , ²² , ²³ ] furthermore, it gives the possibility to extend the studies to situations of nonequilibrium ^[24] and to the interface with fluid dynamics. ^[25] The paper is organized as follows: the section “Methodologies” provides a basic description for the the path integral technique and for the AdResS methodology. Such a description is sufficient for the comprehension of the current work and is complemented by a rich literature list. Next the model that includes the path integral technique in the latest version of the AdResS set up is described and applied to liquid water at standard ambient temperature and pressure. Simulation results are discussed to prove the validity of the open system approach for path integral; this is done by comparing the AdResS results with those of a full path integral simulation of reference. A discussion regarding the potential perspectives of applications to solvation problems concludes the paper.

Methodologies

PIMD Technique in a Nutshell

Spatial delocalization of atoms in space due to their quantum nature can be described by the path integral formalism of Feynman. ^[26] For systems at low temperature, in particular, this formalism captures their essential quantum features; ^[27] however even for molecular liquids at standard temperature, whose molecules include light atoms, the path integral description can clarify relevant aspects of the observed properties. Liquid water is a particularly relevant case because of the key role played by hydrogen atoms in the bonding network of the liquid. ^[28] The employment of the path integral formalism in the design of molecular dynamics techniques is well established in the field thus we recall here only the aspects relevant for this work and suggest the interested reader to consult specialist work as that of Refs. [3, 4]. For molecular simulation, the key point is the mapping of a classical Hamiltonian of N distinguishable particles onto a quantized Hamiltonian. This latter is formally equivalent to a classical Hamiltonian of interacting polymer rings that represent now, in an effective manner, the atoms. The formal derivation consist of the following steps: given a classical Hamiltonian of atoms of coordinates ($\mathbf{p},\mathbf{r}$ ), mass m_j (j‐th atom mass) characterized by interatomic potential, $V({\mathbf{r}}_1,....{\mathbf{r}}_N)$ :

$${\displaystyle H=\sum _{j=1}^N\frac{{\mathbf{p}}_j^2}{2m_j}+U({\mathbf{r}}_1,....{\mathbf{r}}_N),}$$ (1)

the transformation via the path integral formalism leads to:

$${\displaystyle H_P=\sum _{i=1}^P\left\{\sum _{j=1}^N\frac{1}{2}{m}_j{\omega }_P^2{({\mathbf{r}}_j^{\left(i\right)}-{\mathbf{r}}_j^{(i+1)})}^2+\frac{1}{P}U({\mathbf{r}}_1^i,....{\mathbf{r}}_N^i)\right\},}$$ (2)

that is the classical atomic kinetic term becomes an effective polymer ring where its P beads are connected through a first‐neighbor harmonic interaction. Instead the original interatomic potential is distributed among the polymer beads with the characteristic that only corresponding beads of two distinct polymers are allowed to interact, that is bead 1 with bead 1, bead 2 with bead 2 and so on. Accordingly, one has ${\omega }_P=\sqrt{P}/\beta \hslash$ $(\beta =1/k_{B}T)$ and $U({\mathbf{r}}_1^i,....{\mathbf{r}}_N^i)$ is the potential connecting beads with same index i of two different atoms (see also Figure 1).

Figure 1.

Quantization scheme of two interacting classical atoms with the path integral formalism, that is an effective mapping of the two atoms onto two (classical) ring polymers. Here $P=5$ is used only as a graphical simplification, in reality one needs a much larger number of beads to properly describe the quantum spatial fluctuation of the atoms.

In essence, the spatial delocalization of the atom is effectively described by the spatial fluctuation of the polymer ring and by the delocalization of the atom‐atom interaction over the polymer beads. As a consequence the sampling of spatial configurations of the classical polymer rings via molecular simulation corresponds to a quantum statistical description of the atomistic system. As underlined above, the full procedure to transform such a formalism in solid algorithms of PIMD can be read in detail in Refs. [3, 4]; regarding the current work, we use the PIMD technique presented in Refs. [29–31].

Molecular Dynamics of Open Systems with the AdResS Technique

Spatially adaptive molecular resolution in numerical simulations has became a subject of rather high interest within different communities. ^[32] The central aim of this approach is to identify (open) regions of physical interest where molecules are treated at atomistic (high) resolution while molecules outside are treated with drastically simplified models (coarse‐grained). The reaction‐field method[ ³³ , ³⁴ ] is used to mimic the electrostatic properties of the missing charges of the molecules of the reservoir. As anticipated, the specific numerical scheme employed in this work is the AdResS approach. Figure 2 pictorially summarizes the evolution of the AdResS method from the original empirical version up to the latest development in terms of open system embedded in a generic mean‐field particle reservoir which is of interest in this work.

Figure 2.

(a) Graphical illustration of the original idea of AdResS; (b) Abrupt version of AdResS where the switching function w(x) in the Δ region is no more required. Atomistically resolved molecules interact with coarse‐grained molecules (and vice versa) via a coarse‐grained potential acting on the center of mass of each molecule. (c) The CG region is simplified into a region, TR, of non‐interacting point‐particles (tracers). The figure is reproduced from Ref. [13]. Copyright 2019, the Authors.

The original model (panel (a) in Figure 2) was built on the physical intuition that a smooth change of the dynamics of a molecules from full atomistic to coarse‐grained type of molecular representation would ensure that coupling‐induced perturbations at the interface region are negligible for the rest of the system. This concept was translated into a numerical scheme with a space dependent interpolation of the force acting between two molecules, $\alpha ,\beta$ ,

$${\displaystyle F_{\alpha \beta }=w\left(X_{\alpha }\right)w\left(X_{\beta }\right)F_{\alpha \beta }^{AT}+\left[1-w\left(X_{\alpha }\right)w\left(X_{\beta }\right)\right]F_{\alpha \beta }^{CG}.}$$ (3)

$F_{\alpha \beta }^{AT}$ and $F_{\alpha \beta }^{CG}$ are the forces obtained from the atomistic and coarse‐grained potentials, w(x) is an interpolating function of the coordinate x of the molecule center of mass; it varies monotonously from zero to unity when passing from the coarse‐grained region to the atomistic region. The action of an external thermostat and of an additional one‐particle force acting on the center of mass of the molecules in Δ, named thermodynamic force, ${\mathbf{F}}_{th}\left(x\right)$ , provides thermodynamic stability with respect to the thermodynamic state of reference. ${\mathbf{F}}_{th}\left(x\right)$ , whose concept is derived from statistical mechanics considerations, is self‐consistently calculated during the equilibration of a simulation run and assures that the Δ and AT regions are at the target particle density.[ ⁷ , ⁸ ] It must be reported that in this study the thermostat acts over the whole simulation box and assures thermal stability of the simulation in the AT region. Despite the empirical character and simplicity of concepts, results of AdResS simulations for various challenging systems were satisfactory. However, the complicated coding needed to implement the interpolation scheme and its lack of transferability from code to code together with the need of a clearer statistical mechanics picture of the physical model, led to the idea of considering the AT region as an open subsystem embedded in a reservoir designed as simple as possible. First a relevant technical result was the drastic simplification of the AdResS model, as illustrated in panel (b) of Figure 2, with the removal of the space‐dependent switching function w(x) of Eq. 1 (see also Ref. [35]) leading to an abrupt atomistic‐coarse‐grained interface. Subsequently in Ref. [13] an even more drastic simplification, pictorially reported in panel (c) of Figure 2, was implemented with the substitution of the coarse‐grained model with non‐interacting point‐like particles called tracers. Such a technical simplification not only made the numerical implementation more efficient, but also offered a simulation set up which is ideal for mathematical abstraction and formalization so that the model becomes rigorous (see e. g. Ref. [36]). For example, the long lasting question on whether a global Hamiltonian with physical meaning can be written ^[37] was no more an issue. ^[10] The one‐body thermodynamic force in Δ is now recast into a one‐body potential: $\phi \left(x\right)=-{\int }_{x_0}^x{\overrightarrow{F}}_{th}\left(x{}^{\text{'}}\right)·{\overrightarrow{e}}_x\mathrm{d}x{}^{\text{'}}$ with x ₀ the position of the AT/Δ interface and the resulting total interaction potential of this set up reads:

$${\displaystyle U_{\mathrm{tot}}=U_{\mathrm{tot}}^{\mathrm{AT}}+\sum _{k\in \Delta \cup \mathrm{TR}}\phi \left(X_k\right)}$$

where $U_{\mathrm{tot}}^{\mathrm{AT}}$ is the total potential energy due to atomistic force fields in the AT region and the k‐sum runs over all molecules in Δ and all tracers. Numerical instabilities are avoided by a force capping in the Δ region, that is, by truncating each Cartesian component of the total force vector at a prescribed maximum value. The capping force is applied to molecules which, upon entering the atomistic region, are getting too close to each other. It must be noticed that the thermodynamic force acts also in the tracer region at the border with the Δ region, thus it imposes on the tracers at the border, within a certain error, the wished average density of the Δ region. With such a constrain it is expected that tracers entering the Δ region are at distances contained in the molecule‐molecule distance distribution of the full path integral simulation. However, since tracers are non‐interacting particles it can occur that, due to local fluctuations, few tracers entering into the Δ region are at distances smaller than those normally occurring and thus create numerical instability. It has been verified that the total number of capping events per time step only affects a small fraction (around 1 %) of the total number of molecule‐molecule interactions in the Δ region and affects the AT region not in a relevant way. ^[19] Thus, since it has merely a technical role, it can be neglected in the formal treatment of the global potential. Since the action of the neighborhood on each tracer depends only on the position of the tracer in space, independent of the global tracer configuration, each tracer experiences $\phi \left(x\right)$ and a thermostat (to fix the temperature in TR) as an effective mean field. Thus the AT region is embedded effectively in a mean field particle‐based reservoir. A rigorous statistical mechanics formalization of the AT region as an open system, accompanied by corresponding numerical tests of validation strengthen the physical consistency of the model.[ ¹⁹ , ²⁰ ] It must be clarified that, for studying problems out of thermodynamic equilibrium, for example fluid flows, where equilibrium statistical mechanics cannot be applied, and where conserved properties as linear momentum (e. g. in hydrodynamics) play a key important role, AdResS must be modified. In such case it is needed a thermostat that preserves the momentum in the $\Delta +TR$ region enforced by boundary conditions on expected mass flow.[ ³⁸ , ³⁹ ] Furthermore the capping method may be smoothed, if technically required, by the technique of insertion of tracers in the Δ region via quick local energy minimization. ^[40]

PIMD with AdResS for Liquid Water: from Structureless Tracers to a Molecule with 120 Interaction Sites and Back

In PIMD each bead represents a degree of freedom, so the cost of simulation of every atom is increased by the number of beads of its representation which implies a sizable increase of the simulations costs. Even simulations of system with thousand water molecules represented by three‐site water models with each atom represented by a ring‐polymer of 32 beads (thus 96 degrees of freedom per molecule) is essentially prohibitive. ^[15]

The consequence of the demanding costs of simulation implies the restriction of PIMD applications to relatively small systems and short time scales. However, atoms’ delocalization in space may play an important role in the structure and dynamics of the hydrogen bonding network in water, thus leading to, possibly, relevant effects of solvation and aggregation of solutes, as discussed earlier. The AdResS methodology offers a solution to the problem of high costs of PIMD simulations since it drastically reduces the number of degrees of freedom in the particle reservoir region, and thus the amount of water molecules that need to be treated with the ring‐polymer representation becomes accessible with standard computational resources. The AdResS methodology, in the original version illustrated in panel (a) of Figure 2, as anticipated earlier, has already been used with the PIMD technique.[ ¹⁴ , ¹⁵ , ¹⁶ , ²¹ ] However, beside the conceptual limitations of the previous formulation, the change of resolution was neither technically simple nor efficient, although not drastic, as the molecule‐tracer transition of the model in panel (c) of Figure 2. In addition, in the previous work only a technically convenient, but not physically accurate, three‐site model of water was used. ^[15] Here a four‐site model, physically sound, where each atom is represented by a ring‐polymer of 30 beads ^[41] will be instead employed. The current challenge, pictorially illustrated in Figure 3, is to show that the tracer‐based AdResS version can accurately and efficiently handle a transition from point‐like particles to water molecules with 120 degrees of freedom each. Below we discuss the results of the PIMD simulation and also report its corresponding technical details.

Figure 3.

Graphical illustration of the AdResS set up for a path integral (ring‐polymer) simulation of liquid water (top panel). In the bottom panel is illustrated the four‐site water model used in this simulation and its path integral/ring‐polymer resolution. For simplicity only 10 beads per atom are drawn, however in our simulation we have 30 beads per atom/molecular site. The transition from fully resolved molecules to non‐interacting point‐like tracers implies a reduction of 120 degrees of freedom to one per molecule (and vice versa).

Technical Details

PIMD simulations were performed in the normal mode formalism using a modified GROMACS 5.1. ^[42] A simulation box of dimensions 5.8 nm×2.6 nm×2.6 nm was solvated with 1320 water molecules giving a density of approximately 1007 kg m⁻³. The water model used here is the 4‐site water model of Habershon et al. ^[41] and each atom was decomposed into a ring polymer with 30 beads. The size of the full path‐integral resolution region considered in the AdResS simulations was 1.2 nm×2.6 nm×2.6 nm with the adjacent Δ regions having a size of 0.9 nm×2.6 nm×2.6 nm leaving the rest of the simulation box treated at non‐interacting tracer resolution. The reaction field method with a dielectric constant of 80 was used to calculate electrostatic interactions. Electrostatic and van der Waals interactions were truncated at 0.9 nm. In both the AdResS and fully atomistic path integral cases, all properties were calculated from 1.8 ns long trajectories performed at 298 K with a time step of 0.5 fs and a friction coupling constant of 0.05 ps. The thermodynamic force for the AdResS simulations was obtained from 28 iterations, each 250 ps in length, using 6 polymer ring beads per atom.

Results

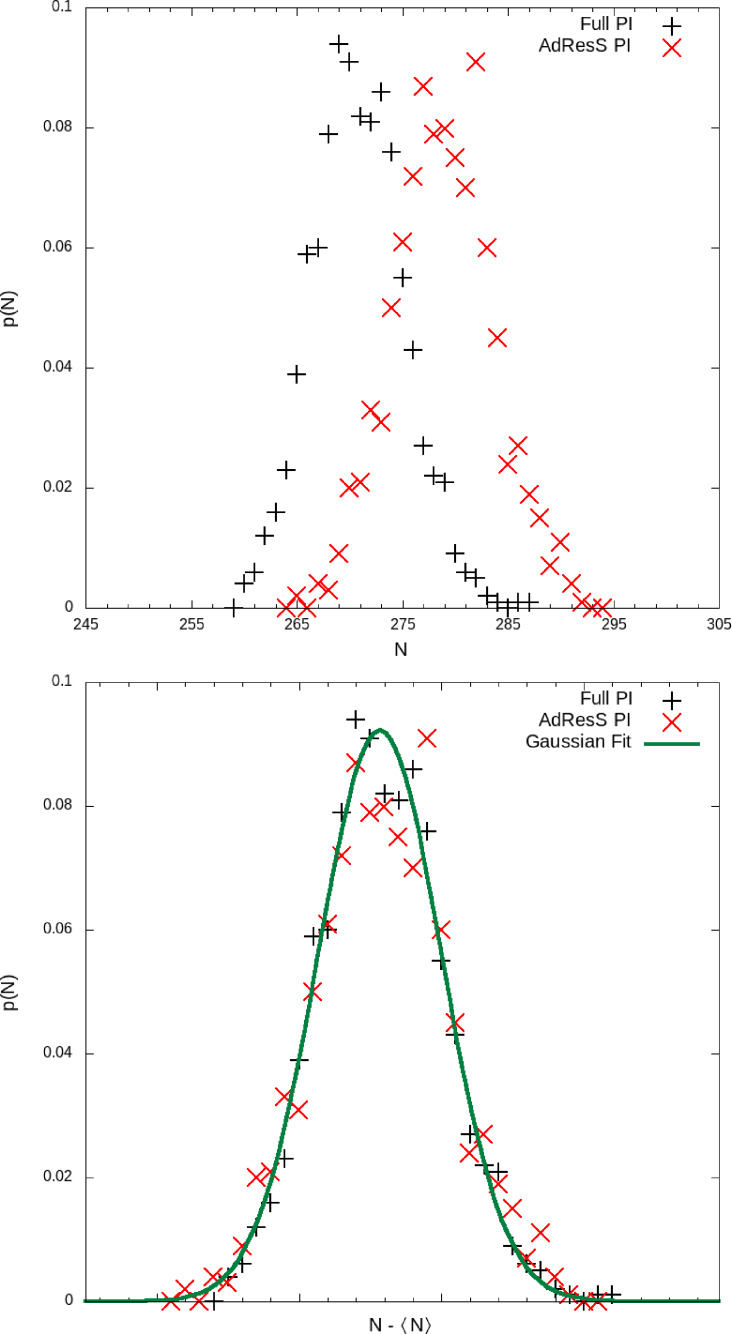
The conditions that the AdResS simulations must satisfy so that we can be sure to define a proper, physically meaningful, open system for the high resolution region of AdResS, concerns basic structural and statistical properties. ^[43] Here we study liquid water at standard ambient temperature and pressure and verify the conditions of physical consistency of AdResS in this context. The first criterion concerns water density in the AT$+\Delta$ region. The density should be equal, within some numerical accuracy, to the value obtained with full‐PIMD simulations taken as reference. This criterion confirms that the action of the thermodynamic force in Δ, fixes the thermodynamic state point of the AdResS system to the wished thermodynamic state point (full‐PIMD simulation of reference). Figure 4 shows a satisfactory agreement between the AdResS simulation and the full‐PIMD simulation of reference. The discrepancy in the AT region is always below a threshold of 5 %. It must be reported that for the testing pourposes of this paper, we have considered the worst case scenario, that is we allow the maximum density fluctuations that we have seen to be reasonable in many AdResS simulations. Even in this case with molecules with 120 degrees of freedom each, this threshold is sufficient for obtaining accurate results. However, the thermodynamic force can be iterated to have fluctuations of density of 1 %. Next criterion concerns radial distribution functions; they represent relevant structural properties that uniquely characterize a liquid in a certain state, furthermore their combination expresses the probability distribution function of the system in configuration space up to the two‐body approximation. In fact $P({\mathbf{R}}_1........{\mathbf{R}}_N)\approx {\Pi }_{i,j}g\left(r_{ij}\right)$ where ${\mathbf{R}}_1........{\mathbf{R}}_N$ is the space configuration of the system, i and j label atoms belonging to different molecules at a distance r_ij . The knowledge of $P({\mathbf{R}}_1........{\mathbf{R}}_N)$ implies the possibility of calculating statistical averages of physical quantities, which implies that the approximation of $P({\mathbf{R}}_1........{\mathbf{R}}_N)$ as factorization of the radial distribution functions provides a statistical knowledge of the system up to the two‐body approximation. In the case of path integral/ring‐polymer representation of atoms/molecules, the criterion of the radial distribution functions is an even more challenging test with respect to the classical case. In fact such functions are calculated as the average of the bead‐bead radial distribution function for each pair of atoms. Figure 5 shows an excellent agreement between the AdResS simulation and the simulation of reference. Finally the simulation must satisfy a statistical criterion, that is to reproduce the reference probability distribution function of the particle number in AT, P(N). This criterion assures that the exchange of particles between high resolution region and the reservoir (TR) occurs in a physically meaningful manner, that is the average number of molecules and average particle number fluctuation in the high resolution region of AdResS are consistent with that of the reference case, which is a mandatory condition of a physically consistent open system. Figure 6 show a satisfactory agreement and thus one can be assured that the exchange through the open boundaries is statistically consistent with that of a reference full‐PIMD simulation. The combined results of Figures 4–6 allow one to conclude that the AdResS set up with tracers with the four‐site water model can handle PIMD simulations of liquid water at standard ambient temperature assuring that its basic liquid properties are properly reproduced. A natural question arising is whether more detailed structural properties, that reflect the microscopic structure of the liquid more specifically, can be reproduced with an equal precision. To this aim we have calculated four more quantities, (i) the average molecular dipole orientation as a function of the position along the direction of change of resolution (Figure 7), (ii) the probability distribution of the average molecular dipole orientation that shows the corresponding statistical fluctuations along the trajectory (Figure 8), (iii) the tetrahedral order parameter, q_tetra , as a function of the position along the direction of change of resolution (Figure 9), (iv) its probability distribution that takes into account the corresponding statistical fluctuations along the trajectory (Figure 10). The tetrahedral order parameter for the i‐th molecule is defined as: $q_{tetra}^i=1-\frac{3}{8}\sum _{j=1,3}\sum _{k=j+1,4}{(\cos {\psi }_{ijk}+\frac{1}{3})}^2$ where ψ_ijk is the angle formed by the Oxygen atom of molecule i and the two nearest neighbor Oxygen atoms j and k. q_tetra is obtained by averaging over the molecules and the trajectories. In all cases the results show a highly satisfactory agreement between the AdResS simulation and the simulation of reference which implies that the AdResS method, in the high resolution region, can faithfully reproduce relevant structural properties and the corresponding statistics of path integral simulations.

Figure 4.

Particle number density in AdResS compared with the density calculated in the simulation of reference with fully resolved details. The discrepancy in the region of relevance (AT) is always below a threshold of 5 %.

Figure 5.

Bead‐bead radial distribution functions for Oxygen‐Oxygen (top panel), Oxygen‐Hydrogen (middle panel) and Hydrogen‐Hydrogen (bottom panel), calculated in the explicit region of AdResS and in the equivalent subregion of a reference simulation with fully resolved details.

Figure 6.

Particle number probability distribution calculated in the explicit region of path integral AdResS and in the equivalent subregion of a reference full path integral simulation (top panel), corrected for the slight discrepancy in the peak values (bottom panel). The figure in the top panel shows a discrepancy of about 3 % in the value of the peak, which is negligible, however, importantly, the shape of the curve is also relevant and in the bottom panel it is shown that by placing the two curves on top of one another, they both agree in a satisfactory manner with the expected Gaussian behavior.

Figure 7.

Average molecular dipole orientation along the x‐axis (direction along which molecules change resolution) as a function of the position in the high resolution region (i. e. region of interest). The comparison with the results of the reference, full‐PIMD, simulation is highly satisfactory; also the results follow the expected behaviors of a uniform liquid. The average is performed over the trajectory and is normalized with respect to the average number of molecules in the path integral region.

Figure 8.

Probability distribution of the average molecular dipole orientation over the trajectory. As expected from the previous figure, the most probable average value is 0.5 within some small fluctuations of about 4 %. The interesting result is the strong agreement between the AdResS simulation and the result of the full path integral simulation. The shapes of the two curves tightly overlap and this shows that the AdResS approach is able to reproduce with high accuracy also the statistical fluctuations of the simulation of reference.

Figure 9.

Tetrahedral order parameter calculated in the path integral region of AdResS compared to the same quantity calculated in the equivalent subregion in a full‐PIMD simulation of reference. The average is performed over the trajectory and is normalized with respect to the average number of molecules in the path integral region.

Figure 10.

Probability distribution of the tetrahedral order parameter. There is a strong agreement between the AdResS simulation and the full‐PIMD simulation. The shapes of the two curves overlap and thus AdResS reproduces the statistical fluctuations of the simulation of reference.

Thermal Stability of the AT Region: the Reservoir Encoded as a Boundary Condition

The use of a global thermostat may rise the question whether the thermalization of the system is uniform all over the simulation box. In reality the relevant question to answer is whether the wished thermalization can achieved, in the AT region, with a simple global thermostat. According to the analytic model, once the boundary conditions are properly enforced at the interface between AT and Δ, then the AT region is assured to be at the wished thermodynamic state point (the thermodynamic force imposes the wished pressure at the wished density, while the thermostat imposes the wished temperature) ^[7] . Following the theoretical model, the thermal condition of the Δ region (away from the border at the AT region) and of the TR region should not have any influence on the thermal conditions of AT. Figures 11 and 12 show that, despite the TR region and the Δ region away from the Δ/AT interface are not thermalized at the reference values, the AT region is perfectly thermalized. Indeed this is the case even when the coupling to the thermostat is not strong enough to impose the reference temperature in the whole Δ and TR regions (due to the large density fluctuations and the strong thermodynamic force at the Δ/TR interface). This means that the thermodynamic force, calculated with the given strength of the thermostat, is able to enforce the boundary conditions required for the AT region (see also supplemental material in Ref. [24]). However, it must be added that here we put ourselves in a worst case scenario, that is we use a thermostat with a mild coupling strength, so that we could prove the power of the theoretical model. In case the coupling strength of the thermostat is increased, the thermal stabilization of $\Delta +$ TR improves (see Figures 13 and 14), however for the AT region it does not make a relevant difference. These results express the fact that the simulation model, designed by formalizing physical conditions for open systems, allows for a computational implementation where the entire physics of the reservoir can be encoded in a boundary condition. The TR region acts only as a technical tool that stores the unphysical material point‐particles for the AT region filtered through the Δ region; the thermostat in TR is actually needed for avoiding that the tracers become too hot and lead to numerical instabilities, but its application does not carry any physical meaning.

Figure 11.

Average molecular velocity fluctuation as a function of the position along the direction x of changing resolution, $\Delta v\left(x\right)$ , normalized by the average molecular velocity of the AT region, $⟨v⟩$ : global system (top panel), only AT region (bottom panel). The plots show that the velocity behaviour in the AT region is perfectly consistent with the result of a full path integral simulation. As expected in the Δ region far from the AT/Δ interface, and above all, in the TR region there is less agreement. At the interface between the Δ and TR region there is a jump; this due to the sharp action of the thermodynamic force which at the interface also displays a large jump due to the discontinuity of resolution (see also, e. g., Ref. [20]).

Figure 12.

Local temperature, T(x), as a function of the position along the direction x of changing resolution: global system (top panel), only AT region (bottom panel). The plots show that the behaviour in the AT region is perfectly consistent with the result of a full path integral simulation. As expected in the Δ and above all, in the TR region the temperature reaches up to the double of the reference temperature. However, in the Δ region the temperature rapidly converges to the target temperature as one approaches the AT/Δ interface. Obviously, being the system non‐homogeneous, one expects such behavior, since the tracers are characterized by much higher density fluctuations than the AT and Δ region, thus a stronger coupling to the thermostat would be required if the temperature of reference was mandatory in such region. However this is not the case and the prescriptions of the theoretical model are sufficient to assure the physical consistency of the simulation in the AT region.

Figure 13.

As in Figure 11, but with a stronger coupling to the thermostat (friction coupling constant of 0.02 ps). The fluctuations in $\Delta +$ TR are much closer to the target value of the AT region, however for the AT region there are no sizable changes compared with the case of a weaker thermostat.

Figure 14.

As in Figure 12, but with a stronger coupling to the thermostat (friction coupling constant of 0.02 ps). The temperature in the $\Delta +$ TR is much closer to the target temperature, however for the AT region there are no sizable changes compared with the case of a weaker thermostat.

Computational Gain

As underlined in the previous sections, the practical relevance of the AdResS method, above all for PIMD, consists of making computationally feasible simulations of processes occurring in a localized region of a large liquid environment. This is a typical situations occurring for a large variety of molecular liquids, in particular for water with its role as solvent. By drastically reducing the number of degrees of freedom that need to be explicitly treated, AdResS allows for a sizable reduction of the computational resources required. The computational gain is usually measured in terms of speed up factor of AdResS simulations compared to reference full atomistic simulations. This factor, in this case, turns out to be about 3.0, without any (AdResS) code optimization that removes technical bottlenecks for the distributed computation; ^[44] such a value, although not yet optimal, is certainly already relevant. In fact it must be also taken into account that the full path integral simulations considered here are modest in size (1320 molecules) while typical simulations of interest, for example in solvation of proteins, consider 10000 molecules at least (see e. g. Ref. [23]). It follows that the gain discussed here is only a lower bound because with larger systems the reduction of number of degrees of freedom is much higher. In this sense a method as AdResS can be crucial for the treatment of relevant systems at large scale and at high physical accuracy by groups not equipped with a large amount of computational resources. For this simulation of 1.8 ns, 6 nodes, with 96 cores per node running for 28.8 hours were needed for the full path integral simulation. Instead 6 nodes with 96 cores per node, running for 8.4 hours were needed for the AdResS simulation. It must be added that since the tracers are non interacting particles, they do not have any physical meaning, but have only a technical meaning as particles of a reservoir for the AT region, filtered through the equilibration in the Δ region according to the instantaneous density fluctuations. This means that two technical options, both under development, are possible: (i) create and annihilate tracers according to the average density fluctuations of molecules in the AT region, thus natural density fluctuations in the AT region are regulated by the thermodynamic conditions imposed in Δ by the thermodynamic force and the thermostat. This implies that a reasonable small AT region of AdResS can mimic a large full resolution simulation. ^[23] (ii) Deposit a very large amount of tracers in the TR region, that is a dense reservoir of particles. The communication between the AT region and the Δ region with the imposition of the thermodynamic force regulates the density fluctuations and thus the amount of tracers that need to enter into the $AT+\Delta$ region or molecules from the AT$+\Delta$ region that need to go in the tracer reservoir. As for the case (i) a small AT region can mimic density fluctuations of a large full resolution system.

Conclusions

We have validated the AdResS method in the most recent version with a mean‐field reservoir of non‐interacting particles for the case in which the open subsystem at high resolution consists of molecules represented within the formalism of path integral. Such a formalism gives, in essence, the possibility of mimicking the quantum delocalization of atoms in space through an effective classical simulation where each atom is represented as a polymer ring with a large number of connected beads. From the technical point of view, the challenge for AdResS is the abrupt transformation of a tracer into a molecule whose atoms are each characterized by a large number of degrees of freedom (beads) and vice versa, that is, from one to 120 degrees of freedom and back, keeping physical consistency with respect to a reference system treated at full quantum resolution. We have simulated liquid water at standard temperature and pressure and have shown a satisfactory level of consistency between the AdResS simulations and the simulation of reference. Moreover, the successful test with liquid water opens the possibility of studying water mediated effects in many solvation problems with the possibility of exploring the effect of the spatial delocalization of hydrogens and the corresponding impact onto the hydrogen bonding network. Full‐PIMD simulations are often still prohibitive on the large scale considered in solvation studies, instead the AdResS technique allows to focus on small regions where the physics of interest takes place, making the study computationally feasible. It must be noticed that the method does not need further validation for solvation studies. In fact in solvation problems the solute is located at the center of the simulation box surrounded by structured solvation shells of water up to the bulk with the characteristics of the system studied here. In AdResS the region of the bulk water beyond the structured solvation shells corresponds to the AT region interfacing the Δ region. It follows that it is sufficient to show that the method reproduces bulk properties to be sure that the solvation problem can be properly addressed. ^[23] In the introduction it has been suggested few practical examples of application as the aggregation of hydrophobic molecules or the determination of the potential of mean force between protein fragments in water; in perspective, such applications will be the subject of future work. In addition, since the tracers are non‐interacting point‐particles, it will be possible in the near future to reduce the reservoir to a continuum description as in fluid dynamics. The equations of fluid dynamics will assure the macroscopic characteristics of the environment while the system‐reservoir exchange of particles via the Δ region occurs through the tracers, which can be created and destroyed according to the density instantaneously determined by the continuum‐atomistic exchange of information. ^[25]

Conflict of interest

The authors declare no conflict of interest.

A. Evangelakis, S. Panahian Jand, L. Delle Site, ChemistryOpen 2022, 11, e202100286.

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.