Summary
We consider evaluating new or more accurately measured predictive biomarkers for treatment selection based on a previous clinical trial involving standard biomarkers. Instead of rerunning the clinical trial with the new biomarkers, we propose a more efficient approach which requires only either conducting a reproducibility study in which the new biomarkers and standard biomarkers are both measured on a set of patient samples, or adopting replicated measures of the error-contaminated standard biomarkers in the original study. This approach is easier to conduct and much less expensive than studies that require new samples from patients randomized to the intervention. In addition, it makes it possible to perform the estimation of the clinical performance quickly, since there will be no requirement to wait for events to occur as would be the case with prospective validation. The treatment selection is assessed via a working model, but the proposed estimator of the mean restricted lifetime is valid even if the working model is misspecified. The proposed approach is assessed through simulation studies and applied to a cancer study.
Keywords: Conditional score, Measurement error, Predictive biomarker, SIMEX, Survival
1. Introduction
A biomarker used to predict the response to a treatment is called a predictive biomarker. For example, patients with colon cancer can be treated by surgery alone or surgery plus chemotherapy. Surgery alone is less expensive and has fewer side effects than surgery plus chemotherapy, but it may be less effective as well, at least for some patients. For an individual patient, it is desirable to identify whether or not the patient will benefit more from the extra chemotherapy based on a biomarker or a set of biomarkers. A possible useful biomarker in this context is the c-myc gene, which is over-expressed in approximately 70 percent of human colonic tumors. Based on a study conducted by the Eastern Cooperative Oncology Group (ECOG), Augenlicht and others (1997) suggested that the c-myc gene may be of clinically prognostic importance in patients with colon cancer. Using a subset of the cases from this clinical trial, Li and Ryan (2006) found that there is an interaction between the c-myc gene expression levels and the two treatments for the response of disease progression-free survival; Song and Zhou (2011) investigated using the observed c-myc gene expression level for treatment selection.
To evaluate the potential of biomarkers for treatment selection, approaches have been proposed that try to minimize the population event rate under (optimal) treatment selection criteria (Song and Pepe, 2004; Brinkley and others, 2010; Cai and others, 2011,Zhang and others, 2012,Janes and others, 2011, 2014) or maximize the population mean (restricted lifetime) (Song and Zhou, 2011).
However, biomarker measurements may contain measurement error, or the current biomarkers may not be very effective for treatment selection. In the ECOG study, the c-myc gene expression levels were measured with error (Li and Ryan, 2006). It is of interest to evaluate the amount of gain that could be achieved with respect to treatment selection if the biomarkers were accurately measured. In another aspect, a new technology may improve the measurement of biomarkers or a new biomarker may be identified with better predictability capacity. For example, with the development of polymerase chain reaction technique, the measurement of c-myc gene expression level may become more accurate. If we call the measurement of c-myc gene level in the original study the standard biomarker, and the improved measurement using advanced techniques the new biomarker, then we would like to assess the capacity of the new biomarker for making treatment selections. With a slight abuse of terminology, we refer both newly identified biomarkers and more accurately measured biomarkers as new biomarkers. Ideally, one would like to re-run the previous study, or perform a new study very similar to it, so that one could measure the new biomarkers using prospectively collected samples. But this is often not feasible. Such a procedure would entail large additional costs associated with obtaining samples of tumor tissues with measurement of disease progression-free survival through a multi-year randomized clinical trial. Moreover, it may not even be feasible to perform such a study. We propose a more efficient approach which requires only conducting a reproducibility study where the new biomarkers and the standard biomarkers will be measured on a set of patient samples or replicated measurements of the inaccurately measured standard biomarkers. Importantly, there is no need to re-run the clinical trial. This makes the study easier to conduct and much less expensive. In addition, it will make it possible to perform the estimation of the clinical performance of the new biomarkers quickly, since there will be no requirement to wait for events to occur. The idea of our approach is summarized in Figure 1. The outcome and the standard biomarkers are observed in the clinical trial, while the new biomarkers and the standard biomarkers are observed in the reproducibility study. We make inference on the new biomarkers versus the outcome to assess the capacity of the new biomarkers on treatment selection. There are related studies in the literature (Boostra and others, 2013a, 2013b) aiming to predict outcome with new biomarkers observed on a subset in the original study, but their objectives are different from what is considered in this article.
Fig. 1.
Overview of the three cases, where 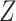 denotes the standard
biomarkers,
denotes the standard
biomarkers,  denotes the new biomarkers, and
denotes the new biomarkers, and
 denotes the treatment.
denotes the treatment.
In this article, we consider the setting in which the outcome is time to an event of interest (survival time), which may be subject to right censoring. To characterize the inter-relations between the biomarkers and the treatment arms, we adopt a working proportional hazards model with interactions between the treatment and the biomarkers. The relation between the standard markers and the new markers is modeled through a classical measurement error model. Various approaches have been proposed to estimate the regression coefficients in the presence of covariate measurement error under the proportional hazards model, however, most were derived under the assumption of linear covariate effects. These include regression calibration (Prentice, 1982; Dafni and Tsiatis, 1998; Wang and others, 2000), SIMEX (Greene and Cai, 2004), likelihood based approaches (Wulfsohn and Tsiatis, 1997; Faucett and Thomas, 1996; Henderson and others, 2000; Xu and Zeger, 2001; Song and others, 2002b), conditional score (Tsiatis and Davidian, 2001; Song and others, 2002a), and correction approaches (Huang and Wang, 2000), among others. Here, we extend the conditional score approach to the proportional hazards model with interactions. In addition, we propose to use the mean restricted lifetime to evaluate the performance of the predictive biomarkers and derive the optimal treatment selection strategy under the working model. To estimate the mean restricted lifetime, we propose a SIMEX estimator and establish the asymptotic properties using the empirical process and stochastic integral techniques.
The novelty of this article includes the following aspects. First, our idea of evaluating new biomarkers without re-running the clinical trial is novel, which could greatly reduce the study time and cost. Second, the adoption of the measurement error model and techniques under this circumstance is novel. Third, we propose well-justified resampling-based inference which extends the technique of Peng and Huang (2008). To the best of our knowledge, the overlay of the resampling-based inference with the already resampling-based SIMEX approach is new.
The article is organized as follows. In Section 1, we give the model definition. We derive an empirical estimator for the optimal treatment selection and propose an approach to evaluate and compare the new biomarkers and standard biomarkers on treatment selection in Section 2. We investigate the finite sample performance of the proposed approach in Section 3, and we apply the approach to the ECOG data in Section 4. Some discussions are given in Section 5. The regularity conditions and sketched proofs are given in the supplementary material available at Biostatistics online.
2. Model definition
Let 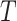 denote the survival time, and
denote the survival time, and
 denote the censoring time. The observed
survival data are
denote the censoring time. The observed
survival data are  and
and  , where
, where
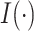 is the indicator function. Let
is the indicator function. Let
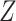 denote a vector of
denote a vector of 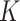 continuous standard biomarkers, and
continuous standard biomarkers, and  denote a vector of
denote a vector of
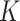 continuous new biomarkers. Remember that,
with a slight abuse of terminology, we refer both newly identified biomarkers and more
accurately measured biomarkers as new biomarkers. Let
continuous new biomarkers. Remember that,
with a slight abuse of terminology, we refer both newly identified biomarkers and more
accurately measured biomarkers as new biomarkers. Let  denote
the treatment, where
denote
the treatment, where 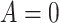 denotes the control or standard
treatment, and
denotes the control or standard
treatment, and 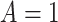 denotes the new treatment. Suppose a
randomized clinical trial has been conducted to evaluate the standard biomarkers for
treatment selection with the observed data
denotes the new treatment. Suppose a
randomized clinical trial has been conducted to evaluate the standard biomarkers for
treatment selection with the observed data 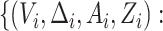
 We are interested in
evaluating the treatment selection capacity of the new biomarkers
We are interested in
evaluating the treatment selection capacity of the new biomarkers  .
.
For an individual with the new biomarkers  , intuitively, we may
assign the subject to treatment
, intuitively, we may
assign the subject to treatment  if
if
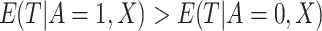 |
and 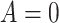 otherwise. That is,
otherwise. That is,
 where
where
 |
This is an extension of the treatment rule for binary outcomes where the probability of
success is compared for the two treatments (Janes
and others, 2014). However, when censoring exists, the mean
(unrestricted) survival time may not be estimable if the largest observed survival time is
censored without some tail correction on the estimated survival function (Klein and Moeschberger, 2003). Alternatively, we consider
the mean restricted survival time (lifetime) up to a given time 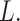 The
technique of restricting survival time has been used previously in estimating the mean
lifetime and quality-adjusted lifetime (Zhao and Tsiatis,
1997; Chen and Tsitais, 2001) . Specifically,
Let
The
technique of restricting survival time has been used previously in estimating the mean
lifetime and quality-adjusted lifetime (Zhao and Tsiatis,
1997; Chen and Tsitais, 2001) . Specifically,
Let 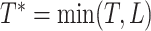 be the restricted
survival time, and
be the restricted
survival time, and
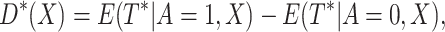 |
then the optimal treatment 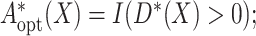 that is, if
that is, if  select
select
 otherwise, select
otherwise, select
 The capacity of treatment selection
based on
The capacity of treatment selection
based on  can be evaluated by
the population mean restricted lifetime under the optimal treatment selection, that is,
can be evaluated by
the population mean restricted lifetime under the optimal treatment selection, that is,
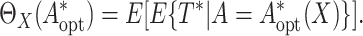 |
(2.1) |
Without loss of generality, we assume an additive measurement error model
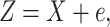 |
(2.2) |
where  and
and
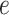 is independent of
is independent of 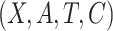 .
This is a natural model when the new biomarkers are obtained by improving the accuracy of
measurement, but may represent a more general relationship between standard biomarkers and
“true” new biomarkers. For example, if we have standard biomarkers
.
This is a natural model when the new biomarkers are obtained by improving the accuracy of
measurement, but may represent a more general relationship between standard biomarkers and
“true” new biomarkers. For example, if we have standard biomarkers 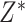 and new biomarkers
and new biomarkers 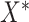 and there exist functions
and there exist functions
 and
and  which could be vector valued, such that
which could be vector valued, such that
 |
(2.3) |
it reduces to model (2.2) with  and
and
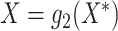 . For simplicity of
presentation, we assume that
. For simplicity of
presentation, we assume that  and
and 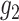 are
known. When
are
known. When  and
and 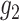 are
unknown, the relationship between the standard biomarkers and the new biomarkers can be
estimated as discussed in Section 6.
are
unknown, the relationship between the standard biomarkers and the new biomarkers can be
estimated as discussed in Section 6.
To ensure the identifiability of model (2.2), we need to have either validation data or replicated data on
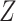 . We consider three cases. In case 1, a
validation data set is available from an external reproducibility study. The observations in
the reproducibility study are
. We consider three cases. In case 1, a
validation data set is available from an external reproducibility study. The observations in
the reproducibility study are 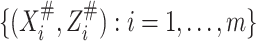 .
In case 2, an internal validation data set of a size
.
In case 2, an internal validation data set of a size 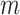 is
available in the original data set. Although we may directly evaluate the new marker using
the validation set in this case, it would be more efficient to use the whole data set. In
case 3, replicated error-contaminated observations are available on some subjects in the
original study. Case 3 is only feasible when the new biomarkers are obtained by improving
the accuracy of measurement while cases 1 and 2 also cover the situation when the new
biomarkers are truly different variables. To unify the notations in the three cases, the
observed data in the original study is denoted by
is
available in the original data set. Although we may directly evaluate the new marker using
the validation set in this case, it would be more efficient to use the whole data set. In
case 3, replicated error-contaminated observations are available on some subjects in the
original study. Case 3 is only feasible when the new biomarkers are obtained by improving
the accuracy of measurement while cases 1 and 2 also cover the situation when the new
biomarkers are truly different variables. To unify the notations in the three cases, the
observed data in the original study is denoted by 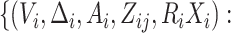
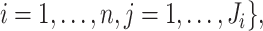 where
where
 denotes the number of replicates for
subject
denotes the number of replicates for
subject 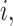 which always equals one in cases 1 and 2;
which always equals one in cases 1 and 2;
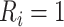 for a subset of
for a subset of
 . The
set
. The
set 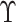 contains
contains 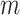 elements
for case 2, while it is empty for cases 1 and 3.
elements
for case 2, while it is empty for cases 1 and 3.
3. Estimation
3.1. Estimation of the optimal treatment
To estimate 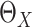 , we adopt a working model,
which assumes the survival time depends on the new biomarkers
, we adopt a working model,
which assumes the survival time depends on the new biomarkers 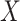 and the
treatment
and the
treatment  through a proportional hazards model
through a proportional hazards model
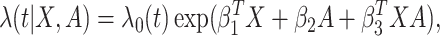 |
(3.1) |
where 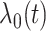 is an
unspecified baseline hazard function, and
is an
unspecified baseline hazard function, and 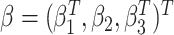 are the regression parameters. Extension to more flexible survival models is discussed in
Section 6.
are the regression parameters. Extension to more flexible survival models is discussed in
Section 6.
Under model (3.1), we have
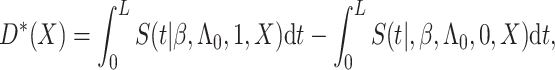 |
where 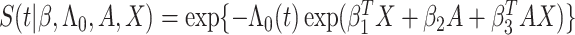 with
with 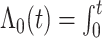
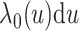 being the baseline
cumulative hazard function. Thus
being the baseline
cumulative hazard function. Thus 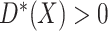 if and only
if
if and only
if 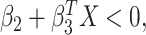 which implies
which implies
 .
In fact, it can be easily seen that
.
In fact, it can be easily seen that  under
model (3.1); that is, the optimal
treatment based on the mean restricted survival time equals the optimal treatment based on
the mean unrestricted survival time.
under
model (3.1); that is, the optimal
treatment based on the mean restricted survival time equals the optimal treatment based on
the mean unrestricted survival time.
If  were observed, an ideal estimator
were observed, an ideal estimator
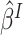 of
of
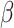 could be obtained by the standard
partial likelihood approach, and the ideal estimator of
could be obtained by the standard
partial likelihood approach, and the ideal estimator of 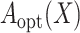 is
is  .
Here and henceforth, we use the superscript “
.
Here and henceforth, we use the superscript “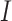 ” to denote the ideal
approach. Since
” to denote the ideal
approach. Since  is not observed in the original study or
only observed in a subset
is not observed in the original study or
only observed in a subset 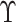 , we may estimate
, we may estimate
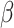 through measurement error
approaches.
through measurement error
approaches.
We adopt the conditional score approach (Song and
others, 2002a) for cases 1 and 3 as it is simple to compute.
The conditional score
estimator was originally derived for the proportional hazards model without interactions.
Here we extend it to model (3.1).
Specifically, assume 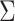 is known for now. Following similar
arguments as those in Song and others
(2002b), we may obtain the “complete sufficient statistic” for
is known for now. Following similar
arguments as those in Song and others
(2002b), we may obtain the “complete sufficient statistic” for
 ,
, 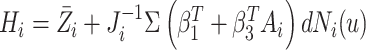 .
Here
.
Here 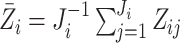 .
The conditional score estimating equation can be written as
.
The conditional score estimating equation can be written as
 |
(3.2) |
where 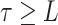 is a fixed
time,
is a fixed
time, 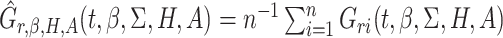 ,
,
 |
with 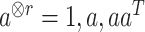 for a vector
for a vector 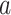 and
and 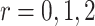 ,
respectively;
,
respectively; 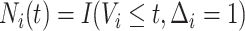 is
the counting process for the events, and
is
the counting process for the events, and  is
the at-risk process. The error variance
is
the at-risk process. The error variance 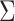 may be estimated
by the method of moments estimator
may be estimated
by the method of moments estimator 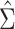 from the
validation data or the replicated data (Song and
others, 2002a).
from the
validation data or the replicated data (Song and
others, 2002a).
In case 2, 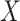 is observed in a subset
is observed in a subset
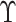 . The partial likelihood estimator
. The partial likelihood estimator
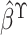 of
of
 may be obtained using observations
in
may be obtained using observations
in 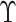 only. But this approach is not
efficient as the information not in
only. But this approach is not
efficient as the information not in 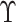 is not used. To
improve the efficiency, following Wang and Song
(2016), an improved estimator can be obtained. Specifically, it is the best
linear combination of
is not used. To
improve the efficiency, following Wang and Song
(2016), an improved estimator can be obtained. Specifically, it is the best
linear combination of 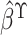 and
and
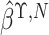 , which equals
, which equals
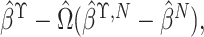 where
where 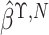 and
and
 are the naive estimates of
are the naive estimates of
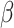 obtained by substituting
obtained by substituting
 for
for  using
the observations in
using
the observations in 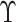 and the whole data set,
respectively, and
and the whole data set,
respectively, and  is given in Appendix A in the
supplementary material
available on Biostatistics online. For simplicity, both this estimator
and the conditional score estimator are referred to as error-corrected estimators
henceforth.
is given in Appendix A in the
supplementary material
available on Biostatistics online. For simplicity, both this estimator
and the conditional score estimator are referred to as error-corrected estimators
henceforth.
Denote the error-corrected estimators of 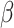 by
by
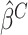 . The optimal treatment can
be estimated by
. The optimal treatment can
be estimated by 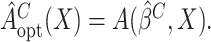 Here and henceforth, we use the superscript “
Here and henceforth, we use the superscript “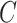 ” to denote the
error-corrected approach. For now, assume model (3.1) holds.
” to denote the
error-corrected approach. For now, assume model (3.1) holds.
Proposition 1
Under the conditions C1–C4 given in Appendix B available on Biostatistics online, almost surely,
exists and converges to
. In addition,
converges to a mean zero normal distribution.
If model (3.1) is not the true
model, it is used as a working model to obtain the treatment selection criterion. Fine (2002) showed that even if model (3.1) does not hold, the partial
likelihood estimator 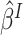 still converges to some
constant
still converges to some
constant  It can be shown that the error-corrected estimators are consistent estimators of
It can be shown that the error-corrected estimators are consistent estimators of
 . Given the value of
. Given the value of
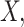
 will converge to a
valid treatment selection criterion
will converge to a
valid treatment selection criterion 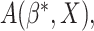 which is equal to
which is equal to 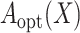 when model (3.1) is correctly specified. When model
(3.1) is misspecified,
when model (3.1) is correctly specified. When model
(3.1) is misspecified,
 is the optimal
treatment under (3.1), but may not
equal to the optimal treatment
is the optimal
treatment under (3.1), but may not
equal to the optimal treatment  We
consider evaluating
We
consider evaluating  and propose an
empirical estimator of
and propose an
empirical estimator of 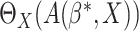 .
.
3.2. Estimation of 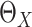
With some algebra, it can be shown that
 |
(3.3) |
where for 
 is the
cumulative hazard function conditional on
is the
cumulative hazard function conditional on 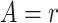 and
and
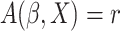 . If
. If  were
observed in the clinical trial,
were
observed in the clinical trial, 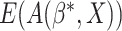 could be estimated by the empirical estimator
could be estimated by the empirical estimator 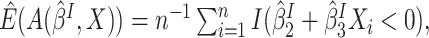 and
and  could
be estimated by Nelson–Aalen type estimators
could
be estimated by Nelson–Aalen type estimators 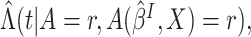 where
where
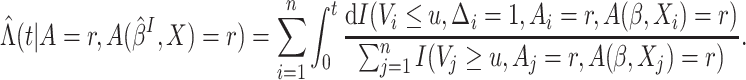 |
Then an estimator of 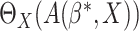 could be
could be
 |
(3.4) |
However, 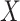 is not observed in the original study or
only observed in a subset
is not observed in the original study or
only observed in a subset 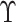 . To deal with the measurement
error, we may apply the SIMEX approach (Carroll and
others, 2006). Assuming
. To deal with the measurement
error, we may apply the SIMEX approach (Carroll and
others, 2006). Assuming 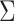 is known for now,
for an increasing sequence of value of
is known for now,
for an increasing sequence of value of 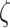 starting from 0,
for example,
starting from 0,
for example, 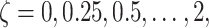 and
and
 let
let
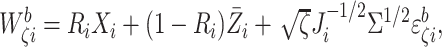 where
where 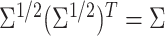 ,
and
,
and 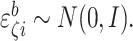 Calculate the naive estimator
Calculate the naive estimator 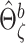 by replacing
by replacing  by
by  and
and  by
by 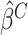 in (3.4). Let
in (3.4). Let
 |
Extrapolate  to
to
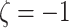 to get the SIMEX estimator
to get the SIMEX estimator
 . A regression model is
usually adopted for the extrapolation, such as the quadratic and nonlinear (rational
linear) extrapolation (Carroll and others,
2006). Specifically, suppose that
. A regression model is
usually adopted for the extrapolation, such as the quadratic and nonlinear (rational
linear) extrapolation (Carroll and others,
2006). Specifically, suppose that 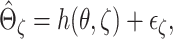 where
where  is an error term with
mean 0. Let
is an error term with
mean 0. Let 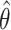 be the least square estimator
of
be the least square estimator
of 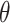 . Then the SIMEX estimator can be
written as
. Then the SIMEX estimator can be
written as
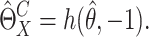 |
When 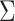 is not known, it can be replaced by
the estimator
is not known, it can be replaced by
the estimator 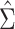 obtained from the validation
data or the replicated data. Specifically,
obtained from the validation
data or the replicated data. Specifically, 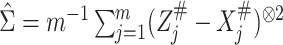 in case 1,
in case 1, 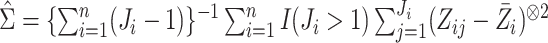 in case 3 and
in case 3 and  in case 2.
in case 2.
Proposition 2
Under the regularity conditions C1–C3 given in Appendix B available on Biostatistics online,
is a consistent estimator of
and
converges to a mean zero normal distribution. Further, with the additional conditions C4–C6,
is a consistent estimator of
and
converges to a mean zero normal distribution.
Proposition 2 indicates that even if the model (3.1) is misspecified, the empirical estimator
 is still a valid
estimator of the mean restricted lifetime under the treatment selection criterion
constructed based on the working model.
is still a valid
estimator of the mean restricted lifetime under the treatment selection criterion
constructed based on the working model.
Model-based estimation. If the working model is the true model, a model-based estimator can be obtained. Noting that
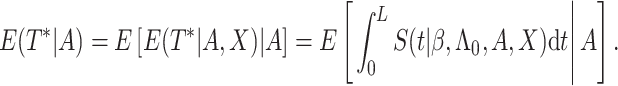 |
(3.5) |
If  were observed, an ideal estimator of
were observed, an ideal estimator of
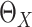 could be
could be
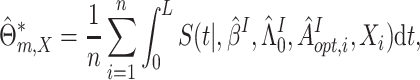 |
(3.6) |
where 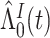 is the Breslow estimator of
is the Breslow estimator of  This cannot be applied
directly since
This cannot be applied
directly since 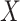 is not observed in the clinical trial. By
analogy to the empirical estimator, the SIMEX approach can be adopted to estimate
is not observed in the clinical trial. By
analogy to the empirical estimator, the SIMEX approach can be adopted to estimate
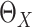 when
when 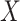 is not
observed.
is not
observed.
If model (3.1) is misspecified, it
can be shown that the model-based estimator 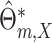 actually estimate
actually estimate
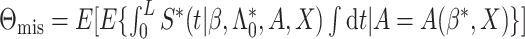 with
with  and
and 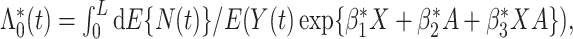 which is different from the optimal mean restricted lifetime
which is different from the optimal mean restricted lifetime  under
the working model. For example, under the scenario considered in our simulation studies in
Section 4, if the true model is
under
the working model. For example, under the scenario considered in our simulation studies in
Section 4, if the true model is
 ,
the optimal mean restricted lifetime is 6.82, the optimal mean restricted lifetime is 6.79
under working model (3.1), while
,
the optimal mean restricted lifetime is 6.82, the optimal mean restricted lifetime is 6.79
under working model (3.1), while
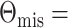 6.60. Therefore the
model-based estimator may not work well for estimation of the mean restricted lifetime
under the working model in this case, while the empirical estimator is still a valid
estimator.
6.60. Therefore the
model-based estimator may not work well for estimation of the mean restricted lifetime
under the working model in this case, while the empirical estimator is still a valid
estimator.
We will focus on the empirical estimation for its robustness. This approach may be applied to the standard biomarkers as described in Section 3.4, which will facilitate the comparison of the standard biomarkers and the new biomarkers.
3.3. Marker-independent treatment selection
Marker-independent treatment selection would assign all subjects to one treatment
 (
( or
or
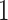 ) if it has been shown significantly
better than the other treatment without taking into consideration of their marker values,
for example, through the log-rank test. The corresponding mean restricted lifetime is
) if it has been shown significantly
better than the other treatment without taking into consideration of their marker values,
for example, through the log-rank test. The corresponding mean restricted lifetime is
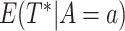 , which can be estimated by
, which can be estimated by
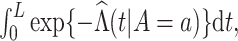 where
where
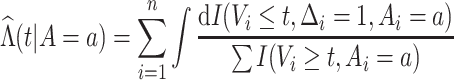 |
is the Nelson–Aalen estimator of the cumulative
hazard function  given
given

3.4. Compare the standard and new biomarkers
To compare the new biomarkers to the standard biomarkers, we need to estimate the
capacity of the standard biomarkers  on treatment selection.
This can be evaluated by a working model that replaces
on treatment selection.
This can be evaluated by a working model that replaces 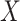 by
by
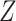 in (3.1), that is,
in (3.1), that is,
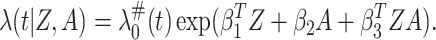 |
(3.7) |
This approach is called the naive approach under the literature of measurement error
models. Let  be the partial likelihood
estimator based on the working model (3.7), where the superscript “
be the partial likelihood
estimator based on the working model (3.7), where the superscript “ ” is used to denote
naive estimators. It can be shown that
” is used to denote
naive estimators. It can be shown that  converges
to some constant
converges
to some constant  (Fine, 2002). Given
(Fine, 2002). Given  , the optimal treatment
selection criterion under the working model is
, the optimal treatment
selection criterion under the working model is 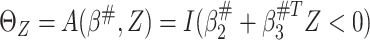 and can be estimated by
and can be estimated by 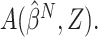 The mean
restricted lifetime
The mean
restricted lifetime  can be
estimated empirically by
can be
estimated empirically by which is obtained by substituting
which is obtained by substituting 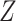 for
for
 and
and  for
for 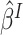 in (3.4).
in (3.4).
Another way to evaluate a treatment selection rule  is to
evaluate the probabilities of subjects mis-assigned to the non-optimal treatment. If the
optimal treatment is 1, the misassignment probability is
is to
evaluate the probabilities of subjects mis-assigned to the non-optimal treatment. If the
optimal treatment is 1, the misassignment probability is
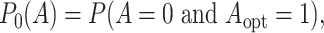 |
(3.8) |
and if the optimal treatment is 0, the misassignment probability is
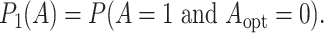 |
(3.9) |
The overall misclassification probability  Thus, we may compare the treatment selection rules
Thus, we may compare the treatment selection rules 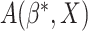 and
and
 based on (3.8) and (3.9).
based on (3.8) and (3.9).
In the simulation studies, if 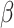 is estimated by
is estimated by
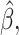 t he misassignment
probabilities
t he misassignment
probabilities 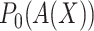 and
and  of using biomarker
of using biomarker
 can be estimated by
can be estimated by
 and
and  and
and
 and
and 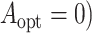 , and the estimated
misassignment probabilities of using
, and the estimated
misassignment probabilities of using  are obtained by
substituting
are obtained by
substituting 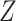 for
for 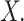 Note
that
Note
that 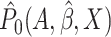 and
and
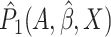 converge to
zero for a consistent estimator
converge to
zero for a consistent estimator 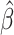 of
of
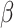 .
.
In practice, 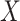 is not observed in the original study or
only observed in a subset
is not observed in the original study or
only observed in a subset 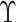 . If (3.1) is correctly specified, the overall misassignment
probability of using
. If (3.1) is correctly specified, the overall misassignment
probability of using 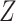 equals
equals
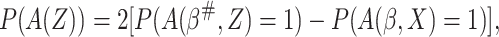 |
where 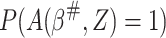 can be estimated
by
can be estimated
by  and
and 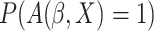 can be estimated by
can be estimated by
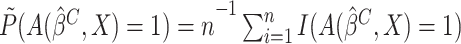 if
if  were observed. Since
were observed. Since
 is not observed, we may apply the SIMEX
approach to obtain the estimate of
is not observed, we may apply the SIMEX
approach to obtain the estimate of  .
.
When the original data contain replicated observations, 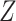 may be
replaced by the mean
may be
replaced by the mean  of the replicated observations,
which has better performance than
of the replicated observations,
which has better performance than 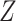 with reduced
measurement error, and we may compare the treatment selection using
with reduced
measurement error, and we may compare the treatment selection using
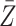 vs.
vs. 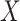 .
.
3.5. Resampling-based inference
Since the asymptotic variance for the empirical estimator depends on the unknown density
and hazard functions, the estimation requires smoothing and may not work well when
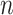 is not large. We develop a
resampling-based approach by analogy to that used in Peng
and Huang (2008). We describe how to derive the variance estimator for
is not large. We develop a
resampling-based approach by analogy to that used in Peng
and Huang (2008). We describe how to derive the variance estimator for
 in case 3; the process
is similar in the other two cases. Specifically, we generate
in case 3; the process
is similar in the other two cases. Specifically, we generate 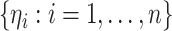 from a known
nonnegative distribution with mean 1. Using
from a known
nonnegative distribution with mean 1. Using 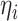 as weights in
the method of moment estimating equation, we first obtain the perturbed estimator
as weights in
the method of moment estimating equation, we first obtain the perturbed estimator
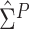 of
of
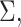 where the superscript
“
where the superscript
“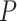 ” stands for the perturbed estimator. Then
using
” stands for the perturbed estimator. Then
using 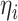 as weights and replacing
as weights and replacing
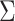 by
by 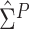 in the conditional score
estimating equation (3.2), we
obtain the perturbed estimator
in the conditional score
estimating equation (3.2), we
obtain the perturbed estimator 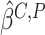 of
of
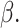 Next, we obtain the perturbed
estimator
Next, we obtain the perturbed
estimator 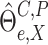 through the
perturbed SIMEX process where for each
through the
perturbed SIMEX process where for each 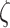 and
and
 replace
replace  by
by
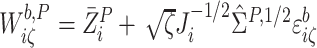 in
in  with
with 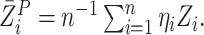 By repeatedly generating
By repeatedly generating 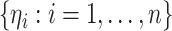 , we obtain a
large number of realization of
, we obtain a
large number of realization of 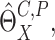 denoted by
denoted by 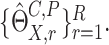 It can be shown that conditional on the observed data,
It can be shown that conditional on the observed data, 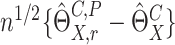 has asymptotically the same distribution as
has asymptotically the same distribution as 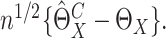 Thus the variance of
Thus the variance of 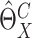 can be estimated by
the sample variance of
can be estimated by
the sample variance of 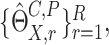 and the confidence interval of
and the confidence interval of 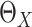 can be
constructed through Wald method or by the percentiles of
can be
constructed through Wald method or by the percentiles of  When the error
variance is estimated from the validation data in case 1, the perturbed estimator of
When the error
variance is estimated from the validation data in case 1, the perturbed estimator of
 of
of
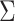 is obtained from the validation
data with a separately generated set of perturbation variables
is obtained from the validation
data with a separately generated set of perturbation variables 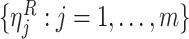 .
.
4. Simulation studies
We conducted simulation studies to evaluate the performance of the proposed approaches.
Mimicking the case of c-myc gene in the ECOG study, we consider treatment selection using
one biomarker. The new biomarker 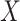 was generated from a
standard normal distribution, and the measurement error was generated from a normal
distribution with mean 0 and variance
was generated from a
standard normal distribution, and the measurement error was generated from a normal
distribution with mean 0 and variance 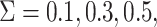 or
or
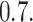 The survival data contains observations
of (
The survival data contains observations
of ( ) on
) on  or
or
 subjects, where
subjects, where
 was generated from a Bernoulli distribution
with probability
was generated from a Bernoulli distribution
with probability 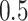 , mimicking treatment assignment in a
randomized clinical trial. The survival time was generated based on model (3.1) with
, mimicking treatment assignment in a
randomized clinical trial. The survival time was generated based on model (3.1) with 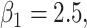
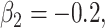
 and
and 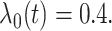 The optimal mean
restricted lifetime under
The optimal mean
restricted lifetime under  equals 6.93. The censoring time
was generated from an exponential distribution with mean 20 and truncated at 12. The
censoring rate was 30%. We considered three cases: (i) the error variance is estimated from
an external validation data set that contains observations of (
equals 6.93. The censoring time
was generated from an exponential distribution with mean 20 and truncated at 12. The
censoring rate was 30%. We considered three cases: (i) the error variance is estimated from
an external validation data set that contains observations of (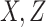 ) on
500 subjects; (ii) the error variance is estimated from replicated observations of
) on
500 subjects; (ii) the error variance is estimated from replicated observations of
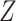 in the original data with
in the original data with
 for
for 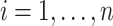 ; (iii) an internal validation
data set is available with
; (iii) an internal validation
data set is available with 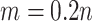 . For each setting, 500 simulated data
sets were generated.
. For each setting, 500 simulated data
sets were generated.
We obtained the error-corrected estimators and naive estimators of
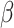 ,
,  , and
, and 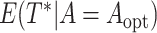 as described in
Section 3 . As a benchmark, we also obtained the
ideal estimators of
as described in
Section 3 . As a benchmark, we also obtained the
ideal estimators of  ,
, 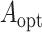 , and
, and 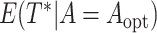 , assuming
, assuming
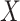 is observed in the survival data. When the
error is large, the root to the conditional score estimating equation
is observed in the survival data. When the
error is large, the root to the conditional score estimating equation
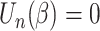 may not exist, and there may
exist some “outliers.” We calculate the bias based on the median of the estimates, and the
standard error by the normalized median absolute deviation (MAD) via the resampling method.
The 95% Wald confidence intervals were calculated correspondingly. For the SIMEX approaches,
we adopted the rational linear extrapolation, and used the quadratic extrapolation as a
backup if the rational extrapolation failed (Carroll
and others, 2006). The perturbation variable
may not exist, and there may
exist some “outliers.” We calculate the bias based on the median of the estimates, and the
standard error by the normalized median absolute deviation (MAD) via the resampling method.
The 95% Wald confidence intervals were calculated correspondingly. For the SIMEX approaches,
we adopted the rational linear extrapolation, and used the quadratic extrapolation as a
backup if the rational extrapolation failed (Carroll
and others, 2006). The perturbation variable
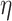 was generated from a location-scale
transformation of beta(
was generated from a location-scale
transformation of beta(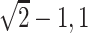 ) and we set
) and we set
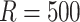 in the resampling process and
in the resampling process and
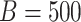 in the SIMEX process.
in the SIMEX process.
The results of estimating  for
for  and
and
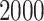 are shown in Tables S1 and S2 in the
supplementary material available
at Biostatistics online, respectively. Compared to the ideal estimates, the
naive estimates show clear bias with the coverage probabilities well below the nominal
level; the coverage probabilities worsen when the sample size increases and error variance
gets larger. The error-corrected estimates perform reasonably well for
are shown in Tables S1 and S2 in the
supplementary material available
at Biostatistics online, respectively. Compared to the ideal estimates, the
naive estimates show clear bias with the coverage probabilities well below the nominal
level; the coverage probabilities worsen when the sample size increases and error variance
gets larger. The error-corrected estimates perform reasonably well for
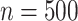 , and the performance improves when the
sample size increases to
, and the performance improves when the
sample size increases to 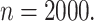
We also estimated the misassignment probabilities using the standard biomarker and the new
biomarker for 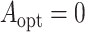 and
and 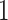 separately. The misassignment probabilities would be zero if the treatment assignment was
based on the true model with the true regression coefficients. The estimated misassignment
probabilities are shown in Table 1. The estimated
misassignment probabilities of the error-corrected estimates based on the new marker are
close to the ideal estimates, and they are much lower than those from the naive approach
based on the standard biomarker. When
separately. The misassignment probabilities would be zero if the treatment assignment was
based on the true model with the true regression coefficients. The estimated misassignment
probabilities are shown in Table 1. The estimated
misassignment probabilities of the error-corrected estimates based on the new marker are
close to the ideal estimates, and they are much lower than those from the naive approach
based on the standard biomarker. When 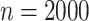 and error standard
variance increases from 0.1 to 0.7, the estimated total misassignment rate increases from
0.49% to 2.03% in case 1, 0.64% to 0.84% in case 2, and 0.44% to 0.93% in case 2 from the
error-corrected approaches based on the new biomarker, while from 9.76% to 22.21% in case 1,
9.76% to 22.14% in case 2, and 6.96% to 17% in case 3 from the naive approach based on the
standard marker. This shows the advantage of adopting the new biomarker, especially when the
measurement error is large.
and error standard
variance increases from 0.1 to 0.7, the estimated total misassignment rate increases from
0.49% to 2.03% in case 1, 0.64% to 0.84% in case 2, and 0.44% to 0.93% in case 2 from the
error-corrected approaches based on the new biomarker, while from 9.76% to 22.21% in case 1,
9.76% to 22.14% in case 2, and 6.96% to 17% in case 3 from the naive approach based on the
standard marker. This shows the advantage of adopting the new biomarker, especially when the
measurement error is large.
Table 1.
Simulation results for estimation of treatment misassignment rate (%).

|
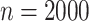
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
A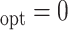
|
A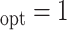
|
A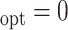
|
A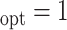
|
|||||||||||
|
Marker | Method | Est | SD | Est | SD | Est | SD | Est | SD | ||||
| New | Ideal | 0.35 | 0.61 | 0.41 | 0.64 | 0.19 | 0.30 | 0.18 | 0.28 | |||||
| Case 1 | ||||||||||||||
| 0.1 | New | EC | 0.49 | 0.79 | 0.56 | 0.89 | 0.26 | 0.38 | 0.23 | 0.36 | ||||
| Standard | Naive | 4.91 | 1.06 | 4.93 | 1.07 | 4.94 | 0.54 | 4.82 | 0.52 | |||||
| [0.05in]0.3 | New | EC | 0.77 | 1.24 | 0.75 | 1.21 | 0.40 | 0.62 | 0.38 | 0.57 | ||||
| Standard | Naive | 8.00 | 1.27 | 7.99 | 1.26 | 8.12 | 0.64 | 7.84 | 0.61 | |||||
| [0.05in]0.5 | New | EC | 1.02 | 1.62 | 1.07 | 1.81 | 0.69 | 1.17 | 0.54 | 0.87 | ||||
| Standard | Naive | 10.00 | 1.40 | 9.63 | 1.39 | 9.98 | 0.73 | 9.61 | 0.71 | |||||
| [0.05in]0.7 | New | EC | 1.31 | 2.33 | 1.92 | 3.62 | 1.04 | 2.04 | 0.99 | 1.97 | ||||
| Standard | Naive | 11.46 | 1.51 | 10.85 | 1.48 | 11.37 | 0.77 | 10.84 | 0.71 | |||||
| Case 2 | ||||||||||||||
| 0.1 | New | EC | 0.60 | 0.95 | 0.66 | 0.96 | 0.32 | 0.47 | 0.32 | 0.48 | ||||
| Standard | Naive | 4.91 | 1.08 | 4.83 | 1.03 | 4.91 | 0.54 | 4.85 | 0.53 | |||||
| 0.3 | New | EC | 0.71 | 1.07 | 0.75 | 1.08 | 0.38 | 0.55 | 0.38 | 0.57 | ||||
| Standard | Naive | 8.05 | 1.26 | 7.82 | 1.24 | 8.09 | 0.67 | 7.88 | 0.64 | |||||
| 0.5 | New | EC | 0.73 | 1.11 | 0.78 | 1.12 | 0.41 | 0.59 | 0.41 | 0.61 | ||||
| Standard | Naive | 9.93 | 1.41 | 9.54 | 1.33 | 9.95 | 0.70 | 9.63 | 0.71 | |||||
| 0.7 | New | EC | 0.74 | 1.13 | 0.80 | 1.14 | 0.42 | 0.61 | 0.42 | 0.63 | ||||
| Standard | Naive | 11.30 | 1.45 | 10.78 | 1.43 | 11.30 | 0.74 | 10.84 | 0.75 | |||||
| Case 3 | ||||||||||||||
| 0.1 | New | EC | 0.47 | 0.73 | 0.43 | 0.71 | 0.21 | 0.33 | 0.23 | 0.35 | ||||
| Standard | Naive | 3.59 | 0.96 | 3.47 | 0.88 | 3.50 | 0.48 | 3.46 | 0.47 | |||||
| [0.05in]0.3 | New | EC | 0.60 | 0.94 | 0.57 | 0.91 | 0.25 | 0.40 | 0.31 | 0.45 | ||||
| Standard | Naive | 5.96 | 1.13 | 5.80 | 1.08 | 5.92 | 0.56 | 5.80 | 0.55 | |||||
| [0.05in]0.5 | New | EC | 0.75 | 1.27 | 0.71 | 1.09 | 0.31 | 0.49 | 0.39 | 0.56 | ||||
| Standard | Naive | 7.43 | 1.23 | 7.26 | 1.19 | 7.44 | 0.62 | 7.25 | 0.59 | |||||
| [0.05in]0.7 | New | EC | 0.78 | 1.28 | 0.96 | 1.56 | 0.47 | 0.76 | 0.46 | 0.72 | ||||
| Standard | naive | 8.60 | 1.26 | 8.30 | 1.34 | 8.64 | 0.68 | 8.36 | 0.65 | |||||
EC, error corrected; Est, estimate; SD, empirical standard deviation.
We further estimated the mean restricted lifetime within 10 years using the new biomarker
and the standard biomarker. The results are shown in Table
2. The optimal mean restricted lifetime is 6.93 using the new marker, whereas when
 increases from 0.1 to 0.7, the
mean restricted lifetime based on the standard marker decreases from 6.72 to 6.02 in cases 1
and 2 and 6.82 to 6.35 in case 3. The estimates perform reasonably well for
increases from 0.1 to 0.7, the
mean restricted lifetime based on the standard marker decreases from 6.72 to 6.02 in cases 1
and 2 and 6.82 to 6.35 in case 3. The estimates perform reasonably well for
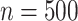 and improves when
and improves when
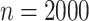 .
.
Table 2.
Simulation results for estimation of  and
and
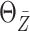 .
.

|
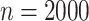
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|

|
True | Method | B | MAD | RMAD | CP | B | MAD | RMAD | CP | ||
Estimation of 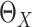
| ||||||||||||
| [0.05in] | 6.931 | Ideal |
 0.034
0.034 |
0.245 | 0.247 | 0.950 |
 0.013
0.013 |
0.122 | 0.123 | 0.982 | ||
| Case 1 | ||||||||||||
| 0.1 | 6.931 | EC | 0.007 | 0.379 | 0.474 | 0.948 |
 0.007
0.007 |
0.168 | 0.197 | 0.978 | ||
| 0.3 | 6.931 | EC |
 0.041
0.041 |
0.498 | 0.637 | 0.942 |
 0.032
0.032 |
0.242 | 0.272 | 0.950 | ||
| 0.5 | 6.931 | EC |
 0.101
0.101 |
0.582 | 0.805 | 0.913 |
 0.104
0.104 |
0.283 | 0.345 | 0.948 | ||
| 0.7 | 6.931 | EC |
 0.211
0.211 |
0.632 | 0.894 | 0.922 |
 0.141
0.141 |
0.333 | 0.411 | 0.910 | ||
| Case 2 | ||||||||||||
| 0.1 | 6.931 | EC | 0.013 | 0.402 | 0.452 | 0.906 |
 0.007
0.007 |
0.176 | 0.195 | 0.964 | ||
| 0.3 | 6.931 | EC |
 0.033
0.033 |
0.440 | 0.603 | 0.940 |
 0.041
0.041 |
0.211 | 0.256 | 0.962 | ||
| 0.5 | 6.931 | EC |
 0.016
0.016 |
0.578 | 0.776 | 0.920 |
 0.064
0.064 |
0.286 | 0.324 | 0.936 | ||
| 0.7 | 6.931 | EC |
 0.059
0.059 |
0.700 | 0.966 | 0.890 |
 0.086
0.086 |
0.320 | 0.394 | 0.936 | ||
| Case 3 | ||||||||||||
| 0.1 | 6.931 | EC | 0.001 | 0.353 | 0.412 | 0.934 | 0.015 | 0.149 | 0.179 | 0.952 | ||
| 0.3 | 6.931 | EC |
 0.019
0.019 |
0.367 | 0.477 | 0.964 |
 0.012
0.012 |
0.186 | 0.211 | 0.958 | ||
| 0.5 | 6.931 | EC |
 0.026
0.026 |
0.425 | 0.549 | 0.970 |
 0.025
0.025 |
0.228 | 0.249 | 0.958 | ||
| 0.7 | 6.931 | EC |
 0.043
0.043 |
0.550 | 0.676 | 0.920 |
 0.013
0.013 |
0.265 | 0.293 | 0.938 | ||
Estimation of 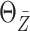
| ||||||||||||
| Case 1 | ||||||||||||
| 0.1 | 6.720 | Naive |
 0.039
0.039 |
0.255 | 0.255 | 0.940 |
 0.009
0.009 |
0.114 | 0.127 | 0.958 | ||
| 0.3 | 6.411 | Naive |
 0.032
0.032 |
0.283 | 0.263 | 0.968 |
 0.040
0.040 |
0.119 | 0.132 | 0.956 | ||
| 0.5 | 6.186 | Naive |
 0.053
0.053 |
0.271 | 0.270 | 0.942 |
 0.013
0.013 |
0.142 | 0.134 | 0.964 | ||
| 0.7 | 6.017 | Naive |
 0.035
0.035 |
0.264 | 0.274 | 0.938 |
 0.011
0.011 |
0.135 | 0.136 | 0.974 | ||
| Case 2 | ||||||||||||
| 0.1 | 6.720 | Naive |
 0.036
0.036 |
0.262 | 0.255 | 0.940 |
 0.011
0.011 |
0.125 | 0.127 | 0.958 | ||
| 0.3 | 6.411 | Naive |
 0.026
0.026 |
0.257 | 0.265 | 0.952 |
 0.015
0.015 |
0.121 | 0.131 | 0.952 | ||
| 0.5 | 6.186 | Naive |
 0.022
0.022 |
0.255 | 0.271 | 0.942 |
 0.008
0.008 |
0.126 | 0.134 | 0.954 | ||
| 0.7 | 6.017 | Naive |
 0.019
0.019 |
0.261 | 0.274 | 0.940 |
 0.011
0.011 |
0.121 | 0.136 | 0.962 | ||
| Case 3 | ||||||||||||
| 0.1 | 6.818 | Naive |
 0.023
0.023 |
0.251 | 0.253 | 0.958 |
 0.001
0.001 |
0.121 | 0.126 | 0.940 | ||
| 0.3 | 6.629 | Naive |
 0.023
0.023 |
0.243 | 0.258 | 0.958 | 0.000 | 0.135 | 0.129 | 0.942 | ||
| 0.5 | 6.476 | Naive |
 0.016
0.016 |
0.258 | 0.262 | 0.954 | 0.003 | 0.131 | 0.131 | 0.954 | ||
| 0.7 | 6.347 | Naive |
 0.018
0.018 |
0.274 | 0.267 | 0.938 |
 0.005
0.005 |
0.136 | 0.132 | 0.948 | ||
EC, error corrected; B, empirical bias based on the median; MAD, empirical median absolute deviation; RMAD, resampling median absolute deviation; CP, empirical coverage probability of 95% confidence interval.
Under this setting, the average survival time for treatment 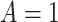 is
significantly longer than
is
significantly longer than 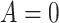 without adjusted for the biomarker value.
Therefore, marker-independent treatment selection will assign all subjects to treatment 1.
The corresponding mean restricted lifetime within 10 years is 3.984, which is much shorter
than marker based estimates. The corresponding misassignment rate is 48.4%, which is much
higher than marker based estimates.
without adjusted for the biomarker value.
Therefore, marker-independent treatment selection will assign all subjects to treatment 1.
The corresponding mean restricted lifetime within 10 years is 3.984, which is much shorter
than marker based estimates. The corresponding misassignment rate is 48.4%, which is much
higher than marker based estimates.
We also consider a simulation setting when the true model is misspecified as (3.1). The simulation setting is the same
as case 1 above except that the true model is  with
with 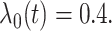 In this case, the
treatment selection based on the working model (3.1) is not optimal overall. Based on the working models (3.1) and (3.7), we estimated the misassignment probabilities and the mean
restricted lifetime using the new biomarker and the standard biomarker, respectively. The
results for
In this case, the
treatment selection based on the working model (3.1) is not optimal overall. Based on the working models (3.1) and (3.7), we estimated the misassignment probabilities and the mean
restricted lifetime using the new biomarker and the standard biomarker, respectively. The
results for 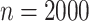 are shown in Tables S3 and S4 in the
supplementary material available
at Biostatistics online. For estimation of the overall misassignment rate,
the estimate is 3.53% from the ideal approach. When the error variance increases from 0.1 to
0.7, the estimates from the error-corrected approach based on the new biomarker are close to
that from the ideal approach, while the estimates based on the standard biomarker increase
considerably from 10.21% to 22.53% for the naive approach with the error variance increases
from 0.1 to 0.7. The optimal mean restricted lifetime based on the new marker is 6.79 under
model (3.1), while the mean
restricted lifetime based on the standard marker decreases from 6.59 to 5.92 when
are shown in Tables S3 and S4 in the
supplementary material available
at Biostatistics online. For estimation of the overall misassignment rate,
the estimate is 3.53% from the ideal approach. When the error variance increases from 0.1 to
0.7, the estimates from the error-corrected approach based on the new biomarker are close to
that from the ideal approach, while the estimates based on the standard biomarker increase
considerably from 10.21% to 22.53% for the naive approach with the error variance increases
from 0.1 to 0.7. The optimal mean restricted lifetime based on the new marker is 6.79 under
model (3.1), while the mean
restricted lifetime based on the standard marker decreases from 6.59 to 5.92 when
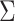 increases from 0.1 to 0.7. The
estimates of the mean restricted lifetime perform well.
increases from 0.1 to 0.7. The
estimates of the mean restricted lifetime perform well.
5. Application
We applied the proposed approach to a subset of the ECOG clinical trial, which was analyzed in Li and Ryan (2006), where c-myc expression level was measured via dot plots on 92 patients randomized to receive surgery alone or surgery plus chemotherapy, both progression-free survival and overall survival were recorded. The results for overall survival are presented as follows while the results for progression-free survival are presented in the supplementary material available at Biostatistics online.
Based on the log-rank test, surgery plus chemotherapy is better than surgery alone for
overall survival (p-value = 0.0186). Thus marker-independent treatment selection would
assign all patients to surgery plus chemotherapy. Using this subset of data, Li and Ryan (2006) found marginally significant
interaction between treatment 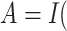 surgery plus
chemotherapy
surgery plus
chemotherapy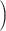 and log c-myc gene expression level
and log c-myc gene expression level
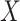 for progression-free survival
(
for progression-free survival
( -value
-value 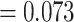 )
and overall survival (
)
and overall survival ( -value
-value  )
under model (3.1 ), and Song and Zhou (2011) evaluated bisecting the observed
c-myc gene expression level
)
under model (3.1 ), and Song and Zhou (2011) evaluated bisecting the observed
c-myc gene expression level  for treatment selection. It is conjectured
that a more accurate measurement of c-myc gene expression level might improve its capacity
for treatment selection. In this subset, 26 subjects have replicated c-myc gene expression
measurements with the estimated measurement error standard deviation equal to
for treatment selection. It is conjectured
that a more accurate measurement of c-myc gene expression level might improve its capacity
for treatment selection. In this subset, 26 subjects have replicated c-myc gene expression
measurements with the estimated measurement error standard deviation equal to
 . The plot of the residuals
. The plot of the residuals
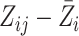 and the corresponding Q–Q
plot indicate that it is reasonable to assume the error is normal with constant variance
(Figure 2).
and the corresponding Q–Q
plot indicate that it is reasonable to assume the error is normal with constant variance
(Figure 2).
Fig. 2.
Left, residual plot; right, Q–Q plot of the residuals.
We checked the proportional hazards assumption in model (3.7 ) using the method in Therneau and Grambsch (2006, Chapter 6.2). To check the proportional hazards
assumption in model (3.1), as
 is not available, we adopted SIMEX approach
to obtain the error-corrected p-values. There is no evidence of violation of the
proportional hazards assumptions in both models.
is not available, we adopted SIMEX approach
to obtain the error-corrected p-values. There is no evidence of violation of the
proportional hazards assumptions in both models.
We would like to assess the amount of gain of improving c-myc gene expression level
measurement on treatment selection and to compare treatment selection based on the true
value 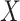 and the error-contaminated observation. To
reduce variation from SIMEX and bootstrap, we took larger values of
and the error-contaminated observation. To
reduce variation from SIMEX and bootstrap, we took larger values of
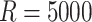 in the resampling process and
in the resampling process and
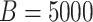 in the SIMEX process. Under the
working proportional hazards model (3.1) and (3.7), the
estimated coefficients and standard errors are shown in Table 3. The error-corrected estimates of log c-myc level and the interaction are
larger in magnitude. Among the 92 subjects, 48 (47.8%) patients were assigned to surgery
alone and 44 to surgery plus chemotherapy. An estimate of 87% patients would be assigned to
surgery plus chemotherapy if the treatment is selected using
in the SIMEX process. Under the
working proportional hazards model (3.1) and (3.7), the
estimated coefficients and standard errors are shown in Table 3. The error-corrected estimates of log c-myc level and the interaction are
larger in magnitude. Among the 92 subjects, 48 (47.8%) patients were assigned to surgery
alone and 44 to surgery plus chemotherapy. An estimate of 87% patients would be assigned to
surgery plus chemotherapy if the treatment is selected using 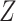 , and 82%
if the treatment is selected using
, and 82%
if the treatment is selected using  . This suggested that 10%
patients might be assigned to the wrong treatment if model (3.1) is true and the treatment is selected using
. This suggested that 10%
patients might be assigned to the wrong treatment if model (3.1) is true and the treatment is selected using
 . The estimated mean restricted lifetime
within 5 years is 3.85 if all patients are assigned to surgery alone, and 4.10 if all are
assigned to surgery plus chemotherapy. The estimated mean restricted lifetime within 5 years
is 4.40 when the treatment is selected using
. The estimated mean restricted lifetime
within 5 years is 3.85 if all patients are assigned to surgery alone, and 4.10 if all are
assigned to surgery plus chemotherapy. The estimated mean restricted lifetime within 5 years
is 4.40 when the treatment is selected using 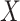 while 4.13 when the
treatment is selected using
while 4.13 when the
treatment is selected using  . There is no significant difference between
the mean restricted life times (95% confidence interval
. There is no significant difference between
the mean restricted life times (95% confidence interval  ,
0.61). With the consideration of the possible side effects of chemotherapy, the treatment
selection based on the new marker seems to be better as less patients are assigned to
surgery plus chemotherapy.
,
0.61). With the consideration of the possible side effects of chemotherapy, the treatment
selection based on the new marker seems to be better as less patients are assigned to
surgery plus chemotherapy.
Table 3.
Analysis of the ECOG data for overall survival.
| Estimation of Cox model coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|
| log(c-myc) | TRT | log(c-myc) TRT TRT |
||||||
| Est (RMAD) | Est (RMAD) | Est (RMAD) | ||||||
Model based on 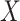
|
0.715 (0.548) |
 0.027 (0.488)
0.027 (0.488) |
 1.355 (0.975)
1.355 (0.975) |
|||||
Model based on 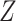
|
0.582 (0.396) |
 0.105 (0.428)
0.105 (0.428) |
 1.126 (0.691)
1.126 (0.691) |
|||||
| Estimation of 5-year restricted lifetime | ||||||||
| Est | CI | |||||||
| All assigned to surgery alone | 3.85 | (3.41–4.29) | ||||||
All assigned to surgery chemotherapy chemotherapy |
4.10 | (3.66–4.53) | ||||||
Treatment selection using 
|
4.39 | (3.79–5.00) | ||||||
Treatment selection using 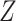
|
4.13 | (3.71–4.55) | ||||||
Est, estimate; RMAD, resampling median absolute deviation; CI, 95% confidence interval.
6. Discussion
We have proposed a novel method to evaluate a new biomarker based on data from a reproducibility study. Our approach assumes that the reproducibility study samples and the clinical trial samples are randomly drawn from a common target population. It is beyond the scope of this article to address the impact of violations of this assumption.
We have aimed on maximizing the population mean-restricted lifetime. This method can be
extended to other statistical measures, for example, 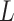 -year
survival rate, or a more flexible utility function that incorporates notions of cost and
quality of life. Although we have focused on survival time as outcomes, the approach can be
adapted to discrete and continuous outcomes with minor modifications.
-year
survival rate, or a more flexible utility function that incorporates notions of cost and
quality of life. Although we have focused on survival time as outcomes, the approach can be
adapted to discrete and continuous outcomes with minor modifications.
For simplicity, we have adopted proportional hazards models as working models. The estimation of mean restricted lifetime under the treatment selection criterion based on the working model is still valid even if the model is misspecified. Our approaches may also be extended to more flexible models, for example, by allowing time-varying treatment or covariate effects, or including nonparametric functions of covariates in the survival model. Other types of survival models, such as the accelerated failure time model or the additive hazards model, may also be used. Such extensions may warrant further investigation.
In addition, we have assumed a classical measurement error model between the new marker and
the standard marker. An more flexible model such as (2.3) with  and
and
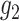 unknown may be adopted and could be
estimated using data from the reproducibility study with validation data based on parametric
models or spline approximation. In some situations, both markers might involve measurement
error while the measurement error for the new marker might be smaller. It would be of
interest to extend our approaches to accommodate such complexity.
unknown may be adopted and could be
estimated using data from the reproducibility study with validation data based on parametric
models or spline approximation. In some situations, both markers might involve measurement
error while the measurement error for the new marker might be smaller. It would be of
interest to extend our approaches to accommodate such complexity.
The model of equation (2.2) assumes that the new assay reduces error compared to the existing assay. This is motivated by the fact that often newer technologies provide better measurements than existing technologies. However, the new technologies are often more expensive as well. There is a cost–benefit tradeoff for many new assays. Our modeling approach can help in the quantification of how large the potential benefit might be from a new assay that is under consideration. This can be used to make the “go” versus “no go” decision on whether or not to switch to the new marker in the future. In other words, by quantifying the benefit, our method gives the information needed to make this decision. Another application of our approach is to the setting where a gold standard treatment-selection biomarker exists along with an approximation to the biomarker. The approximation may be based for example on pathological evaluations, like the Magee score as an approximation to the OncotypeDX score (Farrugia and others, 2017). Our approach provides a framework in which to understand the relationship between two such scores as predictors of a clinically important survival outcome.
7. Software
The R code and a sample data set are available on GitHub (https://github.com/xsong88/Evaluate-Biomarkers).
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
National Institutes of Health (CA201207 to X.S. and K.K.D.; R43GM134768 to X.S.); and NSF (DMS-1916411 to X.S.).
References
- Augenlicht, L., Wadler, S., Corner, G., Richards, C., Ryan, L., Multani, A., Pathak, S., Benson, A., Hailer, D., and Heerdt, B. (1997). Low-level c-myc amplification in human colonic carcinoma cell lines and tumors: a frequent, p53-independent mutation associated with improved outcome in a randomized multi-institutional trial. Cancer Research 99, 1769–1775. [PubMed] [Google Scholar]
- Boonstra, P., Mukherjee, B., and Taylor, J. (2013). Bayesian shrinkage methods for partially observed data with many predictors. The Annals of Applied Statistics 7, 2272–2292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boonstra, P., Taylor, J., and Mukherjee, B. (2013). Incorporating auxiliary information for improved prediction in high dimensional datasets: an ensemble of shrinkage approaches. Biostatistics 14, 259–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinkley, J., Tsiatis, A. A., and Anstrom, K. J. (2010). A generalized estimator of the attributable benefit of an optimal treatment regime. Biometrics 66, 512–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai, T., Tian, L., Wong, P., and Wei, L. J. (2011). Analysis of randomized comparative clinical trial data for personalized treatment selections. Biostatistics 12, 270–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll, R. J., Ruppert, D., Stefanski, L. A., and Crainiceanu, C. M. (2006). Measurement Error in Nonlinear Models. New York: Chapman and Hall/CRC. [Google Scholar]
- Chen, P. Y. and Tsitais, A. A. (2001). Causal inference on the difference of the restricted mean lifetime between two groups. Biometrics 57, 1030–1038. [DOI] [PubMed] [Google Scholar]
- Dafni, U. G. and Tsiatis, A. A. (1998). Evaluating surrogate markers of clinical outcome measured with error. Biometrics 54, 1445–1462. [PubMed] [Google Scholar]
- Farrugia, D., Landmann, A., Zhu, L., Diego, E., Johnson, R., Bonaventura, M., Soran, A., Dabbs, D., Clarek, B., Puhalla, S.. and others (2017). Magee equation 3 predicts pathologic response to neaoadjuvant systemic chemotehrapy in estrogen receptor positive, her2 negative/equivocal breast tumors. Modern Pathology 30, 1078–1085. [DOI] [PubMed] [Google Scholar]
- Faucett, C. J. and Thomas, D. C. (1996). Simultaneously modeling censored survival data and repeatedly measured covariates: a Gibbs sampling approach. Statistics in Medicine 15, 1663–1685. [DOI] [PubMed] [Google Scholar]
- Fine, J. (2002). Comparing nonnested Cox models. Biometrika 89, 635–647. [Google Scholar]
- Greene, W. and Cai, J. (2004). Measurement error in covariates in the marginal hazards model for multivariate failure time data. Biometrics 60, 987–996. [DOI] [PubMed] [Google Scholar]
- Henderson, R., Diggle, P., and Dobson, A. (2000). Joint modeling of longitudinal measurements and event time data. Biostatistics 4, 465–480. [DOI] [PubMed] [Google Scholar]
- Huang, Y. and Wang, C. Y. (2000). Cox regression with accurate covariates unascertainable: a nonparametric correction approach. Journal of the American Statistical Association 95, 1209–1219. [Google Scholar]
- Janes, H., Brown, M. D., Pepe, M. S., and Huang, Y. (2014). An approach to evaluating and comparing biomarkers for patient treatment selection. International Journal of Biostatistics 10, 99–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janes, H., Pepe, M. S., Bossuyt, P. M., and Barlow, W. E. (2011). Measuring the performance of markers for guiding treatment decisions. Annals of Internal Medicine 154, 253–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein, J. P. and Moeschberger, M. L. (2003). Survival Analysis: Techniques for Censored and Truncated Data. New York: Springer. [Google Scholar]
- Li, Y. and Ryan, L. (2006). Inference on survival data with covariate measurement error an imputation-based approach. Scandinavian Journal of Statistics 33, 169–190. [Google Scholar]
- Peng, L. and Huang, Y. (2008). Survival analysis with quantile regression models. Journal of the American Statistical Association 103, 637–649. [Google Scholar]
- Prentice, R. (1982). Covariate measurement errors and parameter estimates in a failure time regression model. Biometrika 69, 331–342. [Google Scholar]
- Song, X., Davidian, M., and Tsiatis, A. A. (2002a). An estimator for the proportional hazards model with multiple longitudinal covariates measured with error. Biostatistics 3, 511–528. [DOI] [PubMed] [Google Scholar]
- Song, X., Davidian, M., and Tsiatis, A. A. (2002b). A semiparametric likelihood approach to joint modeling of longitudinal and time-to-event data. Biometrics 58, 742–753. [DOI] [PubMed] [Google Scholar]
- Song, X. and Pepe, M. S. (2004). Evaluating markers for selecting a patient’s treatment. Biometrics 60, 874–883. [DOI] [PubMed] [Google Scholar]
- Song, X. and Zhou, X. H. (2011). Evaluating markers for treatment selection based on survival outcome. Statistics in Medicine 30, 2251–2264. [DOI] [PubMed] [Google Scholar]
- Therneau, T. M. and Grambsch, P. M. (2006). Modeling Survival Data: Extending the Cox Model. New York: Springer. [Google Scholar]
- Tsiatis, A. and Davidian, M. (2001). A semiparametric estimator for the proportional hazards model with longitudinal covariates measured with error. Biometrika 88, 447–458. [DOI] [PubMed] [Google Scholar]
- Wang, C. Y. and Song, X. (2016). Robust best linear estimator for Cox regression with instrumental variables in whole cohort and surrogates with additive measurement error in calibration sample. Biometrical Journal 58, 1465–1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, C. Y., Wang, N., and Wang, S. (2000). Regression analysis when covariates are regression parameters of a random effect model for observed longitudinal measurements. Biometrics 56, 487–495. [DOI] [PubMed] [Google Scholar]
- Wulfsohn, M. S. and Tsiatis, A. A. (1997). A joint model for survival and longitudinal data measured with error. Biometrics 53, 330–339. [PubMed] [Google Scholar]
- Xu, J. and Zeger, S. L. (2001). Joint analysis of longitudinal data comprising repeated measures and times to events. Applied Statistics 50, 375–387. [Google Scholar]
- Zhang, B., Tsiatis, A. A., Laber, E. B., and Davidian, M. (2012). A robust method for estimating optimal treatment regimes. Biometrics 68, 1010–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, H. and Tsiatis, A. A. (1997). A consistent estimator for the distribution of quality adjusted lifetime. Biometrika 84, 339–348. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




