Differential RNA methylation using multivariate statistical methods

Abstract

Motivation

m6A methylation is a highly prevalent post-transcriptional modification in eukaryotes. MeRIP-seq or m6A-seq, which comprises immunoprecipitation of methylation fragments , is the most common method for measuring methylation signals. Existing computational tools for analyzing MeRIP-seq data sets and identifying differentially methylated genes/regions are not most optimal. They either ignore the sparsity or dependence structure of the methylation signals within a gene/region. Modeling the methylation signals using univariate distributions could also lead to high type I error rates and low sensitivity. In this paper, we propose using mean vector testing (MVT) procedures for testing differential methylation of RNA at the gene level. MVTs use a distribution-free test statistic with proven ability to control type I error even for extremely small sample sizes. We performed a comprehensive simulation study comparing the MVTs to existing MeRIP-seq data analysis tools. Comparative analysis of existing MeRIP-seq data sets is presented to illustrate the advantage of using MVTs.

Results

Mean vector testing procedures are observed to control type I error rate and achieve high power for detecting differential RNA methylation using m6A-seq data. Results from two data sets indicate that the genes detected identified as having different m6A methylation patterns have high functional relevance to the study conditions.

Availability

The dimer software package for differential RNA methylation analysis is freely available at https://github.com/ouyang-lab/DIMER.

Supplementary information

Supplementary data are available at Briefings in Bioinformatics online.

1 Introduction

N6-Methyladenosine (m6A) is one of the several known transcriptomic modifications in eukaryotes [4]. It is the most prevalent modification found in mature RNA, occurring at an average of 1 in every 2000 bases [14]. Besides a high abundance around the stop codons, it is also observed in non-coding RNAs (ncRNA) and long ncRNAs [28], transfer RNAs [33] and ribosomal RNAs [19]. Despite being first detected in the 1970s [13], its exact mechanism and implications are not entirely known. In recent years, there has been increased interest in understanding the role of m6A methylation in gene regulation [15], RNA splicing and stability [14] and cell differentiation and proliferation [38]. It is also observed to play a role as pacesetter in the mammalian circadian clock [18]. Besides regulating cellular mechanism, recent work has shed light on the role of m6A methylation in cancer biology as a regulator of tumorigenesis and self-renewal in glioblastoma stem cells. Researchers have shown that tumorigenesis and self-renewal of glioblastoma stem cells is regulated by m6A modification [9].

Unlike DNA methylation, which can be determined at the base pair level through bisulphite sequencing, there is no exact method for studying m6A methylation. Determining m6A methylation at the base pair level is challenging because methylated and unmethylated adenosine bases have nearly identical chemical properties. Hence, reverse transcription of an m6A base does not yield a comparable method like bisulfite sequencing in DNA. The standard and widely used method to measure RNA methylation is through immunoprecipitation sequencing, m6A-seq or MeRIP-Seq [28]. Using antibodies that target m6A nucleosides in fragmented transcripts, libraries are prepared for the transcripts carrying the m6A-methyl group, called the immunoprecipitated (IP) fragments. Library size of the IP fragments depends on the capture rate of the experiment and the quality of transcripts in the sample. To account for this variability in transcript abundance in the samples, a control library is also prepared. Combining the immunoprecipated and control samples, the relative transcript abundance is used as a measure of methylation signal. While some recent techniques have been developed to study RNA methylation at near nucleotide resolution [22], such experiments have low throughput and are not exact nucleotide-level. To better localize the exact location of methylated adenosines, motif finding algorithms are generally used. 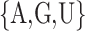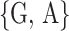For example, [8, 17] have identified that most methylated adenosines are found in the consensus DRACH (D = , R = , H = 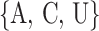) motif.

Besides identifying methylated nucleosides at the base pair level, a clinically important computational challenge in understanding RNA methylation is to compare the methylation profiles of transcriptomes under two or more conditions. Differential methylation analysis is an important step in understanding the role of methylation/demethylation enzyme complexes such as METTL3-METTL14 complex [23], WTAP [31], FTO [36], etc. There are two main methods used for detecting regions with high levels of differential methylation: peak-calling and window-based.

Peak-calling algorithms first identify contiguous regions with high levels of methylation called peaks on the two conditions (e.g. wild-type versus knockout) and then do a comparison of the peaks. Similar to MACS [37] for ChIP-Seq experiments, peaks in MeRIP-Seq are defined as regions enriched in the IP samples compared to control samples. Several methods have been developed targeting m6A methylation data sets such as exomePeak [27], HEPeak [10], SRAMP [39], m6aPred [7] and iRNA-Methyl [6]. When differential analysis is our primary interest, these methods have a notable drawback. Since the same data are used for calling peaks and testing differential methylation, there is potential for over-fitting the data and type I error in the hypothesis testing part may not be controlled [26].

Window-based methods do not involve peak-calling and thus do not suffer from over-fitting as the data are used only for differential analysis. In window-based methods, the region of interest—typically an entire gene or an exon—is divided into windows of pre-defined width. These windows are then used to impart methylation signals. Differential analysis is then performed by comparing the signals across all the windows within a given region of interest. For example, a simple method is to calculate the total methylation signal in the gene by adding the signals across all the windows and using a Fisher’s exact test. Without loss of generality, we consider a gene as our region of interest for the remainder of the paper.

Statistical methods for comparing the window-based methylation signals in a region of interest can be broadly classified into two categories: univariate and multivariate. In univariate methods, the signals within each window are modeled independently using parametric models. The region of interest is then deemed differentially methylated by combining the results of all the windows. Higher-level methods involve modeling the parameters across the windows using another parametric model, similar to applying a prior distribution in a Bayesian model. Differential methylation of the region is then defined based on the parameters of the higher-level model. Currently existing methods such as MeTDiff [11] and DRME [24] use univariate methods to model these window-based signals. Likelihood based tests are then used for detecting differentially methylated regions. In multivariate methods, signals across all the windows are considered simultaneously as a data vector and modeled using multivariate distributions. The number of windows will correspond to the dimension of the distribution. The mean signal across all the windows can be compared using standard multivariate test statistics such as the Hotelling’s 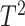test.

The main advantage of using multivariate distributions is that this approach allows specifying a non-zero dependence structure between the windows. Univariate methods have the drawback of ignoring the dependence structure of the methylation signals between windows. In MeRIP-Seq experiments, the sequences are typically 50 base pairs (bp) long and could potentially overlap multiple windows. Thus, incorporating the dependence structure in the testing procedure is of utmost importance to control error rates.

2 Approach

In traditional multivariate analysis, inference is based on the assumption that the number of samples is larger than the dimension. For a given window size, the number of windows can be as large as a few thousands. However, in most MeRIP-Seq experiments, the number of replicates is small, usually less than 10 per condition. Methods such as Hotelling’s 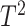test suffer from the curse of dimensionality and are not applicable when the number of windows is larger than the number of replicates. Dimension reduction methods such as principal component analysis (PCA) can be used to make the dimension smaller than the sample size. However, vast amounts of information could potentially be lost when reducing the dimension from thousands to as low as two or three.

To address the issue of small sample size in multivariate analysis, several test statistics have been proposed when the mean is the parameter of interest. High-dimensional mean vector tests (MVTs) construct the test statistic by avoiding operations (e.g. inversion of sample covariance matrix), which are affected by the curse of dimensionality. They have been shown as an alternative with good performance in comparison to univariate methods for capture-based DNA methylation studies [3]. Inspired by those results, we studied the performance of MVTs when applied to MeRIP-Seq data. We designed a simulation study emulating data from existing MeRIP-Seq experiments to study how the MVTs perform in comparison to univariate methods currently available. We then applied the four methods considered to two publicly available data sets (GSE 61995 [16]; GSE 87516 [21]) to study the functional importance of RNA methylation.

The rest of the article is organized as follows. In Section 3, we discuss the issues with existing MeRIP-seq analysis tools. Mathematical formulation of the data and hypothesis test and description of existing univariate methods are also provided in detail. The MVTs and their mathematical details are discussed in section 3.3. In section 4, simulation studies designed based on MeRIP-Seq data sets are presented. Results from our analysis of two data sets are presented in section 5. Implementation of our analysis tool dimer is discussed in section 7.

3 Methods

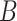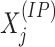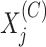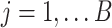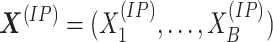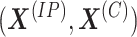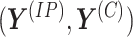Consider a gene that is covered by disjoint adjacent windows. Denote by and the number of reads mapped to the bin, for the IP and control samples, respectively. The vectors of signals, denoted by and , define the methylation signal of the gene. The windows give a measure of resolution and are generally shorter than the immunoprecipitated sequences. Let and denote the pair of methylation signal vectors for the two conditions, respectively. 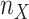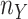Let and denote the sample sizes for the two groups, respectively. Our goal is to test if the gene is differentially methylated between two conditions, e.g. wild-type versus knockout. A regression-based approach for studying the association between the treatment condition and RNA methylation would be to fit a multivariate logistic regression model. Since the number of bins is larger than the sample size in most studies, a regularized model is more suitable. However, the performance of this approach based on either deviance-based likelihood ratio test (LRT) or existence of non-zero regression coefficients is not good due to the extremely low sample size (see Supplementary Material).

Generally, differential methylation is mathematically defined in one of two ways: difference in mean or difference in distribution. The MVTs use a non-parametric approach, i.e. no specific form of distribution for the model, to establish difference in the mean methylation signals. Univariate methods use parametric models and establish difference in distribution by showing difference in the parameters. While the former is the most preferred description of differential methylation, the latter is more complete.

3.1 MeTDiff

In MeTDiff [11], differential methylation is defined as the difference in distribution of signals for the two conditions. Proposed as a method for detecting differentially methylated peaks, MeTDiff can be generalized for a gene. In MeTDiff, the methylation counts of the windows in a gene are modeled using a beta-binomial model with a single pair of parameters,

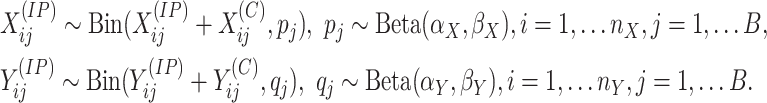(1)

A gene is defined as differentially methylated if the two distributions differ, i.e. 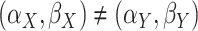. An LRT statistic is calculated and compared against the 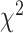-distribution with appropriate degrees of freedom. Note that the asymptotic properties of the LRT statistic are on the number of windows within the gene. Depending on the window size, the number of windows is generally large enough to have good approximation. This is the main advantage of MeTDiff, since the test can be applied even for studies with a single replicate.

The Beta-Binomial mixture is a logical choice to model this kind of data due to conjugacy of the distributions. But when the signals are sparse, the distribution of the probabilities 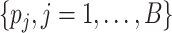tends to be multimodal. Sparsity of signals also induces a mode around zero, a feature that is not addressed by MeTDiff. Empirical distribution of the probability of methylation for some genes (see Supplementary Material) shows that a mixture of Beta distributions is a more appropriate model. The beta-binomial model also does not incorporate the dependence between adjacent windows as mentioned above.

3.2 DRME

Differential RNA methylation (DRME) [24] models the IP and input read counts using a negative binomial model. Differential methylation of the gene is parametrized determined by the mean of the distribution, which is parameterized to account for the total abundance of the gene and variable library size between samples. Estimation of the parameters and construction of the test statistic for this method are inspired by the DESeq [2] approach.

A major drawback of this method is representation of the entire methylation signal of a gene using a single count. The univariate measure of methylation allows for testing one-sided alternative. The parametrization accounts for technical variability. However, adding the methylation signals across all the windows ignores the biological variability within the gene. For nucleotide-level modifications such as methylation, using genewise measures is not accurate as it can potentially average out the difference over the entire region. For example, effects of regions with hyper- and hypo-methylation can be canceled out since they are combined through addition.

3.3 Mean vector tests

In window-based methylation signal estimation methods such as HEPeak [10] and exomePeak [27], the region of interest is divided into bins of equal size. When the resolution is set to be very small, the bin size is generally small enough for a single fragment to cover multiple bins. When a fragment overlaps multiple bins, the signal is shared equally among all the bins. While the dependence of true methylation status at the nucleotide level is unknown, this method of assigning signals imparts a strong dependence structure on neighboring bins.

Reads overlapping multiple windows imposes a strong dependence structure on the read counts across the gene. Univariate models fail to address this dependence, even with higher-level models such as MeTDiff. Multivariate models consider all the windows simultaneously and are parameterized to model both the mean signal and the dependence structure. Univariate approaches model the read counts within the windows using discrete distributions, such as Poisson or negative binomial. Multivariate distributions of discrete random variables are not very well characterized. Since both IP and control samples have to be modeled simultaneously, a canonical extension of the univariate methods is not feasible. This is because standard models such as additive Poisson model [25] allow only very restricted covariance structures. Multivariate generalizations of binomial distribution [1, 35] are not well studied for high dimensions.

To avoid modeling discrete multivariate discrete signals, the methylation read counts need to be transformed to a continuous measure. Using both IP and control samples simultaneously, define the relative read count

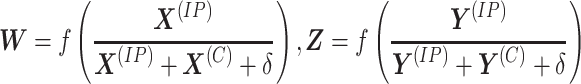(2)

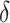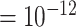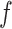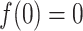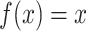as the measure of methylation signal for all the windows in a gene. An infinitesimally small quantity () is added to the denominator to handle the situation when both IP and control samples have zero read count. The function is a monotonically increasing function with . In our analysis, we used the identity function for simplicty. Alternatively, the inverse hyperbolic function, 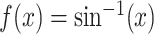, can be used.

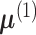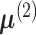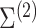Parametrizing the first two moments of the methylation signal vectors, let and be the mean vector and covariance matrix for the first condition. For samples from the second condition, denote these parameters by and , respectively,

Defining differential methylation through the mean vectors, the hypothesis can be formulated as

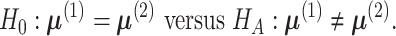(3)

Traditional Hotelling’s 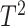-test cannot be used for testing the hypothesis because the data violate all the necessary conditions. The number of bins in a gene, 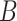, is generally large while the sample size for most studies, , is very small for most studies. This results resulting in what is called a large p small n situation. Also, the covariance matrices of the two groups are not necessarily equal and cannot be assumed to be otherwise.

With increasing interest in high-dimensional data analysis, several test statistics have been proposed for testing the hypothesis in (4). The key to constucting the test statistic is to find a function of the data, which estimates the difference between the means 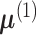and 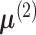, commonly through the Euclidean distance,

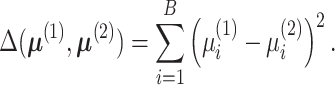(4)

A large value of observed 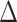will serve as an indication of difference in the mean methylation signals of the two groups. Among such testing procedures, three tests are known to outperform their predecessors in terms of performance: Chen–Qin test (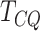) [5], Park–Ayyala test (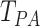) [30] and Srivastava–Katayama–Kano test (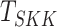) [34].

An attractive feature of this class of MVT statistics is that they are distribution free, hence the error of model misspecification can be avoided. They are applicable for a large set of population parameter values and are also applicable for unequal covariance matrices. These test statistics are established to be asymptotically normal, therefore critical values for the tests at a given significance level can be easily calculated. These methods have been applied previously in capture-based DNA methylation studies for detection of differential methylation [3]. It has been found that while the small sample sizes affect the type I error rates, the MVT is still conservative as compared to other methods. Among the three mean vector tests, 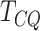is shown to have better performance over 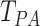and 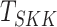. Under a wide range of models, was observed to control type I error at a specified significance level and attain reasonable power even for very sparse signals and small number of replicates. In this paper, 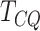is applied as a multivariate method for detection of differentially methylated genes in m6A RNA methylation studies.

From the MeRIP-Seq experiment, the IP and control read vectors for a given gene are recorded for all the replicates. Let 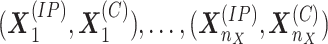denote the read count vectors of IP and control samples from the first condition. Similarly, denote the read count vectors observed under the second condition by 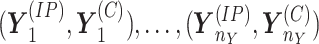. Using the relative measure defined in (3), obtain the vectors 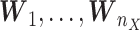for the first condition and 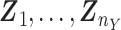under the second condition, respectively. The length of the vector is denoted by 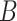, which is determined by the length of the gene and the window size chosen. The test statistic 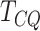is given by

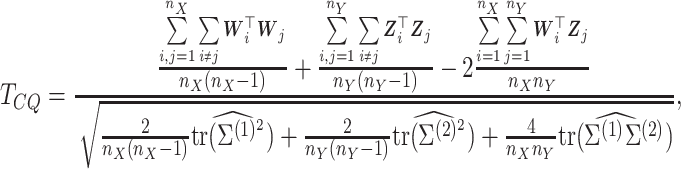(5)

where

$$\begin{array}{c}\widehat{\text{tr}({\mathrm{\Sigma }}^{(1{)}^2})}=\frac{1}{n_X(n_X-1)}\sum _{i\ne j}{\mathit{W}}_j^{\mathrm{\top }}({\mathit{W}}_i-{\overline{\mathit{W}}}_{(i,j)}){\mathit{W}}_i^{\mathrm{\top }}({\mathit{W}}_j-{\overline{\mathit{W}}}_{(i,j)}),\\ \widehat{\text{tr}({\mathrm{\Sigma }}^{(2{)}^2})}=\frac{1}{n_Y(n_Y-1)}\sum _{i\ne j}{\mathit{Z}}_j^{\mathrm{\top }}({\mathit{Z}}_i-{\overline{\mathit{Z}}}_{(i,j)}){\mathit{Z}}_i^{\mathrm{\top }}({\mathit{Z}}_j-{\overline{\mathit{Z}}}_{(i,j)}),\\ \widehat{\text{tr}({\mathrm{\Sigma }}^{(1)}{\mathrm{\Sigma }}^{(2)})}=\frac{1}{n_X{n}_Y}\sum _{i,j}{\mathit{W}}_i^{\mathrm{\top }}({\mathit{Z}}_j-{\overline{\mathit{Z}}}_{(j)}){\mathit{Z}}_j^{\mathrm{\top }}({\mathit{W}}_i-{\overline{\mathit{W}}}_{(i)}),\end{array}$$

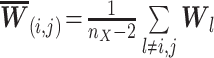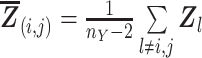and , and 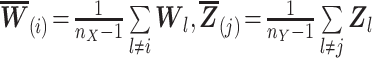. The test statistic is asymptotically normal and the 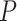-value is given by 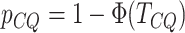, where 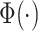is the normal cumulative distribution function. To adjust for multiple testing when analyzing all the genes, we use false discovery rate (FDR) to control the type I error.

Note that although the alternative in (4) is two-sided, the rejection region is right-sided. This is because the function 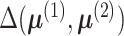is non-negative and the null hypothesis is rejected for large positive values of 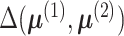. The hypothesis in (4) can be equivalently written as 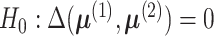versus .

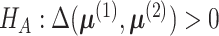4 Simulation study

To compare the performance of 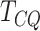, MeTDiff, DRME and Fisher’s exact test, we performed a comprehensive simulation study. We generated the data sets using parameters estimated from real data sets. The read counts for IP and control samples for the two conditions were randomly generated using a mixture beta-binomial model. Read count vectors were generated for 10 000 regions, with the lengths randomly selected from the mouse genome. Each region is divided into equally sized bins of size 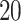and 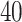. For regions that are not differentially methylated, the count vectors are generated using a mixture beta-binomial model,

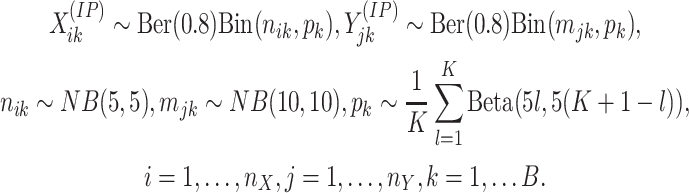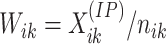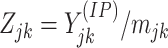Relative counts of IP samples can be obtained as and , respectively.

The Bernoulli component is added to induce sparsity into the model. These components for a given window can be different for all the samples, modeling the irregularity in observed reads. It reflects the absence of uniform methylation across all samples either due to non-methylation or lack of sequencing depth. The beta mixture model is proposed based on the multi-modal distribution of IP read proportions observed in real data (GSE 61995; see Supplementary Material). For the differentially methylated regions, the counts are generated similarly except for the proportions,

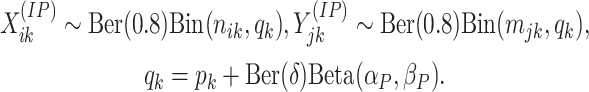The proportion of windows differing between the two groups can be controlled by 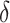. The beta distribution parameters 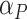and 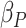also control the difference between the two groups. The number of mixture components 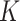determines multimodality of the distribution of proportions. We varied 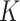between 1 and 3 to study robustness of the tests to distribution misspecification. For each value of 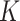, we studied four models (Models I–IV) varying the values of 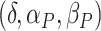. 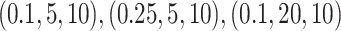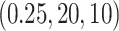The values of parameters used are and , respectively. Sample sizes for the two groups were set to four, .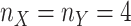

The methods were compared using three measures: area under the curve (AUC) of the receiver operating curve (ROC) constructed using the 20000 tests; the type I error rate based on the 10000 non-differentially methylated regions and the power based on the 10000 differentially methylated regions. Average AUC is reported by replicating each simulation setting 100 times.

4.1 Results

Figure 1 shows the ROC curves for the four models when 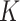equals 3. Results for 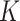equal to 1 and 2 are presented in Supplementary Material (Figures S1 and S2). The ROC curves were plotted using average sensitivity and specificity based on 100 replicates. The average AUC calculated from 100 replicates is also presented in the plots, which shows an increasing trend for 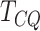with increasing distance between null and alternative. The AUC increases with both proportion of differently methylated windows (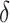) and parameters of the negative binomial (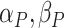). Both DRME and Fisher’s exact test show very similar results, they are only slightly better than random guess for all four settings. Under all the four models, MeTDiff is seen to have the least AUC and is at most as good as a random guess. This lack of performance of MeTDiff can be attributed to deviations in the distributional assumptions (distribution modality, dependence) of the method.

Figure 1.

ROC Curves of the four simulation models, Models I–IV, for mixture of 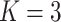components. The numbers in the legend correspond to the average AUC (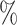) of the plot calculated over 100 random simulations.

For the four methods, type I error and power are calculated at the nominal significance level of 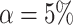to compare their performance. The results are presented in Table 1. For the type I error, which is equal to 1 - specificity, values close to 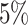indicate good performance. For the power, which is the sensitivity of the test, higher values indicate that the test is able to correctly identify true positives. Under all scenarios, 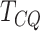controls type I error and achieves good power, which increases with increasing difference between the groups. The univariate methods, MeTDiff, DRME and Fisher, all have inflated false positive rates and low power.

Table 1.

Type I error and power for the Models I–IV defined in the simulation study setup for 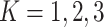. The values presented are based on a nominal significance level of and averaged over 100 replicates

		Type I error				Power
	Model	MeTDiff	CQ	DRME	Fisher	MeTDiff	CQ	DRME	Fisher
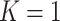
	I	0.465	0.044	0.137	0.242	0.471	0.161	0.169	0.278
	II	0.466	0.043	0.137	0.243	0.472	0.446	0.207	0.312
	III	0.465	0.044	0.136	0.243	0.471	0.485	0.207	0.317
	IV	0.466	0.044	0.137	0.247	0.474	0.849	0.280	0.380
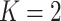
	I	0.466	0.044	0.135	0.237	0.471	0.172	0.168	0.272
	II	0.466	0.043	0.135	0.237	0.473	0.469	0.208	0.308
	III	0.467	0.044	0.135	0.236	0.472	0.496	0.207	0.312
	IV	0.466	0.044	0.134	0.236	0.475	0.853	0.282	0.379
	I	0.467	0.045	0.130	0.222	0.471	0.199	0.169	0.264
	II	0.467	0.045	0.131	0.224	0.473	0.524	0.212	0.303
	III	0.466	0.045	0.131	0.224	0.472	0.514	0.207	0.303
	IV	0.467	0.045	0.131	0.223	0.476	0.861	0.283	0.372

The results presented in Figure 1 and Table 1 are based on the identity function for 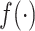in (3). To study how monotone transformation of the signals will affect 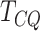, we repeated the simulation with signals transformed as 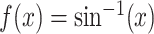. The results are presented in Supplementary Material (Table S1). Under all models, the type I error has increased slightly, but is still controlled at 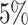significance level. The MVT shows a significant increase power for the arcsine-transformed data under all the settings.

5 Data analysis

In previously published m6A methylation studies, analysis of the data has commonly focused on detecting regions with enhanced methylation signal (peaks) and understanding their importance. In our analysis, we have focused on doing a gene-level analysis. At the gene level, one can further investigate the detected genes for their functional importance and explore significant canonical pathways. To the best of our knowledge, there are no results reported for comparison of RNA methylation at the gene level.

We applied the four methods to two data sets to detect differentially methylated genes and investigate their biological relevance in the context of the respective experimental setup. For each data set, we aligned the sequences to the appropriate reference transcriptome to obtain gene-wise read counts. To study robustness of the methods to window size, we used window sizes of 10, 20, 30, 40 and 50 for assigning read counts. For each window size, the 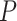-values calculated for the genes were adjusted for multiple testing correction using FDR. 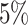Genes expressing differentially methylated transcripts were reported using the nominal significance level as cut-off. Downstream analysis of selected genes was performed using Ingenuity Pathway Analysis (IPA) (QIAGEN Inc.) [20].

5.1 Study I

The first data set we analyzed was collected by Geula et al. [16]. In this study, the effects of methyltransferase knockout in cellular development of mice were studied. Particularly, the role of m6A in pluripotency transitions by comparing METTL3 methyltransferase knock-out samples against wild-type in mouse embryonic stem cells (mESCs) was investigated. The data set consists of three replicates (IP+control) from wild-type mESC and three replicates from knock-out mESC samples. Raw sequence files for the samples were acquired from NCBI (accession number GSE 61995). Using the Ensembl reference transcriptome (GRCm67) for alignment, We reported the read counts for a total of 37 991 genes. After preliminary processing of the data and filtering of genes (see Supplementary Materials), the four test statistics were applied to the remaining genes. The number of differentially expressed genes after FDR correction for the five window sizes is reported in Table 2. As seen from the table, 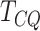is the most conservative among the four methods, followed by DRME. Fisher’s exact test and MeTDiff are extremely liberal, detecting almost half of the genes in the analysis as differentially methylated.

Table 2.

Number of differentially methylated genes detected by the four methods when using five different windows sizes for Study I

Bin size		MeTDiff	DRME	Fisher
10	1739	22 445	4067	22 356
20	1796	22 487	3637	19 342
30	1890	22 235	3336	17 169
40	1899	22 313	3106	15 866
50	1952	22 336	2912	14 815

To measure robustness of the set of genes detected across the five window sizes, we calculated the overlap of genes at different window size. A method is deemed robust if the overlap across all five window sizes is relatively higher compared to the remaining overlaps. This can be calculated by comparing the number in the middle to the maximum of the remaining numbers in the Venn diagram. Figure 2 shows the common number of genes detected when using different window sizes for the four methods. To compare robustness of the methods across window sizes, proportion of commonly detected genes adjusted for the total number of genes detected was calculated. This measure is an adjusted Jaccard index (see Supplementary Material). It can be seen from the figure that 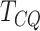(adj. 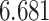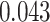Jaccard index of ) and DRME () detect a very high proportion of genes common to all window sizes as compared to MeTDiff () and Fisher’s exact test ().

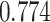Figure 2.

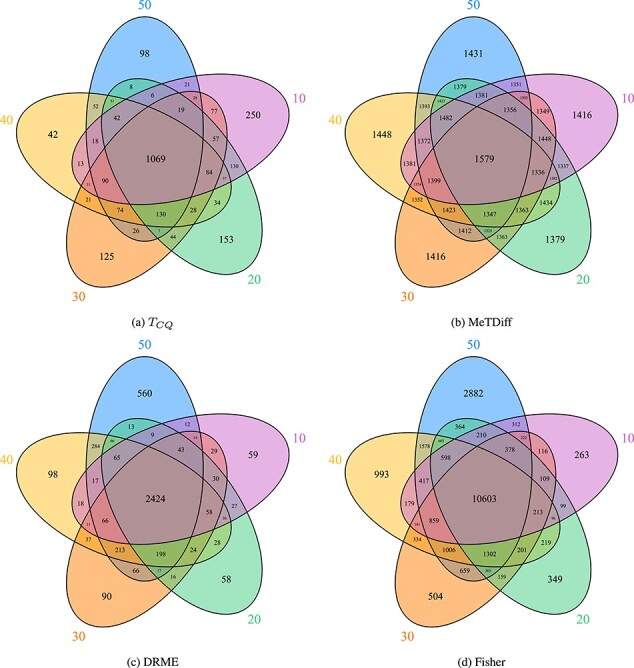
Venn diagrams showing the common sets of genes detected to be differentially methylated for Study I when using different bin sizes for assigning methylation signals. The circles correspond to different bin sizes from 10 to 50 base-pairs.

IPA analysis To better understand the role of the genes detected by the four methods in the growth of mESCs, we studied their molecular and cellular functions. For each method, the top five cellular functions detected using IPA are presented in Table 3 in the decreasing order of -values. The output from IPA analysis is presented in Supplementary Material. To accommodate the large number of genes detected by MeTDiff and Fisher’s exact test in IPA, the top 1000 genes (based on smallest -value) were selected for analysis. For 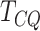and DRME, all the genes selected by the testing procedure were used in the analysis. Genes detected using 50 bp window-size were used for this analysis.

Table 3.

Top five molecular and cellular functions detected as significant using IPA for Study I. The functions are presented in the decreasing order of signficance (determined by the 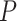-value). The results are based on the top 1000 genes for DRME and MeTDiff and all the genes are used for 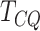and DRME

Method	Molecular and cellular functions detected as significant
	Cellular development; cellular growth and proliferation; cellular function and maintenance; cellular movement; cell cycle
MeTDiff	Cell death and survival; cellular movement; cellular development; cellular growth and proliferation; cell morphology
DRME	Cell morphology; amino acid metabolism; lipid metabolism; molecular transport; small molecule biochemistry
Fisher’s test	Cell cycle; cellular development; cellular growth and proliferation; cell morphology; gene expression

A majority of the functions detected by DRME are not related to cellular development. All five functions highlighted by 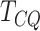and MeTDiff are related to cell growth. A majority of the functions (four out of five) detected by Fisher’s exact test are also associated with cellular development. This indicates that the genes identified by 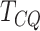, MeTDiff and Fisher’s test to have strongest evidence of differential methylation (in terms of the smallest 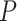-value) have very high functional relevance. Table 4 shows that MeTDiff and Fisher’s test detect a very large number of genes. As evident from the inflated type I error rates of these two methods from the simulation study, there is a high chance that most of these genes detected could be false positives. The high specificity of 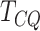is a strong indication that there is a relatively smaller chance of the genes detected by 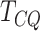to be false positives.

Table 4.

Number of differentially methylated genes detected by the four methods for data in Study II. The five rows correspond to the window sizes used to assign read counts to genes

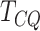
Window size		MeTDiff	DRME	Fisher
10	460	17 320	1749	12 370
20	451	17 283	1248	8023
30	455	17 203	1046	5946
40	452	16 937	983	4783
50	470	16 827	974	3870

5.2 Study II

The second data set we analyzed was from the study by Lichinchi et al. (NCBI accession number GSE 87516) [21]. In this study, the authors focused on exploring m6A methylation in human cells, comparing the methylation topologies between normal human (HEK293T) cells and those infected with Zika (MR766) virus. The data set consists of three replicates each (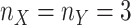) from normal and Zika-infected samples, respectively. Aligning the sequences to GRCh38 reference transcriptome, methylation signals are calculated for 58 233 genes. After preliminary screening and testing as described in Supplementary Materials, we studied genes exhibiting differential methylation and the subsequent pathways detected. The number of genes detected by the four methods are presented in Table 4.

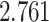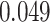Venn diagrams presented in Figure 3 show how consistent the results are across different window sizes. The adjusted Jaccard index for the four methods are —, MeTDiff—, DRME— 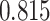and Fisher’s exact test—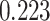. This is an indication that selects a small number of genes robustly across all window sizes. However, it can be observed that the Venn diagrams do not show consistency (percentage of overlap) in the genes selected by the five window sizes. Greater consistency has been achieved when window size 10 is removed from this list (see Supplementary Materials). This suggests that the data are very noisy when window size of 10 bp is considered.

Figure 3.

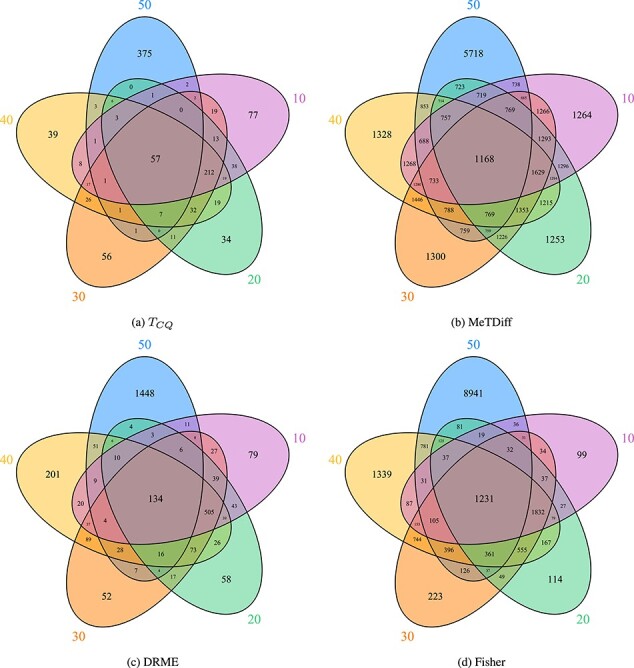
Venn diagrams showing the common sets of genes detected to be differentially methylated for Study II when using different window sizes for assigning methylation signals. The circles correspond to different window sizes from 10 to 50 base pairs.

To understand the functional relevance of genes detected, the diseases and functions associated with these genes were studied using IPA analysis (Table 4). Heatmaps of the IPA results are presented in Supplementary Material. Zika virus infection in humans is known to be positively associated with microcephaly [29], which can lead to developmental and neurological disorders. The results indicate that the genes detected by show strong evidence of association with neurological and developmental disorders. The other three methods detect diseases such as cancer, which are not known to be associated with Zika virus infection.

6 Conclusions and discussions

In this paper, we proposed using MVT procedures as a multivariate alternative for testing gene-wise or region-wise differential methylation of RNA. In comparison to existing methods that use univariate distributions, the MVT approach uses signals from all the windows simultaneously. As observed from the simulation studies, the MVT is better at controlling type I error and also achieves higher power than the other procedures being compared. The MVT has a higher area under the curve in the ROC curves, indicating better detection of methylated genes the method has high specificity and low false positive rate.

Read counts from the immunoprecipitation data are converted to methylation signals using the ratio of IP read count to the total read count (IP + Control). Using the raw methylation signal and an arcsine transformation have shown to control type I error rate of MVTs well. Both methods have high sensitivity, with the arcinse transformation having higher power compared to the raw signal. Some functions that can be considered instead of the arcsine are 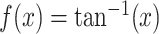or . 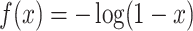While any monotone increasing transformation would increase the power, it is important to evaluate its efficiency at controlling type I error.

We analyzed two data sets using MVT and compared the results to three existing univariate methods. Pathway analysis of genes detected by MVT are observed to be of high functional relevance to the experimental conditions, while keeping the number of genes detected small. All four testing procedures have shown consistency of results across window sizes ranging from 10 to 50. However, read counts for smaller window sizes are noisy. As seen in Study II, smaller window sizes could reduce consistency of the results. For optimal trade-off between window size and accuracy, we recommend using a 20–50 bp window size.

The MVT is applicable only when there are at least three biological replicates. However, many studies report only one or two replicates. Univariate methods such as MeTDiff are capable of handling data sets with single replicate, as the windows are treated as replicates. But the accuracy of such methods for single replicate data sets has not been extensively validated. Lack of replicates can result in erroneous results, due to biological and technical variability across samples. There is a need to develop and assess tools for analyzing data sets with smaller number of replicates using multivariate techniques.

7 Software availability

For calculating window based read-counts and testing differential methylation, we developed dimer. dimer, standing for differential methylation of RNA, is a Python-based package. The package uses other bioinformatics tools such as bedtools [32] and pybedtools [12] for faster calculations. Using aligned sequence files in BAM format as input, dimer provides the test statistic and 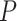-value for each gene in the provided annotation file. Additionally, the package also creates bedgraph files for visualization using a genome browser. dimer gains an advantage in run-time (see Supplementary Materials) compared to MeTDiff. The package is available from the GitHub website: https://github.com/ouyang-lab/DIMER.

Key Points

1. High-dimensional multivariate tests are more accurate for detection of differentially methylated genes in RNA methylation studies.

2. The features detected by 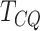have high specificity and very high functional relevance as compared to the other univariate test procedures.

3. The test procedure is robust for window sizes 20–50 bp. Caution needs to be applied when using 10 bp window as the results are prone to error.

Deepak Nag Ayyala is an assistant professor of biostatistics and data science at the Medical College of Georgia, Augusta University. His research interests are primarily in high dimensional statistical inference, with applications in epigenomics and transcriptomics.

Jianan Lin is an assistant computational scientist at The Jackson Laboratory for Genomic Medicine. His research interests include analyzing the next generation sequencing data and developing computational methods to solve biological problems.

Zhengqing Ouyang is an associate professor of biostatistics at the University of Massachusetts, Amherst. His research interests are mainly in the development of statistical and computational methods for elucidating the structures and regulations of genomes and RNAs.

Funding

National Institutes of Health/National Institute of General Medical Sciences (R35 GM124998 to Z.O.).