Abstract
The best crystal identification (CI) algorithms proposed so far for phoswich detectors are based on adaptive filtering and pulse shape discrimination (PSD). However, these techniques require free running analog to digital converters, which is no longer possible with the ever increasing pixelization of new detectors. We propose to explore the dual-threshold time-over-threshold (ToT) technique, used to measure events energy and time of occurence, as a more robust solution for crystal identification with broad energy windows in phoswich detectors. In this study, phoswich assemblies made of various combinations of LGSO and LYSO scintillators with decay times in the range 30 to 65 ns were investigated for the LabPET II detection front-end. The electronic readout is based on a 4 × 8 APD array where pixels are individually coupled to charge sensitive preamplifiers followed by first order CR-RC shapers with 75 ns peaking time. Crystal identification data were sorted out based on the measurements of likeliness between acquired signals and a time domain model of the analog front-end. Results demonstrate that crystal identification can be successfully performed using a dual-threshold ToT scheme with a discrimination accuracy of 99.1% for LGSO (30 ns)/LGSO (45 ns), 98.1% for LGSO (65 ns)/LYSO (40 ns) and 92.1% for LYSO (32 ns)/LYSO (47 ns), for an energy window of [350–650] keV. Moreover, the method shows a discrimination accuracy >97% for the two first pairs and ~90% for the last one when using a wide energy window of [250–650] keV.
Index Terms—: Crystal identification, depth of interaction, phoswich, time-over-threshold, radial spatial resolution, positron emission tomography, front-end electronics, signal processing, LGSO, LYSO
I. Introduction
Positron Emission Tomography (PET) scanners with a cylindrical geometry present a common artifact known as parallax [1] when the source of radiation is away from the center of the scanner. Depth of interaction (DOI) measurement in the detector has demonstrated the ability to mitigate this problem [2] and has been already used in some preclinical and clinical scanners to improve radial spatial resolution [3]–[12]. DOI techniques can be divided into three classes: discrete, continuous and segmented (Fig. 1).
Fig. 1:

Common depth-of-interaction techniques: a) discrete, b) continuous, c) segmented. (figure edited from [13], open source)
The discrete design consists in stacking two or more detector layers having their own read-out electronics [14]–[16], while the continuous detectors measure the light ratio or spreading among two or more independent readouts located on opposite side of the crystal [17]–[21]. Unlike the discrete and continuous methods, the segmented approach uses subdivided crystals stacked together according to various schemes and a reduced number of front-end readouts, which is more affordable way to realize crystal identification (CI). The light sharing [22]–[29] and phoswich are the most common segmented methods, where the latter consists in stacking two or more crystals with different scintillating properties on the same photodetector [5], [30]–[34]. This method generally requires digital signal processing techniques to identify the crystal where the annihilation photon was absorbed. Various CI approaches have been proposed, which can be classified as pulse shape discrimination (PSD) in the time domain [35]–[37], PSD in the frequency domain [38] and adaptive filtering [39], [40]. So far, the latter achieved the best performance with > 98% accuracy even with crystals having similar properties [39]–[42]. However, this technique requires sampling the signal at the output of a shaping filter and applying real-time signal processing, an approach no longer possible in highly pixelated systems such as in the LabPET II detection modules, for both space and power consumption considerations. The multi-threshold sampling [43], [44] and the time-over-threshold (ToT) [45], [46] techniques were introduced some time ago to overcome these limitations. The latter was more recently implemented in the LabPET II 64-channel front-end ASIC to measure the energy and time of the interaction at a low power budget (~9.4 mW per channel) and reduced silicon real estate [47]. This method with a single discrimination threshold was previously used by Chang et al. [48] to discriminate between 3 × 3 × 10 mm3 LSO and LYSO with decay times of 33 ns and 42 ns, respectively, on SiPM. The method showed an excellent discrimination accuracy of 97.2% [48]. However, it was tested only for photopeak events, which can be a limiting factor for the sensitivity of PET systems. In this study, we explore a CI method based on a dual-threshold ToT technique in an avalanche photodiode-based (APD) detection module using broad energy windows [49]. This dual-threshold ToT technique was selected to optimise the timing measurement on both the rising and falling edges since APD signals over a broad range of signal amplitude are noisier compared to SiPM signals. The detection module, the different phoswich samples used, the LabPET II data acquisition system (DAQ) and its signal processing model will be first detailed. Then, the CI method will be described and the different parameters affecting its performance will be investigated. Finally, the results will be presented and discussed in the context of implementation in an application specific integrated circuit (ASIC) for the Scanner Approaching in Vivo Autoradiographic Neuro Tomography (SAVANT) [50].
II. MATERIALS
A. Detection module and scintillators
The LabPET II APD-based detector module [51] was used to assess the crystal identification performance with three phoswich pairs consisting of 30 and 45 ns LGSO (LGSO30ns/LGSO45ns), 65 ns LGSO and 40 ns LYSO (LGSO65ns/LYSO40ns), and 32 and 47 ns LYSO (LYSO32ns/LYSO47ns) of various size and form factor. The characteristics of the three phoswich assemblies investigated in this work are detailed below and summarized in Table 1. The photodetector module consists of two monolithic 4 × 8 APD arrays with 1.1 × 1.1 mm2 active area pixels at a 1.2 mm pitch (Fig. 2a). The two APD arrays are bump bonded onto a custom built ceramic holder. This APD module was designed for one-to-one coupling between the APD and scintillator pixels. In this study, only one APD pixel was tested as shown by Fig. 2a.
TABLE 1:
Characteristics of phoswich pairs in the experiment.
| Phoswich Pair (Bottom/Top) | Crystal | Decay time (ns) | Light output (APD readout, % LYSOref)* | Crystal volume (mm3) | Manufacturer (year) |
|---|---|---|---|---|---|
| LGSO30ns/LGSO45ns | LGSO:Ce (90% Lu) | 30 | 73 | 1.2 × 1.2 × 6 | Hitachi (2015) |
| LGSO:Ce (90% Lu) | 45 | 107 | 1.2 × 1.2 × 6 | ||
| LGSO65ns/LYSO40ns | LGSO:Ce (40% Lu) | [65–75] | 70 | 2 × 2 × 12 | Hitachi (2007) |
| LYSO:Ce (95% Lu) | 40 | 98 | 2 × 2 × 14 | CPI (2007) | |
| LYSO32ns/LYSO47ns | LYSO:Ce (95% Lu) | 32 | 79 | 3 × 3 × 3 | Sichuan Tianle |
| LYSO:Ce (95% Lu) | 47 | 100 | 3 × 3 × 3 | Photonics Co. (2019) | |
| LYSO reference | LYSO:Ce (95% Lu) | 40 | 100 | 1.2 × 1.2 × 10.6 | Proteus (2016) |
Light output was measured on individual crystals before phoswich assembly and reported relative to that of LYSO with a decay time of 40 ns (internal reference).
Fig. 2:

Detectors modules: a) APD array, b) LGSO30ns/LGSO45ns, c) LGSO65ns/LYSO40ns, and d) LYSO32ns/LYSO47ns phoswiches.
1). LGSO30ns/LGSO45ns:
The first experiment used a 12 mm long 8 × 8 phoswich scintillator block made of two 6 mm long LGSO30ns and LGSO45ns crystal arrays. Each scintillator pixel measures 1.12 × 1.12 × 6 mm3. The pixels were saw cut, mechanically polished and bonded to 3M ESR reflector with an optical adhesive of refractive index of 1.5 (Dymax OP-20). The LGSO30ns and LGSO45ns arrays were glued together using Dymax Op-20 and were coupled to the APD array using optical epoxy of refractive index of 1.53 (EPO-TEK 301–2) (Fig. 2b). In this first study, the LGSO30ns was placed in contact with the APD to avoid unnecessary light loss since it had the lowest light yield of the two crystals as described in Table 1. The module was irradiated by a 68Ge (511 keV) rod source placed at a fixed distance above the crystals.
2). LGSO65ns/LYSO40ns:
The second experiment used a phoswich assembly of 2 × 2 mm2 crystals of 12 mm for LGSO65ns and 14 mm for LYS040ns, respectively (Fig. 2c). The two pixels were wrapped together with 5 layers of Teflon tape and deposited on the APD module (Fig. 2c) using optical grease (Bicron BC-630). For this phoswich, the LGSO65ns was in contact with the APD array. Given the total phoswich length of 26 mm, side irradiation with a 68Ge source was applied to obtain a similar number of interactions in both crystals.
3). LYSO32ns/LYSO47ns:
The third experiment used 3 × 3 × 3 mm3 cubic crystals of LYSO32ns and LYSO47ns (Fig. 2d). These detectors were coated with a 200 μm thickness barium sulfate (BaSO4) and wrapped together with 5 layers of Teflon tape to avoid misalignment and light loss. The phoswich was deposited on the APD module using optical grease (Bicron BC-630) and irradiated from above using a 68Ge source.
B. Measurement setup
A test PCB was designed to support both the LabPET II APD detection module and its front-end electronics along with an analog buffer stage to enable oscilloscope probing (Fig. 3). A Lecroy 6100 Series oscilloscope with a vertical resolution of 11 bits, a sensitivity of 200 mV/div, a bandwidth of 1 GHz and a sampling rate of 5 GS/s was used for data acquisition. The LabPET II front-end electronics is based on a 64-channel ASIC designed in TSMC 0.18 μm CMOS. The ASIC measures 5.9 × 4.6 mm2 and contains two 32-channel analog blocks and one digital block operating at 100 MHz [47].
Fig. 3:

Test setup showing a phoswich detector mounted on a front-end circuit board.
Each analog channel (Fig. 4) includes a charge sensitive preamplifier (CSP) with a pole-zero cancellation circuit and a 0.93 mV/fC to 88.9 mV/fC adjustable gain, followed by a first order CR-RC shaper with a peaking time of 75 ns and a baseline holder. The shaper output feeds two comparators used to discriminate the signal amplitude and generate the rising and falling edge timestamps required to compute both the timing and energy information based on a dual-threshold ToT scheme [47]. The two thresholds were meticulously chosen to optimize timing performance (Threshold 1) and energy resolution (Threshold 2) by reducing the time jitter on each measurement (Fig. 5). The digital block harvests the time (t1) and energy information (Δt = t3 − t1) with a time to digital converter (TDC) and transfers the data to an external FPGA through a LVDS port clocked at 100 MHz [47].
Fig. 4:

ASIC’s analog channel adapted from [47].
Fig. 5:

Dual time-over-threshold principle (adapted from [52]).
In the current LabPET II ASIC, each event triggers 4 timestamps (t1, t2, t3, and t4), but only t1 and t3 are routed to the output, which is not sufficient for this study. Therefore, digital acquisition with an oscilloscope was performed using the analog output of the ASIC’s test channel to assess the minimum number of thresholds needed to perform crystal identification. Consequently, only one APD pixel of the array was read out in this study (Fig. 2a).
C. Channel model
The channel model is divided into two parts: the detection module and the electronic readout channel (Fig. 6). The detection module consists of a Cerium-activated inorganic scintillator optically coupled to an avalanche photodiode modeled as:
| (1) |
where I0 is proportional to the deposited energy and depends on the crystal light yield and the APD gain. And, τdecay is the crystal decay time. Each block of the electronic readout channel was modeled by its transfer function Hk(s) in the Laplace domain. Eq. 2 and eq. 3 are examples of transfer functions of the CSP (resulting from the pole at its input) and the shaper, respectively. Then Hchannel was determined by the product of all individual transfer functions (eq. 4) [53]. Finally, the impulse response h(t) is calculated as the Laplace inverse of Hchannel.
| (2) |
| (3) |
| (4) |
| (5) |
where τCSP and τShaper are the time constant of the CSP and the CR-RC shaper respectively, Gain is the channel’s electronic gain including the gain of the PZ and the shaper.
Fig. 6:

Channel model.
Hence, the signal y(t) (in Volt) is the convolution of current induced in the APD by the scintillation signal i(t) and the impulse response of the electronic channel h(t).
| (6) |
The signal at the different stages of the channel (scintillator, charge sensitive preamplifier and shaper output) is displayed in Fig. 7. The rise and decay of the signal at the CSP output is determined by the scintillator decay time and CSP decay constant, respectively. The rise and decay of the signal at the output of the shaper, in turn, is determined respectively by the decay and rise time of the CSP signal, and by the shaper time constant.
Fig. 7:

Signal from the scintillator and at the output of the charge sensitive preamplifier and shaper.
III. Methods
In this section, the channel model validation is first presented and the crystal identification method is introduced. The effects of time offset and energy windows on the CI performance is then described. Finally, the effect of varying the number of thresholds (accordingly the number of samples) and its impact on the CI compared to 5 GHz sampled signals is studied. Recommendations for an implementation in an ASIC then follows.
A. Channel model validation
Knowing all a priori parameters of the electronic channel extracted from the computer-aided Cadence design software and scintillators parameters (decay time and light yield), one model per scintillator was produced in Matlab. The model was then validated with an acquisition of 30,000 events from single crystals of each phoswich pair using a 68Ge source by measuring the fit error R2 between the acquired signals and the model.
B. Crystal identification
The crystal identification method is based on the estimation of the R-square error between the acquired samples yi of the signal and its predicted samples computed from the theoretical model of the electronic channel including the scintillator, the APD and the shaper along with all auxiliary electronics dedicated to the experimental test (PCB and scope). R2 is defined as:
| (7) |
where,
| (8) |
Thus, the likeliness between the acquired event data set and the simulated data generated from just one crystal of the phoswich pair and the DAQ is compared.
For this experiment, 50,000 events from each phoswish pair were acquired with the scope using the 68Ge rod source and processed using Matlab to extract the amplitude and to compute the equivalent time of occurrence t1. The scope trigger was set to have a low energy threshold around 200 keV for the crystal having the lowest light output to allow data to be reused for further experiments. For each data set, the R2 spectra were obtained by measuring the fit error between the acquired signal and both the fast and slow model of the crystal-DAQ pair in Matlab. Discrimination accuracy was calculated using eq. 9:
| (9) |
where N is the total number of events and M is the number of events in the overlapped region of the two gaussian distributions. The model giving the best identification accuracy for an energy window of [250–650] keV was selected for each pair. Once the discrimination was performed, the energy spectra after identification were extracted based on the maximum amplitude of the digitized signals for each crystal of the phoswich pair. Finally, the method was verified by applying the algorithm on the data sets acquired separately from the crystals forming the 3rd pair (LYSO32ns/LYSO47ns).
C. Effect of time offset correction
As described in the Materials section, time information is determined by the the first threshold crossing time t1. However, this information is slightly offset from the effective time of occurrence of the event due to the time walk in the leading edge discriminator and must be compensated. Moreover, this value is affected also by propagation delay induced by comparators due to energy variation. Thus, to improve the CI performance, t1 must be corrected for each event by determining the occurrence time t0.
In this experiment, the same set of 50,000 events from each phoswich of the previous experiment was used. All events were normalized according to their maximum amplitude and the energy window was set to [350–650] keV. The t1 correction was based on a linear interpolation of the two thresholds signal crossing times t1 and t2 (Fig. 8). The first threshold was set slightly above the DC noise, while the second one was swept over the entire dynamic range of the normalized signal from 0.1 to 0.5 with a step of 0.05 and from 0.5 to 0.9 with a step of 0.1. t0 was computed using eq. 10,
| (10) |
where Y1 and Y2 are the amplitude of threshold 1 and threshold 2, respectively. R2 was recalculated and the discrimination error was evaluated for each threshold. Then, Threshold 2 was set to the best discrimination accuracy. Finally, an equivalent discrimination error was computed for each phoswich without time offset correction.
Fig. 8:

Method for t0 determination by linear interpolation.
D. Effect of energy windows on crystal identification
For this experiment, the same acquisition of 50,000 events was used and t0 was computed according to the last experiement. Different energy windows were applied using Matlab to explore the sensitivity of the method related to the energy measurement. Since only one energy threshold can be applied on a phoswich arrangement, the lower energy threshold was set in reference of the crystal having the lowest light output (LGSO30ns for the first phoswich, LGSO65ns for the second one and LYSO32ns for the last one). It was varied from 250 keV to 500 keV with a step of 25 keV. However, the higher energy threshold was fixed to 650 keV based on the crystal having the highest light output. For each energy window, crystal identification was performed and discrimination accuracy was evaluated. Then, discrimination accuracy as a function of the low cut energy for each phoswich pair was plotted.
E. Effect of number of thresholds
As the current LabPET II electronics depends on a dual ToT scheme, only 4 timestamps (t1, t2, t3 and t4) are available. This last experiment is aimed at evaluating the minimum number of timestamps required for a good CI and, thus, to provide design guidelines for the LabPET II ASIC upgrade. As a ToT scheme is selected, the experiment boils down to determining the number of thresholds and timing accuracy required for an implementation in the ASIC. Here, one must notice that the measurement yi of the acquired signal and its predicted value are no more the normalized amplitude values but the timestamps determined when the signal crosses the thresholds. All events were normalized to an amplitude of 1. Matlab was used to set iteratively 2 to 4 thresholds (T1 to T4) at different levels and extract the corresponding timestamps on which CI methods were applied. The CI performance was computed for the different energy windows as described in Section III-D. For the 2 thresholds measurement, T1 was set slightly above the noise floor, while T2 was swept from 0.1 V to 1 V with steps of 50 mV to find the best discrimination accuracy for each phoswich pair. For the 3 thresholds measurement, T1 and T2 were set based on the measurement made with the 2 thresholds experiment and T3 was swept from T2 level to 1 V with steps of 50 mV and the discrimination accuracy was evaluated. The same methodology was used for the last measurement where T4 was swept from the level of T3 up to 1 V with steps of 50 mV. For each phoswich pair, the discrimination accuracy was plotted as a function of the energy windows based on the entire original signal, 2 thresholds, 3 thresholds and 4 thresholds. The low energy threshold was varied from 250 keV to 500 keV with a step of 25 keV.
IV. Results
A. Channel model validation
Figs. 9 to 11 display acquired events (black) from single crystals of each phoswich and the associated models based on slow-decay-time crystal (blue) and fast-decay-time crystal (red) for the single crystals of the LGSO30ns/LGSO45ns, LGSO65ns/LYSO40ns and LYSO32ns/LYSO47ns phoswich pairs, respectively. When the acquired event follows the selected model, R2 values are close to 1, meaning a good prediction. For example, R2 was about ~ 0.9 when the model of the other crystal was used for LGSO30ns/LGSO45ns, ~0.8 for LYSO32ns/LYSO47ns and ~ 0.6 for LGSO65ns/LYSO40ns. As the difference of decay time between crystals of the phoswich pair increases, the value of R2 decreases when the model of the other crystal is used and, consequently the discrimination accuracy should increase.
Fig. 9:

Acquired signals compared to the models for single crystals of the LGSO30ns/LGSO45ns phoswich pair.
Fig. 11:

Acquired signals compared to the models for single crystals of the LYSO32ns/LYSO47ns phoswich pair.
B. Crystal identification
Table II presents discrimination accuracies for each phoswich pair using the fast and slow models for an energy window of [250–650] keV. The difference between models does not exceed ~2% for LGSO30ns/LGS45ns, ~1.5% for LGSO65ns/LYSO40ns and ~6% for LYSO32ns/LYSO47ns. According to these results, the model giving the best discrimination accuracy was selected for each phoswich pair to complete the study.
TABLE II:
Comparison of discrimination accuracy using fast and slow models for each phoswich pair for an energy window of [250–650] keV and the selected model for each pair (blue).
| Fast model | Slow model | |
|---|---|---|
| LGSO30ns/LGSO45ns | 96.9% | 99.0% |
| LGSO65ns/LYSO40ns | 96.7% | 98.0% |
| LYSO32ns/LYSO47ns | 90.0% | 85.9% |
The discrimination performance between the LGSO30ns and LGSO45ns (Fig. 12) shows an excellent identification accuracy of 99.5% for a reduced energy window of [350–650] keV based on the model of the LGSO45ns. The reconstructed energy spectra show a good separation with energy resolutions of 20.8% FWHM for the LGSO45ns and 27.8% FWHM for the LGSO30ns (Fig. 13). Fig. 14 shows the discrimination spectra between the LGSO65ns and LYSO40ns based on the model of the LGSO65ns. The identification accuracy was estimated to 98.7% for an energy window of [350–650] keV. Energy spectra show an energy resolution of 25.1% FWHM for the LYSO40ns and 37.9% FWHM for the LGSO65ns (Fig. 15). The fair energy resolution of LGSO65ns can be explained by its poor light output. For the LYSO32ns/LYSO47ns, an identification accuracy around 92% is measured using the model of LYSO32ns (Fig. 16). As a confirmation, the R2 histogram from the individual LYSO47ns (orange line) and LYSO32ns (brown line) crystals are superposed to the R2 histogram measured from the phoswich pair (blue) in Fig. 16 Results show that the method reliably separates the scintillators. Energy spectra show an energy resolution of 31.2% FWHM for the LYSO32ns and 29.6% FWHM for the LYSO47ns (Fig. 17).
Fig. 12:

Crystal identification of LGSO30ns/LGSO45ns based on the slow crystal model.
Fig. 13:
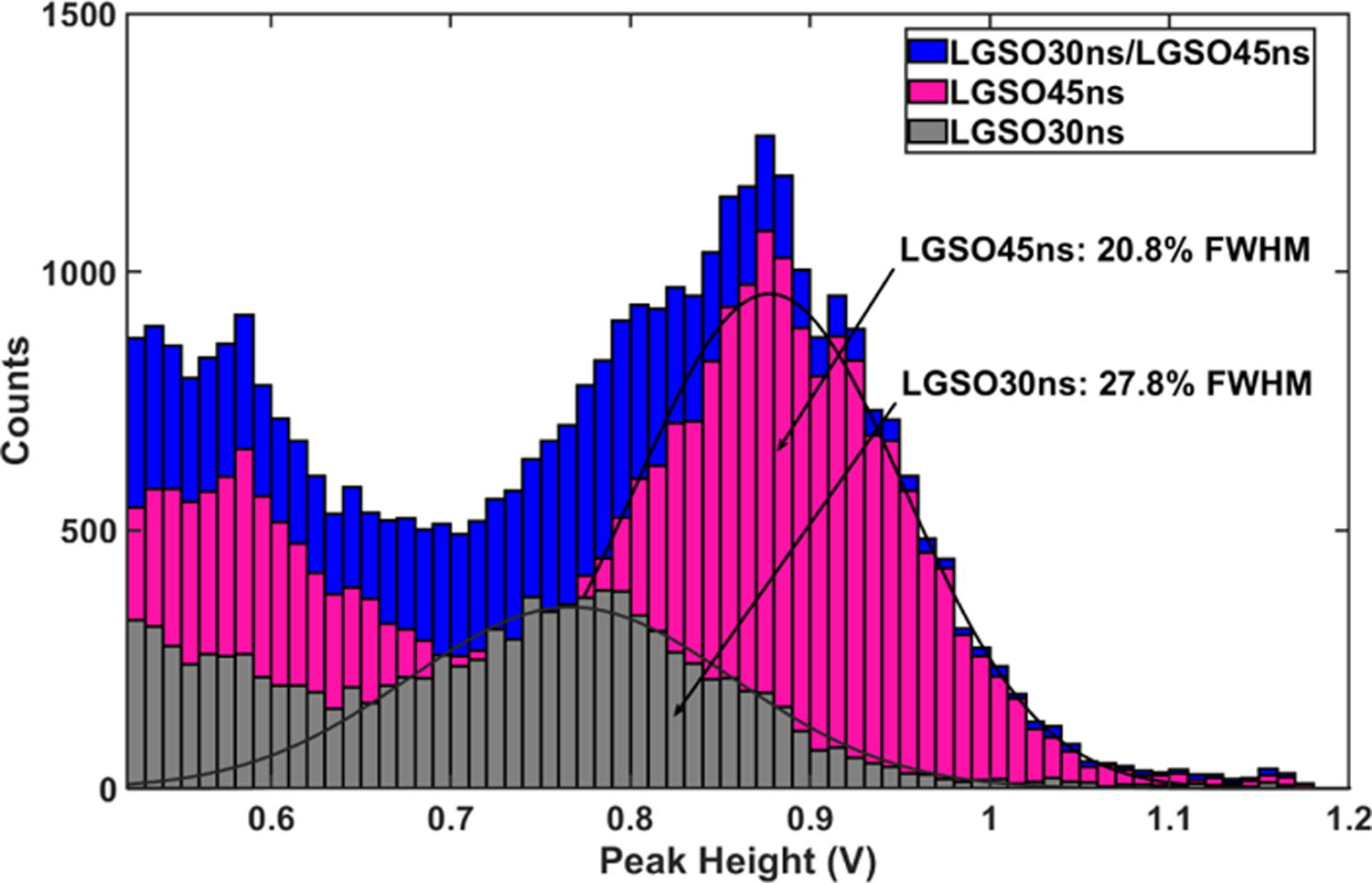
Energy spectra of the LGSO30ns/LGSO45ns phoswich after crystal identification.
Fig. 14:

Crystal identification of LGSO65ns/LYSO40ns based on the slow crystal model.
Fig. 15:

Energy spectra of the LGSO65ns/LYSO40ns after crystal identification.
Fig. 16:

Crystal identification of LYSO32ns/LYSO47ns based on the fast crystal model.
Fig. 17:

Energy spectra of the LYSO32ns/LYSO47ns after crystal identification.
C. Effect of time offset correction
Fig. 18 presents the effect of varying the second threshold level on the discrimination accuracy for the three phoswich pairs. Results indicate that the discrimination accuracy is optimal when the level of the second threshold was set between 0.3 V and 0.35 V. An equivalent measurement of discrimination accuracy without correcting the time offset on t1 was performed. An improvement of ~0.5%, ~3% and ~6% was observed for LGSO30ns/LGSO45ns, LGSO65ns/LYSO40ns and LYSO32ns/LYSO47ns pairs, respectively when the time offset correction is applied. For the latter, the improvement was more significant because signals have a lower amplitude, which increase the time walk and propagation delay due to energy variations compared to the other pairs.
Fig. 18:

Effect of time offset correction on discrimination accuracy.
D. Effect of energy windows on crystal identification
Fig. 19 shows the discrimination accuracy of the three phoswich pairs for different energy windows. One can notice that the discrimination accuracy improves when narrowing the energy window. For the LGSO30ns/LGSO45ns, the discrimination accuracy increases from 99% for an energy window of [250–650] keV to 99.7% for an energy window of [500–650] keV. For the LGSO65ns/LYSO40ns, the discrimination accuracy improved from 98% to 99.3% for the same energy windows. However, the discrimination accuracy is observed to drop more steeply for the LYSO32ns/LYSO47ns when enlarging the energy windows.
Fig. 19:

Effect of energy window on crystal identification.
E. Effect of number of thresholds
Fig. 20 to Fig. 22 display the variation of discrimination accuracy as a function of the number of thresholds for the three phoswich pairs and for different energy windows. The difference of discrimination accuracy when using the entire digitized signal and only 2 thresholds does not exceed 1.1% for the LGSO30ns/LGSO45ns and 0.9% for the LGSO65ns/LYSO40ns for an energy window of [250–650] keV. For the LYSO32ns/LYSO47ns, the discrimination accuracy is relatively unaffected for the same energy window of [250–650] keV, when using only two thresholds. However, for narrower energy windows, the difference between the entire signal and 2 thresholds is under 1% for the three phoswich pairs. One can notice that the identification accuracy based on thresholds may sometimes achieve better performance compared to the entire signal. In fact, by judiciously setting the thresholds, samples are selected to minimize the time jitter effect which is not the case when using the entire signal.
Fig. 20:

Effect of the number of thresholds on discrimination accuracy of LGSO30ns/LGSO45ns phoswich.
Fig. 22:

Effect of the number of thresholds on discrimination accuracy of LYSO32ns/LYSO47ns phoswich.
Fig. 23 shows the energy spectra for LGSO30ns/LGSO45ns, LGSO65ns/LYSO40ns and LYSO32ns/LYSO47ns (from left to right) when discrimination is applied using the entire signal (top) and using 2 thresholds (bottom). The discriminations were based on using the model of the crystal having the slow decay time. Results show that the proposed CI scheme have a good ability to distinguish between crystals of each pair.
Fig. 23:

Comparison of the energy spectra after crystal identification for the three phoswich pairs discriminated using the entire digitized signal (top) and only 2 thresholds (bottom).
V. Discussion
Results demonstrate that despite the similar decay time difference of ~15 ns for the 1st and 3rd phoswich assemblies (LGSO30ns/LGSO45ns and LYSO32ns/LYSO47ns), there is a noticeable difference in discrimination accuracy. This discrepancy can be explained by the difference of light output between the two pairs as can be observed from the pulse height spectra of Fig. 13 and Fig. 17. In fact, with a higher light output, the signal-to-noise ratio (SNR) improves and consequently the discrimination accuracy also improves as we are measuring the fit error between a model and the signal from acquired events. Similarly, the poorer performance of the LGSO65ns/LYSO40ns pair relative to the LGSO30ns/LGSO45ns phoswich can be partly explained by the much lower light output of the LGSO65ns scintillator, despite the larger decay time difference of 25 ns (Fig. 15). Moreover, this phoswich assembly was handmade with optical grease and wrapped in Teflon tape, which is suboptimal for light extraction from long thin crystals of 12 mm and 14 mm. Despite the more favorable form factor of the LYSO pair (Fig. 2d) compared to the LGSO phoswich array (Fig. 2b), and irrespective of the different polishing quality of the scintillators and the reflector selection, the main cause of light loss with the former is the poor coupling fraction between the 3 × 3 mm2 cross section crystal pair and the 1.1 × 1.1 mm2 APD pixel. Therefore, the discrimination accuracy of this phoswich pair is impaired by the signal loss, but results show that crystals can still be identified with fairly high confidence.
The proposed method can be classified as a pulse shape discrimination technique since we are analyzing the shape of the signal to discriminate between two crystals. Therefore, the main parameter that may differentiate between crystals is the decay time. Obviously, the length of crystals, light output, reflector type, and polishing quality may also affect the discrimination accuracy [54], [55] since they all affect the SNR. However, the aim of the study was to demonstrate the concept of a new robust method that can be integrated in the LabPET II electronic readout for implementation in a DOI scanner.
Normalizing the amplitude of events in the proposed model-based method is very important to eliminate the effect of energy variation. After normalization, all the acquired signals can be compared with respect to one crystal-DAQ model, which greatly facilitates computing. Moreover, using different threshold levels with non-normalized events would cause variations in energy windows, since it is the level of the highest threshold in the ToT approach that determines the dynamic range of the signals. Hence, if the signal does not reach the level of this highest threshold, the event will be ignored. Measuring the amplitude of the signals is a limitation in the current version of the LabPET II ASIC as the energy is deduced from ToT. A peak detector would need to be implemented in the next ASIC upgrade to mitigate this problem.
The choice of the crystal model (fast or slow) used in CI was based on the one giving the best discrimination accuracy. Nevertheless, the difference of discrimination accuracy between either models does not exceed 2% for the first two phoswich pairs and 4% for the third one with the same [250–650] keV energy window. This difference is not significant and is within the error margin. Whereas the discrimination accuracy may vary by only 0.7% when raising the lower threshold of the energy window for the LGSO30ns/LGSO45ns (Fig. 20, Entire Signal), in all other instances the variations exceed 1% to 2% (Fig. 20–22).
It was shown that when time offset correction on t1 was applied, discrimination accuracy was improved for some phoswiches. On one hand, t1 is determined by the crossing of the signal with the first threshold. Its value will vary as a function of the energy due to the time walk in the leading edge discrimination and the propagation delay of the comparator, thus inducing an error on the time of occurrence. On the other hand, the CI method is based on the measurement of the fit error between a signal and its model. Therefore, both of them must be temporally aligned to minimize the fit error and maximise the discrimination accuracy.
The results presented so far were based on a 5 GS/s rate acquisition. However, the LabPET-II ASIC uses a dual-threshold time-over-threshold technique to extract energy and timestamps. Different numbers of thresholds were tested to evaluate the performance of the CI method proposed here for further implementation in the ASIC. Even using a dual threshold approach, the results demonstrate that satisfactory discrimination accuracy can be achieved with well above 90% correct identification in all cases. The poorer CI performance of the technique using the fit error between the entire signal and the model in some instance (Fig. 22) can be explained by the fact that, a lot of noise was included, especially on the low amplitude sections of the signal, while the timestamps are taken at the time points optimizing the signal-to-noise ratio.
Finally, timestamps were measured with a precision of 200 ps at the sampling rate of 5 GS/s, while timestamps will be measured with a precision of 312.5 ps in the ASIC. This difference is expected to have a negligible impact on the discrimination accuracy, since the two thresholds will be meticulously selected to minimize the time jitter effect.
VI. Conclusion
In this paper, a crystal identification (CI) method based on the time-over-threshold (ToT) approach was proposed and investigated with three phoswich scintillator assemblies of diverse configurations. Results demonstrates that when one successively applies amplitude-based normalization and appropriately selects the thresholds, CI with discrimination accuracy better that 97% can be achieved by using a limited number of thresholds for a wide energy window of [250–650] keV. Even when using only two thresholds, discrimination accuracies of 99.1%, 98.1% and 92.1% for a narrower energy window of [350–650 keV] can be reached for LGSO30ns/LGSO45ns, LGSO65ns/LYSO40ns and LYSO32ns/LYSO47ns, respectively. Therefore, the proposed method can easily be implemented in a future upgrade of LabPET II ASIC incorporating a peak detector with an analog-to-digital converter for maximum amplitude extraction, if the scintillators are carefully chosen. Future work using scintillators of the same configuration, with optimal polishing and bonding conditions, will further refine the results.
Fig. 10:

Acquired signals compared to the models for single crystals of the LGSO65ns/LYSO40ns phoswich pair.
Fig. 21:

Effect of the number of thresholds on discrimination accuracy of LGSO65ns/LYSO40ns phoswich.
Acknowledgment
The authors would like to thank all the members of Groupe de recherche en appareillage médical de Sherbrooke (GRAMS) and Centre d’imagerie moléculaire de Sherbrooke (CIMS) for their support. This work was realised in part thanks to these granting organizations: Natural Sciences and Engineering Research Council of Canada (NSERC), PROMPT, MEDTEQ, MITACS, Regroupement Stratégique en Microsystèmes du Québec (RESMIQ), Université de Sherbrooke and National Institutes of Health (NIH-P41EB 022544 and U01EB027003).
Contributor Information
Haithem Bouziri, Interdisciplinary Institute for Technological Innovation (3IT) and with the Department of Electrical and Computer Engineering, Université de Sherbrooke, Sherbrooke, QC, Canada J1K 0A5..
Catherine M. Pepin, Sherbrooke Molecular Imaging Center, Department of Nuclear Medicine and Radiobiology, Université de Sherbrooke, Sherbrooke, QC, Canada J1H 5N4.
Konin Koua, Interdisciplinary Institute for Technological Innovation (3IT) and with the Department of Electrical and Computer Engineering, Université de Sherbrooke, Sherbrooke, QC, Canada J1K 0A5..
Maher Benhouria, Interdisciplinary Institute for Technological Innovation (3IT) and with the Department of Electrical and Computer Engineering, Université de Sherbrooke, Sherbrooke, QC, Canada J1K 0A5..
Caroline Paulin, Interdisciplinary Institute for Technological Innovation (3IT) and with the Department of Electrical and Computer Engineering, Université de Sherbrooke, Sherbrooke, QC, Canada J1K 0A5..
Jinsong Ouyang, Gordon Center for Medical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, 02114 USA..
Marc Normandin, Gordon Center for Medical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, 02114 USA..
Jean-François Pratte, Interdisciplinary Institute for Technological Innovation (3IT) and with the Department of Electrical and Computer Engineering, Université de Sherbrooke, Sherbrooke, QC, Canada J1K 0A5..
Georges El Fakhri, Gordon Center for Medical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, 02114 USA..
Roger Lecomte, Sherbrooke Molecular Imaging Center, Department of Nuclear Medicine and Radiobiology, Université de Sherbrooke, Sherbrooke, QC, Canada J1H 5N4..
Réjean Fontaine, Interdisciplinary Institute for Technological Innovation (3IT) and with the Department of Electrical and Computer Engineering, Université de Sherbrooke, Sherbrooke, QC, Canada J1K 0A5..
References
- [1].Michaud J-B, Fontaine R, and Lecomte R, “ARMAX model and recursive least-squares identification for DOI measurement in PET,” in 2003 IEEE Nuclear Science Symposium. Conference Record, vol. 4, October 2003, pp. 2386–2390. [Google Scholar]
- [2].Green MV, Ostrow HG, Seidel J, and Pomper MG, “Experimental evaluation of depth-of-interaction correction in a small-animal positron emission tomography scanner,” Molecular Imaging, vol. 9, no. 6, pp. 311–318, 2010. [PMC free article] [PubMed] [Google Scholar]
- [3].Carrier C, Martel C, Schmitt D, and Lecomte R, “Design of a high resolution positron emission tomograph using solid state scintillation detectors,” IEEE Transactions on Nuclear Science, vol. 35, no. 1, pp. 685–690, February 1988. [Google Scholar]
- [4].Akamatsu G, Tashima H, Iwao Y, Wakizaka H, Maeda T, Mohammadi A, Takyu S, Nitta M, Nishikido F, Rutherford H, Chacon A, Safavi-Naeini M, Yoshida E, and Yamaya T, “Performance evaluation of a whole-body prototype PET scanner with four-layer DOI detectors,” Physics in Medicine and Biology, vol. 64, April 2019. [DOI] [PubMed] [Google Scholar]
- [5].Sempere Roldan P, Chereul E, Dietzel O, Magnier L, Pautrot C, Rbah L, Sappey-Marinier D, Wagner A, Zimmer L, Janier M, Tarazona V, and Dietzel G, “Raytest ClearPET™, a new generation small animal PET scanner,” Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 571, no. 1–2, pp. 498–501, February 2007. [Google Scholar]
- [6].Krishnamoorthy S, Blankemeyer E, Mollet P, Surti S, Holen RV, and Karp JS, “Performance evaluation of the MOLECUBES β-CUBE - A high spatial resolution and high sensitivity small animal PET scanner utilizing monolithic LYSO scintillation detectors,” Physics in Medicine and Biology, vol. 63, July 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Sato K, Shidahara M, Watabe H, Watanuki S, Ishikawa Y, Arakawa Y, Nai Y, Furumoto S, Tashiro M, Shoji T, Yanai K, and Gonda K, “Performance evaluation of the small-animal PET scanner ClairvivoPET using NEMA NU 4–2008 Standards,” Physics in Medicine and Biology, vol. 61, pp. 696–711, December 2015. [DOI] [PubMed] [Google Scholar]
- [8].Wienhard K, Schmand M, Casey ME, Baker K, Bao J, Eriksson L, Jones WF, Knoess C, Lenox M, Lercher M, Luk P, Michel C, Reed JH, Richerzhagen N, Treffert J, Vollmar S, Young JW, Heiss WD, and Nutt R, “The ECAT HRRT: Performance and First Clinical Application of the New High Resolution Research Tomograph,” February 2002.
- [9].Yamaya T, Yoshida E, Toramatsu C, Nishimura M, Shimada Y, Inadama N, Shibuya K, Nishikido F, and Murayama H, “Preliminary study on potential of the jPET-D4 human brain scanner for small animal imaging,” Annuals of Nuclear Medicine, vol. 23, pp. 183–190, February 2009. [DOI] [PubMed] [Google Scholar]
- [10].Gonzalez AJ, Gonzalez-Montoro A, Vidal LF, Barbera J, Aussenhofer S, Hernandez L, Moliner L, Sanchez F, Correcher C, Pincay EJ, Cañizares G, Lamprou E, Sanchez S, Catret JV, Jiménez-Serrano S, Cabello J, Schwaiger M, Iborra A, Merlin T, Visvikis D, and Benlloch JM, “Initial Results of the MINDView PET Insert Inside the 3T mMR,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. 3, no. 3, pp. 343–351, May 2019. [Google Scholar]
- [11].Tashima H, Yoshida E, Iwao Y, Wakizaka H, Mohammadi A, Nitta M, Kitagawa A, Inaniwa T, Nishikido F, Tsuji AB, Nagai Y, Seki C, Minamimoto T, Fujibayashi Y, and Yamaya T, “Development of a multi-use human-scale single-ring OpenPET system,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. Early access, November 2020. [Google Scholar]
- [12].Won JY, Park H, Lee S, Son JW, Chung Y, Ko GB, Kim KY, Song J, Seo S, Ryu Y, Chung JY, and Lee JS, “Development and Initial Results of a Brain PET Insert for Simultaneous 7-Tesla PET/MRI Using an FPGA-Only Signal Digitization Method,” IEEE Transactions on Medical Imaging, vol. Early access, February 2021. [DOI] [PubMed] [Google Scholar]
- [13].Mohammadi I, Castro IF, Correia PM, Silva AL, and Veloso JF, “Minimization of parallax error in positron emission tomography using depth of interaction capable detectors: Methods and apparatus,” Biomedical Physics and Engineering Express, vol. 5, no. 6, October 2019. [Google Scholar]
- [14].McElroy DP, Pimpl W, Pichler BJ, Rafecas M, Schüler T, and Ziegler SI, “Characterization and readout of MADPET-II detector modules: Validation of a unique design concept for high resolution small animal PET,” IEEE Transactions on Nuclear Science, vol. 52, no. 1, pp. 199–204, February 2005. [Google Scholar]
- [15].Vandenbroucke A, Foudray AMK, Olcott PD, and Levin CS, “Performance characterization of a new high resolution PET scintillation detector,” Physics in Medicine and Biology, vol. 55, no. 19, pp. 5895–5911, September 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Beltrame P, Bolle E, Braem A, Casella C, Chesi E, Clinthorne N, De Leo R, Dissertori G, Djambazov L, Fanti V, Heller M, Joram C, Kagan H, Lustermann W, Meddi F, Nappi E, Nessi-Tedaldi F, Oliver JF, Pauss F, Rafecas M, Renker D, Rudge A, Schinzel D, Schneider T, Séguinot J, Solevi P, Stapnes S, and Weilhammer P, “The AX-PET demonstrator - Design, construction and characterization,” Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 654, no. 1, pp. 546–559, October 2011. [Google Scholar]
- [17].Cuddy S, Reznik A, Rowlands JA, and Taghibakhsh F, “Effect of scintillator crystal geometry and surface finishing on depth of interaction resolution in PET detectors: Monte Carlo simulation and experimental results using silicon photomultipliers,” in Medical Imaging 2010: Physics of Medical Imaging, vol. 7622. SPIE, March 2010, pp. 561–568. [Google Scholar]
- [18].Huber JS, Moses WW, Andreaco MS, and Petterson O, “An LSO scintillator array for a PET detector module with depth of interaction measurement,” IEEE Transactions on Nuclear Science, vol. 48, no. 3, pp. 684–688, June 2001. [Google Scholar]
- [19].Joung J, Miyaoka RS, and Lewellen TK, “cMiCE: a high resolution animal PET using continuous LSO with a statistics based positioning scheme,” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 489, no. 1, pp. 584–598, August 2002. [Google Scholar]
- [20].Ling T, Lewellen TK, and Miyaoka RS, “Depth of interaction decoding of a continuous crystal detector module,” Physics in Medicine and Biology, vol. 52, no. 4, pp. 2213–2228, March 2007. [DOI] [PubMed] [Google Scholar]
- [21].Yang Q, Wang X, Kuang Z, Zhang C, Yang Y, and Du J, “Evaluation of Two SiPM Arrays for Depth-Encoding PET Detectors Based on Dual-Ended Readout,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. Early Access, July 2020. [Google Scholar]
- [22].Ito M, Lee JS, Kwon SI, Lee GS, Hong B, Lee KS, Sim KS, Lee SJ, Rhee JT, and Hong SJ, “A four-layer DOI detector with a relative offset for use in an animal PET system,” IEEE Transactions on Nuclear Science, vol. 57, no. 3, pp. 976–981, June 2010. [Google Scholar]
- [23].Liu H, Omura T, Watanabe M, and Yamashita T, “Development of a depth of interaction detector for γ-rays,” Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 459, no. 1–2, pp. 182–190, February 2001. [Google Scholar]
- [24].Pizzichemi M, Polesel A, Stringhini G, Gundacker S, Lecoq P, Tavernier S, Paganoni M, and Auffray E, “On light sharing TOF-PET modules with depth of interaction and 157 ps FWHM coincidence time resolution,” Physics in Medicine & Biology, vol. 64, no. 15, p. 155008, August 2019. [DOI] [PubMed] [Google Scholar]
- [25].Yoshida E, Obata F, Kamada K, and Yamaya T, “A crosshair light sharing PET detector with DOI and TOF capabilities using four-to-one coupling and single-ended readout,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. Early Access, October 2020. [Google Scholar]
- [26].Yoshida E, Kamada K, Obata F, and Yamaya T, “Development of Single-Ended Readout DOI Detector With Quadrisected Crystals,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. 4, no. 5, pp. 563–569, September 2020. [Google Scholar]
- [27].Zhang X, Ye B, Yu H, Zhang Y, Xie S, Xu J, and Peng Q, “Depth of interaction measurements based on rectangular light sharing window technology and nine-crystals-to-one-SiPM coupling method,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. Early Access, September 2020. [Google Scholar]
- [28].Brown JMC, Brunner SE, and Schaart DR, “A High Count-Rate and Depth-of-Interaction Resolving Single-Layered One-Side Readout Pixelated Scintillator Crystal Array for PET Applications,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. 4, no. 3, pp. 361–370, October 2020. [Google Scholar]
- [29].Teimoorisichani M and Goertzen AL, “Geometry Optimization of a Dual-Layer Offset Detector for Use in Simultaneous PET/MR Neuroimaging,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. 3, no. 3, pp. 275–284, May 2019. [Google Scholar]
- [30].Saoudi A, Pepin CM, Dion F, Bentourkia M, Lecomte R, Andreaco M, Casey M, Nutt R, and Dautet H, “Investigation of depth-of-interaction by pulse shape discrimination in multicrystal detectors read out by avalanche photodiodes,” IEEE Transactions on Nuclear Science, vol. 46, no. 3, pp. 462–467, June 1999. [Google Scholar]
- [31].Seidel J, Vaquero JJ, Siegel S, Gandler WR, and Green MV, “Depth identification accuracy of a three layer phoswich PET detector module,” IEEE Transactions on Nuclear Science, vol. 46, no. 3, pp. 485–490, June 1999. [Google Scholar]
- [32].Bergeron M, Cadorette J, Beaudoin JF, Lepage MD, Robert G, Selivanov V, Tétrault M-A, Viscogliosi N, Norenberg JP, Fontaine R, and Lecomte R, “Performance evaluation of the LabPET APD-based digital PET scanner,” IEEE Transactions on Nuclear Science, vol. 56, pp. 10–16, February 2009. [Google Scholar]
- [33].Yamamoto S, Watabe H, Kawachi N, Fujimaki S, Kato K, and Hatazawa J, “Three-layer GSO depth-of-interaction detector for high-energy gamma camera,” Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 743, pp. 124–129, April 2014. [Google Scholar]
- [34].Chandrikamohan P and DeVol TA, “Comparison of pulse shape discrimination methods for phoswich and CsI:Tl detectors,” IEEE Transactions on Nuclear Science, vol. 54, no. 2, pp. 398–403, April 2007. [Google Scholar]
- [35].Roncali E, Phipps JE, Marcu L, and Cherry SR, “Pulse shape discrimination and classification methods for continuous depth of interaction encoding PET detectors,” Physics in Medicine and Biology, vol. 57, no. 20, pp. 6571–6585, September 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Wiener RI, Surti S, and Karp JS, “DOI determination by rise time discrimination in single-ended readout for TOF PET imaging,” IEEE Transactions on Nuclear Science, vol. 60, no. 3, pp. 1478–1486, June 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Mosset JB, Devroede O, Krieguer M, Rey M, Vieira JM, Jung JH, Kuntner C, Streun M, Ziemons K, Auffray E, Sempere-Roldan P, Lecoq P, Bruyndonckx P, Loude JF, Tavernier S, and Morel C, “Development of an optimized LSO/LuYAP phoswich detector head for the lausanne ClearPET demonstrator,” IEEE Transactions on Nuclear Science, vol. 53, no. 1, pp. 25–29, February 2006. [Google Scholar]
- [38].Streun M, Brandenburg G, Larue H, Saleh H, Zimmermann E, Ziemons K, and Hailing H, “Pulse Shape Discrimination of LSO and LuYAP Scintillators for Depth of Interaction Detection in PET,” in IEEE Nuclear Science Symposium and Medical Imaging Conference, November 2002, pp. 1636–1639. [Google Scholar]
- [39].Michaud J-B, Pepin CM, Lecomte R, and Fontaine R, “ARMAX-RLS parameter-estimation crystal identification in phoswich PET detectors,” IEEE Transactions on Nuclear Science, vol. 57, no. 3, pp. 982–989, June 2010. [Google Scholar]
- [40].Semmaoui H, Viscogliosi N, Bélanger F, Michaud JB, Pepin CM, Lecomte R, and Fontaine R, “Crystal identification based on recursive-least-squares and least-mean-squares auto-regressive models for small animal PET,” IEEE Transactions on Nuclear Science, vol. 55, no. 5, pp. 2450–2454, October 2008. [Google Scholar]
- [41].Viscogliosi N, Riendeau J, Berard P, Tetrault M-A, Lefebvre R, Lecomte R, and Fontaine R, “Real Time Implementation of a Wiener Filter Based Crystal Identification Algorithm,” IEEE Transactions on Nuclear Science, vol. 55, no. 3, pp. 925–929, June 2008. [Google Scholar]
- [42].Yousefzadeh HC, Viscogliosi N, Tetrault M-A, Pepin CM, Berard P, Bergeron M, Semmaoui H, Lecomte R, and Fontaine R, “A Fast Crystal Identification Algorithm Applied to the LabPET™ Phoswich Detectors,” Nuclear Science, IEEE Transactions on, vol. 55, no. 3, pp. 1644–1651, June 2008. [Google Scholar]
- [43].Kim H, Kao CM, Xie Q, Chen CT, Zhou L, Tang F, Frisch H, Moses WW, and Choong WS, “A multi-threshold sampling method for TOF-PET signal processing,” Nuclear Instruments and Methods in Physics Research A, vol. 602, no. 2, pp. 618–621, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Xie Q, Chen Y, Zhu J, Liu J, Wang X, Liu W, Chen X, Niu M, Wu Z, Xi D, Wang L, Xiao P, Chen C, and Kao C, “Implementation of LYSO/PSPMT Block Detector With All Digital DAQ System,” IEEE Transactions on Nuclear Science, June. [Google Scholar]
- [45].Kipnis I, Collins T, DeWitt J, Dow S, Frey A, Grillo A, Johnson R, Kroeger W, Leona A, Luo L, Mandelli E, Manfredi PF, Melani M, Momayezi M, Morsani F, Nyman M, Pedrali-Noy M, Poplevin P, Spencer E, Re V, and Roe N, “A Time-over-threshold machine: The readout integrated circuit for the BABAR Silicon Vertex Tracker,” IEEE Transactions on Nuclear Science, vol. 44, no. 3, pp. 289–297, June 1997. [Google Scholar]
- [46].Powolny F, Auffray E, Hillemanns H, Jarron P, Lecoq P, Meyer TC, and Moraes D, “A novel time-based readout scheme for a combined PET-CT detector using APDs,” IEEE Transactions on Nuclear Science, vol. 55, no. 5, pp. 2465–2474, October 2008. [Google Scholar]
- [47].Arpin L, Koua K, Panier S, Bouziri H, Abidi M, Ben Attouch MW, Paulin C, Maille P, Geoffroy C, Lecomte R, Pratte JF, and Fontaine R, “Embedded real time digital signal processing unit for a 64-channel PET detector module,” in 2011 IEEE Nuclear Science Symposium and Medical Imaging Conference, October 2011, pp. 1545–1550. [Google Scholar]
- [48].Chang CM, Cates JW, and Levin CS, “Time-over-threshold for pulse shape discrimination in a time-of-flight phoswich PET detector,” Physics in Medicine and Biology, vol. 62, no. 1, pp. 258–271, December 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Bergeron M, Thibaudeau C, Cadorette J, Tetrault M-A, Pepin CM, Clerk-Lamalice J, Loignon-Houle F, Davies M, Dautet H, Deschamps P, Fontaine R, and Lecomte R, “LabPET II, an APD-based Detector Module with PET and Counting CT Imaging Capabilities,” IEEE Transactions on Nuclear Science, vol. 62, no. 3, pp. 756–765, June 2015. [Google Scholar]
- [50].Gaudin E, Toussaint M, Thibaudeau C, Croteau E, Fontaine R, Normandin MD, Petibon Y, Ouyang J, Fakhri GE, and Lecomte R, “Simulation Studies of the SAVANT High Resolution Dedicated Brain PET Scanner Using Individually Coupled APD Detectors and DOI Encoding,” vol. 60, no. 1, 2019, p. 531, 2019 SNMMI, Anaheim, CA. [Google Scholar]
- [51].Bérard P, Bergeron M, Pepin CM, Cadorette J, Tétrault M-A, Viscogliosi N, Fontaine R, Dautet H, Davies M, Deschamps P, and Lecomte R, “Development of a 64-channel APD detector module with individual pixel readout for submillimetre spatial resolution in PET,” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 610, no. 1, pp. 20–23, October 2009. [Google Scholar]
- [52].Gaudin E, Arpin L, Bouchard J, Paille M, Bouziri H, Bergeron M, Pepin CM, Cadorette J, Fontaine R, and Lecomte R, “Performance characterization of a dual-threshold time-over-threshold APD-based detector front-end module for PET imaging,” in 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference, October 2016, pp. 1–3. [Google Scholar]
- [53].Bouziri H, “Identification de cristaux dans un phoswich par la méthode de mesure de temps au dessus d’ un seuil (ToT) pour le scanner LabPET II,” M.Sc. thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, p. 116, January 2014. [Google Scholar]
- [54].Kang HG, Yamaya T, Han YB, Song SH, Ko GB, Lee JS, and Hong SJ, “Crystal surface and reflector optimization for the SiPM-based dual-ended readout TOF-DOI PET detector,” Biomedical Physics & Engineering Express, vol. 6, no. 6, November 2020. [DOI] [PubMed] [Google Scholar]
- [55].Roncali E, Stockhoff M, and Cherry SR, “An integrated model of scintillator-reflector properties for advanced simulations of optical transport,” Physics in Medicine and Biology, vol. 62, no. 12, pp. 4811–4830, May 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]


