More (Adjustment) is Not Always Better: How Directed Acyclic Graphs Can Help Researchers Decide Which Covariates to Include in Models for the Causal Relationship Between an Exposure and an Outcome in Observational Research

Introduction

When constructing a model for an outcome of interest (e.g., a linear regression model), the choice of covariates^a to be included depends in part on the researcher’s aims. If the aim is to build a predictive model [1], covariate selection focuses on improving model predictions while also limiting overfitting, which occurs when an overly complex model yields predictions that are too specific to a particular dataset, reducing its generalizability [2, 3]. Alternatively, the aim may be to build a causal model [1]. (Note that Table 1 contains a glossary with definitions for all key terms, which are italicized.) For instance, one might build a causal model in order to quantify the average causal effect of an exposure on an outcome. The average causal effect can be defined as the average difference in outcome had each individual in the population experienced the exposure, as compared to if no one had experienced the exposure [4]. As an illustration for this commentary, we will consider a causal model of the effect of the exposure preterm birth on the outcome attention-deficit/hyperactivity disorder (ADHD) during childhood. Because this example is offered purely for illustrative purposes, we have deliberately simplified it and ignored methodological difficulties that would complicate a real-world investigation of this issue (e.g., mismodeling the functional form of the variables, measurement error, presence of unmeasured confounders).

Table 1.

Glossary of Key Terms

Term	Definition
Average causal effect	The contrast in mean counterfactual outcomes in a population, had two different interventions been applied to the population.
Blocked path	On a DAG, a path is blocked if and only if it contains a variable that is not a collider and has been adjusted for, or if it contains a collider and neither that collider nor its descendants have been adjusted for.
Causal model	A model used to estimate differences in the distribution of an outcome had different interventions been applied (for example, to estimate the average causal effect of an exposure on an outcome).
Collider	A variable on a DAG path that is directly affected by two other variables. On a DAG, this is represented by a node at which two edges collide.
Collider stratification bias	Bias resulting from adjusting for a collider, which opens a path between the variables that directly affect the collider.
Counterfactual outcome	The potential outcomes that would have been observed in individuals had they received a particular intervention. Here, intervention is used in a loose sense that includes exposures (e.g., to a risk factor for an outcome).
Directed acyclic graph (DAG)	A kind of diagram consisting of nodes and edges, where the edges are directed (i.e., unidirectional arrows) and the diagram is acyclic (i.e., one cannot return to the same node by following a path in the direction of the arrows). A causal DAG refers to a DAG that represents all causal relationships between included variables.
Edge	Directed arrows on a DAG. On a causal DAG, these arrows represent causal effects of different variables (i.e., nodes) on each other.
Open path	On a DAG, a path that is not blocked.
Node	A vertex on a DAG. On a causal DAG, these vertices represent random variables.
Path	A connection between two nodes on a DAG through a particular continuous sequence of edges. Note that the path does not have to follow the direction of the arrows.

With causal models, the aim is to obtain the least biased possible estimate of the average causal effect, where the term “bias” is used to mean any deviation from an accurate measurement [5]. Thus, covariate selection should focus on eliminating or reducing bias. One type of bias occurs when the estimated causal effect reflects not only the causal relationship between the exposure and the outcome, but also other relationships between the exposure and the outcome [6], as is typically the case in observational studies [7]. In our example, the unadjusted association between preterm birth and ADHD may be a biased estimate of the causal effect of interest if there are other variables that link preterm birth and ADHD, aside from the intermediate variables that mediate the exposure’s causal effect on the outcome (i.e., variables in the causal pathway between preterm birth and ADHD).

When selecting covariates, researchers may choose to include certain variables because they believe them to be potential confounders (i.e., common causes of the exposure and outcome) that, if not included in the model, will lead to biased estimates of the average causal effect. For example, researchers might adjust for maternal smoking during pregnancy because they believe that it has a causal effect on both preterm birth and ADHD. If this were the case, then unadjusted estimates of the association between preterm birth and ADHD would be biased, because these estimates would reflect not only the association due to the causal effect of preterm birth on ADHD, but also the association due to the common effects of maternal smoking during pregnancy on exposure and outcome. Additionally, researchers at times choose to include certain covariates because existing research has identified them as risk factors for the outcome, or as correlates of the exposure. However, adjusting for covariates can, in certain circumstances, do more harm than good, by introducing new bias into an estimate of the causal effect [8, 9].

To examine the potential perils of covariate adjustment, we provide an introduction to causal directed acyclic graphs (DAGs). Causal DAGs can clarify how adjustment for a given covariate might impact bias, by providing a simple way to visualize assumptions about the statistical relationships between the exposure, outcome, and covariates in question. We illustrate their use with the example of preterm birth and ADHD.

An Introduction to DAGs

The development and use of DAGs to clarify causal models in epidemiologic research has been described elsewhere [10–12]. Causal DAGs are a kind of causal diagram consisting of nodes, which represent variables, and directed edges (i.e., arrows), which represent causal relationships between variables. As an example, see Figure 1, which presents a DAG for a simplified causal model for preterm birth and ADHD, which we consider in detail in the next section. An arrow on a DAG does not imply that there is definitely a causal relationship between the two variables, but only that there might be a relationship between them. In contrast, the absence of an arrow between two variables implies that the researcher is certain that one variable does not cause the other. These graphs are acyclic, which means that if one follows the direction of arrows on a DAG, no path from a variable will lead back to itself.

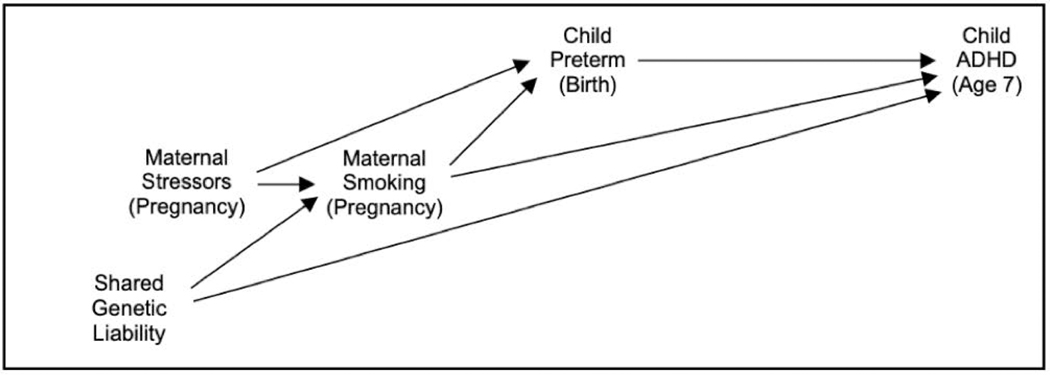
Fig. 1. Example of Directed Acyclic Graph (DAG) for the Causal Effect of Child Preterm Birth on Child ADHD.

Variables are represented by nodes on a DAG. Assumed causal relationships between variables are represented by directed edges (i.e., arrows) between nodes. Typically, variables later in terms of temporal order appear farther to the right. (Abbreviations: ADHD = attention-deficit/hyperactivity disorder)

Researchers can apply several graphical rules to DAGs to help decide which, if any, covariates to include in the causal model (see Fig. 2). These rules relate to paths between the variables depicted in the graph. A path is a connection between two variables on a DAG through a particular continuous sequence of arrows. Note that the presence of a path through a series of variables is independent of the directions of the arrows involved in the path, and does not imply any particular type of association between those variables. In other words, a path does not need to follow the direction of the arrows involved (e.g., in Fig. 1, there is a path between preterm birth and ADHD that passes through maternal smoking during pregnancy). However, the direction of the arrows does affect whether a path is open or blocked. An open path can be thought of as a path along which one can travel unimpeded, in the sense that one does not encounter blocks at any of the nodes between the endpoints; determining whether a path is blocked at a particular node involves the application of several rules that are described in the following paragraph. Notably, open paths imply statistical associations between the endpoint variables, whereas blocked paths imply the absence of an association. If a path is open, then it will contribute to the estimated association between the variables on the two ends of the path. Thus, aside from paths representing the causal effect of interest (e.g., paths from preterm birth to ADHD), all other paths between the exposure and outcome will ideally be blocked. If not, then the resulting estimate of the average causal effect will be biased, although the magnitude of this bias will vary depending on the strength and nature of the causal relationships represented in the other open paths, as we illustrate in the following section. Of course, it is possible that all other open paths between exposure and outcome might cancel each other exactly, meaning that the net bias due to other open paths would be null. However, such balancing is empirically untestable, and seems unlikely to occur in practice.

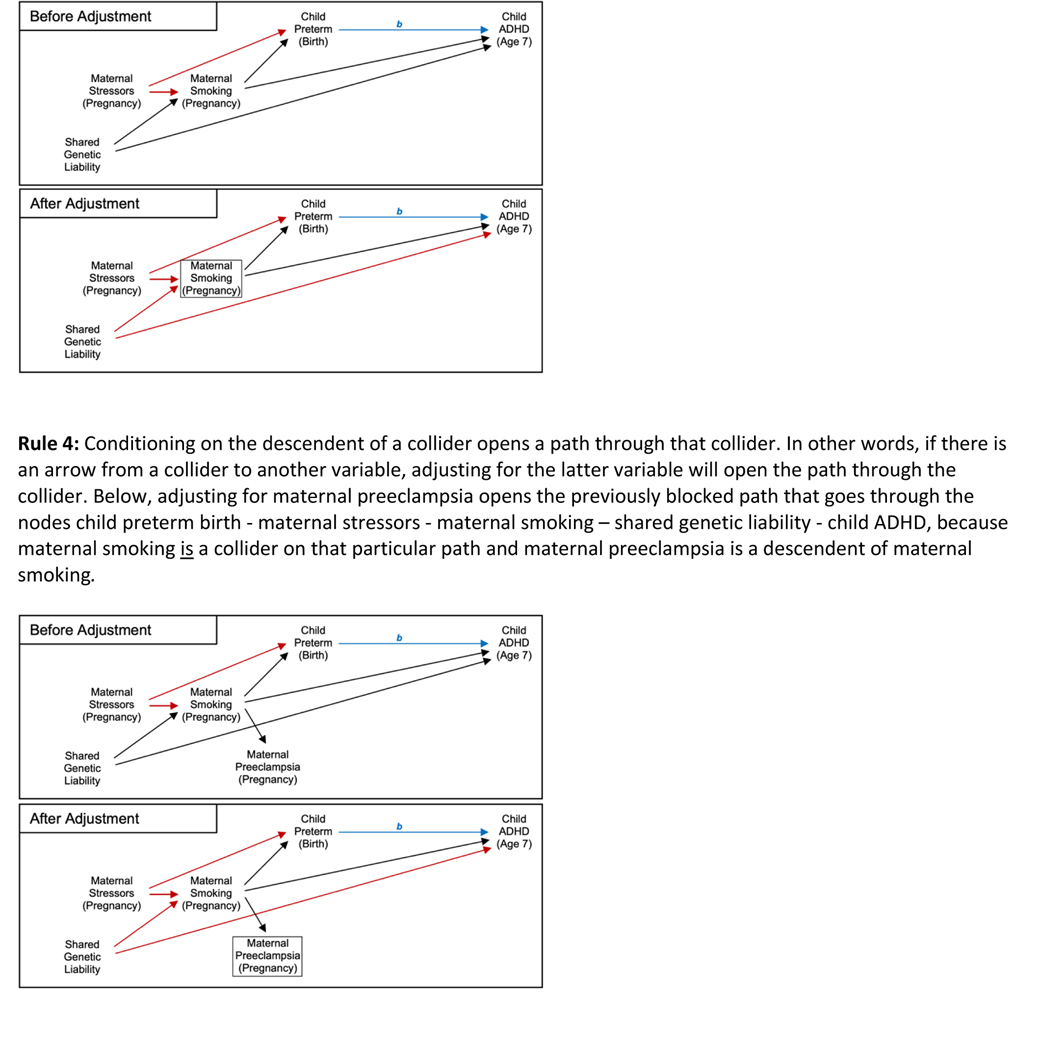
Fig. 2.

Graphical Rules for Directed Acyclic Graphs (DAGs). For illustrative purposes, the blue arrow represents the relationship of interest (the causal effect of Child Preterm Birth on Child ADHD), and the letter b denotes the average causal effect one seeks to estimate. Also, in the examples below, red is used to highlight how far one can travel along a given path from Child Preterm Birth toward Child ADHD before the path is blocked. (Abbreviations: ADHD = attention-deficit/hyperactivity disorder)

Whether a path is open or blocked depends on the relationships between the variables on that path and on which of those variables are included as covariates in the causal model. In a simple unadjusted model, paths between the exposure and outcome are open unless they pass through a collider (Rule 1). A collider is a variable that is caused by the two adjacent variables along that path, as represented by edges pointing toward the variable. To understand why the presence of a collider blocks the path, suppose that maternal stressors during pregnancy and shared genetic liability both cause maternal smoking during pregnancy, which in turn causes both preterm birth and ADHD (see Fig. 1). (Note that we use the variable name “shared genetic liability” as short-hand for overlapping risk factors for maternal smoking during pregnancy and child ADHD.) Maternal smoking is a collider on the path between preterm birth and ADHD that passes through both maternal stressors, maternal smoking, and shared genetic liability; this type of path is referred to as an M-shaped path (because it appears in the shape of the letter “M” when viewed sideways on our graph). Although maternal stressors can affect maternal smoking during pregnancy, this effect will not be transmitted to shared genetic liability because the latter is a cause, not an effect, of maternal smoking. Thus, the maternal smoking variable blocks this particular path.

Notably, adjusting for a variable can block a previously open path or open a previously blocked path, depending on the relationships between the variables in question. More specifically, adjusting for a variable that is not a collider on a particular path will block that path (Rule 2). For example, if maternal smoking during pregnancy caused both child preterm birth and child ADHD, adjusting for maternal smoking would block the path from preterm birth to ADHD that goes through maternal smoking and represents confounding. In this instance, adjusting for maternal smoking would reduce bias due to confounding. However, adjusting for a variable that is a collider (Rule 3) or its descendent (Rule 4) opens the path previously blocked by that collider. To illustrate this, let us return to the example of maternal smoking. Since it is a collider on the aforementioned M-shaped path between preterm birth and ADHD, that path is blocked without adjusting for maternal smoking in the causal model (Rule 1). In fact, adjusting for maternal smoking would actually induce a relationship between shared genetic liability and maternal stressors, thereby opening the M-shaped path between preterm birth and ADHD and introducing bias into the estimate of the average causal effect. This bias can be positive or negative and is referred to as collider stratification bias (the more general term) or M-bias (a specific type of collider stratification bias that occurs, e.g., when adjusting for a covariate that shares a common cause with the exposure and another common cause with the outcome) [8]. To understand how adjusting for a collider introduces bias, recall that adjusting for a variable amounts to holding it constant. At a constant level of maternal smoking, knowing the mother’s stressors tells you something about their shared genetic liability, because maternal smoking is a function of shared genetic liability and maternal stressors. In this example, adjusting for maternal smoking both reduces bias (by blocking the path through maternal smoking that represents confounding) and introduces bias (by opening the M-shaped path through maternal smoking).

To eliminate bias due to other open paths between the exposure and outcome, the researcher must select a set of covariates such that all paths between the exposure and outcome are blocked, except for the path representing the causal effect of interest. Of course, in some situations (e.g., if the exposure is randomly assigned), no adjustment is needed because there are no longer any paths that have edges directed to the exposure because the only cause of the exposure is the random process. Alternatively, in other situations, even if every variable were measured, there is no set of covariates that can block all other paths. These types of situations necessitate using more complex methods of estimation [13, 14], which require their own, similarly strong assumptions. These complex methods can also be useful in situations where there is a set of covariates that block all other paths, but some or all of the covariates in that set have not been measured [15].

Illustrative Example

We now return to our example of preterm birth and ADHD. By way of background, the potential effect of preterm birth on ADHD has received considerable attention from researchers [16–20]. Most studies have documented a positive association between the two variables, and various causal mechanisms have been proposed [21, 22]. However, the interpretation of these findings is complicated by the researchers’ choice of covariates, since adjusting for additional variables in the causal model could introduce bias, depending on those variables’ actual relationship to preterm birth and ADHD. As noted above, researchers often choose to include certain covariates because they believe that they may confound the exposure-outcome relationship. For example, maternal smoking during pregnancy has been considered a potential confounder [16], leading to its inclusion as a covariate in models used to examine the relationship between preterm birth and ADHD [17, 18, 20]. However, although there is a consistent association between maternal smoking during pregnancy and child ADHD [23], maternal smoking is not necessarily a cause of ADHD; instead, the association may reflect a common cause, such as a shared genetic liability [24].

Since our example is intended for didactic purposes, we introduce several simplifying assumptions, beginning with the assumption that relevant constructs (e.g., ADHD in childhood, maternal smoking) can be measured by single variables. Critically, we assume that the DAG depicted in Figure 1 includes all paths between preterm birth and ADHD, including paths that pass through maternal smoking during pregnancy, a potential confounder. We also assume that maternal stressors during pregnancy and shared genetic liability have not been measured in the study, and it is thus not possible to include them as covariates. We recognize that, in practice, these assumptions are unlikely to be met, and thus our example is not meant to be taken as a valid analysis of the actual causal effects involved.

The DAG in Figure 1, which represents the assumed causal relationships among the variables involved, depicts several pathways by which maternal smoking could relate to preterm birth and ADHD. One of these ways is through a confounder, i.e., a cause of both preterm birth and ADHD. However, maternal smoking could also relate to the exposure and outcome through common causes (e.g., maternal stressors during pregnancy and shared genetic liability, respectively). Depending on which of these paths is present, including maternal smoking as a covariate (i.e., in the causal model for the effect of preterm birth on ADHD) could increase bias, reduce bias, or both.

Applying the graphical rules presented in Figure 2 to the question of how to handle maternal smoking, we can see that, without adjusting for maternal smoking, there are three open paths between preterm birth and ADHD, aside from the path representing the causal effect of preterm birth on ADHD. These other open paths between preterm birth and ADHD, which represent confounding, include the path that goes through maternal smoking only, the one that goes through both maternal stressors and maternal smoking, and the one that goes through both maternal smoking and shared genetic liability. Due to these open paths through maternal smoking, we can expect that unadjusted estimates of the average causal effect (of preterm birth on ADHD) will be biased. Including maternal smoking as a covariate in our causal model will block these paths, eliminating these particular sources of bias. However, adjusting for maternal smoking will also introduce collider stratification bias, as noted above. This happens because maternal smoking is a collider on the M-shaped path that connects preterm birth and ADHD via maternal stressors, maternal smoking, and shared genetic liability.

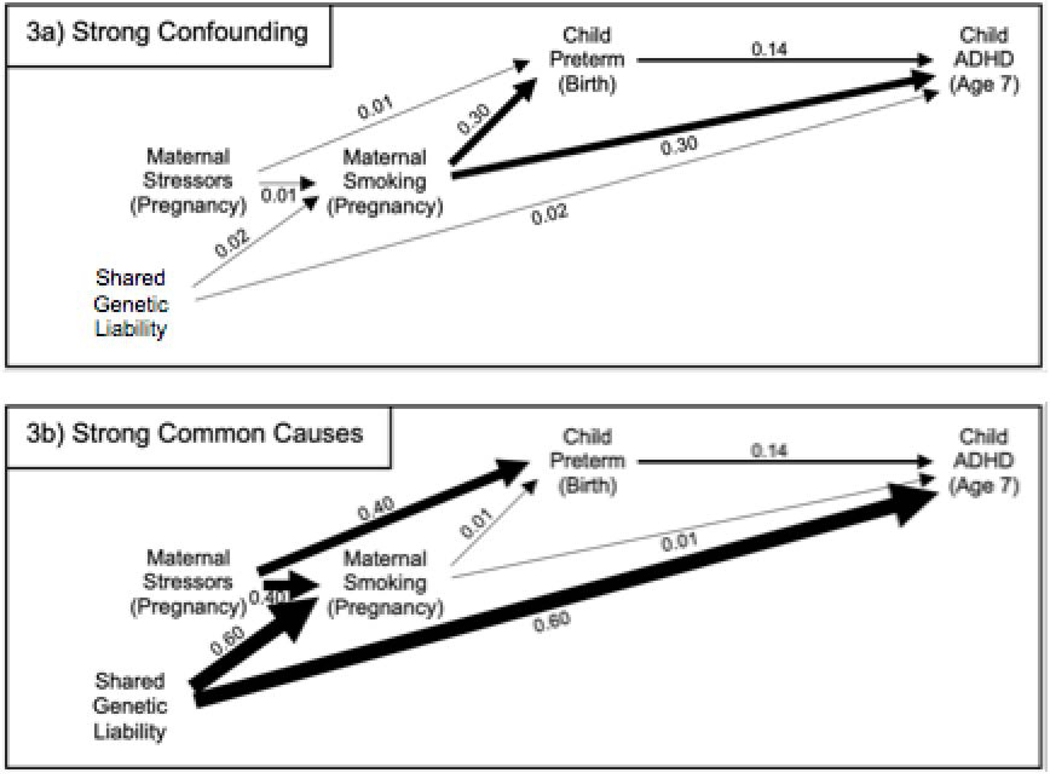
Whether blocking the three previously open paths, or opening the one previously blocked path, introduces more bias depends on the strengths of the relationship between the variables on these paths through maternal smoking. To illustrate this point, we performed simulations for two scenarios where the strengths of these relationships differ markedly (note that the selected values of the parameters were not based on actual empirical evidence from the literature, but rather were chosen to illustrate scenarios for didactic purposes). In these simulations, we make several additional simplifying assumptions,^b including assumptions that the models in our simulations are correctly specified and that predictors (e.g., preterm birth) can be measured without error; in reality, violations of these assumptions may represent additional sources of bias. In the first scenario we examine (Fig. 3a), maternal smoking during pregnancy has strong effects on preterm birth and ADHD, reflecting a scenario where maternal smoking does confound the relationship between the two. Further, in this scenario, the unmeasured common causes (i.e., maternal stressors in pregnancy and shared genetic liability) have minimal effects on maternal smoking and preterm birth and on maternal smoking and ADHD, respectively. In this scenario, the unadjusted estimate (=0.23) of the coefficient for preterm birth (i.e., in a linear regression model for ADHD fitted to the simulated data) is heavily biased away from the true value (=0.14), whereas the estimate adjusted for maternal smoking (=0.14) is effectively unbiased. This contrasts with the second scenario (Fig. 3b), where maternal smoking is a very weak confounder of the relationship between preterm birth and ADHD, but the unmeasured common causes (i.e., maternal stressors during pregnancy and shared genetic liability) have strong effects on maternal smoking and preterm birth and on maternal smoking and ADHD, respectively. In this scenario, the estimate adjusted for maternal smoking (=0.08) is more biased than the unadjusted estimate (=0.15), which is close to the true value (=0.14) of the average causal effect of preterm birth on ADHD in our simulation. Notably, neither estimate in this scenario is as biased as the unadjusted estimate in the first scenario. These results are consistent with prior theoretical work [8] and simulation studies [26, 27] of the situation where a potential covariate is both a true confounder of the exposure-outcome relationship and also a collider on another path between the exposure and outcome. These studies suggest that the bias introduced by adjusting for that covariate could be less than the bias present in an unadjusted analysis, unless the confounding effects are small compared to the effects of the unmeasured common causes.

Fig. 3. Two Scenarios for How Maternal Smoking During Pregnancy Relates to Child Preterm Birth and to Child ADHD.

It is not standard practice to include numeric values corresponding to paths, or differing edge widths in DAGs; however, we do so in Figures 3a-3b for illustrative purposes, to highlight the differing strength of the relationships depicted in the two contrasting scenarios. The magnitude of the value appearing next to an edge, and the width of the edge, both reflect the strength of the (directed) relationship between the two variables connected by the edge, in the model used to generate simulated data consistent with the DAG. (Abbreviations: ADHD = attention-deficit/hyperactivity disorder)

Discussion

As the above example illustrates, when constructing a causal model, adjusting for a given variable can reduce bias, introduce bias, or both, depending on the true causal structure between the variables in question. If the potential covariate is both a confounder of the exposure-outcome relationship and a collider on another path between them, research suggests that the confounding bias eliminated by adjusting for the covariate will likely outweigh the collider stratification bias introduced by doing so, unless the confounding effects are small compared to the effects of the unmeasured common causes. Many real-world examples, including the relationship between preterm birth and ADHD, may more closely resemble the first scenario, meaning adjusting for the potential confounder (e.g., maternal smoking) would result in less bias than failing to adjust for it. However, there are other situations where adjusting for a covariate is more likely to result in a net increase in bias. The most obvious situation is adjusting for a covariate that is an intermediate variable (i.e., a mediator) on one of the paths through which the exposure causes the outcome [28, 29]. If that path contributes substantially to the average causal effect of interest, then adjusting for an intermediate covariate can introduce considerable bias. For example, researchers examining the relationship between preterm birth and ADHD might choose to adjust for perinatal hypoxic-ischemic events because they have been considered a potential risk factor for negative cognitive outcomes [30]. However, adjusting for hypoxic-ischemic events would bias estimates of the average causal effect of preterm birth on ADHD if hypoxic-ischemic events mediate at least some of this effect. More subtly, adjusting for a covariate that is caused by an intermediate variable, but not itself on the causal path between the exposure and outcome, can introduce bias when that covariate shares an unmeasured common cause with the outcome [28]. In this scenario, the degree of bias increases the stronger the relationship between the intermediate variable and the downstream covariate and the stronger the causal path through the intermediate variable [28]. In the above example, adjusting for low Apgar scores [16, 17, 20] could bias estimates of the average causal effect of preterm birth on ADHD if low Apgar scores are caused by an intermediate variable (e.g., perinatal hypoxic-ischemic events) and also share other unmeasured common causes with child ADHD. Additionally, adjusting for a covariate that is an effect of the outcome can cause a net increase in bias, for example if the exposure has a direct effect (i.e., an effect not mediated via the outcome) on the covariate.

The challenges involved in deciding which covariates (if any) to include extends to many other situations where adjusting for particular covariates can either reduce or introduce bias, depending on the true causal structure (for examples, see [10, 31–33]). Thus, the potential inclusion of any covariate in a causal model requires careful consideration. DAGs can facilitate this consideration by illuminating the assumed underlying causal structure of the variables under study and thereby revealing the consequences of adjusting for particular covariates under a variety of assumptions. Further, the use of DAGs becomes even more helpful when relationships are more complicated, since attempts to apply simple rules without graphical justification often fails completely in such instances.

Of note, selecting covariates and interpreting causal models requires not only careful consideration, but also expert knowledge. Observational data alone are not typically sufficient to determine whether any given DAG is the true DAG, or whether any given causal model is correct [9].^c For instance, in our example, the potential covariate maternal smoking during pregnancy may be associated with the outcome ADHD because the former causes the latter; because both are caused by another, unmeasured variable (i.e., shared genetic liability); or both. We cannot determine from the dataset alone which of these is true and must instead make assumptions regarding the relationship between these variables. In common practice, both DAGs and causal models rely on the assumptions made by the researcher about the relationship of all measured and unmeasured variables in an analysis, assumptions that are typically based on previous research or knowledge of processes (e.g., biological processes) under investigation [9].

Despite causal DAGs’ utility, there are limitations that should be noted. To begin with, as illustrated in the above example, DAGs alone are insufficient to determine the direction or magnitude of bias introduced by adjustment, or lack of adjustment, for a covariate. Additionally, DAGs cannot depict the influence of effect measure modification (for example, gender as a moderator of the effect of preterm birth on ADHD) [37], although there have been attempts to extend DAGs to consider such features. Additional potential limitations to the use of causal DAGs have been raised, including the possibility of oversimplification, but are beyond the scope of this commentary [38–40].

Conclusion

In observational psychiatric research, interest often lies in the causal relationship between an exposure and outcome. To estimate this relationship, researchers fit a causal model (i.e., a model for the relationship between the exposure and the outcome) to data. Researchers often include a variety of covariates in the model, typically in hopes of obtaining more accurate estimates of the causal effect of interest. However, as we have discussed and illustrate in an example, depending on the covariates’ true relationships to the exposure and outcome, adjustment for covariates can actually introduce new bias, instead of, or in addition to, reducing bias. Therefore, researchers should carefully consider which covariates to include in a causal model, rather than simply including all covariates potentially related to the exposure or the outcomes. DAGs are a useful tool for clarifying how covariate adjustment might impact bias in an estimate. By allowing researchers to visualize the assumptions required for a particular set of covariates to block all other paths between the exposure and outcome aside from the path of interest, DAGs allow researchers to contemplate whether those assumptions are reasonable.

Appendix A: R Code for Simulations

N <- 10000
n <- 250

# Scenario 1: Strong Confounding

# True values of parameters:
Path.MatStress.to.Preterm <- 0.01
Path.MatStress.to.MatSmoke <- 0.01

Path.GenLiab.to.ChildADHD <- 0.02
Path.GenLiab.to.MatSmoke <- 0.02

Path.MatSmoke.to.Preterm <- 0.30
Path.MatSmoke.to.ChildADHD <- 0.30

Path.Preterm.to.ChildADHD <- 0.14 # Path of interest

# Store coefficient estimates from simulation
ResultsB.Unadjusted <- c()
ResultsB.Adjusted <- c()

# Conduct simulation:
set.seed(192)
for(j in 1:N)
{
    MatStress.j <- rnorm(n, 0, 1)
    GenLiab.j <- rnorm(n, 0, 1)
    
    MatSmoke.j <- Path.MatStress.to.MatSmoke*MatStress.j + Path.GenLiab.to.MatSmoke*GenLiab.j +
                  rnorm(n, 0, sd = sqrt(1 - Path.MatStress.to.MatSmokê2 - Path.GenLiab.to.MatSmokê2))
    
    Preterm.j <- Path.MatStress.to.Preterm*MatStress.j + Path.MatSmoke.to.Preterm*MatSmoke.j +
                 rnorm(n, 0, sd = sqrt(1 - Path.MatStress.to.Preterm^2 - Path.MatSmoke.to.Preterm^2))
    
    ChildADHD.j <- Path.Preterm.to.ChildADHD*Preterm.j + Path.GenLiab.to.ChildADHD*GenLiab.j +
                   Path.MatSmoke.to.ChildADHD*MatSmoke.j +
	          rnorm(n, 0, sd = sqrt(1 - Path.Preterm.to.ChildADHD^2 - Path.GenLiab.to.ChildADHD^2 - Path.MatSmoke.to.ChildADHD^2))
    
    ResultsB.Unadjusted[j] <- summary(lm(ChildADHD.j ~ Preterm.j))$coef[2,1]
    ResultsB.Adjusted[j] <- summary(lm(ChildADHD.j ~ Preterm.j + MatSmoke.j))$coef[2,1]
    
}

# View and summarize results:
ResultsB.Unadjusted
ResultsB.Adjusted

mean(ResultsB.Unadjusted)
mean(ResultsB.Adjusted)
# Scenario 2: Strong Common Causes

# True values of parameters:
Path.MatStress.to.Preterm <- 0.40
Path.MatStress.to.MatSmoke <- 0.40

Path.GenLiab.to.ChildADHD <- 0.60
Path.GenLiab.to.MatSmoke <- 0.60

Path.MatSmoke.to.Preterm <- 0.01
Path.MatSmoke.to.ChildADHD <- 0.01

Path.Preterm.to.ChildADHD <- 0.14 # Path of interest

# Store coefficient estimates from simulation
ResultsB.Unadjusted <- c()
ResultsB.Adjusted <- c()

# Conduct simulation:
set.seed(192)
for(j in 1:N)
{
    MatStress.j <- rnorm(n, 0, 1)
    GenLiab.j <- rnorm(n, 0, 1)
    
    MatSmoke.j <- Path.MatStress.to.MatSmoke*MatStress.j + Path.GenLiab.to.MatSmoke*GenLiab.j +
                  rnorm(n, 0, sd = sqrt(1 - Path.MatStress.to.MatSmokê2 - Path.GenLiab.to.MatSmokê2))
			 
    Preterm.j <- Path.MatStress.to.Preterm*MatStress.j + Path.MatSmoke.to.Preterm*MatSmoke.j +
                 rnorm(n, 0, sd = sqrt(1 - Path.MatStress.to.Preterm^2 - Path.MatSmoke.to.Preterm^2))
			
    ChildADHD.j <- Path.Preterm.to.ChildADHD*Preterm.j + Path.GenLiab.to.ChildADHD*GenLiab.j +
                   Path.MatSmoke.to.ChildADHD*MatSmoke.j +
	          rnorm(n, 0, sd = sqrt(1 - Path.Preterm.to.ChildADHD^2 - Path.GenLiab.to.ChildADHD^2 - Path.MatSmoke.to.ChildADHD^2))
			 
    ResultsB.Unadjusted[j] <- summary(lm(ChildADHD.j ~ Preterm.j))$coef[2,1]
    ResultsB.Adjusted[j] <- summary(lm(ChildADHD.j ~ Preterm.j + MatSmoke.j))$coef[2,1]

}

# View and summarize results:
ResultsB.Unadjusted
ResultsB.Adjusted

mean(ResultsB.Unadjusted)
mean(ResultsB.Adjusted)