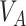Abstract
Heart-lung interaction mechanisms are generally not well understood. Mechanical ventilation, for example, accentuates such interactions and could compromise cardiac activity. Thereby, assessment of ventilation-induced changes in cardiac function is considered an unmet clinical need. We believe that mathematical models of the human cardiopulmonary system can provide invaluable insights into such cardiorespiratory interactions. In this article, we aim to use a mathematical model to explain heart-lung interaction phenomena and provide physiologic hypotheses to certain contradictory experimental observations during mechanical ventilation. To accomplish this task, we highlight three model components that play a crucial role in heart-lung interactions: 1) pericardial membrane, 2) interventricular septum, and 3) pulmonary circulation that enables pulmonary capillary compression due to lung inflation. Evaluation of the model’s response under simulated ventilation scenarios shows good agreement with experimental data from the literature. A sensitivity analysis is also presented to evaluate the relative impact of the model’s highlighted components on the cyclic ventilation-induced changes in cardiac function.
Keywords: Cardiopulmonary Model, Heart-Lung Interactions, Mechanical Ventilation
I. Introduction
The human body is a complex dynamic system with sophisticated neurohumoral control mechanisms. Besides autonomic and humoral regulatory processes, direct mechanical heart-lung interactions also exist. These arise from to the fact that the heart resides within the thoracic cavity. Respiratory activity causes cyclic variations in lung volume and in intrathoracic (pleural) pressure. Such variations are, in turn, transferred to all cardiovascular structures within the thoracic cavity, such as thoracic veins, heart, pulmonary circulation, and aorta, thus leading to cyclic changes in cardiac function. These respiratory-induced cardiac variations appear in normal breathing (pulsus paradoxus) [1], but they become accentuated in mechanically ventilated subjects under positive pressure ventilation (reversed pulsus paradoxus) [2].
Positive pressure ventilation (PPV) is a life support therapy that is typically instituted when a patient is unable to maintain adequate ventilation on their own. It is estimated that, even before the pandemic, every year nearly 1.5 million patients across the United States require some form of mechanical ventilation support [3], [4] and this number is set to increase. Despite the undoubted benefits of this therapy, PPV may cause adverse consequences as a result of the aforementioned mechanical effects of respiration on cardiac function. Selection of inappropriate ventilator settings, such as elevated pressure support or positive end-expiratory pressure (PEEP) levels, can induce substantial changes in pleural pressure and potentially compromise cardiac performance.
Balancing such ventilatory interventions requires a comprehensive understanding of the interactions between the different components of the cardiopulmonary system. These interactions can be captured 1) by black-box models, where input-output relationships are described by some form of mathematical representations without a direct physiological interpretation [5], or 2) by physiology-based mathematical models which incorporate a mechanistic description of the system being modeled. In this paper, we focus on this latter category of modeling approaches as we believe that this is better suited to the understanding of cardio-respiratory interactions. Model-based computer simulations could be effective tools to conduct 1) virtual physiological experiments, 2) analyze cardiopulmonary dynamics, 3) investigate different clinical scenarios, and 4) assess the outcomes of specific treatments [6].
Over the past few years, several investigators [7]–[10] have proposed mathematical models of the integrated cardiorespiratory physiology. However, most of the earlier work was not tailored to simulate mechanical ventilation scenarios. The model proposed by Cheng et al. [9], though comprehensive, is primarily focused on the response of the autonomic nervous system (ANS) during sleep, like Cheyne-Stokes respiration and sleep apnea. The model from Lu et al. [10], on the other hand, has more rigor in describing the dynamics associated with mechanical heart-lung interactions. However, this model is less detailed in the description of the short-term neural mechanisms that are involved in the cardiovascular and respiratory control systems. The integrated cardiopulmonary model (CP Model) that was recently introduced by our group [7], [8] features all major cardiorespiratory control mechanisms as well as cardiovascular circulation, respiratory mechanics, alveolar and tissue gas exchange, and gas transport. However, despite its rigor in neural pathways, the CP Model presented limitations in mechanical heart-lung interaction mechanisms, as highlighted by Albanese et al. [7].
Experimental studies [11] have shown that the cyclic respiratory-induced changes in cardiac activity are predominantly attributed to four elements: thoracic cavity, pericardial membrane (pericardium), interventricular septum, and pulmonary peripheral vessels whose resistance to blood flow changes as a function of alveolar volume. In this paper, we 1) incorporate an enhanced cardiac model with septum and pericardium into the original CP Model, and 2) revise the pulmonary circulation model to include a varying pulmonary peripheral resistance as a function of alveolar volume.
The manuscript is organized as follows. First, in the Methods section, we describe the CP Model and highlight the pericardial membrane, interventricular septum, and pulmonary circulation model. Second, in the Results & Validation section, we demonstrate the model’s validity by comparing its response during simulated ventilation conditions against experimental data from mechanically ventilated subjects. We also perform a sensitivity analysis to evaluate the relative impact of the model’s highlighted components to variations in cardiac function that are induced by mechanical ventilation. Additionally, we provide physiologic explanations to contradictory experimental results. Lastly, in the Discussion section, we discuss the limitations of such a model and outline future improvements.
II. Methods
A. The Cardiopulmonary Model
Fig. 1 shows the high-level block diagram of the cardiopulmonary model (CP Model). The original CP Model was developed by Albanese et al. [7] using data from healthy, spontaneously breathing, individuals and validated under hypoxia and hypercapnia by Cheng et al. [8], while Karamolegkos et al. [12] improved the model by including the Hering-Breuer reflex. Model parameters were assigned in reference to a generic 70-kg healthy subject.
Figure 1.
High-level block diagram of the cardiopulmonary model.
B. Modeling Highlights
Fig. 2 presents the cardiovascular system components that are important for studying heart-lung interactions during mechanical ventilation. Detailed description of the original CP Model can be found in [7], while we now present the details of the cardiovascular system components which gave rise to an enhanced CP Model (Fig. 2) and allowed us to study heart-lung interactions.
Figure 2.
Schematic block diagram of the cardiovascular system of the enhanced CP Model. 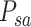 and
and 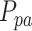 , systemic and pulmonary arterial blood pressures;
, systemic and pulmonary arterial blood pressures; 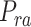 and
and 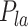 , right and left atrial pressures;
, right and left atrial pressures; 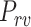 and
and 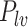 , right and left ventricular pressures;
, right and left ventricular pressures; 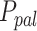 , pulmonary arteriolar pressure;
, pulmonary arteriolar pressure; 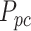 , pulmonary capillary pressure;
, pulmonary capillary pressure; 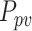 , pulmonary venous pressure;
, pulmonary venous pressure;  , pericardial pressure;
, pericardial pressure; 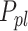 , pleural (intrathoracic) pressure;
, pleural (intrathoracic) pressure;  , alveolar pressure;
, alveolar pressure;  and
and 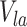 , right and left atrial volumes;
, right and left atrial volumes;  and
and  , right and left ventricular volumes;
, right and left ventricular volumes; 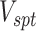 , septal volume;
, septal volume; 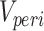 , pericardial volume;
, pericardial volume; 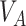 , alveolar volume;
, alveolar volume; 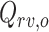 and
and 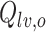 , right and left ventricular output blood flows;
, right and left ventricular output blood flows; 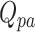 , pulmonary arterial blood flow;
, pulmonary arterial blood flow; 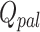 , pulmonary arteriolar blood flow;
, pulmonary arteriolar blood flow; 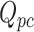 , pulmonary capillary blood flow;
, pulmonary capillary blood flow; 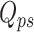 , pulmonary shunt blood flow; MV, mitral valve; AV, aortic valve; TV, tricuspid valve; PV, pulmonary valve;
, pulmonary shunt blood flow; MV, mitral valve; AV, aortic valve; TV, tricuspid valve; PV, pulmonary valve;  , imaginary plane defining the volumes of the septum and of the right and left ventricular free walls.
, imaginary plane defining the volumes of the septum and of the right and left ventricular free walls.
1). Pericardium
The pericardium is the membrane that contains the heart and serves as the connective medium between the heart and the chest wall. The mechanical behavior of the pericardium resembles that of a passive fluid chamber with nonlinear elastic properties. Thus, its pressure-volume characteristics are modeled with an exponential function as proposed by Chung et al.
[13]. Such a function relates the transmural pressure across the pericardium ( ) to the total blood volume (
) to the total blood volume ( ) enclosed by it as
) enclosed by it as
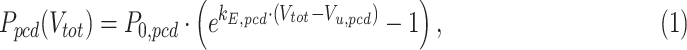 |
where 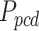 is the difference between the pressure inside the pericardial membrane (
is the difference between the pressure inside the pericardial membrane ( ) and the pleural pressure (
) and the pleural pressure (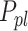 ) outside of it,
) outside of it, 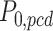 is a scaling factor,
is a scaling factor, 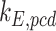 is an elastance coefficient, and
is an elastance coefficient, and 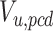 is the volume enclosed by the pericardium when the transmural pressure
is the volume enclosed by the pericardium when the transmural pressure 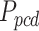 is zero (unstressed volume). The values of the parameters in (1) have been adopted from [10] and are reported in Table I.
is zero (unstressed volume). The values of the parameters in (1) have been adopted from [10] and are reported in Table I.  comprises the volumes of all four heart chambers and the volume of fluid within the pericardial space (
comprises the volumes of all four heart chambers and the volume of fluid within the pericardial space (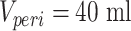 [14]). The volumes of the myocardial tissue and coronary circulation are neglected in this model.
[14]). The volumes of the myocardial tissue and coronary circulation are neglected in this model.
TABLE I. Parameters of the Heart Model in Basal Conditions.
| Parameter | RV free wall | LV free wall | Pericardium | Septum |
|---|---|---|---|---|
 (ml (ml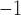 ) ) |
0.011 [15] | 0.014 [15] | 0.005 [10] | 0.175 [16] |
 (mmHg) (mmHg) |
1.5 [15] | 1.5 [15] | 0.5 [10] | 1.11 [16] |
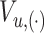 (ml) (ml) |
35.904 [7] | 14.758 [7] | 200 [10] | 0 [16] |
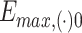 (mmHg/ml) (mmHg/ml) |
1.412 [17] | 2.392 [17] | — | 32.4 |
Note that the subscript 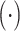 indicates the respective compartment, namely
indicates the respective compartment, namely  for the right (RV) ventricular free wall,
for the right (RV) ventricular free wall, 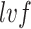 for the left ventricular (LV) free wall,
for the left ventricular (LV) free wall, 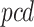 for the pericardium, and
for the pericardium, and  for the septum.
for the septum.  , elastance coefficient;
, elastance coefficient; 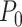 , scaling factor;
, scaling factor;  , unstressed volume;
, unstressed volume; 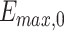 , basal value of wall elastance at the maximum contraction point (end-systole) which is subject to changes by the autonomic nervous system.
, basal value of wall elastance at the maximum contraction point (end-systole) which is subject to changes by the autonomic nervous system.
2). Interventricular Septum
The CP Model features four heart chambers. The two ventricles interact with each other due to the presence of the interventricular septum, whereas the two atria are assumed to be connected through a rigid wall since atrial interference has a minimal contribution to the overall cardiovascular hemodynamics.
To describe the interventricular septum, we follow the model proposed by Chung et al.
[13] which was validated with echocardiographic images. An imaginary plane  is assumed to split the total ventricular space into three functional volumes (see Fig. 2): a right ventricular free wall volume (
is assumed to split the total ventricular space into three functional volumes (see Fig. 2): a right ventricular free wall volume ( ), a left ventricular free wall volume (
), a left ventricular free wall volume (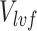 ), and a septal volume (
), and a septal volume (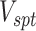 ). Each one of these three volumes represents blood volume that is bounded by the corresponding wall (namely, left and right ventricular free walls and septal wall, respectively) and the plane
). Each one of these three volumes represents blood volume that is bounded by the corresponding wall (namely, left and right ventricular free walls and septal wall, respectively) and the plane  . Furthermore, due to the natural position of the interventricular wall protruding into the right ventricle (Fig. 2), right and left ventricular volumes are defined as
. Furthermore, due to the natural position of the interventricular wall protruding into the right ventricle (Fig. 2), right and left ventricular volumes are defined as 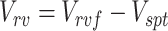 and
and  , respectively.
, respectively.
Heart contraction is simulated by the activation of the three walls delineated above. Their contractile activities are modeled by means of variable-elastance models such that the pressure-volume relationships vary between end-systolic and end-diastolic states. The transition between end-systolic and end-diastolic states is governed by a half-sine activation function 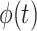 whose period is equal to the heart period [7]. The pressure-volume relationships of the two ventricular free walls remain as in [7]. For instance, the maximal isometric transmural pressure across the left ventricular free wall (
whose period is equal to the heart period [7]. The pressure-volume relationships of the two ventricular free walls remain as in [7]. For instance, the maximal isometric transmural pressure across the left ventricular free wall (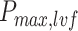 ) is defined as a function of
) is defined as a function of 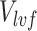 according to the equation
according to the equation
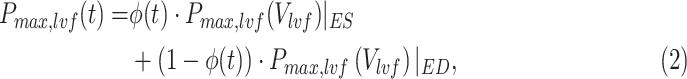 |
where  and
and 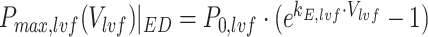 are the end-systolic (
are the end-systolic ( ) and end-diastolic (
) and end-diastolic ( ) pressure-volume relationships, respectively; these determine the elastic behavior of the free wall during a cardiac cycle.
) pressure-volume relationships, respectively; these determine the elastic behavior of the free wall during a cardiac cycle.  is the wall elastance at the maximum contraction point (end-systole),
is the wall elastance at the maximum contraction point (end-systole),  is the unstressed volume of the ventricular wall, and
is the unstressed volume of the ventricular wall, and 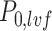 ,
,  are the parameters that characterize the end-diastolic exponential function. The maximal pressure of the left ventricle (prior to any viscous losses due to blood flow over the aortic valve) can be computed by taking into account
are the parameters that characterize the end-diastolic exponential function. The maximal pressure of the left ventricle (prior to any viscous losses due to blood flow over the aortic valve) can be computed by taking into account  , which acts as the external (reference) pressure of the ventricular free wall. Hence,
, which acts as the external (reference) pressure of the ventricular free wall. Hence,  . For the sake of brevity, the equations to simulate ventricular function, including ventricular filling, valve operation, and ventricular ejection, are omitted from this article. A detailed description of these elements can be found in [15].
. For the sake of brevity, the equations to simulate ventricular function, including ventricular filling, valve operation, and ventricular ejection, are omitted from this article. A detailed description of these elements can be found in [15].
As for the elastic properties of the right ventricular free wall and septum, an analogous approach is considered. The right ventricular free wall adheres to the same formulation of the biphasic pressure-volume relationship as in (2). On the other hand, the behavior of the septal wall is modeled via a nonlinear volume-pressure relationship similar to the approach followed in [13]. The values of the parameters that characterize the elastic properties of all three cardiac walls are reported in Table I, along with the corresponding reference sources.
Note that  in Table I indicates the basal elastance value that is modulated by the autonomic nervous system (ANS), whereas
in Table I indicates the basal elastance value that is modulated by the autonomic nervous system (ANS), whereas 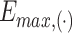 , like the one used in (2), is the resultant elastance value due to the ANS action. This is so, because the ANS efferent sympathetic pathway regulates the magnitude of cardiac contraction by controlling the elastance values of the two ventricular free walls and of the septum. The equations describing the ANS actions on the ventricular free wall elastances are kept the same as the ones in [7], which were taken from Ursino and Magosso [17]. As for the septal elastance, we follow the same approach as in [17]. The equations are reported in the Appendix.
, like the one used in (2), is the resultant elastance value due to the ANS action. This is so, because the ANS efferent sympathetic pathway regulates the magnitude of cardiac contraction by controlling the elastance values of the two ventricular free walls and of the septum. The equations describing the ANS actions on the ventricular free wall elastances are kept the same as the ones in [7], which were taken from Ursino and Magosso [17]. As for the septal elastance, we follow the same approach as in [17]. The equations are reported in the Appendix.
3). Pulmonary Circulation
Fig. 3 shows the pulmonary circulation model that is developed based on the work by Lu et al.
[10]. The model consists of four pressure nodes (pulmonary arteries ( ), pulmonary arterioles (
), pulmonary arterioles (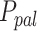 ), pulmonary capillaries (
), pulmonary capillaries ( ), and pulmonary veins (
), and pulmonary veins (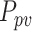 )), a pulmonary shunt compartment, and three variable resistances (pulmonary arteriolar (or pre-capillary) resistance (
)), a pulmonary shunt compartment, and three variable resistances (pulmonary arteriolar (or pre-capillary) resistance (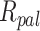 ), pulmonary shunt resistance (
), pulmonary shunt resistance (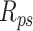 ), and pulmonary post-capillary resistance (
), and pulmonary post-capillary resistance ( )). By considering two nodes (
)). By considering two nodes (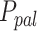 and
and  ) for the pulmonary peripheral compartment, we achieve an explicit separation between the extra-alveolar peripheral vessels (arterioles) and the capillary vessels that are near the alveoli. Pleural pressure (
) for the pulmonary peripheral compartment, we achieve an explicit separation between the extra-alveolar peripheral vessels (arterioles) and the capillary vessels that are near the alveoli. Pleural pressure (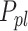 ) can then be set as the external pressure of the pulmonary arterioles (node
) can then be set as the external pressure of the pulmonary arterioles (node  in Fig. 3), while the pressure at the pulmonary capillaries (node
in Fig. 3), while the pressure at the pulmonary capillaries (node 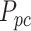 in Fig. 3) is referenced to alveolar pressure (
in Fig. 3) is referenced to alveolar pressure (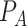 ). This configuration follows experimental evidence that the extravascular pressure of the capillaries that participate in gas exchange resembles alveolar rather than pleural pressure [11]. Additionally, this configuration allows a more accurate representation of the pulmonary shunt. Anatomically, the shunt is located between the pulmonary arteries and the pulmonary veins and comprises the pulmonary peripheral vessels that do not participate in gas exchange. Hence, it is more reasonable to model the shunt as a compartment that originates from the arteriolar pressure node and is parallel to the pulmonary capillaries (see Fig. 3).
). This configuration follows experimental evidence that the extravascular pressure of the capillaries that participate in gas exchange resembles alveolar rather than pleural pressure [11]. Additionally, this configuration allows a more accurate representation of the pulmonary shunt. Anatomically, the shunt is located between the pulmonary arteries and the pulmonary veins and comprises the pulmonary peripheral vessels that do not participate in gas exchange. Hence, it is more reasonable to model the shunt as a compartment that originates from the arteriolar pressure node and is parallel to the pulmonary capillaries (see Fig. 3).
Figure 3.
Electrical diagram of the pulmonary circulation model of the CP Model.  , air/blood pressure;
, air/blood pressure;  , blood flow;
, blood flow;  , resistance;
, resistance; 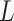 , inertance;
, inertance; 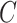 , capacitance (compliance). Subscripts:
, capacitance (compliance). Subscripts: 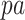 , pulmonary arteries;
, pulmonary arteries;  , pulmonary arterioles;
, pulmonary arterioles; 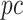 , pulmonary capillaries;
, pulmonary capillaries; 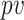 , pulmonary veins;
, pulmonary veins; 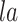 , left atrium;
, left atrium; 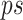 , pulmonary shunt;
, pulmonary shunt; 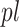 , pleural space;
, pleural space; 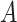 , alveolar space. The variable resistances
, alveolar space. The variable resistances 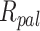 ,
, 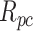 , and
, and 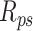 are indicated by diagonal arrows.
are indicated by diagonal arrows.
Next, we seek to capture the physiology of the compression of the pulmonary capillaries due to lung expansion [18]. Such an interaction is considered the primary factor for the increase in pulmonary impedance (thus, in right ventricular afterload), typically observed during inspiration in positive pressure ventilation [19]. To capture this phenomenon, we introduce a variable resistance (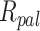 ) that changes as a function of alveolar volume (
) that changes as a function of alveolar volume ( ) and shunt fraction (
) and shunt fraction ( ):
):
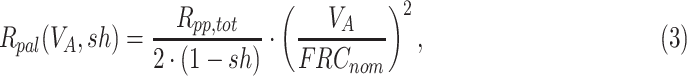 |
where 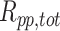 is the total resistance of the pulmonary peripheral circulation at steady-state conditions and at a nominal functional residual capacity (
is the total resistance of the pulmonary peripheral circulation at steady-state conditions and at a nominal functional residual capacity (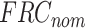 ),
),
 |
The nominal functional residual capacity ( ) is here calculated to be 2.25 liters for a nominal set of respiratory system parameters (airway resistance of 1.7459 cmH
) is here calculated to be 2.25 liters for a nominal set of respiratory system parameters (airway resistance of 1.7459 cmH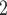 O
O s/l, and lung and chest wall compliances of 0.2 l/cmH
s/l, and lung and chest wall compliances of 0.2 l/cmH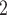 O and 0.2445 l/cmH
O and 0.2445 l/cmH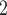 O, respectively). The complete set of equations that describe the pulmonary circulation model is presented in the Appendix.
O, respectively). The complete set of equations that describe the pulmonary circulation model is presented in the Appendix.
Table II presents the parameters of the pulmonary circulation model of Fig. 3 along with their reference sources. Note that the compliance and unstressed volume values of the pulmonary arterioles and pulmonary capillaries (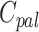 and
and 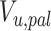 , and
, and 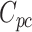 and
and 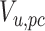 , respectively) have been computed such that their parallel arrangement (assuming zero-flow conditions) provides values equivalent to those published in [7] and [17]; namely,
, respectively) have been computed such that their parallel arrangement (assuming zero-flow conditions) provides values equivalent to those published in [7] and [17]; namely,  ml/mmHg, which is indeed the compliance of the pulmonary peripheral compartment in [17], and
ml/mmHg, which is indeed the compliance of the pulmonary peripheral compartment in [17], and 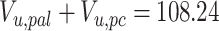 ml, which is the unstressed volume of the pulmonary peripheral circulation in [7]. To complete the calculation, we follow the convention used by Lu et al.
[10] where
ml, which is the unstressed volume of the pulmonary peripheral circulation in [7]. To complete the calculation, we follow the convention used by Lu et al.
[10] where 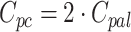 and
and 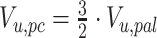 .
.
TABLE II. Parameters of the Pulmonary Circulatory System.
| Compliance (ml/mmHg) | Unstressed volume (ml) | Resistance (mmHg s/ml) s/ml) |
Inertance (mmHg s s /ml) /ml) |
|---|---|---|---|
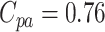 [7]
[7]
|
 [7]
[7]
|
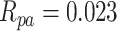 [7]
[7]
|
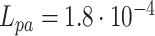 [7]
[7]
|

|

|
 [17]
[17]
|
|

|
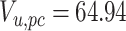
|
||
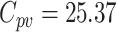 [7]
[7]
|
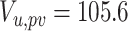 [7]
[7]
|
 [7]
[7]
|
See text and Fig. 3 legend for explanation of symbols.
III. Results & Validation
In this section, we demonstrate the capability of the CP Model in 3 steps. As a first step, we prove the model’s validity during normal resting conditions. As a second step, we perform three validation studies with real patient data followed by a sensitivity analysis, and as a third step we use the model to explain important physiological phenomena. A stability analysis of the dynamic model was omitted from this paper for brevity.
The dynamic equations of the CP Model were programmed in Simulink (MathWorks, Natick, MA). Simulation results presented in the following sections were obtained using the fourth-order Runge-Kutta method with a fixed-size integration step of 0.0005 seconds (2 kHz rate).
A. Results in Normal Resting Conditions
Table III presents the static values (at end-expiration) of the main hemodynamic variables predicted by the CP Model in normal resting conditions, along with the normal ranges observed in the general population. All variables fell within expected normal physiological ranges.
TABLE III. Static Values of Main Hemodynamic Variables in Normoxic Conditions.
| Variable | Model | Normal range |
|---|---|---|
Systemic arterial pressure,  (mmHg) (mmHg) | ||
| Mean | 89.39 | 70–105 [7] |
| Systolic | 121.85 | 100–140 [7] |
| Diastolic | 76.77 | 60–90 [7] |
Left ventricular pressure, 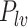 (mmHg) (mmHg) | ||
| Systolic | 121.85 | 90–140 [7] |
| End-diastolic | 4.65 | 4–12 [7] |
Left ventricular volume, 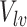 (ml) (ml) | ||
| End-systolic | 55.98 | 37–57 [20] |
| End-diastolic | 136.07 | 121–163 [20] |
Left atrial pressure, 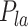 (mmHg) (mmHg) | ||
| Mean | 4.35 | 4–12 [21] |
Pulmonary arterial pressure,  (mmHg) (mmHg) | ||
| Mean | 14.35 | 9–18 [21] |
| Systolic | 26.86 | 15–28 [7] |
| Diastolic | 7.11 | 5–16 [7] |
Right ventricular pressure, 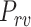 (mmHg) (mmHg) | ||
| Systolic | 26.86 | 15–28 [7] |
| End-diastolic | 1.91 | 0–8 [7] |
Right ventricular volume, 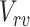 (ml) (ml) | ||
| End-systolic | 49.31 | 36–64 [22] |
| End-diastolic | 127.05 | 121–167 [22] |
Right atrial pressure,  (mmHg) (mmHg) | ||
| Mean | 1.71 | 2–6 [7] |
The model-predicted values are taken from the end-expiratory heart beat after a 2,000-second simulation.
B. Validation in Mechanical Ventilation Conditions
Validation of complex physiological models is a challenging task due to the high number parameters and variables and there has not been an established quantitative approach for validating such models [6], [23]. Nevertheless, Summers et al. [23] have proposed the following set of qualitative criteria that we have adopted in this work: the model predictions are in good agreement with experimental data when the simulated outputs 1) are directionally appropriate in a qualitative manner, 2) have steady-state values that closely match the experimental data, and 3) are fairly accurate during the transient dynamic state of the system’s response.
In this section, we aim to validate the CP Model in mechanical ventilation conditions according to the above criteria. To do so, we leverage data from three different human studies that evaluate the hemodynamic effects of mechanical ventilation during 1) changes in positive pressure ventilation (PPV) in spontaneously breathing healthy subjects [24], 2) step changes in PEEP in sedated patients [25], and 3) constant ventilatory support in sedated patients for investigating the cyclic ventilation-induced changes in cardiac function [26]. As our main goal is to show that the model is able to describe the physiology of an average patient population, rather than matching a specific patient dataset, no quantitative metric of the goodness of fit between simulated and experimental data, such as a root mean squared error, is considered.
For the simulations presented hereafter, a few parameters were adjusted from their nominal values reported in Table III. Such parameter adjustments were necessary because the baseline cardiorespiratory variables of the subjects in the three aforementioned human studies differed from their average normal values. Possible factors include the age distribution of the study population or the disease state characterizing those subjects. Note, however, that parameters were modified at the beginning of each simulation and subsequently kept constant for the duration of the simulation. This further justifies the authors’ choice not to use any goodness of fit metric for evaluating the model’s performance against experimental data.
1). Validation study 1: Changes in PPV in spontaneously breathing healthy subjects
Our first validation study [24] includes data from 18 healthy volunteers who underwent 3 consecutive 30-minute phases under different ventilation regimes while actively breathing: phase 1, normal conditions with no positive pressure ventilation (labeled as PPV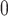 ); phase 2, ventilation with pressure support of 3 cmH
); phase 2, ventilation with pressure support of 3 cmH O and PEEP of 10 cmH
O and PEEP of 10 cmH O (labeled as PPV
O (labeled as PPV ); phase 3, ventilation with pressure support of 3 cmH
); phase 3, ventilation with pressure support of 3 cmH O and PEEP of 20 cmH
O and PEEP of 20 cmH O (labeled as PPV
O (labeled as PPV ). Magnetic resonance imaging was used to measure the volumes of the heart chambers of the study volunteers during each phase. Fig. 4 shows the comparison between experimental data and model predictions in terms of cardiac output (
). Magnetic resonance imaging was used to measure the volumes of the heart chambers of the study volunteers during each phase. Fig. 4 shows the comparison between experimental data and model predictions in terms of cardiac output ( ), heart rate (
), heart rate ( ), left (LV) and right (RV) ventricular stroke volumes (
), left (LV) and right (RV) ventricular stroke volumes ( ), end-diastolic volumes (
), end-diastolic volumes ( ), and end-systolic volumes (
), and end-systolic volumes ( ).
).
Figure 4.

Cardiovascular response to step changes in the level of positive pressure ventilation (PPV). Experimental data (black squares and error bars are means and standard errors of the means, respectively) collected during a human study with 18 spontaneously breathing healthy subjects as published by Kyhl et al.
[24]. Both model-simulated (gray circles) and experimental data are assessed at end-expiratory heart beats at the end of each 30-minute PPV period. LV, left ventricular; RV, right ventricular; 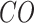 , cardiac output;
, cardiac output;  , heart rate (bpm, beats per minute);
, heart rate (bpm, beats per minute); 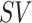 , stroke volume;
, stroke volume;  , end-diastolic volume;
, end-diastolic volume;  , end-systolic volume.
, end-systolic volume.
The baseline values (at PPV ) of
) of  and
and  of the study volunteers were abnormally high compared to the average population values in Table III. Hence, the following parameter adjustments were applied:
of the study volunteers were abnormally high compared to the average population values in Table III. Hence, the following parameter adjustments were applied:  was set to 3.05 mmHg/ml,
was set to 3.05 mmHg/ml, 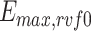 was set to 0.8 mmHg/ml,
was set to 0.8 mmHg/ml, 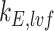 was set to 0.008 ml
was set to 0.008 ml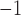 , and
, and  was set to 0.007 ml
was set to 0.007 ml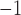 .A possible explanation for the high experimental
.A possible explanation for the high experimental 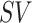 and
and 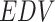 could be a low average age of the study population (16–71 years). In fact, based on the studies by Maceira et al.
[20], [22], end-diastolic and stroke volumes are inversely related to age, with younger subjects exhibiting higher cardiac volumes due to higher ventricular compliances (i.e., low elastance coefficients
could be a low average age of the study population (16–71 years). In fact, based on the studies by Maceira et al.
[20], [22], end-diastolic and stroke volumes are inversely related to age, with younger subjects exhibiting higher cardiac volumes due to higher ventricular compliances (i.e., low elastance coefficients 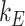 ).
).
The simulation results in Fig. 4 show that our model is able to mimic the effects of step changes in PPV on cardiac activity. All experimental and simulated cardiac volumes are reduced during positive pressure ventilation (see PPV and PPV
and PPV ), while heart rate increases due to sympathetic activation. Despite the increase in
), while heart rate increases due to sympathetic activation. Despite the increase in 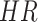 , left ventricular
, left ventricular  markedly drops as PPV is increased, thus leading to a reduction in cardiac output. The drop in
markedly drops as PPV is increased, thus leading to a reduction in cardiac output. The drop in 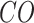 is expected since systemic venous return is reduced due to the increase in pleural pressure following the step changes in PPV. In addition, model predictions, except RV
is expected since systemic venous return is reduced due to the increase in pleural pressure following the step changes in PPV. In addition, model predictions, except RV 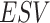 , are within one standard deviation of the sampling distribution (standard error) of the subjects for all PPV levels. Although simulated RV
, are within one standard deviation of the sampling distribution (standard error) of the subjects for all PPV levels. Although simulated RV 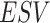 changes are directionally in agreement with those reported in [24], their magnitude is small, especially at PPV
changes are directionally in agreement with those reported in [24], their magnitude is small, especially at PPV . Such a discrepancy between model and experimental RV
. Such a discrepancy between model and experimental RV  at PPV
at PPV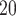 could be due to a disproportionately high model-predicted right ventricular afterload when PPV is increased which causes a high RV
could be due to a disproportionately high model-predicted right ventricular afterload when PPV is increased which causes a high RV 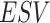 value. Right ventricular afterload is indeed directly associated with pulmonary capillary collapse, which is shown to be affected by the respiratory system’s mechanical properties (more detailed explanation is provided in the Explanation of physiological phenomena section).
value. Right ventricular afterload is indeed directly associated with pulmonary capillary collapse, which is shown to be affected by the respiratory system’s mechanical properties (more detailed explanation is provided in the Explanation of physiological phenomena section).
2). Validation Study 2: Step Changes in PEEP on Sedated Patients
Our second validation study [25] analyzes the cardiovascular response to step changes in PEEP and blood infusion (volume expansion, VE) in 8 ARDS patients. The results are summarized in Fig. 5, where model simulation results are compared against the corresponding experimental data in terms of cardiac index (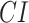 ),
), 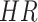 , stroke volume index (
, stroke volume index (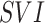 ), LV and RV end-diastolic (
), LV and RV end-diastolic (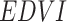 ) and end-systolic (
) and end-systolic (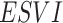 ) volume indices, and ejection fractions (
) volume indices, and ejection fractions (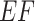 ). All volumetric indices are normalized by the body surface area (
). All volumetric indices are normalized by the body surface area (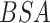 ). According to the study in [25], PEEP was adjusted from 0 to 20 cmH
). According to the study in [25], PEEP was adjusted from 0 to 20 cmH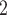 O in increments of 5 cmH
O in increments of 5 cmH O (PEEP
O (PEEP , PEEP
, PEEP , PEEP
, PEEP , PEEP
, PEEP , and PEEP
, and PEEP ). At PEEP
). At PEEP , plasma expanders (VE) were administered in order to normalize the cardiac index at a level similar to baseline (PEEP
, plasma expanders (VE) were administered in order to normalize the cardiac index at a level similar to baseline (PEEP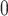 ). Each ventilatory period lasted 20 minutes and the experimental data in Fig. 5 were reported as the average values over the last 10 minutes. All other ventilator settings, besides PEEP, were kept unchanged throughout the study, with tidal volume set to 10–14 ml/kg of body weight and
). Each ventilatory period lasted 20 minutes and the experimental data in Fig. 5 were reported as the average values over the last 10 minutes. All other ventilator settings, besides PEEP, were kept unchanged throughout the study, with tidal volume set to 10–14 ml/kg of body weight and  set to 50%. No medications were administered to the subjects during the study.
set to 50%. No medications were administered to the subjects during the study.
Figure 5.

Cardiovascular response to step changes in positive end-expiratory pressure (PEEP) and blood volume expansion (VE) in ARDS subjects. Experimental data (black squares, and error bars are means and standard errors of the means, respectively) as reported by Dhainaut et al.
[25] from a human study with 8 ARDS patients. Each PEEP level is applied for 20 minutes. Both model-simulated (gray circles) and experimental data are computed at end-expiratory heart beats during the last 10 minutes of each PEEP segment. The model’s volumetric indices are normalized by assuming a nominal body surface area of 1.9 m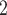 . PEEP
. PEEP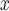 , PEEP at x cmH
, PEEP at x cmH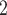 O where x = {0, 5, 10, 15, 20}; PEEP
O where x = {0, 5, 10, 15, 20}; PEEP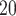 + VE, PEEP at 20 cmH
+ VE, PEEP at 20 cmH O and blood volume expansion with 625
O and blood volume expansion with 625 72 ml of plasma expanders;
72 ml of plasma expanders;  , stroke volume index;
, stroke volume index; 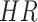 , heart rate (bpm, beats per minute);
, heart rate (bpm, beats per minute); 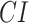 , cardiac index;
, cardiac index; 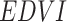 , end-diastolic volume index;
, end-diastolic volume index; 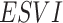 , end-systolic volume index;
, end-systolic volume index;  , ejection fraction; LV, left ventricular; RV, right ventricular.
, ejection fraction; LV, left ventricular; RV, right ventricular.
In our simulation, the experimental basal values of 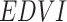 and
and 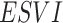 were matched by initially setting
were matched by initially setting  ,
, 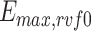 ,
, 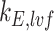 , and
, and 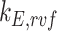 to 4 mmHg/ml, 0.4 mmHg/ml, 0.007 ml
to 4 mmHg/ml, 0.4 mmHg/ml, 0.007 ml , and 0.0065 ml
, and 0.0065 ml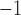 , respectively. Such parameter changes were justified because of the study population’s low average age (36 years). In order to match the elevated heart rate reported in [25], the basal heart period (
, respectively. Such parameter changes were justified because of the study population’s low average age (36 years). In order to match the elevated heart rate reported in [25], the basal heart period (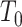 ) of the model was adjusted, from its nominal value of 0.58 seconds [7], [15] to 0.27 seconds. Additionally, the basal values of systemic and pulmonary peripheral resistances (splanchnic peripheral resistance,
) of the model was adjusted, from its nominal value of 0.58 seconds [7], [15] to 0.27 seconds. Additionally, the basal values of systemic and pulmonary peripheral resistances (splanchnic peripheral resistance, 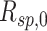 = 1 mmHg
= 1 mmHg s/ml, extrasplanchnic resistance,
s/ml, extrasplanchnic resistance, 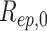 = 0.5 mmHg
= 0.5 mmHg s/ml, and total pulmonary peripheral resistance,
s/ml, and total pulmonary peripheral resistance, 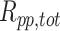 = 0.23 mmHg
= 0.23 mmHg s/ml) were changed in order to match the data in [25], i.e., a systemic and a pulmonary vascular resistance of 0.51 mmHg
s/ml) were changed in order to match the data in [25], i.e., a systemic and a pulmonary vascular resistance of 0.51 mmHg s/ml and 0.16 mmHg
s/ml and 0.16 mmHg s/ml, respectively. As for the respiratory system, we adjusted the lung and chest wall mechanical properties to be:
s/ml, respectively. As for the respiratory system, we adjusted the lung and chest wall mechanical properties to be: 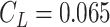 l/cmH
l/cmH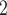 O,
O, 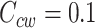 l/cmH
l/cmH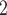 O,
O,  l, and
l, and  l. These initial changes allowed us to achieve a tidal volume of about 0.75 liters (about 11 ml/kg of body weight) and a basal mean
l. These initial changes allowed us to achieve a tidal volume of about 0.75 liters (about 11 ml/kg of body weight) and a basal mean 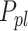 value of -1.07 cmH
value of -1.07 cmH O, compared to 0
O, compared to 0 1.6 cmH
1.6 cmH O in [25]. Also, since the experimental data were obtained from sedated patients, the ventilation control model was modified by setting the sensitivities of the central and peripheral chemoreflex mechanisms as well as the basal breathing amplitude to zero. Finally, venous admixture (pulmonary shunt fraction) and
O in [25]. Also, since the experimental data were obtained from sedated patients, the ventilation control model was modified by setting the sensitivities of the central and peripheral chemoreflex mechanisms as well as the basal breathing amplitude to zero. Finally, venous admixture (pulmonary shunt fraction) and  were set to 0.35 (35%) and 50%, respectively, as reported by Dhainaut et al.
[25].
were set to 0.35 (35%) and 50%, respectively, as reported by Dhainaut et al.
[25].
The results in Fig. 5 show that the model captures well the effect of PEEP on the overall cardiac function. Left and right ventricular  are reduced as PEEP is progressively increased due to a reduction in systemic venous return. Reduction in
are reduced as PEEP is progressively increased due to a reduction in systemic venous return. Reduction in  then leads to a decrease in
then leads to a decrease in 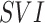 as explained by the Frank-Starling mechanism. Moreover, left ventricular
as explained by the Frank-Starling mechanism. Moreover, left ventricular 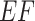 is relatively constant across the entire PEEP range, indicating that LV afterload is not significantly affected by PEEP application. In contrast, right ventricular
is relatively constant across the entire PEEP range, indicating that LV afterload is not significantly affected by PEEP application. In contrast, right ventricular 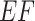 is lower at high PEEP values in both experimental and simulation results. This effectively demonstrates an elevated pulmonary impedance owing to the compression of the pulmonary capillaries by the PEEP-induced lung expansion. However, the response of the model to the VE protocol (PEEP
is lower at high PEEP values in both experimental and simulation results. This effectively demonstrates an elevated pulmonary impedance owing to the compression of the pulmonary capillaries by the PEEP-induced lung expansion. However, the response of the model to the VE protocol (PEEP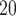 + VE) is somewhat in disagreement with the experimental results in [25]. While simulated left ventricular volume indexes return to basal values (PEEP
+ VE) is somewhat in disagreement with the experimental results in [25]. While simulated left ventricular volume indexes return to basal values (PEEP levels) after VE, in agreement with the experimental observations in [25], the model predicts an increase in RV
levels) after VE, in agreement with the experimental observations in [25], the model predicts an increase in RV 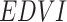 and
and  beyond their basal values, which is not found experimentally. Such a disparate behavior in RV
beyond their basal values, which is not found experimentally. Such a disparate behavior in RV 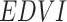 and
and  after VE has also been exhibited in human studies. The study under investigation [25] shows a complete return of RV
after VE has also been exhibited in human studies. The study under investigation [25] shows a complete return of RV 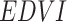 to baseline. However, an earlier study from Dhainaut et al.
[27] demonstrated a marked increase in right ventricular afterload and hence RV
to baseline. However, an earlier study from Dhainaut et al.
[27] demonstrated a marked increase in right ventricular afterload and hence RV 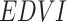 , like what our model predicts. We therefore conjecture, just as the investigators in [27] stipulate, that model simulations indicate right ventricular overload (i.e., increase in afterload) due to the collapse of the pulmonary capillaries when PEEP is increased.
, like what our model predicts. We therefore conjecture, just as the investigators in [27] stipulate, that model simulations indicate right ventricular overload (i.e., increase in afterload) due to the collapse of the pulmonary capillaries when PEEP is increased.
3). Validation Study 3: Constant Ventilatory Support on Sedated Patients
Our third validation study [26] examines the cyclic respiratory-induced variations in left and right ventricular functions during positive pressure ventilation. The study is performed on 31 sedated patients who were mechanically ventilated under a pressure-control mode with tidal volume of 7–9 ml/kg, respiratory rate of 15 breaths/minute, end-inspiratory pause of 0.5 seconds, and PEEP of 5 cmH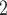 O. During the study, hemodynamic measurements were acquired via transesophageal echocardiography and the evolutions of beat-to-beat
O. During the study, hemodynamic measurements were acquired via transesophageal echocardiography and the evolutions of beat-to-beat 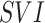 ,
, 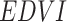 , and
, and 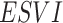 during a breathing cycle were analyzed.
during a breathing cycle were analyzed.
To match the baseline conditions of the subjects in the study, some parameters of the cardiovascular and respiratory systems in our model were modified. Namely, we set 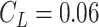 l/cmH
l/cmH O,
O, 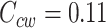 l/cmH
l/cmH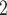 O,
O, 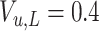 l, and
l, and  l in order to get: a total respiratory system compliance of 0.039 l/cmH
l in order to get: a total respiratory system compliance of 0.039 l/cmH O (the average compliance reported in [26] is 0.038
O (the average compliance reported in [26] is 0.038 0.007 l/cmH
0.007 l/cmH O), a tidal volume of about 0.6 liters (about 8.5 ml/kg of body weight, compared with 7–9 ml/kg in [26]) and a pleural pressure value of −1.75 cmH
O), a tidal volume of about 0.6 liters (about 8.5 ml/kg of body weight, compared with 7–9 ml/kg in [26]) and a pleural pressure value of −1.75 cmH O at the end of expiration (
O at the end of expiration (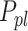 = −2.04
= −2.04 0.14 cmH
0.14 cmH O in [26]). In the cardiovascular compartment, we modified the following parameters:
O in [26]). In the cardiovascular compartment, we modified the following parameters: 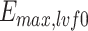 ,
, 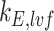 ,
, 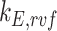 ,
,  , and
, and  to 1.9 mmHg/ml, 0.016 ml
to 1.9 mmHg/ml, 0.016 ml , 0.011 ml
, 0.011 ml , 0.8 mmHg, and 1.5 mmHg, respectively. As in the previous ARDS study, we altered the model’s systemic peripheral resistances (
, 0.8 mmHg, and 1.5 mmHg, respectively. As in the previous ARDS study, we altered the model’s systemic peripheral resistances (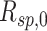 = 3 mmHg
= 3 mmHg s/ml and
s/ml and 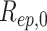 = 1 mmHg
= 1 mmHg s/ml) in order to match the basal systemic vascular resistance (
s/ml) in order to match the basal systemic vascular resistance (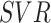 ) that was computed from the data in [26] as the ratio between mean arterial blood pressure (
) that was computed from the data in [26] as the ratio between mean arterial blood pressure (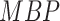 ) and cardiac output, i.e.,
) and cardiac output, i.e., 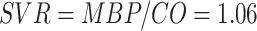 mmHg
mmHg s/ml. Finally, to simulate the effects of sympathomimetic drugs, we decreased the basal heart period to 0.35 seconds to get a basal heart rate close to the experimental value (94
s/ml. Finally, to simulate the effects of sympathomimetic drugs, we decreased the basal heart period to 0.35 seconds to get a basal heart rate close to the experimental value (94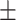 13 bpm).
13 bpm).
The results are summarized in Fig. 6 and demonstrate that the model outputs follow the trends in the experimental data for most of the indices. In particular, left ventricular 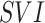 reaches its minimum at end-expiration and its maximum at the end of inhalation. A similar trend is also observed for LV
reaches its minimum at end-expiration and its maximum at the end of inhalation. A similar trend is also observed for LV  as per the Frank-Starling mechanism. The increase in left ventricular
as per the Frank-Starling mechanism. The increase in left ventricular 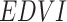 with inhalation is ascribed to the compression of the pulmonary peripheral vessels that promotes more blood into the left atrium and increases left ventricular filling. As to LV
with inhalation is ascribed to the compression of the pulmonary peripheral vessels that promotes more blood into the left atrium and increases left ventricular filling. As to LV  , Vieillard-Baron et al.
[26] report a statistically insignificant change in
, Vieillard-Baron et al.
[26] report a statistically insignificant change in 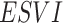 during the breathing cycle. Although the simulated variations in LV
during the breathing cycle. Although the simulated variations in LV  are not directionally similar to the experimental data, we notice that their magnitude is considerably smaller than the intra-breath changes in
are not directionally similar to the experimental data, we notice that their magnitude is considerably smaller than the intra-breath changes in 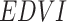 and
and 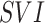 . The inspiratory decrease in LV
. The inspiratory decrease in LV 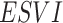 predicted by our model is nevertheless supported by other investigators [28].
predicted by our model is nevertheless supported by other investigators [28].
Figure 6.

Cyclic intra-breath changes in left (left column) and right (right column) ventricular functions during positive pressure ventilation. Experimental data (black squares, and error bars are means and standard errors of the means, respectively) as reported by Vieillard-Baron et al.
[26] from a study with 31 fully sedated patients under mechanical ventilation. Both model (gray circles) and experimental data are with reference to the left vertical axes in each subfigure. Note that [26] does not report measurements for RV 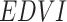 and
and 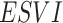 . LV, left ventricular; RV, right ventricular;
. LV, left ventricular; RV, right ventricular; 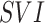 , stroke volume index;
, stroke volume index; 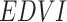 , end-diastolic volume index;
, end-diastolic volume index; 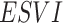 , end-systolic volume index;
, end-systolic volume index; 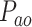 (overlaid on the right vertical axes), airway opening pressure.
(overlaid on the right vertical axes), airway opening pressure.
The right ventricle, on the other hand, is primarily affected by changes in pleural pressure. An increase in pleural pressure during inhalation decreases systemic venous return and hence right ventricular filling (end-diastolic volume). This, in turn, leads to a reduction of right ventricular stroke volume as per the Frank-Starling mechanism. RV 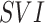 reaches its minimum value during the end-inspiratory pause and then increases back to baseline during exhalation, which is also linked to the withdrawal of pressure support. Model simulations of right ventricular
reaches its minimum value during the end-inspiratory pause and then increases back to baseline during exhalation, which is also linked to the withdrawal of pressure support. Model simulations of right ventricular 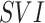 are directionally in agreement with the experimental data, although the simulated beat-to-beat changes are more pronounced in magnitude. Such a discrepancy cannot be sufficiently explained due to lack of RV
are directionally in agreement with the experimental data, although the simulated beat-to-beat changes are more pronounced in magnitude. Such a discrepancy cannot be sufficiently explained due to lack of RV 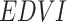 and
and 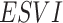 data as reported by [26]. However, in line with previous studies [29], the model-predicted intra-breath variation in RV
data as reported by [26]. However, in line with previous studies [29], the model-predicted intra-breath variation in RV 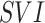 (about 10 ml/m
(about 10 ml/m ) is larger than the variation in LV
) is larger than the variation in LV  (about 5 ml/m
(about 5 ml/m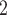 ). This phenomenon is ascribed to the damping effect of the pulmonary circulation (i.e., pulmonary hydraulic impedance); namely, at every breath, for any given respiratory-induced increase in RV stroke volume, the corresponding increase in LV stroke volume is of smaller amplitude [29]. This is because the pulmonary circulation effectively accommodates for part of the blood volume that is ejected from the right ventricle before it reaches the left heart [30].
). This phenomenon is ascribed to the damping effect of the pulmonary circulation (i.e., pulmonary hydraulic impedance); namely, at every breath, for any given respiratory-induced increase in RV stroke volume, the corresponding increase in LV stroke volume is of smaller amplitude [29]. This is because the pulmonary circulation effectively accommodates for part of the blood volume that is ejected from the right ventricle before it reaches the left heart [30].
C. Sensitivity Analysis
In the previous sections, we demonstrated the capability of the CP Model to replicate the physiological effects of mechanical ventilation on cardiac function. As a next step, we conduct a sensitivity analysis to examine the relative impact of the three highlighted model components (septum, pericardium, and pulmonary circulation model) on the CP Model’s capability to capture the heart-lung interactions during a breathing cycle. Such a sensitivity analysis complements the parameter sensitivity analysis conducted in [31].
For each of the three model components, we choose a key model parameter (physical property) for which a deviation from its nominal value would be indicative of a specific clinical pathology. For the pericardium, we choose the pericardial elastance (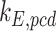 in Table I) because an increase in
in Table I) because an increase in 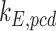 is associated with a stiffer pericardium, and thus indicative of constrictive pericarditis. For the septum, we choose the septal elastance (
is associated with a stiffer pericardium, and thus indicative of constrictive pericarditis. For the septum, we choose the septal elastance (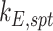 in Table I) because an increase in
in Table I) because an increase in 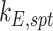 may be indicative of ventricular hypertrophy. Lastly, for the pulmonary circulation, we choose the total peripheral resistance of the pulmonary circulation (
may be indicative of ventricular hypertrophy. Lastly, for the pulmonary circulation, we choose the total peripheral resistance of the pulmonary circulation ( in (3)) since an increase in
in (3)) since an increase in  may represent a condition of pulmonary embolism.
may represent a condition of pulmonary embolism.
We then simulate changes in the values of the aforementioned parameters (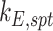 ,
,  , or
, or  ) by setting them to 0.5 x baseline and 2 x baseline while examining stroke volume variations (
) by setting them to 0.5 x baseline and 2 x baseline while examining stroke volume variations ( ) of both left and right ventricles.
) of both left and right ventricles.  is an index that is widely used clinically [28] to characterize the heart-lung interactions by summarizing the extent to which cardiac function is affected by mechanical ventilation. It is computed as:
is an index that is widely used clinically [28] to characterize the heart-lung interactions by summarizing the extent to which cardiac function is affected by mechanical ventilation. It is computed as:
 |
where 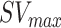 and
and  are the maximum and minimum
are the maximum and minimum 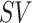 values within a breathing cycle, respectively.
values within a breathing cycle, respectively.
Table IV and Table V present the values of LV and RV 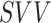 as the septal and pericardial elastances and the total pulmonary peripheral resistance are perturbed from their baseline values reported in Table I and Table II. We examined changes in the parameter values by 0.5 x baseline and 2 x baseline. Table IV and Table V also include the ratio (P/B, perturbed over baseline) between perturbed and baseline
as the septal and pericardial elastances and the total pulmonary peripheral resistance are perturbed from their baseline values reported in Table I and Table II. We examined changes in the parameter values by 0.5 x baseline and 2 x baseline. Table IV and Table V also include the ratio (P/B, perturbed over baseline) between perturbed and baseline  values. A P/B ratio larger (or smaller) than one indicates that the associated parameter change resulted in an increase (or decrease) in
values. A P/B ratio larger (or smaller) than one indicates that the associated parameter change resulted in an increase (or decrease) in 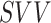 .
.
TABLE IV. Effects of Septal and Pericardial Elastances on Ventricular Stroke Volume Variation.
LV 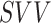
|
RV 
|
||||
|---|---|---|---|---|---|
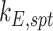
|

|
Value (%) | P/B | Value (%) | P/B |
| 0.5 x baseline | 0.5 x baseline | 13.92 | 1.20 | 21.85 | 1.10 |
| baseline | 14.27 | 1.23 | 21.94 | 1.10 | |
| 2 x baseline | 15.16 | 1.31 | 22.62 | 1.14 | |
| baseline | 0.5 x baseline | 11.30 | 0.97 | 19.42 | 0.98 |
| baseline | 11.59 | — | 19.86 | — | |
| 2 x baseline | 12.47 | 1.08 | 20.29 | 1.02 | |
| 2 x baseline | 0.5 x baseline | 10.19 | 0.88 | 18.65 | 0.94 |
| baseline | 10.31 | 0.89 | 18.75 | 0.94 | |
| 2 x baseline | 11.06 | 0.95 | 19.18 | 0.97 | |
Left and right ventricular stroke volume variation ( ) are computed over a breathing cycle as septal (
) are computed over a breathing cycle as septal (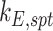 ) and pericardial (
) and pericardial ( ) elastances are perturbed from their baseline values, and ratio (P/B, perturbed over baseline) of perturbed LV and RV
) elastances are perturbed from their baseline values, and ratio (P/B, perturbed over baseline) of perturbed LV and RV 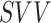 with respect to baseline.
with respect to baseline.
TABLE V. Effect of Total Pulmonary Peripheral Resistance on Stroke Volume Variation.
LV 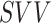
|
RV 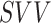
|
|||
|---|---|---|---|---|
|
Value (%) | P/B | Value (%) | P/B |
| 0.5 x baseline | 12.40 | 1.07 | 19.65 | 0.99 |
| baseline | 11.59 | — | 19.86 | — |
| 2 x baseline | 10.81 | 0.93 | 21.29 | 1.07 |
Left and right ventricular stroke volume variation (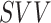 ) are computed over a breathing cycle as total pulmonary peripheral resistance (
) are computed over a breathing cycle as total pulmonary peripheral resistance (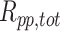 ) is perturbed from its baseline value, and ratio (P/B) of perturbed LV and RV
) is perturbed from its baseline value, and ratio (P/B) of perturbed LV and RV  with respect to baseline.
with respect to baseline.
Table IV reinforces the fact that the septum has a predominant role in affecting left ventricular performance, which has also been supported by studies in the literature [11]. A twofold decrease in septal elastance (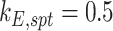 x baseline) causes an appreciable increase in LV
x baseline) causes an appreciable increase in LV  , while the same fold decrease in pericardial elastance (
, while the same fold decrease in pericardial elastance (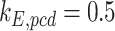 x baseline) causes a decrease in LV
x baseline) causes a decrease in LV  (P/B of 1.23 vs 0.97, respectively). On the other hand, stiffening the pericardium (
(P/B of 1.23 vs 0.97, respectively). On the other hand, stiffening the pericardium (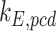 = 2 x baseline) compresses the pericardial space, hence resulting in larger intra-breath swings in stroke volume and a larger
= 2 x baseline) compresses the pericardial space, hence resulting in larger intra-breath swings in stroke volume and a larger  . Table IV also shows that RV
. Table IV also shows that RV 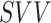 is less affected by changes in septal and pericardial elastances because it is primarily driven by the cyclic respiratory-induced variations in venous return (this physiological fact is also evident in the model). Table V demonstrates that changes in pulmonary peripheral resistance have minimal impact on LV and RV
is less affected by changes in septal and pericardial elastances because it is primarily driven by the cyclic respiratory-induced variations in venous return (this physiological fact is also evident in the model). Table V demonstrates that changes in pulmonary peripheral resistance have minimal impact on LV and RV 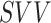 . Nevertheless, it is valuable to note that changes in
. Nevertheless, it is valuable to note that changes in 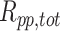 affect the two ventricles in opposite ways; that is, an increase in
affect the two ventricles in opposite ways; that is, an increase in  reduces LV
reduces LV 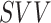 , but increases RV
, but increases RV 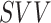 . This is so since the pulmonary circulation is anatomically positioned between the right and left ventricles.
. This is so since the pulmonary circulation is anatomically positioned between the right and left ventricles.
D. Explanation of physiological phenomena
The following sections show how the CP Model can be used to explain physiologic phenomena that occur during mechanical ventilation conditions. First, we analyze the effects of PEEP on left and right ventricular functions via the Frank-Starling curves. Second, we illustrate the significance of the mechanical properties of the respiratory system in altering the effects of PEEP application on RV function and on the septum. This analysis also allows for the explanations of contradictory experimental results reported in the literature. Third, we demonstrate the intra-breath hemodynamic effects of mechanical ventilation on left and right ventricular preload, afterload, ejection fraction, and arterial pulse pressure.
1). Frank-Starling Curves
As shown in Figs. 4 and 5, the CP Model is able to capture the effect of PEEP on cardiac activity. The marked drop in the simulated cardiac output as PEEP is increased can be explained by the Frank-Starling mechanism and it is primarily due to a reduction in ventricular filling (preload). The decrease in preload is attributed to a reduction in venous return that is driven by the step increase in the external positive pressure. The underlying effects of the Frank-Starling mechanism on both left and right ventricular functions can be illustrated in Fig. 7. Fig. 7 presents left and right ventricular cardiac indices as functions of the corresponding 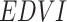 (preload) for all PEEP levels and it shows model outputs reproducing the Frank-Starling law. Note that, as mentioned in the Results & Validation section, volume expansion (VE) entirely reversed the output of both ventricles; namely, right and left cardiac indices at PEEP
(preload) for all PEEP levels and it shows model outputs reproducing the Frank-Starling law. Note that, as mentioned in the Results & Validation section, volume expansion (VE) entirely reversed the output of both ventricles; namely, right and left cardiac indices at PEEP + VE returned to about the same levels as those at PEEP
+ VE returned to about the same levels as those at PEEP . However, right ventricular
. However, right ventricular  at PEEP
at PEEP + VE was higher than its basal value (PEEP
+ VE was higher than its basal value (PEEP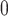 ), an indication of right ventricular overload. This phenomenon resulted in the deviation of the “PEEP
), an indication of right ventricular overload. This phenomenon resulted in the deviation of the “PEEP + VE” point from the right ventricular function curve in Fig. 7.
+ VE” point from the right ventricular function curve in Fig. 7.
Figure 7.
Model-simulated Frank-Starling curves describing cardiac index (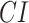 ) with end-diastolic volume index (
) with end-diastolic volume index ( ) for left (black curve) and right (gray curve) ventricles. Filled circles indicate
) for left (black curve) and right (gray curve) ventricles. Filled circles indicate 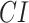 versus
versus 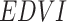 at different PEEP levels from 0 cmH
at different PEEP levels from 0 cmH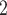 O to 20 cmH
O to 20 cmH O. Hollow circles represent
O. Hollow circles represent  versus
versus 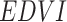 at PEEP
at PEEP and volume expansion (VE).
and volume expansion (VE).
Fig. 7 also reveals that the inotropic states of the two ventricles remain relatively unchanged with PEEP application since all respective points fall close to a fitted quadratic ventricular function curve (an increase in ventricular inotropy is indicated by a shift of the Frank-Starling curve upward and to the left). Further evidence of a constant inotropic states is provided by the model-predicted maximal ventricular elastances (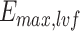 and
and 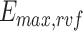 ). Both neural-modulated elastances attain values close to their basal conditions (at PEEP
). Both neural-modulated elastances attain values close to their basal conditions (at PEEP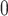 ) for all PEEP levels; that is,
) for all PEEP levels; that is,  , 4.540, 4.542, 4.554, and 4.577 mmHg/ml and
, 4.540, 4.542, 4.554, and 4.577 mmHg/ml and  , 0.721, 0.722, 0.729, and 0.742 mmHg/ml for PEEP
, 0.721, 0.722, 0.729, and 0.742 mmHg/ml for PEEP , PEEP
, PEEP , PEEP
, PEEP , PEEP
, PEEP , and PEEP
, and PEEP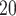 , respectively. These model predictions are in agreement with Huemer et al.
[32] and Jardin et al.
[33] who demonstrated that ventricular inotropy is independent of preload and constant over a wide range of afterload. In particular, they showed that changes in PEEP have moderate effects on the end-systolic left and right ventricular contractilities (i.e., inotropic states), despite the presence of some compensatory sympathetic activation due to the decrease in cardiac output (especially at high PEEP levels).
, respectively. These model predictions are in agreement with Huemer et al.
[32] and Jardin et al.
[33] who demonstrated that ventricular inotropy is independent of preload and constant over a wide range of afterload. In particular, they showed that changes in PEEP have moderate effects on the end-systolic left and right ventricular contractilities (i.e., inotropic states), despite the presence of some compensatory sympathetic activation due to the decrease in cardiac output (especially at high PEEP levels).
2). PEEP Effects on RV Function and Septum
The mechanism of reduction in venous return due to an increase in PEEP is well established in the literature. However, contradictory results have been reported regarding the effects of PEEP on right ventricular volume. For instance, Dhainaut et al.
[25] showed that a reduction in systemic venous return driven by a PEEP increase ultimately reduces right ventricular volumes (see RV  and
and 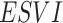 in Fig. 5). On the other hand, an earlier study by the same authors [27] as well as experimental data by Jardin et al.
[30] had demonstrated an increase in the size of the right ventricle when PEEP was instituted. This phenomenon was attributed to an increase in pulmonary system impedance (RV afterload) that could, in turn, lead to right ventricular overloading (if excessive PEEP levels are applied) [27], [30].
in Fig. 5). On the other hand, an earlier study by the same authors [27] as well as experimental data by Jardin et al.
[30] had demonstrated an increase in the size of the right ventricle when PEEP was instituted. This phenomenon was attributed to an increase in pulmonary system impedance (RV afterload) that could, in turn, lead to right ventricular overloading (if excessive PEEP levels are applied) [27], [30].
A way to explain such contradictory experimental results is to investigate how changes in right ventricular function relate to the partitioning of the respiratory system elastance ( ) into lung (
) into lung (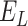 ) and chest wall components (
) and chest wall components (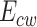 ). We hypothesize that the
). We hypothesize that the 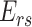 partitioning alters the effects of PEEP on right ventricular preload and afterload. It is a known fact that for a given value of
partitioning alters the effects of PEEP on right ventricular preload and afterload. It is a known fact that for a given value of 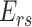 (
(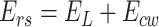 ), the same change in PEEP would result in different changes in pleural pressure (
), the same change in PEEP would result in different changes in pleural pressure (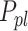 ) depending on the ratio between
) depending on the ratio between 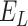 and
and  . Specifically, a low
. Specifically, a low  (high lung compliance) coupled with a high
(high lung compliance) coupled with a high 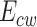 would induce a notable increase in
would induce a notable increase in 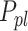 as a response to an increase in PEEP level. In contrast, a high
as a response to an increase in PEEP level. In contrast, a high  coupled with a low
coupled with a low 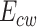 would produce a smaller increase in
would produce a smaller increase in 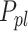 in response to the same PEEP variation. In addition, as previously illustrated, 1) right ventricular preload (
in response to the same PEEP variation. In addition, as previously illustrated, 1) right ventricular preload (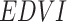 ) is influenced by pleural pressure via changes in systemic venous return, and 2) right ventricular afterload (
) is influenced by pleural pressure via changes in systemic venous return, and 2) right ventricular afterload ( ) depends on the level of pulmonary capillary compression (pulmonary impedance) from lung expansion. As such, the different
) depends on the level of pulmonary capillary compression (pulmonary impedance) from lung expansion. As such, the different  partitioning could be the explanation behind the contradictory experimental results found in the studies by Dhainaut et al.
[25] and Jardin et al.
[27], [30].
partitioning could be the explanation behind the contradictory experimental results found in the studies by Dhainaut et al.
[25] and Jardin et al.
[27], [30].
To investigate this hypothesis, we set up our CP Model to simulate the response of subjects with different 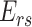 partitioning into
partitioning into 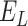 and
and  . In the literature, profound differences in the
. In the literature, profound differences in the  partitioning have been reported between two groups of ARDS patients: 1) ARDS patients with pulmonary diseases such as pneumonia (ARDS
partitioning have been reported between two groups of ARDS patients: 1) ARDS patients with pulmonary diseases such as pneumonia (ARDS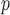 ), and 2) ARDS patients with extra-pulmonary diseases such as peritonitis (ARDS
), and 2) ARDS patients with extra-pulmonary diseases such as peritonitis (ARDS ). In a study by Gattinoni et al.
[34], the ARDS
). In a study by Gattinoni et al.
[34], the ARDS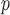 group had
group had 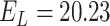 cmH
cmH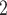 O/l and
O/l and  cmH
cmH O/l, whereas the ARDS
O/l, whereas the ARDS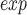 group had
group had 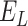 = 15.95 cmH
= 15.95 cmH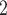 O/l and
O/l and  = 15.88 cmH
= 15.88 cmH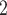 O/l (all values are at zero PEEP), with
O/l (all values are at zero PEEP), with  being approximately the same between the two groups. Based on this, we use the CP Model to simulate the response of the two ARDS groups (ARDS
being approximately the same between the two groups. Based on this, we use the CP Model to simulate the response of the two ARDS groups (ARDS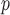 and ARDS
and ARDS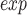 ) under a PEEP-step protocol. Fig. 8 compares the simulated cardiovascular responses (LV and RV
) under a PEEP-step protocol. Fig. 8 compares the simulated cardiovascular responses (LV and RV 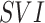 ,
, 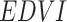 , and
, and 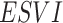 ) for ARDS
) for ARDS (black squares) and ARDS
(black squares) and ARDS (gray circles) as PEEP is increased from 0 to 20 cmH
(gray circles) as PEEP is increased from 0 to 20 cmH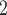 O in steps of 5 cmH
O in steps of 5 cmH O. The notable discrepancy in the direction of change of the RV
O. The notable discrepancy in the direction of change of the RV  as PEEP increases (lower right subfigure of Fig. 8) clearly illustrates that the different
as PEEP increases (lower right subfigure of Fig. 8) clearly illustrates that the different  partitioning between ARDS
partitioning between ARDS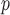 and ARDS
and ARDS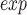 alters the effect of PEEP on the loading status of the right ventricle. It is clear from simulation that right ventricular
alters the effect of PEEP on the loading status of the right ventricle. It is clear from simulation that right ventricular  decreases for ARDS
decreases for ARDS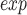 due to a marked drop in
due to a marked drop in  , whereas it increases for ARDS
, whereas it increases for ARDS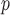 . The increase in RV
. The increase in RV 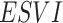 for ARDS
for ARDS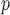 is a direct consequence of 1) the increased right ventricular afterload (pulmonary impedance) that is caused by the compression of the pulmonary peripheral vessels, and 2) the moderate decrease in RV preload (
is a direct consequence of 1) the increased right ventricular afterload (pulmonary impedance) that is caused by the compression of the pulmonary peripheral vessels, and 2) the moderate decrease in RV preload (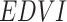 ). The small decrease in
). The small decrease in 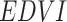 is attributed to the combination of stiff lungs (high
is attributed to the combination of stiff lungs (high  ) with a more compliant chest wall (low
) with a more compliant chest wall (low  ) that characterizes the ARDS
) that characterizes the ARDS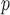 condition. It is worth noting that these opposite RV
condition. It is worth noting that these opposite RV 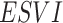 responses between ARDS
responses between ARDS and ARDS
and ARDS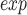 occur despite the overall decrease in systemic venous return that causes a reduction in left and right ventricular
occur despite the overall decrease in systemic venous return that causes a reduction in left and right ventricular 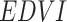 and
and 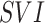 in both cases. These observations then suggest that institution of PEEP on a patient with ARDS
in both cases. These observations then suggest that institution of PEEP on a patient with ARDS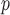 may lead to right ventricular overloading, potentially causing right ventricular failure [35], despite the overall decrease in systemic venous return.
may lead to right ventricular overloading, potentially causing right ventricular failure [35], despite the overall decrease in systemic venous return.
Figure 8.

Cardiovascular response to step changes in the level of positive end-expiratory pressure (PEEP) of a virtual patient with either pulmonary ARDS (ARDS , black squares) or extra-pulmonary ARDS (ARDS
, black squares) or extra-pulmonary ARDS (ARDS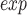 , gray circles). Each PEEP level is applied for a period of 20 minutes and simulation results are averaged over the last 10 minutes of each PEEP segment. LV, left ventricular; RV, right ventricular;
, gray circles). Each PEEP level is applied for a period of 20 minutes and simulation results are averaged over the last 10 minutes of each PEEP segment. LV, left ventricular; RV, right ventricular; 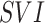 , stroke volume index;
, stroke volume index; 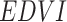 , end-diastolic volume index;
, end-diastolic volume index; 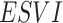 , end-systolic volume index.
, end-systolic volume index.
Contradictory experimental findings have also been reported regarding the movement of the septum in response to changes in PEEP. Some researchers, like Jardin et al.
[30], [33], demonstrated that PEEP application increases the septal curvature by shifting the interventricular septum leftwards (the curvature is an indication of the position of the septum inside the heart). Such a septal movement effectively constricts the left ventricle, thereby reducing left ventricular filling and ejection capacity. In contrast, studies by Dhainaut et al.
[27] and Huemer et al.
[32] showed negligible ventricular interdependence with a minimal change in the radius of the septal curvature. To explain such contradictory observations, again, we simulated results for ARDS and ARDS
and ARDS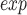 . In the ARDS
. In the ARDS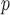 case, the model outputs show that the increased right ventricular afterload (
case, the model outputs show that the increased right ventricular afterload (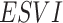 ) after a PEEP increase reduces the septal volume, effectively pushing the septum toward the left ventricular free wall. Specifically,
) after a PEEP increase reduces the septal volume, effectively pushing the septum toward the left ventricular free wall. Specifically, 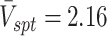 , 2.12, 2.06, 1.99, and 1.93 ml for PEEP = 0, 5, 10, 15, and 20 cmH
, 2.12, 2.06, 1.99, and 1.93 ml for PEEP = 0, 5, 10, 15, and 20 cmH O, respectively, where
O, respectively, where  is the average septal volume over the last 10 minutes of each PEEP interval. In contrast, the ARDS
is the average septal volume over the last 10 minutes of each PEEP interval. In contrast, the ARDS simulations show an increase in septal volume from 2 ml at PEEP
simulations show an increase in septal volume from 2 ml at PEEP to 2.37 ml at PEEP
to 2.37 ml at PEEP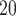 , indicating a septal movement toward the right ventricular free wall. This direction in the movement of the septum is attributed to the marked reduction in the right ventricular
, indicating a septal movement toward the right ventricular free wall. This direction in the movement of the septum is attributed to the marked reduction in the right ventricular 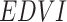 in the ARDS
in the ARDS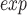 case (see Fig. 8).
case (see Fig. 8).
3). Intra-Breath Hemodynamic Effects of Mechanical Ventilation
In the previous sections, we described heart-lung interaction phenomena during PEEP application. We now focus on the hemodynamic effects of mechanical ventilation over a breathing cycle. Ventricular function is usually described by three indicators: preload, afterload, and ejection fraction. Preload is defined as the level of stretching of the cardiac myocytes immediately before contraction. Afterload is the maximal stress applied on the ventricular wall during contraction and is associated with the load that the ventricle needs to overcome to eject blood. Finally, ejection fraction is the proportion of blood pumped by a ventricle per cardiac cycle, and depends on both preload and afterload. Positive pressure ventilation is known to affect all three indicators. For instance, Fig. 9 qualitatively summarizes, based on experimental evidence by Michard and Teboul [28], the changes induced by mechanical ventilation on left and right ventricular functions. Fig. 10 depicts beat-to-beat changes in preload, afterload, and ejection fraction as simulated by our CP Model. It is evident that the simulations in Fig. 10 are qualitatively in good agreement with Fig. 9. We know that positive pressure inhalation induces lung expansion by increasing transpulmonary and pleural pressures. We then observe that these positive swings in pleural pressure reduce right ventricular preload via a reduction in systemic venous return (see Fig. 9 and black bars in right plot of Fig. 10). Such pleural pressure swings also increase pericardial pressure, which prompts a decrease in left ventricular transmural pressure. Since afterload depends on the pressure across the ventricular wall, a reduction in transmural systolic pressure lowers the afterload of the left ventricle (see Fig. 9 and gray bars in left plot of Fig. 10). At the same time, inspiratory elevation of alveolar pressure and compression of the pulmonary peripheral vessels due to lung inflation have two consequences: 1) an increase in RV afterload (due to an increase in pulmonary system impedance, see Fig. 9 and gray bars in right plot of Fig. 10), and 2) an increase in LV preload (due to the compression of the pulmonary peripheral vessels which promotes blood flow into the left ventricle, see Fig. 9 and black bars in left plot of Fig. 10). As for the ejection fraction, the decrease in right ventricular preload during inhalation, along with the concomitant increase in right ventricular afterload, generates a reduction in right ventricular ejection fraction (see Fig. 9 and white bars in right plot of Fig. 10). In addition, the increased preload of the left ventricle (accompanied by a decrease of its afterload) generates a transient increase in LV ejection fraction toward the end of inhalation (see Fig. 9 and white bars in left plot of Fig. 10). During exhalation, the inspiratory reduction in right ventricular ejection lowers the filling of the left ventricle which, in turn, reduces LV stroke volume and ejection fraction as per the Frank-Starling mechanism.
Figure 9.

Hemodynamic effects of mechanical ventilation in relation to changes in airway opening pressure (gray waveform). White dashed boxes indicate changes in respiratory system variables, whereas light and dark gray boxes respectively refer to changes in right (RV) and left (LV) ventricular functions. Transpulmonary pressure is defined as the difference between alveolar and pleural pressures. The figure is adapted from [28].
Figure 10.

Percent change (left vertical axes) in left (left plot) and right (right plot) ventricular preload (black bars), afterload (gray bars), and ejection fraction (white bars) during a breathing cycle (P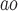 , right vertical axes). Ventricular function indices have been computed based on the simulation results in Fig. 6 as follows: preload
, right vertical axes). Ventricular function indices have been computed based on the simulation results in Fig. 6 as follows: preload 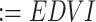 ; afterload
; afterload  ventricular wall stress,
ventricular wall stress,  , where
, where  is the end-systolic transmural pressure and
is the end-systolic transmural pressure and  is the corresponding end-systolic volume [32]; ejection fraction,
is the corresponding end-systolic volume [32]; ejection fraction, 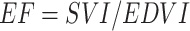 . The gray horizontal dotted line indicates the zero percent level of the change in preload, afterload, or ejection fraction.
. The gray horizontal dotted line indicates the zero percent level of the change in preload, afterload, or ejection fraction.
4). Intra-Breath Variations in Pulse Pressure
Intra-breath variations in cardiac activity, such as those summarized in Figs. 9 and 10, result in changes in stroke volume, and consequently in arterial pulse pressure (pulse pressure ( ) is considered to be proportional to stroke volume assuming a constant arterial compliance). Since
) is considered to be proportional to stroke volume assuming a constant arterial compliance). Since  is monitored at the bedside, intra-breath variations in
is monitored at the bedside, intra-breath variations in  have been proposed as dynamic predictors to two clinical interventions: PEEP application [36] and fluid resuscitation (volume expansion) [37], [38]. Both interventions, though distinct, share the same underlying mechanism affecting cardiac activity; they induce a change in preload (negative for PEEP application, positive for volume expansion) that leads to a shift in the heart’s operating point on the Frank-Starling curve (see Fig. 7). Such a shift effectively alters the variation in pulse pressure for any given intra-breath change in cardiac preload (
have been proposed as dynamic predictors to two clinical interventions: PEEP application [36] and fluid resuscitation (volume expansion) [37], [38]. Both interventions, though distinct, share the same underlying mechanism affecting cardiac activity; they induce a change in preload (negative for PEEP application, positive for volume expansion) that leads to a shift in the heart’s operating point on the Frank-Starling curve (see Fig. 7). Such a shift effectively alters the variation in pulse pressure for any given intra-breath change in cardiac preload (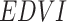 ).
).
Given the clinical relevance of PEEP and volume expansion (VE) therapies, we simulate them both using the CP Model. We measure the percent change in pulse pressure over a breathing cycle as originally proposed by Michard et al. [36], [38]:
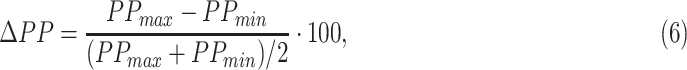 |
where  and
and  are the maximum and minimum pulse pressure values within a breathing cycle, respectively. Following our analysis on stroke volume (see Fig. 10), we expect that
are the maximum and minimum pulse pressure values within a breathing cycle, respectively. Following our analysis on stroke volume (see Fig. 10), we expect that  occurs at peak inspiration whereas
occurs at peak inspiration whereas 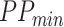 during exhalation. For both PEEP and volume expansion scenarios, we simulate two patient groups with different pathologies: one with low blood volume (hypovolemia) and one with low systemic vascular resistance (e.g., sepsis). Considering that both pathologies are clinically manifested by low blood pressure (hypotension), we select the model parameters such that the two groups have the same (low) baseline mean arterial blood pressure. The model predictions in terms of
during exhalation. For both PEEP and volume expansion scenarios, we simulate two patient groups with different pathologies: one with low blood volume (hypovolemia) and one with low systemic vascular resistance (e.g., sepsis). Considering that both pathologies are clinically manifested by low blood pressure (hypotension), we select the model parameters such that the two groups have the same (low) baseline mean arterial blood pressure. The model predictions in terms of 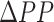 demonstrate a good agreement with experimental findings from literature studies [36], [38]; namely, a high
demonstrate a good agreement with experimental findings from literature studies [36], [38]; namely, a high  value, prior to intervention (whether PEEP or VE therapy), is indicative of a hypovolemic subject.
value, prior to intervention (whether PEEP or VE therapy), is indicative of a hypovolemic subject.
Table VI summarizes the results of the simulation studies. The septic virtual patient in the first scenario (PEEP application) has a  of about 9.5% with an average cardiac index of 4.15 (l/min)/m
of about 9.5% with an average cardiac index of 4.15 (l/min)/m at zero PEEP. On the other hand, in the hypovolemic case,
at zero PEEP. On the other hand, in the hypovolemic case,  is initially 15.5% and
is initially 15.5% and  is 3.15 (l/min)/m
is 3.15 (l/min)/m . As expected, the hypovolemic patient has a lower cardiac index due to a reduced overall blood volume, and thus reduced cardiac preload. When PEEP of 10 cmH
. As expected, the hypovolemic patient has a lower cardiac index due to a reduced overall blood volume, and thus reduced cardiac preload. When PEEP of 10 cmH O is applied, the hypovolemic subject shows a decrease in
O is applied, the hypovolemic subject shows a decrease in  of about 10% to 2.83 (l/min)/m
of about 10% to 2.83 (l/min)/m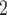 (
(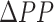 increases to 19.2%), while the cardiac index of the septic virtual patient reduces by only 2.6% to 4.04 (l/min)/m
increases to 19.2%), while the cardiac index of the septic virtual patient reduces by only 2.6% to 4.04 (l/min)/m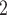 (
( increases to just 9.9%). Obviously, there is a correlation between
increases to just 9.9%). Obviously, there is a correlation between 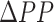 at zero PEEP and the magnitude of change in cardiac index after a PEEP increase. This is in agreement with what was observed in [36]; namely, the higher the
at zero PEEP and the magnitude of change in cardiac index after a PEEP increase. This is in agreement with what was observed in [36]; namely, the higher the 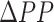 at zero PEEP, the larger the drop in
at zero PEEP, the larger the drop in 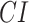 . It is also worth noting that the simulated increase in
. It is also worth noting that the simulated increase in 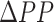 in both hypovolemic and septic cases after PEEP application is in agreement with the experimental results reported by Michard et al.
[36] and Kubitz et al.
[39]. Such an increase is due to the fact that PEEP reduces cardiac volumes, effectively forcing the heart to work on a steeper portion of the Frank-Starling curve (see Fig. 7, for example). Thus, the magnitude of change in stroke volume and in pulse pressure (
in both hypovolemic and septic cases after PEEP application is in agreement with the experimental results reported by Michard et al.
[36] and Kubitz et al.
[39]. Such an increase is due to the fact that PEEP reduces cardiac volumes, effectively forcing the heart to work on a steeper portion of the Frank-Starling curve (see Fig. 7, for example). Thus, the magnitude of change in stroke volume and in pulse pressure (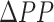 ) for any given change in left ventricular filling (preload) depends on the level of PEEP; the higher the PEEP, the larger the
) for any given change in left ventricular filling (preload) depends on the level of PEEP; the higher the PEEP, the larger the 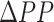 , as also indicated by [40].
, as also indicated by [40].
TABLE VI. 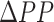 as Clinical Predictor of PEEP Application and Volume Expansion (VE) Therapies.
as Clinical Predictor of PEEP Application and Volume Expansion (VE) Therapies.
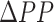
|
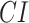 ((l/min)/m ((l/min)/m ) ) |
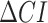
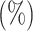
|
|||
|---|---|---|---|---|---|
PEEP
|
PEEP
|
PEEP
|
PEEP
|
||
| Hypovolemic | 15.5 | 19.2 | 3.5 | 2.83 |
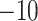
|
| Septic (normovolemic) | 9.5 | 9.9 | 4.15 | 4.04 |
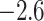
|
| Before VE | After VE | Before VE | After VE | ||
| Hypovolemic | 18.2 | 11.7 | 2.93 | 3.41 | 16.4 |
| Septic (normovolemic) | 9.8 | 7.5 | 4.1 | 4.48 | 9.2 |
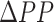 , percent change in pulse pressure over a breathing cycle;
, percent change in pulse pressure over a breathing cycle; 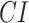 , cardiac index;
, cardiac index;  , percent change in
, percent change in 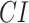 before and after the intervention; PEEP
before and after the intervention; PEEP 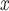 , PEEP at x cmH
, PEEP at x cmH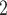 O where x = {0, 10}.
O where x = {0, 10}.
Similar conclusions on  can be drawn for the fluid resuscitation (or volume expansion, VE) scenario; that is, the higher the
can be drawn for the fluid resuscitation (or volume expansion, VE) scenario; that is, the higher the 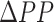 before VE, the larger the effect of fluid resuscitation in augmenting
before VE, the larger the effect of fluid resuscitation in augmenting  (see Table VI). For the hypovolemic case,
(see Table VI). For the hypovolemic case, 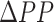 and
and  are initially (i.e., before VE) 18.2% and 2.93 (l/min)/m
are initially (i.e., before VE) 18.2% and 2.93 (l/min)/m , respectively. After a 500 ml fluid administration (similar to the experimental protocol in [38]),
, respectively. After a 500 ml fluid administration (similar to the experimental protocol in [38]),  reduces to 11.7%, while
reduces to 11.7%, while  increases to 3.41 (l/min)/m
increases to 3.41 (l/min)/m , a 16.4% increase. In contrast, the septic virtual patient shows much smaller changes in both
, a 16.4% increase. In contrast, the septic virtual patient shows much smaller changes in both  and
and 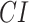 ;
; 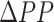 is initially 9.8% and then reduces to 7.5%, while cardiac index increases by only 9.2%, from 4.1 to 4.48 (l/min)/m
is initially 9.8% and then reduces to 7.5%, while cardiac index increases by only 9.2%, from 4.1 to 4.48 (l/min)/m . We can therefore conclude that the model predictions adhere to the 13% threshold in the
. We can therefore conclude that the model predictions adhere to the 13% threshold in the  value before VE, which allowed Michard et al.
[38] to discriminate between responders (increase in
value before VE, which allowed Michard et al.
[38] to discriminate between responders (increase in  after VE greater than 15%) and non-responders with 94% sensitivity and 96% specificity.
after VE greater than 15%) and non-responders with 94% sensitivity and 96% specificity.
IV. Discussion
In this study, we have developed an integrated cardiopulmonary model to 1) analyze heart-lung interactions during mechanical ventilation, and 2) evaluate effects of those interactions on cardiac activity. Mechanical ventilation is typically instituted as a life-saving therapy, however, it can profoundly compromise cardiac performance. Mathematical models of the cardiopulmonary physiology can be especially useful to interpret the interactions between heart and lungs and to analyze the potential negative effects of mechanical ventilation therapy on cardiac function. The cardiopulmonary model (CP Model) presented in this paper captures the main mechanisms of cardiorespiratory interactions and it includes a pericardial membrane, an interventricular septum, and a pulmonary circulation model that accounts for the effects of pulmonary capillary compression during inhalation (see Figs. 2 and 3). The CP Model was validated with patient data in normal resting conditions (see Table III) and under mechanical ventilation scenarios (see Figs. 4–6). Ventilation conditions were simulated via a simple ventilator model able to replicate common ventilator settings, such as pressure control level, PEEP, and inspiration-to-expiration ratio. The ventilator model includes all necessary elements to simulate any type of ventilation modes, such as pressure-control ventilation (PCV), pressure support ventilation (PSV), and volume-control ventilation (VCV). Despite the proven capability of the proposed model in describing heart-lung interaction mechanisms, it is necessary to point out some limitations. These can also serve as a basis for future work.
First, all scenarios and validation processes presented in this paper pertain to passively breathing subjects. Indeed, spontaneously breathing subjects under mechanical ventilation support exhibit more elaborate dynamics due to neural and mechanical reflexes. Nevertheless, the present CP Model due to its basis on the work by Albanese et al. [7], [31] includes a comprehensive neural control module. The neural component models short-term neural control mechanisms acting on both the cardiovascular and the respiratory functions, such as baroreceptors, peripheral and central chemoreceptors as well as lung-stretch receptors. An example of the capability of the model to simulate spontaneously breathing subjects has been presented in [12].
Second, the CP Model does not consider the effects of PEEP on alveolar recruitment and gas exchange. For instance, it is well known that institution of PEEP on ARDS patients is recommended to improve gas exchange by inflating the collapsed alveoli and reducing edema and intrapulmonary shunt [41]. Alveolar recruitment is typically modeled via a nonlinear pressure-volume relationship [42], where lung compliance increases as the collapsed lung regions are being recruited with PEEP application. Consequently, the recruited alveoli can participate in gas exchange, effectively prompting a reduction in intrapulmonary shunt. However, the proposed model assumes a linear pressure-volume relationship (hence, constant lung compliance) and a constant value for the shunt fraction. Besides gas exchange, the assumption of a constant lung compliance has disadvantages regarding the mechanism that describes the effects of PEEP on cardiac output (see Fig. 11). Specifically, Dhainaut et al.
[25] found a curvilinear relationship between PEEP and cardiac index (black squares in left plot of Fig. 11), whereas our model predicts a linear relationship between the two (gray circles in left plot of Fig. 11). At the same time, 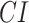 and pleural pressure are linearly related for both simulated and experimental data (right plot in Fig. 11). It is worth noticing, however, the effect of PEEP on pleural pressure. Each step increase in PEEP results in a constant step increment in pleural pressure in our CP Model, whereas the experimental data show larger step increments at higher PEEP levels (compare the x-axis increments in the right hand-side plot of Fig. 11). Like Dhainaut et al.
[25], we conjecture that the varying step increments in pleural pressure with each PEEP increase are attributed to a nonlinear lung compliance. The increased compliance at higher PEEP levels allows a larger lung expansion. This, in turn, leads to a larger compression of the pleural space which translates into a larger increase in
and pleural pressure are linearly related for both simulated and experimental data (right plot in Fig. 11). It is worth noticing, however, the effect of PEEP on pleural pressure. Each step increase in PEEP results in a constant step increment in pleural pressure in our CP Model, whereas the experimental data show larger step increments at higher PEEP levels (compare the x-axis increments in the right hand-side plot of Fig. 11). Like Dhainaut et al.
[25], we conjecture that the varying step increments in pleural pressure with each PEEP increase are attributed to a nonlinear lung compliance. The increased compliance at higher PEEP levels allows a larger lung expansion. This, in turn, leads to a larger compression of the pleural space which translates into a larger increase in  compared to that at low PEEP. Based on these observations, we can conclude that since pleural pressure directly affects venous return, the nonlinear lung compliance and the varying step increments in
compared to that at low PEEP. Based on these observations, we can conclude that since pleural pressure directly affects venous return, the nonlinear lung compliance and the varying step increments in 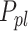 after each PEEP increase are responsible for the curvilinear relationship between
after each PEEP increase are responsible for the curvilinear relationship between  and PEEP that is reported in literature [25].
and PEEP that is reported in literature [25].
Figure 11.

Comparison of the effects of positive end-expiratory pressure (PEEP, left plot) and pleural pressure (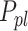 , right plot) on cardiac index (
, right plot) on cardiac index ( ) between model-predicted (gray circles) and experimental (black squares) data. Experimental data are taken from Dhainaut et al.
[25] and are reported with their mean and standard error of the means. Notice that each
) between model-predicted (gray circles) and experimental (black squares) data. Experimental data are taken from Dhainaut et al.
[25] and are reported with their mean and standard error of the means. Notice that each 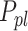 point represents the average pleural pressure (or its surrogate, esophageal pressure) at each corresponding PEEP level.
point represents the average pleural pressure (or its surrogate, esophageal pressure) at each corresponding PEEP level.
Third, some limitations also exist in the heart model. 1) As indicated in the Methods section, the proposed CP Model does not consider any mechanical interdependence between the two atria [43]. 2) Furthermore, a constant left ventricular diastolic pressure-volume relationship is used. Although studies [30], [44] have shown that right ventricular overload may lead to a reduction in left ventricular diastolic elastance, the current model implementation only considers the leftward movement of the septum as the sole reason for right-to-left ventricular interference that causes a decrease in left ventricular volume. 3) Finally, activations of the left and right ventricular free walls are assumed to happen simultaneously. This assumption is based on the absence of concrete experimental evidence regarding the delay between left and right ventricular contractions in healthy individuals [45]–[47]. Nevertheless, we have included a provision in our model to simulate contraction delays due to pathological conditions, such as left or right bundle branch blocks.
Lastly, it is known that systemic venous return depends on the pressure gradient between the extra-thoracic veins (upstream pressure) and the venae cavae inside the thorax (downstream pressure). These two pressure points are, in turn, affected by abdominal and pleural pressures, respectively. While mechanical ventilation induces positive swings in pleural pressure, it also causes the diaphragm to descend, thereby raising abdominal pressure [48], [49]. Consequently, while pleural pressure swings are considered the primary determinants in decreasing venous return, the concomitant increase in abdominal pressure is expected to minimize the effect of  in reducing venous return. In our model, we assume abdominal pressure equal to atmospheric pressure (zero). Thus, any simulated changes in venous return depend solely on changes in pleural pressure, potentially resulting in model simulations with larger than expected decrease in venous return as compared with experimental data.
in reducing venous return. In our model, we assume abdominal pressure equal to atmospheric pressure (zero). Thus, any simulated changes in venous return depend solely on changes in pleural pressure, potentially resulting in model simulations with larger than expected decrease in venous return as compared with experimental data.
V. Conclusion
In conclusion, we have hereby presented a mathematical cardiopulmonary model with a pericardial membrane, an interventricular septum, and a pulmonary circulation model that accounts for the compression of the pulmonary peripheral vessels due to lung inflation. Such a model allows for a better understanding of heart-lung interactions during mechanical ventilation. For instance, the inclusion of the pericardium allows to simulate cardiac diseases, such as pericarditis and cardiac tamponade. The model was validated with experimental data, both in transient (intra-breath) and steady-state conditions (PEEP application). Moreover, model simulations were used to provide physiologic explanations to a few contradictory experimental observations, thus proving the potentials of such a model to improve the current understanding of complex physiological phenomena. We therefore believe that this CP Model can serve as a tool to study, analyze, and evaluate the effects of mechanical ventilation therapy on cardiac function, contributing in making such a therapy safer for patients, including COVID-19 patients who require intubation due to their comorbidities and who may suffer of a high risk of cardiovascular complications.
Appendix. Interventricular septum
The septal elastance effector response to the ANS sympathetic activity is modeled according to the approach proposed by Ursino and Magosso [17]. Such a model includes a logarithmic function to describe the effector’s static response, a pure delay, and a low-pass first-order filter to simulate its dynamic behavior. Specifically, the maximal elastance of the septum ( ) changes with respect to the frequency of the sympathetic efferent fibers (
) changes with respect to the frequency of the sympathetic efferent fibers (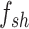 ) according to the following equations:
) according to the following equations:
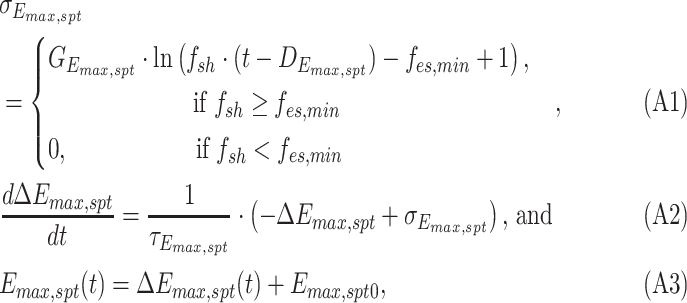 |
where 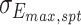 is the output of the logarithmic static function of (A1) that is used to calculate the maximal septal elastance in (A3),
is the output of the logarithmic static function of (A1) that is used to calculate the maximal septal elastance in (A3),  is a gain factor,
is a gain factor, 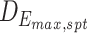 is the latency in the static response,
is the latency in the static response, 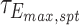 is the time constant of the first-order filter, and
is the time constant of the first-order filter, and 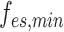 is a threshold for sympathetic stimulation. Following the method by Ursino and Magosso [17],
is a threshold for sympathetic stimulation. Following the method by Ursino and Magosso [17], 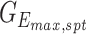 and
and  are respectively set to 16.1% and 81% of the original septal elastance value reported in [16]. The parameter values, besides
are respectively set to 16.1% and 81% of the original septal elastance value reported in [16]. The parameter values, besides 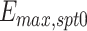 (see Table I), of this reflex regulatory mechanism are reported in Table VII.
(see Table I), of this reflex regulatory mechanism are reported in Table VII.
TABLE VII. Parameters of the Septal Elastance Reflex Effector Model.
See text for explanation of symbols.
Pulmonary peripheral vessels
The equations describing the pulmonary circulation model are obtained by applying the conservation of mass (continuity equation) and momentum (compatibility equation) laws on the electrical analog in Fig. 3.
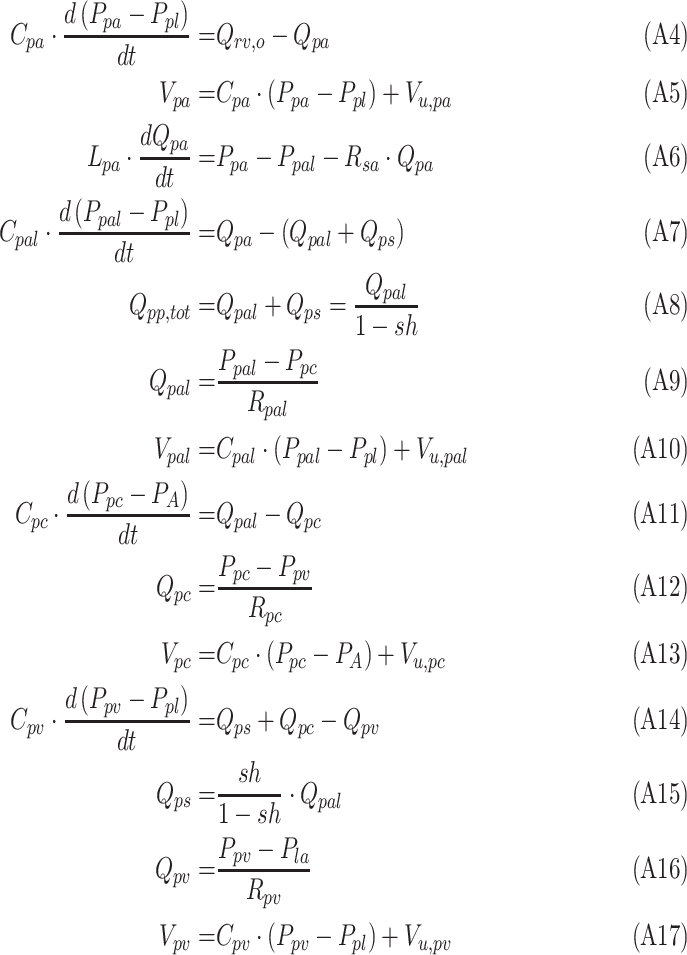 |
Equation (3), which defines the 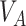 -dependent arteriolar resistance, is based on the equation proposed by Lu et al.
[10]:
-dependent arteriolar resistance, is based on the equation proposed by Lu et al.
[10]:
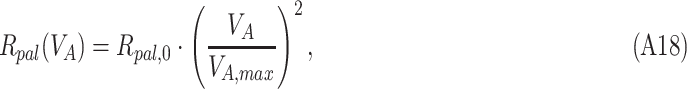 |
where  is a constant value that represents the arteriolar resistance when alveolar volume has reached its maximum value
is a constant value that represents the arteriolar resistance when alveolar volume has reached its maximum value 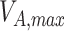 . However, (A18), as originally proposed by Lu et al.
[10], does not account for the pulmonary shunt (the amount of blood that does not contribute to gas exchange) that is included in the pulmonary circulation model of our CP Model (see Figs. 2 and 3). To introduce the effects of anatomical shunting in our model, we consider that the resistances of shunted (
. However, (A18), as originally proposed by Lu et al.
[10], does not account for the pulmonary shunt (the amount of blood that does not contribute to gas exchange) that is included in the pulmonary circulation model of our CP Model (see Figs. 2 and 3). To introduce the effects of anatomical shunting in our model, we consider that the resistances of shunted (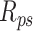 ) and non-shunted (
) and non-shunted ( and
and 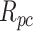 ) pulmonary peripheral compartments are functions of the selected shunt fraction (
) pulmonary peripheral compartments are functions of the selected shunt fraction (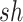 ) such that the distribution of blood between the two segments matches the
) such that the distribution of blood between the two segments matches the  value (
value (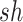 is equal to 1.7% in normal physiological conditions). Derivation of (3) from (A18) is based on the following two assumptions:
is equal to 1.7% in normal physiological conditions). Derivation of (3) from (A18) is based on the following two assumptions:
- 1)
-
2)Similar to the model by Lu et al. [10], the resistance
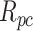 does not change with respect to
does not change with respect to 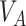 . Its value is considered equal to
. Its value is considered equal to 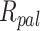 when alveolar volume is equal to
when alveolar volume is equal to 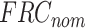 ,
,

Consequently, at steady-state conditions when  ,
,
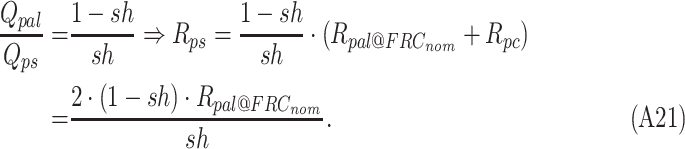 |
Hence, (A19) becomes:
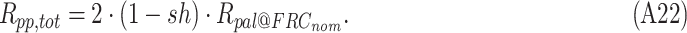 |
Using the definition for 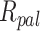 in (A18), (A22) gives us the constant, but unknown, quantity
in (A18), (A22) gives us the constant, but unknown, quantity 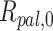 as:
as:
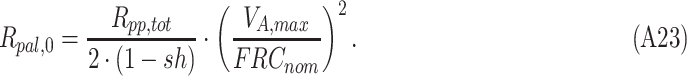 |
Then,
 |
Note that the shunt resistance  does not need to be explicitly specified because the flow over the pulmonary shunts,
does not need to be explicitly specified because the flow over the pulmonary shunts, 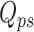 , is replaced by
, is replaced by  according to (A15).
according to (A15).
Contributor Information
Nikolaos Karamolegkos, Email: n.karamolegkos@columbia.edu.
Antonio Albanese, Email: antonio.albanese2@gmail.com.
Nicolas W. Chbat, Email: chbat@quadrusmedical.com.
References
- [1].McGregor M., “Pulsus paradoxus,” N Engl. J. Med., vol. 301, no. 9, pp. 480–482, Aug. 1979. [DOI] [PubMed] [Google Scholar]
- [2].Scharf S. M., Brown R., Saunders N., and Green L. H., “Hemodynamic effects of positive-pressure inflation,” J. Appl. Physiol., vol. 49, no. 1, pp. 124–131, Jul. 1980. [DOI] [PubMed] [Google Scholar]
- [3].Schmitz R., Lantin M., and White A., “Future needs in pulmonary and critical care medicine,” Abt Associates Inc., Tech. Rep., 1998. [Google Scholar]
- [4].Wunsch H., Wagner J., Herlim M., Chong D. H., Kramer A. A., and Halpern S. D., “ICU occupancy and mechanical ventilator use in the United States,” Crit. Care Med., vol. 41, no. 12, pp. 2712–2719, Dec. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Porta A., Bari V., Bassani T., Marchi A., Pistuddi V., and Ranucci M., “Model-based causal closed-loop approach to the estimate of baroreflex sensitivity during propofol anesthesia in patients undergoing coronary artery bypass graft,” J. Appl. Physiol., vol. 115, no. 7, pp. 1032–1042, Oct. 2013. [DOI] [PubMed] [Google Scholar]
- [6].Hester R. L. et al. , “HumMod: A modeling environment for the simulation of integrative human physiology,” Front. Physiol., vol. 2, p. 12, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Albanese A., Cheng L., Ursino M., and Chbat N. W., “An integrated mathematical model of the human cardiopulmonary system: Model development,” Amer. J. Physiol. Heart Circulatory Physiol., vol. 310, no. 7, pp. H899–H921, Apr. 2016. [DOI] [PubMed] [Google Scholar]
- [8].Cheng L., Albanese A., Ursino M., and Chbat N. W., “An integrated mathematical model of the human cardiopulmonary system: Model validation under hypercapnia and hypoxia.” Amer. J. Physiol. Heart Circulatory Physiol., vol. 310, no. 7, pp. H922–H937, Apr. 2016. [DOI] [PubMed] [Google Scholar]
- [9].Cheng L., Ivanova O., H.-H. Fan, and Khoo M. C., “An integrative model of respiratory and cardiovascular control in sleep-disordered breathing,” Respir Physiol. Neurobiol., vol. 174, no. 1-2, pp. 4–28, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lu K., Clark J. W., Ghorbel F. H., Ware D. L., and Bidani A., “A human cardiopulmonary system model applied to the analysis of the valsalva maneuver,” Amer. J. Physiol. Heart Circulatory Physiol., vol. 281, no. 6, pp. H 2661–H2679, Dec. 2001. [DOI] [PubMed] [Google Scholar]
- [11].Pinsky M. R., “Hemodynamic effects of ventilation and ventilatory maneuvers” in Respiratory-Circulatory Interactions in Health and Disease, New York, NY, USA: CRC Press, 2001, pp. 216–251. [Google Scholar]
- [12].Karamolegkos N., Albanese A., Isaza F., and Chbat N. W., “Patient emulator: A tool for testing mechanical ventilation therapies,” in Proc. 38th Annu. Int. Conf. IEEE Eng. Med. Biol. Soc., vol. 2006, 2016, pp. 4321–4324. [DOI] [PubMed] [Google Scholar]
- [13].Chung D. C. et al. , “A dynamic model of ventricular interaction and pericardial influence,” Amer. J. Physiol., vol. 272, no. 6Pt 2, pp. H 2942–H2962, Jun. 1997. [DOI] [PubMed] [Google Scholar]
- [14].Takata M. and Robotham J. L., “Mechanical Heart-Pericardium-Lung Interactions” in Respiratory-Circulatory Interactions in Health and Disease, New York, NY, USA: CRC Press, 2001, pp. 290–311. [Google Scholar]
- [15].Ursino M., “Interaction between carotid baroregulation and the pulsating heart: A mathematical model,” Amer. J. Physiol. Heart Circulatory Physiol., vol. 275, no. 5, pp. H 1733–H1747, Nov. 1998. [DOI] [PubMed] [Google Scholar]
- [16].Luo C., Ware D. L., Zwischenberger J. B., and Clark J. W., “Using a human cardiopulmonary model to study and predict normal and diseased ventricular mechanics, septal interaction, and atrio-ventricular blood flow patterns,” Cardiovasc. Eng., vol. 7, no. 1, pp. 17–31, Apr. 2007. [DOI] [PubMed] [Google Scholar]
- [17].Ursino M. and Magosso E., “Acute cardiovascular response to isocapnic hypoxia. i. a. mathematical model,” Amer. J. Physiol. Heart Circulatory Physiol., vol. 279, no. 1, pp. H149–H165, Jul. 2000. [DOI] [PubMed] [Google Scholar]
- [18].Whittenberger J. L., McGregor M., Berglund E., and Borst H. G., “Influence of state of inflation of the lung on pulmonary vascular resistance.” J. Appl. Physiol., vol. 15, no. 5, pp. 878–882, Sep. 1960. [DOI] [PubMed] [Google Scholar]
- [19].Roos A., Thomas L. J., Nagel E. L., and Prommas D. C., “Pulmonary vascular resistance as determined by lung inflation and vascular pressures,” J. Appl. Physiol., vol. 16, no. 1, pp. 77–84, 1961. [DOI] [PubMed] [Google Scholar]
- [20].Maceira A. M., Prasad S. K., Khan M., and Pennell D. J., “Normalized left ventricular systolic and diastolic function by steady state free precession cardiovascular magnetic resonance,” J. Cardiovasc. Magn. Reson., vol. 8, no. 3, pp. 417–426, Jul. 2006. [DOI] [PubMed] [Google Scholar]
- [21].Edwards Lifesciences LLC, “Normal hemodynamic parameters and laboratory,” 2009. [Google Scholar]
- [22].Maceira A. M., Prasad S. K., Khan M., and Pennell D. J., “Reference right ventricular systolic and diastolic function normalized to age, gender and body surface area from steady-state free precession cardiovascular magnetic resonance,” Eur. Heart J., vol. 27, no. 23, pp. 2879–2888, 2006. [DOI] [PubMed] [Google Scholar]
- [23].Summers R. L. et al. , “Validation of a computational platform for the analysis of the physiologic mechanisms of a human experimental model of hemorrhage,” Resuscitation, vol. 80, no. 12, pp. 1405–1410, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Kyhl K. et al. , “The decrease of cardiac chamber volumes and output during positive-pressure ventilation.” Amer. J. Physiol. Heart Circulatory Physiol., vol. 305, no. 7, pp. H1004–H1009, 2013. [DOI] [PubMed] [Google Scholar]
- [25].Dhainaut J. F., Devaux J. Y., Monsallier J. F., Brunet F., Villemant D., and Huyghebaert M. F., “Mechanisms of decreased left ventricular preload during continuous positive pressure ventilation in ARDS,” Chest, vol. 90, no. 1, pp. 74–80, 1986. [DOI] [PubMed] [Google Scholar]
- [26].Vieillard-Baron A. et al. , “Cyclic changes in arterial pulse during respiratory support revisited by doppler echocardiography,” Amer. J. Respir. Crit. Care Med., vol. 168, no. 6, pp. 671–676, 2003. [DOI] [PubMed] [Google Scholar]
- [27].Dhainaut J. F., Schlemmer B., Monsallier J. F., Fourestie V., and Carli A., “Behavior of the right ventricle following PEEP in patients with mild and severe ARDS,” Amer. Rev. Respir. Dis., vol. 129, p. A99, 1984. [Google Scholar]
- [28].Michard F. and Teboul J. L., “Using heart-lung interactions to assess fluid responsiveness during mechanical ventilation,” Crit. Care, vol. 4, pp. 282–289, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Pinsky M. R., “Heart-lung interactions,” Curr. Opin. Crit. Care, vol. 13, pp. 528–531, 2007. [DOI] [PubMed] [Google Scholar]
- [30].Jardin F., J.-C. Farcot, Gueret P., J.-F. Prost, Ozier Y., and J.-P. Bourdarias, “Echocardiographic evaluation of ventricles during continuous positive airway pressure breathing,” J. Appl. Physiol., vol. 56, no. 3, pp. 619–627, 1984. [DOI] [PubMed] [Google Scholar]
- [31].Chen W. W., Gao H., Luo X. Y., and Hill N. A., “Study of cardiovascular function using a coupled left ventricle and systemic circulation model.” J. Biomech., vol. 49, no. 12, Mar. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Huemer G., Kolve N., Kurz A., and Zimpfer M., “Influence of positive end-expiratory pressure on right and left ventricular performance assessed by doppler two-dimensional echocardiography,” Chest, vol. 106, no. 1, pp. 67–73, Jul. 1994. [DOI] [PubMed] [Google Scholar]
- [33].Jardin F., J.-C. Farcot, Boisante L., Curien N., Margairaz A., and J.-P. Bourdarias, “Influence of positive end-expiratory pressure on left ventricular performance,” New. England, J. Med., vol. 304, no. 7, pp. 387–392, Feb. 1981. [DOI] [PubMed] [Google Scholar]
- [34].Gattinoni L., Pelosi P., Suter P. M., Pedoto A., Vercesi P., and Lissoni A., “Acute respiratory distress syndrome caused by pulmonary and extrapulmonary disease different syndromes?,” Amer. J. Respir. Crit. Care. Med., vol. 158, no. 1, pp. 3–11, 1998. [DOI] [PubMed] [Google Scholar]
- [35].Vieillard-Baron A. and Jardin F., “Why protect the right ventricle in patients with acute respiratory distress syndrome?,” Curr. Opin. Crit. Care, vol. 9, no. 1, pp. 15–21, 2003. [DOI] [PubMed] [Google Scholar]
- [36].Michard F. et al. , “Clinical use of respiratory changes in arterial pulse pressure to monitor the hemodynamic effects of PEEP,” Amer. J. Respir. Crit. Care Med., vol. 159, pp. 935–939, 1999. [DOI] [PubMed] [Google Scholar]
- [37].Marik P. E., Cavallazzi R., Vasu T., and Hirani A., “Dynamic changes in arterial waveform derived variables and fluid responsiveness in mechanically ventilated patients: A systematic review of the literature,” Crit. Care Med., vol. 37, no. 9, pp. 2642–2647, 2009. [DOI] [PubMed] [Google Scholar]
- [38].Michard F. et al. , “Relation between respiratory changes in arterial pulse pressure and fluid responsiveness in septic patients with acute circulatory failure,” Amer. J. Respir. Crit. Care Med., vol. 162, no. 1, pp. 134–138, 2000. [DOI] [PubMed] [Google Scholar]
- [39].Kubitz J. C. et al. , “The influence of positive end-expiratory pressure on stroke volume variation and central blood volume during open and closed chest conditions,” Eur. J. Cardiothorac Surg., vol. 30, no. 1, pp. 90–95, 2006. [DOI] [PubMed] [Google Scholar]
- [40].Michard F., “Changes in arterial pressure during mechanical ventilation,” J. Amer. Soc. Anesthesio., vol. 103, no. 2, pp. 419–428, 2005. [DOI] [PubMed] [Google Scholar]
- [41].Ranieri V. M. et al. , “Effects of positive end-expiratory pressure on alveolar recruitment and gas exchange in patients with the adult respiratory distress syndrome,” Amer. Rev. Respir. Dis., vol. 144, no. 3pt1, pp. 544–551, Sep. 1991. [DOI] [PubMed] [Google Scholar]
- [42].Mols G., Priebe H. J., and Guttmann J., “Alveolar recruitment in acute lung injury,” Brit. J. Anaesth., vol. 96, no. 2, pp. 156–166, 2006. [DOI] [PubMed] [Google Scholar]
- [43].Goldstein J. A., Tweddell J. S., Barzilai B., Yagi Y., Jaffe A. S., and Cox J. L., “Hemodynamic effects of atrial interaction,” Coron. Artery. Dis., vol. 4, no. 6, pp. 545–553, 1993. [DOI] [PubMed] [Google Scholar]
- [44].Bove A. A. and Santamore W. P., “Ventricular interdependence,” Prog. Cardiovasc. Dis., vol. 23, no. 5, pp. 365–388, 1981. [DOI] [PubMed] [Google Scholar]
- [45].Burkhoff D., Kronenberg M. W., Yue D. T., Maughan W. L., Hunter W. C., and Sagawa K., “Quantitative comparison of canine right and left ventricular isovolumic pressure waves,” Amer. J. Physiol. Heart Circ. Physiol., vol. 253, no. 2, pp. H475–H479, 1987. [DOI] [PubMed] [Google Scholar]
- [46].Ellinger G. F., Gillick F., Boone B. R., and Chamberlain W., “Electrokymographic studies of asynchronism of ejection from the ventricles: Normal subjects and patients with bundle branch block,” Amer. Heart J, vol. 35, no. 6, pp. 971–979, 1948. [DOI] [PubMed] [Google Scholar]
- [47].Luisada A. A. and Fleischner F. G., “Temporal relation between contraction of right and left sides of the normal human heart,” Exp. Biol. Med., vol. 66, no. 2, pp. 436–440, Nov. 1947. [DOI] [PubMed] [Google Scholar]
- [48].Fessler H. E., Brower R. G., Wise R. A., and Permutt S., “Effects of positive end-expiratory pressure on the canine venous return curve,” Amer. Rev. Respir. Dis., vol. 146, no. 1, pp. 4–10, Jul. 1992. [DOI] [PubMed] [Google Scholar]
- [49].Takata M. and Robotham J. L., “Effects of inspiratory diaphragmatic descent on inferior vena caval venous return,” J. Appl. Physiol., vol. 72, no. 2, pp. 597–607, 1992. [DOI] [PubMed] [Google Scholar]