Skip to main content
PMC home page
International Journal of Sports Physical Therapy logoLink to International Journal of Sports Physical Therapy
. 2022 Apr 1;17(3):390–399. doi: 10.26603/001c.32380

Machine Learning Does Not Improve Humeral Torsion Prediction Compared to Regression in Baseball Pitchers

Garrett S Bullock 1,✉, Charles A Thigpen 2, Gary S Collins 3, Nigel K Arden 1, Thomas K Noonan 4, Michael J Kissenberth 5, Ellen Shanley 2
PMCID: PMC8975570  PMID: 35391864

Abstract

Background

Humeral torsion is an important osseous adaptation in throwing athletes that can contribute to arm injuries. Currently there are no cheap and easy to use clinical tools to measure humeral torsion, inhibiting clinical assessment. Models with low error and “good” calibration slope may be helpful for prediction.

Hypothesis/Purpose

To develop prediction models using a range of machine learning methods to predict humeral torsion in professional baseball pitchers and compare these models to a previously developed regression-based prediction model.

Study Design

Prospective cohort

Methods

An eleven-year professional baseball cohort was recruited from 2009-2019. Age, arm dominance, injury history, and continent of origin were collected as well as preseason shoulder external and internal rotation, horizontal adduction passive range of motion, and humeral torsion were collected each season. Regression and machine learning models were developed to predict humeral torsion followed by internal validation with 10-fold cross validation. Root mean square error (RMSE), which is reported in degrees (°) and calibration slope (agreement of predicted and actual outcome; best = 1.00) were assessed.

Results

Four hundred and seven pitchers (Age: 23.2 +/-2.4 years, body mass index: 25.1 +/-2.3 km/m2, Left-Handed: 17%) participated. Regression model RMSE was 12° and calibration was 1.00 (95% CI: 0.94, 1.06). Random Forest RMSE was 9° and calibration was 1.33 (95% CI: 1.29, 1.37). Gradient boosting machine RMSE was 9° and calibration was 1.09 (95% CI: 1.04, 1.14). Support vector machine RMSE was 10° and calibration was 1.13 (95% CI: 1.08, 1.18). Artificial neural network RMSE was 15° and calibration was 1.03 (95% CI: 0.97, 1.09).

Conclusion

This is the first study to show that machine learning models do not improve baseball humeral torsion prediction compared to a traditional regression model. While machine learning models demonstrated improved RMSE compared to the regression, the machine learning models displayed poorer calibration compared to regression. Based on these results it is recommended to use a simple equation from a statistical model which can be quickly and efficiently integrated within a clinical setting.

Levels of Evidence

2

Keywords: humeral retrotorsion, deep learning, gradient boosting machines, non-linear transformations

INTRODUCTION

Baseball throwing generates high velocity and forces through the arm,1–3 which contribute to unique osseous and soft tissue glenohumeral joint adaptations.4,5 These shoulder adaptations contribute to changes in shoulder range of motion, specifically to increased external rotation and decreased internal rotation in comparison to the nondominant arm.6 These unique throwing specific shoulder adaptations have been associated with arm injuries in baseball players.4,7

While soft tissue adaptations affect throwing specific shoulder range of motion,8 the underlying osseous structural transformations also contribute to throwing shoulder range of motion.9 These osseous shoulder structural adaptations are termed humeral torsion (HT). HT is measured through the line that bisects the humeral head articular surface and the transepicondylar axis.10 During youth and adolescence, the high humeral forces generated during pitching effect osseous growth and development, contributing to the diminution of humeral anatomical neck and head antetorsion that occurs with aging.11 These structural adaptations are important for throwing development12; however, they are also linked to arm injury risk.9

Within clinical practice, HT can be calculated indirectly through ultrasonic methods.5 However, this equipment is expensive, preventing many clinics and clinicians from assessing HT, hindering clinical examination. One way to arrive at clinical measures is through prediction modelling.13 Statistical prediction modelling uses traditional regression based methods to obtain a risk or probability.14 More recently, machine learning algorithms (such as random forests, gradient boosting machines, support vector machines, and neural networks) have been purported to offer increased flexibility to capture nonlinearities and higher order interactions.15,16 Machine learning uses general purpose algorithms that identify data patterns, using minimal data assumptions,17 and are being increasingly used in the medical setting.18,19 As a result, there is widespread interest in exploring the usefulness of modern machine learning methods for increasing prediction accuracy compared to more regression based statistical approaches.20

Humeral torsion is an important osseous adaptation in throwing athletes that can contribute to arm injuries.9 Machine learning algorithms offer an alternative strategy to predict outcomes in data with high complexity. Comparing and contrasting regression based statistical and machine learning approaches can help identify the most promising prediction model to be implemented in the clinical setting. Therefore, the purpose of this study was to develop prediction models using a range of machine learning methods to predict professional baseball pitcher HT and compare these models to a traditional regression-based prediction model.

METHODS

Study Design

A prospective cohort study was conducted from 2009 to 2019 on Minor League pitchers in one Major League Baseball organization. Only preseason data were utilized in this study and pitchers were only included once within the dataset. Participants were excluded from the study if 1) the athlete played a primary position other than pitcher, 2) they were being treated for a shoulder or elbow injury at the beginning of the season, or 3) they were unable to participate on the first day of practice because of upper extremity injury. Prior to data collection, all participants were informed of the risks and benefits of study participation and participants gave verbal and written consent to study participation. The PRISMA health system Institutional Review Board approved this study.

Data Collection

Before the beginning of the season, all baseball players were questioned for arm dominance, prior baseball experience, injury history, and position(s) played. Participants were then examined for current height (cm) and mass (kg). Participants were then examined for passive shoulder PROM and HT. Shoulder PROM testing was randomized for each participant, and examiners were blinded to hand dominance throughout the study.21 Two examiners performed all measurements for the entire cohort.

Predictors

Predictors included player demographics (age, hand dominance, previous baseball participation, injury history, position played, and continent of origin), shoulder PROM, and injury history. Shoulder ROM and injury history are further described below.

Shoulder Range of Motion

All shoulder PROM (external rotation [ER], internal rotation [IR] and horizontal adduction [HA]) was measured supine on a standardized plinth table by two examiners using a digital inclinometer per previously described methods.22–25 Two trials were performed per shoulder measurement, and the average of these two trials was used for data analysis. Shoulder PROM was calculated on 10 participants prior to data collection for the two examiners. Shoulder PROM intra- and inter-rater reliability was excellent for ER and IR (ICC(2,1) and ICC (2,k) = 0.92-0.99) and HA (ICC(2,1) and ICC (2,k) = 0.92-0.99), and the standard error of measurement was 2°-4° for shoulder ER, IR, and HA.

Injury History

A shoulder or elbow injury was defined as any traumatic or overuse injury that occurred during any baseball team sponsored activity (from the beginning of preseason through the last post season game) to any muscle, joint, tendon, ligament, bone, or nerve that required medical attention.26 Injuries were further designated by dominant and nondominant arm. An independent examiner, blinded to physical measurements, reviewed medical documents to determine the diagnosis, duration of treatment, and the time to clearance for return to full sport participation.

Outcome

Humeral Torsion (HT)

Dominant HT was measured supine on a standardized plinth table with the shoulder in 90° of abduction. One examiner, using a 5 mHz ultrasonographic transducer (Sonosite Inc, Bothell, WA, USA) measured HT. The ultrasonographic transducer was placed level, confirmed with a bubble level, on the anterior shoulder, perpendicular to the long axis of the humerus. The humerus was then rotated until the apexes of the greater and lesser tubercles could be visualized parallel to the horizontal plane. The second examiner placed a digital inclinometer on the ulnar side of the forearm, measuring the forearm inclination angle with respect to the horizontal, which indirectly measures HT.5 Two trials were performed per HT measurement, and the average of these two trials was used for data analysis. HT reliability was calculated on 10 participants prior to data collection for the two examiners. Humeral torsion intra- and inter-rater reliability was excellent (ICC(2,1) and ICC (2,k) 0.93-0.97) and the standard error of measure was 2-4°.

Statistical Analyses

All data were investigated for missingness prior to analyses, using the R package naniar. Missing data were low (Shoulder ROM: 3%, age: <1%, HT: 2%), thus complete case analyses were performed. Descriptive statistics were reported by mean (standard deviation), median (interquartile range), and frequencies and percentages for categorical variables.

Sample Size Considerations

For the statistical modelling, an a priori sample size calculation was performed with the R package pmsampsize.27 Referencing a previous meta-analysis and meta-regression,9 mean HT was 28°, standard deviation was 4°, and R2 was 0.38. The a priori statistical regression prediction model was determined to incorporate ten degrees of freedom (i.e., parameters). As a result, a total of 246 baseball players were required to reduce the risk of overfitting.

Model Development

The transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) were followed for all model development.28

Statistical Model

A linear regression model to predict HT was developed, using predictor variables including: Predictor variables included: (1) age,29 (2) arm dominance (Left or Right handed),30,31 (3) shoulder IR,9 (4) shoulder ER,9 (5) shoulder HA,32 (6) continent of origin (North America or Latin America),33 (7) previous shoulder or elbow injury.34 Linearity was not assumed; as a result, continuous predictors were assessed for non-linearity with restricted cubic splines. Restricted cubic splines were calculated with three, four, and five knots with the R package rms. All continuous predictors demonstrated a linear relationship to HT. Interactions were also analyzed, with no predictors observed to have an interaction relationship with HT. Internal validation was performed with a 10-fold cross validation. Internal validation is performed to reduce optimism bias, as models are overly optimistic on the developed dataset.35,36 The R package caret was used to performed cross validation.

Four machine learning models (Random Forest, Gradient Boosting Machine [GBM], Support Vector Machine Regression [SVM], and Artificial Neural Networks [ANN]) were developed to predict HT using an iterative hyperparameter tuning process. Hyperparamter tuning consisted of using a grid search process. All machine learning models incorporated all the same predictors used to develop the linear regression model. The R packages randomForest, gbm, kernlab and e1071, and neuralnet were used for random forest, GBM, SVM, and ANN models. For full description of the machine learning models, tuning variables, final hyperparameters, and complete code, please refer to the Appendix. Following model development, all machine learning models, besides ANN, were internally validated with a 10-fold cross validation. The ANN model was replicated 100 times.

Model performance was assessed with root mean square error (RMSE), calibration and R2. Root mean square error is the error of the model reported in outcome units (i.e., degrees), with lower error demonstrating improved prediction performance. Calibration is the agreement of predicted and actual outcome (i.e., HT), with a calibration of 1 equalling best calibration.35,36

RESULTS

A total of 407 pitchers with a mean age of 23.2 years (sd = 2.4), BMI of 25.1 km/m2 (sd = 2.3) were eligible and included (Table 1).

Table 1. Pitcher demographics, presented as mean (SD) or percentage.

Professional Pitchers
(n = 407)
Age (years) 23.2 (2.4)
Hand Dominance
Left
Right
17%
83%
BMI (kg/m2) 25.1 (2.3)
Arm Injury History Prevalence 43%
Dominant Humeral Torsion (°) 8.2 (12.7)
Dominant Internal Rotation (°) 35.2 (11.4)
Dominant External Rotation (°) 126.9 (10.9)
Dominant Horizontal Adduction (°) -1.4 (13)
Nondominant Humeral Torsion (°) 25.7 (13.0)
Nondominant Internal Rotation (°) 48.1 (10.6)
Nondominant External Rotation (°) 118.3 (11.6)
Nondominant Horizontal Adduction (°) 16.5 (14.6)
Open in a new tab

Generalized Linear Regression Model

Final model RMSE was 12°, calibration was 1.00 (95% CI: 0.94, 1.06); Table 2; Figure 1A), and R2 was 0.41. The mean distribution of the final model linear predictors was 17°, the standard deviation was 10°, the minimum was -19°, and the maximum was 48°. For full model report, please refer to the Appendix.

Table 2. Statistical and Machine Prediction Model Performance.

Prediction Model Root Mean Square Error Calibration Slope
Generalized Linear Regression 12° 1.00 (95% CI: 0.94, 1.06)
Random Forest 9° 1.33 (95%CI: 1.29, 1.37)
Gradient Boosting Machine 9° 1.09 (95% CI: 1.04, 1.14)
Support Vector Machine Regression 10° 1.13 (95% CI: 1.08, 1.18)
Artificial Neural Network 15° 1.03 (95% CI: 0.97, 1.09)
Open in a new tab

Figure 1. Calibration Plot for Regression (A) and Artificial Neural Network (B).

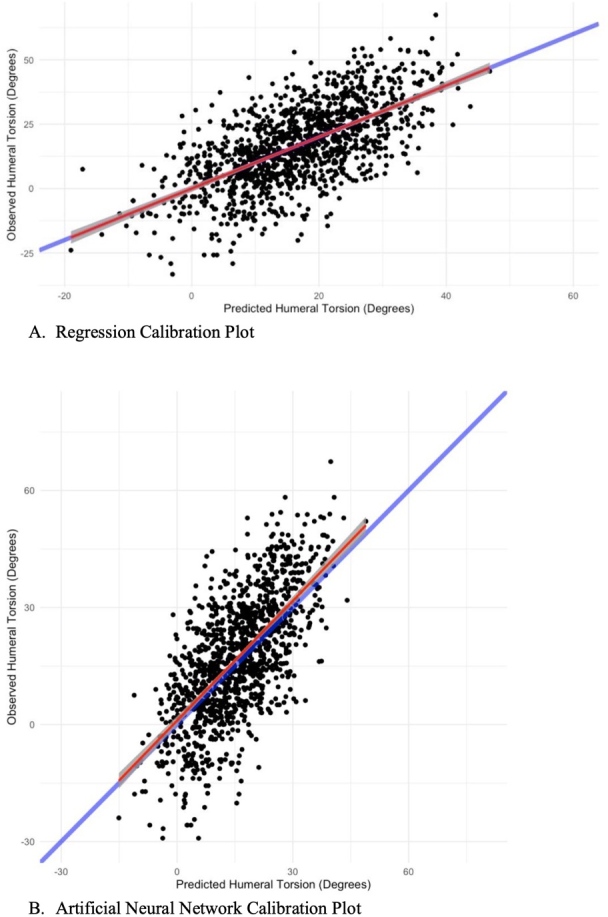
Figure 1.

Open in a new tab

The blue line depicts perfect calibration, while the red line reports actual calibration.

Machine Learning Models

The random forest and GBM demonstrated the best RMSE (Table 2). The random forest demonstrated the worst calibration (Table 2) and the ANN demonstrated the best calibration (Table 2; Figure 1B). The mean distribution of the final model linear predictors was 16° to 17°, the standard deviation was ranged from 9° to 10°, the minimum ranged from -2°1 to -11°, and the maximum was ranged from 44° to 52°. For each calibration plot and a full pictorial description of the final ANN architecture, please refer to the Appendix.

DISCUSSION

The machine learning models, besides ANN, demonstrated improved RMSE, compared to the statistical prediction model. Interestingly, the random forest and GBM RMSE difference compared to the linear regression model was similar to the HT standard error of measure (2-4°). However, all machine learning models demonstrated poor calibration compared to the linear regression prediction model. All prediction models demonstrated similar mean and variance calculations for predicted values. These findings suggest that prediction model performance should be evaluated through multiple performance metrics.

The machine learning models demonstrated decreased RMSE compared to the linear regression model. RMSE reports the average prediction model error in the units of the outcome of interest, which in this case is degrees of HT.37 This allows for a clinically pertinent and interpretable comparison of model performance. The random forest and GBM demonstrated decreased RMSE similar to the reliability HT standard error of measure, which may demonstrate a clinically significant difference. Both the random forest and GBM methods employ ensemble methods to generate prediction models.38,39 Ensemble methods have been shown to increase overall prediction precision due to the meta-aggregation of multiple models, allowing for increased generalizability in highly complex data.40 Further, the SVM model demonstrated a RMSE difference just below to the standard error of measure in comparison to the statistical model. SVMs utilize spatial kernel-based methods to inform predictions. Due to the individuality affecting HT development,12 the visual hyperplane demarcation methods used by SVM may generate improved HT prediction.

Although ML methods demonstrated decreased RMSE, calibration was poor. All machine learning methods demonstrated worse calibration compared to the statistical model, with the ANN a three-point slope difference. Calibration assesses the prediction outcome versus the actual outcome, and is important in understanding the accuracy of predictions.41 Over calibration has been reported as potentially harmful in the clinical setting, with miscalibration above 5% potentially affecting clinical decisions.42 These worse calibration performing machine learning methods, besides the ANN model, demonstrated a calibration slope in excess of 1.09, with the random forest model having a calibration slope of 1.33. Upon visual inspection of the calibration plots, all three models had significant demarcation at both tails of the calibration slope. These calibration discrepancies may be due to the biological volatility of individual outliers. Baseball players may have different genetic, environmental, and overall baseball loading factors, which all contribute to HT. Due to the algorithmic nature of machine learning, these outliers may have indiscriminately affected overall calibration. However, the ANN model had similar calibration compared to the statistical mode. ANN’s are high performers in predictions involving complex and multiple interaction data.43 As stated above, the complex issue individual variability, may allow for ANN’s to demonstrate high calibration performance.

All machine learning and linear regression models demonstrated similar mean and variance of predicted outcomes. These predictions are greater than those reported in a previous meta-analysis.9 While all models demonstrated similar prediction HT outcomes, there were distinct differences in model performance parameters. These findings highlight that model performance should be evaluated on multiple parameters, and not just on one specific performance finding. Clinicians need to integrate multiple prediction model performance outcomes, including discrimination, calibration, and model error, where appropriate, when evaluating the efficacy of a prediction model.41

These findings warrant future research. External validation is required to evaluate the generalizability of these models. HT development may be influenced by the volume and speed of throwing.12 Further research is needed to decipher if incorporating lifetime baseball exposure and throwing velocity could aid in prediction model precision. Other genetic factors such as collagen phenotype and familial history may also affect HT. Incorporating these predictors would be beneficial in evaluating the prediction ability of these models. Finally, the clinical utility of these prediction models needs to be evaluated. Understanding how these models may affect clinical practice and decisions in comparison to standard evidence-based practice is needed.

Clinical Implications

Model RMSE ranged from 9° to 15° for all models, with the statistical regression model RMSE was 12. The HT standard error of measure in professional pitchers is 2 degrees.44 Professional pitchers with 5 degrees HT difference between their throwing and non-throwing arms has been previously determined to pose greater risk for arm injury.45 As RMSE was reported in degrees, the RMSE may be beyond the clinically important error, and affect pitching arm risk assessment.5 However, arm injury examination encompasses multiple factors,4,46,47 and this HT prediction model could be used in conjunction of multiple other clinical tests and measures in order to prescribe a personalized injury mitigation program.

Practical Example

To aid in clinical applicability an example is described. As the machine learning models did not improve HT prediction, the ease of use and interpretability of the statistical model is recommended for clinical implementation. The statistical model is calculated through a mathematical equation to predict HT. This equation can be inputted into a standardized Excel or other basic computer program. For example, consider a 22-year-old right-handed pitcher from North America, with 35 degrees of IR, 103 degrees of ER, and 2 degrees of HA. During the clinical interview, the pitcher did not report any current or prior arm injuries. Using the equation reported in the supplement: 33.01 (The Intercept) + 22*0.15 (Age) – 1.83 (Right-Handed) + 35*0.37 (IR) - 103*0.30 (ER) + 2*0.31 (HA) + 0 (North America) + 0 (No Injury History) the model predicts this pitcher’s right HT is 18 degrees.48

Strengths and Potential Limitations

This study utilized a large sample of professional baseball pitchers that exceeded the a priori required sample size which increases the precision of these results. Multiple models were performed, incorporating both machine learning and statistical prediction model techniques, which increases the comparability of these findings. Internal validation was performed on all findings, allowing for a realistic optimism corrected model estimate, increasing the validity of these results. External validation was not performed on these models, decreasing the generalizability of these models. While many machine learning methods suggest splitting data into training and testing sets,49,50 this decreases the power and precision of these models.51,52 While this data met the a priori sample size calculations for linear regression, this sample size calculation may be too small for machine learning models.53 Further, these data did not allow for a training and testing split to maintain proper power. Previous authors51,52,54 have recommended to utilize all data during model development, and use robust internal validation methods to correct for optimism. As a result, cross-validation was used for internal validation on these prediction models.

Conclusions

Machine learning models demonstrated improved root mean square error and poorer calibration compared to the statistical model. Machine learning did not improve HT prediction in professional baseball players compared to a traditional statistical model. The root mean square error of all models was greater than the standard error of measure and clinically important difference, which may hinder the clinical usefulness of these models. It is recommended that clinicians use the statistical model in practice in conjunction with other examination factors, as this model provides an easy-to-use equation, that can quickly and efficiency be integrated within a clinical setting. Future research is needed to evaluate if environmental and genetic factors can improve HT prediction.

Declarations of interest

The authors declare no conflicts of interest.

Supplementary Material

Appendix 1
ijspt_2022_17_3_32380_81315.docx (904.4KB, docx)

Funding Statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

References

  1. Effect of a 6-Week weighted baseball throwing program on pitch velocity, pitching arm biomechanics, passive range of motion, and injury rates. Reinold M. M., Macrina L. C., Fleisig G. S., Aune K., Andrews J. R. 2018Sports Health. 10(4):327–333. doi: 10.1177/1941738118779909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Kinematic and kinetic comparison of baseball pitching among various levels of development. Fleisig Glenn S, Barrentine Steve W, Zheng Nigel, Escamilla Rafael F, Andrews James R. 1999J Biomech. 32(12):1371–1375. doi: 10.1016/s0021-9290(99)00127-x. [DOI] [PubMed] [Google Scholar]
  3. Kinetics of baseball pitching with implications about injury mechanisms. Fleisig Glenn S, Andrews James R, Dillman Charles J, Escamilla Rafael F. 1995Am J Sport Med. 23(2):233–239. doi: 10.1177/036354659502300218. [DOI] [PubMed] [Google Scholar]
  4. Deficits in glenohumeral passive range of motion increase risk of shoulder injury in professional baseball pitchers: a prospective study. Wilk Kevin E, Macrina Leonard C, Fleisig Glenn S, Aune Kyle T, Porterfield Ron A, Harker Paul, Evans Timothy J, Andrews James R. 2015Am J Sport Med. 43(10):2379–2385. doi: 10.1177/0363546515594380. [DOI] [PubMed] [Google Scholar]
  5. Humeral torsion as a risk factor for shoulder and elbow injury in professional baseball pitchers. Noonan T. J., Thigpen C. A., Bailey L. B., Wyland D. J., Kissenberth M., Hawkins R. J., Shanley E. 2016Am J Sports Med. 44(9):2214–9. doi: 10.1177/0363546516648438. [DOI] [PubMed] [Google Scholar]
  6. Reinold Michael M, Gill Thomas J. Sports Health. 1. Vol. 2. Current concepts in the evaluation and treatment of the shoulder in overhead-throwing athletes, part 1: physical characteristics and clinical examination; pp. 39–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Correlation of glenohumeral internal rotation deficit and total rotational motion to shoulder injuries in professional baseball pitchers. Wilk Kevin E, Macrina Leonard C, Fleisig Glenn S, Porterfield Ronald, Simpson Charles D, Harker Paul, Paparesta Nick, Andrews James R. 2011Am J Sport Med. 39(2):329–335. doi: 10.1177/0363546510384223. [DOI] [PubMed] [Google Scholar]
  8. Changes in shoulder and elbow passive range of motion after pitching in professional baseball players. Reinold Michael M, Wilk Kevin E, Macrina Leonard C, Sheheane Chris, Dun Shouchen, Fleisig Glenn S, Crenshaw Ken, Andrews James R. 2008Am J Sport Med. 36(3):523–527. doi: 10.1177/0363546507308935. [DOI] [PubMed] [Google Scholar]
  9. The relationship between humeral torsion and arm injury in baseball players: A systematic review and meta-analysis. Helmkamp Joshua K, Bullock Garrett S, Rao Allison, Shanley Ellen, Thigpen Charles, Garrigues Grant E. 2020Sports Health. 12(2):132–138. doi: 10.1177/1941738119900799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. The torsion of the humerus: its localization, cause and duration in man. Krahl Vernon E. 1947Am J Anatomy. 80(3):275–319. doi: 10.1002/aja.1000800302. [DOI] [PubMed] [Google Scholar]
  11. Biomechanics of the shoulder in youth baseball pitchers: implications for the development of proximal humeral epiphysiolysis and humeral retrotorsion. Sabick Michelle B, Kim Young-Kyu, Torry Michael R, Keirns Michael A, Hawkins Richard J. 2005Am J Sport Med. 33(11):1716–1722. doi: 10.1177/0363546505275347. [DOI] [PubMed] [Google Scholar]
  12. Playing level achieved, throwing history, and humeral torsion in Masters baseball players. Whiteley Rod, Adams Roger, Ginn Karen, Nicholson Leslie. 2010J Sport Sci. 28(11):1223–1232. doi: 10.1080/02640414.2010.498484. [DOI] [PubMed] [Google Scholar]
  13. Development and validation of a prediction model for fat mass in children and adolescents: meta-analysis using individual participant data. Hudda Mohammed T, Fewtrell Mary S, Haroun Dalia, Lum Sooky, Williams Jane E, Wells Jonathan CK, Riley Richard D, Owen Christopher G, Cook Derek G, Rudnicka Alicja R. 2019BMJ. 366:l4293. doi: 10.1136/bmj.l4293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Prognosis and prognostic research: what, why, and how? Moons Karel G M, Royston Patrick, Vergouwe Yvonne, Grobbee Diederick E, Altman Douglas G. 2009BMJ. 338:b375. doi: 10.1136/bmj.b375. [DOI] [PubMed] [Google Scholar]
  15. Adequate sample size for developing prediction models is not simply related to events per variable. Ogundimu Emmanuel O, Altman Douglas G, Collins Gary S. 2016J Clin Epidemiol. 76:175–182. doi: 10.1016/j.jclinepi.2016.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Sample size considerations for the external validation of a multivariable prognostic model: a resampling study. Collins Gary S, Ogundimu Emmanuel O, Altman Douglas G. 2016Stat Med. 35(2):214–226. doi: 10.1002/sim.6787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Points of significance: statistics versus machine learning. Bzdok Danilo, Altman Naomi, Krzywinski Martin. 2018Nature. :1–7. doi: 10.1038/nmeth.4642. [DOI] [PMC free article] [PubMed]
  18. Applications of machine learning and high‐dimensional visualization in cancer detection, diagnosis, and management. Mccarthy John F, Marx Kenneth A, Hoffman Patrick E, Gee Alexander G, O'neil Philip, Ujwal M L, Hotchkiss John. 2004Ann New York Acad Sci. 1020(1):239–262. doi: 10.1196/annals.1310.020. [DOI] [PubMed] [Google Scholar]
  19. The use of artificial neural networks in decision support in cancer: a systematic review. Lisboa Paulo J, Taktak Azzam F G. 2006Neural Networks. 19(4):408–415. doi: 10.1016/j.neunet.2005.10.007. [DOI] [PubMed] [Google Scholar]
  20. Predicting the future—big data, machine learning, and clinical medicine. Obermeyer Ziad, Emanuel Ezekiel J. 2016New Eng J Sport Med. 375(13):1216. doi: 10.1056/NEJMp1606181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Shoulder range of motion measures as risk factors for shoulder and elbow injuries in high school softball and baseball players. Shanley Ellen, Rauh Mitchell J, Michener Lori A, Ellenbecker Todd S, Garrison J Craig, Thigpen Charles A. 2011Am J Sport Med. 39(9):1997–2006. doi: 10.1177/0363546511408876. [DOI] [PubMed] [Google Scholar]
  22. Glenohumeral joint total rotation range of motion in elite tennis players and baseball pitchers. Ellenbecker T. S., Roetert E. P., Bailie D. S., Davies G. J., Brown S. W. 2002Med Sci Sports Exerc. 34(12):2052–6. doi: 10.1097/00005768-200212000-00028. [DOI] [PubMed] [Google Scholar]
  23. Reliability and validity of a new method of measuring posterior shoulder tightness. Tyler T. F., Roy T., Nicholas S. J., Gleim G. W. 1999J Orthop Sports Phys Ther. 29(5):262–9; discussion 270. doi: 10.2519/jospt.1999.29.5.262. [DOI] [PubMed] [Google Scholar]
  24. Changes in passive range of motion and development of glenohumeral internal rotation deficit (GIRD) in the professional pitching shoulder between spring training in two consecutive years. Shanley E, Thigpen C, Clark J C, Wyland D J, Hawkins R J, Noonan T J, Kissenberth M J. 2012J Shoulder Elbow Surg. 21(11):1605–1612. doi: 10.1016/j.jse.2011.11.035. [DOI] [PubMed] [Google Scholar]
  25. Shanley E., Kissenberth M. J., Thigpen C. A., Bailey L. B., Hawkins R. J., Michener L. A., Tokish J. M., Rauh M. J. J Shoulder Elbow Surg. 7. Vol. 24. Preseason shoulder range of motion screening as a predictor of injury among youth and adolescent baseball pitchers; pp. 1005–13. [DOI] [PubMed] [Google Scholar]
  26. High school cross country running injuries: a longitudinal study. Rauh M. J., Margherita A. J., Rice S. G., Koepsell T. D., Rivara F. P. 2000Clin J Sport Med. 10(2):110–6. doi: 10.1097/00042752-200004000-00005. [DOI] [PubMed] [Google Scholar]
  27. Calculating the sample size required for developing a clinical prediction model. Riley Richard D, Ensor Joie, Snell Kym I E, Harrell Frank E, Martin Glen P, Reitsma Johannes B, Moons Karel G M, Collins Gary, Van Smeden Maarten. 2020BMJ. 368 doi: 10.1136/bmj.m441. [DOI] [PubMed] [Google Scholar]
  28. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. Collins G. S., Reitsma J. B., Altman D. G., Moons K. G. 2015BMJ. 350:g7594. doi: 10.1136/bmj.g7594. [DOI] [PubMed] [Google Scholar]
  29. Shoulder range of motion in elite tennis players: effect of age and years of tournament play. Kibler W Ben, Chandler T Jeff, Livingston Beven P, Roetert E Paul. 1996Am J Sport Med. 24(3):279–285. doi: 10.1177/036354659602400306. [DOI] [PubMed] [Google Scholar]
  30. Left-handed skeletally mature baseball players have smaller humeral retroversion in the throwing arm than right-handed players. Takenaga Tetsuya, Goto Hideyuki, Sugimoto Katsumasa, Tsuchiya Atsushi, Fukuyoshi Masaki, Nakagawa Hiroki, Nozaki Masahiro, Takeuchi Satoshi, Otsuka Takanobu. 2017J Shoulder Elbow Surg. 26(12):2187–2192. doi: 10.1016/j.jse.2017.07.014. [DOI] [PubMed] [Google Scholar]
  31. The differences of humeral torsion angle and the glenohumeral rotation angles between young right-handed and left-handed pitchers. Takeuchi Satoshi, Yoshida Masahito, Sugimoto Katsumasa, Tsuchiya Atsushi, Takenaga Tetsuya, Goto Hideyuki. 2019J Shoulder Elbow Surg. 28(4):678–684. doi: 10.1016/j.jse.2018.09.002. [DOI] [PubMed] [Google Scholar]
  32. Influence of humeral torsion on interpretation of posterior shoulder tightness measures in overhead athletes. Myers Joseph B, Oyama Sakiko, Goerger Benjamin M, Rucinski Terri Jo, Blackburn J Troy, Creighton R Alexander. 2009Clin J Sport Med. 19(5):366–371. doi: 10.1097/JSM.0b013e3181b544f6. [DOI] [PubMed] [Google Scholar]
  33. Humeral retroversion and participation age in professional baseball pitchers by geographic region. Thomas Stephen J, Sheridan Scott, Reuther Katherine E. 2020J Athl Train. 55(1):27–31. doi: 10.4085/1062-6050-563-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. A comparison of glenoid morphology and glenohumeral range of motion between professional baseball pitchers with and without a history of SLAP repair. Sweitzer Brett A, Thigpen Charles A, Shanley Ellen, Stranges Gregory, Wienke Jeffrey R, Storey Troy, Noonan Thomas J, Hawkins Richard J, Wyland Douglas J. 2012Arthroscopy. 28(9):1206–1213. doi: 10.1016/j.arthro.2012.02.023. [DOI] [PubMed] [Google Scholar]
  35. Methods matter: clinical prediction models will benefit sports medicine practice, but only if they are properly developed and validated. Bullock Garrett S, Hughes Tom, Sergeant Jamie C, Callaghan Michael J, Riley Richard, Collins Gary. 2021Br J Sport Med. 55(23):1319–1321. doi: 10.1136/bjsports-2021-104329. [DOI] [PubMed] [Google Scholar]
  36. Clinical prediction models in sports medicine: A guide for clinicians and researchers. Bullock Garrett S, Hughes Tom, Sergeant Jamie C, Callaghan Michael J, Riley Richard D, Collins Gary S. 2021J Orthop Sport Phys Ther. 51(10):517–525. doi: 10.2519/jospt.2021.10697. [DOI] [PubMed] [Google Scholar]
  37. Statistics for the evaluation of model performance. Willmott C J, Ackleson S G, Davis R E, Feddema J J, Klink K M, Legates D R, O’donnell J, Rowe C M. 1985J. Geophys. Res. 90(C5):8995–9005. [Google Scholar]
  38. Greedy function approximation: a gradient boosting machine. Friedman Jerome H. 2001Ann Stat. :1189–1232.
  39. Liaw Andy, Wiener Matthew. R news. 3. Vol. 2. Classification and regression by randomForest; pp. 18–22. [Google Scholar]
  40. Martelli Pier Luigi, Fariselli Piero, Casadio Rita. Bioinformatics. suppl_1. Vol. 19. An ENSEMBLE machine learning approach for the prediction of all-alpha membrane proteins; pp. i205–i211. [DOI] [PubMed] [Google Scholar]
  41. Assessing the performance of prediction models: a framework for some traditional and novel measures. Steyerberg Ewout W, Vickers Andrew J, Cook Nancy R, Gerds Thomas, Gonen Mithat, Obuchowski Nancy, Pencina Michael J, Kattan Michael W. 2010Epidemiol. 21(1):128. doi: 10.1097/EDE.0b013e3181c30fb2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Calibration of risk prediction models: impact on decision-analytic performance. Van Calster Ben, Vickers Andrew J. 2015Med Dec Making. 35(2):162–169. doi: 10.1177/0272989X14547233. [DOI] [PubMed] [Google Scholar]
  43. An introduction to artificial neural networks in bioinformatics—application to complex microarray and mass spectrometry datasets in cancer studies. Lancashire Lee J, Lemetre Christophe, Ball Graham R. 2009Briefings Bioinformatics. 10(3):315–329. doi: 10.1093/bib/bbp012. [DOI] [PubMed] [Google Scholar]
  44. Influence of humeral torsion on interpretation of posterior shoulder tightness measures in overhead athletes. Myers J. B., Oyama S., Goerger B. M., Rucinski T. J., Blackburn J. T., Creighton R. A. 2009Clin J Sport Med. 19(5):366–71. doi: 10.1097/JSM.0b013e3181b544f6. [DOI] [PubMed] [Google Scholar]
  45. Humeral torsion as a risk factor for shoulder and elbow injury in professional baseball pitchers. Noonan Thomas J, Thigpen Charles A, Bailey Lane B, Wyland Douglas J, Kissenberth Michael, Hawkins Richard J, Shanley Ellen. 2016Am J Sport Med. 44(9):2214–2219. doi: 10.1177/0363546516648438. [DOI] [PubMed] [Google Scholar]
  46. Preseason shoulder strength measurements in professional baseball pitchers: identifying players at risk for injury. Byram Ian R, Bushnell Brandon D, Dugger Keith, Charron Kevin, Harrell Jr Frank E, Noonan Thomas J. 2010Am J Sport Med. 38(7):1375–1382. doi: 10.1177/0363546509360404. [DOI] [PubMed] [Google Scholar]
  47. Associations among hip and shoulder range of motion and shoulder injury in professional baseball players. Scher Steve, Anderson Kyle, Weber Nick, Bajorek Jeff, Rand Kevin, Bey Michael J. 2010J Athl Train. 45(2):191–197. doi: 10.4085/1062-6050-45.2.191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Development and internal validation of a humeral torsion prediction model in professional baseball pitchers. Bullock Garrett S, Shanley Ellen, Collins Gary S, Arden Nigel K, Noonan Thomas K, Kissenberth Michael J, Wyland Douglas J, Arnold Amanda, Bailey Lane B, Thigpen Charles A. 2021J Shoulder Elbow Surg. (12):2832–2838. doi: 10.1016/j.jse.2021.05.022. [DOI] [PubMed]
  49. Assessment and validation of machine learning methods for predicting molecular atomization energies. Hansen Katja, Montavon Grégoire, Biegler Franziska, Fazli Siamac, Rupp Matthias, Scheffler Matthias, Von Lilienfeld O Anatole, Tkatchenko Alexandre, Müller Klaus-Robert. 2013J Chem Theory Comp. 9(8):3404–3419. doi: 10.1021/ct400195d. [DOI] [PubMed] [Google Scholar]
  50. A study on SMO-type decomposition methods for support vector machines. Chen Pai-Hsuen, Fan Rong-En, Lin Chih-Jen. 2006IEEE transactions Neural Networks. 17(4):893–908. doi: 10.1109/TNN.2006.875973. [DOI] [PubMed] [Google Scholar]
  51. Prediction models need appropriate internal, internal–external, and external validation. Steyerberg Ewout W, Harrell Frank E. 2016J Clin Epidemiol. 69:245–247. doi: 10.1016/j.jclinepi.2015.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. Steyerberg Ewout W, Harrell Frank E, Jr., Borsboom Gerard J J M, Eijkemans M J C, Vergouwe Yvonne, Habbema J Dik F. 2001J Clin Epidemiol. 54(8):774–781. doi: 10.1016/s0895-4356(01)00341-9. [DOI] [PubMed] [Google Scholar]
  53. Modern modelling techniques are data hungry: a simulation study for predicting dichotomous endpoints. van der Ploeg Tjeerd, Austin Peter C, Steyerberg Ewout W. 2014BMC Med Res Methodol. 14(1):137. doi: 10.1186/1471-2288-14-137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Key steps and common pitfalls in developing and validating risk models. Wynants Laure, Collins Gary S, Van Calster Ben. 2017BJOG. 124(3):423–432. doi: 10.1111/1471-0528.14170. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Appendix 1
ijspt_2022_17_3_32380_81315.docx (904.4KB, docx)

Articles from International Journal of Sports Physical Therapy are provided here courtesy of North American Sports Medicine Institute

RESOURCES