RNA chain length and stoichiometry govern surface tension and stability of protein-RNA condensates

Summary

Proteomic studies have shown that cellular condensates are frequently enriched in diverse RNA molecules, which is suggestive of mechanistic links between phase separation and transcriptional activities. Here, we report a systematic experimental and computational study of thermodynamic landscapes and interfacial properties of protein-RNA condensates. We have studied the affinity of protein-RNA condensation as a function of variable RNA sequence length and RNA-protein stoichiometry under different ionic environments and external crowding. We have chosen the PolyU sequences for RNA and arginine/glycine-rich intrinsically disordered peptide (RGG) for proteins as a model system of RNA-protein condensates, which we then investigate through in vitro microscopy measurements and coarse-grained molecular dynamics simulations. We find that crowding and RNA chain length can have a major stabilizing effect on the condensation. We also find that the RNA-protein charge ratio is a crucial variable controlling stability, interfacial properties, and the reentrant phase behavior of RGG-RNA mixtures.

Graphical abstract

Highlights

• •LLPS with long RNAs is favored because of the lower entropic penalty of dissociation
• •RNA chain length modulates interfacial and material properties of condensates
• •Crowding can stabilize condensates with shorter RNAs
• •Salt reduces the reentrant LLPS window but does not change the optimal stoichiometry

Physical chemistry; Biophysical chemistry; Biophysics; Biophysical Chemistry

Introduction

Eukaryotic cells contain a large variety of membraneless organelles, which create transient and dynamic microcompartments for spatiotemporal organization and regulation of biomolecules (Mitrea and Kriwacki, 2016; Banani et al., 2017). Research over the last decade has shown that biomolecular condensation, which often occurs via liquid-liquid phase separation (LLPS) of proteins and nucleic acids, is the primary mechanism for the biogenesis of membraneless organelles (MLOs) (Shin and Brangwynne, 2017; Uversky, 2019, 2020; Zaslavsky et al., 2019). Biomolecular condensates encompass many types of intracellular bodies and can vary in size, lifetime, and composition (Brangwynne et al., 2009, 2015). The functional roles of condensates are yet to be fully elucidated. On the grounds of thermodynamic and kinetic control of phase transitions, however, many studies have already proposed functions of condensates which encompass transcriptional noise buffering (Simpson-Lavy and Kupiec, 2021; Riback et al., 2020), enhancement of enzymatic catalysis (O’Flynn and Mittag, 2021; Nakashima et al., 2021; Peeples and Rosen, 2021), and formation of heterochromatin domains in the nucleus (Rippe, 2021; Machida et al., 2018; Nakagawa et al., 2014). When it comes to possible gene-regulatory functions of condensation, RNA molecules are very likely to play significant roles because proteomic studies find ubiquitous enrichment of RNAs and RNA-binding proteins in the majority of membranless nuclear bodies (Hubstenberger et al., 2017; Youn et al., 2019). In particular, ribonucleoprotein (RNP) condensates appear at all stages of gene regulation, from RNA synthesis to transcription and degradation. Misregulation of RNA-containing condensates is a cause of many neurodegenerative diseases (Tatomer et al., 2016; Duronio and Marzluff, 2017; Galganski et al., 2017; Ma and Mayr, 2018).

Despite the functional importance of RNAs in phase separation, the biophysics of RNP condensate formation has often been viewed as protein-centric, which emphasizes the roles of low complexity domains of proteins as drivers of condensation while relegating more passive supporting roles for RNAs (Tauber et al., 2020; Wiedner and Giudice, 2021; Roden and Gladfelter, 2020). However, recent evidence is beginning to suggest more central roles for RNA molecules in the condensation and regulation of RNPs (Garcia-Jove Navarro et al., 2019; Kaur et al., 2021). In particular, it is found that RNAs can regulate the onset of phase separation and control the stoichiometry window of reentrant transitions. Further, RNAs can serve as nucleation seeds for condensate formation and act in synergy with proteins to give rise to multiphasic condensates (Kaur et al., 2021; Alshareedah et al., 2019, 2020). For instance, in vitro studies have discovered the formation of micellar and hollow vesicular nucleoprotein phases driven by simple polyU RNA strands mixed with disordered Arg-rich proteins (Alshareedah et al., 2019). Besides regulating phase behavior, it was also found that RNAs modulate the biophysical properties of liquid condensates by tuning their viscosity, surface tension, and structural order within liquid biomolecular condensates (Kaur et al., 2021; Alshareedah et al., 2019, 2020, 2021b; Zhang et al., 2015; Wei et al., 2017). Understanding the generic principles by which RNA contributes to the formation and structure of protein condensates would serve as an important foundation for the design of novel condensates.

Theoretical models (Choi et al., 2020a; Ruff et al., 2018; Zeng et al., 2020; Pappu, 2020; Lin et al., 2020; Huihui and Ghosh, 2020), molecular simulations (Shea et al., 2021; Regy et al., 2020; Dignon et al., 2020; Ruff et al., 2018; Choi et al., 2019), and field theoretical simulations (Pal et al., 2021; McCarty et al., 2019; Laghmach and Potoyan, 2020) of biomolecular phase transitions have emerged to play an increasingly important role alongside experiments in shedding light on the sequence-encoded driving forces as well as biophysical and material properties of condensates. One of the emerging theoretical frameworks from these studies is the stickers-and-spacers framework (Choi et al., 2020a, 2020b; Brangwynne et al., 2015; Chong and Mir, 2021) inspired from the field of associative polymers. This framework has become particularly helpful for rationalizing sequence-specific cases of protein-RNA phase transitions by providing an explanation for context-dependent affinity changes of key aromatic and charged residues (Chong and Mir, 2021; Martin et al., 2020; Yang et al., 2019). To give proper context for the present work, it is instructive that we briefly review the prior computational work on protein-RNA condensation. A pioneering work by Boeyaems et al. (Boeynaems et al., 2019) has looked at mechanisms of forming multilayered protein-RNA condensates and gave a glimpse that RNA structure and the interplay of RNA-RNA, protein-protein, and protein-RNA interactions govern the mesoscale structure and material properties of liquid condensates. Subsequently, more complex topologies including multilayered, micellar, and hollow vesicles were revealed by exploring the non-stoichiometric protein-RNA ratios (Kaur et al., 2021; Alshareedah et al., 2020). The protein sequence-dependent material properties (Alshareedah et al., 2021a) were recently explained utilizing the stickers-and-spacers framework. The thermodynamics of protein-RNA phase separation was further elucidated using minimalist patchy particle and residue-level models, showing that fine-tuning the interaction strengths and stoichiometries of components can indeed enhance or downregulate condensation (Joseph et al., 2021). It is important to note that most of these pioneering computational studies of biomolecular phase transitions, with a few exceptions (Mazarakos and Zhou, 2021), have largely focused on computing sequence-dependent phase-coexistence diagrams (Choi et al., 2020a; Regy et al., 2020) and have not investigated the sequence and composition dependence of interfacial properties. However, it is expected that interfacial tension and viscosity of condensates govern the dynamics of droplet fusion, extent of wetting, and topology with respect to other coexisting condensates (Kaur et al., 2021; Ghosh et al., 2021; Alshareedah et al., 2021a). The manner in which molecular interactions, sequence patterning, and stoichiometric composition of mixed chain condensates contribute to their interfacial properties is still not well understood.

In this work, we systematically investigate how essential aspects of RNA chains, namely their length and the stoichiometric ratio in conjunction with the external environmental conditions (pressure, salt, and temperature), contribute to the interfacial properties and thermodynamic stability of protein-RNA condensates (Figure 1). We employ optical microscopy experiments and a variety of computer simulation methodologies with coarse-grained molecular models to shed light on the nature of protein-RNA condensation and suggest new experiments for probing the roles of RNAs in regulating LLPS. In this work, we have adopted a minimalistic polyelectrolyte coarse-grained model of protein-RNA mixtures with bead per residue/base for RNA and RGG chains (Kaur et al., 2021; Alshareedah et al., 2019, 2020). Carrying out multiple distinct ways of sampling protein-RNA condensates, we have managed to distill the basic interplay of short-range and long-range forces with the configurational chain entropy, which underlies the observed experimental trends. In particular, we find that the polyelectrolyte charge ratio $q_{-}/q_{+}$, defined as the ratio of the number of RNA to protein charge units, is a key parameter that correlates with the window of the reentrant phase transition in excellent agreement with the experiments (Figure 1B). We also show that salt and external crowding can significantly tune the window of reentrant phase transitions of protein-RNA condensates. In sum, the study provides a comprehensive account of how RNA can modulate the formation of protein-RNA condensates through general non-sequence specific forces. Therefore, these findings serve as a useful guide for the experimental design of novel condensates and as a starting point for developing sequence-specific computational models of protein-RNA condensation.

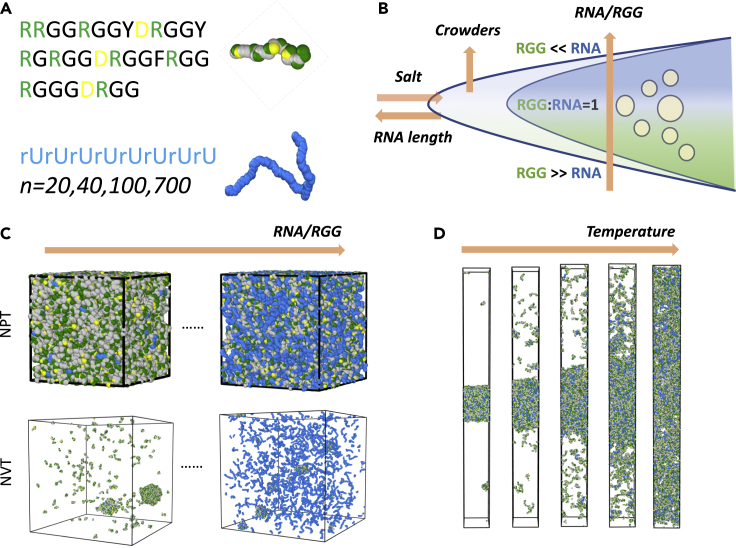
Figure 1.

Overview of simulations for probing the reentrant transitions of RGG-PolyU mixtures

(A) Coarse-grained model protein and RNA chains and the pairwise potentials employed in modeling RNA-RGG condensation.

(B) Schematic depiction of reentrant transition and the impact of external (salt and crowders) and internal (RNA length and concentration) factors.

(C) Setup of NVT and NPT simulations for investigating how the variation in RGG:PolyU ratio, salt, and external crowding impacts the stability of condensates.

(D) Setup of liquid-vapor equilibrium coexistence simulations to study the impact of RNA chain length on critical temperature and surface tension for 1:1 stoichiometries.

Results and discussion

Interplay of stoichiometry and RNA chain length governs the interfacial tension and thermodynamic stability of protein-RNA condensates

To study the impact of RNA chain length on the vapor-liquid phase coexistence, we have first set up mixtures with 1:1 polyelectrolyte charge $q_{-}/q_{+}$ ratio of rU_n:RGG systems, where we have varied the PolyU RNA chain length by setting n = 20, 40, 100, and 700 values (Figure 2). Through chain length variation with a fixed polyelectrolyte charge ratio, $q_{-}/q_{+}$, we aim to dissect the contribution of RNA chain connectivity in the condensate formation separately from the pure electrostatics-driven attraction of RNA-protein monomeric units. All of the simulations start from a previously equilibrated dense slab in the middle of the simulation box, which is then further simulated until the 1D density profile is equilibrated following the standard protocol of liquid-vapor complex fluids (Figure 1D, see STAR Methods).

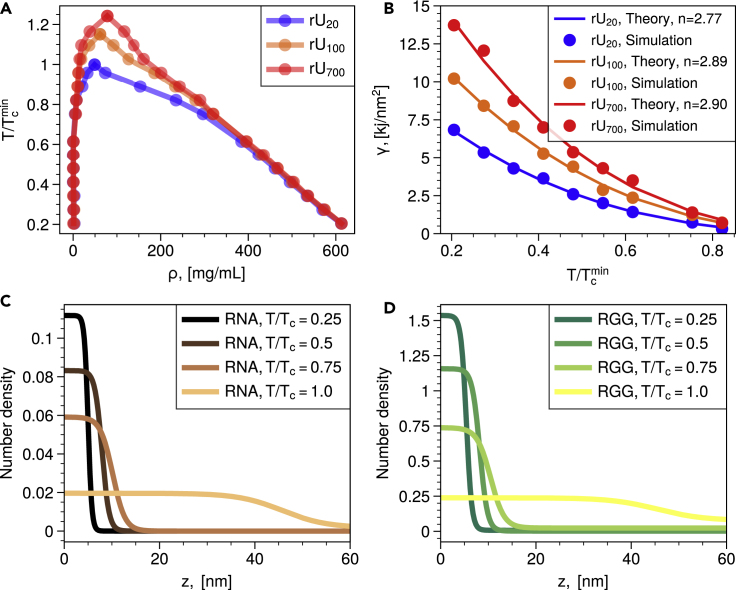
Figure 2.

Calculation of the phase diagrams and interfacial tensions of RGG-PolyU mixtures in the space of temperature and density

(A) Surface tension as a function of temperature for three RNA chain lengths (20, 100, and 700) under constant charge stoichiometry.

(B) Phase diagrams in the space of density and temperature. Critical temperature of U₂₀ is taken as a reference referred to as $T_c^{\min }$ with respect to which all other critical temperatures of longer PolyU lengths are compared.

(C) Density profiles of RNA chains along the z direction of the simulation box.

(D) Density profile of the RGG chains along the z direction of the simulation box.

As a measure of effective RNA-protein interactions and a key variable governing topology of multiphasic condensates (Kaur et al., 2021), we have first analyzed surface tension of RGG-PolyU mixtures for different temperatures (Figure 2A). We are guided by the Guggenheim-Katayama formula (Rowlinson and Widom, 2013; De Gennes et al., 2004) $\gamma \left(T\right)\sim {\gamma }_0{\left(1-T/T_c\right)}^n$, where n = 11/9 is predicted for complex and organic fluids (Rowlinson and Widom, 2013). T_c stands for critical temperature of protein-RNA mixtures which are obtained by mapping phase diagram in the space of density vs temperature and subsequently fitting the obtained binodal curve to $A{\left(T-T_c\right)}^{\beta }$, where β = 0.325 is the critical exponent for the 3D Ising model. We find that protein-RNA condensates do follow the Guggenheim-Katayama formula with a best fit obtained with an exponent, $n\sim 3$. The value of the exponent deviates from the range which is often used for organic fluids. This difference in exponents is reflective of the long-range electrostatic interactions dominating the protein-RNA interactions as opposed to weaker cohesive forces in organic liquids (Duchemin et al., 2021) (Figure 2A). Based on a fit to the Guggenheim-Katayama formula, one expects a trend of growing T_c as a function of the RNA chain. Indeed, mapping the binodal lines in the temperature-density plane, we find that the critical temperature grows as a function of RNA chain length for a fixed polyelectrolyte charge ratio (Figures 2B–2D).

These observations of elevated critical temperature and enhanced surface tension appear to have a simple rationalization in entropic arguments, which favor the stability of condensates with longer RNA chains. There are a host of similar phenomena where entropic forces allow simple rationalization of the location of molecular association/dissociation equilibrium known in physical chemistry under the name of a ligand effect (Ruff et al., 2021). The essence of the ligand effect is in reducing the entropic penalty for RNA-protein association by having greater connectivity of monomeric units/ligands. The longer RNA chains are thus more favored to form condensates than the shorter RNAs because of a reduced entropy penalty of association. As a consequence, condensates with longer RNA chain length display enhanced density (Figures 2C–2D), higher critical temperatures (Figure 2B), and higher surface tensions (Figure 2A). We note that carrying out mixed chain liquid-vapor coexistence simulations with long-range electrostatic forces is challenging, especially for polyelectrolyte charge disproportionate stoichiometries, which could lead to heterogeneities and a slow convergence rate of the density distribution. For the $q_{-}/q_{+}=1$ ratio, we have obtained a well-mixed liquid condensate slab configuration that smoothly transitions to a uniform distribution in vapor state with respect to both components (Figures 2C and 2D). On the other hand, for highly charged disproportionate mixtures, $q_{-}/q_{+}\gg 1\text{,}$ we have encountered heterogeneous slow-converging distributions often accompanied by interface formation. Thus, we seek alternative sampling methods for studying mixed chain condensates with heterogeneous distributions and attractive long-range forces. These challenges have also been discussed (Mazarakos and Zhou, 2021) in a recent study on mixed Lennard-Jones chain vapor-liquid phase equilibrium. Therefore, in the following section, we employ a multi-replica NVT sampling of protein-RNA droplet formation and NPT grid sampling of liquid state equilibrium.

Although the coexistence simulations are not an optimal setup for computationally probing highly heterogeneous mixtures, we can employ NVT simulations initiated from single droplet states to visualize the stability of protein-RNA condensates for varying RNA chain length and stoichiometric ratios. By carrying out twenty replicas of simulations with an RNA chain length of 40 and 120, we have confirmed the generality of findings from the coexistence simulations by showing that RNA chain length indeed stabilizes the formation of droplets (Figures 3A and 3B). We also find that increasing RNA concentration leads to a reentrant transition. In particular, we can see that even at high charge disproportionate states, longer RNA chains can become active nucleating centers, stabilizing the formation of large and small droplets. At the same time, the shorter RNA chains are entropically more favored to be in dissociated states relative to longer RNA chains. By analyzing the radii of gyration of the largest clusters (cutoff set at 3 nm) in these simulations, we see that longer RNA tends to generate larger droplets that are able to maintain their size against the excess RNA concentration. In contrast, shorter RNAs tend to dissolve droplets much faster. In the next section, we provide a deeper and more quantitative examination of the thermodynamic stability of liquid protein-RNA condensates as a function of RNA length and stoichiometry coupled with external conditions.

Figure 3.

Constant volume simulations of RGG-PolyU condensates initiated from dense droplet states for two PolyU lengths

(A) PolyU of length of 40.

(B) PolyU of length 120. The snapshots from left to right correspond to polyelectrolyte charge ratios of $q_{-}/q_{+}=\mathrm{1,5,10}$. The histogram on the right shows the distribution of radii of gyration of clusters observed in the independent replicas of cubic box NVT simulations.

External crowding and degree of ionic screening govern the reentrant transition window in protein-RNA condensates

The study of the liquid-vapor equilibrium of protein-RNA condensates in the previous sections provided a robust picture of how RNA chain length contributes to the stability of condensates. However, one encounters many challenges when quantitatively studying liquid-vapor phase equilibrium of mixed protein-RNA condensates with stoichiometries that are strongly deviating from the 1:1 polyelectrolyte charge ratio, rendering the equilibrium density estimation of smaller components unreliable. In this section, we start from an observation that for mixed chain systems, the density of the chain packing at a given temperature and pressure is a natural proxy for estimating the location with respect to the binodal line (Mazarakos and Zhou, 2021).

Therefore, we turn to liquid state equilibrium under NPT conditions where we use mass density in the simulation box under constant pressure as a proxy for measuring the affinity of distinct stoichiometries to form condensates. In addition, to understand the impact of pressure, we have looked at standard pressure conditions (p = 1atm) and a high-pressure condition (p = 10atm) which we use as a way of mimicking condensate formation under in vitro and cellular crowding, respectively. To dissect the contributions of stoichiometry and chain length on the thermodynamic stability of RGG-RNA condensate, we have carried out a large grid of simulations sampling ten stoichiometries distributed between 1:10 to 10:1 ratios (Figure 4) with each condition also being replicated for ten values of ionic strengths, each with two values of pressures totaling in 200 unique simulations. In agreement with experiments presented in the following section (see Figure 6), we see that under higher pressure (p = 10atm), the reentrant window is drastically expanded (Figures 4 and S2). Unsurprisingly, the short RNA chain length mixtures appear as more sensitive to external pressure, because, in our setup, external pressure counters the entropic drive of shorter chains to dissociate into the dilute region of the solution. One can envision crowding-induced phase transitions in the cell as a mechanism to respond to both global changes in the cellular environment (Delarue et al., 2018).

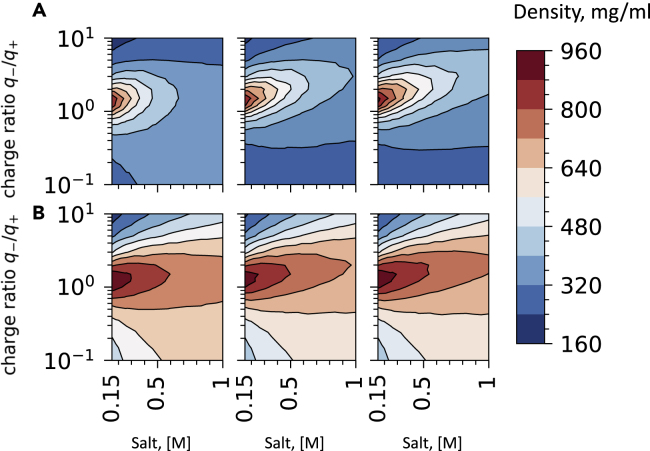
Figure 4.

Liquid state equilibrium of RNA-RGG condensates under constant pressure as a function of salt concentration and charge ratio

(A) From left to right corresponds to the RNA chain length of 20, 100, and 700 under pressure p = 1 atm.

(B) From left to right corresponds to the RNA chain length of 20, 100, and 700 under pressure p = 10 atm.

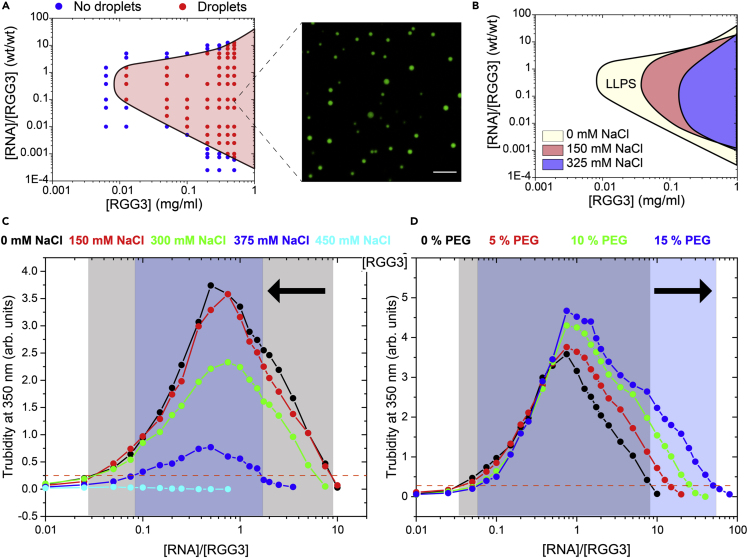
Figure 6.

Experimental evidence for the stoichiometry-dependent liquid-liquid phase separation of RGG-polyU mixtures

(A) A state diagram indicating the RGG (FUS^RGG3) and polyU concentrations at which condensates form (red-filled circles) and the concentrations at which the mixture forms a homogeneous state (blue-filled circles). The solid black line is a guide to the eye. The red shaded region marks the LLPS regime. Inset shows a fluorescence microscopy image of RGG-polyU condensates formed at an RGG concentration of 0.33 mg/mL and polyU-to-RGG ratio of 0.75 (w/w). The buffer contains 25 mM Tris-HCl (pH 7.5), 125 mM NaCl, and 20 mM DTT. Scale bar represents 10 micron.

(B) A state diagram showing the effect of increasing ionic strength of the buffer on the LLPS region of RGG-polyU mixtures. Higher salt concentration leads to the shrinkage of the LLPS region in the state diagram because of weaker intermolecular interactions (see Figure S1).

(C) The turbidity of RGG-polyU mixtures as a function of RGG-to-polyU ratio (w/w) is shown for several salt concentrations (NaCl). The shaded regions indicate the LLPS condition (turbidity >0.25) for the lowest and highest salt concentrations used in this study and are drawn as a guide to the eye. The black arrow marks the shrinkage of the LLPS window upon increasing salt concentration. The sample was prepared by fixing RGG concentration to 0.347 mg/mL and varying polyU concentration in a 25 mM Tris-HCl (pH 7.5) buffer with 20 mM DTT and the desired NaCl concentration.

(D) Similar data to (C) but at different crowding conditions. The arrow indicates the enlargement of the LLPS window upon increasing crowder concentration (PEG8000), indicating more favorable LLPS at high crowding conditions. RGG concentration is kept at 0.347 mg/mL, and polyU concentration is varied. The sample was prepared by fixing RGG concentration to 0.347 mg/mL and varying polyU concentration in a 25 mM Tris-HCl (pH 7.5) buffer with 150 mM NaCl, 20 mM DTT, and the desired PEG concentration (w/v).

Results from the NPT simulations (Figures 4 and S2) also capture the salt-induced trend in the reentrant transitions showing that the condensate coexistence region is mostly centered around polyelectrolyte charge ratio of $q_{-}/q_{+}\sim 1-5$. In agreement with coexistence and NVT simulations, we again see the same robust trend of longer RNA chains having larger densities and broader coexistence windows. It is also notable that the salt-dependent profiles converge under high pressure to nearly identical coexistence windows. This is readily explained by the fact that in high-density mixtures, the effect of RNA chain connectivity effectively disappears. The fact that high external pressure/crowding conditions counter the ligand effect is seen in the emergence of similar reentrant windows for all PolyU lengths for the high-pressure conditions (Figures 4 and S2)

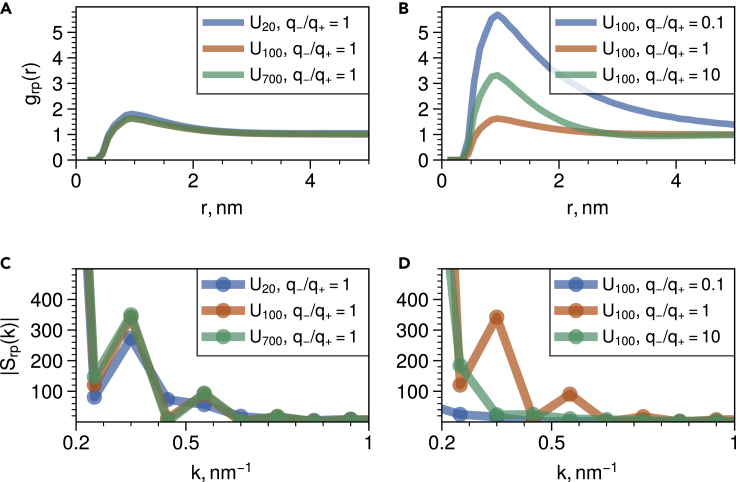
To better understand the nature of chain packing in $RNA:RGG$ liquid condensates, we next turn to the analysis of radial distribution functions (RDF) and static Debye structure factors of protein-RNA condensates (Figures 5A and 5B). The radial distribution functions are especially useful for visualizing the dense protein-RNA mixtures obtained through NPT simulations for varying stoichiometry and chain length of RNA. Specifically, the RDF plots allow one to see the ligand effect at play by quantifying how many RNA base units are positioned near each RGG chain.

Figure 5.

Radial distributions and structure factors for liquid state condensates of RGG-PolyU mixtures

(A) Radial distribution functions of RGG-U monomers for fixed polyelectrolyte charge stoichiometry and varying PolyU length.

(B) Radial distribution functions of RGG-U monomers for varying polyelectrolyte charge stoichiometry and fixed PolyU length.

(C) Static structure factor of RGG-U monomers for fixed polyelectrolyte charge stoichiometry and varying PolyU length (D) Static structure factor of RGG-U monomers for varying polyelectrolyte charge stoichiometry and fixed PolyU length.

When looking at the radial distribution functions for a varying PolyU length and fixed stoichiometry, we find that spatial distribution of protein and RNA units is similar in all liquid condensates (Figure 5A). This implies that we have a well-mixed protein-RNA condensate in the absence of interfaces. On the other hand, when looking at radial distribution functions with varying stoichiometry and fixed RNA length, we find different organization of RNA units depending on the stochiometry (Figure 5B). Specifically, in the condensates containing disproportionate number of RNA chains, we see that on an average there are more U units in the first shell of RGG residues. When looking at cross-species structure factors (Figures 5C and 5D), we see that longer RNA chains and charge proportionate stoichiometries tend to generate condensates with larger characteristic length scales.

In addition to basic structure-centric analysis, it is also informative to provide an approximate assessment of the entropy-energy interplay in the condensates with varying stoichiometry (Figure S3). To do this, we have converted simulation snapshots into pixelated images (via Gaussian blurring) and used the information-theoretic measure of entropy, i.e., Shannon entropy, $S=-{\sum }_i{p}_i\log p_i$ where p_i stands for the probability of a pixel. The energetic contribution is assessed by computing intermolecular pair energy per chain pair $U_{\text{inter}}=\frac{1}{N_{\text{pairs}}}⟨U_{DH}+U_{LJ}⟩$ where we have included only excluded volume U_LJ and U_DH contributions between RNA−RNA, RNA−RGG, and RGG−RGG chain pairs averaged over simulation frames. We see that shorter RNA chains incur a larger entropic penalty of condensation (Figure S3A). From the analysis of the energetic term, we find that stoichiometric ratios beyond 1:1 can still be favorable energetically, especially for longer RNA chains because of reduced entropic penalty (Figure S3B).

Experimental evidence for RNA chain length, stoichiometry, and salt-dependent reentrant condensation

Previously, we have reported that mixtures of RNA and Arg-rich proteins/peptides can undergo a reentrant liquid-liquid phase separation with respect to RNA:protein mixture stoichiometry (Alshareedah et al., 2019, 2021a, 2020, 2021b; Banerjee et al., 2017; Kaur et al., 2021). Other reports have indicated that such reentrant behavior is observed for several protein-RNA and protein-protein heterotypic phase separating systems (Babinchak and Surewicz, 2020; Iserman et al., 2020; Maharana et al., 2018). In this section, to test some of the predictions reported in the last two sections, we probe the effect of salt and crowding conditions on the full state diagram of protein-RNA condensates. We utilize the third RGG box of Fused in Sarcoma (FUS^RGG3 or RGG) as a model Arg-rich protein in the presence of generic homopolymeric RNA polyU as our model protein-RNA system. Using bright-field microscopy, we constructed an isothermal state diagram of RGG-polyU mixtures (See STAR Methods). At low total concentration (both RGG and polyU), no phase separation was observed across the tested mixture stoichiometry values. Increasing the total concentration led to the emergence of LLPS at a window of mixing ratios (0.1–1.5, Figure 6A). The LLPS is reentrant, because no LLPS was observed at extremely low (<0.1) and (>1.5) high mixing. Increasing the total concentration caused a broadening of the LLPS window, where the coexistence lines in both sides of the LLPS region shifted toward more extreme ratios (0.001–10, Figure 6A). We next probed the effect of increasing the ionic buffer strength via the addition of salt (NaCl) on the global state diagram of RGG-polyU mixtures. We found that the lowest total concentration where LLPS s observed is shifted to a higher concentration upon the addition of salt (from [RGG] = 0.0125 mg/mL at 0 mM NaCl to [RGG] = 0.2 mg/mL at 325 mM NaCl, Figures 6B and S1). In addition, the LLPS window shrinks considerably upon the addition of salt (Figure 6B). These results are affirmed by solution turbidity measurements that showed that the phase-separation of the RGG-polyU mixtures decreases significantly upon increasing the salt concentration with a concurrent shrinkage in the LLPS window (Figure 6C). These results are consistent with simulations reported here and also with previous experimental studies on the effect of salt on protein-RNA phase separation (Alshareedah et al., 2021b; Banerjee et al., 2017). The effect of salt can be understood as an effective attenuation of electrostatic interactions between the RGG chains and polyU chains, which leads to the diminishing of protein-RNA complexes and weaker inter-complex interactions.

Heterotypic interactions between RGG chains and polyU chains can also be affected by crowding. Previous reports explored the effect of crowding on LLPS and found orthogonal results depending on the crowding agent and the specific protein system. For example, Protter et al. showed that increasing crowding diminished the phase separation of hnRNPA1 protein (Protter et al., 2018) (using BSA and lysozyme as a crowder). Alternatively, our previous work showed that crowding enhances LLPS of the prion-like low complexity domain of FUS (PLD) (Kaur et al., 2021) (using PEG and dextran as crowders). Further, Lin and coworkers suggested that BSA can enhance phase separation of FUS-IDR with RNA at 10% concentration (Lin et al., 2015). Zosel et al. showed (Zosel et al., 2020) that crowding enhances the affinity between the activation domain of the steroid receptor coactivator 3 (ACTR, negatively charged) and the coactivator binding domain of CBP/p300 protein (NCBD, positively charged). The enhancement of such interaction is thought to be a manifestation of depletion forces (Zosel et al., 2020). In the present work, we used turbidity measurements to probe the effect of crowding (mimicked by the addition of PEG8000) on the heterotypic phase separation of RGG-polyU mixtures. We found that increasing the concentration of PEG in the solution led to a significant enlargement of the LLPS window of RGG-polyU mixtures. At 0% PEG, RGG-polyU mixtures phase-separated between [polyU]/[RGG] mixing ratios of 0.05 and 7.5. At 15% PEG (w/v), we observe LLPS over a much broader window of mixing ratios (from 0.1 to 50, Figure 6D). These results indicate that increasing PEG concentration leads to more favorable LLPS conditions for RGG-polyU mixtures. The effect of PEG on the phase behavior of heterotypic protein-RNA mixtures has been measured previously for Spermine-polyU mixtures (Marianelli et al., 2018). However, this effect of PEG enhancing the phase separation may not be generalized to different crowders, and the underlying mechanism may be more complex than simple depletion interactions. Previous reports indicated that although PEG enhanced polyU-Spermine phase separation, Ficoll-70, another commonly used crowding agent, had little effect on the same system (Marianelli et al., 2018). Fluorescence micrographs showed that PEG is depleted from the polyU-Spermine condensates, whereas Ficoll-70 was enriched in the same condensates (Marianelli et al., 2018). Andre and Spruijt have written a thorough review of crowding agents’ distinct effects on the LLPS of various protein and protein-RNA systems (André and Spruijt, 2020). Overall, our results are in harmony with coarse-grained molecular dynamics simulations, showing that RGG-polyU phase separation is reentrant, diminished by increasing salt concentration and enhanced by crowding with PEG.

Conclusion

It has been shown that mixtures of RNA and Arg-rich proteins/peptides can undergo a reentrant liquid-liquid phase separation upon the change in RNA:protein stoichiometry (Alshareedah et al., 2019, 2021a, 2020, 2021b; Banerjee et al., 2017; Kaur et al., 2021; Babinchak and Surewicz, 2020; Iserman et al., 2020; Maharana et al., 2018). However, the ability of the external environment and length-scale of polymeric RNA chains to control the window of reentrant transitions and influence interfacial properties of protein-RNA condensates has not been studied. In addition, the molecular-scale details underlying the thermodynamic stability of condensates have so far remained elusive.

In this work, we have carried out a systematic study to elucidate the interplay of RNA chain length, RNA-protein stoichiometry, and environmental conditions that jointly shape the thermodynamic landscapes and interfacial properties of protein-RNA condensates. Using RGG and PolyU constructs as model systems, we have employed optical microscopy experiments and many different molecular simulations to probe the nature of the liquid state and liquid-vapor equilibrium of protein-RNA condensates. We show that the polyelectrolyte charge ratio of RNA:protein chains is a key variable governing the stability of condensates and the coexistence window of reentrant transitions. Simulations also show that basic polymeric and electrostatic forces capture a broad range of RNA-RGG condensation features by also providing several interesting molecular insights. We find that RNA chain length is a key variable affecting surface tension and thermodynamic stability of protein-RNA condensates through a mechanism reminiscent of the “ligand effect” (Ruff et al., 2021) known in chemical and material sciences. We find that the impact of RNA chain length on condensate formation takes place through enhanced localization of RNA units which effectively enhance protein-RNA interactions, leading to high critical temperatures and surface tensions. Analysis of radial distribution functions and condensates structure factors provides additional insight into why RNAs can form droplets that significantly deviate from the 1:1 polyelectrolyte charge ratio. Interestingly both simulations and experiments show that external crowding can largely offset the destabilizing effect of shorter RNA chains and extend the coexistence window. Overall, the study provides a comprehensive account of how molecular characteristics and stoichiometric ratio in protein RNA mixtures govern thermodynamic and interfacial properties of condensates. The findings of this paper should be helpful both as a guide for the experimental design of novel synthetic condensates and as a starting point for developing sequence-specific computational models of protein-RNA condensation.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
RGG3 box of FUS	GenScript Inc., USA	FUS472-505-Cys
polyuridylic acid pottasium salt (poly(U))	Sigma-Aldrich	P9528
Water, (For RNA Work) (DEPC-Treated, DNASE, RNASE free/Mol. Biol.)	Fisher Bioreagents	CAS 7732-18-5
DL-Dithiothreitol (DTT)	Sigma-Aldrich	D0632
Alexa Fluor™ 488 C5 Maleimide	Invitrogen, Molecular Probes	A10254
Polyethylene glycol MW 8000	Fisher Scientific	CAS 25322-68-3
UltraPureTM 1 M Tris-HCl pH 7.5	Invitrogen	15-567-027 (Fisher Scientific)
Sodium Chloride	Fisher Bioreagents	BP358-212
Software and algorithms
Origin Pro v2021	OriginLabs	https://www.originlab.com/
Ovito Pro		https://www.ovito.org/
Hoomd-Blue v2.7		https://hoomd-blue.readthedocs.io/en/latest/
freud v2.7		https://freud.readthedocs.io/en/latest/
gsd v2.5		https://gsd.readthedocs.io/en/stable/#

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by Davit A Potoyan potoyan@iastate.edu

Materials availability

Study did not generate new materials.

Method details

Minimal poly-electrolyte model for RNA-protein condensation

This work has employed a single-residue and single-base resolution coarse-grained polyelectrolyte model for protein and RNA chains which is commonly adopted in computational studies of biomolecular condensates (Dignon et al., 2018b; Alshareedah et al., 2020; Mazarakos and Zhou, 2021). The model and a few of its variations have been used in the previous studies of binary and ternary systems (Kaur et al., 2021; Alshareedah et al., 2019, 2020). Briefly, this model uses particles sizes, bond lengths, and harmonic constants, which were originally used in the studies by Dignon et al. (Dignon et al., 2018a, 2018b, 2019, ) for parametrizing the hydropathy based models of the intrinsically disordered protein sequence. Since our simulations are using coarse-grained representation of biomolecules, we adopt the following derived units τ = 1 ps, σ = 1 nm and ε = 1 kJ/mol.

The energy function describing the protein-RNA mixture can be broken down to three terms U = U_b + U_LJ + U_DH corresponding to bonded interactions, non-bonded short-range repulsion/attraction and long-range electrostatic interactions respectively. The term U_b describes bonded interactions of protein and RNA chains, which are modeled by a harmonic potential k_r (r–r₀)² with a spring constant k_r = 10 kJ/nm² and on equilibrium bond length of r₀ = 0.38 and r₀ = 0.34 for protein and RNA chains respectively. Unlike the protein chain, the RNA chain also includes an additional harmonic angular term k_θ (θ–θ₀)² which models the stiffness of the RNA chains (Kaur et al., 2021; Alshareedah et al., 2019, 2020). Here, the spring constant is k_θ = 1.0 kJ and the equilibrium angle is θ₀ = 1.78 rads. Electrostatic interactions are modeled by using a Coulombic term with Debye-Hückel electrostatic screening to account for salt concentration: $U_{DH}\left(r,i,j\right)=\frac{q_i{q}_j}{4\pi Dr}\exp \left(-\kappa r\right)$ where ${\kappa }^{-1}$ is the Debye screening length and _D = 80, is the dielectric constant of the solvent (water). Debye Huckel’s term acts on all charged pairs within and between chains. The Debye screening length ${\kappa }^{-1}$ is varied in the simulations to study the impact of salt concentration (0.1–1 M). The short-range attraction/repulsion models all short-range interactions, including hard-core repulsion of coarse-grained units and short-range attractions due to RNA base-pairing and residue-base interactions. In this study, we have set the energetic scale of short range-attractions to be uniform ${\epsilon }_{LJ}^{pp}={\epsilon }_{LJ}^{rp}={\epsilon }_{LJ}^r=1$ which is done to ensure the formation of well-mixed droplets without sub-compartments in agreement with experimental findings presented in the next section (Figure 6A). Prior studies have shown that the interplay of scales in short-range attraction can lead to the formation of multiphasic condensattion and different degrees of wetting of multicomponent droplets (Kaur et al., 2021; Hazra and Levy, 2021; Mazarakos and Zhou, 2021). We note, however, that when it comes to nucleic-acids the breakdown of interactions into short vs long range contributions may not be as trivial. This is due to the presence of multiple interactions between sugar, base and phosphate groups which involve water and ion mediated multi-valent interactions (Potoyan et al., 2013).

We utilized the third RGG box of Fused in Sarcoma (AA: 472–505; FUS^RGG3 or RGG) as a model Arg-rich polypeptide (Thandapani et al., 2013). The sequence length of RGG is fixed in all simulations to be 34 amino acids long. The length of PolyU is varied to study the impact of RNA chain length on condensation. We have looked at four different PolyU lengths corresponding to U₂₀, U₄₀, U₁₀₀ and U₇₀₀ (Figure 1). The protein-to RNA charge ratio is varied from $q_{-}/q_{+}=10$ (RNA-rich condensates) to $q_{-}/q_{+}=0.1$ (protein-rich condensates). For each PolyU: RGG mixture, we have sampled the salt-induced screening lengths from the near-physiological up to 10 times the physiological concentration. Finally, we have looked at variable crowding conditions to determine how the condensate phase boundaries are modulated by external pressure mimicking intracellular crowding. Further details on simulation, including snapshots, parameter table, and methodology, can be found in the Supporting Information (see Table S1).

Setup of vapor-liquid coexistence and liquid state simulations

We carried out two distinct simulations for probing liquid state and liquid-vapor equilibrium of protein-RNA condensates (Figures 1C and 1D). Both simulations are first initialized at a low density by randomly placing the protein and RNA chains in the large cubic simulation box of 100 nm³. Because we had to run a large number of grid-based simulations, this protocol serves two purposes: first, to eliminate blowups during the first few hundred time steps by reducing the number of beads placed within very close proximity by the random initialization, secondly, this setup avoids the tangling of long RNA chain molecules in some of the simulations.

We have then used high external pressure of p = 10atm on all sides of the box to generate condensed slabs of varying RNA length, condensate density, external crowding, stoichiometry, and salt concentrations. For liquid-liquid equilibrium state, the condensates were further equilibrated under p = 1atm and under p = 10atm pressures using NPT ensemble in order to reveal the density fluctuations of condensates with varying composition and environmental conditions (Figure 1C). In order to visualize the formation of the condensates, we have also carried out a series of NVT simulations using the previously condensed state obtained from NPT simulations as a starting point.

The box with a dense condensate state was slowly elongated to 200 nm along the z axis and further equilibrated under the NVT ensemble for the liquid-vapor coexistence simulations. Once equilibrated, one has a slab of liquid condensate surrounded by its coexisting saturated vapor of RNA and protein chains. The binodal of liquid-vapor equilibrium is numerically estimated by fitting density histogram of simulated particles of protein and RNA along the elongated box axis (z) to hyperbolic tangent profile $\left(\tanh \right)$ as is done in previous studies (Mazarakos and Zhou, 2021; Silmore et al., 2017; Stephan et al., 2019). The coexistence simulations have also been used to calculate the value of condensate surface tension as a function of temperature γ (T). For these calculations, we make use of pressure tensors extracted from the z-slabs of coexistence simulations $\gamma ={\int }_{-\infty }^{\infty }dz\left[⟨P_{zz}⟩-0.5\cdot \left(⟨P_{xx}⟩+⟨P_{yy}⟩\right)\right]$ to obtain temperature-dependent surface tension which is then fitted to Guggenheim-Katayama formula (De Gennes et al., 2004; Rowlinson and Widom, 2013) γ = γ₀(1–T/T_c)ⁿ where γ₀ is a constant obtained after fitting and exponent n for simple fluids is predicted to be n ∼ 1.

The NPT molecular dynamics simulations were run at T = 300 K using p = 10atm and τ_P = 0.5 to dense generate liquid slabs. The NVT molecular dynamics (MD) simulations were run at T = 300 K using the Langevin thermostat with a friction coefficient of η = 0.01 and time step of 0.01. MD runs were performed on graphical processing units (GPUs) using the HOOMD-Blue package. The equilibrium run was performed for 10⁶ with a time step of 0.01, and the production run was performed for an additional ${10}^7$ steps. Convergence of liquid sate simulations is checked by conducting multiple replicas using the norm of the dot product of radial distribution functions of replicas as a metric for convergence. The convergence of liquid-vapor coexistence was checked by monitoring the time evolution of the density profile for the two components.

Materials

The third RGG box of FUS (FUS AA: 472–505) was synthesized by GenScript Inc, USA (>90% purity) and used without further purification. The RGG sequence has a C-terminal Cysteine for site-specific fluorescence labeling. Concentrated stock solutions of the peptide were prepared by dissolving in RNase-free water with 50 mM DTT and stored at −20°C. Polyuridylic acid potassium salt (MW 600–1000 kDa) was purchased from Sigma Aldrich and reconstituted in RNase-free water, and stored at −20°C. To ensure no insoluble aggregates existed in the stock solutions, both peptide and polyU stocks were checked under the microscope.

State diagram measurements

Peptide-RNA mixtures were prepared by mixing RGG and polyU solutions in a 25 mM Tris-HCl buffer (pH 7.5) with 20 mM DTT. The NaCl concentration is indicated in the corresponding figures and figure legends. Samples were mixed thoroughly and imaged using a Zeiss Primovert inverted microscope with 40x objective lens and a Zeiss Axiocam 503 monochrome camera. Samples that formed condensates were marked as LLPS and samples that did not form condensates were marked as no LLPS. The complete state diagram was plotted using OriginPro software (v2021). The fluorescence image in Figure 6A was collected using a Zeiss LSM 710 Laser scanning confocal microscope with a 63x oil immersion objective (Plan-Apochromat 63x/1.4 oil DIC M27). The sample contained 1% Alexa 488 (C5-maleimide derivative, Molecular Probes) labeled RGG peptide. The labeling was done through Cysteine-maleimide chemistry as described in our earlier work (Banerjee et al., 2016).

Turbidity measurements

Samples were prepared identically as described in the state diagram measurement section. Turbidity was measured using a NanoDrop oneC UV-Vis spectrophotometer with 1.0 mm path length at 350 nm wavelength. For samples containing PEG8000, the PEG was added to the buffer before adding RGG and polyU. The turbidity plots were produced by gradually titrating the polyU concentration in a single 100 μL sample. The RGG concentration was kept at 0.347 mg/mL for all the turbidity curves.

Published: April 15, 2022

Data and code availability

All of the python scripts used for the analysis of molecular simulation data reported in the manuscript can be accessed via https://doi.org/10.5281/zenodo.6108088.