Dosimetric Quantities in Neuroendocrine Tumors over Treatment Cycles with 177Lu-DOTATATE

Daniel Roth; Johan Gustafsson; Carl Fredrik Warfvinge; Anna Sundlöv; Anna Åkesson; Jan Tennvall; Katarina Sjögreen Gleisner

doi:10.2967/jnumed.121.262069

. 2022 Mar;63(3):399–405. doi: 10.2967/jnumed.121.262069

Dosimetric Quantities in Neuroendocrine Tumors over Treatment Cycles with ¹⁷⁷Lu-DOTATATE

Daniel Roth ^1,^*, Johan Gustafsson ^1,^*, Carl Fredrik Warfvinge ², Anna Sundlöv ^1,², Anna Åkesson ³, Jan Tennvall ², Katarina Sjögreen Gleisner ^1,^✉

PMCID: PMC8978188 PMID: 34272319

Visual Abstract

graphic file with name jnumed.121.262069absf1.jpg

Keywords: ¹⁷⁷Lu-DOTATATE, neuroendocrine tumors, absorbed dose, fractionation

Abstract

Tumor dosimetry was performed for ¹⁷⁷Lu-DOTATATE with the aims of better understanding the range and variation of the tumor-absorbed doses (ADs), how different dosimetric quantities evolve over the treatment cycles, and whether this evolution differs depending on the tumor grade. Such information is important for radiobiologic interpretation and may inform the design of alternative administration schemes. Methods: The data came from 41 patients with neuroendocrine tumors (NETs) of grade 1 (n = 23) or 2 (n = 18) who had received between 2 and 9 treatment cycles. Dosimetry was performed for 182 individual lesions, giving a total of 880 individual AD assessments across all cycles. Hybrid planar–SPECT/CT imaging was used, including quantitative SPECT reconstruction, voxel-based absorbed-dose-rate calculation, semiautomatic image segmentation, and partial-volume correction. Linear mixed-effect models were used to analyze changes in tumor ADs over cycles, absorbed-dose rates and activity concentrations on day 1, effective half-times, and tumor volumes. Tumors smaller than 8 cm³ were excluded from analyses. Results: Tumor ADs ranged between 2 and 77 Gy per cycle. On average, the AD decreased over the cycles, with significantly different rates (P < 0.05) of 6% and 14% per cycle for grade 1 and 2 NETs, respectively. The absorbed-dose rates and activity concentrations on day 1 decreased by similar amounts. The effective half-times were less variable but shorter for grade 2 than for grade 1 (P < 0.001). For grade 2 NETs, the tumor volumes decreased, with a similar tendency in grade 1. Conclusion: The tumor AD, absorbed-dose rate, and activity uptake decrease, in parallel with tumor volumes, between ¹⁷⁷Lu-DOTATATE treatment cycles, particularly for grade 2 NETs. The effective half-times vary less but are lower for grade 2 than grade 1 NETs. These results may indicate the development of radiation-induced fibrosis and could have implications for the design of future treatment and dosimetry protocols.

DOTATATE with ¹⁷⁷Lu is well established for the treatment of neuroendocrine tumors (NETs). A protocol of 4 cycles of 7.4 GBq administered at an interval of approximately 2 mo has been proven safe and effective (1–3). Since the therapy is based on ionizing radiation, the likelihood of tumor response is expected to be related to the absorbed dose (AD) (4–11). Current data indicate that the tumor ADs vary considerably between patients, from a few grays to nearly 200 Gy (8,9,12–15). Most studies on tumor dosimetry have focused on a single lesion in each patient, and there are currently limited data on the variation in AD between metastases within patients and variation across treatment cycles. Such information is important to advance the understanding of how the AD delivery is currently fractionated and to inform the design of alternatives in which the activity per cycle, number of cycles, or time between cycles in the standard administration scheme are modified (4,7–9,11,16).

The AD is essentially calculated from a combination of an initial absorbed-dose rate and an effective half-time, in turn derived from estimates of the activity concentration over time. Understanding changes in these input quantities is essential for a deeper understanding of any systematic changes in the AD. Such information is also important from a practical perspective. A varying initial absorbed-dose rate but a stable half-time implies that the latter needs to be determined at cycle 1 only, thereby simplifying the dosimetry protocol.

Tumor biology adds another level of complexity. Gastroenteropancreatic NETs are divided into grades G1, G2, and G3 based on Ki-67 staining representing the proliferation rate. G1 tumors (Ki-67 < 3%) are indolent, whereas G3 tumors (Ki-67 > 20%) are more aggressive. G2 tumors have a proliferation rate of 3%–20%, with a moderate aggressiveness. Additionally, there is an inverse relationship between somatostatin-receptor expression and grade (17).

The aim of this work is to improve the understanding of how the tumor AD is delivered over the treatment cycles, including the effect of tumor grade. Further aims are to elucidate which underlying quantity is mainly responsible for any changes in the tumor ADs and whether dosimetry can be simplified.

MATERIALS AND METHODS

Patient Data

Data were obtained from the Iluminet trial (NCT01456078), for which a detailed description has been published elsewhere (18). The Iluminet trial was a phase II, nonrandomized clinical trial that included 103 patients at 2 sites in Sweden from 2011 to 2018. The trial included patients with somatostatin-receptor–expressing NETs of gastroenteropancreatic or bronchopulmonary origin, with a Ki-67 index of up to 20% (G1 and G2) based on the most recent biopsy before inclusion in the study. They were given repeated cycles of ¹⁷⁷Lu-DOTATATE (7.4 GBq) at intervals of 10 ± 2 wk. Treatment was continued up to a renal biologically effective dose of 27 ± 2 Gy unless tumor progression or treatment-limiting toxicity occurred earlier. Patients with a good renal and hematologic tolerance, and no signs of tumor progression, were invited to continue up to a renal biologically effective dose of 40 ± 2 Gy. The final analysis of the trial results is under way. This study is based on a subset of the Iluminet patients, acquired at one of the study sites, and includes 41 patients who received 2–9 cycles.

Image Data

Two SPECT/CT systems were used, a GE Discovery VH and a GE Discovery 670 (GE HealthCare). Images were acquired using medium-energy collimators and energy windows centered on 208 keV, with widths of 20% (GE Discovery VH) or 15% (GE Discovery 670).

Whole-body images were acquired at nominal times 1 h, 24 h (day 1), 96 h (day 4), and 168 h (day 7) after administration. The γ-camera images were coregistered to a scout radiograph to enable pixelwise attenuation and scatter correction (19).

SPECT/CT images were acquired on day 1, with 60 projections of 45 s each, a 128 × 128 matrix, and a pixel size of 4.42 × 4.42 mm² (GE Discovery 670) or 4.02 × 4.02 mm² (GE Discovery VH). The low-dose CT images were rescaled to mass density using a 2-segment linear function based on calibration measurements. For each set of projection data, 3 different settings were used for the OS-EM reconstruction (overview of image data analysis is shown in Supplemental Fig. 1; supplemental materials are available at http://jnm.snmjournals.org). The reason for this 3-fold reconstruction was that different steps in the dosimetry process required images with different characteristics (20,21). The first reconstruction (AS-8) was used for segmentation and applied 8 iterations and 6 angles per subset with compensation for attenuation and scatter (22). The second reconstruction (ASR-8), used for visual inspection, also included distance-dependent resolution compensation. The third reconstruction (ASR-40) was used for image-based quantification, with 40 iterations and 6 angles per subset and compensations for attenuation, scatter, and resolution. All SPECT images were calibrated to reflect the activity per voxel by application of a calibration factor from measurements in air (23). Absorbed-dose-rate maps were calculated from the SPECT images (ASR-40) using a voxel-based Monte Carlo program based on the EGS4 code with the PRESTA (23,24).

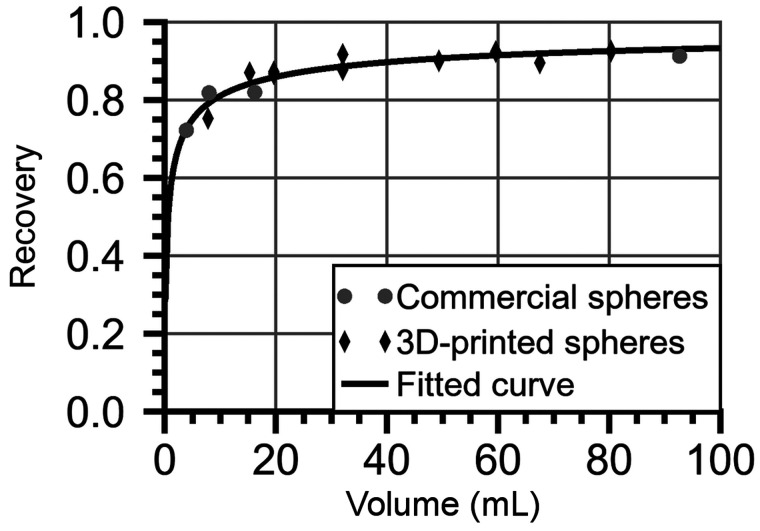
Recovery coefficients (RCs) were determined by phantom measurements of an elliptic water-filled Jaszczak phantom with 12 spheric inserts with ¹⁷⁷Lu-DOTATATE with volumes of 3.9–93 mL. Four spheres were from a commercial vendor, whereas 8 spheres were 3D-printed by fused filament fabrication. Images were acquired for 1–3 spheres at a time using the same acquisition settings as for patients and reconstructed as ASR-40. The RC was calculated as the ratio of the sphere activity estimated from images and the activity from phantom preparation, and a function of the RC versus volume was fitted (21).

Image Analysis

Tumors were delineated in the SPECT images using a semiautomatic 3-dimensional segmentation method based on Fourier surfaces (21). Initialization was done by manual delineation of volumes of interest (VOIs) that roughly encompassed the tumor, using the ASR-8 SPECT image for guidance. A closed surface was adapted to the tumor boundary as represented by high image gradients in the AS-8 SPECT images, which has been shown to preserve volume well (21). The VOI was applied in the ASR-40 images, and the mean activity concentration was calculated. The mean absorbed-dose rate was determined by applying the same VOI in the absorbed-dose-rate maps. The RC for the VOI volume was applied to both the activity concentration and the absorbed-dose rate.

Planar images were analyzed by identifying the tumors using an in-house graphic user-interface. Segmentation was performed using a semiautomatic method (20), which, when applied in the time sequence of images, yielded tumor-specific time–activity data (in relative units). Absorbed-dose rate as a function of time was determined by rescaling the planar-derived data to the SPECT-derived absorbed-dose rate on day 1. A curve was fitted, consisting of a monoexponential function for the last 3 data points and a quadratic function for the early phase (20). The AD was obtained by analytic integration of the absorbed-dose rate.

The SPECT VOIs and planar regions of interest were verified by the responsible oncologists using diagnostic images, such as contrast-enhanced CT or MRI. In a few cases, the VOIs and regions of interest were adjusted or redelineated, using the Otsu method (25) or a manually selected threshold. Verification also aimed at ensuring that the planar-derived data fulfilled the validity criteria described previously (20).

To make image-derived quantities consistent for statistical analysis, the ADs, absorbed-dose rates, and activity concentrations were recalculated to a nominal administered activity of 7.4 GBq. The absorbed-dose rates and activity concentrations were also adjusted to a reference time point, set to the average time point of all SPECT/CT images acquired on day 1 (21.7 ± 1.5 h). This adjustment was based on the effective half-time for the individual tumor or, if unavailable, the mean half-time for other tumors within the same patient or else across all patients. Different exclusion criteria were set for the analyses of different quantities. A volume cutoff of 8 cm³ was applied to avoid the bias observed for small volumes (21). For the AD and effective half-time, tumors that suffered from substantial superposition of activity in the planar images were excluded (20). An additional criterion was set for the effective half-time, to exclude cycles in which, for practical reasons, not all 4 planar images were acquired.

Different alternatives for simplifying the dosimetry process were evaluated in terms of how well the cumulative AD across all cycles could be estimated. As a reference, tumors that met the selection criteria for all cycles were identified and the cumulative ADs determined. These were compared with the cumulative ADs when assuming a constant AD estimated from the first cycle (A), using a constant half-time estimated from the first cycle (B), or using grade-specific mean half-time (C). Both B and C were combined with a cycle-specific estimate of the absorbed-dose rate, assuming monoexponential washout. The possibility of using the fitted linear mixed-effect model (LMM) for interpolation of missing cycle data was also explored (D) and, as a consistency check, the cumulative ADs obtained from Equation 1 (E). Evaluation was made by means of Bland–Altman plots (Supplemental Fig. 4).

Statistical Analysis

Changes over the treatment cycles were analyzed using an LMM in R, version 4.0.2 (26, 27). Dependent variables were the AD, the absorbed-dose rate on day 1, the activity concentration on day 1, the effective half-time, and the tumor volume. The model was

Q {(n, g)}_{i, j} = \exp [q_{1} + q_{2} \cdot g + n \cdot (k_{1} + k_{2} \cdot g) + Δ q_{i} + Δ k_{i} \cdot n + Δ q_{i, j} + Δ k_{i, j} \cdot n]

Eq. 1

where n was the cycle number, g the grade status for the patient (G1, $g = 0$ ; G2, $g = 1$ ), and $Q {(n, g)}_{i, j}$ the dependent variable for tumor j in patient i. Parameters $q_{1}$ and $q_{2}$ described the global intercepts—and $k_{1}$ and $k_{2}$ the mean rates of change with respect to the cycle number—for G1 and G2. These parameters were treated as fixed effects. Parameters $Δ q_{i}$ , $Δ k_{i}$ , $Δ q_{i, j}$ , and $Δ k_{i, j}$ constituted the random effects, where $Δ q_{i}$ and $Δ k_{i}$ described the patient-specific differences from the global intercepts and rates of change, whereas $Δ q_{i, j}$ and $Δ k_{i, j}$ described the tumor-specific differences from the sum of the fixed effects and the patient-specific random effects. The 95% CIs for the rates of change and the difference between G1 and G2 were also derived (28).

The mean value across all cycles was calculated using a second LMM. This was constructed by omitting the cycle-dependent terms in Equation 1, according to

\bar{Q} (g) = q_{1} + q_{2} \cdot g + Δ q_{i} + Δ q_{i, j}

Eq. 2

The global mean for G1 and G2 were thus $q_{1}$ and $(q_{1} + q_{2})$ , respectively. The 95% CIs were constructed using the Confint function in R.

RESULTS

Of the G1 patients (n = 23), the primary-tumor origin was pancreas (n = 1), small intestine or right colon (n = 20), and lung (n = 2). For G2 patients (n = 18), it was pancreas (n = 7), small intestine or right colon (n = 9), lung (n = 1), and unknown (n = 1).

Altogether, dosimetry was performed for 182 tumors in 41 patients given between 2 and 9 treatment cycles, resulting in 880 AD assessments. Of these, the criterion for activity concentration and absorbed-dose rate analysis was fulfilled for 500 data points, representing 138 tumors in 40 patients. From these, 404 fulfilled the criteria for AD estimation, representing 109 tumors in 39 patients. The criteria for the effective half-time were fulfilled in 301 cases, representing 104 tumors in 39 patients. As a result of the inclusion criteria, not every patient and tumor was represented at every cycle.

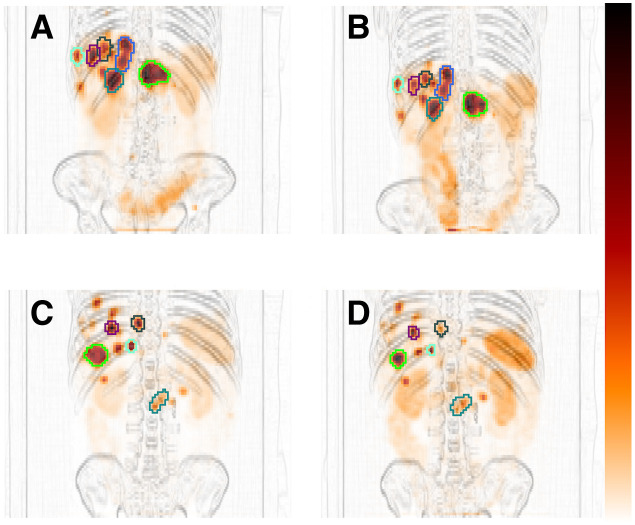
Figure 1 shows examples of SPECT VOIs from the semiautomatic segmentation that in most cases yielded results consistent with image data (21). The RC curve is shown in Figure 2. The in-house–manufactured spheres provided a relevant volume range with respect to partial-volume correction.

FIGURE 2. — Measured RCs and fitted curve.

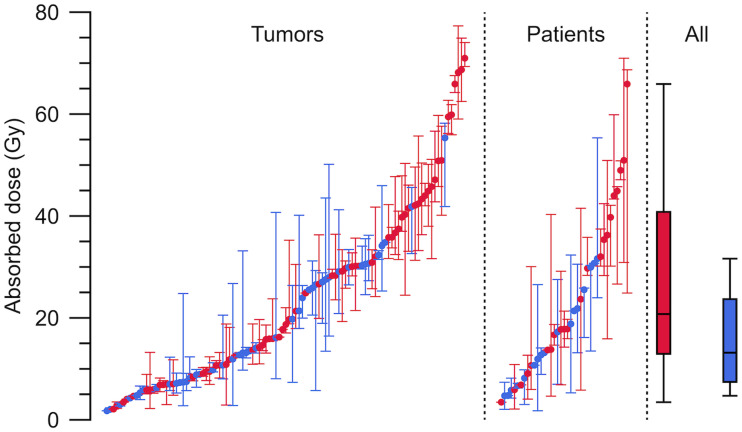
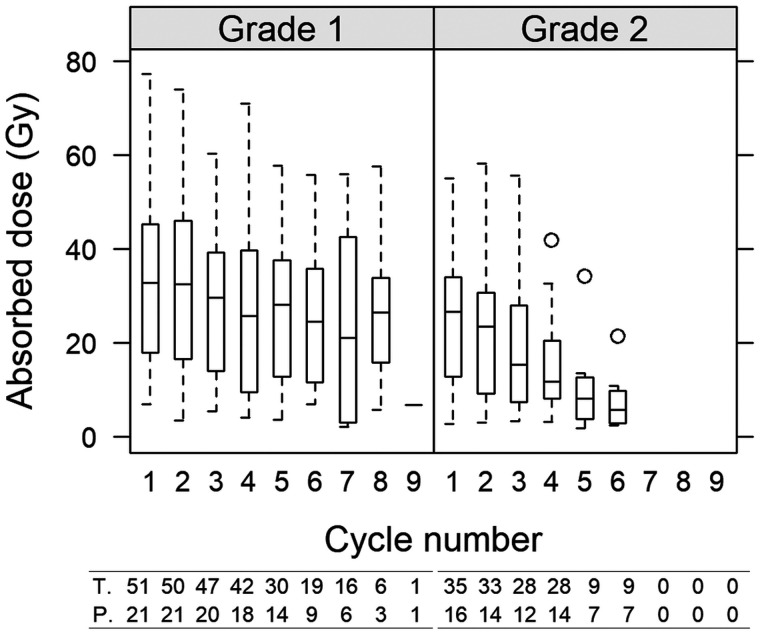
Figure 3 summarizes the AD per cycle, its variability, and how the variability is decomposed over cycles for individual tumors, between tumors, and between patients. The tumor AD ranged between 2 and 77 Gy, and there was substantial variation both between cycles and between tumors. The median AD for G1 patients was 21 Gy (first and third quartiles, 13 and 41; range, 3.5–66 Gy) (rightmost panel). For G2 patients, the median was 13 Gy (first and third quartiles, 7.4 and 24; range, 4.7 to 32 Gy). The overall difference between G1 and G2 was caused mainly by a more pronounced AD decrease over the cycles for G2 (Fig. 4). Calculated across all tumors, for G1, the medians for cycles 1–5 were 33, 33, 30, 26, and 28 Gy, respectively, and 24 Gy for 6 cycles or more. For G2, medians for cycles 1–5 were 27, 23, 15, 12, 8 Gy, respectively, and 6 Gy for 6 cycles or more.

FIGURE 4. — AD as function of cycle for G1 NETs (left) and G2 NETs (right) across all patients and all tumors. Whiskers indicate 5th and 95th percentiles. At bottom, numbers of tumors and patients are indicated beneath each box.

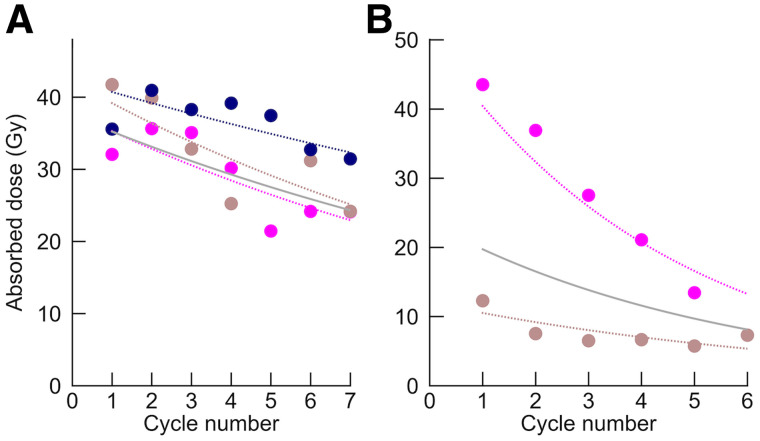
Figure 5 shows examples of the AD evolution for individual tumors over treatment cycles and how the LMM (Eq. 1) decomposes the intercepts and rates of change with respect to the individual patient and tumor. The fixed-effect intercepts over all patients and tumors for G1 ( $exp (q_{1})$ ) and G2 ( $\exp (q_{1} + q_{2})$ ) were 24.6 and 19.4 Gy, respectively, and were not significantly different (P = 0.3). The changes between consecutive cycles are summarized in Table 1. On average, the AD rate of change for G2 was −0.15, corresponding to a 14% decrease between consecutive cycles. For G1, the decrease was less pronounced, with a mean rate of change of −0.06, or a 6% decrease between cycles, and the upper limit of the 95% CI was near zero. The AD changes of G1 and G2 were significantly different.

TABLE 1.

Fixed-Effect Percentage Change from Previous Cycle

	Change (% from previous cycle)
	G1		G2
Dependent variable	Mean	95% CI	Mean	95% CI	P (G1 vs. G2)
Activity concentration (MBq/mL)	−6.1	−11 to −0.89	−14	−20 to −8.4	0.04
Absorbed-dose rate (mGy/h)	−6.2	−11 to −0.93	−14	−20 to −8.3	0.04
Effective half-time (h)	−0.69	−2.1 to 0.77	−1.2	−3.4 to 1.1	0.7
Volume (cm³)	−1.1	−5.0 to 3.0	−6.4	−11 to −1.4	0.1
AD (Gy)	−5.7	−11 to −0.12	−14	−20 to −7.9	0.04

Open in a new tab

Data are calculated from rates of change from the LMM, such that for G1, change = $\exp (k_{1}) - 1$ , and for G2, change = $\exp (k_{1} + k_{2}) - 1$ , with $k_{1}$ and $k_{2}$ as in Eq.1.

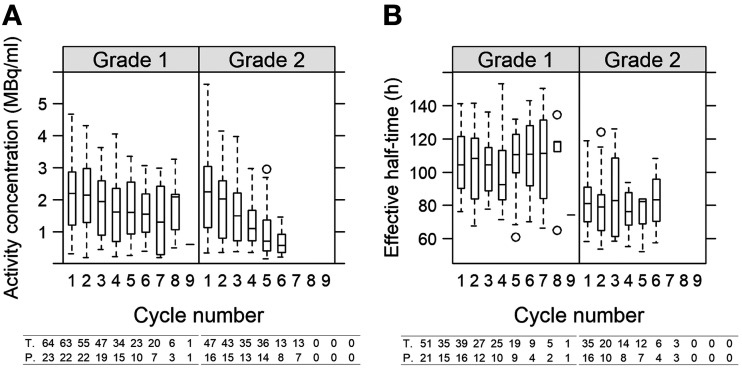
The activity concentration exhibited a decrease similar to the AD (Fig. 6), as did the absorbed-dose rate (Table 1). The median absorbed-dose rates for G1 were 187, 175, 163, 136, 133, and 127 mGy/h for cycles 1–5 and for 6 cycles or more, respectively, whereas for G2 they were 184, 167, 125, 87, 58, and 50 mGy/h. The decreased AD over the cycles was thus associated with a decreased absorbed-dose rate, in turn governed by a decreasing activity concentration. The tumor volumes did not change for G1, whereas for G2 a per-cycle decrease of 6% was observed (Table 1). The fixed-effect intercepts were 20 cm³ and 16 cm³ for G1 and G2 patients, respectively, and were not significantly different (P = 0.4). The distributions of all tumor volumes at cycle 1 are shown in Supplemental Fig. A2. For the effective half-time, a cycle-dependent change was not observed (Table 1; Fig. 6). The averages over all patients, all cycles, and all tumors (Eq. 2) were 103 h for G1 (95% CI, 96–109 h) and 81 h (95% CI, 73–90 h) for G2. The difference between G1 and G2 was significant (P < 0.001).

FIGURE 6. — Activity concentration (A) and effective half-time (B) as functions of cycle number for G1 and G2 NETs across all patients and all tumors. At bottom, numbers of tumors and patients are indicated beneath each box. For activity concentration in G1, 2 outliers at cycle 1 (6.8 and 7.5 MBq/mL) are excluded.

The cumulative ADs obtained using complete dosimetry and the simplification alternatives are shown in Table 2 and Supplemental Fig. 3. The median cumulative AD was 137 Gy (range, 33–403 Gy) for G1 and 80 Gy (range, 11–211 Gy) for G2. The assumption of a constant effective half-time across cycles yielded a negligible systematic deviation both when estimated from the first cycle (B) and as the grade-specific cohort means (C), whereas the limits of agreement were wider when using the population means. Assuming a constant AD across cycles (A) yielded the largest deviations among the alternatives. The modest deviations obtained using Equation 1 (E) confirmed the fit of the LMM to data.

TABLE 2.

Relative Difference in Cumulative AD for 65 Individual Tumors over 2–9 Cycles When Introducing Simplifications to Dosimetry Protocol, When Using LMM to Interpolate Missing Cycle Data, and When Using Complete LMM

Alternative	Description	Mean (%)	Limits of agreement (%)
A	Simplification using constant AD/cycle, from first cycle	15	55
B	Simplification using constant effective half-time, from first cycle	0.43	13
C	Simplification using constant effective half-time, global means (G1, 103 h; G2, 81 h)	0.01	31
D	Interpolation, LMM intercept patient- and tumor-effective half-time (Eq. 2)	1.6	7.9
E	Complete LMM for effective half-time or AD (Eq. 1)	−1.0	3.3

Open in a new tab

Relative difference is calculated as (AD simplified protocol/AD complete dosimetry – 1). Limits of agreement are derived from Bland–Altman plots (Supplemental Fig. A4).

DISCUSSION

We have found that when ¹⁷⁷Lu-DOTATATE is given with a fixed activity in repeated cycles, the tumor AD decreases over the course of treatment, especially for G2 NETs. This decrease is caused by a decreasing activity uptake in the tumors. We have also found that there is a large variability in tumor ADs, both between cycles for individual tumors and within and between patients. This is an important observation for dosimetry-based treatment planning with the objective of reaching a minimum cumulative AD to tumors since it may be difficult to decide which tumor AD should guide treatment.

The observed decline in activity uptake and volume for G2 may be consistent with the development of radiation-induced stroma and fibrosis observed in pancreatic NETs (29). For G1, the declines are less pronounced, as could possibly be related to the rate of cell necrosis (2). A low Ki-67 index means that a higher proportion of cells are in the G0 phase of the cell cycle, and the progression to cell death may thus be slower for G1 than G2 NETs. This is also consistent with the published relationships between tumor shrinkage and cumulative AD at the time of best response, which required a longer follow-up time for small-intestinal NETs than for pancreatic NETs, which generally have a higher Ki-67 (8,9,11).

The effective half-times are not observed to change over the treatment cycles and are in rather narrow ranges, with significantly shorter half-times for G2 than G1. The lower ability to retain ¹⁷⁷Lu-DOTATATE for G2 NETs could be associated with tumor-cell necrosis, recruitment of immune cells, and washout via the lymphatic system (29,30). The limited variation in the effective half-times opens the possibility of simplifying the dosimetry method by estimating the tumor-specific effective half-time for the first cycle and then assuming an equal half-time for remaining cycles. The amplitude of the curve will still need to be estimated for each cycle but requires only 1 SPECT/CT examination.

A limitation in this study is that image segmentation and estimation of the tumor volume are based on SPECT, thereby making the VOI definition dependent on the activity distribution. The low-dose CT acquired as part of SPECT/CT does not provide sufficient quality for tumor identification, and the alternative would be to use contrast-enhanced CT and coregistration of the SPECT image. However, coregistration is known to introduce undesired interpolation effects, and in view of the comparably small and differently located tumors, this approach was not considered feasible. The volume cutoff of 8 cm³ was applied to avoid negative bias in the activity concentration for smaller volumes (21). Another limitation is the use of planar imaging for assessing the effective half-time. In previous studies, we have found good agreement with SPECT-derived data for tumors without a substantial activity overlap in the planar images (20).

LMMs are suitable for analysis of data that have complex covariance structures, including longitudinal and hierarchical data. For this study, the rates of change are based on repeated measurements with variance components both between patients and between tumors in the same patient. Technically, a linear function is fitted to the logarithm of the data (Eq. 1), thereby assuming an exponential relationship between the dependent variable and cycle number. We deemed a multiplicative change (e.g., −10% per cycle) to be more appropriate than an additive change (e.g., 3 Gy per cycle).

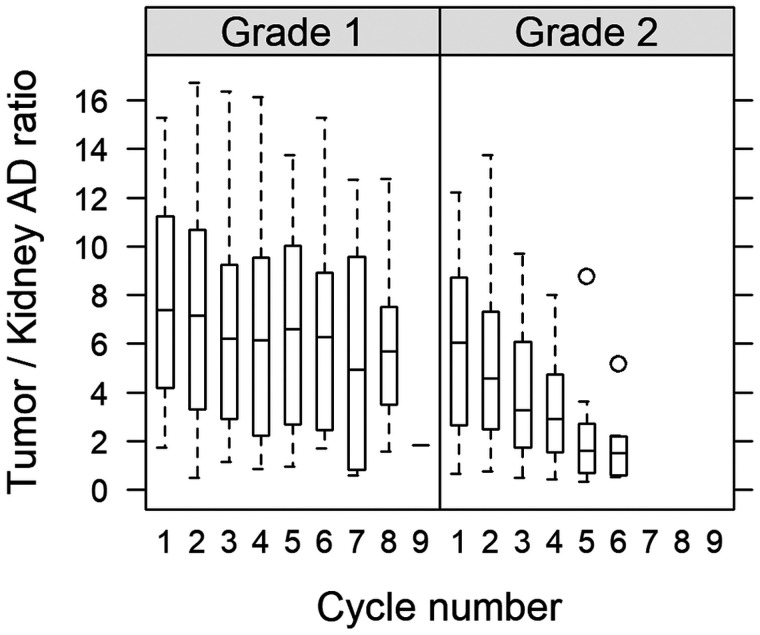
For future treatment optimization, the ADs to healthy tissues also need consideration. On the basis of previously reported renal dosimetry data (18,31), we calculated tumor-to-kidney AD ratios as a function of cycle (Fig. 7), obtaining values of between 0.33 and 17. For consistency, the rate of change in the kidney AD was also analyzed by omitting the tumor-specific terms in Equation 1, giving 95% CIs that covered zero for both G1 and G2. The decreasing tumor-to-kidney ratio, observed mainly for G2, is thus governed by the decreasing tumor AD. These results raise the question of whether it would be more beneficial to administer fewer cycles with a higher activity for G2. However, the specifics of such a protocol would require detailed consideration of the tumor-to-kidney AD ratios, as well as the risk of hematologic and pituitary toxicity (4,7,16,32).

FIGURE 7. — Ratio of AD to tumor and kidneys (mean left and right) for G1 and G2 NETs.

CONCLUSION

The tumor AD decreases between cycles in ¹⁷⁷Lu-DOTATATE treatment. The trend is more pronounced for G2 NETs than for G1 NETs and is governed mainly by a decreased activity uptake. G2 NETs also exhibit a decreasing volume over the cycles. The effective half-times do not demonstrate a systematic trend but are, on average, lower for G2 than G1 NETs. These results have implications for the design of alternative administration schemes and dosimetry protocols in ¹⁷⁷Lu-DOTATATE treatment.

DISCLOSURE

Anna Sundlöv has been a consultant for Novartis, Ipsen, and Spago Nanomedical. Katarina Sjögreen Gleisner has been a consultant for Fusion Pharmaceuticals Inc. Economic support was granted by the Swedish Cancer Society (contract 180747) and the Mrs. Berta Kamprad’s Foundation (BKS-2020-13-293 and BKS-2020-8-270). No other potential conflict of interest relevant to this article was reported.

ACKNOWLEDGMENTS

We express our gratitude to the included patients and to our coworkers Fanny Mörnsjö Centofanti, Paula Gluchowski, Cecilia Hindorf, Erik Larsson, Johanna Svensson, and Peter Bernhardt.

KEY POINTS.

QUESTION: Does the tumor AD change over treatment cycles in therapy of NETs with ¹⁷⁷Lu-DOTATATE?

PERTINENT FINDINGS: An exploratory analysis of 41 patients showed a decrease in tumor ADs by 6% per cycle for G1 tumors and 14% per cycle for G2 tumors, both statistically significant. The per-cycle decrease was caused by a lower activity uptake in the tumors and a decreasing volume, whereas the effective half-times were less variable.

IMPLICATIONS FOR PATIENT CARE: The results have implications for the design of future administration protocols and for the implementation of tumor dosimetry for ¹⁷⁷Lu-DOTATATE therapy.

REFERENCES

1. Strosberg J, El-Haddad G, Wolin E, et al. Phase 3 trial of ¹⁷⁷Lu-Dotatate for midgut neuroendocrine tumors. N Engl J Med. 2017;376:125–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Kwekkeboom DJ, de Herder WW, Kam BL, et al. Treatment with the radiolabeled somatostatin analog [¹⁷⁷Lu-DOTA⁰, Tyr³]octreotate: toxicity, efficacy, and survival. J Clin Oncol. 2008;26:2124–2130. [DOI] [PubMed] [Google Scholar]
3. Kim SJ, Pak K, Koo PJ, Kwak JJ, Chang S. The efficacy of ¹⁷⁷Lu-labelled peptide receptor radionuclide therapy in patients with neuroendocrine tumours: a meta-analysis. Eur J Nucl Med Mol Imaging. 2015;42:1964–1970. [DOI] [PubMed] [Google Scholar]
4. Hagmarker L, Svensson J, Ryden T, et al. Bone marrow absorbed doses and correlations with hematological response during ¹⁷⁷Lu-DOTATATE treatments are influenced by image-based dosimetry method and presence of skeletal metastases. J Nucl Med. 2019;60:1406–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Barone R, Borson-Chazot F, Valkema R, et al. Patient-specific dosimetry in predicting renal toxicity with ⁹⁰Y-DOTATOC: relevance of kidney volume and dose rate in finding a dose-effect relationship. J Nucl Med. 2005;46(suppl 1):99S–106S. [PubMed] [Google Scholar]
6. Pauwels S, Barone R, Walrand S, et al. Practical dosimetry of peptide receptor radionuclide therapy with ⁹⁰Y-labeled somatostatin analogs. J Nucl Med. 2005;46(suppl 1):92S–98S. [PubMed] [Google Scholar]
7. Sundlöv A, Sjögreen-Gleisner K, Tennvall J, et al. Pituitary function after high-dose ¹⁷⁷Lu-DOTATATE therapy and long-term follow-up. Neuroendocrinology. 2021;111:344–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Ilan E, Sandström M, Wassberg C, et al. Dose response of pancreatic neuroendocrine tumors treated with peptide receptor radionuclide therapy using ¹⁷⁷Lu-DOTATATE. J Nucl Med. 2015;56:177–182. [DOI] [PubMed] [Google Scholar]
9. Jahn U, Ilan E, Sandström M, Garske-Roman U, Lubberink M, Sundin A. ¹⁷⁷Lu-DOTATATE peptide receptor radionuclide therapy: dose response in small intestinal neuroendocrine tumors. Neuroendocrinology. 2020;110:662–670. [DOI] [PubMed] [Google Scholar]
10. Chansanti O, Jahangiri Y, Matsui Y, et al. Tumor dose response in yttrium-90 resin microsphere embolization for neuroendocrine liver metastases: a tumor-specific analysis with dose estimation using SPECT-CT. J Vasc Interv Radiol. 2017;28:1528–1535. [DOI] [PubMed] [Google Scholar]
11. Jahn U, Ilan E, Sandström M, Lubberink M, Garske-Roman U, Sundin A. Peptide receptor radionuclide therapy (PRRT) with ¹⁷⁷Lu-DOTATATE; differences in tumor dosimetry, vascularity and lesion metrics in pancreatic and small intestinal neuroendocrine neoplasms. Cancers (Basel). 2021;13:962. [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Cremonesi M, Ferrari ME, Bodei L, et al. Correlation of dose with toxicity and tumour response to ⁹⁰Y- and ¹⁷⁷Lu-PRRT provides the basis for optimization through individualized treatment planning. Eur J Nucl Med Mol Imaging. 2018;45:2426–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Wehrmann C, Senftleben S, Zachert C, Muller D, Baum RP. Results of individual patient dosimetry in peptide receptor radionuclide therapy with ¹⁷⁷Lu DOTA-TATE and ¹⁷⁷Lu DOTA-NOC. Cancer Biother Radiopharm. 2007;22:406–416. [DOI] [PubMed] [Google Scholar]
14. Kupitz D, Wetz C, Wissel H, et al. Software-assisted dosimetry in peptide receptor radionuclide therapy with ¹⁷⁷lutetium-DOTATATE for various imaging scenarios. PLoS One. 2017;12:e0187570. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Rudisile S, Gosewisch A, Wenter V, et al. Salvage PRRT with ¹⁷⁷Lu-DOTA-octreotate in extensively pretreated patients with metastatic neuroendocrine tumor(NET): dosimetry, toxicity, efficacy, and survival. BMC Cancer. 2019;19:788. [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Del Prete M, Buteau FA, Arsenault F, et al. Personalized ¹⁷⁷Lu-octreotate peptide receptor radionuclide therapy of neuroendocrine tumours: initial results from the P-PRRT trial. Eur J Nucl Med Mol Imaging. 2019;46:728–742. [DOI] [PubMed] [Google Scholar]
17. Hofman MS, Lau WFE, Hicks RJ. Somatostatin receptor imaging with ⁶⁸Ga DOTATATE PET/CT: clinical utility, normal patterns, pearls, and pitfalls in interpretation. Radiographics. 2015;35:500–516. [DOI] [PubMed] [Google Scholar]
18. Sundlöv A, Sjögreen-Gleisner K, Svensson J, et al. Individualised Lu-177-DOTATATE treatment of neuroendocrine tumours based on kidney dosimetry. Eur J Nucl Med Mol Imaging. 2017;44:1480–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Sjögreen K, Ljungberg M, Strand SE. An activity quantification method based on registration of CT and whole-body scintillation camera images, with application to ¹³¹I. J Nucl Med. 2002;43:972–982. [PubMed] [Google Scholar]
20. Roth D, Gustafsson J, Sundlöv A, Sjögreen Gleisner K. A method for tumor dosimetry based on hybrid planar-SPECT/CT images and semiautomatic segmentation. Med Phys. 2018;45:5004–5018. [DOI] [PubMed] [Google Scholar]
21. Gustafsson J, Sundlöv A, Sjögreen Gleisner K. SPECT image segmentation for estimation of tumour volume and activity concentration in ¹⁷⁷Lu-DOTATATE radionuclide therapy. EJNMMI Res. 2017;7:18. [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Frey EC, Tsui BMW. A new method for modeling the spatially-variant, object-dependent scatter response function in SPECT. In: 1996 IEEE Nuclear Science Symposium Conference Record. IEEE; 1996:1082–1086.
23. Ljungberg M, Frey E, Sjögreen K, Liu XW, Dewaraja Y, Strand SE. 3D absorbed dose calculations based on SPECT: evaluation for 111-In/90-Y therapy using Monte Carlo simulations. Cancer Biother Radiopharm. 2003;18:99–107. [DOI] [PubMed] [Google Scholar]
24. Bielajew AF, Rogers DWO. PRESTA: the parameter reduced electron-step transport algorithm for electron Monte-Carlo transport. Nucl Instrum Meth B. 1987;18:165–181. [Google Scholar]
25. Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern. 1979;SMC-9:62–66. [Google Scholar]
26.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. R Project website. https://www.R-project.org/.2020. Accessed December 1, 2021.
27. Bates D, Mächler M, Bolker BM, Walker SC. Fitting linear mixed-effects models using lme4. J Stat Softw. 2015;67:1–48. [Google Scholar]
28.Lenth R. emmeans: Estimated marginal means, aka Least-squares means. R package version 1.5.2 - 0010002. R Project website. https://cran.r-project.org/web/packages/emmeans/emmeans.pdf. Updated November 29, 2021. Accessed December 1, 2021.
29. Schiavo Lena M, Partelli S, Castelli P, et al. Histopathological and immunophenotypic changes of pancreatic neuroendocrine tumors after neoadjuvant peptide receptor radionuclide therapy (PRRT). Endocr Pathol. 2020;31:119–131. [DOI] [PubMed] [Google Scholar]
30. Örbom A, Eriksson SE, Elgström E, et al. The intratumoral distribution of radiolabeled ¹⁷⁷Lu-BR96 monoclonal antibodies changes in relation to tumor histology over time in a syngeneic rat colon carcinoma model. J Nucl Med. 2013;54:1404–1410. [DOI] [PubMed] [Google Scholar]
31. Sundlöv A, Gustafsson J, Brolin G, et al. Feasibility of simplifying renal dosimetry in ¹⁷⁷Lu peptide receptor radionuclide therapy. EJNMMI Phys. 2018;5:12. [DOI] [PMC free article] [PubMed] [Google Scholar]
32. Bergsma H, van Lom K, Raaijmakers M, et al. Persistent hematologic dysfunction after peptide receptor radionuclide therapy with ¹⁷⁷Lu-DOTATATE: incidence, course, and predicting factors in patients with gastroenteropancreatic neuroendocrine tumors. J Nucl Med. 2018;59:452–458. [DOI] [PubMed] [Google Scholar]

[bib1] 1. Strosberg J, El-Haddad G, Wolin E, et al. Phase 3 trial of ¹⁷⁷Lu-Dotatate for midgut neuroendocrine tumors. N Engl J Med. 2017;376:125–135. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] 2. Kwekkeboom DJ, de Herder WW, Kam BL, et al. Treatment with the radiolabeled somatostatin analog [¹⁷⁷Lu-DOTA⁰, Tyr³]octreotate: toxicity, efficacy, and survival. J Clin Oncol. 2008;26:2124–2130. [DOI] [PubMed] [Google Scholar]

[bib3] 3. Kim SJ, Pak K, Koo PJ, Kwak JJ, Chang S. The efficacy of ¹⁷⁷Lu-labelled peptide receptor radionuclide therapy in patients with neuroendocrine tumours: a meta-analysis. Eur J Nucl Med Mol Imaging. 2015;42:1964–1970. [DOI] [PubMed] [Google Scholar]

[bib4] 4. Hagmarker L, Svensson J, Ryden T, et al. Bone marrow absorbed doses and correlations with hematological response during ¹⁷⁷Lu-DOTATATE treatments are influenced by image-based dosimetry method and presence of skeletal metastases. J Nucl Med. 2019;60:1406–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] 5. Barone R, Borson-Chazot F, Valkema R, et al. Patient-specific dosimetry in predicting renal toxicity with ⁹⁰Y-DOTATOC: relevance of kidney volume and dose rate in finding a dose-effect relationship. J Nucl Med. 2005;46(suppl 1):99S–106S. [PubMed] [Google Scholar]

[bib6] 6. Pauwels S, Barone R, Walrand S, et al. Practical dosimetry of peptide receptor radionuclide therapy with ⁹⁰Y-labeled somatostatin analogs. J Nucl Med. 2005;46(suppl 1):92S–98S. [PubMed] [Google Scholar]

[bib7] 7. Sundlöv A, Sjögreen-Gleisner K, Tennvall J, et al. Pituitary function after high-dose ¹⁷⁷Lu-DOTATATE therapy and long-term follow-up. Neuroendocrinology. 2021;111:344–353. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib8] 8. Ilan E, Sandström M, Wassberg C, et al. Dose response of pancreatic neuroendocrine tumors treated with peptide receptor radionuclide therapy using ¹⁷⁷Lu-DOTATATE. J Nucl Med. 2015;56:177–182. [DOI] [PubMed] [Google Scholar]

[bib9] 9. Jahn U, Ilan E, Sandström M, Garske-Roman U, Lubberink M, Sundin A. ¹⁷⁷Lu-DOTATATE peptide receptor radionuclide therapy: dose response in small intestinal neuroendocrine tumors. Neuroendocrinology. 2020;110:662–670. [DOI] [PubMed] [Google Scholar]

[bib10] 10. Chansanti O, Jahangiri Y, Matsui Y, et al. Tumor dose response in yttrium-90 resin microsphere embolization for neuroendocrine liver metastases: a tumor-specific analysis with dose estimation using SPECT-CT. J Vasc Interv Radiol. 2017;28:1528–1535. [DOI] [PubMed] [Google Scholar]

[bib11] 11. Jahn U, Ilan E, Sandström M, Lubberink M, Garske-Roman U, Sundin A. Peptide receptor radionuclide therapy (PRRT) with ¹⁷⁷Lu-DOTATATE; differences in tumor dosimetry, vascularity and lesion metrics in pancreatic and small intestinal neuroendocrine neoplasms. Cancers (Basel). 2021;13:962. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib12] 12. Cremonesi M, Ferrari ME, Bodei L, et al. Correlation of dose with toxicity and tumour response to ⁹⁰Y- and ¹⁷⁷Lu-PRRT provides the basis for optimization through individualized treatment planning. Eur J Nucl Med Mol Imaging. 2018;45:2426–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib13] 13. Wehrmann C, Senftleben S, Zachert C, Muller D, Baum RP. Results of individual patient dosimetry in peptide receptor radionuclide therapy with ¹⁷⁷Lu DOTA-TATE and ¹⁷⁷Lu DOTA-NOC. Cancer Biother Radiopharm. 2007;22:406–416. [DOI] [PubMed] [Google Scholar]

[bib14] 14. Kupitz D, Wetz C, Wissel H, et al. Software-assisted dosimetry in peptide receptor radionuclide therapy with ¹⁷⁷lutetium-DOTATATE for various imaging scenarios. PLoS One. 2017;12:e0187570. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] 15. Rudisile S, Gosewisch A, Wenter V, et al. Salvage PRRT with ¹⁷⁷Lu-DOTA-octreotate in extensively pretreated patients with metastatic neuroendocrine tumor(NET): dosimetry, toxicity, efficacy, and survival. BMC Cancer. 2019;19:788. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib16] 16. Del Prete M, Buteau FA, Arsenault F, et al. Personalized ¹⁷⁷Lu-octreotate peptide receptor radionuclide therapy of neuroendocrine tumours: initial results from the P-PRRT trial. Eur J Nucl Med Mol Imaging. 2019;46:728–742. [DOI] [PubMed] [Google Scholar]

[bib17] 17. Hofman MS, Lau WFE, Hicks RJ. Somatostatin receptor imaging with ⁶⁸Ga DOTATATE PET/CT: clinical utility, normal patterns, pearls, and pitfalls in interpretation. Radiographics. 2015;35:500–516. [DOI] [PubMed] [Google Scholar]

[bib18] 18. Sundlöv A, Sjögreen-Gleisner K, Svensson J, et al. Individualised Lu-177-DOTATATE treatment of neuroendocrine tumours based on kidney dosimetry. Eur J Nucl Med Mol Imaging. 2017;44:1480–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib19] 19. Sjögreen K, Ljungberg M, Strand SE. An activity quantification method based on registration of CT and whole-body scintillation camera images, with application to ¹³¹I. J Nucl Med. 2002;43:972–982. [PubMed] [Google Scholar]

[bib20] 20. Roth D, Gustafsson J, Sundlöv A, Sjögreen Gleisner K. A method for tumor dosimetry based on hybrid planar-SPECT/CT images and semiautomatic segmentation. Med Phys. 2018;45:5004–5018. [DOI] [PubMed] [Google Scholar]

[bib21] 21. Gustafsson J, Sundlöv A, Sjögreen Gleisner K. SPECT image segmentation for estimation of tumour volume and activity concentration in ¹⁷⁷Lu-DOTATATE radionuclide therapy. EJNMMI Res. 2017;7:18. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] 22. Frey EC, Tsui BMW. A new method for modeling the spatially-variant, object-dependent scatter response function in SPECT. In: 1996 IEEE Nuclear Science Symposium Conference Record. IEEE; 1996:1082–1086.

[bib23] 23. Ljungberg M, Frey E, Sjögreen K, Liu XW, Dewaraja Y, Strand SE. 3D absorbed dose calculations based on SPECT: evaluation for 111-In/90-Y therapy using Monte Carlo simulations. Cancer Biother Radiopharm. 2003;18:99–107. [DOI] [PubMed] [Google Scholar]

[bib24] 24. Bielajew AF, Rogers DWO. PRESTA: the parameter reduced electron-step transport algorithm for electron Monte-Carlo transport. Nucl Instrum Meth B. 1987;18:165–181. [Google Scholar]

[bib25] 25. Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern. 1979;SMC-9:62–66. [Google Scholar]

[bib26] 26.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. R Project website. https://www.R-project.org/.2020. Accessed December 1, 2021.

[bib27] 27. Bates D, Mächler M, Bolker BM, Walker SC. Fitting linear mixed-effects models using lme4. J Stat Softw. 2015;67:1–48. [Google Scholar]

[bib28] 28.Lenth R. emmeans: Estimated marginal means, aka Least-squares means. R package version 1.5.2 - 0010002. R Project website. https://cran.r-project.org/web/packages/emmeans/emmeans.pdf. Updated November 29, 2021. Accessed December 1, 2021.

[bib29] 29. Schiavo Lena M, Partelli S, Castelli P, et al. Histopathological and immunophenotypic changes of pancreatic neuroendocrine tumors after neoadjuvant peptide receptor radionuclide therapy (PRRT). Endocr Pathol. 2020;31:119–131. [DOI] [PubMed] [Google Scholar]

[bib30] 30. Örbom A, Eriksson SE, Elgström E, et al. The intratumoral distribution of radiolabeled ¹⁷⁷Lu-BR96 monoclonal antibodies changes in relation to tumor histology over time in a syngeneic rat colon carcinoma model. J Nucl Med. 2013;54:1404–1410. [DOI] [PubMed] [Google Scholar]

[bib31] 31. Sundlöv A, Gustafsson J, Brolin G, et al. Feasibility of simplifying renal dosimetry in ¹⁷⁷Lu peptide receptor radionuclide therapy. EJNMMI Phys. 2018;5:12. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib32] 32. Bergsma H, van Lom K, Raaijmakers M, et al. Persistent hematologic dysfunction after peptide receptor radionuclide therapy with ¹⁷⁷Lu-DOTATATE: incidence, course, and predicting factors in patients with gastroenteropancreatic neuroendocrine tumors. J Nucl Med. 2018;59:452–458. [DOI] [PubMed] [Google Scholar]

PERMALINK

Dosimetric Quantities in Neuroendocrine Tumors over Treatment Cycles with ¹⁷⁷Lu-DOTATATE

Daniel Roth

Johan Gustafsson

Carl Fredrik Warfvinge

Anna Sundlöv

Anna Åkesson

Jan Tennvall

Katarina Sjögreen Gleisner

Visual Abstract

Abstract