Principles of Tracer Kinetic Analysis in Oncology, Part I: Principles and Overview of Methodology

Abstract

Learning Objectives: On successful completion of this activity, participants should be able to describe (1) describe principles of PET tracer kinetic analysis for oncologic applications; (2) list methods used for PET kinetic analysis for oncology; and (3) discuss application of kinetic modeling for cancer-specific diagnostic needs.

Financial Disclosure: This work was supported by KL2 TR001879, R01 CA211337, R01 CA113941, R33 CA225310, Komen SAC130060, R50 CA211270, and K01 DA040023. Dr. Pantel is a consultant or advisor for Progenics and Blue Earth Diagnostics and is a meeting participant or lecturer for Blue Earth Diagnostics. Dr. Mankoff is on the scientific advisory boards of GE Healthcare, Philips Healthcare, Reflexion, and ImaginAb and is the owner of Trevarx; his wife is the chief executive officer of Trevarx. The authors of this article have indicated no other relevant relationships that could be perceived as a real or apparent conflict of interest.

CME Credit: SNMMI is accredited by the Accreditation Council for Continuing Medical Education (ACCME) to sponsor continuing education for physicians. SNMMI designates each JNM continuing education article for a maximum of 2.0 AMA PRA Category 1 Credits. Physicians should claim only credit commensurate with the extent of their participation in the activity. For CE credit, SAM, and other credit types, participants can access this activity through the SNMMI website (http://www.snmmilearningcenter.org) through March 2025

PET enables noninvasive imaging of regional in vivo cancer biology. By engineering a radiotracer to target specific biologic processes of relevance to cancer (e.g., cancer metabolism, blood flow, proliferation, and tumor receptor expression or ligand binding), PET can detect cancer spread, characterize the cancer phenotype, and assess its response to treatment. For example, imaging of glucose metabolism using the radiolabeled glucose analog ¹⁸F-FDG has widespread applications to all 3 of these tasks and plays an important role in cancer care. However, the current clinical practice of imaging at a single time point remote from tracer injection (i.e., static imaging) does not use all the information that PET cancer imaging can provide, especially to address questions beyond cancer detection. Reliance on tracer measures obtained only from static imaging may also lead to misleading results. In this 2-part continuing education paper, we describe the principles of tracer kinetic analysis for oncologic PET (part 1), followed by examples of specific implementations of kinetic analysis for cancer PET imaging that highlight the added benefits over static imaging (part 2). This review is designed to introduce nuclear medicine clinicians to basic concepts of kinetic analysis in oncologic imaging, with a goal of illustrating how kinetic analysis can augment our understanding of in vivo cancer biology, improve our approach to clinical decision making, and guide the interpretation of quantitative measures derived from static images.

Molecular imaging with PET quantifies emissions from radiopharmaceuticals designed to measure specific biologic processes in vivo. As a method that measures absolute radionuclide concentration, PET is an inherently quantitative imaging modality. Indeed, the SUV of ¹⁸F-FDG, obtained as a measure of tracer uptake at a single time point (static) in standard clinical practice, has found widespread clinical acceptance in oncology (1,2). The quantitative capabilities of PET, however, extend well beyond simple static uptake measures. PET can quantify important features of radiopharmaceutical kinetics such as tissue delivery, retention, and release back to the blood that provide a more comprehensive picture of in vivo cancer biology and can improve clinical decision making (3).

This 2-part series is intended for nuclear medicine trainees and practitioners not familiar with pharmacokinetic principles and tracer kinetic analysis. Part 1 provides the rationale for kinetics analysis in PET cancer imaging, along with a framework for modeling, quantifying, and interpreting PET tracer kinetics. Part 2 illustrates specific implementations of kinetic analysis for cancer PET, the added benefits over standard clinical static imaging, and cases in which kinetic principles can guide the interpretation of static PET images to avoid pitfalls related to single-time-point imaging of a dynamic process (4). We focus on methods and examples relevant to common oncologic applications, with an emphasis on ¹⁸F-FDG as the currently most commonly used radiopharmaceutical for PET cancer imaging. We also discuss additional examples of other illustrative or emerging cancer imaging probes.

This review is intended to serve as a primer for kinetic analysis in oncology. For those wanting a more detailed review of these topics, including the underlying mathematic principles, we refer readers to more comprehensive references (5–10). Additionally, this review focuses on dynamic imaging and kinetic analysis. We do not, therefore, discuss static measures of ¹⁸F-FDG uptake beyond SUV, such as metabolic tumor volume and total lesion glycolysis; these topics are more thoroughly discussed in other sources (11).

WHY DO KINETIC MODELING?

After injection into the bloodstream, radiopharmaceuticals undergo a series of complex molecular interactions with tissues. The resulting image represents the combination of several key steps from injection to uptake in cancer cells, including the following (Fig. 1) (12,13): delivery to the tumor by regional blood flow; transit across the tumor capillary membranes and through the interstitial fluid; transport into the cell, often by specific membrane transporters; binding to target molecules (e.g., tumor receptors) or trapping after enzymatic alteration (e.g., ¹⁸F-FDG conversion to ¹⁸F-FDG-6-phosphate [¹⁸F-FDG-6-P] by hexokinase); and release from the cell by disassociation from the binding target or by reverse enzymatic alteration that no longer traps the molecule (e.g., conversion of ¹⁸F-FDG-6-P back to ¹⁸F-FDG by glucose-6-phosphatase).

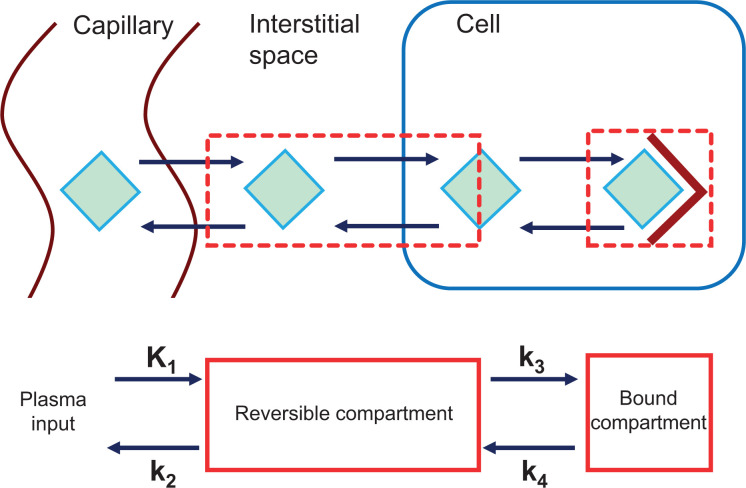
FIGURE 1.

(Top) Depiction of movement of tracer (green diamond) from vasculature to its intracellular tumor target (maroon V). Tracer is delivered to tumor via regional blood flow; travels from capillary, through interstitial space, and into cell, where it interacts with its target in this example; and may also follow reverse path. Static PET image represents summation of tracer in each of these steps in tissue. For kinetic analysis, compartments are constructed that represent key states of tracer (e.g., reversible compartment representing tracer in interstitial space and in cell, and bound compartment representing tracer engaging with target. Rate constants (K₁, k₂, k₃, and k₄) represent transfers between compartments (defined in Table 1), which may depict multiple tracers moving through multiple barriers.

This complex series of steps cannot be fully characterized by imaging at a single time point remote from tracer injection. Time-resolved PET imaging can, however, be performed continuously from the start of tracer injection to provide a dynamic series of images that fully capture all steps in radiopharmaceutical delivery, retention, and release (Fig. 1). By capturing the time course of tissue uptake and applying pharmacokinetic models that represent radiopharmaceutical pharmacology and biochemistry, PET can quantify specific biologic phenomena—for example, transport and metabolic rate—that cannot be measured by simple static imaging and SUV (3). So why go through the additional time and complexity of dynamic imaging and tracer kinetic analysis, given the ease and efficiency of taking a single snapshot sometime later after injection? There are several reasons.

The first is that tracer kinetic parameters provide biologic insights related to the radiopharmaceutical target and the disease process (8). For example, dynamic ¹⁸F-FDG can measure both the rate of delivery of glucose to cancers and the rate of its metabolism. Demonstrating a balance or imbalance between substrate delivery and use may predict important outcomes such as therapeutic response and survival (14).

Second, tracer kinetic analysis provides more precise interpretations of PET images. For example, for ¹⁸F-FDG PET, tracer remains in the blood at notable concentrations for several hours after injection. As such, static tumor images at the typical 1-h-postinjection time point reflect a mixture of unmetabolized ¹⁸F-FDG exchanged with the blood and ¹⁸F-FDG-6-P trapped by tumor glucose metabolism (the biologic target of ¹⁸F-FDG). Static PET imaging cannot distinguish between ¹⁸F-FDG and ¹⁸F-FDG-6-P since both have the same positron-emitting isotope detected by the scanner. Dynamic imaging and kinetic analysis, however, can use the time course of radioactive ¹⁸F-FDG in the blood (plasma) and the total ¹⁸F-FDG plus ¹⁸F-FDG-6-P in the tissue to infer the rate of intracellular ¹⁸F-FDG-6-P accumulation and provide a much more specific estimate of tumor glucose metabolism (12,13). This ability can have important implications in the clinic and clinical trials—for example, for measuring therapeutic response (14–16).

Third, kinetic principles can help avoid pitfalls in interpreting standard clinical static uptake images. For example, the persistence of ¹⁸F-FDG in the blood after injection leads to ongoing trapping of tracer as ¹⁸F-FDG-6-P over time. For tumors with high glucose metabolic rates, SUV can increase over 30% in as little as 15 min at 1 h after injection (17). Variability of uptake time in serial scans can therefore considerably confound the assessment of therapeutic response both in the clinic and in clinical trials (14,18). Kinetic analysis avoids this pitfall and can inform static imaging correction schemes.

These points illustrate that static uptake measures (e.g., SUV) provide a clinically practical, albeit limited, approximation of information carried by radiopharmaceutical uptake kinetics. Furthermore, the optimum timing of imaging and the optimum approach to uptake quantification are not necessarily the same for all tracers and all tumors. Particularly, in the development and early testing of a new radiotracer, or the application of an existing tracer to a new tumor or treatment, initial testing should focus on dynamic imaging and rigorous kinetic characterization to guide image interpretation and clinical translation (3,13). Through detailed kinetic analysis, tracer uptake can be characterized to guide the development of rational simplified protocols more amenable to the clinic. An understanding of tracer kinetics is necessary before protocol simplification to avoid or mitigate pitfalls of the simplified approaches discussed above (8). A recent example can be seen in the development of a novel radiotracer for imaging poly[adenosine diphosphate-ribose] polymerase expression in ovarian cancer, in which a study of tracer kinetics helped determine the nature of tracer retention in patients and guided the approach to static imaging (19). Even when reasonable static imaging approximations are possible, dynamic acquisition and full kinetic analysis can still yield important clinical data and biologic insights not possible with static imaging. Such examples are highlighted in part 2 of this review.

PET KINETIC ANALYSIS: PRINCIPLES AND REQUIREMENTS

Overview

Figure 2 illustrates the conceptual framework for dynamic PET imaging (top) and kinetic modeling or analysis (middle). An important difference from standard clinical imaging is the need to collect dynamic volumetric 4-dimensional (3 spatial dimensions and time) imaging data over time. Key patient data obtained during scanning include the measurement of the time-varying target tissue uptake curves (time–activity curves), as well as data on tracer clearance from the plasma. Target tissue uptake curves are obtained from direct dynamic imaging, whereas plasma clearance curve can be measured by blood sampling, image analysis, or a hybrid of both methods (8).

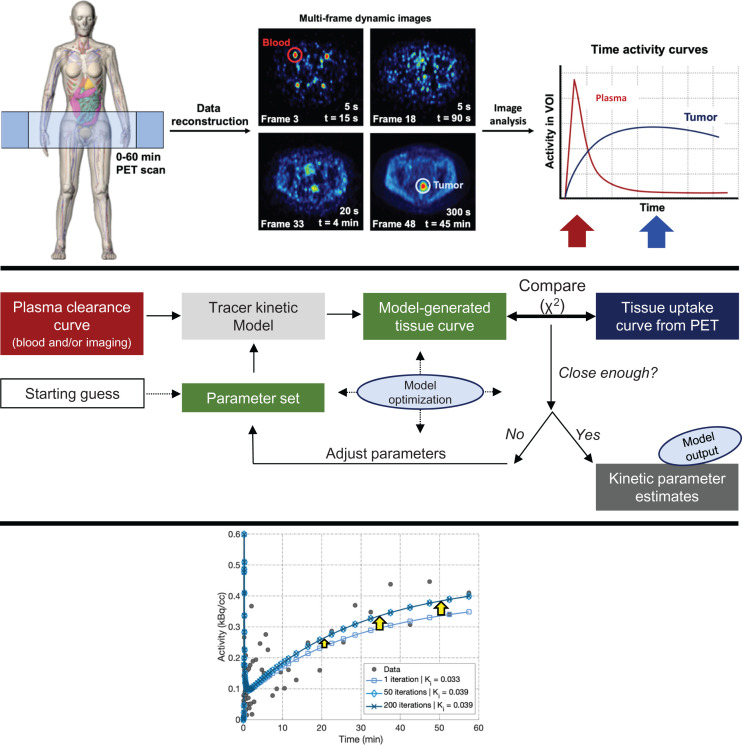
FIGURE 2.

(Top) Data are acquired at single bed position (left) and reconstructed into multiframe dynamic images (middle), on which regions of interest are drawn to create time–activity curves (right). Blood time–activity curve peaks early in scan (red arrow, corresponding to early dynamic frames), whereas tumor activity peaks later (blue arrow, corresponding to later dynamic frames). (Middle) In this schematic overview of the approach to kinetic analysis, raw whole-blood time–activity curve must be partitioned into plasma vs. red blood cell activity and corrected for metabolites to obtain plasma time–activity curve, which is then used as input to kinetic modeling process. Dynamic tissue time–activity curves act as standard of truth against which model estimates are compared in iterative process of kinetic parameter estimation. (Bottom) Kinetic parameter estimation (model-generated tissue curve) improves through model optimization as iterations increase.

The middle of Figure 2 provides an overview of the approach to kinetic analysis. The plasma clearance curve serves as an input—or driving function—to a model describing tracer pharmacokinetic behavior in the tissue of interest (5,9). A set of parameters describes quantitative tracer kinetic features that include tracer delivery to the tissue, retention or trapping in tissue, and efflux back to the blood. Using the plasma clearance curve as input into the kinetic model, the kinetic parameter set—typically in the form of a set of differential equations—can be mathematically integrated to generate a simulated (model-generated) tissue curve. This curve is then compared with the measured tissue curve from patient imaging to estimate the goodness of fit, typically assessed with the χ² function. The process of parameter estimation involves iterative guesses of the parameter values toward the goal of minimizing the difference (χ² value) between the model-generated and measured blood curve from a predefined goal. This process is known as optimization of the model fit to the measured data (Fig. 2, bottom), and the parameter values that yield the closest fit of the model to the measured PET data are reported as kinetic parameter estimates—the goal of kinetic analysis.

Data Acquisition

Dynamic data are typically acquired at a single bed position over time to measure the time course of tracer uptake and generate 4-dimensional datasets of time-varying regional tracer concentration (Fig. 2, top).

To capture the time course of radiotracer uptake for the tissues of interest, the PET axial field of view is typically centered over a single anatomic area of interest for the duration of the scan. Given the limited axial field of view of PET scanners—typically 16–25 cm—the investigator must choose the most ideal axial position to image. If all sites of interest are not contained in a single axial field of view, the investigator must select the optimal area to scan, with the inclusion of some lesions at the expense of others. Additionally, if an image-derived input function is to be used, the imaging axial field of view should also include a large arterial blood pool—for example, the aorta—to measure the blood time–activity curve in a location ideally just upstream of the organ or lesion of interest (20).

After the patient is positioned in the scanner, the radiotracer is injected and imaged continuously for a period that is dictated by radiotracer kinetics. Although a sharp bolus injection is often ideal for modeling, other protocols may be better suited for certain applications: for example, a bolus-plus-infusion protocol (21). Additionally, for extended studies (e.g., hour-long studies), motion correction may be needed if the patient shifts during the scan (22,23).

Dynamic imaging data either are collected in list mode, to be parsed into time bins (hereafter referred to as frames) after acquisition, or are directly binned into sinograms with predetermined frame durations. Most current dynamic imaging protocols parse the data into short (5–10 s for typical ¹⁸F tracers) frames early after injection to capture the fast dynamics of the tracer in both larger blood vessels and the smaller vasculature within organs. After the initial bolus, frame durations are typically lengthened (1–5 min) to decrease image noise when count rates are lower and the kinetics are no longer as rapidly changing (Fig. 2, top). Each frame is then individually reconstructed (8).

To be compared and used for kinetic analysis, all time–activity curves must be calibrated to be in common units for either SUV (typically mg/mL) or activity concentration (e.g., Bq/mL) (8,9). This calibration happens naturally for image-derived blood clearance and tissue curves but requires cross calibration between a well counter and the PET scanner for plasma curves obtained by blood sampling. Arterial blood sampling, commonly used for brain PET imaging and kinetic analysis, is less common for oncologic PET since, first, large blood-pool structures such as the heart and aorta are frequently in the dynamic imaging field and, second, oncologic patients often undergo serial scans and toxic systemic therapy that make arterial sampling a challenge. What often works well is a hybrid approach using image analysis of a large blood-pool structure (e.g., aorta or ventricle) and venous blood samples to determine fractional radioactivity in red cells versus plasma and parent radiotracer versus labeled metabolites (8).

Kinetic Model Formulation

The next step in kinetic analysis requires a model, typically a compartmental model. Model formulation needs to encompass the complexity of biology and biochemistry in living systems but, at the same time, meet the challenge of estimating each facet of in vivo biology given the spatial, temporal, and statistical limitations of the 4-dimensional datasets measured by PET (5,9,10,24). As such, compartmental models used for PET typically represent only the key, rate-limiting, steps that determine the time course of tracer uptake: tracer delivery, metabolism, or target binding. Radiotracer biochemistry and pharmacology investigated during preclinical development and early human trials should inform model design to yield model parameters of clinical and biologic interest that can be estimated with reasonable accuracy and precision (10,24). In interpreting the parameter estimates yielded by kinetic analysis, it is important to consider the biologic complexity of the processes underlying the parameter estimates and the influence of common factors such as tissue perfusion, cellular density, and possible drug effects on the kinetics of the PET tracer (Fig. 1).

In compartmental models for PET, the plasma clearance curve (plasma time–activity curve) serves as the input (driving function) to one or more tissue compartments. Compartments are virtual constructs representing tracer label present between the key steps that mediate tracer delivery, retention, and release (10,24). A tissue compartment can represent whole tissue, tumor cells, a subcellular location, or, frequently, a biochemical state associated with a particular cell type. For example, ¹⁸F-FDG tissue kinetics are typically modeled as having 2 compartments (13,25,26). The first is a free or reversible compartment representing ¹⁸F-FDG delivered to all components of tissue outside the blood vessels (cells and interstitial space) but not trapped by phosphorylation. The second is a trapped compartment for ¹⁸F label retained in the cell as ¹⁸F-FDG-6-P. This compartment consists of ¹⁸F-FDG that has been phosphorylated by hexokinase and is retained inside cells, unless it is released to the reversible ¹⁸F-FDG compartment via dephosphorylation by glucose-6-phosphatase. In typical model illustrations, compartments are indicated by boxes, and transfers to and from the blood and between compartments are illustrated by arrows. The blood, considered a driving function for PET kinetic analysis, represents systemic delivery and clearance from the total-body blood pool. The driving function is not a compartment and is assumed to be unaffected by incremental tracer delivery to or clearance from the tissue. In this formalism, each arrow indicates a physical or biochemical transition and represents a difference equation (as an approximation of a differential equation) describing mass transit. Parameters of interest for typical oncologic models are described below and summarized in Table 1.

TABLE 1.

Parameters of Interest for Typical Oncologic Models

Model type	Parameter of interest
Microparameters
1-tissue-compartment model	K1 (blood-tissue transfer constant), k2 (tissue-blood transfer content),
2-tissue-compartment model	K1, k2, k3 (representing substrate-target binding or metabolism rate constant), k4 (off-binding or metabolic degradation rate constant)
Macroparameters
VT (1-tissue compartment)	VT = K1/k2
VT (2-tissue compartments)	VT = (K1/k2) × (1 + [k3/k4])
Ki	Ki = K1k2/(k2 + k3)
Typical units
K rate constant	mL/min/cm3
k rate constant	1/min
VT	mL/cm3

Figure 3 illustrates the 1-tissue-compartment and 2-tissue-compartment models most commonly used for PET oncologic radiotracers (top and middle, respectively) and an ¹⁸F-FDG kinetic model as a specific implementation of a 2-compartment model (bottom). In PET nomenclature, the plasma input curve serves as the driving function for the model and does not count as a compartment by convention, although in other fields such as drug pharmacology, the blood or plasma clearance curve is an important focus of kinetic analysis and is included as a compartment (27).

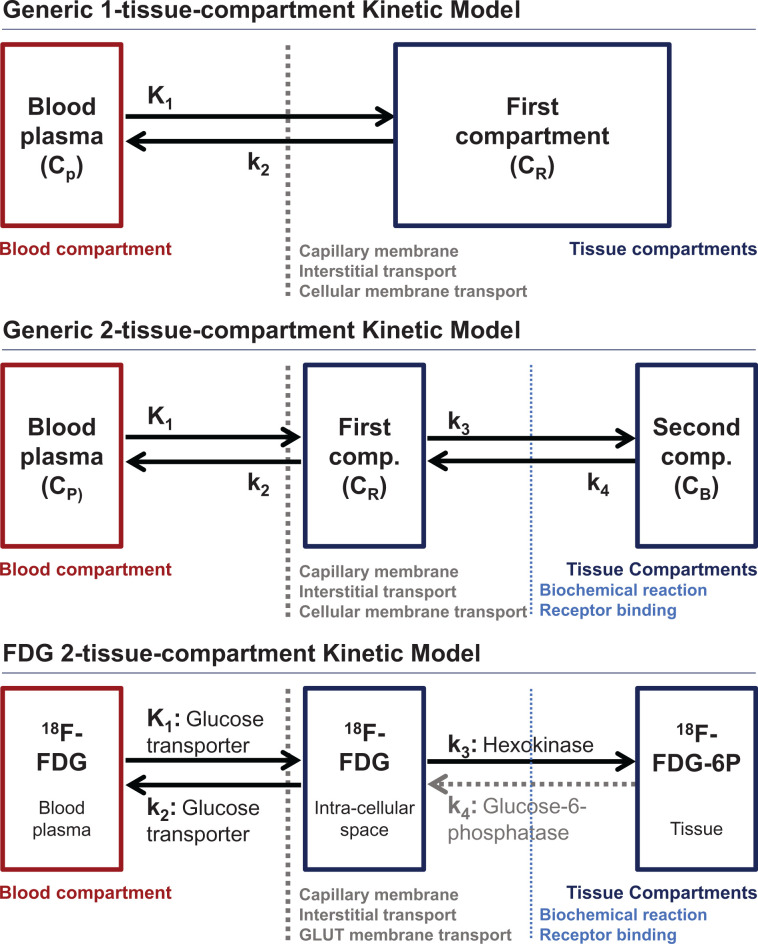
FIGURE 3.

Kinetic model for generic 1-tissue-compartment model (top), generic 2-tissue-compartment model (middle), and 2-tissue-compartment model for ¹⁸F-FDG (bottom). Barriers encountered by radiotracer as it moves between compartments are also noted.

To illustrate the formulation of a kinetic model, we start with the simple 1-tissue-compartment model (Fig. 3, top), which describes tracers that are only reversibly transported into and out of tissues. Such models have been used to estimate tissue perfusion (K₁) using ⁸²Rb or ¹⁵O-water (28–31), as described in part 2. This simple model includes only transfer from the blood into the tissue compartment (K₁ [mL/min/cm³]) and efflux from the tissue compartment back into the blood (k₂, [1/min]) (28). To illustrate how the model’s graphic depiction relates to the model’s mathematic formula, we consider the arrows leading into the tissue compartment (blood-to-tissue transport described by K₁ applied to the plasma time–activity curve, C_p) and out of the tissue compartment (efflux described by k₂) applied to the compartment activity concentration (C_R) of the single tissue compartment over a small time increment (Δt). The 1-tissue-compartment model reversible compartment difference equation is as follows:

$$\frac{\mathrm{\Delta }{C}_R}{\mathrm{\Delta }t}=K_1{C}_P-k_2{C}_R.$$

The blood concentration is typically measured in Bq/mL, and the compartment concentrations are considered as Bq/cm³ of tissue, or, if density is known or estimated, Bq/g of tissue.

A common convention is to use an uppercase K to represent a parameter that can be related directly to a physical quantity (5,9). For example, K₁ for ¹⁵O-water is equal to tissue blood flow (perfusion, typically described in units of mL/min/cm³ of tissue) (28), which can be measured by a variety of other methods that include both imaging and nonimaging approaches. Those parameters that originate in a compartment are typically assigned a lowercase k and have time constant units, typically 1/min. The lowercase k parameters are critical to model optimization but are often hard to relate to measurable quantities. However, when referenced to uppercase K parameters, the k parameters can describe steady-state kinetic features that can be related to measurable quantities. For example, the volume of distribution for a 1-tissue-compartment model, often termed V_T, represents the ratio of tracer in the compartment compared with the blood at equilibrium, and is given by K₁/k₂ (mL/cm³). For ¹⁵O-water, V_T is interpreted as tissue water, a quantity that can be readily measured by drying tissue samples and that can provide an indirect estimate of tumor cellularity in some cases such as breast cancer (28,32). In practice, most oncologic radiopharmaceuticals have biochemical or molecular targets that retain the tracer in or on cancer cells. This requires a second tissue compartment to describe radiopharmaceutical interaction with the specific metabolic or binding target (Fig. 3, middle). The 2-tissue-compartment model includes, similar to the 1-tissue-compartment model, delivery to (K₁ [mL/min/cm³]) and efflux from (k₂ [1/min]) a reversible compartment. However, in addition, the model includes the rate of substrate-to-target binding or metabolic conversion (k₃ [1/min]) leading from the reversible compartment to a second bound or trapped tissue compartment. The second compartment can also have an efflux pathway (k₄ [1/min]) from the bound or trapped second compartment back to the reversible first compartment.

For illustration purposes, we consider the difference equation for the 2-tissue-compartment model in comparison to the 1-tissue-compartment model equation. The reversible compartment now has 2 source of input (plasma transport, described by K₁, and bound or trapped compartment efflux, described by k₄) and 2 paths for efflux (to the plasma, described by k₂, and to the trapped or bound compartment, described by k₃), resulting in the following 2-tissue-compartment model reversible compartment difference equation:

$$\frac{\mathrm{\Delta }{C}_R}{\mathrm{\Delta }t}=K_1{C}_P+k_4{C}_B-(k_2+k_3)C_R.$$

For many metabolized tracers used in oncology, including ¹⁸F-FDG in most tumors (2,33,34), the second compartment is largely irreversible (k₄ equal to or close to 0). In this case, overall tracer uptake and retention are best described by a metabolic flux constant (K_i) representing the rate at which the tracer moves from the blood to its trapped stated in tissue, for example, ¹⁸F-FDG-6-P for ¹⁸F-FDG PET. By considering equilibrium concentrations, K_i can be expressed as a combination of K₁, k₂, and k₃:

$$K_i= \frac{(K_1\cdot k_3)}{(k_2+ k_3)}.$$

K_i is often called a macroparameter, comprising individual rate parameters (microparameters). It is denoted with a capital K similar to K₁ to indicate that it has the same units as K₁ (mL/min/g), and it can be related to real-life measurements, such as cellular glucose consumption for ¹⁸F-FDG. The rate of metabolism of the native (traced) substance can be estimated by multiplying K_i by the plasma concentration of the substance (μmol/mL) to provide a metabolic rate (μmol/min/cm³) (9), as is described in more detail for ¹⁸F-FDG below.

For completeness, we note that if both compartments of the 2-tissue-compartment model are fully reversible (k₄ ≠ 0), as is the case for some tumors signaling receptors that serve as drug targets, then V_T is a more biologically or clinically relevant parameter to described specifically retained tracer. The 2-compartment model, V_T, differs from the 1-compartment model in that it includes both the reversible compartment and the bound compartment, the latter of which carries relevant information regarding tracer binding to its intended target. The 2-tissue-compartment model V_T is given by…

$$V_T\hspace{0.17em}=\hspace{0.17em}(K_1/k_2)\hspace{0.17em}\times \hspace{0.17em}(1\hspace{0.17em}+\hspace{0.17em}[k_3/k_4]).$$

In this case, V_T (mL/cm³) indicates an equilibrium partition coefficient ratio of tissue concentration (μmol/cm³) to blood concentration (μmol/mL) that can be related to real-world measures. This approach is a mainstay of neuroreceptor imaging but is somewhat less common for cancer applications. One limitation for cancer target binding studies, unlike most noncancer brain studies (27), is the lack of an appropriate reference tissue for nonspecific radioligand binding. Nevertheless, V_T can be a useful measure to, for example, guide the dosing of receptor-targeted cancer drugs (35).

To further illustrate the nature of compartmental models, we highlight the model most widely used for ¹⁸F-FDG (Fig. 3, bottom) (25). ¹⁸F-FDG can be modeled with an irreversible 2-tissue-compartment model in tumors with absence of glucose-6-phophorylase and therefore a k₄ of 0. As a glucose analog, ¹⁸F-FDG is relatively permeable to normal capillaries throughout the body, and after transiting the interstitial fluid, ¹⁸F-FDG enters the cell through membrane glucose transporters. This series of steps is described by the 1-tissue delivery parameter, K₁, which reflects a complex combination of blood flow, capillary permeability, interstitial transport, and membrane transport that has a modest correlation with blood flow in many tumors (32). Once inside the cell, ¹⁸F-FDG can either leave the cell through the same bidirectional transporters (k₂) or become phosphorylated to ¹⁸F-FDG-6-P by hexokinase (k₃), the same enzyme that converts glucose to glucose-6-phosphate. ¹⁸F-FDG-6-P cannot be metabolized to the next step in glycolysis and is not transported out of the cell unless the phosphate group is cleaved by glucose-6-phosphatase (36). Administered ¹⁸F-FDG that enters the glucose metabolic pathway is therefore effectively trapped in the cell for the duration of imaging for most types of cancer, although several normal tissues that actively make glucose or consume glycogen (liver, brain, muscle) and some tumors (well-differentiated hepatocellular cancer) have finite glucose-6-phosphatase activity to convert ¹⁸F-FDG-6-P back to ¹⁸F-FDG (k₄) (25,33). The first tissue compartment represents any unmetabolized ¹⁸F-FDG in tissue that is outside the vascular space, whereas the second compartment represents ¹⁸F-FDG-6-P trapped in the intracellular space. ¹⁸F-FDG mimics glucose up to the common rate-limiting step of phosphorylation conversion glucose-6-P/¹⁸F-FDG-6-P. The K_i for ¹⁸F-FDG therefore describes the rate of glucose metabolism through hexokinase, including glucose transport from the plasma to cancer cells. Multiplying the ¹⁸F-FDG K_i by the plasma glucose measured at the time of imaging (μmol/mL) provides an estimate of the tumor metabolic rate of glucose in μmol/min/cm³ of tissue. This estimate comes with a note of caution that the transport and hexokinase kinetics of glucose and ¹⁸F-FDG are not identical (26,34), particularly in cancer (37), leading some to describe estimates of tumor glucose metabolism from dynamic ¹⁸F-FDG PET as the “metabolic rate of glucose assessed by ¹⁸F-FDG,” or MR¹⁸F-FDG (13).

Parameter Estimation

As seen in Figure 2, the process of kinetic parameter estimation involves iterative adjustment of the kinetic model parameters from biologically reasonable starting guesses to values that optimize the model’s fit to the measured tissue curves. This optimization is done by comparing the model-generated tissue time–activity curve with the PET-measured patient tissue time–activity curve at each iteration and then making adjustments to the parameters until an acceptable fit is achieved. To match the measured tissue curves, the model-generated curves need to include the contribution of circulating blood in the small vessels and capillaries that are present in all living tissue but are below PET spatial resolution. As such, total activity concentration (C_TOT, Bq/mL) in each image voxel or the tissue volume of interest (VOI) is a mixture of the tissue compartment time–activity curves (C_R and C_B for 2-tissue-compartment models) and the whole-blood time–activity curve (C_WholeBlood) (5,9), noting the contribution of whole blood to the image, whereas the driving function uses the plasma time–activity curve. The contribution of the blood to the total tissue time–activity curve can be included in the kinetic model using a fractional blood fraction volume parameter (V_B), assumed to be a constant fraction across the time scale of the imaging study using the following formula (for a 2-tissue-compartment model), with the convention that C′_TOT indicates the model-generated time–activity curve versus the measures time–activity curve, C_TOT:

$$C{\prime }_{\mathit{TOT}}= V_B\times C_{\mathit{WholeBlood}}+\left(1-V_B\right)\times (C_R+C_B).$$

Using the units described in Table 1, the model generates tissue compartment curves having units of Bq/cm³, the same as measured by PET systems. If a density correction were used with resultant tissue compartment curves having units of Bq/g, the model output must be multiplied by tissue density (g/mL) to have comparable data for the model and measured data. Most use the approximation of unit water density (1 g/mL), but tissues such as lung and bone may require more accurate density corrections. Other formulations consider models on a purely volumetric basis (7,27), avoiding this issue and performing separate density corrections when needed to compare parameter estimates with in vitro assays, which are typically done on a tissue weight basis.

During parameter estimation, the compartment activity concentrations, C_R and C_B, are generated by the model and C_WholeBlood is provided either by an image-based input function from a blood-pool structure or from the whole-blood activity measured by blood sampling. The blood volume parameter V_B can be measured using imaging methods such as ¹¹CO PET that label red blood cells (38); however, this adds complexity and radiation dose to oncologic imaging protocols and is infrequently used in clinical practice and clinical research. Alternatively, V_B can be estimated as a parameter as part of the kinetic modeling. This estimation may pose a challenge for highly permeable tracers for which the early tissue uptake curve has a strong contribution from both blood pool and tissue delivery (V_B and K₁ parameters), and estimates of the 2 parameters may vary with one another (32). In addition to adding a blood volume component to match PET-measured tissue curves, model-generated C′_TOT curves are integrated over the same time intervals as the patient imaging protocol to have the model mimic the imaging process as closely as possible. Most kinetic analysis approaches assume that the measured blood and tissue time–activity curves are corrected for physical isotope decay. It is also possible to directly include physical decay in the compartmental model for those cases in which the physical decay constants are close to pharmacologic transfer constants (e.g., ¹⁵O-water studies (32)) to avoid pitfalls during the model integration step in the kinetic analysis.

Parameter estimation requires adjustment, or optimization, of the parameter set to minimize the difference between the model-generated curve (C′_TOT) and the measured curve (C_TOT), typically known as the χ² function (39):

$${\chi }^2\hspace{0.17em}=\hspace{0.17em}(C{\prime }_{\mathit{TOT}1}\hspace{0.17em}–\hspace{0.17em}{C}_{\mathit{TOT}1}{)}^2/w_1\hspace{0.17em}+\hspace{0.17em}(C{\prime }_{\mathit{TOT}2}\hspace{0.17em}–\hspace{0.17em}{C}_{\mathit{TOT}1}{)}^2/w_2+\dots \hspace{0.17em}(C{\prime }_{\mathit{TOT}L}\hspace{0.17em}–\hspace{0.17em}{C}_{\mathit{TOT}L}{)}^2/w_L+,$$

where the numbers 1, 2 … L indicate the time bins starting from the first time bin at the start of tracer injection to the last time bin (bin L) collected during scanning. The w’s are weights applied to the square of the model-versus-measured time–activity curve difference for each time bin. These weights are typically calculated to be proportional to the statistical uncertainty of the PET measurement for the time point. This approach reduces the influence of noisy time bins with large statistical variability that typically occurs in short early time bins used to measure the rapidly changing time–activity curve early after injection and late time bins that are impacted by physical decay of the tracer isotope. These weights can have a significant impact on model performance and can be tuned to optimize estimates of the parameters identified as being most important for specific applications (39).

Model optimization methods seek to efficiently adjust model parameters to reach the smallest possible χ² value. Since the differential equations that define most models do not have a closed-form solution, nonlinear optimization approaches are used (e.g., Marquardt–Levenberg algorithm) (39). Most nonlinear estimation algorithms require initial parameter estimates (starting guess) and parameter range limits to constrain the search to parameter values that are within biologically possible ranges. These values are typically taken from preclinical and other early tracer studies and guided by the expected biology (40,41). Even with appropriate weighting, good starting guesses, and appropriate parameter limits, nonlinear optimization algorithms applied to standard PET data are susceptible to local minima, overfitting, sensitivity to noise, and parameter covariance (39). As a result, some kinetic parameters may not be able to be estimated independently of each other or with reasonable precision (8). As such, it is possible, and perhaps likely, that not all model parameters can be reliably estimated, and the model should therefore be mathematically tested before implementation and use.

Mathematic Testing and Validation

Model forms are typically chosen on the basis of the known biology and pharmacology of the radiopharmaceutical and the biology of the tissue and target. However, since all models require some simplification of complex in vivo conditions, it can be difficult in some cases to select the correct model. In such cases, a series of mathematic calculations and simulations based on measured time–activity curves can be used to test the ability of the model to estimate relevant parameters. The ultimate goal of a kinetic model is to estimate relevant macroparameters (e.g., flux or V_T) and microparameters (e.g., k₂ or k₃) accurately (i.e., recover the true value of the parameter without bias) and precisely (i.e., recover the same value with repeat testing). More complex models with a greater number of parameters will undoubtedly improve the overall fit of a model to the tissue time–activity curve. However, more complex models may result in overfitting such that kinetic parameters are poorly determined, precluding reliable quantification of the underlying biologic process. To account for a trade-off between goodness of fit and model complexity, several statistical tests have been developed, including the Akaike information criterion (42), model selection criterion (MSE), and Schwartz criterion, in which a penalty is given for the number of parameters included in the model (43). These criteria quantify the fit of a model with consideration of model complexity to offer an easy means of comparison among candidate models (44).

Additional mathematic tests and simulation approaches have been developed to study the ability of a model to estimate parameters under realistic imaging conditions (39). Through such rigorous mathematic testing, the ability of a model to quantify relevant biology can be optimized (9,41). These approaches include sensitivity analysis, identifiability analysis, and simulations that can provide expectations for the bias, precision, and covariance of the estimated parameters (9). Sensitivity and identifiability analyses use closed-form calculations based on typical model parameter values and resulting tissue time–activity curves. Sensitivity analysis estimates the model’s ability to estimate each parameter on the basis of its impact on the model-generated tissue curve. If a small change in a parameter induces a large change in model output, that parameter is likely to be estimated accurately; conversely, parameters that have a low impact on the generated tissue curve cannot be estimated accurately. Identifiability analysis, including both analytic calculations and mathematic simulations, can estimate the ability to measure parameters independently. This analysis may reveal that some microparameters, although needed for overall parameter estimation, cannot be reliably estimated independently of other parameters. An example of this is discussed in part 2 (4) in the context of ¹⁸F-FDG and 3′-deoxy-3′-¹⁸F-fluorothymidine (¹⁸F-FLT), where studies show that only K₁ and K_i (and not k₂ and k₃) can be accurately estimated for typical cancer imaging conditions.

Simulations are particularly helpful to mimic the typical statistical noise encountered in the PET-measured tissue time–activity curves. By adding noise to idealized time–activity curves, the precision and bias of the parameter estimates can be estimated. Such estimates are key for interpreting kinetic analysis results and relating them to cancer biologic properties and clinical outcomes (9). Several existing kinetic analysis software packages include estimates of parameter precision as part of their analysis.

Since PET kinetic modeling seeks to quantify relevant biology, the kinetic model should ideally be validated against independent measures of the biologic characteristic of interest. For instance, for a tracer that measures receptor expression, correlation of uptake measures with in vitro tissue expression of that receptor on excised tissue can be used for validation. For ¹⁸F-fluoroestradiol, PET uptake has been shown to correlate well with tissue estrogen receptor expression as measured by a quantitative radioligand binding assay (45) and by immunohistochemistry, with both qualitative and semiquantitative measures on immunohistochemistry (46,47). As the latter measure is used in the clinic to direct therapy, validation against this marker facilitates clinical translation (46), noting that ¹⁸F-fluoroestradiol has recently been granted Food and Drug Administration approval. The radiolabeled thymidine analog ¹⁸F-FLT has also been validated as a measure of tumor proliferation through correlation with Ki-67, a protein that is expressed only during cellular proliferation. Studies have shown a good correlation between FLT K_i values versus tissue assays of percentage of cells with Ki-67, supporting clinical relevance (48). Ultimately, though, for translation into the clinic, PET uptake measures must be tested in the context of clinical care. Carefully designed clinical trials are required to test the added value of PET to the prediction and improvement of clinical outcomes, as described in part 2.

Alternative Approaches to Lesion Identification

Traditional approaches to PET kinetic analysis often use tissue time–activity curves derived from the average activity in VOIs to help reduce the statistical noise in the curve compared with single-voxel curves. This approach generates a single set of parameter values for each region drawn and represents an average of biologic properties across the VOI. Whereas maximum uptake in a voxel is often used for semiquantitative static measures (e.g., SUV_max), kinetic analysis typically uses mean uptake in a VOI, which is more robust to differences in image noise. In addition to simple geometric shapes (e.g., a sphere), VOIs can be drawn using threshold or edge-based methods (49), using a peak VOI for more heterogeneous lesions (50), or mapping to an atlas of regions of interest for neurologic applications (51,52). As an alternative to VOI-based methods, voxel-based methods generate 3-dimensional images of tracer kinetic parameters, called parametric images, that better reflect the spatial distribution of tissue properties and tumor heterogeneity than do VOI-based approaches (53,54). Voxel-based analysis, however, is associated with more statistical uncertainty in the tissue time–activity curves, which can lead to considerable noise in the parametric image. Methods that consider the 4-dimensional PET image as a combination of a common set of fundamental tissue time–activity curves—for example, mixture analysis, wavelet decomposition, and others—can mitigate this challenge and add computational efficiency (55,56). When successful, this approach can improve the precision with which parameters are estimated and dramatically improve parametric image quality (Fig. 4 (57)).

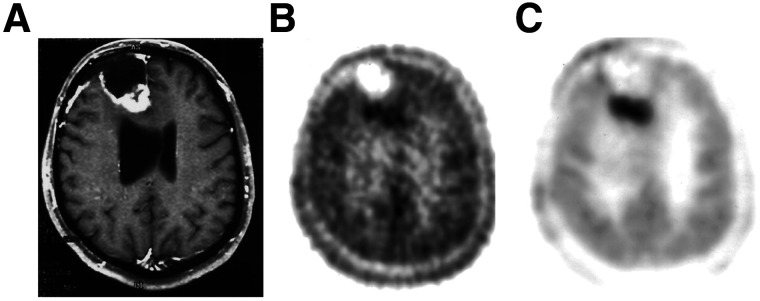
FIGURE 4.

(A) MRI demonstrates contrast enhancement in recurrent right frontal glioma, with viable tissue predominately seen posteriorly. (B) Summed 20- to 60-min 2-[¹¹C-11]thymidine PET image demonstrates relatively high background uptake of tracer throughout brain, with mildly increased tracer uptake in enhancing portion of recurrent glioma. (C) 2-[¹¹C-11]thymidine K_i parametric image from mixture analysis demonstrates increased contrast of tumor compared with normal brain, underscoring benefits of kinetic analysis. (Modified with permission of (57).)

Interpreting Kinetic Parameter Estimates

Part 2 of this review provides several examples of how kinetic parameter estimates can offer unique insights into the clinical biology of cancer that can help guide treatment selection and evaluate therapeutic efficacy. Some common themes apply to these interpretations. For the most part, parameters that quantify tracer delivery and retention yield the most reliable and clinically important measures that provide information on delivery of drugs and metabolic substrates (K₁), metabolic flux through rate-limiting steps (K_i), and drug target availability and binding (2-compartment V_T). Although (lowercase) k-type microparameters are important for tracer kinetic insights and model optimization, these parameters are theoretic constructs of compartmental models influenced by in vivo native metabolite concentrations that are often not easily measured directly (see, for example, early studies of ¹¹C-labeled glucose and thymidine (41)). Additionally, in some cases, microparameters are not reliably estimated independently of other variables, especially in the context of the heterogeneity (58) common in cancer imaging. Therefore, new cancer radiopharmaceuticals—or new applications of existing tracers—require rigorous studies of kinetics in preclinical and early clinical studies to determine the utility and validity of tracer kinetic parameters as measures of cancer biology and tools for guiding clinical practice.

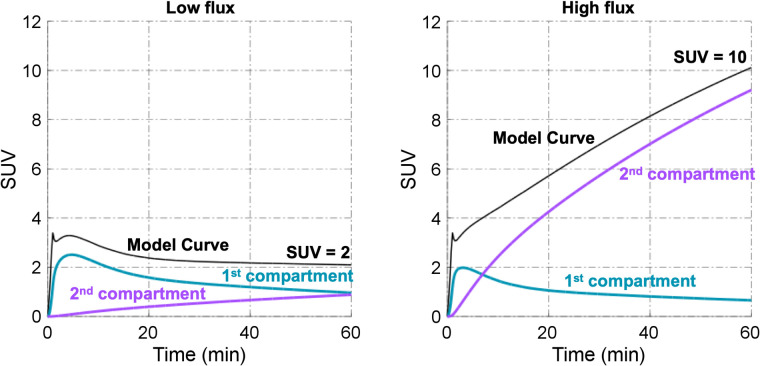
Once established and validated, kinetic models may be used to gain insight into the composition of a static PET image obtained at any single time point. That is, kinetic analysis can predict the contribution of the different pools of tracer pharmacologic state to the total image signal. This is exemplified for ¹⁸F-FDG in Figure 5, showing how an understanding of ¹⁸F-FDG kinetics can provide insight into how to interpret SUVs. Using a 2-compartment kinetic model to generate curves based on the range of kinetic constants seen in breast cancer (14), Figure 5 depicts the contribution of the free (¹⁸F-FDG) and trapped (¹⁸F-FDG-6-P) components of the ¹⁸F label detected in tumor tissue. For tumors with low SUVs, uptake reflects a nearly equal mix of free and trapped ¹⁸F-FDG, even late after injection. As such, SUVs for tumors with modest uptake (SUV < 3–4) reflects a nearly equal—and confusing—mix of transport and tissue distribution (reversible tissue ¹⁸F-FDG) and glucose metabolism (¹⁸F-FDG-6-P). However, for tumors with a high SUV, most of the label is in the form of ¹⁸F-FDG-6-P by 60 min after injection, and the 60-min SUV provides a reasonable indication of tumor glucose metabolism. This insight has several important implications: first, changes in uptake with treatment should be interpreted carefully for tumors with low baseline uptake, as they may reflect changes in tracer delivery or tissue distribution as a side effect of therapy rather than changes in tumor health and viability as indicated by glucose metabolism. Similarly, low ¹⁸F-FDG uptake may also impact the precision and interpretation of posttherapy uptake measures in treated tumors, which often carries prognostic information that can be measured more accurately by kinetic measures such as K_i than by static measures such as SUV (14).

FIGURE 5.

Representative low-flux and high-flux lesions in plots of individual components of model curve. Radiotracer is freely exchanged in first compartment but is trapped in second compartment. Major contributor of uptake in low-flux lesion is reversible (first) compartment, whereas trapped (second) compartment is major contributor of uptake in high-flux lesion.

Another insight from kinetic analysis is the variable behavior of static SUV measures over time after injection. Low-uptake tumors will have flat or even declining uptake since the free ¹⁸F-FDG component will follow the decline in plasma activity due primarily to renal clearance of ¹⁸F-FDG, an observation that may be misinterpreted as glucose-6-phosphatase activity (not included in the Fig. 5 simulated data, which had a k₄ of 0). Highly glycolytic tumors with high ¹⁸F-FDG uptake, as indicated by high SUVs, will have increasing SUVs over time because of increased trapping of ¹⁸F-FDG, confounding comparison of serial scans when uptake time is variable (18). These illustrations provide a clinically relevant example of the benefit of kinetic analysis, including providing insights into how to interpret the static imaging uptake measures most often used in the clinic.

ALTERNATIVE APPROACHES TO ESTIMATING TRACER KINETICS: GRAPHICAL ANALYSIS AND OTHER MODEL-FREE APPROACHES

Although compartmental analysis provides a rigorous approach to studying tracer kinetics, these methods have some undesirable properties. Most notably, compartmental models require nonlinear optimization to estimate kinetics parameters, a computationally demanding task often associated with bias, covariance, and a lack of precision in parameter estimates (9). This limitation spurred the development of alternative approaches to estimating selected kinetic parameters—such as metabolic flux and V_T—by linear estimation methods. Linear estimation—for example a simple line fit to 2-dimensional data—has closed-form solutions that typically do not require iterative optimization. Unlike nonlinear approaches, these approaches are computationally efficient, not dependent on starting guesses, and generally tolerant to statistical noise in the data (39).

The most popular approaches to radiotracer imaging, often called graphical analysis, exploit the fact that most clinically relevant PET tracers distribute fairly quickly into target tissues and settle into a period of exponential blood or plasma clearance, typically 20–40 min after injection. This quick distribution results in a pseudo steady-state when, even though blood and tissue curves change over time, tissue tracer uptake kinetics are driven largely by rate-limiting steps of metabolism or target binding in the second bound or trapped tissue compartment and not by transport and early tissue distribution. This process can be understood using the 2-tissue-compartment model illustrated in Figure 3. Early after injection, when there is a rapid rise and early fall in the plasma time–activity curve, target tissues will largely exchange tracer back and forth with the blood in the first, reversible, tissue compartment reflecting early tracer delivery. Once this transient period has passed, and the plasma clearance curve settles into more stable—typically exponential—clearance, the reversible compartment comes into a pseudo equilibrium with the blood. Tracer uptake then reflects steady-state tracer movement into the second compartment, which represents trapped metabolic products or reversible target binding. Seminal works by Patlak and Logan (59,60) recognized that these conditions lead to a late linear relationship between time-varying tissue-to-blood uptake ratios and measures of plasma tracer availability, which can be customized to yield flux (K_i, Patlak analysis) or V_T (Logan analysis) estimates from a simple line fit (Fig. 6), at some time after tracer injection. Although an underlying model is not required for graphical methods, knowledge of tracer pharmacology and kinetics in the target tissue is key to ensuring that the assumptions of the chosen graphical method are satisfied.

FIGURE 6.

Graphical methods of data analysis, including Patlak (A) and Logan (B) plots, where C_Plasma is blood time–activity curve and C_Tissue is tissue time–activity curve. t = time.

Because of the popularity of ¹⁸F-FDG PET (a trapped tracer) for oncology, Patlak analysis is often used to describe flux into tissue for cancer imaging applications. The irreversible uptake of ¹⁸F-FDG in most malignancies lends itself to evaluation with Patlak analysis (Fig. 6A), which can be understood in the context of the compartmental model illustrations in Figures 3 and 5, where the steady rise in the trapped compartment (¹⁸F-FDG-6-P) time–activity curve over time, together with a fall in both the plasma and the reversible-compartment time–activity curves, lead to an increase in the tissue-to-blood ratio over time in those tissues with active glucose metabolism by hexokinase (i.e., k₃ > 0). When plotted in Patlak space, later time points, after the tracer has mostly reached pseudo steady state (with the first compartment reaching steady state), can be fit to a line in which the slope estimates the flux (K_i,¹⁸F-FDG) and the intercept reflects the V_T of the first tissue compartment plus the vascular space (i.e., the Patlak does not completely correct for blood volume) (59). For trapped tracers with labeled metabolites, modifications to this graphical method have been proposed (61). For tracers that bind targets reversibly (i.e., no appreciable trapping), Logan graphical analysis may be used. If blood input data are available, the original Logan graphical analysis method (Fig. 6B) may be used to calculate the macroparameter V_T (60). These graphical methods provide computational advantages (8) that lend themselves well to parametric imaging and other clinically relevant approaches. Specifically, these graphical methods do not suffer from noise amplification (62) and can even be applied to raw scan data before reconstruction (63). A limitation of these approaches is that although they provide robust estimates of macroparameters specific to the tracer and its target cancer biology, they do not provide estimates of other key measures, such as drug or substrate delivery (K₁). Additionally, the reparametrized x- and y-axes constructed for linear estimation are not independent of each other, and as such, measures of variability of the estimated macroparameter are difficult to obtain (62).

Other model-free approaches to estimating kinetics have been proposed that include the consideration of tracer uptake curves as a combination of exponential clearance curves (64), recognizing clearance as a key pharmacologic property highly relevant to drug therapy. An alternative approach leverages the residue method of Zierler and Meier (65) as an alternative to compartmental analysis for PET oncology tracers (66). The approach uses linear regression to estimate regional tracer delivery (tracer flow) and retention (tracer tissue residue). This approach has the advantage of being a linear estimation method that is computationally efficient and robust, well suited to parametric imaging. Advances in imaging data science, including radiomics and artificial intelligence, offer the promise of new approaches to 4-dimensional PET image analysis that may yield new insights, as demonstrated by a recent study applied to locally advanced breast cancer (67).

CONCLUSION

Through kinetic analysis of dynamic PET imaging, specific interactions between the radiotracer and tissue can be quantified. Kinetic measures may better capture relevant biology to inform patient management. In the initial development of a kinetic model, both biologic and mathematic factors must be considered. A kinetic model should be able to accurately estimate kinetic parameters that have biologic relevance. Once a model is thoroughly tested, imaging protocols may be optimized to eliminate the burden of imaging on the patient and staff and possibly decrease scan time. Static imaging protocols may also be developed and optimized to enable translation into a busy clinic. Of course, the ultimate utility of a radiotracer lies in its application, whether in research or clinical care. In part 2, we will discuss such applications and emphasize cases that provide examples for ¹⁸F-FDG and other oncologic tracers, as well as the benefits of kinetic analysis over static approaches.