Abstract
Herein, the geometric, electronic, and nonlinear optical properties of excess electron zintl clusters Ge5AM3, Ge9AM5, and Ge10AM3 (AM = Li, Na, and K) are investigated. The clusters under consideration demonstrate considerable electronic stability as well as superalkali characteristics. The NBO charge is transferred from the alkali metal to the Ge-atoms. The FMO analysis shows fabulous conductive properties with a significant reduction in SOMO–LUMO gaps (0.79–4.04 eV) as compared with undoped systems. The designed clusters are completely transparent in the deep UV-region and show absorption in the visible and near-IR region. Being excess electron compounds these clusters exhibit remarkable hyperpolarizability response up to 8.99 × 10−26 esu, where a static second hyperpolarizability (γo) value of up to 2.15 × 10−30 esu was recorded for Ge9Na5 superatom clusters. The excitation energy is the main controlling factor for hyperpolarizability as revealed from the two-level model study. The electro-optical Pockel's effect and the second harmonic generation phenomenon (SHG) are used to investigate dynamic nonlinear optical features. At a lower applied frequency (=532 nm), the dynamic hyperpolarizability and second hyperpolarizability values are significantly higher for the studied clusters. Furthermore, for the Ge9K5 cluster, the hyper Rayleigh scattering (HRS) increases to 5.03 × 10−26 esu.
Herein, the geometric, electronic, and nonlinear optical properties of excess electron zintl clusters Ge5AM3, Ge9AM5, and Ge10AM3 (AM = Li, Na, and K) are investigated.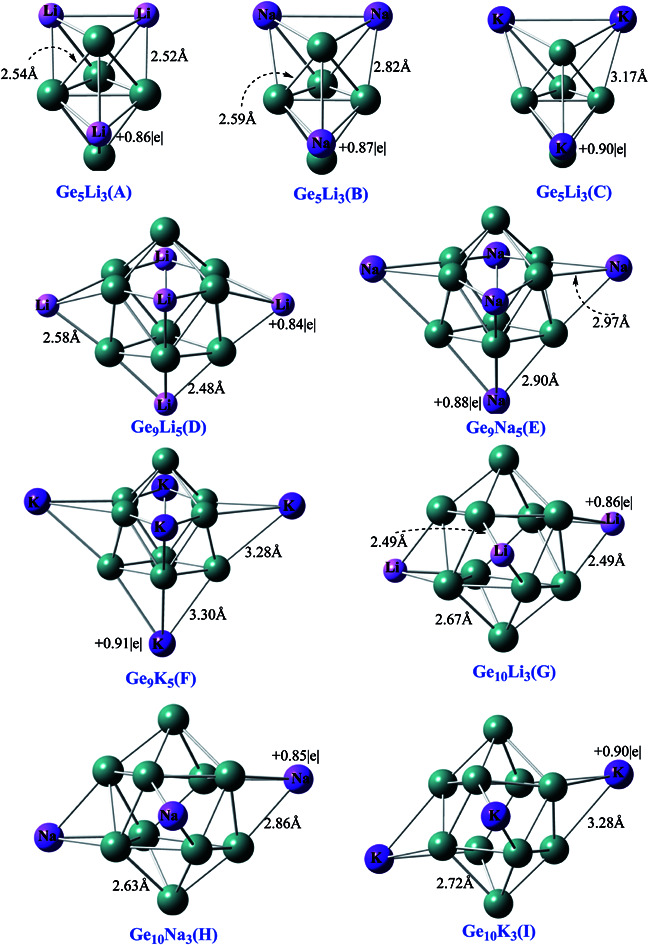
1. Introduction
The past several decades have witnessed increasing scientific and technology-driven interest in developing nonlinear optical (NLO) materials because of their tremendous importance in photonic applications.1,2 The developments in the field of nonlinear optics and laser-based technologies started after the discovery of the ruby laser by Maiman in 1960.3 Thus nonlinear optical materials have emerged rapidly during the last few decades, mainly due to their extensive applications in optoelectronic and photonic devices, second harmonic generation (SHG), endoscopy, and laser surgery4–8 To date, numerous approaches for designing nonlinear optical materials with high hyperpolarizability have been used, including diradical character,9 designing octupolar molecules,10 the push–pull effect in conjugated chromophores,11 multidecker sandwich complexes,12 and excess electron models.13 Among the studied nonlinear optical materials inorganic materials exhibit prime interest because of their physicochemical stability and thermal stability.14
The excess electron system is well-known for triggering second and third-order nonlinearity.15,16 In the family of excess electron compounds, electride,17 alkalides,18 and alkaline-earthides19,20 are well known.
Electrides are compounds in which electron trapping into the complexant acts as an anion.21 Similarly, the alkalides are compounds in which alkali metals possess a negative charge and become anion (Li−, Na−, K−).22 Alkaline-earthides are also a fabulous excess electron system that contains a negative charge on alkaline-earth metals (Be−, Mg−, Ca−).23 Excess electron compounds can be designed by doping any complexant with alkali metals,24,25 alkaline earth metals,26 transition metals27,28 and superalkali clusters.29,30
Superalkali clusters belong to the superatom clusters family and exhibit alkali-like characteristics with tunability in their electronic and geometric properties.31 The term ‘superalkalis’ was first time introduced by Gutsev and Boldyrev for Li3O, Li2F, NLi4etc. through DVMxα calculations. The superalkali clusters materials are of prime interest and show significant applications in numerous fields including, catalysis,32 reduction of CO2 and N2,33 hydrogen storage materials, and nonlinear optics.34 Thus, being excess electron compounds superalkali clusters can be adopted for making high-performance nonlinear optical materials. Furthermore, several studies have been proposed that reveal that superalkali being excess electron clusters can be doped with different molecules and nanocages to form excess electron compounds for triggering the NLO response. In this regard, superalkali-doped nanocages Li3O@Al12N12 were theoretically designed with electride characteristics for enhanced nonlinear optical response.35 Similarly, superalkali doped 2D graphdiyne M2X@GDY (where M = Li, Na, K, and X = F, Cl, Br) were studied, and it was observed that there is a significant decrease in the HOMO–LUMO gap with a notecable increase in hyperpolarizability response.36 Moreover, superalkali clusters were doped with different 2D materials and nanocages to get excess electron compounds i.e. alkalide, alkaline earthides. These excess electron compounds were reported as excellent nonlinear optical materials with significant hyperpolarizality.24,37,38 However, a very limited number of studies were reported that reveal the nonlinear optical response of pure superalkali clusters as efficient nonlinear optical materials.
A few number of pure superalkali clusters are investigated as excess electron compounds and show remarkable hyperpolarizability. In this regard, Misra et al., investigated the electronic and nonlinear optical response of hyper lithiated superalkali clusters and reported these clusters as efficient NLO materials. The nonlinear optical response increases up to 1.2 × 104 au.39 Subsequently, another class of superalkali clusters CNLin (n = 1–10) was investigated for nonlinear optical response and second-order NLO response was much pronounced.40 The literature reveals that only conventional types of superalkali clusters are explored for optical and nonlinear optical studies however several models can be efficiently utilized to be used as nonlinear optical responses. Literature also reveals, there are several superatom clusters (silicon-based) encapsulated by transition metals which were also studied for optical and magnetic excitation41,42
Zintl polyanions, discovered by Eduard zintl in 1930 belong to the group (14,15) and show excellent physicochemical stability.43 It is previously reported that zintl P73− anion as core material can be used to design organo-zintl superalkali clusters which contain superb electron properties.44 Similarly, zintl based superalkalis as a building block, when treated with superhalogens make novel supersalt compounds with significant electronic and nonlinear optical properties.45 Moreover, superalkali clusters other than alkali metals might possess better stability and a high nonlinear optical response. We become interested in zintl-based superatoms, particularly germinum-based superatoms (which belong to group 14 elements) for electronic and optical properties. Furthermore, the stoichiometry of these clusters obeys magic number nuclei, in which their valence shells are organised as 1S2, 1P6, 1D10, 2S2, 1F14 after losing one electron, achieving electronic shell closure (according to Jellium model). When designed with alkali metals, Ge semimetallic clusters may have improved optoelectronic and NLO features. Although the Ge5Li3, Ge9Li5, and Ge10Li3 were theoretically studied by Sun et al.46 Their investigations were limited to electronic properties whereas we adopted the alkali decorated zintl clusters Ge5AM3, Ge9AM5 and Ge10AM5 (where AM = Li, Na, K) for exploring optoelectronic and nonlinear optical properties.
In these studied clusters, we are mainly concerned with the following issues. Do these clusters belong to superalkali with better thermal and electronic stability than conventional superalkalis do these clusters possess nonlinear optical responses for declaring them as efficient NLO materials. The NLO response was confirmed by hyperpolarizability calculation and second hyperpolarizability.
2. Computational details
Initially, all the studied alkali decorated zintl polyanions Ge5AM3, Ge9AM5, and Ge10AM3 (where AM = Li, Na, K) are considered and optimized at CAM-B3LYP/6-311+G(d,p) level of theory. The geometries of Ge5Li3, Ge9Li5, and Ge10Li3 were reported in the previous literature and we adopted the similar design for the rest of the alkali metals.46 All the calculations were performed with Gaussian 09 software.47 The CAM-B3LYP (Coulomb attenuating method) is a hybrid exchange–correlation functional that includes the hybrid properties of B3LYP functional and long-range corrected Coulomb-Attenuating Method (CAM).48 B3LYP is a hybrid part of the above method that contains Beckes 3-parameters for exchange functional and Lee–Yang–Parr-correlation functional. This hybrid density functional theory-based method comprises 0.19 HF plus 0.81 (B88) exchange interactions at short range and 0.65 HF plus 0.35 (B88) long-range interactions.49 The CAM-B3LYP is a well-known approach for linear and nonlinear optical characteristics of various clustered materials, and it has already been demonstrated to give appropriate geometries and comparable hyperpolarizability values with CCDST.50–53 Besides, the triple zeta split valence basis set 6-311+G(d,p) with diffuse and polarized function is adopted throughout the calculations.
To explore the electronic stabilities of these clusters, we calculated vertical ionization potential and electron affinity.
| IE = EX+ − EX0 | 1 |
| EA = EX− − EX0 | 2 |
The chemical hardness is also calculated to understand their reactivity and soft nature and given by equation below 54
| Chemical hardness (η) = VIP − VEA | 3 |
To further explore the electronic properties, we performed frontier molecular orbital (FMOs) analysis which included SOMO, LUMO, and EH–L gap. The FMOs analysis also provides evidence of the excess electron nature of studied superalkali clusters. Natural bonding orbitals (NBO) study is conducted to explore the nature and charge distribution as studied superatom clusters. The time-dependent density functional (TD-DFT) theory is adopted to calculate the excited state parameters and absorbance behavior of studied zintl superatom clusters. The time-dependent density functional (TD-DFT) is well know for obtaining excited states parameters and absorption spectra of molecules and clusters. The TD-DFT was chosen because of its performance and its correspondence to experimental results. For this purpose excited-state calculations with TD-CAM-B3LYP/6-311+G(d,p) are performed. Mathematically system under the constant field can be expressed as:
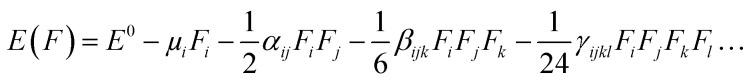 |
4 |
where F is an external applied electric field on the molecular system, Fi is its component of force along i direction; E0 is the total energy of the superalkali clusters without a static electric field, μi,αij, βijk, and γijkl are dipole moment, polarizability, hyperpolarizability, and second-order hyperpolarizability, respectively. Thus regarding nonlinear optical properties, the following parameters are estimated including the mean dipole moment (μo), change in dipole moment (Δμ), static polarizability (α) and static first hyperpolarizability (β).
| αo = 1/3(αxx + αyy + αzz) | 5 |
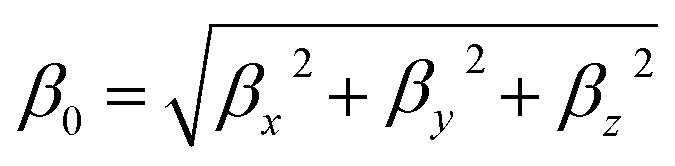 |
6 |
where βx = βxxx + βxyy + βxzz, βy = βyyy + βyzz + βyxx and βz = βzzz + βzxx + βzyy.
| μo = (μx2 + μy2 + μz2)½ | 7 |
Besides, the second static hyperpolarizability (γo) and the projection of hyperpolarizability on the dipole moment vector (βvec) is also calculated for our studied superalkali clusters at the same level of theory. Vector part of hyperpolarizability (βvec) and second hyperpolarizability (γ) are expressed defined as
| 〈γ〉 = 1/5(γxxxx + γyyyy + γzzzz + γxxyy + γxxzz + γyyxx + γyyzz + γzzxx) | 8 |
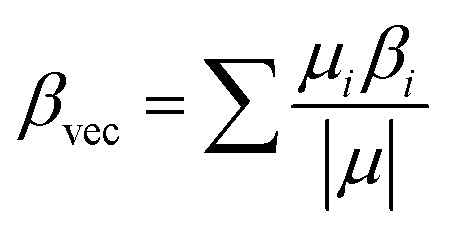 |
9 |
Mathematically βHRS can be expressed as;
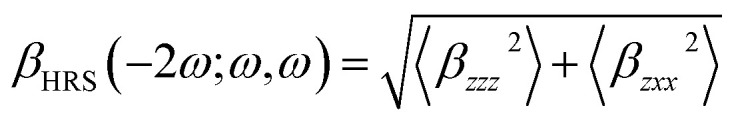 |
10 |
where 〈βzzz2〉 and 〈βzxx2〉 are average of orientational (β) tensor.
While the related depolarization ratio for these superalkali clusters (DR) ratio is also given by;DR = 〈βzzz2〉/〈βzxx2〉
The frequency-dependent NLO analysis was conducted at 532 and 1064 nm wavelength. Frequency-dependent hyperpolarizability involves the electro-optic Pockel's effect (EOPE) β(−ω;ω,0) and electric field induced second harmonic generation (ESHG) β(−2ω;ω,ω) respectively. While for second hyperpolarizability (γ), dc-Kerr γdc-Kerr (ω) = γ(−ω;ω,0,0) and second harmonic generation γESHG(ω) = γ(−2ω;ω, ω,0) were considered.
3. Results and discussion
3.1. Geometries and electronic properties
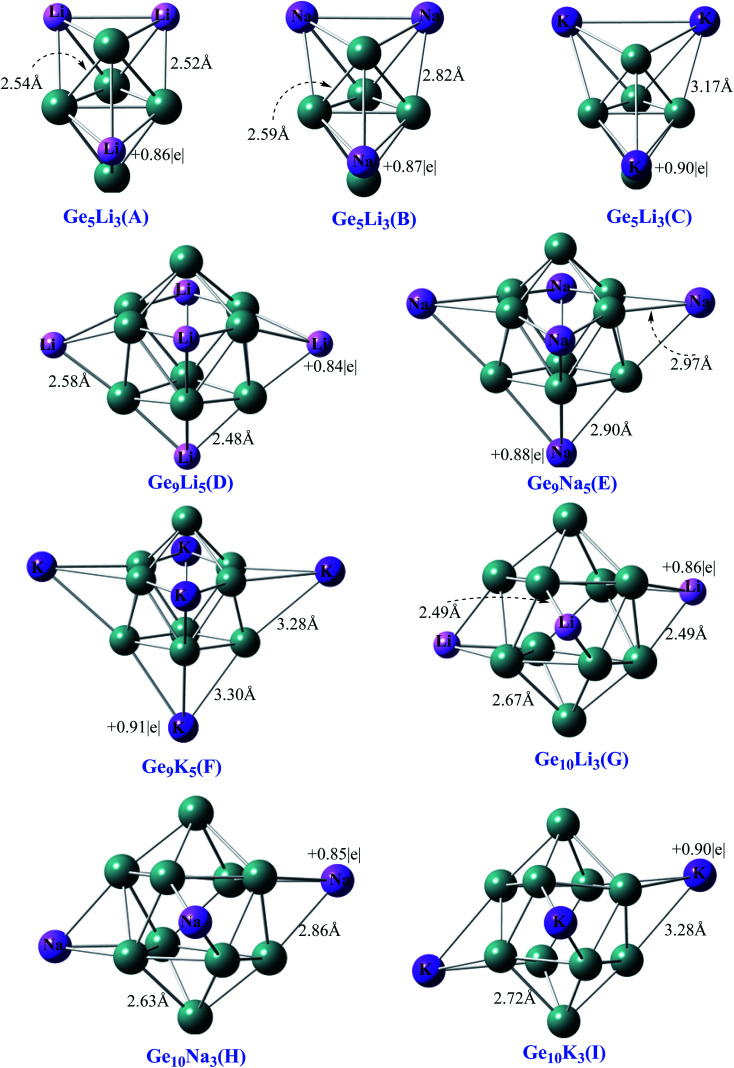
All the optimized geometries of Ge5AM3, Ge9AM5, and Ge10AM3 (where AM = Li, Na, K) zintl superalkali clusters and their equilibrium bond length are depicted in Fig. 1. The geometric parameters of these clusters are identical to those reported in the earlier literature46 and are included in the ESI† (S1).
Fig. 1. Optimized geometries with NBO charge of Ge5AM3, Ge9AM5 and Ge10AM3 clusters.
These clusters have no imaginary frequency (negative frequency) according to the frequency calculations, hence they are true minima on the potential energy surface (PES).
The computed ionization potential and electron affinity are used to analyze the electronic stability and superalkali nature of the investigated clusters. The difference in ground state energy between the cationic and neutral systems is described as the ionization potential (IP), meanwhile, the difference in ground state energy between the neutral and anionic systems is defined as the electron affinity.
The vertical ionization potential (VIP) values for Ge9AM3 are in the range of 5.49 to 3.91 eV, and it decreased dramatically as the alkali-metal size rose (Li to k). The VIP values for the Ge9AM5 series follow a similar pattern, reaching to 2.15 eV for F (Table 1). On the other hand, the VIP values for Ge10AM3 are slightly higher than for Ge9AM5 (Table 1). The lower VIPS values for the Ge9AM5 series can be attributed to the higher number of alkali metals (AM = 5), which is responsible for the cluster's electropositive nature. Additionally, their superalkali nature is demonstrated by their relatively low ionization potential values than Li atoms (5.4 eV).
Vertical ionization potential (VIP, in eV), vertical electron affinity (VEA in eV), maximum chemical hardness (η in eV), average NBO charge upon germanium (QGe in |e|), an average charge upon alkali metal (QAM in |e|), of Ge5AM3 Ge9AM5 and Ge10AM3 (where AM = Li, Na, K).
| Superalkalis | VIP | VEA | η | Q Ge | Q AM |
|---|---|---|---|---|---|
| Ge 5 AM 3 (where AM = Li, Na, K) | |||||
| Ge5Li3 (A) | 5.49 | 0.98 | 4.51 | −0.69 | 0.86 |
| Ge5Na3 (B) | 4.69 | 0.64 | 4.05 | −0.65 | 0.87 |
| Ge5K3 (C) | 3.91 | 0.29 | 3.62 | −0.65 | 0.90 |
| Ge 9 AM 5 | |||||
| Ge9Li5 (D) | 4.36 | 0.65 | 3.71 | −0.61 | 0.85 |
| Ge9Na5 (E) | 2.81 | 0.07 | 2.74 | −0.52 | 0.88 |
| Ge9K5 (F) | 2.15 | 0.02 | 2.13 | −0.50 | 0.90 |
| Ge 10 AM 3 | |||||
| Ge10Li3 (G) | 4.98 | 1.15 | 3.83 | −0.38 | 0.86 |
| Ge10Na3 (H) | 4.34 | 0.67 | 3.67 | −0.36 | 0.85 |
| Ge10K3 (I) | 3.50 | 0.11 | 3.39 | −0.46 | 0.90 |
The calculated vertical electron affinity (VEA) values of these superalkali clusters range from 0.02 to 1.15 eV. In the designed series, Ge9AM5 has a smaller VEA value than those of Ge3AM3 and Ge10AM3. The electro-positive feature of the examined superalkalis is revealed by the tiny VEA values. Furthermore, the reduced VEA values indicate that these alkali-decorated zintl clusters are unable to completely grasp the valence (loosely bound) electron, which could result in interesting electrical properties. Table 1 shows that the examined clusters are polarizable and soft, based on the computed minimal values of chemical hardness. The calculated chemical hardness (η) values decrease with increased alkali metals size within these clusters. Among the series, Ge9AM5 clusters shows lower values of chemical hardness which may be attributed to the higher number of alkali smaller metals (soft) in these clusters.
3.2. Natural bonding orbital (NBO) analysis
The NBO analysis is a useful tool for interpreting intramolecular and intermolecular interactions and conjugative interactions in compounds and clusters.55 For Ge5AM3 clusters, the obtained charges on alkali metals (QAM) vary from 0.86 to 0.90|e| (positive magnitude). The C cluster has the highest computed positive charge of 0.90|e|, while A has the lowest value of 0.86|e| in the Ge5AM3 family. Similarly, the Ge9AM5 clusters, computed average charge (QAM) ranges from 0.85 to 0.90|e| (Table 1). For the Ge10AM3 superalkali clusters, similar NBO (positive magnitude) charges are observed. Hence, the computed positive NBO charges upon alkali metals shows the significant charge transfer (from alkali metals to Ge-atom) within the superalkali clusters. Additionally, the compted NBO charges upon germanium metals (QGe) for Ge5AM3 range from −0.13 to −0.69|e| (negative in magnitude). Therefore from the computed NBO charges (Table 1) one can observe the excellent separation of charges within the clusters. Likewise, the computed NBO charges (QGe) for the Ge9AM3 clusters are range from −0.09 to −0.61|e| where the highest value of −0.61|e| is obtained for Ge9Li5 while the lowest value (−0.50) is obtained for Ge9K5 superalkali. However, the reported NBO charges (QGe) for the third series Ge10AM3 are reduced (in negative magnitude) with corresponding increased cluster size. The overall NBO charges is an order of Ge5AM3 > Ge9AM5 > Ge10AM3.
3.3. Frontier molecular orbital (FMO) analysis and excess electron character
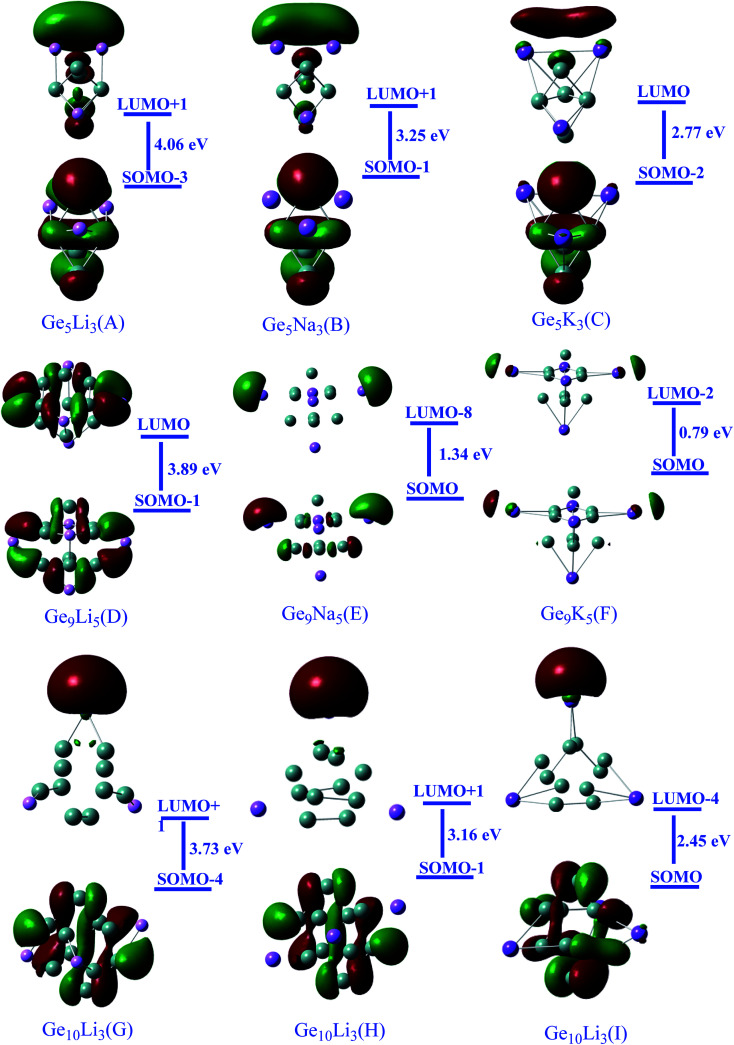
FMO analysis is adopted to validate the reactivity of the studied cluster system. Thus according to the frontier molecular orbital treatment of chemical reactivity, the rate, and site of reactivity of a molecule with a nucleophile is dominated by the interaction of the LUMO of the molecule in question with the HOMO of the nucleophile. The closer these orbitals are in energy, the more intensely they will interact, and the higher is the reactivity will be. Result in Table 2 show that the computed values for singly occupied molecular orbitals (SOMO), LUMO, and ES–L gaps. For the Ge5AM3, the obtained values of singly occupied molecular orbitals (SOMO) vary from −4.99 to −3.51 eV and increase from A to C. For Ge9AM5, predicted SOMO energies are in the range of −3.97 to −1.80 eV, as well. The Ge10AM3 clusters, on the other hand, have lower SOMO energies than those of Ge9AM5 clusters, and these range from −4.46 to −3.14 eV. It can also be concluded that the SOMO energies of the examined superalkali clusters rise monotonically as the size of the alkali metals increases. Thus the observed trend of SOMO energies for studied superalkali clusters is Ge9AM5 < Ge10AM3 < Ge5AM3. Furthermore, the estimated LUMO energies for Ge5AM3 clusters vary with cluster size. However, the estimated energies of virtual orbitals for the Ge9AM5 series are increasing, while the Ge10AM3 clusters are increasing even high.
Energies of SOMO and LUMOs (in eV), HOMO–LUMO gaps (EH–L in eV), excitation energies (ΔE in eV), the wavelength of maximum absorbance (λmax in nm), oscillator strength (fo in au), ground-state dipole moment (μo in au), and excited-state dipole moment (Δμ in au) of Ge5AM3, Ge9AM5 and Ge10AM3 superalkali clusters.
| Superalkalis | SOMO | LUMO | E H–L | ΔE | λ max | f o | μ | Δμ |
|---|---|---|---|---|---|---|---|---|
| Ge 5 AM 3 (where AM = Li, Na, K) | ||||||||
| Ge5Li3 (A) | −4.99 | −0.94 | 4.04 | 2.16 | 571 | 0.015 | 1.63 | 1.05 |
| Ge5Na3 (B) | −4.24 | −0.99 | 3.25 | 2.16 | 572 | 0.015 | 2.26 | 1.14 |
| Ge5K3 (C) | −3.51 | −0.73 | 2.77 | 2.24 | 553 | 0.041 | 3.12 | 2.34 |
| Ge 9 AM 5 | ||||||||
| Ge9Li5 (D) | −3.97 | −0.07 | 3.89 | 2.25 | 548 | 0.007 | 0.27 | 0.62 |
| Ge9Na5 (E) | −2.42 | −1.07 | 1.34 | 1.77 | 688 | 0.076 | 1.69 | 2.49 |
| Ge9K5 (F) | −1.80 | −1.02 | 0.79 | 1.12 | 1101 | 0.219 | 2.21 | 1.86 |
| Ge 10 AM 3 | ||||||||
| Ge10Li3 (G) | −4.40 | −0.87 | 3.73 | 2.31 | 534 | 0.007 | 1.45 | 0.62 |
| Ge10Na3 (H) | −4.00 | −0.83 | 3.16 | 2.47 | 500 | 0.008 | 1.55 | 0.65 |
| Ge10K3 (I) | −3.14 | −0.69 | 2.45 | 2.14 | 578 | 0.005 | 1.67 | 0.49 |
For Ge5AM3 clusters, there is a considerable reduction in the SOMO–LUMO gap, with values ranging from 4.06 to 2.77 eV. The HOMO–LUMO gaps for Ge5AM3 clusters are around 4.06 to 2.77 eV, indicating that these compounds behave like semiconductors. Similarly, the observed reduction in Ge9AM5EH–L values from 3.89 to 0.79 eV could be attributable to their higher SOMO energies. Furthermore, the Ge10AM3 series' HOMO–LUMO gap values are slightly higher than the Ge9AM3 series, and range from 3.37 to 2.45 eV (Table 2). The significant reduction in HOMO–LUMO gaps reveals the soft nature (higher reactivity) and conductive properties of these clusters. Furthermore, the observed reduced SOMO–LUMO gap within clusters is attributed to the larger size of alkali metals (ease in the transition of electron from occupied to virtual orbitals).
Moreover, the excess electron character of clusters can be seen in the electronic density distribution (Fig. 2). The excess electron cloud is indicated by the electronic density of SOMO and LUMO scattered throughout the alkali metals that resemble to s-orbital. The LUMO electronic density for Ge10AM3 clusters wraps around the alkali metals, whereas the LUMO densities for Ge9AM5 clusters move away from the alkali metals.
Fig. 2. Representation of Frontier molecular orbital densities along with orbitals contribution of superalkali clusters (iso-value of 0.030).
3.4. TD-DFT analysis of clusters
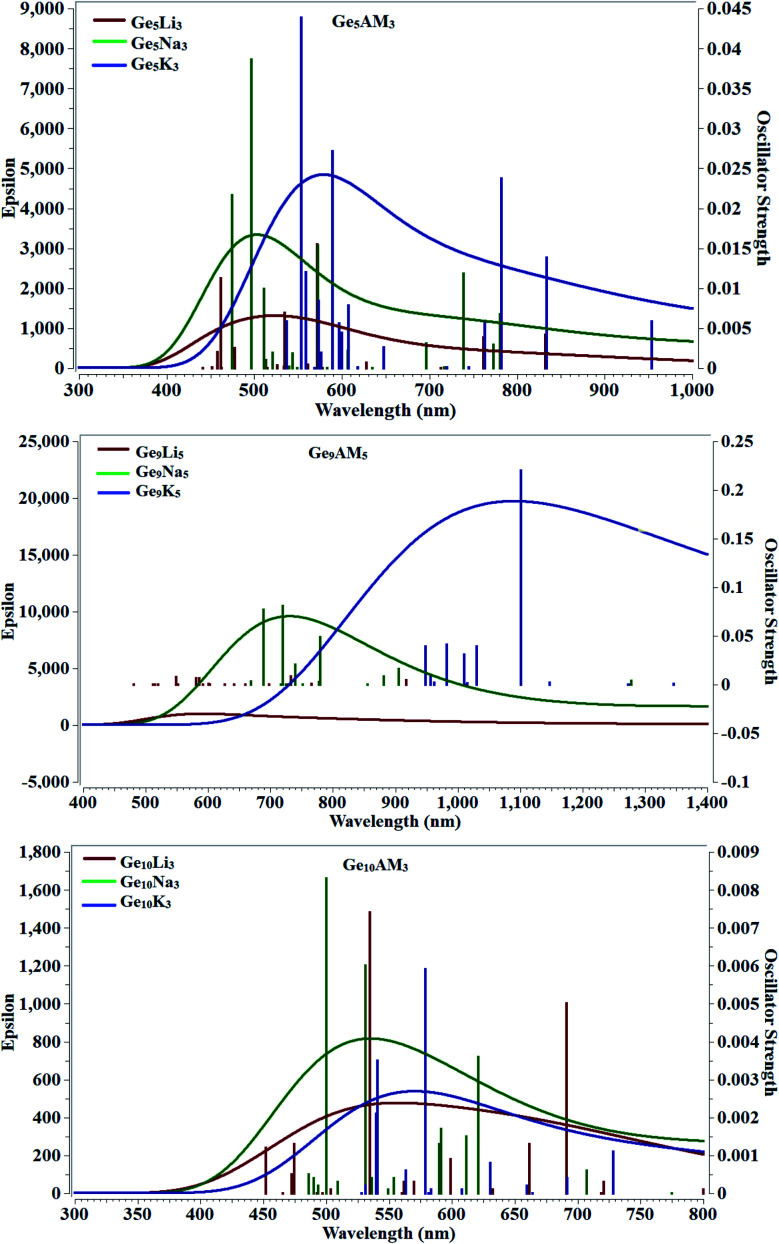
Time-dependent density functional theory was used to examine the absorbance behavior of Ge5AM3, Ge9AM5, and Ge10AM3 superalkali clusters. For nonlinear optical applications, the cluster materials employed should be transparent in the used region. In the absorption study, we calculated the maximum absorbance, excitation energy, and oscillator strength (during the electronic transition). The computed excited state parameters for the studied superalkali clusters are given in Table 2. From the computed results one can observe that the studied clusters are completely transparent in the UV-region (<400 nm) and show broadband absorbance in the visible region. The longer absorbance wavelength for the Ge5AM3 (λmam = 572 nm) is observed for the Ge5Na3 superalkali cluster whereas the lowest absorbance maxima (λmam = 553 nm) is obtained for the Ge5K3 superalkali cluster (Fig. 3). However, the Ge9AM5 series shows higher absorbance maxima (λmam = 1101 nm) for Ge9K5 clusters. Similarly, for the second series, the highest absorbance maxima (λmam = 578 nm) is observed for the Ge10K3 cluster in the Ge10AM3 series. Overall, the clusters of Ge9AM5 series shows absorption maxima at a longer wavelength (bathochromic shift) whereas the Ge5AM3 and Ge10AM3 have slightly blue-shifted wavelengths. As a result of their total transparency under deep UV-region, the optoelectronic properties of the examined clusters fall under the UV-region. Furthermore, the excitation energies (ΔE) of Ge5AM3 (i.e. excitation of an electron from HOMO to LUMO) are also very small and ranges from 2.16 to 2.24 eV whereas the observed excitation energies (ΔE) for the Ge9AM5 are further reduced and lie in the range of 1.12 to 2.25 eV. Alternatively, the computed excitation energies of the Ge10AM3 series are slightly higher than those of Ge9AM5 and display a range of 2.14 to 2.47 eV. Moreover, the calculated oscillator strength (probability of absorbance during excitation) shows significant values for Ge5AM3 superalkali clusters while the Ge9AM5 and Ge10AM3 have slightly reduced values of oscillator strength (fo).
Fig. 3. Absorbance spectra of Ge5AM3, Ge9AM5, and Ge10AM3.
3.5. Dipole moment and change in dipole moment
Table 2 shows the computed values of mean dipole moment (μo) and change in dipole moment (Δμ). The magnitude of polarisation in clusters and the asymmetric charge distribution are shown by the significant values of dipole moments. For the Ge5AM3 series, the observed mean dipole moments range from 1.63 to 3.13 au. As the size of alkali metals grows larger (Li to K), the dipole moment gradually increase. Likewise, the calculated values of the dipole moment of Ge9AM5 range from 0.27 to 2.21 au. Thus the calculated values of dipole moment for the Ge9AM5 are slightly smaller than those of Ge5AM3 clusters. On the other hand, the computed mean dipole moments are enhanced for the Ge10AM3 series and the values lie in the range of 1.42 to 1.67 au. Hence, from the computed results, one can conclude that a significant dipole moment that is associated with the Ge5AM3 series would result in larger polarization. Our calculations also show that the studied alkali decorated zintl polyanions clusters possess polar bonds (asymmetric electronic density) that might be an important factor for imparting optical and nonlinear optical properties. Besides, the computed changes in dipole momen between the ground state and crucial excited state for Ge5AM3 clusters lies in the range of 1.05 to 2.34 au where the highest value of 2.34 au is observed for Ge5K3 while the lowest value of 1.05 au is obtained for the Ge5Li3 cluster. A similar decreasing trend of change in dipole moment is observed for the Ge9AM5 clusters. The value of excited-state dipole moment for the Ge9AM5 series lie in the range of 0.62 to 1.86 au. However, the computed values of the excited-state dipole moment are increasing with the increased size of alkali metals within clusters. Finally, the Ge10AM3 series of clusters show further decreased values of change in dipole moment. As a result of the fascinating electronic features of clusters examined, increased optical and nonlinear optical properties might be expected.
3.6. Static nonlinear optical properties
The alkali-like superatom clusters Ge5AM3, Ge9AM5, and Ge10AM3 examined here have an excess electron nature. As a result, large optical and nonlinear optical (NLO) responses are reasonable predictions. Literature reveals that compounds and clusters with excess electrons characteristics are significantly adopted for triggering nonlinear optical response.19,36,39,56–65 Hence, the calculated polarizability (αo), hyperpolarizability (βo), second hyperpolarizability (γo), and associated electronic parameters are computed and given in Table 3. The calculated values of polarizability (linear optical response) of Ge5AM3 lie in the range of 3.70 × 10−23 to 5.3 × 10−23 esu. Similarly, the computed values of polarizability (αo) for Ge9AM5 series are significantly enhanced and lie in the range of 6.5 × 10−23 to 1.9 × 10−21 esu. Alternatively, the obtained values of polarizability of Ge10AM3 series are slightly smaller than those of Ge9AM5 and lie in range of 60 × 10−24 to 71 × 10−24 au. The increasing trend of polarizability may be seen as the size of alkali metals increases (Li to K). Overall, the highest value of 1.9 × 10−21 esu is obtained for F wheres the lowest value of 37 × 10−24 esu is observed for A. Furthermore, the significant polarizability values obtained demonstrate the amount of polarity within the examined clusters. Asymmetric distribution of charges and electronic densities inside clusters also contributed to the higher linear optical response.
Polarizability (αo in ×10−24 esu), first static hyperpolarizability (βo in ×10−33 esu) scattering hyperpolarizability (βvec in ×10−33 esu), static second hyperpolarizability (γo in ×10−40 esu), HOMO–LUMO gaps (EH–L in au), and vertical ionization potential (VIP in au) of Ge5AM3, Ge9AM5 and Ge10AM3 superalkali clusters.
| Superalkalis | α o | β o | β vec | γ o | E H–L | VIP |
|---|---|---|---|---|---|---|
| Ge 5 AM 3 | ||||||
| Ge5Li3 (A) | 3.7 × 10−23 | 3.44 × 10−29 | 3.39 × 10−30 | 1.37 × 10−34 | 4.04 | 5.49 |
| Ge5Na3 (B) | 4.5 × 10−23 | 1.01 × 10−27 | 9.94 × 10−30 | 5.5 × 10−34 | 3.25 | 4.69 |
| Ge5K3 (C) | 5.3 × 10−23 | 3.41 × 10−28 | 2.97 × 10−29 | 2.80 × 10−33 | 2.77 | 3.91 |
| Ge 9 AM 5 | ||||||
| Ge9Li5 (D) | 6.5 × 10−23 | 1.80 × 10−28 | 1.81 × 10−29 | 4.07 × 10−34 | 3.89 | 4.36 |
| Ge9Na5 (E) | 3.6 × 10−22 | 1.57 × 10−26 | 1.57 × 10−26 | 2.15 × 10−30 | 1.34 | 2.81 |
| Ge9K5 (F) | 1.9 × 10−21 | 8.99 × 10−26 | 8.99 × 10−27 | 7.68 × 10−34 | 0.79 | 2.15 |
| Ge 10 AM 3 | ||||||
| Ge10Li3 (G) | 6.0 × 10−23 | 1.88 × 10−29 | 1.88 × 10−29 | 2.26 × 10−34 | 3.73 | 4.98 |
| Ge10Na3 (H) | 6.8 × 10−23 | 3.87 × 10−29 | 3.87 × 10−29 | 3.87 × 10−34 | 3.16 | 4.34 |
| Ge10K3 (I) | 7.1 × 10−23 | 4.57 × 10−29 | 4.57 × 10−29 | 7.68 × 10−34 | 2.45 | 3.50 |
Furthermore, the calculated values of static hyperpolarizability (βo) lie in the range of 3.44 × 10−29 to 8.99 × 10−26 esu. The calculated static first and second hyperpolarizabilities values are significant. Hyperpolarizability values in the proposed superalkali clusters follow the order Ge9AM5 > Ge5AM3 > Ge10AM3. The hyperpolarizability values obtained for the Ge5M3 series rise monotonically with alkali metal size. The highest value of 3.41 × 10−28 esu is observed for the C cluster while the lowest value (3.44 × 10−29 esu) is calculated for the A cluster. Similarly, the obtained values of the βo for the Ge9AM5 series range from 1.80 × 10−28–8.99 × 10−26 esu. With the increased metal size and the number of alkali metals in the Ge9AM5 clusters, there is a huge increase in βo values. In particular, the Ge9K5 shows a remarkable βo value (8.99 × 10−26 esu) which may be attributed to the larger size of alkali metal (K). In comparison, the Ge10AM3 (AM = Li, Na, and K) clusters have range of 1.88 × 10−29 to 4.57 × 10−29, which is lower than the Ge9AM5 and Ge5AM3 clusters. In our designed and studied clusters the hyperpolarizability response is quite larger than previously reported LinF (n = 2–5) superalkali clusters,39 and M2OCN & M2NCO (M = Li, Na, K) clusters.64 Excess electron nature might account for considerable hyperpolarizability response found in these clusters. Furthermore, the studied fabulous electronic properties contribute to the hyperpolarizabilities values. As a result, decreased EH–L gaps and ionization potential (IP) with increasing alkali metals (AM) size ultimately prompt the βo response.
We used a conventional two model with the sum-over-state (SOS) method to develop a full understanding of hyperpolarizability and its governing factors. The two-level model can be written as follows: βtl = Δμ × fo/ΔE3
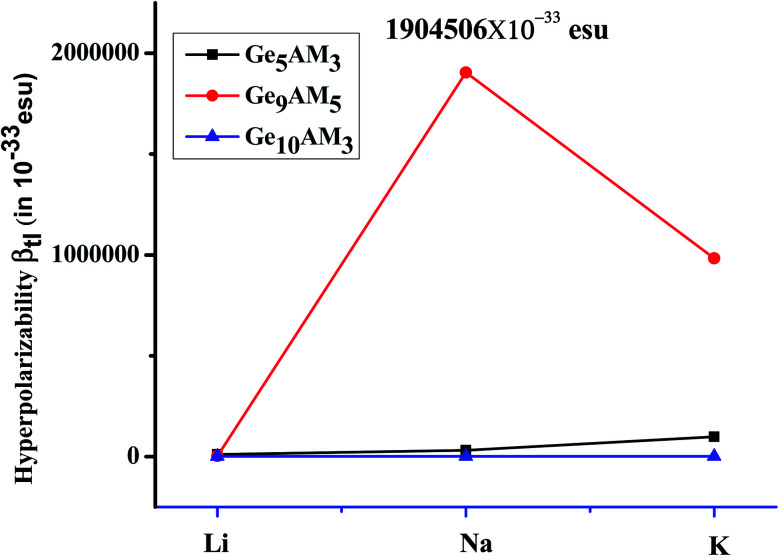
Where the Δμ, fo, and ΔE are changes in dipole moment, oscillator strength, and excitation energy for crucial excitation (excitation with maximum oscillator strength). From the above model, one can observe that βtl has a direct relation with change in dipole moment and oscillator strength (fo) while it is inversely related with cubic of excitation energy (ΔE). The obtained values of βtl range from 1.03 × 10−29–1.90 × 10−27 esu (Table 4). The Ge9AM5 has the largest βtl values in the examined clusters series, which is comparable to βo. For the first series (Ge5AM3), the βtl is increased with an increase in Δμ and oscillator strength. In this series, Ge5K3 shows a significant βtl response which may be attributed to its noticeable change in dipole moment (2.34 au) and small excitation energy (1.58 eV). As a result, excitation energy (E) is considered to be extremely vital in impacting hyperpolarizability response. A similar trend is observed for the second series (Ge9AM5) where the Ge9Na5 shows a notable value (1.90 × 10−27 esu) of βtl which is due to small excitation energy (transition energy) and higher change in dipole moment (2.49 au). Likewise, βtl values for the Ge10AM3 series, there is an increase βtl with reduced excitation energy (ΔE). Hence, the excitation energy is deciding factor in triggering the hyperpolarizability response from the two-level model where its effect is inversely related to βtl. Furthermore, the estimated βo and βtl values are highly correlated, providing additional insight into the hyperpolarizability response. From the plotted graph (Fig. 4), one can observe that overall, the βtl values increase dramatically for the Ge9Na5 cluster.
Computed hyperpolarizability from the two-level model (βtl in ×10−33 esu), change in dipole moment (Δμ in au), excitation energy (ΔE in eV), oscillator strength (fo in au) hyper Rayleigh scattering (βHRS in ×10−33 esu), and depolarization ratio (DR in au) of superalkali clusters.
| Superalkalis | β tl | Δμ | ΔE | f o | β HRS | DR |
|---|---|---|---|---|---|---|
| Ge 5 AM 3 | ||||||
| Ge5Li3 (A) | 1.03 × 10−29 | 1.05 | 2.16 | 0.05 | 1.31 × 10−29 | 6.87 |
| Ge5Na3 (B) | 3.11 × 10−29 | 1.14 | 1.67 | 0.04 | 4.23 × 10−29 | 5.61 |
| Ge5K3 (C) | 9.79 × 10−29 | 2.34 | 1.58 | 0.16 | 1.32 × 10−28 | 6.41 |
| Ge 9 AM 5 | ||||||
| Ge9Li5 (D) | 2.90 × 10−30 | 0.62 | 1.69 | 0.01 | 1.13 × 10−29 | 2.44 |
| Ge9Na5 (E) | 1.90 × 10−27 | 2.49 | 0.01 | 0.002 | 9.61 × 10−27 | 2.41 |
| Ge9K5 (F) | 9.83 × 10−28 | 1.86 | 0.75 | 0.06 | 5.03 × 10−26 | 2.45 |
| Ge 10 AM 3 | ||||||
| Ge10Li3 (G) | 1.54 × 10−30 | 0.62 | 1.87 | 0.01 | 1.21 × 10−29 | 2.37 |
| Ge10Na3 (H) | 1.79 × 10−30 | 0.65 | 2.02 | 0.21 | 2.08 × 10−29 | 2.45 |
| Ge10K3 (I) | 9.64 × 10−31 | 0.49 | 1.86 | 0.11 | 2.73 × 10−29 | 2.57 |
Fig. 4. Representation of βtl for Ge5AM3, Ge9AM5, and Ge10AM3 superalkali clusters.
Projection of hyperpolarizability on dipole moment vector is also evaluated through βvec simulations. The βvec is a vector part of hyperpolarizability and is very important to characterize the nonlinearity of molecules and clusters. The calculated βvec values are given in Table 3. From Table 3, the observed βvec response of designed clusters strongly correlates with total hyperpolarizability which indicates the dipole moment has the same direction projection of hyperpolarizability (βo). Furthermore, the quite comparable values of first hyperpolarizabilities with βvec also indicate that the charge transfer is parallel to the molecular dipole moments. The resemblance of βo and βvec also suggests that these clusters can be synthesized in laboratory.
We also carried out calculations for estimation of static second hyperpolarizability (γo) which is a third rank tensor (χ3). The obtained values of γo for the Ge5AM3 range from 1.37 × 10−34–2.80 × 10−33 esu which shows an increasing trend with the increased size of alkali metals. Similarly, for the second series (Ge9AM5), the γo response increases up to 2.15 × 10−30 esu for E cluster. The γo values for the Ge10AM3 superalkali clusters, on the other hand, decrease considerably. Clusters with a higher number of alkali metals (AM) have a substantial γo response. Likewise, the γo response for the Ge10AM3 clusters lie in the range of 2.26 × 10-34 to 7.68 × 10−34 esu and a slight increase is observed with growing alkali metals size. Hence, the γo values vary in order of Ge9AM5 > Ge5AM3 > Ge10AM3.
3.7. Hyper Rayleigh scattering measurement (βHRS)
The hyperpolarizability of nonlinear optical molecules can be determined using hyper-Rayleigh scattering. The βHRS is a widely used method for determining the nonlinear optical characteristics of centrosymmetric molecules with zero dipole moment. At the same level of theory, we theoretically evaluated the βHRS response for these clusters. Overall, the calculated highest value (5.03 × 10−26 esu) of βHRS is obtained for Ge9K5 while the lowest value 1.13 × 10−29 esu is observed for D. For the Ge5AM3 series βHRS lie in the range of 1.31 × 10−29 esu to 1.32 × 10−28 esu, and are increased with size (Li to K). In the Ge9AM5 series, the usual trend of beta-HRS value of Ge9Li5 may be attributed to the small size of Li-atom. Similarly, other nonlinear optical parameters for Ge9Li5 are also small. It has been reported in the literature previously that dominating factor changes from structure to structure (and it ultimately leads to irregular trends). However, factors affecting the βHRS response might be the same as total hyperpolarizability values. A similar increasing trend of βHRS with the size of metal (AM) can be seen for the second series of clusters(Ge9AM5). Furthermore, βHRS values do not increase with clusters size, rather these show dependence upon the size of and the number of alkali metals. As a result, the βHRS values for the Ge10AM3 become slightly smaller, ranging from 1.22 × 10−29 to 2.73 × 10−29 esu. Interestingly, the Ge9K5 exhibits a significant HRS response which suggests better NLO properties. Additionally, the depolarization ratio (DR) is higher for Ge5AM3 clusters and increases up to 6.87 au for Ge5Li3.
3.7.1. Dynamic nonlinear optical properties
The frequency-dependent NLO properties are the fundamental molecular parameters that are required for the description of many nonlinear optical phenomena. The theoretical understanding and accurate determination of the frequency-dependent hyperpolarizabilities β(ω) and second hyperpolarizabilities γ(ω) are therefore crucial to classify nonlinearity of materials. The frequency-dependent NLO response is estimated at dispersion frequencies of 532 and 1064 nm, and we calculated electro-optic pockel's effect (EOPE) with β(−ω;ω,0) and electric field induced second harmonic generation (EFSHG) with β(−2ω;ω,ω) at applied frequency. The obtained values of electro-optical pockel's effect (EOPE) for Ge5AM3 clusters at dispersion frequency of 532 nm range from. The EOPE effect is much pronounced at a small dispersion frequency of 532 nm. Similarly, the obtained dynamic hyperpolarizabilities β(−2ω;ω,ω) values noticeably at smaller frequencies. Overall, the highest values (3.54 × 10−26 esu) of EOPE is obtained for C whereas the lowest value of 3.02 × 10−28 esu is observed for D (Table 5). The is a gradual increase in β(ω) with an increased size of alkali metals metal. Both EOPE and SHG show significant values at smaller applied frequencies, and their values slightly decrease at higher dispersion frequency (1064 nm).
Frequency-dependent hyperpolarizability β(ω) in form of electro-optic pockel's effect (EOPE) β(−ω;ω,0) in ×10−33 esu, and electric field induced second harmonic generation (EFSHG) with β(2 − ω;ω,ω) in ×10−33 esu at ω = 532 nm and ω = 1064 nm.
| Superalkalis | ω = 0.0856 au (532 nm) | ω = 0.0428 au (1064 nm) | ||
|---|---|---|---|---|
| β(−ω;ω,0) | β(−2ω;ω,0) | β(−ω;ω,0) | β(−2ω;ω,0) | |
| Ge 5 AM 3 | ||||
| Ge5Li3 (A) | 3.28 × 10−27 | 4.42 × 10−27 | 6.99 × 10−29 | 1.81 × 10−28 |
| Ge5Na3 (B) | 1.29 × 10−27 | 3.63 × 10−27 | 2.50 × 10−28 | 3.72 × 10−28 |
| Ge5K3 (C) | 3.54 × 10−26 | 1.30 × 10−26 | 2.24 × 10−28 | 9.50 × 10−28 |
| Ge 9 AM 5 | ||||
| Ge9Li5 (D) | 3.02 × 10−29 | 3.28 × 10−29 | 7.86 × 10−29 | 1.47 × 10−30 |
| Ge9Na5 (E) | 7.68 × 10−28 | 4.42 × 10−27 | 1.56 × 10−26 | 2.94 × 10−27 |
| Ge9K5 (F) | 6.39 × 10−27 | 1.04 × 10−26 | 4.93 × 10−29 | 1.39 × 10−27 |
| Ge 10 AM 3 | ||||
| Ge10Li3 (G) | 9.67 × 10−29 | 1.98 × 10−28 | 2.24 × 10−29 | 6.99 × 10−29 |
| Ge10Na3 (H) | 5.71 × 10−28 | 3.71 × 10−28 | 2.85 × 10−29 | 5.62 × 10−29 |
| Ge10K3 (I) | 1.21 × 10−27 | 1.04 × 10−27 | 5.87 × 10−29 | 2.42 × 10−28 |
The calculated frequency-dependent second hyperpolarizability γ(ω) that includes dc-Kerr γdc−Kerr (ω) = γ(−ω;ω,0,0) and second harmonic generation with γESHG(ω) = γ(−2ω;ω,ω,0) are calculated at the same level of theory. The calculated values of dynamic second hyperpolarizability are given in Table 6. The calculated dc-Kerr constant and EFSHG are higher at 532 nm and their values slightly decreased at higher dispersion frequency (1064 nm). Likewise, Ge9AM5 and Ge10AM3 are also larger at a small dispersion frequency of 532 nm. Hence, the studied clusters offer tremendous dynamic NLO properties at the smaller external applied frequency.
Frequency-dependent second hyperpolarizability with dc-Kerr effect γ (−ω;ω,0,0) and electric field induced second harmonic generation (ESHG) γ(−2−ω;ω,ω,0) in ×10−40 esu at ω = 532 and 1064 nm.
| Superalkalis | ω = 0.0856 au (532 nm) | ω = 0.0428 au (1064 nm) | ||
|---|---|---|---|---|
| γ(−ω;ω,0,0) | γ(−2ω;ω,ω,0) | γ(−ω;ω,0,0) | γ(−2ω;ω,ω,0) | |
| Ge 5 AM 3 | ||||
| Ge5Li3 (A) | 7.84 × 10−31 | 1.37 × 10−30 | 3.39 × 10−34 | 1.40 × 10−30 |
| Ge5Na3 (B) | 1.30 × 10−32 | 1.64 × 10−31 | 2.45 × 10−33 | 2.31 × 10−33 |
| Ge5K3 (C) | 5.43 × 10−36 | 2.52 × 10−29 | 7.37 × 10−32 | 2.09 × 10−31 |
| Ge 9 AM 5 | ||||
| Ge9Li5 (D) | 1.36 × 10−33 | 5.74 × 10−32 | 3.16 × 10−32 | 1.19 × 10−33 |
| Ge9Na5 (E) | 1.76 × 10−29 | 8.80 × 10−30 | 1.58 × 10−31 | 1.03 × 10−32 |
| Ge9K5 (F) | 5.23 × 10−32 | 2.53 × 10−32 | 2.15 × 10−30 | 3.76 747 508 × 10−32 |
| Ge 10 AM 3 | ||||
| Ge10Li3 (G) | 8.45 × 10−32 | 1.24 × 10−31 | 3.24 × 10−40 | 5.28 × 10−34 |
| Ge10Na3 (H) | 1.22 × 10−32 | 6.84 × 10−34 | 1.72 × 10−32 | 2.41 × 10−33 |
| Ge10K3 (I) | 5.23 × 10−32 | 2.53 × 10−32 | 2.15 × 10−30 | 3.76 × 10−32 |
4. Conclusion
In the summary, we explored the zintl-based superalkali for geometric, electronic and nonlinear optical properties. The studied zintl superalkali clusters Ge5AM3, Ge9AM5, and Ge10AM3 (AM = Li, Na, K) belong to excess electron compounds. These are superalkali clusters as their calculated vertical ionization potential (VIP) values are smaller than Li atom (5.39 eV). The calculated significant VIP values suggest their electronic stability. The calculated chemical hardness (η) lie in the range of 2.13 to 4.51 eV, and Ge9AM5 shows the higher softness among the series. There is a significant charge (positive in magnitude) on alkali metals, and the charge is transferred from alkali to Ge-atom. The charge is transferred from alkali metals to Ge-atoms within the clusters. There is a notable reduction in EH–L (0.79–4.04 eV) which reveals their conductive applications. These clusters are completely transparent in the deep UV region, and show absorption maxima (λmax) at the longer wavelength. Being excess electron compounds these clusters shows remarkable hyperpolarizability response up to 8.99 × 10−26 esu where the static second hyperpolarizability (γo) value recorded up to 2.15 × 10−30 esu for Ge9AM5 clusters. The adopted two-level model study reveals the controlling factors of hyperpolarizability. The obtained significant βtl value of 1.90 × 10−27 esu may attributed to smaller excitation energy (0.01 eV) The frequency-dependent hyperpolarizabilities and second hyperpolarizabilities values are much higher at smaller dispersion frequencies (ω = 532 nm). Moreover, the hyper Rayleigh scattering (βHRS) increases up to 5.03 × 10−27 esu for the Ge9K5 cluster.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
The authors acknowledge the financial and technical support from the Higher Education Commission of Pakistan and COMSATS University, Abbottabad Campus.
Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08192f
References
- Chen C. Liu G. Recent advances in nonlinear optical and electro-optical materials. Annu. Rev. Mater. Sci. 1986;16(1):203–243. doi: 10.1146/annurev.ms.16.080186.001223. [DOI] [Google Scholar]
- Qin S. J. and Badgwell T. A., An overview of nonlinear model predictive control applications, in Nonlinear model predictive control, Springer, 2000, pp. 369–392 [Google Scholar]
- Maiman T. H. Stimulated optical radiation in ruby. Nature. 1960;187(4736):493–494. doi: 10.1038/187493a0. [DOI] [Google Scholar]
- Agranovich V. M. Gartstein Y. N. Litinskaya M. Hybrid resonant organic–inorganic nanostructures for optoelectronic applications. Chem. Rev. 2011;111(9):5179–5214. doi: 10.1021/cr100156x. [DOI] [PubMed] [Google Scholar]
- Guo J. et al., 2D GeP as a novel broadband nonlinear optical material for ultrafast photonics. Laser Photon. Rev. 2019;13(9):1900123. doi: 10.1002/lpor.201900123. [DOI] [Google Scholar]
- Yu H. Koocher N. Z. Rondinelli J. M. Halasyamani P. S. Pb2BO3I: A Borate Iodide with the Largest Second-Harmonic Generation (SHG) Response in the KBe2BO3F2 (KBBF) Family of Nonlinear Optical (NLO) Materials. Angew. Chem. Int. Ed. 2018;57(21):6100–6103. doi: 10.1002/anie.201802079. [DOI] [PubMed] [Google Scholar]
- Lukic A. et al., Endoscopic fiber probe for nonlinear spectroscopic imaging. Optica. 2017;4(5):496–501. doi: 10.1364/OPTICA.4.000496. [DOI] [Google Scholar]
- Wang B. Riemann I. Schubert H. Schweitzer D. König K. Halbhuber K. Multiphoton microscopy for monitoring intratissue femtosecond laser surgery effects. Lasers Surg. Med. 2007;39(6):527–533. doi: 10.1002/lsm.20523. [DOI] [PubMed] [Google Scholar]
- Nakano M. et al., Second Hyperpolarizabilities (γ) of Bisimidazole and Bistriazole Benzenes: Diradical Character, Charged State, and Spin State Dependences. J. Phys. Chem. A. 2006;110:4238. doi: 10.1021/jp056672z. [DOI] [PubMed] [Google Scholar]
- Lee Y.-K. Jeon S.-J. Cho M. Molecular polarizability and first hyperpolarizability of octupolar molecules: donor-substituted triphenylmethane dyes. J. Am. Chem. Soc. 1998;120(42):10921–10927. doi: 10.1021/ja9803456. [DOI] [Google Scholar]
- Karki L. Vance F. W. Hupp J. T. LeCours S. M. Therien M. J. Electronic Stark Effect Studies of a Porphyrin-Based Push− Pull Chromophore Displaying a Large First Hyperpolarizability: State-Specific Contributions to β. J. Am. Chem. Soc. 1998;120(11):2606–2611. doi: 10.1021/ja973593v. [DOI] [Google Scholar]
- Wang S.-J. Wang Y.-F. Cai C. Multidecker Sandwich Complexes VnBenn+1 (n = 1, 2, 3) as Stronger Electron Donor Relative to Ferrocene for Designing High-Performance Organometallic Second-Order NLO Chromophores: Evident Layer Effect on the First Hyperpolarizability and Two-Dimensional N. J. Phys. Chem. C. 2015;119:5589. doi: 10.1021/jp5123272. [DOI] [Google Scholar]
- Zhong R. L. Xu H. L. Li Z. R. Su Z. M. Role of excess electrons in nonlinear optical response. J. Phys. Chem. Lett. 2015;6(4):612–619. doi: 10.1021/jz502588x. [DOI] [PubMed] [Google Scholar]
- Halasyamani P. S. and Zhang W., inorganic materials for UV and deep-UV nonlinear-optical applications, ACS Publications, 2017 [DOI] [PubMed] [Google Scholar]
- Li X.-H. Zhang L. Zhang X.-L. Ni B.-L. Li C.-Y. Sun W.-M. Designing a new class of excess electron compounds with unique electronic structures and extremely large nonlinear optical responses. New J. Chem. 2020;44:6411–6419. doi: 10.1039/D0NJ00896F. [DOI] [Google Scholar]
- He H. M. et al., Effects of the Cage Number and Excess Electron Number on the Second Order Nonlinear Optical Response in Molecular All-Metal Electride Multicage Chains. J. Phys. Chem. C. 2017;121(45):25531–25540. doi: 10.1021/acs.jpcc.7b06464. [DOI] [Google Scholar]
- Ma F. et al., Lithium salt electride with an excess electron pair - A class of nonlinear optical molecules for extraordinary first hyperpolarizability. J. Phys. Chem. A. 2008;112(45):11462–11467. doi: 10.1021/jp8040023. [DOI] [PubMed] [Google Scholar]
- Sun W. M. et al., Designing Alkalides with Considerable Nonlinear Optical Responses and High Stability Based on the Facially Polarized Janus all-cis-1,2,3,4,5,6-Hexafluorocyclohexane. Organometallics. 2017;36(17):3352–3359. doi: 10.1021/acs.organomet.7b00491. [DOI] [Google Scholar]
- Ahsan A. Ayub K. Adamanzane based alkaline earthides with excellent nonlinear optical response and ultraviolet transparency. Opt. Laser Technol. 2020;129:106298. doi: 10.1016/j.optlastec.2020.106298. [DOI] [Google Scholar]
- Srivastava A. K. Misra N. M2X (M= Li, Na; X= F, Cl): the smallest superalkali clusters with significant NLO responses and electride characteristics. Mol. Simul. 2016;42(12):981–985. doi: 10.1080/08927022.2015.1132840. [DOI] [Google Scholar]
- Dye J. L. Electrides: Early Examples of Quantum Confinement. Acc. Chem. Res. 2009;42(10):1564–1572. doi: 10.1021/ar9000857. [DOI] [PubMed] [Google Scholar]
- Huang R. H. Eglin J. L. Huang S. Z. McMills L. E. H. Dye J. L. Complexation of the cations of six alkalides and an electride by mixed crown ethers. J. Am. Chem. Soc. Oct. 1993;115(21):9542–9546. [Google Scholar]
- Ahsan A. Ayub K. Extremely large nonlinear optical response and excellent electronic stability of true alkaline earthides based on hexaammine complexant. J. Mol. Liq. 2020;297:111899. doi: 10.1016/j.molliq.2019.111899. [DOI] [Google Scholar]
- Ullah F. Kosar N. Ayub K. Mahmood T. Superalkalis as a source of diffuse excess electrons in newly designed inorganic electrides with remarkable nonlinear response and deep ultraviolet transparency: A DFT study. Appl. Surf. Sci. 2019;483:1118–1128. doi: 10.1016/j.apsusc.2019.04.042. [DOI] [Google Scholar]
- Iqbal J. Ludwig R. Ayub K. Phosphides or nitrides for better NLO properties? A detailed comparative study of alkali metal doped nano-cages. Mater. Res. Bull. 2017;92:113–122. doi: 10.1016/j.materresbull.2017.03.065. [DOI] [Google Scholar]
- Ullah F. Kosar N. Ali A. Mahmood T. Ayub K. Alkaline earth metal decorated phosphide nanoclusters for potential applications as high performance NLO materials; A first principle study. Phys. E. 2020;118:113906. doi: 10.1016/j.physe.2019.113906. [DOI] [Google Scholar]
- Rad A. S. Ayub K. Nonlinear optical and electronic properties of Cr-, Ni-, and Ti-substituted C20 fullerenes: a quantum-chemical study. Mater. Res. Bull. 2018;97:399–404. doi: 10.1016/j.materresbull.2017.09.036. [DOI] [Google Scholar]
- Rad A. S. Ayub K. Substitutional doping of zirconium-, molybdenum-, ruthenium-, and palladium: An effective method to improve nonlinear optical and electronic property of C20 fullerene. Comput. Theor. Chem. 2017;1121:68–75. doi: 10.1016/j.comptc.2017.10.015. [DOI] [Google Scholar]
- Kosar N. Shehzadi K. Ayub K. Mahmood T. Theoretical study on novel superalkali doped graphdiyne complexes: Unique approach for the enhancement of electronic and nonlinear optical response. J. Mol. Graphics Modell. 2020:107573. doi: 10.1016/j.jmgm.2020.107573. [DOI] [PubMed] [Google Scholar]
- Sajid H. Ayub K. Mahmood T. Exceptionally high NLO response and deep ultraviolet transparency of superalkali doped macrocyclic oligofuran rings. New J. Chem. 2020;44(6):2609–2618. doi: 10.1039/C9NJ05065E. [DOI] [Google Scholar]
- Brito B. G. A. Hai G.-Q. Cândido L. Analysis of the ionization potentials of small superalkali lithium clusters based on quantum Monte Carlo simulations. Chem. Phys. Lett. 2018;708:54–60. doi: 10.1016/j.cplett.2018.07.062. [DOI] [Google Scholar]
- Cochran E. Muller G. Meloni G. Stability and bonding of new superalkali phosphide species. Dalton Trans. 2015;44(33):14753–14762. doi: 10.1039/C5DT02277K. [DOI] [PubMed] [Google Scholar]
- Zhao T. Wang Q. Jena P. Rational design of super-alkalis and their role in CO2 activation. Nanoscale. 2017;9(15):4891–4897. doi: 10.1039/C7NR00227K. [DOI] [PubMed] [Google Scholar]
- Hou N. Wu Y.-Y. Wu H.-S. He H.-M. The important role of superalkalis on the static first hyperpolarizabilities of new electrides: Theoretical investigation on superalkali-doped hexamethylenetetramine (HMT) Synth. Met. 2017;232:39–45. doi: 10.1016/j.synthmet.2017.07.021. [DOI] [Google Scholar]
- Sun W.-M. et al., A theoretical study on superalkali-doped nanocages: unique inorganic electrides with high stability, deep-ultraviolet transparency, and a considerable nonlinear optical response. Dalton Trans. 2016;45(17):7500–7509. doi: 10.1039/C6DT00342G. [DOI] [PubMed] [Google Scholar]
- Shehzadi K. Ayub K. Mahmood T. Theoretical study on design of novel superalkalis doped graphdiyne: A new donor–acceptor (D-π-A) strategy for enhancing NLO response. Appl. Surf. Sci. 2019;492:255–263. doi: 10.1016/j.apsusc.2019.06.221. [DOI] [Google Scholar]
- Sun W. M. Fan L. T. Li Y. Liu J. Y. Wu D. Li Z. R. On the potential application of superalkali clusters in designing novel alkalides with large nonlinear optical properties. Inorg. Chem. 2014;53(12):6170–6178. doi: 10.1021/ic500655s. [DOI] [PubMed] [Google Scholar]
- Wang J. J. et al., The interaction between superalkalis (M 3 O, M = Na, K) and a C 20 F 20 cage forming superalkali electride salt molecules with excess electrons inside the C 20 F 20 cage: Dramatic superalkali effect on the nonlinear optical property. J. Mater. Chem. 2012;22(19):9652–9657. doi: 10.1039/C2JM15405F. [DOI] [Google Scholar]
- Srivastava A. K. Misra N. Nonlinear optical behavior of LinF (n = 2–5) superalkali clusters. J. Mol. Model. 2015;21(12):1–5. doi: 10.1007/s00894-015-2849-0. [DOI] [PubMed] [Google Scholar]
- Hou D. Wu D. Sun W. M. Li Y. Li Z. R. Evolution of structure, stability, and nonlinear optical properties of the heterodinuclear CNLin (n = 1-10) clusters. J. Mol. Graphics Modell. 2015;59:92–99. doi: 10.1016/j.jmgm.2015.04.004. [DOI] [PubMed] [Google Scholar]
- Oliveira M. J. T. Medeiros P. V. C. Sousa J. R. F. Nogueira F. Gueorguiev G. K. Optical and magnetic excitations of metal-encapsulating Si cages: A systematic study by time-dependent density functional theory. J. Phys. Chem. C. 2014;118(21):11377–11384. doi: 10.1021/jp4096562. [DOI] [Google Scholar]
- Oliveira M. I. A. Rivelino R. de Brito Mota F. Gueorguiev G. K. Optical properties and quasiparticle band gaps of transition-metal atoms encapsulated by silicon cages. J. Phys. Chem. C. 2014;118(10):5501–5509. doi: 10.1021/jp409967a. [DOI] [Google Scholar]
- Scharfe S. Kraus F. Stegmaier S. Schier A. Fässler T. F. Zintl ions, cage compounds, and intermetalloid clusters of group 14 and group 15 elements. Angew. Chem. Int. Ed. 2011;50(16):3630–3670. doi: 10.1002/anie.201001630. [DOI] [PubMed] [Google Scholar]
- Giri S. Reddy G. N. Jena P. Organo-Zintl Clusters [P7R4]: A New Class of Superalkalis. J. Phys. Chem. Lett. 2016;7(5):800–805. doi: 10.1021/acs.jpclett.5b02892. [DOI] [PubMed] [Google Scholar]
- Reddy G. N. Kumar A. V. Parida R. Chakraborty A. Giri S. Zintl superalkalis as building blocks of supersalts. J. Mol. Model. 2018;24(11):1–13. doi: 10.1007/s00894-018-3806-5. [DOI] [PubMed] [Google Scholar]
- Sun W. Decorating Zintl polyanions with alkali metal cations : A novel strategy to design superatom cations with low electron affinity. J. Alloys Compd. 2018;740:400–405. doi: 10.1016/j.jallcom.2017.12.075. [DOI] [Google Scholar]
- Frisch M. J. et al. , Gaussian 09 (Revision A. 02)[Computer software], Gaussian Inc., Wallingford CT, 2009 [Google Scholar]
- Yanai T. Tew D. P. Handy N. C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP) Chem. Phys. Lett. 2004;393(1–3):51–57. doi: 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Beerepoot M. T. P. Friese D. H. List N. H. Kongsted J. Ruud K. Benchmarking two-photon absorption cross sections: performance of CC2 and CAM-B3LYP. Phys. Chem. Chem. Phys. 2015;17(29):19306–19314. doi: 10.1039/C5CP03241E. [DOI] [PubMed] [Google Scholar]
- Li M. Reimers J. R. Ford M. J. Kobayashi R. Amos R. D. Accurate prediction of the properties of materials using the CAM-B3LYP density functional. J. Comput. Chem. 2021:1486–1497. doi: 10.1002/jcc.26558. [DOI] [PubMed] [Google Scholar]
- Limacher P. A. V Mikkelsen K. Luthi H. P. On the Accurate Calculation of Polarizabilities and Second Hyperpolarizabilities of Polyacetylene Oligomer Chains using the CAM-B3LYP Density Functional. J. Chem. Phys. 2009;130:194114. doi: 10.1063/1.3139023. [DOI] [PubMed] [Google Scholar]
- Ahsin A. Ayub K. Remarkable electronic and NLO properties of bimetallic superalkali clusters: a DFT study. J. Nanostruct. Chem. 2021:1–17. [Google Scholar]
- Oviedo M. B. V Ilawe N. Wong B. M. Polarizabilities of π-conjugated chains revisited: improved results from broken-symmetry range-separated DFT and new CCSD (T) benchmarks. J. Chem. Theory Comput. 2016;12(8):3593–3602. doi: 10.1021/acs.jctc.6b00360. [DOI] [PubMed] [Google Scholar]
- Vijayaraj R. Subramanian V. Chattaraj P. K. Comparison of Global Reactivity Descriptors Calculated Using Various Density Functionals: A QSAR Perspective. J. Chem. Theory Comput. Oct. 2009;5(10):2744–2753. doi: 10.1021/ct900347f. [DOI] [PubMed] [Google Scholar]
- Pathak S. K. et al., Experimental (FT-IR, FT-Raman, UV and NMR) and quantum chemical studies on molecular structure, spectroscopic analysis, NLO, NBO and reactivity descriptors of 3,5-Difluoroaniline. Spectrochim. Acta, Part A. 2015;135:283–295. doi: 10.1016/j.saa.2014.06.149. [DOI] [PubMed] [Google Scholar]
- Ahsin A. Ali A. Ayub K. Alkaline earth metals serving as source of excess electron for alkaline earth metals to impart large second and third order nonlinear optical response; A DFT study. J. Mol. Graphics Modell. 2020;101:107759. doi: 10.1016/j.jmgm.2020.107759. [DOI] [PubMed] [Google Scholar]
- Ullah F. Kosar N. Ayub K. Gilani M. A. Mahmood T. Theoretical study on a boron phosphide nanocage doped with superalkalis: novel electrides having significant nonlinear optical response. New J. Chem. 2019;43(15):5727–5736. doi: 10.1039/C9NJ00225A. [DOI] [Google Scholar]
- Kosar N. et al., Significant nonlinear optical response of alkaline earth metals doped beryllium and magnesium oxide nanocages. Mater. Chem. Phys. 2020;242:122507. doi: 10.1016/j.matchemphys.2019.122507. [DOI] [Google Scholar]
- Rad A. S. Ayub K. Change in the electronic and nonlinear optical properties of Fullerene through its incorporation with Sc-, Fe-, Cu-, and Zn transition metals. Appl. Phys. A. 2019;125(6):430. doi: 10.1007/s00339-019-2721-7. [DOI] [Google Scholar]
- Sajjad S. Ali A. Mahmood T. Ayub K. Journal of Molecular Graphics and Modelling Janus alkaline earthides with excellent NLO response from sodium and potassium as source of excess electrons ; a fi rst principles study. J. Mol. Graphics Modell. 2020;100:107668. doi: 10.1016/j.jmgm.2020.107668. [DOI] [PubMed] [Google Scholar]
- Ullah F. Ayub K. Mahmood T. Remarkable second and third order nonlinear optical properties of organometallic C6Li6− M3O electrides. New J. Chem. 2020;44:9822–9829. doi: 10.1039/D0NJ01670E. [DOI] [Google Scholar]
- Ayub K. Are phosphide nano-cages better than nitride nano-cages? A kinetic, thermodynamic and non-linear optical properties study of alkali metal encapsulated X 12 Y 12 nano-cages. J. Mater. Chem. C. 2016;4(46):10919–10934. doi: 10.1039/C6TC04456E. [DOI] [Google Scholar]
- Munsif S. et al., Remarkable nonlinear optical response of alkali metal doped aluminum phosphide and boron phosphide nanoclusters. J. Mol. Liq. 2018;271:51–64. doi: 10.1016/j.molliq.2018.08.121. [DOI] [Google Scholar]
- Ahsin A. Ayub K. Theoretical Investigation of Superalkali Clusters M2OCN and M2NCO (where M= Li, Na, K) as Excess Electron System with Significant Static and Dynamic Nonlinear optical response. Opt. 2020:166037. [Google Scholar]
- Ahsin A. Ayub K. Superalkali-based alkalides Li3O@[12-crown-4]M (where M= Li, Na, and K) with remarkable static and dynamic NLO properties; A DFT study. Mater. Sci. Semicond. Process. 2022;138:106254. doi: 10.1016/j.mssp.2021.106254. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.