A BRIEF VISIT FROM THE FIRST INTERSTELLAR ASTEROID REVEALS A RED EXTREMELY ELONGATED BODY

Abstract

Until recently, none of the ~750,000 known asteroids and comets were thought to have originated outside our solar system. Many decades of asteroid and comet characterization have yielded formation scenarios that explain the mass distribution, chemical abundances and planetary configuration of today’s solar system, but up until now there has been no way to tell if our solar system is typical. Solar system formation models suggest that orbital migration of the giant planets as they formed ejected a large fraction of the original planetesimals into interstellar space¹. The predicted interstellar number density² of icy interstellar objects of 2.4 × 10⁻⁴ au⁻³ suggested that these should have been detected by surveys, yet none had ever been seen. Here we report on the discovery and characterization of 1I/2017 U1 (‘Oumuamua), the first object known to originate outside our solar system. Follow-up observations and subsequent analysis verified the extrasolar trajectory of ‘Oumuamua. Our observations reveal the object to be asteroidal, with no hint of cometary activity despite an approach within 0.25 au of the Sun. Spectroscopic measurements show that the object’s surface is consistent with comets or organic-rich asteroid surfaces found in our own solar system. Light-curve observations of ‘Oumuamua indicate that the object has an extreme oblong shape, with a 10:1 axis ratio and a mean radius of 102±4 m assuming an albedo of 0.04. Very few objects in our solar system have such an extreme lightcurve. The discovery of ‘Oumuamua suggests that previous estimates of the density of interstellar objects were pessimistically low. Imminent upgrades to contemporary asteroid survey instruments and improved data processing techniques are likely to produce more interstellar objects in the upcoming years, creating opportunities to interrogate the mineralogical, elemental or isotopic composition of material from other solar systems.

On 2017 October 19 the Pan-STARRS1 telescope system detected an object moving rapidly west at 6.2 degrees per day (Figure 1A). A search of images from the previous nights found the object had also been imaged on October 18. Additional images acquired with the Canada-France-Hawaii Telescope (CFHT) on October 22 confirmed that this object is unique, with the highest known hyperbolic eccentricity of 1.188 ± 0.016³. Data obtained by our team and other researchers between October 14–30 refined its orbital eccentricity to 1.1956 ± 0.0006 which is at a level of precision that confirms the hyperbolic nature to > 100σ. Designated as 1I/2017 U1, this object is clearly from outside our solar system (Figure 2), and as such is the first detected interstellar object (ISO). Given its discovery and follow-up observations from multiple Hawai‘i observatories, 1I/2017 U1 has been named ‘Oumuamua, which in Hawaiian reflects the way this object is like a scout or messenger sent from the distant past to reach out to us.

Figure 1. ‘Oumuamua’s Asteroidal appearance.

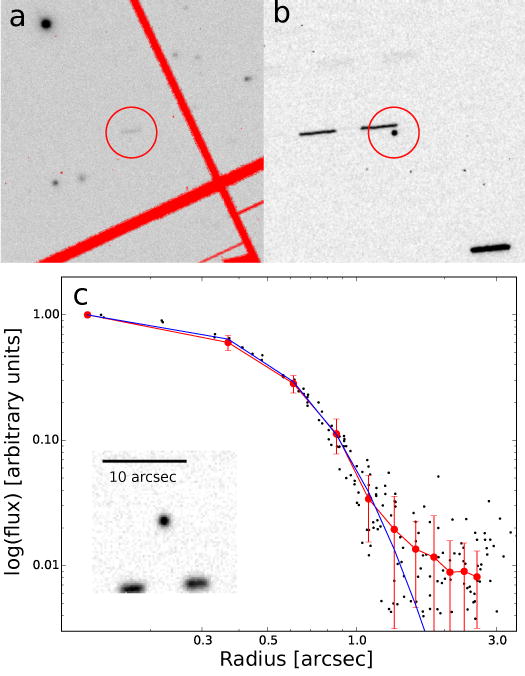
[a] Pan-STARRS1 discovery image of ‘Oumuamua on 2017 October 19. ‘Oumuamua is the faint trail centered in the circle. Red regions are masked pixels. [b] CFHT image obtained on October 22 showing no hint of coma. [c] Deep image combining Gemini and VLT g and r-band data. The black dots mark the flux in individual pixels. The red dots show the average flux in annuli at each radius (the error bars are the RMS dispersion) and the blue line is a Moffat profile with a FWHM of 0.87″. The difference between the two curves provides a very sensitive upper limit to any possible activity.

Figure 2. The path of ‘Oumuamua through our solar system in comparison to the orbit of a typical Halley-type comet.

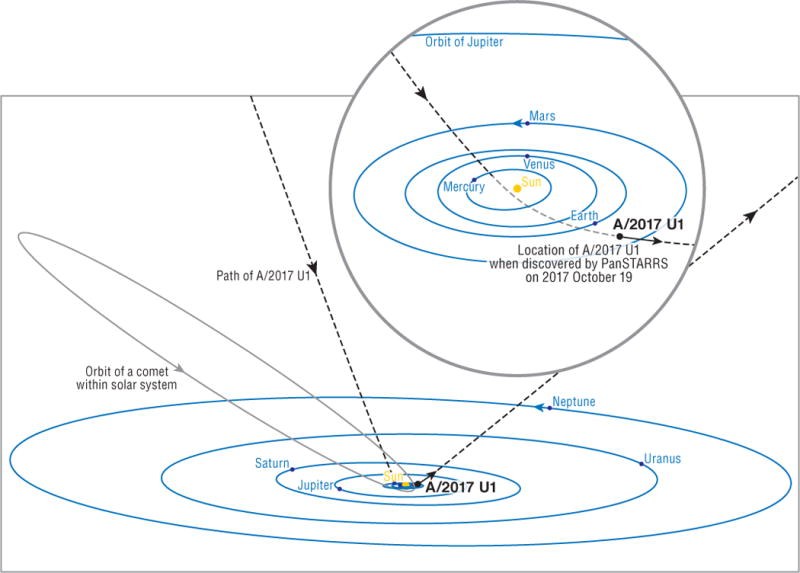
The inset shows the inner solar system, with the solid line segment along ‘Oumuamua’s trajectory indicating the short window of two weeks during which it was bright enough (median magnitude of lightcurve V~20-24) to be studied by large telescopes on Earth. The path is shown as a lighter shade when the object was below the ecliptic. Credit: Brooks Bays/SOEST Publication Services/UH Institute for Astronomy.

The October 22 CFHT observations were tracked at the object’s rate of motion and ‘Oumuamua’s point spread function was consistent with a stellar profile with no asymmetry and no coma, implying that it is asteroidal (Figure 1B). Additional time-resolved sequences of images at multiple wavelengths between October 25–27 UT with the European Southern Observatory Very Large Telescope and the Gemini South Telescope, further strengthened ‘Oumuamua’s asteroidal identification (Figure 1C). The upper limit for the dust coma brightness is g > 25.8 in the wings of the object’s point-spread function (1-2″ from the center), and g > 29.8 ± 0.05 mag/arcsec² at the 5σ level outside the point spread function (>5″ from the center). Using the upper limit to the light that could be scattered by dust we determined that less than 1.7×10⁻³ kg/s of dust could be released from the surface. This is 7-8 orders of magnitude less than a typical long-period comet would produce if there was near-surface water ice (see Methods).

An analysis of ‘Oumuamua’s lightcurve (Figure 3, see Methods) indicates its rotation period is ~7.34±0.06 hours under the customary assumption that the double-peaked lightcurve is dominated by the shape of the object. No other period gives a satisfactory re-phased lightcurve and the value is not unusual for objects of this size.

Figure 3. Lightcurve of ‘Oumuamua.

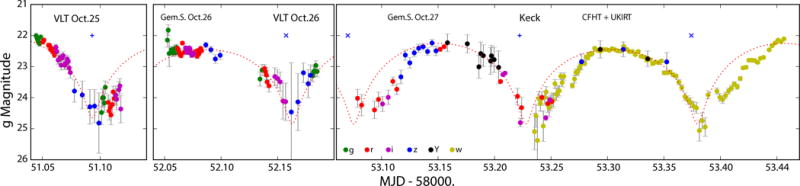
All the magnitudes have been scaled to g-band using the measured colors, and to the geometry of Oct. 25.0. Epochs are corrected for travel time for Oct. 25.0. The errorbars are the 1σ photometric errors. The dotted line corresponds to a 10:1:1 triaxial ellipsoid with a 20% hemispheric variation of albedo, rotating with a 7.34 hour period; the “+” and “X” identify the two minima of the double-peaked lightcurve.

‘Oumuamua’s median magnitude gives it an average radius of ~100 m assuming an albedo of 0.04, but the very large 2.5 magnitude lightcurve range implies that it is extremely elongated–with an axis ratio of at least 10:1 (see Methods) or that it has large albedo variations or both. ‘Oumuamua’s red surface color is consistent with the organic-rich surfaces of comets, D-type asteroids, and outer solar system small bodies (Figure 4). Its measured colors (g-r = 0.84 ± 0.05, g-i = 1.15 ± 0.10, g-z = 1.25 ± 0.10, g-Y = 1.60 ± 0.20), corresponding to a spectral slope of S_v = 23±3%/100nm), are consistent with uniform colors over the whole surface of the object (see Methods). This suggests that ‘Oumuamua’s reflectivity is indistinguishable from small bodies in our own solar system but the inferred shape is unique.

Figure 4.

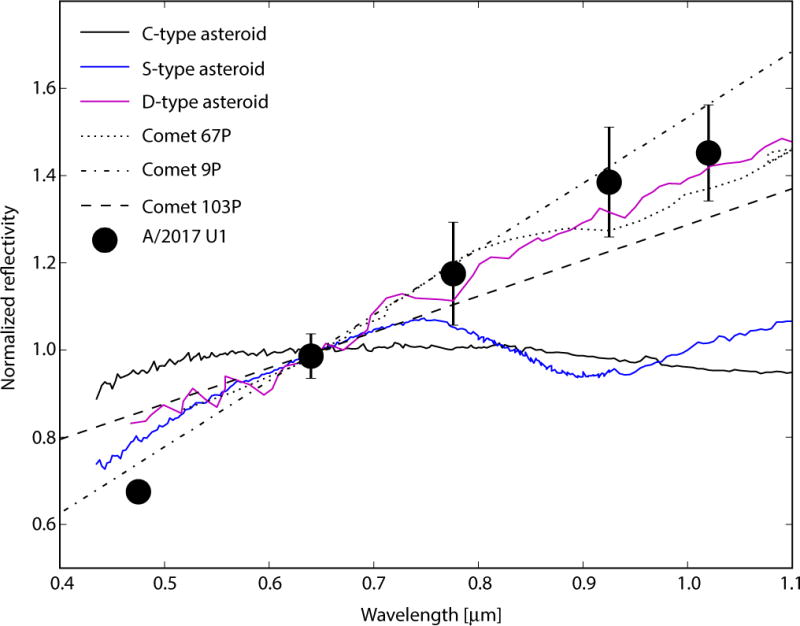
Reflectivity of the surface of ‘Oumuamua. ‘Oumuamua’s surface reflectivity is consistent with D-type asteroids¹² and comets. Data are normalized to 1.0 at 0.65 μm and the error bars reflect the 1-sigma standard deviation.

The highly elongated shape of ‘Oumuamua implied by its large lightcurve range is very unusual. If the object is cigar-shaped and rotating around its shortest axis, it must have at least some tensile strength (> few Pa, see Methods). An albedo p=0.04 results in an object 800×80×80 m across. The case of a contact or quasi-contact binary consisting of two elongated lobes can be rejected as it would require unrealistically high physical densities. Alternatively, if the object has no tensile strength, then the rotation axis must be the longest, and its density can be in the range of asteroids. As its rotation would be less stable, we consider the cigar morphology more likely. For comparison, strengthless triaxial ellipsoids have a maximum lightcurve amplitude of 0.9 mags⁴ but five known objects⁵ have maximum lightcurve ranges ≥ 2.2 mags and the 1.6 km diameter asteroid (1865) Cerberus has a 2.3 mag range⁵.

Since a kilometer-scale object can exhibit such a large lightcurve range it may be expected that smaller objects like ‘Oumuamua are more likely to have greater mechanical strength capable of sustaining a highly elongated shape. However, there are few objects of comparable size in our solar system with lightcurve ranges approaching that of ‘Oumuamua and it raises the question of why the first known ISO is so unusual.

It has been suggested⁶ there is a flux of very small (< 100 μm) interstellar meteoroids from the debris disk around β-Pictoris. Could ‘Oumuamua have similarly originated from a nearby debris disk? For ‘Oumuamua, the asymptotic radiant is toward right ascension 18^h42^m and declination +34.3° (± 5′), located near the current position of the Vega debris disk⁷ at 18^h 36^m +38.8°. However, the travel time to Earth from the distance of Vega is ~600,000 years accounting for Vega’s proper motion. Thus ‘Oumuamua is not likely to have been ejected from the Vega system. The outgoing asymptote is 23^h 52^m +24.8°.

Alternatively, a close encounter between a long period comet and a small undiscovered nearby planet⁸ could possibly perturb the smaller object onto a hyperbolic orbit. For such a planet to remain undiscovered for so long, it must be located near the Galactic Plane (which most NEO surveys avoid) and we note that ‘Oumuamua’s radiant has a galactic latitude of ~16°. It is also possible that a more distant, larger undiscovered planet in our own solar system could have perturbed ‘Oumuamua into an unbound orbit. The best estimate for the location of a distant ~10M_Earth planet is many hundreds of au from the Sun⁹, but the estimate of its orbital plane does not contain ‘Oumuamua’s radiant direction. Although we believe it unlikely that an undiscovered planet could have produced the motion of ‘Oumuamua, we cannot yet rule it out. A deep search for distant planets in the radiant direction of ‘Oumuamua would help to confirm or reject this possibility.

The heliocentric incoming velocity of ‘Oumuamua in right-handed Galactic coordinates is v_∞(U, V, W)=(−11.2, −22.4, −7.6) km s⁻¹. This is remarkably close to the mean motion of stars in the solar neighborhood¹², with an especially small deviation from the mean in U and W. Younger stars have smaller velocity dispersions than older systems, so this close proximity to the exact local mean velocity suggests an origin in a young stellar system, although the possibility that ‘Oumuamua has been orbiting the Galaxy for billions of year cannot be ruled out. This encounter has transformed ‘Oumuamua’s orbit from one that is particularly close to the local mean to one that is typically dispersed from the mean, hinting that this may be its first close approach to a star, and its first chance to lose volatiles.

The asteroidal nature of ‘Oumuamua is surprising given that the predicted ratio of cometary to asteroidal material in our solar system’s Oort cloud ranges from 200:1 to 10000:1 depending on the formation model for our planetary system¹⁰. Thus, we expected that most ISOs would be cometary assuming that this range of ratios is also applicable to objects that were ejected into interstellar space. Indeed, asteroidal objects on long period comet orbits in our own solar system have only recently been discovered¹⁰ and are known as Manx-type comets. A population of interstellar asteroids could arise from scattering events in their host system when major planets migrated through strong resonances and ejected objects with more mature processed inner solar system material than those in their Oort cloud. If the typical ISO is asteroid-like then the ISO number density could be much higher than contemporary limits^2,11 because models assume that cometary material is more likely ejected and cometary ISOs should be the easiest to detect because of selection effects.

The ‘Oumuamua discovery suggests there are likely additional ISOs in our solar system at any given time and raises the tantalizing prospect of many future ISO discoveries. These objects will enable the measurement of elemental abundances in other solar systems and test planetary formation theories. Calculating a formal interstellar influx number density and predicting their future discovery rate by existing and planned sky surveys from the single ‘Oumuamua discovery is beyond the scope of this work and would require a detailed simulation of the surveys’ ISO detection efficiency², which is complicated by regular improvements to the surveys’ operations. Indeed, it is likely that the ‘Oumuamua discovery was made possible by recent improvements to the Pan-STARRS1 detection pipeline which resulted in increased efficiency of finding trailed objects as some were incorrectly rejected as spurious detections. Our estimates suggest that there is always about one ISO of about 250 m diameter (assuming a 4% albedo) within 1 au of the Sun, that is, interior to Earth’s orbit (see Methods).

The discovery of an interstellar object adds a new component, albeit small, to the Earth impact risk: impact from an interstellar object would be far more energetic than from a solar system object with similar mass, due to the larger impact speed. Meteorites resulting from such an impact would show an age inconsistent with that of our solar system, of which no example is known to date.

Methods

Discovery and orbit determination

The October 19 detection of ‘Oumuamua by the Pan-STARRS1 telescope³ used four sidereally tracked w_P1-band images obtained in poor seeing conditions (with a stellar FWHM of 2.2″) during normal survey observations for near-Earth objects¹³. Two additional w_P1-band -band pre-discovery images from 2017 October 18 were then identified in images with stellar FWHMs of 1.8″ and 2.4″. It was not possible to detect low-level cometary activity in these images due to poor seeing and the object being trailed.

Both elliptical and parabolic heliocentric orbits gave atypically large fit residuals when additional astrometry beyond the original detections were included. Follow-up observations with the ESA Optical Ground Station also did not fit and were blocked by the Minor Planet Center (MPC) automated routines as suspected outliers. Our investigation revealed that this object could be explained using a hyperbolic orbit with a preliminary eccentricity of e ~ 1.13, the largest ever recorded (the next largest being comet Bowell at e = 1.057 due to a Jupiter encounter). ‘Oumuamua was first classified as an Aten-type object (semimajor axis, a = 0.74 au, e = 0.449, inclination, i=10°) when it was posted to the Near-Earth Object Confirmation Page (NEOCP). The Aten-type orbit induced a 5 arc minute error in its predicted location 24 hours later and increased to 34 arc minutes after 48 hours. It was later classified as a Halley-family comet when the Minor Planet Center revised the orbit to (a = 50 au, e = 0.997, i = 107°) after including the Catalina Sky Survey observations on October 20 and the ephemeris error for our pre-discovery observations decreased from 34 to 0.5 arc minutes. The object’s orbit was seen to be clearly hyperbolic after the arc was extended to October 22 by our CFHT observations. With additional Canada-France-Hawaii Telescope astrometry on 2017 October 22 UT (Figure 1B) the eccentricity was revised to e = 1.188 ± 0.016. With a total of 131 observations (eleven of which were rejected as outliers) ‘Oumuamua’s orbital eccentricity is now securely hyperbolic at the > 100 σ confidence level, having a barycentric eccentricity of e = 1.1929 ± 0.0006 (Extended Data Table 1). The two most significant planetary close approaches were with the Earth (0.16 au ~ 16 Hill radii) and Jupiter (4.82 au ~ 14 Hill radii) but even they are too distant to significantly perturb ‘Oumuamua during its approach towards the Sun (nevertheless, the corresponding perturbations have all been modeled in the discussion presented here).

Survey strategy improvements

Many objects that are first detected moving as fast as ‘Oumuamua are lost if they are not immediately targeted for more observations. The ISO discovery rate could be improved by increasing the survey depth, sky coverage rate, and search strategies (see Methods). The surveys could also self followup¹⁴ but this would reduce the NEO discovery rate from which the surveys derive their funding. The ISO detection rate may also be improved with enhanced source detection algorithms for trailed and/or non-stellar sources in images. One reason for the inefficiency in detecting ISOs is because of a biased search strategy. ISOs with high rates of motion may have posted to the Near Earth Object Confirmation Page (NEOCP) but recovery efforts would have targeted incorrect predicted positions assuming they are small, nearby, and with elliptical orbits. In general, one night after discovery an ISO would be located to the west of the predicted position of an NEO with similar motion, and outside the region that is assumed as a realistic uncertainty for regular elliptical orbits. In ‘Oumuamua’s case the geometry was such that some elliptical solutions overlapped with the true hyperbolic solution and its predicted location on the sky was therefore serendipitously imaged in follow-up observations.

Complicating the ISO discovery rate even more, two-thirds of ISOs that display cometary activity would not rank high enough to post to the NEOCP upon discovery based only upon their apparent rates of motion². Instead, the detections would have to be identified as unusual (cometary) based on their non-stellar point-spread function and then subsequent targeted follow-up observations would allow their identification as ISOs.

Discovery and characterization observations

Pan-STARRS1

The Panoramic Survey Telescope and Rapid Response System¹⁵) is a 1.8 m diameter wide field astronomical imaging and data processing facility, having a 3° field of view with 0.25″ pixels. The data are processed to remove instrumental artifacts, and most objects are automatically detected and photometrically and astrometrically calibrated^16,17,14. Fast moving objects that leave trails on the image, like ‘Oumuamua, must be remeasured before submission to the MPC.

Canada-France-Hawaii Telescope, CFHT

Observations taken with the 3.6 m diameter CFHT used the MegaCam wide-field imager, an array of forty 2048×4612 pixel CCDs with a plate scale of 0.187″ per pixel and a 1.1 square degree FOV. The data were obtained using queue service observing and processed to remove the instrumental signature through the Elixir pipeline¹⁸. Three 60-second exposures were obtained on 2017 October 22 UT using a wide gri-band filter with the full width half maximum (FWHM) of 0.5″ seeing. The exposures were tracked at the predicted motion of the object and obtained in excellent conditions (Fig. 1b). The immediate area surrounding the object was searched for faint companions with similar motion but none were found.`Oumuamua was at a heliocentric distance of 1.22 au, just 43 days past 0.25 au perihelion on September 09. A series of MegaCam observations were also obtained on 2017 October 27 UT using the wide gri-band filter to obtain a light curve. Integration times were initially 70 seconds but were increased to 180 seconds to improve the signal to noise ratio. The weather during the period October 23–26 on Maunakea was poor and no observations could be obtained.

Gemini South Telescope

We were awarded 3.5 h of Director’s Discretionary (DD) time for rapid observations of ‘Oumuamua using the 8 m Gemini South telescope. Data were obtained using the Gemini Multi-Object Spectrograph (GMOS) in imaging mode that uses three 2048×4176 Hamamatsu chips. The data were obtained through Sloan Digital Sky Survey (SDSS) filters using queue service observing. The detector was read out with pixels binned 2×2 with slow read (read noise=3.98 e⁻) and low gain (1.83 e⁻/ADU). Exposures were kept to 30 s to minimize trailing.

Very Large Telescope, VLT

Observations were performed at the ESO 8.2 m diameter VLT UT1 on Paranal, Chile, using DD time, tracking the object with short exposures (30 s) to minimize trailing of the stars. We used the FORS2¹⁹ instrument and the g-HIGH+115, R-SPECIAL+76, I-BESS+77, and z-Gunn+78 filters with the “red” CCD, a 2k×4k MIT detector. The pixels were read-binned 2×2 resulting in an image scale of 0.25″/pix.

United Kingdom Infrared Telescope, UKIRT

The data were taken using the 3.8 m diameter UKIRT in 30 s frames while tracking non-sidereally according to the ‘Oumuamua ephemeris. Alternating blocks in z and Y bands were de-trended, registered, and stacked manually. The magnitudes are calibrated in the SDSS (z) and UKIDSS (Y) systems.

Keck 2 Telescope

Observations were performed on Keck 2 10-m telescope using DEIMOS (DEep Imaging Multi-Object Spectrograph) in imaging mode. DEIMOS has a 2×4 array of 2k×4k MIT/Lincoln Labs CCDs to cover the full spectra range. In imaging mode, four of these detectors are illuminated by the sky with a plate scale of 0.1185″ per 15 μm pixel. The object was observed with CCD #6 using non-sidereal guiding or tracking. Image quality during these observations was 1.5″ (FWHM). A total of 18 exposures were obtained of the object using Johnson B, R, I filters with 100 second exposures. Guiding failed during two of these exposures; of the remaining 16 exposures the object was not detected in the two B-band images, nor in 5 of the images near the minimum of the light curve. Because of substantial residual background variations in the images, photometry was measured for the object using a 1.8″ diameter aperture, corrected to the standard 4″ aperture using bright stars in a sidereal-tracked image in the same period. Zero points and color corrections were measured to transform the photometry to SDSS magnitudes in r and i-bands using stars from the PS1 3π survey^{15, 16}, assuming a color of r – i = 0.3.

Visual-band CCD data reduction

We reduced all visual-band CCD data using custom code for bias subtraction and flat-fielding to establish a uniform detector response. We use the Terapix/Astromatic tools²⁰ to fit world coordinates (RA and Dec) using reference stars from the SDSS and 2MASS catalogs. We used expanded SExtractor²⁰ automatic apertures to measure the magnitudes of trailed stars and computed a photometric zero point for each image using stars from the PS1 database¹⁶ 3π survey¹⁵ or the Sloan Digital Sky survey²¹. The final griz magnitudes are in the SDSS system, and the Y magnitudes in the UKIDSS system. Finally, we measured ‘Oumuamua’s apparent magnitude by summing the flux inside a 4″ diameter aperture placed at the adjusted ephemeris location and correcting for the zero point.

Solving for the rotation period and colors

The lightcurve data were first corrected for the observing geometry to normalize the heliocentric and geocentric distances to those of October 25.0 and preliminary color corrections were applied to all the data points. An initial rotation period was then determined using the Phase Dispersion Minimization (PDM) technique²². Then the color indexes (g – r, g – i, g – z, g – Y) were included in the PDM to minimize the dispersion between the lightcurve segments to obtain the final period and colors.

We estimated the uncertainty on the period and colors by individually “scanning” through each value. The phased lightcurve for the values at the limit of the interval of confidence were also visually checked to be “almost but not quite as good” as the best fit. Rotation periods were scanned in the range from 2 to 20~h to ensure that no other period could reproduce the observations. In particular, the half-period of ~3.65 h fails to produce a satisfactory single-peaked phased curve (which would be difficult to explain physically). A period of 11.0 h is marginally acceptable with the PDM metric but produces a 3-peaked lightcurve.

Shape and size

The light curve of a triaxial ellipsoid²³ with axis ratio a > b > c was fit to ‘Oumuamua’s lightcurve. As the geometry of the rotation axis is unknown, the aspect angle (between the line-of-sight and the rotation axis) was set to the most probable value of 90°, and results in a lower limit on the elongation. Asteroids usually rotate on their shortest axis, c, for stability. The fit yields an axis ratio of 10:1:c with large uncertainties on a = 10±1 (dominated by the noise of the faintest points, see Figure 3). The value of c is not directly constrained by the lightcurve. We accounted for a small asymmetry between the lightcurve maxima with a periodic signal of 0.2 mag amplitude intended to represent a hemispherical relative albedo variation of 20%. Since the albedo and geometric cross-section are degenerate this interpretation is not strong. The resulting model is not unique but is useful to guide the eye. It is clear that ‘Oumuamua’s lightcurve has systematic deviations with respect to the fit ellipsoid and these likely correspond to large areas where the object is flat or concave (flat and concave cannot be distinguished by the lightcurve as as they produce the same cross-section). A roughly spherical object would require extreme variations of albedo to reproduce the range and sharp minima of the lightcurve but this is unlikely based on our current understanding of the surfaces of most asteroids in our solar system and the absence of any sign of volatiles.

The brightest g = 22.15 and faintest g = 24.65 lightcurve values show a range of 2.5 magnitudes which implies a 10:1 axis ratio for 2 sides of the ellipsoid. The median g magnitude can be converted to an absolute magnitude of H_V = 22.4 (in the H-G asteroid photometric system) after accounting for ‘Oumuamua’s colors. Using a cometary albedo of p = 0.04 yields an effective radius of 102 ± 4 m (the uncertainties are based only on the magnitude uncertainties). Kuiper belt objects show a range of albedos (0.04–0.28) and higher albedos are associated with icy objects²⁴. ‘Oumuamua is not icy and billions of years of irradiation by galactic cosmic rays and ionizing radiation should darken its surface, thus we assume that the surface has a low albedo. It is meaningless to directly convert the brightest and faintest magnitudes into linear dimensions because a/c is not directly constrained by the lightcurve.

The c axis can however be constrained together with the density of the object ρ and its albedo p, so that the πpac and πpbc cross-sections match the lightcurve maximum and minimum, and the gravity at the tip of the a radius matches the centrifugal force. An additional constraint comes from the fact that the rotation must take place along the shortest axis, so a > b > c, or possibly along the longest axis, with c > a > b (rotation along the intermediate axis is not stable). The densities corresponding to a strengthless short-axis rotator are un-physically high (>20,000 kg/m³). This suggests that a cigar-shaped short-axis rotator must have some internal tensile strength. This also rules-out a binary or close binary. To estimate this strength, the centrifugal force and gravitation force were estimated cutting the object in two parts along its long axis. Scanning density values in the 500–10,000 kg/m³ range leads to a very moderate minimum required strength of 3 Pa. With b = c and an albedo p = 0.2, this results in radii 180 × 18 × 18 m, and 400 × 40 × 40 m with p = 0.04.

Alternatively, a long-axis rotator can be held by gravity for densities > 1500 kg/m³, and resulting in physical radii of the order of a × b × c = 40 × 4 × 80 m for an asteroid-like albedo p = 0.2 and 90 × 9 × 180 m for a dark albedo p = 0.04. Both the density and the c axis are lower limits.

Assessment of lack of activity

In order to reach the faintest possible surface-brightness, a stack of the g and r images from Gemini and VLT was produced, totaling 1920 s exposure time. By coincidence, the photometric zero points of these two filters are virtually equal, with ZPg = ZPr = 27.98 (for adu/s/pix). The profile of the object was estimated by averaging its flux in annuli. A Moffat function²⁵ was adjusted to an average profile, resulting in α = 1.1″ that corresponds to a FWHM of 0.87″. The individual pixels and profiles are displayed in Fig. 1. The Moffat profile represents the object’s profile well out to ~2″, where the sky noise dominates. We assume that all the flux difference between the object profile and the Moffat profile corresponds to a coma; this gives g_coma = 25.8 for the ring between 1 and 2″ (to be compared to g_`Oumuamua = 22.5). This magnitude can be converted into a total diffusing area of dust grains. Assuming an albedo of 0.04/0.2, a bulk density of 1,000 or 3,000 kg/m³ (typical values for fluffy and compact cometary grain densities seen from the Rosetta mission²⁵), and a grain radius a = 1 μm, up to 0.5/0.3 kg of dust could be present around in the direct vicinity of the object.

At larger radii from the object, any (not visible) coma would be fainter than the noise background, which is N = 0.147 ± 0.005 adu/s/pix in 0.25″ pixels. The 3σ (5σ) limits correspond to surface brightnesses of g = r =30.4 (29.8) ± 0.05 mag arcsec⁻². Using the same assumptions as above, up to 13/8 g (8/4 g), at the 3σ (5σ) level of comet/asteroidal dust per pixel could be present. In the 2-2.5″ annulus (covering ~100 pixels), this could represent up to 1 kg.

Most LPCs were originally scattered into the Oort cloud during our solar system’s formation and the comets we see now are being dislodged from the Oort cloud and returned to the solar system after ~4.6 Gyr of exposure to an interstellar environment, yet most are active objects and are expected to be active for thousands of perihelion passages. Given that LPCs retain their volatiles over Gyr time scales and the fact that ‘Oumuamua has been at the temperatures of interstellar space for a long time, any ice should have survived for billions of years. However, since no similar sized inactive objects on LPC orbits have been discovered in our own solar system, and Manx-type comets are rare, it is difficult to reconcile ‘Oumuamua’s lack of volatiles with our current understanding of LPC formation and composition. Computing a water ice thermal sublimation model²⁶ shows that the maximum dust production for 1 μm grains that can be sustained and remain below the coma detection limits above is 1.668 10⁻³ kg/s (assuming a dust to gas ratio of 1), which corresponds to the order of a few kg within the aperture and in agreement with the previous estimate.

Estimating the interstellar object number density

We estimate the ISO number density (ρ_IS), i.e. the spatial number density of ISOs far from the influence of any stars, by scaling from earlier upper confidence limits². They calculated a 90% upper confidence limit on ρ_IS = 2.4 10⁻² au⁻³ for inactive (asteroidal) objects with H < 19 assuming an albedo p_V = 0.04 typical of cometary nuclei (corresponding roughly to objects with diameters > 0.5 km diameter). Their limit was based on the lack of discovery of any ISOs during ~18 integrated years of surveying using the Pan-STARRS1¹⁵ and Catalina Sky Surveys²⁷. Those surveys subsequently acquired another ~12 years of data, so we normalize the survey time based on the discovery rate of H < 22 NEOs¹ during and subsequent to the original time period. Due to surveying, hardware, and software improvements, the surveys have since discovered roughly 1930 NEOs with H < 22 compared to about 1740 objects during the original study. We extrapolate from the H < 19 (> 0.5 km diameter) size to H < 22 using the size-frequency distribution (SFD) for a self-similar collisional cascade²⁸ of N(<H) ∝ 10^0.5H as this SFD is broadly representative of most small body populations in the solar system in this size range²⁹. Finally, we account for the decreased survey depth (geocentric distance) for objects with H = 19 and H = 22 because the Pan-STARRS1 system with a V-band limiting magnitude¹⁴ of ~21.7 can detect objects of these absolute magnitudes out to geocentric distances of ~1.4 au and ~0.55 au respectively. Assuming that most ISOs are inactive, asteroid-like, objects similar to ‘Oumuamua, the interstellar ISO number density of ρ_IS (H < 19) ~ 0.003 au⁻³ is close to earlier upper confidence limits². Scaling down in size to H = 22, comparable to ‘Oumuamua, and accounting for the 3× density enhancement due to the Sun’s gravity², suggests that there is always about one ISO with H < 22 (about 250 m diameter assuming pV = 0.04) closer to the Sun than 1 au. i.e. interior to Earth’s orbit.

Code availability

Software used to perform DEIMOS photometry is available from http://svn.pan-starrs.ifa.hawaii.edu/trac/ipp/browser. The UKIRT data were detrended by the standard WFCAM data processing pipeline. We have opted not to make the custom calibration and photometry software used to reduce imaging data from the VLT, Gemini and CFHT available because the components relevant to this work cannot be readily isolated. Various short, custom scripts were developed for the analysis; they are available on request. We have also opted not to make the sublimation model software available because it is being upgraded and will may become part of work for a graduate thesis.

Data availability

The Gemini GMOS and ESO FORS2 raw data will be available in the Gemini and ESO archives respectively after the expiration of the proprietary period. CFHT raw and reduced images are available on request. The raw UKIRT data will become available from the UKIRT archive, reduced data is available upon request. DEIMOS raw images are available on request.

Extended Data

Extended Data Table 1.

Orbital elements of ‘Oumuamua based on observations collected between 2017 October 14–30.

Element	Heliocentric	Barycentric†
υ∞ (km/s)	–	26.15 ± 0.05
q (au)	0.25383 ± 0.00023	0.25066 ± 0.00023
e	1.1956 ± 0.0006	1.1929 ± 0.0006
i (deg)	122.545 ± 0.021	122.592 ± 0.021
Ω (deg)	24.6056 ± 0.0009	24.2570 ± 0.0009
ω (deg)	241.43 ± 0.04	241.44 ±0.04
T	2017-09-09.461 ±0.004	2017-09-09.091 ±0.004
Epoch	2017-09-09.0	1838-01-01.0

^†The barycentric elements account for periodic terms connected with the motion of the Sun around the barycenter. The elements were integrated backwards in time until the object was 1000 au from the Sun to remove any possible effects from close encounters during the incoming trajectory. The time-of-passage at pericenter (T) should be interpreted as peribarion in this case. The elements were computed using the software Find_Orb by Bill Gray.