Violations. How Nature Circumvents the Woodward–Hoffmann Rules and Promotes the Forbidden Conrotatory 4n + 2 Electron Electrocyclization of Prinzbach’s Vinylogous Sesquifulvalene

Abstract

Woodward and Hoffmann, in their treatise on orbital symmetry in 1969, stated “Violations. There are none!” Prinzbach reported in 1978 that the electrocyclization of vinylogous sesquifulvalene occurs exclusively through the Woodward–Hoffmann orbital-symmetry-forbidden 14π-electron conrotatory pathway, despite the availability of a variety of orbital-symmetry-allowed processes. Prinzbach later demonstrated that an 18π-electron homologue exhibits the same forbidden behavior. And yet, the analogous vinylogous pentafulvalene and heptafulvalene both follow the orbital symmetry rules, each proceeding through its allowed conrotatory 12π and 16π process, respectively. We report the investigation of these reactions with ωB97X-D DFT. The physical origins of the flagrant Prinzbach violations of the Woodward–Hoffmann orbital symmetry selection rules have now been elucidated by these calculations in conjunction with extensive analyses and comparisons to electrocyclizations that obey the Woodward–Hoffmann rules. This remarkable reversal of the Rules (the 14π-electron-forbidden process is found to be 11 kcal/mol more energetically facile than the allowed process) occurs due to the high degree of polarization of this hydrocarbon, such that conrotatory electrocyclization of vinylogous sesquifulvalene behaves like a cyclopentadienide combining with a tropylium. These results are compared to other forbidden pericyclic processes driven by steric constraints and strain release or by diradical character of the reactants that facilitates the formation of diradical transition states for symmetry-forbidden reactions. We predict how strong donor–acceptor substitution can modify nodal properties to level the difference between allowed and forbidden electrocyclic reaction barriers, and we provide computational predictions of two such cases.

Graphical Abstract

■ INTRODUCTION

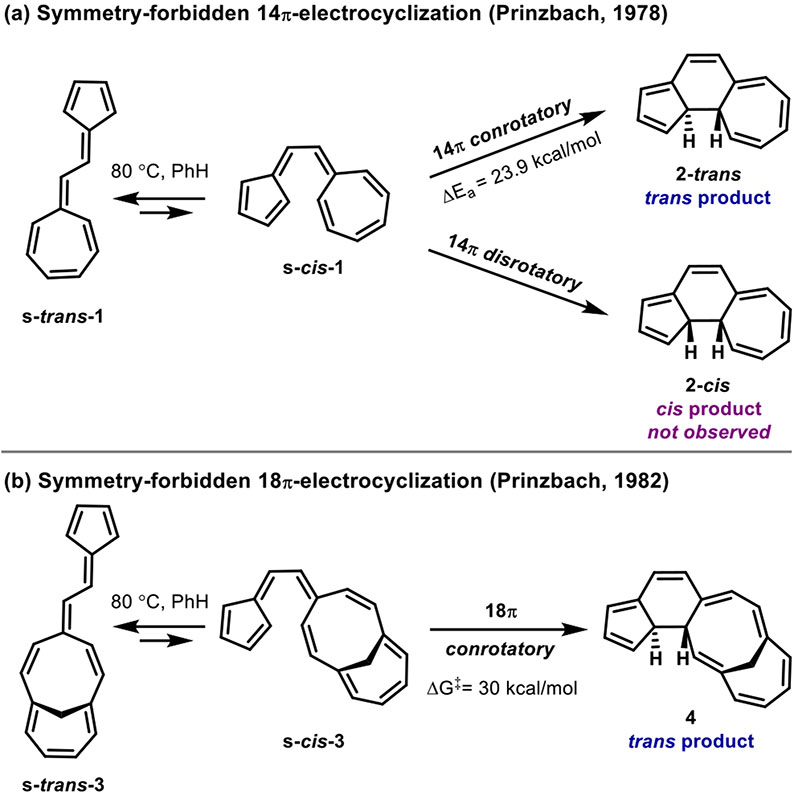
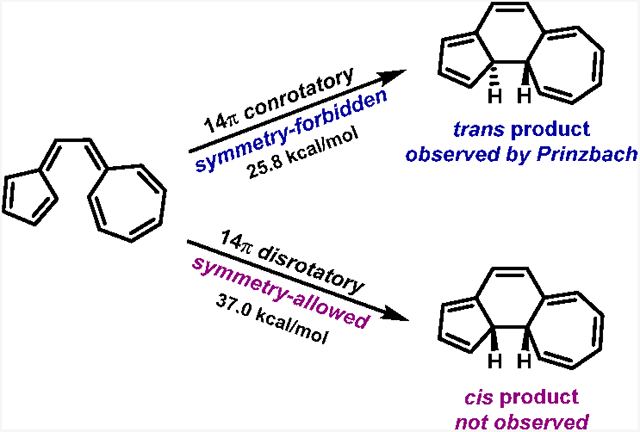
The electrocyclization of vinylogous sesquifulvalene was investigated experimentally by Prinzbach and co-workers in 1978 (Figure 1a)^1,2 For this 14π electrocyclization, Prinzbach and co-workers observed that the symmetry-forbidden conrotatory pathway occurred “almost certainly exclusively” to form the trans product (2-trans).³ The cis product (2-cis) that would be formed from a symmetry-allowed disrotatory pathway was not observed. Similarly, in 1982, Prinzbach and co-workers reported that a related system containing a hendecafulvene linked to a fulvene undergoes a symmetry-forbidden conrotatory 18π electrocyclization (Figure 1b).⁴ These results are in violation of the outcome that would be expected from the Woodward–Hoffmann rules.^5,6 Perhaps the most famous quote in the history of orbital symmetry—“Violations. There are none!”—from the Woodward and Hoffmann review of their work on the conservation of orbital symmetry emphasizes the generality of these rules and the expectation that only very special circumstances could cause deviations.⁶ Nevertheless, the blatant violations reported by Prinzbach have received remarkably little attention and no explanation.

Figure 1.

Symmetry-forbidden conrotatory electrocyclizations of (a) 14π vinylogous sesquifulvalene and (b) the related 18π fulvene–hendecafulvene system reported by Prinzbach. Reactions were performed in benzene. Energetics were measure by Prinzbach.^1,2

In an electrocyclization reaction, the termini must rotate away from a nearly planar arrangement of the conjugated π system to allow the p orbitals at the termini to overlap and form a σ bond between the terminal carbons. This rotation may occur in the same direction (conrotatory) or in the opposite direction (disrotatory). Rotations that cause the terminal p orbitals of the HOMO to overlap in-phase lead to a symmetry-allowed reaction according to the Woodward–Hoffmann rules.^5,6. Those in which the terminal orbitals of the HOMO overlap out-of-phase are called symmetry-forbidden. Allowed electrocyclizations are conrotatory for 4n π-electron systems and disrotatory for 4n + 2 π-electron electrocyclizations. On page 174, Woodward and Hoffmann state that “A very powerful Maxwell demon… He could seize a molecule of cyclobutene at its methylene groups, and tear it open in a disrotatory fashion to obtain butadiene. But without such demoniac intervention, molecules will very rarely comport themselves in like fashion.”⁶ The 4π–electron butadiene—cyclobutene interconversion of various derivatives serve as a testament to this: several experimental results show an activation energy that is 15 kcal/mol lower for allowed conrotatory versus forbidden disrotatory electrocyclization in these derivatives.⁷

We have investigated the Prinzbach exceptions to the Woodward–Hoffmann rules with modern computational methods. We begin this report with a brief review of previous, well-documented exceptions to the Rules, then explore the Prinzbach sesquifulvalene system with a variety of theoretical methods, and compare these results to those obtained for electrocyclizations that do follow the Rules. Finally, we propose an explanation of why these systems violate the Rules and predict other examples that should violate them as well.

■ PREVIOUSLY REPORTED VIOLATIONS

Although exceptions to the Woodward–Hoffmann rules are rare, some examples have been reported in the literature. Symmetry-forbidden electrocyclizations have been reported in constrained ring systems where a conrotatory ring-opening is not possible, as in Dewar benzene ring-opening to benzene; the 4π-electron system should undergo a conrotatory opening, but that would form a trans-benzene, which is impossibly strained.⁸ Similarly, geometrically constrained cyclobutenes^9,10 or cyclopropyl anions^11,12 fused to small rings have been shown to undergo symmetry-forbidden disrotatory ring-openings. Such systems have high transition state barriers and are highly exergonic, but they undergo forbidden disrotatory electrocyclizations (slowly) because there is no other option.

In addition to those reactions described above, examples that are more relevant to the systems reported by Prinzbach are shown in Figure 2. The pleiadene system, 5, studied by Michl et al. undergoes the forbidden disrotatory pathway to 6 with a barrier more characteristic of allowed reactions (21.3 kcal/mol).^13,14 In this reaction, 5 has significant diradical character and can easily achieve the forbidden diradical transition state.¹⁴ The ground state mixes with and is stabilized by the doubly excited reactant configuration to stabilize the diradical transition state.

Figure 2.

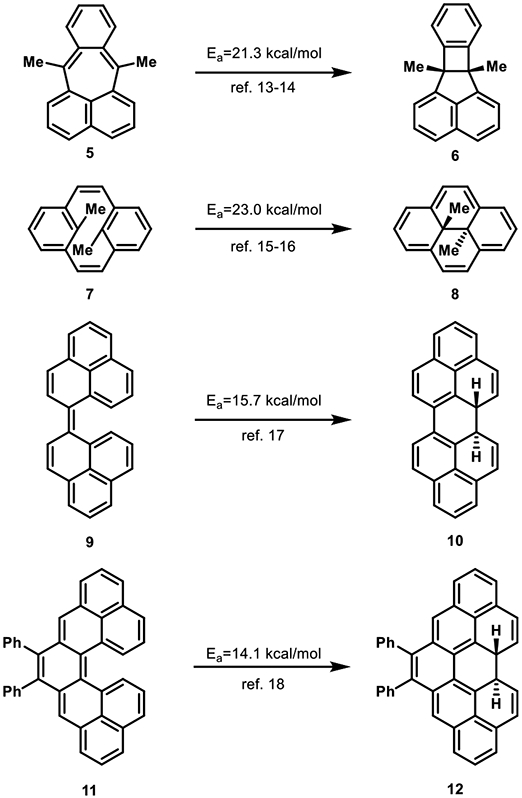
Experimental activation energies for energetically preferred, symmetry-forbidden electrocyclizations.

The second example in Figure 2 involves a relatively facile thermal conversion of 7 to trans-15,16-dimethyldihydropyrene (8) by a forbidden 6π-electron conrotatory electrocyclization, with a transition state barrier of only 23.0 kcal/mol.^15,16 Here, structural strain prevents disrotatory electrocyclization, but the forbidden reaction is energetically facile.

The biphenalenylidene system, 9, also undergoes a forbidden conrotatory 6π-electron electrocyclization with a low experimental barrier of 15.7 kcal/mol. Kubo et al. explored this process experimentally and theoretically and proposed that the allowed reaction gives a highly distorted transition state and product.¹⁷ The allowed disrotatory process was computed to have a barrier of 30.8 kcal/mol, while the forbidden conrotatory process has a computed activation energy of only 22.6 kcal/mol. Kubo et al. attributed this to the diradical character of the ground state of 9.

Juríček et al. studied the diphenylcethrene system, 11, experimentally and the parent cethrene system computationally.¹⁸ Experimentally, the forbidden conrotatory cyclization activation energy for 11 is only 14.1 kcal/mol. With a variety of density functionals, the forbidden conrotatory cyclization of cethrene was calculated to be significantly easier than the allowed disrotatory cyclization: the forbidden reaction has an activation barrier of >18 kcal/mol, whereas that of the allowed is >27 kcal/mol. Juríček et al. suggested that the forbidden reaction is facilitated by mixing of the ground with the doubly excited state at the transition state, and the allowed process is disfavored due to steric distortions in its transition state.

Rzepa reported an interesting 10π-electron “double-twist Möbius aromatic” transition state which is formally conrotatory at the bond-forming position but allowed in terms of transition state aromaticity.¹⁹ Mauksch and Tsogoeva pointed out that the common use of Möbius to describe conrotatory processes is different from “genuine Möbius topology” where both faces of the π system may overlap without a node throughout the conjugated cycle. These authors conceive and calculate the 12π-electron electrocyclization of a “true Möbius aromatic transition state” that is Hückel aromatic and only formally violates the Woodward–Hoffmann Rules.^20,21

■ COMPUTATIONAL METHODS

Computations were performed with Gaussian 16.²² Reactant and transition-state geometries were optimized in the gas phase by using the ωB97X-D²³ functional and 6-31G(d) basis set.²⁴ Frequency analyses were performed at the same level of theory as that used for geometry optimizations to characterize the stationary points as either minima (no imaginary frequencies) or saddle points (one imaginary frequency) on the potential energy surface and to obtain thermal corrections for Gibbs free energies and enthalpies. Single point energies were calculated with the ωB97X-D functional and the 6-311++G(d,p) basis set. Molecular structures were visualized by using PyMol.²⁵

■ RESULTS AND DISCUSSION

Hexatriene and Stilbene.

The energetic difference between allowed disrotatory versus forbidden conrotatory electrocyclization in the 6π-electron hexatriene system has been established, and the allowed reaction has invariably been observed.^26-29 We calculate that the symmetry-allowed disrotatory 6π electrocyclization of cis-hexatriene is 15.1 kcal/mol below the forbidden conrotatory reaction, calculated with an unrestricted, broken-symmetry wave function (Figure 3a). This system follows orbital symmetry predictions, even though the boat-like TS-1b is obviously destabilized by H─H interactions. The all-cis conformation of hexatriene has a NICS(0) value of 2.1 (nonaromatic), the allowed disrotatory TS is aromatic (NICS(0) = −13.9), and the forbidden conrotatory TS is antiaromatic (NICS(0) = 19.5).

Figure 3.

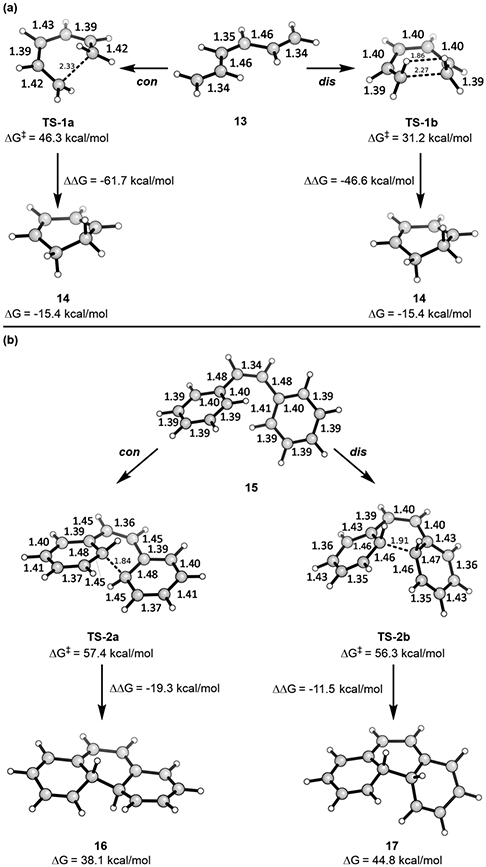
Bond lengths and free energies of the transition states of (a) cis-hexatriene (con TS is open-shell) and (b) cis-stilbene (con TS is open-shell).

cis-Stilbene (15) is another related system, a 14π-electron “alternant” analogue to Prinzbach’s “nonalternant” system, possessing two phenyls instead of a cyclopentadiene and a cycloheptatriene. This system is known to readily undergo photochemical allowed conrotatory electrocyclization and to then revert to cis-stilbene via a thermally forbidden electrocyclic opening. We have computed the conrotatory and disrotatory transition states for the thermal reactions, which are shown in Figure 3b. The forbidden con TS is an open-shell singlet. In this reaction, the difference between the allowed and forbidden pathways is remarkably small. TS-2a, leading to the forbidden conrotatory product, is a chair transition state, which has been shown to be lower in energy than the corresponding boat transition state in reactions like the Cope rearrangement.³⁰ Conversely, TS-2b is a boat. The forbidden transition state is similar to the reaction of two benzenes to form dicyclohexadienyl, which has previously been calculated by using semiempirical methods.³¹ Note that in TS-2a the double bond linking the two phenyls is nearly a normal double bond, indicating that it does not participate in the TS in a significant way.

The high transition state barrier for the allowed pathway (56.3 kcal/mol) is due in part to the high energy of the product 17, which is related to its boatlike character. Figure 3 also shows the energies of the ring-opening reactions. The conrotatory retrocyclization barrier to form cis-stilbene from 16 has been measured to be E_a = 17.5 kcal/mol,³² which is close to our calculated barrier of ΔH^‡ = 19.8 kcal/mol. Unsurprisingly, the allowed disrotatory ring-opening of 17 was calculated to go through an 8 kcal/mol lower barrier of ΔH^‡ = 11.4 kcal/mol.

In Figure 4, we show typical orbital correlation diagrams for allowed and forbidden reactions.⁵ In allowed reactions, all the occupied orbitals of the reactant smoothly correlate with those of the product. In forbidden reactions, one of the occupied orbitals of the reactant, usually the HOMO, correlates with a vacant orbital, usually the LUMO. When the HOMO and LUMO cross along the reaction path, a diradical state is formed that allows correlation of the electronic structure of the ground state of the reactant with that of the product, but at the expense of a relatively higher (“forbidden”) activation energy. The activation energy is often around 15 kcal/mol above that of the allowed process, as seen in hexatriene, above, but it is not so large in cis-stilbene, where the diradical state of the forbidden TS is only 1 kcal/mol above the allowed TS. Woodward and Hoffmann stated that “The essential and decisive factor in making a reaction forbidden is that in the transition state there is at least one level [orbital] that is no longer bonding…” As shown in Figure 2, this can be avoided in formally forbidden reactions by stabilization. Open-shell UDFT calculations, or CASSCF calculations, are generally required to compute forbidden pathways. However, as shown below, we had no difficulty computing the forbidden pathway for the vinylogous sesquifulvalene system using closed-shell, single-Slater methods, and we confirmed that these methods are sufficient to accurately model our system.

Figure 4.

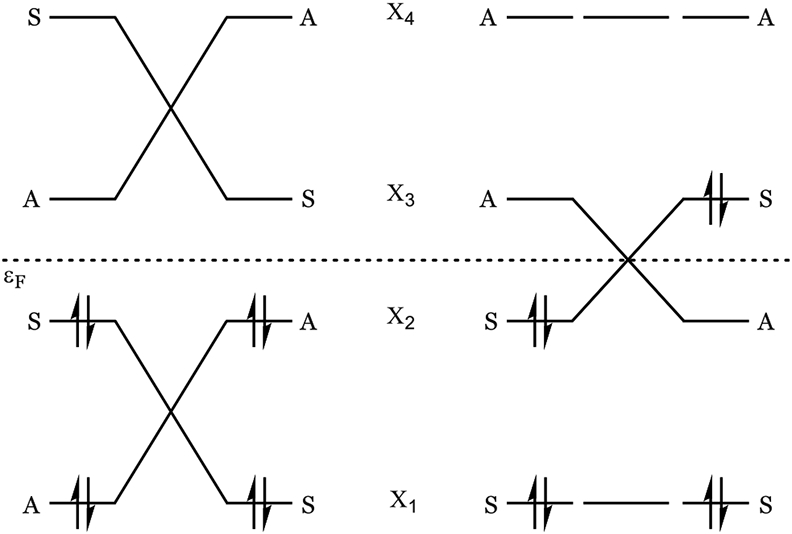
Typical correlation diagrams for allowed (left) and forbidden (right) reactions. In the forbidden reactions, the crossing of HOMO and LUMO results in a diradical state (one electron in each of two degenerate orbitals).

Comparison to Biphenalenylidene and Cethrene Forbidden Reaction Pathways.

The intrinsically diradical character of forbidden transition states makes it such that they usually must be computed as open-shell systems. For this reason, we were hesitant to base our analysis on single configuration DFT calculations. To provide further validation of our calculations on a forbidden transition state, we studied the allowed, but disfavored, and forbidden, but preferred, reactions of cethrene, introduced in Figure 2. The results are shown in Table 1.

Table 1.

Energy Barriers for the Electrocyclization of Cethrene and Biphenalenylidene^a

structure	ΔH‡	ΔG‡	ΔEa (expt)
cethrene: dis TS	26.1	27.0	unknown
cethrene: con TS	17.4	18.7	14.1
biphenalenylidene: con TS	14.1	15.1	15.7

^aAll transition states listed have open-shell wave functions except for the cethrene dis TS.

The computed barriers for the electrocyclization of cethrene and biphenalenylidene using our single configuration DFT methods are in good agreement with those established by prior CASSCF calculations and experiment.^17,18 Using open-shell calculations, we computed a ΔH^‡ for the conrotatory transition state of cethrene of 17.4 kcal/mol. This compares reasonably well to the barrier of ΔE_a = 14.1 kcal/mol for the diphenylcethrene established experimentally by Juríček et al.¹⁸ In addition, our computed barrier for the conrotatory ring closure of biphenalenylidene of ΔH^‡ = 14.1 kcal/mol is in good agreement with the experimental value of ΔE_a^‡ = 15.7 kcal/mol.¹⁷ We conclude that DFT is indeed well-suited for computations of the forbidden processes studied here.

14π Electrocyclizations of Prinzbach’s Vinylogous Sesquifulvalene.

Finally, we arrive on the focus of our investigation: vinylogous sesquifulvalene, which undergoes a clean, forbidden, conrotatory electrocyclization.

The ground-state geometry of vinylogous sesquifulvalene is planar and s-trans, so there must be a rotation from the s-trans to the s-cis configuration to bring the appropriate atoms together for the 14π electrocyclization. The transition state for the rotation of the centrally connecting single bond from the s-trans to the s-cis conformation was located. The free energy barrier of this conformational change is 7.4 kcal/mol, which is significantly lower than the transition state for electrocyclization to give the cyclized product (ΔG^‡ = 25.8 kcal/mol for the trans product). The geometries of the s-trans and s-cis conformers and the two electrocyclization transition states are shown in Figure 5. Interestingly, the conformers of the reactant that are related to the allowed dis and forbidden con transition states are 7.1 and 8.7 kcal/mol above the global minimum, respectively.

Figure 5.

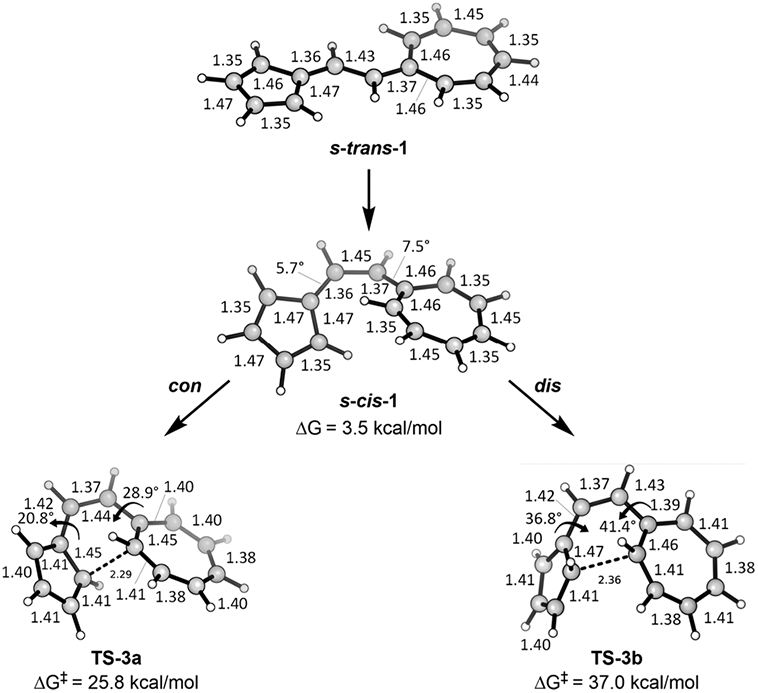
Geometries of s-trans and s-cis reactants and transition state geometries for conrotatory and disrotatory 14π electrocyclizations.

The ease with which we located the forbidden transition state is unusual because, as noted above, forbidden transition states are often singlet diradical states, and they are often quite unsymmetrical.

The forbidden conrotatory and allowed disrotatory transition states shown in Figure 5 are extremely similar structurally, with the 5- and 7-membered rings having all “aromatic” bond lengths of 1.40 ± 0.02 Å except for the six C─C bonds involved in the forming 6-membered ring; these have bond lengths of 1.45 ± 0.01, 1.43 ± 0.01, 1.37, 1.42, 1.46 ± 0.01, and 2.33 ± 0.04 Å. These geometries suggest that the transition state has the character of a cyclopentadienide adding to a tropylium, connected by a vinyl group linker. Analysis of charges, later in this paper, reinforces this image, but the NICS(0) values described below present a more complicated picture.

The vinylogous sesquifulvalene in its ground-state s-trans conformation has a nonaromatic 5-membered ring (NICS(0) = −0.3) and an antiaromatic 7-membered ring (NICS(0) = 8.7), very similar to those of fulvene (NICS(0) = 0.7) and heptafulvene (NICS(0) = 9.5). In the forbidden but favored conrotatory transition state, the 5-, 6 (forming)-, and 7-membered rings have NICS(0) values of 7.6, 6.7, and 15.7, respectively—all antiaromatic as expected for a forbidden reaction. The corresponding values in the allowed disrotatory (but disfavored) transition state are −6.6, −8.7, and −0.6, aromatic or nonaromatic.

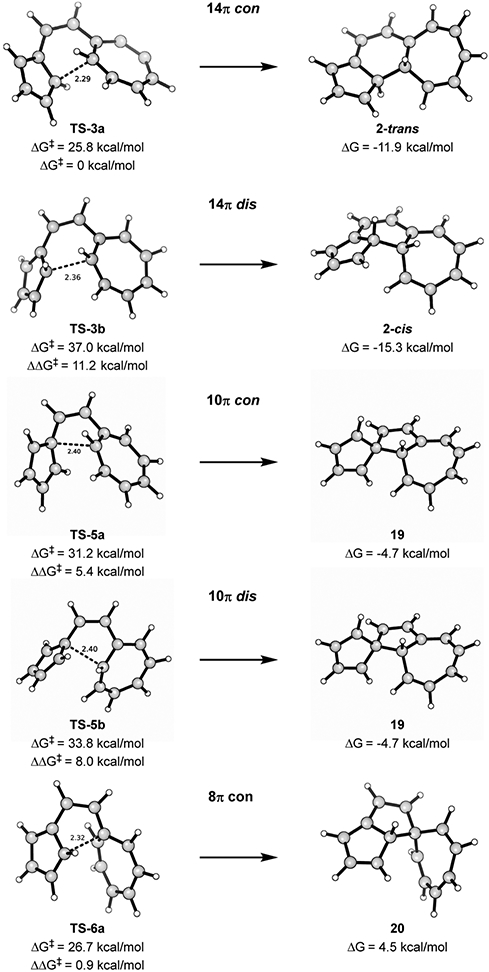
The forbidden conrotatory transition state for formation of the trans product was computed to have a free energy barrier of 25.8 kcal/mol (ΔH^‡ = 23.7)—the same as the experimental value of ΔH^‡ = 23.9 ± 0.5 kcal/mol—whereas the transition state for the allowed disrotatory reaction to form the cis product was computed to have a free energy barrier of 37.0 kcal/mol (Figure 5). As supported by experiment, TS-3a is energetically preferred. We predict that the disrotatory counterpart, TS-3b, is disfavored by an impressive 11.2 kcal/mol. There is something fundamental about the nature of this system that not only favors the forbidden process but also disfavors the allowed process.

We compared the steric parameters of the allowed, disfavored TS of sesquifulvalene to the analogous allowed and favored transition state of hexatriene described in Figure 3. The disrotatory TS of cis-hexatriene has an “inside-H” distance of 1.86 Å, whereas the “inside-H” distance of the disrotatory 14π TS of the vinylogous sesquifulvalene is 1.91 Å. These distances are particularly short in comparison to the disrotatory TSs of the difulvene and diheptafulvene systems, which have “inside-H” distances of 2.54 and 2.38 Å, respectively (Figure 9). While this steric clash might increase the barrier of these disrotatory reactions to some degree, we cannot attribute the preference for the conrotatory TS in the 14π system solely to the “inside-Hs” being too close in the disrotatory TS. This is made evident by the observation that the “inside-H” distance in the allowed, disrotatory TS of cis-hexatriene is even shorter than in the vinylogous sesquifulvalene, and yet cis-hexatriene’s disrotatory TS is still significantly favored energetically to its conrotatory TS. There are some features of the boatlike disrotatory processes that make them energetically disfavored relative to the chairlike conrotatory processes. This will be discussed in detail later in this paper.

Figure 9.

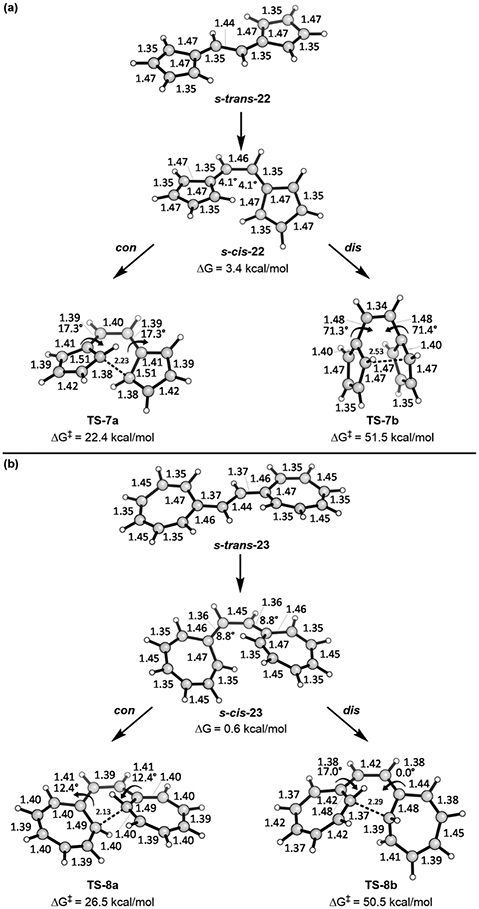
Bond lengths and torsion angles of (a) vinylogous pentafulvalene and (b) vinylogous heptafulvalene along with transition states for their electrocyclizations. All are closed-shell wave functions.

Other factors have been shown to lower the difference between allowed and forbidden reaction barriers. For example, Wolfgang Roth postulated, and theory confirmed, that the constraint of a cyclobutene to a planar geometry reduced the allowed (con)–forbidden (dis) energy difference for ring-opening from >11 kcal/mol to about 3 kcal/mol by reducing the orbital overlap between the termini of the diene and consequently reducing the stabilization of the allowed transition state.³³

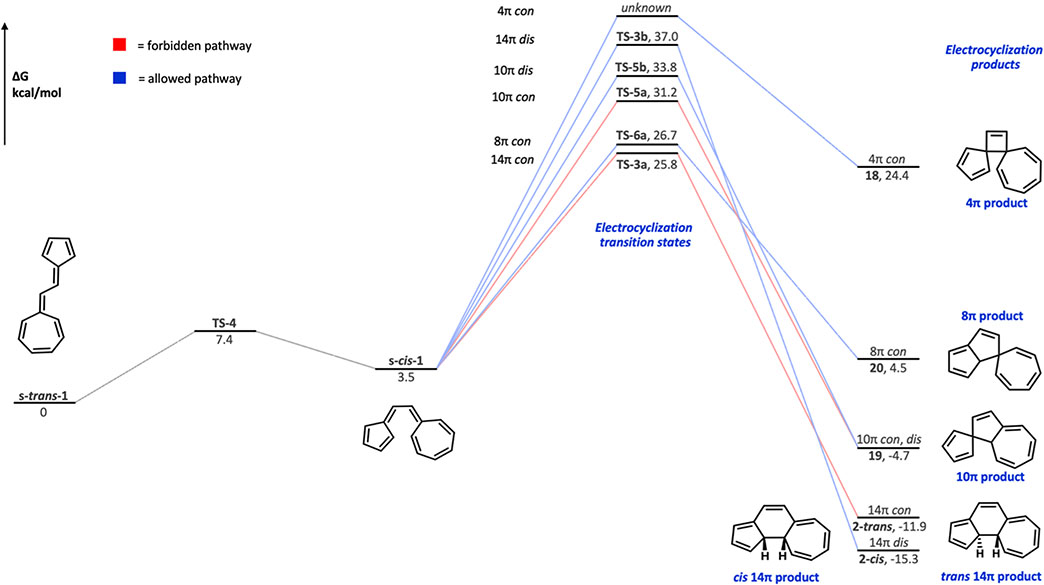
In addition to the 14π electrocyclization that was observed by Prinzbach and co-workers, we investigated the 10π, 8π, and 4π electrocyclizations (Figure 6) of the vinylogous sesquifulvalene. The transition states and products were computed for each of these pathways.

Figure 6.

Free energy diagram for electrocyclization of s-cis-1 via 4π, 8π, 10π, and 14π conrotatory and disrotatory pathways. All structures have closed-shell wave functions except for TS-5a.

The energetics are shown in Figure 6 and Table 2, and the transition state structures are shown in Figure 7. While expected from the experimental results, we were amazed to find that the symmetry-forbidden TS (TS-3a) for formation of the 14π trans product (2-trans) is highly favored kinetically even though the product is not the most stable. The trans product is destabilized by 3.4 kcal/mol relative to the cis product (2-cis); evidently, the thermodynamics of these products are not the factors that determine the activation barriers leading to them.

Table 2.

Energy Barriers for the Electrocyclizations of s-cis-1 (in kcal/mol)

structure	ΔH‡	ΔG‡	ΔΔG‡
TS-3a	23.7	25.8	0
TS-3a (exp)	23.9 ± 0.5
TS-3b	35.2	37.0	11.2
TS-5a	29.6	31.2	5.4
TS-5b	31.8	33.8	8.0
TS-6a	24.4	26.7	0.9
4π TS	unknown	unknown	unknown

Figure 7.

Transition states of 14π-, 10π-, and 8 π-electron electrocyclizations of s-cis-1.

Another feasible path is through the allowed 8π conrotatory electrocyclization TS, which has a free energy barrier of 26.7 kcal/mol—this is higher than the forbidden TS-3a by only 0.9 kcal/mol. However, since the 8π product is unstable, at a free energy relative to reactants of 4.5 kcal/mol, it will revert to starting material and eventually follow the irreversible TS-3a reaction pathway. The most stable product (2-cis), which would be formed by the allowed disrotatory pathway, is not formed at all because of its high TS barrier of 37.0 kcal/mol. Another possible cyclization is the 10π electrocyclization (TS-5a and TS-5b). Interestingly, the 10π con and dis electrocyclization TSs act similarly to their 14π counterparts. We observe that the forbidden, conrotatory 10π TS (computed with an open-shell, broken-symmetry wave function) is 2.6 kcal/mol lower in energy than the allowed, disrotatory 10π TS—a second violation of the Woodward–Hoffmann rules within the same system!

Although a transition state for formation of the 4π product could not be located, its high-energy product (ΔG = 24.4 kcal/mol) indicates that it will have a very high-energy TS. Taken together, the TS and product energies described in the free energy diagram explain why the 14π electrocyclization trans product (2-trans) is the only observed product for this reaction.

Prinzbach and co-workers observed rapid conversion of the 14π trans product to a hydrogen shifted product 21 (Figure 8). Our calculations are consistent with experiments: product 21 is calculated to be 42.3 kcal/mol lower in energy than the starting material and 30.4 kcal/mol below trans-product 21-trans. Product 21 can be formed from 2-trans by two facile 1,5-sigmatropic hydrogen shifts.

Figure 8.

Final product formed by thermolysis of 2-trans.

We also studied two other systems investigated by Prinzbach: the 12π- and 16π-electron vinylogous pentafulvalene and heptafulvalene. The s-trans and s-cis conformers of these compounds and their allowed conrotatory and forbidden disrotatory transition states are shown in Figure 9.

These 4n π-electron systems follow the Woodward–Hoffmann rules faithfully, perhaps more faithfully than any other known systems. For the 12π system, the allowed conrotatory barrier is 29.1 kcal/mol below the forbidden barrier! For the 16π system, that difference is 24.0 kcal/mol—nearly as large. The allowed transition state geometries have primarily aromatic bond lengths of 1.38–1.42 Å, except for the ring bonds involved in formation of six-membered rings (1.39–1.51 Å). The transition state of the forbidden path of the vinylogous heptafulvalene is quite different, and the lengths of the bonds that are not involved in the formation of the new six-membered ring range from 1.37 to 1.45 Å. For the vinylogous pentafulvalene, the transition state located appears to be the transition state for the Cope rearrangement of the disrotatory electrocyclization product. Note the full double bond connecting the two cyclopentadienyl moieties in TS-7b.

Returning to the 14π system, we explored whether the forbidden pathway might occur by a more or less stepwise process, involving rotation of the s-cis-reactant to a diradical or zwitterionic structure with both rings perpendicular to the connecting ethylene linkage. Figure 10 shows the geometry of this structure and the Hirshfeld charges on each CH and C unit.

Figure 10.

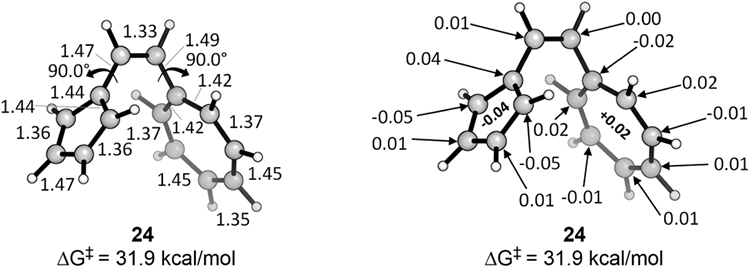
Diradical structure formed from the vinylogous sesquifulvalene by rotating both rings to 90° relative to the connecting ethylene moiety. Geometries and Hirshfeld charges (Hs summed into Cs) are shown.

This structure is an open-shell singlet diradical. A localized double bond forms at the centrally connecting bond between the rings, and the two bonds attaching this double bond to the rings are single bonds. As expected, some positive charge localizes onto the tropylium ring, while negative charge accumulates on the cyclopentadiene substructure, but the degree of charge separation is very small—far less than in the transition states (see Figure 12). At a free energy of 31.9 kcal/mol, the perpendicular structure lies between the 14π allowed and forbidden transition states energetically. This structure is very different from the transition state of the 14π electrocyclization of vinylogous sesquifulvalene, in terms of both charges and bond lengths, which indicates that this cyclization does not occur through a diradical process.

Figure 12.

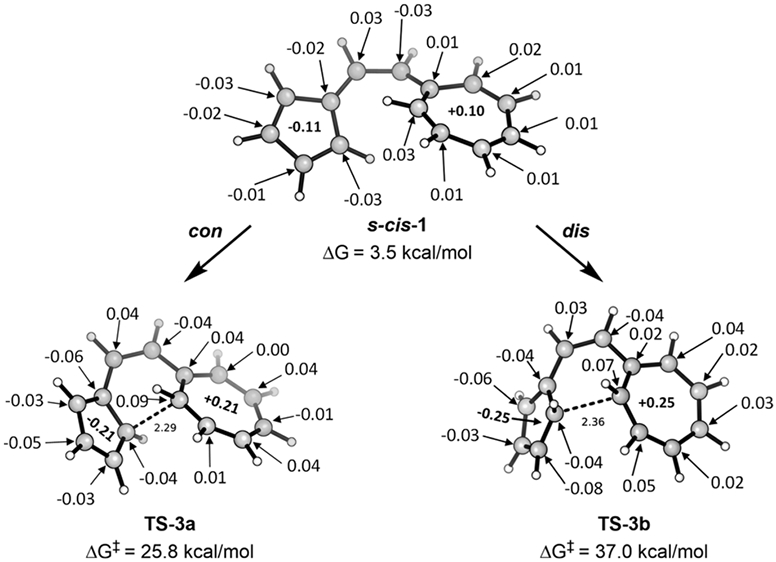
Charges in s-cis vinylogous sesquifulvalene and the forbidden and allowed 14π transition states.

We also considered the possibility of direct interconversion between certain transition states shown in Figures 6 and 7. Because TS-3a and TS-6a are so similar structurally and energetically, Roald Hoffmann suggested that we search for a second-order saddle point on the potential energy surface connecting these two first-order saddle points—this would correspond to the second-order transition state between TS-3a and TS-6a. Unfortunately, we were not able to locate such a second-order saddle point, despite trying numerous and diverse approaches. We generated a series of intermediate structures between TS-3a and TS-6a, but every structure in which we allowed either of the two forming-bonds of interest to lengthen became reactant-like, and these structures were all lower in energy than both TSs. Finally, we froze the 14π forming bond at its length in TS-3a and the 8π forming bond at its length in TS-6a, allowing the rest of the molecule to optimize freely (Figure 11).

Figure 11.

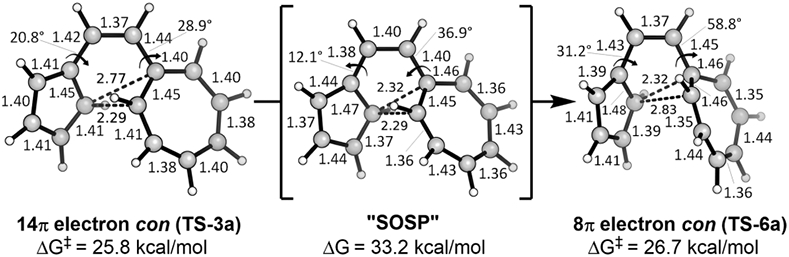
Bond lengths, torsion angles, and energies of TS-3a, approximate second-order saddle point “SOSP”, and TS-6a.

We label this approximate second-order saddle point “SOSP” and use it as an approximate barrier between TS-3a and TS-6a. Our approximation indicates that conversion from the 14π cyclization TS to the 8π cyclization TS costs an additional 7.4 kcal/mol. Further analysis of the geometries of the two transition states and the dihedral angles shows that the rotations of the two odd-membered rings are actually quite different between TS-3a and TS-6a.

Next, we describe the charge separation in the vinylogous sesquifulvalene and the transition states. As shown in Figure 12, the reactant involves notable charge transfer between the cycloheptatriene and cyclopentadiene rings, creating 6π-electron tropylium and 6π-electron cyclopentadienide aromatic character. This increases to 0.21 electrons in the forbidden con and 0.25 electrons in the allowed dis transition states. Indeed, this indicates that the transition states possess substantial zwitterionic character.

Orbitals of Vinylogous Sesquifulvalene and the Transition States for Disrotatory and Conrotatory Electrocyclizations.

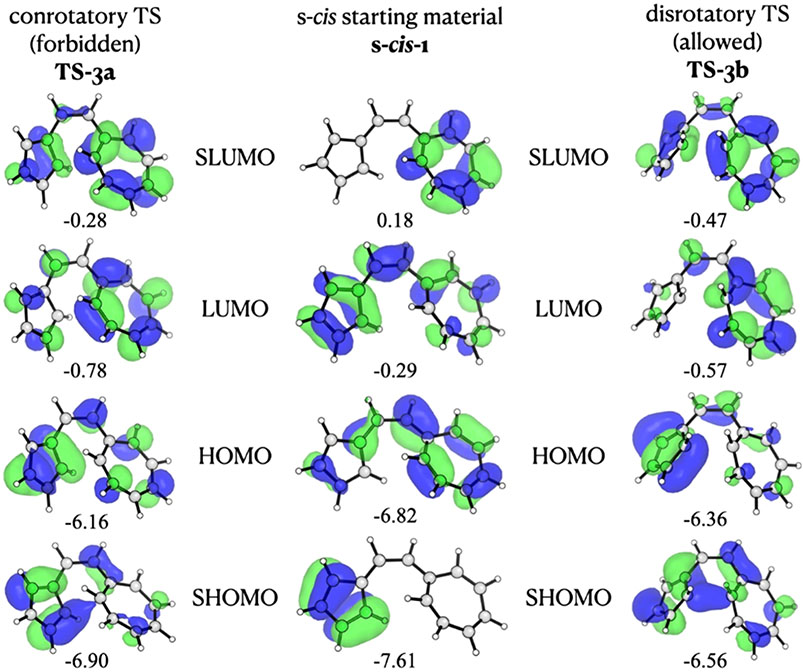
In this section, we analyze the shapes of the orbitals involved in these reactions to better understand their behavior as the reactions proceed. Figure 13 shows the computed Kohn–Sham orbital shapes and energies (in eV) corresponding to the top two occupied and lowest two vacant orbitals in the s-cis reactant and the transition states of vinylogous sesquifulvalene. In their original communication on electrocyclizations,⁵ Woodward and Hoffmann noted that the favored electrocyclic process is that which increases bonding orbital overlap upon cyclization and later showed that this indicates correlation with a bonding orbital in the product. However, as shown in Figure 13, there is a node at the bond-forming carbon of the 5-membered ring in the HOMO of the s-cis reactant. This node shifts to the bond-forming carbon of the 7-membered ring in the transition states for both the allowed disrotatory and forbidden conrotatory 14π electrocyclizations.

Figure 13.

Two highest occupied and two lowest vacant orbitals of vinylogous sesquifulvalene in the s-cis conformation and in the 14π con and dis transition states.

Prinzbach noted that the sites that became bonded in the reaction have relatively small coefficients in the HMO HOMO. Perhaps even more interesting is that the SHOMO of the reactant has essentially no density in the cycloheptatriene, while the SLUMO has no density in the cyclopentadiene. In the two transition states, the HOMO and SHOMO are mainly on the cyclopentadiene, while the LUMO and SLUMO are mainly on the cycloheptatriene, which, like the charges, suggests that the TSs have considerable cyclopentadienide–tropylium character. Also, there is little or no partial bonding for either TS in either the HOMO or the SHOMO, whereas the usual situation would be bonding in the HOMO for the allowed and antibonding for the forbidden. These nodal differences from normal linear polyenes form a basis for the behavioral differences between these systems and linear polyenes.

Forbidden pathways usually begin with the rise of the HOMO, a typical behavior in forbidden cycloadditions due to the antibonding interaction at the forming bond centers and expected due to distortion of the π system. Similarly, the LUMO drops due to the bonding interactions that ensue upon ring-closing motion and reduction of antibonding by distortion. It is important to note that the Woodward–Hoffmann values do not depend upon maintenance of exact symmetry. Woodward and Hoffmann note on page 797 of the Angewandte review that “A slight perturbation … may destroy total symmetry, but cannot be expected to change dramatically the mechanism of a reaction.”⁶ In the case studied here, we suggest that this reaction has considerable character of an attack of a cyclopentadienide on a tropylium: a reaction which has no orbital symmetry restriction.

We conclude that formally forbidden reactions may become favored by strong polarization of the system that disrupts the normal nodal behavior of linear polyenes. The vinylogous sesquifulvalene is also nonalternant, but that in itself is not sufficient to overturn the Rules, as demonstrated by the vinylogous pentafulvalene and heptaffilvalene (Figure 9).

We illustrate in Figure 14 how polarization can disrupt the nodal properties of a polyene and cause nodes to be present at the sites of bond formation in electrocyclic reactions.

Figure 14.

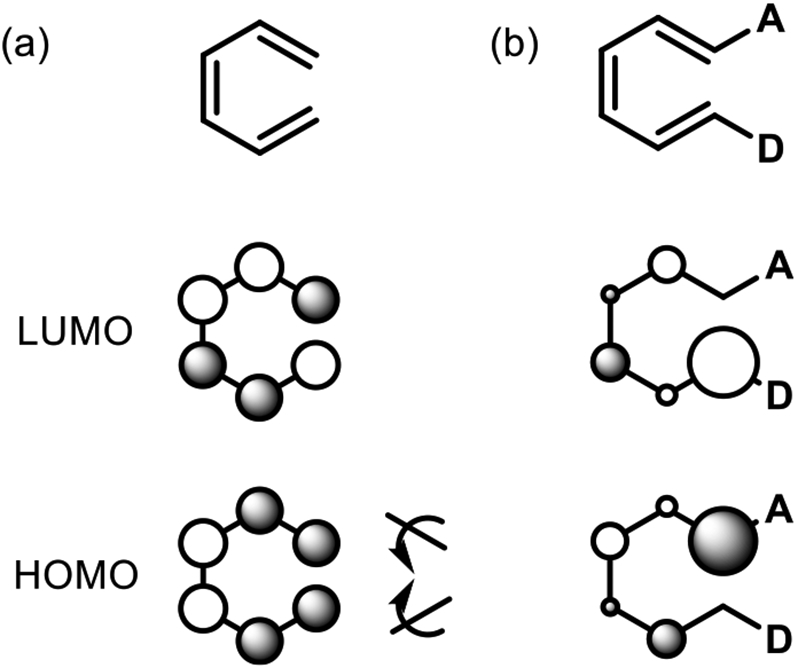
HOMO and LUMO of (a) hexatriene and (b) a 1-D, 6-A substituted triene (D = strong donor; A = strong acceptor).

The familiar HOMO and LUMO of hexatriene are shown in Figure 14a. If there is a sufficiently powerful acceptor at one terminus, it will concentrate the HOMO on that carbon to form what is essentially a localized carbanion. A donor at the opposite terminus will cause that terminus to become a carbocation, reflected in the large coefficient at that terminus in the LUMO. The nodes at the termini imply that there is no preference between conrotatory or disrotatory electrocyclization.

The suggestion that polar effects could influence, or even reverse, the Woodward–Hoffmann Rules was made previously by both Epiotis and Inagaki. In a series of papers in 1971 and 1972, Epiotis proposed that donor and acceptor substituents could decrease the preference for the W–H allowed path.^25,34-41 For electrocyclizations, he noted that donors or acceptors could cause configuration interaction that would instigate partial electron transfer from HOMO to LUMO. The transfer of electron density from the HOMO to the LUMO was proposed to cause a change in the rules. Hückel MO calculations on allyl and butadiene systems were cited to support his theory.¹³ While our explanation does not invoke configuration interaction and his papers do not deal with alterations of coefficients by substituents, we do note Epiotis’ prescience about the influence of donors and acceptors on the Rules. In a later review of his new theory, Epiotis ends his discussion of polar effects on electrocyclic reaction stereochemistries by concluding that “A concerted polar hexatriene ring closure will occur thermally in a disrotatory manner…”⁴¹ That is, the CI is predicted to accelerate both disrotatory and conrotatory electrocyclizations, maintaining the Woodward–Hoffmann predictions, contrary to the violations described here.

Inagaki, like Epiotis, described the possibility of forbidden [π²_s + π²_s] cycloadditions becoming favored when they involve a donor-substituted alkene reacting with an acceptor-substituted alkene.⁴² He described this as “pseudoexcitation”, related to Epiotis’ configuration interaction model. We note alternatively that alteration of FMO coefficients can reduce the forbiddenness in these cases, although this will also promote stepwise processes via zwitterions.

Our model emphasizes coefficient changes that arise from mixing of the orthogonal orbitals of the unsubstituted system. Whereas hexatriene must electrocyclize in a disrotatory fashion to maintain bonding in the HOMO, the D and A substitutents tend to produce nodes on the termini of the HOMO or LUMO, so that previously forbidden conrotatory or disrotatory electrocyclizations are now allowed.

These considerations rationalize the origins of the favorability of the formally forbidden reaction but leave open the question of why the formally allowed is so unfavorable. Some local effects influence this, such as the resemblance of the forming 6-membered ring to a chair in the conrotatory transition state and to a boat in the disrotatory transition state,⁴³ which also causes partial eclipsing about the forming bond in the dis TS. Shea has shown that the chair transition states of hydrocarbon Cope rearrangements are ΔΔG^‡ = 6–9 (ΔΔH^‡ = 11–16) kcal/mol lower in energy than the corresponding boat transition states.³⁰

In addition, in his original paper,¹ Prinzbach claimed that the higher energy of the allowed, disrotatory transition state of sesquifulvalene is due to excessive strain at its exocyclic carbons. We measured the dihedral angles about the exocyclic carbons in each pathway and found the following: in the conrotatory pathway, these angles change from 20.8° and 28.9° in TS-3a to 22.2° and 13.1° in the product, 2-trans. The dihedral angles of the disrotatory pathway decrease from 36.8° and 41.4° in TS-3b to 20.0° and 4.1° in the product, 2-cis. The dihedral angles in the disrotatory TS are 12°–16° greater than those in the conrotatory TS, causing greater strain in these partial double bonds that raises the energy of the allowed, dis TS, even above that of the forbidden, con TS. This pattern reverses as each pathway forms its respective product and partial double bonds become single bonds. The high distortion of the dis TS is relieved as it goes to the cis product. The con TS goes to the trans product (2-trans), which reduces its dihedral angles, but they are not quite as small as in 2-cis. This slightly higher strain of the trans product contributes to it being higher in energy than the cis product, and it explains why the two pathways switch in thermodynamic favorability.

Design of a Polarized Nonalternant Hydrocarbon and Substituted Hexatriene and Their Conrotatory and Disrotatory Electrocyclizations.

We probed whether significant stabilization of a typically orbital-symmetry-forbidden reaction would occur in other highly polarized systems. To test this, we studied the 10π electrocyclization of 6-triafulvenylfulvene. The results are shown in Figure 15.

Figure 15.

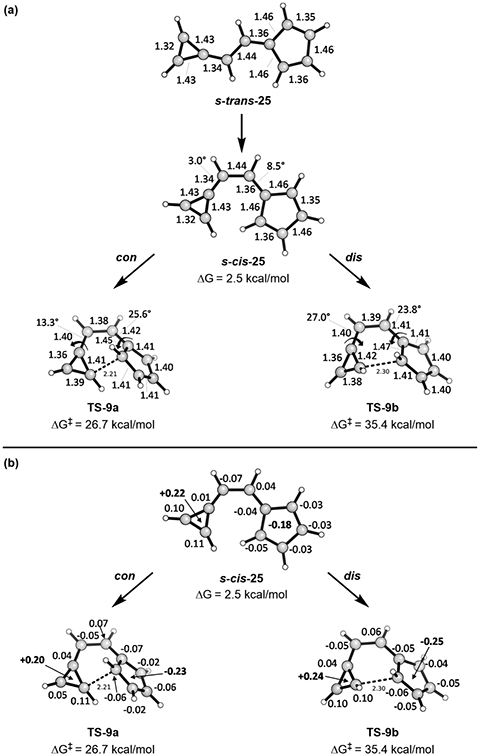
Forbidden conrotatory and allowed disrotatory transition states for electrocyclization of 6-triafulvenylfulvene. In (a) geometries are shown. In (b) Hirshfeld charges are shown by each atom.

As expected, significant positive charge accumulates on the triafulvene while significant negative charge accumulates on the fulvene (Figure 15b). This charge separation gives each ring some aromatic character, similar to the sesquifulvalene system. This polarization changes the nodal properties of the hydrocarbon and eliminates the orbital symmetry restriction. Once again, the geometrical preference for a chairlike TS causes the forbidden conrotatory process to be preferred. This is another flagrant violation of the Woodward–Hoffmann rules! And indeed, it agrees with our hypothesis that significant polarization can eliminate the orbital symmetry forbiddeness.

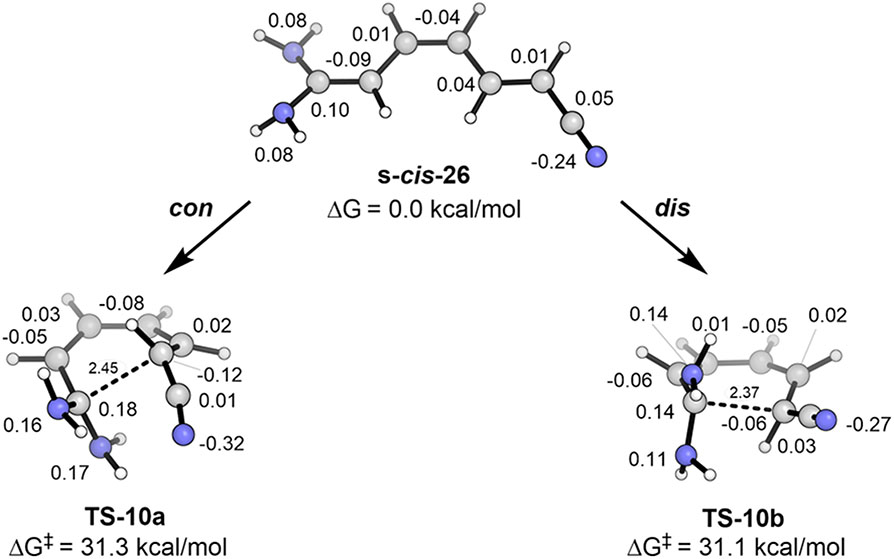
To demonstrate these effects on a linear polyene, we studied the formal 6π electrocyclization of a highly polar, substituted hexatriene. We were unable to locate transition states for cis-1,1-diamino-6,6-dicyanohexatriene, so instead we studied the nearly as highly polar cis,trans-1,1-diamino-6-cyanohexatriene (s-cis-26). The results are shown in Figure 16.

Figure 16.

Forbidden conrotatory and allowed disrotatory transition states for electrocyclization of cis,trans-1,1-diamino-6-cyanohexatriene. Hirshfeld charges are shown by each atom.

This reaction involves, in effect, an iminium cation reacting with a cyanomethide anion. As expected, the cyano group nitrogen accumulates significant negative charge while the NH₂ groups and carbon-1 become very positively charged. In accordance with our theory, this significant charge separation leads to remarkable stabilization of the orbital-symmetry-forbidden, conrotatory transition state; the two transition states have an essentially identical barrier near 31 kcal/mol. This occurs because the polarization eliminates the orbital symmetry forbiddeness, but there is no additional driving force pushing the energy of the allowed, disrotatory TS above that of the forbidden, conrotatory TS. It is primarily the termini that rotate in these transition states, so neither conformation has significant boat or chair character. These two transition states have merely been made energetically equal by polarization. The systems described above serve to confirm our proposal about the stabilization of symmetry-forbidden electrocyclization transition states for highly polarized molecules.

■ VIOLATIONS

Our findings reproduce the exclusive selectivity for a single regioisomeric and diastereomeric product in the electrocyclization reaction of vinylogous sesquifulvalene, studied experimentally by Prinzbach in 1978. The forbidden conrotatory 14π electrocyclization pathway has the lowest free energy barrier out of all the available electrocyclizations. While the 8π conrotatory electrocyclization is only slightly more difficult, this reaction is reversible, and the product is higher in energy than the starting material. The high polarization of vinylogous sesquifulvalene leads to nodal effects that allow it to achieve a reaction that formally violates the Woodward–Hoffmann rules. Such effects are likely to be common in highly polar systems, such as the model 6-triafulvenylfulvene and diaminocyanohexatriene systems we studied. An alternative mode of circumventing the rules described earlier involved highly conjugated systems, such as cethrene, that have many low-lying electronic configurations, some of which have the correct symmetry to stabilize the forbidden diradical transition state. As to when violations of the Woodward–Hoffmann rules can occur, we have discovered that highly polar units can profoundly alter the local symmetry properties of π-systems and can make formally forbidden reactions favorable.

We are now seeking to evolve this hypothesis into a general theory of pericyclic reactions of polar systems.