Abstract
Goal: We propose novel supervised control architectures to regulate the cognitive stress state and close the loop. Methods: We take information present in underlying neural impulses of skin conductance signals and employ model-based control techniques to close the loop in a state-space framework. For performance enhancement, we establish a supervised knowledge-based layer to update control system in real time. In the supervised architecture, the controller parameters are being updated in real-time. Results: Statistical analyses demonstrate the efficiency of supervised control architectures in improving the closed-loop results while maintaining stress levels within a desired range with more optimized control efforts. The model-based approaches would guarantee the control system-perspective criteria such as stability and optimality, and the proposed supervised knowledge-based layer would further enhance their efficiency. Conclusion: Outcomes in this in silico study verify the proficiency of the proposed supervised architectures to be implemented in the real world.
Keywords: Closed-loop, cognitive stress, skin conductance, state-space, supervised control
I. Introduction
In The modern world, any challenge might be a source of cognitive stress [1]. The fast-paced life has the potential to induce emotional and cognitive stress [2]. Feeling overwhelmed, anxiety, and agitation are among the symptoms associated with the high levels of cognitive stress [3]. Conversely, loss of cognitive engagement might also prevent individuals from following their goals [4]. A low level of positive stress, which is also called eustress, might cause memory problems, lack of motivation, and poor concentration [5]. It can also negatively affect persons’ productivity in work places. While it is important to track internal stress levels [6], it is also critical to establish a mechanism for keeping internal cognitive stress state within a favorable range [7]. In this research, we aim to track the internal cognitive stress and propose novel control architectures to maintain it within the pleasant range. Advances in the fields of control and automation have opened avenues of applications in various area such as autonomous vehicles, robotics, and financial systems [8]. Recently, there has been much interest in investigating the use of modern control techniques in physiological systems [9]. Researchers are actively working on automating multiple clinical processes such as: artificial pancreas for regulating blood glucose levels [10], [11], feedback control mechanism in neuroprosthesis [12], internal energy regulation in patients with cortisol-related disorders [13]–[15], anesthesia delivery system for medically induced coma [16]–[18], and deep brain stimulation for treating neurodegenerative disorders [19]. Hence, we propose to employ control methods in internal cognitive stress regulation.
As internal cognitive stress state is a hidden state and can not be measured, we approach this problem indirectly [20]. In human body, the autonomic nervous system (ANS) is responsible for a vast number of functions in response to the mental stress [21]. Changes in the arousal of the sympathetic nervous system (SNS) and parasympathetic nervous systems (PSNS), as branches of ANS, are presented in different physiological signals[22]. In fact, the human brain employs SNS and PSNS to react to environmental stimuli. As a result of SNS and PSNS activation, we observe changes in physiological signals such as heart rate, respiration, and skin conductivity [23]. In response to internal/external stress stimuli, brain changes the sweat gland activation via SNS [24]–[26]. Consequently variations in sweat glands activation could be reflected in skin conductance signal monitored by sensors located in wrist-worn devices [27]. Skin conductance signal or electrodermal activity has been shown to be an indicator of mental arousal and cognitive stress [6], [28]–[30]. Therefore, we follow the approaches presented in [31] for further analysis. In the simulation system presented in [31], the hidden cognitive stress state is connected to the changes in skin conductance response (SCR) events via a state-space approach. Employing experimentally collected data, a real-time simulation system is developed to investigate the control design algorithm for closing the loop [31].
In the system presented in [7], [31], we took SCR events as the binary observation and estimated the hidden stress state in real time. While SCR time events carry important information about internal arousal state [6], [30], focusing on only the events’ time as the binary observations and ignoring their amplitudes may cause loss of valuable details. As reported in several articles [21], [29], SCR amplitudes includes information about internal arousal state. In [20], a modified version of the filtering approach, which incorporates continuous-valued information from the SCR amplitudes (i.e., phasic amplitude and tonic levels) is presented. In their proposed approach, they have reported overfitting to the continuous values [20]. To solve this issue, authors in [32] proposed the marked point process (MPP) filtering approach. The MPP filter is applied to estimate internal arousal state from SCR events and their corresponding amplitudes to address the overfitting problem [32]. Compared to our previous approach [31], which we only included SCR time events as binary observations, here we enhance the state estimation process by incorporating the event amplitudes and estimate the internal state with MPP approach.
Exploiting the state-space representation which will lead us to track internal arousal state in a systematic way, we aim to invest in control system techniques to regulate the estimated arousal state and close the loop. In recent years, there exists a growing interest in employing control methods to automate various procedures [33], [34]. Researchers in [35] developed a novel boundary control scheme to regulate a rigid-flexible wing system and close the loop. He et al. considered distributed disturbances and designed a robust control strategy to reject them [36]. Similarly, in present research, we propose novel control approaches to close the loop, regulate the estimated stress state, and keep it within the desired range. The state-space model and the real-time estimation enable us to handle this physiological system as a control-theoretic problem. Hence, we propose to employ well-established model-based optimal control techniques, including linear quadratic regulator (LQR) and model predictive control (MPC) to close the loop. In both LQR and MPC, by optimizing corresponding objective functions, the optimal control would be derived in a real-time manner. The performance of both LQR and MPC depends on the selection of the objective functions [37]. Additionally, due to the nature of this physiological system, the inter- and intra-subject variability make the objective function selection process a challenging task. Among available approaches that address the challenges associated with the objective function selection, research in [38] proposed to use genetic algorithm for optimal tuning of MPC weights. Ramasamy et al. have established a mechanism to update the cost functions based on the system performance as well as the operator input in an offline manner [38]. In their proposed approach, they use an interactive decision tree to get feedback from the operator and infer the optimal gain weights. Researchers in [39] proposed a multi-scenario approach for designing a robust MPC system. They evaluated the operational system for each scenario and considered them while tuning the MPC. Van et al. also proposed to combine the genetic algorithm with a multi objective fuzzy decision making system for MPC tuning [40]. In their proposed approach, they rank the predefined objective functions based on the fuzzy systems [40]. Zhao et al. in [41] implemented a real-time system for adjusting the MPC tuning parameters in an adaptive cruise control system. The expert system proposed in [41] adjusts the tune parameters based on if-then rules. The corresponding cost functions are regulated based on the changes in sign of error terms [41]. To address the need for creating a system to dynamically update the control tune parameters, we propose to establish a supervised layer on top of the implemented model-based control systems. In the proposed architectures, a knowledge-based fuzzy system would supervise the LQR and MPC and adjusts the objective functions in real-time.
The combination of fuzzy systems and model-based control techniques have been explored in the literature [42]–[44]. The researchers in [42] have used fuzzy logic methodology to address the output constraints while designing the MPC. Researchers in [43] use the fuzzy system to decouple the modeling process and use LQR approach to control the power plant. In a similar approach, researchers in [44] apply fuzzy system to model building heating system and implemented the MPC for the process control. However, the present work is the first attempt to use a fuzzy system as the supervised layer to adjust tuning parameters in model-based control structures. Moreover, the proposed supervised control architectures provide a setting to include the relevant medical expertise to enhance the closed-loop system. These novel supervised control approaches could be further expanded to deliver adaptive and robust closed-loop characteristics. The key contributions of the present research include (i) implementing real-time MPP Bayesian-type filter to estimate the hidden arousal state from amplitude and timings of skin conductance response events, (ii) taking advantage of state-space representation of internal arousal state and utilizing model-based LQR and MPC structures to regulate the hidden state, and (iii) presenting novel supervised fuzzy-LQR and fuzzy-MPC architectures to adjust control tuning parameters in real-time.
II. Materials and Methods
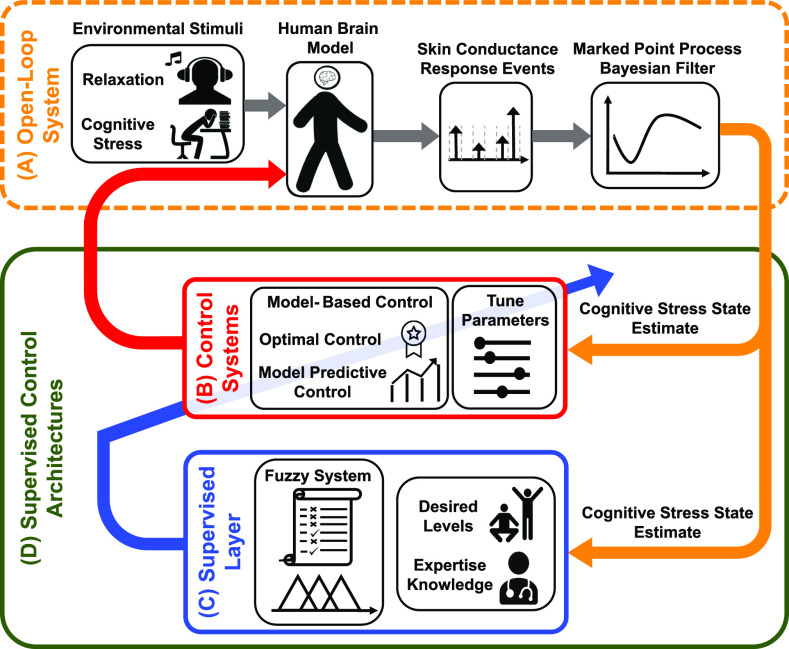
An overview of the proposed closed-loop supervised control architectures is presented in Fig. 1. We utilize the simulation system presented in [31]. The idea presented in [31] is associated with employing experimental data [45] and simulating the environmental stimuli for two scenarios: cognitive stress and relaxation. In a state-space representation, we take simulated SCR events and estimate the hidden cognitive stress state in real-time. To this end, we employ the MPP Bayesian-type filtering ((A) in Fig. 1). To design the control signal and close the open-loop system, we use the model-based approaches LQR and MPC ((B) in Fig. 1). We establish a supervised fuzzy system on top of the LQR and MPC structures to automatically update the control tune parameters ((C) in Fig. 1). The supervised layer executes this task based on feedback from the estimated cognitive stress state, desired state levels, and expertise knowledge.
Fig. 1.
Closed-Loop Supervised Control Architectures Overview. (A) The orange dashed box displays the open-loop system. The solid green box, shows the supervised control architectures. (D) We take the SCR events generated by human brain model and utilize the MPP Bayesian filter to estimate the cognitive stress state. (B) To close the loop, we use the optimal control and model predictive control structures. (C) We establish a knowledge-based fuzzy system, as a supervised layer, and (D) apply expertise knowledge for updating the control tune parameters in a real-time manner.
A. Human Brain Stimulus-Response Model
We use the simulation model that is based on the experimental data [45] and presented in [31]. Non-EEG Dataset for Assessment of Neurological Status [45] is publicly available through the PhysioNet database [45], [46]. This study contains multiple experiments that induce different types of the stress to the subjects. The simulation model is based on two sessions: cognitive stress and relaxation, as the most representative cases [31]. In the original study [45], multiple physiological data were collected (i.e., skin conductance, body temperature, 3D accelerometer signals, heart rate, and blood oxygenation levels). In this research, we aim to track and regulate internal stress state by monitoring skin conductance measurements which were collected using Affectiva Q Curve wearable device to build the simulation environment. Similar to [6], [31], we analyze profiles associated with six selected participants whose data were clean and reliable. More information regarding this experiments and simulation system could be found in [6], [31], [45].
In the simulation system presented in [31], to model individual’s brain responses, we relate the internal cognitive stress-related state to the changes in skin conductance signal by employing a first-order state-space model [6], [30]:
 |
where 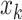 stands for the hidden stress-related state,
stands for the hidden stress-related state, 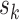 reflects the environmental stimuli, and
reflects the environmental stimuli, and 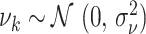 represents the process noise [20], [30].
represents the process noise [20], [30]. 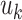 denotes the control input signal designed and applied in real-time to regulate the simulated stress-related state. It is worth mentioning that we include the
denotes the control input signal designed and applied in real-time to regulate the simulated stress-related state. It is worth mentioning that we include the 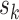 in (1) for the simulation purpose. In a real-world scenario, the human’s internal cognitive stress state is affected by real environmental stimuli. The details of modeling the environmental stimuli is presented in [31]. We also assume the occurrence of SCR events,
in (1) for the simulation purpose. In a real-world scenario, the human’s internal cognitive stress state is affected by real environmental stimuli. The details of modeling the environmental stimuli is presented in [31]. We also assume the occurrence of SCR events, 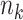 , follows a Bernoulli distribution with the following probability function:
, follows a Bernoulli distribution with the following probability function:
 |
where the probability 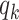 is connected to the stress state
is connected to the stress state 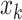 , via the following Sigmoid function [47]:
, via the following Sigmoid function [47]:
 |
where 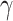 is the person-specific baseline parameter that should be determined. Similar to [31], we first assume
is the person-specific baseline parameter that should be determined. Similar to [31], we first assume 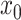 approximately equals to zero. We then calculate the
approximately equals to zero. We then calculate the 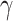 based on the average probability of an SCR occurring in the whole data. According to (3), with increase in the levels of the cognitive stress state, the probability of receiving the SCR events is also increased.
based on the average probability of an SCR occurring in the whole data. According to (3), with increase in the levels of the cognitive stress state, the probability of receiving the SCR events is also increased.
To incorporate all the information included in SCR events, we extend our previous research [31], which only employs the SCR events’ time, to comprise the amplitudes associated with the SCR events. To this end, we assume there exists a linear relationship between the internal cognitive stress state 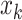 and the SCR amplitudes:
and the SCR amplitudes:
 |
where 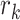 is assumed to be the log transformation of the continuous-valued associated with each SCR event’s amplitude.
is assumed to be the log transformation of the continuous-valued associated with each SCR event’s amplitude. 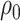 and
and 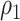 are constant values derived by the offline expectation maximization algorithm [31], [32].
are constant values derived by the offline expectation maximization algorithm [31], [32]. 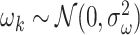 is measurement noise with variance
is measurement noise with variance 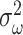 . Accordingly, the joint density function on the probability of receiving the SCR event
. Accordingly, the joint density function on the probability of receiving the SCR event 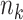 with the corresponding amplitude
with the corresponding amplitude 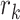 is:
is:
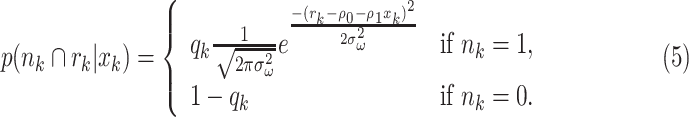 |
As presented in (5), the amplitude information will not be included when there is no impulse 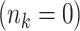 [32].
[32].
It is worth mentioning that the log transformation, discussed in  modeling (4), is only considered in this in silico study [20]. In real-world implementation of the proposed algorithm, we take amplitude and timing of SCR events to model and estimate cognitive arousal state [32].
modeling (4), is only considered in this in silico study [20]. In real-world implementation of the proposed algorithm, we take amplitude and timing of SCR events to model and estimate cognitive arousal state [32].
B. Cognitive Stress State Estimation via MPP Filtering
Taking the SCR events time and their corresponding amplitudes 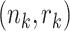 , as the binary and continuous observations, we follow the MPP-based Bayesian filtering approach to estimate the hidden cognitive stress state
, as the binary and continuous observations, we follow the MPP-based Bayesian filtering approach to estimate the hidden cognitive stress state 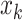 [32]. While the estimation process includes the forward filter and a backward smoother, we only implement the forward part of the filter for further real-time analysis. At each time step, a Gaussian approximation is applied to the posterior density. Combining the prediction and the update steps in the forward filter [32], we estimate the stress state and its variance using the following recursive equations:
[32]. While the estimation process includes the forward filter and a backward smoother, we only implement the forward part of the filter for further real-time analysis. At each time step, a Gaussian approximation is applied to the posterior density. Combining the prediction and the update steps in the forward filter [32], we estimate the stress state and its variance using the following recursive equations:
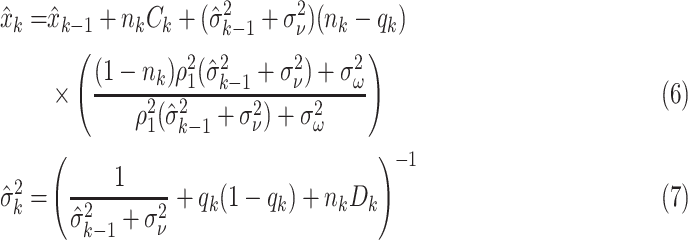 |
where,
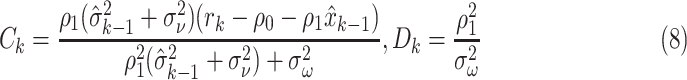 |
when there exists a SCR event 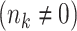 . Otherwise (i.e.,
. Otherwise (i.e., 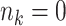 ),
), 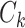 and
and 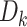 equal zero
equal zero 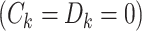 . In fact, the terms
. In fact, the terms 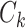 and
and 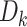 presented in (6) and (7) incorporate the continuous-valued information (
presented in (6) and (7) incorporate the continuous-valued information (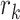 in (4)) associated with the observed SCR event
in (4)) associated with the observed SCR event  at time step
at time step 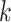 . So, these terms are applied only when there exists a SCR event
. So, these terms are applied only when there exists a SCR event 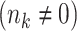 . The probability
. The probability 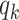 presented in (6) and (7) is being related to the state
presented in (6) and (7) is being related to the state 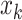 via (3). So, it will results in a nonlinear problem that should be solved by employing numerical methods such as Newton-Raphson [34]. Consequently, we estimate the cognitive stress-related state
via (3). So, it will results in a nonlinear problem that should be solved by employing numerical methods such as Newton-Raphson [34]. Consequently, we estimate the cognitive stress-related state 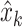 and its corresponding variance parameter
and its corresponding variance parameter  in a real-time manner.
in a real-time manner.
C. Control Design
In this part, we follow the goal of establishing a knowledge-based fuzzy system ((C) in Fig. 1) as a supervised layer in model-based control approaches ((B) in Fig. 1) to close the loop and regulate the estimated cognitive stress state. Particularly, we implement the fuzzy control structure as a supervised layer in LQR and MPC structures. In the supervised architectures, the fuzzy system will automatically adjust the control tune parameters in real-time. In what follows, we discuss both model-based control approaches.
1). LQR
Taking advantage of the state-space model and estimates of cognitive stress state, in LQR framework, we find the optimal solution of a predefined cost function. Hence, the obtained control signal 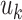 will minimize the following objective function:
will minimize the following objective function:
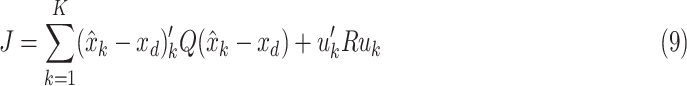 |
where 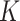 is the ultimate time of the process.
is the ultimate time of the process. 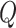 and
and 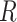 are positive definite weight matrices to penalize the state deviations and the input efforts, respectively.
are positive definite weight matrices to penalize the state deviations and the input efforts, respectively. 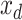 in (9) also stands for the desired levels of estimated stress state. Solving this optimization problem, the optimal control signal
in (9) also stands for the desired levels of estimated stress state. Solving this optimization problem, the optimal control signal 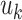 is derived as a linear state feedback controller:
is derived as a linear state feedback controller:
 |
where, the feedback gain  is derived recursively:
is derived recursively:
 |
where 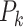 is the discrete solution of the following algebraic Riccati equation:
is the discrete solution of the following algebraic Riccati equation:
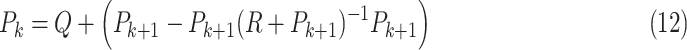 |
with the 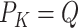 initial condition.
initial condition.
2). MPC
To advance the optimal control LQR, we propose to use MPC structure as the second model-based control technique. In MPC framework, we first project the state values for whole time-window horizon [48]. Then, we derive the control input for all future prediction window and apply the first control action. To this end, we introduce the following quadratic function that needs to be minimized:
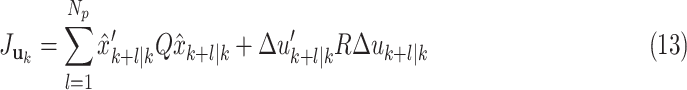 |
where 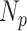 is the prediction horizon,
is the prediction horizon, 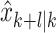 denotes to the state estimate prediction, and
denotes to the state estimate prediction, and 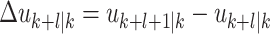 is the predicted variation of control input at each time step. Similar to LQR,
is the predicted variation of control input at each time step. Similar to LQR, 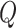 and
and 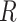 are positive definite weight matrices to penalize the predicted state deviations and control efforts. To find the control signal, we aim to derive
are positive definite weight matrices to penalize the predicted state deviations and control efforts. To find the control signal, we aim to derive 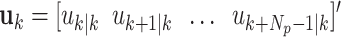 which is the control input for whole time horizon window prediction. To this end, we first define
which is the control input for whole time horizon window prediction. To this end, we first define 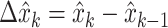 and
and 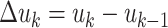 . Using these terminologies, general state-space model (1) would be simply transferred to
. Using these terminologies, general state-space model (1) would be simply transferred to 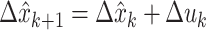 . By considering the estimated state as the output equation,
. By considering the estimated state as the output equation,  , and defining a new augmented variable, we build:
, and defining a new augmented variable, we build:
 |
So, the augmented system dynamics would be such as:
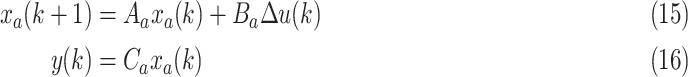 |
where the augmented system matrices of (1) are:
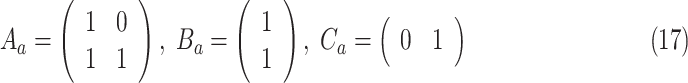 |
Employing the output equation in the augmented system (16), we build the predicted future observation for whole prediction horizon 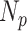 such that:
such that:
 |
where:
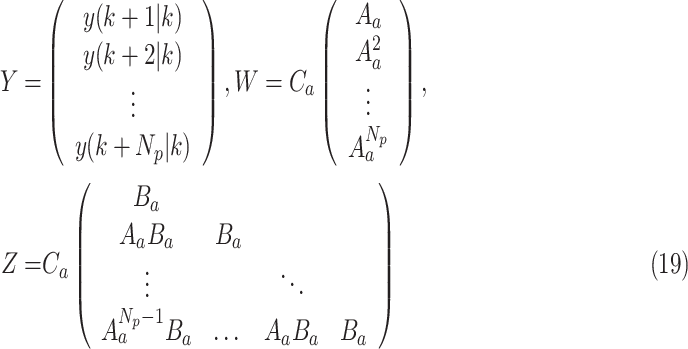 |
Now, the goal of finding control action 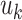 is converted to calculating the sequence of
is converted to calculating the sequence of 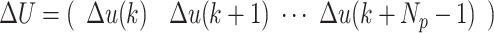 . Consequently, this sequence will provide the predicted state variables
. Consequently, this sequence will provide the predicted state variables 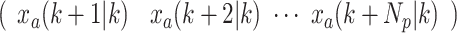 .
.
To find the sequence 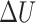 in (18), by knowing
in (18), by knowing 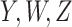 and
and 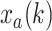 , minimizing the cost function presented in (13) would be equal to minimizing the following objective function:
, minimizing the cost function presented in (13) would be equal to minimizing the following objective function:
 |
where 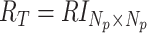 and
and 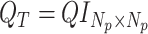 are diagonal matrices for penalizing the control effort and deviations in the estimated state, respectively. Assuming there is no constraint, by setting
are diagonal matrices for penalizing the control effort and deviations in the estimated state, respectively. Assuming there is no constraint, by setting 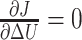 , we derive the optimal solution:
, we derive the optimal solution:
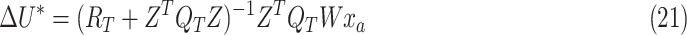 |
It is also worth mentioning that positive definite matrices 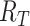 and
and 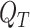 (i.e.,
(i.e., 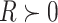 ,
, 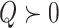 ) will guarantee the second order necessary condition in the computed
) will guarantee the second order necessary condition in the computed 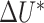 . Finally, the first element in
. Finally, the first element in 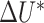 , which is
, which is 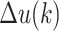 , includes required control action signal for each time step (i.e.,
, includes required control action signal for each time step (i.e., 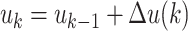 ).
).
It should be also noted that by any selections of positive definite weight matrices 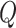 and
and 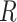 , finding the optimal control would be equal to solving a quadratic program optimization problem (20). Solution
, finding the optimal control would be equal to solving a quadratic program optimization problem (20). Solution 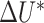 in (21) only relies on the current state, past control input, and the desired level. Consequently, it will result in a closed-loop well-posed system that always has a unique solution [49].
in (21) only relies on the current state, past control input, and the desired level. Consequently, it will result in a closed-loop well-posed system that always has a unique solution [49].
In MPC design, while there exist methods for ensuring stability in infinite time horizon cases, utilizing a straightforward method for delivering rigorous stable property with finite time horizon remains challenging. In this research, to invest the stability, we evaluate prediction tail and consider terminal constraint [50]. Assuming terminal constraint 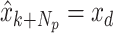 in (13) also provides with recursive feasibility. To this end, we consider the general form of optimal control input as Lyapunov function:
in (13) also provides with recursive feasibility. To this end, we consider the general form of optimal control input as Lyapunov function:
 |
where  . In
. In 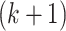 time instant, the first component of
time instant, the first component of 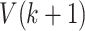 has been occurred and is no longer prediction. This unused part is called prediction tail (i.e.,
has been occurred and is no longer prediction. This unused part is called prediction tail (i.e., 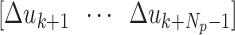 ) [50], [51]. For the sake of simplicity, we assume zero terminal constraint at this stage (i.e.,
) [50], [51]. For the sake of simplicity, we assume zero terminal constraint at this stage (i.e., 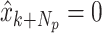 ). Next, we follow the steps presented in [52] and derive
). Next, we follow the steps presented in [52] and derive 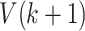 :
:
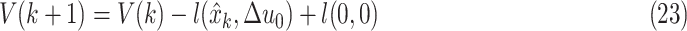 |
where initial cost 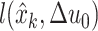 is subtracted and corresponding cost for staying at terminal state is added (i.e,
is subtracted and corresponding cost for staying at terminal state is added (i.e, 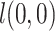 ) [50]. Hence,
) [50]. Hence,
 |
Since 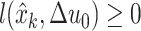 , we may conclude that
, we may conclude that 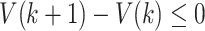 and the Lyapunov function candidate is stable.
and the Lyapunov function candidate is stable.
D. Supervised Control Architectures
As illustrated, in both LQR and MPC approaches, the selection of weight matrices 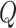 and
and 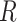 plays an important role in the control design process. In fact, derived control gain in these model-based approaches highly depends on the weight matrices presented in (9) and (13). To update the weight matrices in real-time, we consider a knowledge-based system as a supervised layer in the design process. Therefore, we establish a fuzzy system on top of the pure LQR and MPC structures to (i) take the intrinsic advantages of the modeled dynamics employed in LQR and MPC, (ii) enhance the performance of the conventional architectures by adjusting the tune-parameters in real-time, and (iii) overcome the heuristic nature of the pure fuzzy control design (i.e., presented in [31]). To this end, we define the corresponding rule-base and fuzzy structure to change the tune-parameters (i.e.,
plays an important role in the control design process. In fact, derived control gain in these model-based approaches highly depends on the weight matrices presented in (9) and (13). To update the weight matrices in real-time, we consider a knowledge-based system as a supervised layer in the design process. Therefore, we establish a fuzzy system on top of the pure LQR and MPC structures to (i) take the intrinsic advantages of the modeled dynamics employed in LQR and MPC, (ii) enhance the performance of the conventional architectures by adjusting the tune-parameters in real-time, and (iii) overcome the heuristic nature of the pure fuzzy control design (i.e., presented in [31]). To this end, we define the corresponding rule-base and fuzzy structure to change the tune-parameters (i.e., 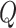 and
and 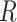 matrices) in real-time. On the basis of LQR and MPC, the larger
matrices) in real-time. On the basis of LQR and MPC, the larger 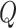 and
and 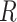 values are, the more we penalize state deviations and control effort, respectively. Therefore, we set to use higher values for
values are, the more we penalize state deviations and control effort, respectively. Therefore, we set to use higher values for 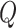 while the error between the estimated state and target state levels is large and decrease it once the estimated stress state is within a predefined range. Following a similar logic, while the error term between the estimated state and the desired value is large, we set not to penalize the control input and let it minimize the error. Once the estimated state tends to a predefined range of the target level, we set to increase the
while the error between the estimated state and target state levels is large and decrease it once the estimated stress state is within a predefined range. Following a similar logic, while the error term between the estimated state and the desired value is large, we set not to penalize the control input and let it minimize the error. Once the estimated state tends to a predefined range of the target level, we set to increase the 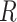 and penalize the control effort to minimize it. Hence, we build the fuzzy rule base as presented in Table I.
and penalize the control effort to minimize it. Hence, we build the fuzzy rule base as presented in Table I.
TABLE I. Supervised Fuzzy Rule Base.
| Rule number | IF | Then | |
| e error | Q parameter | R parameter | |
Rule
|
Large | Strong | Weak |
Rule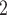
|
Moderate | Moderate | Moderate |
Rule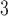
|
Small | Weak | Strong |
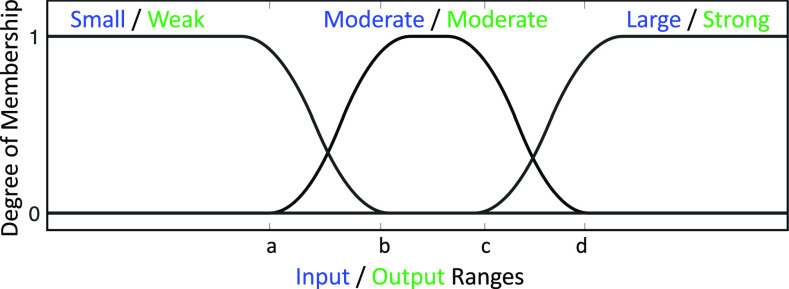
To quantify the linguistic variables presented in Table I, we employ the membership functions depicted in Fig. 2. According to the rule base (Table I), three sets of membership function for each input and output variables (i.e., error between the estimated state and the target level, 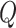 parameter, and
parameter, and 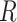 parameter) are considered.
parameter) are considered.
Fig. 2.
Input and Output Membership Functions. For each error input 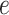 and the tune parameters
and the tune parameters 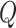 and
and 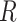 , three membership functions are employed to quantify the linguistic variables presented in Table I. Blue notations are for the error input and the green notations associated with the output tune parameters.
, three membership functions are employed to quantify the linguistic variables presented in Table I. Blue notations are for the error input and the green notations associated with the output tune parameters.
For each sets of input and outputs in Fig. 2, the middle functions belong to 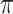 -shaped membership functions with parameters
-shaped membership functions with parameters 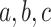 and
and 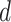 . The left one and the right ones are z-shape function with the parameter
. The left one and the right ones are z-shape function with the parameter 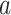 and
and 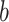 and s-shape function with parameters
and s-shape function with parameters 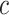 and
and 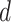 , respectively. To illustrate the shape of the membership function presented in Fig. 2, we present the middle
, respectively. To illustrate the shape of the membership function presented in Fig. 2, we present the middle 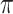 -functions as:
-functions as:
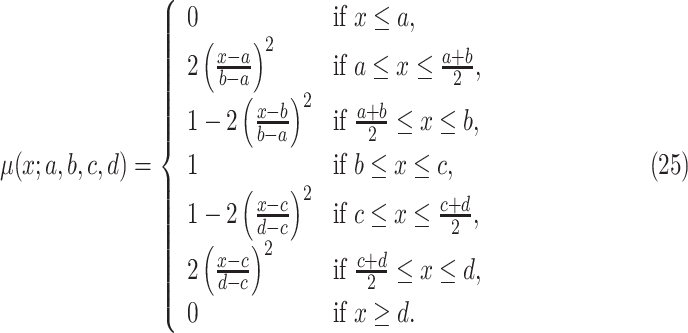 |
The s-shaped and z-shaped functions are spacial cases of the 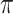 -shaped function. The values associated with variables
-shaped function. The values associated with variables 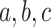 and
and 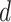 for each input and output are presented in Table II. We also use the Mamdani inference engine and centroid defuzzification to execute the fuzzy system in the proposed supervised control architectures.
for each input and output are presented in Table II. We also use the Mamdani inference engine and centroid defuzzification to execute the fuzzy system in the proposed supervised control architectures.
TABLE II. Membership Function Values in Supervised Layer (25).
| Membership Function | Variable | a | b | c | d |
| Input Error |
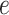 value value |
0.1 | 0.3 | 0.5 | 0.7 |
| Output Fuzzy-LQR |
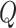 parameter parameter |
100 | 300 | 500 | 800 |
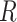 parameter parameter |
5 | 20 | 30 | 45 | |
| Output Fuzzy-MPC |
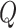 parameter parameter |
1000 | 1500 | 2000 | 2500 |
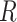 parameter parameter |
3 | 6 | 9 | 12 |
III. Results
Implementing the model-based LQR and MPC methods in addition to the proposed supervised fuzzy-LQR and fuzzy-MPC approaches, we present the results. To show the performance of MPP filter in tracking cognitive stress state and demonstrate the efficiency of implementing the proposed supervised architectures, we present open-loop and closed-loop results. We follow the developed simulation environment in the order of first inducing cognitive stress and then causing the relaxation [31]. To analyze the accuracy of proposed control architectures, we present two closed-loop scenarios: inhibition for reducing the cognitive stress levels in the first half, and excitation to increase the levels of cognitive stress estimates in the second half of the simulation. In open-loop case, there is no control applied (i.e., 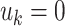 in (1)). Fig. 3 depicts The results associated with the Participant 1. The results correspond to the rest of simulated profiles are presented in supplementary materials.
in (1)). Fig. 3 depicts The results associated with the Participant 1. The results correspond to the rest of simulated profiles are presented in supplementary materials.
Fig. 3.
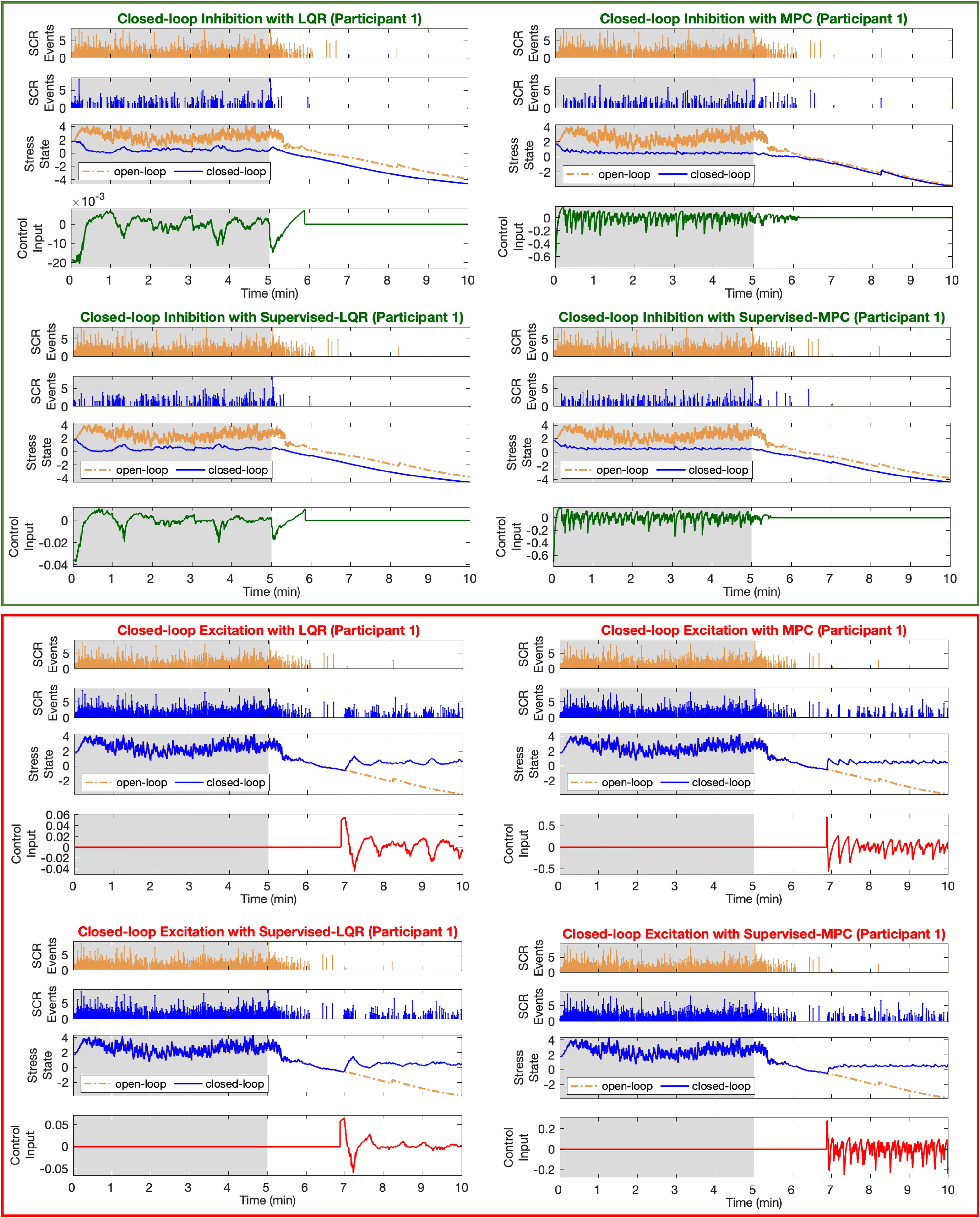
Closed-Loop Results (Participant 1). The top four panels show the closed-loop inhibition results. The bottom four panels show the closed-loop excitatory results. In each panel, the top two sub-panels show the SCR events along with their amplitudes in open-loop (orange color) and closed-loop (blue color) cases. The third sub-panel shows the estimated cognitive stress-related state. The bottom sub-panel shows the designed control implemented in real-time to close the loop and either inhibit or excite the estimated stress levels. The gray and white backgrounds correspond to the high and low arousal environmental stimuli, respectively (i.e., cognitive stress condition vs relaxing condition).
In each panel of Fig. 3, the top two sub-panels shows the simulated SCR events. The third sub-panel shows the estimated stress state. Orange and blue colors stand for open-loop and closed-loop results, respectively. The bottom sub-panels depict the resulted control signal (inhibitory control in green and excitatory control in red color).
A. Closed-Loop Inhibition
The main goal in inhibitory closed-loop case is to design the control action to reduce the levels of the estimated cognitive stress state in the first half of the simulation. To investigate the effects of supervised layer, we present each model-based LQR and MPC methods along with their fuzzy supervised pairs (top four panels of Fig. 3). As presented in Fig. 3, control system detects high arousal levels and, by deriving the appropriate action, reduces the high levels of cognitive stress state in the first half of the simulation. As the second half is related to the low arousal period (or relaxation), there is no need to apply any control (i.e., 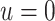 ). The left panels in Fig. 3 present the results of applying LQR and supervised fuzzy-LQR controllers. The right panels in Fig. 3 present the results of applying MPC and supervised fuzzy-MPC controllers.
). The left panels in Fig. 3 present the results of applying LQR and supervised fuzzy-LQR controllers. The right panels in Fig. 3 present the results of applying MPC and supervised fuzzy-MPC controllers.
B. Closed-Loop Excitation
The main objective in excitatory closed-loop case is to design the control action for increasing the levels of the estimated cognitive stress state in the second half of the simulation (with low arousal environmental stimuli). The results of applying each model-based LQR and MPC method along with their fuzzy supervised pairs are presented in bottom four panels of Fig. 3. The excitatory control aims to detect the low levels of estimated cognitive stress state in the second half of the simulation and derive the appropriate control action to enhance it. As the first half is related to the high arousal (or cognitive stress stimuli), there is no need to apply any control action in this period (i.e., 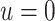 ). The left panels in Fig. 3 present the results of applying LQR and supervised fuzzy-LQR controllers. The right panels in Fig. 3 present the results of applying MPC and supervised fuzzy-MPC controllers.
). The left panels in Fig. 3 present the results of applying LQR and supervised fuzzy-LQR controllers. The right panels in Fig. 3 present the results of applying MPC and supervised fuzzy-MPC controllers.
IV. Discussion
In this research, as one of the very first in the context of closed-loop cognitive stress regulation, we proposed to use MPP filtering along with novel supervised control approaches to enhance the closed-loop control performance. In this regard, we utilized a simulation environment [31] based on the experimental data [45] to investigate the proposed methodologies in tracking and regulating internal cognitive stress state. To this end, we investigated skin conductance signal measurements and related them to the hidden stress state. To estimate the hidden state in real-time, we employed the MPP Bayesian-type filter and incorporated the information regarding the time and the amplitudes of SCR events.
The open-loop results, presented in Fig. 3, illustrate the sufficiency of internal stress state tracking in response to the changes in simulated environmental stimuli. The higher numbers/values of SCR events (i.e., orange spikes in the first sub-panel) and levels of estimated stress state (i.e. orange graph in the third sub-panel) in the first half of the simulation is because of the applied high arousal environmental stimuli. Moving toward the low arousal session (white background in Fig. 3), both the numbers/values of SCR events and the estimated stress levels drop significantly, which is due to the induced relaxing environmental stimuli in the second half of the simulation. These changes in the estimated stress state are in good agreement with the changes in SCR events: higher levels of the estimated stress state in the first half of the simulation (i.e., cognitive stress), and lower levels for the second half of the simulation (i.e., relaxation). These results verify the efficiency of the state-space approach along with the MPP filter in tracking the cognitive stress state in real-time.
To regulate the estimated stress levels in a closed-loop manner, we proposed novel supervised control approaches. Taking advantage of the state-space model as well as the real-time state estimation, we first presented the results of applying model-based system-theoretic control approaches: LQR and MPC. As the performance in these controllers highly depends on adjusting tune-parameters (i.e., weight matrices), we proposed a novel knowledge-based fuzzy supervised layer to enhance the control systems and update the control tuning parameters in real-time. The fuzzy system performs this task based on the insights into the system and changes in the control design criteria. The results of the proposed supervised control approaches in both inhibition and excitation cases are presented in Fig. 3.
In the closed-loop inhibition task (top four panels of Fig. 3), the goal is to reduce the levels of the estimated stress state in the stress session (i.e., first half of the simulation). During this period, we assume that the environmental stimuli cause the subject to feel stressed. As a result, SNS would activate the sweat glands and skin conductivity would be increased. Consequently, more activation on SCRs would be observed (top sub-panels of Fig. 3). By tracking the estimated stress state, the designed control system derives the required action for inhibition task. The control signal, presented in third sub-panel, is mainly active in the first half and results in lowering the stress state. The results of implementing supervised fuzzy-LQR approach is presented in the bottom left panel of Fig. 3. Establishing a supervised layer on top of the LQR approach results in achieving the control goal more precisely (second sup-panel) with more optimized control efforts. The results of applying MPC and supervised fuzzy-MPC approaches to inhibit the cognitive stress state are depicted in the right panels of Fig. 3. The control signal, presented in third sub-panel, is active in the first half of the simulation and tries to lower the estimated stress state. The results of implementing the supervised fuzzy system on top of the MPC system are presented in the bottom right panel of Fig. 3. This supervised architecture has improved the state tracking accuracy. Besides, the supervised layer has resulted in achieving the control goal with a more optimal control effort.
Compared to the inhibition task, the goal of implementing excitation class of controllers is to excite the low levels of arousal state. It is also important to keep the positive stress (i.e., eustress) in a desired range. The second half of the simulation in the presented environment is assumed to induce low cognitive stress condition on the person. We assume that the similar condition might happen while the subject is supposed to concentrate on the task, but due to multiple possible reasons, the cognitive engagement would be lost. The goal of elevating the estimated stress-related state has been followed by both designing the LQR and MPC approaches. The results of closed-loop excitation task are presented in the bottom four panels of Fig. 3.
First, by implementing the pure LQR method, the control action is active in the second half of the simulation, which is associated with the low arousal environmental stimuli. The LQR control action results in more activation in the simulated SCRs (first sub-panel), and leads to a higher level of estimated cognitive stress state (middle sub-panel). Enhancing the LQR closed-loop system by considering the supervised layer and updating the control tune-parameters in real-time, improves the results on both state tracking and control effort criteria. As presented in the bottom left panel of Fig. 3, the supervised fuzzy-LQR has led to a more precise state tracking with more optimal control efforts. As the second model-based approach, we implemented MPC method. First, by applying the pure MPC, the control action (third sub-panel) has elevated the levels of estimated stress state (second sub-panel). By enhancing the pure MPC structure with supervised fuzzy layer, we derive the results presented in the bottom right panel of Fig. 3. Similar to fuzzy-LQR, the supervised fuzzy-MPC architecture has improved the performance of the closed-loop excitation in both tracking accuracy and control effort minimization. To better evaluate the results of establishing supervised fuzzy system on top of model-based LQR and MPC approaches, we analyze the closed-loop results. Hence, we consider two criteria: (1) the effectiveness in reducing error term and improving the state tracking, and (2) achieving the closed-loop goal with optimized control efforts (see Table III).
TABLE III. Closed-Loop Performance Analysis (Participant 1).
| Closed-Loop Class | Controller |
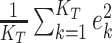
|
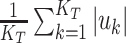
|
| Inhibition | LQR | 0.1642 | 0.0045 |
| Supervised LQR | 0.1260 | 0.0052 | |
| MPC | 0.0658 | 0.0662 | |
| supervised MPC | 0.0592 | 0.0590 | |
| Excitation | LQR | 0.0664 | 0.0074 |
| supervised LQR | 0.0640 | 0.0054 | |
| MPC | 0.0181 | 0.0621 | |
| supervised MPC | 0.0154 | 0.0338 |
In Table III, 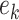 and
and 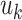 represent the tracking error and the control input, respectively.
represent the tracking error and the control input, respectively. 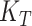 is the total time that the control is active in the loop. As presented in Table III, the supervised layer in LQR structure has decreased the tracking error
is the total time that the control is active in the loop. As presented in Table III, the supervised layer in LQR structure has decreased the tracking error 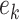 in inhibition task (0.1260 compared to 0.1642). Supervised fuzzy-LQR approach has improved state tracking accuracy by 23% with a 14% increase in the control efforts. In the excitation class, establishing supervised layer on top of the LQR system has resulted in a small improvement in state tracking accuracy (0.0640 compared to 0.0664) with a 27% decrease in total control efforts (0.0054 compared to 0.0074). Implementing the supervised fuzzy-MPC approach has resulted in more promising results. In comparison to the pure MPC, the supervised fuzzy-MPC system has reduced the tracking error by 10% and 15% in inhibition and excitation tasks, respectively. The supervised fuzzy-MPC architecture has also lead to applying less control efforts. It has reduced the total control effort by 10% and 45% in inhibition and excitation closed-loop tasks, respectively. The similar results for the rest of the simulated profiles are presented in the supplementary materials. We also analyzed the results of implementing supervised approaches on all six simulated profiles [6], [31]. A summary of overall closed-loop performance analysis for all simulated profiles are presented in Table IV.
in inhibition task (0.1260 compared to 0.1642). Supervised fuzzy-LQR approach has improved state tracking accuracy by 23% with a 14% increase in the control efforts. In the excitation class, establishing supervised layer on top of the LQR system has resulted in a small improvement in state tracking accuracy (0.0640 compared to 0.0664) with a 27% decrease in total control efforts (0.0054 compared to 0.0074). Implementing the supervised fuzzy-MPC approach has resulted in more promising results. In comparison to the pure MPC, the supervised fuzzy-MPC system has reduced the tracking error by 10% and 15% in inhibition and excitation tasks, respectively. The supervised fuzzy-MPC architecture has also lead to applying less control efforts. It has reduced the total control effort by 10% and 45% in inhibition and excitation closed-loop tasks, respectively. The similar results for the rest of the simulated profiles are presented in the supplementary materials. We also analyzed the results of implementing supervised approaches on all six simulated profiles [6], [31]. A summary of overall closed-loop performance analysis for all simulated profiles are presented in Table IV.
TABLE IV. Overall Closed-Loop Performance Analysis.
| Closed-Loop Class | Criteria | Controller | Improvement |
| Inhibition | Average Error | Supervised LQR | +22.6% |
| Supervised MPC | +23.0% | ||
| Control Effort | Supervised LQR | -35.4% | |
| Supervised MPC | +7.6% | ||
| Excitation | Average Error | Supervised LQR | +5.4% |
| Supervised MPC | +20.4% | ||
| Control Effort | Supervised LQR | -0.0% | |
| Supervised MPC | +32.9% |
As presented in Table IV, establishing supervised fuzzy system has significantly improved the MPC performance in both inhibition and excitation closed-loop systems. The proposed supervised fuzzy-MPC architecture has resulted in an enhanced tracking accuracy with more optimized control efforts. These analyses verify how the proposed supervised control architectures result in a more accurate state tracking with more optimal control efforts in MPC design. While the supervised fuzzy layer has also improved the tracking accuracy in LQR design, it has not been effective in accomplishing this task by reducing the control efforts. Supervised fuzzy-LQR system has decreased the tracking error on all six simulated profiles by average of 22.6% and 5.4% in inhibition and excitatory closed-loop classes, respectively. However, these improvements are not achieved by reducing the control efforts. Instead, in inhibition task, supervised LQR resulted in an average of 35% increase in control efforts. These analysis show that the proposed supervised architecture has great potential in improving state tracking accuracy in LQR design.
The results in this in silico study confirm that the proposed supervised architectures have great potentials to be implemented in real-world. The idea of applying a supervised layer on top of the model-based control approaches would result in performance improvement in closed-loop systems. It can also provide an excellent structure to incorporate medical expertise while designing the control. As we are dealing with a human-in-the-loop system, it is highly crucial to supervise the control systems. In the proposed supervised architectures, with respect to the nature of model-based LQR and MPC approaches, we ensure that the essential control system design criteria, such as stability and optimality, would be guaranteed. In fact, the supervised knowledge-based network would further enhance their efficiency by adjusting the control tune parameters in real-time. The proposed supervised methodologies are well-aligned to the human physiology basis and could be further investigated in similar closed-loop disorder treatments. These architectures could also be further expanded to result in adaptive and person-specific closed-loop tools.
V. Conclusion
Influenced by the recent advances in wearable technologies and inspired by the fact that skin conductance carries important information regarding internal arousal state, we developed novel closed-loop architectures for regulating the hidden arousal state. To this end, we implemented marked point process filtering approach and included the amplitude and timing of skin conductance responses. To close the loop, we proposed supervised control techniques to take advantage of the state-space representation and model-based control methods. Hence, we established supervised LQR and supervised MPC structures for regulating the cognitive stress state. We investigated the efficiency of the proposed architecture in two class of closed-loop scenarios: inhibition and excitation. The results verify the effectiveness of proposed architectures in keeping the estimated stress state within a target range with more optimal control efforts.
VI. Future Directions
As the next step of this research, we intend to investigate effects of possible safe actuation effective in regulating cognitive arousal state. By designing and performing human-subject experiments and modeling the actuation dynamics, we aim to include practical actuation while closing the loop. To this end, we can suggest to design different sets of experiments for inhibition and excitation purposes. For inhibition, one may consider designing the tasks that could increase individuals’ cognitive stress state. An example of these tasks is fear conditioning (e.g., watching the clips that may induce fear of heights in humans with acrophobia [53], [54]). While watching the clips, subjects should wear wearable devices that may collect their physiological data [55]. The goal of closing the loop would be incorporating the actuation to help them feel more relaxed. An example of real actuation in this example could be listening to relaxing music [56], [57] or performing diaphragmatic breathing [58]. For excitation purposes, one may design and perform experiments to help the subjects with enhancing their arousal state. In this regard, we can suggest to perform memory-related tasks [59] and analyze the effects of safe actuation helpful in elevating their arousal levels. In these experiments, subjects should fully engage with the tasks. The goal of closing the loop would be enhancing arousal state and improving cognitive performance. Therefore, one may measure performance state and further examine impacts of exciting actuation in both increasing arousal state and improving cognitive performance. Examples of safe exciting actuation could be drinking beverages like coffee or energy drinks [60], [61]. Employing experimental data in these closed-loop experiments, one may perform system identification to model these safe actuation’s dynamics. Once we learn how a specific actuation would affect one’s arousal state, we may incorporate their dynamics while closing the loop.
In the aforementioned experiments, we expect to observe variable responses among different subjects. Moreover, as uncertainty in model parameters presented in the state-space representation is unavoidable, it is also beneficial to research on adaptive and robust control design to further enhance the control systems [62]. Another future direction of this research could be extending the proposed architectures and considering adaptive and robust properties in both the state estimation and control design stages. The perspective closed-loop systems would be adaptive to the uncertainty in the modeled dynamics and robust to unexpected disturbances. Consequently, the idea of closed-loop cognitive stress regulation would be applicable in real-world situations. In an actual environment, a wrist-worn device would collect the skin conductance signal. Utilizing the proposed methods, the internal arousal state would be estimated in real-time. Taking advantage of the proposed experiments, one may incorporate actuation dynamics while implementing supervised control architectures for closing the loop regulating the arousal state.
Supplementary Materials
Supplementary materials.
Funding Statement
This work was supported in part by NSF CAREER Award through Multimodal Intelligent Noninvasive brain state Decoder for WearableAdapTive Closed-loop arcHitectures (MINDWATCH) under Grant 1942585, in part by NSF Grant through Wearable-Machine Interface Architectures (CRII: CPS) under Grant 1755780, and in part by New York University Start-up funds.
Contributor Information
Hamid Fekri Azgomi, Email: hfekriazgomi@uh.edu.
Rose T. Faghih, Email: rfaghih@nyu.edu.
References
- [1].Bubonya M., Cobb-Clark D. A., and Wooden M., “Mental health and productivity at work: Does what you do matter?,” Labour Econ., vol. 46, pp. 150–165, 2017. [Google Scholar]
- [2].G. . Kassymova et al. , “Impact of stress on creative human resources and psychological counseling in crises,” Int. J. Educ. Inf. Technol., vol. 13, no. 1, pp. 26–32, 2019. [Google Scholar]
- [3].Simblett S., Birch J., Matcham F., Yaguez L., and Morris R., “A systematic review and meta-analysis of e-mental health interventions to treat symptoms of posttraumatic stress,” JMIR Ment. Health, vol. 4, no. 2, 2017, Art. no. e5558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Mackersie C. L. and Calderon-Moultrie N., “Autonomic nervous system reactivity during speech repetition tasks: Heart rate variability and skin conductance,” Ear Hear., vol. 37, pp. 118S–125S, 2016. [DOI] [PubMed] [Google Scholar]
- [5].Kupriyanov R. and Zhdanov R., “The eustress concept: Problems and outlooks,” World J. Med. Sci., vol. 11, no. 2, pp. 179–185, 2014. [Google Scholar]
- [6].Wickramasuriya D. S., Amin M., and Faghih R. T., “Skin conductance as a viable alternative for closing the deep brain stimulation loop in neuropsychiatric disorders,” Front. Neurosci., vol. 13, 2019, Art. no. 780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Azgomi H. F., Wickramasuriya D. S., and Faghih R. T., “State-space modeling and fuzzy feedback control of cognitive stress,” in Proc. 41st Annu. Int. Conf. IEEE Eng. Med. Biol. Soc., 2019, pp. 6327–6330. [DOI] [PubMed] [Google Scholar]
- [8].Leondes C. T., Advances in Control Systems: Theory and Applications. Amsterdam, Netherlands: Elsevier, 2014. [Google Scholar]
- [9].Khodaei M. J., Candelino N., Mehrvarz A., and Jalili N., “Physiological closed-loop control (PCLC) systems: Review of a modern frontier in automation,” IEEE Access, vol. 8, pp. 23965–24005, 2020. [Google Scholar]
- [10].Copp D. A., Gondhalekar R., and Hespanha J. P., “Simultaneous model predictive control and moving horizon estimation for blood glucose regulation in type 1 diabetes,” Optimal Control Appl. Methods, vol. 39, no. 2, pp. 904–918, 2018. [Google Scholar]
- [11].Chakrabarty A., Zavitsanou S., Doyle F. J., and Dassau E., “Event-triggered model predictive control for embedded artificial pancreas systems,” IEEE Trans. Biomed. Eng., vol. 65, no. 3, pp. 575–586, Mar. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Seel T., Werner C., Raisch J., and Schauer T., “Iterative learning control of a drop foot neuroprosthesis-generating physiological foot motion in paretic gait by automatic feedback control,” Control Eng. Pract., vol. 48, pp. 87–97, 2016. [Google Scholar]
- [13].Azgomi H. F., Hahn J.-O., and Faghih R. T., “Closed-loop fuzzy energy regulation in patients with hypercortisolism via inhibitory and excitatory intermittent actuation,” Front. Neurosci., vol. 15, 2021, Art. no. 909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Wickramasuriya D. S. and Faghih R. T., “A cortisol-based energy decoder for investigation of fatigue in hypercortisolism,” in Proc. 41st Annu. Int. Conf. IEEE Eng. Med. Biol. Soc., 2019, pp. 11–14. [DOI] [PubMed] [Google Scholar]
- [15].Azgomi H. F. and Faghih R. T., “A wearable brain machine interface architecture for regulation of energy in hypercortisolism,” in Proc. 53rd Asilomar Conf. Signals Syst. Comput., 2019, pp. 254–258. [Google Scholar]
- [16].Yang Y. and Shanechi M. M., “An adaptive and generalizable closed-loop system for control of medically induced coma and other states of anesthesia,” J. Neural Eng., vol. 13, no. 6, 2016, Art. no. 66019. [DOI] [PubMed] [Google Scholar]
- [17].Savoca A. and Manca D., “A physiologically-based approach to model-predictive control of anesthesia and analgesia,” Biomed. Signal Process. Control, vol. 53, 2019, Art. no. 101553. [Google Scholar]
- [18].Krieger A. and Pistikopoulos E. N., “Model predictive control of anesthesia under uncertainty,” Comput. Chem. Eng., vol. 71, pp. 699–707, 2014. [Google Scholar]
- [19].McDermott H. J. and Sinclair N. C., “Feedback control for deep brain stimulation for motor disorders,” Healthcare Technol. Lett., vol. 7, no. 3, pp. 72–75, 2020. [Google Scholar]
- [20].Wickramasuriya D. S. and Faghih R. T., “A Bayesian filtering approach for tracking arousal from binary and continuous skin conductance features,” IEEE Trans. Biomed. Eng., vol. 67, no. 6, pp. 1749–1760, Jun. 2020. [DOI] [PubMed] [Google Scholar]
- [21].Amin M. R. and Faghih R. T., “Inferring autonomic nervous system stimulation from hand and foot skin conductance measurements,” in Proc. 52nd Asilomar Conf. Signals Syst. Comput., 2018, pp. 655–660. [Google Scholar]
- [22].Rosebrock L. E., Hoxha D., Norris C., Cacioppo J. T., and Gollan J. K., “Skin conductance and subjective arousal in anxiety, depression, and comorbidity,” J. Psychophysiol., vol. 31, pp. 145–157, 2017. [Google Scholar]
- [23].Buss K. A., Jaffee S., Wadsworth M. E., and Kliewer W., “Impact of psychophysiological stress-response systems on psychological development: Moving beyond the single biomarker approach.” Develop. Psychol., vol. 54, no. 9, pp. 1601–1605, 2018. [DOI] [PubMed] [Google Scholar]
- [24].Huang J. et al. , “Impact of brain arousal and time-on-task on autonomic nervous system activity in the wake-sleep transition,” BMC Neurosci., vol. 19, no. 1, 2018, Art. no. 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Amin M. R. and Faghih R. T., “Identification of sympathetic nervous system activation from skin conductance: A sparse decomposition approach with physiological priors,” IEEE Trans. Biomed. Eng., vol. 68, no. 5, pp. 1726–1736, May 2021. [DOI] [PubMed] [Google Scholar]
- [26].Tang Y.-Y. et al. , “Central and autonomic nervous system interaction is altered by short-term meditation,” Proc. Nat. Acad. Sci., vol. 106, no. 22, pp. 8865–8870, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Menghini L., Gianfranchi E., Cellini N., Patron E., Tagliabue M., and Sarlo M., “Stressing the accuracy: Wrist-worn wearable sensor validation over different conditions,” Psychophysiol., vol. 56, no. 11, 2019, Art. no. e13441. [DOI] [PubMed] [Google Scholar]
- [28].Nepal O., Jha R., Bhattarai A., Khadka P., and Kapoor B., “Galvanic skin response as a simple physiology lab teaching tool-an alternative indicator of sympathetic arousal,” Kathmandu Univ. Med. J., vol. 62, no. 2, pp. 156–160, 2018. [PubMed] [Google Scholar]
- [29].Amin M. R. and Faghih R. T., “Sparse deconvolution of electrodermal activity via continuous-time system identification,” IEEE Trans. Biomed. Eng., vol. 66, no. 9, pp. 2585–2595, Sep. 2019. [DOI] [PubMed] [Google Scholar]
- [30].Wickramasuriya D. S., Qi C., and Faghih R. T., “A state-space approach for detecting stress from electrodermal activity,” in Proc. 40th Annu. Int. Conf. IEEE Eng. Med. Biol. Soc., 2018, pp. 3562–3567. [DOI] [PubMed] [Google Scholar]
- [31].Azgomi H. F., Cajigas I., and Faghih R. T., “Closed-loop cognitive stress regulation using fuzzy control in wearable-machine interface architectures,” IEEE Access, vol. 9, pp. 106202–106219, 2021. [Google Scholar]
- [32].Wickramasuriya D. S. and Faghih R. T., “A marked point process filtering approach for tracking sympathetic arousal from skin conductance,” IEEE Access, vol. 8, pp. 68499–68513, 2020. [Google Scholar]
- [33].Vissani M., Isaias I. U., and Mazzoni A., “Deep brain stimulation: A review of the open neural engineering challenges,” J. Neural Eng., vol. 17, no. 5, 2020, Art. no. 051002. [DOI] [PubMed] [Google Scholar]
- [34].He W., Meng T., He X., and Ge S. S., “Unified iterative learning control for flexible structures with input constraints,” Automatica, vol. 96, pp. 326–336, 2018. [Google Scholar]
- [35].He W., Wang T., He X., Yang L.-J., and Kaynak O., “Dynamical modeling and boundary vibration control of a rigid-flexible wing system,” IEEE/ASME Trans. Mechatronics, vol. 25, no. 6, pp. 2711–2721, Dec. 2020. [Google Scholar]
- [36].He W., Meng T., He X., and Sun C., “Iterative learning control for a flapping wing micro aerial vehicle under distributed disturbances,” IEEE Trans. Cybern., vol. 49, no. 4, pp. 1524–1535, Apr. 2019. [DOI] [PubMed] [Google Scholar]
- [37].Hajizadeh I., Samadi S., Sevil M., Rashid M., and Cinar A., “Performance assessment and modification of an adaptive model predictive control for automated insulin delivery by a multivariable artificial pancreas,” Ind. Eng. Chem. Res., vol. 58, no. 26, pp. 11506–11520, 2019. [Google Scholar]
- [38].Ramasamy V., Sidharthan R. K., Kannan R., and Muralidharan G., “Optimal tuning of model predictive controller weights using genetic algorithm with interactive decision tree for industrial cement kiln process,” Processes, vol. 7, no. 12, 2019, Art. no. 938. [Google Scholar]
- [39].Santos J. E. W., Trierweiler J. O., and Farenzena M., “Robust tuning for classical mpc through the multi-scenarios approach,” Ind. Eng. Chem. Res., vol. 58, no. 8, pp. 3146–3158, 2019. [Google Scholar]
- [40].Lee J. Van der, Svrcek W., and Young B., “A tuning algorithm for model predictive controllers based on genetic algorithms and fuzzy decision making,” ISA Trans., vol. 47, no. 1, pp. 53–59, 2008. [DOI] [PubMed] [Google Scholar]
- [41].Zhao R., Wong P., Xie Z., and Zhao J., “Real-time weighted multi-objective model predictive controller for adaptive cruise control systems,” Int. J. Automot. Technol., vol. 18, no. 2, pp. 279–292, 2017. [Google Scholar]
- [42].Ali E. and Al-Ghazzawi A., “On-line tuning of model predictive controllers using fuzzy logic,” Can. J. Chem. Eng., vol. 81, no. 5, pp. 1041–1051, 2003. [Google Scholar]
- [43].Ko H.-S. and Jatskevich J., “Power quality control of wind-hybrid power generation system using fuzzy-LQR controller,” IEEE Trans. Energy Convers., vol. 22, no. 2, pp. 516–527, Jun. 2007. [Google Scholar]
- [44].Killian M., Mayer B., and Kozek M., “Hierachical fuzzy MPC concept for building heating control,” IFAC Proc. Volumes, vol. 47, no. 3, pp. 12048–12055, 2014. [Google Scholar]
- [45].Birjandtalab J., Cogan D., Pouyan M. B., and Nourani M., “A non-EEG biosignals dataset for assessment and visualization of neurological status,” in Proc. IEEE Int. Workshop Signal Process. Syst., 2016, pp. 110–114. [Google Scholar]
- [46].Goldberger A. L. et al. , “Physiobank, physiotoolkit, and physionet: Components of a new research resource for complex physiologic signals,” Circulation, vol. 101, no. 23, pp. e215–e220, 2000. [DOI] [PubMed] [Google Scholar]
- [47].McCullagh P. and Nelder J. A., Generalized Linear Models. Evanston, IL, USA: Routledge, 2019. [Google Scholar]
- [48].Zenere A. and Zorzi M., “Model predictive control meets robust Kalman filtering,” IFAC-PapersOnLine, vol. 50, no. 1, pp. 3774–3779, 2017. [Google Scholar]
- [49].Bemporad A., Heemels W. M. H., and Schutter B. De, “On hybrid systems and closed-loop MPC systems,” IEEE Trans. Autom. Control, vol. 47, no. 5, pp. 863–869, May 2002. [Google Scholar]
- [50].Kwon W. and Pearson A., “A modified quadratic cost problem and feedback stabilization of a linear system,” IEEE Trans. Autom. Control, vol. AC-22, no. 5, pp. 838–842, Oct. 1977. [Google Scholar]
- [51].Keerthi S. and Gilbert E. G., “Optimal infinite-horizon feedback laws for a general class of constrained discrete-time systems: Stability and moving-horizon approximations,” J. Optim. Theory Appl., vol. 57, no. 2, pp. 265–293, 1988. [Google Scholar]
- [52].Worthmann K., “Stability analysis of unconstrained receding horizon control schemes,” Ph.D. dissertation, Bayreuth Univ., 2011. [Google Scholar]
- [53].Diemer J., Lohkamp N., Mühlberger A., and Zwanzger P., “Fear and physiological arousal during a virtual height challenge-effects in patients with acrophobia and healthy controls,” J. Anxiety Disord., vol. 37, pp. 30–39, 2016. [DOI] [PubMed] [Google Scholar]
- [54].Wiederhold B. K. and Bouchard S., “Fear of heights (acrophobia): Efficacy and lessons learned from psychophysiological data,” in Advances in Virtual Reality and Anxiety Disorders. Berlin, Germany: Springer, 2014, pp. 119–144. [Google Scholar]
- [55].Kritikos J., Tzannetos G., Zoitaki C., Poulopoulou S., and Koutsouris D., “Anxiety detection from electrodermal activity sensor with movement & interaction during virtual reality simulation,” in Proc. 9th Int. IEEE/EMBS Conf. Neural Eng., 2019, pp. 571–576. [Google Scholar]
- [56].Russo F. A. et al. , “Predicting musically induced emotions from physiological inputs: Linear and neural network models,” Front. Psychol., vol. 4, 2013, Art. no. 468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Du M., Jiang J., Li Z., Man D., and Jiang C., “The effects of background music on neural responses during reading comprehension,” Sci. Rep., vol. 10, no. 1, pp. 1–10, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Hopper S. I., Murray S. L., Ferrara L. R., and Singleton J. K., “Effectiveness of diaphragmatic breathing for reducing physiological and psychological stress in adults: A quantitative systematic review,” JBI Evidence Synth., vol. 17, no. 9, pp. 1855–1876, 2019. [DOI] [PubMed] [Google Scholar]
- [59].N. von Janczewski, Wittmann J., Engeln A., Baumann M., and Krauß L., “A meta-analysis of the n-back task while driving and its effects on cognitive workload,” Transp. Res. Part F: Traffic Psychol. Behav., vol. 76, pp. 269–285, 2021. [Google Scholar]
- [60].McLellan T. M., Caldwell J. A., and Lieberman H. R., “A review of caffeine’s effects on cognitive, physical and occupational performance,” Neurosci. Biobehavioral Rev., vol. 71, pp. 294–312, 2016. [DOI] [PubMed] [Google Scholar]
- [61].Quinlan P. T. et al. , “The acute physiological and mood effects of tea and coffee: The role of caffeine level,” Pharmacol. Biochem. Behav., vol. 66, no. 1, pp. 19–28, 2000. [DOI] [PubMed] [Google Scholar]
- [62].Bolus M. F., Willats A. A., Rozell C. J., and Stanley G. B., “State-space optimal feedback control of optogenetically driven neural activity,” J. Neural Eng., vol. 18, no. 3, 2021, Art. no. 036006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.