A Bayesian hierarchical change point model with parameter constraints

Abstract

Alzheimer’s disease is the leading cause of dementia among adults aged 65 or above. Alzheimer’s disease is characterized by a change point signaling a sudden and prolonged acceleration in cognitive decline. The timing of this change point is of clinical interest because it can be used to establish optimal treatment regimens and schedules. Here, we present a Bayesian hierarchical change point model with a parameter constraint to characterize the rate and timing of cognitive decline among Alzheimer’s disease patients. We allow each patient to have a unique random intercept, random slope before the change point, random change point time, and random slope after the change point. The difference in slope before and after a change point is constrained to be nonpositive, and its parameter space is partitioned into a null region (representing normal aging) and a rejection region (representing accelerated decline). Using the change point time, the estimated slope difference, and the threshold of the null region, we are able to (1) distinguish normal aging patients from those with accelerated cognitive decline, (2) characterize the rate and timing for patients experiencing cognitive decline, and (3) predict personalized risk of progression to dementia due to Alzheimer’s disease. We apply the approach to data from the Religious Orders Study, a national cohort study of aging Catholic nuns, priests, and lay brothers.

1. Introduction

As adults age, they undergo subtle cognitive changes that may not initially manifest as clinical symptoms. These cognitive changes are often gradual, making them difficult to distinguish at first from more debilitating cognitive decline. However, as individuals approach dementia, cognitive impairment becomes more obvious, and the decline in cognitive function begins to accelerate. Once dementia sets in, the cognitive decline pattern differs markedly from the pattern in normal aging adults.^1–3 Alzheimer’s disease (AD) is the leading cause of dementia among adults aged 65 or above, resulting in progressive memory loss, impaired thinking and disorientation, as well as changes in personality and mood. AD is marked histologically by the degeneration of brain neurons, primarily in the cerebral cortex, and by the presence of neurofibrillary tangles and plaques containing betaamyloid.⁴

Physiologically, AD presents as a continuum of syndromes ranging from no cognitive impairment (NCI) to mild cognitive impairment (MCI), and finally to dementia.⁵ There is heterogeneity in the onset of the disease: some individuals may experience cognitive decline early, while for others, the onset of disease occurs later in life.¹ There are a number of other defining features associated with the disease. First, for those who develop AD-related dementia, it is believed that an accelerated decline in cognitive function will occur at a certain time point (or “change point”) during the course of cognitive decline, leading ultimately to dementia.^5,6 However, the timing of the change point is highly variable and is influenced by patient-specific factors, such as age, family history, and lifestyle factors.^7,8 It is therefore critical to monitor the occurrence of this acceleration so that clinicians and care providers can pursue timely treatments.⁹ Second, the slope before the change point varies: some adults may show a linear cognitive decline prior to the point of accelerated decline, while others may show relatively stable performance prior to the change point.¹⁰ Third, the slope after the change point is nonincreasing, as cognitive decline progresses more rapidly following the change point.⁵ An appropriate statistical model should therefore take into account the above features. In particular, the model should restrict the change in slope following the change point to be nonpositive, with no change in slope occurring only for adults who do not experience or only temporarily experience cognitive decline.

Numerous random effect change point models have been formulated to examine the acceleration of cognitive change.^{5,6,9,11–13} However, this prior research has focused primarily on methods to characterize the decline in cognitive function for diseased patients only, without attempting to distinguish normal aging from diseased cognitive decline, or to predict the likelihood of cognitive decline in advance of clinical diagnosis. Ji et al.¹⁴ recognized that not every older adult experiences diseased cognitive decline and developed a hypothesis testing approach to assess whether a biomarker change point occurred during long-term follow-up. If the hypothesis test confirmed the presence of a change point, the authors then fit a general bilinear model to estimate a global change point time for all individuals. However, this approach did not allow for subject-specific change points. Slate and Turnbull¹⁵ used a subject-specific change point model to model the growth of prostate-specific antigen. The authors restricted the slope after the change point to be larger than a fixed, positive lower bound. The purpose of this restriction was to aid model identifiability by ensuring that the slopes before and after the change point could be distinguished from one another during estimation. However, the authors assumed a separate normal distribution, independent of other model parameters, for the slope after the change point, which may be restrictive in some settings. In our application, for example, patients with low cognitive scores at baseline will likely have more precipitous declines following AD onset compared to patients with higher baseline scores. In addition, Slate and Turnbull¹⁵ assumed a prespecified value for the lower bound of the slope following the change point rather than allowing this to be estimated from the data. Through simulations, we show that fixing the threshold a priori can lead to poor inference if the threshold parameter is misspecified, which is likely in practice.

In this article, we develop a flexible model to (1) distinguish normal aging patients from patients with diseased cognitive decline who are not yet formally diagnosed as dementia, which will help to identify the profile of healthy cognitive aging and diseased cognitive aging, (2) estimate subject-specific change points and rates of cognitive decline, which will help to characterize cognitive decline, and (3) develop a prediction model to assist with subject-specific disease prognoses to identify patients at high risk of advancing to dementia.

The gold standard diagnosis of AD requires brain autopsy, whereby a neuropathologist diagnoses AD if two pathognomonic signs of AD (amyloid plaques and neuritic tangles) are found in brain tissue. In living patients, the diagnosis of AD is typically performed through clinical evaluation.¹⁶ However, as recent research shows, the sensitivity of the clinical diagnosis ranges from 70.9% to 93%, and the specificity ranges from 44.3% to 91%.^17,18 In addition, physicians often feel uncomfortable in providing a timely diagnosis of AD due to the limitation of the current diagnostic approach.¹⁹ Hence, there is a need to develop a prediction tool to predict the risk of disease progression to dementia in the next several years without increasing healthcare costs. While the clinical practicality of such a tool may be limited at present to research studies that collect large amounts of longitudinal data, such a tool might eventually assist clinicians (e.g. geriatricians, geriatric psychiatrists, neurologists, neuropsychologists) in deciding whether to implement treatment and care management plans in the hopes of delaying dementia onset and improving quality of life. Furthermore, this tool would aid patients in planning ahead while they are still able to make important decisions regarding their care, support, and financial or legal matters. In this study, we focus on using data from a neuropsychological test battery since these are the primary tools for evaluating cognitive decline. These measurements are comprehensive, less invasive, and provide the information needed to determine the syndromal cognitive stage. Although there are other biomarkers and approaches (e.g. neuroimaging) available, the majority are not available for routine use due to expense, risks, and the need for specialized equipment or laboratories.^20,21 Hence, it is critical to develop statistical methods that can be easily implemented to improve the prognosis of cognitive decline and to help triage patients when deciding whether further diagnostic biomarker testing is necessary.

To address these goals, we propose a Bayesian change point model for the analysis of cognitive decline for older adults. Our proposed model has several attractive features. First, it incorporates correlated subject-specific intercepts, slopes before change points, and slopes after change points. Second, it constrains the difference in slope before and after change points to be nonpositive, since it is well documented that cognitive decline accelerates following the onset of AD.^10,14 Third, it defines a clinically meaningful “null region” in which the difference in slope before and after the change point is effectively 0, representing NCI, where the threshold for this null region is estimated from the data rather than fixed at a prespecified value. While this threshold is similar in spirit to Slate and Turnbull,¹⁵ we use it in a fundamentally different way—namely, as a prognostic tool to determine the likelihood of dementia due to AD rather than as a device to ensure identifiable model parameters. Through simulation studies, we demonstrate that a data-driven approach to estimating the threshold leads to more accurate and precise parameter estimates. Fourth, the model allows for a random change point time for each individual. Finally, the model can make personalized prediction of the risk of progression to dementia due to AD as individuals age. For implementation, we propose an efficient Markov chain Monte Carlo (MCMC) algorithm that relies in large part on easily sampled Gibbs steps. Our approach can be useful for clinicians or researchers involved in large cohort AD research studies (such as those in AD research centers) as well as memory clinics where extensive longitudinal cognitive data are available.

In the next section, we describe the Religious Orders Study (ROS) dataset. Then, we present a Bayesian hierarchical random change point model with a parameter constraint and discuss the estimation approach. This is followed by the Simulation study section where we evaluate the model’s performance using a simulation study. In the penultimate section, we apply the approach to the data of ROS and discuss the results. We summarize the approach in the final section.

2. Motivating dataset: The ROS

Our analysis was based on the ROS,¹⁶ a longitudinal clinical cohort study of aging Catholic nuns, priests, and lay brothers from more than 40 religious orders across the United States. Participants without known dementia were enrolled into the study, and data were collected annually for more than 20years. Clinical evaluation of cognitive function was performed annually, and patients were categorized as NCI, MCI, or dementia due to AD (hereafter referred to as “AD”) at each annual visit. Clinical diagnoses were performed by assessment of cognitive impairment by neuropsychologists and determination of disease stages by clinical consensus using standard criteria.⁵ In general, patients’ disease stage could switch between NCI and MCI over the course of the study. However, because AD is currently an irreversible condition,²² it was unlikely for disease stage to return to either MCI or NCI once a patient was diagnosed as AD unless there was a misdiagnosis. The investigators collected measures of cognitive function (e.g. episodic memory, semantic memory, and working memory), motor function (e.g. manual strength, manual dexterity, and gait), disabilities and blood tests, genetic risk factors, and demographic and psychological traits. For our analysis, we used a well-validated, global measure of cognitive function (“global cog”) as the outcome, which is a composite score of cognitive measures.⁴ This composite score is derived from 19 tests that cover five cognitive domains, namely episodic memory, semantic memory, working memory, perceptual speed, and visuo-spatial ability. The composite scores are created by converting each test to a z-score and averaging the z-scores from the five domains. Higher scores indicate better cognitive function. Detailed information about the individual tests and the derivation of the composite measure has been previously reported.^16,23

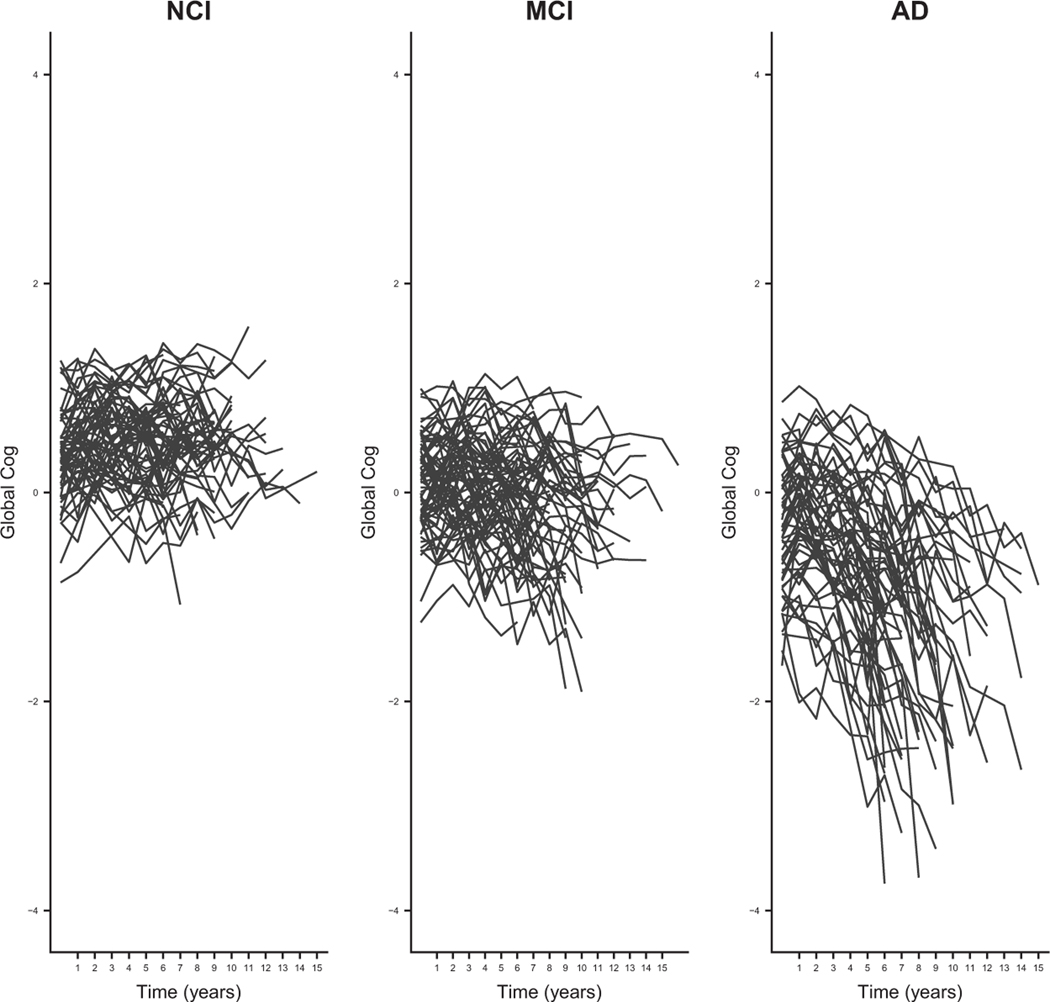
Figure 1 shows 3 panels of global cog functional trajectories for a 20% random sample of ROS patients, resulting in an analytic sample of 189 patients. We chose subsample of patients for illustrative purpose and to expedite the case study presented in the Application to ROS data section. This random sample was more or less equally split between NCI, MCI, and AD patients, where disease stage was defined according to the diagnosis at the final clinical visit. Of these 189 patients, 13.5% of the patients reversed their disease stage from AD to MCI or NCI, 32.8% patients switched between MCI and NCI, 30.7% patients stayed at NCI, 11.6% progressed from NCI to MCI to AD, 3.7% transitioned from NCI to MCI, and 6.3% transitioned directly from NCI to AD based on clinicians’ assessments over the course of the study. The global cog scores ranged from –4 to 2 in the entire available ROS data. As expected, participants with NCI tended to have higher scores compared to patients with MCI and AD, with the mean score at the last clinical visit of 0.44, while MCI patients generally had higher scores than AD patients with the mean score of –0.24. For AD patients, the mean score at the last clinical visit is –1.75. Although no participants had known AD-type dementia at enrollment, over the course of the study, some participants appeared to develop disease more rapidly than others. The left panel shows global cog scores for the NCI participants. The scores fluctuated between –1 and 2, but overall, there was no downward trend in the trajectories. For MCI patients (the middle panel), the global cog measurements fluctuated between –2 and 1, suggesting increased cognitive impairment, with a slight downward trend over time. For AD patients (the right panel), the global cog measurements fluctuated between –4 and 1 and generally showed a sharp decline at some point during the study, potentially heralding the onset of AD.

Figure 1.

Cognitive function trajectories for patients diagnosed with NCI, MCI, and AD at the final clinical visit for the sample of 189 patients in the ROS data.

NCI: no cognitive impairment; MCI: mild cognitive impairment; AD: Alzheimer’s disease.

3. Model and estimation

3.1. Model

In this section, we describe a Bayesian constrained random change point model for cognitive functional trajectories. For each individual, we estimate if and when a change point occurs, as well as the slope before and after the change point. Our model allows for individuals to have unique random intercepts, random slopes before the change points, random change point times, and random slopes after the change points. The slope difference before and after the change point is constrained to be nonpositive, as we expect a more precipitous decline following the change point. However, we do not constrain the slope before the change point since its pattern varies.¹⁰ Thus, our model enables us to achieve two goals simultaneously: (1) to identify whether an individual’s cognitive trajectory experiences a change point during the follow-up and (2) to estimate the rate and timing of rapid cognitive decline if a change point occurs.

We consider a piecewise-linear random change point model characterized by potentially different slopes before and after a random change point

$$Y_{ij}={\beta }_{1i}+{\beta }_{2i}{t}_{ij}+{\beta }_{3i}{\left(t_{ij}-{\kappa }_i\right)}_{+}+z_{ij}^{\prime }{\mathit{\beta }}_{4i}+{ϵ}_{ij}$$ (1)

where for individual $i=1,\dots ,n$ at follow-up visit $j=1,\dots ,n_i$, Y_ij is the continuous outcome measure (e.g. global cog), t_ij is the measurement time, z_ij is a m × 1 vector of individual level predictors (i.e. age and education), $w_{+}=w$ if $w\ge 0$ and 0 otherwise, $k_i$ denotes an unknown random change point, and ϵ_ij is an error term, which follows a normal $\text{N}\left(0,{\sigma }_{ϵ}^2\right)$ distribution; alternative distributions, such as the skew normal or finite mixture models, could be used to accommodate additional features of the data, such as skewness or multimodality.

Because AD onset has a high degree of heterogeneity in its progression, we use subject-specific parameters for all terms in the model. For individual i, β₁i denotes the random intercept, β₂i is the random slope before the change point $k_i$, and β₃i is the difference in random slopes before and after the change point $k_i$. For brevity, we refer to β₃i below as simply the “slope decrement” after the change point $k_i$. As previous research has shown, cognitive decline accelerates after the change point for AD patients, but cognitive trajectories are relatively stable for normal aging patients. Hence, we assume that the slope decrement β_3i is less than or equal to zero, which ensures clinically and statistically meaningful estimation for the slope after the change point. The parameter β_4i is the m × 1 vector of coefficients corresponding to the predictors z_ij. The conditional likelihood function of $\mathit{Y}=\left(y_{ij}\right)$ given all parameters and data ${\mathit{x}}_{ij}={\left(1,t_{ij},{\left(t_{ij}-{\kappa }_i\right)}_{+},z_{ij}^{\prime }\right)}^{\prime }$ and $\mathit{X}=\left({\mathit{x}}_{ij}\right)$, which is an N × q matrix, where $N={\sum }_{i=1}^n{n}_i$, is

$$L\left(\mathit{Y}\mid \mathit{\beta },\mathit{\kappa },{\sigma }_{ϵ}^2,\mathit{X}\right)=\prod _{i=1}^n\prod _{j=1}^{n_i}\frac{1}{\sqrt{2\pi }{\sigma }_{ϵ}}\exp \left\{-\frac{1}{2{\sigma }_{ϵ}^2}{\left(y_{ij}-{\mathit{x}}_{ij}^{\prime }{\mathit{\beta }}_i\right)}^2\right\}$$

where $\mathit{\kappa }={\left({\kappa }_1,{\kappa }_2,\dots ,{\kappa }_n\right)}^{\prime }$ and $\mathit{\beta }={\left({\mathit{\beta }}_1^{\prime },{\mathit{\beta }}_2^{\prime },\dots ,{\mathit{\beta }}_n^{\prime }\right)}^{\prime }$ in which ${\mathit{\beta }}_i={\left({\beta }_{i1},{\beta }_{i2},{\beta }_{i3},{\mathit{\beta }}_{i4}^{\prime }\right)}^{\prime }$ is a q × 1 vector of regression parameter. The conditional likelihood can be maximized subject to the constraint ${\beta }_{3i}\le 0$ for $i=1,2,\dots ,n$. However, calculation of the maximum likelihood estimator subject to constraints is often difficult,²⁴ since estimates of ${\beta }_{3i}$ for individuals without cognitive impairment fall on the boundary of the parameter space (i.e. ${\widehat{\beta }}_{3i}$ is equal to or close to 0). Hence, we use Bayesian methods for parameter estimation, since order constraints can be readily incorporated into the prior distributions for the model parameters.

3.2. Prior specification

For normal aging individuals, the slopes after the change points may be minimal, in which case we can ignore their effects. However, it is not practical to assume the slope decrement is exactly equal to zero. Instead, we introduce a “null region” within which the effect is negligible, representing stable cognitive trajectories. We follow Neelon and Dunson²⁵ to select a prior distribution for β which achieves the following two goals simultaneously: (1) constrains the trajectory to be nonincreasing after the change point and (2) allows for a null region. Hence, we express the constrained slope decrement for patient $i,{\beta }_{3i}$, in terms of a latent, unconstrained slope decrement ${\beta }_{3i}^{\ast }$, namely, we set ${\beta }_{3i}={11}_{\{{\beta }_{3i}^{\ast }<\delta \}}{\beta }_{3i}^{\ast }$, $i=1,2,\dots ,n$, where δ is a threshold parameter representing clinically relevant cognitive decline, and ${11}_{\{.\}}$ is the indicator function. This representation facilitates posterior computation because it is often easier to sample from an unconstrained conditional distribution and apply a suitable constraint as part of the MCMC algorithm than it is to draw directly from a constrained posterior itself.²⁶ The parameter ${\beta }_{3i}^{\ast }$ is an unconstrained latent slope decrement, and d is a small negative threshold above which the slope decrement ${\beta }_{3i}^{\ast }$ is effectively zero. Specifically, for individual i, if ${\beta }_{3i}^{\ast }<\delta$ then ${\mathit{\beta }}_i={\mathit{\beta }}_i^{\ast }={\left({\beta }_{1i}^{\ast },{\beta }_{2i}^{\ast },{\beta }_{3i}^{\ast },{\mathit{\beta }}_{4i}^{\ast \prime }\right)}^{\prime }$, which ensures feature (1); otherwise if $\delta \le {\beta }_{3i}^{\ast }\le 0$, then ${\mathit{\beta }}_i={\mathit{\beta }}_{i0}^{\ast }={\left({\beta }_{1i}^{\ast },{\beta }_{2i}^{\ast },0,{\mathit{\beta }}_{4i}^{\ast \prime }\right)}^{\prime }$ here, we set ${\beta }_{3i}=0$ to ensure feature (2). We choose a conditionally conjugate MVN $\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right)$ prior for the unconstrained parameter ${\mathit{\beta }}_i^{\ast }$, where ${\mathit{\beta }}_0$ is the population mean, and ${\mathbf{\text{Σ}}}_{\beta }$ is an unstructured covariance matrix that accounts for dependence in the model parameters. This is relevant in our application, as we expect AD patients have much steeper slopes before and after change points compared to the MCI and NCI patients.⁵ More formally, given the threshold δ, the joint prior for $\left(\mathit{\beta },{\mathit{\beta }}^{\ast }\right)$ is

$$\begin{gathered} \pi \left(\mathit{\beta },{\mathit{\beta }}^{\ast }\mid \delta ,{\mathbf{\text{Σ}}}_{\beta },{\mathit{\beta }}_0\right)=\prod _{i=1}^n\pi \left({\mathit{\beta }}_i,{\mathit{\beta }}_i^{\ast }\mid \delta ,{\mathbf{\text{Σ}}}_{\beta },{\mathit{\beta }}_0\right) \\ =\prod _{i=1}^n\left({11}_{\{{\beta }_{3i}^{\ast }<\delta \}}{11}_{\left\{{\mathit{\beta }}_i={\mathit{\beta }}_i^{\ast }\right\}}+{11}_{\left\{\delta \le {\beta }_{3i}^{\ast }\le 0\right\}}{11}_{\left\{{\mathit{\beta }}_i={\mathit{\beta }}_0^{\ast }\right\}}\right)\text{MVN}\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right) \end{gathered}$$ (2)

where ${\mathit{\beta }}^{\ast }={\left({\mathit{\beta }}_1^{\ast \prime },{\mathit{\beta }}_2^{\ast \prime },\dots ,{\mathit{\beta }}_n^{\ast \prime }\right)}^{\prime }$. Equation (2) represents a mixture of a point mass at 0 when $\delta \le {\beta }_{3i}^{\ast }\le 0$ and a truncated multivariate normal distribution (MVN) when ${\beta }_{3i}^{\ast }<\delta$. This mixture prior approach is similar to spike- and-slab variable selection and offers a computationally efficient alternative to dimension-switching approaches such as reversible jump.²⁷ Essentially, we fit a fully parameterized model that includes the decrement slope, β_3i, but allow β_3i to equal zero if the unconstrained slope, ${\beta }_{3i}^{\ast }$ falls within the null region. Thus, the dimension of the odel stays fixed, but the prior structure for β_3i is a mixture distribution whose sample space encompasses a point mass at zero. In this way, we partition the constrained parameter space for the slope decrement, β_3i, into two regions: (1) [δ, 0], corresponding to individuals whose β₃s fall into this null region and who do not experience cognitive impairment and (2) $(-\infty ,\delta )$, corresponding to individuals whose β₃s fall into this rejection region and who experience AD-type cognitive decline. By using this joint prior in equation (2), we simultaneously estimate oth the slope decrement β₃, which guarantees the stable or downward trend in cognitive trajectories, and the threshold δ of the null region, which encourages flatness in the trajectories for patients without clinically relevant cognitive decline.

To complete the prior specification and ensure an identifiable model, we assign an MVN $(\mathbf{0},\mathbf{\text{Ω}})$ prior for the population mean ${\mathit{\beta }}_0$. For ${\mathbf{\text{Σ}}}_{\beta }$, we assign an inverse-Wishart $\text{IW}(\nu ,\mathbf{\text{Γ}})$ prior where v is the degree of freedom. Throughout, we assume that $\mathbf{\text{Ω}}$ and $\mathbf{\text{Γ}}$ are known scale matrices (e.g. the q × q identity matrix, ${\mathit{I}}_q$, where q represents the dimension of β₀). We assign an inverse-gamma $\text{IG}\left(a_{ϵ},b_{ϵ}\right)$ prior for ${\sigma }_{ϵ}^2$ To be consistent with prior research,^5,28 we assume ${\kappa }_i\sim \text{N}\left({\mu }_{\kappa },{\sigma }_{\kappa }^2\right)$ truncated between 3 and 8 for $i=1,2,\dots ,n$ likewise, we assume $\delta \sim \text{N}\left({\mu }_{\delta },{\sigma }_{\delta }^2\right)$ truncated between –0.1 and 0, which provides a clinically meaningful null region. Thus, unlike previous work involving change point models, we allow the threshold parameter to be estimated from the data rather than fixed a priori. Using simulation studies, we demonstrate below that estimating d rather than fixing it a prespecified value generally improves inferences.

3.3. Posterior

For posterior computation, we adopt an efficient MCMC algorithm that combines Gibbs steps and Metropolis-Hastings steps. Conditional on the data $\left(y_{ij},{\mathit{x}}_{ij}\right)$ $i=1,2,\dots ,n$ and $j=,1,2,\dots ,n_i$, the joint posterior density of parameters $\mathit{\beta },{\mathbf{\text{Σ}}}_{\beta },\mathit{\kappa },{\sigma }_{ϵ}^2,{\mathit{\beta }}_0$, the latent variable ${\mathit{\beta }}^{\ast }$, and δ is proportional to

$$\begin{gathered} \prod _{i=1}^n\prod _{j=1}^{n_i}\text{N}\left(y_{ij};{\mathit{\beta }}_i,{\sigma }_{ϵ}^2,{\mathit{x}}_{ij},{\kappa }_i\right)\pi \left({\mathit{\beta }}_i,{\mathit{\beta }}_i^{\ast }\mid \delta ,{\mathbf{\text{Σ}}}_{\beta },{\mathit{\beta }}_0\right)\pi \left({\mathit{\beta }}_0\right)\pi (\delta )\pi \left({\kappa }_i\right)\pi \left({\mathbf{\text{Σ}}}_{\beta }\right)\pi \left({\sigma }_{ϵ}^2\right) \\ =\prod _{i=1}^n\prod _{j=1}^{n_i}\text{N}\left(y_{ij};{\mathit{\beta }}_i,{\sigma }_{ϵ}^2,{\mathit{x}}_{ij},{\kappa }_i\right)\pi \left({\mathit{\beta }}_0\right)\pi (\delta )\pi \left({\kappa }_i\right)\pi \left({\mathbf{\text{Σ}}}_{\beta }\right)\pi \left({\sigma }_{ϵ}^2\right) \\ \left({11}_{\{{\beta }_{3i}^{\ast }<\delta \}}{11}_{\left\{{\mathit{\beta }}_i={\mathit{\beta }}_i^{\ast }\right\}}+{11}_{\left\{\delta \le {\beta }_{3i}^{\ast }\le 0\right\}}{11}_{\left\{{\mathit{\beta }}_i={\mathit{\beta }}_{i0}^{\ast }\right\}}\right)\text{MVN}\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right) \end{gathered}$$

where $\pi \left({\mathit{\beta }}_i,{\mathit{\beta }}_i^{\ast }\mid \delta ,{\mathbf{\text{Σ}}}_{\beta },{\mathit{\beta }}_0\right)$ is defined in equation (2), $\pi \left({\mathit{\beta }}_0\right)$ is a prior for ${\mathit{\beta }}_0,\pi (\delta )$ is a prior of $\delta ,\pi \left({\kappa }_i\right)$ is a prior for the change point, $\pi \left({\mathbf{\text{Σ}}}_{\beta }\right)$ is a prior for ${\text{Σ}}_{\beta }$ and $\pi \left({\sigma }_{ϵ}^2\right)$ is a prior for ${\sigma }_{ϵ}^2$. The full conditional distributions for ${\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }$, and ${\sigma }_{ϵ}^2$ have straightforward conjugate forms. We estimate ${\kappa }_i(i=1,2,\dots ,n)$ using a Metropolis-Hastings step. Averaging k_i over the course of the MCMC algorithm results in a smooth posterior estimate of the mean egression function, reflecting our intuition that the change point is not instantaneous but instead represents a smooth transition (or “bent cable”) occurring over a short period of time.²⁹ Following Neelon and Dunson,²⁵ we update the threshold parameter d, the latent slope decrements ${\beta }_{3i}^{\ast }(i=1,\dots ,n)$, and the observed slope decrements ${\beta }_{3i}(i=1,\dots ,n)$ jointly using a Metropolis-Hastings step. Thus, after setting initial values, the sampler iterates through the following steps:

1. Sample ${\sigma }_{ϵ}^2$ from its inverse gamma full conditional

2. Sample ${\text{Σ}}_{\beta }$ from its inverse-Wishart full conditional

3. Sample ${\kappa }_i^{new}(i=1,2,\dots ,n)$ from an $\text{N}\left({\kappa }_i^{old},{\sigma }_{\kappa }^{\ast 2}\right)$ truncated between 3 and 8. Accept or reject the candidate ${\kappa }_i^{new}$ using a random walk Metropolis-Hastings step

4. Sample ${\mathit{\beta }}_0$ from its multivariate normal full conditional

5. Update $\delta ,\mathit{\beta },{\mathit{\beta }}^{\ast }$ in one block as follows:

   1. Sample a candidate value of ${\delta }^{new}$ from an $\text{N}\left({\delta }^{old},{\sigma }_{\delta }^{\ast 2}\right)$ truncated between –0.1 and 0
   2. For $i=1,2,\dots ,n$, sample ${\mathit{\beta }}_i^{\ast new}$ new from its unconstrained MVN full conditional, and if ${\beta }_{3i}^{\ast new}<{\delta }^{new}$ then set ${\mathit{\beta }}_i^{new}={\mathit{\beta }}_i^{\ast new}$; otherwise, if ${\delta }^{new}\le {\beta }_{3i}^{\ast new}\le 0$, then set ${\mathit{\beta }}_i^{new}={\mathit{\beta }}_{i0}^{\ast new}$
   3. Accept or reject the candidate ${\delta }^{new}$, ${\mathit{\beta }}^{new}={\left({\mathit{\beta }}_1^{new\prime },\dots ,{\mathit{\beta }}_n^{new\prime }\right)}^{\prime }$ and ${\mathit{\beta }}^{\ast new}={\left({\mathit{\beta }}_1^{\ast new\prime },\dots ,{\mathit{\beta }}_n^{\ast new\prime }\right)}^{\prime }$ in one block with a Metropolis-Hastings step

6. Repeat steps 1 to 5 until convergence and calculate posterior summaries based on a large number of iterations.

MCMC convergence is monitored by trace plots, and the model fitting is assessed by standardized residual plots. The detailed MCMC algorithm (including priors and posteriors) is described in Online Appendix A. R code (https://www.r-project.org) for fitting the model is available from the first author.

3.4. Personalized prediction of disease progression to AD

In the following, we illustrate how to use the proposed approach to identify patients at high risk to progress to AD at various stages during the follow-up period. Our approach can be applied when extensive longitudinally measured cognitive data are available (such as AD research centers and some memory clinics). Additionally, clinicians with access to longitudinal data can use the model to predict the risk of progressing to AD and to adjust patients’ treatment plans accordingly at each follow-up visit.

Suppose we wish to predict the probability of progression to AD for a new patient i at visit j. We first fit model 1) using the longitudinal cognitive measurements for patient i up to and including visit j (i.e. we observe only the first j measurements for patient i), together with the available data for the remaining patients. Let ${\beta }_{3ij}^{\ast }$ denote the latent slope decrement following the change point for patient i at visit j, and let δ_j be the corresponding threshold indicating the null region boundary. At each MCMC iteration, we compare ${\beta }_{3ij}^{\ast }$ with ${\delta }_j$ to decide whether ${\beta }_{3ij}^{\ast }$ falls into the null region or the rejection region. We then estimate the probability, $p_{ij}$, of ${\beta }_{3ij}^{\ast }$ falling inside the rejection region (i.e. ${11}_{\{{\beta }_{3ij}^{\ast }<{\delta }_j\}}=1$ at visit j over the course of the MCMC iterations. If individual i does not experience a change point at visit j, the majority of the ${\beta }_{3ij}^{\ast }\text{s}$ will fall into the null region (i.e. the majority of ${\beta }_{3ij}=0$) and the corresponding posterior mean probability ${\widehat{p}}_{ij}$ will be small; otherwise, if individual i does experience a change point at visit j, the majority of the ${\beta }_{3ij}^{\ast }\text{s}$ will fall inside the rejection region (i.e. the majority of ${\beta }_{3ij}={\beta }_{3ij}^{\ast }$), and the corresponding posterior mean probability ${\widehat{p}}_{ij}$ will be large. Hence, ${\widehat{p}}_{ij}$ provides an estimate of AD risk at visit j. By refitting the model for various choices of j, we can monitor the changes in the probability of progression to AD over the course of the follow-up.

4. Simulation study

4.1. Simulation model

To evaluate the proposed model, we conducted a simulation study, applying the method to 100 simulated patients in which 50 observations whose cognitive functional trajectories encounter change points (i.e. labeled “AD” patients) and the other 50 observations whose cognitive functional trajectories do not encounter change points (i.e. labeled “non-AD” patients). To illustrate how to fit the model with predictors, we added two risk factors: age at enrollment centered at 76 years old and years of education as a continuous variable. We generated data using the following model

$$Y_{ij}={\beta }_{1i}+{\beta }_{2i}{t}_{ij}+{\beta }_{3i}{\left(t_{ij}-{\kappa }_i\right)}_{+}+{\beta }_{4i}ag{e}_i+{\beta }_{5i}educatio{n}_i+{ϵ}_{ij}$$ (3)

where $i=1,2,\dots ,100$, $j=1,2,\dots ,n_i$. We first made assumptions similar to the preliminary results from the ROS data,⁵ which we refer to Scenario 1. For each individual i, we generated the number of annual visits, n_i, from a discrete uniform U[7, 15] distribution, the change point $k_i$ followed an N(5, 1) truncated between years 3 and 8, the error term ϵ_ij followed an N(0, 0.05), and the years of education followed a uniform distribution U½5; 25]. For observations with change points, we assumed that age followed an $\text{N}(85,64)$, and the parameter ${\mathit{\beta }}_i(i=1,2,\dots ,50)$ followed an $\text{MVN}\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right)$ in which the population mean ${\mathit{\beta }}_0=(-0.18,-0.05,-0.3,-0.04,0.04{)}^{\prime }$. For observations without change points, we assumed that age followed an N(72, 64), and the parameter ${\mathit{\beta }}_i(i=51,\dots ,100)$ followed an $\text{MVN}\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right)$ in which the population mean ${\mathit{\beta }}_0=(-0.18,-0.05,0,-0.04,0.04{)}^{\prime }$. The specification for ${\mathbf{\text{Σ}}}_{\beta }$ is provided in Online Appendix B, which resulted in heterogeneity similar to the ROS data. We assumed the threshold for the null region $\delta =-0.05$ and ${\beta }_3=-0.3$ for AD patients to be consistent with the results in Yu et al.⁵ To assess the robustness of the model, we simulated two additional scenarios, denoted as Scenarios 2 and 3, in which we increased the variability in the data and changed the value of δ to accommodate different null regions (see Online Appendix B).

When fitting model (3), we assumed independent $\text{MVN}\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right)$ priors for the random effects ${\mathit{\beta }}_i^{\ast }$, an $\text{MVN}\left(\mathbf{0},{\mathit{I}}_5\right)$ prior for β₀, an IG(0.001, 0.001) prior for ${\sigma }_{ϵ}^2$, and an IW(5, I₅) prior for ${\mathbf{\text{Σ}}}_{\beta }$. We ran the model for 20000 MCMC terations with a burn-in of 5000, which was sufficient to ensure convergence based on trace plots and to verify that the normality assumption held based on the standardized residual plot.

4.2. Results

Table 1 presents the posterior means and 95% credible intervals (CIs) for the model parameters in Scenario 1, where $\delta =-0.05$, $\rho =0.1$ and ${\sigma }_{ϵ}^2=0.05$. The estimated population mean, ${\widehat{\mathit{\beta }}}_0$, and the estimated threshold of the null region, $\widehat{\delta }=-0.05$ (with acceptance rate of 60%), are close to the true parameter values, and the 95% Cis overlap with the true values used in the simulation.

Table 1.

Simulated and posterior mean parameter estimates for simulation study for Scenarios 1, 2, and 3.

Parameter	True value	Posterior mean (95% CI)
Scenario 1: $\delta$ = −0.05, ${\sigma }_{ϵ}^2$ = 0.05, ρ = 0.1, and ${\mathbf{\text{Σ}}}_{\beta }$ with Specification 1
${\beta }_1$	−0.18	−0.20 [−0.45, 0.06]
${\beta }_2$	−0.05	−0.05 [−0.06, −0.04]
${\beta }_3$	−0.30	−0.26 [−0.32, −0.21]
${\beta }_4$	−0.04	−0.05 [−0.06, −0.035]
${\beta }_5$	0.04	0.04 [0.02, 0.06]
${\sigma }_{ϵ}^2$	0.05	0.05 [0.049, 0.06]
$\delta$	−0.05	−0.05 [−0.07, −0.03]
Scenario 2: $\delta$ = −0.1, ${\sigma }_{ϵ}^2$ = 0.5, ρ = 0.1, and ${\mathbf{\text{Σ}}}_{\beta }$ with Specification 1
${\beta }_1$	−0.18	−0.16 [−0.40, 0.13]
${\beta }_2$	−0.05	−0.06 [−0.08, −0.03]
${\beta }_3$	−0.30	−0.28 [−0.32, −0.23]
${\beta }_4$	−0.04	−0.05 [−0.06, −0.027]
${\beta }_5$	0.04	0.04 [0.02, 0.06]
${\sigma }_{ϵ}^2$	0.5	0.48 [0.45, 0.53]
$\text{Δ}$	−0.1	−0.10 [−0.11, −0.09]
Scenario 3: $\delta$ = −0.05, ${\sigma }_{ϵ}^2$ = 0.05, ρ = 0.2, and ${\mathbf{\text{Σ}}}_{\beta }$ with Specification 1
${\beta }_1$	−0.18	−0.18 [−0.52, 0.09]
${\beta }_2$	−0.05	−0.05 [−0.06, −0.04]
${\beta }_3$	−0.30	−0.26 [−0.31, −0.21]
${\beta }_4$	−0.04	−0.05 [−0.06, −0.03]
${\beta }_5$	0.04	0.04 [0.02, 0.06]
${\sigma }_{ϵ}^2$	0.05	0.05 [0.048, 0.06]
$\delta$	−0.05	−0.05 [−0.06, −0.04]

CI: credible interval. 95% CIs are given in parentheses.

Figure 2 shows the simulated and estimated trajectories. This figure clearly demonstrates the adequate model fit, with the estimated average trajectories overlapping with the simulated average trajectories very well for both AD and non-AD patients. Figure D1 in Online Appendix D presents the simulated trajectories (blue dot curves) and the estimated trajectories (red long-dash curves) for six individuals. The figure shows that the estimated trajectories closely mimic the simulated trajectories. Specifically, AD patients 5, 25, and 42 experience change points in which the ${\widehat{\beta }}_{3}s$ are –0.17, –0.25, and –0.65, respectively, which are outside the null region. The follow-up times for these patients are 14, 15, and 15 years. Non-AD patients 69, 70, and 93 do not experience change points during their follow-up periods, which ranged from 14 to 15 years. As expected, the ${\widehat{\beta }}_{3}s$ for these individuals are –0.001, –0.0003, and –0.02, which are inside the null region. Finally, the standardized residual plot in Figure D2 of Online Appendix D follows a standard normal distribution, indicating that the normality assumption holds.

Figure 2.

Estimated and simulated average cognitive trajectories for Scenario 1 in the simulation study.

AD: Alzheimer’s disease

To assess the robustness of the model performance given the nature of the disease and covariates in the model, we simulated additional scenarios, denoted as Scenarios 2 and 3 (details are provided in Online Appendix B). Scenario 2 corresponds to $\delta =-0.1$, ${\mathbf{\text{Σ}}}_{\beta }$ taking the same values as in Scenario 1, and ${\sigma }_{ϵ}^2=0.5$, which implies greater within-subject variability relative to Scenario 1. Scenario 3 corresponds to $\delta =-0.05$, ${\sigma }_{ϵ}^2=0.05$, $\rho =0.2$ and the diagonal elements in ${\mathbf{\text{Σ}}}_{\beta }$ taking the values given in Scenario 1, leading to higher random effect correlation compared to Scenario 1. As shown in Table 1, for both scenarios, the estimated model parameters closely mimic the true values, with 95% CIs overlapping with the true values in all cases (Scenarios 2 and 3 in Table 1). Figure D3(a) and (b) in Online Appendix D, which is similar to Figure 2, presents estimated trajectories for Scenario 2 and 3, respectively. Both panels clearly demonstrate satisfactory model fit in which the estimated average trajectories overlap with the simulated average trajectories very well for all cases. Figure D4 in Online Appendix D presents estimated global cog trajectories for six patients under Scenario 2 (Panel (a)) and Scenario 3 (Panel (b)). Again, the simulated trajectories and the estimated trajectories mirror one another. Figure D5 in Online Appendix D presents the standardized residual plots for Scenario 2 (Panel (a)) and Scenario 3 (Panel (b)). Both residual plots follow a standard normal distribution indicating that the normality assumption holds.

Finally, we conducted simulations to compare our approach to that of Slate and Turnbull,¹⁵ which prespecifies the threshold parameter, δ, and assumes that the random effect β_3i is uncorrelated with other random effects in the model. We selected four settings for the correlation between ${\beta }_{3i}(i=1,\dots ,n)$ and other random effects in the model, denoted by ρ*, and for the prespecified value of d that reflects an “informed guess” as to the true, unknown δ value:

• Setting 1a: ρ* = 0, true δ = prespecified δ = −0.05. This scenario most closely conforms to the approach of Slate and Turnbull.¹⁵

• Setting 1b: Same settings as in (1a) but with a misspecified δ of –0.03 under the approach of Slate and Turnbull.¹⁵

• Setting 2a: ρ* = 0:2, true δ = prespecified δ = −0.1. This scenario corresponds to a modest correlation between the random effects.

• Setting 2b: Same settings as in (2a) but with a misspecified δ of –0.15 under the approach of Slate and Turnbull.¹⁵

For each setting, we assumed ${\beta }_{01}=-0.18$, ${\beta }_{02}=-0.05$, ${\beta }_{03}=-0.3$, ${\beta }_{04}=-0.04$ and ${\beta }_{05}=0.04$. For Settings a and 1b, where ${\rho }^{\ast }=0$, we assumed that ${\left({\beta }_{1i},{\beta }_{2i},{\beta }_{4i},{\beta }_{5i}\right)}^{\prime }$ followed an MVN distribution with mean ${\left({\beta }_{01},{\beta }_{02},{\beta }_{04},{\beta }_{05}\right)}^{\prime }$ and covariance matrix taking the values of Scenario 1 in Online Appendix B. We further assumed an $\text{N}\left({\beta }_{03},{\sigma }_{33}^2\right)$ distribution for β_3i, where ${\sigma }_{33}^2$ is given in Scenario 1 of Online Appendix B. For Settings 2a and 2b, where ρ* = 0.2, we assumed that ${\left({\beta }_{1i},{\beta }_{2i},{\beta }_{3i},{\beta }_{4i},{\beta }_{5i}\right)}^{\prime }$ followed an MVN distribution with mean ${\left({\beta }_{01},{\beta }_{02},{\beta }_{03},{\beta }_{04},{\beta }_{05}\right)}^{\prime }$ and covariance matrix taking values given in Scenario 1 of Online Appendix B with the common correlation of ρ*. These two settings have the assumed true $\delta =-0.1$, which is different from the above Scenario 3. We then compared the model of Slate and Turnbull¹⁵ to our approach in which δ was estimated as part of the MCMC algorithm.

Table C1 in Online Appendix C presents the posterior means and 95% CIs for the model parameters using both approaches. As expected, when d is incorrectly specified under the approach of Slate and Turnbull,¹⁵ the parameter estimates deviate from their true values, and the 95% CIs often fail to cover the true parameter values. These trends increase as the random effect correlation increases. In contrast, under the proposed approach, the parameter estimates are generally more accurate, and the 95% CIs are more precise. For example, under Setting 1b, where ρ* = 0, the true δ = −0.05, and the prespecified δ = −0.03, which is only a small deviate from the true δ, under Slate and Turnbull¹⁵ approach, ${\widehat{\beta }}_{03}=-0.21(95\text{\%CI}=[-0.24,-0.18])$, which fails to cover the true value of –0.30. Although ${\widehat{\beta }}_{02}$ and ${\widehat{\sigma }}_{ϵ}^2$ are not far away from the true values, their 95% CIs overlap with the true values at one of the boundaries. Conversely, under the proposed approach, ${\widehat{\beta }}_{03}=-0.23(95\text{\%CI}=[-0.32,-0.14])$, and all other parameter estimates are quite accurate with correct posterior intervals around the true values. Even when we correctly specified the δ value, the approach of Slate and Turnbull¹⁵ did not always yield accurate estimates and correct posterior intervals, since it fails to consider the correlation between the random slope after the change point and other random effects in the model. For example, under Setting 2a, where ${\rho }^{\ast }=0.2$ and $\delta$ is correctly specified at $-0.1,{\widehat{\beta }}_{03}=-0.36(95\text{\%CI}=[-0.41,-0.32])$, which fails to cover the true value of –0.30. In addition, ${\widehat{\beta }}_{02}$ and ${\widehat{\sigma }}_{ϵ}^2$ are away from the true values and the corresponding 95% CIs fail to cover the true values. In contrast, under the proposed method, ${\widehat{\beta }}_{03}=-0.34(95\text{\%CI}=[-0.41,-0.20])$, which achieves the proper estimate and posterior interval encompassing the true value. All other parameter estimates are quite accurate with proper posterior intervals. Taken together, these results highlight the importance of estimating the threshold parameter during model fitting and taking into account the potential correlation among all model parameters.

5. Application to ROS data

Next, we applied model (3) to the random sample from the ROS dataset. The follow-up time for each individual ranged from 7 to 15 years. We also included age at enrollment (centered) and years of education in our analyses, as these are known predictors of cognitive decline.⁵ Among those 189 patients, the percentage of NCI, MCI, and AD patients diagnosed at the last clinical visit was 32%, 37%, and 31%, respectively. The average year of education was 15.5 years ranging from 5 to 26 years, and the average age at enrollment was 76.9 years old ranging from 56.7 to 91.3 years old.

5.1. Model fitting

We fit the model based on the estimation approach presented in the Model and estimation section. We assumed an MVN(0; 1000 × I₅) prior for β₀, an IG(0.001, 0.001) prior for ${\sigma }_{ϵ}^2$, an $\text{MVN}\left({\mathit{\beta }}_0,{\mathbf{\text{Σ}}}_{\beta }\right)$ prior for ${\mathit{\beta }}_i^{\ast }$, and an IW(5, 0.01 × I₅) prior for ${\mathbf{\text{Σ}}}_{\beta }$.

We ran the MCMC algorithm for 20,000 iterations with a burn-in of 5000. The acceptance rate for estimating κ_i ranged from 47% to 49%, and the acceptance rate for δ was 46%. The standardized residual plot (Panel (a) of Figure D6 in Online Appendix D) follows a standard normal distribution, and the trace plot (Panel (b) of Figure D6 in Online Appendix D) shows adequate mixing for all parameters. The posterior population mean and 95% CI for each component of β₀ are presented in Table C2 of Online Appendix C. Age at enrollment and years of education are significant predictors of AD. The posterior mean of the threshold for the null region $\widehat{\delta }=-0.05$, which is consistent with previous research.⁵ Figure 3 shows individual trajectory plots for six patients from the ROS data (blue dotdash curves), estimated trajectories (red long-dash curves), and 95% credible bands (shaded area), which follow the trend of and overlap with the observed sample trajectories; $\widehat{p}$ represents the estimated probability of progression to AD at the 11th visit using the prediction algorithm described in the Personalized prediction of disease progression to AD section.

Figure 3.

Observed and estimated trajectories for six selected patients from the ROS study. Shaded regions denote 95% credible bands.

5.2. Potential clinical usage: Personalized risk prediction

Next, we used the model to predict the risk of disease progression to AD on another randomly selected sample. For brevity, we illustrate the approach by randomly selecting 14 new patients from different stages of disease progression. For these patients, seven were diagnosed as AD (the top seven patients in Table 2), three patients’ disease stage switched between NCI and MCI (the middle three patients in Table 2), and four were NCI during the course of the study (the bottom four patients in Table 2). We present the prediction results for additional 18 patients (6 patients in each disease stage) in Table C3 of Online Appendix C, which has the same structure as Table 2. We repeatedly fit model (3) combining these new patients with the 189 patients from the previous analysis. We first fit the model using their global cog measurements from the first six visits (measurements at baseline and the first five follow-up visits), which allowed sufficient time for patients to experience potential change points. We then fit the model again using their global cog measurements from the first seven visits (global cog measurement at baseline and the first six follow-up visits), and repeatedly fitting model (3) with additional observations up to follow-up visit eight, nine, and so on until first AD diagnosis or the eleventh visit for the non-AD patients, where the eleventh visit is the maximal follow-up time for seven AD patients.

Table 2.

Clinical usage: individual risk of progression to AD (${\widehat{\beta }}_3$ and $\widehat{p}(\text{\%})$) for 14 randomly selected patients from the ROS study.

ID	6th visit	7th visit	8th visit	9th visit	10th visit	11th visit	Time to first AD diagnosis
50108200	−0.06	−0.07	−0.09	−0.11	−0.15	−0.18	11th visit
	53	54	71	79	95	99
50102790	−0.09	−0.12	−0.16	−0.18	−0.18	-	10th visit
	70	84	95	98	98
50103679	−0.13	−0.15	−0.16	−0.18	-	-	9th visit
	85	91	96	98
81874628	−0.13	−0.13	−0.14	−0.13	−0.17	-	10th visit
	86	89	94	90	98
64336939	−0.11	−0.15	−0.11	−0.15	−0.17	−0.17	11th visit
	78	92	78	93	98	98
20195344	−0.10	−0.09	−0.12	−0.12	−0.15	−0.19	11th visit
	76	69	84	85	95	100
59796318	−0.08	−0.05	−0.09	-	-	-	8th visit
	61	46	72
5632732	−0.05	−0.05	−0.10	−0.12	−0.06	−0.07	-
	47	44	74	83	60	61
5577538	−0.10	−0.07	−0.06	−0.03	−0.02	−0.02	-
	73	56	50	34	24	22
50108912	−0.09	−0.09	−0.10	−0.08	−0.12	−0.12	-
	70	64	79	62	86	88
5218242	−0.11	−0.07	−0.05	−0.03	−0.03	−0.04	-
	77	54	46	27	30	40
10100448	−0.08	−0.07	−0.04	−0.02	−0.04	−0.05	-
	59	57	37	27	37	52
10100600	−0.08	−0.06	−0.07	−0.07	−0.05	−0.05	-
	65	47	55	58	49	54
31813134	−0.07	−0.06	−0.08	−0.10	−0.11	−0.14	-
	60	52	64	77	82	94

AD: Alzheimer’s disease.

In the following, we suppress the time index j and the individual index i for ${\widehat{\beta }}_3$ and $\widehat{p}$. Table 2 presents the posterior mean of the slope decrement, along with $\widehat{p}$ (as a %), the estimated personalized risk of progression to AD, from the sixth to the eleventh visit. By repeatedly fitting model (3) with additional global cog measurements at each follow-up visit, the slope decrement, ${\widehat{\beta }}_3$, and the probability of progression to AD, $\widehat{p}$, were updated.

Using both the posterior means of ${\widehat{\beta }}_3$ and $\widehat{p}$ at each follow-up visit, we can obtain information about patients’ ikelihood of progression to AD. For example, for patient 50108200, at the sixth visit, ${\widehat{\beta }}_3$ is just outside the null region (where $\widehat{\delta }$ = −0.044 at visit 6), and $\widehat{p}$ is 53%. At the seventh visit, ${\widehat{\beta }}_3$ decreases, and $\widehat{p}$ increases slightly. At the eighth visit, $\widehat{p}$ has a relatively larger jump compared to the previous visits, but ${\widehat{\beta }}_3$ is not far from the null region. These findings may indicate the onset of cognitive decline for this patient. However, at the ninth visit compared to the estimates at the previous visits, ${\widehat{\beta }}_3$ jumps to $-0.11$, which is a steeper decline and is farther away from the null region. Additionally, $\widehat{p}$ is 79%, which represents a relatively large increase compared to the sixth to the eighth visits. These results indicate that this patient’s cognitive decline continues the trend we observed at the eighth visit. Hence, we can view this as an early warning sign of cognitive impairment. At the tenth visit, $\widehat{p}$ is 95%, which is a stronger warning of cognitive decline. Clinicians may consider more frequent visits or enhanced treatments to mitigate the cognitive decline for this patient. At the tenth and eleventh visits, ${\widehat{\beta }}_3\text{s}$ bound well away from the null region, and $\widehat{p}\text{s}$ are nearly 100%. These estimates are in concordance with the clinical diagnosis of AD at the eleventh visit. However, our model is able to provide an early warning of serious cognitive decline at least three years before the actual diagnosis of AD for this patient. For patients 50102790, 50103679, 81874628, 64336939, and 20195344, the model provides a strong warning of cognitive decline ($\widehat{p}$ > 80% and ${\widehat{\beta }}_3$ far away from the null region) at the seventh, sixth, sixth, ninth, and eighth visit, respectively, well in advance of their actual AD diagnoses.

In some cases, there is a discrepancy between the model prediction and clinical diagnosis. For example, patient 59796318’s first AD diagnosis was at the eighth visit. However, the model’s suggestion is different. The estimated posterior mean of β₃ and p at the eighth visit are –0.09 and 72%, which is a suggestive but not conclusive indication of progression to AD. In fact, the AD diagnosis at the eighth visit was a misdiagnosis: this patient was subsequently followed for two more visits and the disease stage was NCI at the ninth visit and MCI at the tenth visit. Thus, the proposed method could be used to identify potential misdiagnoses when the model predictions disagree with clinical assessments.

For the three patients whose disease stage switched between NCI and MCI, the posterior means of ${\widehat{\beta }}_3\text{s}$ and $\widehat{p}\text{s}$ fluctuate along with their global cog trajectories, which indicates that our model is able to capture subtle cognitive changes and the switch of the disease stage from time to time. Consider, for example, patient 5632732. At the sixth and seventh visits, ${\widehat{\beta }}_3\text{s}$ for this patient are just outside the boundary of the null region, and $\widehat{p}\text{s}$ are less than 50%. However, at the eighth visit, $\widehat{p}$ jumps to 74% compared to that of 44% at the seventh visit, and ${\widehat{\beta }}_3$ is farther away from the null region, which can be viewed as an early warning of cognitive decline. At the ninth visit, $\widehat{p}$ increases to 83%, which is a strong indication of cognitive decline. Clinicians may wish to monitor this patient more often, prescribe enhanced medications, or recommend behavioral therapies. For patient 50108912, the cognitive trajectory fluctuates over a larger range. In particular, $\widehat{p}$ at the tenth visit is more than 85%, and it reaches nearly 90% at the eleventh visit, which is a convincing evidence of serious cognitive decline. Although this patient was not diagnosed as AD during the course of the study, our results suggest the potential for AD onset during the study. As a result, clinicians may want to adjust the treatment and monitoring schedule for this patient to delay or prevent the onset of AD.

Among the NCI patients, one patient (ID 5218242) might experience temporary cognitive decline at the sixth visit with ${\widehat{\beta }}_3=-0.11$, which is outside the null region, and $\widehat{p}=77\text{\%}$. These larger estimates may be also due to the learning stage of the model when we fit the model using a shorter trajectory. However, this patient’s cognitive function gradually returned to normal, as ${\widehat{\beta }}_3$ is gradually absorbed back into the null region and $\widehat{p}$ decreases. Clinicians may therefore consider monitoring this patient annually according to routine protocol. For one patient (ID 10100600), the cognitive function was relatively stable throughout the follow-up period: the posterior means $\left({\widehat{\beta }}_3\text{s}\right)$ are close to the boundary $\widehat{\delta }$, and $\widehat{p}\text{s}$ are less than 60% for visits 7 to11. Clinicians and AD researchers may choose to monitor this patient according to the current annual schedule until they see more severe signs of cognitive decline.

The last patient (ID 31813134) was diagnosed as NCI at the last visit. However, the model results suggest this patient may experience AD earlier in the study. In particular, the slope decrement ${\widehat{\beta }}_3$ decreases steadily from the eighth visit to the eleventh visit, where ${\widehat{\beta }}_3=-0.14$ is well outside the null region. The estimated probability $\widehat{p}$ steadily increases over time from 82% at the tenth visit to 94% at the eleventh visit, which is a convincing sign of progression to AD. For this scenario, clinicians may consider monitoring this patient more frequently to avoid potential misdiagnosis, which may delay treatment and jeopardize the patient’s quality of life. More generally, when there is a discrepancy between clinical diagnosis and what model suggests, clinicians may need to pay special attention to the patient.

6. Discussion

In this paper, we proposed a Bayesian hierarchical random change point model with a parameter constraint in which we allow for a random intercept, random change point time, random slope before the change point, and random slope after the change point. The parameter space for the difference in slope before and after the change point was constrained and partitioned into a null region, representing NCI, and a rejection region, representing diseased cognitive impairment. Using this model, we can (1) distinguish normal aging individuals from individuals experiencing diseased cognitive impairment, (2) characterize the rate and timing of the cognitive decline if individuals’ cognitive functional trajectories encounter change points, and (3) identify patients at high risk of progression to AD using both the difference in slope estimates and the probability of advancing to AD. The simulations and the real application illustrate that the proposed model works very well in terms of model fitting and prediction. The model is robust to different parameter values, and estimating the threshold is preferable to assuming a fixed value, as the latter may be misspecified in practice.

Most importantly, the proposed model provides an additional tool to assist clinical evaluation for AD patients. Using the model, we are able to predict the subject-specific probability of progression to AD at various time points by measurements available only from cognitive measurements. Using this predicted probability together with the subject-specific change point and the rate of cognitive decline, clinicians can be assisted to (1) identify individuals with high risk of progression to AD several years before the actual event, (2) adjust individuals’ treatment plan and follow-up visit plan accordingly, which may hopefully delay disease progression and improve patients’ quality of life, and (3) use the model results as an additional tool to assist the diagnosis, particularly when there is a discrepancy between the clinical diagnosis and the model’s suggestion about the changes in cognitive trajectories, thus potentially avoiding misdiagnoses and improving patients’ quality of life.

Because AD is a nonreversible disease with no cure, it is critical to identify individuals at high risk of progression to AD. Doing so may prompt patients and clinicians to better understand their patient’s risk factors and identify effective medication regimens or behavioral therapies that may prevent or delay disease progression. For example, patients can increase their physical activity, eat a heart- (and brain-) healthy diet, quit smoking, and initiate cognitive training to enhance memory, reasoning, and speed of processing.³⁰

While the widespread clinical use of our method may be several years away, the approach might find more immediate application in AD research centers or memory clinics where extensive longitudinal cognitive data are available for clinicians or researchers involved in large cohort AD research studies. Thus, for the time being, the target population might be limited to participants in those large-scale AD research cohort studies and any patients with memory concerns referred by their primary care doctors to clinicians. Despite these limitations, we believe the method will have growing impact as a way to assess patients longitudinally in a noninvasive manner in order to make predictions for the potential onset of dementia. This goal aligns with NIH AD diagnostic guidelines (https://www.nia.nih.gov/health/alzheimers-disease-diagnostic-guidelines), which states that “clinicians should obtain long-term assessment of cognitive whenever possible to gain evidence of progressive decline.”

There are a number potential extensions of this work. First, future extensions of this work could focus on testing these models using cognitive screening instruments (e.g. MMSE, MiniCog) which, while less sensitive than a neuropsychological test battery, are more widely available. Second, the model could be expanded to include two change points and more complex order constraints. This model could be useful since the cognitive measurements could encounter two change points. Because the process of AD is from NCI to MCI, and eventually to AD, the first change point could happen at the time when the disease switches from NCI to MCI, and the second change point could happen at the time when the disease transfers from MCI to AD. In this case, our model can be extended to include three slopes: the slope before the first change point (α₁), the slope between the first and the second change point (α₂), and the slope after the second change point (α₃). We could add order constraints on these slopes, for example, α₁ ≥ α₂ ≥ α₃. Third, we could incorporate imaging or other biomarker data together with clinical evaluation measurements and fit a joint model of multiple outcomes to improve the predictions. Finally, we could model the random change point, κ_i, as a function of certain predictors by fitting a truncated normal regression, with the mean as a function of predictors instead of a fixed value.

A complementary approach would be to model the data via a hidden Markov model (HMM)³¹ which could include measurements available beyond clinical evaluation (e.g. neuroimaging data). Under this approach, patients’ disease stage could transition between NCI and MCI and to AD over the course of the study. Conditional on a patient’s disease state at time t, we could model cognitive impairment score. The HMM model could be used to determine when patients transition to the “absorbing” AD state, which might be used to facilitate clinical practice.

There are some limitations of the proposed approach. First, in the Potential clinical usage: Personalized risk prediction section, we illustrate how to use the proposed method to predict disease progression using estimated values of ${\widehat{\beta }}_3$ and $\widehat{p}$. While our assessments of ${\widehat{\beta }}_3$ and $\widehat{p}$ are at present qualitative in nature, working with clinical investigators, it may be possible to derive clinically meaningful thresholds for these values. Second, the proposed model needs longitudinal data to run, and these data may not be widely available outside of large-scale longitudinal cohort studies, although some of these have publicly available data that might support the use of our model. Additionally, in memory disorder clinics where patients are annually seen with cognitive assessments, reviewing electronic health records or certain algorithms (for example, Natural language processing algorithm) may be used to extract relevant clinical data (e.g. cognitive test scores and other clinical data that are collected over time). In general, we anticipate that the model will find increasing value in settings where longitudinal data related to cognitive decline are available.