Abstract
Cyclic peptides have the potential to vastly extend the scope of druggable proteins and lead to new therapeutics for currently untreatable diseases. However, cyclic peptides often suffer from poor bioavailability. To uncover design principles for permeable cyclic peptides, a promising strategy is to analyze the conformational dynamics of the peptides using molecular dynamics (MD) and Markov state models (MSMs). Previous MD studies have focused on the conformational dynamics in pure aqueous or apolar environments to rationalize membrane permeability. However, during the key steps of the permeation through the membrane, cyclic peptides are exposed to interfaces between polar and apolar regions. Recent studies revealed that these interfaces constitute the free energy minima of the permeation process. Thus, a deeper understanding of the behavior of cyclic peptides at polar/apolar interfaces is desired. Here, we investigate the conformational and kinetic behavior of cyclic decapeptides at a water/chloroform interface using unbiased MD simulations and MSMs. The distinct environments at the interface alter the conformational equilibrium as well as the interconversion kinetics of cyclic peptide conformations. For peptides with low population of the permeable conformation in aqueous solution, the polar/apolar interface facilitates the interconversion to the closed conformation, which is required for membrane permeation. Comparison to unbiased MD simulations with a POPC bilayer reveals that not only the conformations but also the orientations are relevant in a membrane system. These findings allow us to propose a permeability model that includes both ‘prefolding’ and ‘non-prefolding’ cyclic peptides – an extension that can lead to new design considerations for permeable cyclic peptides.
This study uses molecular dynamics and Markov state models to analyse how interfaces interact with cyclic decapeptides and modulate their dynamic and equilibrium properties.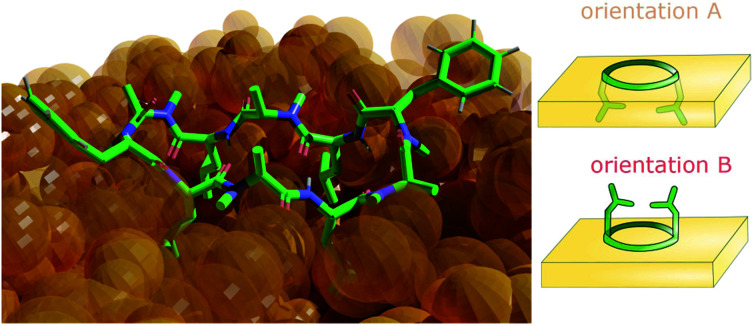
1. Introduction
Existing pharmaceutical drugs cover only a small fraction of the over 20 000 proteins encoded in the human genome.1–3 Most of the druggable proteins share distinct structural features, compared to the undruggable fraction: they have restricted, pocket-shaped binding sites that favor interactions with small organic molecules.4,5 In addition, their amount of well-defined rigid domains is significant. However, bioinformatic studies estimate that 85% to 90% of proteins do not contain suitable pocket-shaped binding sites and/or well-defined rigid domains, and are therefore difficult to target by small-molecule drugs.1,2 In contrast, macrocyclic drugs like cyclic peptides can bind to larger binding sites with flat profiles or protein–protein interfaces.6–12 Cyclization has the added benefit that it prevent rapid metabolic clearance.13 Therefore, cyclic peptides have the potential to vastly extend the scope of druggable proteins and lead to therapeutics for currently untreatable diseases.14
The therapeutic applicability of cyclic peptides is, however, limited by their often low cell permeability and oral bioavailability.15,16 To address this issue, many experimental and computational studies have focused on the molecular mechanism of cell permeation of cyclic peptides with the aim to define strategies for the rational design of permeable cyclic peptides.17–25N-Methylation of the peptide backbone, change of stereocenters, conformational flexibility, and side-chain modifications can all influence the permeability. Unfortunately, their effect is non-linear and highly site-dependent.24,26–30 The cell permeability of cyclic peptides often drops with increasing peptide size.31 Nevertheless, some larger cyclic peptides can display internal conformational changes, which are crucial for membrane permeability.32–34 The different conformations can be distinguished by the amount of intramolecular hydrogen bonds. In the so called ‘closed’ conformation, the internal hydrogen bonds shield the polar groups from the environment leading to a low polar surface area. In contrast, polar groups are exposed to the environment in the ‘open’ conformation.18,33,35 Therefore, cyclic peptides can adapt to polar and apolar environments by changing from one conformation to another, an ability called the ‘chameleonic’ behavior of cyclic peptides.33,36
The shielding of polar groups in the ‘closed’ conformation lowers the desolvation energy barrier for moving into the apolar membrane interior. Therefore, the ‘closed’ conformation is assumed to be the main permeable species.21,33,37,38 However, the possibility to adopt a ‘closed’ conformation in an apolar environment alone does not necessarily imply membrane permeability.21,34 Molecular dynamics (MD) and nuclear magnetic resonance (NMR) studies have revealed that congruent conformational states (i.e. conformations occurring in both polar and apolar environments, of which the ‘closed’ conformation can be one) facilitate the transition between different environments and therefore increase membrane permeability.18,21,24 The peptide composition, size, and hydrophobic surface area heavily influence the conformational behaviour of cyclic peptides and thus also the permeability.21,23,26,27,31 The interplay between all these factors is not trivial to decipher and therefore, it is difficult to establish structure–permeability relationships.
During their path through the membrane, cyclic peptides pass different environments. They start in a polar aqueous environment outside the cell, cross the polar and often charged lipid head-group region, move through the apolar lipid-tail region, and again pass the head-group region in order to reach the interior of the cell. Thus, cyclic peptides not only face different environments, but also multiple interfaces between polar and apolar regions. The conformational and dynamic behavior at these interfaces is hardly understood since previous simulation approaches have focused mainly on homogeneous environments.21,24 Only few studies have been reported that targeted cyclic peptides in non-homogeneous environments.39,40 In these studies, biased enhanced sampling approaches were employed to achieve sufficient sampling in the available simulation time. Wang et al.39 simulated cyclosporine A at a water/chloroform interface as well as in a 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) bilayer system. To enhance sampling, the authors increased the temperature of the system to 490 K and reduced specific force constants acting on the ω-dihedral angles. Sugita et al.40 used steered MD41 and umbrella sampling42 to pull more than 100 different cyclic peptides into a POPC bilayer and calculate their free-energy profile. In addition, they focused on small cyclic peptides with little conformational flexibility in order to obtain converged results. These studies led to important new insights into the permeability of cyclic peptides. The free-energy minimum along the permeation pathway (i.e. the most favorable position of the peptide) was neither in the aqueous phase nor in the apolar lipid-tail region, but directly beneath the lipid head-group region at the polar/apolar interface.39,40 This behavior was conserved over a wide range of peptides with different hydrophilicity. The free-energy minimum was more distinct for more lipophilic peptides, but even very hydrophilic peptides showed this minimum.40 As cyclic peptides are likely to spend a large proportion of their permeation process located at this minimum, a detailed and non-biased understanding of how the interface influences the conformational behavior and dynamics of cyclic peptides is desired.
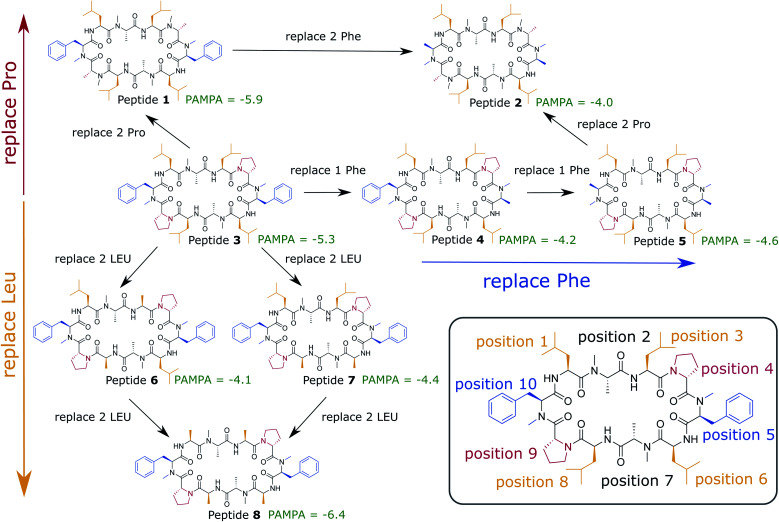
In this work, we use extensive unbiased MD simulations to investigate the behavior of a series of eight cyclic decapeptides (CDPs) at a water/chloroform interface, and compare the results to unbiased simulations with a POPC bilayer. In contrast to the work of Sugita et al.,40 the peptides are chosen to show complex internal conformational dynamics. The simulations are performed without biases and at room temperature to avoid artifacts like the distortion of the interface or POPC bilayer or the formation of pores. In addition, this ensures that the observed conformations and kinetics reflect the natural behavior of the cyclic peptides. The backbone scaffold of the CDPs and their N-methylation pattern was introduced by Fouché et al.43,44 and is kept throughout our series while the side chains are varied. Fig. 1 illustrates the variations that are performed in three dimensions: (i) a switch from leucine to alanine at position 1, 3, 6, and 8, (ii) proline to alanine at position 4 and 9, and (iii) d-phenylalanine to d-alanine at position 5 and 10. In the closed conformation, as observed by NMR and in crystal structures, the peptides form two β-strands (amino acids at position 1, 2, 3 and 6, 7, 8) and two β-turns (amino acids at position 4, 5 and 9, 10). In this conformation, all unmethylated amide nitrogen atoms face towards the peptide interior and build the typical four H-bonds pattern.21 We investigate how the interplay between polar/apolar interfaces and the peptide orientation modulate the conformational and kinetic behavior of the CDPs, and showcase the important role of interfaces in the passive permeation process of cyclic peptides.
Fig. 1. Cyclic decapeptide (CDP) series used in this work. The backbone scaffold was reported by Fouché et al.43,44 and is kept constant. The side-chain residues are systematically varied between leucine/alanine at position 1, 3, 6, and 8 (yellow), proline/alanine at position 4 and 9 (red), and d-phenylalanine/d-alanine at position 5 and 10 (blue). In position 2 and 8 are alanines in all peptides. In position 5 and 10 are d-amino acids to enable the correct β-turn conformation. The parallel artificial membrane permeation assay (PAMPA) data were taken from ref. 24. Note that CDP 1 and 3 in this study correspond to CDP 6 and 4, respectively, in ref. 21 and 24.
2. Methods
2.1. Experimental details
All experimental data has been taken from previous publications. The synthesis of the CDPs and the determination of their solution structures in chloroform by NMR spectroscopy have been described in detail in ref. 43. The PAMPA measurements were described in ref. 21 and 24. The NMR measurements have been used to derive the ‘closed’ starting conformations for MD simulations. Compound purity was determined by analytical liquid chromatography-mass spectrometry (LC-MS) and liquid chromatography-ultraviolet spectroscopy (LC-UV) 220 nm to 400 nm diode array detection (DAD) with an acquity ultra-performance liquid chromatography (UPLC) system. The purity of all compounds was >95%.
2.2. Computational details
2.2.1. MD simulations
2.2.1.1. Initial conformations
All MD simulations were initiated with CDPs in their ‘closed’ or major ‘open’ conformation. The ‘closed’ conformers were obtained from measurements in chloroform by NMR spectroscopy.43 The generation of the major ‘open’ conformers has been described in detail in ref. 21 and 24. Briefly, a set of 100 seed conformers from enhanced sampling runs facilitating an opening of the ‘closed’ conformers was selected to perform repeated parallel MD simulations of 100 ns length until the subsequent core-set Markov model (CSMM) converged. The ‘open’ conformers of CDPs 2 and 4–8 were adapted by in silico mutagenesis from CDP 1 and 3, respectively, and used as an ensemble set of seeds for the corresponding MD simulations.
2.2.1.2. Water/chloroform interface
All MD simulations at the water/chloroform interface were performed using the Groningen Molecular Simulation (GROMOS) software package45 and the GROMOS 54A8 force field.46 The simulations were carried out under NPT conditions with rectangular periodic boundary conditions. The leapfrog scheme47 was used to integrate Newton's equations of motion with a time step of 2 fs. The simple-point-charge (SPC) water solvent model48 was used. Weak coupling49 to three separate temperature baths for the peptide, the chloroform phase and the water solvent was applied with a reference temperature of 300 K and a relaxation time of 0.1 ps. The pressure was maintained around 1.013 bar (1 atm) by weak coupling to a pressure bath with a relaxation time of 0.5 ps and an isothermal compressibility of 0.4575 nm2 N−1 under isotropic scaling of the simulation box. For the nonbonded interaction, a twin-range cutoff scheme was used with 0.8 nm and 1.4 nm cutoffs. A reaction-field force50 with a relative dielectric permittivity of 61.0 (ref. 51) was used for the treatment of electrostatic interactions beyond the long-range cutoff. The SHAKE algorithm52 was used to constrain bond lengths with a relative tolerance of 10−4. Coordinate and energy trajectories were written out every 5 ps for data analysis.
The biphasic simulation system consisted of 400 chloroform molecules and an equal volume of water molecules. The simulation box measured 7.52 nm × 3.76 nm × 3.76 nm. A cyclic peptide in either the ‘closed’ conformation or the major ‘open’ state was placed in the simulation box in various orientations either at the interface of the water and chloroform phases, or at the center of the aqueous phase, with approximately 1.88 nm distance between the CDP's center of mass and the closest chloroform atom at the interface. Each simulation was preceded by 20 ps NVT thermalisation and equilibration under positional restraining of the solute atoms. Initial velocities were generated using a random number generator seed at an initial temperature of 300 K. If not mentioned otherwise, 50 MD simulations with different starting orientations were performed for 200 ns per peptide and starting conformation, resulting in 20 μs of sampling of each CDP. The first 2 ns of each simulation were discarded from the analysis for equilibration.
2.2.1.3. POPC bilayer
The MD simulations at the POPC lipid bilayer (a mimic for a cellular membrane) were performed using the Groningen Machine for Chemical Simulations (GROMACS) 2020.5 software package53 and the GROMOS 54A8 force field.46 Lipid parameters were adopted from the POPC model of Marzuoli et al.54 to improve solvation properties of the head-group region. The simulations were carried out under NPT conditions with rectangular periodic boundary conditions. Again, the SPC48 water model was used as solvent. The leapfrog scheme47 was used to integrate Newton's equations of motion with a time step of 2 fs. Weak coupling49 to three separate temperature baths at 303 K for the peptide, the lipids and the solvent was applied with a relaxation time of 0.1 ps. The pressure was coupled semi-anisotropically to a Parrinello-Rahman barostat55 at 1.0 bar with a coupling constant of 2.0 ps and an isothermal compressibility of 0.45 nm2 N−1. For both the short-range electrostatic and van der Waals interactions, a single cutoff of 1.2 nm was used. The long-range electrostatics were calculated by the particle mesh Ewald (PME) algorithm.56 The linear constraint solver (LINCS) algorithm57 was used to impose constraints on the bond lengths with fourth order expansion. Center-of-mass (COM) motion removal was applied in every simulation step to remove the motion of the bilayer relative to the solvent. Coordinate trajectories were written out every 100 ps for data analysis.
The topology of the simulation box containing 512 POPC lipids in a bilayer (256 per leaflet) was adopted from Marzuoli et al.54 The CDPs were placed either in their ‘closed’ conformation or the major ‘open’ state at the center of the aqueous phase in the simulation box, with approximately 3 nm distance between the CDP's center of mass and the closest head-group atom of the POPC lipids. Each simulation was preceded by 100 ps NVT thermalisation and 1 ns NPT equilibration. In total, 50 runs with 100 ns length were started in the ‘open’ and ‘closed’ conformation of CDP 1 and CDP 3 each. After manual assessment, those runs that showed an initial contact with the membrane were selected. For CDPs 1 and 3, two and three of the 100 runs showed an initial contact with the membrane, respectively. The last frame of these simulations was used as the seed for five continuation runs with 100 ns each.
2.2.2. Construction of Markov models
MSMs provide a statistical framework to describe the complete system dynamics.58 Using MSMs, one can compute stationary quantities and long-time kinetics from ensembles of short simulations. Importantly, these short simulations need to be in ‘local equilibrium’ within the MSM states, but are not required to be in ‘global equilibrium’. Thus, we can combine multiple short simulations of 200 ns to obtain the system's kinetics in the μs regime.
For all trajectories, the sine and cosine of the backbone torsion angles ϕ and ψ were extracted using the PyEMMA Python library,59 representing the first 40 feature dimensions. Additionally, the position in the simulation box and orientation of the CDPs with respect to the simulation box were extracted from the trajectories using the MDTraj60 Python library, resulting in a total of 42 feature dimensions. In the system description, no side-chain information was explicitly included. The 42 feature dimensions were reduced to 6–11 collective coordinates (the exact number depends on the peptide) by time-lagged independent component analysis (TICA).61
The hierarchical density-based Sittel–Stock clustering algorithm62 was used for the spatial clustering. The Sittel–Stock algorithm requires a cutoff for the minimal number of members for a cluster (k). Here, a cutoff k = 100 was used. To obtain effective transition probabilities between the conformational states, the core-set Markov model technique (CSMM)63–66 was used. For the Markov model, a lagtime τ of 1.5 ns was chosen to ensure Markovianity. Furthermore, robust Perron cluster–cluster analysis (PCCA+)67 was performed to group the microstates into metastable conformational states. Depending on the peptide, three or four macrostates were chosen. Visual inspection of these showed that this procedure lead to the separation of a ‘closed’, an ‘open orientation A’, and an ‘open orientation B’ state for each peptide.
The mean first passage times (MFPTs) Ex[Ty] of the interconversion processes describe the expected hitting times of one target state y in Y when starting in state x in X. MFPTs were calculated from the transition matrix T with the following equation,
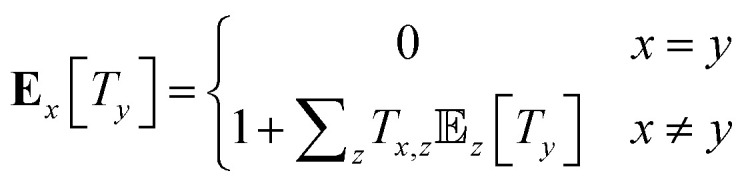 |
1 |
Bootstrapping was performed to obtain the average and standard deviation for the steady-state populations of the Markov models. A total of 50 bootstrapping iterations were performed. In each iteration, n trajectories were picked from the total set of trajectories with replacement, where n equals the total number of trajectories.
2.2.3. Data analysis
If not stated otherwise, all trajectories were analyzed using the MDTraj60 Python library.
2.2.3.1. Position
The position of the CDP inside the biphasic simulation box was calculated by dividing the number of atom–atom contacts within a threshold of 0.5 nm between the CDP and the chloroform molecules with the number of atom–atom contacts between the CDP and molecules of the water and chloroform phase as follows,
 |
2 |
2.2.3.2. Orientation with respect to the simulation box
To calculate the orientation of the peptides with respect to the simulation box, the cosine of α, the scalar product between the normal vector to the plane set up by the CDP (a⃑) and a vector parallel to the length of the simulation box (b⃑) was determined,
| Orientation = cos(α) = cos(a⃑·b⃑) | 3 |
Because of the periodic boundary conditions, the vector parallel to the length of the biphasic simulation box (b⃑) was calculated as the vector pointing from the COM of the aqueous phase to the COM of the chloroform phase. In the simulation with the POPC bilayer, on the other hand, the z-axis of the system was used as b⃑. In each case, these vectors (b⃑) constitute the normal vector to the polar/apolar interface.
2.2.3.3. Orientation with respect to the water/chloroform interface by side-chain interactions
To calculate the orientation of the peptides with respect to the water/chloroform interface by side-chain interactions, the number of atom–atom contacts within a threshold of 0.5 nm between the non-hydrogen atoms of the leucine side chains (alanine if substituted) and chloroform molecules was divided by the number of atom–atom contacts between the non-hydrogen atoms of the leucine side chains (alanine if substituted) and molecules of the water and chloroform phase as follows,
 |
4 |
2.2.3.4. RMSD
The atom-positional backbone root-mean square deviation (RMSD) was calculated with respect to the NMR solution structure of the ‘closed’ state.
2.2.3.5. State assignment
Re-assignment of simulation frames to the macrostates identified by Markov state modelling was used to analyze the distribution of total energies as well as the positions and orientations of the CDPs within these states. If not stated otherwise, only the frames with a probability >90% of belonging to a certain metastable set were included.
2.3. Data and software availability
The structure and topology files of the CDPs in the closed and major open conformation are available on GitHub (https://github.com/rinikerlab/cyclic_peptide_at_interfaces). The GitHub repository also contains a sample Jupyter notebooks for the MSM analysis of CDP 1.
Further information, custom scripts, or production trajectories are available from the corresponding author (S. R.) upon request. The freely available software can be obtained via the following links: GROMOS (http://www.gromos.net/), GROMACS (https://www.gromacs.org/), and PyMol (https://github.com/schrodinger/pymol-open-source).
3. Results and discussion
3.1. 3D hydrophobicity profile
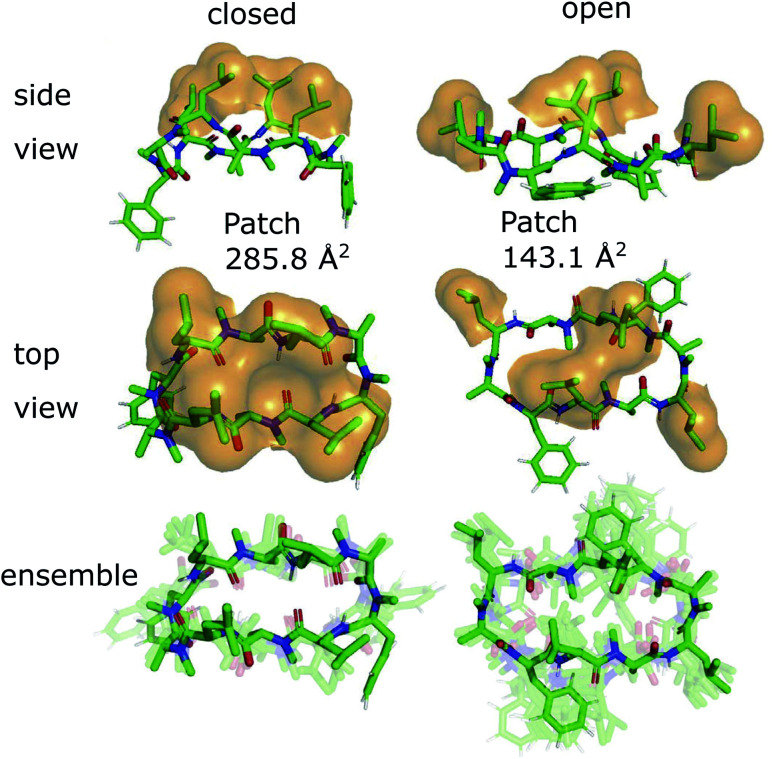
The 3D conformations of the cyclic decapeptides (CDPs) show a directed hydrophobicity profile, i.e. one side of the peptides is more hydrophobic than the other. This directionality is mainly caused by leucine residues, a common feature of the CDP series.44Fig. 2 displays the conformation of CDP 1 in the ‘closed’ and the highest populated ‘open’ state obtained by a MSM of the peptide in water. The solvent-accessible surface of the hydrophobic leucine residues is highlighted in orange. In both the ‘closed’ and ‘open’ conformation, all leucine residues point outwards of the plane defined by the backbone macrocycle. We will call this direction the peptide's ‘normal’. The leucine side-chain orientations are relative stable throughout the simulations. In contrast, the orientation of the phenylalanine side chains is flexible and can span a 180° angle. Thus, the CDPs show a higher occurrence of hydrophobic side chains on one side, which leads to the directed hydrophobicity pattern. In the ‘closed’ conformation, the leucine side chains build a continuous, large hydrophobic patch, while this patch is split into smaller ones in the ‘open’ conformations. The directed hydrophobicity and conformational dependency was observed for all peptides of the series except CDP 8, which contains no leucines (see section ‘Hydrophobicity profile of peptides 2–7’ and Fig. S1 in the ESI†).
Fig. 2. Metastable conformations of CDP 1 in water. The ‘closed’ as well as the highest populated ‘open’ state are shown. In the two top panels, the solvent-accessible surface of the hydrophobic leucine residues is indicated by orange spheres. The conformational ensemble of the metastable states is shown at the bottom.
When the peptides are simulated in an isotropic environment like a water box, the observed directed hydrophobicity has no effect on the conformational dynamics of the peptides. However, this may be different at interfaces between polar and apolar environments. Sugita et al.40 have shown that the most favorable position of cyclic peptides at the membrane is directly underneath the lipid head-group region at the polar/apolar interface. Such an interface has its own directionality that can interact with the directed hydrophobicity of the CDPs and effect the conformational behavior. As previous work has mainly focused on isotropic environments, the role of the directionality could not be captured. The observed differences in the hydrophobic patch between the ‘open’ and ‘closed’ state are thereby of special interest, as Hoang and co-workers23 found that the size of the largest continuous hydrophobic surface patch correlates with the membrane permeability in a series of cyclic hexapeptides and heptapeptides. This raises the question whether the different patch sizes of ‘open’ and ‘closed’ conformers also lead to permeability effects.
3.2. Peptide orientations at interfaces
A water/chloroform interface was chosen as a model system. This combination allows straightforward comparison to previous work that was performed in pure water or pure chloroform.18,21,23,24 We first tested how the CDPs orient towards the interface. Therefore, CDP 1 was placed at the interface in the ‘closed’ and in the major ‘open’ conformation with different orientations and simulated without constraints. Interestingly, only two stable orientations, called A and B in the following, were observed in the open conformation. In the closed conformation, only one stable orientation, orientation A, was seen. All other orientations quickly rotated towards one of the stable ones. In both orientations A and B, the plane defined by the peptide backbone laid flat on the interface. In orientation A, the leucine side chains face towards the chloroform phase, whereas in orientation B they face towards the water phase.
To confirm that the stable orientations occur naturally and are not an artifact of placing the peptide at the interface, 60 short simulations of 20 ns length with the peptides starting in the aqueous phase in random orientations were performed. Indeed, within few nanoseconds of simulation time, the peptides diffused towards the interface and adopted the same stable orientations A and B. Interestingly, 75% of the ‘open’ peptides initially adopted orientation A at the interface, whereas 25% initially interacted with the interface in orientation B. This shows that while establishing the first contact with the interface, there is an initial preference for orientation A. This preference is amplified after a few nanoseconds equilibration time at the interface, resulting in 97% in orientation A versus 3% in orientation B (Table 1). Based on these findings, the simulations of CDPs 2–8 were directly started from the water phase with random orientations. Again, only the two stable orientations A and B were observed (Table 1). Note that Table 1 displays the simulation time spent in the orientations over 50 simulations of 200 ns length. As we show later in this study, the relaxation timescales for this system are in the order of μs. Thus, at this stage, the reported values do not reflect equilibrium distributions but rather mimic an initial distribution after drug administration. For equilibrium populations, we refer the reader to Section 3.5.
Fraction of simulation time spent in orientation A and B after equilibration for CDPs 1–8 in the ‘open’ and ‘closed’ conformation.
| Peptide ID | ‘Open’ | ‘Open’ | ‘Closed’ | ‘Closed’ |
|---|---|---|---|---|
| Orient. A (%) | Orient. B (%) | Orient. A (%) | Orient. B (%) | |
| 1 | 97 | 3 | 100 | 0 |
| 2 | >99 | <1 | 100 | 0 |
| 3 | 76 | 24 | 100 | 0 |
| 4 | 88 | 12 | 100 | 0 |
| 5 | 96 | 4 | 100 | 0 |
| 6 | 54 | 46 | 100 | 0 |
| 7 | 57 | 43 | 100 | 0 |
| 8 | 60 | 40 | 87 | 13 |
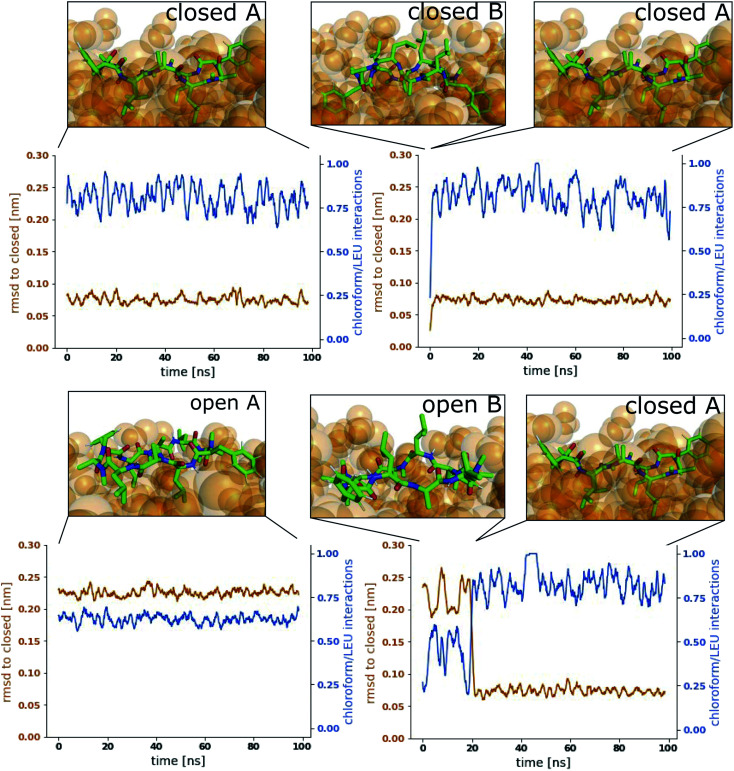
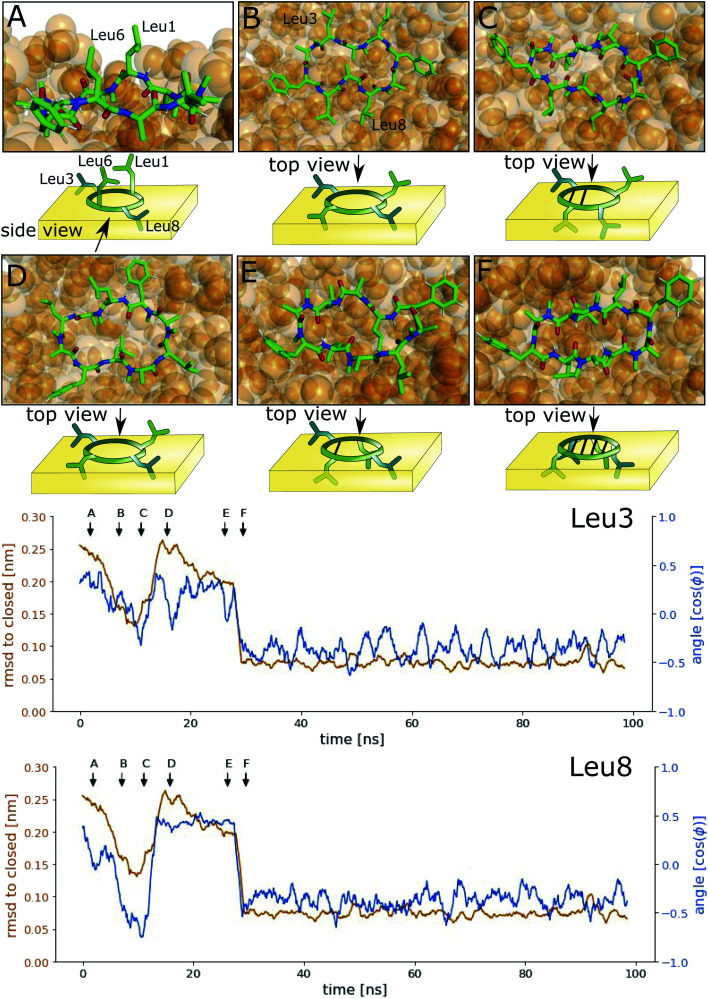
Fig. 3 shows representative simulations of CDP 1 in the stable orientations at the interface. The simulation in the top left panel was started from the ‘closed’ conformation in orientation A. This orientation was stable throughout the full simulation time of 100 ns. In contrast, the simulation in the top right panel was started from the ‘closed’ conformation in orientation B. Within 1 ns of simulation time, the peptide rotates from orientation B to orientation A, indicating that orientation B is less stable in the ‘closed’ conformation. A higher resolution of the rotation process is shown in Fig. S2 in the ESI.† Simulations started from the ‘open’ conformation are shown in the bottom panels of Fig. 3. When the peptide was started from orientation A (left), the orientation was stable throughout the full simulation as in the ‘closed’ case. Interestingly, orientation B appears to be metastable in the ‘open’ conformation (right panel). After starting in orientation B, the peptide remained in this orientation for a few nanoseconds, before rotating as well towards orientation A. During the rotation, the peptide stayed in the ‘open’ conformation in some simulations while it closed in others (as in the example in Fig. 3, a rotation from orientation B to A without closing is depicted in Fig. S3 in the ESI†). The rotation of the peptide occurs along its long axis and thus, the contacts with the chloroform phase are temporarily increased until orientation A is reached.
Fig. 3. Representative simulations of CDP 1 at the water/chloroform interface. Blue lines show the fraction of leucine/chloroform interaction with respect to all leucine/solvent interactions as a measure for the peptide's orientation. The root mean square deviation (RMSD) of the peptide with respect to its ‘closed’ conformation is shown in orange. Snapshots of the simulations are provided to illustrate the location and orientation of the peptide towards the interface. Chloroform molecules are shown as orange spheres. Water molecules are not shown for visual clarity. Simulations were started from the following combinations of conformation and orientation. (Top left): ‘Closed’/A. (Top right): ‘Closed’/B. (Bottom left): ‘Open’/A. (Bottom right): ‘Open’/B.
3.3. Composition effects on the orientation preference at the interface
From Table 1, it is evident that all CDPs favor orientation A at the interface. In the ‘closed’ conformation, all peptides except CDP 8 are even exclusively observed in orientation A. The stronger preference for orientation A in the ‘closed’ state in comparison to the ‘open’ state aligns well with the hydrophobic patches shown in Fig. 2 and S1 in the ESI.† In the ‘closed’ states, the leucine side chains form a large continuous hydrophobic patch, while the patch is broken up in the ‘open’ state. In orientation A, the hydrophobic patch faces the hydrophobic chloroform phase resulting in favorable interactions. These are stronger with the large continuous patch of the ‘closed’ state, leading to a stronger preference for orientation A. Hence, not only the overall amount of hydrophobic surface area is important but also its distribution in different conformers.
The effect of the hydrophobic patch can be confirmed by the orientation preferences of CDPs 6–8, which lack half (two) or all (four) leucines side chains in comparison to the other peptides. In the ‘open’ conformation, CDPs 6 and 7 (lacking two leucines) have nearly equal preference for orientation A and B (Table 1). CDP 8 (lacking all four leucines) is the only peptide for which orientation B in the ‘closed’ conformation is observed. It is also the peptide with the lowest passive membrane permeability. Other amino acids also seem to influence the orientation preference. Phenylalanine even shows a titratable effect. Upon removal of both phenylalanine side chains from CDP 1, the fraction of ‘open’ frames in orientation B drops from 3% to <1%. When removing one phenylalanine from CDP 3, the fraction drops from 24% to 12%, while removing an additional phenylalanine leads to a further decrease to 4%. The presence of proline, on the other hand, seems to reduce the preference for orientation A. CDPs 1 and 3 as well as 2 and 5 only differ in the presence of proline residues. In the first pair, the fraction of orientation B in the ‘open’ conformation increases from 3% to 24%, and in the second pair it increases from <1% to 4% upon introduction of the proline side chain. CDPs that contain proline residues have a more round shape in the ‘open’ states (compare Fig. 2 and S1 in the ESI†). Therefore, the hydrophobic patch of those peptides is more fragmented in the ‘open’ state than for peptides without proline. A more separated hydrophobic patch thus leads to a lower preference for orientation A.
The CDPs can only adopt distinct orientations at polar/apolar interfaces. The preference between the orientations is modulated by the amino-acid composition as well as the conformation of the peptide. This particular feature of cyclic peptides could only be observed by advancing from simulations in simple isotropic environments to anisotropic environments such as a polar/apolar interface. However, the question remains if the observations from the water/chloroform interface are transferable to a real lipid membrane system.
3.4. Comparison with lipid membranes
Lipid membranes and simple polar/apolar interfaces share important features like the directed hydrophobicity, but also differ in many points. Lipid membranes consist of a polar and often charged head-group region and an apolar lipid-tail region. Each layer of the membrane exhibits a dipole moment that points from the membrane's middle plane toward the head-group region. The head-group region is usually hydrated by water molecules. In comparison to chloroform molecules, the lipids are much larger, more bulky, and therefore not that easily displaced. The orientations A and B of the CDPs maximize the interface surface area occupied by the peptide (i.e. the peptide lies parallel to the interface), and are thus expected to distort the membrane surface more than a peptide in a tilted orientation. This raises the question how transferable the results from the water/chloroform system are towards a lipid membrane.
As an approximation for a biological membrane, we used a large patch containing 512 POPC lipids (256 in each layer). This system was chosen to minimize finite size and buckling effects. Due to the increased size and complexity of the system, the simulation program was changed to GROMACS with the same force field (see Method section). To ensure that this change does not cause significant differences in the results, we compared the simulations of CDP 1 in water between the two simulation programs (the MSMs are displayed in Fig. S4 in the ESI†). The kinetic timescales as well as the fraction of ‘closed’ and ‘open’ conformational states were within a ratio of 1.5 of each other. In addition, the stationary distributions of the peptide overlapped in the TICA subspace with the exception of two minor conformational states (marked with red boxes). These small deviations can be explained by statistical fluctuations of the simulations.
Simulations of the POPC patch with CDPs 1 and 3 were performed at room temperature without the addition of any bias. The two peptides were selected as representatives of the peptide classes with and without proline residues. The equilibrium population of ‘closed’ states in water is 45% for CDP 3, but only <1% for CDP 1.21 Therefore, these peptides are good candidates to test the role of conformation preference for entering the membrane interface. We use no biases in the simulations in order to remain as realistic as possible and avoid membrane distortion or pore formation, unwanted effects that would alter the results. The simulations were initialized with peptides placed in the aqueous phase. In the chloroform/water simulations, the peptides moved to the interface within a few nanoseconds. In contrast, it took much longer in the lipid membrane system for the peptide to reach the membrane interface. In most simulations, the peptide remained in the aqueous phase entirely. Due to their conformational flexibility, the peptides adopted conformations according to their equilibrium distribution during the elongated stay in the aqueous phase. CDP 3 adopted both ‘open’ and ‘closed’ conformations in the aqueous phase. Interestingly, the peptide was able to move to the membrane interface in both ‘open’ and ‘closed’ conformations. CDP 1 was nearly exclusively found in ‘open’ conformations in the water phase. Accordingly, only open conformations were seen inserting into the membrane interface.
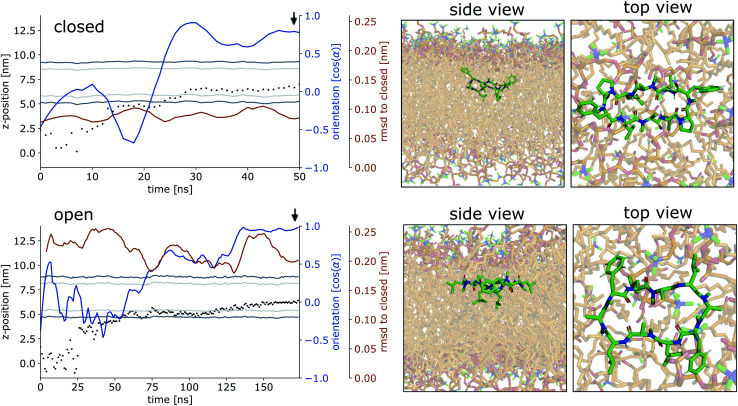
Fig. 4 shows representative simulations of CDPs 1 and 3 inserting into the membrane interface in the ‘closed’ and ‘open’ state, respectively. In the trajectory of CDP 3, the peptide remained in the ‘closed’ conformation throughout the simulation. After an initial phase of diffusion in the water phase (0–15 ns), the peptide stayed in the proximity of the membrane for some time (15–25 ns), before entering the membrane in a tilted orientation (22–28 ns), and eventually moving deeper into the membrane and adopting orientation A (30 ns onward). The membrane thickness was unperturbed by the embedding of the CDP. The area per lipid, which was 0.637 nm2 without the CDP, dropped slightly (0.02 nm2) upon CDP insertion, but relaxed back into the equilibrium value within a few ns. Orientation A was relatively stable over the rest of the simulation. Looking at the snapshots, one can confirm that the peptide is indeed in orientation A with the leucine residues pointing towards the apolar tail region. The lipids were thereby pushed aside to make room for the peptide. In the top view, one can observe that the peptide is not covered by the lipids but still has contacts with the aqueous phase through a water funnel. This water funnel together with the polar head-groups in the proximity of the peptide and the apolar tail region creates a local polar/apolar interface for the peptide. The environment at this interface is comparable with that observed in the water/chloroform system. In some frames in the ‘closed’ conformation (but never in ‘open’ conformations), lipids fully cover the peptide, leading to the disappearance of the water funnel and a slightly deeper penetration of the peptide in the membrane.
Fig. 4. Representative simulations of CDPs 3 and 1 inserting into the membrane interface. (Top): CDP 3 in the ‘closed’ conformation. (Bottom): CDP 1 in the ‘open’ conformation. Black dots show the COM position of the peptide. The position of the membrane is indicated by dark grey (head groups) and light grey (tails) lines. The orientation of the peptide with respect to the membrane is shown in blue, α indicates the angle between the peptide normal and the membrane normal. The orange lines indicate the RMSD of the peptide with respect to its ‘closed’ NMR solution structure. The black arrow indicates the time point corresponding to the snapshots shown on the right. In the snaphots, the peptide is shown in green and the membrane in orange.
CDP 1, which inserts into the membrane in the ‘open’ conformation, shows a similar trajectory. It exhibited more conformational dynamics but never closed. It also entered the membrane in a tilted orientation that is stable between 60–125 ns. Eventually, it adopts orientation A with the leucines pointing towards the tail region (125 ns onward). In contrast to orientation A of the ‘closed’ conformation, the phenylalanine side chains point towards the membrane plane and not towards the head-group region. Nevertheless, the environment is very similar to that in water/chloroform and also shows the characteristic polar/apolar interface formed by the water funnel and the head groups.
Before fully entering the membrane, the peptides position themselves at the membrane/water interface. Our findings highlight that conformationally flexible peptides can do this in both ‘closed’ and ‘open’ conformations. In all simulations with peptides in the ‘open’ conformation and in a majority of the simulations with peptides in the ‘closed’ conformation, the peptide remains in contact with the aqueous phase through a water funnel and also in proximity of the head-group region. Thus, the peptide creates its own local interface environment. Especially peptides that preferentially adopt the ‘open’ conformation in water seem to insert into the membrane in the ‘open’ conformation. For peptides that predominantly enter the membrane in the ‘open’ conformation, the closing dynamics at the interface is potentially the decisive factor for their membrane permeability. Within our simulation time, the peptides appear to be trapped in one leaflet of the membrane, indicating that crossing the interior of the membrane is connected with a substantial energy barrier for the large and flexible CDPs. Unfortunately, the insertion events into the membrane are very rare. A total of 10 μs simulation time per peptide was necessary to sample two and three membrane insertion events for CDPs 1 and 3, respectively. Additionally, simulating a big POPC patch is very computer resource intensive. Therefore, this analysis was only performed for CDPs 1 and 3 and no statistical evaluation of the distribution between orientation A and B was possible.
In summary, striking similarities in terms of positioning, conformation, and orientation preferences of the CDPs were observed between the water/chloroform interface and the membrane interface, indicating that the former model system can be used as an approximation for the conformational dynamics at lipid membranes. Due to its large size, the computational costs to simulate the membrane system are very high. Additionally, the dynamics of the peptides at the membrane are slower due to friction effects with the bulky lipids. Collecting sufficient data to construct an MSM would take considerably more simulation time than available for the membrane system in this study and is unfeasible for a larger number of peptides. Therefore, we continued to study the conformational dynamics of the CDPs using the simpler and faster equilibrating water/chloroform system, where it is possible to obtain sufficient data for the construction of MSMs.
3.5. Interface catalyzes the closing of cyclic peptides
Next, we investigated how the interface influences the conformational dynamics of the CDPs. Fig. 5 shows a trajectory of CDP 1 interconverting from the ‘open’ to the ‘closed’ conformation at the interface. Interestingly, the backbone torsional angle ϕ of leucines 3 and 8 is highly correlated with the change in RMSD with respect to the ‘closed’ state, but not the backbone torsions of leucine 1 and 6 or any other residue. In the trajectory, we can see first half closing of the peptide (at approx. 10 ns) followed by a full closing event (at approx. 28 ns). For the half closing, the characteristic intramolecular hydrogen bonds are only formed on one side of the peptide (see Fig. 5C and E). For the full closing, a change in the backbone torsional angle ϕ of leucines 3 and 8 of around 90° is necessary. In comparison, no closing events were seen in our previous simulations of CDP 1 in pure water (CDP 6 in ref. 21 and 24). Similar closing trajectories were observed for all eight peptides (Fig. S5 and S6 in the ESI† show a selection of these closing and opening events).
Fig. 5. Interconversion of CDP 1 from ‘open’ to ‘closed’ conformation at the interface. The orange line represents the RMSD with respect to the ‘closed’ NMR solution structure, and the blue line the cosine of the backbone ϕ angle. Arrows indicate the time points of the snapshots (A–F) shown on top.
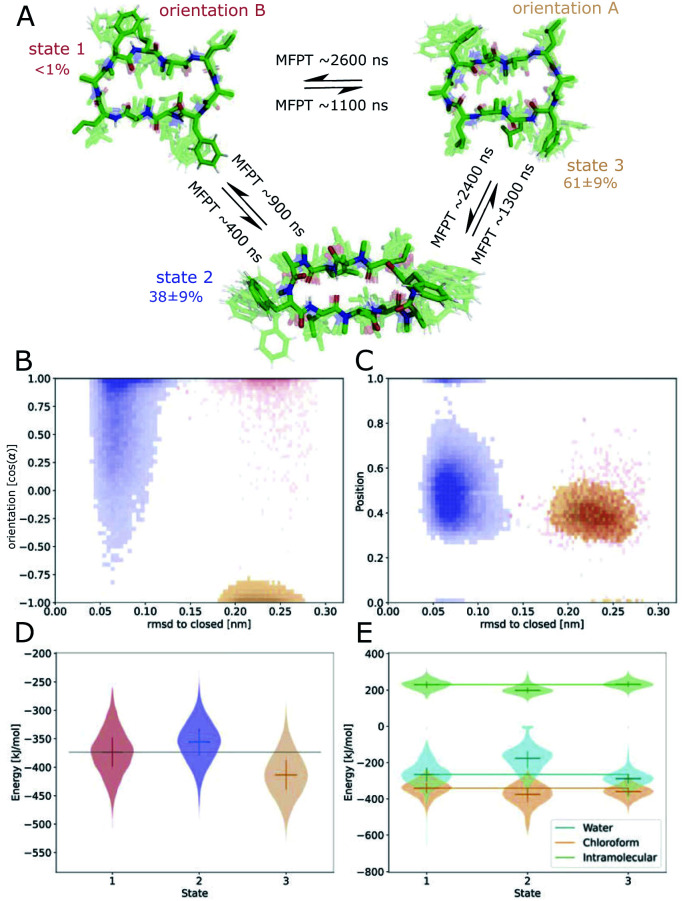
To better understand the kinetics and metastable conformational states of the CDPs, we built MSMs for each of the peptides. Previously, we used the backbone torsional angles as input features for the MSMs.21,24 To take into account the role of the interface, we included two additional features: the position and orientation of the peptide relative to the interface. The position of the peptide with respect to the interface was measured by the ratio between the number of peptide–chloroform contacts and the total number of peptide–solvent contacts. The orientation was described with the angle between the peptide and the membrane normal. Four or three metastable conformational states were identified for CDPs 1–8.
Fig. 6 shows the MSM of CDP 1 based on the interface simulations. The results of all other CDPs are provided in Fig. 7 and S7–S13 in the ESI.† Importantly, the kinetic model distinguishes for all peptides metastable states in orientation A and B for ‘open’ but not ‘closed’ conformations. The model was not biased to make this distinction. The orientation feature was treated as any other of the 42 MSM input features. Its significance for the kinetic model underlines the previous observation that it is important to consider both orientations for ‘open’ conformations. The equilibrium populations as well as the MFPTs between the metastable states are shown in panel A. Interestingly, the ‘closed’ state of CDP 1 is highly populated at the interface (38%). In contrast, its ‘closed’ population in water is <1%.21 Thus, CDP 1 mainly adopts ‘open’ conformations in water and also likely inserts into the interface in an ‘open’ conformation (compare to Fig. 4). Once at the interface, the equilibrium and kinetics of CDP 1 are shifted compared to the aqueous phase. The closing process becomes much faster. Thus, the interface can act as a catalyst for the interconversion between ‘open’ and ‘closed’ conformations. Additionally, the MFPT for the closing process is much shorter for orientation B than for orientation A. In our equilibrium model, orientation B is hardly populated. However, we have found that in 25% of cases CDP 1 initially interacted with the interface in orientation B (section ‘Peptide orientations at interfaces'). Therefore, in a real world non-equilibrium scenario where the cyclic peptide is administered as a drug, the importance of orientation B may be higher than anticipated by the equilibrium model.
Fig. 6. Markov state model (MSM) of CDP 1. (A) Representative members of the metastable states, their equilibrium populations as well as the mean first passage times (MFPTs) between them. (B) Metastable state assignment mapped to the orientation feature and the RMSD with respect to the ‘closed’ state. (C) Metastable state assignment mapped to the position feature and the RMSD with respect to the ‘closed’ state. (D) Violin plot of the interaction energies of the metastable state members. (E) Same as (D), but split into water, chloroform, and intramolecular contributions. Horizontal lines are added to help guide the eye.
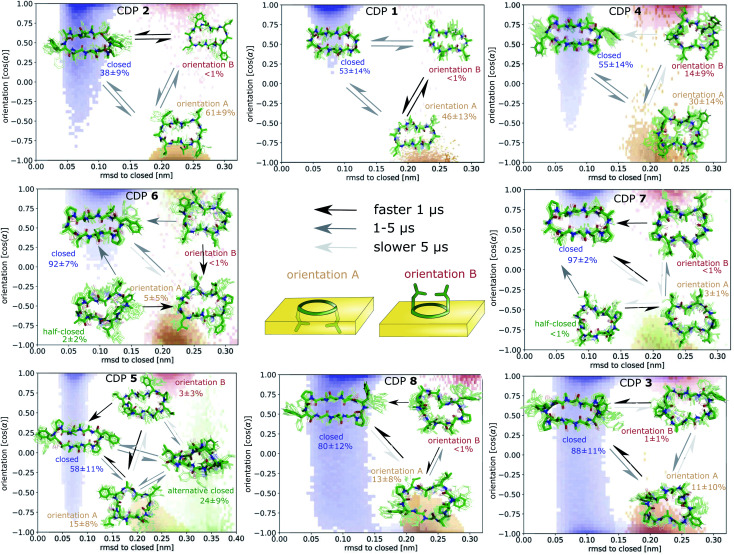
Fig. 7. Markov state models (MSMs) of CDP 1–8. Representative members of the metastable states, their equilibrium populations as well as the mean first passage times (MFPTs) between them are shown on top of the simulation data points mapped to the orientation feature and the RMSD with respect to the ‘closed’ state. Note that the simulation data points represent non-equilibrium data while for the MSMs the equilibrium populations are shown.
Fig. 6B shows the metastable state assignment mapped on the orientation feature and the RMSD with respect to the ‘closed’ conformation. The model clearly distinguishes between a ‘closed’ state (blue) and two different ‘open’ states (red and orange). The two ‘open’ states are separated by their orientation with respect to the interface. The ‘closed’ state can adopt a larger variety of orientations. This first seems to be in contrast with the observed stability of only one orientation in the ‘closed’ state (Table 1). However, as discussed below, the ‘closed’ state can diffuse into the apolar phase. There, it experiences an isotropic environment, which leads to more orientational variety. Therefore, the ‘closed’ state has a highly preferable orientation while positioned at the interface but loses this preference once it diffuses into the apolar phase. Panel C shows the MSM states mapped on the position feature and the RMSD with respect to the ‘closed’ state. From this projection, it can be seen that only the ‘closed’ state (but not the ‘open’ one) can fully diffuse into the apolar phase (position = 1).
The potential energy contributions in the MSM states of CDP 1 are compared in Fig. 6D and E. As expected from the equilibrium populations, the ‘open’ orientation B (state 1) has a higher energy (less favorable) than the ‘open’ orientation A (state 3). The higher energy of state 1 might facilitate the closing process to state 2. Panel E splits the energy into water, chloroform, and intramolecular contributions. In the case of CDP 1, the peptide has more favorable interactions with both water and chloroform in orientation A (state 3) than in orientation B (state 1). For the peptides containing proline, the preference for orientation A can primarily be attributed to more favorable interactions with water molecules.
Fig. 7 displays an overview of the MSMs of all eight peptides. The kinetics and equilibrium populations of the metastable states are shown on top of the simulation data points mapped to the features RMSD to the ‘closed’ state and the orientation. The simulation data points were colored according to their metastable state assignment. All CDPs showed a distinct separation between at least three metastable states: the ‘closed’ conformations and the ‘open’ conformation in orientation A and B. CDPs 4–6 populate an additional metastable state that could be assigned to either the ‘half-closed’ or an ‘alternative closed’ conformation. For all eight CDPs, the ‘closed’ state was highly populated in equilibrium with the interface present (>38% for peptides without proline and >55% for peptides with proline). Additionally, orientation A was always higher populated, and thus energetically more favorable, than orientation B.
We were able to show that the unique environment of the interface alters the conformational equilibrium and favors the ‘closed’ state. This effect is especially strong for peptides that rarely close in aqueous solution. For these peptides, the interface effect can increase the fraction of ‘closed’ conformations by a factor >50. In addition, peptides starting from an ‘open’ conformation in orientation A and B have different closing dynamics with faster closing in orientation B. Next, we will have a closer look at how the ‘closed’ peptides behave at the interface.
3.6. Permeable conformations
Proceeding from the peptide in the ‘closed’ conformation at the interface, a total of ∼500 events of peptides diffusing into the chloroform phase were counted. These events will be referred to as ‘membrane diffusions' in the following. All diffusion events start from the ‘closed’ orientation A with the leucine side chains interacting with the apolar phase. In most cases, the peptide rotates along its long axis until the leucine side chains point towards the aqueous phase. Then, it diffuses into the apolar phase until it is fully surrounded by chloroform molecules. An example trajectory of this process is provided for CDP 1 in Fig. S15 in the ESI.† Not a single event of ‘membrane diffusion’ in the ‘open’ conformation was observed. This is in line with the findings reported in ref. 39 for cyclosporine A.
Interestingly, an ‘alternative closed’ state was identified for CDP 6 (Fig. S16 in the ESI†). In this ‘alternative closed’ state, the phenylalanine and proline side-chains build a cage structure and the backbone resembles a twisted ‘eight’. Four intramolecular hydrogen bonds stabilize the structure with the center carbonyl oxygen contributing to two hydrogen bonds. The MSM revealed that the ‘alternative closed’ state has a significant equilibrium population of around 24% (Fig. S11 in the ESI†). Therefore, it might contribute notably to permeability. The existence of this ‘alternative closed’ state showcases the versatility of cyclic peptides and highlights the need to have detailed knowledge of their conformational behavior.
The finding that ‘membrane diffusion’ events only occur in the ‘closed’ or ‘alternative closed’ conformations strengthens the long-standing hypothesis that large and flexible cyclic peptides can permeate only when they can adopt conformations in which the polar groups are shielded by intramolecular hydrogen bonds. Although cyclic peptides in the ‘open’ state are mainly located at the interface, they cannot fully immerse into the apolar phase.
4. Conclusions
In this study, we investigated the conformational and kinetic behavior of CDPs at a polar/apolar interface. All examined peptides preferred to be located at the interface over a position in pure polar or apolar solvent. Due to their directed hydrophobicity (Fig. 2), the CDPs adopted two distinct orientations with respect to the interface: the hydrophobic patch formed by the leucine residues pointed either towards the apolar (orientation A) or polar phase (orientation B). The existence of these orientations was evident from both visible inspection of the simulations (Fig. 3) and the MSMs (Fig. 6). The same conformations and orientations were also observed in the POPC bilayer system (Fig. 4). Interestingly, the local environment of the peptides in the membrane matched the environment of the water/chloroform interface. On one side the peptide was in contact with the apolar lipid tails, while a water funnel and the head-group region of the lipids formed a polar surrounding on the other side. The equilibrium populations and interaction energies of orientation A and B showed that orientation A is clearly preferred. Interestingly, this preference was modulated by both the conformation and the amino-acid composition of the CDPs (Table 1). These modulations can be linked to changes in the hydrophobic patch on the peptide surface. A larger continuous patch led to a stronger preference for orientation A. Peptides in orientation B showed a faster closing dynamics, probably due to the higher (less favorable) energy of this orientation (Fig. 6). Although the equilibrium population of orientation B was rather low in the MSMs, a significant fraction of CDPs that started in the water phase initially docked to the interface in orientation B. Thus, in a non-equilibrium scenario, the importance of orientation B might be higher than anticipated by the equilibrium kinetic models.
The MSMs furthermore revealed that the unique environment of the interface not only led to distinct orientations but also influenced the conformational equilibrium and kinetics of the CDPs. Importantly, the presence of the interface facilitated the closing process for all examined peptides. Especially for CDP 1, which rarely adopts the ‘closed’ conformation in aqueous solution, the equilibrium population of the ‘closed’ state was increased by a factor of approximately 50 (i.e. from <1% to 38%). Thus, the interface might function as a catalyst for the closing process. This is especially relevant for peptides with low ‘prefolding’ in water. Furthermore, we were able to explicitly show that the peptides can only diffuse into the apolar phase in the ‘closed’ conformation, marking it as the ‘permeable species'.
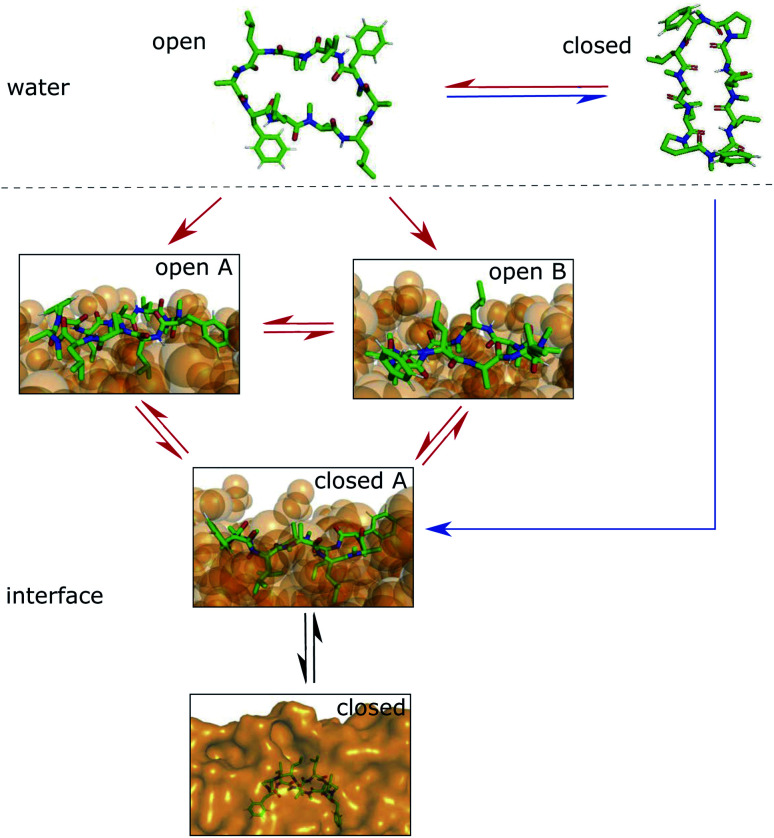
We showed that cyclic peptides can insert into the interface between the head-group and tail regions of the membrane in both the ‘open’ and ‘closed’ conformations (Fig. 4). This, in combination with the observed catalytic ability of the interface, leads to the proposition of a refined hypothesis for membrane permeation (Fig. 8). An equilibrium exists between ‘open’ and ‘closed’ states in water. Peptides with a significant equilibrium population of the ‘closed’ conformation in water (i.e. ‘prefolding’) can insert into the interface directly in the ‘closed’ state, and subsequently diffuse into the apolar phase (blue + black route). Peptides with no or low population of the ‘closed’ conformation in water may still be able to permeate, although along a different route. They insert into the interface in the ‘open’ state. The interface modulates the equilibrium between ‘open’ and ‘closed’ conformations, facilitating the closing process. Once in the ‘closed’ conformation, the peptide is able to diffuse into the apolar phase (red + black route). One can further speculate that different amino acids contribute differently to the closing process in water and in a lipid bilayer. Bulky residues may hinder the dynamics due to steric clashes inside the membrane but not in water. Future work is necessary to test whether different design principles apply for ‘prefolding’ and ‘non-prefolding’ cyclic peptides. In particular, the influence of different amino-acid compositions on the closing dynamics has to be explicitly tested in the presence of a membrane, as the water/chloroform interface is not able to mimic the steric hindrance caused by the lipids. Thus, future work will show the predictive power of the proposed model.
Fig. 8. Hypothesis for the permeation process of ‘prefolding’ (closing in water) and ‘non-prefolding’ (closing in the membrane) cyclic peptides. Peptides with a significant population of the ‘closed’ conformation in water can insert into the interface or membrane directly in the ‘closed’ state (blue route). Peptides with no or a low population of the ‘closed’ conformation in water insert into the interface in the ‘open’ state. There, the conformational dynamics are modulated by the presence of the interface, resulting in a new equilibrium between ‘open A’, ‘open B’ and ‘closed’ states. The interface environment acts as a catalyst, which facilitates the closing process (red route). Once in the ‘closed’ conformation at the interface, the peptide can diffuse into the apolar phase (black arrows).
Abbreviations
- COM
Center of mass
- CSMM
Core-set Markov model
- DAD
Diode array detection
- GROMACS
Groningen machine for chemical simulations
- GROMOS
Groningen molecular simulation
- LC-MS
Liquid chromatography-mass spectrometry
- LC-UV
Liquid chromatography-ultraviolet Spectroscopy
- LINCS
Linear constraint solver
- MD
Molecular dynamics
- MFPT
Mean first passage time
- MSM
Markov state model
- NMR
Nuclear magnetic resonance
- PCCA+
Robust Perron cluster cluster analysis
- PME
Particle mesh Ewald
- POPC
1-Palmitoyl-2-oleoylphosphatidylcholine
- RMSD
Root-mean square deviation
- SPC
Simple-point-charge
- TICA
Time-lagged independent component analysis
- UPLC
Ultra-performance liquid chromatography
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge financial support by the Swiss National Science Foundation (Grant number 200021-178762) and the Scholarship Fund of the Swiss Chemical Industry. S. M. L was also supported by the PhD scholarship of the German National Academic Foundation.
Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra09025a
Notes and references
- Hopkins A. L. Groom C. R. Nat. Rev. Drug Discovery. 2002;1:727–730. doi: 10.1038/nrd892. [DOI] [PubMed] [Google Scholar]
- Russ A. P. Lampel S. Drug Discovery Today. 2005;10:1607–1610. doi: 10.1016/S1359-6446(05)03666-4. [DOI] [PubMed] [Google Scholar]
- Pertea M. Shumate A. Pertea G. Varabyou A. Breitwieser F. P. Chang Y.-C. Madugundu A. K. Pandey A. Salzberg S. L. Genome Biol. 2018;19:208. doi: 10.1186/s13059-018-1590-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X.-P. Du G.-H. Drug Discoveries Ther. 2007;1:23–29. [PubMed] [Google Scholar]
- Caron G. Kihlberg J. Goetz G. Ratkova E. Poongavanam V. Ermondi G. ACS Med. Chem. Lett. 2021;12:13–23. doi: 10.1021/acsmedchemlett.0c00581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driggers E. M. Hale S. P. Lee J. Terrett N. K. Nat. Rev. Drug Discovery. 2008;7:608–624. doi: 10.1038/nrd2590. [DOI] [PubMed] [Google Scholar]
- Marsault E. Peterson M. L. J. Med. Chem. 2011;54:1961–2004. doi: 10.1021/jm1012374. [DOI] [PubMed] [Google Scholar]
- Villar E. A. Beglov D. Chennamadhavuni S. Porco J. A. Kozakov D. Vajda S. Whitty A. Nat. Chem. Biol. 2014;10:723–731. doi: 10.1038/nchembio.1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doak B. C. Zheng J. Dobritzsch D. Kihlberg J. J. Med. Chem. 2015;59:2312–2327. doi: 10.1021/acs.jmedchem.5b01286. [DOI] [PubMed] [Google Scholar]
- Duffy F. J. O'Donovan D. Devocelle M. Moran N. O'Connell D. J. Shields D. C. J. Chem. Inf. Model. 2015;55:600–613. doi: 10.1021/ci500431q. [DOI] [PubMed] [Google Scholar]
- Dougherty P. Qian Z. Pei D. Biochem. J. 2017;474:1109–1125. doi: 10.1042/BCJ20160619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanner M. F. Zoghebi K. Hanna S. Mozaffari S. Rahighi S. Tiwari R. K. Parang K. J. Chem. Inf. Model. 2021;61:3015–3026. doi: 10.1021/acs.jcim.1c00320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zorzi A. Deyle K. Heinis C. Curr. Opin. Chem. Biol. 2017;38:24–29. doi: 10.1016/j.cbpa.2017.02.006. [DOI] [PubMed] [Google Scholar]
- Morioka T. Loik N. D. Hipolito C. J. Goto Y. Suga H. Curr. Opin. Chem. Biol. 2015;26:34–41. doi: 10.1016/j.cbpa.2015.01.023. [DOI] [PubMed] [Google Scholar]
- Adessi C. Soto C. Curr. Med. Chem. 2002;9:963–978. doi: 10.2174/0929867024606731. [DOI] [PubMed] [Google Scholar]
- Wang C. Craik D. Biopolymers. 2016;106:901–909. doi: 10.1002/bip.22878. [DOI] [PubMed] [Google Scholar]
- Tsomaia N. Eur. J. Med. Chem. 2015;94:459–470. doi: 10.1016/j.ejmech.2015.01.014. [DOI] [PubMed] [Google Scholar]
- Witek J. Keller B. G. Blatter M. Meissner A. Wagner T. Riniker S. J. Chem. Inf. Model. 2016;56:1547–1562. doi: 10.1021/acs.jcim.6b00251. [DOI] [PubMed] [Google Scholar]
- Naylor M. Bockus A. Blanco M. Lokey R. Curr. Opin. Chem. Biol. 2017;38:141–147. doi: 10.1016/j.cbpa.2017.04.012. [DOI] [PubMed] [Google Scholar]
- Witek J. Mühlbauer M. Keller B. G. Blatter M. Meissner A. Wagner T. Riniker S. ChemPhysChem. 2017;18:3309–3314. doi: 10.1002/cphc.201700995. [DOI] [PubMed] [Google Scholar]
- Witek J. Wang S. Schroeder B. Lingwood R. Dounas A. Roth H.-J. Fouché M. Blatter M. Lemke O. Keller B. Riniker S. J. Chem. Inf. Model. 2019;59:294–308. doi: 10.1021/acs.jcim.8b00485. [DOI] [PubMed] [Google Scholar]
- Raeder A. F. Reichart F. Weinmüller M. Kessler H. Bioorg. Med. Chem. 2018;26:2766–2773. doi: 10.1016/j.bmc.2017.08.031. [DOI] [PubMed] [Google Scholar]
- Hoang H. N. Hill T. A. Fairlie D. P. Angew. Chem., Int. Ed. 2021;60:8385–8390. doi: 10.1002/anie.202012643. [DOI] [PubMed] [Google Scholar]
- Wang S. König G. Roth H. Fouché M. Rodde S. Riniker S. J. Med. Chem. 2021;64:12761–12773. doi: 10.1021/acs.jmedchem.1c00775. [DOI] [PubMed] [Google Scholar]
- Linker S. Wang S. Ries B. Stadelmann T. Riniker S. Chimia. 2021;75:518–521. doi: 10.2533/chimia.2021.518. [DOI] [PubMed] [Google Scholar]
- Moehle K. Hofmann H. J. J. Pept. Res. 1998;51:19–28. doi: 10.1111/j.1399-3011.1998.tb00412.x. [DOI] [PubMed] [Google Scholar]
- Ono S. Naylor M. R. Townsend C. E. Okumura C. Okada O. Lokey R. S. J. Chem. Inf. Model. 2019;59:2952–2963. doi: 10.1021/acs.jcim.9b00217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cipcigan F. Smith P. Crain J. Hogner A. Maria L. D. Llinas A. Ratkova E. J. Chem. Inf. Model. 2020;61:263–269. doi: 10.1021/acs.jcim.0c00803. [DOI] [PubMed] [Google Scholar]
- Comeau C. Ries B. Stadelmann T. Tremblay J. Poulet S. Fröhlich U. Coté J. Boudreault P.-L. Derbali R. M. Sarret P. Grandbois M. Leclair G. Riniker S. Marsault E. J. Med. Chem. 2021;64:5365–5383. doi: 10.1021/acs.jmedchem.0c02036. [DOI] [PubMed] [Google Scholar]
- Moritsugu K. Takeuchi K. Kamiya N. Higo J. Yasumatsu I. Fukunishi Y. Fukuda I. J. Chem. Inf. Model. 2021;61:1921–1930. doi: 10.1021/acs.jcim.0c01427. [DOI] [PubMed] [Google Scholar]
- Pye C. R. Hewitt W. M. Schwochert J. Haddad T. D. Townsend C. E. Etienne L. Lao Y. Limberakis C. Furukawa A. Mathiowetz A. M. Price D. A. Liras S. Lokey R. S. J. Med. Chem. 2017;60:1665–1672. doi: 10.1021/acs.jmedchem.6b01483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gangwar S. Jois S. Siahaan T. Velde D. V. Stella V. Borchardt R. Pharm. Res. 1996;13:1657–1662. doi: 10.1023/A:1016484522113. [DOI] [PubMed] [Google Scholar]
- Rezai T. Bock J. Zhou M. Kalyanaraman C. Lokey R. Jacobson M. J. Am. Chem. Soc. 2006;128:14073–14080. doi: 10.1021/ja063076p. [DOI] [PubMed] [Google Scholar]
- Riniker S. Future Med. Chem. 2019;11:637–639. doi: 10.4155/fmc-2018-0429. [DOI] [PubMed] [Google Scholar]
- Alex A. Millan D. S. Perez M. Wakenhut F. Whitlock G. A. MedChemComm. 2011;2:669–674. doi: 10.1039/C1MD00093D. [DOI] [Google Scholar]
- Danelius E. Poongavanam V. Peintner S. Wieske L. H. E. Erdélyi M. Kihlberg J. Chem.–Eur. J. 2020;26:5231–5244. doi: 10.1002/chem.201905599. [DOI] [PubMed] [Google Scholar]
- Rezai T. Yu B. Millhauser G. L. Jacobson M. P. Lokey R. S. J. Am. Chem. Soc. 2006;128:2510–2511. doi: 10.1021/ja0563455. [DOI] [PubMed] [Google Scholar]
- Dougherty P. G. Sahni A. Pei D. Chem. Rev. 2019;119:10241–10287. doi: 10.1021/acs.chemrev.9b00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C. K. Swedberg J. E. Harvey P. J. Kaas Q. Craik D. J. J. Phys. Chem. B. 2018;122:2261–2276. doi: 10.1021/acs.jpcb.7b12419. [DOI] [PubMed] [Google Scholar]
- Sugita M. Sugiyama S. Fujie T. Yoshikawa Y. Yanagisawa K. Ohue M. Akiyama Y. J. Chem. Inf. Model. 2021;61:3681–3695. doi: 10.1021/acs.jcim.1c00380. [DOI] [PubMed] [Google Scholar]
- Park S. Khalili-Araghi F. Tajkhorshid E. Schulten K. J. Chem. Phys. 2003;119:3559–3566. doi: 10.1063/1.1590311. [DOI] [Google Scholar]
- Sugita Y. Kitao A. Okamoto Y. J. Chem. Phys. 2000;113:6042–6051. doi: 10.1063/1.1308516. [DOI] [Google Scholar]
- Fouché M. Schäfer M. Berghausen J. Desrayaud S. Blatter M. Piéchon P. Dix I. Garcia A. M. Roth H.-J. ChemMedChem. 2016;11:1048–1059. doi: 10.1002/cmdc.201600082. [DOI] [PubMed] [Google Scholar]
- Fouché M. Schäfer M. Blatter M. Berghausen J. Desrayaud S. Roth H.-J. ChemMedChem. 2016;11:1060–1068. doi: 10.1002/cmdc.201600083. [DOI] [PubMed] [Google Scholar]
- Schmid N. Christ C. D. Christen M. Eichenberger A. P. van Gunsteren W. F. Comput. Phys. Commun. 2012;183:890–903. doi: 10.1016/j.cpc.2011.12.014. [DOI] [Google Scholar]
- Reif M. M. Hünenberger P. H. Oostenbrink C. J. Chem. Theory Comput. 2012;8:3705–3723. doi: 10.1021/ct300156h. [DOI] [PubMed] [Google Scholar]
- Hockney R. W. Methods Comput. Phys. 1970;9:136. [Google Scholar]
- Berendsen H. J., Postma J. P., van Gunsteren W. F. and Hermans J., in Intermolecular Forces, Springer, 1981, pp. 331–342 [Google Scholar]
- Berendsen H. J. Postma J. v. van Gunsteren W. F. DiNola A. Haak J. R. J. Chem. Phys. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]
- Tironi I. G. Sperb R. Smith P. E. van Gunsteren W. F. J. Chem. Phys. 1995;102:5451–5459. doi: 10.1063/1.469273. [DOI] [Google Scholar]
- Heinz T. N. van Gunsteren W. F. Hünenberger P. H. J. Chem. Phys. 2001;115:1125–1136. doi: 10.1063/1.1379764. [DOI] [Google Scholar]
- Ryckaert J.-P. Ciccotti G. Berendsen H. J. J. Comput. Phys. 1977;23:327–341. doi: 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Lindahl E. Hess B. Van Der Spoel D. Mol. Model. Annu. 2001;7:306–317. doi: 10.1007/s008940100045. [DOI] [Google Scholar]
- Marzuoli I. Margreitter C. Fraternali F. J. Chem. Theory Comput. 2019;15:5175–5193. doi: 10.1021/acs.jctc.9b00509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parrinello M. Rahman A. J. Appl. Phys. 1981;52:7182–7190. doi: 10.1063/1.328693. [DOI] [Google Scholar]
- Essmann U. Perera L. Berkowitz M. L. Darden T. Lee H. Pedersen L. G. J. Chem. Phys. 1995;103:8577–8593. doi: 10.1063/1.470117. [DOI] [Google Scholar]
- Hess B. Bekker H. Berendsen H. J. Fraaije J. G. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H. [DOI] [Google Scholar]
- Pande V. S. Beauchamp K. Bowman G. R. Methods. 2010;52:99–105. doi: 10.1016/j.ymeth.2010.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherer M. K. Trendelkamp-Schroer B. Paul F. Pérez-Hernández G. Hoffmann M. Plattner N. Wehmeyer C. Prinz J.-H. Noé F. J. Chem. Theory Comput. 2015;11:5525–5542. doi: 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- McGibbon R. T. Beauchamp K. A. Harrigan M. P. Klein C. Swails J. M. Hernández C. X. Schwantes C. R. Wang L.-P. Lane T. J. Pande V. S. Biophys. J. 2015;109:1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Hernández G. Paul F. Giorgino T. De Fabritiis G. Noé F. J. Chem. Phys. 2013;139:015102. doi: 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Sittel F. Stock G. J. Chem. Theory Comput. 2016;12:2426–2435. doi: 10.1021/acs.jctc.5b01233. [DOI] [PubMed] [Google Scholar]
- Buchete N.-V. Hummer G. J. Phys. Chem. B. 2008;112:6057–6069. doi: 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- Vanden-Eijnden E. Venturoli M. Ciccotti G. Elber R. J. Chem. Phys. 2008;129:174102. doi: 10.1063/1.2996509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütte C. Noé F. Lu J. Sarich M. Vanden-Eijnden E. J. Chem. Phys. 2011;134:204105. doi: 10.1063/1.3590108. [DOI] [PubMed] [Google Scholar]
- Lemke O. Keller B. G. J. Chem. Phys. 2016;145:164104. doi: 10.1063/1.4965440. [DOI] [PubMed] [Google Scholar]
- Deuflhard P. Weber M. Linear Algebra Appl. 2005;398:161–184. doi: 10.1016/j.laa.2004.10.026. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The structure and topology files of the CDPs in the closed and major open conformation are available on GitHub (https://github.com/rinikerlab/cyclic_peptide_at_interfaces). The GitHub repository also contains a sample Jupyter notebooks for the MSM analysis of CDP 1.
Further information, custom scripts, or production trajectories are available from the corresponding author (S. R.) upon request. The freely available software can be obtained via the following links: GROMOS (http://www.gromos.net/), GROMACS (https://www.gromacs.org/), and PyMol (https://github.com/schrodinger/pymol-open-source).