Association Rule Mining in Multiple, Multidimensional Time Series Medical Data

Abstract

Time series pattern mining (TSPM) finds correlations or dependencies in same series or in multiple time series. When numerous instances of multiple time series data are associated with different quantitative attributes, they form a multiple multidimensional framework. In this paper, we consider real-life time series data of muscular activities of human participants obtained from multiple electromyogram (EMG) sensors and discover patterns in these EMG time series data. Each EMG time series data is associated with quantitative attributes such as energy of the signal and onset time, which are required to be mined along with EMG time series patterns. We propose a two-stage approach for this purpose: in the first stage, our emphasis is on discovering frequent patterns in multiple time series by doing sequential mining across time slices. And in the next stage, we focus on the quantitative attributes of only those time series that are present in the patterns discovered in the first stage. Our evaluation with large sets of time series data from multiple EMG sensors demonstrate that our two-stage approach speeds up the process of finding association rules in such multidimensional environment as compared to other methods and scales up linearly in terms of number of time series involved. Our approach is generic in finding association rules in other medical sensor databases containing multiple time series associated with quantitative attributes, which can be used in extending research areas like rehabilitation programs or designing better prosthetic devices.

Introduction

Analyzing multiple time series and multidimensional databases has several real-world applications such in medical, finance, and engineering fields. The main interest lies in discovering the structural and temporal relationships or the dependencies hidden inside the given time-related data. Dependencies give the information on the frequent co-occurrences of events, which are expressed in the form of association rules.

The traditional association rule mining algorithms to recognize frequent events in the form of item-sets were built on quantitative databases such as market basket. Agrawal and Srikant [5] introduced the problem of sequential pattern mining across similar data from transaction database, based on the Apriori property [3, 4]. Later, many studies contributed to the efficient sequential pattern mining [6, 24, 42, 51, 59]. In recent years, some variations in sequential mining were discovering inter-event association, i.e., frequent episodes [58], cyclic association rule mining [7], constraint-based sequential pattern mining [38, 46, 52], and long sequential pattern mining in noisy environment [36, 62]. Algorithms for mining inter-transaction association rules were presented in [34, 55, 56] and [33]. There has also been lot of work on mining sequential patterns in time series data. Several studies [8, 15, 25, 28, 31] proposed the data mining techniques that found correlations and temporal dependencies within time series data and also investigated periodic segments [22, 40], partial periodic patterns [21, 26], constructed decision trees to mine patterns in streaming data [17, 27, 48, 57], and mined tree-like patterns in large data sets [14]. However, these methods did not consider multiple sequences in a single transaction and hence were not suitable to mine frequent patterns in a multi-sequence time series databases, which are becoming ubiquitous and more prominent in today’s world. In recent years, there has been significant focus in mining frequent patterns in multiple time series data [11, 30, 35, 44, 53].

In [43], authors associated sequential pattern mining with multidimensional information to undergo multidimensional sequential pattern mining in databases, where each transaction consisted of single sequence with multidimensional features. To mine multidimensional sequential patterns, [43] explored data cube structure for multidimensional association rule mining, which was originally proposed in [13]. Gosain and Bhugra [18] have surveyed different algorithms to generate association rules of quantitative data.

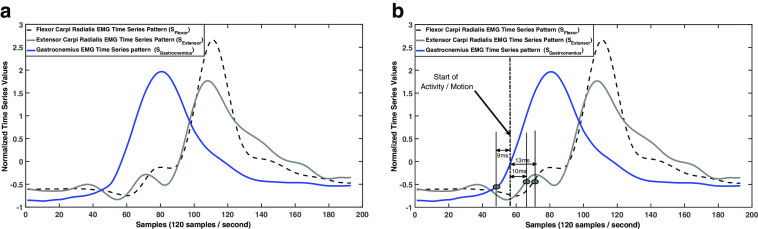
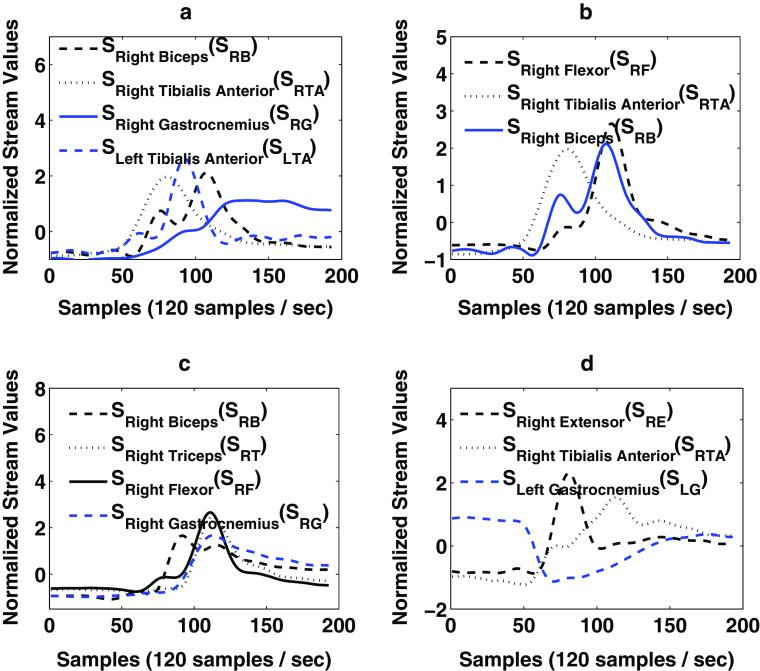
In order to illustrate multi-sequence time series database, we consider a practical biomedical application of monitoring muscular activities in the legs and hands during human motion through electromyography (EMG) signals.The EMG time series signal is defined as the sequence of measured electrical currents generated in muscles during its contraction representing neuromuscular activities [47]. For any given motion (i.e., analogous to a transaction), say for example “raising of the arms,” we have multiple time series sequences in the form of muscular activities of different muscles. As shown as an example in Fig. 1a, we mine a frequent multiple time series pattern P in the form of association rule given by $P=S_{\text{Flexor}}\wedge S_{\text{Extensor}}\to S_{\text{Gastrocnemius}}$, where S _Flexor and S _Extensor are time series EMG patterns from hand muscles “Flexor Carpi Radialis” and “Extensor Carpi Radialis,” respectively, and S _{Gastrocnemius} is the time series EMG pattern from leg muscle “Gastrocnemius.”

Fig. 1.

a An example of only multiple time series sequence pattern. b An example of multiple time series sequence pattern with associated multidimensional information

Though such global frequent muscular patterns are discovered from multiple time series sequential pattern mining, these patterns lack the focus without the proper context, which needs to fit in order to make the discovered rules most meaningful. For example, if the above rule with multiple time series is augmented with the related multidimensional information for each time series sequence as follows:

$$\begin{array}{rcl}\langle S_{\text{Flexor}},\mathit{Onset}\approx 13\text{ms}\rangle \wedge \langle S_{\text{Extensor}},\mathrm{Onset}\approx 10\text{ms}\rangle \Rightarrow & & \\ \langle S_{\text{Gastrocnemius}},\mathit{Onset}\approx -9\text{ms}\rangle ,& & \end{array}$$ 1

where Onset 1 indicates the time difference between the corresponding muscular activation and start of the activity/motion indicated by the movement of joints (e.g., wrist joint for raising of the arms), then this rule (represented in Fig. 1b) is indicated as follows: While raising of the arms, if the flexor carpi radialis muscle with time series pattern S _Flexor has an onset of approximately 13 ms and extensor carpi radialis muscle with time series pattern S _Extensor has an onset of approximately 10 ms after start of activity, then onset of gastrocnemius leg muscle with time series pattern S _{Gastrocnemius} had been activated approximately 9 ms before the start of activity. Thus, by adding the context in the form of multidimensional information in multiple sequence patterns, the rule reveals the fact that when person gets ready to raise his/her arms, just few milliseconds before, his/her legs are prepared with muscular contraction to maintain balance during raising of the arms. These types of association rules related to EMG patterns from different parts of body can be effectively used in designing/training prosthetic devices, and monitoring the longitudinal improvement for the patients in rehabilitative environment by giving real-time biofeedback information. Characterizing the EMG signals in these applications has been vastly studied in the past [1, 10, 12, 37, 45, 50, 54]. However, mining multiple sequence patterns associated with multidimensional information may also be applied in many other biomedical applications such as continuous monitoring of cardiovascular parameters, electroencephalogram, and electrogastrogram. To the best of our knowledge, there have been no previous studies on mining multiple sequence time series with associated multidimensional information in a medical sensor database.

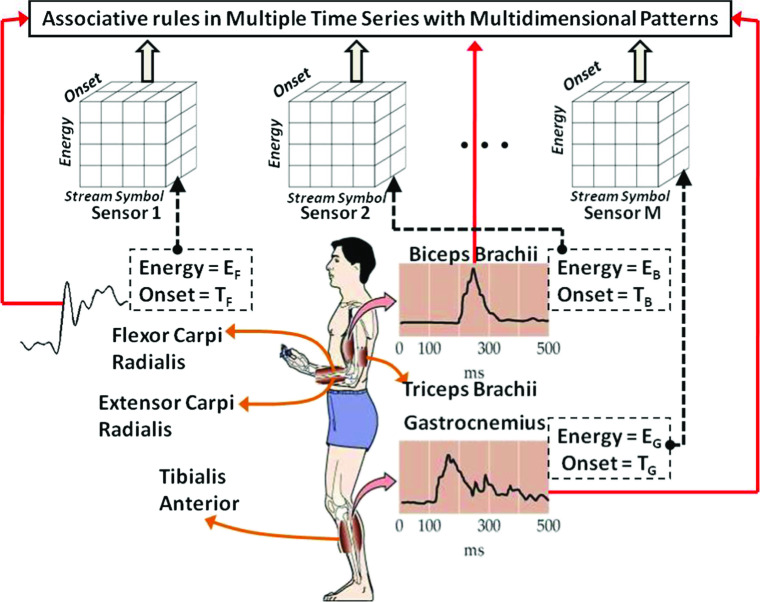
In this paper, we integrate multiple sequences pattern mining with multidimensional information. We can get two types of multidimensional association rules: inter-dimensional, where same kind of attributes/predicates may not be repeated in the same rule and hybrid dimensional, where same kind of attributes/predicates can be repeated. In this paper, we are interested in hybrid multidimensional association rule mining because we plan to explore dependencies between multiple time series, with each series having its own multidimensional information in the form of multiple attributes. To find such kind of hybrid rules, previous approaches [29, 43] that computed the data-cubes by aggregating each and every combination of the multiple dimensions may be too time consuming and inefficient in terms of storage. Figure 2 illustrates our practical focus on large sets of short-length human motions, where each motion is represented by multiple time series of electrical muscular activity recorded by the electromyographic (EMG) surface sensors placed on different parts of human body. As shown in Fig. 2, we target main muscles such as “Biceps Brachii,” “Triceps Brachii,” “Flexor Carpi Radialis,” and “Extensor Carpi Radialis” from upper extremities, and also “Tibialis Anterior” and “Gastrocnemius” from lower extremities. Each EMG time series has important associative multidimensional information (e.g., Onset and Energy) that are useful to analyze the contextual behavior of EMG sensors. The importance of these features is as follows:

Fig. 2.

Association rule mining in multiple sequence time series with multidimensional information in EMG database

Onset of EMG Signal

On active motion/action by the participants’ body segments, different onset times for the corresponding EMG sensors give the temporal relationship with respect to the motion. It has been observed that muscle activation can occur not only after but also before the actual movement of the body segments.

Energy of the Signal

The energy information of the time series data is important to know the power of EMG activity for the corresponding movements of the body segments. The energy of the time series data x(t) from a sensor i for duration T is given by the following:

$$E_i={\int }_1^{T}x{\left(t\right)}^2\mathrm{dt}\mathrm{.}$$ 2

In addition, we may have several other attributes such as “Energy,” “Variance,” “Zero-crossings” [60] that are associated with the muscular time series signals, which add interpretive knowledge to the mined patterns.

Approach

We propose a two-stage approach to mine high confidence patterns/rules in multiple time series sequences with multidimensional data. In the first stage, our emphasis is on discovering frequent patterns in multiple time series by doing sequential pattern mining across time slices using a modified apriori technique. And in the next stage, we perform multidimensional analysis on the attributes of only chosen time series that are involved in the discovered, frequent multiple time series patterns. From our experimental results, we show that our proposed approach is scalable with respect to the database size, i.e., the number of multiple time series sequences considered for mining and runs over an order of magnitude faster than previously developed multidimensional pattern mining algorithm bottom-up computation (BUC) [9]. On quantifying the quality of the discovered association rules, our approach gives twice the number of high-confident rules as compared to bottom-up computation.

Our Earlier Work

We reported preliminary results of our approach in a 4-page workshop paper [44]. The work presented here extends [44] in the following manner:

• Discussion on the significance of mining multiple sequence time series with associated multidimensional information in a medical sensor database.

• Formalization of the problem on mining hybrid multidimensional association rules to describe data mining applications in the real-world medical sensor database containing multiple times series data, with each series having its own multidimensional information in the form of multiple attributes/features.

• Discussion on the processing of multiple time series information and multi-attribute information to mine association rules by exploring various data processing/mining tools such as dimensionality reduction techniques, clustering, and discretization techniques.

• Extension of the approach on discovering structural patterns in multiple time series data by modifying apriori candidate generation criteria in traditional apriori mining algorithm.

• Illustration of the new approach on the multiple time series electromyogram (EMG) sensor database to highlight applicability and implementability in the real-world applications.

• Discussion and illustration of the construction of projected multi-attribute tree to mine frequent attributes based on the projected multi-attribute information.

• Addition of extensive simulation results to evaluate the performance of the proposed approach for mining association rules in EMG sensor database by studying:

  • Scalability over the number of time slices used to represent each of the EMG multiple time series data.
  • Scalability over the number of clusters used to represent time slices during pre-processing of the time series sensor data.
  • Scalability over the cardinality of quantitative attributes used during discretization of multi-attribute information.
  • Scalability over the number of time series considered for mining frequent patterns in multiple time series information with different support thresholds.
  • Scalability over support thresholds used for mining frequent multiple times series and associated multi-attributes.

• Evaluation on the number of rules discovered for different configurations of time series data streams and by varying different levels of minimum confidences and supports.

• Presentation of the real discovered interesting rules from the tested multiple time series EMG sensor database based on high support, confidence, and J-measure [49].

Problem Definition

From the notations in Table 1, for all 1 ≤ i ≤ N, S _i = {s _i1,s _i2, ⋯ , s _iM}, where S _i is one set among the N sets of M multiple time series data each. The time series of type {s _∗r} is generated or captured by r ^th sensor or source. We denote the set of all time series from one sensor r as F(r) = {s _i,r|i = 1⋯N}. Also, all the time series from all sensors have Q quantitative attributes or features A ₁,⋯ ,A _Q. Thus, a schema for the n ^th time series in F(r) is given by 〈n,s _n,r,(a ₁,⋯ ,a _Q)〉, where a _j ∈ A _j. And finally, the schema for multiple, multidimensional sensor database is given as follows: (m I d,$\langle s_1,(a_1^1,\cdots ,a_Q^1)\rangle ,$ ⋯ ,$\langle s_M,(a_1^M,\cdots ,a_Q^M)\rangle )$, where m I d is a motion identifier.

Table 1.

Notation I

Notation	Explanation
N	Total number of motions
M	Total number of EMG sensors
S i	A set of M time series, each from M sensors
	corresponding to the i th motion
s ij	A time series of j th sensor corresponding to the
	i th motion
F(r)	A set of all time series corresponding to the r th
	sensor
Q	Total number of quantitative attributes associated
	with each time series
A k	k th quantitative attribute

A time series data from sensor r, say Y, is contained in a tuple d of sensor database if Y ∼ s _d,r. The support of time series Y in a database D is the number of tuples in the database containing similar pattern to time series Y for sensor r. Given a positive integer m i n_s u p as the support threshold, a time series Y corresponding to sensor r is called a frequent time series pattern of sensor r when it is contained in at least m i n_s u p tuples in the database. Additionally, a multidimensional tuple for sensor r, say H = [Y,(x ₁,⋯ ,x _Q)] is said to be contained in a tuple d of sensor database if and only if, for (1 ≤ j ≤ Q), either $x_j=a_j^r$ or x _j = ∗ and Y ∼ s _dr. Here, ∗ denotes a meta-symbol which does not belong to any domain of A ₁,⋯ ,A _Q. The number of tuples in the database containing H is called the support of H, denoted as s u p p o r t(H). Thus, an association rule is an implication of the form $H\Rightarrow R$, where H and R are the multidimensional tuple for two different sensors or conjunction of multidimensional tuple for multiple sensors. The rule $H\Rightarrow R$ holds in the database D with confidence c if c % of tuples in the database D that contain H also contains R. The rule $H\Rightarrow R$ has support sup if s u p % of tuples in the database D contain both H and R.

Example 1

Let snippet of our database for EMG system be as given in Table 2. For each muscle-sensor, we have two attributes: “Onset of muscle ( ms)” and “Energy of the muscle signal ( m V ² )”. Let say, the support threshold m i n_s u p = 2, and P _b := s _1,b ∼ s _3,b and P _f := s _1,f ∼ s _3,f. Then, support for tuple (H = ) 〈(10m s,∗),P _b〉 is 2 since it is contained in 〈(10 ms,50 mV ²),s _1,b〉 and 〈(10 ms,95 mV ²),s _3,b〉. Similarly, support for tuple (R = ) 〈(30 ms,∗),P _f〉 is also 2 since it is contained in 〈(30 ms,65 mV ²), s _1,f〉 and 〈(30 ms,40 mV ²),s _3,f〉. Now more interestingly, we have a rule as follows:

$$\begin{array}{rcl}\left(\mathit{Onset}\right(\mathit{Biceps})=10\text{ms})\wedge P_b\Rightarrow P_f\wedge \left(\mathit{Onset}\right(\mathit{Flexor})=30\text{ms})& & \\ (\mathit{support}=50\%\mathit{and}\mathit{confidence}=100\%)\mathrm{.}& & \end{array}$$ 3

Table 2.

A multiple time series sequence database for EMG sensors with related multidimensional information

mId	Sensor 1 (biceps)	Sensor 2 (triceps)	Sensor 3 (flexor)	Sensor 4 (extensor)
	Biceps Brachii	Triceps Brachii	Flexor Carpi Radialis	Extensor Flexor Carpi Radialis
	〈Sequence, (Onset, Energy) 〉	〈Sequence, (Onset, Energy) 〉	〈Sequence, (Onset, Energy) 〉	〈Sequence, (Onset, Energy) 〉
1	〈s 1,b, (10m s, 50m V 2)〉	〈s 1,t, (5m s, 65m V 2)〉	〈s 1,f, (30m s, 65m V 2)〉	〈s 1,e, (38m s, 19m V 2)〉
2	〈s 2,b, (15m s, 45m V 2)〉	〈s 2,t, (8m s, 50m V 2)〉	〈s 2,f, (45m s, 20m V 2)〉	〈s 2,e, (56m s, 45m V 2)〉
3	〈s 3,b, (10m s, 95m V 2)〉	〈s 3,t, (25m s, 85m V 2)〉	〈s 3,f, (30m s, 40m V 2)〉	〈s 3,e, (78m s, 19m V 2)〉
4	〈s 4,b, (25m s, 6m V 2)〉	〈s 4,t, (20m s, 90m V 2)〉	〈s 4,f, (25m s, 10m V 2)〉	〈s 4,e, (90m s, 20m V 2)〉
5	〈s 5,b, (10m s, 25m V 2)〉	〈s 5,t, (30m s, 50m V 2)〉	〈s 5,f, (35m s, 10m V 2)〉	〈s 5,e, (60m s, 40m V 2)〉

The confidence is calculated as the ratio of support($H\cup R$) = 2 to support(H) = 2. The rule explains that, whenever a person raises his right arm, 50% of the time his/her bicep muscle get activated after 10 ms of movement and followed by flexor muscle after 30 ms with pattern P _b and P _f, respectively. And confidence suggests that, if biceps behave according to rule H, then flexor will behave according to the rule R with a confidence of 100%.

Pattern Mining Framework

From the mining perspective, for each motion, we have multiple time series information and multi-attribute information that need to be processed in order to discover important relationships between acting muscles while doing movements or exercises.

Multiple Time Series Information

Mining multiple time series pattern is difficult, but if they are represented by the symbols instead of data points interesting patterns can be discovered and moreover, mining becomes easier. But, on the other side, one symbol for each finite time series summarizes the behavior and may worsen the interpretation of the data. To strike a balance between easy mining and interpretation, each time series can be divided into equal time slices. Each time slice can be represented by a symbol, and each time series is modulated into a string of symbols. The granularity of the time slices can be modified, depending on the requirements. Our goal is to develop a generic algorithm that can aid in discovering the knowledge among the M time series for any given width of the time slices based on the requirements.

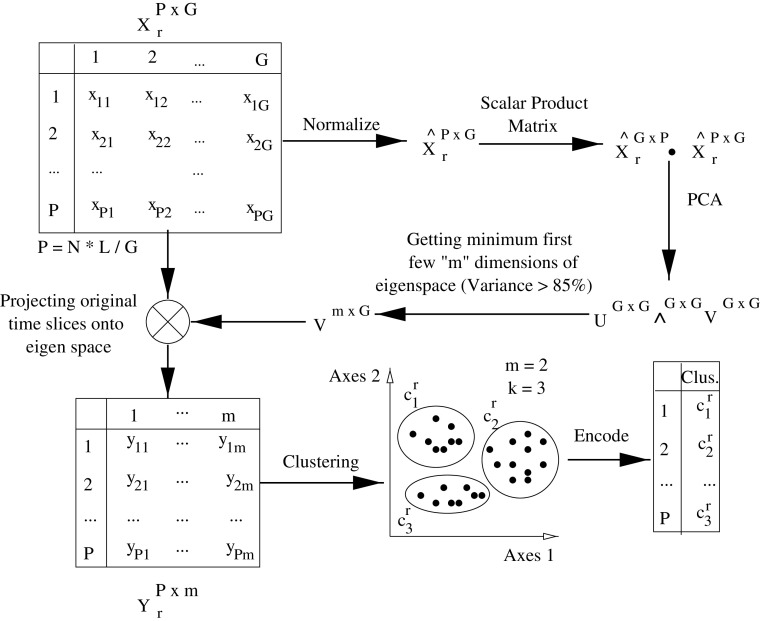
Let L be the length of all time series and G be the granular size of a basic unit of time slice. This gives L/G time slices per time series of each EMG sensor. In a database of N motions, we have total of P = N ∗ L/G time slices for each sensor. For instance, X _r is the P × G order data matrix corresponding to sensor r in Fig. 3. The time-slice space derived for sensor r is substantial, and therefore, we tend to derive lower dimensional space to represent the given time slices. In this work, as our aim is to discover contribution from M muscles for an action, we are interested in more “holistic” trends of the time slices by assessing their structural or shape dependencies between them without considering local variations. As a result, it makes sense that we capture the global properties of the time slices rather than their localized spatial features. Due to this requisite, it suits to apply PCA that tends to minimize the reprojection error, rather than applying ICA that minimizes the statistical dependency between the basis feature vectors. An illustration of the analysis can be seen in Fig. 3 where the space derived for sensor r is normalized and projected into a subspace that span at least 85% of total variance. Further the projected time slices represented in low dimensional m-D space as points are further clustered and encoded into a symbolic representation of the cluster to which it belongs.

Fig. 3.

The process of encoding original time slices for sensor r with corresponding cluster number

Clustering Feature Points

Clustering the feature points is an important step, as we can represent/encode the corresponding time slices of each time series into a symbolic representation of the cluster to which it belongs. We can choose an appropriate clustering approach to cluster the feature points. In our implementation, we chose to use k-means clustering approach to cluster the feature points. Here, one of the challenges is to determine an appropriate number of clusters that can be representative for different time slices. If number of clusters were more, then the occurrences of each symbol would be infrequent, making the mining process difficult. There is a possibility that a rule generated may have 100% confidence, but it may never occur again, and hence the rule becomes useless. On the other hand, if the number of clusters are less, then the support for the symbols may increase but the confidence may not be high affecting the usefulness of the mined rules. We have empirically studied the effect of varying the number of clusters on the performance of our approach. The results are discussed in Section 5.2.

However, other popular clustering techniques such as hierarchical clustering [23], CLARANS [39], DBSCAN [16], BIRCH [61], and CURE [20] can also be used. For further information, recently, [32] has surveyed the approaches for pattern-based clustering in high-dimensional data. In future, we will simulate different clustering techniques along with ICA to study the performance.

Example 2

In multi-block of multiple time series information of Fig. 4, we have shown a string of symbols for each time series of EMG sensors for five motions. The original, equi-length time series data of four EMG sensors (biceps brachii (biceps), triceps brachii (triceps), flexor carpi radialis (flexor), and extensor carpi radialis (extensor)) are spliced into three time slices, and hence, each time series is represented in the form of three symbols. In this example, five clusters were used in k-means clustering of the feature points representing these time slices for each EMG sensor. Figure 14 describes the effect of varying the number of clusters k. The symbol represents the cluster identification and super-script indicates the EMG sensor. The discretization of the multi-attribute information for each time series in Fig. 4 is discussed in Section 3.2.

Fig. 4.

A discretized version of multiple time series information with its associated multi-attribute information for the database of EMG sensors

Fig. 14.

Scalability over number of clusters

Multi-attribute Information

As discussed earlier, each EMG time series data is associated with the quantitative attributes that are distributed in the continuous range of values. Hence, we propose a discretization technique that will produce symbols with equiprobability. According to [41], a normalized time series have a Gaussian distribution. In our case, we normalize all the values of attribute A _i in database, to get a standard normalized distribution of values. We can then determine the “breakpoints” [41] that will produce ‘f’ equally probable areas (i.e., probability = 1/f) under Gaussian distribution. The effect of varying the cardinality for the attributes on the performance of our approach is discussed in Section 5.2.

The discretized version of the multi-attribute information for each sensor in each motion (Table 2) is shown in Fig. 4 (for conciseness, only two attributes are shown; in real, it can be easily extended to represent more attributes). In Fig. 4, for discretized multi-attribute symbols, super-script j indicates the j ^th attribute.

Discovering Association Rules

To discover the structural patterns in multiple time series data along with their attributes, we divide the association rule mining process into two stages: first, mine co-behaviors in multiple time series information and then, find important characteristics/features from the corresponding, projected multi-attribute information. The projected multi-attribute information contains only the attributes that are associated with the time series present in the discovered patterns.

An Iterative Method for Mining Patterns in Multiple Time Series Data

Our proposed algorithm to find frequent patterns in the given multiple time series information requires a sequential procedure for mining patterns in one time slice in each iteration. This approach helps in pruning the patterns that are non-frequent in preceding time slice, as they will always be non-frequent for the next iterations corresponding to subsequent time slices. Next, in traditional apriori algorithm [4], the candidate generation technique considers only a set of discrete symbols, but on the contrary, in our database, we have independent, discrete sets of symbols for each of the multiple sensors. Moreover, as we are mining association rules between multiple time series data, two patterns of same time series do not occur in the same rule. And hence, we need to prevent the original apriori candidate generation approach of joining of two different frequent symbols (that represent time slice) of same time series. For example, let us say, we have two frequent symbols 2¹ and 4¹ representing first time slice patterns for bicep muscle (= 1). On joining these symbols, according to [4], gives frequent pattern 〈2¹,4¹〉, which is invalid because two different patterns cannot occur from the same muscle in the span of first time slice. Considering this, we modified the original approach of candidate generation as follows (Notations in Table 3).

Table 3.

Notation II

Notation	Explanation
L[i,j]	Set of frequent j-length patterns (those with
	minimum support) in first i time slices of
	time series data. Each member of this set has two
	fields: 1. j-length pattern 2. support count
C[i,j]	Set of candidate j-length patterns in first i
	time slices of time series data. Each member of
	this set has two fields: 1. j-length pattern
	2. support count
M S[i + 1]	The multiple time series information gathered in
	iteration i

Modified Apriori Candidate Generation

The n e w_c a n d i d a t e_s e t function in iteration i takes an argument L[i,k − 1], the set of frequent (k − 1)-length patterns in first i time slices. It returns a superset of all frequent k-length patterns in first i time slices. This function works as follows: First, in join step, we join L[i,k − 1] with L[i,k − 1] to get k-length patterns in table C[i,k] as follows:

$$\begin{array}{rcl}\mathbf{\text{insert into}}& & \mathrm{table}C[1,k]\\ \mathbf{\text{select}}& & p\mathrm{.}\mathit{symbo}{l}_1,p\mathrm{.}\mathit{senso}{r}_1,\cdots ,p\mathrm{.}\mathit{symbo}{l}_{k-1},\\ & & p\mathrm{.}\mathit{senso}{r}_{k-1},q\mathrm{.}\mathit{symbo}{l}_{k-1},q\mathrm{.}\mathit{senso}{r}_{k-1}\\ \mathbf{\text{from}}& & L_{k-1}p,L_{k-1}q\\ \mathbf{\text{where}}& & (p\mathrm{.}\mathrm{symbo}{l}_1=q\mathrm{.}\mathit{symbo}{l}_1\wedge p\mathrm{.}\mathit{senso}{r}_1=\\ & & q\mathrm{.}\mathit{senso}{r}_1),\cdots ,(p\mathrm{.}\mathit{symbo}{l}_{k-2}=\\ & & q\mathrm{.}\mathit{symbo}{l}_{k-2}\wedge p\mathrm{.}\mathit{senso}{r}_{k-2}=\\ & & q\mathrm{.}\mathit{senso}{r}_{k-2}),p\mathrm{.}\mathit{senso}{r}_{k-1}\ne p\mathrm{.}\mathit{senso}{r}_{k-1};\end{array}$$

In joining two L[i,k − 1] entries, each of them share (k − 2) same symbols for the same sensors, and the last (k − 1)^th single symbol must be from different sensor regardless of symbol. A condition p.s e n s o r _k−1≠p.s e n s o r _k−1 in join function is to avoid the joining of two frequent symbols from the same sensor. Next, we use the prune step from [4]; we delete the patterns c ∈ C[i,k] such that some (k − 1)-subset of c is not present in L[i,k − 1].

Now, we go for main algorithm as follows:

Algorithm 4.1—Pattern Mining in Multiple Time Series Data

In iteration 1, the frequent 1-length patterns in the first time slice are derived from original multiple time series information (Fig. 4), referred as M S[1].2 These patterns, stored in L[1,1], serve to filter out from M S[1] any sensor entries from the motions that has non-frequent pattern or whole motion entries that has all sensor entries with non-frequent pattern in time slice 1. The result of this filtering process, M S[2], is used in the generation of frequent k-length patterns in iteration 1. In subsequent iterations, say i, M S[i] is scanned to generate the frequent 1-length patterns in the first i time slices to give L[i,1], which are further used to filter out non-frequent patterns from M S[i] to get M S[i + 1]. The frequent k-length patterns in iteration i are derived in two steps, as shown in Fig. 5,

• The new candidates at pass k are formed in C[i,k], using modified apriori candidate generation, by joining two (k − 1)-length patterns in L[i,k − 1] that share (k − 2) same symbols for the same sensors, and the remaining single symbol in both (k − 1)-length patterns from different sensors. And then, according to the pruning property in [4], some k-length patterns formed in C[i,k] are removed, if there exists some of their subsets that are not present in L[i,k − 1].

• For each motion entry t in M S[i + 1], for each of t’s k-length subset c, if c is present in C[i,k], then c’s support count is incremented. L[i,k] is used to store the candidates that has support greater than a minimum threshold.

Fig. 5.

Algorithm 4.1—pattern mining in multiple time series data

Example 3

Figures 6, 7, and 8 shows the step-by-step illustration of an iterative process of mining multiple time series from the multiple time series, multidimensional database (Fig. 4) to get frequent pattern involving three EMG time series from sensors 1 (Biceps), 3 (Flexor), and 4 (Extensor). The discovered pattern p = 〈2¹4¹2¹, 1³3³2³, 2⁴1⁴5⁴〉 is highlighted in multiple time series information as it has been observed in motion 1 and 3 giving support value as 2. In the next stage (discussed in Section 4.2), we get the attribute pattern (highlighted in multi-attribute information) that contain frequent attributes for biceps (attribute 1), flexor (attribute 1), and extensor sensors (attribute 2). From now on for brevity, let us denote pattern p = 〈E ¹ E ³ E ⁴〉.

Fig. 6.

Iteration 1: mining frequent patterns in first time slice

Fig. 7.

Iteration 2: mining frequent patterns in first two time slices

Fig. 8.

Iteration 3: mining frequent patterns in all three time slices

Projected Multi-attribute Tree: Mining Multi-attributes

To mine the frequent attributes, we could have continued the previous iterative mining process; but multi-attribute information is quantitative and unlike time series, it does not have any sequential or temporal significance. So, continuing the mining process sequentially is time-consuming because the total number of attribute symbols increases rapidly. In [19], CUBE operator was proposed that computed aggregates of all possible combinations of attributes to mine multidimensional association rules. Further, in [2], CUBE lattice was converted into hierarchy of aggregate operators to form a processing tree to mine frequent patterns. Also, in bottom-up computation (BUC) [9], a tree mining approach was employed using aggregation on single attribute and then expanded the fan-out of tree by aggregating on pair, then three attributes and so on. All these tree mining approaches worked only on a set of discrete attributes, but on the contrary, in our database, we have independent, discrete sets of attributes corresponding to each of the multiple time series pattern. This may cause high increase in the fan-out of the trees, which further may affect computation time. Hence, to conduct a fast and efficient attribute mining for each frequent time series pattern p, we construct a corresponding projected multi-attribute information for p.

Example 4

From Example 3, the frequent time series pattern p = 〈E ¹ E ³ E ⁴〉 containing sensors 1 (biceps), 3 (flexor), and 4 (extensor) is identified. Then, collecting multi-attribute information of sensors present in p from the tuples containing p, we get {[(4¹, 4²), (2¹, 5²), (2¹, 2²)], [(4¹, 7²), (2¹, 6²), (1¹, 2²)]}. This set is called projected multi-attribute information for p.

A projected multi-attribute tree is constructed using the projected multi-attribute information for p. One advantage of tree formulation is that we can exploit the mining process on the subsets of branches that gives frequent attribute patterns within those corresponding time series. In Fig. 9a, a projected multi-attribute tree for generic pattern p _g = 〈E ¹,E ²,⋯ ,E ^u〉 has u branches with Q levels, one for each of the “Q” attributes. A node inside tree T is defined by T[s e r i e s #] [a t t r.#]. Each member of the node T[i][j] is of the form 〈m I d,a ^j〉, where m I d is the motion identifier, which contains pattern p _g, and a ^j is the discrete value of the j ^th attribute in m I d for the time series E ⁱ in p _g.

Fig. 9.

a Generic projected multi-attribute tree for general pattern with u time series. b Projected multi-attribute tree for pattern p from Example 3 in Section 4.1 (m i n_s u p = 2)

Example 5

Figure 9b shows the projected multi-attribute tree for pattern p = 〈E ¹ E ³ E ⁴〉 from Section 4.1. The nodes in 3^rd branch of the tree corresponds to the 3^rd pattern in p, i.e., E ⁴. In our example, as we consider two attributes, we have two nodes as T[4][1] and T[4][2]. Also, in T[4][1], we have entries as 〈1,2¹〉 and 〈3,1¹〉, which indicates that pattern p is contained in motions 1 and 3.We determine a frequent attribute pattern in form of p A = 〈(4¹),(2¹),(2²)〉 for frequent time series pattern p (shown in Fig. 9b). After decoding, we get an attribute pattern associated with multiple time series pattern p as p A = 〈O n s e t _biceps = 10 ms, O n s e t _flexor = 30 ms, E n e r g y _extensor = 19 mV ²〉.

Combining Frequent Time Series Pattern and Corresponding Frequent Attribute Pattern to Get Association Rules

Using previous examples, the time series in p (Example 3) and, corresponding attributes in p A (Example 5) are merged to get whole set of frequent pattern. In this case, we have V = {〈E ¹(4¹)〉,〈E ³(2¹)〉,〈E ⁴(2²)〉}. For brevity, let us say V = {P,Q,R}, where P = 〈E ¹(4¹)〉, Q = 〈E ³(2¹)〉, and R = 〈E ⁴(2²)〉. To get association rule, we find all non-empty subsets of V. For every such subset say z, the association rule in form of $z\Rightarrow (V-z)$ is generated if the ratio of s u p p o r t(V ) to s u p p o r t(z) is at least m i n i m u m c o n f i d e n c e. A user can set the threshold for m i n i m u m c o n f i d e n c e depending on needs and application.

Performance Evaluation

Test Environment and Datasets

We used real-world time series from EMG AgCl electrodes using Delsys Myomonitor system, that are used to pick the muscle signals of limbs while performing motions. We collected live time series data with a speed of 120 samples/second from EMG sensors. Eight EMG sensors were placed on biceps, triceps, flexor, and extensor muscles of both hands. In addition, four sensors were placed on respective gastrocnemius and tibialis anterior muscles of both legs. That gives us data from a total of 12 sensors for each experiment.The raw time series data from the EMG sensors were smoothed using a fifth-order Butterworth low-pass filter with a 10-Hz cut-off frequency. The filtered non-noisy EMG time series were full-wave rectified for further pattern mining.

There were 20 participants enrolled in this study approved by the University of Texas at Dallas Institutional Review Board (IRB File Number: 05–19). We collected EMG time series data from these 20 participants that were uniformly distributed across ages 20–80, with initial consent. For each participant, procedure for an initial system setup that included placing of EMG sensors was too consuming (about an hour). Each participant then performed ten different kinds of properly planned experiments, each one included 10–15 trials. As the behavior (movement dynamics) and goal-oriented purpose of each experiment/motion is different, we needed to discover different sets of association rules corresponding to each experiment. In following Section 5.2, we show the performance of our technique on an experiment where person raises his both arms on reacting to a visual cue. With 120 samples per second and nearly 2 seconds for each trial of raise motion, we have approximately 50,000 samples each from different EMG sensors (total of 600,000 samples from 20 participants). Each motion is represented by maximum of 12 synchronous time series data, which form the multiple time series information. To form multi-attribute information, we extracted quantitative attributes like “onset” and “energy” from the each time series of EMG sensor as discussed in Section 1.

Experimental Results

We evaluated the performance of our approach by varying support thresholds for mining association rules in EMG sensor database that consisted of multiple time series and multi-attribute information. For comparison purpose, we tested our data set with bottom-up cube computation (BUC) [9] for finding association rules. Since BUC worked on multidimensional data and also took advantage of minimum support pruning property, it was interesting to see the comparative results with our proposed approach. As seen in Fig. 10, our two-stage proposed approach always runs faster than BUC by more than an order for all tested support thresholds.

Fig. 10.

Comparison of running time with BUC across support thresholds

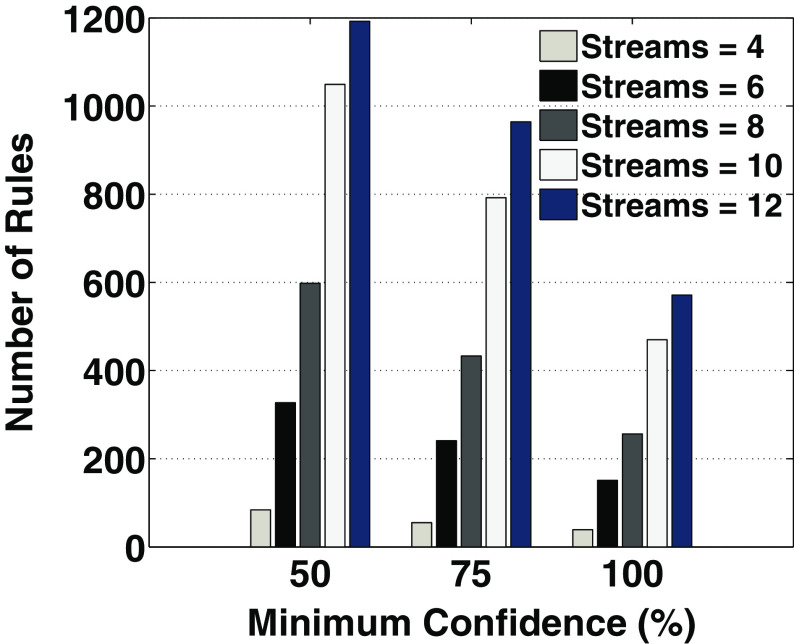
Figure 11 shows the comparative results for the percentage of 100% confidence rules among the total output rules provided by BUC and our two-stage proposed approach. The discovered high-confidence rules identify strong association between the involved multiple time series. Figure 12 shows the plot of number of rules discovered on considering different configurations for the number of time series and by varying the minimum confidence. In this experiment, the support threshold for both multiple time series and multi-attributes was set to 3%.

Fig. 11.

Comparison of percentage of rules with 100% confidence

Fig. 12.

The total number of rules for different minimum confidence

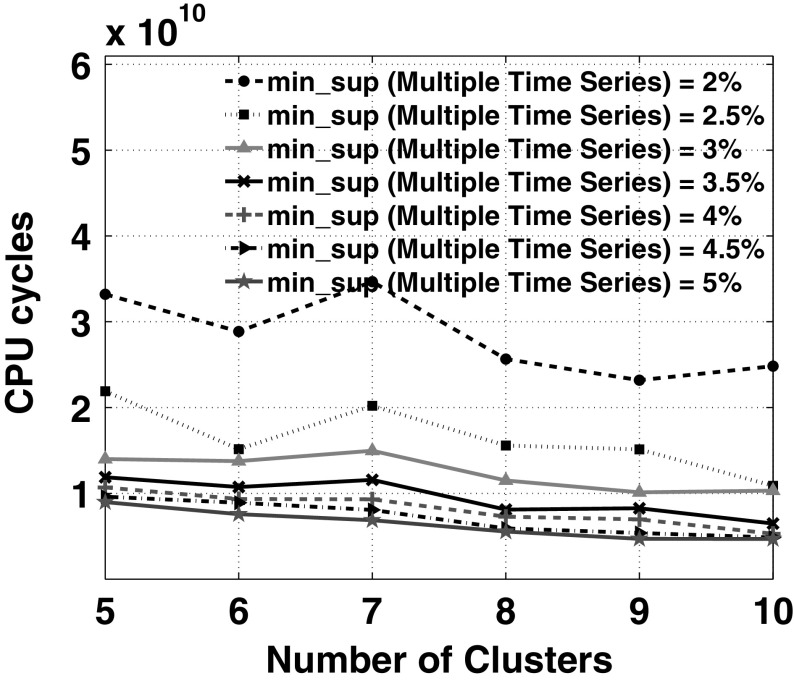
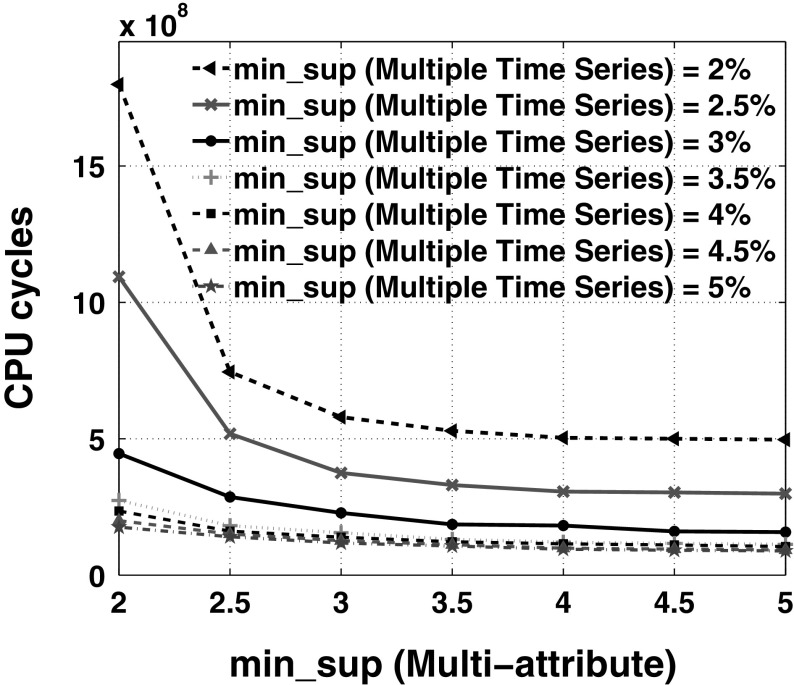
Figure 13 shows the scalability of our approach over the number of time slices used in EMG time series (= 4). From Fig. 13, for finding specific high-confidence rules that have less support in an overall database, we recommend to have less number of time slices per time series (say, 1 − 3) for faster response. The sparsity between the feature points that represents each time slice of the EMG time series data is higher for more number of clusters. Based on the observation of Fig. 14, to get generic rules that have high support, it is appropriate to use any number of clusters as the processing time varies between 1–4 s. In addition, to get high-confidence specific rules, we encourage users to use more number of clusters between 8 and 10 for better response time. Figure 15 shows the scalability of our approach over the cardinality of quantitative attributes while mining multi-attribute information. The users can set higher cardinality for the attributes (7–10) to mine high confidence-low support rules. Figure 16 shows the scalability of our approach over the number of time series considered for mining frequent patterns in multiple time series information with different support thresholds. In these experiments, we have kept equal support thresholds for multiple time series and multi-attribute information. The running cost for 12 time series is almost 5, 10, and 20 times greater than running cost for 8, 6, and 4 time series respectively, when support threshold = 2.5%. Figure 17 shows the performance of our algorithm over both support thresholds with number of time series equal to 4 and cardinality of attributes and number of clusters both set to 10.

Fig. 13.

Scalability over number of time slices in each of the multiple time series data

Fig. 15.

Scalability over cardinality of quantitative attributes

Fig. 16.

Scalability over number of time series

Fig. 17.

Scalability over support thresholds

Sample Rule Discoveries

As we get lots of rules for different sets of experiments with varying confidences and support, it was necessary to find out whether the proposed approach discovers interesting rules from the multiple EMG time series framework. Hence, we used the metric called J-measure proposed in [49] that gave us the quantitative measure of information content present in the rules, using the ideas of information theory. J-measure balances confidence and support, and moreover, is also the simplified measurement as it is dependent on the frequencies of the item-sets present in the corresponding rule. For a mined rule $Y\Rightarrow X$, corresponding J-measure is given as follows:

$$\begin{array}{rcl}J(Y\Rightarrow X)& =& p\left(y\right)\ast \left[p\left(x\right|y)\mathrm{.}log\left(\frac{p\left(x\right|y)}{p\left(x\right)}\right)\right.\\ & & \left.+(1-p(x\left|y\right))\mathrm{.}log\left(\frac{(1-p(x\left|y\right))}{(1-p(x\left)\right)}\right)\right]\mathrm{.}\end{array}$$ 4

J-measure is the product of two terms: p(y), which is probability of the antecedent of the rule (a measure of hypothesis simplicity) and term in square brackets that gives the cross entropy (a measure of the goodness of fit between rule and data). Further information on J-measure is given in [49]. High J-measure indicates an important rule, but a rule with high confidence will not have a high J-measure if the corresponding support is very low. Figure 18 and Table 4 show top-scoring, multiple time series rules involving eight EMG time series with their support, confidence, and J-measure.

Fig. 18.

Significant rules in EMG time series database

Table 4.

Significant multiple time series rules in Fig. 18 with measures

Fig.	Rule	Sup.	Conf.	J-meas.
		(%)	(%)
18a	$S_{\mathrm{RB}}\wedge S_{\mathrm{RTA}}\to S_{\mathrm{RG}}\wedge S_{\mathrm{LTA}}$	4.5	100	0.0084
18b	$S_{\mathrm{RF}}\wedge S_{\mathrm{RTA}}\to S_{\mathrm{RB}}$	3.87	85.7	0.0068
18c	$S_{\mathrm{RB}}\wedge S_{\mathrm{RT}}\wedge S_{\mathrm{RF}}\to S_{\mathrm{RG}}$	3.22	83.33	0.0047
18d	$S_{\mathrm{RE}}\wedge S_{\mathrm{RTA}}\to S_{\mathrm{LG}}$	3.87	75	0.0046

Figure 19 shows the comparison of the corresponding J-measure for rules with 100% confidence. We achieved higher rate of information content for all tested support thresholds, which suggests the better informative rules as compared to BUC approach. Also, from Fig. 19, lower support thresholds gives high amount of redundant rules, which reduces the average information content.

Fig. 19.

Average J-measure for rules with 100% confidence

Conclusions

In this paper, we introduced an efficient technique to discover hybrid-multidimensional associative rules in medical sensor database, where every time series is associated with the multidimensional information in the form of related quantitative features or attributes. In our proposed approach, we first discovered frequent multiple time series patterns using modified apriori technique for sequential pattern mining across time slices. In the second stage, for each frequent time series pattern, we built a corresponding projected multi-attribute tree that mines the frequent multidimensional patterns related to the time series present in multiple time series pattern. By conducting an extensive set of experiments on real-life data set such as electromyogram and by varying input parameters like number of time slices per time series, support thresholds, cardinality of attributes, number of clusters as well as number of time series, we have shown the effectiveness of the algorithm design. Our approach runs over an order of magnitude faster and gives high-confident association rules than bottom-up computation technique for multidimensional pattern mining. It also has linear scalability in terms of the number of time series present in database.

Though we have tested our approach on medical sensor database such as EMG database, the proposed technique should be applicable to any real data sets involving multiple time series sequences that are associated with other multidimensional attributes. Hence, further research is warranted to demonstrate the technique in other time series databases to extent the usability of our proposed approach. The applications of multiple time series sequential pattern mining integrated with multidimensional pattern mining in biomedical fields such as prosthetic designs, physical medicines, and rehabilitations are interesting topics for future research.

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.