Strong neutral sweeps occurring during a population contraction

Abstract

A strong reduction in diversity around a specific locus is often interpreted as a recent rapid fixation of a positively selected allele, a phenomenon called a selective sweep. Rapid fixation of neutral variants can however lead to a similar reduction in local diversity, especially when the population experiences changes in population size, e.g. bottlenecks or range expansions. The fact that demographic processes can lead to signals of nucleotide diversity very similar to signals of selective sweeps is at the core of an ongoing discussion about the roles of demography and natural selection in shaping patterns of neutral variation. Here, we quantitatively investigate the shape of such neutral valleys of diversity under a simple model of a single population size change, and we compare it to signals of a selective sweep. We analytically describe the expected shape of such “neutral sweeps” and show that selective sweep valleys of diversity are, for the same fixation time, wider than neutral valleys. On the other hand, it is always possible to parametrize our model to find a neutral valley that has the same width as a given selected valley. Our findings provide further insight into how simple demographic models can create valleys of genetic diversity similar to those attributed to positive selection.

Introduction

Past demography and natural selection play a critical role in shaping extant genetic diversity. A central question in population genetics is to quantify their respective impact on observed genomic diversity. Because selection interferes with demographic estimates and vice versa, estimation of one of these 2 components is difficult without accounting for the other (Charlesworth et al. 1993, 1995; Kaiser and Charlesworth 2009; O’Fallon et al. 2010; Charlesworth 2013; Nicolaisen and Desai 2013; Johri et al. 2020, 2021b). Moreover, the relative importance of demography and selection as determinants of genome-wide diversity is currently hotly debated and may vary extensively among species (Corbett-Detig et al. 2015; Rousselle et al. 2018; Pouyet and Gilbert 2019; Galtier and Rousselle 2020). It has been shown that selection and demography can leave very similar footprints on the genetic diversity of a population (Andolfatto and Przeworski 2000; Teshima et al. 2006; Thornton and Jensen 2007; Johri et al. 2021a). Disentangling the effects of demography and selection is, therefore, crucial to avoid the erroneous inference of evolutionary scenarios from genomic data (Jensen et al. 2005; Wares 2009; Mathew and Jensen 2015; Johri et al. 2020).

Hard selective sweeps lead to valleys of strongly reduced diversity around positively selected sites due to the hitchhiking of linked neutral loci (Maynard Smith and Haigh 1974), such observations of strong depletions of diversity in some genomic regions are often interpreted as due to past episodes of positive selection because the probability to observe a fast fixation of a neutral variant in a population of constant size is extremely low. However, during a range expansion for instance, some neutral or even mildly deleterious mutations can go quickly to fixation due to the low effective size of populations on the front of the range (Edmonds et al. 2004; Klopfstein et al. 2006; Hallatschek and Nelson 2008; Peischl et al. 2013), a phenomenon termed allele surfing (Klopfstein et al. 2006). Theoretical studies have shown that the average neutral diversity on the wave front decays exponentially as the range expands (Hallatschek and Nelson 2008), similarly to what happens when a population experiences a sudden decay of the population size, i.e. a population contraction, due to a drastic change in the environment for example. In both cases, a mutation appearing when the population size is shrinking might go quickly to fixation, inducing a strong decrease of diversity in the surrounding genomic region, whereas the average level of diversity might stay quite high depending on the strength and the duration of the contraction. As a result, the coalescent tree of alleles sampled in a population with strongly reduced effective population size will have short external branches, and long internal branches, depending on the parameters of the model (Excoffier et al. 2009). The average site frequency spectrum associated to such a tree resembles a neutral Site Frequency Spectrum (SFS), but with a lack of rare alleles and an excess of high frequency sites, i.e. it becomes “flatter” (Sousa et al. 2014; Peischl and Excoffier 2015). The footprint left by the rapid fixation of a neutral allele on the surrounding genomic diversity might thus be like that of a positively selected allele sweeping through a constant size population.

The expected shape of nucleotide diversity in genomic regions surrounding a site undergoing a rapid neutral fixation has been investigated analytically and numerically. Tajima (1990) studied the reduction of diversity during a neutral fixation at a given recombination distance from the fixing site. His results rely on rigorous mathematical arguments based on diffusion theory, but no closed form solution is provided for the shape of a neutral sweep. Johri et al. (2021a) described the valley of diversity occurring around a neutral fixation using an approach introduced for selective sweeps, assuming that the evolution of the allele frequency is that of a selected allele except in the initial stochastic phase. Here, we extend this work by inferring the dynamics of fixation of neutral alleles after a population contraction and we examine their effects on neighboring regions of the genome. We provide an analytical result for the expected coalescence time as a function of the recombination distance from the locus undergoing a fast fixation. Importantly, our results apply regardless of the process driving the allele going to fixation (neutrality, positive selection, background selection), as it only relies on the typical trajectory of an allele going to fixation in a given time, even though this trajectory differs depending on the underlying driver of this fixation (i.e. neutrality or selection). We compare our results against simulations and find that they hold for a wide range of realistic parameter combinations. We compare our results about the signature of neutral sweeps to patterns expected under selective sweeps and discuss potential differences between the signatures that could potentially allow us to discriminate between neutral and selective processes for a given demographic scenario. Finally, we investigate the similarity between the genomic signature of an allele going to fixation either selectively or neutrally and observe that a selective sweep signal can in principle be replicated in a neutral model with an appropriate choice of demographic parameters. We conclude that strong diversity depletions in the genome of a population, often attributed to the effect of positive selection, can be obtained with demographic effects only, and we call for caution when trying to detect signals of adaptation from genomic data, adding support to previous studies reaching similar conclusions (Thornton and Jensen 2007; Crisci et al. 2013; Jensen et al. 2019).

Model

We model here the effect of an instantaneous population contraction on genomic diversity. Throughout the whole manuscript, time is measured backwards. We assume that t_c generations before the present, the population size instantaneously dropped from N₀ diploid individuals to N_c individuals with N_c < N₀. We assume a standard coalescent model (Kingman 1982a,b) with discrete nonoverlapping generations, random mating, monoecious individuals, and no selection. Two haplotypes sampled in the current population at time t = 0 have, as we go backwards in time, a constant probability (2N_c)⁻¹ of coalescing at each generation, for the first t_c generations, and then, this probability switches to (2N₀)⁻¹ as we enter the ancestral uncontracted population. We can approximate the distribution of coalescence time T of these 2 haplotypes as a piecewise exponential distribution (see Appendix A1) with expected value:

$$E\left[T\right]=2\left(N_0-N_c\right) e^{-t_c/2N_c}+2N_c.$$ (1)

We see that the expected coalescence time decreases exponentially with the age of the contraction t_c and that it approaches $2N_c$ for a very old contraction. Coalescence times cannot be measured directly from empirical data, but they are closely related to nucleotide diversity $\pi$. Under the infinitely many sites model, the number of nucleotide differences between 2 homologous DNA segments is proportional to their coalescence time T as π = 2μT, where μ is the total mutation rate for the whole segment. Multiplying Equation (1) by 2μ shows that an instantaneous population contraction leads to an exponential decrease of the expected nucleotide diversity along the genome with the age of the contraction t_c. However, it does not inform us on the distribution of nucleotide diversity $\pi$ along the genome, or on spatially correlated patterns of diversity such as local depletion or excess of diversity relative to the expectation.

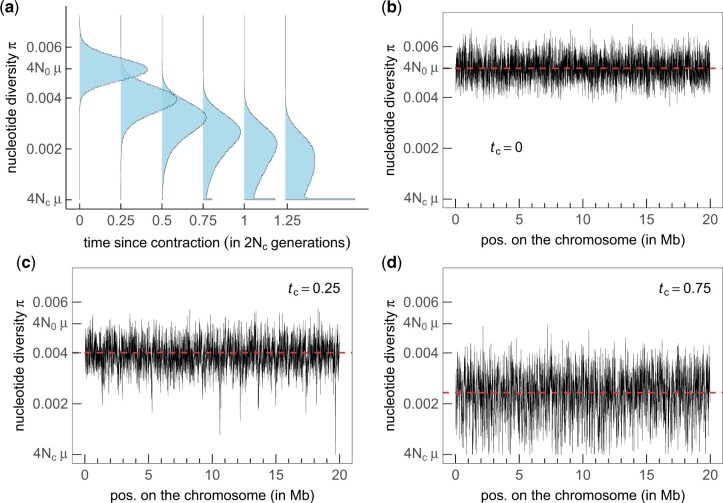
Figure 1 shows the evolution of the distribution of π as a function of the time t_c elapsed since the contraction. For t_c = 0, there is no contraction, and the population size remains constant and equal to N₀. In this case, we see (Fig. 1, a and b, t_c = 0) that the distribution of π is symmetric and centered at E[π] = 4N₀μ. For an older contraction, we see that the distribution is not only shifted to lower values of diversity as expected from Equation (1), but that it also becomes strongly peaked around π = 4N_cμ. This bimodality of the distribution can be understood intuitively in the following way. There are 2 possible types of coalescent trees for haplotypes sampled after the population contraction (note that the tree depends on the locus considered because of recombination). Indeed, the most recent common ancestor (MRCA) of the sample lived either before the contraction (T_MRCA > t_c) or after the contraction (T_MRCA < t_c). In the former case, the tree at this locus has long inner branches and short outer branches, whereas in the latter case, the tree is essentially a (short) neutral tree corresponding to a population of constant size N_c (Excoffier et al. 2009). Both types of trees occur at different loci and correspond to the 2 observed modes in the distribution of the nucleotide diversity along the chromosome. The precise shape of the distribution of nucleotide diversity across sites depends on the relative frequency of both types of trees, which itself depends on the age of the contraction t_c. For a sample of size 2, the probability that the MRCA lived after the contraction, that is T_MRCA < t_c is $1-e^{-t_c/2N_c}$. For a larger sample of haplotypes, there is no closed form solution for this probability, but the trees rooted after the contraction are rare for t_c ≪ 2N_c and very frequent when t_c ≫ 2N_c (Tavaré 1984). Therefore, the evolution of the distribution of π for increasing contraction age t_c appears to be a transition from a unimodal distribution centered at 4N₀μ to another unimodal distribution centered at 4N_cμ, with both modes coexisting for intermediate ages (Fig. 1). This bimodality has been pointed out previously in the context of population bottlenecks (Austerlitz et al. 1997); however, those studies mainly focused on long duration bottlenecks (the effect of a contraction or a bottleneck on nucleotide diversity is the same provided that the bottleneck is not yet finished, or that it finished very recently so that the effect of population recovery is negligible). In the present work, we investigate the effect of short contractions on the genetic diversity and make the claim that this short contraction regime is of particular interest as it can lead, such as in Fig. 1c, to genomic signatures similar to those generated by positive selection acting on a few sites in an otherwise neutral genome. More specifically, we want to quantitatively describe the reduction of diversity along the genome that is observed around a locus with a small T_MRCA (such as in Fig. 1c in the regions around 10–11 and 19–20 Mb), where we observe a valley or trough of diversity. Akin to what is done for selective sweeps, we consider the (neutral) fast fixation of an allele and analyze the impact of hitchhiking on the genetic diversity of neighboring loci, and we refer to this process as a neutral sweep.

Figure 1.

Nucleotide diversity of a population experiencing a contraction, as a function of the time t_c elapsed since the contraction, measured in units of 2N_c. a) Distribution of nucleotide diversity as a function of time, nucleotide diversity along the chromosome at t_c = 0 b), at t_c = 0.25 c) and at t_c = 0.75 d). Population size before contraction N₀ = 2.37 × 10⁶ and after contraction N_c = 4,400. Mutation rate μ = 5.42 × 10⁻¹⁰ per site per generation. Recombination rate r = 3.5 × 10⁻⁸ per site per generation. Chromosome size L = 20 Mb. Window size 10 kb sliding at 1-kb intervals. Sample size: 30 haplotypes. These parameters are taken from Rogers et al. (2010). Simulations were performed with fastsimcoal2 (Excofffier et al. 2021).

To investigate neutral sweeps in our model, we consider the following scenario: t_m generations ago a mutation occurred at a single site on the chromosome, which we call the focal site. We further assume that this mutation has just fixed in the population, i.e. that it was segregating at a frequency strictly lower than 1 in the last generation (at t = 1) and has now (at t = 0) a frequency equal to 1. We assume that the population contraction occurred t_c generations ago, with t_c$\ge$t_m. As the mutant enters the population as a single allelic copy at the focal locus, defined as a nonrecombining region surrounding the focal site, this copy is a common ancestor for all the copies (2N_c) present at fixation. However, it is not necessarily the most recent common ancestor. Figure 2 shows a sketch of our model to help visualize how recombination can maintain diversity at linked loci around a locus where a new mutation quickly fixed in the population.

Figure 2.

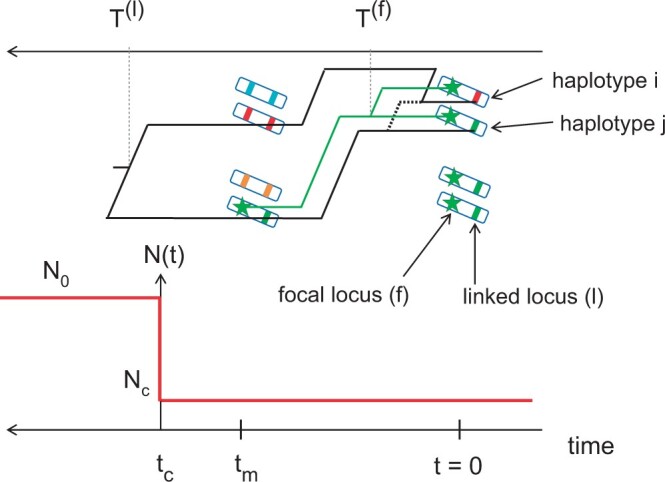
Instantaneous population contraction with a subsequent neutral fixation. A mutant (green star) appeared t_m generations ago and has just fixed neutrally in a diploid population that experienced a contraction t_c generations ago. We represent the population as a set of ${2N}_c$ 2-locus haplotypes that are painted so that the gene copies present at t = 0 can be traced back to t = t_m. Due to recombination, haplotype i carries a red gene copy at the linked locus at t = 0. Correspondingly, the coalescence time T^(l) of the haplotypes i and j at the linked locus (black tree) is larger than t_m. On the other hand, the coalescence time T^(f) at the focal locus (green tree) is smaller than t_m because at this locus all gene copies descend from the same haplotype (due to the fixation of the focal mutation).

Results

Average coalescence time at a linked locus

We can calculate the expected coalescence time T^(l) of 2 randomly sampled haplotypes at a linked locus as a function of the recombination rate r from the focal locus. The idea is to consider 2 haplotypes with a given coalescence time T^(f) at the focal locus, and then follow the genealogy of the gene copies carried by these 2 haplotypes at the linked locus backward in time, while considering possible recombination events. The expected coalescent time at the linked locus is then

$$E\left[T^{\left(\mathit{l}\right)}\right]=\left(1-E\left[e^{-2r{\sum }_{t=1}^{T^{\left(\mathit{f}\right)}}(1-{\overline{x}}_t)}\right]\right)\left(t_m+T_m\right)+E\left[T^{\left(\mathit{f}\right)}\hspace{0.33em}{e}^{-2r\sum _{t=1}^{T^{\left(\mathit{f}\right)}}(1-{\overline{x}}_t)}\right]$$ (2)

where ${\overline{x}}_t$ is the average frequency of the mutant (derived) allele at the focal locus at time t counting backward from present. A detailed derivation of this equation is given in Appendix D. The first term of the right-hand side of Equation (2) corresponds to cases where lineages escape the neutral sweep due to recombination and still have not coalesced after t_m generations. In this case we need to wait on average $T_m=2\left(N_0-N_c\right) e^{-{(t}_c-\mathrm{ }{t}_m)/2N_c}+2N_c$ extra generations before the lineages coalesce, due to the contraction that happened t_c − t_m generations before the focal mutation. The second term of the right-hand side of Equation (2) corresponds to cases where the lineages cannot escape the sweep and are forced to coalesce at a time T^(l) ≤ t_m.

Distribution of coalescence times at the focal locus

To evaluate Equation (2), we need to determine the probability distribution of the pairwise coalescence times T^(f) at the focal locus, as well as the expected frequency trajectory of the derived allele. Even though this allele fixes neutrally in a population of constant size (the contraction occurs prior to the mutation), the distribution of coalescent times at the focal locus T^(f) departs from the usual exponential distribution for a neutral coalescent process because the allele fixes in exactly t_m generations, and hence, the coalescence time for a randomly chosen pair of haplotypes is at most t_m. Slatkin (1996) investigated the coalescent process within a “mutant allelic class” that originated from a single mutation at a given time in the past. He derived exact analytical results for the average pairwise coalescence time, but the coalescence distribution itself can only be expressed with multidimensional integrals and obtaining a closed form expression does not appear feasible. We therefore use a different approach: given a particular fixation trajectory of the mutant allele, i.e. given the number of mutant copies $N_{\mathrm{\mu }}$ at each generation between t = 0 and t = t_m, we can express the coalescence time distribution within the mutant allelic class, using the result of a coalescent in a population with a time-dependent (but deterministic) size $N_{\mathrm{\mu }}\left(t\right)$ (Griffiths and Tavaré 1994). Averaging over all possible trajectories of the mutation, we obtain:

$$P\left(T^{\left(\mathit{f}\right)}\right)=\sum _{{\{x}_t\}}\left[\frac{1}{2N_c{x}_{T^{\left(\mathit{f}\right)}}} \prod _{t=1}^{T^{\left(\mathit{f}\right)}-1}\left(1-\frac{1}{2N_c{x}_t}\right)\right]P\left({\{x}_t\}\right)$$ (3a)

where $x_t=N_{\mathrm{\mu }}\left(t\right)/\left(2N_c\right)$ is the frequency of the mutant t generations from fixation, and $P\left({\{x}_t\}\right)$ is the probability of a given trajectory. $P\left({\{x}_t\}\right)$ can be evaluated (see Appendix B) and the sum in Equation (3a) can in principle be computed numerically; however, the number of trajectories to consider is prohibitive. As a first approximation, we can replace $x_t$ by its expectation ${\overline{x}}_t$, i.e. we neglect the fluctuations of the trajectory around the mean to obtain

$$P\left(T^{\left(\mathit{f}\right)}\right)\simeq \frac{1}{2N_c {\overline{x}}_{T^{\left(\mathit{f}\right)}}}\prod _{t=1}^{T^{\left(\mathit{f}\right)}-1}\left(1-\frac{1}{2N_c {\overline{x}}_t}\right).$$ (3b)

The last step is to determine the average trajectory of an allele fixing in exactly t_m generations. Zhao et al. (2013) as well as Maruyama and Kimura (1975) have investigated the characteristic trajectory of an allele fixing in a given time but they do not provide a closed form solution. Here, we use a different approach (also based on diffusion theory to obtain an approximation for the average trajectory of an allele fixing in exactly t_m generations, starting from a frequency p₀. As detailed in Appendix B, we obtain

$${\overline{x}}_t=1/2\left(1-\left(1-2p_0\right)e^{-\left(t_m-t\right)/N_c}+e^{-t/N_c}\right)$$ (4a)

which is valid for $t_m\gg 2N_c$. For very fast fixations, i.e. when $t_m\ll 2N_c$, the frequency of the allele increases approximately linearly as

$${\overline{x}}_t=1-\left(1-p_0\right)\frac{t}{t_m}.$$ (4b)

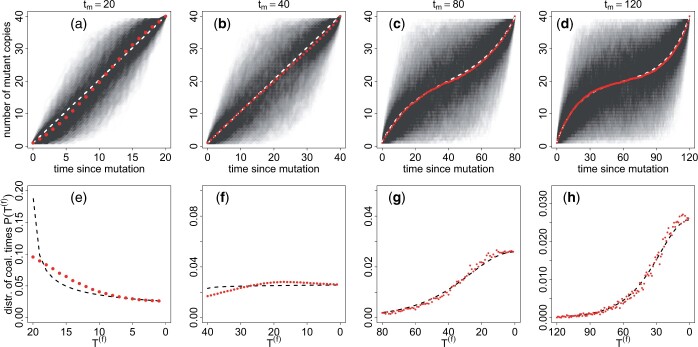
We remind the reader that t is counted backwards from fixation. Figure 3 compares Equations (4a) and (4b) to trajectories obtained from simulations of a Wright–Fisher diploid population. We find good agreement between the simulations and the analytical results. Importantly, the typical neutral trajectory for large values of the fixation time has an “inverse-sigmoid shape” (Fig. 3c), contrary to the typical sigmoid trajectory of a positively selected allele going to fixation in a constant size population (see Fig. 5a). This neutral trajectory occurs because, conditional on nonloss, neutral alleles need to quickly escape loss at the beginning and remain at intermediate frequencies to stay away from both fixation and loss until they eventually fix in the population at t = 0 (i.e. in exactly t_m generations). Figure 3, e–h also shows the coalescence time distribution for several values of the fixation time t_m. The comparison of the distribution of pairwise coalescence time with numerical simulations of a Wright–Fisher model shows that our approximation Equation (3b) is quite accurate but overestimates the probability of coalescence for large coalescence times when t_m is small (Fig. 3d). Notably, coalescence (simulated or theoretical) is more probable at large times (i.e. when the mutant appeared) for short fixation times (Fig. 3d), whereas it is more probable at small times (i.e. close to fixation) for large fixation times (Fig. 3e). The coalescence rate within the mutant allelic class is given by the inverse of the number of mutant copies and is for all values of the fixation time slightly more than 1/2N_c at the first generation. However, when the fixation time is short (Fig. 3e), there is a fast increase of the coalescence rate backwards in time, and many lineages are forced to coalesce at t = t_m. When the fixation time is large (Fig. 3h), the coalescence rate also increases backwards in time, but the increase is much slower. In that case, most coalescence events happen in much less than t_m generations, so that the early increase in frequency of the mutant has almost no influence on the coalescence distribution.

Figure 3.

Average frequency (a–d) and coalescence time distribution (e–h) of an allele fixing in a diploid population of constant size N_c = 20 in exactly $t_m$ generations, starting as a single copy (i.e. p₀ = (2N_c)⁻¹). The red dots are the results of Wright–Fisher simulations, and the black and white dashed lines are calculated with Equations (4b) (first and second columns), (4a) (third and fourth columns), and (3b). In (a)–(d), we show the variability of the fixation process by overlapping 1,780 fixing trajectories. The (numerically estimated) probability, for a mutant that appears at the onset of the contraction, to fix in less than $t_m$ generations is 0.006, 0.16, 0.64, and 0.86 for $t_m$ = 20, 40, 80, and 120, respectively (for this particular value of N_c).

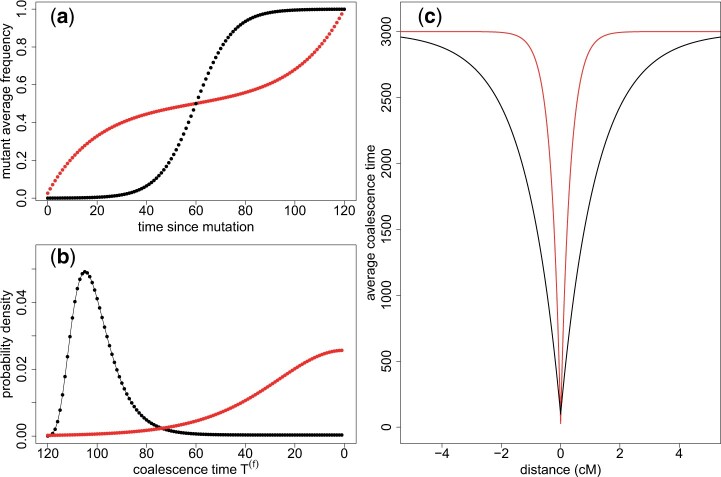
Figure 5.

Comparison between troughs of diversity resulting from a selective sweep (black) and a neutral sweep (red), for the same fixation time $t_m=120$ (corresponding to s ≈ 0.1 in the selective case). Frequency of the fixing allele as a function of time a), coalescence time distribution b), and diversity around the fixing site along the genome using Equation (5) c). N₁ = 1500, N_c = 20, and N₀ = 2.97 × 10⁴.

Effect of a neutral sweep on linked diversity

Combining Equations (3b) and (4a) with Equation (2) allows us to get an approximation for the average coalescence time at linked loci. Since the derivation of Equation (2) assumes that there is at most 1 recombination event in the genealogy of a randomly chosen pair of gene copies, we expect it to be only accurate for small values of the recombination rate r. For large values of r we use a heuristic approach combining the result of Equation (2), which is accurate for small r, and the expected diversity at unlinked loci, which is equal to $T_0=2\left(N_0-N_c\right) e^{-t_c/2N_c}+2N_c$ as stated in Equation (1). We fit the trough of diversity with an exponential function of the form:

$$E\left[T^{\left(\mathit{l}\right)}\right]\left(r\right)=T_0\left(1-c{e}^{-ar}\right)$$ (5)

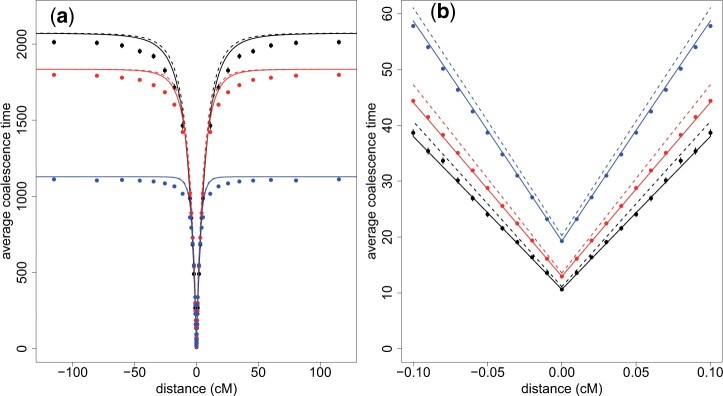
where the coefficients $c=1-E\left[T^{\left(\mathit{f}\right)}\right]/T_0$ and $a=2E[(t_m+T_m-T^{\left(\mathit{f}\right)}){\sum }_{t=1}^{T^{\left(\mathit{f}\right)}}(1-{\overline{x}}_t)]/(T_0-E\left[T^{\left(\mathit{f}\right)}\right])$ are obtained by imposing that Equations (2) and (5) coincide for small values of r (using a linear expansion in r). In Fig. 4, we compare the result of Equation (5) to Wright–Fisher simulations with two recombining loci. We see in Fig. 4a that the exponential function fits the data accurately at large values of the recombination distance, but that the fit is biased for intermediate values of r. In Fig. 4b we see that the approximation is very good for low values of the recombination distance, although there still is a slight bias. This discrepancy at small r can be corrected (solid lines in Fig. 4) if we use numerical estimations of ${\overline{x}}_t$ and $P\left(T^{\left(\mathit{f}\right)}\right)$, instead of Equations (4) and (3b), to evaluate Equation (5).

Figure 4.

Average coalescence time at a linked locus, as a function of the recombination distance from the focal locus where a mutant fixed in exactly t_m generations, starting from a single copy t_m generations ago. t_m = 15 in black, t_m = 20 in red, and t_m = 40 in blue. The dots are calculated with 2-locus WF simulations, and compared to Equation (5) with either a numerical estimation (solid lines) or a theoretical estimation (dashed lines) of ${\overline{x}}_t$ and $P\left(T^{\left(\mathrm{f}\right)}\right)$. N_c = 20. N₀ = 1,500. The population experienced a contraction t_c = t_m generations ago.

We observe, as expected, in Fig. 4 that the troughs of diversity induced by neutral sweeps are wider and deeper for short fixation times. Similarly to what happens after a selective sweep, there is less opportunity for linked loci to escape the sweep by recombination and maintain diversity when the fixation is fast. In addition, the diversity level at the center of the valley is given by the average coalescence time at the focal locus, which quickly decreases for small fixation times t_m.

Comparison of neutral sweeps and selective sweeps

Since we did not make any assumption regarding the process driving the mutant allele to fixation when deriving the average coalescence time at linked loci (Equation (2)) and the coalescence time distribution at the focal locus (Equation (3b)), our framework allows us to directly compare the signatures of different processes that can drive mutations to fixation in a given number of generations. We illustrate this by comparing the effect of neutral and hard selective sweeps on linked diversity. Later, we will discuss how neutral sweeps compare to a larger variety of scenarios (e.g. background selection, small selection coefficients, or dominant alleles). Here we assume that the neutral and selected fixations occurred over the same time interval, that is in both cases in exactly $t_{\mathrm{m}}$ generations. The selected fixation is assumed to be codominant (h=0.5) and occurs on an autosomal locus in a randomly mating diploid population of constant size N₁, and we consider a strong selection strength (2N₁s ≫ 1) so that the allele frequency follows the deterministic trajectory

$${\overline{x}}_t=\frac{1}{1+\left(2N_1-1\right) e^{-2\left(1-t/t_m\right) \text{log} \left(2{\mathrm{N}}_1\right) }}$$ (6)

where the fixation time is given by t_m(s) = 2log(4N₁s)/s (Barton 1995). Then combining Equations (5), (3b), and (6), we can compute the average coalescence time at linked loci as a function of the recombination distance r to the focal locus, after replacing T_m, the average coalescence time at t = t_m, by 2N₁ in Equation (5) and N_c by N₁ in Equation (3b). This approach yields results similar to Charlesworth (2020), where the author investigated signals of selective sweeps correcting for coalescent events that happen during the sweep, thus going beyond the common assumption of a star tree structure at the focal locus. For the sake of simplicity in the neutral case, we consider that the mutant appeared at the time of the contraction, i.e. t_m = t_c. Furthermore, we will assume that the average coalescence times (and consequently the genetic diversity) are equal in both scenarios, i.e. that T₀ = 2N₁ which implies that

$$N_0\left(t_m\right)=\left(N_1-N_c\right) e^{t_m/2N_c}+N_c .$$ (7)

In the neutral case, we want the diversity to remain as high as 4N₁ μ after the contraction, which is possible only if the ancestral diversity was even higher, i.e. we have in general N₀ > N₁ > N_c.

In Fig. 5a, we compare the mutant average frequency as a function of time for a selected and a neutral fixation. The dynamics of the neutral fixation is the opposite of that of the selected allele in the sense that when one is increasing, the other is “resting” and vice versa. These different trajectories translate into different coalescence distributions at the focal locus (Fig. 5b). If selection drives the fixation of the mutation, the distribution of coalescence time is peaked at large coalescence times. In contrast, in the neutral case the distribution is skewed toward small coalescence times. Correspondingly, the coalescence tree for the selected case has a star-like structure (Hermisson and Pennings 2017), whereas the tree for the neutral case has shorter outer branches. Therefore, for a given recombination distance, there will be fewer recombinations on the neutral tree because it has a much smaller total length. As recombination helps maintain diversity at linked loci, we would expect neutral troughs of diversity to be wider than in the selected case. However, this is at odds with the valleys of diversity observed in Fig. 5c, where the selective trough is wider than the neutral trough. Even though recombinations occur less frequently on the neutral tree as compared to a selected tree, a recombination on the neutral tree is more likely to lead to a change of genomic background from derived to ancestral allele due to the inverse sigmoid neutral trajectory of the derived allele. Recombination on the neutral tree will thus more often lead to a lineage escaping the sweep, resulting in more efficient recovery of diversity in the neutral case for a given genomic distance from the focal locus. Furthermore, we see that the trough is deeper in the neutral case (Fig. 5c), since the average coalescence time is smaller at the focal site due to the smaller total length of the coalescence tree.

To determine if these differences between selective and neutral troughs hold for other fixation times and population sizes, we define 2 quantities that characterize the shape of a trough, as well as its propensity to be detected in real data: (1) the trough relative depth and (2) the width of the trough. The relative depth is defined as the difference between the background level of diversity and the diversity at the focal locus, divided by the background diversity, and the width is measured at half depth, i.e. halfway between the background diversity and the diversity at the focal locus. In Fig. 6, we plot the relative depth of neutral and selective troughs as a function of their width for different fixation times t_m, calculated with our analytical expressions. We see that the neutral troughs are not only always narrower than the selective troughs for the same value of t_m, but also deeper. This is due to differences in the focal tree structure between the selective case and the neutral case as well as difference in the ancestral background level in both cases, as explained above. For very short fixation times (corresponding to selection coefficients larger than 0.1), there is almost no difference between troughs generated by selective and neutral sweeps. Indeed, for such values of t_m, in both cases, the focal coalescence tree is essentially a star tree because the increase in frequency is very fast, and the ancestral backgrounds of diversity, 2N₀ and 2N₁, are also practically equal. Note however that at small t_m the corresponding value of the selection coefficient s (see legend of Fig. 6) may be unrealistically high. For realistic values of the selection coefficient/fixation time, the neutral troughs tend to be quite deep but narrow, whereas selective troughs are wider and their depth decreases quickly for low selection coefficients. From Fig. 6, we see that the shape of a neutral trough is generally different from a selective sweep signal, but in practice those differences might be hidden due to the noise inherent present in real genomic data, and it might be difficult to decide whether a genomic signal is a due to a neutral sweep or a selective sweep.

Figure 6.

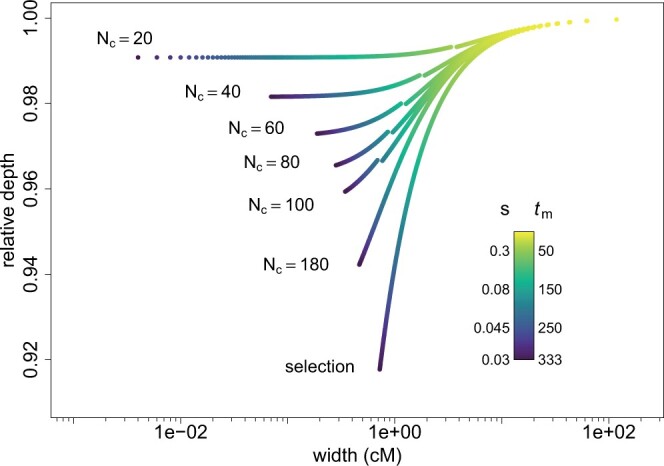
Relative depth as a function of the width of the diversity troughs, for different values of t_m and N_c in the neutral case and for selective scenarios with identical fixation times. t_m goes from 1 to 333 by increments of 1, the corresponding values of the selection coefficient s are indicated on the left of the legend bar (for all of them we have N₁s ≫ 1). N₁ = 1,500. N₀ is given by Equation (7) and depends on N_c and t_m. The jumps in the neutral curves for N_c = 20, 40, 60, 80, and 100 are due to the use of 2 different approximations for the frequency of the mutant, Equations (4a) and (4b) and are located at t_m = 2N_c.

Discussion

It has repeatedly been suggested that strong depletions of diversity in the genome are not necessarily due to the presence of positive selection (Johri et al. 2020) and can also be the result of demographic effects only, such as the allele surfing phenomenon occurring at the front of a range expansion (Klopfstein et al. 2006). In this work, we considered a model of population contraction to analyze quantitatively the genomic signature of the rapid fixation of a mutation during a population contraction, but it should also apply in case of range expansions or recurrent founder events by considering the harmonic mean of population sizes. Taking a step further from previous work that focused on the impact of range expansion on mere allele frequencies, we have studied here the impact of a neutral allele fixation on neighboring genomic diversity. We show that the diversity profile around a recently fixed locus crucially depends on the frequency trajectories of the allele going to fixation, and we outline the fact that neutrally fixing alleles have an inverse-sigmoid trajectory (Fig. 3d), as compared to the standard sigmoid frequencies observed for positively selected alleles. For the same fixation time, this difference translates into different genomic signatures (see Figs. 5c and 6). Our results demonstrate that there is a short period after a demographic contraction (or during a range expansion) where observed profiles of genomic diversity would look like those usually attributed to selection (Fig. 1c) and that selective sweep signals can be mimicked by neutrally fixing mutations without the need to invoke complex histories of population size changes.

Our results allow for a systematic comparison of selective and neutral troughs of diversity, and we used our results to investigate trough shapes for a range of neutral and selected scenarios (see Fig. 6), which in principle can be used to decide whether a given empirical trough is due to selection or demography, and to infer the corresponding parameters. However, we did not consider the whole spectrum of possible selection scenarios. It would be indeed interesting to use our results to study cases of background selection, small selection coefficients, and a variety of dominance coefficients. All these cases should have their own characteristic trajectories of fixation, and hence potentially different genomic signatures. In addition, in our model we do not consider mutations that fixed in the past (we always assume that the allele has just reached fixation), nor do we consider mutations appearing before the population contraction, i.e. with t_m > t_c. The average coalescence time in the former case can be expressed as a function of the coalescence time at fixation using conditional probabilities, and we can show that a sweep signal vanishes exponentially with the time elapsed since fixation (see Appendix D). In the latter case, we can solve the problem by considering the number of gene copies at t_c that descend from the original copy that appeared at t_m. One could extend our results by considering an allele starting from an arbitrary number of copies at t_c, akin to soft selective sweeps; however, the analytic calculations are complex, and we leave this study for future research. In any case, those additional scenarios must be considered when trying to infer models from the study of troughs found in empirical data. Another phenomenon that renders the inference of parameters cumbersome is a possible interference between troughs. Indeed, when two loci fix neutrally in the population, the genetic diversity in the region between those loci will be influenced by both fixations and will differ from the diversity expected in the vicinity of a single fixing locus. As in the case of interference between the fixation of selected alleles (Weissman and Barton 2012), this should limit the number of independent neutral fixations. The effect of trough interference is stronger for neighboring troughs, and the probability to observe close troughs depends on the relative frequency of troughs along the genome, which itself depends on the distribution of the $T_{\mathrm{MRCA}}$. In Fig. 1d, for example the distribution of $T_{\mathrm{MRCA}}$ has a mode centered around 4N_c (not shown) and correspondingly the nucleotide diversity is peaked around 4N_c$\mu$. As a result, we see many regions of the chromosome with a low diversity. It is likely that those troughs interfere with each other and that they do not correspond to the profile of an isolated trough. On the other hand, in Fig. 1c, the first mode of the $T_{\mathrm{MRCA}}$ distribution is truncated because t_c is much smaller than 4N_c, and only $T_{\mathrm{MRCA}}$s equal or close to t_c are observed (plus all the $T_{\mathrm{MRCA}}$s corresponding to the second mode centered at 4N₀). In this case, there is no interference and the (rare) troughs, such as the one in Fig. 7, are correctly fitted by their theoretical expectation. Those considerations imply that, even though we know the forward in time probability that an allele will fix in t_m generations, it is difficult to infer the parameters of a fixation scenario from a single observed neutral valley of diversity. It appears therefore difficult to perform model selection from a single trough signal, i.e. to decide whether a particular trough is due to selection or demographic effects, because alternative demographic scenarios that we did not consider here could also lead to similar signals.

We performed simulations to investigate the signature of a neutral rapid fixation on the SFS (Supplementary Fig. 1). We chose demographic parameters such that troughs are not numerous along the genome and leave a strong footprint on genomic diversity. Out of 10,000 simulations of 20-Mb chromosomes, only 432 exhibit a (single) region of highly reduced diversity (here arbitrarily set to less than 7% of the background diversity). By averaging over all these valleys of diversity, we calculated the average SFS observed in a 15-kb window at the center of the valley and obtained a U-shape SFS, which is also expected around a selective sweep (Huber et al. 2016). However, contrary to a fixation driven by selection (Supplementary Fig. 1), the SFS around a neutral fixation shows a slight excess of variants at intermediate frequencies. This is probably due to the fact that some neutral haplotypes have spent more time at intermediate frequencies before going to fixation than selected haplotypes that rapidly "jump" from very low to very high frequencies (see Fig. 5a). Note also that the background (genome-wide) SFS away from neutral sweeps has a global excess of intermediate and high frequency variants compared to a constant size population. This excess of high frequency variants is typical of populations having gone through a recent population size reduction or a bottleneck (Marth et al. 2004) due to the higher coalescence rate during the population contraction. These differences in expected SFS around neutral and selected sweeps could help decide whether regions of low diversity observed in empirical data are due to selection or to demographic processes. However, since very few variants are usually observed in the vicinity of single troughs, the empirical SFS in such a region might be too noisy to confidently identify the cause of the diversity reduction. In principle, if several troughs of diversity were observed in a genome, one could use the distribution of trough shapes and pooled SFS expected under a given simple demographic model and a distribution of fitness effect to compare neutral and selection models under a likelihood framework, but such an exploration is beyond the scope of the present paper.

In conclusion, our results suggest that any empirical valley of diversity found in empirical data can be reproduced neutrally with a population contraction using appropriate parameters. One could argue that this identifiability problem disappears once the true evolutionary history is correctly inferred. However, inferring the true demographic history requires precise knowledge about how selection has shaped genomic diversity (Johri et al. 2020). In humans, for instance, it has been estimated that roughly 95% of genomic diversity is affected by some form of nonneutral forces such as background selection or biased gene conversion (Pouyet et al. 2018) potentially biasing demographic inference (Ewing and Jensen 2016). These considerations indicate than genome scans in search for signals of adaptation might be more affected by past demography than previously thought. We thus believe that despite current advances using supervised machine learning or similar approaches (Schrider and Kern 2018), it remains important to further study the effect of neutral fixations in various demographic scenarios using localized genomic approaches such as the present analytical work (Johri et al. 2021b), as well as with controlled experiments on real living organisms where both the selected locus and the population history are known (Orozco-terWengel et al. 2012). Such work will be critical in order to develop more appropriate evolutionary null models for statistical inference (Hahn 2008; Johri et al. 2020).

Data availability

The authors affirm that all data necessary for confirming the conclusions of the article are present within the article, figures, and tables.

Supplemental material is available at GENETICS online.

Appendices

Appendix A: Coalescence distribution after a contraction

We want to determine the coalescence time of 2 lineages in a population that experienced a contraction $t_m$ generations ago, from a diploid size N₀ to N_c. As we go backward in time, the coalescence rate switches from $(2N_c{)}^{-1}$ to $(2N_0{)}^{-1}$ at T = t_c. The probability distribution might still be approximated by a piecewise exponential density:

$$\begin{array}{c}{f}_0\left(T\right)=\hspace{0.33em}\frac{1}{2N_c}\mathrm{e}\mathrm{xp}\left(-\frac{T}{2N_c}\right)\hspace{0.33em}\hspace{0.33em}\mathit{for}\hspace{0.33em}\hspace{0.33em}0<T<t_{\mathrm{c}}\\ =\frac{1}{2N_0}\mathrm{e}\mathrm{xp}\left(-\frac{t_{\mathrm{c}}}{2N_c}\right) \exp \left(-\frac{T-t_{\mathrm{c}}}{2N_0}\right)\hspace{0.33em}\hspace{0.33em}\mathit{for}\hspace{0.33em}\hspace{0.33em}T\ge t_{\mathrm{c}}.\end{array}$$

The corresponding expectation for this distribution is

$$\begin{array}{c}E\left[T\right]=T_0={\int }_0^{\mathrm{\infty }}T f_0\left(T\right) \mathrm{d}T\\ =\hspace{0.33em}2N_0 e^{-t_c/2N_c}+2N_c\left(1-e^{-t_c/2N_c}\right).\end{array}$$

Appendix B: Average frequency of an allele fixing in exactly t_m generations

In this section, time is counted forward from the mutation, which appears after the contraction, so that during the fixation the diploid population size is constant and equal to N_c. We condition on the fixation time t_m of the mutant. We define the trajectory of a mutant as the list of frequencies at all generations: ${\{x}_t\}=\left(x_0,x_1,\dots ,x_{t_m-1},x_{t_m}\right)$. We assume that the mutant fixes in exactly t_m generations, starting from a frequency $p_0$, i.e. $x_0=p_0$, $0<x_{t_m-1}<1$, and $x_{t_m}=1$. The probability that the mutant follows a given trajectory might be expressed as the product of the transition probabilities

$$P\left({\{x}_t\}\right)=\prod _{t=0}^{t_m-1}P\left(i,t\to j,t+1\mathrm{ }|\mathrm{ } \text{fix in} t_m,p_0\right).$$

For an unconditional Wright Fisher model, $P\left(i,t\to j,t+1\right)$ is the probability to have $j$ copies of the new allele at $t+1$ given that there were $i$ copies at $t$. We note $P_t\left(i\to j\right)$ for brevity. If we only consider trajectories fixing in exactly $t_m$ generations and starting from a number $2N_c p_0$ of copies at $t=0$, then the transition probabilities are not equal to the transitions of the unconditional Wright–Fisher model. However, thanks to Bayes theorem, we can write

$$\begin{array}{c}{P}_t\left(i\to j | \text{fix in} t_m,p_0\right)=\frac{P_t\left(\text{fix in} t_m | i\to j,p_0\right)P_t\left(i\to j | p_0\right)}{P\left(\text{fix in} t_m | p_0\right)}\\ =\frac{P\left(\text{fix in} t_m | j_{t+1}\right)P_t\left(i\to j\right)}{P\left(\text{fix in} t_m | p_0\right)}.\end{array}$$ (B1)

From the first to the second line, we use the Markov property. The 3 terms involved in the right-hand side of this equation can be approximated thanks to diffusion theory. In this framework, the probability for an allele to fix in $t_m$ generations, given that there were $i$ copies at time $t$ is approximately (Ewens 2004)

$$P\left(\mathrm{fix} \mathrm{in} t_m | i_t\right)=\frac{3}{2N_c}\left(1-\frac{i}{2N_c}\right)\frac{i}{2N_c}\hspace{0.33em}{e}^{-\left(t_m-t\right)/2N_c}.$$ (B2)

The term $P_t\left(i\to j\right)$ is the unconditional binomial transition probability of the Wright Fisher model (which does not depend on $t$). In principle, Equation (B1) can be used to compute the exact distribution of coalescence times at the focal locus, using Equation (3a). However, the huge number of possible trajectories fixing in $t_m$ generations (${\left(2N_c-1\right)}^{t_m-1}$) makes the average over trajectories impossible to evaluate numerically. For this reason, we use the approximation in Equation (3b).

We consider here the probability that the allele has frequency $x$ at time $t$, given that it started at frequency $p_0$ at $t=0$. Again if we only consider trajectories that fix in exactly $t_m$ generations, this probability is not equal to the neutral diffusive result. However, similarly to the previous section, we can use Bayes theorem:

$$P\left(x_t |\mathrm{fix} \mathrm{in} t_m, p_0\right)=\frac{P\left(\mathrm{fix} \mathrm{in} t_m | x_t\right)P\left(x_t | p_0\right)}{P\left(\mathrm{fix} \mathrm{in} t_m | p_0\right)}.$$

From diffusion theory (Ewens 2004), we also have

$$P\left(x_t | p_0\right)=6p_0\left(1-p_0\right) e^{-t/2N_c}\left(1+5\left(1-2p_0\right)\left(1-2x\right)e^{-t/N_c}\right)$$

which is a second order expansion of an infinite series involving vanishing exponential terms ($e^{-k\left(k+1\right)t/4N_c}$ for all $k\ge 1$). This expansion is thus valid in the limit of large times $t\gg 2N_c$. We deduce that the probability that an allele fixing in $t_m$ generations has frequency $x$ at time $t$ is

$$P\left(x_t |\mathrm{fix} \mathrm{in} t_m, p_0\right)=6x\left(1-x\right)\left(1+5\left(1-2p_0\right)\left(1-2x\right)e^{-t/N_c}\right)$$

which yields $E\left[x_t |\mathrm{fix} \mathrm{in} t_m, p_0\right]=1/2\left(1-\left(1-2p_0\right)e^{-t/N_e}\right)$.

This expression is valid for $t_m\gg t\gg 2N_c$ and does not allow one to estimate the frequency close to fixation. If we evaluate this expression for a given value of t, we must assume that t_m is much larger than t (otherwise Equation (B2) is not accurate). It implies that we cannot evaluate the frequency close to fixation, because wherever we “look,” the fixation is always much later in time. Consequently, we see that $E\left[x_t\right]$ tends to $1/2$ when t is very large, which is the only possible value for an average frequency infinitely far away from both fixation (at t = t_m) and loss (at t = 0). However, we know that the frequency should be symmetric, i.e. the allele should on average approach fixation in the same way it escapes loss, because the neutral fixation of a derived allele is the same as the loss of the ancestral allele. We thus write

$$E\left[x_t |\mathrm{ }\mathrm{fix} \mathrm{in} t_m, p_0\right]=1/2\left(1-\left(1-2p_0\right)e^{-t/N_c}+e^{-\left(t_m-t\right)/N_c}\right).$$

When $t_m\ll 2N_c$, we can use a linear approximation for the trajectory (based on the numerical observations)

$$E\left[x_t |\mathrm{fix} \mathrm{in} t_m, p_0\right]=p_0+\left(1-p_0\right)\frac{t}{t_m}.$$

Appendix C: Coalescence distribution at linked loci around a neutral fixation

We now return to the scenario of Fig. 2, with a backward in time approach. Using Bayes theorem, we express the coalescence time of 2 haplotypes at the linked locus $T^{\left(l\right)}$, conditioning on the coalescence time at the focal locus $T^{\left(f\right)}$

$$P\left(T^{\left(l\right)}\right)={\int }_0^{t_m}P\left(T^{\left(l\right)} | T^{\left(f\right)}\right) P\left(T^{\left(f\right)}\right)d{T}^{\left(f\right)}=E\left[P\left(T^{\left(l\right)} | T^{\left(f\right)}\right) \right].$$

We assume that the linked locus is close to the focal locus on the chromosome, more precisely that the recombination rate $r$ is very small $r\ll 1$, so that we consider at most 1 recombination, occurring on one of the 2 focal lineages. We distinguish cases where there is no recombination between t = 0 and t = T^(f), cases where the allele at the linked locus recombines (somewhere between t = 0 and t = T^(f)) onto a haplotype carrying the ancestral allele at the focal locus, and cases where the allele at the linked locus recombines onto a haplotype carrying the derived allele at the focal locus. We call the second and third case heterozygous and homozygous recombinations, respectively, referring to the zygosity at the focal locus of the recombining pair of haplotypes (note that are 3 haplotypes, the 2 first ones have a coalescence time T^(f) and the third one recombines with one of these 2). If there is no recombination, then the coalescence time is the same for both loci, T^(l) = T^(f). To treat the case with a homozygous recombination, it is convenient to name the haplotypes: i and j coalesce at T_ij^(f) = T^(f) at the focal locus, and k is a third haplotype, onto which the linked allele recombines (coming from i). The linked allele carried by j stays on the same haplotype (no more than 1 recombination), and after recombining onto k, the linked allele initially carried by i also stays on k (again, at most 1 recombination). This implies that those 2 linked alleles coalesce at T_ij^(l) = T_jk^(f). This time is in general different than T_ij^(f); however, on average, T_jk^(f) and T_ij^(f) are equal (averaging over all possible coalescence trees at the focal locus). This implies that we can treat the case with homozygous recombination as if there was no recombination. If there is a heterozygous recombination between i and k, at some generation between t = 0 and t = T^(f), then the linked alleles still have not coalesced at t = t_m because after the recombination one of them is linked to a derived focal allele and the other one to an ancestral focal allele (and they stay linked because there is at most 1 recombination). In that case, T_ij^(l) is equal to t_m plus a random time given by (on average) T_m and is independent of T_ij^(f). Using again Bayes theorem and the previous results to write

$$\begin{array}{c}P\left(T^{\left(l\right)} | T^{\left(f\right)}\right)=P\left(T^{\left(l\right)} | T^{\left(f\right)},\mathrm{ }\mathrm{one}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)\\ P\left(\mathrm{one}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)\\ +P\left(T^{\left(l\right)} | T^{\left(f\right)},\mathrm{ }\mathrm{no}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)\\ P\left(\mathrm{no}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)=f_m\left(T^{\left(l\right)}-t_m\right)\\ \left[1-P\left(\mathrm{no}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)\right]\\ +\mathrm{\delta }\left(T^{\left(l\right)}-T^{\left(f\right)}\right)P\left(\mathrm{no}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)\end{array}$$

where $\delta \left(\cdot \right)$ is the Dirac delta function, and $f_m$ is the unconditional coalescence distribution of a pair of lineages sampled at t = t_m, i.e. it is equal to the function $f_0$ introduced above but replacing t_c by t_c − t_m (note also that $f_m\left(t\right)=0$ if t < 0). We then have to evaluate the probability that there is no heterozygous recombination. At generation t (counted backward), the probability that a linked allele recombines onto a haplotype carrying the ancestral allele at the focal locus is $r\left(1-x_t\right)$, where $x_t$ is the frequency of the derived allele at the focal locus, we deduce that the probability that there is no heterozygous recombination on either lineage is

$$\begin{array}{c}P\left(\mathrm{no}\mathrm{ }\mathrm{het}.\mathrm{ }\mathrm{rec}.\mathrm{ }\mathrm{in} \left[0, T^{\left(f\right)}\right]\right)=\prod ^{T^{\left(f\right)}} (1-r[1-x_t]{)}^2\\ \simeq \exp \left(-2r \sum _{t=1}^{T^{\left(f\right)}}\left(1-x_t\right)\right).\end{array}$$

This probability depends explicitly on the allele trajectory, which means that rigorously, all the calculations should be conditioned on a given trajectory and then averaged over all trajectories. To allow for mathematical tractability, and to avoid heavy expressions, we consider that as a good approximation $x_t={\overline{x}}_t$. Finally, we obtain

$$P\left(T^{\left(l\right)}\right)=\hspace{0.33em}E\left[\mathrm{\delta }\left(T^{\left(l\right)}-T^{\left(f\right)}\right) \exp \left(-2r \sum _{t=1}^{T^{\left(f\right)}}\left(1-x_t\right)\right)\right]\mathrm{ }+ f_m\left(T^{\left(l\right)}-t_m\right) E\left[1-\exp \left(-2r \sum _{t=1}^{T^{\left(f\right)}}\left(1-x_t\right)\right)\right].$$

The expectation corresponding to this distribution yields Equation (2).

Appendix D: Average coalescence time at a linked locus around a mutation that completed fixation t_fix generations ago

Thanks to Bayes theorem we can write

$$E\left[T^{\left(l\right)}\right]=E\left[T^{\left(l\right)}|T^{\left(l\right)}<t_{\text{fix}}\right]P\left(T^{\left(l\right)}<t_{\text{fix}}\right)+E\left[T^{\left(l\right)}|T^{\left(l\right)}>t_{\text{fix}}\right]P\left(T^{\left(l\right)}>t_{\text{fix}}\right)$$

i.e. we distinguish coalescence events happening in less than t_fix generations or more than t_fix generations. In the former case, the coalescence is neutral, unconditional (the fixation is completed) and happens in a population of constant size N_c which means that $E\left[T^{\left(l\right)}|T^{\left(l\right)}<t_{\text{fix}}\right]$ and $P\left(T^{\left(l\right)}<t_{\text{fix}}\right)$ can be worked out from the neutral exponential distribution. On the other hand, $E\left[T^{\left(l\right)}|T^{\left(l\right)}>t_{\text{fix}}\right]$ is equal to t_fix plus the expectation from Equation (5), which we note here $E\left[T^{\left(l\right)}\right]\left(t=\mathrm{ }{t}_{\text{fix}}\right)$. We obtain

$$E\left[T^{\left(l\right)}\right]=2N_c\left({1-e}^{-t_{\text{fix}}/2N_c}\right)+E\left[T^{\left(l\right)}\right]\left(t=\mathrm{ }{t}_{\text{fix}}\right){\mathrm{ }e}^{-t_{\text{fix}}/2N_c}.$$

We see that the sweep signal vanishes exponentially with the time elapsed since fixation.