Imputation of Missing Data in Electronic Health Records Based on Patients’ Similarities

Abstract

Using electronic health records (EHR) as the source of data for mining and analysis of different health conditions has become an increasingly common approach. However, due to irregular observation times and other uncertainties inherent in medical settings, the EHR data sets suffer from a large number of missing values. Most of the traditional data mining and machine learning approaches are designed to operate on complete data. In this paper, we propose a novel imputation method for missing data to facilitate using these approaches for the analysis of EHR data. The imputation is based on a set of interpatient, multivariate similarities among patients. For a missing data point in a patient’s lab results during his/her intensive care unit stay, the method ranks other patients based on their similarities with the ego patient in terms of lab values, then the missing value is estimated as a weighted average of the known values of the same laboratory test from other patients, considering their similarities as weights. A comparison of the estimated values by the proposed method with values estimated by several common and state-of-the-are methods, such as MICE and 3D-MICE, shows that the proposed method outperforms them and produces promising results.

Introduction

In the past few years, the development of information systems for patient data in the form of electronic health records (EHR) has progressed substantially. However, the main objective of generating EHR data is not research or analytical studies [15, 16] and adopting this data for research purposes has its own challenges. The EHR data show the trend of patients’ health trajectories through a set of features including lab results and vital signs. Other data collected include patients’ demographic, the medications administered for them, and their medical history [1, 13]. They are generally heterogeneous, temporal (and sometimes spatial), sparse, incomplete, noisy, irregular, and inaccurate [7]. In addition, occurrences of missing data in the EHR are very common. It can be attributed to the irregular ordering of lab tests and collection of vital signs or the fact that not all data are collected at regular intervals. Furthermore, the factors contributing to missing data are not necessarily known in advance. In [19], a classification of missing data in the EHR is provided and it is discussed that one of the reasons for missing data is the lack of documentation. This lack of documentation further complicates the analysis of missing data in EHR as it is difficult to ascertain whether the absence of data is intentional. For example, a clinician may deem the continued monitoring of a clinical analyte unnecessary because the patient’s lab values have stabilized in acceptable ranges. The researchers also categorize the missing data into three categories: the data “missing completely at random,” “missing at random,” and “not missing at random” [6]. The difference between the two first categories is that in “data missing completely at random,” all the data points have the same probability to be missing. However, in the second category, the missingness of the data is attributable to, for example, patients’ conditions, which makes the missingness of the data independent from the value of data. The last category includes missing data which completely depends on the value of the data. The level of bias introduced by each category is different and they may be differently treated.

Because most of the analytical methods developed for data-driven prediction and modeling in different disciplines assume that the input data set has no missing data, there have been extensive efforts both in the health care community and other fields to find the best method for treating missing data. The most basic and common method is complete case (or listwise) deletion, in which the entire records including missing data (for at least one feature) are removed. In [18], it is discussed that this method works very well in data sets with less than 15% missing data. However, [19] states that this method only works well for the “missing completely at random” category, which is not necessarily the case in missing data in the EHR. In addition, removing the whole record because of one missing data point results in information loss for all other features in the record. Therefore, other methods have been proposed in the literature that instead of removing the entire record with the missing value, the missing value should be imputed.

Related Work

The methods for imputation can be categorized into two main categories: univariate and multivariate. In the univariate category, the value of the missing data is estimated using the values of the same feature in the data set. In the case of multivariate imputation, the values of missing data are estimated using the values of other features in addition to the same feature in the data set. The univariate imputation of missing data can be performed in multiple ways. The imputeTS [14] is a R package specifically developed for univariate imputation, covering the most common methods in this category such as the mean (median, mode) imputation which replaces a missing data point with the mean (median, mode) value of the same feature. Another technique is using the closest available data point for the missing data points. It can be the most recent available data (also called last observation carried forward, LOCF) or the first next available data point (also called next observation carried backward, NOCB). Other methods in univariate missing data imputation are linear interpolation (linear interpolation of the value of missing data point using the previous and next available data points), spline interpolation (using polynomial interpolation of values of missing data point using the closest data points), and Kalman smoothing (using Kalman filter to predict the value of missing data).

Considering the richness of the literature on multivariate data analysis, data mining, and machine learning, it is not surprising that numerous techniques have been proposed for the estimation of missing data points. In [5], the said methods are categorized into statistical techniques, such as hot and cold deck imputation (estimating the missing data point in a record using other similar records, found based on the features that both records have), and machine learning techniques, such as decision tree imputation (estimating the value of the missing data using decision trees created by the feature of missing data as target variable, and other features of the data set as predictors, the records with no missing data are used for creating the decision tree). In [8], multiple statistical and machine learning techniques are compared with listwise deletion and it is shown that machine learning techniques outperform statistical techniques, and both are better than the listwise deletion technique in terms of the prognosis accuracy in patients with breast cancer. In [6], a generalized regression neural network-based approach is developed for multiple and single imputations of missing data. They compare the results of their methods with 25 different imputation techniques proposed in the literature on 98 data sets at different rates of data missingness and show that although computationally expensive, their proposed techniques have been able to outperform many of the methods in the literature. Another approach to missing data is to mine and learn from the patterns of missingness and their occurrences and use these patterns as a feature (informative missingness) for prediction of target feature [4, 11].

In many of the previously developed techniques for imputation, it is assumed that the outcomes of patients are known, and the accuracy or other prediction evaluation metrics are used to compare the performance of different imputation techniques. In addition, in most of the proposed techniques, the individual features are used to estimate the values for missing data points. Given that the changes in lab results and vital signs for a patient are not independent events, considering the dynamics among the features as a set might improve the performance of imputation techniques.

In this study, we focus on interpatient similarities and propose a novel method of imputation for data points missing at irregular time intervals. The similarity of two patients is defined as a function of their patterns of changes in their lab results. Then, ranking patients based on their similarities to the patient with missing data, the value corresponding to a missing data point in one patient is estimated from other similar patients which have a known value for the lab test (hereafter analyte) with missing data.

Materials and Methods

Data Set

In the following sections, the method used to impute missing data points and the function used to evaluate the performance of the proposed method are described.

The data set is derived from the MIMIC-III (Medical Information Mart for Intensive Care III) database of patients admitted to the intensive care units (ICU) at the Beth Israel Deaconess Medical Center between 2001 and 2012 [9]. It includes 13 clinical analytes, for which lab results were recorded at irregular time intervals starting from the beginning of the care (chart time t = 0). As part of the Data Analytics Challenge at the 2019 International Conference on Healthcare Informatics (ICHI 2019), the given data set has 8267 patients with 10–260 (mean, 24) lab records each. The ground truth for evaluation is established by randomly masking existing data points in the sets. In the following sections, we discuss our proposed method to impute the missing data points and the evaluation function.

Interpatient Similarity-Based Imputation

The methods proposed in the literature are mainly model-driven. They propose to create models based on the relationships among variables. In some of these methods, a response variable is used and the performance of imputation process is evaluated based on the impacts of the estimated values for missing data on the prediction of the response variables. In others, the variable with the missing value is considered as the target variable and other variables are used as predictors of this variable. It is shown that these approaches can perform very well. However, once a model is developed, it is used for the estimation of missing values without referring back to the source data for verification.

We propose an interpatient similarity-based imputation method for missing data, which is data-driven. For a patient with missing data, it identifies similar patients and uses their known values for estimation of missing data points. In the absence of patient diagnoses, we take into account all 13 analytes to represent a patient’s state of health, and we calculate the Euclidean distance to gauge the similarity between the lab records. In addition, we assume two patients at chart time t = 0 have different baseline states of health and may progress differently during their ICU stays. Therefore, a patient’s record with missing data at t_i needs to be compared with all available lab records taken at t_1:n for other patients to improve the chance of identifying patients with a similar health state. To reduce the impact of randomness, we also compare the similarity of previous and next rows of the row with the missing value. In other words, for two patients to be considered similar, they should exhibit similar states of health at the present moment as well as similar trajectories. To incorporate the temporal information entailed in the data, we weigh the similarity by the differences in time elapsed between two lab records among patients. In this study, we consider the very recent and very next lab records for comparing the trends. However, the approach can be broadened to a wider time window. Last, assuming that patients with similar states of health share similar lab values, we use the known values of other patients to estimate the missing value of interest.

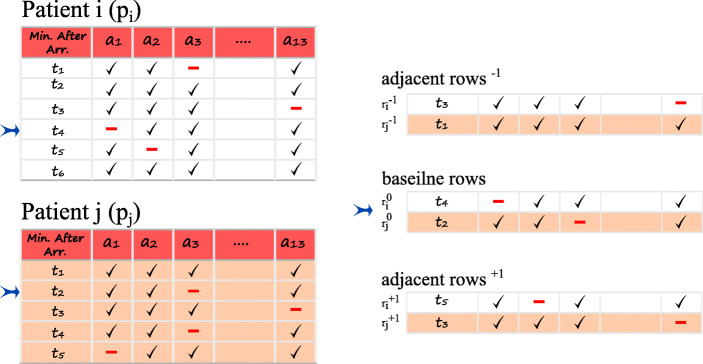
Figure 1 shows a schematic diagram of the similarity calculation for two patients, p_i and p_j. In this example, the analyte a₁ has a missing value at t₄ for p_i. Since the health state of p_i at t₄ is not necessarily identical to that of p_j at t₄, all the rows of p_j should be examined. For instance, we calculate the similarity between the lab record of p_i at t₄ and p_j at t₂. We designate these two rows as baseline rows and denote them as $r_i^0$ and $r_j^0$ respectively. Similarly, the Euclidean distances between adjacent rows of p_i at t₃ and p_j at t₁ (denoted by $r_i^{-1}$ and $r_j^{-1}$), and of p_i at t₅ and p_j at t₃ (denoted by $r_i^{+1}$ and $r_j^{+1}$) are calculated. In addition, we factor in the difference in the time elapsed between two lab orders for two patients (i.e., (t₄ − t₃) of p_i and (t₂ − t₁) of p_j represented as $\delta t_i^{-1}$ and $\delta t_j^{-1}$ respectively for the previous rows, and (t₅ − t₄) of p_i and (t₃ − t₂) of p_j represented as $\delta t_i^{+1}$ and $\delta t_j^{+1}$ respectively for the next rows). In other words, two patients might have similar states of health, but their lab results may come out differently if ordered at different time intervals. To modify the said effect, we use a generalized bell-shaped function which operates on the differences of time elapsed $\mathrm{\Delta }{t}^{-1}=\delta t_i^{-1}-\delta t_j^{-1}$ and $\mathrm{\Delta }{t}^{+1}=\delta t_i^{+1}-\delta t_j^{+1}$ and produces a weight in the range of [0,1]. This function (1) has three parameters: a, b, and c. The parameter c of the function is considered to be 0 because we assume a symmetrical distribution of equal probability for when Δt^− 1 or Δt^+ 1 have opposite signs with the same absolute value. Parameters a and b are experimentally estimated.

$$f\left(x\right)=\frac{1}{1+|\frac{x-c}{a}{|}^{2b}}$$ 1

Fig. 1.

The row at time t₄ for patient p_i with missing data point for analyte a₁ and its previous and next rows are considered for evaluation of similarity with patient p_j at time t₂

The distances between the patient with missing data and each of the other patients are calculated in (2):

$$dist=dist(r_i^0,r_j^0)+dist(r_i^{-1},r_j^{-1})\ast w{t}^{-1}+dist(r_i^{+1},r_j^{+1})\ast w{t}^{+1}$$ 2

where, wt^− 1 = f(Δt^− 1) and wt^+ 1 = f(Δt^+ 1).

With the interpatient similarities computed, the known lab value of the patient with the minimum dist serves as a good estimate for the missing value of interest. However, to reduce the effect of uncertainties in the data, we use a weighted average of the known values from all the patients as an estimate for the missing analyte value. To give more credit to patients’ lab records with higher similarities, we use a weighted average function ($\sum w{t}_d\cdot known\text{\_}values/\sum w{t}_d$), in which weight (wt_d) is computed using a second generalized bell-shaped function operating on the values computed for dist in (2). The parameter c of the function would be the minimum distance, meaning that the row with the maximum similarity has the highest weight, and parameters a and b are experimentally estimated. The range given in (3) is considered as acceptance range for estimated values:

$$\left[min\right(a_{k,i}^{-2\to +2})-0.25\cdot IQR,max(a_{k,i}^{-2\to +2})+0.25\cdot IQR]$$ 3

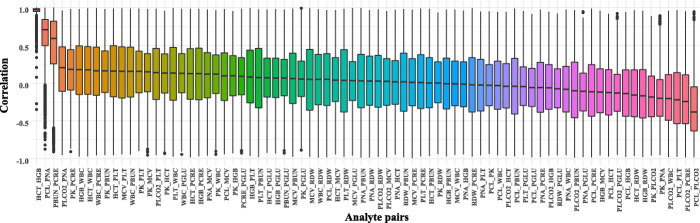
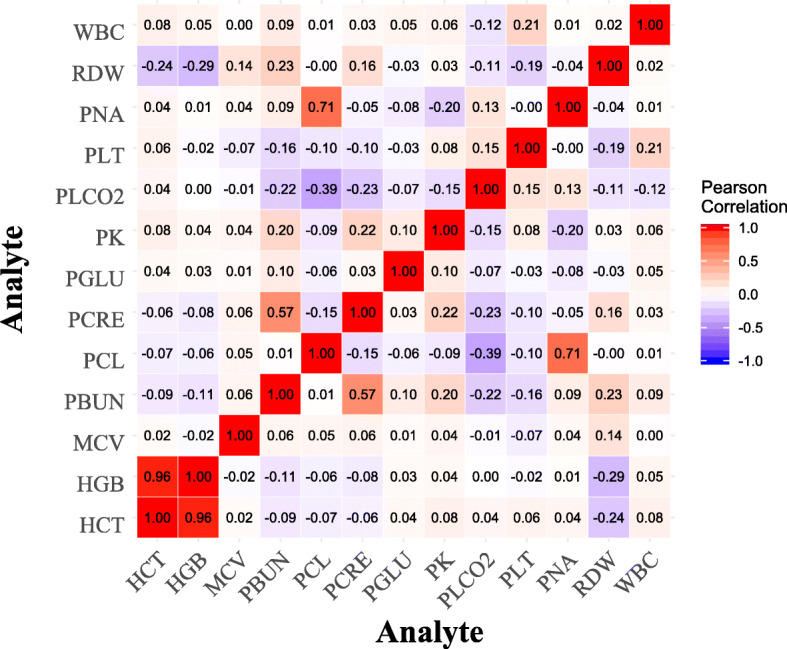
where $a_{k,i}^{-2\to +2}$ represents the list of values of desired analyte k of p_i from two rows before to two rows after the row with the missing value, and IQR computes the interquartile range of the same list. If the weighted average obtained falls outside of this range, it is considered that there are not enough data or similar patients in the data set, based on the assumption that the base values for imputation should be somewhat near the values of the adjacent records to the missing analyte. In that scenario, we resolve to univariate linear interpolation using the zoo library developed for R software [20] to estimate the missing values. This is because the correlation analysis of observations of inter- and intrapatient features showed that the pairwise correlations, except for HCT-HGB and PCL-PNA pairs, are relatively weak as seen in Figs. 2 and 3. The pseudocode of the method is shown in Algorithm 1.

Fig. 2.

The population level correlations among pairs of analytes (PCL, chloride; PK, potassium; PLCO2, bicarb; PNA, sodium; HCT, hematocrit; HGB, hemoglobin; PLT, platelets; WBC, WBC count; PBUN, BUN; PCRE, creatinine; PGLU, glucose)

Fig. 3.

The patient level correlations among pairs of analytes (PCL, chloride; PK, potassium; PLCO2, bicarb; PNA, sodium; HCT, hematocrit; HGB, hemoglobin; PLT, platelets; WBC, WBC count; PBUN, BUN; PCRE, creatinine; PGLU, glucose)

The method is developed in R and the corresponding codes are publicly available at https://github.com/alijazayeri/similarity_based_imputation.

Evaluation

To evaluate the performance of the proposed methods, different metrics are used in the literature. For example, in [6], three interval- and point-based approaches are adopted to compare multiple imputation methods. These metrics are either used to compare the accuracy of algorithms based on the differences between the estimated values and the actual values or based on the impacts of the values estimated on the performance of algorithms adopted to predict some response variables as a function of variables with missing values. Here, we use the normalized root-mean-square deviation (nRMSD) metric as follows:

$$nRMSD\left(a\right)=\sqrt{\frac{\mathrm{\Sigma }{I}_{p,a,i}{\left(\frac{x_{p,a,i}-Y_{p,a,i}}{max\left(Y_{p,a}\right)-min\left(Y_{p,a}\right)}\right)}^2}{{\mathrm{\Sigma }}_{p,i}{I}_{p,a,i}}}$$ 4

Where I is a vector of 0’s and 1’s, and I_p,a,i is 1 if patient p has a missing value at time index i for analyte a and 0 otherwise. And, considering Y_p,a and X_p,a as vectors representing actual and estimated values for analyte a of patient p, then Y_p,a,i and x_p,a,i would be numeric actual and estimated values of analyte a at time index i.

We assume that the imputation is performed without relying on any response variables; therefore, the performance should be evaluated based on the deviation of estimated values from actual values. The root-mean-square deviation is a common metric for evaluation of the performance of different methods following the same approach. We use the normalized version of the root-mean-square deviation because it would be possible to compare the performance of the proposed method for different analyates [12].

Results

We compared the performance of our algorithm with four baseline algorithms applied on the the same data set. These baseline algorithms are mean, multiple imputation with chained equations (MICE) [2, 3], Gaussian processes (GP), and 3-dimensional MICE (3D-MICE) [12]. The mean imputation is one of the most common approaches adopted in the literature. In this method, the missing values are imputed with mean of the known values for the same variable. The MICE algorithm creates different models (e.g., linear regression models) for imputing the missing values of one variable based on the known and imputed values of other variables in the data set. This process is iteratively repeated with updated estimations of missing values. A Gaussian process is defined as a collection of random variables where any subset of this collection has a joint Gaussian distribution with known mean and co-variance functions [17]. In this method, Gaussian processes are trained for each patient and using co-variance relations among variables, the missing values for variables are estimated. The 3D-MICE is a combination of MICE and GP. In 3D-MICE, the data is flattened and MICE is employed for cross-sectional imputation. Then, the GP is used for longitudinal estimation of missing values. Considering the variance of estimated values, a weighted average of estimations is calculated [12].

Table 1 shows the results obtained for the evaluation metric computed based on the imputed values estimated by the proposed method for 2000 random patients (≈ 25% of the population) using other patients’ data in the data set. The data set was composed of 199,695 rows related to 8267 patients. There were 8267 missing values for each analyte in total and each patient had one missing value for each analyte on average. The data for the first four methods in this table are from [12]. As can be seen in this table, the proposed method in this paper outperformed all other methods for all the variables except the MCV, for which the proposed method has similar performance as others. Overall, estimated values by our method are about eight times more accurate than the mean imputation, and it has been able to outperform MICE, GP, and 3D-MICE respectively with 27%, 33%, and 22% more accuracy. In the proposed method, except for generalized bell-shaped functions for which we experimentally find the parameters, it estimates the missing value in a data-driven fashion without relying on any specific mathematical formulation among variables and the variable with missing data. Finally, among these four methods, the 3D-MICE has the closest performance. It can be attributed to the utilization of this method from the advantages of both MICE and GP methods.

Table 1.

The metric values for different methods and analytes (lowest nRMSD value for each analyte is shown in bold)

Analyte	Mean	MICE	GP	3D-MICE	Similarity-based
Chloride	0.785	0.326	0.374	0.325	0.284
Potassium	0.601	0.386	0.391	0.378	0.230
Bicarb	0.798	0.375	0.377	0.364	0.249
Sodium	0.734	0.332	0.379	0.333	0.223
Hematocrit	1.493	0.261	0.380	0.272	0.245
Hemoglobin	1.542	0.262	0.376	0.272	0.261
MCV	3.402	0.379	0.389	0.369	0.389
Platelets	2.968	0.385	0.363	0.351	0.281
WBC count	4.186	0.384	0.369	0.358	0.343
RDW	5.047	0.395	0.353	0.348	0.257
BUN	2.361	0.367	0.324	0.313	0.272
Creatinine	3.451	0.362	0.360	0.340	0.319
Glucose	1.030	0.402	0.405	0.394	0.304
Overall	2.612	0.358	0.373	0.342	0.279

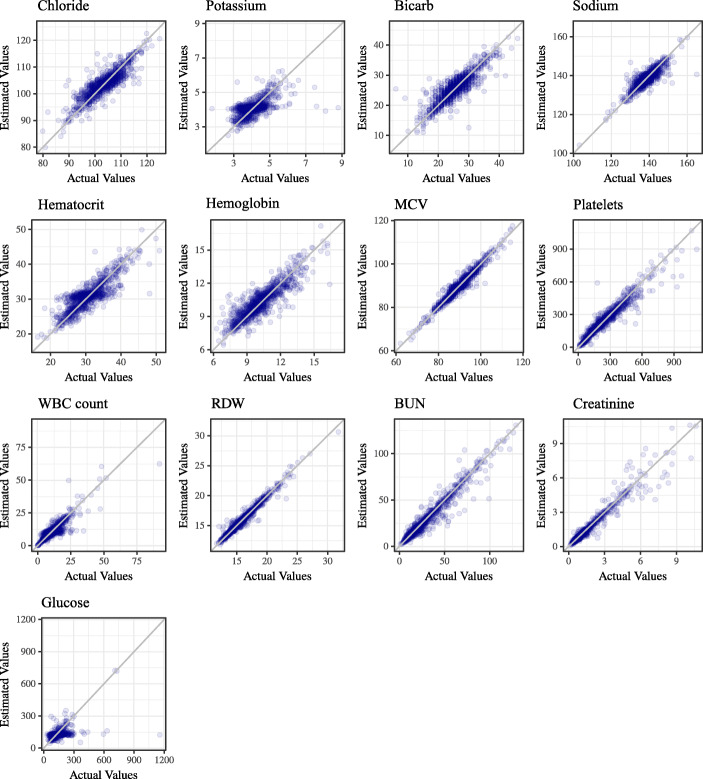
Figure 4 shows the estimated values for missing data points in comparison with actual values. The ideal case is to have all the points over the diagonal in each sub-plot, meaning that the estimated and actual values are equal.

Fig. 4.

The visualization of results for 13 analytes. The ideal estimation is to have all the points on the diagonal line

Conclusion

In this paper, we proposed a novel similarity-based missing data imputation method. The comparison of the performance of the proposed method with some of the state-of-the-art methods developed for the imputation of missing values in time series data shows that it produces more accurate results. This method is completely data-driven rather than model-driven, in the sense that it searches in the whole data set to rank patients (and their corresponding measurements) based on their similarities to the measurements of the patient with missing data, rather than estimates the missing value using a pre-developed model. In other words, the proposed method not only takes advantage of the cross-sectional and longitudinal information of the ego patient as proposed by 3D-MICE, but also factors in information from similar patients by way of calculating interpatient similarity. Then, using similarities, a weighted average is computed based on the known values of other patients to estimate the value of the missing data point. The performance of the method can be attributed to the adopted search strategy for the selection of similar patients. If similar enough patients can be found in the data set based on their current status and their health trajectories for multiple analytes, then the method assumes that the value missing in the patient of interest should be similar to the known values of similar patients as well. A similar assumption has been made in a previous study [10] and it is shown that a similarity-based method can outperform “one-size-fits-all” models for ICU mortality prediction. Considering the dependency of the proposed method to the prior observations of the same patient or other patients, this method shows its best performance when larger data sets are available. As the proposed method is data-driven and searches the whole data set for finding similar patients, this method can work very well in situations where real-time imputation of missing data is needed. On the other hand, the time-consuming step in our method is the calculation of pairwise similarities and prioritization of patients and their observations based on their similarity to the patient with the missing value. Similar to the similarity-based prediction approach proposed in [10], the performance of the proposed method in this paper is obtained at the expense of computational resources required to find similar patients. Therefore, developing more appropriate data structures or indexing of the data set for fast retrieval of similar patients can improve the efficiency of the method. Furthermore, because the proposed method evaluates analytes and each of the missing values independently, this method offers a remarkable potential for parallelization which can be considered a future direction for the current study. Here, we estimated the parameters of the functions experimentally. Using a more systematic approach for parameter optimization of bell-shaped functions might improve the results. In addition, for estimation of missing values when there are not enough similar patients in the data set, we applied linear imputation. Using other techniques might improve performance. Another avenue of further research is considering more adjacent rows (a wider time span) to the row with the missing value. This increases the chance of finding more similar patients with respect to trajectories of their lab results and vital signs, and consequently improves the accuracy of the proposed method.

Funding Information

This work was supported in part by the National Science Foundation under the Grant NSF-1741306, IIS-1650531, and DIBBs-1443019.

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.