Abstract
Clinical time series imputation is recognized as an essential task in clinical data analytics. Most models rely either on strong assumptions regarding the underlying data-generation process or on preservation of only local properties without effective consideration of global dependencies. To advance the state of the art in clinical time series imputation, we participated in the 2019 ICHI Data Analytics Challenge on Missing Data Imputation (DACMI). In this paper, we present our proposed model: Context-Aware Time Series Imputation (CATSI), a novel framework based on a bidirectional LSTM in which patients’ health states are explicitly captured by learning a “global context vector” from the entire clinical time series. The imputations are then produced with reference to the global context vector. We also incorporate a cross-feature imputation component to explore the complex feature correlations. Empirical evaluations demonstrate that CATSI obtains a normalized root mean square deviation (nRMSD) of 0.1998, which is 10.6% better than that of state-of-the-art models. Further experiments on consecutive missing datasets also illustrate the effectiveness of incorporating the global context in the generation of accurate imputations.
Keywords: Missing data imputation, Clinical time series, Electronic health records
Introduction
The rapid development and global adoption of electronic health records (EHR) over the past decade has given researchers valuable opportunities to perform secondary analysis of the EHR data accumulated over the years. In addition to the structured data, such as diagnosis codes and medication prescriptions, the EHR data also contain clinical time series that are crucial for characterization of patients’ health conditions. In particular, bedside monitors and irregularly requested laboratory tests are often used to measure patients’ health status during their hospital stays. Therefore, modeling the clinical time series has become a critical component of healthcare data analytics, and considerable effort has been made to use clinical time series for various tasks like mortality prediction. However, the clinical time series are generally of low quality, primarily due to the complexity of clinical practice, which hinders the application of data-driven approaches [10, 14]. One major issue is missing data. Thus, it is often necessary to fill in missing values in an incomplete clinical time series, which is referred to as time series imputation, before machine learning algorithms can be applied.
However, clinical time series imputation is a nontrivial task for a variety of reasons. First, clinical time series are often irregularly recorded in practice. Taking laboratory tests as an example, some tests, such as that to determine a blood glucose level, are usually repeated at regular intervals, whereas others are only requested when necessary. Second, the missingness of the clinical time series cannot always be regarded as completely at random because laboratory tests could be unrequested when the caregivers do not find them necessary. In other words, the pattern of the missing clinical time series could depend to some extent on the patients’ health states. Third, data are often missing consecutively rather than individually at random. For instance, medical monitors can be disconnected for a time while the patient is being transferred between wards. These circumstances impose additional difficulties and should be considered in attempts to tackle the clinical time series imputation problem.
In view of these challenges, the IEEE ICHI Data Analytics Challenge on Missing data Imputation (DACMI)1 was held in conjunction with the 7th IEEE International Conference on Health Care Informatics (ICHI-19). A shared task was defined as imputing clinical time series with a dataset developed to benchmark the accuracy of submissions. This paper describes our submission to the data analytics challenge.
Numerous methods based on statistics and machine learning have been exploited for time series imputation, including the autoregressive-moving-average model (ARMA), matrix factorization (MF), and recurrent neural networks (RNNs). However, most methods make strong assumptions regarding the data generation process that underlies the imputation. For example, Gaussian process (GP) models [7] adopt the locality assumption, and MF models [17] assume temporal regularity and low rankness. The former means that data points closer in time tend to be similar, and the latter means that data are generated at fixed time intervals and are governed by low-rank factors. Suboptimal performance may result when these assumptions are not met. Recent efforts have also sought to develop time series imputation models without such assumptions, such as the RNN, which summarizes past observations using hidden state vectors and predicts the missing entries based on the learned hidden states [2, 3, 15]. Despite the great success obtained, it has also been found that RNNs tend to capture local properties rather than the global dynamics of the input data [5], which could have great importance for imputing the clinical time series, as mentioned above. For example, a patient with kidney disease may exhibit different temporal patterns of blood urea nitrogen (BUN) tests or blood pressure measurements from most patients.
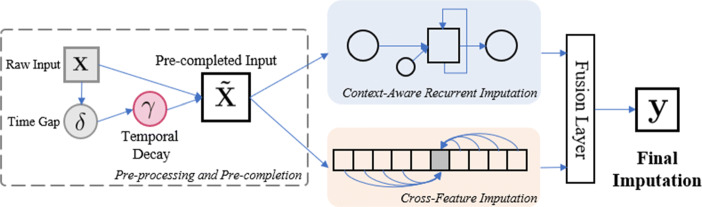
These observations lead us to conjecture that the accuracy could be improved significantly if the patient’s overall health state could be captured from the observed time series so that the imputation could be carried out with reference to the captured health state. To this end, we propose the Context-Aware Time Series Imputation (CATSI) framework, which is depicted in Fig. 1. CATSI consists of two major components: context-aware recurrent imputation and cross-feature imputation. The former is designed based on a bidirectional RNN to model the longitudinal dynamics over time, and the latter uses the cross-feature relationships of the observed variables. Finally, we use a fusion layer to produce the final imputations based on the recurrent and cross-feature imputations.
Fig. 1.
The framework of Context-Aware Time Series Imputation (CATSI) model, consisting of two major components: the context-aware recurrent componenfvt and the cross-feature component. The final imputation is produced by fusing the recurrent imputations and the cross-feature imputations using a fusion layer
Related Works
Many studies on time series imputation have been published, many of which use information on the longitudinal observations of the same variable and the correlations among various variables observed at the same time, and different assumptions are imposed.
Autoregressive models [11] such as ARMA and its variant ARIMA are simple but effective methods to model time series. They usually assume the stationarity of the time series, which means that parameters such as the mean and variance of the variable of interest remain unchanged over time. Although non-stationarity can be partially eliminated by differencing, complex temporal dynamics often cannot be accurately modeled, which can easily lead to inevitable errors. In contrast, GP models [12, 13] allow different assumptions, such as smoothness, stationarity, and periodicity, to be encoded by prior distributions. Under the Bayesian framework, GP is particularly beneficial in handling the uncertainties in the observed data. However, it can be very sensitive to the prior, which is believed to govern the parameters of the process that generates the underlying data. In the context of clinical time series, it could be quite challenging to properly encode patients’ rapidly evolving health states as a prior distribution for the clinical time series. Moreover, GP often uses an implicit constraint of locality, in the sense that data points closer in time generally are closer in their values [10]. MF [16] and its higher-order extension, tensor factorization (TF) [4], can also be used to analyze and impute time series. They assume that the observed data are generated by the linear combination of some low-dimensional latent factors, that is, low rankness, which is, however, often inadequate for clinical time series with complex temporal dynamics. Multiple imputation by chained equations (MICE) [1] is another popular method used for time series imputation. Unlike single imputation, it accounts for the uncertainty by generating multiple imputations instead of only one. However, it assumes that data are missing completely at random, which could result in biased imputations if applied to clinical time series.
RNNs have recently emerged as a promising tool for modeling sequential data and have been introduced to time series imputation. They summarize past observations using a latent vector called a hidden state and generate a prediction for the next time step given the current observation and the learned hidden state. In [3], the missing patterns were found to be related to the labels of the data; thus, a specific design of RNN model is proposed to exploit the missing patterns in clinical time series to handle the missing information. Cao et al. [2] developed a model based on bidirectional long short-term memory (LSTM) to consider not only past observations but also the future trend of the time series.
In general, RNNs do not impose explicit assumptions on the data generation process except for the temporal dependency; that is, the future observations are conditioned on the past ones. Meanwhile, the temporal dynamics can be captured purely by the hidden states learned by RNNs. In principle, RNNs can capture arbitrarily long-term dependencies given sufficient capacity, yet they are often hindered by the difficulties encountered during optimization for model learning. In practice, therefore, RNNs are observed to capture the local properties more than the global dynamics of the input sequential data [5]. To the best of our knowledge, no study has yet explicitly considered the global dynamics when applying RNNs to clinical time series imputation.
Dataset
The dataset used in this data analytics challenge is derived from the publicly available dataset generated in real-world intensive care units (ICUs), MIMIC-III (Medical Information Mart for Intensive Care III) [8], by the organizers of the challenge. Thirteen commonly measured laboratory test analytes are extracted, including PCL (CI), PK, PLCO2 (Bicarb), PNA (sodium), HCT, HGB, MCV, PLT, WBC, RDW, BUN, PCRE (creatinine), and PGLU (glucose). Beginning with the raw data in MIMIC-III, the time points with half or more of the variables missing are excluded, and only the ICU stays for which all variables have at least nine observations are included. The ground truth of the original missing values in the data is unknown. Thus, additional missing data are manually injected by randomly masking one observation per variable per patient so that the performance can be measured for the masked entries. Finally, the time series recorded in the ICU stays for 16,534 patients are extracted; half (8267 patients) are provided as the training dataset, and the remaining half are held out as the test set. The basic characteristics of the 13 analytes are summarized in Table 1.
Table 1.
Basic characteristics of the 13 analytes extracted, where RSD is the relative standard deviation of the empirical mean
| Analyte | Mean | RSD (%) | Interquartile range | Missing rate (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Test | Training | Test | Native | After masking | ||
| PCL | 103.62 | 103.75 | 6.14 | 6.19 | 100–108 | 1.18 | 5.32 |
| PK | 4.1 | 4.09 | 14.88 | 14.91 | 3.7–4.4 | 1.34 | 5.48 |
| PLCO2 | 25.41 | 25.42 | 20.11 | 20.22 | 22–28 | 1.39 | 5.53 |
| PNA | 138.57 | 138.67 | 3.72 | 3.71 | 135–142 | 1.26 | 5.4 |
| HCT | 30.03 | 30.01 | 15.85 | 15.63 | 26.8–32.7 | 12.51 | 16.65 |
| HGB | 10.05 | 10.04 | 16.32 | 16.24 | 8.9–11 | 15.09 | 19.23 |
| MCV | 90.28 | 90.47 | 7.24 | 7.09 | 86–94 | 15.23 | 19.37 |
| PLT | 247.93 | 251.22 | 67.06 | 66.73 | 129–330 | 14.55 | 18.59 |
| WBC | 11.41 | 11.63 | 67.05 | 91.57 | 7–14.1 | 14.8 | 18.94 |
| RDW | 16.23 | 16.13 | 15.16 | 14.82 | 14.5–17.4 | 15.34 | 19.48 |
| PBUN | 33.52 | 32.87 | 76.37 | 76.51 | 16–44 | 0.74 | 4.88 |
| PCRE | 1.64 | 1.59 | 101.83 | 100 | 0.7–1.9 | 0.7 | 4.84 |
| PGLU | 132.38 | 131.81 | 48.25 | 48.3 | 100–148 | 2.7 | 6.84 |
| Mean | – | – | – | – | – | 7.45 | 11.58 |
The empirical mean and the RSD of the training set and the test set are listed separately, and the interquartile range and the missing rates are for the training set
Methodology
Notations
We use a matrix to denote the multivariate time series for a specific patient, where T is the length of the time series, D is the number of variables, and the t th row xt is the observation at the t th time step. The time stamp corresponding to the t th time step is denoted by st. Like the existing work [2, 3], we use a masking matrix M of the same size as the X to indicate missingness in the time series:
| 1 |
In addition, to account for the irregularity of the time series caused by the missing values, we introduce an observation gap matrix Δ, the same size as X, to represent the gap between the current time stamp and the time stamp of the last observation that is not missing [3], i.e.,
| 2 |
The other notations and symbols used in this paper are summarized in Table 2.
Table 2.
Symbols and notations used throughout the paper
| Symbol | Definition |
|---|---|
| ⊙ | Element-wise matrix multiplication |
| D | The number of variables in the time series |
| The input matrix of the multivariate time series with missing values | |
| The masking matrix indicating missingness in the input matrix | |
| The observation gap at time step t | |
| The temporal decay factor at time step t | |
| The precompleted input to the model | |
| W, b | Learnable weighing matrix and the bias vector of linear transformations |
| The hidden states of the bidirectional LSTM | |
| The cell states of the bidirectional LSTM | |
| r | The context vector |
| The coefficient for imputation fusion | |
| The recurrent, cross-feature, and final imputation |
Pre-Processing: Normalization and Completion by Temporal Decay
We first normalize the raw input data for each variable of each patient using the min–max normalization by subtracting the minimum and dividing by the range, that is, the difference between the maximum and minimum values, given as:
| 3 |
To allow the raw input data with missing values to be properly fed into the model, we transform the raw input to a “pre-completed” version by filling in the missing entries using a trainable temporal decay module originally proposed by [3]. This method was inspired by the observation that if a variable has not been observed for a long time, it tends to be closer to a “default” value (in our case, the empirical mean); otherwise, it would be likely to be closer to its historical observations. Formally, a temporal decay factor is computed based on the observation gap δt at time st, and the pre-completion can be computed by taking the convex combination of the last observation and the mean with the decay factor as the coefficient, as follows:
| 4 |
| 5 |
where is the computed pre-completion, is the last observation, and is the empirical mean for the d th variable at time st. We then complete the raw input by replacing the missing values using (5) while keeping the observed ones. Formally,
| 6 |
Note that the temporal decay module is trainable, which means that the parameters and are updated during training, and thus the pre-completions are recomputed in each iteration.
Context-Aware Recurrent Imputation
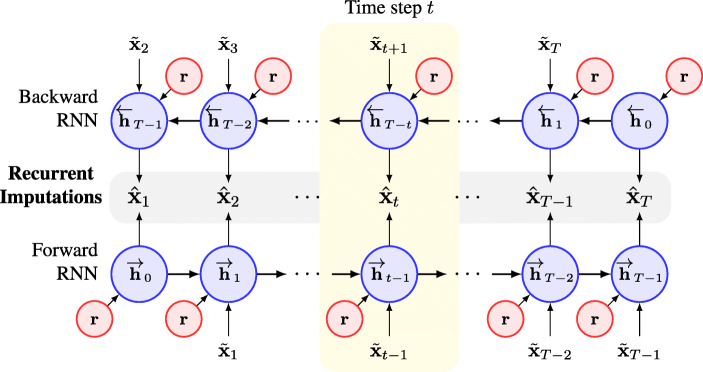
As shown in Fig. 1, our model consists of two major components. We first introduce the recurrent imputation component, which is based on a bidirectional RNN model. We depict the architecture of the recurrent component in greater detail in Fig. 2. The desired recurrent imputation lies in the middle of Fig. 2, below and above which are the forward and backward RNNs, respectively. The time series are fed to the forward RNN in the original temporal order and to the backward RNN in reverse order. By adopting the bidirectional RNN, we can use the information from both the past and future observations in the time series. At the t th time step, the hidden states from the forward and backward RNNs summarize the observations before and after st, and the recurrent imputation can then be produced by combining the two hidden states and applying a linear transformation:
| 7 |
where h is the hidden state, and [⋅;⋅] indicates the concatenation of the two hidden states. The parameters of the forward RNNs are denoted with a right arrow atop the letter (e.g., ), and those of the backward RNNs are denoted with a left arrow (e.g., ).
Fig. 2.
Architecture of the context-aware recurrent component based on a bidirectional LSTM. The vector r denotes the global context vector learned from the entire time series input. At each time step, the global context vector, together with the observations before and after, is used to learn the hidden states of the forward and backward RNNs. The recurrent imputation is then obtained by combining the two hidden states learned
In this paper, we use the LSTM model [6] to extract the hidden states h from the input data. As described above, consideration of the input alone is insufficient because it neglects the patients’ health states, which could be very critical for clinical time series imputation. Therefore, we propose incorporation of patients’ health states when learning the hidden states. Briefly, we introduce a “context vector” for each patient that is learned to capture the global temporal dynamics to represent the corresponding patient’s health state, where C is the dimension of the context vector, which is a pre-specified hyperparameter. At each time step, we then produce the hidden states with reference to the global dynamics of the input time series by feeding the context vector to the LSTM model together with the time series input. Formally, we have:
| 8 |
| 9 |
| 10 |
| 11 |
where h0 and c0 denote the initial hidden states and cell states in the LSTM model, respectively. LSTM(⋅) denotes the update procedure of a standard LSTM model [6]. The initial hidden state of a standard LSTM model is generally set to be a zero vector, whereas that of our method is computed from the global context vector, which is particularly beneficial for imputing the missing values at the first several time steps.
To learn the context vector r from the time series for each patient, we here present two approaches:
Summarizing the Basic Statistics
The easiest way to characterize a patient’s overall health state is to compute the basic descriptive statistics of the time series, i.e., the empirical mean , the standard deviation σd, the missing rate pd, and the length of the time series for the p th patient Tp. A multilayer perceptron (MLP) can then be used to approximate the function f to summarize the patient’s overall baseline characteristics:
| 12 |
This method is simple but effective because the empirical mean and the standard deviation can often provide valuable information related to a patient’s state. For example, patients with uncontrolled hypertension usually have higher blood pressure. However, this method does not account for the dynamics of the time series, and it can lead to situations in which worsening patients cannot be distinguished from recovering patients, such as those whose blood pressure is lowering over time after effectively being controlled.
RNN-Based Encoder
To further capture the complex temporal dynamics of the time series, we can use another RNN model as an encoder. Briefly, we input the entire time series into the encoder RNN and obtain the hidden states at the last time step as the context vector r, in that it summarizes the entire time series. We use a standard gated recurrent unit (GRU) as the encoder RNN because it has a simpler structure than LSTM.
Although the two approaches can be applied separately, we combine them by concatenating the output of the two methods as the context vector, with the expectation that the first part can represent the overall characteristics and the second part can capture the patient’s characterizing dynamics.
The architecture of the recurrent component in CATSI differs from that developed in BRITS [2] in a number of ways. The most significant difference is the use of the context vector c, which explicitly captures the patients’ global temporal dynamics, thus alleviating the issue in which RNN models tend to focus more on local properties than on the global dynamics [5].
Cross-Feature Imputation
Another major component is the cross-feature component, which allows the effective use of feature correlation. Essentially, we can estimate the value of one variable based on other variables observed at the same time by:
| 13 |
| 14 |
where is the cross-feature imputation of the d th feature at time step t. Equation (13) first computes a linear transformation of the raw input with the d th column of being forced to be zeros. This ensures that is not involved in predicting itself. We use another potentially nonlinear function g(⋅) that is approximated by an MLP to generate the cross-feature imputations, which explores the complex feature correlations.
Imputation Fusion
After obtaining the recurrent and the cross-feature imputations, we use a fusion layer similar to that of [2] to produce the final imputation yt by taking their convex combination:
| 15 |
where the coefficient is computed by considering the missing patterns, i.e., the missing masks mt, and the observation time gaps γt by:
| 16 |
Loss Function and End-to-End Training
We use the mean squared deviation (MSD) of the observed entries as the loss function as given by:
| 17 |
where X is the input data, and Y is the produced imputation. M is the binary missing mask matrix, with 1 indicating the observed entries; thus, the square of the Frobenius norm of M is essentially the number of observed data points in the input data X.
As described in BRITS [2], optimizing the loss function of the final imputation alone leads to slow convergence. We accumulate the loss functions for the recurrent imputations and the cross-feature imputations Z as in [2] to derive the overall loss function to accelerate the convergence:
| 18 |
We train the CATSI model end-to-end with Adam [9], a widely adopted optimization method based on stochastic gradient descent. We set the learning rate to 0.001 throughout all experiments.
Experiments and Results
To evaluate the proposed model, we first perform imputation using the original dataset provided by the DACMI organizers, as introduced in Section 3. To demonstrate the effectiveness of the context-aware design, we further conduct experiments with consecutive missingness by randomly masking two to five consecutive entries in each variable to generate new datasets.
In this paper, we measure the performance with the normalized root mean square deviation (n RMSD) defined as:
| 19 |
where p, d, and t indicate the indices of the patient, the analyte, and the time step, respectively, and y and x indicate the ground truth and the imputations, respectively.
Individual Missingness
We first train CATSI with the official training set and perform imputation on the test set provided in the challenge, in which only one entry per analyte per patient was manually masked as missing to evaluate the performance. We use 80% of the training data to train the model and the remaining 20% to determine the hyperparameters. After training the model, we freeze the model to generate the imputation for the test set. This is the official task in the challenge, and here we report the results we submitted for official evaluation. We compare with three baseline models, including:
BRITS [2]: A state-of-the-art time series imputation model based on bidirectional RNN.
3D-MICE [10]: A state-of-the-art model developed to impute clinical time series by combining the MICE method and the longitudinal GP model.
MICE [1]: Multiple Imputation by Chained Equations, a widely adopted and easy-to-use method for imputing time series mainly using the feature correlations of the data.
According to the results in Table 3, CATSI consistently outperforms all three baselines for all variables by a large margin. It obtained an average nRMSD of 0.1998 over all analytes, which is 10.6% lower than that obtained with 3D-MICE and BRITS. By using only the cross-variable correlations without considering any longitudinal information, MICE can only achieve a mean nRMSD of 0.266, 24.89% higher than CATSI. Table 3 further shows that MICE has similar performance on some analytes as BRITS, such as HGB, which means that the imputation for HGB is more sensitive to other variables than to the historical observations. However, CATSI can still obtain better imputation on these analytes, which indicates that the cross-feature imputation component can capture the complex correlations across variables. For other analytes, BRITS achieved better imputation performance than MICE, which shows that longitudinal information is critical for imputing the clinical time series. The further improvement obtained by CATSI also demonstrates its effectiveness in representing patients’ health states by the global context vectors and incorporating them into the imputation process.
Table 3.
Experimental results for individual missingness, the original shared task in the ICHI19 data analytics challenge
| CATSI | 3D-MICE | BRITS | MICE | |
|---|---|---|---|---|
| PCL | 0.1738 | 0.2 | 0.193 | 0.225 |
| PK | 0.2431 | 0.2632 | 0.266 | 0.29 |
| PLCO2 | 0.2026 | 0.2314 | 0.224 | 0.268 |
| PNA | 0.1958 | 0.2145 | 0.215 | 0.233 |
| HCT | 0.1436 | 0.1505 | 0.153 | 0.148 |
| HGB | 0.1349 | 0.1488 | 0.146 | 0.146 |
| MCV | 0.2534 | 0.2713 | 0.279 | 0.309 |
| PLT | 0.1862 | 0.2294 | 0.215 | 0.318 |
| WBC | 0.227 | 0.256 | 0.26 | 0.309 |
| RDW | 0.213 | 0.2458 | 0.241 | 0.332 |
| PBUN | 0.1574 | 0.1846 | 0.194 | 0.29 |
| PCRE | 0.206 | 0.2338 | 0.244 | 0.29 |
| PGLU | 0.2602 | 0.2769 | 0.275 | 0.306 |
| Mean | 0.1998 | 0.2235 | 0.2235 | 0.266 |
| Relative improvement | – | 10.6% | 10.6% | 24.89% |
The performance scores of the 3D-MICE model were provided by the challenge organizers. The italic number indicates the best performance, measured using normalized root mean square deviation (n RMSD). CATSI obtained 10.6% relative improvement over 3D-MICE and BRITS
Consecutive Missingness
The individual missingness considered in the challenge can largely be regarded as missing-at-random, which is generally easier to handle. To demonstrate the effectiveness of introducing the global context vector to represent the patients’ health states, we further consider the consecutive missingness. In particular, based on the ground truth data (without manual masking), we generate new datasets by randomly masking m consecutive values for each variable per patient. The newly generated datasets mimic the more realistic and challenging situations in which the global temporal dynamics of the clinical time series must be considered for accurate imputations. We require that the masked entries do not cover any native missing values, and vary m from 2 to 5. We report the missing rates before and after masking in Table 4, where the missing rates increase dramatically from an average of 11.58% for individual missingness, as shown in Table 1, to 28.15% for five consecutive missing values.
Table 4.
Missing rates of the newly generated consecutive missing datasets, where m indicates the number of consecutive missing values
| Native (%) | Consecutive missing (%) | ||||
|---|---|---|---|---|---|
| m= 2 | m= 3 | m= 4 | m= 5 | ||
| PCL | 1.18 | 9.46 | 13.6 | 17.74 | 21.88 |
| PK | 1.34 | 9.62 | 13.76 | 17.9 | 22.04 |
| PLCO2 | 1.39 | 9.67 | 13.81 | 17.95 | 22.09 |
| PNA | 1.26 | 9.54 | 13.68 | 17.82 | 21.96 |
| HCT | 12.51 | 20.79 | 24.93 | 29.07 | 33.21 |
| HGB | 15.09 | 23.37 | 27.51 | 31.65 | 35.79 |
| MCV | 15.23 | 23.51 | 27.65 | 31.79 | 35.93 |
| PLT | 14.55 | 22.83 | 26.97 | 31.11 | 35.25 |
| WBC | 14.8 | 23.08 | 27.22 | 31.36 | 35.5 |
| RDW | 15.34 | 23.62 | 27.76 | 31.9 | 36.04 |
| PBUN | 0.74 | 9.02 | 13.16 | 17.3 | 21.44 |
| PCRE | 0.7 | 8.98 | 13.12 | 17.26 | 21.4 |
| PGLU | 2.7 | 10.98 | 15.12 | 19.26 | 23.4 |
| Mean | 7.45% | 15.73% | 19.87% | 24.01% | 28.15% |
For this task, we compare the other bidirectional RNN model, BRITS. BRITS has a similar architecture to CATSI, except that CATSI incorporates a global context vector to represent the patient’s health state. Table 5 shows the imputation performance for various numbers of consecutive missing entries. CATSI outperforms BRITS for all numbers of consecutive missing entries by a large margin. In particular, CATSI performs 18.75% better than BRITS when two consecutive values are masked as missing, which is much higher than the performance gap of 10.6% obtained for the individual missing experiments, as reported in Table 3. The reason for the huge increase in the performance gap is that the use of local dynamics information is hindered by the consecutive missing entries. Consequently, accurate imputation must rely more on longer-range temporal dynamics. CATSI effectively captures the global dynamics of the input time series by the context vector, and the imputation is produced with reference to it. Without explicitly considering the global dynamics, it can be observed that BRITS relies more on local information, leading to suboptimal performance.
Table 5.
Imputation performance for consecutive missingness, measured using the normalized root mean square deviation (n RMSD)
| m= 2 | m= 3 | m= 4 | m= 5 | |||||
|---|---|---|---|---|---|---|---|---|
| CATSI | BRITS | CATSI | BRITS | CATSI | BRITS | CATSI | BRITS | |
| PCL | 0.1998 | 0.228 | 0.2304 | 0.243 | 0.251 | 0.26 | 0.2682 | 0.273 |
| PK | 0.2494 | 0.289 | 0.2622 | 0.293 | 0.2678 | 0.299 | 0.2774 | 0.3 |
| PLCO2 | 0.2264 | 0.268 | 0.2488 | 0.281 | 0.2682 | 0.292 | 0.2878 | 0.301 |
| PNA | 0.213 | 0.237 | 0.243 | 0.25 | 0.2588 | 0.262 | 0.2754 | 0.273 |
| HCT | 0.1462 | 0.165 | 0.176 | 0.2 | 0.1984 | 0.213 | 0.2202 | 0.232 |
| HGB | 0.1456 | 0.163 | 0.1788 | 0.198 | 0.1982 | 0.212 | 0.2202 | 0.238 |
| MCV | 0.2694 | 0.32 | 0.2838 | 0.325 | 0.2996 | 0.329 | 0.3098 | 0.334 |
| PLT | 0.2236 | 0.321 | 0.2578 | 0.331 | 0.2872 | 0.338 | 0.3098 | 0.344 |
| WBC | 0.25 | 0.313 | 0.2704 | 0.324 | 0.2922 | 0.327 | 0.3036 | 0.332 |
| RDW | 0.2404 | 0.328 | 0.2654 | 0.336 | 0.2952 | 0.342 | 0.3018 | 0.352 |
| PBUN | 0.2102 | 0.292 | 0.2484 | 0.302 | 0.2772 | 0.312 | 0.301 | 0.32 |
| PCRE | 0.2298 | 0.294 | 0.2506 | 0.296 | 0.2696 | 0.307 | 0.2876 | 0.31 |
| PGLU | 0.2654 | 0.315 | 0.272 | 0.314 | 0.2768 | 0.312 | 0.2834 | 0.316 |
| Mean | 0.221 | 0.272 | 0.245 | 0.284 | 0.265 | 0.293 | 0.28 | 0.302 |
| Relative improvement | – | 18.75% | – | 13.73% | – | 9.56% | – | 7.28% |
The italic numbers indicate the best performance for each value of m. CATSI consistently outperforms BRITS for all values of m
In contrast, we also observe that as the number of consecutive missing entries continues to increase, the performance gap between CATSI and BRITS decreases from 18.75 to 7.28%. This indicates that learning the context vector from the input time series may not be sufficient to fully account for the complex dynamics of patients’ health states. Future studies may incorporate other data modalities to further improve the imputation performance.
Ablation Study: Effect of the Recurrent and Cross-Feature Components
The proposed model, CATSI, contains two major components: the recurrent and the cross-feature components. In this section, we conduct an ablation study to further understand the contribution of the two components to the overall performance improvement.
In the objective function shown in (18), we accumulate the loss function for the recurrent imputation, the cross-feature imputation, and the final imputation. We first examine the effects of this accumulated objective function. We run two experiments, one with the accumulated loss function and the other with only the final imputation loss. The change in the loss function of the recurrent component during training is visualized in Fig. 3. Figure 3 shows that accumulating the three terms in (18) leads not only to faster convergence, but also to lower loss value. In contrast, when using the final imputation loss alone, the recurrent component converges much more slowly.
Fig. 3.
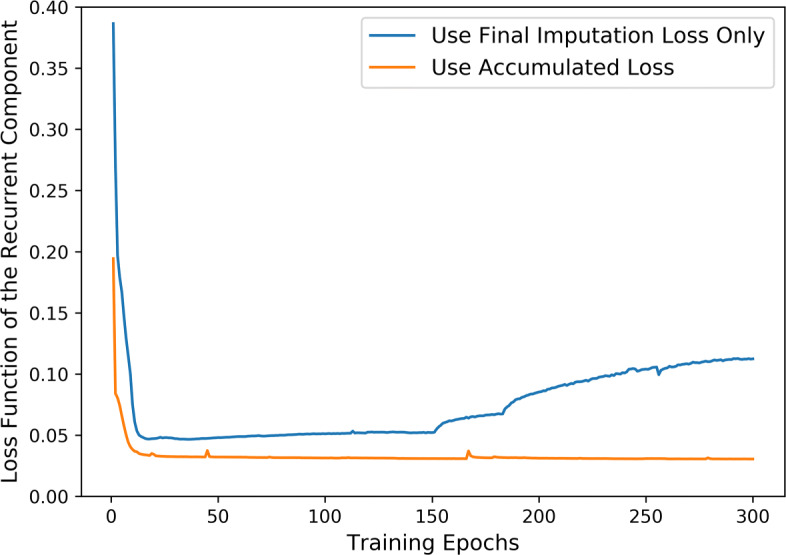
Loss function for the recurrent component during training
We then investigate the effects of the recurrent component and the cross-feature component on the final imputation performance. We turn on one of the two components and run experiments using the individual missing dataset as in Section 5.1. Note that with only one component being used, it is not necessary to fuse the imputation, so we remove the final imputation loss and directly minimize the loss function of the active component in this experiment. The results are reported in Table 6, where the values in bold indicate the best performance for the corresponding analyte, and those in italics indicate the second best. As we observed previously, the two components contribute differently to different analytes. For most analytes, such as PLT, RDW, and PCRE, the results of the recurrent component are significantly better than those of the cross-feature components and even better than those in the final imputation. However, for other variables such as HCT and HGB, the recurrent component performs much worse than the cross-feature component. However, the final imputation obtained by fusing the two components is closer than that obtained by the cross-feature component. In fact, for all analytes, the final imputation obtained by fusing the two components shows either the best or the second best performance, and CATSI obtains the overall best performance, measured by the mean n RMSD. This also suggests that future studies can make use of the differences in terms of the sensitivity to the recurrent information and the feature correlation information to generate better final imputations.
Table 6.
Experimental results of the imputation performance using CATSI and the two components separately
| PCL | PK | PLCO2 | PNA | HCT | HGB | MCV | |
| Recurrent component | 0.192 | 0.238 | 0.205 | 0.213 | 0.212 | 0.203 | 0.243 |
| Cross-feature component | 0.204 | 0.267 | 0.249 | 0.212 | 0.110 | 0.107 | 0.287 |
| Fusion of both components | 0.174 | 0.243 | 0.203 | 0.196 | 0.144 | 0.135 | 0.253 |
| PLT | WBC | RDW | PBUN | PCRE | PGLU | Mean | |
| Recurrent component | 0.179 | 0.221 | 0.213 | 0.152 | 0.201 | 0.250 | 0.209 |
| Cross-feature component | 0.295 | 0.291 | 0.317 | 0.271 | 0.269 | 0.282 | 0.243 |
| Fusion of both components | 0.187 | 0.227 | 0.213 | 0.157 | 0.206 | 0.260 | 0.200 |
Experiments are done with the individual missing dataset as in Section 5.1. The numbers in bold indicate the best performance for the corresponding analyte, and those in italics indicate the second best ones. The performance is measured using normalized root mean square deviation (n RMSD)
Conclusions
In this paper, we propose the Context-Aware Time Series Imputation (CATSI) framework for imputation of clinical time series; its advantage is that the patients’ health states are explicitly considered by introducing a global context vector learned from the input clinical time series data. CATSI consists of two major components: a context-aware recurrent imputation module based on bidirectional LSTM and a cross-feature imputation module to explore the complex feature correlations. An imputation fusion layer is used to produce the final imputation. The empirical evaluations on both the original shared task in the ICHI-19 data analytics challenge and the consecutive missingness configuration show that CATSI consistently outperforms all baselines. Moreover, the relative performance gap between CATSI and BRITS increases from 10.6% for individual missing values to 18.75% for two consecutive missing values, thus validating the effectiveness of introduction of the global context vector as a representation of patients’ health states. In future work, we will focus on integrating other data modalities, such as event sequences in EHR, to further capture the complex dynamics of patients’ health states and further improve the imputation performance.
Funding
This research is partially supported by General Research Fund RGC/HKBU12201219 and RGC/HKBU12202117 from the Research Grants Council of Hong Kong.
Compliance with Ethical Standards
Conflict of Interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Kejing Yin, Email: cskjyin@comp.hkbu.edu.hk.
Liaoliao Feng, Email: liaoliaof@163.com.
William K. Cheung, Email: william@comp.hkbu.edu.hk
References
- 1.Azur MJ, Stuart EA, Frangakis C, Leaf PJ. Multiple imputation by chained equations: what is it and how does it work? Int. J. Methods Psychiatr. Res. 2011;20(1):40–49. doi: 10.1002/mpr.329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cao W, Wang D, Li J, Zhou H, Li L, Li Y (2018) BRITS: Bidirectional recurrent imputation for time series. In: Advances in neural information processing systems, pp 6775–6785
- 3.Che Z, Purushotham S, Cho K, Sontag D, Liu Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018;8(1):6085. doi: 10.1038/s41598-018-24271-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cong F, Lin QH, Kuang LD, Gong XF, Astikainen P, Ristaniemi T. Tensor decomposition of EEG signals: a brief review. J. Neurosci. Methods. 2015;248:59–69. doi: 10.1016/j.jneumeth.2015.03.018. [DOI] [PubMed] [Google Scholar]
- 5.Dieng AB, Wang C, Gao J, Paisley JW (2017) TopicRNN: a recurrent neural network with long-range semantic dependency. In: 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings
- 6.Gers FA, Schmidhuber J, Cummins F (1999) Learning to forget: continual prediction with LSTM [DOI] [PubMed]
- 7.Hori T, Montcho D, Agbangla C, Ebana K, Futakuchi K, Iwata H. Multi-task Gaussian process for imputing missing data in multi-trait and multi-environment trials. Theor. Appl. Genet. 2016;129(11):2101–2115. doi: 10.1007/s00122-016-2760-9. [DOI] [PubMed] [Google Scholar]
- 8.Johnson AE, Pollard TJ, Shen L, Li-wei HL, Feng M, Ghassemi M, Moody B, Szolovits P, Celi LA, Mark RG. MIMIC-III, a freely accessible critical care database. Scientific Data. 2016;3:160035. doi: 10.1038/sdata.2016.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv:https://arxiv.org/abs/1412.6980
- 10.Luo Y, Szolovits P, Dighe AS, Baron JM. 3D-MICE: Integration of cross-sectional and longitudinal imputation for multi-analyte longitudinal clinical data. J. Am. Med. Inform. Assoc. 2017;25(6):645–653. doi: 10.1093/jamia/ocx133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Montgomery DC, Jennings CL, Kulahci M (2015) Introduction to time series analysis and forecasting. Wiley
- 12.Roberts S, Osborne M, Ebden M, Reece S, Gibson N, Aigrain S. Gaussian processes for time-series modelling. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2013;371(1984):20110550. doi: 10.1098/rsta.2011.0550. [DOI] [PubMed] [Google Scholar]
- 13.Tobar F, Bui TD, Turner RE (2015) Learning stationary time series using gaussian processes with nonparametric kernels. In: Advances in neural information processing systems, pp 3501–3509
- 14.Xiao C, Choi E, Sun J. Opportunities and challenges in developing deep learning models using electronic health records data: a systematic review. J. Am. Med. Inform. Assoc. 2018;25(10):1419–1428. doi: 10.1093/jamia/ocy068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yoon J, Zame WR, van der Schaar M (2018) Estimating missing data in temporal data streams using multi-directional recurrent neural networks. IEEE Transactions on Biomedical Engineering [DOI] [PubMed]
- 16.Yu HF, Rao N, Dhillon IS (2016) Temporal regularized matrix factorization for high-dimensional time series prediction. In: Advances in neural information processing systems, pp 847–855
- 17.Yu R, Cheng D, Liu Y (2015) Accelerated online low rank tensor learning for multivariate spatiotemporal streams. In: International Conference on Machine Learning, pp 238–247