A Multi-directional Approach for Missing Value Estimation in Multivariate Time Series Clinical Data

Abstract

Missing values are common in clinical datasets which bring obstacles for clinical data analysis. Correctly estimating the missing parts plays a critical role in utilizing these analysis approaches. However, only limited works focus on the missing value estimation of multivariate time series (MTS) clinical data, which is one of the most challenge data types in this area. We attempt to develop a methodology (MD-MTS) with high accuracy for the missing value estimation in MTS clinical data. In MD-MTS, temporal and cross-variable information are constructed as multi-directional features for an efficient gradient boosting decision tree (LightGBM). For each patient, temporal information represents the sequential relations among the values of one variable in different time-stamps, and cross-variable information refers to the correlations among the values of different variables in a fixed time-stamp. We evaluated the estimation method performance based on the gap between the true values and the estimated values on the randomly masked parts. MD-MTS outperformed three baseline methods (3D-MICE, Amelia II and BRITS) on the ICHI challenge 2019 datasets that containing 13 time series variables. The root-mean-square error of MD-MTS, 3D-MICE, Amelia II and BRITS on offline-test dataset are 0.1717, 0.2247, 0.1900, and 0.1862, respectively. On online-test dataset, the performance for the former three methods is 0.1720, 0.2235, and 0.1927, respectively. Furthermore, MD-MTS got the first in ICHI challenge 2019 among dozens of competition models. MD-MTS provides an accurate and robust approach for estimating the missing values in MTS clinical data, which can be easily used as a preprocessing step for the downstream clinical data analysis.

Introduction

With the development of health informatics in recent years, more and more clinical data have been accumulated, which paves the way for various clinical data analysis, such as disease prediction, medication recommendation, decision support, and so on. Data quality, as revealed in the principle “Garbage In, Garbage Out,” is the foundation of good analytics. Data with poor quality will significantly affect the performance of analysis methods. Missing value is one of the most common quality problems in clinical data. It usually stems from the irregular schedule of the data collection in clinical scenario [1] (e.g., depends on the patient conditions or administrative requirements) or the unexpected accidents. Missing value makes it hard to directly utilize many data mining and machine learning algorithms on the original dataset.

Although excluding the data with missing values is a simple way to handle the problem, it may introduce bias and reduce the data volume. The potential bias and small volume of the remaining data make it hard to get reliable, generalizable, and valuable findings. Therefore, how to estimate the missing values as accurate as possible becomes an essential preprocessing for downstream analysis procedures.

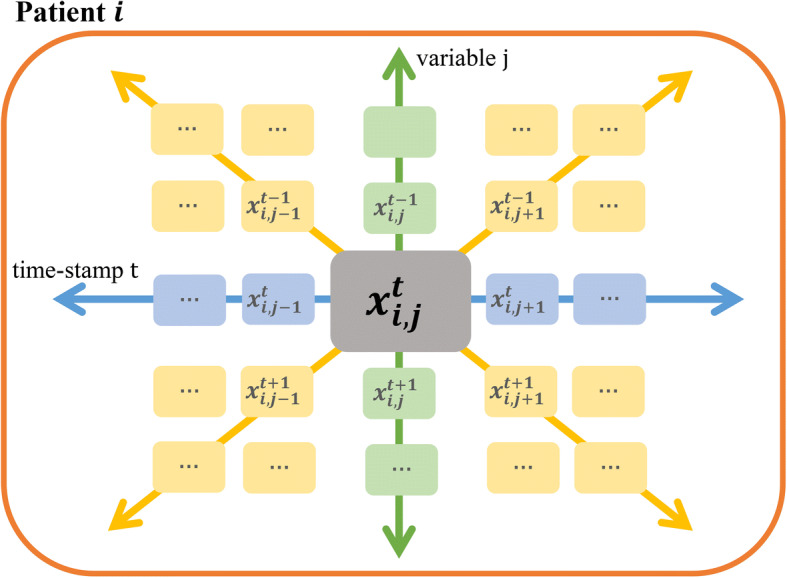
According to the clinical data types, different estimation strategies have been proposed. Multivariate time series (MTS) clinical data is the most challenge one. An example of MTS clinical data is shown in Fig. 1. Given a patient, there are a set of variables, and each variable is a time series. The missing parts may be occurred in any time-stamp for any variables. MTS data type is common in patients’ monitoring data, treatment data, following up data, and so on. A typical application for MTS data is the clinical events prediction calculating the risk of different clinical outcomes based on patients’ historical MTS data [2–4]. Precise estimation for the missing values in MTS data can improve the availability and accuracy of various prediction methods [5].

Fig. 1.

An example of MTS clinical data. “T” is the time axis, and red symbol “X” represents missing value

The core principle of the strategies for missing value estimation is to make full use of the available information in the data. The most common way is the use of mean value and forward/backward value of a time series to filling in the missing parts. However, the simply statistical values can hardly capture the rich information in MTS for estimating miss values. Interpolation and imputation are two main technical directions for addressing the problem. The former one attempts to construct a fitting function for the time series of each variable. However, it ignores the potential relations between multiple variables. The latter one, such as MICE [6], Miss Forest [7], and matrix completion [8], focuses on utilizing correlations between different variables to imputing the missing values in a fixed time-stamp, while the temporal information in time series data has been ignored by them.

Recently, a number of deep learning frameworks, such as M-RNN [9], BRITS [10], and GRUI [11], have been proposed and achieved impressive results on the benchmark datasets. The success of these methods stems from the high-quality representations extracted from a large amount of data, which means that it may not get desire performance with limited training dataset.

In this paper, we proposed a novel method MD-MTS to estimate the missing values in MTS clinical data. MD-MTS is a tree-based algorithm utilizing multi-directional information in the available parts in MTS clinical data. We constructed two kinds of features, temporal and cross variable, as the input of LightGBM, an effective and efficient gradient boosting tree method. The Intensive-Care-Unit (ICU) datasets which contains 13 time series variables, provided in Data Analytics Challenge on Missing Data Imputation (DACMI) of IEEE International Conference on Healthcare Informatics (ICHI) 20191, is used for our model training and evaluation. On the offline-test dataset, MD-MTS achieved significant improvement compared to three baseline models, 3D-MICE [1], Amelia II [12], and BRITS [10]. On the online-test dataset, our method got the best performance among the submitted models.

Dataset

The MTS dataset of DACMI of IEEE ICHI 2019 is derived from MIMIC dataset [13], a real-world ICU data. In total, 13 commonly measured laboratory tests are extracted as the time series variables, including “PCL,” “PK,” “PLCO2,” “HCT,” “HGB,” “MCV,” “PLT,” “WBC,” “RDW”, “PBUN,” “PCRE,” and “PGLU.” They reflect the clinical states of each patient in different time-stamps, which can be used for analysis tasks like sepsis prediction and mortality prediction. Table 1 shows an example about a patient’s data.

Table 1.

An example patient’s MTS data in our datasets

CHARTTIME	PCL	PK	PLCO2	PNA	HCT	HGB	MCV	PLT	WBC	RDW	PBUN	PCRE	PGLU
0	106	4	NA	137	37.6	12.9	84	142	10.4	12.8	45	2.3	111
225	107	3.5	19	137	34.8	11.5	84	133	13.6	12.8	46	2.3	136
800	105	3.9	19	134	33.9	11.7	81	158	20.1	13.2	47	2.2	148
1515	103	3.7	18	133	32.2	10.9	83	152	17.9	13.4	42	1.9	109
3013	106	3.7	23	139	31	10.5	84	141	13.1	13.3	27	1.6	102
3746	106	3.6	24	138	NA	NA	83	151	10.3	13.5	23	1.3	105
4434	105	3.5	25	137	30.7	10.3	83	173	10.7	13.6	23	1.4	NA
4789	109	4	26	143	NA	NA	NA	NA	NA	NA	23	1.5	120
6140	104	3.4	23	138	30.2	9.8	NA	218	10.4	13.9	NA	1.3	257
7497	108	4.1	23	141	31.3	10.5	85	NA	9.8	13.7	23	1.3	116
8940	105	NA	24	140	34.8	11.6	84	314	15.1	13.6	23	1.4	118
9496	105	4.6	24	138	NA	NA	NA	NA	NA	NA	26	1.5	115
10378	104	4.5	22	136	34.3	11.4	85	284	13.2	14	35	1.3	125
11874	108	4.6	20	136	26.3	8.8	84	329	13.9	14.3	65	1.2	133
13161	112	4.3	22	140	30.3	10.5	85	308	10.1	NA	38	NA	110
14639	NA	4	21	137	28.4	9.9	85	264	8.1	14.4	17	1.1	124
16149	109	4.2	21	NA	27.9	9.7	85	295	NA	14.1	12	1	104

Bold and italics values represent the real and masked missing values, respectively

As seen in the table, the first column “CHARTTIME” refers to the sampling time-stamps of the 13 measurements from the patient’s admission (the first row). “NA” represents the missing values which are marked by two different background colors: NA in bold are the real missing parts in the original datasets (the true values are unknown), and NA in italics are the “fake” missing parts whose true values have been artificially masked. Therefore, the yellow ones are used to evaluate the performance of missing value estimation methods because we know their labels (true values). As described by the DACMI challenge, the masked missing values are randomly selected at varying time points, and for each sample, there are 13 masked missing values (one for each variable).

In DACMI, two datasets are released:

• Dataset A contains 8267 samples (a sample refers to a patient’s data like Table 1), 199,695 time-stamps, and 2,596,035 values. In DACMI, this dataset is used for model design. There are totally 193,405 missing values (7.45%), which can be divided into real missing part and masked missing part. The true values of the masked parts have been provided, so that we name them as offline-test dataset.

• Dataset B contains 8267 samples, 196,936 time-stamps, and 2,560,168 values. The dataset in DACMI is used for the performance comparison between the submitted challenge models, including 158,502 missing values (11.58%). Unlike dataset1, DACMI have not provided the true values of the masked parts, which are used to evaluate online the accuracy of the estimated values. Thus, we name them as online-test dataset, which can better demonstrate the generalization of the proposed methods because it is infeasible to optimize the methods based on the test dataset.

The detailed statistics of the missing rate in the two datasets are listed in Table 2.

Table 2.

Statistics of the missing rate

	PCL	PK	PLCO2	PNA	HCT	HGB	MCV	PLT	WBC	RDW	PBUN	PCRE	PGLU
Dataset A	1.18%	1.34%	1.39%	1.26%	12.51%	15.09%	15.23%	14.55%	14.80%	15.34%	0.74%	0.70%	2.70%
Dataset B	5.40%	5.48%	5.60%	5.45%	16.64%	19.13%	19.24%	18.62%	18.89%	19.36%	4.97%	4.94%	6.83%

Method

In this section, we firstly introduce the problem definition formally. Then, we give a data exploration which determines the design of our method. Finally, we detail MD-MTS, including the preprocessing, feature engineering, and tree-based regressor.

Problem Definition

We define a MTS dataset as $\mathcal{D}$ with sample size $\left|\mathcal{D}\right|$. The values in $\mathcal{D}$ are denoted as $x_{i,j}^t\in \mathcal{D}$, where i, j, and t refer to the jth variable in tth time-stamp of ith sample. We define the real missing parts and masked missing parts as ${\mathcal{D}}^R$ and ${\mathcal{D}}^M$. It means that the true value of $x_{i,j}^t\in {\mathcal{D}}^R$ is unknown, while the true value of $x_{i,j}^t\in {\mathcal{D}}^M$ is known. Therefore, the task of estimation missing values in MTS data can be defined as given MTS dataset $\mathcal{D}$, for each value $x_{i,j}^t\in {\mathcal{D}}^M$, the goal is to calculate an estimation value ${\tilde{x}}_{i,j}^t$ to make the difference between $x_{i,j}^t$ and ${\tilde{x}}_{i,j}^t$ as small as possible. We use normalized root-mean-square deviation (nRMSD) of each variable to measure the difference, which is denoted as follows:

$${\mathit{\text{nRMSD}}}_j=\sqrt{\frac{{\sum }_i{\sum }_{x_{i,j}^t\in {\mathcal{D}}^M}{\left(\frac{{\tilde{x}}_{i,j}^t-x_{i,j}^t}{{\mathit{Max}}_{i,j}-{\mathit{Min}}_{i,j}}\right)}^2}{n_j}}$$

where Max_{i, j} and Min_{i, j} is the maximum and minimum values of jth variable of ith sample, and n_j is the number of calculated values of variable j. Methods with less nRMSD represent better performance. In addition, the average nRMSD of all the variables, which is denoted as $\overline{\mathit{\text{nRMSD}}}=\frac{1}{K}{\sum }_{j=1}^K{\mathit{\text{nRMSD}}}_j$ (K is the count of variables in $\mathcal{D}$), represents the overall performance of the estimation method.

For DACMI datasets used in this paper, we define them as ${\mathcal{D}}_A$ and ${\mathcal{D}}_B$ for dataset A and dataset B, respectively. According to the rule of DACMI, the estimation methods can only depend on either ${\mathcal{D}}_A$ or ${\mathcal{D}}_B$. It means that if we want to estimate the masked missing values in ${\mathcal{D}}_A$, the methods can only use the information from ${\mathcal{D}}_A$ (without ${\mathcal{D}}_B$), and vice versa. This rule highlights the generalization of the estimation methods because there is no other external information can be involved in.

Data Exploration

Data exploration is an essential procedure for the model design. Following the DACMI rule, we did a data exploration on ${\mathcal{D}}_A$, and drew inspiration from it.

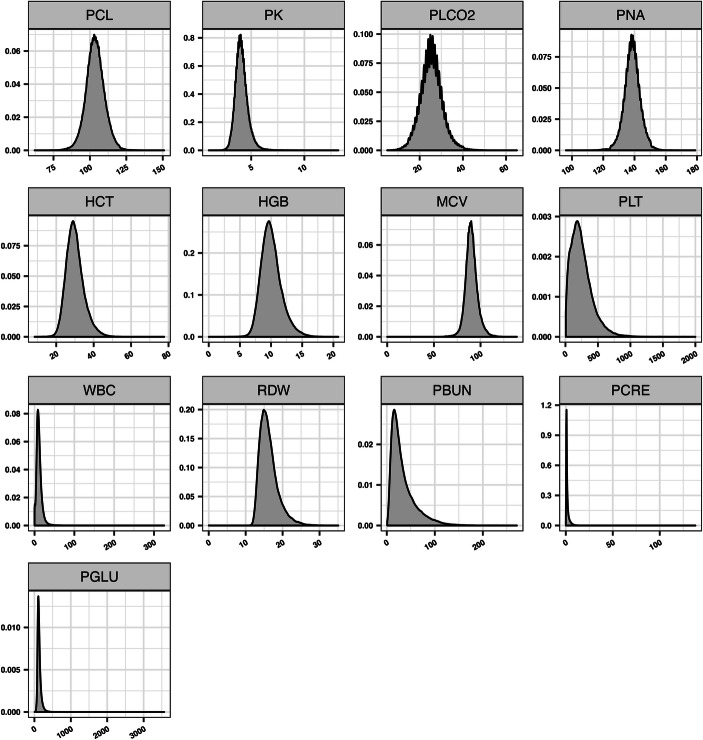
1. Variable distribution. We analyzed the distribution of each variable across the time-stamps as shown in Fig. 2. Most of the variables meet the normal distribution, while 5 variables (PLT, WBC, PBUN, PCRE, PGLU) coincide with long-tail distribution.

   → Variables with long-tail distribution should be processed by special transformation. In this paper, we adopted a log function on these variables.

2. Time-interval. For each sample, the time-intervals between two consecutive time-stamps are irregular. Take Table 1 as an example; the time-intervals vary from 225 (row 1 and 2) to 1510 (row 16 and 17) units. Furthermore, the time-interval in pairwise time-stamps is also different between different samples.

   → The time irregularity in intra/inter samples should be taken into consideration.

3. Missing pattern. As mentioned before, the masked missing values are selected randomly. While for real missing parts, we found that HCT, HGB, MCV, PLT, WBC, and RDW are usually missing together in a time-stamp (as shown in green color in Table 1). It is common in clinical data because some variables are extracted from the same laboratory test. If the patient has not received the test in a time-stamp, none of these variables would be recorded.

   → Solely using imputation methods, which depends on the values in the same time-stamp, can hardly get good performance due to the high missing rate.

Fig. 2.

Variable distributions in dataset A

• 4.Correlations between variables. As shown in Fig. 3, there are few significant linear correlations among the variables.

  → Non-linear methods are preferred for the estimation.

Fig. 3.

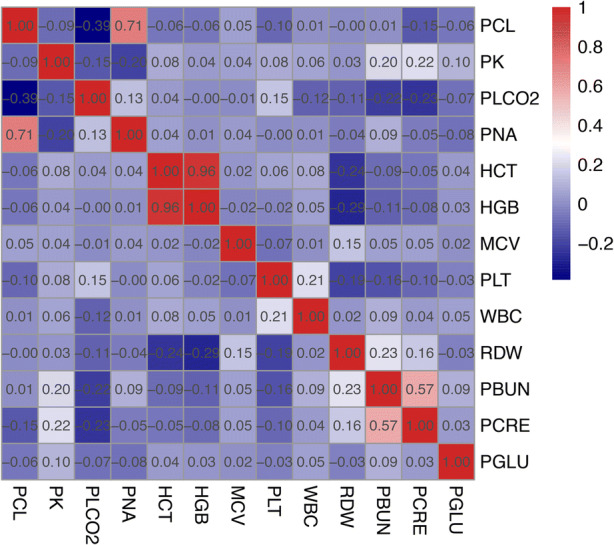
Correlations between 13 variables in dataset A

Although the above explorations are based on DACMI dataset, most of them are common problems in MTS clinical data. We attempt to tackle these problems by a unified framework.

MD-MTS

According to the data exploration, we proposed MD-MTS to estimate the missing values in MTS clinical data. MD-MTS is a machine learning method that constructs a model from training data and then applies the model on testing data. Given $\mathcal{D}={\mathcal{D}}_A$, the training and testing dataset is ${\mathcal{D}}^{\mathit{Tr}}=\left\{x_{i,j}^t|x_{i,j}^t\in \mathcal{D}\backslash \left({\mathcal{D}}^R\cup {\mathcal{D}}^M\right)\right\}$ and ${\mathcal{D}}^{\mathit{Te}}={\mathcal{D}}^M$. And it is similar for ${\mathcal{D}}_B$. The pipeline contains three steps: preprocessing, feature engineering, and tree-based regressor (as shown in Fig. 4).

Fig. 4.

The pipeline of MD-MTS

1. Preprocessing

Besides applied log function on the variables with long-tail distribution (PLT, WBC, PBUN, PCRE, PGLU) as mentioned above, we then did a normalization on all the variables of ${\mathcal{D}}^{\mathit{Tr}}$ as follows:

$$\mathit{norm}\left(x_{i,j}^t\right)=\frac{x_{i,j}^t-{\mathit{Min}}_{\ast ,j}}{{\mathit{Max}}_{\ast ,j}-{\mathit{Min}}_{\ast ,j}}$$

where Max_{∗, j} and Min_{∗, j} are the maximum and minimum values of jth variable in ${\mathcal{D}}^{\mathit{Tr}}$.

• 2.Feature engineering

Proper features are of great importance for machine learning methods. The more information involved in, the better performance of the estimation. As we mentioned before, both interpolation and imputation methods consider only partial information in the MTS data. In our method, we took advantages of both temporal and cross-variable information to construct a multi-directional feature set.

Given a value $x_{i,j}^t\in \mathcal{D}$ to be estimated, the constructed feature set for estimation is listed as follows:

• ${\mathcal{F}}_1$: $\left\{x_{i,k}^t|1\le k\le \mathrm{K}\bigwedge k\ne j\right\}$, the values of the other variables in current time-stamp t, which provide the information about the correlation between variables. Note that if $x_{i,k}^t$ is a missing value ($x_{i,k}^t\in \left({\mathcal{D}}^R\cup {\mathcal{D}}^M\right)$), we set them to NA for the feature set.

• ${\mathcal{F}}_2$: The time-stamp t and the charttime $c_i^t$ in current time-stamp t. Take Table 1 as an example, for the value $x_{i,3}^2$ (2^nd row, 3^rd column), the two features are “2” and “225”, respectively. Absolute time information has been taken into account by these features.

• ${\mathcal{F}}_3$: The charttime interval between the current time-stamp with the pre-time-stamp ($c_i^t-c_i^{t-1}$) and post-time-stamp ($c_i^{t+1}-c_i^t$). These features are used to handle the time-irregularity.

• ${\mathcal{F}}_4$: The values of all the 13 variables in pre- and post-3 time-stamps $\left\{x_{i,k}^{t\prime }|t-3\le t^{\prime }\le t+3\bigwedge t^{\prime }\ne t,1\le k\le 13\right\}$. This is a fusion feature set that combines the information of temporal and cross variable. Similarly, we set missing values in the feature set to NA.

• ${\mathcal{F}}_5$: Sample id i, and the max/min/mean values of all the 13 variables of ith sample. These features bring the unique information of the sample, because there may exist relations between the sample and its variable values.

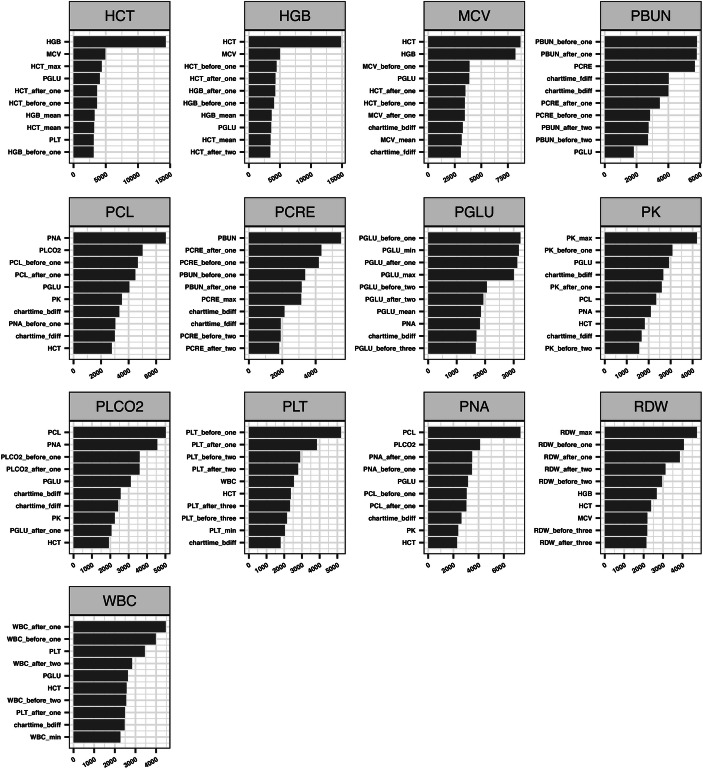
There are totally 134 features in the feature set for ${\mathcal{D}}_A$ or ${\mathcal{D}}_B$ (${\mathcal{F}}_1$:12, ${\mathcal{F}}_2$:2, ${\mathcal{F}}_3$:2, ${\mathcal{F}}_4$:78, ${\mathcal{F}}_5$:40). Figure 5 illustrates a brief summarization for the constructed feature set. As we can see, the temporal and cross-variable information have been captured by the multiple-directions, including global, vertical, horizontal, and diagonal values.

Fig. 5.

A brief summarization for the constructed feature set

• 3.Tree-based regressor

Based on the constructed feature set of each target value $x_{i,j}^t$, we need to select a proper regressor to give an estimation value for it. There are three core requirements for the regressor: (a) finding non-linear correlations, (b) processing noise and missing values (because there is NA in the constructed feature set), and (c) good generalization.

LightGBM [7] is a gradient boosting tree algorithm which is widely used for classification and regression problems. As an ensemble learning approach, many weak learners are iteratively added in each round of training. It is less prone to overfitting and more sensitive to outliers. Missing value is acceptable for LightGBM. While for other regressors, such as logistic regressor and deep learning methods, a coarsely imputation for the missing parts is necessary. It is time-consuming to choose a suitable preliminary imputation strategy for these methods. Therefore, we adopt LightGBM as our regressor to estimate the values.

Due to fact that the values of each variable share the same feature space, we will train K tree-based models for the K variables in dataset. The training and inference procedures are detailed as follows:

• Training procedure

Given all the values of variable j across all the training samples $\left\{x_{i,j}^t|x_{i,j}^t\in {\mathcal{D}}^{\mathit{Tr}},1\le i\le \left|{\mathcal{D}}^{\mathit{Tr}}\right|\right\}$, constructing the feature set for each value as above described. By inputting the feature set to LightGBM, we can get an estimation result ${\tilde{x}}_{i,j}^t$ for $x_{i,j}^t$. The label is the true value of $x_{i,j}^t$. It is worth mentioning that the values in feature set, estimation result, and label are the preprocessed ones. Mean squared error (MSE) is used as the loss metric. After training, we get the tree-based model for variable j which can be used for the missing value estimation. Similarly, the models for other variables will be trained following the procedure.

We used the python-package of LightGBM for our experiments2. The parameters we set for LightGBM includes “learning_rate” = 0.03, “sub_feature” = 0.9, “max_depth” = 10, “max_data” = 50, “min_data_in_leaf” = 50, “feature_fraction” = 0.9, “bagging_fraction” = 0.9, “bagging_freq” = 3, “lambda_l2” = 0.005,“verbose” = − 1, “num_boost_round” = 30,000, and “early_stopping_rounds” = 200. The other parameters are default in LightGBM. Although we trained K models for the K variables in dataset, we adopted the same parameters for different models because of the stable performance of LightGBM.

• Inference procedure

In the inference procedure, we will apply the trained model on the testing dataset ${\mathcal{D}}^{\mathit{Te}}$. Similarly, for each $x_{i,j}^t\in {\mathcal{D}}^{\mathit{Te}}$, we input the constructed feature set to the jth trained model and get the estimation result. Due to the preprocessing in pre-step, we need to transform the estimation results to original scale to calculate the measurement nRMSD.

Experimental results

In this section, we will introduce the experimental results on DACMI datasets, including offline-test and online-test dataset.

Offline-Test Dataset

On the offline-test dataset ${\mathcal{D}}^{\mathit{Te}}\in {\mathcal{D}}_A$, we compared MD-MTS with the following baseline models to demonstrate the method effectiveness.

• 3D-MICE [1]. The method of Gaussian process (GP) can impute single-variate time series data [14]. For multivariable dataset, multiple imputation with chained equations (MICE) can build a conditional model for each variable to be imputed while using the other variables as possible predictors [6]. A new imputation algorithm, 3-dimensional multiple imputation with chained equations (3D-MICE) was developed recently [1]. It combines MICE with GP models to impute missing data based on both cross-sectional and longitudinal information and showed better performance than MICE and GP methods.

• Amelia II [12]. The method uses the bootstrap-based EMB algorithm to impute many variables with many observations. EMB algorithm combines the classic expectation-maximization algorithm with a bootstrap approach. It utilizes both timing and multivariable information at one model, implying that Amelia II is suitable for this task.

• BRITS [10]. The method adopted a bidirectional recurrent neural network (RNN) for imputing missing values. Missing values were regarded as variables of the RNN graph, which could get delayed gradients in both forward and backward directions with consistency constraints.

Table 3 compares the performance of the four missing value estimation methods using nRMSD. It is observed that Amelia II achieves better performance than 3D-MICE for all the 13 variables. MD-MTS outperforms the three baseline models. The $\overline{\mathit{\text{nRMSD}}}$ has been significantly reduced by 23.65%, 9.6%, and 7.7% compared to 3D-MICE, Amelia II, and BRITS. PCL, “PNA”, “HCT”, HGB, and PBUN are the 5 variables with highest performance improvement (> 30% to 3D-MICE, > 10% to Amelia II and > 10% to BRITS).

Table 3.

Performance of the missing value estimation methods on offline-test dataset measured by nRMSD

Variable	3D-Mice	Amelia II	BRITS	MD-MTS
PCL	0.2040	0.1554	0.1506	0.1324
PK	0.2628	0.2445	0.2314	0.2238
PLCO2	0.2357	0.2029	0.1957	0.1809
PNA	0.2180	0.1755	0.1708	0.1534
HCT	0.1467	0.1121	0.1156	0.0983
HGB	0.1444	0.1112	0.1054	0.0915
MCV	0.2707	0.2479	0.2345	0.2251
PLT	0.2289	0.1760	0.1794	0.1601
WBC	0.2585	0.2162	0.2164	0.2006
RDW	0.2512	0.2202	0.2133	0.2093
PBUN	0.1905	0.1467	0.1486	0.1308
PCRE	0.2336	0.1943	0.2017	0.1823
PGLU	0.2792	0.2671	0.2568	0.2444
Avg.	0.2249	0.1900	0.1862	0.1718

The values in italics represent the best performance

The feature importance generated by LightGBM (top 10) for each variable is listed in Fig. 6. We can find that for different variables, there are different important features for the estimation. Most of the common features with great importance among the 13 models are included in ${\mathcal{F}}_1$, ${\mathcal{F}}_3$,${\mathcal{F}}_4$, ${\mathcal{F}}_5$, which cover the temporal and cross-variable information. For the variable pairs with high linear correlations, such as “HCT” and “HGB” and “PCL” and “PNA” (as shown in Fig. 3), they played significantly important roles for the prediction between each other.

Fig. 6.

Feature importance of the models for 13 variables

To further investigate the contribution of each part of the constructed features, we did an ablation study for MD-MTS. In this experiment, we generated the estimation results, which are shown in Table 4, by systematically removing different kinds of features. It is observed that each subset of the constructed features is important for the missing value estimation. From the average of nRMSD in the last row, compared to MD-MTS with whole feature set, we found that the result will be reduced with 32.89% by removing ${\mathcal{F}}_4$, which is composed by the values in pre/post three time-stamps. As a combination of temporal and cross-variable features, ${\mathcal{F}}_4$ contributes most to the result. Similarly, as a cross-variable feature subset, ${\mathcal{F}}_1$ plays a critical role for the estimation. The removing of ${\mathcal{F}}_2$, ${\mathcal{F}}_3$, and ${\mathcal{F}}_5$, which contain information of temporal and patient level, would also degrade the final performance by more than 10%.

Table 4.

Ablation study for MD-MTS measured by nRMSD

Variable	MD-MTS	Without ${\mathcal{F}}_1$	Without ${\mathcal{F}}_2$	Without ${\mathcal{F}}_3$	Without ${\mathcal{F}}_4$	Without ${\mathcal{F}}_5$
PCL	0.1324	0.1888	0.1317	0.1326	0.1608	0.1319
PK	0.2238	0.2322	0.2257	0.2269	0.2473	0.2291
PLCO2	0.1809	0.2053	0.1981	0.1981	0.2379	0.1985
PNA	0.1534	0.2107	0.2034	0.2036	0.2412	0.2042
HCT	0.0983	0.2109	0.0998	0.0995	0.1110	0.1014
HGB	0.0915	0.2111	0.1987	0.1988	0.2346	0.2025
MCV	0.2251	0.2458	0.2443	0.2446	0.2713	0.2534
PLT	0.1601	0.1738	0.1659	0.1683	0.2226	0.1686
WBC	0.2006	0.2129	0.2104	0.2127	0.2558	0.2151
RDW	0.2093	0.2100	0.2103	0.2100	0.2527	0.2204
PBUN	0.1308	0.1472	0.1313	0.1329	0.2098	0.1318
PCRE	0.1823	0.2023	0.2033	0.2038	0.2522	0.2062
PGLU	0.2444	0.2506	0.2510	0.2542	0.2713	0.2536
Avg.	0.1718	0.2078	0.1903	0.1912	0.2283	0.1936

The values in italics font represent the best performance

We also conducted a series of experiments to demonstrate the sensitivity of regressor (LightGBM) in MD-MTS. We selected three popular tree-based regressors, Random Forest, GBDT [15], and XGBoost [16], as the comparison. All of these methods took the same features as the input. Table 5 shows the results. As we can see, XGBoost achieved competitive performance with our MD-MTS (LightGBM-based). Random Forest and GBDT performed worse scores than Amelia II. We think that XGBoost and LightGBM are two similar gradient boosting tree-based classifiers, which can better process the massive constructed features than Random Forest and GBDT.

Table 5.

Sensitivity of regressors with same features on offline-test dataset measured by nRMSD

Variable	MD-MTS	Random Forest	GBDT	XGBoost
PCL	0.1324	0.1730	0.1648	0.1382
PK	0.2238	0.2503	0.2356	0.2289
PLCO2	0.1809	0.2158	0.2036	0.1848
PNA	0.1534	0.1945	0.1825	0.1573
HCT	0.0983	0.1717	0.1497	0.1042
HGB	0.0915	0.1358	0.1330	0.0952
MCV	0.2251	0.2659	0.2713	0.2394
PLT	0.1601	0.2086	0.2121	0.1771
WBC	0.2006	0.2751	0.2458	0.2098
RDW	0.2093	0.2550	0.3061	0.2410
PBUN	0.1308	0.2435	0.1758	0.1390
PCRE	0.1823	0.2465	0.2424	0.1893
PGLU	0.2444	0.2689	0.2532	0.2517
Avg.	0.1718	0.2234	0.2135	0.1812

The values in italics font represent the best performance

The training time for MD-MTS and all the compared methods are shown in Table 6. As we can see, MD-MTS (LightGBM-based) is the most efficient approach. Random forest, GBDT and Amelia II are also trained fast, while 3D-MICE and BRITS would take several hours for training.

Table 6.

Training time of different methods on offline-test dataset

Methods	Time	Methods	Time
MD-MTS	12.8 mins	Random Forest	28.4 min
3D-MICE	361.3 mins	GBDT	26.5 min
Amelia II	23.0 mins	XGBoost	64.2 min
BRITS	275.9 mins

• 4.1Online-test dataset

On the online-test dataset ${\mathcal{D}}^{\mathit{Te}}\in {\mathcal{D}}_B$ measured by nRMSD, MD-MTS is the top performer among all the submitted models of DACMI of ICHI 20193. For the 13 variables, our method achieved 11 optimal and 2 sub-optimal nRMSD. We demonstrate the comparison in online-test dataset between MD-MTS, Amelia II, and the official baseline 3D-MICE in Table 7.

Table 7.

Performance of the missing value estimation methods on online-test dataset measured by nRMSD

Variable	MD-MTS (Rank 1)	3D-MICE	Amelia II
PCL	0.1351	0.2000	0.1581
PK	0.2255	0.2632	0.2478
PLCO2	0.1794	0.2314	0.2005
PNA	0.1561	0.2145	0.1775
HCT	0.1002	0.1505	0.1169
HGB	0.0920	0.1488	0.1131
MCV	0.2289	0.2713	0.2518
PLT	0.1580	0.2294	0.1839
WBC	0.1986	0.2560	0.2240
RDW	0.2021	0.2458	0.2192
PBUN	0.1341	0.1846	0.1489
PCRE	0.1827	0.2338	0.1960
PGLU	0.2440	0.2769	0.2673
Avg.	0.1721	0.2235	0.1927

The values in italics font represent the best performance.

Discussion

In this paper, we investigated the problem of estimating missing values in MTS clinical data. The proposed method MD-MTS outperformed other models by a significant margin in DACMI datasets. According to the method architecture and experiment performance, we make a conclusion about the advantages of MD-MTS as follows:

1. Accurate. MD-MTS is a machine learning method which is consisted by proper preprocessing, comprehensive feature engineering, and powerful gradient boosting tree. The model generated from the training datasets can recognize the core patterns, including temporal and cross-variable dimensions, for the missing value estimation. The accuracy of the proposed method has been demonstrated by the comparison with baseline models and competition models which contains different deep learning, machine learning, and statistical methods.

2. Practical. The feature set for MD-MTS is easy to construct. Given a MTS clinical dataset, all of the features can be found in it, including the multi-directional values in temporal dimension and cross-variable dimension. Neither complex features nor initial imputation strategies that need a lot of manual works are essential for MD-MTS. In addition, LightGBM is an industrial-level algorithm which has been widely used in various production systems. It makes MD-MTS applicable, stable, and trustable in clinical scenario.

3. Generalizable. The generalization ability of MD-MTS is represented in three aspects. Firstly, the parameter space of the proposed method is limited, and only parts of parameters play important roles in the estimation performance. It brings convenience for the parameter tuning in different datasets. Secondly, MD-MTS is insensitive to the minor adjustment of the parameters, which means that only several parameter combinations may be required for searching. The performance on online-dataset, whose true values of the masked missing parts are invisible offline, demonstrated the generalization of MD-MTS. Thirdly, we can easily involve in other features for the tree-based regressor according to the datasets or clinical requirements.

Besides the advantages, we also list the limitations of this study.

1. Limitation of the dataset. In this study, we designed and evaluated the proposed MD-MTS on DCAMI datasets. Although they are extracted from a set of typical MTS data (ICU laboratory tests) in clinical scenario, there are following shortcomings:

• Missing rate. As shown in Table 1, the missing rate of DACMI datasets (real and masked missing parts) is relatively low. The variables with high missing rate, which are common in real-world clinical data, have been excluded from the datasets. While these variables may reduce the completeness of the feature set (a lot of “NA”) and result in worse estimation performance.

• Missing pattern. As described in Sect. 2, besides the real missing values, only one masked missing value was randomly selected for each variable in each sample. The pattern of the masked missing parts in DACMI datasets cannot cover all the possibilities in other clinical data. We can only evaluate the estimation performance on the masked missing parts whose true values are known.

• Number of variables. There are only 13 variables in DACMI datasets. Considering the way of feature set construction, more variables bring larger feature set for MD-MTS, and hence a more complex model.

• 2.Future information. In the temporal dimension, we used both past and future information in the feature set for a target value. However, in some clinical tasks, we can only use the past information, such as predicting the sepsis risk on current time. In these tasks, we need to estimate the missing values based on the features in current and previous time-stamps.
• 3.Performance for downstream tasks. One of the core goals of missing value estimation in MTS data is to improve the performance for the downstream tasks. In this study, we have not given an example to demonstrate the ability of MD-MTS.

For all the limitations mentioned above, we will do further studies on them to evaluate and optimize our method.

Conclusion

In this paper, we study the problem of estimating missing values in MTS clinical data. By exploring the data characteristics, we proposed a novel machine learning method MD-MTS. It combines the temporal and cross-variable information into the multi-directional feature set, which is utilized as the input for a tree-based regressor. Experimental results on DACMI datasets demonstrated that our proposed method outperforms baseline models and competition models.

Compliance with ethical standards

Conflict of interest

The authors declare that there is no conflict of interest.