Abstract
Cortisol is a glucocorticoid hormone that is critical to immune system functioning. Studies show that prolonged exposure to high levels of cortisol can lead to a range of physical health ailments including the progression of tumor growth. The ability to monitor cortisol levels over time can therefore be used to facilitate decision-making during cancer treatment. However, collecting serum or saliva samples to monitor cortisol in situ is inconvenient, costly, and impractical. In this paper, we propose a general predictive modeling process that uses passively sensed actigraphy data to predict underlying salivary cortisol levels using graph representation learning. We compare machine learning models with handcrafted feature engineering and with graph representation learning, which includes Graph2Vec, FeatherGraph, GeoScattering and NetLSD. Our preliminary results generated from data from 10 newly diagnosed pancreatic cancer patients demonstrate that machine learning models with graph representation learning can outperform the handcrafted feature engineering to predict salivary cortisol levels.
Keywords: Salivary cortisol, Predictive modeling, Graph representation learning, Actigraphy data, Mobile sensing
Introduction
Pancreatic cancer is one of the most lethal malignancies, with a 5-year survival rate of 9%. Although it is the eleventh most common form of cancer worldwide, it is the seventh leading cause of cancer-related deaths worldwide [29]. Research demonstrates that the incidence and mortality rates of pancreatic cancer in the USA have increased significantly since 2000 [43]. Importantly, preliminary data suggests that cortisol could influence how pancreatic tumors respond to cancer treatment [33].
Bodily hormones serve as chemical messengers that facilitate complex processes like immune system functioning and behavior. Cortisol, a glucocorticoid hormone, is a primary product of the hypothalamic-pituitary-adrenal (HPA) axis and plays a key role in facilitating the “fight or flight” response. The release of cortisol in response to stressors increases glucose in the bloodstream which supplies an immediate energy source to the large muscles in the body. While cortisol prepares the body for action, repeated and prolonged exposure to high cortisol levels can lead to impaired immune system functioning, gastrointestinal problems, cardiovascular disease, infertility, and insomnia [1]. This is particularly problematic for treating pancreatic cancer given that an increase in cortisol concentration has been found to advance tumor growth [23].
Mobile technology may provide a low-cost and accessible means to continuously approximate cortisol levels in the body though no studies have examined this issue. Existing work on the use of mobile sensing in health has primarily used sensors to approximate behaviors using a layered, hierarchical framework where features are extracted from raw sensor data and translated into markers of behavioral states[25]. The theoretical underpinning of using sensors to approximate hormone levels leverages this hierarchical framework. Studies show that cortisol generally peaks in the morning and gradually decreases throughout the day, although experiential factors such as physical activity and response to acute and chronic stressors lead to individual variabilities in cortisol levels throughout the day [32]. Cortisol level is therefore the product of a predictable diurnal rhythm as well as behavioral states (e.g., physical activity, stress response) that can be sensed by a wearable device. The behavioral features that are extracted from sensor data serve as a bridge that can be used to approximate cortisol levels in pancreatic cancer patients.
Currently, the primary methods for measuring cortisol are through serum and saliva samples which are inconvenient to collect and costly to analyze. The inconvenience of biospecimen collected is pronounced in adults with pancreatic cancer given the impact of their disease on their health, daily functioning, and overall quality of life. Biospecimen collection is also impractical as a means of monitoring cortisol in real-time given the time needed to complete assays. Tracking cortisol levels through mobile technology has the ability to advance our understanding of the trajectory of tumor growth and the potential role it plays on response to anticancer treatment.
The aim of the present study is to present a process for linking passively sensed raw actigraphy data with salivary cortisol levels in adults newly diagnosed with pancreatic cancer. The ultimate goal of this work is to demonstrate that passively collected data can be used to approximate in situ the underlying circulating cortisol level in cancer patients, in lieu of serum or saliva collection. No published work has examined the potential of using passively collected activity data to predict underlying hormone levels.
Related Works
Advancements in sensing technologies enable researchers to employ passive and mobile sensing to collect fine-grained behavioral data via smartphone and wearable embedded sensors. Data collected from these sensors are then extracted and analyzed to characterize health related behaviors through featurization of mobile sensing data, also known as feature engineering [38]. Many different sensors have been used to passively capture information about users’ states, such as accelerometer, which measures acceleration along a three-dimensional coordinate system [16], and gyroscope, which measures the angular rotation rate along three orthogonal axes of the embedded device. Location sensors, such as Global Positioning System (GPS) and Bluetooth Encounter, can identify smartphone users’ geographical locations and relative position with respective to other Bluetooth devices. Light, atmospheric pressure, and relative humidity can also be measured and tracked by light sensors, barometers, and humidity sensors respectively. Feature engineering can be integrated with machine learning techniques to use raw sensor data to predict or recognize target variables, such as activity type (e.g., walking, sitting) and level (e.g., high vs. low) [4, 10, 18, 26].
Numerous studies have examined the relationship between salivary cortisol level and physical activity. For example, McGuigan et al. found that salivary cortisol increased in response to high-intensity acute resistance exercise [24]. In another study, a significant increase in salivary cortisol was found after participants completed 4 weeks of moderate-intensity level exercise [2]. Furthermore, a wealth of studies demonstrate the validity of using salivary cortisol as a biomarker of psychological stress [14], including among cancer patients [17]. In a recent study, Allende et al. found that evening cortisol may be a useful predictor of breast cancer survival, potentially related to accumulated stress over the course of the day [3]. Despite the relevance of cortisol to physical activity and psychological distress and cancer, no studies have used passively collected data to predict cortisol levels. To accomplish this, we first present the two strategies of (1) Handcrafted Feature Engineering, and (2) Automatic Feature Engineering.
Handcrafted Feature Engineering
is the process of using domain knowledge or expertise to manually design features that represent the characteristics of target variables. For example, in the domain of mental health, handcrafted behavioral features can be created based on prior results or domain knowledge of behaviors of people who suffer from mental health issues [34]. In a previous study, eight handcrafted human mobility features were created from location data, including total distance travelled, maximum distance between two locations and radius of gyration, to predict depression levels in adults [6]. These handcrafted features were based on theory and a large amount of research indicating that individuals high in depression tend to be sedentary and avoid physical activity [36]. Representative features related to physical motion, social activities, sleep quality, and smartphone use have also been extracted and applied to the prediction of symptoms of schizophrenia [42]. Researchers have also used handcrafted features from wearable sensors to detect early onset Alzheimer’s disease [40]. Relative to automatic features, the contribution of handcrafted features in prediction algorithms are more easily understood because they are generated by domain experts. However, a critical limitation is that handcrafted features are typically based on theoretical models that may not generalize to a specific population or sample. In these cases, handcrafted feature engineering may provide limited ability to predict an outcome of interest and in most cases of predictive modeling handcrafted features are outperformed by automatic features [41].
Automatic Feature Engineering
is the process of automatically learning users’ states without manually designed feature functions. Deep learning methods, such as convolutional neural network (CNN) and recurrent neural network (RNN), can learn and optimize the features from raw sensor data automatically [22]. In human activity recognition, complex features can be captured by convolutional layers in CNN to predict activity labels (e.g., walking, standing, sitting) with 95.75% accuracy, whereas SVM-trained models with handcrafted features demonstrate 94.61% accuracy [30]. By leveraging the temporal dependency of the time series data from mobile sensors, long short-term memory (LSTM) automatically learns features from raw data and was found to be superior in terms of recognition accuracy against other CNN and shallow machine learning models (e.g., SVM) with handcrafted features [9]. Although deep learning models with automatic feature engineering can be used to generate models with higher prediction accuracy than models with handcrafted features, training deep learning models requires a large number of observations to obtain robust estimations which is not often found in health related studies. For studies with a smaller number of participants and observations, an automatic feature engineering method called graph representation learning can be utilized, which maps structural graph data into numerical spaces. A description of graph representation learning is presented in Section 3.
Methodology: a Process to Predict Salivary Cortisol Levels
In this section, we introduce the general predictive modeling process that takes raw sensor data as input and trains a machine learning model to predict salivary cortisol level. We also provide detailed information about the handcrafted feature engineering methods that were implemented in this study. Finally, we will describe graph representation learning (GRL), and present GRL algorithms including Graph2Vec [19], FeatherGraph [31], GeoScattering [12], and NetLSD [39] which were implemented in this study.
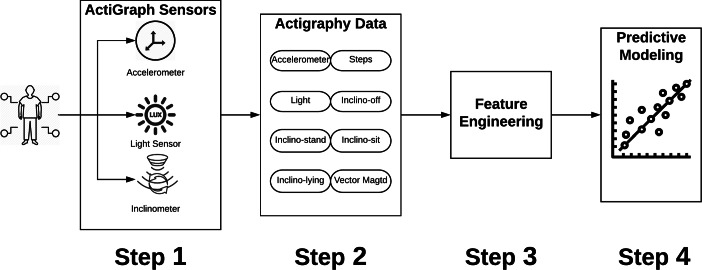
As shown in Fig. 1, the predictive modeling process consists of 4 steps. In the first step, sensor data, including accelerometer, light, and inclinometer are passively generated from ActiGraph devices worn by participants. In the second step, the raw sensor data is pre-processed by using time-window segmentation to reduce noise in the data. Devices are programmed to sample based on a pre-specified epoch (e.g., 30 s, 1 min) which in this study was performed by the ActiLife software.1 By using ActiLife, the raw actigraphy data can be retrieved, sampled, aggregated, and synchronized. In this study, we specified 1-min epoch to aggregate and synchronize the raw actigraphy data. In step three, several feature engineering methods can be used to extract meaningful features including handcrafted engineering methods (i.e., time domain features, frequency domain features) and graph representation learning methods. In the fourth step, the extracted features are used in the training process of predictive modeling. The machine learning model with the lowest testing error is selected to predict salivary cortisol levels.
Fig. 1.
Predictive modeling pipeline of salivary cortisol levels—a general process
Handcrafted Feature Engineering
Handcrafted feature engineering can be applied to extract temporal and spectral features from raw sensor data manually, as shown in Table 1. Generally, given a multi-dimensional time series data , xi, where i = 1,2,..., m and m is the dimensions of actigraphy data, represents one-dimensional time series data collected from one of the sensors. And xit represents the i th dimension of the actigraphy data at time t. Let ts represent the time when we record participants’ salivary cortisol levels. Then, we set the time , where , such that, in the time window , handcrafted-featurized value H can be extracted by applying feature engineering functions , where and k is the number of the features extracted from each sensor and is the segment of the time series framed by the time window. The handcrafted features extracted from time and frequency domains are shown in Table 1. The identified handcrafted features were selected based on prior works indicating the potential importance of mean values, indicators of variance, as well as max/min and the symmetry of distribution in data representing behavior. Because salivary cortisol levels are represented along a continuum, our predictive modeling task is to build regression models to fit cortisol levels with minimum testing error.
Table 1.
Handcrafted features
| Domains | Features |
|---|---|
| Time domain | Mean |
| Standard deviation | |
| Maximum | |
| Minimum | |
| Peak to peak | |
| Shannon entropy | |
| Mean absolute difference | |
| Frequency domain | # Maxpeaks |
| # Minpeaks | |
| Kurtosis | |
| Skewness | |
| Absolute energy |
Automatic Feature Engineering: Graph Representation Learning
Graph representation learning (GRL) can be used to extract structural and synthetic features in lower dimensions to capture interaction and transitions between different sensed behaviors [20]. GRL can be generalized as a process to learn a mapping that embeds graphs into low-dimensional numerical vector spaces such that this embedding can optimally preserve the intrinsic graph properties [7]. Then, the embedded features generated from GRL can be fed into downstream machine learning models to build predictive models. For GRL in this study as shown in Fig. 2, given a sequence of time series data, we apply G-means clustering, which can automatically optimize the number of clusters[13] to assign a cluster label for each time point, and then we transform the sequence of cluster labels to undirected and unweighted graphs that represent the transitions of states in the time series data. Then, GRL algorithms are trained with graph inputs and then generate embedding vectors as the independent variables in modeling regressors. The motivation of including Graph2Vec, FeatherGraph, GeoScattering, and NetLSD are the following: (1) Graph2Vec and NetLSD are the representative methods based random walk and matrix factorization respectively; (2) FeatherGraph [31] and GeoScattering [12] have achieved state-of-art result in graph embedding task. The GRL methods implemented in this study are described below.
Fig. 2.
Feature extraction by graph representation learning
Graph2Vec
learns k-dimensional numerical representations from graphs [28]. Assume a set of undirected and unweighted graphs , where Gi={Vi, Ei, λi}, Vi is a set of nodes, E ∈ (Vi ×Vi) is a set of edges, and assigning an unique label from vocabulary to each node in Vi for i = 1,..., n. Graph2Vec performs as a function f (G) generating the output in k-dimensional vector space, analogous to Doc2vec [19] which maps documents to numerical spaces. Rooted subgraphs are sampled and relabeled by Weisfeiler-Lehman (WL) kernel to train a skipgram model such that Gi and Gj are more similar the f(Gi) and f(Gj) are closer in k-dimensional space[28] .
FeatherGraph
leverages characteristic functions of node features with random walk weights to featurize each node neighborhood and then use mean pooling to average node level features to create graph level features [31]. Assume an unweighted and undirected graph G = (V,E), where V is the set of nodes and E is the set of edges. For node v ∈V, we describe a node feature as a random variable X and specify feature vector xv, where . Given the source node u and target node w, where u, w ∈V and , and evaluation point we define real and imaginary part of the r − scale random walk weighted characteristic function for node u as
| 1 |
| 2 |
where . Then, the concatenated vector of Re(∙) and Im(∙) will be used as feature vector for the node u [31].
GeoScattering
can extract numerical embeddings from graphs by using the moments of wavelet transformed features [31]. Let G = (V, E, W) be a graph, where V is the set of vertices {v1, v2,..., vn}, E is the set of edges (vl, vm) with 1 ≤ l, m ≤ n, and W is the weight matrix W = {w(vl, vm) = 1,: (vl, vm) ∈E}. Then define n × n lazy random walk matrix as , where I is the identity matrix of G, A is the adjacency matrix and D is the diagonal degree matrix. With the definition of wavelet transform matrix at scale 2j,
| 3 |
and signals defined on graph G, the “zero” order scattering moments, first order geometric scattering moment and second order geometric scattering moment can be defined respectively as
| 4 |
| 5 |
| 6 |
, for and 1 ≤ q ≤ Q. Finally, the collection provides the set of features to describe graph G [31].
NetLSD
generates eigenvectors from the factorized normalized Laplacian matrix of the input graph’s adjacency matrix and calculates the heat kernel trace by using the eigenvectors to represent the input graph [39]. Consider an undirected graph and unweighted graph G = (V, E), where V is the set of vertices and E is the set of edges. Then denote the adjacency matrix of a graph G as A and diagonal matrix as D with the degree of node i as entry Dii, a graph’s normalized Laplacian is the matrix can be expressed as . L can be factorized as L = ΦΛΦT, where Λ is a diagonal matrix on the sorted eigenvalues λ1 ≤ ... ≤ λn of which ϕ1,...,.ϕn are the corresponding eigenvectors. Then, the n × n heat kernel matrix at each vertex at time t can be calculated by
| 7 |
, where (H)ij shows how much heat transferred from vi to vj at time t. Finally, a heat trace signature of graph G can be used the graph embedding, which consists of heat traces tr(Ht) at different time t [39].
Participants and Procedure
The inclusion criteria included the following: (1) age 18 years; (2) insomnia symptoms for 6 months; (3) sleep 6.5 hours per night; (4) sleep disturbances (or associated daytime fatigue) that cause significant distress or impairment in social, occupational, or other areas of functioning, as determined by at least a a subthreshold level of severity on the Insomnia Severity Inventory [5] (i.e., a score of 8 out of 22; (5) ability to provide informed consent; (6) histological or cytological proof of pancreatic adenocarcinoma; (7) borderline resectable, locally advanced or metastatic pancreatic cancer and are not candidates for upfront, curative surgical resection; (8) have not received any therapy (cytotoxic chemotherapy, immunotherapy, radiotherapy, biologic therapy, or other investigational therapy directed towards their pancreatic cancer) for their cancer prior to enrollment; and (9) are candidates for systemic therapy based on investigator evaluation. Criteria related to sleep were present given that an original aim of the study was to understand the relationship between insomnia symptoms and pancreatic tumor growth. To control for factors that may artificially inflate salivary cortisol levels, patients that were active smokers (and who reported being unwilling to quit smoking during the study period) were not enrolled, in addition to those taking corticosteroids. Based on these criteria, we recruited 10 adults (6 males, 4 females) newly diagnosed with pancreatic cancer from a cancer clinic. The average age of the participants is 64.6. Nine participants self-identified as White and 1 participant identified as multiracial. The average ± std of sleep time of the participants is 411 ± 135.53 min. Participants were diagnosed with pancreatic cancer on average 15 days before enrolling in the study. The detailed demographics information is shown in Table 2.
Table 2.
Demographics information of the participants
| Age | Sex | Ethnicity | Income ($) | Cancer stage |
|---|---|---|---|---|
| 75 | Male | White | 100, 000 + | 1b |
| 58 | Female | White | 50, 000 − 75, 000 | 3 |
| 67 | Male | Multiracial | 30, 000 − 50, 000c | 2 |
| 81 | Female | White | ≤ 30, 000 | NA |
| 50 | Male | White | ≤ 30, 000 | NA |
| 71 | Female | White | 100, 000 + | NA |
| 47 | Male | White | 50, 000 − 75, 000 | 2 |
| 76 | Male | White | 75, 000 − 100, 000 | NA |
| 66 | Male | White | 75, 000 − 100, 000 | 2 |
| 55 | Female | White | 100, 000 + | 1 |
Clinical research coordinators approached potential participants at a regular medical visit. After signing the consent form, coordinators showed participants how to properly collect (i.e., by salivettes) and store their saliva samples to ensure the most reliable salivary cortisol readings. Participants were asked to collect 3 samples per day (at wake, 5pm, 9pm) for 5 consecutive days in order to capture the diurnal fluctuation in cortisol levels [1]. On average, the saliva samples were collected at the following times: 7:51AM, 5:43 PM, 9:43 PM. For all samples, participants were instructed to not brush their teeth, drink caffeine, vigorously exercise, or eat a major meal within the hour preceding the sample collection. For each sample, the participants placed a sterile cotton swab from the salivette tube under their tongue for 1–2 min, then placed it into the salivette tube upon completion. After collecting the sample, participants recorded the time and date they collected the sample, and put all samples in their refrigerator as quickly as feasible. Participants were also asked to wear a wristworn actigraphy device (ActiGraph GT9X) on their non-dominant hand every day throughout the study. Participants received a postage-paid mailer to return their saliva samples and the actigraph after the 5th day of collection. Salivettes were stored at − 80∘C until shipment for assay.
The saliva assays were completed by the 3rd party vendor (Salimetrics.com) that specializes in accurate testing results for biomarkers in saliva samples. Samples were thawed to room temperature, vortexed, and then centrifuged for 15 min at approximately 3000 RPM (1500×g) immediately before performing the assay. Samples were tested for salivary cortisol using a high sensitivity enzyme immunoassay. Sample test volume was 25μl of saliva per determination. The assay has a lower limit of sensitivity of 0.007μg/dL, a standard curve range from 0.012 − 3.0μg/dL, and an average intra-assay coefficient of variation of 4.60%, and an average inter-assay coefficient of variation 6.00%, which meets the manufacturers’ criteria for accuracy and repeatability in salivary bioscience, and exceeds the applicable NIH guidelines for Enhancing Reproducibility through Rigor and Transparency. The density plot of cortisol level is shown in Fig. 3.
Fig. 3.

Density plot of saliva cortisol level
Experiments and Results
In this section, we present the implementation and results of our predictive modeling approaches to predict salivary cortisol levels at each time point. We also discuss hyperparameter selection (window size and sensor combination), graph construction, and model evaluation.
Experiments
Following the predictive modeling process in Fig. 1, we first collected multi-dimensional time series actigraphy data, which are pre-processed raw sensor data generated from ActiGraph sensors.
For feature engineering, we compared two strategies: handcrafted feature engineering and graph representation learning. For handcrafted feature engineering, we applied the feature extraction functions as shown in Table 1 and then scale features into unit variance. For graph representation learning, we firstly perform G-means clustering on the time series data, and then assign cluster labels for each time series data point. As shown in Fig. 4, the vertices in each graph represent different clusters (participants’ states) of the corresponding input time series data, and edges represent the transitions between different vertices (states). The clusters represented by the vertices reflect semantic meanings, which can be inferred from the cluster centers as shown in Table 3.
Fig. 4.
Sampled graph visualization from one observation in the actigraphy data. The acceleration graph represents acceleration states and state transitions, generated by using G-means clustering for axis x, axis y, axis z 3D accelerometer data. Magnitude of acceleration is vector magnitude of accelerometer’s axis x, axis y, axis z data , which equals to . And magnitude of acceleration plot shows the state transitions of the magnitude. Steps represents the step count state transitions. Inclinometer and light represents the inclinometer and light sensor data state transitions respectively
Table 3.
Sampled cluster centers / representation
| Vertex | Acceleration | Steps | Magnitude of acceleration | Inclinometer | Light |
|---|---|---|---|---|---|
| 0 | (257, 264, 365) | 2 | 1736 | Sitting | 0 |
| 1 | (523, 513, 686) | 8 | 25 | Standing | NA |
| 2 | (16, 13, 25) | 0 | 806 | Lying | NA |
| 3 | (802, 930, 991) | 6 | 417 | Inactive | NA |
| 4 | NA | 12 | 1208 | NA | NA |
| 5 | NA | 4 | NA | NA | NA |
The entries in the the columns of acceleration, steps, magnitude of acceleration, and light represent the values of cluster centers for each cluster; and the entries in inclinometer represent the label of each vertex. To transfer time series data to the graphs, we firstly applied G-means clustering to automatically generate the best cluster allocation. For example, the optimal number of clusters for acclerometer is 4 and the optimal number of clusters for light is 1, which could because the light sensor did not have too much variations during a day and the patients spend most of the times in the hospitals
The vertices in acceleration graph, as shown in Fig. 4, can be explained as physical activities, such as walking, sitting or running. For example, the vertex 2 of acceleration clustering, which has low coordinate values, implies the activity has small body movement extent (such as walk or sit). The edge between vertex 2 and vertex 3 indicate the transition between different activities. Similarly for the graph of Steps, each vertex represents the cluster of number of steps in one minutes (since we sample raw sensor data with processing epoch of 1 minute). The edges between vertex 2 and vertex 4 implies the participant change their average step frequency from 0.17 to 12.44/min as shown in Table 3. This illustration can also be applied to explain magnitude graph in Fig. 4: the vertices represent the activities with different level of vigorousness and edges show the transition between these activities; the lower value of the cluster center in magnitude graph the more sedentary the activity that represented by the vertex should be. The vertices in inclinometer, as shown in Fig. 4 represent the postures of standing, lying, sitting, and off (inactive) which are detected by using inclinometer. The classification accuracy of the postures by using inclinometer has been validated with around 90% [35], thus we do not need to apply G-means to assign cluster labels. And the edges capture the transitions between the detected postures. For the light sensor, the vertex in light graph shown in Fig. 4 represent the cluster of the unit of illumination. High unit of illumination implies a bright environment, such as outdoor, and low unit of illumination implies a dark environment, such as home. As show in Table 3, the value of this only cluster center of Light is 0, meaning that the participant is in a dark environment with much variation. Then, we use the graphs as input to the graph representation learning to generate the unsupervised learned graph features.
Given that saliva cortisol level is recorded at time ts and ActGraphy data X, the window size w defines the feature space such that we extract features from X within the time range between the time ts − w and the time when cortisol level is recorded. To determine the optimal window size and the sufficient combination of sensors, we evaluate the performance of random forest with different combinations of sensors (Acc+Inclin+Light, Acc+Inclin, and Acc) and increasing size of windows (from 0.5- to 12-h increase by 0.5 h) by using 10-fold cross-validation with mean absolute error (MAE). As shown in Fig. 5, the optimal selection of window size and sensor combinations for handcrafted feature engineering is 9.5 h with accelerometer only, and the lowest MAE is 0.090 as shown in Table 4. As shown in Fig. 6, the optimal selection of window size and sensor combinations for graph representation learning by using GeoScattering is 9.5 h with accelerometer only, and the lowest MAE is 0.087 as shown in Table 4.
Fig. 5.

Sensors and window size selection for handcraft feature extraction
Table 4.
Window size (h) selection for handcrafted and graph representation learning feature extraction by random forest
| Sensors | Handcrafted | GeoScattering | ||
|---|---|---|---|---|
| Window size | MAE | Window size | MAE | |
| Acc+Inclin+Light | 8.0 | 0.091 | 4.5 | 0.090 |
| Acc+Inclin | 7.5 | 0.091 | 6.0 | 0.089 |
| Acc | 9.5 | 0.090 | 9.5 | 0.087 |
Bold numbers indicate the best performance of the proposed model
Fig. 6.

Sensors and window size selection for graph representation learning feature extraction
To explore the relationship between activities and cortisol level, we applied a random forest model on handcrafted features by using full sensor data (Acc+Inclin+Light) and selected the top 15 features from 120 features ranked by feature importance, as shown in Fig. 7. These 15 most important features, peak to peak, absolute energy and max all characterize motion signal amplitude which indicates that physical activity behaviors are strong contributors to predicting cortisol levels. The selected features from accelerometer have higher feature importance than the selected features from inclinometer except inclinometer − lie − absolute energy. This implies that accelerometer features are strong predictors of cortisol levels than are light and inclinometer sensors.
Fig. 7.
Random forest feature importance: the features from the same actigraphy sensor are decorated with the same color
To compare the performance between handcrafted feature engineering and graph representation learning approaches, we implemented several machine learning algorithms in the downstream predictive modeling, as shown in Fig. 1. To demonstrate the general predictive framework, as shown in Fig. 1, we applied standard regression models to our dataset. These regression models include lasso regression [37], ridge regression [15], regression of support vector machine (SVM) [11], regression of random forest (RF) [21], regression of Xgboost (XGB) [8], and regression of multi-layer perceptron (MLP) [27]. Thus, for the combinations of feature engineering methods and machine learning models training with the features selected by 9.5-h window size, we use 10-fold cross-valuation with MAE, RMSE, and MAPE to assess the predictive performance of these combinations.
Results
The results of comparing the feature engineering methods across the different machine learning models are shown in Table 5. We use the mean value of cortisol as the vanilla model with 10-fold cross-validation, the mean MAE ± std of the vanilla model is 0.126 ± 0.018, RMSE 0.158 ± 0.034 is, and MAPE is 59.571 ± 9.612. We use the machine learning models with handcrafted features as baseline models. Values in bold in Table 5 indicate the optimal fit between the feature engineering methods (i.e., handcrafted and automatic feature engineering approaches) and machine learning models (i.e., lasso, ridge, SVM, random forest, Xgboost, MLP). Overall, machine learning models with handcrafted and automatic feature engineering were able to predict cortisol hormone level with generally low mean MAE, RMSE, and MAPE. For each individual machine learning model, graph representation learning methods, and in particular FeatherGraph and Geoscattering, produced the lowest mean MAE, RMSE, and MAPE.
Table 5.
MAE, RMSE, MAPE (mean ± std) comparison between handcrafted and graph representation learning feature extraction
| Metrics | Featurization | Machine learning models | |||||
|---|---|---|---|---|---|---|---|
| Lasso | Ridge | SVM | Random Forest | Xgboost | MLP | ||
| MAE | Handcrafted | 0.125 ± 0.026 | 0.106 ± 0.057 | 0.104 ± 0.014 | 0.090 ± 0.017 | 0.099 ± 0.029 | 0.112 ± 0.034 |
| Graph2Vec | 0.124 ± 0.032 | 0.124 ± 0.038 | 0.118 ± 0.022 | 0.092 ± 0.026 | 0.091 ± 0.031 | 0.125 ± 0.030 | |
| FeatherGraph | 0.124 ± 0.032 | 0.096 ± 0.020 | 0.098 ± 0.018 | 0.090 ± 0.019 | 0.089 ± 0.026 | 0.097 ± 0.028 | |
| GeoScattering | 0.123 ± 0.025 | 0.095 ± 0.022 | 0.108 ± 0.013 | 0.087 ± 0.029 | 0.085 ± 0.037 | 0.119 ± 0.038 | |
| NetLSD | 0.124 ± 0.032 | 0.122 ± 0.020 | 0.118 ± 0.028 | 0.091 ± 0.026 | 0.093 ± 0.017 | 0.128 ± 0.032 | |
| RMSE | Handcrafted | 0.159 ± 0.014 | 0.141 ± 0.021 | 0.153 ± 0.017 | 0.140 ± 0.013 | 0.139 ± 0.019 | 0.169 ± 0.059 |
| Graph2Vec | 0.158 ± 0.032 | 0.156 ± 0.044 | 0.155 ± 0.049 | 0.146 ± 0.035 | 0.134 ± 0.039 | 0.159 ± 0.043 | |
| FeatherGraph | 0.156 ± 0.042 | 0.131 ± 0.013 | 0.132 ± 0.018 | 0.136 ± 0.017 | 0.138 ± 0.014 | 0.150 ± 0.051 | |
| GeoScattering | 0.155 ± 0.034 | 0.150 ± 0.036 | 0.135 ± 0.035 | 0.130 ± 0.036 | 0.131 ± 0.037 | 0.167 ± 0.150 | |
| NetLSD | 0.156 ± 0.037 | 0.132 ± 0.035 | 0.139 ± 0.038 | 0.132 ± 0.033 | 0.138 ± 0.030 | 0.187 ± 0.082 | |
| MAPE(%) | Handcrafted | 45.357 ± 7.568 | 36.986 ± 6.142 | 38.612 ± 8.547 | 39.145 ± 9.573 | 39.147 ± 10.472 | 45.201 ± 11.354 |
| Graph2Vec | 43.739 ± 9.957 | 45.171 ± 8.153 | 37.738 ± 12.346 | 32.443 ± 8.248 | 36.539 ± 10.724 | 48.744 ± 8.124 | |
| FeatherGraph | 42.181 ± 8.236 | 32.456 ± 7.341 | 29.388 ± 6.932 | 31.172 ± 8.970 | 31.088 ± 9.991 | 44.763 ± 9.048 | |
| GeoScattering | 41.609 ± 7.251 | 35.031 ± 8.881 | 34.021 ± 5.841 | 35.673 ± 7.724 | 28.992 ± 8.896 | 49.035 ± 8.074 | |
| NetLSD | 43.379 ± 10.236 | 36.031 ± 9.887 | 35.378 ± 9.132 | 34.079 ± 9.316 | 34.016 ± 9.165 | 46.775 ± 10.561 | |
Bold numbers indicate the best performance of the proposed model
Discussion
The proposed process can potentially improve treatment of pancreatic cancer, which has among the lowest 5-year survival rates of all cancer sites. Specifically, given the that cortisol is known to increase tumor growth and inhibit response to cancer treatment, devising a way to continuously monitor cortisol levels may improve clinical decision making that could ultimately improve cancer outcomes. For example, knowing that a patient’s cortisol level has been elevated for a long duration may lead physicians to prescribe behavioral interventions that are known to reduce the stress response.
The combination of mobile sensing and machine learning has the potential to address a need in cancer by providing a way to predict saliva cortisol levels in situ. The process outlined in this paper indicates that extracting the features from accelerometer data with a 9.5-h window size provided the sufficient feature space to fit regression models. By applying graph representation learning, the results indicate that the automatic feature engineering approaches of FeatherGraph and Geoscattering provided the smallest error when using accelerometer data to predict cortisol levels. Furthermore, the random forest feature importance analysis for handcrafted features showed that features that captured motion signal amplitude contributed the most to the prediction of saliva cortisol levels (Fig. 7), suggesting that physical motion could be a strong predictor of salivary cortisol levels.
A major contribution of the proposed process is to enable researchers and clinicians a way to potentially track cortisol in the body with minimal measurement burden. By leveraging passive data streams from wearables, there is an opportunity to bypass costly and inefficient saliva collection and assays. Providing a convenient and accessible way to approximate cortisol is particularly important for cancer patients, who experience significantly greater levels of burden and distress than the general population.
Although the current paper uses data from 10 adults newly diagnosed with pancreatic cancer, our results support the feasibility of a process that uses passively sensed data from wearables to approximate salivary cortisol levels throughout the day. Our findings suggest that automatic feature engineering and machine learning approaches can be applied to temporally dense actigraphy data to predict cortisol levels, although future studies should apply this process to a larger number of patients to determine the reliability of these findings.
Limitations and Future Directions
In addition to those mentioned, the current work should be evaluated in light of some limitations. The size of the learning samples are relative small which may limit generalizability. In the future, this can be mitigated by recruiting more participants or exploring the use of other machine learning methods that can train more robust models in small datasets. Graph representation learning methods does not consider the semantic information of each vertex of the the graphs. This means that the concepts that are represented by vertices cannot be captured by graph representation learning. In addition, hyperparameter optimization (such as min observation, max depth in G-means) and feature selection were not performed given their needs for a powerful computing source.
In a study of predictive modeling of saliva cortisol levels in real time, multimodal sensors (such as heart rate, galvanic skin response) can be applied to extract more related features to further increase prediction accuracy. Further, personalized machine learning models by using transfer learning can be used to build personalized cortisol level machine learning models to address individual characteristics.
Finally, our results suggest that the degree of error in predicting cortisol levels from passively collected data varies at different times throughout the day. Future work should examine the clinical implications of larger versus smaller errors in prediction, which likely depends in part on the way the information is being used in a clinical setting. For example, predictions with larger (vs. smaller) measurement error are still important if the goal is to understand the general trajectory of a patient’s cortisol levels throughout treatment. By contrast, such predictions have limited utility if the intention is to intervene when cortisol levels reach a specific value or at a specific time, with minimal room for error.
Conclusion
In this paper, we propose a general predictive modeling process that uses passively sensed actigraphy data to predict saliva cortisol levels. The proposed process enables researchers to optimize the window size for feature space and selection of sensors to identify the sufficient combination of window size and sensor with the lowest testing error. We demonstrate that GRL can outperform handcrafted feature engineering by generating unsupervised learned graph features to train machine learning models with the lowest MAE.
Acknowledgements
We wish to acknowledge the UVA Clinical Trials Unit for their assistance with patient recruitment.
Funding
This work was possible through a seed grant from the UVA Cancer Center.
Declarations
Conflict of Interest
The authors declare no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Adam EK, Quinn ME, Tavernier R, McQuillan MT, Dahlke KA, Gilbert KE. Diurnal cortisol slopes and mental and physical health outcomes: a systematic review and meta-analysis. Psychoneuroendocrinology. 2017;83:25–41. doi: 10.1016/j.psyneuen.2017.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alghadir AH, Gabr SA, Aly FA. The effects of four weeks aerobic training on saliva cortisol and testosterone in young healthy persons. J Phys Therapy Sci. 2015;27(7):2029–2033. doi: 10.1589/jpts.27.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Allende S, Medina J L, Spiegel D, Zeitzer J M (2020) Evening salivary cortisol as a single stress marker in women with metastatic breast cancer. Psychoneuroendocrinology 104648 [DOI] [PubMed]
- 4.Bardram JE, Matic A. A decade of ubiquitous computing research in mental health. IEEE Pervas Comput. 2020;19(1):62–72. doi: 10.1109/MPRV.2019.2925338. [DOI] [Google Scholar]
- 5.Bastien CH, Vallières A, Morin CM. Validation of the insomnia severity index as an outcome measure for insomnia research. Sleep Med. 2001;2(4):297–307. doi: 10.1016/S1389-9457(00)00065-4. [DOI] [PubMed] [Google Scholar]
- 6.Canzian L, Musolesi M (2015) Trajectories of depression: unobtrusive monitoring of depressive states by means of smartphone mobility traces analysis. In: Proceedings of the 2015 ACM international joint conference on pervasive and ubiquitous computing, pp 1293–1304
- 7.Chen F, Wang Y C, Wang B, Kuo C C J (2020) Graph representation learning: a survey. APSIPA Trans Signal Inf Process:9
- 8.Chen T, Guestrin C (2016) Xgboost: A scalable tree boosting system. In: Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, pp 785–794
- 9.Chen Z, Zhang L, Cao Z, Guo J. Distilling the knowledge from handcrafted features for human activity recognition. IEEE Trans Ind Inf. 2018;14(10):4334–4342. doi: 10.1109/TII.2018.2789925. [DOI] [Google Scholar]
- 10.Cornet VP, Holden RJ. Systematic review of smartphone-based passive sensing for health and wellbeing. J Biomed Inf. 2018;77:120–132. doi: 10.1016/j.jbi.2017.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Drucker H, Burges CJ, Kaufman L, Smola AJ, Vapnik V (1997) Support vector regression machines. In: Advances in neural information processing systems, pp 155–161
- 12.Gao F, Wolf G, Hirn M (2019) Geometric scattering for graph data analysis. In: International Conference on Machine Learning, pp 2122–2131
- 13.Hamerly G, Elkan C (2004) Learning the k in k-means. In: Advances in neural information processing systems, pp 281–288
- 14.Hellhammer DH, Wüst S, Kudielka BM. Salivary cortisol as a biomarker in stress research. Psychoneuroendocrinology. 2009;34(2):163–171. doi: 10.1016/j.psyneuen.2008.10.026. [DOI] [PubMed] [Google Scholar]
- 15.Hoerl AE, Kennard RW. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics. 1970;12(1):55–67. doi: 10.1080/00401706.1970.10488634. [DOI] [Google Scholar]
- 16.Huang Y, Skatova A, Bedwell B, Rodden T, Shipp V, Bertenshaw E (2015) Designing for human sustainability: The role of self-reflection. In: Proceedings of the 17th International Conference on Human-Computer Interaction with Mobile Devices and Services Adjunct, pp 1042–1045
- 17.Hulett JM, Fessele KL, Clayton MF, Eaton LH. Rigor and reproducibility: a systematic review of salivary cortisol sampling and reporting parameters used in cancer survivorship research. Biol Res Nurs. 2019;21(3):318–334. doi: 10.1177/1099800419835321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lane ND, Miluzzo E, Lu H, Peebles D, Choudhury T, Campbell AT. A survey of mobile phone sensing. IEEE Commun Mag. 2010;48(9):140–150. doi: 10.1109/MCOM.2010.5560598. [DOI] [Google Scholar]
- 19.Le Q, Mikolov T (2014) Distributed representations of sentences and documents. In: International conference on machine learning, pp 1188–1196
- 20.Li B, Pi D (2020) Network representation learning: a systematic literature review. Neural Comput Appl:1–33
- 21.Liaw A, Wiener M, et al. Classification and regression by randomforest. R. 2002;2(3):18–22. [Google Scholar]
- 22.Yz Lin, Nie Zh, Ma Hw. Structural damage detection with automatic feature-extraction through deep learning. Comput-Aided Civ Infrastruct Eng. 2017;32(12):1025–1046. doi: 10.1111/mice.12313. [DOI] [Google Scholar]
- 23.Martens B, Drebert Z. Glucocorticoid-mediated effects on angiogenesis in solid tumors. J Steroid Biochem Mol Biol. 2019;188:147–155. doi: 10.1016/j.jsbmb.2019.01.009. [DOI] [PubMed] [Google Scholar]
- 24.McGuigan MR, Egan AD, Foster C. Salivary cortisol responses and perceived exertion during high intensity and low intensity bouts of resistance exercise. J Sports Sci Med. 2004;3(1):8. [PMC free article] [PubMed] [Google Scholar]
- 25.Mohr DC, Zhang M, Schueller SM. Personal sensing: understanding mental health using ubiquitous sensors and machine learning. Ann Rev Clin Psychol. 2017;13:23–47. doi: 10.1146/annurev-clinpsy-032816-044949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mukhopadhyay S, Postolache OA (2014) Pervasive and mobile sensing and computing for healthcare. Technolo Soc Issues
- 27.Murtagh F. Multilayer perceptrons for classification and regression. Neurocomputing. 1991;2(5-6):183–197. doi: 10.1016/0925-2312(91)90023-5. [DOI] [Google Scholar]
- 28.Narayanan A, Chandramohan M, Venkatesan R, Chen L, Liu Y, Jaiswal S (2017) graph2vec: Learning distributed representations of graphs. In: Proceedings of the 13th International Workshop on Mining and Learning with Graphs (MLG)
- 29.Rawla P, Sunkara T, Gaduputi V. Epidemiology of pancreatic cancer: global trends, etiology and risk factors. World J Oncol. 2019;10(1):10. doi: 10.14740/wjon1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ronao CA, Cho SB. Human activity recognition with smartphone sensors using deep learning neural networks. Expert Syst Appl. 2016;59:235–244. doi: 10.1016/j.eswa.2016.04.032. [DOI] [Google Scholar]
- 31.Rozemberczki B, Sarkar R (2020) Characteristic functions on graphs: Birds of a feather, from statistical descriptors to parametric models. arXiv:200507959
- 32.Schlotz W, Hammerfald K, Ehlert U, Gaab J. Individual differences in the cortisol response to stress in young healthy men: Testing the roles of perceived stress reactivity and threat appraisal using multiphase latent growth curve modeling. Biol Psychol. 2011;87(2):257–264. doi: 10.1016/j.biopsycho.2011.03.005. [DOI] [PubMed] [Google Scholar]
- 33.Sephton SE, Sapolsky RM, Kraemer HC, Spiegel D. Diurnal cortisol rhythm as a predictor of breast cancer survival. J Natl Cancer Inst. 2000;92(12):994–1000. doi: 10.1093/jnci/92.12.994. [DOI] [PubMed] [Google Scholar]
- 34.Seppälä J, De Vita I, Jämsä T, Miettunen J, Isohanni M, Rubinstein K, Feldman Y, Grasa E, Corripio I, Berdun J, et al. Mobile phone and wearable sensor-based mhealth approaches for psychiatric disorders and symptoms: systematic review. JMIR Mental Health. 2019;6(2):e9819. doi: 10.2196/mental.9819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Steeves JA, Bowles HR, Mcclain JJ, Dodd KW, Brychta RJ, Wang J, Chen KY. Ability of thigh-worn actigraph and activpal monitors to classify posture and motion. Med Sci Sports Exercise. 2015;47(5):952. doi: 10.1249/MSS.0000000000000497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Teychenne M, Ball K, Salmon J. Sedentary behavior and depression among adults: a review. Int J Behav Med. 2010;17(4):246–254. doi: 10.1007/s12529-010-9075-z. [DOI] [PubMed] [Google Scholar]
- 37.Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc Ser B (Methodol) 1996;58(1):267–288. [Google Scholar]
- 38.Trifan A, Oliveira M, Oliveira JL. Passive sensing of health outcomes through smartphones: systematic review of current solutions and possible limitations. JMIR mHealth uHealth. 2019;7(8):e12649. doi: 10.2196/12649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tsitsulin A, Mottin D, Karras P, Bronstein A, Müller E (2018) Netlsd: hearing the shape of a graph. In: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp 2347–2356
- 40.Varatharajan R, Manogaran G, Priyan MK, Sundarasekar R. Wearable sensor devices for early detection of alzheimer disease using dynamic time warping algorithm. Clust Comput. 2018;21(1):681–690. doi: 10.1007/s10586-017-0977-2. [DOI] [Google Scholar]
- 41.Wang J, Chen Y, Hao S, Peng X, Hu L. Deep learning for sensor-based activity recognition: a survey. Pattern Recogn Lett. 2019;119:3–11. doi: 10.1016/j.patrec.2018.02.010. [DOI] [Google Scholar]
- 42.Wang R, Wang W, Aung MS, Ben-Zeev D, Brian R, Campbell AT, Choudhury T, Hauser M, Kane J, Scherer EA, et al. Predicting symptom trajectories of schizophrenia using mobile sensing. Proc ACM Interact Mob Wearable Ubiquit Technol. 2017;1(3):1–24. [Google Scholar]
- 43.Wu W, He X, Yang L, Wang Q, Bian X, Ye J, Li Y, Li L. Rising trends in pancreatic cancer incidence and mortality in 2000–2014. Clin Epidemiol. 2018;10:789. doi: 10.2147/CLEP.S160018. [DOI] [PMC free article] [PubMed] [Google Scholar]