Abstract
People of rural India often suffer from acute health conditions like diarrhea, flu, lung congestion, and anemia, but they are not receiving treatment even at primary level due to scarcity of doctors and health infrastructure in remote villages. Health workers are involved in diagnosing the patients based on the symptoms and physiological signs. However, due to inadequate domain knowledge, lack of expertise, and error in measuring the health data, uncertainty creeps in the decision space, resulting many false cases in predicting the diseases. The paper proposes an uncertainty management technique using fuzzy and rough set theory to diagnose the patients with minimum false-positive and false-negative cases. We use fuzzy variables with proper semantic to represent the vagueness of input data, appearing due to measurement error. We derive initial degree of belonging of each patient in two different disease class labels (YES/NO) using the fuzzified input data. Next, we apply rough set theory to manage uncertainty in diagnosing the diseases by learning approximations of the decision boundary between the two class labels. The optimum lower and upper approximation membership functions for each disease class label have been obtained using Non-dominated Sorting Genetic Algorithm-II (NSGA-II). Finally, using the proposed disease_similarity_factor, new patients are diagnosed precisely with 98% accuracy and minimum false cases.
Keywords: Boundary uncertainty, Rough set theory, Fuzzy set, Rural healthcare, Optimization
Introduction
Uncertainty is a state, occurred due to lack of knowledge and incomplete information about a problem domain. Uncertainty in healthcare receives wide attention, and researchers look at it from different perspectives, as there are multiple possibilities of creeping uncertainty in this domain. Uncertainty depends on the precision and standardization of the medical equipment, patients’ inability to express their discomfort precisely, and observations by doctors and nurses that may lead to ambiguous decisions. Laboratory reports often have chance to provide a certain degree of error, and no one can exactly determine one’s prognosis. Uncertainty may be the consequence of lack of knowledge of the agents who analyze the facts. Due to various reasons, uncertainty appears in the healthcare domain, resulting inaccurate diagnoses of the patients.
The problem is even worse in rural areas where dearth of experts, limited facilities, and patients’ lack of awareness are the reality, attracting researchers to provide cost-effective solutions to the patients of remote places. At present, health kiosks are set up in remote villages of India, and using different sensors, health assistants measure basic physiological signals like blood pressure, pulse rate, height, weight, SpO2, and body temperature of the people, visiting in the kiosks [1]. The data are collected from rural India, where more than 31.4% of that population suffers from infectious diseases, like “diarrhea” and “flu,” 9.9% from “gastrointestinal disorders,” and 4.2% from respiratory diseases [2]. Studies are conducted on the people of rural India, revealing that the prevalence rate, ranging from 0.2 to 6%, suffers from severe anemia and the disease is very common among adolescent girls which is the cause of many severe health-related issues [3].
Patients often fail to precisely understand or express the sign of their discomfort, which are hidden variables (symptoms/signs) and play a crucial role in diagnosing the diseases. In remote areas, the health assistants, due to their lack of experience and medical knowledge, fail to observe the same, resulting misdiagnosis of the patients. For instance, the primary symptom of viral gastroenteritis (stomach flu) is “diarrhea” (non-bloody). Nausea, vomiting, and abdominal cramping may also accompany “diarrhea.” Mild fever (about 100 F or 37.77 C), chills, headache, and muscle aches along with tiredness may occur in some individuals with viral gastroenteritis but are not considered by the health assistants for diagnosis. Early “flu” symptoms can affect the throat and chest. Some strains of the virus can cause “diarrhea” with sign of nausea, stomach pain, or vomiting. Thus, viral gastroenteritis has a chance to be misdiagnosed with “diarrhea” or “flu.” On the other hand, chest pain (lung congestion) and “diarrhea” are common health issues; however, there is rarely a relationship between the symptoms, according to 2014 study published in the Journal of Emergency Medicine [4]. The other observation is that the patients having flu very rarely are misdiagnosed with “anemia.” Autoimmune hemolytic anemia (AIHA) is characterized by the temperature at which the auto-antibody has the greatest avidity for the target red cell antigen, either warm or cold forms. There have been few case reports describing influenza as a cause of cold agglutinin hemolytic anemia. In maximum cases, the clinical eyes of the doctors can extract the hidden features and diagnose the conditions precisely. However, due to scarcity of doctors in remote areas, health workers are engaged to diagnose the diseases, with high chance of false-positive or false-negative cases.
Regular consultations with doctors are held to understand the remote healthcare framework potential applications. In the paper, an expert is defined as a licensed medical practitioner who examines the material facts of medical-related cases and whose skills and experience qualify them to testify in the medical domain. In particular, doctors from different government and private hospitals are integrated into the system as resource providers, i.e., their domain expertise is used to deliver healthcare services. Prof. (Dr.) Satadal Saha (MS, FRCS (Eng), Honorary Professor, Centre for Nanotechnology, IIT Guwahati, Founder, JSV Innovations Pvt. Ltd., Vice-President, Foundation for Innovations in Health) provides us his expertise in this framework, with a focus on developing community-based healthcare models. Dr. Suman Mallik (MD, DNB, PDCR Consultant) is a senior consultant, Radiation Oncologist of NH Cancer Institute (formerly West bank Cancer Centre); is a member of the Association of Radiation Oncologist of India (AROI), European society for Radiotherapy and Oncology (ESTRO), American Society for Radiation Oncology (ASTRO), and American Brachytherapy Society (ABS); and is also associated with us as an expert. Based on the study and consulting with the experts, we propose the model for diagnosing the common diseases like “flu,” “diarrhea,” “lung congestion,” “anemia,” and “gastrointestinal disorders” with disease class label YES or NO. Here “gastrointestinal disorders” possibly are misdiagnosed with “diarrhea” or “flu.” Through interaction with the patients, the health workers note basic symptoms like cold, breathlessness, body ache, headache, nausea, and abdominal pain. Based on their knowledge and by analyzing the input data, they try to diagnose the patients. However, the measured values are often incorrect due to lack of precision of the sensors, resulting errors in the input data. In such cases, prediction made by the health workers into YES/NO disease class label is not correct, and often for the same input data, the patients are diagnosed differently.
The ultimate goal of disease diagnosis is to minimize the classification error by learning parameters of the classifiers. The estimation of parameters under uncertainty was viewed as a probabilistic problem [5]. However, this approach requires a huge number of training samples for different classes, and we assume feature independencies. But in practical situations, only a finite number of samples are available, which results in a chance of underfitting [6]. Moreover, the dependency among the symptoms is to be considered for predicting the diseases more accurately. Multi-sensor data fusion algorithms reduce the uncertainty by combining data from multiple independent sources, therefore may be inconsistent. Other methods, such as fuzzy set theory and belief measures, are used to model the vague health data set, but they rely on subjective knowledge and human perception. Rough set theory (RST) [7] has been applied to discover structural relationships within imprecise and incomplete data without additional information about the experimental data. Based on Pawlak’s [8] RST, uncertainty in the concepts is described using lower and upper approximation sets, which are crisps. However, in healthcare, the concept as perceived by the health workers is often uncertain, therefore not possible to diagnose the patients into two crisp sets as diseased (YES) or not (NO). Rough fuzzy set theory [9] is applied to address the issue where lower and upper approximation sets representing the uncertain concepts are defined as a pair of fuzzy sets. The membership function of each such fuzzy set is derived based on the approximation space with many membership functions by applying the infimum or supremum operators, ignoring the degree of belonging of individual patients in a particular class label.
Approximation of concepts is an approach to dealing with uncertainty in domain knowledge where data semantics are the primary concern. Semantic is domain and context-dependent; therefore, human intelligence or experts play a crucial role if the concepts do not have well-defined boundaries. In rural areas, dearth of experts is evident, and it becomes a real challenge in healthcare domain to provide services to poor people in a cost-effective manner. Our previous work, “Managing Uncertainty to Rural Primary Health Care using Rough Set Theory” (RSTA) [10], developed rough set theory (RST)-based techniques to managing uncertainty in healthcare for the patients of rural India. Here based on the proposed index, patients in the boundary region (BR) who are not certainly diagnosed might be moved to the positive region (PR), where patients are certainly diagnosed. In one of our recent works, “Knowledge uncertainty management in remote healthcare based on mutual information” (KUMI) [11], information content of the patients in the BR is assessed using mutual information (MI) with respect to the information content of the patients in the PR. Patients with the highest information content residing in the BR have been inducted in the PR, thereby reducing uncertainty in diagnosing the patients.
In the paper, we deal with two types of uncertainty, (a) vagueness in symptoms and physiological signs related to the measurement error and (b) uncertainty in decision space due to incomplete domain knowledge of the health assistants. Contributions of the paper to address the scope of the work are given below.
-
(i)
In order to deal with vagueness in the input dataset, symptoms and physiological signals are represented using semantically appropriate fuzzy variables in reference to the respective standard value.
-
(ii)
The degree of belonging of each patient into two different disease class labels (YES, NO) has been derived using the input data instead of setting discrete labels.
-
(iii)
Uncertainty in the decision space has been dealt with by applying RST where the target sets are partitioned into lower and upper approximation sets, which are fuzzy, unlike crisp sets of Pawlak’s RST [8].
-
(iv)
We apply Non-dominated Sorting Genetic Algorithm-II (NSGA-II) [12] to obtain the optimal membership value of the fuzzy sets by maximizing lower approximation and minimizing upper approximation membership functions.
-
(v)
Using the proposed disease_similarity_factor, new patients are diagnosed with sufficient margin between the two class labels of each disease, which minimizes the false-positive and negative cases.
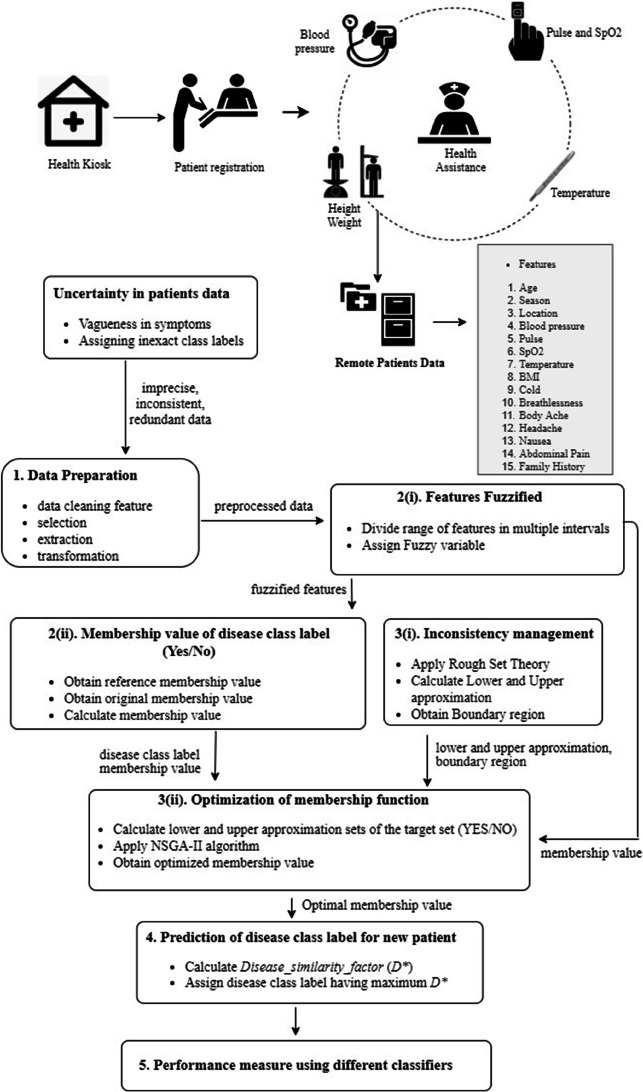
Block diagram of different steps of the proposed methodology is shown in Fig. 1.
Fig. 1.
Block diagram of the proposed methodology
The paper is organized as follows: Section 2 explains the related methods reported in the literature to deal with uncertainty in healthcare. Section 3 describes the method to handle vagueness in input variables that arises due to measurement errors. Management of uncertainty in decision-making to diagnose the patients has been presented in Section 4. Section 5 describes the method of determining the disease class label of the test data and functioning of the classifiers. Section 6 presents the experimental results, and discussions on the results are provided in Section 7. Finally, conclusion appears in Section 8.
Literature Review
Uncertainty in healthcare emerges in situations when it is difficult to diagnose the diseases due to probability variation, high ambiguity, and intricate complexity related to the variables, correlation between the variables, and incomplete knowledge or unknown disease trajectory. In 1957, Renee Fox [13] classified uncertainty into three parts that mainly focused on the impossibility of acquiring the knowledge and complex skills required to tackle medical understanding. In 1979, Light [14] considered five areas where medical students experience uncertainty based on clinical reasoning. On the other hand, a conceptual framework has been proposed by Beresford [15] for the types of clinical uncertainty, which includes conceptual uncertainty (the inability to apply abstract knowledge to concrete situations), technical uncertainty (the absence of scientific data or practical skill), and personal uncertainty (the lack of previous relationship with a patient and knowledge of healthcare assistant). In 2008, Farnan et al. [16] further qualify the domains of Beresford’s model by relating uncertainty to the following six categories: transitions of care, diagnostic decision-making and management conflict (conceptual uncertainty), procedural skills and knowledge of indications (technical uncertainty), and goals of care (personal uncertainty). Further, Hamui and Sutton et al. [17] developed Beresford’s model to include five types of uncertainty. Han et al. [18] proposed a structure of uncertainty in healthcare, which considers the concept along three dimensions: (a) source of uncertainty, (b) substantive issue that gives rise to the uncertainty, and (c) the locus of uncertainty. Managing diagnostic uncertainty in healthcare is special and has warranty consequences that motivate each event to take different actions. Inadequate diagnostic uncertainty management techniques may affect the outcomes. The paper [19] discusses the nature of uncertainty issues delineated in the developed taxonomy across a variety of healthcare fields, professions, and countries. The paper [20] highlights the ubiquitous existence and recognition of irreducible uncertainty in various fields of science, classifies uncertainty depending on perception, and discusses the perspectives and effects of understanding on healthcare practice, healthcare administration, physician–patient contact, basic science research, and clinical investigation. In healthcare, uncertainty tolerance [21, 22] is considered a feature of individuals affecting various outcomes related to wellness.
Systematic assessment of clinical decision support systems (CDSS) [23] defines and proposes potential care for patients based on collected information from the patients, but it needs careful design, implementation, and critical evaluation. Neural network [24], genetic algorithms [25], decision trees [26], and fuzzy set theory [27] are commonly used in medical data analysis under uncertainty. To control uncertainty in predictive healthcare, machine learning methods [28] were studied with the benefits of early disease identification, patient care, and community services. All the existing data analysis approaches are primarily based on assumptions and require large number of experiments, otherwise fail to conclude in the presence of incomplete information.
Pawlak introduced rough sets [29], a mathematical model for processing incomplete information and applying it to extract knowledge. Indiscernible or equivalence relation is the key notion in Pawlak’s rough set model, and various extended models are proposed by different authors, roughly classified into three categories [30–32]: (a) direct extension, (b) the extension in certainty environment, and (c) the extension in uncertainty environment. The first category includes precision rough set [30], probabilistic rough set [33], decision rough set [34], decision-theoretic rough set [35], and parameterized decision-theoretic rough set [36]. In the second category, the generalized rough set [37] is an extension of Pawlak’s rough set obtained by replacing indiscernible relation with generalization relation. Tolerance rough set [38] is an extension of rough set obtained by replacing equivalence relation with tolerance relation and used to measure similarity relation, whereas dominance rough set [39] generalizes rough sets by replacing equivalence relation with dominance relation. In the third category, the rough fuzzy set [40] is extended from Pawlak’s rough set by replacing the crisp target concept to deal with the fuzzy target concept. The fuzzy rough set [41] is extended from rough set by replacing equivalence relation with fuzzy similarity relation. Fuzzy binary relation is employed to characterize the similarity between samples and replace crisp target with fuzzy concept. Rough fuzzy set is a special case of fuzzy rough set.
Uncertainty has been described in rough set theory by lower and upper approximation sets, where the target sets have different decision attribute values for the same set of condition features. However, in many applications, the states of the target concept may be uncertain and fuzzy in practice. To address this problem, Dubois and Prade suggested rough fuzzy set [42] to deal with the target concept, which is fuzzy or uncertain. In rough fuzzy sets, the lower and upper approximation fuzzy sets are considered two boundary fuzzy sets of the target concept. Many researchers have been drawing attention to the uncertainty measurement using rough fuzzy set model since it extracts precise rules from the decision systems. A rough extension of entropy is proposed by Maratea and Ferone [43] to measure uncertainty and ambiguity of samples using lower and upper approximation of rough fuzzy set. New lower and upper approximation operators proposed by Beg and Rashid [44] are a modified soft rough fuzzy set model, which provides better approximations of undefinable sets. Based on rough entropy and information entropy, Wang [45] introduced a method that addressed the uncertainty measure of rough fuzzy sets. Combining the rough degree with the rough entropy, Qin [46] proposed new rough entropy that can measure rough degree induced by boundary region of fuzzy target as well as roughness from knowledge classification. Sun [47] implemented a generalized rough fuzzy sets uncertainty measure based on the Shannon entropy which is efficient and suitable for evaluating the roughness and accuracy of generalized rough fuzzy sets. From a distance perspective, Hu [48] studied the roughness measure of rough fuzzy sets and applied it to incomplete fuzzy decision-making information systems. In the paper [49], an attribute-oriented rough fuzzy set method is applied to solve decision-making problems with multiple attributes, while the paper [50] explores variable precision multigranulation rough fuzzy set approach to multiple attribute group decision-making with uncertainty. To handle uncertainty, rough fuzzy diagraph based method is applied in the paper [51].
However, there exist several shortcomings in the current research on uncertainty measures of rough fuzzy sets in the field of medical diagnosis [52], decision-making [53], and feature selection [54]. Lack of theoretical analysis in the uncertainty of rough fuzzy set is difficult for decision-making precisely. In the view of traditional uncertainty measures, two rough approximation spaces with the same uncertainty are not necessarily equivalent, and the difference between them is difficult to reflect in decision-making. Information-based research using rough set [53] helped medical experts by defining associations between various medical factors to prevent false findings. Identifying minimum sets of clinical measures that impact disease identification, diagnosis, and prediction is the real challenge to deliver cost-effective healthcare systems.
Availability of health dataset is also an issue because rural people do not have much health awareness, and due to limited infrastructure, a large section of people are not tested regularly. Therefore, there is room for research opportunities to develop autonomous systems that address the vulnerability of primary healthcare. Outlier detection [55, 56] refers to the process of identifying the rare objects, here patients (fewer in numbers) in the data set and in general we remove the outlying objects to purify the data for further processing. Outlier detection methods [57–61] have been classified into different techniques such as statistical-based methods, distance-based methods, graphical-based methods, geometric-based methods, depth-based methods, profiling methods, and model-based and density-based methods. Outlier detection is an essential and extensive research branch due to its widespread use in a wide range of applications [62–64]. Outlier detection is important in healthcare [65, 66] in order to obtain significant information, which is often critical. In healthcare databases, outlier detection techniques are used to detect anomalous patterns in the patient records, containing valuable data, for example, rare disease symptoms.
Fuzzy and probability-based methods are available in the remote health field to control uncertainty. However, establishing relationships among the clinical parameters and finding the membership or probability to measure the degree of belongings of the patients into two different disease class labels create a bottleneck for the development of autonomous primary healthcare systems. The status of the target definition is often ambiguous and vague in real-life applications of decision-making. This problem has been tackled by proposing the rough fuzzy set (RFS) [40], which defines the target set as fuzzy. Nevertheless, boundary uncertainty management problem in remote healthcare has not yet been discussed for predicting disease class label of the patients in the presence of symptoms, which are often vague. The paper aims to manage vagueness in input feature space and reduces boundary uncertainty by optimizing the approximations of decision space so that false-negative outcomes are minimized.
Managing Vagueness in Input Variables
Feature Representation
In rural areas, scarcity of doctors hinders people from accessing basic health services. Rural people with basic school level education are trained to measure health-related features (e.g., blood pressure, pulse, temperature, SpO2, and other measurements), and after training, they acquire basic health knowledge. The trained personnel are deployed in health kiosks as health assistants. Health kiosks with minimum health infrastructure are located in different rural areas, viz., Sundarban (21° 57′ N, 87° 11′ E), Barhra (23.7° N, 87.86° E), Suri (23.910° N, 87.527° E), and Sitalkuchi (26° 10′ N, 89° 11′ E). Health assistants collect basic health data of the patients using different sensing devices (blood pressure monitor, Pulse_Oximeter monitor, SpO2 monitor, etc.) who visit the health kiosks. In some medical kiosks, health assistants also collect health data for regular health checkups of rural people. The data are collected either from the kiosks, or the health workers move from door to door with portable sensing devices and consult with the expert doctors as and when required.
Table 1 shows the descriptive summaries of patient features. In this paper, we analyze 5500 patients’ data, which include features like gender (male, female, and others), relationship status (single, married, and others), occupation (currently employed, currently unemployed, retired, and others), family income per month, age, and education (moderate, poor). We collect associated information of the patients such as the season (summer, monsoon, autumn, winter) in which the patients visit the kiosk and their location, shown in Table 1. Basic signs or symptoms (cold, breathlessness, headache, body ache, nausea, abdominal pain) and family history (asthma and allergies, diabetes, habits such as smoking, drinking, heart disease, and history of surgeries) are also included to give demographic information of the patients (Table 1). Among 5500 patients, 3800 are males, 1700 are females, 2695 are single, 1463 are married, and 1342 are others. We also register the features such as 64.38% employed, 22.58% unemployed, 9.09% retired, and 14.23% others. For example, the number and percentage of the patients visiting the kiosks in summer are 1193, i.e., 21.69%.
Table 1.
Patient’s characteristics
| Features/unit | Grade/range | Count (%) |
|---|---|---|
| Number of patients: 5500 | ||
| Gender | Male | 3800 (69.09) |
| Female | 1700 (30.9) | |
| Others | None | |
| Occupation | Currently employed | 3541 (64.38) |
| Currently unemployed | 1242 (22.58) | |
| Retired | 500 (9.09) | |
| Others | 783 (14.23) | |
| Age (A)/(years) | 1 ≤ A < 12 | 610 (11.09) |
| 12 ≤ A < 20 | 609 (11.07) | |
| 20 ≤ A < 40 | 1454 (26.43) | |
| 40 ≤ A < 60 | 1374 (24.98) | |
| 60 ≤ A < 70 | 789 (14.34) | |
| A ≥ 70 | 664 (12.07) | |
| Season (S)/(month) | Summer | 1193 (21.69) |
| Monsoon | 2347 (42.67) | |
| Autumn | 1024 (18.62) | |
| Winter | 936 (17.01) | |
| Location (L) with respect to sea level/(meter) | 0 < L ≤ 1500 | 2000 (36.36) |
| 1500 ≤ L < 2400 | 1500 (27.27) | |
| 2400 ≤ L < 5000 | 1200 (21.81) | |
| L ≥ 5000 | 800 (14.54) | |
| BMI/(kg/m2) | BMI < 16 | 695 (12.63) |
| 16 ≤ BMI < 18.5 | 1943 (35.32) | |
| 18.5 ≤ BMI < 25 | 2104 (38.25) | |
| 25 ≤ BMI < 30 | 614 (11.16) | |
| BMI ≥ 30 | 144 (2.61) | |
| Cold/(grades) | None | 1519 (27.61) |
| Sore throat | 1209 (21.98) | |
| Nasal congestion | 1065 (19.36) | |
| Runny nose | 1230 (22.36) | |
| Sneezing | 477 (8.67) | |
| Body ache (BA)/(grades) | None | 1862 (33.85) |
| Acute | 2097 (38.12) | |
| Chronic | 1541 (28.01) | |
| Nausea (N)/(grades) | None | 1745 (31.72) |
| Mild | 1239 (22.52) | |
| Acute | 1348 (24.51) | |
| Severe | 1168 (21.23) | |
| Asthma and allergies | Yes | 2414 (43.89) |
| No | 3086 (56.11) | |
| Diabetes/sugar disease | Yes | 2286 (41.56) |
| No | 3214 (58.44) | |
| Habits (such as smoking, drinking) | Yes | 3786 (68.84) |
| No | 1714 (31.16) | |
| Relationship status | Single | 2695 (49) |
| Married | 1463 (26.6) | |
| Others | 1342 (24.4) | |
| Family income (FI) per months (Rs) | FI < 5000 | 2037 (37.03) |
| 5000 ≤ FI < 25,000 | 1649 (29.98) | |
| 25,000 ≤ FI < 50,000 | 1045 (19) | |
| FI ≥ 50,000 | 769 (13.98) | |
| Systolic (BPS)/diastolic (BPD)/(mmHG) | BPS < 90/BPD < 60 | 941 (17.10) |
| 90 ≤ BPS < 120/60 ≤ BPD < 80 | 1564 (29.43) | |
| 120 ≤ BPS < 140/80 ≤ BPD < 100 | 1431 (26.01) | |
| 140 ≤ BPS < 160/100 ≤ BPD < 110 | 1008 (18.32) | |
| 160 ≤ BPS < 180/110 ≤ BPD < 120 | 463 (8.42) | |
| BPS ≥ 180/BPD ≥ 120 | 143 (2.6) | |
| Pulse (PU)/(bpm) | PU < 60 | 503 (9.14) |
| 60 ≤ PU < 73 | 956 (17.38) | |
| 73 ≤ PU < 83 | 3259 (59.25) | |
| PU ≥ 83 | 782 (14.21) | |
| SpO2 (SO)/(percentage) | SO < 85 | 547 (9.94) |
| 85 ≤ SO < 90 | 1102 (20.03) | |
| 90 ≤ SO < 95 | 1753 (31.87) | |
| SO ≥ 95 | 2098 (38.14) | |
| Temperature (T)/(degree Fahrenheit) | T < 97 | 93 (1.69) |
| 97 ≤ T < 99.5 | 3101 (56.38) | |
| 99.5 ≤ T < 104 | 2258 (41.05) | |
| T ≥ 104 | 48 (0.87) | |
| Breathlessness (BN)/(grades) | None | 1964 (35.71) |
| Mild | 1505 (27.36) | |
| Moderate | 1543 (28.05) | |
| Severe | 332 (6.03) | |
| Very severe | 156 (2.83) | |
| Headache(H)/(days) | None | 2637 (47.94) |
| Low | 1327 (24.12) | |
| Medium | 1065 (19.36) | |
| Severe | 471 (8.56) | |
| Abdominal pain(AP)/(grades) | None | 1524 (27.71) |
| Mild | 1330 (24.18) | |
| Moderate | 1382 (25.12) | |
| Severe | 1264 (22.98) | |
| Heart disease | Yes | 3247 (59.03) |
| No | 2253 (40.97) | |
| History of surgeries | Yes | 998 (18.15) |
| No | 4502 (81.85) | |
| Education qualification | Moderate | 4872 (88.58) |
| Poor | 628 (11.42) | |
L location, S season, A age, BPS blood pressure systolic, BPD blood pressure diastolic, PU pulse, SO SpO2, T temperature, FI family income, BN breathlessness, H headache, BA body ache, N nausea, AP abdominal pain.
The patients are from different age groups such as child, adolescence, young, middle, senior, and old. When a patient visits at the kiosk, health assistants first collect the following data as (1) picture of the patient, (2) registration of the patient, (3) the status, i.e., new or old patients, (4) date of visit, (5) name of the patient, (6) name of father/mother/husband/wife, (7) address, (8) contact number, and (9) occupation. The health workers measure the health data of the patients, like (1) height and weight, (2) BMI, (3) pulse, (4) temperature, and (5) SpO2 using different sensors and enquire about their family and medical history. Figure 2 shows a sample patient prescription of Barhra health kiosk, established under the sponsored project of Govt. of India.
Fig. 2.
Sample prescription of Barhra Rural Health Kiosk (23.7° N, 87.86° E)
In rural areas, data are collected from the patients, often imprecise, inconsistent, and consist of missing value and redundant too. In addition, the patients’ data are non-homogeneous and may be imbalanced. Therefore, preparation of such data in a homogeneous form is necessary and sampled to remove imbalance problem in the dataset [67] as much as possible. The steps for data preparation include data cleaning (remove redundant features and samples, outlier detection and missing value imputation) [68]. Data is preprocessed that includes the steps of feature selection, extraction, and transformation to obtain important features with suitable representation as feature vectors and used to train the prediction model.
Data cleaning is an operation that is performed first for identifying and correcting the mistakes or errors in the data. There are general data cleaning operations having the steps: first, we define the standard value of the input features in consultation with the experts and medical literature. The data of the patients are collected by the health assistants, and based on the respective standard value, we identify the outliers. Next, the duplicate entry, if any, has been removed. Further, we mark the missing (as shown in Fig. 2 missing symptom of BMI, temperature) and finally imputing missing values using statistics or a learned model. In our previous work [69], imputing missing symptom value is explored using multiple fuzzy-based regression models.
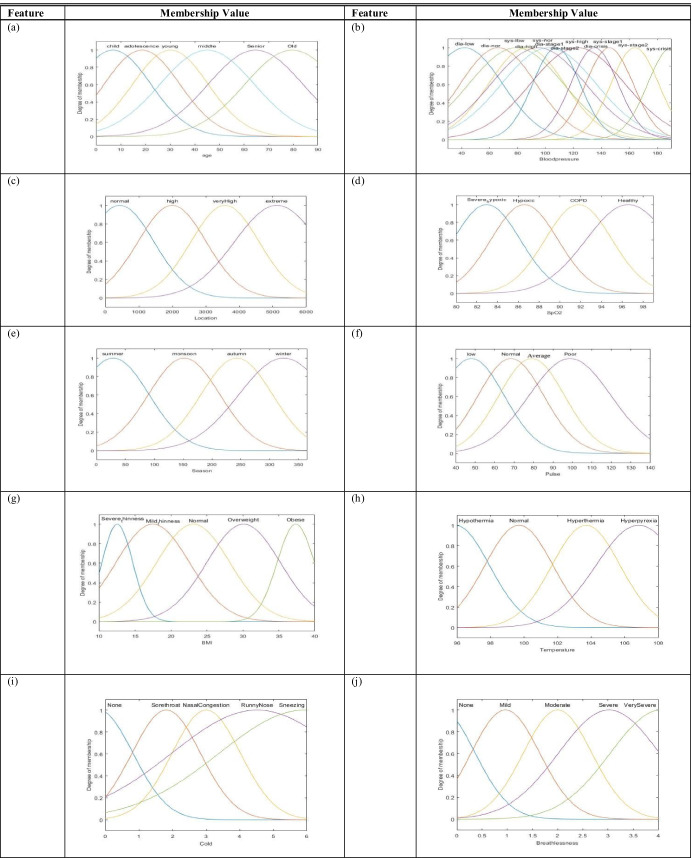
Health workers measure physiological signs of the patients using different sensors and try to interpret the symptoms through interaction with the patients. Due to measurement error and lack of expertise of the health workers, the collected information is unreliable to build a framework for diagnosing the patients of rural areas. In the paper, the measured signals and symptoms of the patients along with other associated attributes like age, location, and seasons are considered to be input features, and patients are objects of the training dataset. We process the measured data by dividing the range of each feature into multiple intervals/levels and assign fuzzy variables to each interval (Table 2) based on the respective standard value available in the literature [70, 71]. Thus, the features are fuzzified (Fig. 3) depending on their property and semantics to represent the vagueness, appearing due to measurement error. In the paper, we consider five diseases as decision attributes like “flu,” “diarrhea,” “lung congestion,” “anemia,” and “gastrointestinal disorders” from which people of rural India suffer.
Table 2.
Discretized features represented using fuzzy variables
| Features/unit | Range | Fuzzy variable |
|---|---|---|
| Age (A)/(years) | 1 ≤ A < 12 | Child |
| 12 ≤ A < 20 | Adolescence | |
| 20 ≤ A < 40 | Young | |
| 40 ≤ A < 60 | Middle | |
| 60 ≤ A < 70 | Senior | |
| A ≥ 70 | Old | |
| Season (S)/(month) | 1st Mar.–31st May | Summer |
| 1st June–31stAug | Monsoon | |
| 1st Sept.–31st Nov | Autumn | |
| 1st Dec.–End_Feb | Winter | |
| Location (L) with respect to sea level/(meter) | 0 < L ≤ 1500 | Normal_level |
| 1500 ≤ L < 2400 | High level | |
| 2400 ≤ L < 5000 | Very high level | |
| L ≥ 5000 | Extreme_level | |
| BMI/(kg/m2) | BMI < 16 | Severe_thinness |
| 16 ≤ BMI < 18.5 | Mild_thinness | |
| 18.5 ≤ BMI < 25 | Normal | |
| 25 ≤ BMI < 30 | Overweight | |
| BMI ≥ 30 | Obese | |
| Cold/(days) | 0 | None |
| 0 ≤ Cold < 3 | Sore throat | |
| 1 ≤ Cold < 3 | Nasal congestion | |
| 3 ≤ Cold < 5 | Runny nose | |
| 4 ≤ Cold < 6 | Sneezing | |
| Body ache (BA)/(days) | 0 ≤ BA < 1 | None |
| 1 ≤ BA < 3 | Acute | |
| 3 ≤ BA < 6 | Chronic | |
| Nausea (N)/(times) | 0 | None |
| 0 ≤ N < 2 | Mild | |
| 2 ≤ N < 4 | Acute | |
| 4 ≤ N < 6 | Severe | |
| Systolic (BPS)/diastolic (BPD)/(mmHG) | BPS < 90/BPD < 60 | Low |
| 90 ≤ BPS < 120/60 ≤ BPD < 80 | Normal | |
| 120 ≤ BPS < 140/80 ≤ BPD < 100 | High | |
| 140 ≤ BPS < 160/100 ≤ BPD < 110 | Stage 1_Hypertensive | |
| 160 ≤ BPS < 180/110 ≤ BPD < 120 | Stage 2_Hypertensive | |
| BPS ≥ 180/BPD ≥ 120 | Crisis_Hypertensive | |
| Pulse (PU)/(bpm) | PU < 60 | Low |
| 60 ≤ PU < 73 | Normal | |
| 73 ≤ PU < 83 | Average | |
| PU ≥ 83 | Poor | |
| SpO2 (SO)/(percentage) | SO < 85 | Severe_hypoxic |
| 85 ≤ SO < 90 | Hypoxic | |
| 90 ≤ SO < 95 | COPD | |
| SO ≥ 95 | Healthy | |
| Temperature (T)/(degree Fahrenheit) | T < 97 | Hypothermia |
| 97 ≤ T < 99.5 | Normal | |
| 99.5 ≤ T < 104 | Hyperthermia | |
| T ≥ 104 | Hyperpyrexia | |
| Breathlessness (BN)/(grades) | 0 | None |
| 0 ≤ BN < 1 | Mild | |
| 1 ≤ BN < 2 | Moderate | |
| 2 ≤ BN < 3 | Severe | |
| 3 ≤ BN < 4 | Very severe | |
| Headache(H)/(days) | 0 | None |
| 0 ≤ H < 2 | Low | |
| 2 ≤ H < 4 | Medium | |
| 4 ≤ H < 6 | Severe | |
| Abdominal pain(AP)/(days) | 0 | None |
| 0 ≤ AP < 2 | Mild | |
| 2 ≤ AP < 4 | Moderate | |
| 4 ≤ AP < 6 | Severe |
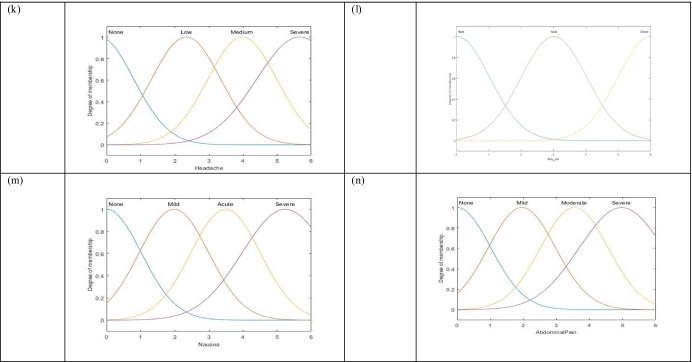
Fig. 3.
Membership functions of features: a age, b blood pressure (systolic/diastolic), c location, d SpO2, e season, f pulse, g BMI, h temperature, i cold, j breathlessness, k headache, l body ache, m, nausea, and n abdominal pain
Membership Value of Disease Class Label
Instead of using discrete class labels (YES/NO) to the patients corresponding to different diseases, we calculate the membership value of each x (x ∈ U, the universe of discourse of patients) belonging to class label YES/NO for a particular disease j by defining Eq. (1):
| 1 |
where l = 1, 2…, N, representing number of features for each observation (patient) in the training dataset. The lth feature value of patient x is used to obtain the reference and original membership value using Table 2, and Fig. 3 is used to calculate and , respectively. The log function is applied to keep the degree of membership value of a particular disease class label in between 0 and 1. Say, k = , therefore, k is always 1 < k < ∞ and so log k is positive assuming that due to measurement error never equals to one or zero, which is certain. Hence, the value of is within the range 0–1 where the numerator is nonzero and ≤ 1. Due to consideration of all features, the summation may be beyond one, and so the summation is divided by the number of features (N) for normalization.
In Eq. (1), each feature is represented by the respective membership value, which implies the weight or degree of contribution of that feature in measuring the membership value of the disease class label. Thus, the impact of each feature is important and contributes to calculating the membership of the respective disease class label value.
The significance of Eq. (1) is to find the membership function of decision attribute value, i.e., whether diseased (YES) or not (NO) by considering the reference value of each symptom within the range 0–1, obtained from the literature [67, 68].
For obtaining the reference membership value, we divide the range of the feature into number of granules and calculate the mid-point of each granule. The midpoint of a particular granule, in which the original feature value lies, is considered for calculating the reference membership value (. For example, normal pulse range is 60–73, which is divided into four granules, i.e., 60–63, 63–66.50, 66.50–69.60, and 69.60–73. Then we evaluate the midpoint of the granules as 61.50, 64.70, 68, and 71, respectively. The reference feature value has been considered the midpoint of the range to which the original feature value of the patient belongs. For obtaining more precision, we may divide the range of a particular symptom/signal into even larger number of granules.
Here we describe how to calculate the degree of membership value of each patient, who may belong to any particular disease class label (YES/NO), using Eq. (1) with an example of Table 3.
Table 3.
Patient data
| Features | Patient | |||||||
|---|---|---|---|---|---|---|---|---|
| P01 | P02 | P03 | P04 | P05 | P06 | P07 | P08 | |
| Associated information | ||||||||
| L | nor_altitude | nor_altitude | nor_altitude | high_altitude | nor_altitude | nor_altitude | nor_altitude | nor_altitude |
| S | Monsoon | Monsoon | Monsoon | Autumn | Summer | Winter | Autumn | Autumn |
| A | Middle | Middle | Middle | Young | Adolescence | Old | Senior | Senior |
| Physiological sign/signals | ||||||||
| BPS | Stage 1_Hypertensive | Stage 1_Hypertensive | Stage 1_Hypertensive | Normal | Low | Very high | Stage 2_Hypertensive | Stage 2_Hypertensive |
| BPD | High | High | High | Normal | Normal | High | Stage 1_Hypertensive | Stage 1_Hypertensive |
| PU | Average | Average | Average | High | Normal | Normal | Poor | Poor |
| SO | Hypoxic | Hypoxic | Hypoxic | Normal | COPD | Severe_hypoxic | Healthy | Healthy |
| T | Normal | Normal | Normal | Normal | High | Normal | Normal | Normal |
| BMI | Normal | Normal | Normal | Normal | Overweight | Mild_thinness | Obese | Obese |
| Symptoms | ||||||||
| Cold | Runny nose | Runny nose | Runny nose | Sore throat | None | Nasal congestion | None | None |
| Breathlessness | Severe | Severe | Severe | None | Very Severe | None | Mild | Mild |
| Body ache | Acute | Acute | Acute | Acute | None | Chronic | None | None |
| Headache | Low | Low | Low | Low | Medium | None | Medium | Medium |
| Nausea | None | None | None | Mild | None | Acute | Mild | Mild |
| Abdominal pain | None | None | None | Mild | None | Severe | None | None |
| Family history | ||||||||
| Asthma and allergies | Yes | Yes | Yes | No | Yes | No | No | No |
| Diabetes/sugar disease | No | No | No | Yes | No | Yes | No | No |
| Habits (such as smoking, drinking) | No | No | No | No | Yes | No | Yes | Yes |
| Heart disease | Yes | Yes | Yes | No | No | Yes | No | No |
| History of surgeries | No | No | No | Yes | No | No | Yes | Yes |
| Decision attribute | ||||||||
| Lung congestion | YES | NO | NO | NO | YES | YES | YES | NO |
L location, S season, A age, BPS blood pressure systolic, BPD blood pressure diastolic, PU pulse, SO SpO2, T temperature.
After field study and based on the opinion of the experts, we consider several features and related diseases, which are common in rural areas. The standard ranges of values for each feature are obtained from the medical literature, like pulse (PU) reading usually varies from 60 to 83 bpm. In consultation with the doctors, rules are framed and we use fuzzy variables with proper semantic to represent impreciseness in measurement, shown in Table 2. For example, if 60 ≤ PU < 73, then it is “average” (fuzzy variable).
Now, when a patient visits to the kiosk, the health workers measure particular features, and fuzzy variables are assigned to the features, using Table 2. Say, patient P01, 50 years of age (A) visited nearest health kiosk from altitude (L) 750 m (from the sea level) in the monsoon season (S). The health workers measured the health data of the patient such as BPS = 155mmHG, BPD = 105mmHG, PU = 80 bpm, SO 89 percentage, T = 98.4 degree Fahrenheit, and BMI = 20 kg/m2. The patient P01 also has symptoms “runny nose cold,” “severe breathlessness (BN),” “acute body ache (BA),” and “low headache (H)” and no symptom of “nausea (N)” and “abdominal pain (AP).” Based on the measured health data, the health assistants predict that the patient P01 may have “lung congestion.”
In order to handle measurement errors, the health data is fuzzified using Table 2. We calculate the membership value of each feature using Fig. 3, such as L = 0.52, S = 0.43, A = 0.5, BPS = 0.65, BPD = 0.56, PU = 0.6, SO = 0.85, T = 0.55, BMI = 0.53, cold = 0.72, BN = 0.82, BA = 0.65, H = 0.3, N = 0.09, and AP = 0.07.
Our next step is to calculate the reference value of corresponding features, respective fuzzy variables, and membership values to determine the degree of belonging of P01 having disease class label “lung congestion = YES” using Eq. (1).
For example, the reference value of feature BPS is calculated as follows: BPS is Stage1_Hypertensive in case of P01, in the range 140mmHG ≤ BPS < 160mmHG, which is divided into four granules (140–144mmHG, 145–149mmHG, 150–154mmHG, 155–159mmHG). We obtain the corresponding midpoints of each granule such as 142mmHG, 147mmHG, 152mmHG, and 157mmHG, respectively. Since the patient P01 has original/actual BPS = 155mmHG, the reference value of BPS is 157 mmHG, which is closest to the original, and the corresponding membership value is 0.6 (Fig. 3). Similarly, the same is calculated for other measured feature values.
Boundary Uncertainty
Decision class values (YES/NO) of the diseases assigned by the health assistants are uncertain, resulting lack of precision in predicting the disease class labels to the patients. The problem is called boundary uncertainty in decision-making. Managing boundary uncertainty improves the accuracy of disease prediction by minimizing false-positive and false-negative cases.
Concept Approximation
For the same feature values, if the disease class labels of two patients are different, inconsistency, one type of uncertainty creeps in the decision system (DS). We apply RST to manage inconsistency by partitioning the target sets into lower and upper approximation sets. For convenience of readers, a brief knowledge of RST has been presented here.
Rough Set Theory
Say, a decision system is a nonempty finite set of objects, A is the set of attributes, where A = C ∪ D, C is condition attribute set, and D is decision attribute set with class label value YES and NO.
V = ∪ a∈AVa, where Va is the domain of attribute a (a ∈ C), i.e., V is the union of attribute domains and f:U × A → V is an information function such that f(x, a) ∈ Va for each x ∈ U and a ∈ A.
An indiscernible relation IND(P) [29] is defined by the following: where .
If IND(P), then x and y are indiscernible with respect to attribute set P.
Given an equivalence relation P on universe U and for any target set X ⊆ U, P-lower and P-upper approximation sets [29] of X:
| 2 |
| 3 |
where is the equivalence class induced by U/P.
The boundary BRP region [29] is defined as follows:
| 4 |
Let us consider the same example (Table 3) where the DS consists of eight objects as patients (P01, P02, P03, P04, P05, P06, P07, P08) and the decision attribute representing disease “lung congestion.”
The equivalent classes are {P01, P02, P03}; {P04}; {P05}; {P06}; and {P07, P08} for the condition attribute set (input features) R = {L, S, A, BPS, BPD, PU, SO, T, BMI, Cold, BN, BA, H, N, AP}.
Table 3 demonstrates uncertain concept “lung congestion” because P01 and P02 and similarly P07 and P08 have the same feature values but different decision attribute (“lung congestion”) values (YES/NO).
The lower approximation and upper approximation (Fig. 4) of target set X1 = {P01, P02, P03, P04, P05, P06, P07, P08}, suffering from “lung congestion = YES” are evaluated as crisp sets = {P05, P06} and = {P01, P02, P03, P05, P06, P07, P08}, respectively. The difference between the two crisp sets is a nonempty set BRP = {P01, P02, P03, P07, P08}; therefore, the target set is rough. Three regions are obtained in a rough approximation space. However, in the healthcare domain, the lower and upper approximation sets of the decision space (here “lung congestion”) are not crisps rather fuzzy sets.
Fig. 4.
Remote patients in lower, upper, and boundary region
Optimization of Membership Functions
The target set or concept is represented as a pair of lower and upper approximation sets using RST; however, they are fuzzy sets unlike RS. The fuzzy sets usually are not singleton set, consisting of multiple objects, and therefore, multiple membership values are used to assess the belonging of the members corresponding to two different disease class labels YES and NO.
Say, for disease j, the lower and upper approximation sets of the target set (YES/NO) have been represented as a pair of membership functions using Eqs. (5) and (6) [9], respectively.
| 5 |
| 6 |
Infimum (inf) and supremum (sup) operators are used to assign a single membership value to the lower and upper approximation sets, where the condition of individual object is not reflected. According to the authors [9], no change in the result has been observed when an object of the same equivalence class with different membership values is considered, suggesting that no calculation with respect to the individual object is necessary. However, there is a possibility of almost infinite number of membership values of a fuzzy variable, and so it is quite difficult to predict the outcomes for all cases. In the paper, the problem has been tackled by optimizing the membership values of the lower and upper approximation sets using NSGA-II. We propose objective functions as maximization of lower approximation and minimization of upper approximation membership functions to obtain corresponding optimum membership values for each disease class label using Eqs. (7) and (8), respectively:
| 7 |
| 8 |
where denote the membership functions of the patients belonging to the lower and upper approximation sets of the target set, representing jth disease with class label k equal to two, i.e., YES/NO. For same feature values, the patients might have “lung congestion” problem, i.e., k is YES or do not have “lung congestion” problem, i.e., k is NO.
In the paper, crowding distance (d) is employed as selection operator of the NSGA-II algorithm, which estimates density around a given individual in a population and expresses using Eq. (9). Crowding distance (d) is measured corresponding to the objective functions as the absolute difference in the function values of the two adjacent solutions of the same front. Overall crowding distance is the sum of individual distance values corresponding to say, m number of objective functions:
| 9 |
where d is the overall crowding distance of solution x, and are the maximum and minimum of objective function , i is the individual of solution set, Fr is the front with identifier r, and is initially set to zero. When the ranks of two non-dominant solutions are different, the smaller rank solutions are selected from the population, and if two solutions belong to the same Pareto frontier, the solution with larger d is chosen.
We modify the searching technique to improve the diversity and uniformity of non-dominated solutions by using Eq. (10). The searching method helps to highlight the best solution points on the Pareto front having separation greater than 0.5 between optimum lower approximation and optimum upper approximation membership functions, shown in Fig. 5a.
| 10 |
Fig. 5.
Functionality of NSGA-II with modification in a searching technique and b termination condition
The termination condition of the algorithm is calculated as an absolute difference in the membership functions of two subsequent solutions in the same front using Eq. (11):
| 11 |
where G1 and G2 are subsequent generations in executing NSGA-II.
Figure 5 shows the functionality of NSGA-II by highlighting the best solution using modified searching technique. The algorithm terminates when the absolute distances are nearly 0.01 between two subsequent generations as shown in Fig. 5b.
Length of each chromosome is fifteen representing the number of input features for diagnosing the diseases. The chromosomes are initialized randomly using the range of membership values of the features, belonging to the respective set of the patients, and for each set, fitness of approximation is applied using Eqs. (7) and (8). After 5000 iterations, a new population has been generated, and by using Eq. (10), we obtain solutions at optimal Pareto front for each disease. The working principle of NSGA-II is described in Algorithm 1.

Figure 6 shows the execution of NSGA-II representing the diseases “flu,” “diarrhea,” “lung congestion,” “anemia,” and “gastrointestinal disorders” with class label YES/NO. The optimum membership values for the YES/NO classes of different diseases are given in Table 4, which shows that there is a wide gap between the two class labels; therefore, the proposed method manages the problem of boundary uncertainty in decision-making.
Fig. 6.
Pareto optimal front for “YES” (a, c, e, g, i) and “NO” (b, d, f, h, j)
Table 4.
Optimal membership value of diseases
| Disease | Flu | Lung congestion | Diarrhea | Anemia | Gastrointestinal | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| YES | NO | YES | NO | YES | NO | YES | NO | YES | NO | |
| Membership | 0.74 | 0.23 | 0.83 | 0.28 | 0.65 | 0.15 | 0.69 | 0.17 | 0.62 | 0.3 |
Disease Similarity
Disease_similarity_factor
The jth disease class label (k) is predicted to a new patient by evaluating disease_similarity_factor (D*(j(k)), given in Eq. (12):
| 12 |
where is the optimal membership function of disease j having kth class label (YES/NO) obtained by NSGA(II) algorithm, represents the kth class membership value of the new patient (xnew), and n is the total number of features. Considering all the diseases, the new patient is diagnosed as having particular disease (j) with class label YES/NO for which the disease_similarity_factor is maximum.
In case there is same or very close D* value for more than one disease class label (YES), then the new patient has the possibility of more than one disease.
Here instead of finding similarities between the new patient and individual patient in the training dataset, we use difference between the optimal membership value of disease class label and corresponding membership value of the new patient. The nonlinear relationship between these two terms is expressed using exponential function, which is inversely proportional with the difference while calculating the disease_similarity_factor. More the difference less is the disease_similarity_factor.
is used to give a constant weightage or bias term to the disease_similarity_factor corresponding to the particular disease class label.
For example, the feature vector of a new patient is represented by the fuzzy variables < “Normal_altitude,” “Monsoon,” “Old,” “High,” “Stage 1_Hypertensive,” “Average,” “Hypoxic,” “Normal,” “Normal,” “Sore throat,” “Mild,” “Acute,” “Low,” “None,” and “None” > for the attributes L, S, A, BPS, BPD, PU, SO, T, BMI, Cold, BN, BA, H, N, and AP, while corresponding membership values (Fig. 3) are < 0.52, 0.43, 0.78, 0.65, 0.72, 0.75, 0.86, 0.55, 0.61, 0.34, 0.25, 0.4, 0.18, 0.05, and 0.11 > . Say, for the new patient, D* of disease “flu” with class label YES is calculated as follows:
Table 5 shows D* of different disease classes and the maximum similarity found with the disease “lung congestion = YES.” Thus, the new patient is diagnosed with disease “lung congestion = YES” which represents maximum similarity value.
Table 5.
Disease_similarity_factor of new patient
| Disease class | D* |
|---|---|
| Flu = YES | 0.65 |
| Flu = NO | 0.20 |
| Lung congestion = YES | 0.70 |
| Lung congestion = NO | 0.25 |
| Diarrhea = YES | 0.59 |
| Diarrhea = NO | 0.15 |
| Anemia = YES | 0.62 |
| Anemia = NO | 0.14 |
| Gastrointestinal = YES | 0.57 |
| Gastrointestinal = NO | 0.28 |
Bold denotes maximum D* value
Classifier Detail
The performance of the proposed method is described using different classifiers like k-nearest neighbor (k-NN) [72], Naive Bayes (NB) [73], decision tree (DT) [74], support vector machine (SVM) [75], logistic regression (LR) [76], and multi-layer perceptron neural network (MLPNN) [77] as shown in Table 6. The brief descriptions of the classifiers are given below.
k-nearest neighbor (k-NN) is a supervised classification algorithm that considers the patient dataset where each data point belongs to a known class (YES/NO). After pre-processing the data, we obtain a space in which each observation or patient data point is represented by its coordinate, and we can interpret the distance between them as their similarity. We want to predict the class of a new patient based on the known observations representing different disease class labels. We choose the class to predict for a new observation by picking the k closest data points to the new observation and to take the most common class among these.
Naive Bayes (NB) algorithm is a probabilistic classifier assuming that the features are independent. The model is used to find the probability of an event A happening, given that another event B has occurred. The Naïve Bayesian equation calculates the posterior probability for each class. The class with the highest posterior probability is the outcome of prediction. Biggest disadvantage is that the features or predictors are to be independent. However, in most real-life cases, the predictors are dependent; this hinders the classifier’s performance.
A decision tree (DT) is constructed by asking a series of carefully crafted questions about the attributes of the test record of the patient. The series of questions and their possible answers are organized to build the decision tree consisting of nodes and directed edges. The root and other internal nodes contain attribute test conditions to separate the patients’ records with different characteristics. A decision node has two or more branches and a leaf node represents classification or decision (YES or NO). The goal is to predict the value of a target variable (YES or NO) by learning simple decision rules (if-else) inferred from the health features.
Support vector machine (SVM) is a supervised classification algorithm to find the optimum hyperplane, called decision boundary in an N-dimensional space (N: the number of features) that distinctly classifies the data points of two different class labels. Support vectors are the data points that are closer to the hyperplane and influence the position and orientation of the hyperplane. Using these support vectors, we maximize the distance between the data points of both classes. In the manuscript, we set regularization parameters to avoid overfitting problems.
Logistic regression (LR) is a statistical method for analyzing the dataset when the dependent variable (target) is categorical. It is an extension of the linear regression model where the logistic function is used to squeeze the output of a linear equation between 0 and 1 instead of fitting a straight line or hyperplane. The goal of LR is to find the best fitting model to describe the relationship between the response variable and a set of independent (predictor or explanatory) variables. In LR, we take the output of the linear function and squash the value within the range of 0–1 using the sigmoid function. If the squashed value is greater than a threshold value (0.5), we assign it a label 1 (YES), else we assign it a label 0 (NO).
Multi-layer perceptron neural network (MLPNN) is a supervised learning algorithm that learns a nonlinear function approximator for classification, given a set of features and a target variable. One or more nonlinear hidden layers are arranged hierarchically between the input and the output layer. In the paper, we use a feed-forward network with one hidden layer and the backpropagation algorithm [78], and the weights are learned in the training phase to classify the patients into two disease class labels (YES or NO).
Table 6.
Performance measures using different classifiers
| Disease | Class | Classifier | Accuracy | Sensitivity | Specificity | Precision | Kappa | |
|---|---|---|---|---|---|---|---|---|
| Flu | YES | BUM | k-NN | 91.45 | 83 | 87 | 0.912 | 0.61 |
| NB | 91.73 | 85 | 91 | 0.934 | 0.63 | |||
| DT | 91.80 | 85 | 91.5 | 0.923 | 0.66 | |||
| LR | 93.57 | 86 | 93.7 | 0.941 | 0.74 | |||
| SVM | 94.27 | 86.01 | 94 | 0.948 | 0.82 | |||
| MLPNN | 95.70 | 88.25 | 95 | 0.951 | 0.83 | |||
| AUM | k-NN | 92.32 | 84 | 89.5 | 0.923 | 0.64 | ||
| NB | 93.21 | 86 | 92.1 | 0.947 | 0.65 | |||
| DT | 94.10 | 86 | 92.9 | 0.953 | 0.68 | |||
| LR | 94.53 | 87.9 | 93 | 0.951 | 0.8 | |||
| SVM | 96.32 | 88.01 | 94.5 | 0.958 | 0.88 | |||
| MLPNN | 97.21 | 89.30 | 95.6 | 0.961 | 0.90 | |||
| Lung congestion | YES | BUM | k-NN | 89.31 | 80.01 | 82 | 0.894 | 0.54 |
| NB | 91.89 | 81.04 | 84 | 0.901 | 0.61 | |||
| DT | 91.76 | 82.04 | 84 | 0.910 | 0.64 | |||
| LR | 92.92 | 84.08 | 86.04 | 0.921 | 0.69 | |||
| SVM | 93.48 | 86.43 | 87.09 | 0.93 | 0.78 | |||
| MLPNN | 94.35 | 88.34 | 88.56 | 0.93 | 0.80 | |||
| AUM | k-NN | 89.45 | 81.45 | 82.65 | 0.905 | 0.57 | ||
| NB | 93.46 | 82.13 | 85.1 | 0.91 | 0.64 | |||
| DT | 94.10 | 82.65 | 85.3 | 0.92 | 0.66 | |||
| LR | 94.82 | 85.43 | 87.02 | 0.92 | 0.74 | |||
| SVM | 96.12 | 87.05 | 88.48 | 0.94 | 0.84 | |||
| MLPNN | 97.10 | 89.55 | 90.10 | 0.94 | 0.86 | |||
| Diarrhea | YES | BUM | k-NN | 89.34 | 81.5 | 83.08 | 0.9 | 0.51 |
| NB | 92.01 | 81.4 | 82.37 | 0.91 | 0.62 | |||
| DT | 92.50 | 82.32 | 82.55 | 0.92 | 0.66 | |||
| LR | 92.95 | 84.31 | 84.12 | 0.908 | 0.76 | |||
| SVM | 93.5 | 86.52 | 86.39 | 0.935 | 0.85 | |||
| MLPNN | 94.5 | 88.75 | 88.40 | 0.950 | 0.87 | |||
| AUM | k-NN | 89.5 | 81.7 | 83.2 | 0.905 | 0.55 | ||
| NB | 93.5 | 82.52 | 85.5 | 0.91 | 0.69 | |||
| DT | 94.1 | 83.25 | 86.2 | 0.91 | 0.70 | |||
| LR | 94.9 | 86.01 | 87.1 | 0.923 | 0.84 | |||
| SVM | 95.5 | 87.15 | 87.8 | 0.94 | 0.91 | |||
| MLPNN | 97.1 | 88.05 | 89.1 | 0.95 | 0.93 | |||
| Anemia | YES | BUM | k-NN | 92.31 | 83.41 | 87.65 | 0.92 | 0.65 |
| NB | 92.73 | 85.05 | 91.87 | 0.94 | 0.66 | |||
| DT | 93.10 | 85.54 | 91.90 | 0.94 | 0.68 | |||
| LR | 93.87 | 86.18 | 93.98 | 0.95 | 0.78 | |||
| SVM | 95.01 | 87.12 | 94.41 | 0.96 | 0.82 | |||
| MLPNN | 96.21 | 87.50 | 94.51 | 0.96 | 0.84 | |||
| AUM | k-NN | 92.4 | 84.05 | 90.15 | 0.93 | 0.7 | ||
| NB | 93.62 | 86.24 | 92.7 | 0.95 | 0.75 | |||
| DT | 94.10 | 86.34 | 93.1 | 0.95 | 0.79 | |||
| LR | 94.8 | 88.05 | 93.4 | 0.96 | 0.85 | |||
| SVM | 96.4 | 88.01 | 94.8 | 0.965 | 0.88 | |||
| MLPNN | 97.4 | 90.08 | 95.7 | 0.971 | 0.89 | |||
| Gastrointestinal | YES | BUM | k-NN | 89.04 | 80.5 | 81.8 | 0.91 | 0.60 |
| NB | 90.92 | 81.70 | 81.7 | 0.91 | 0.64 | |||
| DT | 92.50 | 82.54 | 84.01 | 0.92 | 0.68 | |||
| LR | 92.10 | 84.10 | 85.25 | 0.93 | 0.74 | |||
| SVM | 93.85 | 86.28 | 86.95 | 0.935 | 0.82 | |||
| MLPNN | 94.75 | 89.75 | 87.40 | 0.950 | 0.86 | |||
| AUM | k-NN | 91.5 | 82.7 | 82.2 | 0.91 | 0.59 | ||
| NB | 92.6 | 82.8 | 84.5 | 0.91 | 0.70 | |||
| DT | 93.5 | 83.45 | 86.3 | 0.92 | 0.75 | |||
| LR | 94.5 | 85.01 | 87.1 | 0.923 | 0.85 | |||
| SVM | 95.1 | 87.50 | 88.8 | 0.94 | 0.92 | |||
| MLPNN | 96.6 | 89.50 | 90.1 | 0.96 | 0.94 | |||
| Flu | NO | BUM | k-NN | 86.65 | 81.2 | 85.1 | 0.9 | 0.71 |
| NB | 86.7 | 81.8 | 86.4 | 0.91 | 0.74 | |||
| DT | 87.1 | 82.4 | 86.9 | 0.92 | 0.75 | |||
| LR | 88.5 | 83 | 88.3 | 0.94 | 0.82 | |||
| SVM | 89.3 | 83.8 | 89.3 | 0.95 | 0.88 | |||
| MLPNN | 92.3 | 84.3 | 91.3 | 0.96 | 0.90 | |||
| AUM | k-NN | 88.5 | 84.8 | 87.5 | 0.92 | 0.75 | ||
| NB | 89.1 | 85.2 | 88.3 | 0.92 | 0.78 | |||
| DT | 89.5 | 86.9 | 89.9 | 0.93 | 0.81 | |||
| LR | 91.3 | 87.2 | 90.1 | 0.94 | 0.85 | |||
| SVM | 94.6 | 88.6 | 91.5 | 0.94 | 0.93 | |||
| MLPNN | 95.6 | 91.5 | 92.8 | 0.95 | 0.95 | |||
| Lung congestion | NO | BUM | k-NN | 86.54 | 82.3 | 80.0 | 0.85 | 0.64 |
| NB | 87.2 | 82.9 | 81.0 | 0.85 | 0.68 | |||
| DT | 88.6 | 83.8 | 82.0 | 0.87 | 0.69 | |||
| LR | 89.2 | 84.5 | 82.1 | 0.89 | 0.74 | |||
| SVM | 89.5 | 85.2 | 84.5 | 0.91 | 0.82 | |||
| MLPNN | 90.5 | 88.4 | 85.6 | 0.93 | 0.84 | |||
| AUM | k-NN | 87.8 | 84.9 | 82.2 | 0.90 | 0.66 | ||
| NB | 88.5 | 85.7 | 83.1 | 0.91 | 0.72 | |||
| DT | 89.1 | 86.8 | 84.2 | 0.92 | 0.75 | |||
| LR | 89.3 | 87 | 85.2 | 0.92 | 0.78 | |||
| SVM | 93.1 | 87.8 | 86.8 | 0.93 | 0.92 | |||
| MLPNN | 94.7 | 89.8 | 88.1 | 0.95 | 0.94 | |||
| Diarrhea | NO | BUM | k-NN | 85.2 | 79.5 | 82.8 | 0.88 | 0.54 |
| NB | 87.1 | 80.2 | 82.3 | 0.90 | 0.63 | |||
| DT | 88.4 | 81.3 | 83.7 | 0.91 | 0.68 | |||
| LR | 90.3 | 82.2 | 84.6 | 0.91 | 0.72 | |||
| SVM | 91.5 | 83.5 | 86.9 | 0.92 | 0.84 | |||
| MLPNN | 93.5 | 86.5 | 88.9 | 0.94 | 0.86 | |||
| AUM | k-NN | 86.2 | 80.9 | 84.2 | 0.90 | 0.62 | ||
| NB | 86.8 | 81.5 | 85.8 | 0.92 | 0.69 | |||
| DT | 87.4 | 83.2 | 86.1 | 0.92 | 0.72 | |||
| LR | 89.9 | 84 | 87.4 | 0.93 | 0.77 | |||
| SVM | 92.3 | 84.15 | 88.8 | 0.94 | 0.84 | |||
| MLPNN | 94.1 | 87.70 | 90.8 | 0.95 | 0.86 | |||
| Anemia | NO | BUM | k-NN | 86.7 | 80.4 | 80.5 | 0.89 | 0.58 |
| NB | 86.3 | 82.1 | 81.7 | 0.91 | 0.66 | |||
| DT | 87.1 | 82.9 | 84.1 | 0.92 | 0.68 | |||
| LR | 88.3 | 84.8 | 83.8 | 0.92 | 0.71 | |||
| SVM | 88.1 | 83.1 | 84.4 | 0.93 | 0.83 | |||
| MLPNN | 90.2 | 85.4 | 86.3 | 0.95 | 0.85 | |||
| AUM | k-NN | 87.4 | 84.8 | 80.9 | 0.93 | 0.64 | ||
| NB | 88.1 | 85.2 | 81.7 | 0.93 | 0.74 | |||
| DT | 89.3 | 86.4 | 83.5 | 0.94 | 0.77 | |||
| LR | 90.8 | 87.05 | 84.4 | 0.94 | 0.83 | |||
| SVM | 92.8 | 88.01 | 84.8 | 0.95 | 0.92 | |||
| MLPNN | 95.1 | 90.21 | 86.6 | 0.96 | 0.93 | |||
| Gastrointestinal | NO | BUM | k-NN | 84.7 | 80.5 | 81.3 | 0.89 | 0.61 |
| NB | 86.5 | 81.3 | 83.3 | 0.92 | 0.64 | |||
| DT | 87.3 | 82.5 | 84.1 | 0.93 | 0.72 | |||
| LR | 90.3 | 83.7 | 84.6 | 0.93 | 0.74 | |||
| SVM | 91.5 | 84.1 | 87.9 | 0.93 | 0.85 | |||
| MLPNN | 92.7 | 86.2 | 89.7 | 0.94 | 0.88 | |||
| AUM | k-NN | 86.5 | 81.9 | 84.2 | 0.90 | 0.62 | ||
| NB | 87.9 | 82.5 | 86.8 | 0.92 | 0.66 | |||
| DT | 88.4 | 83.7 | 87.9 | 0.93 | 0.75 | |||
| LR | 89.1 | 84.7 | 88.4 | 0.93 | 0.86 | |||
| SVM | 92.3 | 85.6 | 89.8 | 0.94 | 0.93 | |||
| MLPNN | 94.6 | 88.7 | 92.8 | 0.95 | 0.95 |
k-NN k-nearest neighbor, NB Naive Bayes, DT decision tree, SVM support vector machine, LR logistic regression, MLPNN multi-layer perceptron neural network. Bold denotes better performance.
Experimental Results
The proposed method is demonstrated using the kiosk datasets and compared with other methods followed by performance evaluation measures. The training dataset comprises patients’ information like age, season, location, and physiological signs like systolic/diastolic blood pressure, pulse, SpO2, BMI, temperature, and symptoms like cold, breathlessness, body ache, headache, nausea, and abdominal pain. Common diseases like “lung congestion,” “flu,” “diarrhea,” “anemia,” and “gastrointestinal disorder” are considered, and their class labels YES/NO are initially assigned by the health workers. Five thousand samples are used as training set, and five hundred test samples are considered to classify into appropriate disease classes. The training dataset consists of fifteen features of both male and female patients with variations in the feature values.
The membership values of the features are calculated using the following steps: (a) in consultation with the experts and medical literature, determine the set of fuzzy rules and assign fuzzy variables with proper semantic to the feature. For example, if pulse is less than 60, then pulse is low; similarly if pulse is less than 73 and pulse is greater than or equal to 63, then pulse is normal; (b) calculate the membership value of the fuzzy variable, representing the input feature using Gaussian function, which represent real-life measurement values following a normal distribution where an equal number of measurements are above and below the mean value. The membership value is the quantile, i.e., how many values in the distribution are above or below the certain limit of Gaussian distribution. The membership is calculated by the median (middle quantile, 50th percentile) value of the Gaussian distribution (Fig. 3) of the membership curve of respective features.
Performance of the proposed method is evaluated based on different metrics, (i) accuracy, (ii) sensitivity, (iii) specificity, and (iv) precision, using tenfold cross-validation technique. Table 7 shows the performance measures, which increase (3 to 5%) after managing boundary uncertainty. However, the small amount of random variation indicates the increase of precision after uncertainty management. Figure 7 depicts the boxplots [79] of percentage accuracy (AC), sensitivity (SC), specificity (SP), and precision (PR) before uncertainty management (BUM) and after uncertainty management (AUM). It has been observed that for most of the cases, the plot is more compact. It also indicates that the proposed method achieves better performance measures with lesser standard deviation and higher median value.
Table 7.
Average performance measure
| Class label | Performance | Flu | Lung congestion | Diarrhea | Anemia | Gastrointestinal | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BUM | AUM | BUM | AUM | BUM | AUM | BUM | AUM | BUM | AUM | ||
| YES | AC in % | 86.10 | 94.20 | 85.50 | 96.50 | 84.20 | 94.70 | 83.60 | 93.80 | 84.10 | 93.90 |
| SC in % | 82.80 | 86.60 | 81.70 | 86.20 | 81.70 | 85.80 | 80.20 | 84.80 | 80.90 | 85.70 | |
| SP in % | 85.40 | 88.50 | 84.10 | 89.20 | 82.50 | 87.50 | 83.70 | 89.50 | 82.30 | 87.50 | |
| PR in % | 88.20 | 92.30 | 90.50 | 94.10 | 89.10 | 93.20 | 87.70 | 91.20 | 88.70 | 93.50 | |
| NO | AC in % | 82.70 | 88.10 | 80.30 | 85.50 | 79.10 | 84.00 | 81.40 | 86.60 | 80.40 | 84.60 |
| SC in % | 80.20 | 85.20 | 82.50 | 86.10 | 80.10 | 82.80 | 80.10 | 84.20 | 79.10 | 82.20 | |
| SP in % | 81.50 | 84.10 | 82.00 | 84.40 | 82.20 | 85.70 | 82.40 | 86.70 | 81.80 | 84.30 | |
| PR in % | 86.20 | 89.10 | 84.80 | 89.10 | 84.60 | 89.70 | 85.20 | 90.10 | 84.10 | 87.80 | |
BUM before uncertainty management, AUM after uncertainty management. Bold denotes better performance.
Fig. 7.
Boxplot of accuracy (a–e, a1–e1), sensitivity (f–j, f1–j1), specificity (k–o, k1–o1), and precision (p–t, p1–t1) (percentage) performed on “flu,” “diarrhea,” “lung congestion,” “anemia,” and “gastrointestinal” for class label “YES” and “NO” before and after management of boundary uncertainty
From the experimental result, it has been observed that MLPNN and SVM classifiers perform well in most of the cases and improve 3 to 5% in terms of accuracy, sensitivity, specificity, and precision. Moreover, in some cases, MLPNN and SVM give similar performance, but as the sample size increases, MLPNN performs better than SVM. To verify this, we perform paired t-test at 5% level of significance to determine whether the mean difference between the two sets of observations is zero.
Statistical significant results are given in Table 8 for the disease class labels, and the result shows that MLPNN classifier performs better than other classifiers.
Table 8.
Paired t-test result by MLPNN and other classifier w.r.t. p score value < 0.05
| Disease | Class | Classifier | Accuracy | Sensitivity | Specificity | Precision |
|---|---|---|---|---|---|---|
| Flu | YES | MLPNNV/s k-NN | 3.33 × 10−5 | 3.31 × 10−5 | 2.21 × 10−5 | 4.1 × 10−5 |
| MLPNNV/s NB | 2.32 × 10−5 | 1.48 × 10−4 | 1.03 × 10−5 | 2.05 × 10−4 | ||
| MLPNN V/s DT | 1.89 × 10−5 | 1.07 × 10−4 | 1.01 × 10−5 | 1.78 × 10−4 | ||
| MLPNN V/s LR | 0.037 | 0.030 | 0.038 | 0.088 | ||
| MLPNN V/s SVM | 0.031 | 0.025 | 0.030 | 0.058 | ||
| Lung congestion | YES | MLPNN V/s k-NN | 3.3 × 10−6 | 5.9 × 10−5 | 2.9 × 10−7 | 1.9 × 10−4 |
| MLPNN V/s NB | 2.8 × 10−5 | 2.4 × 10−5 | 1.96 × 10−5 | 1.95 × 10−5 | ||
| MLPNN V/s DT | 1.9 × 10−5 | 1.1 × 10−5 | 0.99 × 10−5 | 1.25 × 10−5 | ||
| MLPNN V/s LR | 0.0013 | 0.083 | 0.094 | 0.0287 | ||
| MLPNN V/s SVM | 0.0003 | 0.013 | 0.054 | 0.087 | ||
| Diarrhea | YES | MLPNN V/s k-NN | 4.5 × 10−5 | 4.42 × 10−5 | 2.88 × 10−5 | 4.7 × 10−5 |
| MLPNN V/s NB | 3.9 × 10−5 | 3.19 × 10−5 | 2.43 × 10−5 | 2.27 × 10−5 | ||
| MLPNN V/s DT | 2.9 × 10−5 | 3.09 × 10−5 | 2.14 × 10−5 | 1.97 × 10−5 | ||
| MLPNN V/s LR | 0.019 | 0.033 | 0.058 | 0.039 | ||
| MLPNN V/s SVM | 0.07 | 0.03 | 0.35 | 0.26 | ||
| Anemia | YES | MLPNN V/s k-NN | 8.3 × 10−7 | 7.8 × 10−6 | 3.8 × 10−7 | 2.3 × 10−3 |
| MLPNN V/s NB | 3.9 × 10−5 | 5.2 × 10−5 | 1.8 × 10−5 | 2.9 × 10−5 | ||
| MLPNN V/s DT | 1.9 × 10−5 | 4.2 × 10−5 | 0.8 × 10−5 | 0.9 × 10−5 | ||
| MLPNN V/s LR | 0.0094 | 0.0065 | 0.0029 | 0.0078 | ||
| MLPNN V/s SVM | 0.0054 | 0.0045 | 0.0008 | 0.0028 | ||
| Gastrointestinal | YES | MLPNN V/s k-NN | 5.5 × 10−5 | 5.02 × 10−5 | 7.88 × 10−5 | 5.7 × 10−5 |
| MLPNN V/s NB | 6.9 × 10−5 | 4.19 × 10−5 | 6.43 × 10−5 | 2.27 × 10−5 | ||
| MLPNN V/s DT | 1.9 × 10−5 | 2.19 × 10−5 | 3.44 × 10−5 | 1.97 × 10−5 | ||
| MLPNN V/s LR | 0.059 | 0.073 | 0.068 | 0.059 | ||
| MLPNN V/s SVM | 0.027 | 0.023 | 0.045 | 0.046 | ||
| Flu | NO | MLPNN V/s k-NN | 8.2 × 10−5 | 5.2 × 10−5 | 5.3 × 10−5 | 3.2 × 10−5 |
| MLPNN V/s NB | 4.9 × 10−5 | 4.1 × 10−5 | 4.1 × 10−5 | 2.6 × 10−5 | ||
| MLPNN V/s DT | 0.89 × 10−5 | 3.7 × 10−4 | 2.01 × 10−5 | 1.18 × 10−4 | ||
| MLPNN V/s LR | 0.077 | 0.080 | 0.098 | 0.058 | ||
| MLPNN V/s SVM | 0.0018 | 0.0021 | 0.0029 | 0.0022 | ||
| Lung congestion | NO | MLPNN V/s k-NN | 2.2 × 10−6 | 1.7 × 10−6 | 1.5 × 10−5 | 1.3 × 10−6 |
| MLPNN V/s NB | 1.4 × 10−5 | 2.7 × 10−5 | 1.7 × 10−5 | 1.5 × 10−5 | ||
| MLPNN V/s DT | 0.29 × 10−5 | 6.6 × 10−4 | 2.5 × 10−5 | 3.8 × 10−4 | ||
| MLPNN V/s LR | 0.044 | 0.081 | 0.098 | 0.058 | ||
| MLPNN V/s SVM | 0.019 | 0.013 | 0.017 | 0.019 | ||
| Diarrhea | NO | MLPNN V/s k-NN | 6.4 × 10−4 | 5.8 × 10−3 | 4.6 × 10−3 | 4.1 × 10−4 |
| MLPNN V/s NB | 4.8 × 10−3 | 3.5 × 10−3 | 2.7 × 10−3 | 2.8 × 10−3 | ||
| MLPNN V/s DT | 5.9 × 10−5 | 4.5 × 10−5 | 6.4 × 10−5 | 4.7 × 10−5 | ||
| MLPNN V/s LR | 0.045 | 0.071 | 0.088 | 0.066 | ||
| MLPNN V/s SVM | 0.033 | 0.028 | 0.015 | 0.014 | ||
| Anemia | NO | MLPNN V/s k-NN | 3.4 × 10−5 | 1.5 × 10−5 | 1.7 × 10−5 | 1.9 × 10−5 |
| MLPNN V/s NB | 3.1 × 10−5 | 2.8 × 10−5 | 2.6 × 10−5 | 2.1 × 10−5 | ||
| MLPNN V/s DT | 2.9 × 10−5 | 4.2 × 10−5 | 0.8 × 10−5 | 0.9 × 10−5 | ||
| MLPNN V/s LR | 0.01 | 0.0085 | 0.005 | 0.007 | ||
| MLPNN V/s SVM | 0.0019 | 0.0017 | 0.001 | 0.004 | ||
| Gastrointestinal | NO | MLPNN V/s k-NN | 4.4 × 10−4 | 3.8 × 10−3 | 4.1 × 10−3 | 4.8 × 10−4 |
| MLPNN V/s NB | 6.1 × 10−3 | 2.8 × 10−3 | 3.7 × 10−3 | 3.7 × 10−3 | ||
| MLPNN V/s DT | 3.7 × 10−5 | 1.5 × 10−5 | 2.4 × 10−5 | 7.7 × 10−5 | ||
| MLPNN V/s LR | 0.040 | 0.071 | 0.098 | 0.046 | ||
| MLPNN V/s SVM | 0.03 | 0.020 | 0.055 | 0.01 |
k-NN k-nearest neighbor, NB Naive Bayes, DT decision tree, SVM support vector machine, LR logistic regression, MLPNN multi-layer perceptron neural network.
We deduce kappa values that measure interrater reliability to represent the extent to which the data collected is correct. The scale of kappa value less than zero indicates no agreement, within range 0–0.20 implies light, 0.20–0.40 implies fair, 0.41–0.60 implies moderate, 0.61–0.80 implies substantial, and 0.81–1 implies perfect. The value increases subsequently after managing uncertainty and lies in the scale perfect for MLPNN classifier.
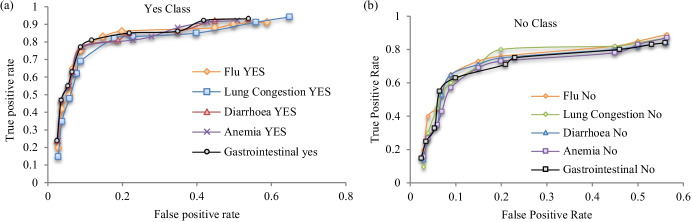
Figure 8 gives ROC [80] curves which depict the highest true positive rate with the lowest false-positive rate for both disease class YES/NO of the diseases “flu,” “diarrhea,” “lung congestion,” “anemia,” and “gastrointestinal disorders” after managing boundary uncertainty.
Fig. 8.
ROC of “flu,” “diarrhea,” “lung congestion,” “anemia,” and “gastrointestinal” for a YES and b NO class
Results are verified by calculating the Pearson correlation coefficient between the symptoms/signals of new patients and the value obtained from the Pareto optimal front. The interpretation of the Pearson correlation coefficient is shown in Table 9, according to Chan et al. [81, 82]. The result of Table 5 is verified by the Pearson correlation coefficient, and interpretation of the result is shown in Table 10. The new patient is very strongly related to the decision attribute “lung congestion” with class label YES and moderately to “flu” with class label YES as given in Table 10. We take 500 test cases of new patients, and in 98% cases, the prediction is correctly interpreted.
Table 9.
Interpretation of Pearson’s correlation coefficient
| Pearson correlation coefficient | Chan et al. interpretation | |
|---|---|---|
| + 1 | − 1 | Perfect |
| + 0.9 | − 0.9 | Very strong |
| + 0.8 | − 0.8 | Very strong |
| + 0.7 | − 0.7 | Moderate |
| + 0.6 | − 0.6 | Moderate |
| + 0.5 | − 0.5 | Fair |
| + 0.4 | − 0.4 | Fair |
| + 0.3 | − 0.3 | Fair |
| + 0.2 | − 0.2 | Poor |
| + 0.1 | − 0.1 | Poor |
| 0 | 0 | None |
Table 10.
Pearson’s correlation coefficient of Pnew and Pareto optimal value
| Disease class | Pearson correlation coefficient | Chan et al. interpretation |
|---|---|---|
| Flu YES | 0.64 | Moderate |
| Flu NO | 0.2 | Poor |
| Lung congestion YES | 0.85 | Very strong |
| Lung congestion NO | 0.1 | Poor |
| Diarrhea YES | 0.4 | Fair |
| Diarrhea NO | − 0.2 | Poor |
| Anemia YES | 0.3 | Fair |
| Anemia NO | 0.1 | Poor |
| Gastrointestinal YES | 0.35 | Fair |
| Gastrointestinal NO | − 0.1 | Poor |
Bold denotes better belonging to disease class label.
Finally, the proposed approach is compared with the existing measures which include rough fuzzy digraphs (RFD) [51], multiple attribute group decision-making (MAGDM) method [49], and technique for prediction estimation by least deviation to two predictions (TPELDTP) method [50]. RFD method is based on rough fuzzy digraph, MAGDM method establishes on variable precision multigranulation rough fuzzy set, and TPELDTP method forecasts the growth based on attribute-oriented RFS. Performance of this method is estimated using NB, k-NN, SVM, LR, and MLPNN classifiers with tenfold cross-validation techniques. Table 11 clearly shows that the classification accuracy (AC) and precision (PR) of the proposed method are higher than the other methods in most of the cases, while MLPNN classifier performs better compared to other classifiers.
Table 11.
Comparison of accuracy and precision of different classifiers with other methods
| Classifier | Method | Flu = YES | Flu = NO | LC = YES | LC = NO | Diarrhea = YES | Diarrhea = NO | Anemia = YES | Anemia = NO | Gas = YES | Gas = NO | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | PR | AC | PR | AC | PR | AC | PR | AC | PR | AC | PR | AC | PR | AC | PR | AC | PR | AC | PR | ||
| NB | RFD | 75.6 | 0.81 | 77.3 | 0.78 | 76.4 | 0.80 | 76.5 | 0.8 | 78.4 | 0.79 | 77.5 | 0.8 | 79.8 | 0.81 | 80.7 | 0.80 | 77.4 | 0.78 | 80.5 | 0.8 |
| MAG | 77.1 | 0.81 | 78.6 | 0.79 | 76.7 | 0.81 | 76.8 | 0.81 | 78.7 | 0.81 | 78.3 | 0.81 | 80.3 | 0.81 | 80.5 | 0.82 | 80.7 | 0.82 | 78.8 | 0.81 | |
| TPEL | 82.7 | 0.85 | 80.0 | 0.82 | 80.6 | 0.83 | 80.5 | 0.84 | 81.2 | 0.83 | 80.0 | 0.83 | 83.0 | 0.84 | 83.8 | 0.84 | 83.2 | 0.83 | 81.5 | 0.82 | |
| Prop | 82.5 | 0.86 | 82.5 | 0.84 | 81.5 | 0.85 | 81.8 | 0.84 | 82.3 | 0.83 | 81.1 | 0.85 | 83.4 | 0.85 | 84.1 | 0.84 | 84.1 | 0.83 | 82.1 | 0.84 | |
| k-NN | RFD | 78.6 | 0.83 | 82.0 | 0.83 | 80.9 | 0.83 | 80.4 | 0.82 | 82.8 | 0.81 | 80.5 | 0.86 | 80.1 | 0.81 | 81.5 | 0.83 | 81.8 | 0.81 | 82.5 | 0.84 |
| MAG | 78.8 | 0.83 | 82.5 | 0.84 | 81.0 | 0.84 | 82.6 | 0.83 | 81.1 | 0.81 | 81.0 | 0.86 | 81.2 | 0.82 | 82.9 | 0.84 | 81.9 | 0.81 | 82.5 | 0.85 | |
| TPEL | 85.1 | 0.86 | 85.1 | 0.86 | 84.9 | 0.87 | 85.0 | 0.86 | 81.2 | 0.84 | 83.8 | 0.87 | 85.5 | 0.84 | 84.8 | 0.85 | 82.2 | 0.83 | 83.8 | 0.85 | |
| Prop | 85.6 | 0.86 | 87.6 | 0.86 | 84.8 | 0.87 | 85.4 | 0.87 | 85.0 | 0.85 | 84.1 | 0.88 | 85.8 | 0.85 | 86.0 | 0.86 | 84.7 | 0.85 | 85.6 | 0.88 | |
| DT | RFD | 80.6 | 0.81 | 82.9 | 0.83 | 81.9 | 0.82 | 81.4 | 0.81 | 81.8 | 0.81 | 82.0 | 0.86 | 81.1 | 0.81 | 82.6 | 0.83 | 80.8 | 0.81 | 82.5 | 0.84 |
| MAG | 79.1 | 0.83 | 83.5 | 0.84 | 81.8 | 0.84 | 82.3 | 0.83 | 82.1 | 0.82 | 82.7 | 0.85 | 81.7 | 0.83 | 83.9 | 0.85 | 82.9 | 0.82 | 83.5 | 0.85 | |
| TPEL | 83.1 | 0.84 | 85.4 | 0.85 | 83.5 | 0.86 | 84.8 | 0.86 | 83.2 | 0.84 | 83.1 | 0.87 | 83.5 | 0.84 | 84.6 | 0.85 | 84.3 | 0.84 | 83.9 | 0.85 | |
| Prop | 85.3 | 0.86 | 86.8 | 0.86 | 85.8 | 0.87 | 85.7 | 0.87 | 85.0 | 0.86 | 84.7 | 0.89 | 85.5 | 0.86 | 86.3 | 0.87 | 85.7 | 0.85 | 85.1 | 0.87 | |
| LR | RFD | 80.6 | 0.86 | 85.1 | 0.84 | 85.8 | 0.85 | 85.9 | 0.86 | 86.5 | 0.85 | 85.4 | 0.86 | 86.1 | 0.84 | 86.8 | 0.85 | 82.1 | 0.81 | 82.7 | 0.83 |
| MAG | 81.4 | 0.85 | 86.3 | 0.86 | 86.7 | 0.85 | 87.1 | 0.89 | 87.3 | 0.87 | 86.3 | 0.86 | 88.2 | 0.85 | 87.2 | 0.87 | 82.9 | 0.84 | 83.5 | 0.85 | |
| TPEL | 89.2 | 0.90 | 88.2 | 0.89 | 90.5 | 0.90 | 90.1 | 0.90 | 90.2 | 0.89 | 89.2 | 0.89 | 90.5 | 0.88 | 89.4 | 0.9 | 83.8 | 0.86 | 85.1 | 0.87 | |
| Prop | 90.9 | 0.90 | 89.2 | 0.90 | 91.1 | 0.91 | 90.5 | 0.90 | 91.2 | 0.90 | 90.2 | 0.91 | 91.7 | 0.90 | 90.8 | 0.91 | 85.7 | 0.88 | 84.9 | 0.89 | |
| SVM | RFD | 85.6 | 0.88 | 86.8 | 0.87 | 85.3 | 0.87 | 87.2 | 0.87 | 87.4 | 0.89 | 87.4 | 0.88 | 87.7 | 0.87 | 88.1 | 0.88 | 86.4 | 0.89 | 87.1 | 0.88 |
| MAG | 86.4 | 0.89 | 87.1 | 0.87 | 86.2 | 0.88 | 88.5 | 0.88 | 87.8 | 0.90 | 88.2 | 0.89 | 88.6 | 0.88 | 88.8 | 0.9 | 87.6 | 0.90 | 88.2 | 0.89 | |
| TPEL | 92.4 | 0.91 | 90.3 | 0.92 | 90.4 | 0.92 | 91.2 | 0.91 | 91.4 | 0.92 | 90.4 | 0.92 | 92.1 | 0.92 | 91.6 | 0.92 | 90.4 | 0.91 | 91.4 | 0.92 | |
| Prop | 94.8 | 0.93 | 94.5 | 0.93 | 95.7 | 0.92 | 93.8 | 0.92 | 94.5 | 0.93 | 95.1 | 0.94 | 94.1 | 0.93 | 95.5 | 0.94 | 92.5 | 0.92 | 93.1 | 0.94 | |
| MLP | RFD | 86.6 | 0.88 | 87.7 | 0.87 | 87.3 | 0.87 | 88.1 | 0.87 | 89.1 | 0.89 | 86.4 | 0.88 | 88.1 | 0.86 | 89.1 | 0.89 | 86.4 | 0.89 | 89.1 | 0.88 |
| MAG | 87.3 | 0.90 | 89.1 | 0.89 | 88.5 | 0.90 | 89.8 | 0.89 | 89.8 | 0.91 | 88.7 | 0.90 | 88.7 | 0.88 | 89.8 | 0.91 | 88.6 | 0.90 | 90.2 | 0.88 | |
| TPEL | 93.6 | 0.92 | 92.3 | 0.92 | 90.8 | 0.92 | 92.2 | 0.90 | 90.4 | 0.92 | 91.1 | 0.92 | 91.5 | 0.92 | 92.6 | 0.92 | 92.4 | 0.92 | 91.4 | 0.92 | |
| Prop | 95.8 | 0.95 | 95.5 | 0.94 | 95.6 | 0.96 | 94.8 | 0.93 | 94.8 | 0.95 | 95.7 | 0.95 | 95.3 | 0.94 | 95.7 | 0.95 | 95.8 | 0.94 | 96.1 | 0.95 | |
LC lung congestion, Gas gastrointestinal, k-NN k-nearest neighbor, NB Naive Bayes, DT decision tree, SVM support vector machine, LR logistic regression, MLP multi-layer perceptron neural network, RFD rough fuzzy digraphs, MAGDM multiple attribute group decision-making method, TPEL technique for prediction estimation by least deviation to two predictions method, PROP proposed method, AC accuracy, PR precision. Bold denotes better performance.
Discussion
Experimental results show that the performance of the proposed model in terms of minimum false cases is best using MLPNN and nonlinear SVM classifiers. Considering all aspects of performance measure, we observe that the MLPNN classifier has high prediction accuracy, precision, specificity, sensitivity, and kappa value and low overfitting problem among other classifiers discussed in the revised manuscript. Performance of the NB classifier for the training and test datasets are close to each other, indicating that the model is free from overfitting. However, the NB classifier is not acceptable for real-life data analysis due to feature independence issue. The k-NN algorithm is not useful for prediction of health condition of the patients since no training is imparted on the dataset and, therefore, shows poor performance in prediction. The DT classifier has overfitting problem, and performance is not satisfactory in case of many features with continuous value. The LR classifier takes quite a long time to train data and does overfit due to selection of parameters and model complexity. Nonlinear SVM with Gaussian kernel is suitable, even for not so large health datasets, and shows high prediction score without overfitting issues. Table 6 shows that using MLPNN classifier, we achieve prediction accuracy nearly 97% for most of the diseases with YES class label and nearly 95% for NO class label. For most of the diseases, with both YES/NO class labels, sensitivity is nearly 90%, specificity is more than 90%, and precision is nearly 0.95, therefore overall increase of 2–4% performance compared to other classifiers after managing uncertainty. To minimize the overfitting problem, tenfold cross-validation is conducted where the dataset is randomly partitioned into 10 mutually exclusive subsets, each of approximately equal size. At each turn, one is kept for testing, while others are used for training, and the process is iterated throughout the tenfold. Further, it has been observed from the ROC curves corresponding to different disease class labels that the MLPNN model shows that the area under the curve (AUC) is nearly one.
The proposed technique has practical implications in the rural areas where doctors have scarce and health infrastructure is inadequate. The rural health kiosks are set up with sensors for collecting primary health data from the patients. However, the data is not uniform and precise, so it needs preprocessing to automatically diagnose the patients’ health condition by analyzing the data. In consultation with the experts, we frame a rule base to represent the feature values using fuzzy variables with reference to the standard value obtained from the medical literature. The relation between the health attributes and associated attributes (age, etc.) is also considered. We fuzzify the input feature variables using Gaussian functions. Due to the scarcity of doctors, health assistants are involved in classifying the patients with disease class label YES/NO, which invites uncertainty in diagnosing the disease due to their lack of knowledge. The health workers are trained regularly using online mode, which improves their expertise by gaining experience while treating patients, consulting experts via the internet, and transferring their knowledge to improve rural people’s primary healthcare. Since increasing expert manpower and developing infrastructure is time-consuming, the pilot project was implemented in various villages with the help of the local administration, and the proposed model demonstrates its practical application in diagnosing common diseases in a more precise and accurate manner with minimum false cases.
The paper focuses the challenges on the primary healthcare and extends services to the people living in (remote) rural India, especially for elderly, women, children, and distressed people. In addition, the work aims to train the health assistants and enable them to use the current technology for establishing communication between the patients and the doctors (experts). However, few limitations could be highlighted for further investigation, including (i) infrastructure, like uninterrupted electrical power supply, which is not always guaranteed in remote villages; (ii) the issues of acquiring data from the patients by overcoming the social inhibitions; (iii) further investigation is required to check if the model developed using a particular dataset is valid for other disease-related dataset by fine tuning the hyperparameters only; (iv) preprocessing of data is needed to convert in a homogeneous form; (v) making the ground truth with consulting expert doctors and medical literature is a tedious job; and finally (vi) the latent/hidden features are to be extracted to reduce misdiagnosis of the diseases.
Conclusion
In remote areas, due to a lack of doctors and skilled manpower, diagnosing diseases is often imprecise. The paper proposes a method for diagnosing the people with minimum false events whether diseased or not by managing vagueness in input variables and boundary uncertainty in decision space. The performance with respect to accuracy, sensitivity, specificity, and precision increases (3 to 5%) after uncertainty management, and MLPNN classifier performs better than k-nearest neighbor, Naive Bayes, LR, and SVM classifiers. Various measures with respect to accuracy, sensitivity, specificity, and precision are used to measure performance of the proposed method and after uncertainty management performance increases (3 to 5%). The paper deduces kappa values that lie in the scale perfect for MLPNN classifier, which performs better than other classifiers to classify the disease class labels of the new patients. The Pearson correlation coefficient between the symptom/signal values of the new patients and the value obtained from the Pareto optimal front indicates that in most of the cases, the class interpretation is correct. Thus, the false-negative cases have been reduced using the proposed uncertainty management method where experts’ involvement is minimum. The paper uses a particular dataset to develop the model; however, whether the model is applicable for other datasets with different health conditions needs further investigation, which is the future scope of this work. Accessibility of huge patient information is the fundamental bottleneck to create the proposed rural healthcare model. In some cases, there may not exist any definite boundary between normal and pathological conditions. In such cases, we must rely on the opinions of experts.
Acknowledgements
We acknowledge Prof. (Dr.) Satadal Saha (MS, FRCS (Eng), Honorary Professor, Centre for Nanotechnology, IIT Guwahati, Founder, JSV Innovations Pvt. Ltd., Vice-President, Foundation for Innovations in Health) and Dr. Suman Mallik (MD, DNB, PDCR Consultant) senior consultant, Radiation Oncologist of NH Cancer Institute (formerly West bank Cancer Centre)) for their expert doctor opinion.
Author Contribution
Conception and design of study: Jaya Sil and Sayan Das.
Methodology: Sayan Das and Jaya Sil.
Acquisition of data: Sayan Das and Jaya Sil.
Formal analysis and investigation: Sayan Das and Jaya Sil.
Writing-original draft preparation: Sayan Das and Jaya Sil.
Writing-review and editing: Jaya Sil and Sayan Das.
Approval of the version of the manuscript: Jaya Sil and Sayan Das.
Supervision: Jaya Sil.
Funding
This work is supported by the Information Technology Research Academy (ITRA), Digital India Corporation (formerly Media Lab Asia), Government of India, under ITRA-Mobile Grant (ITRA/15(59)/Mobile/Remote Health/01).
Declarations
Conflict of Interest
The authors declare no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Das S, Sil J (2017) Uncertainity management of health attributes for primary diagnosis. 2017 International Conference on Big Data Analytics and Computational Intelligence (ICBDAC) 360 365. 10.1109/ICBDACI.2017.8070864
- 2.Bennett, Coleman & Co. Ltd (2021) Infections top illness list for rural, Urban Indians. India times, Times of India webpage. https://timesofindia.indiatimes.com/india/infections-top-illness-list-for-rural-indians-heart-ailment-for-urbanites/articleshow/72949987.cms.Accessed 25 Dec 2019
- 3.Chandrakumari AS, Sinha P, Singaravelu S, Jaikumar S. Prevalence of anemia among adolescent girls in a rural area of Tamil Nadu. India J Family Med Prim Care. 2019;8(4):1414–1417. doi: 10.4103/jfmpc.jfmpc_140_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Panikkath R, et al. Chest pain and diarrhea: a case of Campylobacter jejuni-associated myocarditis. J Emerg Med. 2014;46(2):180–83. doi: 10.1016/j.jemermed.2013.08.060. [DOI] [PubMed] [Google Scholar]
- 5.Uusitalo L, et al. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environ Model Softw. 2015;63:24–31. doi: 10.1016/j.envsoft.2014.09.017. [DOI] [Google Scholar]
- 6.Waleed AA, Alaa K ( 2013) Handling data uncertainty and inconsistency using multisensor data fusion. Adv Artif Intell 241260:11 10.1155/2013/241260
- 7.Skowron A, Dutta S. Rough sets: past, present, and future. Nat Comput. 2018;17(4):855–876. doi: 10.1007/s11047-018-9700-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rissino S, Germano L-T ( 2009) Rough set theory—fundamental concepts, principals, data extraction, and applications. Data mining and knowledge discovery in real life applications. IntechOpen 10.5772/6440
- 9.Jie Y, Taihua X, Fan Z ( 2018) Modified uncertainty measure of rough fuzzy sets from the perspective of fuzzy distance. Math Prob Eng 4160905:11 10.1155/2018/4160905
- 10.Das S, Sil J (2018) Managing uncertainty to rural primary health care using rough set theory. 2018 4th International Conference on Computing Communication and Automation (ICCCA) 1–7 10.1109/CCAA.2018.8777566
- 11.Das S, Sil J (2020) Knowledge uncertainty management in remote healthcare based on mutual information. 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS) 236–241 10.1109/ICACCS48705.2020.9074480
- 12.Deb K, Agrawal S, Pratap A, Meyarivan T (2000) A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In: Schoenauer M. et al. (eds) Parallel problem solving from nature PPSN VI. PPSN 2000. Lecture Notes in Computer Science, vol. 1917. Springer, Berlin, Heidelberg. 10.1007/3-540-45356-3_83
- 13.Fox RC. Medical uncertainty revisited. Handb Soc Stud Health Med. 2000;409:425. [Google Scholar]
- 14.Light D Jr. (1979) Uncertainty and control in professional training. J Health Soc Behav 310–322 [PubMed]
- 15.Beresford EB. Uncertainty and the shaping of medical decisions. Hastings Cent Rep. 1991;21(4):6–11. doi: 10.2307/3562993. [DOI] [PubMed] [Google Scholar]
- 16.Farnan J M et al. (2008) Resident uncertainty in clinical decision making and impact on patient care: a qualitative study. BMJ Qual Saf 17(2):22–126 [DOI] [PubMed]
- 17.Hamui-Sutton A, Vives-Varela T, Gutiérrez-Barreto S, et al. A typology of uncertainty derived from an analysis of critical incidents in medical residents: a mixed methods study. BMC Med Educ. 2015;15:198. doi: 10.1186/s12909-015-0459-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Han, Paul KJ, William MP Klein, Neeraj KA (2011) Varieties of uncertainty in health care: a conceptual taxonomy. Med Decis Making 31.6 828–838.10.1177/0272989X10393976 [DOI] [PMC free article] [PubMed]
- 19.Pomare C et al (2019) A revised model of uncertainty in complex healthcare settings: a scoping review. J Eval Clin Prac 25(2):176–182. 10.1111/jep.13079 [DOI] [PubMed]
- 20.Bhise V, Rajan SS, Sittig DF, et al. Defining and measuring diagnostic uncertainty in medicine: a systematic review. J Gen Intern Med. 2018;33:103–115. doi: 10.1007/s11606-017-4164-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Borkowski N, Katherine AM (2020) Organizational behavior in health care. Jones & Bartlett Publishers
- 22.Strout TD et al (2018) Tolerance of uncertainty: a systematic review of health and healthcare-related outcomes. Patient Educ Couns| 101(9):1518–1537.10.1016/j.pec.2018.03.030 [DOI] [PubMed]
- 23.Wasylewicz ATM, Scheepers-Hoeks AMJW. Clinical decision support systems. Cham: Fundamentals of Clinical Data Science. Springer; 2019. pp. 153–169. [PubMed] [Google Scholar]
- 24.Shahid N, Rappon T, Berta W. Applications of artificial neural networks in health care organizational decision-making: a scoping review. PLoS ONE. 2019;14(2):e0212356. doi: 10.1371/journal.pone.0212356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bessa MA, et al. A framework for data-driven analysis of materials under uncertainty: countering the curse of dimensionality. Comput Methods Appl Mech Eng. 2017;320:633–667. doi: 10.1016/j.cma.2017.03.037. [DOI] [Google Scholar]
- 26.Djulbegovic B, Hozo I. Transforming clinical practice guidelines and clinical pathways into fast and frugal decision trees to improve clinical care strategies. J Evaluation Clin Prac. 2018;24(5):1247–1254. doi: 10.1111/jep.12895. [DOI] [PubMed] [Google Scholar]
- 27.Wang H, Zeshui X, Witold P (2017) An overview on the roles of fuzzy set techniques in big data processing: trends, challenges and opportunities. Knowl-Based Syst 118:15–30.10.1016/j.knosys.2016.11.008
- 28.Chen M, Hao Y, Hwang K, Wang L, Wang L (2017) Disease prediction by machine learning over big data from healthcare communities. IEEE Acc 5:8869–8879. 10.1109/ACCESS.2017.2694446
- 29.Qinghua Z, Qin X, Guoyin W (2016) A survey on rough set theory and its applications. CAAI Trans Intell Technol 1.4:323–333.10.1016/j.trit.2016.11.001
- 30.Zhai J, Zhang Y, Zhu H. Three-way decisions model based on tolerance rough fuzzy set. Int J Mach Learn Cyber. 2017;8:35–43. doi: 10.1007/s13042-016-0591-2. [DOI] [Google Scholar]
- 31.Wei W, Liang J. Information fusion in rough set theory: an overview. Inf Fus. 2019;48:107–118. doi: 10.1016/j.inffus.2018.08.007. [DOI] [Google Scholar]
- 32.Qinghua Z, Qin X , Guoyin W (2016) A survey on rough set theory and its applications. CAAI Trans IntelliTechnol 1.4:323–333
- 33.Huang Y, et al. Dynamic variable precision rough set approach for probabilistic set-valued information systems. Knowl-Based Syst. 2017;122:131–147. doi: 10.1016/j.knosys.2017.02.002. [DOI] [Google Scholar]
- 34.Sun B, et al. Three-way decision making approach to conflict analysis and resolution using probabilistic rough set over two universes. Info Sci. 2020;507:809–822. doi: 10.1016/j.ins.2019.05.080. [DOI] [Google Scholar]
- 35.Sun B, Ma W, Xiao X. Three-way group decision making based on multigranulation fuzzy decision-theoretic rough set over two universes. Int J Approx Reas. 2017;81:87–102. doi: 10.1016/j.ijar.2016.11.001. [DOI] [Google Scholar]
- 36.Lang G, Miao D, Mingjie C. Three-way decision approaches to conflict analysis using decision-theoretic rough set theory. Inf Sci. 2017;406:185–207. doi: 10.1016/j.ins.2017.04.030. [DOI] [Google Scholar]
- 37.Dou H, et al. Decision-theoretic rough set: a multicost strategy. Knowl-Based Syst. 2016;91:71–83. doi: 10.1016/j.knosys.2015.09.011. [DOI] [Google Scholar]
- 38.Dai J, Gao S, Zheng G. Generalized rough set models determined by multiple neighborhoods generated from a similarity relation. Soft Comput. 2018;22:2081–2094. doi: 10.1007/s00500-017-2672-x. [DOI] [Google Scholar]
- 39.Jothi G. Hybrid Tolerance Rough Set-Firefly based supervised feature selection for MRI brain tumor image classification. Appl Soft Comput. 2016;46:639–651. doi: 10.1016/j.asoc.2016.03.014. [DOI] [Google Scholar]
- 40.Zhang X, Chen D, Tsang ECC. Generalized dominance rough set models for the dominance intuitionistic fuzzy information systems. Inf Sci. 2017;378:1–25. doi: 10.1016/j.ins.2016.10.041. [DOI] [Google Scholar]
- 41.Dubois D, Henri P (1990) Rough fuzzy sets and fuzzy rough sets. Int J Gen Syst 17.2–3, pp. 191–209 .10.1080/03081079008935107
- 42.Fuzzy rough set-based attribute reduction using distance measures Wang, Changzhong, et al. Knowl-Based Syst. 2019;164:205–212. doi: 10.1016/j.knosys.2018.10.038. [DOI] [Google Scholar]
- 43.Maratea A, Ferone A (2019) Rough–fuzzy entropy in neighbourhood characterization. In: Montella R., Ciaramella A., Fortino G., Guerrieri A., Liotta A. (eds) Internet and distributed computing systems. IDCS 2019. Lecture Notes in Computer Science, vol. 11874. Springer, Cham. 10.1007/978-3-030-34914-1_41
- 44.Beg I, Tabasam R (2017) An extension of soft rough fuzzy sets. Korean J Math 25.1:71–85
- 45.Wang H, Zhang WX, Li HR (2005) Uncertainty measures of rough-fuzzy sets. Comput Eng Appl 3:31–37
- 46.Huani Q, Darong L (2014 ) New uncertainty measure of rough fuzzy sets and entropy weight method for fuzzy-target decision-making tables. J App Math 487036:7. 10.1155/2014/487036
- 47.Bingzhen S, Ma W (2013) Uncertainty measure for general relation-based rough fuzzy set. Kybernetes
- 48.Hu J, Witold P, Guoyin W (2016) A roughness measure of fuzzy sets from the perspective of distance. Int J Gen Syst 45.3 352–367
- 49.Yu Bet al. (2020) A novel approach to predictive analysis using attribute-oriented rough fuzzy sets. Expert Syst Appl :113644
- 50.Sun B, Weimin M, Xiangtang C (2019) Variable precision multigranulation rough fuzzy set approach to multiple attribute group decision-making based on λ-similarity relation. Comput Ind Eng 127 : 326–343
- 51.Akram M, Zafar F. Rough fuzzy digraphs with application. J Appl Math Comput. 2019;59:91–127. doi: 10.1007/s12190-018-1171-2. [DOI] [Google Scholar]
- 52.Straszecka E. Combining uncertainty and imprecision in models of medical diagnosis. Inf Sci. 2006;176(20):3026–3059. doi: 10.1016/j.ins.2005.12.006. [DOI] [Google Scholar]
- 53.Yager RR. Decision making under measure-based granular uncertainty. Granul Comput. 2018;3:345–353. doi: 10.1007/s41066-017-0075-0. [DOI] [Google Scholar]
- 54.Dai W. Wang, Xu Q. An uncertainty measure for incomplete decision tables and its applications. IEEE Trans Cybern. 2013;43(4):1277–1289. doi: 10.1109/TSMCB.2012.2228480. [DOI] [PubMed] [Google Scholar]
- 55.Suri, NNR, Ranga G (2019) Athithan Outlier detection. Outlier detection: techniques and applications, pp. 13–27. Springer, Cham
- 56.Aggarwal CC, Saket S (2017) Outlier ensembles: an introduction. Springer
- 57.Wang H, Bah MJ, Hammad M. Progress in outlier detection techniques: a survey. IEEE Access. 2019;7:107964–108000. doi: 10.1109/ACCESS.2019.2932769. [DOI] [Google Scholar]
- 58.Hodge V, Austin J. A survey of outlier detection methodologies. Artif Intell Rev. 2004;22:85–126. doi: 10.1023/B:AIRE.0000045502.10941.a9. [DOI] [Google Scholar]
- 59.Cao F et al (2006) Density-based clustering over an evolving data stream with noise. Proceedings of the 2006 SIAM international conference on data mining. Soc Ind Appl Math
- 60.Angiulli F, Basta S, Pizzuti C. Distance-based detection and prediction of outliers. IEEE Trans Knowl Data Eng. 2006;18(2):145–160. doi: 10.1109/TKDE.2006.29. [DOI] [Google Scholar]
- 61.Domingues R, et al. A comparative evaluation of outlier detection algorithms: experiments and analyses. Pattern Recognit. 2018;74:406–421. doi: 10.1016/j.patcog.2017.09.037. [DOI] [Google Scholar]
- 62.Ayadi Aya, et al. Outlier detection approaches for wireless sensor networks: a survey. Comp Netw. 2017;129:319–333. doi: 10.1016/j.comnet.2017.10.007. [DOI] [Google Scholar]
- 63.Cai Z, He Z, Guan X, Li Y. Collective data-sanitization for preventing sensitive information inference attacks in social networks. IEEE Trans Dependable Secure Comput. 2018;15(4):577–590. doi: 10.1109/TDSC.2016.2613521. [DOI] [Google Scholar]
- 64.Djenouri Y, Belhadi A, Lin JC, Djenouri D, Cano A. A survey on urban traffic anomalies detection algorithms. IEEE Access. 2019;7:12192–12205. doi: 10.1109/ACCESS.2019.2893124. [DOI] [Google Scholar]
- 65.Duraj A (2017) Outlier detection in medical data using linguistic summaries. 2017 IEEE International Conference on INnovations in Intelligent SysTems and Applications (INISTA), pp. 385–390 10.1109/INISTA.2017.8001191
- 66.Gaspar J et al. (2011) A systematic review of outliers detection techniques in medical data-preliminary study. HEALTHINF
- 67.Rahman MM, Darryl ND (2013) Addressing the class imbalance problem in medical datasets. Int J Mach Learn Comp 224–228
- 68.Zhang S, Chengqi Z, Qiang Y (2003) Data preparation for data mining. Appl Artif Intell 17.5–6 375–381
- 69.Das S, Sil J. Managing uncertainty in imputing missing symptom value for healthcare of rural India. Health Inf Sci Syst. 2019;7:5. doi: 10.1007/s13755-019-0066-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Jameson, J. Larry 2018 Harrison’s principles of internal medicine. McGraw-Hill Education
- 71.Glynn, Michael, and William M. Drake 2017 Hutchison’s clinical methods e-book: an integrated approach to clinical practice. Elsevier Health Sciences
- 72.Chandel K, Kunwar V, Sabitha S, et al. A comparative study on thyroid disease detection using K-nearest neighbor and Naive Bayes classification techniques. CSIT. 2016;4:313–319. doi: 10.1007/s40012-016-0100-5. [DOI] [Google Scholar]
- 73.Shen Y, Li Y, Zheng HT, et al. Enhancing ontology-driven diagnostic reasoning with a symptom-dependency-aware Naïve Bayes classifier. BMC Bioinf. 2019;20:330. doi: 10.1186/s12859-019-2924-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Azar AT, El-Metwally SM. Decision tree classifiers for automated medical diagnosis. Neural Comput Appl. 2013;23:2387–2403. doi: 10.1007/s00521-012-1196-7. [DOI] [Google Scholar]
- 75.Kumar TS et al. (2017) Brain tumor detection using SVM classifier. 2017 Third International Conference on Sensing, Signal Processing and Security (ICSSS). IEEE
- 76.Ranganathan P, Pramesh CS, Rakesh A (2017) Common pitfalls in statistical analysis: logistic regression. Perspect Clinical Res 8.3:148 [DOI] [PMC free article] [PubMed]
- 77.Weng C-H, Huang TC-K, Han R-P (2016) Disease prediction with different types of neural network classifiers. Telematics Inform 33(2):277–292
- 78.Rojas R. The backpropagation algorithm. Berlin, Heidelberg: Neural networks. Springer; 1996. pp. 149–182. [Google Scholar]
- 79.Nuzzo RL. The box plots alternative for visualizing quantitative data. PM&R. 2016;8(3):268–272. doi: 10.1016/j.pmrj.2016.02.001. [DOI] [PubMed] [Google Scholar]
- 80.Kumar R, Indrayan A. Receiver operating characteristic (ROC) curve for medical researchers. Indian Pediatr. 2011;48:277–287. doi: 10.1007/s13312-011-0055-4. [DOI] [PubMed] [Google Scholar]
- 81.Chan YH. Biostatistics 104: correlational analysis. Singapore Med J. 2003;44(12):614–619. [PubMed] [Google Scholar]
- 82.Akoglu H (2018) User’s guide to correlation coefficients. Turk J Emerg Med 18.3 91–93 [DOI] [PMC free article] [PubMed]