Abstract
Targeted intervention and resource allocation are essential in effective control of infectious diseases, particularly those like malaria that tend to occur in remote areas. Disease prediction models can help support targeted intervention, particularly if they have fine spatial resolution. But, choosing an appropriate resolution is a difficult problem since choice of spatial scale can have a significant impact on accuracy of predictive models. In this paper, we introduce a new approach to spatial clustering for disease prediction we call complexity-based spatial hierarchical clustering. The technique seeks to find spatially compact clusters that have time series that can be well characterized by models of low complexity. We evaluate our approach with 2 years of malaria case data from Tak Province in northern Thailand. We show that the technique’s use of reduction in Akaike information criterion (AIC) and Bayesian information criterion (BIC) as clustering criteria leads to rapid improvement in predictability and significantly better predictability than clustering based only on minimizing spatial intra-cluster distance for the entire range of cluster sizes over a variety of predictive models and prediction horizons.
Keywords: Malaria prediction, Spatial epidemiology, Spatial clustering, Akaike information criterion, Bayesian information criterion
Introduction
Targeted intervention and resource allocation are essential elements of effective control strategies for infectious disease. This is particularly the case for diseases like malaria that are prevalent in less developed and more remote areas in which public health resources are often scarce. A valuable supporting technology is the ability to predict disease with sufficient spatial resolution to effectively target the disease. With case data on infectious disease as well as on related environmental variables now increasingly available in high spatial resolution [1], the data to build high resolution models is often not a limiting factor. One is then faced with the choice of a wide range of possible spatial resolutions to use. This is a complex problem since too fine or too coarse a resolution can negatively affect model prediction accuracy and at the same time very coarse resolutions are not helpful in targeting intervention. While the issue of choice of spatial resolution for modeling has been recognized and discussed in the epidemiological literature [2, 3], previous work has typically chosen spatial resolution for modeling based on existing government administrative boundaries or on boundaries of responsibility of medical clinics. There is as yet no work that has sought to generate spatial partitions from fine grained data in such a way as to retain spatial resolution while maximizing predictability.
In this paper1 we introduce a new approach to spatial clustering for disease prediction we call complexity-based spatial hierarchical clustering. Following the minimum description length principle (MDL) [4, 5], a formalization of Occam’s Razor, we seek to find compact clusters that have time series that can be well characterized by models of low complexity. This is achieved by fitting ARIMA models to the time series and using Akaike information criterion (AIC) and the Bayesian information criterion (BIC) as the MDL metrics. We evaluate the effectiveness of the technique using 2 years of weekly village level malaria case data from Tak Province in northern Thailand. We show that we can greatly increase the predictability of malaria cases for a variety of prediction methods with only a relatively small amount of clustering and that inclusion of AIC and BIC as clustering metrics results in significantly better predictability than clustering based only on minimizing physical compactness for clusters. Comparison with hotspot clusters produced by SatScan on this data set shows that our clustering algorithm discovers some clusters with better predictability than the SatScan clusters of the same size. Furthermore, the hierarchical clusters produced by our algorithm allow the user to easily and flexibly explore alternative spatial groupings.
Related Work
Appropriate choice of spatial resolution has been recognized as one of the most important research issues in the field of spatial epidemiology [2, 3]. For example, in examining the impact of environmental factors on diabetes, Dagliati et al. [6] note that “one of the main efforts was to define the level of detail through which to derive meaningful patterns and observe events of interest.” As Meiker and Sloan [3] point out, resolutions that are too fine can suffer from the small number problem [7] in which sparsely populated areas can have few disease cases, resulting in unstable rate estimates. A common solution is to apply spatial smoothing of the data, but this changes the spatial character of the original data and can introduce autocorrelation in the resulting map [8]. In contrast, the approach in this paper is to cluster regions rather than smoothing the data. In this way, while precision is lost, accuracy of the data is maintained. A second problem in working with geographic data is the sensitivity of statistical results to the definition of spatial units over which the data are collected. This is known as the modifiable areal unit problem (MAUP) and is applicable to predictive and spatial statistical models [9, 10]. This problem can be avoided by using the objectives of the analysis to guide the selection of the spatial resolution. In the current paper, since the objective is population-level malaria prediction, this is addressed by using MDL applied to the time series of malaria cases as a primary criterion in spatial aggregation.
While spatial clustering has been extensively studied in epidemiology, most work has focused on use of spatial scan statistics to perform geographical surveillance of disease and to test whether a disease is randomly distributed over space, over time, or over space and time. Kulldorf’s spatial scan statistic [13] is the most widely used approach and has been implemented in the SatScan package [24]. SatScan moves a scanning window of variable size across space and/or time, noting the number of observed and expected observations inside the window at each space/time location. The scanning window can be a circle or ellipse in space, an interval in time, or a cylinder in space-time with circular or elliptical base designating the spatial area and the height designating the time interval. For each location and size of the window, the number of observed cases is counted and expected cases are calculated assuming an even distribution of cases across the population. A likelihood ratio test is used to compare the prevalence of disease transmission inside the window to that outside and identify areas of higher than expected or lower than expected transmission. When an elliptic window shape is used, there is an option to use a non-compactness penalty to favor more compact clusters. This is to avoid generating long narrow ellipses.
Spatial scan statistics are commonly used to identify hotspots of disease transmission [11, 12]. A hotspot is a geographical area with significantly more disease cases than would be expected by chance. Hotspots are often used for prediction and targeting of intervention since some studies have shown that they often tend to persist over time [14]. Indeed, a cluster-randomized control trial of targeting hotspots for intervention [15] achieved modest reductions inside the hotspots. But, a recent large study in sub-Saharan Africa [16] has found that hotspots may not be temporally stable and may be more difficult to identify at high transmission, bringing into question the value of identifying hotspots as a strategy for targeted intervention.
There is a large body of work on malaria prediction using a variety of techniques including various types of regression, ARIMA models, SIR-based models, and neural networks [17]. Models are most commonly built with weekly or monthly temporal resolution. Spatial resolutions include village, district, province, and catchment, with district being the most common. But, only a limited amount of work has explored the direct impact of spatial resolution on malaria prediction. Giardina et al. [18] assess the effect of the spatial resolution of remotely sensed land cover and elevation on malaria risk estimation. They investigate three resolutions: 1 km, 500 m, and 100 m and find that finer resolution models tend to overestimate the number of infections. Teklehaimanot et al. [19] use data on weekly confirmed malaria cases in ten districts of Ethiopia as well as temperature and rainfall to produce weekly predictions. Districts with similar climactic characteristics are grouped to reduce random error and produce more reliable and precise estimates of weather effects.
Montero and Vilar [20] present a number of model-based, complexity-based, and prediction-based time series clustering techniques implemented in R. Their model-based approach fits time series with ARIMA models and measures the similarity between the fitted models. The complexity-based approach determines similarity between complexity measures of time series. Their approach is fundamentally different from our work in that they treat the individual time series separately in fitting the ARIMA models or computing complexity and follow a standard clustering approach. In our work, similarity is determined in terms of a model fitted to a merger of the time series being considered for clustering. In addition, they do not consider reduction in complexity as a clustering criterion. Other work on time series abstraction and clustering comes from the field of granular computing [21]. The work examines how to define and operate with granulation (aggregation) and de-granulation (disaggregation) operators within the frameworks of fuzzy sets, interval analysis, and rough sets and how to reason with granular data [22]. The work on time series analysis is largely concerned with abstraction of high frequency data. For example, Maciel et al. [23] present a possibilistic fuzzy modeling approach to prediction with interval time series in which the time series over an interval of time is characterized by upper and lower bounds.
Algorithm
The objective of our clustering algorithm is to support targeted intervention, by producing geographic regions that are physically compact and have time series of disease incidence that can be well modeled so that it can be accurately predicted. As a prelude to presenting our algorithm, we discuss two possible approaches to clustering and explain why they are not suitable for solving this problem. Throughout the remainder of the paper, the time series of cases in a cluster will be considered to be the sum of the time series of cases of its constituent geographic regions.
As discussed, the most widely used approach to spatio-temporal clustering in epidemiology uses Kulldorf’s spatial scan statistic [13], implemented in the SatScan package [24]. SatScan examines total disease incidence in a spatial and/or temporal region. While this approach can be of some help in prediction by indicating areas of higher than normal (hotspots) or lower than normal (cold spots) disease incidence, it is too abstract and coarse a measure for our purposes. SatScan can also be used to evaluate spatial variation in temporal trends, but this is again too abstract a notion, examining only the overall rate of increase or decrease of a time series over a period of time. We require an approach that can characterize the predictability of a time series, which requires a finer grained characterization of the time series. In addition, the SatScan approach is based on measuring the difference between incidence inside and outside the cluster, while our purposes need an approach that focuses on similarly within the cluster. An empirical comparison of our approach with that of SatScan is presented in Sect. 6.
A more direct approach to producing geographic clusters with good time series predictability is to cluster geographic regions when this produces time series of low complexity. Three commonly used measures of time series complexity are LZ complexity [25], approximate entropy [26], and Hurst exponent [27]. The LZ complexity measures the number of changes in a time series and so gives a high complexity to time series that have a regular pattern of change and a low value to time series with many constant values. This is not a suitable measure to characterize predictability since time series with regular patterns of change are typically easily modeled. The approximate entropy quantifies the amount of regularity of fluctuations in a time series, and Hurst exponent is a measure of the long-term memory of a time series. As with LZ complexity, they both indicate low complexity of time series with many zero values and occasional non-zero values. They also require that the time series span sufficient time to have repeating patterns, which may not be the case with many data sets. Empirical investigation of these measures shows that they generally indicate low levels of complexity for individual village level time series and a higher level of complexity for the time series representing larger geographic regions. This is opposite to predictability, with predictive models tested generally performing better for larger regions in our data.
Yet a third approach, and the one taken in this paper, is to more directly measure predictability of the time series by fitting a model to it and to measure the parsimony and goodness of fit of that model. The modeling approach should take into account inherent temporal properties such as the variations specific to a particular time frame/seasonality and the trend. The analysis of such properties is commonly carried out by using the mixed modeling approaches from the family of auto-regressive moving average models (ARIMA). ARIMA attempts to describe the movements in a stationary time series as a function of autoregressive and moving average parameters. Auto-regressive terms (AR) of the model consider the dependent relationship between an observation and some number of lagged observations, integration (I) refers to the process of differencing/subtracting an observation from an observation at the previous time step in order to make the time series stationary, and the moving average (MA) terms of the model refer to the dependency between an observation and a residual error from a moving average model applied to lagged observations.
The transmissibility and seasonality aspects of malaria lead to the wide adoption of ARIMA models in malaria prediction and studies have shown them to have higher forecast accuracy than conventional linear models [28]. Moreover, ARIMA models are reasonably simple and relatively stable even in the absence of detailed data, which would make it difficult to calculate parameters required in building more complex prediction models [29].
In characterizing a time series by a model, it is important to guarantee that the model considers enough parameters to adequately model the underlying relationships among variables in the data (sensitivity) while ensuring that the model is not overfitting the data (specificity). In this respect, the performance evaluation measure should consider of a goodness-of-fit term along with a penalty to control overfitting to provide a way to balance sensitivity and specificity. Penalized-likelihood information theoretic criteria such as AIC and BIC are widely used to estimate model parsimony and goodness-of-fit. These criteria measure whether the model’s description of the observed data is achieved in the simplest manner. AIC estimates the expected relative Kullback-Leibler (KL) distance between the fitted likelihood function of the model and unknown true likelihood function of the data, whereas BIC is an estimate of a function of the posterior probability of a given model [30]. The AIC or BIC for a model can be represented in the form [− 2logL + kp], where L is the likelihood function, p is the number of parameters in the model, and k is 2 for AIC and log (n) for BIC. For both measures, smaller values indicate better models. AIC or BIC can be computed easily once the maximum likelihood estimators of the parameters of a model are determined. Since ARIMA models fit well for highly regular univariate time series, finding the best fit model and using its AIC or BIC value which accounts for fit and model complexity works well to characterize time series predictability. We implement this measure using the auto.arima function in R [31] by finding the best-fit ARIMA model in terms of AICc or BIC and using its AIC or BIC value.
Since we wish to support users in selecting appropriate spatial clusters for prediction, we use agglomerative hierarchical clustering so that the cluster membership does not change dramatically as we move between clustering levels. The clustering algorithm uses greedy search. It computes the distance between all pairs of regions, starting with the smallest and clusters those with highest similarity. The two regions in the cluster are removed from the set of candidate regions and the clustered region is added. The distance between the new cluster and all other regions is then computed. The algorithm continues until there is only one cluster, which forms the top level of the cluster hierarchy.
The distance between a pair of clusters is computed by using any distance function to combine physical distance and reduction in either AIC or BIC. Each cluster is associated with a time series of disease cases, and when two clusters are merged, their time series are combined by summing them so that the new time series represents the number of cases in the cluster region at each time point. The complexity of each time series is computed by finding the best fit ARIMA model and computing its AIC or BIC value. The reduction in time series complexity that results from clustering two regions (C1 and C2) is computed by taking the difference between the complexity of the time series for the cluster and the average complexity of the time series for the two regions being merged: IC (C1 ∪ C2) − (IC (C1) + IC (C2))/2, where IC is the information criterion AIC or BIC. The flow diagram of the clustering algorithm is shown in Fig. 1.
Fig. 1.
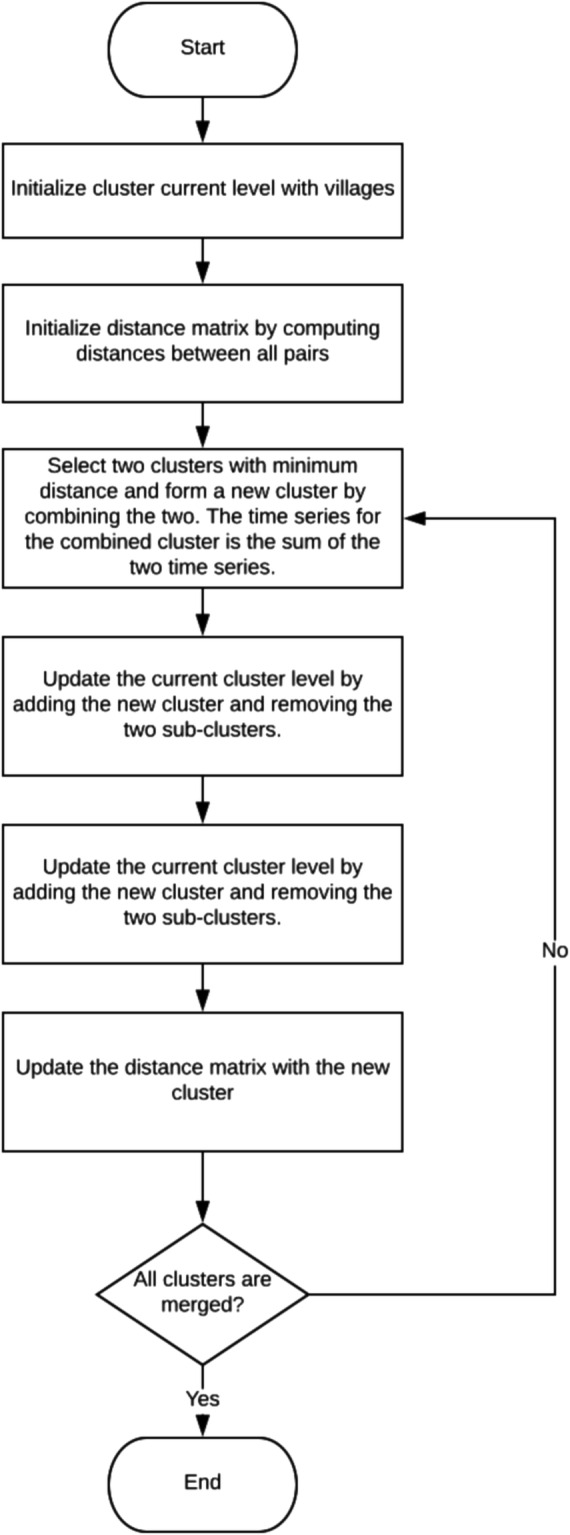
Flow diagram of the clustering algorithm
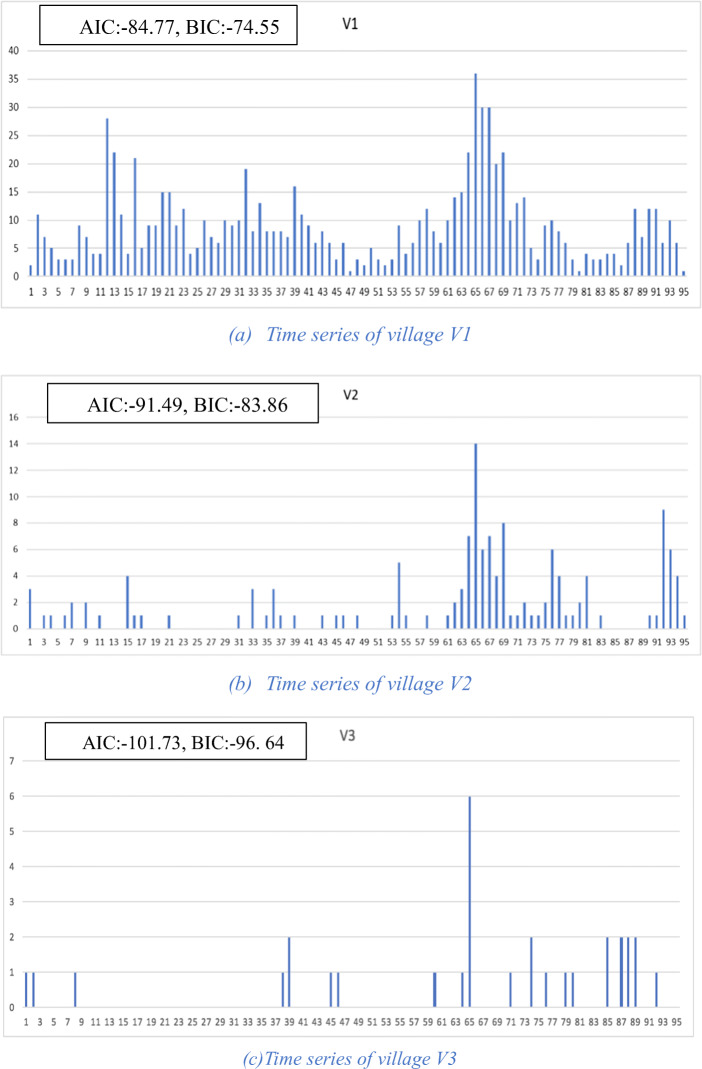
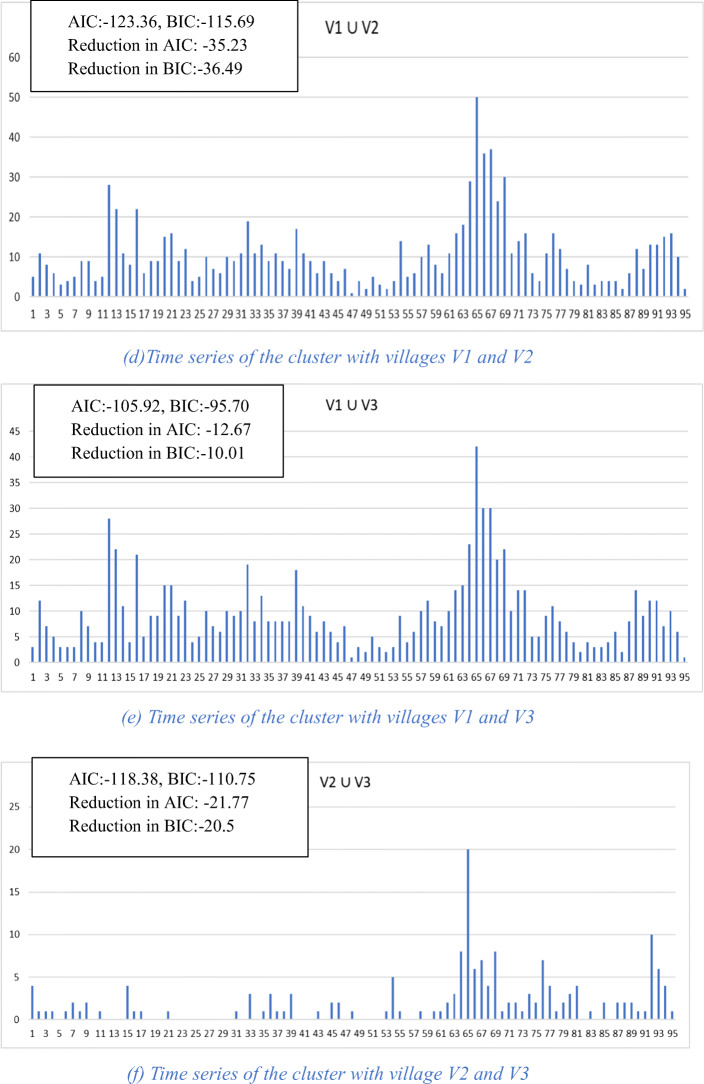
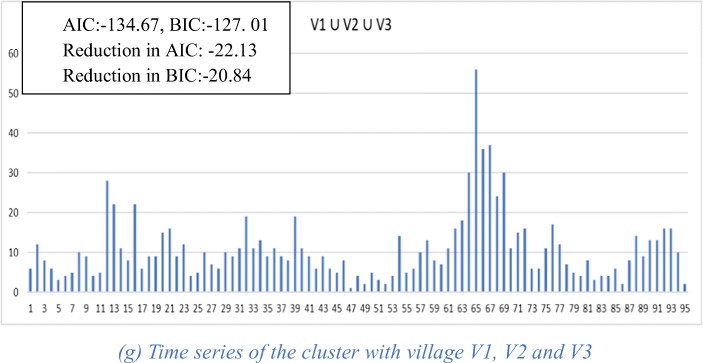
An example of the functioning of the algorithm is given in Fig. 2. For simplicity, we leave physical distance out and work only with complexity of the time series. Figure 2a–c shows the three village-level time series with their corresponding AIC and BIC values. Figure 2d–f shows the three possible pairwise clusters that can be formed and their corresponding AIC and BIC values as well as their reductions in AIC and BIC. Since the cluster (V1 ∪ V2) results in the largest reduction in AIC of − 35.23, when using AIC for clustering, this cluster would be chosen among the three. Figure 2g shows the time series for the cluster formed by adding village V3 to the previous cluster and the corresponding values for AIC, BIC, and reduction in AIC and BIC. It can be seen from these values that this larger cluster results in yet a further improvement in time series complexity as measured by AIC and BIC reduction.
Fig. 2.
Village and cluster level time series
Data
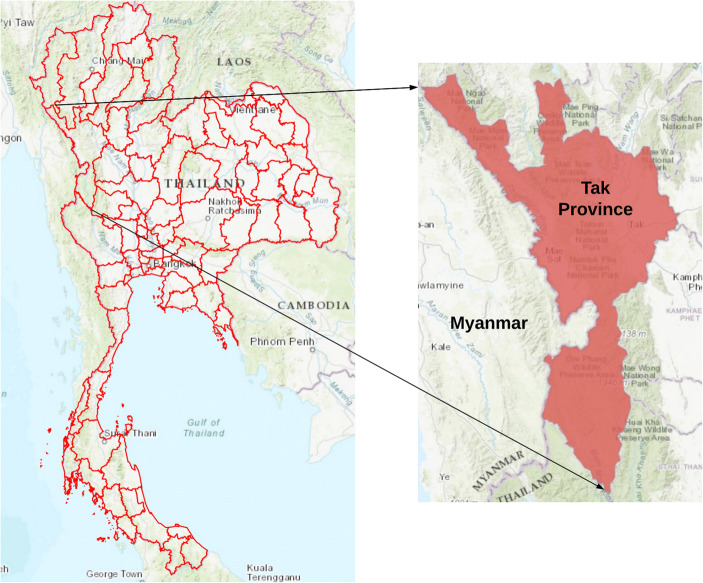
We demonstrate our approach with the problem of weekly malaria prediction in Tak Province of Thailand, shown in the map in Fig. 3. Tak is in the northwest of the country and has a long border with Myanmar. Tak comprises 333 villages, from among which 279 in which malaria is prevalent were selected for analysis. The villages left out of the analysis are those with fewer than two cases in 2 years. All of these except 12 are beyond longitude 99° east, i.e., the portion of Tak farthest from the Myanmar border. The case data for our experiments consists of weekly microscopically confirmed malaria cases obtained from Thailand’s national E-Malaria Information System [1]. The data covers each of the villages for the years 2012 and 2013 (99 weeks), providing a total of 27,621 weekly village reports with 23,201 total cases (Plasmodium falciparum, Plasmodium vivax) over all reports. The number of cases per village per week ranges from 0 to 97 with a mean of 0.84. Predictive models for malaria typically make use of environmental factors as determinants of mosquito vector density and infectivity. So, in addition to the case data, we make use of land surface temperature (LST) and slope in constructing the predictive models. Previous studies [32, 33] found LST to be the most influential temporal environmental variable for this data set and slope to be among the most influential non-temporal environmental variables. LST is taken from monthly satellite data at 5 km resolution from MOD11C3, and slope is calculated as the average in a 1 km buffer around each village, computed from elevation data.
Fig. 3.
Map showing the study area of Tak Province generated with ArcGIS software
Experimental Setup
Five different cluster hierarchies were generated using five similarity measures: physical distance alone as a baseline, AIC and BIC alone, and each of AIC and BIC combined with physical distance with weight 5. This weight was empirically determined to yield compact clusters and retain good influence of the information criterion. Euclidean distance was used for the similarity measure.
The impact of clustering on prediction accuracy was evaluated using 10-fold cross validation. A cluster hierarchy was generated using the training data for each fold, and a predictive model was generated for each cluster in the hierarchy. The same hierarchy was then applied to the test data and predictive models were tested on the clusters there. For malaria prediction, we selected three of the most commonly used techniques: linear regression, ARIMA, and ARIMAX. The predictor variables for ARIMA and ARIMAX were the previous week’s cases and LST lagged by 5 weeks. For linear regression, slope was additionally used. It could not be used for the ARIMA and ARIMAX models since it is constant over time. For each predictive model, we evaluated the effect of clustering on short-term (1-week) and long-term (4-week) prediction accuracy. The horizon of 1 week was chosen as representative of short-term prediction because this is the shortest horizon supported by the temporal granularity of the data. The horizon of 4 weeks was chosen to represent longer range prediction since a previous study of malaria prediction in Tha Song Yang District of Tak Province showed a marked difference in accuracy between models used for short-term predictions of 1–3 weeks and the same types of models used for longer-term predictions of 4–6 weeks [32]. Since the incidence values generally increase with cluster size, to compare prediction accuracy of clusters of varying size, we need an evaluation metric that is independent of magnitude. We thus use the Symmetric Mean Absolute Percentage Error (SMAPE) [34] which has a range of 0 to 100 (Tables 4, 5, 6, and 7).
Table 4.
Cumulative moving average of SMAPE for 1- and 4-week ARIMAX predictions using AIC alone, AIC with physical distance, and physical distance alone. Repeated entries indicate that there were no clusters of that size, and so, the cumulative average value remains unchanged
| Physical distance only | Physical distance with AIC | AIC only | ||||
|---|---|---|---|---|---|---|
| Cluster size | Cum. moving avg. | Cum. moving avg. | Cum. moving avg_ | |||
| 1 week | 4 weeks | 1 week | 4 weeks | 1 week | 4 weeks | |
| 1 | 87.7 | 87.7 | 87.7 | 87.7 | 87.7 | 87.7 |
| 2 | 79.8 | 79.8 | 79.2 | 79.2 | 77.4 | 77.4 |
| 3 | 78.3 | 78.3 | 76.7 | 76.7 | 73.8 | 73.8 |
| 4 | 75.7 | 75.7 | 74.5 | 74.5 | 71.1 | 71.1 |
| 5 | 75.1 | 75.1 | 72.7 | 72.7 | 69.0 | 69.0 |
| 6 | 73.7 | 73.7 | 71.3 | 71.3 | 67.3 | 67.3 |
| 7 | 72.9 | 72.9 | 69.9 | 69..9 | 65.7 | 65.7 |
| 8 | 72.5 | 72.5 | 69.1 | 69.1 | 64.7 | 64.7 |
| 9 | 72.0 | 72.0 | 68.3 | 68.3 | 63.7 | 63.7 |
| 10 | 71.8 | 71.8 | 67.8 | 67.8 | 63.1 | 63.1 |
| 11 | 71.3 | 71.3 | 67.3 | 67.3 | 62.4 | 62.4 |
| 12 | 70.7 | 70.7 | 66.8 | 66.8 | 61.9 | 61.9 |
| 13 | 70.5 | 70.5 | 66.4 | 66.4 | 61.3 | 61.3 |
| 14 | 69.9 | 69.9 | 66.2 | 66.2 | 60.9 | 60..9 |
| 15 | 64.7 | 69.7 | 66.0 | 66.0 | 60.4 | 60.4 |
| 16 | 69.7 | 69.7 | 65.7 | 65.7 | 60.1 | 60.1 |
| 17 | 69.5 | 69.5 | 65.5 | 65.5 | 59.9 | 59.9 |
| 18 | 69.3 | 69.7 | 65.3 | 65.3 | 59.6 | 59.6 |
| 19 | 69.2 | 69.2 | 65.1 | 65.1 | 59.4 | 59.4 |
| 20 | 68.9 | 68.9 | 64.9 | 64.9 | 59.1 | 59.1 |
| 21 | 68.7 | 68.7 | 64.8 | 64.8 | 58.9 | 58.9 |
| 22 | 68.6 | 68.6 | 64.7 | 64.7 | 58.7 | 58.7 |
| 23 | 68.6 | 68.6 | 64.6 | 64.6 | 585 | 58.5 |
| 24 | 68.6 | 68.6 | 64.5 | 64.5 | 58.4 | 58.4 |
| 25 | 68.6 | 68.6 | 64.5 | 64.5 | 58.3 | 58.3 |
| 26 | 68.6 | 68.6 | 64.4 | 64.4 | 58.2 | 58.2 |
| 27 | 68.6 | 68.6 | 64.3 | 64.3 | 58.1 | 58.1 |
| 28 | 68.5 | 68.5 | 64.2 | 64.2 | 58.0 | 58.0 |
| 29 | 68.5 | 68.5 | 64.1 | 64.1 | 57.9 | 57.9 |
| 30 | 68.5 | 615 | 64.0 | 64.0 | 57.8 | 57.8 |
| ... | ... | ... | ... | ... | ... | ... |
| 279 | 66.3 | 66.3 | 60.6 | 60.6 | 54.4 | 54.4 |
Table 5.
Cumulative moving average of SMAPE for 1- and 4-week linear regression predictions using AIC alone, AIC with physical distance, and physical distance alone. Repeated entries indicate that there were no clusters of that size, and so, the cumulative average value remains unchanged
| Physical distance only | Physical distance with AIC | AIC only | ||||
|---|---|---|---|---|---|---|
| Cluster size | Cum. moving avg. | Cum. moving avg. | Cum. moving avg. | |||
| 1 week | 4 weeks | 1 week | 4 weeks | 1 week | 4 weeks | |
| 1 | 88.8 | 89.8 | 88.8 | 89.8 | 88.8 | 89.8 |
| 2 | 80.4 | 81.0 | 80.6 | 81.8 | 79.7 | 81.5 |
| 3 | 78.7 | 76.7 | 77.6 | 79.0 | 75.1 | 79.9 |
| 4 | 76.4 | 74.2 | 75.7 | 77.3 | 72.4 | 78.0 |
| 5 | 75.8 | 71.9 | 74.0 | 75.6 | 70.0 | 77.3 |
| 6 | 74.5 | 70.1 | 72.5 | 74.3 | 68.1 | 76.2 |
| 7 | 73.8 | 68.8 | 71.5 | 73.3 | 66.8 | 75.6 |
| 8 | 73.4 | 67.8 | 70.5 | 72.4 | 65.6 | 75.1 |
| 9 | 72.9 | 66.8 | 69.8 | 71.8 | 64.6 | 74.6 |
| 10 | 72.7 | 66.2 | 69.2 | 71.2 | 63.9 | 74.4 |
| 11 | 72.2 | 65.6 | 68.6 | 70.7 | 63.2 | 74.0 |
| 12 | 71.7 | 65.0 | 68.0 | 70.2 | 62.6 | 73.4 |
| 13 | 71.3 | 64.5 | 67.6 | 69.8 | 62.2 | 73.1 |
| 14 | 70.6 | 64.1 | 67.3 | 69.5 | 61.7 | 72.5 |
| 15 | 70.4 | 63.8 | 67.0 | 69.2 | 61.3 | 72.3 |
| 16 | 70.4 | 63.4 | 66.6 | 68.9 | 60.9 | 72.3 |
| 17 | 70.1 | 63.1 | 66.4 | 68.7 | 60.6 | 72.0 |
| 18 | 69.9 | 62.8 | 66.1 | 68.5 | 60.3 | 71.9 |
| 19 | 69.7 | 62.4 | 65.9 | 68.3 | 59.9 | 71.7 |
| 20 | 69.5 | 62.3 | 65.7 | 68.1 | 59.8 | 71.4 |
| 21 | 69.3 | 62.1 | 65.5 | 67.9 | 59.6 | 71.2 |
| 22 | 69.1 | 61.9 | 65.4 | 67.8 | 59.4 | 71.1 |
| 23 | 69.1 | 61.8 | 65.3 | 67.7 | 59.2 | 71.1 |
| 24 | 69.1 | 61.3 | 65.1 | 67.6 | 59.1 | 71.1 |
| 25 | 69.1 | 61.6 | 65.0 | 67.5 | 59.0 | 71.1 |
| 26 | 69.1 | 61.4 | 64.8 | 67.4 | 58.9 | 71.1 |
| 27 | 69.1 | 64.3 | 64.7 | 67.3 | 58.8 | 71.1 |
| 28 | 69.0 | 61.2 | 64.6 | 67.2 | 58.6 | 71.0 |
| 29 | 69.0 | 61.1 | 64.5 | 67.1 | 58.5 | 71.0 |
| 30 | 69.0 | 61.1 | 64.4 | 67.0 | 58.5 | 71.0 |
| ... | ... | ... | ... | ... | ... | ... |
| 279 | 66.4 | 68.7 | 60.3 | 63.2 | 54.9 | 57.6 |
Table 6.
Cumulative moving average of SMAPE for 1- and 4-week ARIMAX predictions using BIC alone, BIC with physical distance, and physical distance alone. Repeated entries indicate that there were no clusters of that size, and so, the cumulative average value remains unchanged
| Physical distance only | Physical distance with BIC | BIC only | ||||
|---|---|---|---|---|---|---|
| Cluster size | Cum. moving avg. | Cum. moving avg. | Cum. moving avg. | |||
| 1 week | 4 weeks | 1 week | 4 weeks | 1 week | 4 weeks | |
| 1 | 87.7 | 87.7 | 87.7 | 87.7 | 87.7 | 87.7 |
| 2 | 79.8 | 79.8 | 79.2 | 79.2 | 77.4 | 77.4 |
| 3 | 78.3 | 78.3 | 76.7 | 76.7 | 73.8 | 73.8 |
| 4 | 75.7 | 75.7 | 74.5 | 74.5 | 71.1 | 71.1 |
| 5 | 75.1 | 75.1 | 72.7 | 72.7 | 69.0 | 69.0 |
| 6 | 73.7 | 7307 | 71.3 | 71.3 | 67.3 | 67.3 |
| 7 | 72.9 | 72.9 | 69.9 | 69.9 | 65.7 | 65.7 |
| 8 | 72.5 | 72.5 | 69.1 | 69.1 | 64.7 | 64.7 |
| 9 | 72.0 | 72.0 | 68.3 | 68.3 | 63.7 | 63.7 |
| 10 | 71.8 | 71.8 | 67.8 | 67.8 | 63.1 | 63.1 |
| 11 | 71.3 | 7103 | 67.3 | 67.3 | 62.4 | 62.4 |
| 12 | 70.7 | 70.7 | 66.8 | 66.8 | 61.9 | 61.9 |
| 13 | 70.5 | 70.5 | 66.4 | 66.4 | 61.3 | 61.3 |
| 14 | 69.9 | 69.9 | 66.2 | 66.2 | 60.9 | 60.9 |
| 15 | 69.7 | 69.7 | 66.0 | 66.0 | 60.4 | 60.4 |
| 16 | 69.7 | 69.7 | 65.7 | 65.7 | 60.1 | 60.1 |
| 17 | 69.5 | 69.5 | 65.5 | 65.5 | 59.9 | 59.9 |
| 18 | 69.3 | 69.3 | 65.3 | 65.3 | 59.6 | 59.6 |
| 19 | 69.2 | 69.2 | 65.1 | 65.1 | 59.4 | 59.4 |
| 20 | 68.9 | 68.9 | 64.9 | 64.9 | 59.1 | 59.1 |
| 21 | 68.7 | 68.7 | 64.8 | 64.8 | 58.9 | 58.9 |
| 22 | 68.6 | 68.6 | 64.7 | 64.7 | 58.7 | 58.7 |
| 23 | 68.6 | 68.6 | 64.6 | 64.6 | 58.5 | 58.5 |
| 24 | 68.6 | 68.6 | 64.5 | 64.5 | 58.4 | 58.4 |
| 25 | 68.6 | 68.6 | 64.5 | 64.5 | 58.3 | 58.3 |
| 26 | 68.6 | 68.6 | 64.4 | 64.4 | 58.2 | 58.2 |
| 27 | 68.6 | 68.6 | 64.3 | 64.3 | 58.1 | 58.1 |
| 28 | 68.5 | 68.5 | 64.2 | 64.2 | 58.0 | 58.0 |
| 29 | 68.5 | 68.5 | 64.1 | 64.1 | 57.9 | 57.9 |
| 30 | 68.5 | 68.5 | 64.0 | 64.0 | 57.8 | 57.8 |
| ... | ... | ... | ... | ... | ... | ... |
| 279 | 66.3 | 66.3 | 60.6 | 60.6 | 54.4 | 54.4 |
Table 7.
Cumulative moving average of SMAPE for 1- and 4-week linear regression predictions using BIC alone, BIC with physical distance, and physical distance alone. Repeated entries indicate that there were no clusters of that size, and so, the cumulative average value remains unchanged
| Physical distance only | Physical distance with BIC | BIC only | ||||
|---|---|---|---|---|---|---|
| Cluster size | Cum. moving avg. | Cum. moving avg. | Cum. moving avg. | |||
| 1 week | 4 weeks | 1 week | 4 weeks | 1 week | 4 weeks | |
| 1 | 87.7 | 87.7 | 87.7 | 87.7 | 87.7 | 87.7 |
| 2 | 79.8 | 79.8 | 79.2 | 79.2 | 77.4 | 77.4 |
| 3 | 78.3 | 78.3 | 76.7 | 76.7 | 73.8 | 73.8 |
| 4 | 75.7 | 75.7 | 74.5 | 74.5 | 71.1 | 71.1 |
| 3 | 75.1 | 75.1 | 72.7 | 72.7 | 69.0 | 69.0 |
| 6 | 73.7 | 73.7 | 71.3 | 71.3 | 67.3 | 67.3 |
| 7 | 72.9 | 72.9 | 69.9 | 69.9 | 65.7 | 65.7 |
| 8 | 72.5 | 72.5 | 69.1 | 69.1 | 64.7 | 64.7 |
| 9 | 72.0 | 72.0 | 68.3 | 68.3 | 63.7 | 63.7 |
| 10 | 71.8 | 71.8 | 67.8 | 67.8 | 63.1 | 63.1 |
| 11 | 71.3 | 71.3 | 67.3 | 67.3 | 62.4 | 62.4 |
| 12 | 70.7 | 70.7 | 66.8 | 66.8 | 61.9 | 61.9 |
| 13 | 70.5 | 70.5 | 66.4 | 66.4 | 61.3 | 61.3 |
| 14 | 69.9 | 69.9 | 66.2 | 66.2 | 60.9 | 60.9 |
| 15 | 69.7 | 69.7 | 66.0 | 66.0 | 60.4 | 60.4 |
| 16 | 69.7 | 69.7 | 65.7 | 65.7 | 60.1 | 60.1 |
| 17 | 69.5 | 69.5 | 65.5 | 65.5 | 59.9 | 59.9 |
| 18 | 69.3 | 69.3 | 65.3 | 65.3 | 59.6 | 59.6 |
| 19 | 69.2 | 69.2 | 65.1 | 65.1 | 59.4 | 59.4 |
| 20 | 68.9 | 68.9 | 64.9 | 64.9 | 59.1 | 59.1 |
| 21 | 68.7 | 68.7 | 64.8 | 64.8 | 58.9 | 58.9 |
| 22 | 68.6 | 68.6 | 64.7 | 64.7 | 58.7 | 58.7 |
| 23 | 68.6 | 68.6 | 64.6 | 64.6 | 58.5 | 58.5 |
| 24 | 68.6 | 68.6 | 64.5 | 64.5 | 58.4 | 58.4 |
| 25 | 68.6 | 68.6 | 64.5 | 64.5 | 58.3 | 58.3 |
| 26 | 68.6 | 68.6 | 64.4 | 64.4 | 58.2 | 58.2 |
| 27 | 68.6 | 68.6 | 64.3 | 64.3 | 58.1 | 58.1 |
| 28 | 68.5 | 68.5 | 64.2 | 64.2 | 58.0 | 58.0 |
| 29 | 68.5 | 68.5 | 64.1 | 64.1 | 57.9 | 57.9 |
| 30 | 68.5 | 68.5 | 64.0 | 64.0 | 57.8 | 57.8 |
| ... | ... | ... | ... | ... | ... | ... |
| 279 | 66.3 | 66.3 | 60.6 | 60.6 | 54.4 | 54.4 |
Results and Discussion
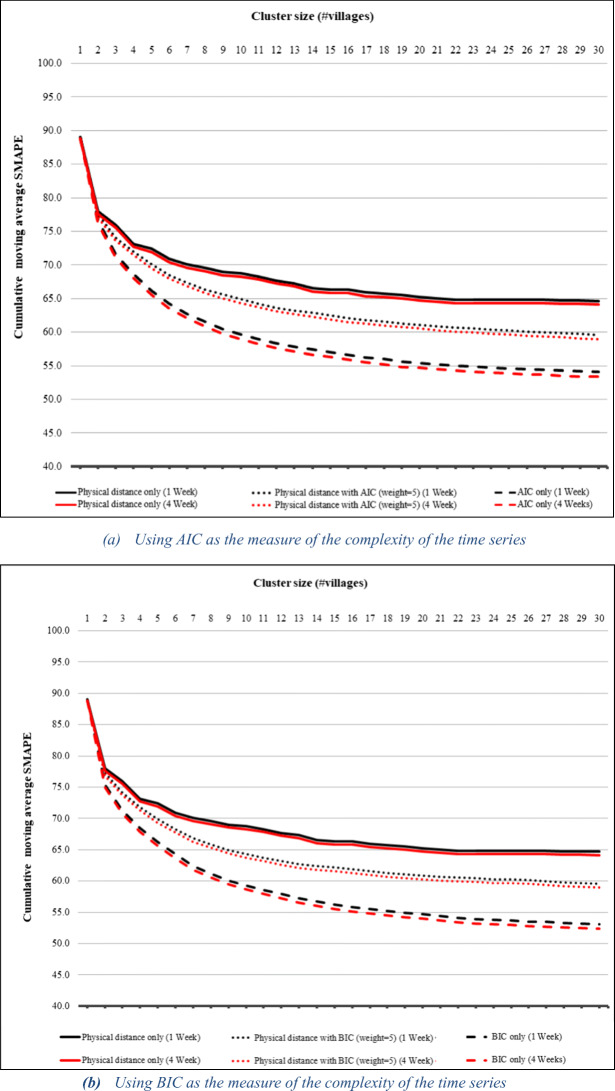
Initial experimentation showed much higher prediction accuracy in terms of SMAPE at the province level than at the individual village level for all three prediction models. We thus expect the prediction accuracy to roughly increase as a function of cluster size. Figure 4a, b shows the cumulative moving average of SMAPE as a function of cluster size for 1-week and 4-week ARIMA predictions for clusters created using AIC-based and BIC-based clustering, respectively. They show SMAPE reduction using AIC/BIC and using physical distance with weighted AIC/BIC against physical distance alone as a baseline. The graphs start with individual villages and go up to a cluster size of 30 since they are quite flat for the remaining portion. Each point on the graph shows the average SMAPE for all clusters of that size or smaller. Note that the curves for 1-week and 4-week prediction are indistinguishable because they are almost identical. Figure 4a shows an initial rapid reduction in SMAPE for all three similarity measures. But, while the curve for physical distance alone begins to flatten already at cluster size 4, those for the AIC-based similarity measures continue to decline, with the two AIC-based similarity measures outperforming physical distance alone. Overall, AIC alone has the best performance, followed by AIC with physical distance. The exact values for the points in the graph are shown in Table 1. The last row in the table represents the average SMAPE for all clusters generated by the clustering algorithm, i.e., for the entire cluster hierarchy. It shows that AIC with physical distance outperforms physical distance by 10.5% and AIC alone outperforms it by 18.4% over all clusters. The results for BIC-based clustering shown in Fig. 4b and Table 2 are similar.
Fig. 4.
Cumulative moving average of SMAPE for 1- and 4-week ARIMA predictions using the AIC- and BIC-based cluster results compared to physical distance alone
Table 1.
Cumulative moving average of SMAPE for 1- and 4-week ARIMA predictions using AIC alone, AIC with physical distance, and physical distance alone. Repeated entries indicate that there were no clusters of that size, and so, the cumulative average value remains unchanged
| Physical distance only | Physical distance with AIC | AI C only | ||||
|---|---|---|---|---|---|---|
| Cluster size | Cum_ moving avg. | Cum_ moving avg. | Cum_ moving avg. | |||
| 1 week | 4 weeks | 1 week | 4 weeks | 1 week | 4 weeks | |
| 1 | 89.0 | 88.9 | 89.0 | 88.9 | 89.0 | 88.9 |
| 2 | 77.5 | 77.5 | 76.6 | 77.1 | 76.6 | 76.2 |
| 3 | 74.1 | 75.5 | 71.6 | 73.6 | 71.6 | 71.1 |
| 4 | 72.0 | 72.7 | 68.7 | 71.5 | 68.7 | 68.1 |
| 5 | 70.0 | 71.9 | 66.2 | 69.5 | 66.2 | 65.6 |
| 6 | 68.5 | 70.4 | 64.2 | 68.0 | 64.2 | 63.5 |
| 7 | 67.4 | 69.6 | 62.7 | 66.8 | 62.7 | 62.1 |
| 8 | 66.4 | 69.1 | 61.5 | 65.8 | 61.5 | 60.9 |
| 9 | 65.6 | 68.5 | 60.5 | 65.1 | 60.5 | 59.8 |
| 10 | 64.9 | 68.3 | 59.7 | 64.3 | 59.7 | 59.0 |
| 11 | 64.3 | 67.8 | 59.0 | 63.7 | 59.0 | 58.3 |
| 12 | 63.7 | 67.2 | 58.4 | 63.1 | 58.4 | 57.6 |
| 13 | 63.2 | 66.8 | 57.9 | 62.7 | 57.9 | 57.1 |
| 14 | 62.9 | 66.0 | 57.4 | 62.3 | 57.4 | 56.7 |
| 15 | 62.5 | 65.8 | 57.0 | 61.9 | 57.0 | 56.3 |
| 16 | 62.1 | 65.8 | 56.6 | 61.5 | 56.6 | 55.9 |
| 17 | 61.8 | 65.4 | 56.3 | 61.3 | 56.3 | 55.5 |
| 18 | 61.6 | 65.2 | 56.0 | 61.0 | 56.0 | 55.2 |
| 19 | 61.3 | 65.0 | 55.6 | 60.7 | 55.6 | 54.9 |
| 20 | 61.1 | 64.7 | 55.4 | 60.5 | 55.4 | 54.7 |
| 21 | 60.9 | 64.5 | 55.2 | 60.3 | 55.2 | 54.5 |
| 22 | 60.7 | 64.4 | 55.0 | 60.1 | 55.0 | 54.3 |
| 23 | 60.6 | 64.4 | 54.9 | 60.0 | 54.9 | 54.1 |
| 24 | 60.3 | 64.4 | 54.7 | 59.7 | 54.7 | 54.0 |
| 25 | 60.2 | 64.4 | 54.6 | 59.6 | 54.6 | 53.9 |
| 26 | 60.1 | 64.4 | 54.5 | 59.5 | 54.5 | 53.7 |
| 27 | 60.0 | 64.4 | 54.4 | 59.3 | 54.4 | 53.7 |
| 28 | 64.8 | 64.3 | 59.8 | 59.2 | 54.3 | 53.5 |
| 29 | 64.8 | 64.3 | 597 | 59.1 | 54.2 | 53.4 |
| 30 | 64.7 | 64.2 | 59.6 | 59.0 | 54.1 | 53.4 |
| ... | ... | ... | ... | .... | ... | ... |
| 279 | 62.0 | 61.5 | 55.5 | 54.8 | 50.6 | 49.9 |
Table 2.
Cumulative moving average of SMAPE for 1- and 4-week ARIMA predictions using BIC alone, BIC with physical distance, and physical distance alone. Repeated entries indicate that there were no clusters of that size, and so, the cumulative average value remains unchanged
| Physical distance only | Physical distance with BIC | BIC only | ||||
|---|---|---|---|---|---|---|
| Cluster Size | Cum. moving avg. | Cum. moving avg. | Cum. moving avg. | |||
| 1 week | 4 weeks | 1 week | 4 weeks | 1 week | 4 weeks | |
| 1 | 89.0 | 88.9 | 89.0 | 88.9 | 89.0 | 88.9 |
| 2 | 78.0 | 77.5 | 77.2 | 76.8 | 75.4 | 74.9 |
| 3 | 76.0 | 75.5 | 74.2 | 73.7 | 71.3 | 70.8 |
| 4 | 73.1 | 72.7 | 71.8 | 71.3 | 68.5 | 67.9 |
| 5 | 72.4 | 71.9 | 69.8 | 69.3 | 66.2 | 65.6 |
| 6 | 70.9 | 70.4 | 68.3 | 67.7 | 64.3 | 63.7 |
| 7 | 70.1 | 69.6 | 66.8 | 66.2 | 62.4 | 61.8 |
| 8 | 69.6 | 69.1 | 65.9 | 65.3 | 61.2 | 60.6 |
| 9 | 69.0 | 68.5 | 65.0 | 64.4 | 60.1 | 59.4 |
| 10 | 68.8 | 68.3 | 64.3 | 63.7 | 59.3 | 58.6 |
| 11 | 68.3 | 67.8 | 63.7 | 63.2 | 58.6 | 57.9 |
| 12 | 67.7 | 67.2. | 63.1 | 62.6 | 57.9 | 57.2 |
| 13 | 67.3 | 66.8 | 62.7 | 62.1 | 57.2 | 56.5 |
| 14 | 66.5 | 66.0 | 62.4 | 61.8 | 56.7 | 56.0 |
| 15 | 66.3 | 65.8 | 62.2 | 61.6 | 56.2 | 55.5 |
| 16 | 66.3 | 65.8 | 61.8 | 61.3 | 55.8 | 55.1 |
| 17 | 65.9 | 65.4 | 61.6 | 61.0 | 55.5 | 54.8 |
| 18 | 65.7 | 65.2 | 61.3 | 60.7 | 55.2 | 54.4 |
| 19 | 65.5 | 65.0 | 61.1 | 60.5 | 54.9 | 54.2 |
| 20 | 65.2 | 64.7 | 60.9 | 60.3 | 54.7 | 53.9 |
| 21 | 65.0 | 64.5 | 60.7 | 60.1 | 54.4 | 53.6 |
| 22 | 64.9 | 64.4 | 60.5 | 59.9 | 54.1 | 53.4 |
| 23 | 64.9 | 64.4 | 60.5 | 59.9 | 53.9 | 53.1 |
| 24 | 64.9 | 64A | 60.3 | 59.7 | 53.8 | 53.0 |
| 25 | 64.9 | 64A | 60.2 | 59.6 | 53.7 | 52.9 |
| 26 | 64.9 | 64.4 | 60.1 | 59.5 | 53.5 | 52.8 |
| 27 | 64.9 | 64.4 | 59.9 | 59.3 | 53.4 | 52.7 |
| 28 | 64.8 | 64.3 | 59.8 | 59.2 | 53.3 | 52.6 |
| 29 | 64.8 | 64.3 | 59.7 | 59.1 | 53.2 | 52.5 |
| 30 | 64.7 | 64.2 | 59.6 | 59.0 | 53.1 | 52.4 |
| ... | ... | ... | ... | ... | ... | ... |
| 279 | 62.0 | 61.5 | 55.2 | 54.5 | 49.6 | 48.9 |
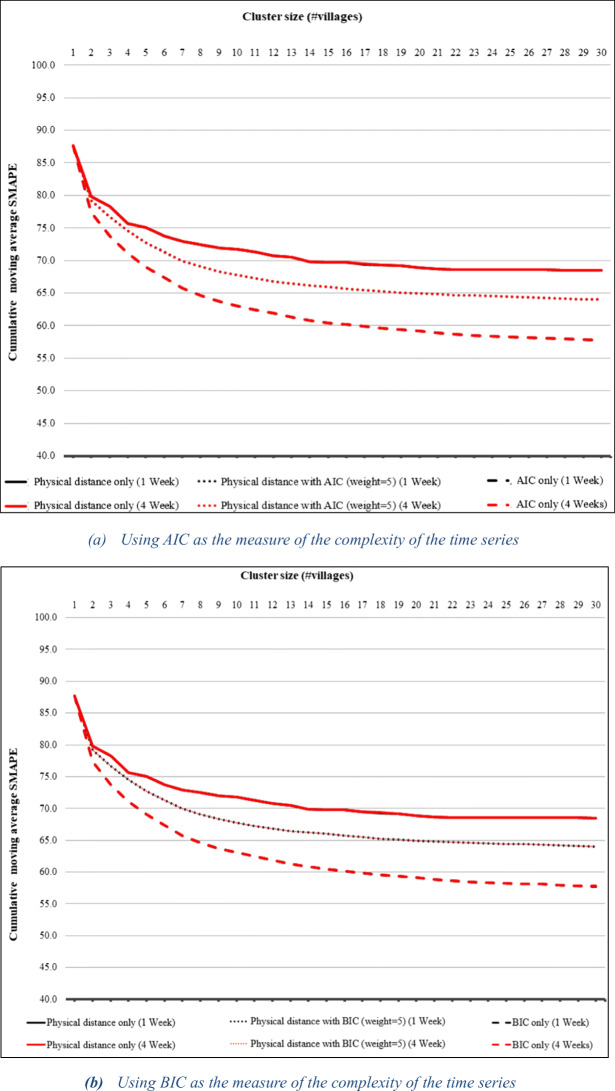
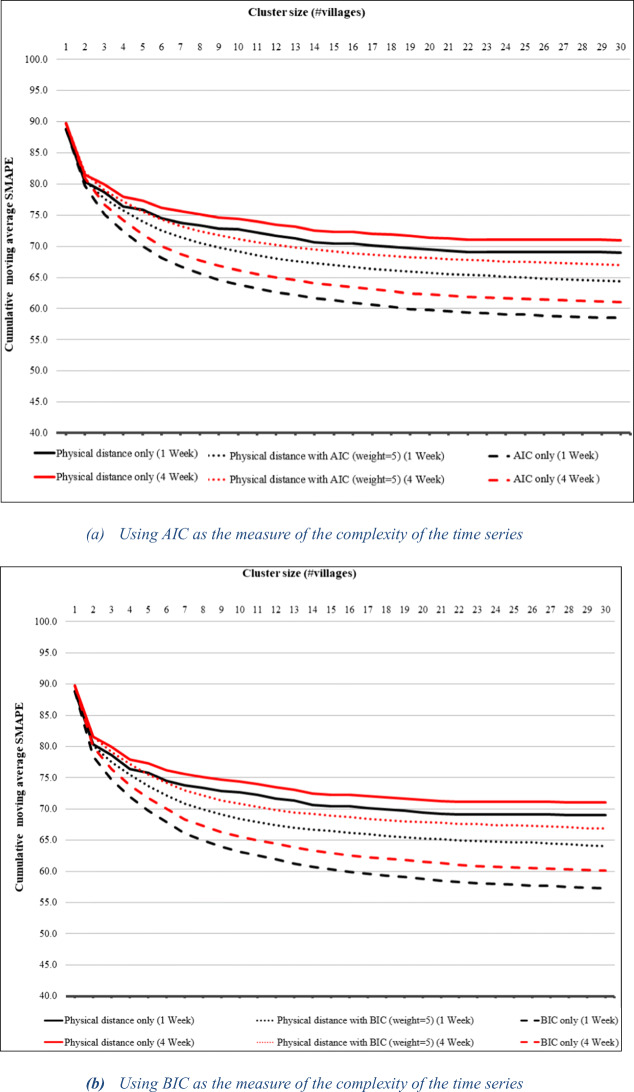
Figure 5a, b shows the cumulative moving average of SMAPE for AIC- and BIC-based clustering versus physical distance alone for ARIMAX predictions, while Fig. 6a, b shows the same graphs for linear regression prediction. The results are similar to those for ARIMA prediction except that in the case of linear regression, 1-week prediction benefits from the AIC- and BIC-based clustering slightly more than 4-week prediction. The tables showing exact values appear in the appendix. The fact that we obtain similar benefits from the clustering with three different prediction models suggests that our clustering technique is an effective general means of improving prediction.
Fig. 5.
Cumulative moving average of SMAPE for 1- and 4-week ARIMAX predictions using the AIC- and BIC-based cluster results compared to physical distance alone
Fig. 6.
Cumulative moving average of SMAPE for 1- and 4-week linear regression predictions using the AIC- and BIC-based cluster results compared to physical distance alone
We also examined the average SMAPE values, which contain significantly more noise than the cumulative moving average values. We compared the average SMAPE for each cluster size between all pairs of the similarity measures for AIC-based clustering and BIC-based clustering for the three prediction models. While the statistical significance differs among the sets, the results are consistent with the cumulative moving average graphs and are consistently statistically significant for cluster sizes 3, 4, 5, 7–10, 19, 52, 53, 66, and 160 for both 1-week and 4-week predictions (two-tailed paired t test p < 0.05). For 4-week predictions for AIC vs physical distance, the t test statistic cannot be computed due to zero standard deviation.
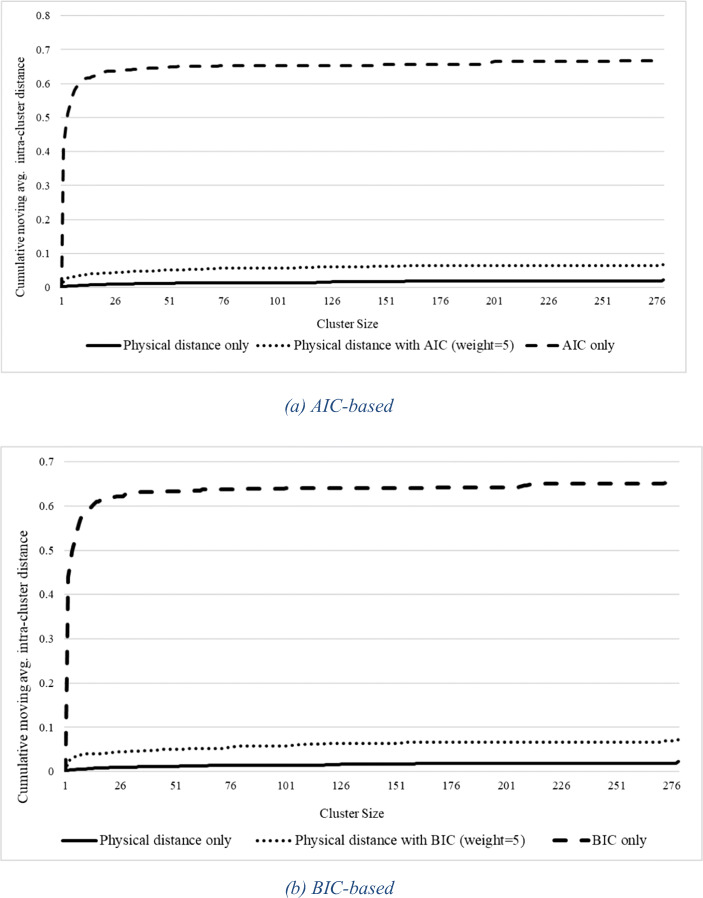
In addition to accurate prediction, targeted intervention requires clusters to be spatially compact. Figure 7a shows the cumulative moving average of intra-cluster distance as a function of cluster size for clusters based on AIC alone and AIC with physical distance against a baseline of physical distance alone. Not surprisingly, use of physical distance alone yields the tightest clusters. Use of AIC alone results in rather high intra-cluster distances, while AIC with weighted physical distance results in intra-cluster distances very close to those of physical distance alone. The results for BIC-based clustering shown in Fig. 7b are similar.
Fig. 7.
Cumulative moving average of intra-cluster distance as a function of cluster size for AIC-based clustering (a) and BIC-based clustering (b) against physical distance alone as a baseline. Intra-cluster distance is taken as the maximum distance between points in the cluster
Putting together the various results, we can see that the average prediction accuracy of AIC/BIC with weighted physical distance is significantly better than that of physical distance alone, and the intra-cluster distance is almost as good as that of physical distance, while the intra-cluster distance of AIC and BIC alone is significantly worse. This makes AIC/BIC with physical distance the clear best choice of similarity measures.
Since SatScan is the most commonly used technique for discovering clusters for malaria prediction, we compare the effectiveness of our clustering algorithm against SatScan in terms of effectiveness of the clusters in improving prediction accuracy. Running SatScan on our data set produces six clusters of villages identified as hotspots, with clusters of sizes 3, 4, 5, 8, 9, and 13. We compare the SMAPE of 1-week ARIMA predictions for these clusters with that of clusters of the same size when using AIC + physical distance (weight 5). The results are shown in Table 3. Our algorithm generates several clusters of sizes 3, 4, 5, 8, 9, and 13, so we show the range of SMAPE for all these clusters as well as the mean. Since SatScan generates only best clusters in terms of its optimization criterion, it is most reasonable to compare the minimum SMAPE for our algorithm’s clusters of the same size. The prediction accuracy of our algorithm’s clusters is better for clusters of sizes 3, 8, and 13. The SMAPE values for cluster size 4 are similar, while those for the SatScan clusters are better for cluster sizes 5 and 9. So, while SatScan discovers some clusters that result in better predictive accuracy than those of the same size discovered by our algorithm, our algorithm also discovers some that perform better than the SatScan clusters. It should be emphasized that SatScan is discovering only a few clusters, so it is not a technique for improving predictability for an entire geographic region. Thus, the two algorithms should not be viewed as competing but rather as complementary.
Table 3.
Comparison of SMAPE for hotspot clusters formed with SatScan vs clusters of same size formed using AIC + physical distance (weight 5) for 1 week ARIMA predictions
| SatScan | AIC + physical distance (weight 5) | |||
|---|---|---|---|---|
| Cluster size | SMAPE | Min SMAPE | Max SMAPE | Mean SMAPE |
| 3 | 85.76 | 59.0 | 67.7 | 65.1 |
| 4 | 54.23 | 55.3 | 64.6 | 59.7 |
| 5 | 15.82 | 39.9 | 66.7 | 50.5 |
| 8 | 41.36 | 28.9 | 54.2 | 41.1 |
| 9 | 17.64 | 31.2 | 51.5 | 41.0 |
| 13 | 74.5 | 12.4 | 48.1 | 32.4 |
Conclusion
This paper has introduced an approach to spatial hierarchical clustering that finds compact geographic regions with good time series predictability. This is done by clustering based on physical distance and reduction in time series complexity as measured by AIC and BIC. Using malaria data from northern Thailand, we have shown that use of the technique can yield rapid returns, greatly improving prediction accuracy with only a small amount of clustering. Furthermore, use of AIC and BIC reduction as clustering criteria provides significantly better results than use of physical distance alone for all tested prediction models over a range of prediction horizons. We plan to apply the technique to malaria prediction in other regions to further verify our results as well as to apply the technique to prediction of other diseases such as dengue.
The predictive models in this study used previous malaria incidence, land surface temperature, and slope to predict future incidence. In practice, predictive models often also make use of a wide variety of environmental variables [17, 32]. A next step in this work is to verify the value of our clustering technique with more complex prediction models as well as to investigate its applicability to prediction of other diseases such as dengue.
Acknowledgements
We thank Oliver Grübner for helpful comments on an earlier draft. This paper is based upon work supported by the U.S. Army ITC-PAC under Contract No. FA5209-15-P-0183. This work was also partially supported through a fellowship from the Hanse-Wissenschaftskolleg Institute for Advanced Study, Delmenhorst, Germany, to Haddawy and a Santander BISIP scholarship to Su Yin.
Appendix A
Compliance with Ethical Standards
Conflict of Interest
The authors declare that they have no conflict of interest.
Footnotes
This paper is an extended version of a previous short workshop paper [35] which presented preliminary results.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Peter Haddawy, Email: peter.had@mahidol.ac.th.
Myat Su Yin, Email: myatsuyinmaung@gmail.com.
Tanawan Wisanrakkit, Email: tanawan.wis@outlook.com.
Rootrada Limsupavanich, Email: rootrada.lim@gmail.com.
Promporn Promrat, Email: promporn.kam@gmail.com.
Saranath Lawpoolsri, Email: saranath.law@mahidol.ac.th.
Patiwat Sa-angchai, Email: patiwat.saa@mahidol.ac.th.
References
- 1.Khamsiriwatchara A, Sudathip P, Sawang S, Vijakadge S, Potithavoranan T, Sangvichean A, Satimai W, Delacollette C, Singhasivanon P, Lawpoolsri S, Kaewkungwal J. Artemisinin resistance containment project in Thailand.(I): implementation of electronic-based malaria information system for early case detection and individual case management in provinces along the Thai-Cambodian border. Malar J. 2012;11(1):247. doi: 10.1186/1475-2875-11-247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Graham A, Atkinson P, Danson F. Spatial analysis for epidemiology. Acta Trop. 2004;91:219–225. doi: 10.1016/j.actatropica.2004.05.001. [DOI] [PubMed] [Google Scholar]
- 3.Meliker JR, Sloan CD. Spatio-temporal epidemiology: principles and opportunities. Spat Spatio-temporal Epidemiol. 2011;2(1):1–9. doi: 10.1016/j.sste.2010.10.001. [DOI] [PubMed] [Google Scholar]
- 4.Rissanen J. Modeling by shortest data description. Automatica. 1978;14(5):465–658. doi: 10.1016/0005-1098(78)90005-5. [DOI] [Google Scholar]
- 5.Hansen MH, Yu B. Model selection and the principle of minimum description length. J Am Stat Assoc. 2001;96(454):746–774. doi: 10.1198/016214501753168398. [DOI] [Google Scholar]
- 6.Dagliati A, Marinoni A, Cerra C, Decata P, Chiovato L, Gamba P, Bellazzi R. Integration of administrative, clinical, and environmental data to support the management of type 2 diabetes mellitus: from satellites to clinical care. J Diabetes Sci Technol. 2016;10(1):19–26. doi: 10.1177/1932296815619180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Waller LA. Gotway CA. John Wiley & Sons: Applied spatial statistics for public health data; 2004. [Google Scholar]
- 8.Gelman A, Price PN. All maps of parameter estimates are misleading. Stat Med. 1999;18(23):3221–3234. doi: 10.1002/(SICI)1097-0258(19991215)18:23<3221::AID-SIM312>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 9.Openshaw S, Taylor PJ. The modifiable areal unit problem. In: Wrigley N, Bennett R, editors. Quantitative geography: a British view. London: Routledge and Degan Paul; 1981. pp. 60–69. [Google Scholar]
- 10.Fotheringham AS, Wong DW. The modifiable areal unit problem in multivariate statistical analysis. Environ Plan A. 1991;23(7):1025–1044. doi: 10.1068/a231025. [DOI] [Google Scholar]
- 11.Glaz J, Naus J, Wallenstein S. Scan statistics. New York, NY: Springer; 2001. [Google Scholar]
- 12.Alemu K, Worku A, Berhane Y, Kumie A. Spatiotemporal clusters of malaria cases at village level, Northwest Ethiopia. Malar J. 2014;13(1):223. doi: 10.1186/1475-2875-13-223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kulldorff M. A spatial scan statistic. Commun Stat-Theory Methods. 1997;26(6):1481–1496. doi: 10.1080/03610929708831995. [DOI] [Google Scholar]
- 14.Mosha JF, Sturrock HJ, Greenwood B, Sutherland CJ, Gadalla NB, Atwal S, Hemelaar S, Brown JM, Drakeley C, Kibiki G, Bousema T. Hot spot or not: a comparison of spatial statistical methods to predict prospective malaria infections. Malar J. 2014;13(1):53. doi: 10.1186/1475-2875-13-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bousema T, Stevenson J, Baidjoe A, Stresman G, Griffin JT, Kleinschmidt I, Remarque EJ, Vulule J, Bayoh N, Laserson K, Desai M. The impact of hotspot-targeted interventions on malaria transmission: study protocol for a cluster-randomized controlled trial. Trials. 2013;14(1):36. doi: 10.1186/1745-6215-14-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mogeni P, Omedo I, Nyundo C, Kamau A, Noor A, Bejon P. Effect of transmission intensity on hotspots and micro-epidemiology of malaria in sub-Saharan Africa. BMC Med. 2017;15(1):121. doi: 10.1186/s12916-017-0887-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zinszer K, Verma AD, Charland K, Brewer TF, Brownstein JS, Sun Z, Buckeridge DL. A scoping review of malaria forecasting: past work and future directions. BMJ Open. 2012;2(6):e001992. doi: 10.1136/bmjopen-2012-001992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Giardina F, Franke J, Vounatsou P (2015) Geostatistical modelling of the malaria risk in Mozambique: effect of the spatial resolution when using remotely-sensed imagery. Geospat Health 10 [DOI] [PubMed]
- 19.Teklehaimanot Hailay D, Lipsitch Marc, Teklehaimanot Awash, Schwartz Joel. Malaria Journal. 2004;3(1):41. doi: 10.1186/1475-2875-3-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Montero P and Vilar JA (2014) TSclust: an R Package for time series clustering, Journal of Statistical Software, vol. 62, no. 1
- 21.Pedrycz W. Granular computing—the emerging paradigm. J Uncertain Syst. 2007;1(1):38–61. [Google Scholar]
- 22.Pedrycz W (2013 May 9) Granular computing: analysis and design of intelligent systems. CRC press
- 23.Maciel L, Ballini R, Gomide F. Evolving granular analytics for interval time series forecasting. Granular Computing. 2016;1(4):213–224. doi: 10.1007/s41066-016-0016-3. [DOI] [Google Scholar]
- 24.Kulldorff M. SaTScan user guide for version 9.0. Retrieved 18 June 2018 from http://www.satscan.org
- 25.Lempel A, Ziv J. On the complexity of finite sequences. IEEE Trans Inf Theory. 1976;22(1):75–81. doi: 10.1109/TIT.1976.1055501. [DOI] [Google Scholar]
- 26.Pincus S. Approximate entropy (ApEn) as a complexity measure. Chaos. 1995;5(1):110–117. doi: 10.1063/1.166092. [DOI] [PubMed] [Google Scholar]
- 27.Rasheed BQ, Qian B. Hurst exponent and financial market predictability. InIASTED conference on Financial Engineering and Applications (FEA 2004) 2004 (pp. 203–209)
- 28.Nobre FF, Monteiro ABS, Telles PR, Williamson GD. Dynamic linear model and SARIMA: a comparison of their forecasting performance in epidemiology. Stat Med. 2001;20(20):3051–3069. doi: 10.1002/sim.963. [DOI] [PubMed] [Google Scholar]
- 29.Pascual M, Cazelles B, Bouma MJ, Chaves LF, Koelle K. Shifting patterns: malaria dynamics and rainfall variability in an African highland. Proc R Soc Lond B Biol Sci. 2008;275(1631):123–132. doi: 10.1098/rspb.2007.1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Burnham KP, Anderson DR. Multimodel inference: understanding AIC and BIC in model selection. Sociol Methods Res. 2004;33(2):261–304. doi: 10.1177/0049124104268644. [DOI] [Google Scholar]
- 31.Khandakar Y, Hyndman RJ (2008) Automatic time series forecasting: the forecast Package for R. Journal of Statistical Software 27(03)
- 32.Haddawy P, Hasan AHMI, Kasantikul R, Lawpoolsri S, Sa-angchai P, Kaewkungwal J, Singhasivanon P. Spatiotemporal Bayesian networks for malaria prediction. Artif Intell Med. 2018;84:127–138. doi: 10.1016/j.artmed.2017.12.002. [DOI] [PubMed] [Google Scholar]
- 33.Hasan A.H.M.I, Haddawy P, Lawpoolsri S. (2017) A comparative analysis of Bayesian network approaches to malaria outbreak prediction, Proc. 13thInt’l Conf. on Computing and Information Technology (IC2IT2017), Bangkok
- 34.Makridakis S. Accuracy measures: theoretical and practical concerns. Int J Forecast. 1993;9:527–529. doi: 10.1016/0169-2070(93)90079-3. [DOI] [Google Scholar]
- 35.Haddawy P, Su Yin M, Wisanrakkit T, Limsupavanich R, Promrat P and Lawpoolsri S (2017) AIC-driven spatial hierarchical clustering: case study for malaria prediction in Northern Thailand, In: Multi-disciplinary Trends in Artificial Intelligence, Proc. MIWAI 2017, Brunei