Mathematical modeling and analysis of the SARS-Cov-2 disease with reinfection

Abstract

The COVID-19 infection which is still infecting many individuals around the world and at the same time the recovered individuals after the recovery are infecting again. This reinfection of the individuals after the recovery may lead the disease to worse in the population with so many challenges to the health sectors. We study in the present work by formulating a mathematical model for SARS-CoV-2 with reinfection. We first briefly discuss the formulation of the model with the assumptions of reinfection, and then study the related qualitative properties of the model. We show that the reinfection model is stable locally asymptotically when ${\mathcal{R}}_0<1$. For ${\mathcal{R}}_0\le 1$, we show that the model is globally asymptotically stable. Further, we consider the available data of coronavirus from Pakistan to estimate the parameters involved in the model. We show that the proposed model shows good fitting to the infected data. We compute the basic reproduction number with the estimated and fitted parameters numerical value is ${\mathcal{R}}_0\approx 1.4962$. Further, we simulate the model using realistic parameters and present the graphical results. We show that the infection can be minimized if the realistic parameters (that are sensitive to the basic reproduction number) are taken into account. Also, we observe the model prediction for the total infected cases in the future fifth layer of COVID-19 in Pakistan that may begin in the second week of February 2022.

Graphical Abstract

1. Introduction

The COVID-19 infection that has not yet been eliminated from the world but in some parts the cases are decreasing day by day. It is expected that with the passage of time and following the recommendations of the World Health Organization (WHO) we can reduce the risk of infection with fewer cases. With the continued efforts of researchers in many countries, the number of cases has decreased. It is noted that the new variants of the COVID-19 cases are still an alarm for many countries of the world with the new number of infected cases. It is also documented that a person infected with COVID-19 can recover depending on his/her age. While it is observed that a person infected with COVID-19 has some other respiratory infection can be in danger and may die. A person infected with some particular disease and recovered after some time maybe with treatment, vaccination, etc., and infected again with that particular infection is known as reinfected. Related to COVID-19, it is observed that a person infected with COVID-19 and after recovery, the same person has been infected with another variant of COVID-19. In Anon (2022c), it is shown that individuals that are unvaccinated can be expected to be reinfected with COVID-19 every 16 months on average. It is shown further, that reinfection of new cases may occur when the winter approaches. The natural immunity to coronavirus infection begins to dwindle with the passage of time. It is shown in Anon (2022b), that people older than 65 after the recovery from the COVID-19 infection cannot be considered immune from the second attack of COVID-19 infection. A study from Denmark (Anon, 2022b) shows that individuals with greater than 65 age, have only 47% protection against reinfection, while with less than 65 age, can have 80% protection (Anon, 2022b). The study revealed that reinfection can occur to the older age people maximum while less to teenagers. The reinfection cases are also recorded in the UK (Anon, 2021). The first case of COVID-19 with reinfection is reported after two months from the complete recovery of SARS-COV-2 infection (Hanif et al., 2020). Due to the emergence of the omicron variant, a number of reinfection cases are documented in South Africa (Pulliam et al., 2021). It is documented further that 35,670 out of 2,796,982 individuals with SARS-COV-2 confirmed laboratory cases are found suspected reinfections. The people had a positive test at least 90 days prior to 27 November 2021 (Pulliam et al., 2021).

Mathematical modeling in science and engineering has a vital role to understand the complex behaviors of the problems arising in physical and biological modeling, see for disease epidemiology (Li et al., 2021a, Okuonghae and Omame, 2020, Deressa and Duressa, 2021), in fluid-related studies (Chu et al., 2021, Li et al., 2021b). While observing from the above facts about the reinfection of the COVID-19 cases, may the world face a new number of infected cases and deaths. Before we formulate a new mathematical model to study the impact of SARS-COV-2 with reinfection, we first highlight some mathematical models that addressed the COVID-19 infection. Mathematical modeling and its optimal control analysis to curb the coronavirus infection is considered in Shen et al. (2021). A case study related to COVID-19 in Thailand using a mathematical model is given in Riyapan et al. (2021). Using the third layer of COVID-19 cases in Li et al. (2021c), the authors formulated a mathematical model and suggested the results for infection control. A study on the coronavirus infection fractional order is suggested in Li et al. (2021d). The infection of COVID-19 in Nigeria through a mathematical model is explored in Iboi et al. (2020a). The early information about the COVID-19 with the prediction of vaccine to save mankind is discussed in Atangana (2020). A mathematical study has been conducted in López and Rodo (2021) to explore the dynamics of coronavirus infection in Italy and France. The COVID-19 pandemic with isolation and quarantine with a case study is discussed in Memon et al. (2021). The modeling and control of the COVID-19 infection in Bangladesh has been discussed in Ullah et al. (2021). The application of optimal control theory to the mathematical assessment of novel coronavirus is analyzed in Zhang et al. (2021). An artificial intelligence study to forecast the infection of COVID-19 is discussed and analyzed in Elsheikh et al. (2021). The authors in Price and Holm (2021) studied the impact of the social distancing on the coronavirus infection. The authors studied the COVID-19 infection model in Shah et al. (2020) with a detailed explanation of their qualitative properties. The statistical and mathematical analysis has been used in Yousaf et al. (2020) to predict the coronavirus infection for the future months in Pakistan. A non-integer order model has been used to study the COVID-19 infection by the authors in Ahmad et al. (2020).

The aim of this study is to construct a new mathematical model for SARS-COV-2 with reinfection. It is documented that a person after recovery from the infection may face reinfection with COVID-19. We will explore in detail the impact of the reinfection on the disease burden and its future implications. The section-wise division is as follows: The construction of the model and its detailed description is given in Section 2. Section 3, discusses the analysis of the model. In Section 4, we study the stability analysis of the model for its equilibrium points. The existence of the backward bifurcation phenomenon for the COVID-19 reinfection model is discussed in Section 5. Section 6, presents the estimations of the parameters and the numerical simulations of the model. Section 7 concludes the results.

2. Model formulation

Here, we construct a new mathematical model for the dynamical analysis of COVID-19 with reinfection. In this regard, first, we denote the total human populations by N(t) and divide into five different compartments: such as the individuals that attract the disease easily denoted by S(t), individuals after getting an infection and remains in incubation period that is become exposed, shown by E(t). After completing the incubation period, the individuals infected with no symptoms or infected with visible symptoms are shown respectively by A(t) and I(t). After some treatments or isolation at home or hospital, the individuals become recovered is shown by R(t). So that N(t) = S(t) + E(t) + A(t) + I(t) + R(t). The description of the transmission of the parameters flow from one compartment to another has been shown in Fig. 1. The above consideration in the form of evolutionary differential equations can be shown given by:

$$\begin{array}{ccc}\frac{dS(t)}{dt}\hfill & =\hfill & \mathrm{\Lambda }-\frac{({\beta }_{1}I+{\beta }_{2}A)}{N}S-\mu S,\hfill \\ \frac{dE(t)}{dt}\hfill & =\hfill & \frac{({\beta }_{1}I+{\beta }_{2}A)}{N}S-(\tau +\mu )E,\hfill \\ \frac{dA(t)}{dt}\hfill & =\hfill & \tau \psi E+\frac{\theta {\beta }_{2}RA}{N}-({\varphi }_1+\mu )A,\hfill \\ \frac{dI(t)}{dt}\hfill & =\hfill & (1-\psi )\tau E+\frac{\rho {\beta }_{1}RI}{N}-({\varphi }_2+\mu +d_1)I,\hfill \\ \frac{dR(t)}{dt}\hfill & =\hfill & {\varphi }_{1}A(t)+{\varphi }_{2}I(t)-\frac{\rho {\beta }_{1}RI}{N}-\frac{\theta {\beta }_{2}RA}{N}-\mu R(t),\hfill \end{array}$$ (1)

Fig. 1.

Flow chart for the model.

In the above model 1, the healthy individual populations are generated through the birth rate while the natural death rate for each class of the model is μ. The parameters β ₁ and β ₂ denote the disease transmission rate due to the interaction of healthy people with symptomatic infected, and asymptomatic infected with no visible symptoms respectively. The incubation period of the disease is given by τ, which distributes the infected people into class A(t) and I(t) respectively. The individuals that complete their incubations period with no visible symptoms join class A at the rate of τψ while the rest join the class I(t) with (1 − ψ)τ. The parameters ϕ ₁ and ϕ ₂ are a recovery of asymptomatic and symptomatic infected individuals. The symptomatic infected people die due to infection with a rate d ₁. The infected individuals either in class A or I after recovering fully from the infections may experiences reinfection while coming in close contact with individuals either asymptomatic or symptomatic, such reinfections of the individuals are shown by the parameters ρ and θ. The parameter ρ defines the infected individuals becoming reinfected with the close contact of symptomatic infected individuals while θ is due to asymptomatic individuals.

3. Model analysis

Here, we discuss some fundamental analysis related to the model 1. We have the total dynamics of the system 1 after adding all its equations, and get the following,

$$\frac{dN}{dt}=\mathrm{\Lambda }-\mu N.$$

We have for the above equation,

$$N(t)=\frac{\mathrm{\Lambda }}{\mu }+\left(\right)N_0-\frac{\mathrm{\Lambda }}{\mu }\left)\right)e^{-\mu t}.$$ (2)

Equation 2 approaches to $\frac{\mathrm{\Lambda }}{\mu }$ whenever t → ∞ and so the involved variables in the system 1 are nonnegative for each value of t ≥ 0. Therefore, all the restated solutions of the system 1 will remain positive for each t ≥ 0. Thus, the system proposed 1 is well-posed mathematically and hence its dynamics can be studded in the region shown by

$$\sum =\left\{\left(S,E,I,A,R,\right)\in {\mathbb{R}}_{+}^5:S+E+I+A+R\le \frac{\mathrm{\Lambda }}{\mu }\right\}.$$

Next, we consider the positivity and boundedness results for the considered system (1). We have the following:

3.1. Positivity and boundedness

Theorem 1

If the variables of the system 1 at t = 0 (S(0) = E(0) = I(0) = A(0) = R(0) > 0) then the solution for t > 0 of the model variables will be positive for every t > 0.

Proof

Let us consider the first equation of model 1,

$$\begin{array}{ccc}\frac{dS}{dt}\hfill & =\hfill & \mathrm{\Lambda }-\lambda (t)S-dS\hfill \\ \hfill & \ge \hfill & -(\lambda (t)+\mu )S,\hfill \end{array}$$

where $\lambda (t)=\frac{({\beta }_{1}I+{\beta }_{2}A)}{N}$. We get the following after applying the taking integration,

$$S(t)\ge S_0\exp \left(\right)-{\int }_0^t(\lambda (t)+\mu )\left)\right)d\zeta >0.$$

S ₀ is the initial population and is positive and hence, S(t) is positive. The same approach can be used to show the rest, i.e., E(t) > 0, I(t) > 0, A(t) > 0, and R(t) > 0. □.

Further, the positive solution discussed in the above theorem are bounded. It can be shown easily from 2 when t → ∞ .

4. Equilibrium points and its stability analysis

The disease free equilibrium of the system 1 can be denoted by E ₀ and is given by

$$E_0=(S^0,0,0,0,0)=\left(\right)\frac{\mathrm{\Lambda }}{\mu },0,0,0,0\left)\right).$$

The computation of the basic reproduction number ${\mathcal{R}}_0$ can be obtained through the next generation approach (Driessche and Watmough, 2002). We have the following results after applying the method in Driessche and Watmough (2002),

$$\begin{array}{c}F=\left(\begin{array}{ccc}0\hfill & {\beta }_2\hfill & {\beta }_1\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ \hfill \end{array}\right),V=\left(\begin{array}{ccc}\mu +\tau \hfill & 0\hfill & 0\hfill \\ -\tau \psi \hfill & \mu +{\varphi }_1\hfill & 0\hfill \\ -\tau (1-\psi )\hfill & 0\hfill & \mu +d_1+{\varphi }_2\hfill \\ \hfill \end{array}\right).\hfill \end{array}$$

The spectral radius of ϱ(FV ⁻¹), gives the basic reproduction number given by

$${\mathcal{R}}_0=\underset{{\mathcal{R}}_1}{\underbrace{\frac{{\beta }_2\tau \psi }{(\mu +\tau )\left(\mu +{\varphi }_1\right)}}}+\underset{{\mathcal{R}}_2}{\underbrace{\frac{{\beta }_1\tau (1-\psi )}{(\mu +\tau )\left(d_1+\mu +{\varphi }_2\right)}}}.$$

Here ${\mathcal{R}}_1$ accounts for the infection generated through the contact of healthy people versus asymptomatic infected people, while ${\mathcal{R}}_2$ can produce secondary infections after contact of healthy with asymptomatic infected people.

4.1. Endemic equilibria

We denote the endemic equilibrium of the model 1 by E * ₁ and can be obtained in the following,

$$E{*}_1=(S*,E*,A*,I*,R*),$$

where

$$\left\{S*=\frac{\mathrm{\Lambda }}{\lambda *+\mu },E*=\frac{\lambda S}{(\tau +\mu )},A*=\frac{N*\tau \psi E*}{N*(\mu +{\varphi }_1)-{\beta }_2\theta R*},I*=\frac{\tau (1-\psi )E*N*}{N*(d_1+\mu +{\varphi }_2)-{\beta }_1\rho R*},R*=\frac{\left({\varphi }_{1}A*+{\varphi }_{2}I*\right)N*}{A*{\beta }_2\theta +{\beta }_{1}I*\rho +\mu N*}.\right\}$$

where N * = S* + E * + A* + I* + R* .

Theorem 2

The COVID-19 reinfection model is locally asymptotically stable at infection free equilibrium E ₀ when ${\mathcal{R}}_0<1$.

Proof

To get the stability results, we compute the Jacobian of model 1 at E ₀, given by

$$\begin{array}{c}J(E_0)=\left(\begin{array}{ccccc}-\mu \hfill & 0\hfill & -{\beta }_2\hfill & -{\beta }_1\hfill & 0\hfill \\ 0\hfill & -(\tau +\mu )\hfill & {\beta }_2\hfill & {\beta }_1\hfill & 0\hfill \\ 0\hfill & \tau \psi \hfill & -({\varphi }_1+\mu )\hfill & 0\hfill & 0\hfill \\ 0\hfill & \tau (1-\psi )\hfill & 0\hfill & -({\varphi }_2+\mu +d_1)\hfill & 0\hfill \\ 0\hfill & 0\hfill & {\varphi }_1\hfill & {\varphi }_2\hfill & -\mu \hfill \\ \hfill \end{array}\right)\hfill \end{array}$$

The characteristics equation for the Jacobian matrix above is given by

$${(\lambda +\mu )}^2[{\lambda }^3+{\mathrm{\Phi }}_1{\lambda }^2+{\mathrm{\Phi }}_2\lambda +{\mathrm{\Phi }}_3=0],$$ (3)

where

$$\begin{array}{ccc}{\mathrm{\Phi }}_1\hfill & =\hfill & d_1+3\mu +\tau +{\varphi }_1+{\varphi }_2,\hfill \\ {\mathrm{\Phi }}_2\hfill & =\hfill & \left(\mu +{\varphi }_1\right)\left(d_1+\mu +{\varphi }_2\right)+(\mu +\tau )\left(\mu +{\varphi }_1\right)(1-{\mathcal{R}}_1)\hfill \\ \hfill & \hfill & +(\mu +\tau )\left(d_1+\mu +{\varphi }_2\right)\left(1-{\mathcal{R}}_2\right)\hfill \\ {\mathrm{\Phi }}_3\hfill & =\hfill & (\mu +\tau )\left(\mu +{\varphi }_1\right)\left(d_1+\mu +{\varphi }_2\right)\left(1-{\mathcal{R}}_0\right).\hfill \end{array}$$ (4)

Here two eigenvalues have negative real part, while to ensure the rest have negative real part, then we show the condition of Routh-Hurtwiz criteria to be fulfilled, that is Φ_i > 0 for i = 1, 2, 3. It can be easily seen that Φ₁ > 0 and Φ₂ and Φ₃ can be easily satisfied if ${\mathcal{R}}_0<1$. Then the result Φ₁Φ₂ − Φ₃ > 0 can be adjusted below:

$$\begin{array}{ccc}{\mathrm{\Phi }}_1{\mathrm{\Phi }}_2-{\mathrm{\Phi }}_3\hfill & =\hfill & \left(\mu +{\varphi }_1\right)\left(d_1+\mu +{\varphi }_2\right)\left(d_1+2(\mu +\tau )+2\mu +{\varphi }_1+{\varphi }_2\right)\hfill \\ \hfill & \hfill & +(\mu +\tau )\left(\mu +{\varphi }_1\right)\left(2\mu +\tau +{\varphi }_1\right)\left(1-{\mathcal{R}}_1\right)\hfill \\ \hfill & \hfill & +(\mu +\tau )\left(d_1+\mu +{\varphi }_2\right)\left(d_1+2\mu +\tau +{\varphi }_2\right)\left(1-{\mathcal{R}}_2\right)>0.\hfill \end{array}$$ (5)

After fulfilling the requirements of Routh- Hurtwiz criteria (that is all the eigenvalues associated to the model 1 will contain negative real parts), then, the model 1 is locally asymptotically stable at the infection free state if ${\mathcal{R}}_0<1$. □.

Next, we present the global asymptotical stability of the system 1 at E ₀ for the special case when ρ = 0 and θ = 0.

Theorem 3

The model 1 at E ₀ when ρ = 0 and θ = 0 is globally asymptotically stable if ${\mathcal{R}}_0\le 1$.

Proof

We define the Lyapunov function given by

$$\mathcal{M}={\mathcal{L}}_{1}E+{\mathcal{L}}_{2}A+{\mathcal{L}}_{3}I,$$ (6)

where ${\mathcal{M}}_i$, for i = 1, 2, 3 can be adjusted later. Differentiating $\mathcal{L}$ with respect to t and then using the system 1, we have

$$\begin{array}{ccc}\dot{\mathcal{M}}\hfill & =\hfill & {\mathcal{L}}_1\dot{E}+{\mathcal{L}}_2\dot{A}+{\mathcal{L}}_3\dot{I},\hfill \\ \hfill & =\hfill & {\mathcal{L}}_1\left[\right]\frac{({\beta }_{1}I+{\beta }_{2}A)}{N}S-(\tau +\mu )E\left]\right)+{\mathcal{L}}_2[\tau \psi E-({\varphi }_1+\mu )A]\hfill \\ \hfill & \hfill & +{\mathcal{L}}_3[(1-\psi )\tau E-({\varphi }_2+\mu +d_1)I],\hfill \\ \hfill & =\hfill & \left[\right]{\mathcal{L}}_1\frac{{\beta }_{1}S}{N}-{\mathcal{L}}_3({\varphi }_2+d_1+\mu )\left]\right)I+\left[\right]{\mathcal{L}}_1\frac{{\beta }_{2}S}{N}-\left({\varphi }_1+\mu \right){\mathcal{L}}_2\left]\right)A\hfill \\ \hfill & \hfill & +\left[\right]{\mathcal{L}}_2\tau \psi +{\mathcal{L}}_3(1-\psi )\tau -\left(\tau +\mu \right){\mathcal{L}}_1\left]\right)E.\hfill \end{array}$$

Assume S≤ N and further assign value to the constants, ${\mathcal{L}}_1=({\varphi }_1+\mu )$, ${\mathcal{L}}_2={\beta }_2$ and ${\mathcal{L}}_3=\frac{{\beta }_1({\varphi }_1+\mu )}{({\varphi }_2+\mu +d_1)}$, then we have

$$\dot{\mathcal{M}}=(\tau +\mu )({\varphi }_1+\mu )({\mathcal{R}}_0-1)E.$$

Here $\dot{\mathcal{M}}\le 0$ when ${\mathcal{R}}_0\le 1$ and $\dot{\mathcal{M}}=0$ if and only if E = 0. Upon using E = 0, in the model 1, we have (S, E, I, A, R) approaches to (S ⁰, 0, 0, 0, 0) when t → ∞ . So, the largest invariant set will be the DFE Q ₀. Hence the LaSalle’s Invariance Principle ensures that the system 1 for ${\mathcal{R}}_0\le 1$ is globally asymptotically stable in ∑. □.

5. Bifurcation analysis of the model

The backward bifurcation analysis is considered to be a very important tool for studying the model to determine the possible existence of the backward bifurcation. If there is possibly a backward bifurcation, the disease-free equilibrium will coexist with the endemic equilibrium, and there may not be the possibility of the global stability of the model at the infection-free state. The occurrence of the backward bifurcation in the disease model is important in a practical sense because the controls must reduce the value of ${\mathcal{R}}_0$ below than unity in order to eliminate the infection. The backward bifurcation phenomenon can be studied for a biological model using the standard approach given in Castillo-Chavez and Song (2004). We consider here the center manifold theory (Castillo-Chavez and Song, 2004) is to investigate the existence of backward bifurcation for the COVID-19 reinfection model 1. To investigate the backward bifurcation phenomenon for the COVID-19 model, we consider ${\mathcal{R}}_0=1$ if and only if

$${\beta }_1=\beta {*}_1=\frac{\left(d_1+\mu +{\varphi }_2\right)\left((\mu +\tau )\left(\mu +{\varphi }_1\right)-{\beta }_2\tau \psi \right)}{\tau (1-\psi )\left(\mu +{\varphi }_1\right)}.$$

We rename the state variables involved in the system 1 by S = z ₁, E = z ₂, A = z ₃, I = z ₄ and R = z ₅, and hence N = z ₁ + z ₂ + z ₃ + z ₄ + z ₅. Using the vector notation $\overrightarrow{z}=(z_1,z_2,z_3,z_4,z_5)$, then we represent the COVID-19 reinfection model by $dz∕dt=F\overrightarrow{z}$ where $F={(k_1,k_2,k_3,k_4,k_5)}^T$, we have the following update system,

$$\begin{array}{ccc}\frac{d{z}_1(t)}{dt}\hfill & =\hfill & \mathrm{\Lambda }-\frac{({\beta }_1{z}_4+{\beta }_2{z}_3)}{N}S-\mu z_1,\hfill \\ \frac{d{z}_2(t)}{dt}\hfill & =\hfill & \frac{({\beta }_1{z}_4+{\beta }_2{z}_3)}{N}{z}_1-(\tau +\mu )z_2,\hfill \\ \frac{d{z}_3(t)}{dt}\hfill & =\hfill & \tau \psi z_2+\frac{\theta {\beta }_2{z}_5{z}_3}{N}-({\varphi }_1+\mu )z_3,\hfill \\ \frac{d{z}_4(t)}{dt}\hfill & =\hfill & (1-\psi )\tau z_2+\frac{\rho {\beta }_1{z}_5{z}_4}{N}-({\varphi }_2+\mu +d_1)z_4,\hfill \\ \frac{d{z}_5(t)}{dt}\hfill & =\hfill & {\varphi }_1{z}_3(t)+{\varphi }_2{z}_4(t)-\frac{\rho {\beta }_1{z}_5{z}_4}{N}-\frac{\theta {\beta }_2{z}_5{z}_3}{N}-\mu z_5(t),\hfill \end{array}$$ (7)

We have for the infection free state the Jacobian of the above the system 7.

$$\begin{array}{c}{J}_1=\left(\begin{array}{ccccc}-\mu \hfill & 0\hfill & -{\beta }_2\hfill & \frac{\left((\mu +\tau )\left(\mu +{\varphi }_1\right)-\tau \psi {\beta }_2\right)\left(\mu +d_1+{\varphi }_2\right)}{\tau (\psi -1)\left(\mu +{\varphi }_1\right)}\hfill & 0\hfill \\ 0\hfill & -\mu -\tau \hfill & {\beta }_2\hfill & -\frac{\left((\mu +\tau )\left(\mu +{\varphi }_1\right)-\tau \psi {\beta }_2\right)\left(\mu +d_1+{\varphi }_2\right)}{\tau (\psi -1)\left(\mu +{\varphi }_1\right)}\hfill & 0\hfill \\ 0\hfill & \tau \psi \hfill & -\mu -{\varphi }_1\hfill & 0\hfill & 0\hfill \\ 0\hfill & \tau (1-\psi )\hfill & 0\hfill & -\mu -d_1-{\varphi }_2\hfill & 0\hfill \\ 0\hfill & 0\hfill & {\varphi }_1\hfill & {\varphi }_2\hfill & -\mu \hfill \\ \hfill \end{array}\right)\hfill \end{array}$$

It is observed that there exists one simple eigenvalue for the matrix J ₁ and the rest contain negative real parts. Thus, we can apply the procedure of center manifold theory further. Next step is to compute the left and right eigenvectors of J ₁, and we show it respectively by $\overrightarrow{v}=(v_1,v_2,v_3,v_4,v_5)$ and $\overrightarrow{w}={(w_1,w_2,w_3,w_4,w_5)}^T$. We get the result in the following,

$$v_1=0,v_3=\frac{{\beta }_2{v}_2}{\mu +{\varphi }_1},v_4=-\frac{v_2\left((\mu +\tau )\left(\mu +{\varphi }_1\right)-{\beta }_2\tau \psi \right)}{\tau (\psi -1)\left(\mu +{\varphi }_1\right)},v_5=0,v_2=v_2>0,$$

and

$$\begin{array}{ccc}{w}_1\hfill & =\hfill & -\frac{w_2(\mu +\tau )}{\mu },w_3=\frac{\tau w_2\psi }{\mu +{\varphi }_1},w_4=\frac{\tau w_2(1-\psi )}{d_1+\mu +{\varphi }_2},\hfill \\ w_5\hfill & =\hfill & w_2\left(\frac{\tau (1-\psi ){\varphi }_2}{\mu \left(d_1+\mu +{\varphi }_2\right)}+\frac{\tau \psi {\varphi }_1}{\mu \left(\mu +{\varphi }_1\right)}\right),w_2=w_2>0.\hfill \end{array}$$

In order to decide the existence of the backward bifurcation for the model 1, we need to compute the value of a and b, which are given by

$$a=\frac{2\mu w_5\left({\beta }_2\theta \left(v_3-v_4\right)w_3-{\beta }_1\rho v_4{w}_4\right)-2\mu v_2\left(w_2+w_3+w_4+w_5\right)\left({\beta }_1{w}_4+{\beta }_2{w}_3\right)}{\mathrm{\Lambda }}$$

and

$$b=\frac{\tau v_2{w}_2(1-\psi )}{d_1+\mu +{\varphi }_2}>0.$$

Here b > 0 and if a > 0 then the exists the backward bifurcation for the model 1 where the disease free equilibrium coexists with the endemic equilibrium and the disease free equilibrium may or may nor not be globally asymptotically stable.

6. Estimation of parameters and numerical results

6.1. Parameters estimations

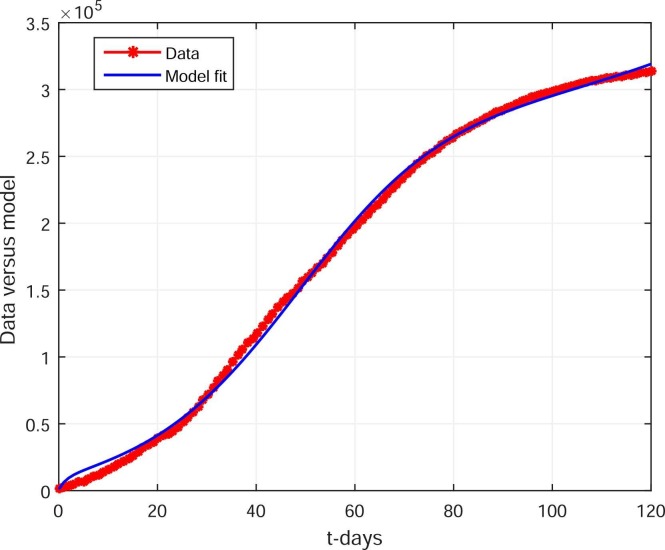
Here, we apply the nonlinear least square curve fitting technique to the model 1 with the real cases from Pakistan from July 01, 2021, till October 28, 2021. We have taken the cases from Anon (2022a) on a daily basis. Before fitting the data to the model 1, we need to determine first some of the information related to the parameters that can be estimated for the model. The total population of Pakistan approximately considered in 2021 to be N(0) = 22, 00, 00, 000 and the values of the variables of the model 1 are obtained is as follows: The infection cases at the beginning of the fourth wave at Pakistan on July 01, 2021, with infected cases I(0) = 1037, and the value for the A(0) = 1000, the value for the exposed individuals is considered for the data to match well the model E(0) = 2,000,000, R(0) = 1000 and we can determine the value of S(0) = 217,996,963. We have some parameters already from literature, such as ϕ ₁ = 1∕(5.1), ϕ ₂ = 0.1, d ₁ = 0.015, see Table 1. The value of Λ is estimated from Λ = μ * N(0), while μ = 1∕(67.7 *365) is the average per day life expectancy in Pakistan (Pakistan population, 1950–2021). We performed the simulations and the desired graphical result to data fitting is shown in Fig. 2. We have the numerical value for the basic reproduction number ${\mathcal{R}}_0\approx 1.4962$, while for the sub-basic reproduction number ${\mathcal{R}}_1\approx 1.4570$ and ${\mathcal{R}}_2\approx 0.0392$. It shows that the asymptomatic infected people generate more infected cases than the symptomatic. One of the reasons is the no visible symptoms of infection. The data is well fitted to the symptomatic infected population (I) of the model 1. It should be noted that there is no available data for the reinfection cases in Pakistan yet, and hence we considered the real data of the fourth wave in cumulative form and presented the result for data fitting. Although, we will explore in the next subsection, the parameters that are account for reinfection and how they minimized the infection cases by studying those parameters. The numerical values of the parameters obtained through the data fitting are shown in Table 1 and will be used further in onward analysis.

Table 1.

Estimated parameters.

Symbol	Definition	Value/per day	Source
Λ	Birth rate	μ × N(0)	Estimated
μ	Natural death rate	$\frac{1}{67.7\times 365}$	Pakistan population - (Pakistan population, 1950–2021)
ψ	Incubation period	0.9920	Fitted
τ	Individuals progress to A	0.4162	Fitted
ϕ1	Recovery of asymptomatic people	1/(5.1)	(Iboi et al., 2020b, Shen et al., 2021)
ϕ2	Recovery of symptomatic people	1/10	(Iboi et al., 2020b, Shen et al., 2021)
d1	Infection death rate of symptomatic people	0.015	(Iboi et al., 2020b, Shen et al., 2021)
θ	Reinfection of asymptomatic people	0.0196	Fitted
ρ	Reinfection of symptomatic people	0.3330	Fitted
β1	Contact among S and I people	0.5621	Fitted
β2	Contact among S and A people	0.2881	Fitted

Fig. 2.

Cases versus model fit: July 1, 2021-October 28, 2021. The * denote the real daily cases of COVID-19 in Pakistan while the bold line is the model infected curve.

6.2. Numerical results

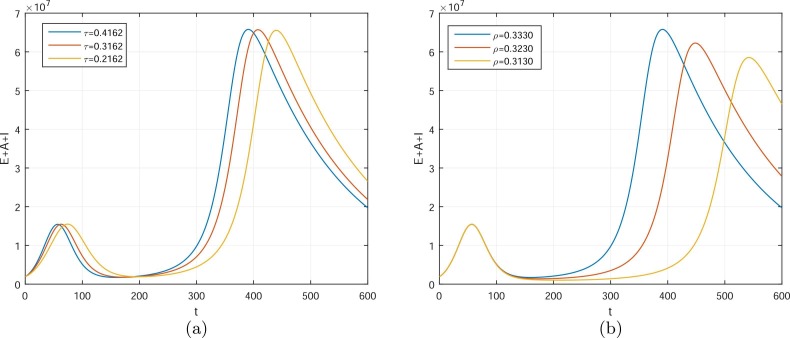
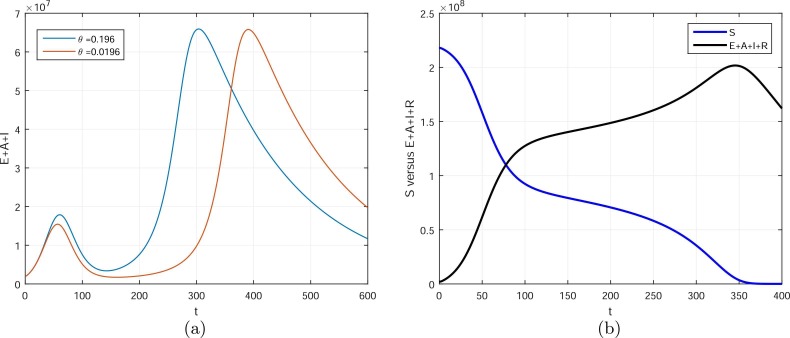
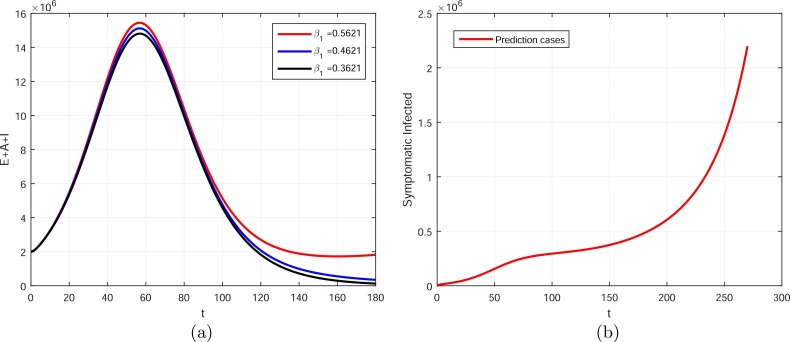
In order to obtain the numerical solution of the model 1, we need to use the Runge-Kutta order four scheme. The numerical values of the parameters given in Table 1 while the initial values of the variables are mentioned in the above subsection are used to obtain the graphical results. The prevention from the COVID-19 dynamics as suggested by World Health Organization, i.e., washing hands, maintaining social distances, wearing face masks, avoiding gathering, etc, can minimize the infection spread in the community, and this is shown graphically in Fig. 3. By decreasing the value of β ₁ and β ₂, the number of symptomatic infected are decreasing faster. The impact of the parameters ρ, τ, and θ on symptomatic infected population are shown in Fig. 4. The subgraphs Fig. 4(a) shows the variations in the value of reinfection parameter ρ, which can best decrease the infected population. It is important to note that the reinfection of the individuals that already experienced the COVID-19 after testing and verified reinfected with COVID-19 should be isolated until their upcoming tests are negative. The subgraph in 4(b) shows that the individuals upon testing and notified asymptomatic or asymptomatic must be isolated, and it is shown graphically with the variation in the parameter value, the cases are decreasing. The subgraph in Fig. 4(c) shows the reinfection parameter responsible for the asymptomatic cases and its impact on the symptomatic cases is shown. It can be observed with the variations in θ, the number of infected cases is decreasing effectively. Fig. 5 represents the total infected cases E + A + I and its simulation results when varying the numerical value of the parameters β ₁ and β ₂. The total infected cases predict the occurrence of the next wave of COVID-19 in Pakistan in the second week of February 2022. We show some variations in the values of β ₁ and β ₂ that can reduce the further infected cases in the second layer. If the prevention mechanics suggested by WHO are properly followed then we may control the infection onward cases. Fig. 6 shows the impact of τ and ρ on the total infected cases E + A + I. A slight variation in these parameters’ values can decrease well the infected cases. Fig. 7 (a) represents the behavior of θ on the total infected cases, a decrease can occur with the decrease in the value of θ. Fig. 7 (b) is obtained by plotting the susceptible individuals versus E + A + I + R, while R that generates the reinfection cases is considered. The prediction of the ending of the fourth wave in the country is shown graphically in Fig. 8. The result in Fig. 8 gives good agreement to the ending period of the COVID-19 cases of the fourth wave in Pakistan, see Anon (2022a). The subgraph in Fig. 8(b) predicts the COVID-19 cumulative cases to be 2,197,600 when the parameters θ and ρ are active otherwise there cannot determine the future fifth wave predictions as well as the cumulative infected cases. The result shows if no proper attention to the reinfected cases is given maybe the healthy individuals could be infected very fast. Although, this prediction is given when there is less recovery from undetected cases.

Fig. 3.

The parameters β₁ and β₂ and its impact on the symptomatic populations when β₁ = 0.5621, 0.4621, 0.3621, 0.2621, 0.1621 and β₂ = 0.2881, 0.2681, 0.2481, 0.2281.

Fig. 4.

The parameters ρ, τ and θ on asymptomatic infected population with different values. Subgraphs show (a) ρ = 0.3330, 0.2330, 0.1330, 0.0330, (b) τ = 0.4162, 0.3162, 0.2162, 0.1162, (c) θ = 0.196, 0.0196.

Fig. 5.

The impact of the parameters β₁ and β₂ on the total infected cases E + A + I. Subgraph shows (a) β₁ = 0.5621, 0.5521, 0.5421, 0.5321, (b) β₂ = 0.2881, 0.2861, 0.2841, 0.2821.

Fig. 6.

The impact of parameters τ and ρ on the prediction cases. Subgraphs show (a) τ = 0.4162, 0.3162, 0.2162, (b) ρ = 0.3330, 0.3230, 0.3130.

Fig. 7.

The parameter θ impact on E + A + I. Subgraphs show (a) θ = 0.196, 0.0196, (b) comparison of susceptible versus E + A + I + R over long time.

Fig. 8.

The prediction of the ending of the fourth wave, for different values of β₁ = 0.5621, 0.4621, 0.3621. Sub-figure (b) determines the future cumulative cases at fourth wave, since july, 01, 2021 till March 2021.

7. Conclusion

In the present work, we constructed a new mathematical model for the SARS-COV-2 with reinfection. We studied in detail the model formulation with the occurring of reinfection cases. After formulation of the model, we studied the model properties such as the positivity of the model solution, boundedness. We studied the stability of the equilibrium solution at the disease-free case and found that the model behaves locally asymptotically stable when ${\mathcal{R}}_0<1$. We considered the real cumulative cases of COVID-19 in Pakistan and estimated the model parameters. The numerical values are used further to estimate the basic reproduction number ${\mathcal{R}}_0\approx 1.4962$. We used the numerical method and presented the graphical results for various values of the parameters. The impact of parameters that are very sensitive has been used to show its impact on the symptomatic population. We observed that the infected cases can be minimized if the values of the parameters are decreased slightly. Moreover, we also considered the impact of the variations of the parameters on the total number of infected cases and found that there may be the fifth layer of COVID-19 in Pakistan. If the number of infected with reinfection are not isolated or quarantined then we may face a large number of new cases. Therefore, identifying the reinfection cases and their isolations, and quarantine can be beneficial to minimize future cases in the country.

Authors statements

All authors equally contributed in this paper and agreed on the final draft of the manuscript.

Declaration of Competing Interest

The authors declare no competing interests regarding the publication of this work.