Estimands and Estimation of COVID-19 Vaccine Effectiveness Under the Test-Negative Design

Abstract

The test-negative design is routinely used for the monitoring of seasonal flu vaccine effectiveness. More recently, it has become integral to the estimation of COVID-19 vaccine effectiveness, in particular for more severe disease outcomes. Because the design has many important advantages and is becoming a mainstay for monitoring postlicensure vaccine effectiveness, epidemiologists and biostatisticians may be interested in further understanding the effect measures being estimated in these studies and connections to causal effects. Logistic regression is typically applied to estimate the conditional risk ratio but relies on correct outcome model specification and may be biased in the presence of effect modification by a confounder. We give and justify an inverse probability of treatment weighting (IPTW) estimator for the marginal risk ratio, which is valid under effect modification. We use causal directed acyclic graphs, and counterfactual arguments under assumptions about no interference and partial interference to illustrate the connection between these statistical estimands and causal quantities. We conduct a simulation study to illustrate and confirm our derivations and to evaluate the performance of the estimators. We find that if the effectiveness of the vaccine varies across patient subgroups, the logistic regression can lead to misleading estimates, but the IPTW estimator can produce unbiased estimates. We also find that in the presence of partial interference both estimators can produce misleading estimates.

The test-negative design is a type of observational study design routinely used to estimate seasonal influenza vaccine effectiveness.^1,2 It is currently being employed internationally to estimate coronavirus disease 2019 (COVID-19) vaccine effectiveness.^3,4 When prospectively implemented, this design recruits individuals who are seeking care or testing in response to COVID-like illness.^5,6 Participants are tested for severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection, for example, by reverse transcription polymerase chain reaction test. The results of this test determine whether the participant is categorized as a COVID-positive “case” or a COVID-negative “control”. COVID-19 vaccination history and other patient information are then obtained, possibly from health records.⁵ Another implementation of this design involves using electronic health data to retrospectively identify patients who sought care or testing due to COVID-like symptoms, their SARS-CoV-2 infection test results and vaccination status at the time of care-seeking, and demographic and clinical information about the patient.^7,8 In either version, vaccine effectiveness is typically estimated using a multivariable logistic regression of the test result (i.e., case status) conditional on vaccination status and measured confounders^6–8 but inverse probability of treatment weighting has also recently been used.⁵

Jackson and Nelson¹ provided the first formal framework for the test-negative design. Using contingency tables of a hypothetical population stratified by binary vaccination status, infection status, and binary propensity to seek care, they showed that case status odds-ratio estimands simplify to risk ratios for medically attended illness under certain assumptions.¹ Foppa et al. ⁹ justified the design and use of the case status odds ratio through mathematical models of infectious disease transmission. Several studies^2,10,11 used causal directed acyclic graphs (DAGs)¹² to explore different sources of bias that may manifest when estimating seasonal flu vaccine effectiveness with the test-negative design. Shi et al.¹¹ investigated bias of the standard test-negative design parameter with respect to the marginal risk ratio parameter under a multiplicative model with binary variables. Vandenbroucke et al.¹³ and Schnitzer et al.¹⁴ investigated the identification of risk factors for COVID-19 disease and SARS-CoV-2 infection, respectively, under the test-negative design with additional population controls. Lewnard et al.¹⁵ reviewed the test negative design in the COVID-19 context and proposed multiple strategies to limit bias due to confounding and misclassification of case status. Important insights arising from past literature include (1) Because only those seeking and accessing care can be enrolled in the study, the test-negative design can better control for confounding due to care-seeking behavior than case–control studies though residual bias is possible when care-seeking behavior is nonbinary.^10,15 However, a consequence is that vaccine effectiveness is only estimated in the subpopulation that has access to care.^1,4 (2) Because all subjects are tested for infection, the test-negative design may be less subject to measurement error than cohort studies¹; however, there is also a danger of important bias when patients falsely testing negative for SARS-CoV-2 are considered to be “controls.”¹⁵ (3) The test-negative design can only estimate vaccine effectiveness to prevent medically attended illness, such as illness leading to hospitalization. (4) Under this design, logistic regression is only valid when the vaccine has no effect on disease with similar presentations to the one being studied.¹

Although many of the above-cited studies contributed to the theoretical justification of the test-negative design,^1,9–11,15 none formally derived the estimands under a statistical sampling framework such as the one used to justify the now-standard analytical methods used for case–control studies¹⁶ or investigated connections to counterfactual causal parameters. Furthermore, no study has justified estimation with inverse probability of treatment weighting (IPTW) though at least one applied study has made use of this method.⁵

In this article, we postulate a nonparametric model, represented by a DAG, of the relevant variables at play when the test-negative design is used to study vaccine effectiveness for medically attended COVID-19. Under this model, we derive the estimand of the test-negative design that is estimated with a correctly specified logistic regression. Under the assumption that the vaccine does not impact the probability of infection or disease due to another infection, the estimand is interpretable as an adjusted risk ratio for medically-attended COVID-19 with respect to vaccination status.^1,11 We also give the marginal risk ratio and show that it can be estimated using inverse probability of treatment weighting when the propensity score model (i.e., model for the probability of vaccination status) is fit using only the control data. In observational and experimental studies of vaccines for infectious disease, one person’s disease occurrence may be impacted by the vaccination status of those in their entourage. This is called “interference” and complicates causal analysis.¹⁷ We discuss potential connections of the statistical estimands to causal parameters under the assumptions of noninterference and partial interference, respectively. We conduct a simulation study to illustrate how estimates and estimands vary under effect modification and partial interference.

STATISTICAL ESTIMANDS

We consider a test-negative design that recruits all patients admitted to hospital on the basis of specific symptoms of COVID-like illness which may be another infectious disease. The patients are then tested for SARS-CoV-2 infection. Administrative databases are then used to ascertain patients’ history of COVID-19 vaccination.

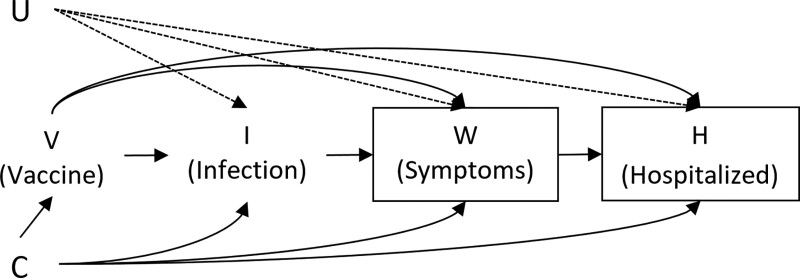
The directed acyclic graph (DAG) in Figure represents a model of the progression of the variables considered in this study. First, individuals have some status of vaccination against COVID-19 V, for example, “unvaccinated,” “fully vaccinated + x days”, etc. Subsequently, they may become infected with some virus (I). Let I = 2 denote infection by SARS-CoV-2, I = 1 other infection, and I = 0 the infection-free state. If an infection is present, the individual may develop severe symptoms W. These symptoms may lead to hospitalization H and thus inclusion in the study. Because this design is observational, there may be common causes C and U of any of the aforementioned variables, where U is unmeasured and assumed to not affect V. Confounders C may include age, comorbidities, employment sector, etc. The variable U could include latent COVID-19 susceptibility.

The test-negative design in this context presumably samples those with some infection (I ≠ 0), with severe symptoms (W = 1) who are then hospitalized (H = 1). Assuming a perfect test for SARS-CoV-2 infection, those who test positive, I = 2, have the outcome of interest and are considered cases. Those who test negative, I = 1, are considered controls. The index date of the study is the date of hospitalization and vaccination status is considered as of that date. This design is distinct from a standard case–control¹⁶ because the participants are selected before knowledge of the nature of their infection.¹

The Conditional Risk Ratio Estimand

The observed data z = (c,v) are samples of Z = (C,V) from the probability function $Pr(Z=z|I\ne \mathrm{0,}W=\mathrm{1,}H=1)$. The infection type i = {1,2} is sampled from a Bernoulli distribution with probability $Pr(I=i|Z=z\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}H=1)$. From this sampling, we can identify the odds ratio of data z versus some comparator z₀ with respect to infection type by

$$\begin{array}{l}\frac{Pr(Z=z\mathrm{,}I=2|I\ne \mathrm{0,}W=\mathrm{1,}H=1)}{Pr(Z=z_0\mathrm{,}I=2|I\ne \mathrm{0,}W=\mathrm{1,}H=1)}/\frac{Pr(Z=z\mathrm{,}I=1|I\ne \mathrm{0,}W=\mathrm{1,}H=1)}{Pr(Z=z_0\mathrm{,}I=1|I\ne \mathrm{0,}W=\mathrm{1,}H=1)}\\ =\frac{Pr(Z=z|I=\mathrm{2,}W=\mathrm{1,}H=1)}{Pr(Z=z_0|I=\mathrm{2,}W=\mathrm{1,}H=1)}/\frac{Pr(Z=z|I=\mathrm{1,}W=\mathrm{1,}H=1)}{Pr(Z=z_0|I=\mathrm{1,}W=\mathrm{1,}H=1)}\mathrm{.}\end{array}$$ (1)

For example, we may contrast those fully vaccinated $z=(c\mathrm{,}v="\text{fully}\text{vaccinated}+\text{14 days"})$ vs. those unvaccinated $z_0=(c\mathrm{,}v="\text{unvaccinated"})$. By the identity

$$\begin{array}{l}Pr(I=i\mathrm{,}W=\mathrm{1,}H=1|Z=z)\\ =\frac{Pr(Z=z\mathrm{,}I=i|I\ne \mathrm{0,}W=\mathrm{1,}H=1)Pr(I\ne \mathrm{0,}W=\mathrm{1,}H=1)}{Pr(Z=z)}\mathrm{,}\end{array}$$

for i = 1,2 we can rewrite Equation (1) as

$$\frac{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|Z=z)}{Pr(I=\mathrm{1,}W=\mathrm{1,}H=1|Z=z)}/\frac{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|Z=z_0)}{Pr(I=\mathrm{1,}W=\mathrm{1,}H=1|Z=z_0)}$$ (2)

which represents the prospective adjusted odds ratio of being hospitalized for COVID-19 vs. being hospitalized for another infection between fully vaccinated and unvaccinated individuals. Under the assumption that the COVID-19 vaccine has no impact on any other type of infection, the ensuing disease severity and potential for hospitalization, $Pr(I=\mathrm{1,}W=\mathrm{1,}H=1|Z=z)=Pr(I=\mathrm{1,}W=\mathrm{1,}H=1|Z=z_0)$ and the odds ratio in Equation (2) simplifies to

$${\psi }_{\text{cRR}}=\frac{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|Z=z)}{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|Z=z_0)}\mathrm{,}$$ (3)

which is the prospective adjusted risk ratio of hospitalization for COVID-19 between fully vaccinated and unvaccinated individuals. The “vaccine effectiveness” estimand is typically given as $1-{\psi }_{\text{cRR}}$.

Now applying the identity

$$\begin{array}{l}Pr(I=i\mathrm{,}W=\mathrm{1,}H=1|Z=z)=Pr(I=i|Z=z\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}\\ H=1)Pr(I\ne \mathrm{0,}W=\mathrm{1,}H=1|Z=z)\end{array}$$

we can rewrite Equation (2) as

$$\begin{array}{l}\frac{Pr(I=2|Z=z\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}H=1)}{Pr(I=1|Z=z\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}H=1)}/\\ \frac{Pr(I=2|Z=z_0\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}H=1)}{Pr(I=1|Z=z_0\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}H=1)}\mathrm{.}\end{array}$$ (4)

A multivariable logistic regression of I = 2 vs. I = 1, conditional on C and a factorization of V using the data sampled under the test-negative design will yield estimates of the odds ratios in Equation (4) under the assumption that the logistic regression model for $\text{Pr}(I=i|Z=z\mathrm{,}I\ne \mathrm{0,}W=\mathrm{1,}H=1)$ is correctly specified.¹⁶ Because of the equivalence of Equation (4) with Equation (3), we can say that the exponential of the coefficient related to vaccination status in the logistic regression is an estimate of the adjusted risk ratio for hospitalization with COVID-19.

Thus, under the assumed DAG and logistic regression model, the conditional risk ratio in Equation (3) is the interpretable estimand. Importantly, this risk ratio is an association between vaccination and a combined outcome that involves three steps: becoming infected with SARS-CoV-2, having severe symptoms, and accessing (being admitted to) a hospital due to these symptoms.¹

The Marginal Risk Ratio

The risk ratio is collapsible, so its value does not depend on the variables in the conditioning set beyond adjustment for confounding. But estimation using logistic regression relies on correct model specification, which may be implausible in practice. In particular, if vaccine effectiveness differs by subgroup, then estimating an overall effect with logistic regression will inevitably result in misspecification because the model cannot include interactions with vaccination. One may choose to instead directly estimate the marginal risk ratio.

$${\psi }_{\text{mRR}}=\frac{\mathbb{E}\{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|Z=z)\}}{\mathbb{E}\{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|Z=z_0)\}}\mathrm{.}$$ (5)

Under effect modification where a third variable can change the effect of vaccination on infection, disease, or hospitalization, this estimand is not equal to the conditional risk ratio.

Due to the biased sampling design, one cannot directly estimate the conditional probability of experiencing an outcome. However, under the previous assumption that the vaccine has no impact on other infections, we have that

$$\begin{array}{l}Pr(V=v|I=\mathrm{1,}W=\mathrm{1,}H=\mathrm{1,}C=c)\\ =\frac{Pr(I=\mathrm{1,}W=\mathrm{1,}H=\mathrm{1,}Z=z|V=v\mathrm{,}C=c)Pr(V=v|C=c)}{Pr(I=\mathrm{1,}W=\mathrm{1,}H=\mathrm{1,}Z=z|C=c)}\end{array}$$

$$=Pr(V=v|C)$$

This means that we can estimate the propensity score by (1) modeling the conditional probability of vaccine status using only the controls, then (2) using this model to estimate probabilities for the whole sample.

It is then possible to use IPTW to estimate the marginal risk ratio directly. This involves taking a ratio of weighted means between subjects with different vaccination statuses. Consider a sample of n hospitalized patients with observed data $(c_k\mathrm{,}{v}_k\mathrm{,}{i}_k;k=\mathrm{1,}\mathrm{...}\mathrm{,}n)$ corresponding to measured confounders, vaccination status, and SARS-CoV-2 infection status, respectively. The latter IPTW estimator contrasting vaccination status v vs. v₀ can be written as follows:

$$\frac{1}{n}{\displaystyle \sum _{k=1}^n}\frac{\mathbb{I}(i_k=2{}^{}\text{and}{v}_k=v)}{\widehat{Pr}(V=v|C=c_k)}/\frac{1}{n}{\displaystyle \sum _{k=1}^n}\frac{\mathbb{I}(i_k=2{}^{}\text{and}{v}_k=v_0)}{\widehat{Pr}(V=v_0|C=c_k)},$$

where $\mathbb{I}(\cdot )$ represents the indicator function and $\widehat{Pr}(V=v_0|C=c_k)$ represents the estimate of the propensity score for the kth patient. One could alternatively run a weighted logistic regression. Estimation with IPTW in the biased sample is justified theoretically in the Appendix and empirically in the simulation study.

CAUSAL INTERPRETATION

Whether statistical estimands can be connected to causal estimands depends on additional assumptions. Causal estimands are often defined based on potential outcomes. A potential outcome under a given treatment is the outcome a participant would have had if they had received that treatment, for example, the outcome they would have under a given vaccination status. Causal inference operating under Rubin’s “stable unit treatment value assumption”¹⁸ requires that the treatment (vaccination) of one individual does not impact the potential outcome of another. This assumption, also referred to as the absence of interference, is likely violated in studies of COVID-19 vaccination effectiveness due to widespread vaccination programs and reduced infectiousness among fully vaccinated people.^17,19 We explore the relationships between the statistical estimands defined above and causal estimands under the hypothetical assumptions of no interference and partial interference.

Causal Interpretation Assuming No Interference

In the absence of interference, one patient’s infection, illness, and hospitalization under their vaccination status could not depend on another patient’s vaccination status. We would then assume consistency where assignment to a vaccination status V = v yields the same outcome as when the observed vaccination status is V = v. If we define the potential outcome under vaccination status v as $\{I(v)\mathrm{,}W(v)\mathrm{,}H(v)\},$ this means that $\left\{I\mathrm{,}W\mathrm{,}H\right\}=\{I(v)\mathrm{,}W(v)\mathrm{,}H(v)\}$ when V = v. Under the DAG in the figure, we must assume that we have measured all variables C. Specifically, we must satisfy the conditional ignorability assumption $\{I(v)\mathrm{,}W(v)\mathrm{,}H(v)\}\perp \perp VC.$ This also means that any common cause of vaccination status with any of the three outcome variables must be measured.

In addition, the probability of an individual having any vaccination status must be non-zero for any possible value of C. This last assumption would be violated if, for instance, the study covers a time-period where some of the recruited patients could not have possibly been fully vaccinated due to age-restrictions during the roll-out period.

Supposing that the above assumptions were true, the risk ratio in equation (3) contrasting some vaccination statuses v = 1 versus v = 0 could be rewritten as

$${\psi }_{\text{cCausalRR}}=\frac{Pr(I(1)=\mathrm{2,}W(1)=\mathrm{1,}H(1)=1|C=c)}{Pr(I(0)=\mathrm{2,}W(0)=\mathrm{1,}H(0)=1|C=c)}$$ (6)

which is the conditional causal risk ratio of being hospitalized with COVID-19. The marginal risk ratio can be rewritten as

$${\psi }_{\text{mCausalRR}}=\frac{Pr(I(1)=\mathrm{2,}W(1)=\mathrm{1,}H(1)=1)}{Pr(I(0)=\mathrm{2,}W(0)=\mathrm{1,}H(0)=1)}\mathrm{.}$$ (7)

However, given that interference is likely in vaccine studies of infectious diseases, these causal parameters may not be well-defined.

Causal Interpretation Under Interference

Under general interference, one person’s potential outcome, indexed by j, depends on the full vector of other individuals’ treatment statuses, $v_{-j}=(v_1\mathrm{,}{v}_2\mathrm{,...}\mathrm{,}{v}_{j-1}\mathrm{,}{v}_{j+1}\mathrm{,...,}{v}_n)$. This individual’s potential outcome can be denoted $Y_j(v_j\mathrm{,}{v}_{-j})$. If interference is limited to known blocks or networks, causal effects can be defined and potentially estimated. For example, in a multisite study, suppose that participants are geographically connected by site so that interference only exists between individuals accessing care at a common site. We say that these individuals are in the same “block.”²⁰ Let $v^m$ denote a vector of vaccination statuses for the mth block and let $v_{-j}^m$ denote the same vector with the jth element removed. Suppose that we can define the potential outcome of the jth individual in block m as depending on a one-dimensional summary $f(v_{-j}^m)$ of the block’s overall vaccine uptake (called “vaccination coverage”).²¹ The potential outcome for individual j in block m could then be rewritten as $Y_j(v_j\mathrm{,}{v}_{-j})=Y_j(v_j\mathrm{,}f(v_{-j}^m))$. Given two block vaccination coverage levels f and f' and two individual vaccination statuses v and v', estimands of interest in this framework include the direct effect $\mathbb{E}\{Y(v\mathrm{,}f)\}/\mathbb{E}\{Y(v^{\prime }\mathrm{,}f)\}$, which is the effect of changing an individual’s vaccination status but fixing the vaccination status of others in the block; the indirect effect $\mathbb{E}\{Y(v\mathrm{,}f)\}/\mathbb{E}\{Y(v\mathrm{,}{f}^{\prime })\},$ which is the effect of changing the block’s vaccination coverage when the individual’s vaccination status is held fixed; and the total effect $\mathbb{E}\{Y(v\mathrm{,}f)\}/\mathbb{E}\{Y(v^{\prime }\mathrm{,}{f}^{\prime })\}$ of changing both the individual vaccination status and block’s vaccination coverage.¹⁷

In standard contexts, these causal estimands can be estimated under challenging assumptions about measured confounding.²⁰ First, all confounders of individual vaccination and outcome must be adjusted for. But because we also need to unconfound the relationship between the individual outcome and the block’s vaccination coverage, it may also be necessary to adjust for summaries of the block’s covariates.²² Examples of such covariates are summaries of the political orientations of the block’s members and leadership which can impact vaccination uptake and are related to health risk-taking behavior. Let $c_{-j}^m$ denote the vector of all covariates in block m except individual j. The block-level summary can be denoted $g_m=g(c_{-j}^m)$. If these measured variables allow for the adjustment for confounding, then we have that

$$E(Y|C=c\mathrm{,}G=g(c)\mathrm{,}V=v\mathrm{,}F=f)=E(Y(v\mathrm{,}f)|C=c\mathrm{,}G=g(c))\mathrm{.}$$

In the test negative design, the outcome for individual j in block m is $Y_j=\left\{I_j\mathrm{,}{W}_j\mathrm{,}{H}_j\right\}$ which we assume is equal to the potential outcomes $\{I_j(v\mathrm{,}{f}_m)\mathrm{,}{W}_j(v\mathrm{,}{f}_m)\mathrm{,}{H}_j(v\mathrm{,}{f}_m)\}$ when we observe $V_j=v$ and $f(V_{-j}^m)=f_m$. And so we can write the conditional risk ratio estimated by the standard logistic regression as

$${\psi }_{cRR}=\frac{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|C=c\mathrm{,}G=g(C)\mathrm{,}V=v)}{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|C=c\mathrm{,}G=g(C)\mathrm{,}V=v^{\prime })}$$

$$=\frac{{\displaystyle {\sum }_{m=1}^{M}Pr(S_m){\mathbb{E}}_{P_m}(Y|C=c\mathrm{,}G=g_m\mathrm{,}V=v\mathrm{,}F=f_m)}}{{\displaystyle {\sum }_{m=1}^{M}Pr(S_m){\mathbb{E}}_{P_m}(Y|C=c\mathrm{,}G=g_m\mathrm{,}V=v^{\prime }\mathrm{,}F=f_m)}},$$

where $Pr(S_m)$ is the proportion of the source population in block m and the second-line expectations are taken under P_m, the block-specific density function. With no unmeasured confounders, ${\psi }_{cRR}$ is equal to

$$\frac{{\displaystyle {\sum }_{m=1}^{M}Pr(S_m){\mathrm{Pr}}_{Pm}(I(v\mathrm{,}{f}_m)=\mathrm{2,}W(v\mathrm{,}{f}_m)=\mathrm{1,}H(v\mathrm{,}{f}_m)=1|C=c\mathrm{,}G=g_m)}}{{\displaystyle {\sum }_{m=1}^{M}Pr(S_m){\mathrm{Pr}}_{Pm}(I(v^{\prime }\mathrm{,}{f}_m)=\mathrm{2,}W(v^{\prime }\mathrm{,}{f}_m)=\mathrm{1,}H(v^{\prime }\mathrm{,}{f}_m)=1|C=c\mathrm{,}G=g_m)}}\mathrm{.}$$

So if block-level confounder summaries are adjusted for in the analysis and if those and the individual-level confounders are sufficient to identify block-specific causal effects, then the overall conditional risk ratio estimand can roughly be interpreted as a contrast between the weighted averages of the block-specific probabilities of medically-attended disease. However, because f_m is the observed vaccination coverage in block m and because this coverage can vary by block, this is not a causal contrast in the sense that it does not represent a marginal or conditional effect of intervening on vaccination. In the simulation study, we explore the potential deviation between the estimates from the test-negative design and the causally-interpretable direct effect risk ratio

$${\psi }_{\text{cRR}\mathrm{,}{f}^{*}}=\frac{Pr(I(v\mathrm{,}{f}^{*})=\mathrm{2,}W(v\mathrm{,}{f}^{*})=\mathrm{1,}H(v\mathrm{,}{f}^{*})=1|C=c\mathrm{,}G=g(C))}{Pr(I(v^{\prime }\mathrm{,}{f}^{*})=\mathrm{2,}W(v^{\prime }\mathrm{,}{f}^{*})=\mathrm{1,}H(v^{\prime }\mathrm{,}{f}^{*})=1|C=c\mathrm{,}G=g(C))}$$

under vaccination coverage f*.

SIMULATION STUDIES

The objective of the simulation study is to compare the values of statistical and causal estimands and to evaluate estimation by logistic regression and the proposed IPTW in the test-negative design. We generated three scenarios, summarized in Table 1. The first two followed the DAG in the Figure with single continuous confounder C and all other variables binary. Two binary unmeasured variables impacted the risks of SARS-CoV-2 infection, severe symptoms due to COVID-19, and hospitalization if the severe symptoms were present. The second unmeasured variable also impacted the risk of other infection and severe symptoms due to other disease. Severe disease symptoms were generated separately for infection with SARS-CoV-2 and other infection. Hospitalization was only possible with severe disease. Vaccination offered protection from infection, severe disease, and hospitalization. For the first two scenarios, no interference was present.

TABLE 1.

Data Generation Structure in the Simulation Study

Variable Name and Type	Description	Generated Conditional On
Scenarios 1 and 2: generated from single population.
Scenario 3: generated in 10 blocks of fixed size.
C, conts	Baseline confounder	None
(Scenario 3 only:)	Study-level baseline confounder (common value within block), e.g., local incidence	None
X, conts
U1 and U2, bin	Unmeasured covariates (causes of outcome)	None
		Scenario 3: U2 depends on X
V, bin	Vaccination	C
		Scenario 3: +X and block
I1 = 1, bin	Infection with other virus	C, U1
I2 = 1, bin	Infection with SARS-CoV-2	C, V, U1, U2, (1 − V) * U2
		Scenario 2: +V * C
		Scenario 3: +X
W[I == 1], bin	Severe disease due to other virus	C, V, U1
W[I == 2], bin	Severe COVID-19	C, V, U1,
		Scenarios 1 and 2: +(1 − V ) * U2
		Scenario 3: +U2 and interaction between V and % vaccinated in block
H[W == 1], bin	Hospitalization with severe symptoms	C, V, U1
		Scenario 3: +% vaccinated in block
Study sample, scenarios 1 and 2: randomly sample n patients with H = 1
Study sample, scenario 3: randomly sample n = 10 patients with H = 1 per block

Each given variable is univariate and generated randomly conditional on the variables given in the rightmost column.

bin indicates binary (generated as Bernoulli), conts: continuous (generated as Gaussian).

FIGURE.

Directed acyclic graph representing the hypothetical relationship between baseline confounders C, vaccination status V, infection I (none/SARS-CoV-2/other infection), severe symptoms W, hospitalization H, and unmeasured common causes of I, W, and H. The variable U represents any (possibly unmeasured) common causes of infection, symptoms, and hospitalization that do not also affect vaccination. The boxes around W and H represent how the study sampling method conditions on these variables. Note that this conditioning also results in all participants having some kind of infection that can lead to severe COVID-19-like symptoms.

• Scenario 1 (Basic Setting): No effect modification of vaccination V by covariate C in any model, no effect of the vaccine on non-SARS-CoV-2 infection or disease. The effects of the vaccine V and symptoms W on hospitalization did not depend on infection type.

• Scenario 2 (Effect modification): Same as Scenario 1 except with an added interaction term between C and V in the model for infection with SARS-CoV-2. This represents a different individual effect depending on the patient’s value of C. For example, if C represents age, then this represents a scenario where older people do not benefit as much from the vaccine as younger people.

The third scenario introduced partial interference.

• Scenario 3 (Partial interference): The subjects in the simulation belonged to 10 blocks of fixed sizes. We generated three subject-level covariates: one continuous and measured, and two binary and unmeasured. We also generated a continuous block-level covariate, X, representing a measure of local incidence of infection with SARS-CoV-2. The probability of vaccination depended on the block, and the local incidence X where greater incidence encouraged vaccination. Infection with SARS-CoV-2 was affected by vaccination status, the block- and individual-level covariates, and the overall vaccine uptake (proportion vaccinated) in the rest of the block. The proportion vaccinated was included as an effect modifier of vaccination with the hypothesis that there is less exposure to the virus when more surrounding people are vaccinated, and that vaccination in addition to lower viral exposure is more protective than the sum of each individual element.

In all scenarios, logistic regression and IPTW adjusted for the baseline confounder C. In the third scenario, the models also adjusted for the block-level covariate X.

The results are presented in Table 2. In all scenarios, the vaccine is more effective at reducing hospitalization than infection. When there was no interference, both the conditional (${\psi }_{cRR}$) and marginal (${\psi }_{mRR}$) risk ratio estimands have a causal interpretation, corresponding to the counterfactual parameters ${\psi }_{cCausalRR}$ and ${\psi }_{mCausalRR}$, respectively.

TABLE 2.

Simulation Study Results

	Truth	Mean Est	MC SE	% Cov cRR	% CovmRR
Scenario 1: Basic setting
Estimands
1 − ψcRR	0.96
1 − ψmRR	0.96
1 − mRR for SARS-CoV-2	0.84
Estimators
Logistic regression		0.97	0.01	89	-
IPTW
πcontrols		0.96	0.02	-	92
πall		0.44	0.06	-	0
Scenario 2: Effect modification by C for SARS-CoV-2 infection
Estimands
1 − ψcRR	0.77
1 − ψmRR	0.75
1 − mRR for SARS-CoV-2	0.44
Estimators
Logistic regression		0.91	0.06	39	-
IPTW
πcontrols		0.74	0.15	-	93
πall		0.18	0.05	-	0
Scenario 3: Partial interference by block vaccination prevalence, f
Estimands
1 − ψcRR	0.86
1 − ψmRR	0.85
1 − mRR for SARS-CoV-2	0.48
1 − ψcRR,75	0.86
1 − ψcRR,50	0.80
1 − ψcRR,25	0.76
Estimators
Logistic regression		0.88	0.04	89	-
IPTW
πcontrols		0.85	0.06	-	92
πall		0.14	0.04	-	0

Aggregate results of the application of each method to 1,000 simulated datasets of n hospitalized patients where n = 500 for Scenarios 1 and 2 and n =1000 for Scenario 3. The results are given with respect to one minus the risk ratios, often referred to as “vaccine effectiveness.” ${\psi }_{cRR}$: the conditional risk ratio for hospitalization with COVID-19 in Equation (3); ${\psi }_{mRR}$: the marginal risk ratio for hospitalization with COVID-19 in Equation (5).

% Cov indicates % of 95% confidence intervals that contain the true vaccine effectiveness (optimal is 95%); Mean est, mean estimate; MC SE, Monte-Carlo standard error of the estimate; mRR marginal risk ratio.

In the first scenario, there was no effect modification so the conditional and marginal risk ratios were equal. The effect of vaccination on infection with SARS-CoV-2 (0.84) was lower than for hospitalization with COVID-19 (0.96). In terms of estimation, the logistic regression performed well although standard confidence intervals undercovered the true conditional causal effect. IPTW performed better with higher coverage of the marginal causal effect when the propensity score was estimated using the controls. The IPTW with propensity score estimated using all of the data was highly biased in all scenarios.

In the second scenario, effect modification resulted in subpopulation vaccine effectiveness that differed by value of C: vaccine effectiveness was 0.98 in the first three quartiles of C, 0.70 in the fourth quartile, and only 0.56 in the 95th percentile. This is akin to vaccine effectiveness dropping off substantially only for the elderly. The overall marginal and conditional vaccine effectiveness were slightly different (0.75 and 0.77, respectively). Logistic regression incorrectly averaged over subgroup effects, resulting in a large overestimate of vaccine effectiveness. When we stratified the logistic regression on subjects with C values in the fourth quartile, we obtained a mean estimate of 0.84, which was also biased for the vaccine effectiveness in that quartile (0.70). IPTW with the control-estimated propensity score performed very well for the estimation of the marginal causal effect. Logistic regression had a lower variance than IPTW because the former ignores the variability in vaccine effectiveness across members of the population.

In the third scenario, we calculated the true conditional and marginal risk ratios. Because interference was present, these no longer have a causal interpretation. We also computed the direct effect of vaccination $1-{\psi }_{cRR\mathrm{,}f}$, defined as the risk ratio of hospitalization with COVID-19 contrasting vaccination status and fixing the proportion vaccinated in a block (f). We give this estimand for three values of $f=\mathrm{0.75,}\mathrm{0.5,}0.25$. The impact of vaccination was the highest (0.86) when 75% of a block was vaccinated. The impact was lower when half or a quarter of the block was vaccinated, with direct effects of 0.80, and 0.76, respectively. In this scenario, logistic regression slightly overestimated the conditional association between the vaccine and hospitalization with COVID-19. IPTW accurately estimated the marginal association. Both estimators gave misleading estimates if they were to be interpreted in a population with lower vaccination coverage.

Under partial interference by block, one may stratify estimation by block to directly estimate the causal parameters ${\psi }_{cRR\mathrm{,}{f}_m}$for the block-specific vaccination prevalence value f_m. Table 3 compares the results of pooled and block-stratified estimation for a single simulated dataset, representing a census of the hospitalized patients (note that in the previous analysis, we took a random subset of patients from each block to represent participants in the study). The analyses of the pooled data had a large sample size of 13,731, and both estimates produced little error relative to the true risk ratios. However, the stratified estimators had smaller sample sizes (particularly for controls) leading to much greater error in the estimates, in particular for the studies with lower vaccination prevalence.

TABLE 3.

Single Simulated Dataset From Scenario 3: Block-Stratified and Pooled Estimation of Vaccine Effectiveness With Logistic Regression and IPTW

Block	Population Size	Sample Size (n. Controls)	Population Vaccination Prevalence, f*	True Values 1 − ψcRR, f*	Logistic Regression, Est (95% CI)	IPTW, Controls, Est (95% CI)
2	250,000	1,832 (31)	0.24	0.76	0.44 (−0.70, 0.77)	0.0 (−2.2, 0.65)
3	250,000	895 (26)	0.32	0.77	0.73 (0.35, 0.88)	0.64 (0.17, 0.84)
1	250,000	523 (48)	0.37	0.77	0.69 (0.38, 0.84)	0.66 (0.34, 0.82)
5	500,000	1,665 (73)	0.58	0.82	0.86 (0.77, 0.92)	0.86 (0.75, 0.92)
4	250,000	346 (38)	0.69	0.84	0.89 (0.77, 0.96)	0.92 (0.81, 0.96)
8	500,000	1,578 (78)	0.75	0.86	0.84 (0.73, 0.91)	0.79 (0.64, 0.88)
10	1,000,000	2,816 (134)	0.77	0.87	0.93 (0.88, 0.96)	0.90 (0.84, 0.94)
9	1,000,000	2,379 (147)	0.78	0.87	0.89 (0.83, 0.93)	0.85 (0.76, 0.90)
6	500,000	1,121 (78)	0.79	0.87	0.88 (0.78, 0.93)	0.84 (0.71, 0.91)
7	500,000	576 (77)	0.83	0.88	0.91 (0.82, 0.96)	0.87 (0.74, 0.94)
Analysis of pooled data, n = 13,731:			Adjusting for X		0.87 (0.84, 0.89)	0.85 (0.81, 0.87)
			Adjusting for block		0.86 (0.84, 0.87)	0.83 (0.80, 0.86)

This analysis was conducted on a single simulated dataset representing a census of hospitalized patients, allowing for a larger sample size in each block. IPTW was implemented with weighted logistic regression where only controls were used to fit the propensity score model. The stratified analyses used 10% weight truncation, but this had negligible impact on the estimates of all blocks except for block 2 where the estimation was unstable due to only having five vaccinated controls.

DISCUSSION

The test-negative design is being increasingly used to study postlicensure vaccine effectiveness for COVID-19.⁴ In this article, we placed the design in a causal inference context by presenting a nonparametric model related to vaccination for SARS-CoV-2, infection, disease symptoms, and reception of care, such as hospitalization. Under this model, we derived the identifiable conditional risk ratio estimand under the statistical sampling framework that differentiated between inclusion criteria (symptoms and accessing care) and measured data (covariates, vaccination status, and infection status). We demonstrated that an IPTW estimator for the risk ratio can be implemented when the propensity score model is fit using only control data. This approach has also been used for case–control studies^23,24 where the validity of the propensity score estimation relies instead on a rare disease assumption. In the test-negative design, neither estimator requires a rare disease assumption. However, both estimators require that vaccination for COVID-19 has no impact on other diseases with similar symptoms.

The major benefit of IPTW is that, unlike logistic regression, it estimates marginal effects even when effect modification is present. While one may present stratified estimates of vaccine effectiveness for different age subgroups, for instance, effect modification is likely to be high-dimensional, also depending on comorbidities and immunosuppressant drug usage. Thus there is likely effect modification occurring even within age groups, leading to potential bias in the logistic regression estimator. IPTW avoids the issue of needing to stratify on a subset where there is no residual effect modification. This also avoids having only small sample sizes to estimate the effects of interest.

In vaccine studies, including randomized controlled trials, interference typically complicates the definition and estimation of causal estimands.¹⁷ In our discussion on interference, we made the strong assumption that one person’s outcome (infection, severe symptoms, and hospitalization) can only be affected by their block’s vaccination coverage, and not the vaccination statuses of the individuals inside or outside of the block. A block may be approximately defined by the geographic region of the medical facility where the patient was admitted.⁵ If all confounders of individual vaccination and block vaccination coverage with the individual’s outcome are measured, then the conditional risk ratio is a ratio of weighted sums of block-specific causal risks. This means that we are contrasting averages of block-vaccination-rate-specific risks under (counterfactual) assignment of vaccination status to the individual. In the simulation study, we presented a scenario where the conditional and marginal risk ratios represented the impact of vaccination only under high vaccination coverage. If we were to interpret either risk ratio as the impact of vaccination, we would be overestimating the vaccination effectiveness except when vaccination coverage is high. Note that this is one specific scenario but it illustrates that average associations over populations with heterogeneous vaccination coverage can be misleading and not represent a causal effect. We also showed that when presenting results by block,⁵ we target a causally interpretable block-stratified parameter, but risk greater estimation error due to smaller sample sizes.

Similarly, we could repeat this exercise by considering interference and effect-modification by local infection rates. The noted challenges point to the importance of stratifying the analysis by block when sample sizes are sufficiently large and developing valid pooled estimators under various types of interference for this design.

Although the test-negative design is not new, emerging evidence of COVID-19 vaccination effectiveness has put it in the international spotlight. Careful study of this design and the interpretation of estimates obtained under this design are ongoing research priorities.

APPENDIX: PROOF OF CONSISTENCY FOR THE IPTW ESTIMATOR

Claim: Let ${\mathbb{E}}_{TND}$ represent an expectation under test-negative design biased sampling and $\mathbb{E}$ be an expectation under unbiased sampling. Let $Y=\mathbb{I}(I=\mathrm{2,}W=\mathrm{1,}H=1)$, the outcome of interest. Let $q_0=Pr(I\ne \mathrm{0,}W=\mathrm{1,}H=1)$ be the marginal probability of having the inclusion criteria for the study. Then, we have that

$${\mathbb{E}}_{\text{TND}}\left\{\frac{Y\mathbb{I}(V=v)q_0}{Pr(V=v|C=c)}\right\}=\mathbb{E}\{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|V=v\mathrm{,}C=c)\}\mathrm{.}$$

Proof. Let ${\text{pr}}_C(c)$ and $p_C(c|I\ne \mathrm{0,}W=\mathrm{1,}H=1)$ be the probability density functions of the covariates C under simple random sampling and test-negative design sampling, respectively. Also let $S=\mathbb{I}(I\ne \mathrm{0,}W=\mathrm{1,}H=1)$ indicate the presence of inclusion criteria for the test-negative design.

$${\mathbb{E}}_{\text{TND}}\left\{\frac{Y\mathbb{I}(V=v)q_0}{Pr(V=v|C=c)}\right\}$$

$$={\displaystyle {\int }_c}\frac{Y\mathbb{I}(V=v)q_0}{Pr(V=v|C=c)}{p}_C(c|S=1)dc$$

$$={\displaystyle {\int }_c}\frac{Pr(Y=\mathrm{1,}V=v|S=\mathrm{1,}C=c)}{Pr(V=v|C=c)}Pr(S=1|C=c)p_C(c)dc$$

$$={\displaystyle {\int }_c}\frac{Pr(Y=\mathrm{1,}V=v\mathrm{,}S=1|C=c)}{Pr(V=v|C=c)}{p}_C(c)dc$$

$$={\displaystyle {\int }_c}Pr(Y=\mathrm{1,}S=1|V=v\mathrm{,}C=c)p_C(c)dc$$

$$={\displaystyle {\int }_c}Pr(Y=1|V=v\mathrm{,}C=c)p_C(c)dc$$

$$=\mathbb{E}\{Pr(I=\mathrm{2,}W=\mathrm{1,}H=1|V=v\mathrm{,}C=c)\}\mathrm{.}$$

Thus, if we weight observations by the inverse of $Pr(V=v|C=c)$ (which, as we recall, must be modeled using only the control data), we can recover the marginal mean of the outcome under a vaccination status v up to the constant q₀. Therefore, one can only estimate the marginal probability of the outcome (i.e., the numerator of Equation 5) with knowledge of q₀. But by taking a ratio, q₀ cancels out, so it is not needed for estimating the risk ratio.