Abstract
Introduction
Clinical trials for sporadic Alzheimer's disease generally use mixed models for repeated measures (MMRM) or, to a lesser degree, constrained longitudinal data analysis models (cLDA) as the analysis model with time since baseline as a categorical variable. Inferences using MMRM/cLDA focus on the between‐group contrast at the pre‐determined, end‐of‐study assessments, thus are less efficient (eg, less power).
Methods
The proportional cLDA (PcLDA) and proportional MMRM (pMMRM) with time as a categorical variable are proposed to use all the post‐baseline data without the linearity assumption on disease progression.
Results
Compared with the traditional cLDA/MMRM models, PcLDA or pMMRM lead to greater gain in power (up to 20% to 30%) while maintaining type I error control.
Discussion
The PcLDA framework offers a variety of possibilities to model longitudinal data such as proportional MMRM (pMMRM) and two‐part pMMRM which can model heterogeneous cohorts more efficiently and model co‐primary endpoints simultaneously.
Keywords: Alzheimer's disease, proportional constrained longitudinal data analysis model (PcLDA), MMRM, proportional MMRM (pMMRM), proportional treatment effect
1. INTRODUCTION
Currently, phase 2/3 efficacy clinical trials in sporadic Alzheimer's disease (AD) generally use the mixed model for repeated measures (MMRM) or, to a lesser degree, the constrained longitudinal data analysis model (cLDA) as the primary analysis model 1 , 2 , 3 , 4 , 5 , 6 , 7 with time since baseline as a categorical variable. The MMRM models the change from baseline with the baseline value as a covariate, whereas cLDA includes the baseline value in the response vector together with the post baseline values and imposes a constraint of a common baseline mean across treatment groups as a result of randomization. 5 , 6 , 7 , 8 The MMRM/cLDA model concept is well accepted by regulatory agencies such as the Food and Drug Administration (FDA) and the European Medicines Agency because of its minimal restrictions on the disease progression during the follow‐up (cLDA to a lesser degree due to its constraint on the baseline mean). However, the tradeoff is that MMRM/cLDA directly uses only the baseline and the end‐of‐study assessments for the estimate of the treatment effect, thus intermediate time points and participants who drop out early contribute less to the treatment effect comparison. Furthermore, MMRM/cLDA requires the same exposure duration for all participants. That means early enrollees need to stop the exposure once reaching the pre‐determined treatment duration while late enrollees are continuing to complete the treatment. Thus, the extended follow‐up for early enrollees does not directly contribute to power. To overcome these inefficiencies, the linear mixed effects (LME) model with random effects (eg, random intercept and random slope) 9 with first‐order time as a continuous variable, which estimates common slopes from baseline to end of study for the treatment group and for the placebo group, respectively, has gained interest. 10 LME provides greater power than MMRM/cLDA given the same sample size. 10 , 11 However, compared with MMRM/cLDA, LME has stronger restrictions; notably, it requires the disease progression during the follow‐up to be linear, which is not likely as demonstrated by real trial data. 2 , 3 Other LME models with curvilinear trends, such as polynomial regression models, have not been used in any AD clinical trials as primary analysis models as the real data rarely meet the pre‐specified curvilinear trends. For these reasons, LME is not preferred by regulatory agencies over MMRM/cLDA.
To overcome the inefficiency of MMRM/cLDA and the linear/curvilinear restriction of LME, we propose the proportional cLDA (PcLDA) (Table 1) or proportional MMRM (supplemental Section 4 in the Supporting Information). Conceptually, PcLDA is similar to the Cox proportional hazards model which estimates the hazard ratio of two groups as a constant over time and thus assumes a proportional treatment effect over time, 12 that is, PcLDA models the treatment effect as a single proportional difference at each post‐baseline visit (Section 2). PcLDA uses time as a categorical variable like MMRM/cLDA and thus releases the linearity/curvilinear assumption of LME. On the other hand, PcLDA directly uses all assessments (baseline, intermediate, end‐of‐study, and extended follow‐up) to estimate the treatment effects, thus naturally yielding higher power than MMRM/cLDA. Furthermore, PcLDA can also incorporate random effects like the LME model, which is able to yield individual‐level disease progression trajectories. When presenting a treatment effect, it is a common practice to convert the difference in the change from baseline between the treatment group and the placebo group to a percent treatment effect using the outputs from cLDA/MMRM. For example, it is widely reported that the FDA‐approved aducanumab demonstrated a 22% slowing of decline on the Clinical Dementia Rating Sum of Boxes in the EMERGE trial, 13 which was calculated as the mean difference (0.39) in the change between the two groups divided by the mean change from baseline in the placebo group (1.74). However, as pointed out by the FDA's review statistician, this percent treatment effect “doesn't represent the analysis scale or acknowledge the standard error of the percent reduction which is needed for proper context.” 14 The PcLDA model overcomes this issue by directly estimating an average percent treatment effect (ie, the proportion ) and its 95% confidence interval (CI) using data from all post‐baseline visits based on the maximum likelihood method. Overall, PcLDA offers a more delicate balance between model efficiency and the acceptability requirements of regulatory agencies than both the MMRM/cLDA and LME models.
TABLE 1.
Model assumptions for the three types of models
| Models | Linearity∼ | Time variable | Treatment effect | Extended follow‐up |
|---|---|---|---|---|
| cLDA/MMRM | No | Categorical | Non‐proportional | Not contribute to treatment effect estimation* |
| LME | Yes | Continuous | Proportional | Contribute to treatment effect estimation |
| PcLDA | No |
Continuous/ Categorical |
Proportional | Contribute to treatment effect estimation |
Abbreviations: cLDA, constrained longitudinal data analysis; MMRM, mixed model for repeated measures; LME, linear mixed effects with first‐order continuous time; PcLDA, proportional cLDA.
*cLDA/MMRM can allow the extended follow‐up, but the assessments in the extended follow‐up do not contribute directly to the treatment effect estimation.
∼Linearity: disease progression is linear during the follow‐up for LME with first‐order continuous time variable.
As it has been demonstrated, cLDA has equal or higher power than MMRM given the same sample size, 5 , 6 thus we choose to evaluate the behavior of PcLDA relative to cLDA with the comparison between PcLDA and MMRM in the appendix. The remainder of this paper is as follows. Section 2 presents the model formulation and its comparison with cLDA. Section 3 evaluates model behavior relative to cLDA through simulated hypothetical clinical trials. Section 4 contains the extension of the PcLDA model. Section 5 concludes with the discussion.
2. MATERIALS AND METHODS
2.1. Proportional cLDA without random effects (marginal model)
Let denote the longitudinal assessments for subject at time for group , , , with representing the baseline visit, and representing the placebo group and the treatment group, respectively, and let be the mean change from baseline at time for group . We define the proportional treatment effect (ie, a percent treatment effect relative to the mean change of the placebo group) as:
| (1) |
thus, . Because is assumed to be the same from visit to visit, thus the time index is not needed for . We assume that due to disease progression, the change from baseline in the placebo group is non‐zero and can be positive or negative. PcLDA can be written as:
| (2) |
where, is the baseline mean that is constrained to be the same across groups because of randomization; is the indicator function; the within‐subject error is assumed to follow the same multivariate normal distribution for both groups: , where is an unstructured variance‐covariance matrix and is the number of repeated measures for subject . A description of cLDA is presented in the corresponding supplemental section 2.1 for reference.
PcLDA assumes that the proportional treatment effect is the same at each post‐baseline visit , and the method to test this assumption is described in Section 2.3. When the assumption is not met, the model can be fit with a different proportion at each visit.
Without loss of generality, we assume that a positive change from baseline in the placebo group represents more severe disease progression. Under this assumption, indicates no treatment effect at all; indicates the treatment completely stops the disease progression; indicates the treatment speeds up the disease progression compared to placebo; indicates the treatment slows down the disease progression compared to placebo. The primary test is whether is significantly different from 0. The parameters in the marginal PcLDA model can be estimated using (restricted) maximum likelihood method. 9
2.2. Proportional cLDA with random effects
PcLDA can be adapted to include random effects (random intercept and random change) like the LME model. PcLDA models with random effects still use time as a categorical variable, thus do not restrict the mean trajectory during the follow‐up to be linear (first‐order continuous time) or curvilinear (polynomial continuous time) as required by LME. PcLDA with random effects can be presented as:
| (3) |
where , , , and have the same meaning as those in (2); is defined in the same way as in (1) with the same assumptions; are the random effects for the intercept and the change from baseline and are assumed to follow the same bivariate normal distribution for both groups: ; the within‐subject error is assumed to follow the same normal distribution for both groups . Like in the LME model, we also consider a linear random change effect. A description of LME (first‐order time) is presented in the corresponding supplemental section 2.2 for reference.
Parameters in this model can be estimated using the (restricted) maximum likelihood method, the first order approximation method, 15 or integration of the likelihood over the random effects using adaptive and/or non‐adaptive Gauss‐Hermite quadrature method. 16
2.3. Test of the proportional treatment effect
The assumption of the proportional treatment effect can be tested using an approximate F statistic. The null hypothesis is:
,
and the alternative hypothesis is:
, for some ,
where, is the proportional treatment effect at post‐baseline visit , is the total number of post‐baseline visits. Let be the estimated treatment effect at each post‐baseline visit, be the design matrix for testing the null hypothesis with each row representing the comparison between two and the null hypothesis can be re‐written as , be an estimate of the generalized inverse of the covariance matrix of the fixed effects, and , then the test statistic can be constructed in a standard way 9 as follows:
.
The test statistic can be approximated by an distribution. The numerator degrees of freedom in the approximation are , and the denominator degrees of freedom can be estimated using methods such as the containment method, the residual method, the Satterthwaite method, and the Kenward‐Roger method. If the null hypothesis that all the proportions are equal is rejected, post hoc pairwise tests using the test statistic can be composed similarly to determine the pairs that are significantly different.
2.4. Computational procedures
The marginal PcLDA and the PcLDA with random effects were implemented using standard SAS computational procedures nlinmix macro and nlmixed, respectively (details are given in the corresponding supplemental materials section 2.4). All analyses were conducted using SAS 9.4 (SAS Institute Inc., Cary, NC).
3. RESULTS
The model behavior of PcLDA was compared to cLDA using simulations, and the simulation parameters were selected for easy interpretation (eg, baseline mean is 1) or based on clinical trial practice (eg, 20% minimum treatment effect, sample size ranging from 100 to 400/arm). Although the difference in power between PcLDA and cLDA may vary when different simulation parameters are used, the overall conclusion that PcLDA has power advantage over cLDA remains unchanged.
3.1. Power comparison between marginal PcLDA and cLDA
Due to the word limit, simulation details are presented in the corresponding supplemental Section 3.1.
3.1.1. Simulation results
The type I error in all cases is within 2% of the nominal 5% for all models (Supplemental Figure 1), similar to the reported type I error rate for mixed effects models based on simulation. 10 , 17 The simulations showed that PcLDA has greater power than cLDA with power gains as much as over 30% between a 4‐year cLDA and a 6‐year PcLDA at sample size of 200 (Figure 1). Specifically, for a 4‐year trial, PcLDA gained about 15% greater power than cLDA; the extra year‐5 data (50% of the non‐dropout subjects) led to another approximately 10% to 15% gain; and the extra year‐6 data (25% of the non‐dropout subjects) produced another 2% to 7% power gain (Figure 1). The difference in power remains similar even with a 10% annual dropout but decreased as the sample size increased (Figure 1). Table 2 presents the bias, mean square error (MSE), and the 95% coverage probability for the proportional treatment effect of 20%. Both the bias and the MSE were very small and the 95% coverage probability was within 2% of the nominal level. Similar results were observed with a 10% treatment effect (supplemental Figure 5).
FIGURE 1.
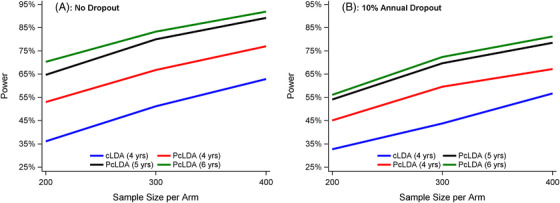
Power comparison by sample sizes and dropout rates for a 20% proportional treatment effect (A, no dropout; B, 10% annual dropout). Results are shown for the following simulations with constrained longitudinal analysis (CLDA) versus proportional cLDA (PcLDA): cLDA (4 years) = cLDA 4‐year trial model; PcLDA (4 years) = PcLDA 4‐year trial model; PcLDA (5 years) = PcLDA 4‐year trial model with 1‐year extended follow‐up for 50% of the remaining subjects; PcLDA (6 years) = PcLDA 4‐year trial model with 1‐year extended follow‐up for 50% of the remaining subjects and 2‐year extended follow‐up for 25% of the remaining subjects. Marginal PcLDA led to a power increase up to 34% over cLDA
TABLE 2.
Bias, MSE, and 95% coverage probability of the proportional treatment effect of 20% (4‐year trial only) for marginal PcLDA
| Sample Size/Arm | No Dropout | 10% Annual Dropout | ||||
|---|---|---|---|---|---|---|
| Bias | MSE | CP | Bias | MSE | CP | |
| 200 | −0.0044 | 0.0109 | 94.3% | −0.0055 | 0.0152 | 94.5% |
| 300 | −0.0030 | 0.0067 | 94.8% | −0.0017 | 0.0095 | 93.9% |
| 400 | −0.0027 | 0.0054 | 94.3% | −0.0012 | 0.0074 | 94.5% |
Bias is the mean of the difference between the estimated parameter and its true value (1000 replicates). Abbreviations: CP, coverage probability of the corresponding 95% confidence interval; MSE, mean of the squared error; PcLDA, proportional constrained longitudinal data analysis model.
3.2. Power comparison between PcLDA with random effects and cLDA
Due to the word limit, simulation details are presented in the corresponding supplemental Section 3.2.
3.2.1. Simulation results
Similarly, the type I error is typically within 2% of the nominal 5% for both models (Figure S2). The PcLDA model with random effects yielded larger power than the cLDA model, with power gains up to 20% between a 4‐year cLDA and a 6‐year PcLDA at a sample size of 100 (Figure 2). For example, without dropout and for a sample size of 100/arm, the cLDA yielded approximately 60% power, whereas a 4‐year PcLDA yielded 71%, a 5‐year PcLDA yielded 76%, and a 6‐year PcLDA yielded 80% (Figure 2). Table 3 presents the bias, MSE, and the 95% coverage probability for the proportional treatment effect of 20%. Both the bias and MSE were very small and the 95% coverage probability was within 2% of the nominal level. Similar results were observed with a 10% treatment effect (Figure S5).
FIGURE 2.
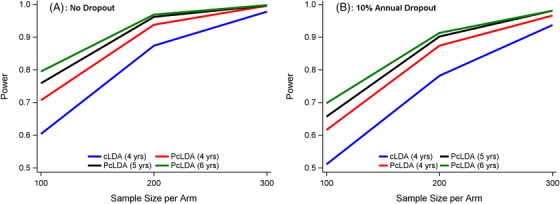
Power comparison by sample sizes and dropout rates for a 20% proportional treatment effect (A, no dropout; B, 10% annual dropout). Results are shown for the following simulations with constrained longitudinal analysis (CLDA) versus proportional cLDA (PcLDA) with random effects: cLDA (4 years) = cLDA 4‐year trial model; PcLDA (4 years) = PcLDA 4‐year trial model; PcLDA (5 years) = PcLDA 4‐year trial model with 1‐year extended follow‐up for 50% of the remaining subjects; PcLDA (6 years) = PcLDA 4‐year trial model with 1‐year extended follow‐up for 50% of the remaining subjects and 2‐year extended follow‐up for 25% of the remaining subjects. PcLDA with random effects led to a power increase up to 20% over cLDA
TABLE 3.
Bias, MSE, and 95% coverage probability of the proportional treatment effect of 20% (4‐year trial only) for PcLDA with random effects
| No Dropout | 10% Annual Dropout | |||||
|---|---|---|---|---|---|---|
| Sample Size/Arm | Bias | MSE | CP | Bias | MSE | CP |
| 100 | −0.0041 | 0.0058 | 95.6% | −0.0032 | 0.0084 | 93.8% |
| 200 | −0.0007 | 0.0028 | 95.2% | −0.0027 | 0.0037 | 94.9% |
| 300 | −0.0017 | 0.0018 | 96.8% | −0.0027 | 0.0025 | 94.4% |
Bias is the mean of the difference between the estimated parameter and its true value (1000 replicates). Abbreviations: CP, coverage probability of the corresponding 95% confidence interval; MSE; mean of the squared error; PcLDA, proportional constrained longitudinal data analysis model.
3.3. Violation of the proportional treatment effect
As pointed out earlier, when presenting a treatment effect, it is a common practice to convert the difference in the change from baseline between the treatment group and the placebo group to a percent treatment effect, to evaluate the model performance when the assumption of proportional treatment effect is violated, and the estimated percent treatment effect of PcLDA will be compared to that derived using the cLDA model output. Data were simulated with different proportional treatment effects at each visit (violation of the proportionality assumption) and were then analyzed using PcLDA with a single proportion to evaluate the robustness of the estimated proportional treatment effect. The simulation details are presented in the corresponding supplemental Section 3.3.
Table 4 shows the means and standard deviations of the estimated percent treatment effect and the power for both models. In all scenarios, PcLDA yielded a smaller estimated mean percent treatment effect than cLDA while maintaining power advantage. As expected, when the treatment effect is smaller at the later stage, the power advantage diminishes. Figure S3 demonstrates the true trajectories (mean change from baseline) versus the mean trajectories of the 1000 estimated clinical trials. Because PcLDA estimates a single proportional treatment effect over all the post‐baseline visits and leverages toward the effect at the end of the follow‐up due to the larger absolute change at the later visits, its estimated mean trajectories for both groups fall within the true trajectories when the treatment effect decreases in the late visits (eg, 30% vs 20%, 40% vs 20%), leading to a smaller estimated mean percent treatment effect than the treatment effect at the late visits (eg, 20%).
TABLE 4.
Percent treatment effect and power comparison between PcLDA and cLDA
| (30%, 30%, 20%, 20%)a | (20%, 20%, 30%, 30%) | (40%, 40%, 20%, 20%) | (20%, 20%, 40%, 40%) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean (SD)a | Power | Mean (SD) | Power | Mean (SD) | Power | Mean (SD) | Power | |
| PcLDA | 18.2% (12.2%) | 38.9% | 28.3% (11.4%) | 71.0% | 15.5% (13.1%) | 33.6% | 34.5% (12.7%) | 82.8% |
| cLDA∼ | 19.1% (12.8%) | 30.6% | 29.5% (11.9%) | 59.7% | 19.2% (12.6%) | 30.6% | 39.5% (12.1%) | 82.4% |
Abbreviations: cLDA, constrained longitudinal data analysis model; PcLDA, proportional constrained longitudinal data analysis model.
aTreatment effect at each post‐baseline visit, for example, 30% means the treatment group has 30% less decline at the first post‐baseline visit than the placebo group.
bMean (SD) of percent treatment effect based on 1000 simulations with the sample size 200/arm.
cPercent treatment effect is calculated as the mean difference in change at the last‐study visit between the treatment group and the placebo group divided by the mean placebo change at the last‐study visit.
3.4. Application to real AD trial data
We applied the marginal PcLDA model to the data from an AD clinical trial. 18 The data were included in a meta‐database of clinical trials and observational studies, whose details have been reported elsewhere. 19 Because practice effects can affect cognitive tests for more than 6 months, 20 , 21 the proportional treatment effect was modelled starting from year‐1 assessment only, and the mean change over every 6 months was estimated. The 11‐item ADAS‐Cog was the cognitive test used in this analysis. The ADAS‐Cog is a brief cognitive test scored as a composite from 0 to 70 errors with higher scores indicating worse impairment. 22 The model output for cLDA and PcLDA are presented in Table S1. Overall, the estimated mean trajectories are almost identical between the two models. Compared to the placebo group, the estimated proportional treatment effect is −11.5% (95% CI [−40.5%, 17.6%]), indicating the treatment group progressed 11.5% faster than placebo during the follow‐up. From cLDA, the estimated mean difference (treatment minus placebo) in change from baseline at year 2 is 1.50 and the estimated mean change from baseline to year 2 in the placebo group is 13.6, leading to 11.0% (ie, 1.5/13.6) faster progression in the treatment group. When comparing the treatment group and the placebo group, although both models failed to reach significance at type I error level 0.05, PcLDA yielded a smaller P‐value (.44) due to the use of data from multiple visits compared to cLDA (P‐value of .51). Given that the overall proportional treatment effect is not significant, not surprisingly, the testing of the proportionality assumption indicated the treatment effect was not statistically different from visit to visit.
4. OTHER VARIATIONS OF THE PROPORTIONAL LONGITUDINAL DATA ANALYSIS MODELS
The concept of proportionality offers a variety of flexibilities to adapt the traditional longitudinal data analysis models. Some examples of the marginal models are presented in the corresponding supplemental Section 4. Models with random effects can be described similarly.
5. DISCUSSION
In this paper, we proposed the PcLDA and the pMMRM to estimate the average proportional (ie, the percent) treatment effect during the follow‐up using the maximum likelihood method. The model is inspired by the well‐established Cox proportional hazards model, and thus is easy to interpret and conceptualize. Through simulated hypothetical clinical trials, we demonstrated that PcLDA yields accurate estimations of the treatment effect, controls type I error, and leads to large increases in power compared with cLDA. Type I error fluctuated within 2% of the nominal level, which is in the range of previous studies. 10 , 17 Compared to cLDA, simulations showed that PcLDA can lead to power increases ranging from over 5% to over 30%, depending on the sample size and the extended follow‐up. Because we did not assume linearity, we did not directly compare the power between PcLDA and LME. PcLDA demonstrated similar power advantage over MMRM (Figure S4). When the baseline mean is not constrained to be the same across groups because of randomization, a non‐constrained proportional longitudinal data analysis (PLDA) model can be used, and it demonstrated similar power advantage over a non‐constrained LDA (supplemental section 2.4.2 and Figure S6).
The power increase can be attributed to the use of the proportional treatment effect which allows all the assessments to directly contribute to the estimate of the treatment effect. Because of the proportional treatment effect, PcLDA can model participants with different durations of follow‐up, thus allows early enrollees to contribute beyond the pre‐determined duration while waiting for the late enrollees to complete the trial. This is relevant as the most valuable information for neurodegenerative disease such as AD is from those participants with the longest exposure, 23 and the financial cost for extending follow‐up is less than the recruitment of new participants. 24 While using data from the extended follow‐up can be appealing, the dropout patterns and dropout reasons in the extended follow‐up should be examined carefully in both the treatment and the placebo groups. If data are not missing at random, sensitivity analyses such as only using data before the extended follow‐up should be conducted to evaluate a treatment effect less affected by the biased dropout.
The proportional treatment effect assumption can be tested using the test proposed in Section 2.3. If the proportions are not significantly different, PcLDA will estimate the average proportional treatment effect. If statistical tests following the procedure listed in Section 2.3 show that, for example, two different proportions appear to be more appropriate than one proportion, then PcLDA can be modified to incorporate two proportions; however, the more proportions used, the less power advantage PcLDA will have over cLDA. Theoretically, if a different proportion is used for each post‐baseline visit, then PcLDA would have minimum advantage over cLDA as the efficacy inference for both models will rely on the end‐of‐study comparison. Our simulations also demonstrated when the proportionality assumption is moderately violated, PcLDA still provides a conservative percent treatment effect estimation compared to cLDA. All things considered, it is recommended to include cLDA/MMRM as sensitivity analysis models. An effective drug should manifest its treatment effect in all models although not all of them will reach statistical significance.
Our study has some limitations. First, PcLDA assumes a proportional treatment effect over time which can be relaxed by increasing the number of proportional parameters. However, this assumption is not unique to PcLDA, as the Cox proportional hazards model employed this assumption as well. Additionally, the change over time in recently published AD clinical trials indicated approximately proportional treatment effects from baseline to the end of study. 2 , 4 , 25 , 26 Some clinical trial data showed that potential practice effect led to a bump on the first post‐baseline visit. 3 , 27 There are several ways to overcome this limitation. One is to simply use two proportions. The first one will take care of the “bump” and the second one will demonstrate the treatment effects. Another possibility is to model the treatment effect from the second post‐baseline visit or from a certain post‐baseline time point as demonstrated in the real data example. However, under these circumstances, an algorithm must be pre‐determined so that the primary analysis will not become post hoc and rely on any information obtained by checking the data. A second limitation is that if a drug has only a symptomatic treatment effect, meaning the treatment effect appears early and vanishes at later time points, the trial duration must be calculated such that the assumption of proportional treatment effect can be tested (as presented in Section 2.3). If the trial duration is too short, the test may fail to detect a significant difference in the proportions and thus falsely conclude the drug is equally effective during both the early stage and the late stage. The average duration for clinical trial is 34.6 weeks for symptomatic treatments and 62.1 weeks for disease‐modifying treatments, 28 and thus we recommend researchers to design the duration in reference to these numbers. Additionally, PcLDA/pMMRM models also require the change of the placebo group to be non‐zero, and for clinical trials without any change over time, the model may become problematic. Therefore, it is critical to choose the outcomes and the visit duration (eg, 6 months or longer) so that the change of the placebo group is non‐zero. Furthermore, when planning a trial, the number of post‐baseline visits which meet the proportionality assumption cannot be easily determined a priori and can only be tested after the trial completion. Since the statistical test for the primary endpoint has to be stated a priori in the protocol, this approach may be impractical for planning a clinical trial without appropriate pilot data. With such pilot data it is a novel way to improve the assessment of the effectiveness of a treatment.
In summary, we propose the proportional mixed models that (1) estimate the proportional/percent treatment effect and its confidence interval directly; (2) combine the merits of the traditional MMRM/cLDA and LME models, (3) lead to large increases in power, and (4) can be easily implemented with widely used SAS procedures. Application of PcLDA in AD clinical trials may facilitate the development of effective drugs by reducing the sample size, shortening the trial duration, and maximizing the use of participants by allowing extended and unequal follow‐up for each participant.
CONFLICT OF INTEREST
None
HUMAN SUBJECT INFORMED CONSENT
Not Necessary. All data used are de‐identified data, which are available to public.
Supporting information
Supporting Information
ACKNOWLEDGMENT
This work was supported by NIH under grant U01AG042791, NIH under grant U01AG042791‐S1, NIH under grant R01AG046179, NIH under grant number R01/R56 AG053267.
Wang G, Liu L, Li Y, et al. Proportional constrained longitudinal data analysis models for clinical trials in sporadic Alzheimer's disease. Alzheimer's Dement. 2022;8:e12286. 10.1002/trc2.12286
REFERENCES
- 1. Dysken MW, Sano M, Asthana S, et al. Effect of vitamin E and memantine on functional decline in Alzheimers disease: the TEAM‐AD VA cooperative randomized trial. JAMA. 2014;311: 33‐44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Doody RS, Thomas RG, Farlow M, et al. Phase 3 trials of solanezumab for mild‐to‐moderate Alzheimer's disease. N Engl J Med. 2014;370:311‐321. [DOI] [PubMed] [Google Scholar]
- 3. Honig LS, Vellas B, Woodward M, et al. Trial of solanezumab for mild dementia due to Alzheimer's disease. N Engl J Med. 2018;378:321‐330. [DOI] [PubMed] [Google Scholar]
- 4. Howard R, McShane R, Lindesay J, et al. Donepezil and memantine for moderate‐to‐severe Alzheimer's disease. N Engl J Med. 2012;366:893‐903. [DOI] [PubMed] [Google Scholar]
- 5. Lu K. On efficiency of constrained longitudinal data analysis versus longitudinal analysis of covariance. Biometrics. 2010;66:891‐896. [DOI] [PubMed] [Google Scholar]
- 6. Liu GF, Lu K, Mogg R, Mallick M, Mehrotra DV. Should baseline be a covariate or dependent variable in analyses of change from baseline in clinical trials? Stat Med. 2009;28:2509‐2530. [DOI] [PubMed] [Google Scholar]
- 7. Liang KY and Zeger SL. Longitudinal data analysis of continuous and discrete responses for pre‐post designs. Sankhyā: Indian J Stat, Ser B. 2000:62;134‐148. [Google Scholar]
- 8. Mallinckrodt CH, Clark WS, David SR. Accounting for dropout bias using mixed‐effects models. J Biopharm Stat. 2001;11:9‐21. [DOI] [PubMed] [Google Scholar]
- 9. Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons, 2012. [Google Scholar]
- 10. Chen YF, Ni X, Fleisher AS, Zhou W, Aisen P, Mohs R. A simulation study comparing slope model with mixed‐model repeated measure to assess cognitive data in clinical trials of Alzheimer's disease. Alzheimers Dement (N Y). 2018;4:46‐53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Delrieu J, Payoux P, Carrié I, et al. Multidomain intervention and/or omega‐3 in nondemented elderly subjects according to amyloid status. Alzheimer's Dement. 2019;15:1392‐1401. [DOI] [PubMed] [Google Scholar]
- 12. Allison PD. Survival Analysis Using SAS: A Practical Guide. 2nd ed. SAS Institute; 2010. [Google Scholar]
- 13. Cummings J, Aisen P, Lemere C, Atri A, Sabbagh M, Salloway S. Aducanumab produced a clinically meaningful benefit in association with amyloid lowering. Alzheimers Res Ther. 2021;13:98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. FDA Statistical Review , Center for Drug Evaluation and Research. Application Number: 761178orig1s000. Statistical Review. U.S. Food and Drug Administration. https://www.accessdata.fda.gov/drugsatfda_docs/nda/2021/761178Orig1s000StatR_Redacted.pdf [Google Scholar]
- 15. Beal S, Sheiner L. Heteroscedastic nonlinear regression. Technometrics. 1988;30:327‐338. [Google Scholar]
- 16. Abramowitz M, Stegun IA. Handbook of mathematical functions: with formulas, graphs, and mathematical tables. Courier Corp. 1965. [Google Scholar]
- 17. Mallinckrodt CH, WS Clark, David SR. Type I error rates from mixed effects model repeated measures versus fixed effects ANOVA with missing values imputed via last observation carried forward. Drug Inf J. 2001;35:1215‐1225. [Google Scholar]
- 18. Sano M, Ernesto C, Thomas RG, et al. A controlled trial of selegiline, alpha‐tocopherol, or both as treatment for Alzheimer's disease. The Alzheimer's Disease Cooperative Study. N Engl J Med. 1997;336:1216‐1222. [DOI] [PubMed] [Google Scholar]
- 19. Kennedy RE, Cutter GR, Schneider LS. Effect of APOE genotype status on targeted clinical trials outcomes and efficiency in dementia and mild cognitive impairment resulting from Alzheimer's disease. Alzheimer's Dement. 2014;10:349‐359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Duff K, Lyketsos CG, Beglinger LJ, et al. Practice effects predict cognitive outcome in amnestic mild cognitive impairment. Am J Geriatr Psychiatry. 2011;19:932‐939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Wang G, Kennedy RE, Goldberg TE, Fowler ME, Cutter GR, Schneider LS. Using practice effects for targeted trials or sub‐group analysis in Alzheimer's disease: how practice effects predict change over time. PLoS One. 2020;15:e0228064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Mohs RC, Knopman D, Petersen RC, et al. Development of cognitive instruments for use in clinical trials of antidementia drugs: additions to the Alzheimer's Disease Assessment Scale that broaden its scope. The Alzheimer's Disease Cooperative Study. Alzheimer Dis Assoc Disord. 1997;11:13‐21. [PubMed] [Google Scholar]
- 23. Bateman RJ, Benzinger TL, Berry S, et al. The DIAN‐TU Next Generation Alzheimer's prevention trial: Adaptive design and disease progression model. Alzheimer's Dement. 2017;13:8‐19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Sheffet AJ, Flaxman L, Tom M, et al. Financial management of a large multisite randomized clinical trial. Int J Stroke. 2014;9:811‐813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Liu‐Seifert H, Andersen SW, Lipkovich I, Holdridge KC, Siemers E. A novel approach to delayed‐start analyses for demonstrating disease‐modifying effects in Alzheimer's disease. PLoS One. 2015;10:e0119632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Doody RS, Raman R, Farlow M, et al. A phase 3 trial of semagacestat for treatment of Alzheimer's disease. N Engl J Med. 2013;369:341‐350. [DOI] [PubMed] [Google Scholar]
- 27. Mulnard RA, Cotman CW, Kawas C, et al. Estrogen replacement therapy for treatment of mild to moderate Alzheimer disease: a randomized controlled trial. Alzheimer's Disease Cooperative Study. JAMA. 2000;283:1007‐1015. [DOI] [PubMed] [Google Scholar]
- 28. Cummings J, Lee G, Mortsdorf T, Ritter A, Zhong K. Alzheimer's disease drug development pipeline: 2017. Alzheimer's Dement (N Y). 2017;3:367‐384. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


