Teacher Mindsets Help Explain Where a Growth-Mindset Intervention Does and Doesn’t Work

Abstract

A growth-mindset intervention teaches the belief that intellectual abilities can be developed. Where does the intervention work best? Prior research examined school-level moderators using data from the National Study of Learning Mindsets (NSLM), which delivered a short growth-mindset intervention during the first year of high school. In the present research, we used data from the NSLM to examine moderation by teachers’ mindsets and answer a new question: Can students independently implement their growth mindsets in virtually any classroom culture, or must students’ growth mindsets be supported by their teacher’s own growth mindsets (i.e., the mindset-plus-supportive-context hypothesis)? The present analysis (9,167 student records matched with 223 math teachers) supported the latter hypothesis. This result stood up to potentially confounding teacher factors and to a conservative Bayesian analysis. Thus, sustaining growth-mindset effects may require contextual supports that allow the proffered beliefs to take root and flourish.

Psychological interventions change the ways that people make sense of their experiences and have led to improvement in a wide variety of domains of importance to society and to public policy (Harackiewicz & Priniski, 2018; Walton & Wilson, 2018). These interventions offer people new beliefs that encourage them to tackle rather than avoid a challenge or to persist rather than give up. To the extent that people put these beliefs into practice, the interventions can improve outcomes months or even years later (see Brady et al., 2020).

For instance, a growth-mindset-of-intelligence intervention conveys to students the malleability of intellectual abilities in response to hard work, effective strategies, and help from other people. Short (< 50 min), online growth-mindset interventions evaluated in randomized controlled trials—including two preregistered replications—have improved the academic outcomes of lower achieving high school students and first-year college students (e.g., Yeager et al., 2019; see Dweck & Yeager, 2019). These interventions are intended to dispel a fixed mindset, the idea that intellectual abilities cannot be changed, which has been associated with more “helpless” responses to setbacks and lower achievement around the world (Organisation for Economic Co-operation and Development, 2021).

Is successfully teaching students a growth mindset enough? A fundamental tension centers on the role of the educational context. Should psychological interventions be thought of as giving people adaptive beliefs that they can apply and reap the benefits from in almost any context, even ones that do not directly support the use of those mindsets? Or do interventions simply offer beliefs that must later be supported by the context if they are to bear fruit?

In a previous article (Yeager et al., 2019), we examined the role of a school factor, namely, the peer norms in a school, and found that the student growth-mindset intervention could not overcome the obstacle of a peer culture that did not share or support growth-mindset behaviors, such as challenge seeking. Here, we asked how the growth-mindset intervention might fare in classrooms led by teachers who endorse more of a fixed mindset (a less supportive context for students’ growth mindsets) as opposed to classrooms led by teachers who endorse more of a growth mindset (a more supportive context).

Why Might a Growth-Mindset Intervention Depend on Teacher Beliefs?

The present research tested the viability of the mindset-plus-supportive-context hypothesis. In this hypothesis, a teacher’s growth mindset acts as an “affordance” (Walton & Yeager, 2020; also see Gibson, 1977) that can draw out a student’s nascent growth mindset and make it tenable and actionable in the classroom. ¹ This hypothesis grows out of the recognition that as people try to implement a belief or behavior in a given context, they become aware of whether it is beneficial and legitimate in that context by attending cues in their environments.

According to the mindset-plus-supportive-context hypothesis, teachers with a growth mindset may convey how, in their class, mistakes are learning opportunities, not signs of low ability, and back up this view with assignments and evaluations that reward continual improvement (Canning et al., 2019; Muenks et al., 2020). This could encourage a student to continue acting on their growth mindsets. By contrast, teachers with more of a fixed mindset may implement practices that make a budding growth mindset inapplicable and locally invalid. For instance, they may convey that only some students have the talent to get an A or say that not everyone is a “math person” (Rattan et al., 2012; also see Muenks et al., 2020). These messages could make students think that their intelligence would be evaluated negatively if they had to work hard to understand the material or if they asked a question that revealed their confusion, discouraging students from acting out key growth-mindset behaviors. According to this hypothesis, the intervention is like planting a “seed,” but one that will not take root and flourish unless the “soil” is fertile (a classroom with growth-mindset affordances; see Walton & Yeager, 2020).

Statement of Relevance.

The growth mindset is the belief that intellectual abilities can be developed and are not fixed. Growth mindsets have received a great deal of attention in schools and among researchers, in part because of the potential for short, highly scalable interventions delivered over the Internet to benefit struggling students. In this article, we show that the positive effect of a short growth-mindset intervention on ninth-grade students’ math grades was concentrated among students whose teachers themselves had growth mindsets. Interestingly, we discovered that students who reported more of a fixed mindset at baseline benefited more from the intervention. This work shows that students at the intersection of vulnerability (a prior fixed mindset) and opportunity (a growth-mindset environment) are the most likely to benefit from growth-mindset interventions.

Despite its intuitive appeal, verification of the mindset-plus-supportive-context hypothesis was not a foregone conclusion. Perhaps students are more like independent agents who can achieve in any classroom context as long as they bring adaptive beliefs to the context and put forth effective effort. Therefore, teachers’ mindsets could be irrelevant to the effectiveness of the intervention. Research could even find stronger effects in a classroom led by teachers espousing more of a fixed mindset. This would imply that the intervention fortifies students to find ways to achieve (e.g., by being less daunted by difficult tasks, working harder, persisting longer) even in contexts that are not directly encouraging these behaviors (Canning et al., 2019; Leslie et al., 2015; Muenks et al., 2020). In this view, a student’s growth mindset could be like an asset that can compensate for something lacking in the environment. Because no study has examined classroom context moderators of the growth-mindset intervention, a direct test of the mindset-plus-supportive-context hypothesis was needed.

The Importance of Studying Treatment-Effect Heterogeneity

Our attention to teachers’ mindsets as a moderating agent continues an important development in psychological-intervention research: a focus on treatment-effect heterogeneity (Tipton et al., 2019). Psychologists have often viewed heterogeneous effects as a limitation, as meaning that the effects are unreliable, small, or applicable in too limited a way, and therefore not important (for a discussion, see Miller, 2019). ² But this view is shifting. First, heterogeneity is now seen as the way things in the world actually are (Bryan et al., 2021; Gelman & Loken, 2014). Nothing, and particularly no psychological phenomenon, works the same way for all people in all contexts. This fact has been pointed out for generations (Bronfenbrenner, 1977; Cronbach, 1957; Lewin, 1952), but it has only recently begun to be appreciated sufficiently. Second, systematically probing where an intervention does and does not work provides a unique opportunity to develop better theories and interventions (Bryan et al., 2021; McShane et al., 2019), including by revealing mechanisms through which the intervention operates.

The Present Research

This study analyzed data from the National Study of Learning Mindsets (NSLM; Yeager, 2019), which was an intervention experiment conducted with a representative U.S. sample of ninth-grade students (preregistration: https://osf.io/tn6g4/). The NSLM focused on the start of high school because this is when academic standards often rise and when students establish a trajectory of higher or lower academic achievement with lifelong consequences (Easton et al., 2017). The NSLM was designed primarily to study treatment-effect heterogeneity. The first article, as mentioned, focused on a school’s peer norms as a moderator (Yeager et al., 2019). The second planned analysis, presented here, focused on teacher factors. Teachers are important to students directly because they lead the classroom and establish its culture. For example, teachers create the norms for instruction, set the parameters for student participation, and control grading and assessments, thereby influencing student motivation and engagement (Jackson, 2018; Kraft, 2019).

The present focus on math grades (rather than overall grade point average [GPA], as in Yeager et al., 2019) is motivated by the fact that students tend to find math challenging and anxiety inducing (Hembree, 1990), and therefore, a growth mindset might help students confront those challenges productively. Further, our focus on math is relevant to policy. Success in ninth-grade math is a gateway to a lifetime of advanced education, profitable careers, and even longevity (Carroll et al., 2017).

In this study of heterogeneous effects, what kinds of effect sizes should be expected? Brief online growth-mindset interventions have tended to improve the grades of lower achieving high school students by about 0.10 grade points (or 0.11 SD; Yeager et al., 2016, 2019). This may seem small relative to benchmarks from laboratory research, but that is not an appropriate comparison for understanding intervention effects obtained in field settings (Kraft, 2020). An entire year of learning in ninth-grade math is worth 0.22 SD as assessed by achievement tests (Hill et al., 2008), and having a high-quality math teacher for a year during adolescence, compared with an average one, is worth 0.16 SD (Chetty et al., 2014). Expensive and comprehensive education reforms for adolescents show a median effect of 0.03 SD. The largest effects top out at around 0.20 SD, and effects this large represent striking outliers (Boulay et al., 2018). Thus, Kraft (2020) concluded that “effects of 0.15 or even 0.10 SD should be considered large and impressive” (p. 248), especially if the intervention is scalable, rigorously evaluated, and assessed in terms of consequential, official outcomes (e.g., grades).

Method

Data

Data came from the NSLM, which as noted was a randomized trial conducted with a nationally representative sample of ninth-grade students during the 2015–2016 school year (Yeager, 2019). The NSLM was approved by the institutional review boards at Stanford University, The University of Texas at Austin, and ICF International. The current analysis, which focused on math teachers, was central to the original design of the study, appeared in our grant proposals, and was referenced as the next analysis in our previous preregistered analysis plan (https://osf.io/afmb6/). The present study followed the Yeager et al. (2019) preregistered analysis plan for every step that could be repeated from the first article (e.g., data processing, stopping rule, covariates, and statistical model). Analysis steps unique to the present article are outlined in detail in the Supplemental Material available online and previewed below. There was no additional preregistration for the present article. Instead, we used a combination of a conservative Bayesian analysis and a series of robustness tests to guard against false positives and portray statistical uncertainty more accurately for analysis steps not specified in the preregistration. The two planned analyses (i.e., for the present article and Yeager et al., 2019) were conducted sequentially. The present study’s math-teacher variables were not merged with the student data until after the Yeager et al. (2019) analyses were completed.

The analytic sample contained students with a valid condition variable, a math grade, and their math teacher’s self-reported mindset (see Table S6 in the Supplemental Material). This sample included 9,167 records (8,775 unique students because some students had more than one math teacher) nested within 223 unique teachers. It composes 76% of the overall NSLM sample of students with a math grade. Students who are missing data could not be matched to a math teacher or their math teacher did not answer the mindset questions. Missing data did not differ by condition (see Table S7 in the Supplemental Material). We retained students who took two math courses with different teachers, each of whom completed the survey. Listwise deletion of them produced the same results (see Table 1). In terms of math level, 7% of records were from a math class at a level below algebra I, 70% were in algebra I, 19% were in geometry, and 3% were in algebra II or above. Students were 50% female and racially diverse (14% Black/African American, 22% Latinx, 6% Asian, 4% Native American or Middle Eastern, and 53% White), and 37% reported that their mother held a bachelor’s degree. Teachers’ characteristics were similar to population estimates: 58% were female, 86% were White non-Latinx, and 51% reported having earned a master’s degree; they had been teaching an average of 13.83 years (SD = 9.95).

Table 1.

Effect of Growth-Mindset Intervention on Math Grades in Ninth Grade Among Students With Math Teachers Holding a Fixed Versus Growth Mindset, Estimated in Linear Mixed-Effects Models

Model specification	Teachers who reported more of a fixed mindset	Teachers who reported more of a growth mindset	Student Intervention × Teacher Mindset (continuous) interaction
Primary model specification
Teacher mindset as moderator + potential teacher confounds (N = 9,167)	CATE = −.02 [−.074, .038], t(8723) = −0.63, p = .531	CATE = .11 [.046, .167], t(8723) = 3.46, p < .001	b = 0.09 [0.026, 0.150], t(8723) = 2.79, p = .005
Robustness test: accounting for school-level moderators from Yeager et al. (2019)
Plus school-level moderators (N = 9,167)	CATE = −.02 [−.075, .039], t(8722) = −0.61, p = .542	CATE = .10 [.045, .168], t(8722) = 3.37, p < .001	b = 0.09 [0.025, 0.151], t(8722) = 2.76, p = .006
Robustness tests: alternative subsamples a
Only students with only one math teacher (N = 8,383)	CATE = −.04 [−.108, .026], t(7953) = −1.20, p = .230	CATE = .11 [.040, .170], t(7953) = 3.18, p = .001	b = 0.09 [0.028, 0.159], t(7953) = 2.81, p = .005
Only previously lower achieving (i.e., below-median preintervention GPA) students b (N = 4,811)	CATE = .02 [−.050, .097], t(4402) = 0.63, p = .527	CATE = .13 [.067, .196], t(4402) = 4.01, p < .001	b = 0.09 [0.008, 0.165], t(4402) = 2.17, p = .030
Only students previously without straight As (N = 6,958)	CATE = −.01 [−.062, .041], t(6543) = −0.39, p = .696	CATE = .14 [.071, .203], t(6543) = 4.07, p < .001	b = 0.11 [0.040, 0.180], t(6543) = 3.10, p = .002

Note: The conditional average treatment effect (CATE), in grade point average (GPA) units (0–4.3), was estimated with the “margins” postestimation command in Stata/SE while holding potentially confounding moderators constant at their population means. All CATEs were estimated using teacher survey weights provided by ICF International to make the estimates generalizable to the nation as a whole. Teachers with more of a growth mindset in this analysis are those who reported a mindset at +1 SD for the continuous teacher-mindset measure, whereas teachers with more of a fixed mindset are at −1 SD. Numbers in brackets represent 95% confidence intervals. The regression model is specified in Equation 1. The focal treatment effects in the growth-mindset-supportive contexts are presented in boldface.

^aThese models included all teacher-level moderators. ^bThis was the preregistered subgroup in Yeager et al. (2019).

The previous, between-schools analysis (Yeager et al., 2019) examined grades in all subjects (math, science, English, and social studies). That analysis focused on the preregistered group of lower achieving students (whose pretreatment grades were below their school median) because it would be harder to detect improvement among students who were already higher achieving and because a previous preregistered study had shown the effects to be concentrated among the lower achievers (Yeager et al., 2016), which replicated our prior work (Paunesku et al., 2015). The current focus on math teachers and math grades, however, required us to include students at all achievement levels, a decision we made before seeing the results. This is because classrooms are smaller units than schools, so excluding half the sample would have left us with too few students in many teachers’ classrooms and could have made estimates too imprecise. In addition, math grades are on average substantially lower than in other subjects, probably because students in the United States are tracked into advanced math classes earlier than in other subject areas, which suggests that students overall tend to be in math classes that they find challenging. This means that fewer students were already earning As, and more students’ grades could improve in response to an intervention, particularly one focused on helping students engage with and learn from challenges (for supplementary analyses among low achievers, see Table 1).

Procedure

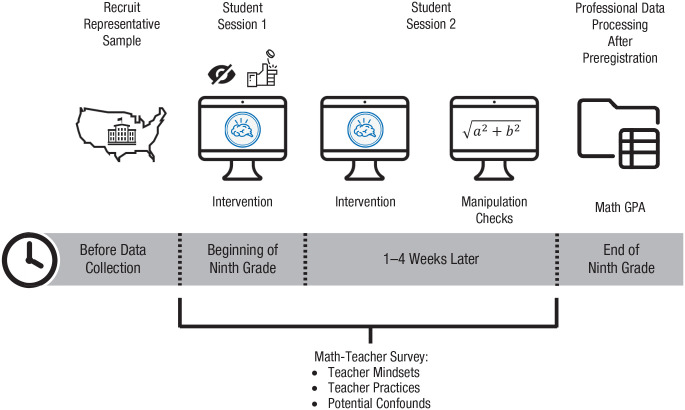
The NSLM implemented a number of procedures that allowed it to be informative with respect to contextual sources of intervention-effect heterogeneity (Tipton et al., 2019). First, each student was randomly assigned on an individual basis (i.e., within classroom and school) to a growth-mindset intervention or a control group, and math teachers (who were unaware of condition and study procedures) were surveyed to measure their mindsets. Thus, each teacher in the analytic sample had some students in the control group and some students in the treatment group. Consequently, we could estimate a treatment effect for each teacher and examine variation in effects across teachers. The study procedures appear in Figure 1 and are described in more detail next. Additional information is reported in the technical documentation available from the Inter-university Consortium for Political and Social Research (Yeager, 2019) and in the supplemental material in Yeager et al. (2019).

Fig. 1.

The student and teacher data-collection procedure in the National Study of Learning Mindsets. The sample was drawn from a nationally representative selection of public schools in the United States during the 2015–2016 academic year. Each student was randomly assigned to a growth-mindset intervention or a control group at the beginning of ninth grade. The non-seeing-eye icon represents masking of condition assignments from teachers, students, and researchers, and the coin-flip icon represents the moment of random assignment. About 85% of students took the first intervention session during the fall semester before the Thanksgiving break, as planned; the rest took it in January or early February to accommodate school schedules. Immediately after the second intervention session (generally 1 to 4 weeks after the first), students completed self-reports of mindsets (which served as a manipulation check). During the intervention, student’s teachers were surveyed to determine their mindsets, their practices, and any potential confounds. After the intervention was complete, data were processed according to a preregistered analysis plan (see https://osf.io/afmb6/) by MDRC, an independent research firm unaware of condition assignment or results. GPA = grade point average.

Data collection and processing

To reduce bias in the research process, we contracted three professional research firms to form the sample, administer the intervention, and collect all the data. ICF International selected and recruited a nationally representative sample of public schools in the United States during the 2015–2016 academic year. Students within those schools completed online surveys hosted by the firm Project for Education Research That Scales (PERTS), during which each student was randomly assigned to a growth-mindset intervention or a control group. The final student response rates were high (median student response rate across schools = 98%), and the recruited sample of schools closely matched the population of interest (Gopalan & Tipton, 2018).

Random assignment to condition was conducted by the survey software at the student level, with 50/50 probability, when students logged on to the survey for the first time. To prevent expectancy effects, we masked condition information from involved parties: Students did not know there were two conditions (i.e., a treatment and a control), and teachers in the school were not allowed to take the treatment, were not told the hypotheses of the study, and were not told that students were randomly assigned to alternative conditions. The treatment and control conditions looked remarkably similar to reduce the likelihood that teachers saw a difference. The intervention sessions generally occurred during electives (such as health or physical education), and schools were discouraged from conducting sessions in math classes. Math teachers were not used as proctors (usually, nonteaching staff coordinated data collection) to keep math teachers as unaware of the study as possible. The intervention involved two sessions of approximately 25 min each, generally 1 to 4 weeks apart, and lasted less than 50 min in total for nearly all students. Immediately after the second intervention session, students completed self-reports of mindsets (which served as a manipulation check).

Prior to data collection, schools provided the research firm with a list of all instructors who taught a math class that academic year with more than two ninth-grade students—the definition of a ninth-grade math teacher used here. This sample restriction was necessary because each teacher would need both treated and control students to provide a within-teachers treatment-effect estimate. All such teachers were invited to complete an approximately 1-hr online survey in return for a $40 incentive, and a large majority of teachers (86.8%) did so. This high response rate reduced the likelihood that biased nonresponse could have affected the distribution or validity of the teacher-mindset measure.

The independent research firm ICF International obtained student survey data from the technology vendor PERTS and administrative data (e.g., grades) from the schools and readied both for final processing. MDRC, another independent research firm, then processed these data following a preregistered analysis plan. They were all unaware of students’ condition assignments. Only then did our research team access the data and execute the planned analyses. (In parallel, MDRC developed an independent evaluation report that reproduced the overall intervention impacts and between-schools heterogeneity results; Zhu et al., 2019.)

Growth-mindset intervention

The growth-mindset intervention presented students with information about how the brain learns and develops using this metaphor: The brain is like a muscle that grows stronger (and smarter) when it learns from difficult challenges (Aronson et al., 2002). Then, the intervention unpacked the meaning of this metaphor for experiences in school, namely, that struggles in school are not signs that one lacks ability but instead that one is on the path to developing one’s abilities. Trusted sources—scientists, slightly older students, prominent individuals in society—provided and supported these ideas. Students were then asked to generate their own suggestions for putting a growth mindset into practice, for example, by persisting in the face of difficulty, seeking out more challenging work, asking teachers for appropriate help, and revising one’s learning strategies when needed, among others.

The intervention involved a number of other exercises designed to help students articulate the growth mindset, how they could use it in their lives, and how other students like them might use it. It was deliberately not a lecture or an “exhortation,” so as to avoid the impression that the intervention was telling young people what to think, because we know that for adolescents, an autonomy-threatening framing could be ineffective or even backfire. Instead, the intervention treated young people as collaborators in the improvement of the intervention, sharing their own unique expertise on what it is like to be a high school student. Additional detail on the intervention (and control) groups appears in the supplement to the Yeager et al. (2019) study (also see the Supplemental Material).

Control group

The control group was provided with interesting information about brain functioning and its relation to memory and learning, but the program did not mention the malleability of the brain or intellectual abilities. As in the growth-mindset condition, trusted sources—scientists, older peers, and prominent individuals in society—provided this information, and students were asked for their opinions and treated as having their own unique expertise. The graphic art, headlines, and overall visual layout were very similar to the treatment, to help students and teachers remain masked and to discourage comparison of materials. Because most students were taking biology at the time, the neuroscience taught in the control group would have added content above and beyond what students were learning in class and could even have increased interest in science and in school. Indeed, students have sometimes found the control material more interesting than the treatment material (Yeager et al., 2016). In sum, the active control condition was designed to provide a rather rigorous test of the effectiveness of the growth-mindset intervention.

Measures

Primary outcome: math grades

The primary dependent variable was students’ posttreatment grades in their math course, which were generally recorded 7 or 8 months after the intervention. All math grades were obtained from schools’ official records. Grades ranged from 0 (an F) to 4.3 (an A+). The mean math GPA was 2.44, leaving considerable room for improvement for many students.

Grades were the dependent variable of interest, not test scores, for three reasons. First, grades are typically better predictors of college enrollment and life-span outcomes than test scores, and the signaling power of grades is apparent even though schools and teachers could potentially inflate their grading scales (Pattison et al., 2013). Thus, grades are relevant for policy and for understanding trajectories of development. Second, grades represent the accumulation of many different assignments (homework, quizzes, tests) and therefore signal the kind of dedicated persistence that a growth mindset is designed to instill. Third, test scores were not an option in this study because ninth grade is not always a grade in which state achievement tests are administered, and most students did not have a math test score.

Primary moderator: teacher mindset

Math teachers rated two fixed-mindset statements: “People have a certain amount of intelligence and they really can’t do much to change it” and “Being a top math student requires a special talent that just can’t be taught” (1 = strongly agree, 6 = strongly disagree; M = 4.74, SD = 0.76). The first is a general fixed-mindset item intended to capture beliefs that might lead to mindset practices that are not specific to math, such as not allowing students to revise and resubmit their work or discouraging low achievers’ questions. The second item captures a belief that could lead to more math-specific mindset practices (see Leslie et al., 2015). The two items were correlated (r = .48, p < .001) and were averaged. We scored them so that higher values corresponded to more growth-mindset beliefs. We note that respondent time on this national math-teacher survey was limited to encourage participation and survey completion, so every construct, even teacher mindset, was limited to a small number of items.

The two mindset items used for the composite had never been administered to large samples of high school math teachers, so we assessed their concurrent validity by administering them to a large, pilot sample of high school teachers along with items that assessed teacher practices (N = 368 teachers). (The details of the sample and the exact item wordings are reported in the Supplemental Material.) In the pilot study, we found that teachers’ mindsets in fact predicted their endorsement of practices expected to follow from teachers’ mindsets on the basis of theory and past research (Canning et al., 2019; Haimovitz & Dweck, 2017; Leslie et al., 2015; Muenks et al., 2020). Specifically, teachers’ endorsement of a growth mindset was positively associated with learning-focused practices (r = .30, p < .001; e.g., saying to a hypothetical struggling student, “Let’s see what you don’t understand and I’ll explain it differently,” and not agreeing that “it slows my class down to encourage lower achievers to ask questions”). Further, teacher mindsets were negatively associated with ability-focused practices (emphasizing raw ability and implying that high effort was a negative sign about ability; r = .28, p < .001; e.g., comforting a hypothetical struggling student by saying, “Don’t worry, it’s okay to not be a math person,” a la Rattan et al., 2012, and praising a succeeding student by saying, “You’re lucky that you’re a math person,” or “It’s great that it’s so easy for you”). This is by no means an exhaustive list of potential mindset teacher practices, and this is certainly not the only way to measure teacher practices. But this validation study suggests that the teacher-mindset measure captures differences in teachers that extend to classroom practices—practices that the student growth-mindset treatment could overcome or that could afford the opportunity for the treatment to work.

Potential confounds for teacher mindsets

Because only the student mindset intervention, and not teachers’ mindsets, was randomly assigned, other characteristics of teachers could be correlated with their mindsets and with the magnitude of the intervention effect. For instance, perhaps teachers’ growth mindsets are simply a proxy for competent and fair instructional practices in general. To account for this possibility, we measured several potential confounds for teacher mindsets: a video-based assessment of pedagogical content knowledge, a fluid intelligence test for teachers, teachers’ masters-level preparation in education or math, and an assessment of implicit racial bias. We call these “potential” confounds because, during the design of the study, these were raised by at least one advisor to the study as something that could interfere with the interpretation of teacher-mindset effects (although, in the end, these factors showed rather weak associations with teacher mindsets; see Table S10 in the Supplemental Material). To this list of a priori, theoretically motivated teacher confounds, we added teacher race, gender, years teaching, and whether they had ever heard of a growth mindset. We describe the potential confounds in the Supplemental Material because their inclusion or exclusion does not change the sign, significance, or magnitude of the key moderation results. To these potential teacher-level moderators, we also added the preregistered school-level moderators (challenge-seeking norms among students and peers, school achievement level, and school racial/ethnic-minority percentage; see Yeager et al., 2019). Adding these school factors in interaction with the treatment did not change the teacher-mindset interaction (see Table 1), suggesting that these factors examined previously (Yeager et al., 2019) and the classroom-level factors examined here account for independent sources of moderation. Last, in a post hoc analysis, we examined three student perceptions of the classroom climate that could be confounded with teacher mindset: the level of cognitive challenge in the course, how interesting the course was, and how much students thought that the teacher was “good at teaching.” None of these factors were moderators and none altered the teacher-mindset interaction (see Table S11 in the Supplemental Material).

Manipulation check and moderator: students’ mindset beliefs

At pretest and again at immediate posttest, participants indicated their level of agreement with the three fixed-mindset statements used as a manipulation check by Yeager et al. (2019; e.g., “You have a certain amount of intelligence, and you really can’t do much to change it”; 1 = strongly agree, 6 = strongly disagree). We averaged responses (pretest: M = 2.95, SD = 1.14, α = .72; posttest: M = 2.70, SD = 1.19, α = .79); higher values corresponded to more of a fixed mindset. An extensive discussion of the validity of this three-item mindset measure and its relation to the growth-mindset “meaning system” appears in the work by Yeager and Dweck (2020). The scale at pretest was used in exploratory moderation analyses. The scale at posttest was used as a planned manipulation check.

Student-level covariates

Student-level control variables related to achievement included the pretreatment measure of low-achieving student status specified in the overall NSLM preregistered analysis plan (https://osf.io/afmb6/), which indicates that the student received an eighth-grade GPA below the median of other incoming ninth graders in the school; students’ expectations of how well they would perform in math class (“Thinking about your skills and the difficulty of your classes, how well do you think you’ll do in math in high school?”; 1 = extremely poorly, 7 = extremely well); students’ racial minority status; students’ gender; and whether their mothers had earned a bachelor’s degree or above. These covariates were specified in the NSLM preregistered analysis plan because each could be related to achievement, and so a chance imbalance with respect to any of these within a teacher’s classroom could bias treatment-effect estimates. Controlling for these factors reduces the influence of chance imbalances. Covariates were school-mean-centered.

Analysis plan

Estimands

The primary analysis focused on the sign and significance of the Student Growth Mindset Intervention × Teacher Growth Mindset interaction. If the interaction was positive and significant, it would be more consistent with the mindset-plus-supportive-context hypothesis.

The primary estimands of interest (i.e., values we wished to estimate) were the simple effects listed in Table 2. The models in Row 1 assume that teacher mindsets are unassociated with other teacher factors, but this is not sufficiently conservative, so it is not our primary analysis of interest. The models in Row 2 account for potential confounding in the interpretation of teachers’ mindsets by fixing the levels of potentially confounding moderators to their population averages (denoted by c in Table 2). Thus, the key results presented in Table 1 correspond to the estimands in Row 2 of Table 2.

Table 2.

Estimands of Interest: Conditional Average Treatment Effects (CATEs)

Analysis	Teachers reporting fixed mindsets	Teachers reporting growth mindsets
Assuming no confounding of the moderator	CATES = Fixed = $\begin{array}{l}\mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Mindset},S_j=\mathrm{Fixed}\right]-\\ \mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Control},S_j=\mathrm{Fixed}\right]\end{array}$	CATES = Growth = $\begin{array}{l}\mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Mindset},S_j=\mathrm{Growth}\right]-\\ \mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Control},S_j=\mathrm{Growth}\right]\end{array}$
$\mathbb{E}$ Adjusting for potential confounding (primary estimand of interest)	CATES = Fixed, C = c = $\begin{array}{l}\mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Mindset},S_j=\mathrm{Fixed},C_j=c\right]-\\ \mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Control},S_j=\mathrm{Fixed},C_j=c\right]\end{array}$	CATES = Growth, C = c = $\begin{array}{l}\mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Mindset},S_j=\mathrm{Growth},C_j=c\right]-\\ \mathbb{E}\left[Y_{ij}|T_{ij}=\mathrm{Control},S_j=\mathrm{Growth},C_j=c\right]\end{array}$

Note: CATE refers to the treatment effect within a subgroup; i indexes students, j indexes teachers. Y = math grades, T (for treatment) = treatment status, S = teacher mindset, C (for confounds) = vector of teacher-mindset confounds, c = population average for potential teacher or school confounds. See proofs and justifications in the article by Yamamoto et al. (2019).

Primary statistical model: linear mixed-effects analysis

The primary analysis examined the cross-level interaction using a typical multilevel, linear mixed-effects model, with a random treatment effect that varied across teachers and was predicted by teacher-level factors, but with one twist: fixed teacher intercepts. Such a model has become the standard approach for multisite trial-heterogeneity analyses (Bloom et al., 2017) because the fixed intercept for each group prevents biases from chance imbalances in the random assignment to treatment within small groups. This “hybrid” (fixed intercept, random slope) approach can make a big difference in the present analysis because some teachers may have small numbers of students and, because of random sampling error, be more likely to have chance imbalances. ³ This is why the fixed-intercept, random-slope model was specified in the NSLM preregistered analysis plan (Yeager et al., 2019). As in all standard multilevel models, the random slope allows different teachers’ students to have different treatment effects, but it uses corrections to avoid overstating the heterogeneity (called an empirical Bayesian shrinkage estimator). Specifically, the model we estimated appears in Equation 1:

$$y_{ij}={\alpha }_j+{\sum }_{h=1}^p{\beta }_h{x}_{ijh}+\left[{\tau }_1{s}_j+{\sum }_{l=2}^k{\tau }_l{c}_{jl}+{\gamma }_j\right]t_{ij}+{ϵ}_{ij},$$ (1)

where y_ij is the math grade for student i in teacher j’s classroom. At the student level, x is a vector of k − 2 student-level covariates (prior achievement, prior expectations for success, race/ethnicity, gender, and parents’ education, all school centered). At the teacher level, α _j is a fixed intercept for each teacher. The large section in brackets represents the multilevel moderation portion of the model, our main interest. The student-level treatment status, $t_{ij}$ , interacts with the continuous measure of teachers’ mindset beliefs ( $s_j$ ) with controls for potential confounds of teacher-mindset beliefs ( $c_j$ , a vector that includes implicit bias, pedagogical content knowledge, fluid intelligence, and teacher master’s certification). The teacher-level random error is γ _j , and the student-level error term is ε _j .

The primary hypothesis test concerns the regression coefficient τ₁, which is the cross-level Student Treatment × Teacher Mindset interaction. When τ₁ is positive and significant, it means that treatment effects are higher when teachers’ growth-mindset scores are higher. The case for a stronger interpretation of τ₁ is bolstered if the coefficient’s sign and significance persist even when the model accounts for the potential confounds indexed by $c_j$ . The model in Equation 1 allows $s_j$ (teachers’ mindsets, the primary moderator) to remain a continuous variable. We estimated the conditional average treatment effects (CATEs) in Table 2 by implementing a standard approach in psychology: calculating the treatment simple effect at −1 SD (teachers who reported relatively more of a fixed mindset) and +1 SD (teachers who reported relatively more of a growth mindset), while holding confounding moderators constant. We used the “margins” postestimation command in Stata/SE (Version 15.1; StataCorp, 2017) to do so. We refer to the former teachers as having a “relatively” more fixed mindset because their position on the scale suggests that they are in an intermediate group—not clearly holding a growth mindset but, on the whole, not an extremely fixed mindset.

Secondary statistical model: Bayesian analysis

The primary model had at least one major limitation: It presumed that all student- and teacher-level variables had linear effects and did not interact. The preregistered analysis plan for the NSLM therefore stated that we would follow up the primary analysis by using a multilevel application of a flexible but conservative approach called Bayesian causal forest (BCF), which relaxes the assumptions of nonlinearity and of no higher order interactions. The BCF approach has been found, in multiple open competitions and simulation studies, to detect true sources of complex treatment-effect heterogeneity while not lending much credence to noise (Hahn et al., 2020). See Equation 2:

$$y_{ij}={\alpha }_j+\beta \left(x_{ij}\right)+\left[\tau \left(s_j,c_j\right)+{\gamma }_j\right]t_{ij}+{ϵ}_{ij}.$$ (2)

The BCF model in Equation 2 retained the key features of the primary statistical model in Equation 1: teacher-specific intercepts, student-level covariates, random variation in the treatment effect across teachers (unexplained by covariates), and potential confounds for teacher-mindset beliefs (collected in the vector $c_{ij}$ ). The most notable change is that the BCF approach replaces the additive linear functions from the primary model with the nonlinear functions $\beta (x)$ and $\tau (s,c)$ . These nonlinear functions have “sum-of-trees” representations that can flexibly represent interactions and other nonlinearities (thus avoiding the researcher degree of freedom of specifying a functional form) and that can allow the data to determine how and whether a given covariate contributes to the model predictions (thus avoiding the researcher degree of freedom of covariate selection). The nonlinear functions are estimated using machine-learning techniques. Bayesian additive regression trees (BART) prior distributions shrink the functions toward simpler structures (such as additive or nearly additive functions) while allowing the data to speak. For more detail about the priors used for the BCF model, see the Supplemental Material.

From the BCF output, there is no single regression coefficient to interpret, as there would be in a typical linear regression model, because the output of the BCF model is a richer posterior distribution of treatment-effect estimates for each of the 9,167 teacher-mindset/student-grade records in the sample. This means that we do not have to set the moderator to +1 or −1 SD. Instead, we can summarize the subgroup treatment effects for each level of teacher mindsets while holding all of the potential confounds constant at their population means (see Fig. 2 for the plot). We note that conducting subgroup comparisons or hypothesis tests does not entail changes to the model fit or prior specifications. The data were used exactly one time, to move from the prior distribution over treatment effects to the posterior distribution. This facilitates honest Bayesian inference concerning subgroup effects and subgroup differences and eliminates concerns with multiple hypothesis testing that can threaten the validity of a frequentist p value (Woody et al., 2020).

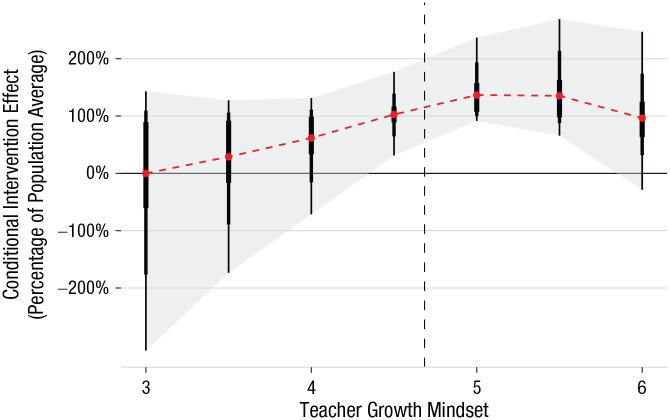
Fig. 2.

Evidence for the mindset-plus-supportive-context hypothesis regarding teacher mindsets and a student-mindset intervention—up to a point—in a flexible Bayesian causal-forest model. Posterior distributions are of the conditional average treatment effect (CATE) as a proportion of the average treatment effect (ATE). Thus, 100% means that the CATE is equal to the population ATE. Red dots represent the estimated intervention effect (posterior means) at each level of teacher mindset. The widths of the bars, from wide to narrow, represent the middle 50% (i.e., interquartile range), 80%, and 90% of the posterior distribution, respectively. The teacher-mindset measure ranges from 1 to 6. The dashed vertical line represents the population mean for teacher mindsets. However, the x-axis stops at 3 because only five teachers had a mindset score below this, and the model cannot make precise predictions with so few teachers.

The BCF analysis had another advantage: It could accommodate the fact that there were researcher degrees of freedom about which aspect of math classrooms might moderate the treatment effect—teacher mindsets, the other teacher variables, or qualities of the schools in which teachers were embedded. The BCF approach allowed all of these teacher and school factors to have the same possibility of moderating the treatment effect and gave them equal likelihood in the prior distribution. In other words, the BCF approach built uncertainty into the model output, which helped to guard against spurious findings (see the Supplemental Material).

Results

Preliminary analyses

Effectiveness of random assignment

The intervention and control groups did not differ in terms of pre-random-assignment characteristics (see Table S5 in the Supplemental Material; also see Yeager et al., 2019).

Average effect on the manipulation check

The manipulation check was successful on average. The growth-mindset intervention led students to report lower fixed-mindset beliefs relative to the control group (control: M = 2.91, SD = 1.17; growth mindset: M = 2.48, SD = 1.16), t(8433) = 16.82, p < .001, d = 0.37.

Homogeneity of the manipulation check

The immediate treatment effect on student mindsets (the beliefs that students reported on the posttreatment manipulation check) was not significantly moderated by teachers’ mindsets, b = 0.04, 95% confidence interval (CI) = [−0.031, 0.102], t(7993) = 1.04, p = .297. Further, there was very little cross-teacher variability in effects on the manipulation checks to explain. According to the BCF model’s posterior distribution, the standard deviation of the intervention effect across teachers was just 5% of the average intervention effect, which means that the posterior prediction interval ranged from 90% to 110% of the average intervention effect, a very narrow range. Here is what this means: Treated students, regardless of their math-teacher mindsets, ended the intervention session with similarly strong growth mindsets that could be tried out. If we later found heterogeneous effects on math grades, measured months into the future, it could reflect differences in the affordances that allowed students to act on their mindsets in class.

Preliminary analyses of effect on math grades

A previous article (Yeager et al., 2019, Extended Data Table 1) and an independent impact evaluation (Zhu et al., 2019) reported the significant main effect of the growth-mindset treatment on math grades for the sample overall (p = .001). Next, the present study’s BCF model found that there was about as much heterogeneity in treatment effects across teachers (47% of the variation) as there was across schools (49%, with the remaining 4% of variation coming from covariation between the two). Combined, these analyses mean that in the present research, we were justified in focusing on heterogeneity in the treatment effect on math grades independently from the school factors reported by Yeager et al. (2019).

Primary analyses: moderation by teachers’ mindsets

Linear mixed-effects model

Teachers’ mindsets positively interacted with the intervention effect on math grades: Student Intervention × Teacher Mindset interaction, b = 0.09, 95% CI = [0.026, 0.150], t(8723) = 2.79, p = .005; see Equation 1. This result was robust to changes to the model, including consideration of the school-level moderators previously reported by Yeager et al. (2019), and changes in the subsample of participating students (see Table 1).

Thus, the data were consistent with the mindset-plus-supportive-context hypothesis: The intervention could alter students’ mindsets, but a growth-affording context was necessary for students’ grades to be improved. Students whose teachers did not clearly endorse growth-mindset beliefs showed a significant manipulation-check effect immediately after the treatment, but their math grades did not improve.

Effect sizes

The CATEs for students who had teachers with a relatively more fixed mindset than a relatively more growth mindset are presented in Table 1. The effect for students in classrooms with growth-mindset teachers was 0.11 grade points and was significant (p < .001), and there was no significant effect in classrooms of teachers who reported more of a fixed mindset (compare Columns 2 and 3). Notably, our primary analyses did not exclude students whose grades could not have been lifted any further. If we limit our sample to the three fourths of students who were not already making straight As across all of their core classes before the study and who therefore had room to improve their grades, the estimated effect among students in classrooms with growth-mindset teachers becomes slightly larger, 0.14 grade points (see Table 1, Row 5).

The present analysis included a representative sample and used intent-to-treat analyses. This means that we included students who could not speak or read English, who had visual or physical impairments, who had attentional problems, whose computers malfunctioned, and more. Thus, there were many students in the data who could not possibly have shown treatment effects. This study therefore estimated effects that could be anticipated under naturalistic circumstances.

Bayesian machine-learning analysis

The BCF analyses yielded conclusions consistent with the primary linear mixed-effects model. First, there was a positive zero-order correlation, r(223) = .55, between teachers’ mindsets and the estimated magnitude of the classroom’s treatment effect (i.e., the posterior mean for the CATE for each teacher), which mirrors the moderation results of the primary linear model. Figure 2, which depicts the posterior distribution for each level of teacher mindset, holding all other moderators constant at the population mean, shows no overlap between the interquartile range for teachers with more of a growth mindset (5 or 5.5) and the interquartile range for teachers with more of a fixed mindset (4 or lower). This supports the conclusion of a positive interaction, again consistent with the mindset-plus-supportive-context hypothesis.

The model also shows that teachers who strongly endorse growth-mindset beliefs show a positive average intervention effect greater than zero with approximately 100% certainty (see Fig. 2), confirming the results of the simple-effects analysis from the linear model. We note again that the BCF model is relatively conservative. It uses a prior distribution centered at a homogeneous treatment effect of zero. This should be taken as strong evidence of moderation and strong evidence that the intervention was effective for students of growth-mindset teachers.

The BCF analysis also yielded new evidence that extended the primary linear model’s results. Figure 2 shows that teachers’ growth mindsets were related to higher treatment-effect sizes in a linear fashion for most of the distribution, but there was no marginal increase in treatment effects when teachers endorsed a growth mindset to an even greater extent once they were already high on the scale (see the rightmost groups of teachers in Fig. 2). The nonlinearity, discovered by the BCF analysis, should invite further investigation into whether teachers already endorsing a very high growth mindset are using practices that encourage all of their students (even those in the control group) to engage in growth-mindset behaviors, potentially narrowing the contrast between students in the treatment and control groups.

Exploratory analyses of baseline student mindsets

The brief, direct-to-student growth-mindset intervention did not appear to overcome local contextual factors that can suppress achievement (e.g., a teacher with a fixed mindset). Could it address individual risk factors suppressing achievement, such as the student’s own fixed mindset? A slight suggestion of this possibility appeared in one of the original growth-mindset-intervention experiments (Blackwell et al., 2007); a student’s prior growth mindset negatively interacted with the intervention effect, but the result was imprecise (p = .07). To revisit this question, we added students’ baseline mindsets as a moderator in the present study’s primary linear mixed-effects model. We found a significant negative interaction with student baseline growth mindsets, b = −0.06, 95% CI = [-0.098, -0.018], t(8717) = 2.85, p = .004, suggesting stronger effects for students with more of a fixed mindset. Thus, the (marginal) Blackwell et al. (2007) moderation finding was borne out. This interaction was additive with, but not interactive with, the teacher-mindset interaction, which did not change in magnitude or significance by including the student-mindset interaction (two-way interaction: still p = .005; three-way interaction: p > .20). Exploring the CATEs, we found that students who reported more fixed mindsets at baseline (–1 SD) in classrooms with a teacher who reported more of a growth mindset (+1 SD) showed an intervention effect on their math grades of 0.16 grade points, 95% CI = [0.079, 0.234], t(8717) = 3.957, p < .001. By contrast, there was no significant effect among students who already reported a strong growth mindset in growth-mindset classes and, as noted, no effect overall in more fixed-mindset classes.

Discussion

In this nationally representative, double-blind clinical trial, successfully teaching a growth mindset to students lifted math grades overall, but this was not enough for all students to reap the benefits of a growth-mindset intervention. Supportive classroom contexts also mattered. Students who were in classrooms with teachers who espoused more of a fixed mindset did not show gains in their math grades over ninth grade compared with the control group, whereas students in classrooms with more growth-mindset teachers showed meaningful gains. This finding suggests that students cannot simply carry their newly enhanced growth mindset to any environment and implement it there. Rather, the classroom environment needs to support, or at least permit, the mindset by providing necessary affordances (see Walton & Yeager, 2020).

In addition, we discovered that students who formerly reported more of a fixed mindset and who went back into a classroom with a teacher who had more of a growth mindset showed larger gains in achievement than did students who began the study with more of a growth mindset. This finding supports the Walton and Yeager (2020) hypothesis that individuals at the intersection of vulnerability (prior fixed mindset) and opportunity (high affordances) are the most likely to benefit from psychological interventions.

The national sampling, and the use of an independent firm to administer the intervention, permits strong claims of generalizability to U.S. public high school math classrooms. Future studies could use or adapt a similar methodology to assess generalizability to other age groups, content areas, or cultural contexts. In general, materials may need to be adapted, sometimes extensively (see Yeager et al., 2016), to be appropriate to new settings.

A main limitation in our study is that teachers’ mindsets were measured, not manipulated. The fact that teacher mindsets were moderators above and beyond other possible teacher confounds lends support to our hypotheses about the importance of classroom affordances. But more research is needed to determine whether teachers’ mindset beliefs, or the practices that follow from them, play a direct, causal role. Thus, the Mindset × Context approach opens the window to a new, experimental program of research.

If a future experimental intervention targeted both students and teachers, what kinds of moderation patterns might be expected? There, we actually might see the largest effects for teachers who formerly reported having a fixed mindset. That is, the benefits of both planting a seed and fertilizing the soil should be greatest where soil was formerly inhospitable and smaller where the soil was already adequate.

In general, we view the testing and understanding of the causal effect of teacher mindsets as the next step for mindset science. Such research will be challenging to carry out, however. For example, we do not think it will be enough to simply copy or adapt the student intervention and provide it to teachers. A new intervention for teachers will need to be carefully developed and tested. We do not yet know which teacher beliefs or practices (or combinations thereof) may be most important in which learning environments. Even if we did, there is much to be learned about how to best encourage and support key beliefs and practices in teachers. The current findings, along with other recent findings about the importance of instructors’ mindsets in promoting achievement for all groups and reducing inequalities between groups (Canning et al., 2019; Leslie et al., 2015; Muenks et al., 2020), point to the urgency and value of this research.

Transparency

Action Editor: Patricia J. Bauer

Editor: Patricia J. Bauer

Author Contributions

D. S. Yeager was the principal investigator for this study. D. S. Yeager, R. Crosnoe, C. Muller, C. Hulleman, A. L. Duckworth, G. M. Walton, and C. S. Dweck developed the study concept, study design, and intervention materials. N. Kersting contributed novel measures to the study. D. S. Yeager, J. M. Carroll, J. Buontempo, S. Woody, J. Murray, and M. Kudym analyzed the data and produced the results. S. Woody and J. Murray developed the Bayesian statistical models, independently conducted confirmatory Bayesian analyses, and produced data visualizations. A. Cimpian and M. Murphy contributed to the study concept, the interpretation of the results, and the writing of the manuscript. P. Mhatre contributed to the study design and analyses. D. S. Yeager, J. M. Carroll, and C. S. Dweck wrote the manuscript and received comments from all the authors. All the authors approved the final manuscript for submission.