Skip to main content
NCBI home page
The Angle Orthodontist logoLink to The Angle Orthodontist
. 2010 May;80(3):554–561. doi: 10.2319/042809-232.1

The Essential Work of Fracture of Thermoplastic Orthodontic Retainer Materials

Albert L Pascual a, Cynthia S Beeman b,✉, E Preston Hicks c, Heather M Bush d, Richard J Mitchell e
PMCID: PMC8985721  PMID: 20050752

Abstract

Objective:

To investigate whether oral cleansing agents affect the essential work of fracture (EWF) and plastic work of fracture (PWF) for two types of orthodontic thermoplastic retainer materials.

Materials and Methods:

Polyethylene-terephthalate-glycol (PETG; Tru-Tain Splint) and polypropylene/ethylene-propylene rubber (PP-EPR) blend (Essix-C+) sheets were compared. For each material, six sets of 25 sheets were thermoformed into double-edge-notched-tension specimens; subsets of five specimens were formed with internotch distances (L) equal to 6, 8, 10, 12, or 14 mm, respectively. Sets were stored (160 hours, 25°C) in air (DRY), distilled water (DW), Original Listerine (LIS), mint Crest ProHealth (CPH), 3% hydrogen peroxide (HP), or Polident solution (POL). Specimens were fractured in tension at 2.54 mm/min. Areas under load-elongation curves were measured to determine total work of fracture (Wf). Linear regressions (Wf vs L [n  =  25]) yielded intercepts (EWF) and slopes (PWF). Ninety-five percent confidence intervals were used to evaluate differences in EWF and PWF estimates.

Results:

PP-EPR blends showed higher EWFs after storage in HP vs storage in DW. PP-EPR blend showed higher EWFs after storage in CPH vs PETG. After HP storage, PP-EPR exhibited lower PWFs than with any other storage conditions. PP-EPR exhibited higher PWFs than PETG after storage in DRY, DW, and LIS.

Conclusions:

Compared with DW, none of the cleansers decreased the energy to initiate fracture. With one exception, no cleanser decreased the energy to continue plastic fracture extension. In PP-EPR blend, increased resistance to fracture initiation was observed with CPH and HP, yet, surprisingly, HP decreased resistance to plastic fracture growth.

Keywords: Essential, Work, Fracture, Orthodontic, Thermoplastic, Retainer

INTRODUCTION

The goal of this investigation is to better understand clinical fracture of clear thermoplastic retainers. Such understanding could not only reduce the frequency of fracture, thereby saving patients the financial costs of replacement, but it could also reduce the risk of orthodontic relapse if fractured retainers are not replaced in a timely manner. Although conversations with orthodontists indicate that retainer fracture is problematic in orthodontic practice, there have been no reports of fracture frequency. To date, only two studies have evaluated the properties of orthodontic thermoplastic retainers. Gardner et al1 compared the wear resistances of three different retainer thermoplastics and found that when they are placed in water and rubbed with a weighted steatite abrader, polyethylene-terephthalate-glycol (PETG) thermoplastics exhibited greater resistance to wear than did two polypropylene-based thermoplastics. In a study of eight different retainer thermoplastics, Ryokawa et al2 found that aging for 24 hours in 37°C distilled water (DW) reduced tensile yield strengths compared with specimens that had not been thermoformed and with specimens that were thermoformed and stored dry. Neither study evaluated the effects of solutes in water or other solvents.

In this investigation we explore the hypothesis that commonly used oral cleansers increase the likelihood that thermoplastic retainers will fracture in service. To determine whether tested cleansers are capable of affecting retainer fracture, the retainers will be subjected to exaggerated, continuous exposure to the cleansers for a period equivalent to 2 years' exposure in service.

It is unknown how these thermoplastics fracture in orthodontic service. Consequently, we decided to use a relatively simple test in which test specimens fracture under moderately fast monotonic loading, as opposed slow monotonic, impact, or cyclic loading.

The dilemma is that many methods used to evaluate a material's fracture toughness are suitable for brittle materials, but not for ductile materials displaying plastic flow during fracture. In response, the Essential Work of Fracture (EWF) Test was recently developed to evaluate the fracture toughness of ductile, thin, plastic sheets.3,4 In the most frequently used EWF test, which uses a double-edge-notched-tension specimen, a series of specimens with equal thicknesses (t) and systematically different internotch distances, or ligament lengths (Ls), are each loaded in tension until complete fracture occurs (Figure 1A). Integrating the area under the load-elongation curve generated during testing of each specimen yields that specimen's total work of fracture (Wf), representing the energy needed for complete specimen fracture (Figure 1B). In EWF theory, Wf is divided into two components: essential work and nonessential work.3

Figure 1.

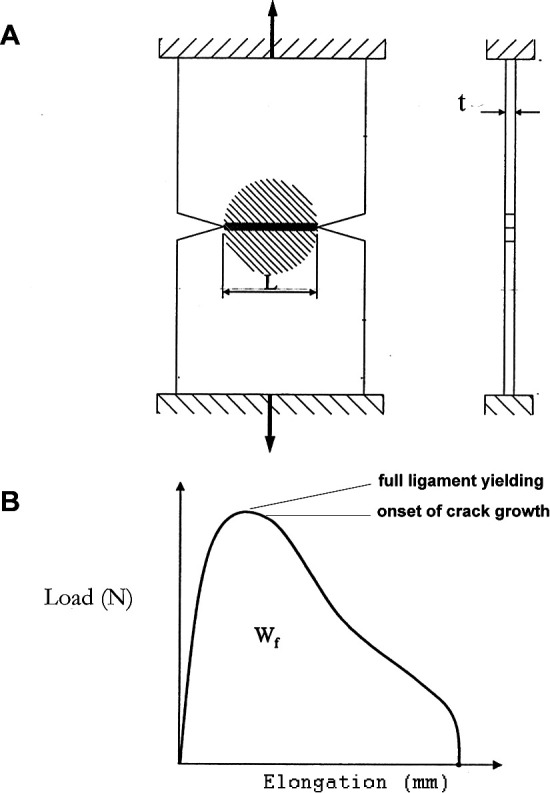
Figure 1

Open in a new tab

(A) Arrows represent loads placed on double-edge-notched-tension (DENT) specimens of thickness (t). The bold center line shows the path of fracture originating from notch tips and extending inward across distance ligament length (L). The shaded circle illustrates the plastic deformation zone. (B) The total work of fracture (Wf) is the area under the curve. The first requirement for essential work of fracture (EWF) test validity: full ligament yielding prior to crack onset.

The EWF, or We, is the energy that is “essential” in generating new fracture surfaces. This energy is concentrated near the plane of fracture and crack tip.4–6 Since EWF depends only on fracture surface area, it is an intrinsic material property. EWF has been regarded as a measure of “resistance to crack initiation.”6,7

The nonessential work, or Wp, is the energy dissipated plastically throughout the zone surrounding the fracture and is therefore known as the plastic work of fracture (PWF). PWF is “nonessential,” given that it has no involvement in generating new fracture surface areas but instead depends on specimen volume, geometry, and loading configuration (and is therefore not an intrinsic material property). PWF is regarded as a measure of “resistance to crack propagation”6 and an indicator of ductility.8

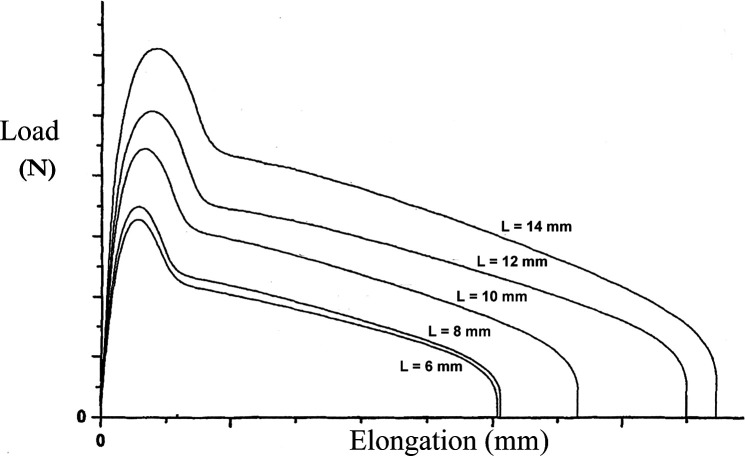
Figure 2 illustrates superimposed load-elongation curves for a series of specimens with varying L, from which Wf values are measured and plotted on a Wf vs L graph (Figure 3). The data should appear linear, assuming that the two requirements of the EWF test are fulfilled: the full ligament yielding occurs just prior to crack onset at the notch tips (Figure 1B), and relative shapes of load-elongation curves in the series are similar (Figure 2).9 The intercept of the line, we, is the evaluated material's EWF. The slope, βwp, is the material's PWF, where β is a shape factor proportional to the area of the plastic zone (Figure 3). The linearity of the EWF theory is described by the following equations10:

Figure 2.

Figure 2

Open in a new tab

Load-elongation curves for a range of ligament lengths (Ls). The second requirement for essential work of fracture (EWF) test validity: curves must appear similar in shape.

Figure 3.

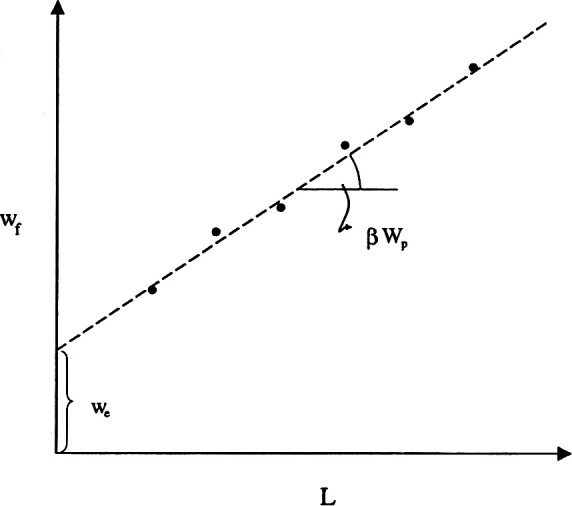
Figure 3

Open in a new tab

Linearity of work of fracture (Wf) × ligament length (L) data: Slope  =  plastic work of fracture (PWF, or Wp); Intercept  =  essential work of fracture (EWF, or We).

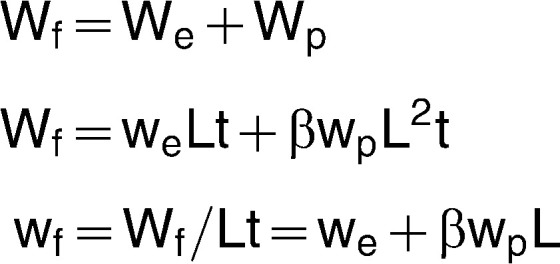graphic file with name i0003-3219-80-3-554-e01.jpg

In this study, the EWF method is used to investigate whether storage in various oral cleansers affects the EWF and PWF for two different orthodontic thermoplastic retainer materials.

MATERIALS AND METHODS

Polypropylene/ethylene-propylene rubber (PP-EPR) blend and PETG thermoplastic polymer sheets (1.0 mm × 125 mm diameter circle) were compared. Each polymer type was stored across the following six conditions: air control (DRY), DW control, and the four cleansers Original Listerine (LIS), mint Crest ProHealth (CPH), Polident solution (POL), and 3% hydrogen peroxide (HP) (Table 1).

Table 1.

Materials Used in this Study

graphic file with name i0003-3219-80-3-554-t01.jpg

Open in a new tab

For each polymer type, six sets of 25 sheets (each set designated for a different condition) were vacuum-thermoformed (Biostar Thermoformer; Scheu-Dental, Iserlohn, Germany) over a 80 × 50 × 10–mm orthodontic stone model (Ortho-Stone; OrthoCast Inc, High Bridge, NJ). A 35 × 70–mm rectangle was then cut from the broad-flat surface of each thermoformed sheet. Rectangles were notched at the center of each long edge using 0.1 mm–thick razor blades (Electron Microscopy Sciences, Hatfield, Pa), producing double-edge-notched-tension specimens. To ensure consistently sharp notches, fresh blades were used per notch. For each set of 25 specimens, five specimens were constructed with L  =  6, 8, 10, 12, and 14 mm, then replicated five times.

For sets stored in DW and the four cleansers, immersions were for 160 hours at 25°C (fluids changed every 24 hours). Full-strength LIS and CPH were used, while POL and HP were prepared to manufacturers' specifications (Table 1).

After storage in their designated groups, each specimen was loaded in tension to fracture (Figure 4A–F) at 2.54 mm/min using a dual-screw mechanical testing machine (Instron Model TTC; Instron Corporation, Canton, NY). Areas under the load-elongation curves were calculated to determine Wf by numerical integration of digitized curves (DigitizeIt; Sharelt!, Eden Prairie, Minn). Data reduction followed the ESIS TC-4 protocol.11

Figure 4.

Figure 4

Open in a new tab

Double-edge-notched-tension (DENT) specimen under tension loading: (A) Just before crack onset. (B) Just after crack onset. (C) Crack extension inward from notches. (D and E) Necking and plastic flow phenomena as polymer cross-section between notches decreases during elongation. (F) After complete fracture.

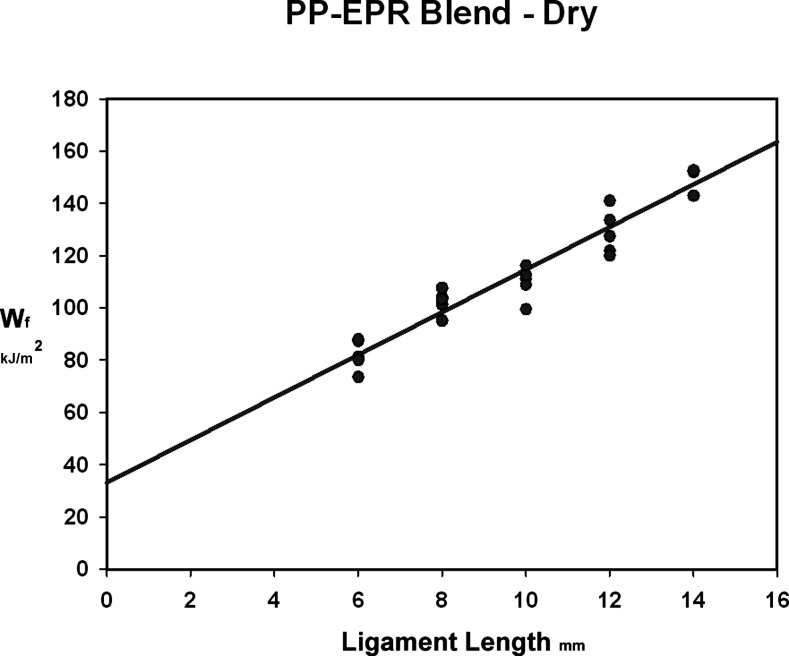
EWF theory predicts that Wfvs L data will be linear. For each thermoplastic-storage combination, least-square regressions were calculated to estimate a best fit line for 25 pairs of Wf vs L data points, with assistance from a graphics software (SigmaStatistics; SigmaPlot 11; Systat Software Inc, San Jose, Calif). Data points were obtained by plotting the Wf values that resulted when length was varied (L  =  6, 8, 10, 12, and 14 mm) with intercept and with slope being EWF and PWF estimates, respectively (Figure 5). Coefficients of determination (R2) for this line are an estimate of the fraction of the variance in the total work fracture that is explained by ligament length.

Figure 5.

Figure 5

Open in a new tab

Linear regression of work of fracture (Wf) × ligament length (L) for polypropylene/ethylene-propylene rubber (PP-EPR) blend specimens in air (DRY) storage (slope  =  8.2 MJ/m3; y  =  33.1 kJ/m2; R2  =  0.96).

When both slope and intercept vary, comparing them from regression analysis is complex, often requiring analysis of covariance and the introduction of interaction terms.12 A more straightforward approach is to provide estimates of intercept and slope with 95% confidence intervals (CIs). Resulting interval estimates can then be used to assess the magnitude and precision of the effect for different treatments.13 CIs can also be used to compare EWF and PWF estimates. However, this comparison is more conservative than traditional hypothesis tests (failing to reject the null hypothesis more often). In fact, nonoverlapping 95% CIs are associated with P-values of <.05 and can be considered statistically different. However, nonoverlapping 95% CIs do not necessarily indicate solely that parameters are different. Partial overlap of 95% CIs still corresponds to P-values of <.05, indicating that there must be considerable overlap before a P-value of >.05 results.14,15 Given the exploratory nature of this work and the number of possible comparisons (a maximum of 36 each for EWF and PWF), a conservative approach regarding partially overlapping groups was employed. In the present investigation, the standard used was that parameters were likely to be in separate ranges only when the overlap was small (less than 0.10 “proportional overlap,” using a term defined by Cumming and Finch14).

RESULTS

Linear regression models were produced for each condition, and R2 values ranged from 0.76 to 0.95, indicating that regression models explained a significant amount of the variability in Wf (eg, Figure 5).

EWF estimates for each polymer and storage condition are presented in Figure 6. With PP-EPR blend, the 95% CIs of EWFs for most storage conditions overlapped one another, indicating that storage conditions did not affect work to initiate fracture. However, the 95% CIs of EWFs for DW (25.6 ± 11.5 kJ/m2) and HP (49.0 ± 12.8 kJ/m2) storage overlapped a small amount, indicating plausible separate ranges for population means of EWF; therefore, more energy is required to initiate fracture of PP-EPR after HP storage vs DW. For PETG, the 95% CIs of EWFs for the storage conditions overlapped one another, indicating that storage conditions did not affect work to initiate fracture.

Figure 6.

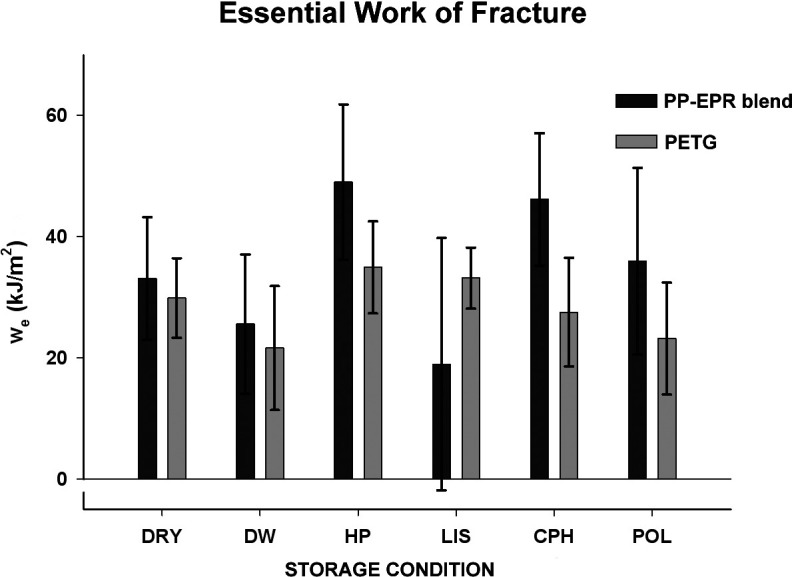
Figure 6

Open in a new tab

Essential work of fracture (EWF) estimates and 95% confidence intervals for polypropylene/ethylene-propylene rubber (PP-EPR; dark bars) and polyethylene-terephthalate-glycol (PETG; light bars) shown across storage conditions.

When comparing the effects of storage condition on the two polymers, 95% CIs for EWFs for most storage conditions overlapped one another, indicating that polymer type did not affect work to initiate fracture. The exception was the 95% CIs for EWFs of the two polymers after CPH storage. These CIs slightly overlapped, indicating that after CPH storage, more energy is required to initiate fracture in PP-EPR (46.1 ± 10.9 kJ/m2) than in PETG (27.5 ± 9.0 kJ/m2).

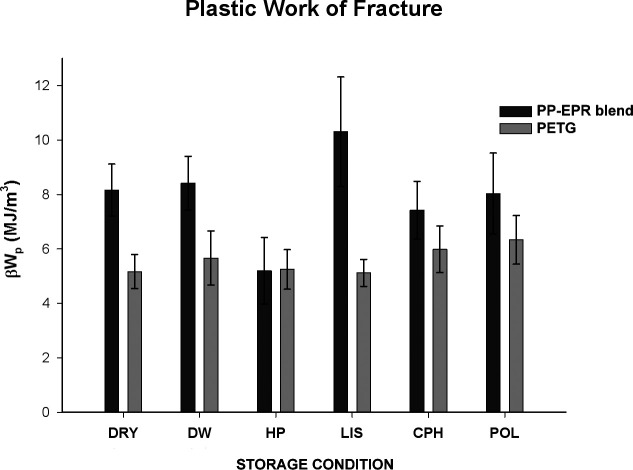
PWF estimates for each polymer and storage condition are presented in Figure 7. For PP-EPR, the 95% CIs of PWFs for all storage conditions except HP (5.2 ± 1.2 MJ/m3) overlapped, indicating that after HP storage, PP-EPR required a smaller amount of energy to continue fracture extension than was observed after storage in all other conditions. For PETG, the 95% CIs of PWFs for the six storage conditions overlapped one another, indicating that storage conditions did not affect the energy required for fracture extension.

Figure 7.

Figure 7

Open in a new tab

Plastic work of fracture (PWF) estimates and 95% confidence intervals for polypropylene/ethylene-propylene rubber (PP-EPR; dark bars) and polyethylene-terephthalate-glycol (PETG; light bars) shown across storage conditions.

When comparing the effects of storage condition on the two polymers, we found the following: after HP, CPH, and POL storage, the 95% CIs of PWFs overlapped one another, indicating that in these conditions, polymer type did not affect the energy required to continue fracture extension. However, the 95% CIs of PWFs did not overlap between the two polymers within DRY (PP-EPR  =  8.2 ± 1.0 MJ/m3; PETG  =  5.2 ± 0.6 MJ/m3), DW (PP-EPR  =  8.4 ± 1.0 MJ/m3; PETG  =  5.7 ± 1.0 MJ/m3), and LIS (PP-EPR  =  10.3 ± 2.0 MJ/m3; PETG  =  5.1 ± 0.5 MJ/m3) conditions, indicating that PP-EPR required more energy than PETG to continue fracture extension.

DISCUSSION

Several EWF studies have evaluated PETG polymer and PP-EPR blend dry sheets. EWFs reported for PETG include 30.3,16 36.1,10 and 31.917 kJ/m2. These values agree with the data in the present study. PWFs reported for PETG from these same studies include 7.7,16 7.5,10 and 8.217 MJ/m3, which are slightly larger than those found in the present study (Figure 7). The only EWF and PWF values found for PP-EPR blends (30 vol. % EPR) are approximately 22 kJ/m2 and approximately 4 kJ/m3, respectively.5 This EWF is close to that found in the present study, but the PWF is less than half that reported here. It should be noted that the vol. % EPR in the materials evaluated in the present study is unknown. At loading rates similar to those used in this study, Grein et al5 found that both EWF and PWF decrease as rubber content increases.

No previous EWF studies evaluated water's effects on the thermoplastics tested in this study. One EWF study did evaluate the aging of polyethylene terephthalate sheets in water.18 Polyethylene terephthalate is a cousin of PETG, but unlike PETG, it can crystallize. The polyethylene terephthalate sheets studied were noncrystalline, so their results may have some relevance to the present study. Aging the sheets in 60°C water for 100 hours reduced the EWF measured at room temperature from 76.8 kJ/m2 before aging to 5.9 kJ/m2.18 Interestingly, PWF was unaffected. The authors attribute EWF decreases to the plasticizing effects of adsorbed water.18 This raises questions if aging in body temperature degrades the EWFs of the thermoplastics tested in this study.

Ryokawa et al2 found that PETG absorbed more water than PP-EPR. They suggested that this difference could influence the mechanical properties of these materials, and they noted that since PP-EPR is a semicrystalline (opaque) thermoplastic, it will have a higher density than an amorphous polymer like PETG. The lower free volume of the semicrystalline polymer limits the water that can be absorbed. Generally, water plasticizes polymers by interfering with secondary bonds between polymer molecules and thereby facilitates the untangling of the polymer ensemble in response to stress.

Such findings with water were not evident in the present investigation. Although reductions were found in EWF after DW storage, these differences were not significant. It was surprising that PETG changed much less than PP-EPR, given that PETG absorbs more water.

Storage of PP-EPR blend in HP and CPH produced increases in EWF. Caudill19 found alterations to outer surface contours occurring on isotactic polypropylene specimens after HP exposure as a result of surface polarity changes. This phenomenon may explain reduced PWF estimates, but it does not address the higher EWF values found in PP-EPR after HP storage.

The mechanisms for the actions of CPH are unknown, leaving us with speculation only. Could the glycerin in CPH be sealing cracks or creating a diffusion barrier that keeps water out of the polymer, consequently increasing the resistance to crack opening?

The number of specimens that EWF tests require has been questioned.4 The present study designated five groups of five specimens (total  =  25) for each treatment group, based on established EWF protocols and previous data20,21 indicating that exceeding 20 specimens gives a satisfactory standard deviation over the mean value of we of <0.1.

This study's intent was not to simulate “clinical” retainer use but rather to determine cleansers' potential to increase fracture risk. Treatments exposed thermoplastics continuously for prolonged periods (an abuse test, not a “use” test). If solvents decreased EWFs or PWFs, additional tests would be necessary under more realistic conditions. However, since no such affects on EWF or PWF were generally observed under abuse, it can be assumed that fracture frequency would not increase under the less abusive conditions that prevail during retainer service.

Given that EWF testing has never before been used to study dental materials, evaluating tear strengths of dental impression materials is one promising application. In addition to fracture behavior, creep behavior (slow gradual plastic deformation over time) of retainers may also be important to evaluate, since loss of intimate retainer adaptation to teeth may occur with creep, leading to undesired tooth movement and relapse.22

CONCLUSIONS

  • Compared to DW, no cleanser decreased resistance to fracture initiation or growth in PETG.

  • Compared to DW, HP increased resistance to fracture initiation yet decreased resistance to fracture growth in PP-EPR.

  • After storage in CPH, an increased resistance to fracture initiation was found in PP-EPR vs PETG.

  • Overall, all tested cleansers can be used to clean thermoplastic orthodontic retainers without increasing risk of fracture.

REFERENCES

  • 1.Gardner G. D, Dunn W. J, Taloumis L. Wear comparison of thermoplastic materials used for orthodontic retainers. Am J Orthod Dentofacial Orthop. 2003;124:294–297. doi: 10.1016/s0889-5406(03)00502-x. [DOI] [PubMed] [Google Scholar]
  • 2.Ryokawa H, Fujishima A, Maki K. The mechanical properties of dental thermoplastic materials in a simulated intraoral environment. Orthodontic Waves. 2006;65:64–72. [Google Scholar]
  • 3.Mai YW On the essential work of ductile fracture in polymers. Int J Fracture. 1986;32:105–125. [Google Scholar]
  • 4.Williams J. G, Rink M. The standardization of the EWF test. Eng Fracture Mech. 2007;74:1009–1017. [Google Scholar]
  • 5.Grein C. P. C, Germain Y, Kausch H. H, Beguelin P. Essential work of fracture of polypropylene and polypropylene blends over a wide range of test speeds. Polymer Eng Sci. 2003;43:223–233. [Google Scholar]
  • 6.Karger-Kocsis J. Toward understanding the morphology-related crack initiation and propagation behavior in polypropylene systems as assessed by the essential work of fracture approach. J Macromol SciPhysics. 1999;B38:635–646. [Google Scholar]
  • 7.Pardoen T. M. Y, Delannay F. Essential work of fracture mechanics—towards a thickness independent plane stress toughness. Eng Fracture Mech. 2002;69:617–631. [Google Scholar]
  • 8.Peres F. M. Application of the essential work of fracture method in ranking the performance in service of high-density polyethylene resins employed in pressure pipes. J Mater Sci. 2008;43:1844–1850. [Google Scholar]
  • 9.Karger-Kocsis J. For what kind of polymer is the toughness assessment by the essential work concept straightforward? Polymer Bull. 1996;37:119–126. [Google Scholar]
  • 10.Karger-Kocsis J, Barany T, Moskala E. J. Plane stress fracture toughness of physically aged plasticized PETG as assessed by the essential work of fracture (EWF) method. Polymer. 2003;44:5691–5699. [Google Scholar]
  • 11.Gray A. Testing Protocol for Essential Work of Fracture. European Structural Integrity Society (ESIS) – TC4 Task Group, 1993 [Google Scholar]
  • 12.Milliken G. A, Johnson D. E. Analysis of messy data nonreplicated experiments 2. New YorkNY: Van Nostrand Reinhold; 1989. [Google Scholar]
  • 13.Cumming G, Finch S. A primer on the understanding, use, and calculation of confidence intervals that are based on central and noncentral distributions. Educ Psychol Meas. 2001;61:532–574. [Google Scholar]
  • 14.Cumming G, Finch S. Inference by eye: confidence intervals and how to read pictures of data. Am Psychol. 2005;60:170–180. doi: 10.1037/0003-066X.60.2.170. [DOI] [PubMed] [Google Scholar]
  • 15.Cumming G. Inference by eye: reading the overlap of independent confidence intervals. Stat Med. 2009;28:205–220. doi: 10.1002/sim.3471. [DOI] [PubMed] [Google Scholar]
  • 16.Karger-Kocsis J. For what kind of polymer is the toughness assessment by the essential work concept straightforward? Polymer Bull. 1996;37:119–126. [Google Scholar]
  • 17.Ching E. C. Y, Li R. K. Y, Mai Y. W. Effects of gauge length and strain rate on fracture toughness of polyethylene terephthalate glycol (PETG) film using the Essential Work of Fracture analysis. Polymer Eng Sci. 2000;40:310–319. [Google Scholar]
  • 18.Barany T, Karger-Kocsis J, Czigany T. Effect of hygrothermal aging on the essential work of fracture response of amorphous poly(ethylene terephthalate) sheets. Polymer Degrad Stability. 2003;82:271–278. [Google Scholar]
  • 19.Caudill V. Polypropylene surface characteristics after exposure to hydrogen peroxide and heat processing. J Plast Film Sheeting. 1992;8:140–154. [Google Scholar]
  • 20.Marchal Y, Walhin J. F, Delannay F. Statistical procedure for improving the precision of the measurement of the essential work of fracture of thin sheets. Int J Fracture. 1997;87:189–199. [Google Scholar]
  • 21.Clutton E. ESIS-TC4: Experience with the Essential Work of Fracture method. ESIS Publ. 2000;27:187. [Google Scholar]
  • 22.Barbagallo L. J, Shen G, Jones A. S, Swain M. V, Petocz P, Darendeliler M. A. A novel pressure film approach for determining the force imparted by clear removable thermoplastic appliances. Ann Biomed Eng. 2008;36:335–341. doi: 10.1007/s10439-007-9424-5. [DOI] [PubMed] [Google Scholar]

Articles from The Angle Orthodontist are provided here courtesy of Edward H Angle Education and Research Foundation, Inc

RESOURCES