Meta-regression methods to characterize evidence strength using meaningful-effect percentages conditional on study characteristics

Abstract

Meta-regression analyses usually focus on estimating and testing differences in average effect sizes between individual levels of each meta-regression covariate in turn. These metrics are useful but have limitations: they consider each covariate individually, rather than in combination, and they characterize only the mean of a potentially heterogeneous distribution of effects. We propose additional metrics that address both limitations. Given a chosen threshold representing a meaningfully strong effect size, these metrics address the questions: “For a given joint level of the covariates, what percentage of the population effects are meaningfully strong?” and “For any two joint levels of the covariates, what is the difference between these percentages of meaningfully strong effects?” We provide semiparametric methods for estimation and inference and assess their performance in a simulation study. We apply the proposed methods to meta-regression analyses on memory consolidation and on dietary behavior interventions, illustrating how the methods can provide more information than standard reporting alone. To facilitate implementing the methods in practice, we provide reporting guidelines and simple R code.

1 ∣. INTRODUCTION

Meta-regression analyses usually focus on estimating and testing differences in average effect sizes between individual levels of each meta-regression covariate in turn.¹ These estimates are certainly useful, but do have limitations as standalone metrics. First, they consider each meta-regression covariate individually and do not directly characterize differences in effect sizes associated with combinations of covariates that are of scientific interest. For example, if the covariates represent possible components of a behavior intervention, it may be useful to consider the strength of effects in studies with a particular combination of components rather than only estimating average effects of each component individually. This approach could be particularly useful given recent calls to conduct meta-analyses that deliberately include studies representing a broad range of interventions, populations, and environments.² Similarly, when meta-regression is used to assess the association of studies' risk-of-bias characteristics with their effect sizes,¹ it would often be useful to consider the strength of effects in studies with low risks of bias on all measures jointly, rather than individually (although one can never be certain that all relevant risks of bias have been assessed, nor that they have been rated with complete accuracy).

Second, and more fundamentally, the usual estimates of average effect sizes characterize only the mean of a potentially heterogeneous distribution of effects. We therefore propose additional metrics that supplement standard reporting by directly addressing questions of fundamental interest in meta-regression and characterizing the potentially heterogeneous distribution of effect sizes conditional on specified levels of the meta-regression covariates. Specifically, in a manner we formalize below, the proposed metrics address two questions: (1) For a given joint level of the covariates, what percentage of the population effects are “meaningfully strong”? (2) For any two joint levels of the covariates, what is the difference between these percentages of meaningfully strong effects?

These metrics extend methods we previously proposed for standard meta-analysis.^3-5 Specifically, we had previously recommended choosing a minimum threshold representing a meaningfully strong effect size (q) and estimating the percentage or proportion of population effects above this threshold. Second, we and others^3,6 have suggested estimating the percentage of effects below a second, possibly symmetric, threshold in the opposite direction from the estimated mean. We discussed a number of methods to choose these thresholds, which included considering the size of discrepancies between naturally occurring groups of interest, effect sizes produced by well-evidenced interventions, cost-effectiveness analyses, or minimum subjectively perceptible thresholds.³ We demonstrated that these percentage metrics could help convey evidence strength for meaningfully strong effects under effect heterogeneity in a manner that provides more information than meta-analytic point estimates alone³ and also that they could sometimes help adjudicate apparent conflicts between meta-analyses.^7,8 In practice, the metrics have been successfully and informatively applied to meta-analyses on a variety of topics.^7,9-13

Here, we provide extensions to meta-regression that address the two questions above by characterizing, for a chosen level of the meta-regression covariates, the percentage of population effects that are above or below the threshold q. This metric helps characterize evidence strength for meaningfully strong effects in studies with a particular level of the covariates, and it could also be used as a hypothesis-generating method to identify which joint levels of the covariates are associated with the largest estimated percentages of meaningfully strong effects. Naturally, this metric also allows one to characterize the complementary cumulative distribution function of the population effects (i.e., the percentage of effects stronger than any arbitrary threshold), which could be displayed graphically. The methods also allow one to estimate the difference in these percentages for any two joint levels of the covariates.

We provide methods to estimate these metrics along with inference (Section 2.2). The methods involve first fitting a standard meta-regression (e.g., using semiparametric methods that do not make assumptions on the distribution of population effects^14-16), using the resulting estimates to appropriately “shrink” studies' point estimates toward the mean, and then estimating the proposed metrics using the empirical distribution of these shrunken estimates. We illustrate by reanalyzing data from two previously published meta-analyses,^13,17 demonstrating that the proposed metrics can provide more information than standard reporting alone (Section 4). We assess the methods' performance in a simulation study that includes a variety of realistic and challenging scenarios (Section 5) and use the results to inform practical reporting guidelines (Section 2.3). The methods are straightforward to implement in practice, and we provide simple example R code to do so (Supplementary material or https://osf.io/gs7fp/).

2 ∣. METHODS

2.1 ∣. Existing methods for standard meta-analysis

We first briefly review the previously proposed methods^3-5 to estimate the percentage of meaningfully strong effects, termed “${\widehat{P}}_{>q}$”, in the context of standard meta-analysis. Let θ_i, ${\widehat{\theta }}_i$, and ${\widehat{\sigma }}_i$ respectively denote the population effect size, point estimate, and estimated standard error of the i^th study. Consider a standard meta-analysis of k independent studies, with $\widehat{\mu }$ denoting the estimated mean and ${\widehat{\tau }}^2$ denoting the estimated heterogeneity (i.e., the estimated variance of the population effects). To estimate ${\widehat{P}}_{>q}$, existing methods begin by calculating a “calibrated” estimate⁵ for each meta-analyzed study, defined as

$${\tilde{\theta }}_i=\widehat{\mu }+\sqrt{\frac{{\widehat{\tau }}^2}{{\widehat{\tau }}^2+{\widehat{\sigma }}_i^2}}({\widehat{\theta }}_i-\widehat{\mu })$$ (2.1)

Intuitively, the calibrated estimate ${\tilde{\theta }}_i$ shrinks the point estimate ${\widehat{\theta }}_i$ toward the estimated mean $\widehat{\mu }$ with a degree of shrinkage that is inversely proportional to the study's precision: relatively imprecise estimates ${\widehat{\theta }}_i$ (i.e., those with large ${\widehat{\sigma }}_i^2$) receive strong shrinkage toward $\widehat{\mu }$, while relatively precise estimates receive less shrinkage and remain closer to their original values. Thus, these calibrated estimates have been appropriately shrunk to correct the overdispersion such that their variance is equal to, the estimated variance of the population effects.⁵ The shrinkage factor $\sqrt{{\widehat{\tau }}^2∕\left({\widehat{\tau }}^2+{\widehat{\sigma }}_i^2\right)}$ minimizes the distance between the empirical cumulative distribution function of the calibrated estimates and of the population effects,¹⁸ which is the relevant loss function for estimating ${\widehat{P}}_{>q}$. Then, ${\widehat{P}}_{>q}$ can be easily estimated⁴ as a sample proportion of the calibrated estimates that are stronger than q:

$${\widehat{P}}_{>q}={\sum }_{i=1}^{k}1\left\{\widehat{\mu }+\sqrt{\frac{{\widehat{\tau }}^2}{{\widehat{\tau }}^2+{\widehat{\sigma }}_i^2}}({\widehat{\theta }}_i-\widehat{\mu })>q\right\}$$ (2.2)

Naturally, analogous methods can be used to estimate the proportion of effects below another threshold, for example to consider the percentage of effects that are in the direction opposite the overall estimated mean.^3,6 Inference can be conducted using bias-corrected and accelerated (BCa) bootstrapping.^4,19,20 If the point estimates are potentially non-independent because, for example, some articles in the meta-analysis contribute multiple estimates from studies with similar study designs or populations, then one should resample clusters of estimates (e.g., articles) with replacement while leaving intact the estimates within each cluster (Davison and Hinkley²¹ Section 3.8). We will refer to this as the “cluster bootstrap”.

2.2 ∣. Extension to meta-regression

We now extend the above methods to a meta-regression with the mean model E[θ ∣ Z] = β₀ + Zβ₁, where Z is a k × p matrix of study-level covariates of any type (binary, categorical, continuous, etc.) with realized levels in study i of z_i and where β₁ is a p-vector of coefficients. We assume that the residual variance of the population effects, Var(θ ∣ Z), is a constant ${\tau }_{ϵ}^2$. This is a standard estimand in meta-regression and is often simply called “τ²” in the literature and in software; here, we adopt the notation “${\tau }_{ϵ}^2$” to clarify that this is the residual heterogeneity conditional on the meta-regression covariates rather than the marginal τ² of a standard meta-analysis. One would first estimate the parameters (β₀, β₁, ${\tau }_{ϵ}^2$) via standard meta-regression; in practice, we would recommend using semiparametric methods similar to generalized estimating equations that do not require assumptions on the distribution of population effects.^14-16,22 Asymptotic and finite-sample theory establishing that this approach provides consistent coefficient estimates under arbitrary distributions was provided elsewhere.^14,22

The proportion of population effects above q, conditional on level z of the covariates, is P(θ > q ∣ Z = z), termed “P _{> q}(z).” While it may seem intuitive to estimate P _{> q}(z) by simply analyzing a subset of the studies and applying the existing methods for standard meta-analysis,^3,4 that approach would preclude consideration of continuous covariates and would be inefficient, especially when considering specific combinations of covariates that do not occur frequently in the observed studies. Instead, we propose estimating P _{> q}(z) as follows. Define a point estimate for each study that has been “shifted” to the chosen covariate level z as ${\widehat{\theta }}_i(Z=z)={\widehat{\theta }}_i-(z_i-z){\widehat{\beta }}_1$, such that $E\left[{\widehat{\theta }}_i(Z=z)\right]={\beta }_0+z{\beta }_1$. An analog to the calibrated estimate ${\tilde{\theta }}_i$ that has been shifted to Z = z is then:

$$\begin{gathered} {\tilde{\theta }}_i(Z=z)=\widehat{E}[\theta \mid Z=z]+\sqrt{\frac{{\widehat{\tau }}_{ϵ}^2}{{\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2}}\left({\widehat{\theta }}_i(Z=z)-\widehat{E}[\theta \mid Z=z]\right) \\ ={\widehat{\beta }}_0+z{\widehat{\beta }}_1+\sqrt{\frac{{\widehat{\tau }}_{ϵ}^2}{{\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2}}\left({\widehat{\theta }}_i-\left[{\widehat{\beta }}_0+z_i{\widehat{\beta }}_1\right]\right) \end{gathered}$$ (2.3)

In the second line, upon canceling the $z{\widehat{\beta }}_1$ terms, the term ${\widehat{\theta }}_i-\left[{\widehat{\beta }}_0+z_i{\widehat{\beta }}_1\right]$ is simply the (unshifted) residual of ${\widehat{\theta }}_i$ with respect to its estimated expectation conditional on its realized Z = z_i. Highly imprecise point estimates (i.e., those with a small ${\widehat{\tau }}_{ϵ}^2∕\left({\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2\right)$) are strongly shrunk toward $\widehat{E}[\theta \mid Z=z]={\widehat{\beta }}_0+z{\widehat{\beta }}_1$, while more precise estimates remain close to the studies' own residuals, ${\widehat{\theta }}_i-\left[{\widehat{\beta }}_0+z_i{\widehat{\beta }}_1\right]$.

Analogously to the fact that standard calibrated estimates approximately match the first two moments of the marginal distribution of population effects,⁵ the shifted, calibrated estimates ${\tilde{\theta }}_i(Z=z)$ approximately match the first two moments of the distribution of the population effects conditional on Z = z. That is, $E\left[{\tilde{\theta }}_i(Z=z)\mid Z=z\right]={\beta }_0+z{\beta }_1=E[\theta \mid Z=z]$, and for large k:

$$\begin{gathered} \text{Var}\left({\tilde{\theta }}_i(Z=z)\mid Z=z\right)\approx \frac{{\widehat{\tau }}_{ϵ}^2}{{\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2}\text{Var}({\widehat{\theta }}_i\mid Z=z) \\ \approx \frac{{\widehat{\tau }}_{ϵ}^2}{{\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2}({\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2) \\ ={\widehat{\tau }}_{ϵ}^2 \\ \approx \text{Var}(\theta \mid Z=z) \end{gathered}$$

The proportion of meaningfully strong effects can then be estimated as:

$$\begin{gathered} {\widehat{P}}_{>q}(z)=\widehat{P}\left({\widehat{\beta }}_0+z{\widehat{\beta }}_1+\sqrt{\frac{{\widehat{\tau }}_{ϵ}^2}{{\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2}}({\widehat{\theta }}_i-[{\widehat{\beta }}_0+z_i{\widehat{\beta }}_1])>q\right) \\ =\sum _{i=1}^{k}1\left\{{\widehat{\beta }}_0+\sqrt{\frac{{\widehat{\tau }}_{ϵ}^2}{{\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2}}({\widehat{\theta }}_i-z_i{\widehat{\beta }}_1-{\widehat{\beta }}_0)>q-z{\widehat{\beta }}_1\right\} \end{gathered}$$ (2.4)

The estimated difference in these proportions comparing level z to a chosen reference level z₀ is simply ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$. Again, analogous methods can be used to estimate the proportion of effects below another threshold, or their difference.

To apply Equation (2.4) in practice, one could simply plug in the meta-regression estimates ${\widehat{\beta }}_0$, ${\widehat{\beta }}_1$, and ${\widehat{\tau }}_{ϵ}^2$; we call this the “one-stage” method. When considering multiple choices of q or z, one can simply compute a single value of ${\widehat{\beta }}_0+\sqrt{{\widehat{\tau }}_{ϵ}^2∕\left({\widehat{\tau }}_{ϵ}^2+{\widehat{\sigma }}_i^2\right)}({\widehat{\theta }}_i-z_i{\widehat{\beta }}_1-{\widehat{\beta }}_0)$ for each study and then compare these to various shifted thresholds, $q-z{\widehat{\beta }}_1$. An essentially equivalent method, which we call the “two-stage” method, can further illustrate the connection between these methods and the existing methods for standard meta-analysis.^4,5 That is, rather than applying Equation (2.4) directly using the meta-regression estimates ${\widehat{\beta }}_0$, ${\widehat{\beta }}_1$, and ${\widehat{\tau }}_{ϵ}^2$, as in the one-stage method, one could instead use only the meta-regression estimate ${\widehat{\beta }}_1$ to shift the point estimates themselves to Z = 0, that is, ${\widehat{\theta }}_i(Z=0)={\widehat{\theta }}_i-z_i{\widehat{\beta }}_1$. Because $E\left[{\widehat{\theta }}_i(Z=0)\mid Z=0\right]={\beta }_0$ and $\text{Var}({\widehat{\theta }}_i(Z=0)\mid Z=0)={\widehat{\tau }}_{ϵ}^2+{\sigma }_i^2$, one could then apply Equation (2.4) by simply fitting a standard intercept-only meta-analysis (without covariates) to the ${\widehat{\theta }}_i(Z=0)$ and then using the pooled point estimate and estimated heterogeneity from this meta-analysis, ${\widehat{\tau }}^2$, to compute standard calibrated estimates⁵ (e.g., using the R package MetaUtility::calib_ests). These estimates could then be compared to the threshold that has also been shifted to Z = 0, that is, $q-z{\widehat{\beta }}_1$. Although these methods are not exactly numerically equivalent,^* simulation results (Section 5) indicated that they performed almost identically in practice. We use the one-stage method for the applied example and code example below.

As in standard meta-analysis,⁴ inference for ${\widehat{P}}_{>q}(z)$ or ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ can proceed via bootstrapping. Specifically, one can resample rows of the original sample, (${\widehat{\theta }}_i$, ${\widehat{\sigma }}_i$, z_i, fit a meta-regression model to the resampled datasets to obtain new estimates ${\widehat{\beta }}_0$, ${\widehat{\beta }}_1$, and ${\widehat{\tau }}_{ϵ}^2$, and finally estimate ${\widehat{P}}_{>q}(z)$ via Equation (2.4). Note that meta-regression estimation of $\widehat{{\beta }_0}$, $\widehat{{\beta }_1}$, and ${\widehat{\tau }}_{ϵ}^2$ must be included in the bootstrapping process to adequately capture the propagation of their sampling errors to the estimates of interest. If the point estimates are clustered, the cluster bootstrap should be used, as described in Section 2.1. A bias-corrected and accelerated (BCa) confidence interval^19,20 can then be constructed from the bootstrapped values of ${\widehat{P}}_{>q}(z)$ or ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$. Informed by simulation results (Section 5), we provide the following four suggested guidelines for reporting ${\widehat{P}}_{>q}(z)$ or ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ to help ensure that the metrics will provide accurate and interpretable results.

2.3 ∣. Guidelines for applying and reporting these metrics

We developed the guidelines below such that, based on an extensive simulation study including both realistic and extreme scenarios (Section 5), the metrics' performances conformed to the following thresholds: the bias was within ±5 percentage points in at least 90% of simulation scenarios, the coverage was no lower than 90% in at least 90% of simulation scenarios, and no more than 2% of simulation scenarios had coverage less than 85%. We required these criteria to hold regardless of the number of meta-analyzed studies, subject to the fourth guideline below. Determining criteria for adequate estimator performance is inherently somewhat arbitrary; we consider these criteria to represent adequate performance based on the performance of existing standard estimators in meta-regression (Section 5). Meta-analysts who wish to apply the metrics according to more or less stringent criteria for the estimators' performance can browse comprehensive results for all simulation scenarios in a publicly available, documented dataset (https://osf.io/gs7fp/). The guidelines are:

1. Include confidence intervals when reporting ${\widehat{P}}_{>q}(z)$ or ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$. The confidence intervals help convey that while these metrics are overall unbiased, they may have considerable sampling variability in some settings and then could potentially be far from the truth for a given single analysis. For example, if ${\widehat{P}}_{>q}(z)$ is large (e.g., 85%), but its confidence interval also includes small values (e.g., [15%, 100%]), or vice versa, investigators should comment on this when interpreting the metrics (as we demonstrate in the applied examples).

2. If point estimates are clustered (for example, within articles), investigate whether the population effects are also skewed by examining a density or cumulative distribution plot of the calibrated estimates (e.g., Section 4). The estimates ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ and/or their confidence intervals may not perform well when the population effects are both clustered and skewed. In such cases, consider eliminating clustering by averaging estimates and variances within clusters (Sutton et al.¹ Section 15.3) and using these average estimates to estimate ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$.^†

3. When choosing a contrast to examine via ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$, avoid specifying extreme quantiles or rare values of the covariates (as described in Section 5.1.3). Choosing extremes can compromise the performance of ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$, though did not appear to compromise ${\widehat{P}}_{>q}(z)$ or ${\widehat{P}}_{>q}(z_0)$ themselves.

4. Apply the metric ${\widehat{P}}_{>q}(z)$ only to meta-regressions with at least 10 studies, and apply ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ only to meta-regressions at least 20 studies. The metrics can perform poorly when there are fewer studies than this. In meta-regressions of 10–20 studies, the metrics show adequate statistical performance as defined above but may have substantial sampling variability, such that the absolute error for any given sample may be large and the confidence intervals may accordingly be highly imprecise.

3 ∣. ADDITIONAL CONSIDERATIONS

3.1 ∣. Types of meta-regression covariates

At least two kinds of meta-regression covariates may be of interest. First, some covariates may be scientifically interesting in their own right because they are hypothesized to be associated with a study's true population effect size; for example, the baseline clinical characteristics of a study's subjects might be associated with a treatment's effectiveness. Second, some covariates may not be of inherent scientific interest, but rather may be associated with a study's point estimate because they relate to the bias with which its true population effect is estimated; for example, observational studies might have typically larger or smaller estimates than randomized trials due to confounding. The proposed methods, like meta-regression more broadly, aim only to characterize effect sizes conditional on study characteristics; they cannot isolate the causal effect that “changing” a study's characteristics would have on its population effect, the bias in its estimate, or both. As such, covariates falling into either or both categories can be handled identically in analysis. When considering specific biases in causal estimation, such as unmeasured confounding, the proposed methods could be combined with sensitivity analysis methods that do focus on causal estimation.^4,24

3.2 ∣. Choices of effect-size measures

There is a large literature on choosing effect-size measures with which to conduct meta-analyses; we summarize here only a few points that are not specific to the methods we have proposed here. First, analyses of binary outcomes can be conducted on either a multiplicative scale (e.g., risk ratios or odds ratios) or an additive scale (e.g., risk differences). For modeling purposes, the choice of an additive or multiplicative scale can be informed by scientific considerations regarding hypothesized mechanisms of the exposure or intervention, by statistical goodness of fit, and by parsimony.²⁵ Multiplicative measures are also sometimes used in contexts when converting studies' estimates to a common, additive scale would invoke potentially unrealistic distributional assumptions, as was the case in the second applied example.¹³ Additive measures are often more relevant to assessing interventions' effects on public health, for example when estimating the “number needed to treat” based on a risk difference or when identifying which subgroup to treat based on an additive interaction measure.²⁶ When assessing public health effectiveness in this sense, then regardless of the scale on which analyses are conducted, the effect measures should be converted to public healthrelevant measures before one considers whether effects are meaningfully strong.

Second, analyses of continuous outcomes are often conducted on the standardized mean difference scale. This scale has limitations: for example, if two interventions produce the same absolute change in the same outcome measure, but are studied in different populations in which the variability on the outcome differs substantially, the interventions would produce different standardized mean differences.^27,28 Some meta-analysts argue against the use of SMDs^27,28 or feel that the scale should never be used in any context (a point raised, for example, during the peer review of this paper). Whether and how SMDs should be used is a current debate in the field of meta-analysis. Our views are as follows. When meta-analyzing studies that measure the outcome on the same scale (e.g., blood pressure in terms of mmHg), it may often be preferable to use raw mean differences.²⁸ However, in many scientific fields, studies do not measure outcomes on exactly the same scale, as in both applied examples provided here; in such cases, using standardized mean differences may enable some approximate comparison and synthesis of effect sizes across studies. Additionally, when outcomes use arbitrary or unitless raw measures (e.g., points on a Likert scale), expressing effect sizes using standardized mean differences may provide some sense of effect sizes relative to variability in that sample, similar to measures of genetic heritability. For some outcomes, such as income or grades in high school, absolute changes may in fact be less substantively meaningful than effects relative to variability in the population, for example expressed by SMDs with appropriately chosen denominators. Alternative metrics characterize effect sizes relative to a specified minimally important difference, rather than to sample variability,²⁹ and we look forward to other metrics that might be proposed. Similar considerations and caveats apply when considering standardized versus absolute contrasts in continuous exposures.³⁰

If the meta-analyst chooses to apply the metrics we propose with effect sizes on the SMD scale, a few caveats should be kept in mind. Selecting a single threshold representing a meaningfully strong effect size across studies makes most sense when either the outcome has similar variability across studies or when, as described above, effects relative to the population are themselves of substantive interest. Second, population effects that exceed the chosen threshold may be those that arise in populations with very limited variability on the outcome measure rather than those in which the absolute effect size is very large.

4 ∣. APPLIED EXAMPLES

All data and R code required to reproduce the analyses and plots for both applied examples is publicly available and documented (https://osf.io/gs7fp/).

4.1 ∣. Sleeping targeted memory recall

In sleeping targeted memory recall (TMR), a specific sensory cue, such as an odor, is first paired with training stimuli during learning, and then the same sensory cue is presented again while the learner is sleeping. This is thought to aid natural processes of memory reactivation and consolidation during sleep. Hu et al.¹⁷ conducted a meta-analysis investigating the effects of sleeping TMR on memory consolidation, the process by which recent learned experiences are crystallized into long-term memory. They meta-analyzed studies that measured memory improvements after a period of sleep during which sleeping TMR was either used or not used. They used subset analyses and meta-regression to investigate various candidate covariates representing specific sleeping TMR methods and types of memory outcomes.

For our re-analysis, we focused on two candidate covariates: (1) the sleep stage during which the sensory cue was presented (dichotomized as slow-wave sleep versus any other stage); and (2) the duration in hours that subjects were allowed to sleep between learning and testing. We considered effect sizes larger than SMD = 0.20 to be meaningfully strong. We informed this choice of threshold by conventional criteria for a “small” effect size³¹ and by comparison to well-evidenced interventions,³ namely conscious mnemonic methods that are known to improve memory consolidation. For example, mnemonics such as rehearsal and the method of loci produce average effect sizes of approximately SMD = 0.31 compared to no training,³² and distributed practice produces effects of approximately SMD = 0.46 compared to massed practice.³³ Sleeping TMR is an unconscious and probably subtler method than these conscious mnemonics, so we selected an effect-size threshold somewhat smaller than the SMD = 0.31 to 0.46 seen for the latter. Of course, our choice of threshold is arbitrary. In practice, it is often reasonable to consider multiple thresholds or to present a plot of the estimated complementary cumulative distribution function of population effects conditional on z (i.e., ${\widehat{P}}_{>q}(z)$ as a function of the threshold q), as we illustrate below. A pointwise confidence interval could be constructed by bootstrapping selectively for the thresholds at which the value of ${\widehat{P}}_{>q}(z)$ changes.

We first robustly meta-analyzed k = 208 point estimates from 87 experiments,^‡ using a working exchangeable correlation structure to model clustering of estimates within experiments,^14,15 to estimate an overall average effect size on the standardized mean difference (SMD) scale of 0.29 (95% CI: [0.19, 0.35]; p <0.0001). We used existing methods for standard meta-analysis⁴ with cluster-bootstrapping to estimate that, overall, 49% (95% CI: [39%, 58%]) of effects were meaningfully strong by our chosen criterion.^§ To investigate effect-measure modification using our proposed methods, we conducted a robust meta-regression^14,15 using the mean model E[θ ∣ Z] = β₀ + β_1sZ_s + β_1dZ_d, where Z = (Z_s, Z_d), Z_s indicated that the cue was presented during slow-wave sleep versus any other sleep stage, and Z_d was the duration of sleep in hours. We estimated the percentage of meaningfully strong effects when the cue was presented during slow-wave sleep and subjects were allowed to sleep for 8 h (i.e., Z = (1, 8)). We also estimated the percentage of meaningfully strong effects when the cue was presented during any other sleep stage and subjects were allowed to sleep for only 2 h (i.e., Z = (0, 2)), and we estimated the difference between these two percentages.

From the meta-regression, the estimated intercept was $\widehat{{\beta }_0}=0.10$ (95% CI: [−0.16, 0.37]; p = 0.42), the estimated effect of cue presentation during slow-wave sleep was ${\widehat{\beta }}_{1s}=0.13$ (95% CI: [−0.11, 0.36]; p = 0.27), and the estimated effect of an additional hour of sleep was ${\widehat{\beta }}_{1d}=0.003$ (95% CI: [−0.02, 0.03]; p = 0.80). The estimated heterogeneity was ${\widehat{\tau }}_{ϵ}^2=0.07$. We used these estimated regression coefficients and Equation (2.4) to calculate shifted, calibrated estimates (Figure 1) and to estimate that, for cue presentation during slow-wave sleep and with 8 h of sleep, 53% of effects were meaningfully strong (95% CI: [34%, 72%]). Figure 2 shows the estimated complementary cumulative distribution function for such studies. In contrast, for cue presentation during any other sleep stage and with only 2 h of sleep, we estimated that 38% of effects were meaningfully strong (95% CI: [16%, 73%]). The estimated difference in the sleeping TMR effect, comparing these two joint levels of the covariates, was thus 15 percentage points (95% CI: [−24, 51]).

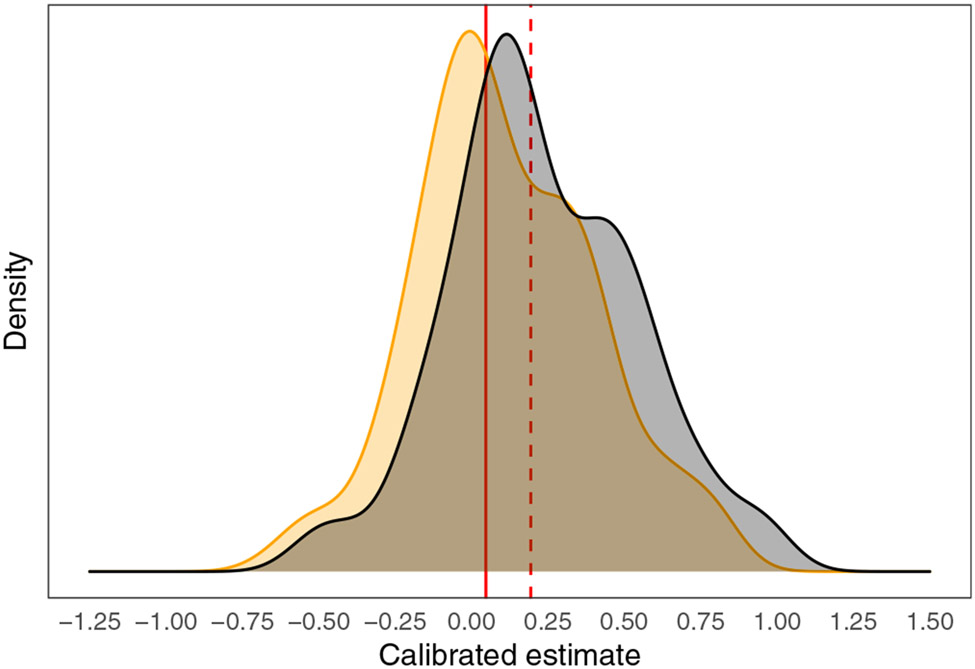
FIGURE 1.

For the applied example on memory consolidation, a smoothed density estimate for standard calibrated estimates⁵ that do not condition on covariates (black curve) and for calibrated estimates that have been shifted to covariate level Z = 0 (orange curve), as in Equation 2.4. Solid red line: the shifted threshold $q-z{\widehat{\beta }}_1$ for q = 0.20 and for covariate level z = (1,8). Dashed red line: the shifted threshold $q-z_0{\widehat{\beta }}_1$ for reference covariate level z₀ = (0,2)

FIGURE 2.

For the applied example on memory consolidation, the estimated complementary cumulative distribution function of population effects in studies with z = (1,8). The black dashed line represents the null. Shaded bands are 95% cluster-bootstrapped pointwise confidence intervals

Considering these results holistically, the point estimates from the meta-regression suggested fairly small, “statistically nonsignificant” average increases in effect sizes associated with presentation during slow-wave sleep (${\widehat{\beta }}_{1s}=0.13$ (95% CI: [−0.11, 0.36]; p = 0.27) and with an additional hour of sleep (${\widehat{\beta }}_{1d}=0.003$ (95% CI: [−0.02, 0.03]; p = 0.80). However, using our proposed metrics to compare joint levels of these two covariates simultaneously and to better characterize heterogeneity, rather than only average effect sizes, suggests that a majority of population effects were meaningfully strong when the cue was presented during slow-wave sleep and with 8 h of sleep, with the confidence interval bounded above 34%. The proposed metrics also suggested that this percentage of meaningfully strong effects may have been somewhat larger than when the cue was presented during any other sleep stage and with only 2 h of sleep, though the confidence interval was wide.

4.2 ∣. Behavior interventions to reduce meat consumption

Mathur et al.^13,34 conducted a meta-analysis to assess the effectiveness of educational behavior interventions that attempt to reduce meat consumption by appealing to animal welfare. They meta-analyzed 100 studies (from 34 articles) of such interventions, all of which measured behavioral or self-reported outcomes related to meat consumption, purchase, or related intentions and had a control condition. Mathur et al.¹³ concluded that the interventions appeared to consistently reduce meat consumption, purchase, or related intentions at least in the short term with meaningfully large effects (meta-analytic average risk ratio [RR] = 1.22; 95% CI: [1.13, 1.33] with 71% of population effects estimated to be stronger than RR = 1.1; 95% CI: [59%, 80%]) and additionally used meta-regression to assess whether various characteristics regarding interventions' contents were associated with their effect sizes. As discussed in Section 3.2, these effect sizes should, when possible, also be considered on the risk difference scale before assessing substantive meaningfulness. Although not all studies reported sufficient information to calculate risk differences directly, most studies for which a risk ratio was extracted used a median split on the outcome in the control group, so the pooled RR = 1.22 corresponds approximately to a risk difference [RD] of 0.11, and the threshold RR = 1.1 corresponds approximately to RD = 0.05. Mathur et al. noted important methodological limitations in this field, including the predominant use of outcomes based on self-reported food consumption or intentions, the potential for social desirability bias, and the potential for confounding in studies that were not randomized or that had differential dropout between intervention arms.

For our re-analysis, we estimated the percentage of meaningfully strong effects in interventions that contained graphic visual or verbal depictions of factory farms, a suspected effect-measure modifier. This component has been controversial, as it could usefully invoke cognitive dissonance³⁵ and harness deep-seated connections between physical and moral disgust,^36,37 or alternatively might backfire for some individuals.³⁵ We excluded two studies for which the meta-analysts had been unable to determine whether the intervention contained graphic content, leaving 98 analyzed studies, of which 61 (62%) had graphic interventions. We considered effect sizes larger than RD = 0.05 (corresponding approximately to RR = 1.1 in this meta-analysis) to be meaningfully large based on the effect sizes of similar behavior interventions.^¶

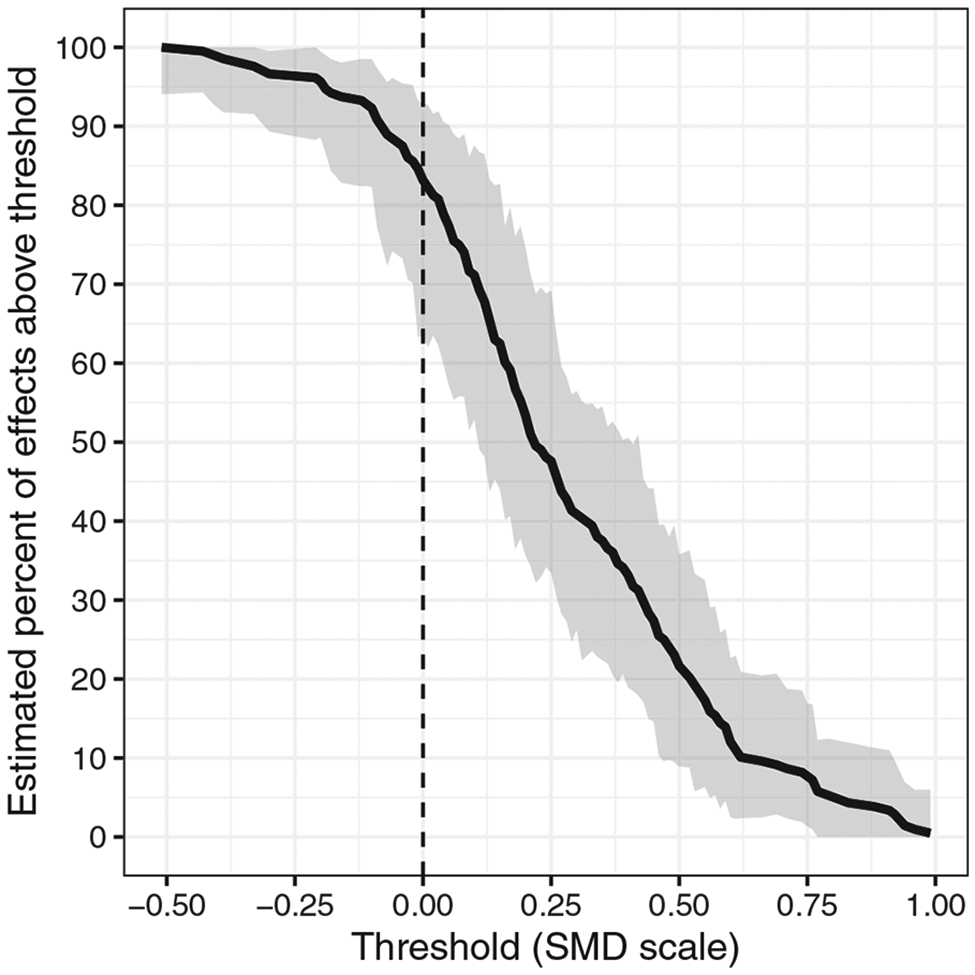
We first estimated the percentage of meaningfully strong effects among studies of graphic interventions while averaging over the distribution of all other study characteristics; that is, we fit a meta-regression with an intercept term and a covariate indicating the use of graphic content. We again used cluster bootstrapping when estimating inference for the percentage metrics. In this first meta-regression, we estimated that effect sizes in studies of graphic interventions were comparable to those in studies of non-graphic interventions (effect-measure modification RR = 0.96; 95% CI: [0.79, 1.17]) and that 70% (95% CI: [49%, 86%]) of effects in studies of graphic interventions were stronger than RR = 1.1. Figure 3 shows the estimated complementary cumulative distribution function for studies of graphic interventions.

FIGURE 3.

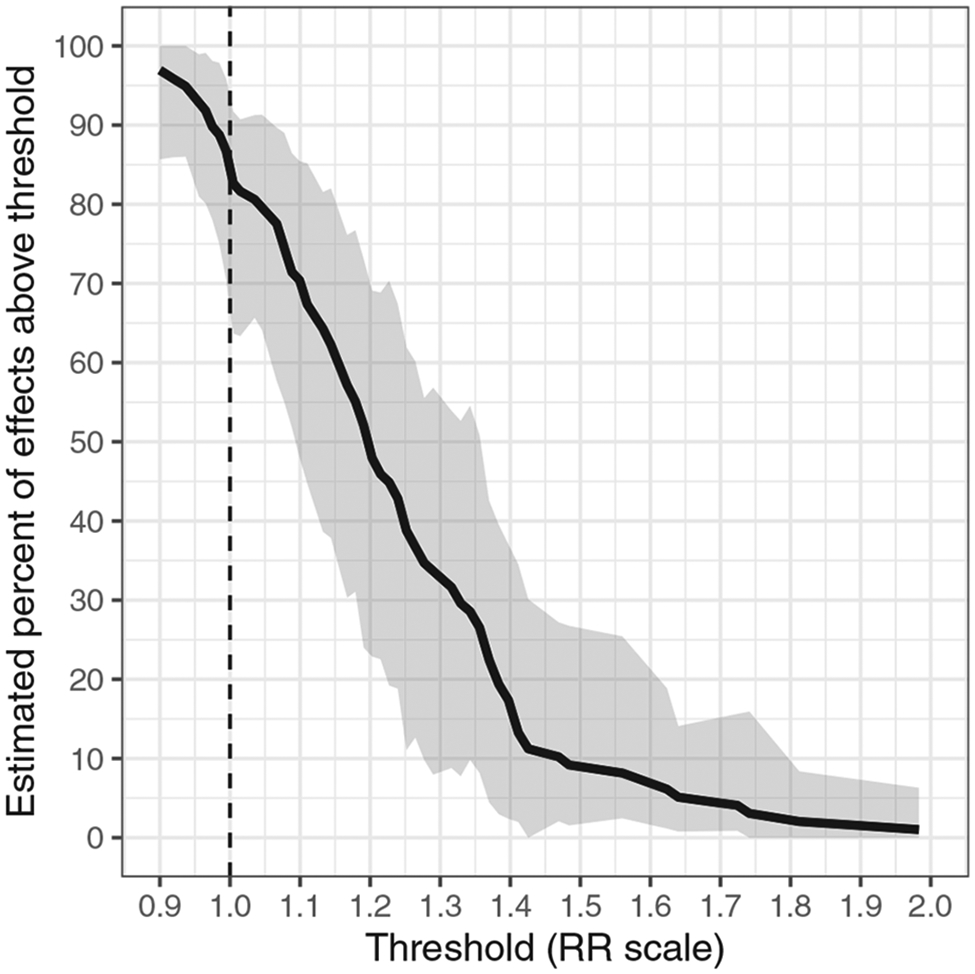
For the applied example on meat consumption, the estimated complementary cumulative distribution function of population effects in studies whose interventions contained graphic content, regardless of risks of bias. The black dashed line represents the null. Shaded bands are 95% cluster-bootstrapped pointwise confidence intervals

Second, we estimated the percentage again upon more stringently considering studies that not only used graphic interventions, but that were also of relatively high methodological quality based on four risk-of-bias covariates. We speculated that these covariates might be associated with the bias in studies' estimates, though they could also be associated with measured or unmeasured effect-measure modifiers. Specifically, we conditioned on studies' having received “low” risk-of-bias ratings¹³ (i.e., indicating higher methodological quality) with respect to the exchangeability of their intervention and control groups, their susceptibility to social desirability bias, and the external generalizability of their recruited subjects. We also conditioned on studies' use of direct behavioral measures of meat consumption (e.g., based on meal purchases at a university dining hall) or self-reports (e.g., via food frequency questionnaires) rather than mere intentions. Although a number of studies (13–53%) fulfilled each of these risk-of-bias criteria individually, no single study of a graphic intervention fulfilled all four simultaneously, which would have precluded conducting a subset analysis. However, the proposed meta-regression methods allowed us to estimate that, in hypothetical high-quality studies of graphic interventions, the percentage of meaningfully strong effects would in fact increase to 97% (95% CI: [18%, 100%]). (See the Discussion for important considerations about assuming additive risks of bias.) This finding corroborates the meta-analysts' observation that higher-quality studies in fact tended to have somewhat larger effect sizes. However, it is also important to note that the confidence interval is quite wide given the near-ceiling point estimate of 97% and is much wider than the confidence interval we obtained when conditioning only on graphic content (i.e., [49%, 86%]). This decrease in precision upon conditioning on risks of bias is itself informative: it quantitatively corroborates the meta-analysts' impression that to more precisely and confidently characterize these interventions' effects will require that future studies prioritize methodological rigor over, perhaps, the introduction of new interventions.

5 ∣. SIMULATION STUDY

5.1 ∣. Simulation methods

We conducted an extensive simulation study to assess the performance of the proposed point estimation and inference methods for ${\widehat{P}}_{>q}(z)$ and the difference ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$, including in scenarios with extreme values of the estimands, skewed population effects, and clustering.

5.1.1 ∣. Data generation

We considered a meta-regression on two covariates, Z = (Z_c, Z_b), in which Z_c was a standard normal variable and Z_b was a binary variable with prevalence 50% that we generated independently of Z_c. To generate data, we first assigned k total studies (k∈{10, 20, 50, 100, 150}) to M clusters, where M was either equal to k (for no clustering) or equal to k/2, such that each cluster contained two estimates.^** We varied the residual heterogeneity^†† ${\tau }_{ϵ}^2\in \{0.0025,0.01,0.04,0.25,0.64\}$. For scenarios with clustering, we set the between-cluster variance, Var(ζ), to $0.75\times {\tau }_{ϵ}^2$, such that 75% of the residual heterogeneity was due to between-cluster heterogeneity and 25% was due to within-cluster heterogeneity. Within each cluster, studies' random intercepts were either normally or exponentially distributed, and the distribution of total sample sizes within each study was either N_i ~ Unif (50, 150) or N_i ~ Unif (800, 900).

We generated the population effect for the i^th study in the m^th cluster from the mean model:

$$\begin{gathered} {\theta }_{mi}={\beta }_0+{\beta }_{1c}{Z}_c+{\beta }_{1b}{Z}_b+{\zeta }_m+{\gamma }_{mi} \\ {\zeta }_m\tilde{N}(0\text{Var}(\zeta ))(\text{cluster -level random effects}) \\ {\gamma }_{mi}\tilde{N}(0{\tau }_{ϵ}^2-\text{Var}(\zeta ))\text{or}{\gamma }_{mi}\stackrel{\stackrel{~}{}}{\text{Exp}}\left(({\tau }_{ϵ}^2-\text{Var}(\zeta ){)}^{-1∕2}\right)(\text{study -level random effects}) \end{gathered}$$

We fixed the intercept to β₀ = 0 and covariate effect strengths to β_1c. = 0.5 and β_1b = 1. We held constant these effect sizes for all simulation scenarios but manipulated the parameters of interest, namely P _>q(z) and the difference P_>q(z) − P_>q(z₀), across a broad range by choosing the threshold q appropriately. We considered three choices of covariate levels of interest, (Z_c, Z_b), which are described in Table 1. Within each cluster (suppressing the "m" subscript notation) and for each of k meta-analyzed studies, we generated a population effect, θ_i, on the raw mean difference scale from a normal distribution or a shifted exponential distribution. We chose each distribution's parameters to provide the desired intercept β₀ and heterogeneity ${\tau }_{ϵ}^2$.

TABLE 1.

Covariate contrasts used in the simulation study. z₀ and z list the value of the continuous covariate followed by the value of the binary covariate.

Acronym for covariate contrast	z 0	z	E[θ ∣ Z = z0]	E[θ ∣ Z = z]	Description
B (“binary”)	(0, 0)	(0, 1)	0	1	Compares levels of the binary covariate while holding the continuous covariate constant at its mean.
BC (“binary and continuous”)	(−0.5, 0)	(0.5, 1)	−0.25	1.25	Compares levels of the binary covariate along with a contrast in the continuous covariate from its 31st percentile to its 69th percentile.
BC-rare (“binary and continuous involving a rare covariate value”)	(2, 0)	(0.5, 1)	1	1.25	Compares levels of the binary covariate along with a contrast in the continuous covariate from its 98th percentile to its 69th percentile.

We then simulated subject-level data for a control group with mean 0 and for a treatment group with mean θ_i; each group was of size N_i/2 with a standard deviation of 1. Thus, the within-study standard error of the estimated mean difference, ${\widehat{\theta }}_i$, was approximately ${\widehat{\sigma }}_i=\sqrt{4∕N_i}$. For the meta-regression, the proportion of the total residual variance attributable to residual effect heterogeneity,^43,44 I², was approximately ${\tau }_{ϵ}^2∕\left({\tau }_{ϵ}^2+4∕E[N]\right)$ (Table 2). We chose values of q to vary the first parameter of interest, P(z), in {0.05, 0.10, 0.20, 0.50}. We then calculated the parameter P _{> q}(z₀) and difference P _{> q}(z) − P _{> q}(z₀) based on q, β_1c, β_1b, ${\tau }_{ϵ}^2$, and the appropriate distributional parameters. Table 3 summarizes the full-factorial design of the simulation study. There were 2400 unique sets of parameters, each analyzed with all of the estimation methods described below.

TABLE 2.

Approximate values of relative residual heterogeneity (I²) for each combination of simulation parameters pertaining to the mean within-study sample size (E[N]) and residual heterogeneity (${\tau }_{ϵ}^2$)

	${\tau }_{ϵ}^2=0.0025$	${\tau }_{ϵ}^2=0.01$	${\tau }_{ϵ}^2=0.04$	${\tau }_{ϵ}^2=0.25$	${\tau }_{ϵ}^2=0.64$
E[N] = 100	0.06	0.20	0.50	0.86	0.94
E[N] = 850	0.25	0.68	0.89	0.98	0.99

TABLE 3.

Possible values of data-generation simulation parameters, manipulated in a full-factorial design

Covariate contrast	k	E[N]	${\tau }_{ϵ}^2$	Clustered	γ distribution	P(z)
B	10	100	0.0025	No: M = k	Normal	0.05
BC	20	850	0.01	$Var(\zeta )=0.75\times {\tau }_{ϵ}^2\text{Yes:}M=k∕2$	Exponential	0.10
BC-rare	50		0.04			0.20
	100		0.25			0.50
	150		0.64

5.1.2 ∣. Estimation procedures

We assessed both the one-stage and the two-stage methods described in Section 2.2. For both methods, for each scenario and iteration, we first estimated the metaregression parameters using a meta-regression model with robust variance estimation as recommended in Section 2.2; for scenarios with clustering, we used a hierarchical working model.¹⁴ In this approach, weighted least squares is used to estimate the meta-regression coefficients. The heterogeneity τ² is estimated using a method-of-moments estimator detailed elsewhere.¹⁴ We fit this model using the robumeta package in R.¹⁵

Then, for the one-stage method, we use the metaregression estimates to directly calculate shifted calibrated estimates as in Equation (2.3). For the two-stage method, as described in Section 2.2, we shifted the point estimates themselves and then fit a standard intercept-only meta-analysis (without covariates) to the shifted estimates, thus obtaining calibrated estimates in the usual manner for a standard meta-analysis.⁵ This second-stage meta-analysis used the Dersimonian-Laird heterogeneity estimator,²³ the usual choice for calculating calibrated estimates.⁵ We fit the second-stage meta-analysis using the R package metafor⁴⁵ and obtained the calibrated estimates using MetaUtility.⁴⁶

To obtain inference, we bootstrapped the meta-regression estimation process as well as, for the two-stage method, the standard meta-analysis estimation process. In scenarios with clustering, we used the cluster bootstrap and constructed bias-corrected and accelerated confidence intervals^19,20 as described in Section 2.1. We implemented bootstrapping using custom-written code and the R package boot.⁴⁷

5.1.3 ∣. High-level simulation structure

We ran simulations representing all 2400 possible combinations of the varying data generation parameters (Table 3). For computational convenience, we generated separate datasets for the one-stage and two-stage methods, resulting in a total of 4800 “scenarios.” We ran 500 simulation iterates per scenario^‡‡ and used 1000 bootstrap iterates for all inference.

5.1.4 ∣. Exploration of bootstrap bias corrections

Second, we explored whether the bootstrap estimates could be used to correct any bias in the estimation of ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$; we calculated the bias-corrected versions of these estimates by subtracting from each original estimate the bootstrapped estimate of its bias (i.e., the difference between the mean of the bootstrapped sampling distribution and the estimate from the original sample itself; Davison & Hinkley,²¹ Section 2.1.2). Because the sampling distributions of ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ can be highly skewed when their estimands are close to 0 or 1, we speculated that applying a variance-stabilizing transformation to the estimates might make the estimators more approximately pivotal and therefore improve the fidelity of the bootstrapped sampling distribution.⁴⁸ Accordingly, we calculated bias-corrected versions of the estimates with and without first taking the logit of the proportion estimates after truncating the proportions to [0.001, 0.999].

5.1.5 ∣. Metrics of estimators' performance

For each scenario, we assessed the point estimators' performance and variability in terms of their mean bias and mean absolute error, defined as follows for a generic parameter ω:

$$\begin{gathered} \text{Bias}=\frac{1}{500}\sum _{r=1}^{500}({\widehat{\omega }}_r-\omega ) \\ \text{Absolute error}=\frac{1}{500}\sum _{r=1}^{500}\mid {\widehat{\omega }}_r-\omega \mid \end{gathered}$$

where r indexes simulation iterates. Second, to compare of our proposed estimators' performance to that of standard estimators from meta-regression (i.e., coefficient estimates and heterogeneity estimates), we assessed relative bias, defined for a generic nonnegative parameter ω as:

$$\text{Relative bias}=\frac{1}{500}\sum _{r=1}^{500}\frac{{\widehat{\omega }}_r-\omega }{\omega }$$

For each scenario, we assessed inference in terms of the mean coverage and mean width of 95% confidence intervals. When summarizing results across scenarios, we report medians because the metrics were often skewed across scenarios. Regarding inference, we also report the proportion of scenarios for which coverage was less than 85%. To help characterize variability in results across scenarios, we report 10^th and/or 90^th percentiles of the performance metrics across scenarios.^§§ Throughout, we collapse over the results of the one-stage and two-stage method because they performed comparably.

5.2 ∣. RESULTS

Comprehensive results for all simulation scenarios, including additional performance metrics, are publicly available as a dataset (https://osf.io/gs7fp/). A small percentage of the 4800 total scenarios (2.5%) proved computationally infeasible to run because their data generation parameters consistently produced extreme datasets for which standard meta-regression estimation failed. We analyzed the remaining 4679 scenarios, representing 2388 of the 2400 possible combinations of data-generation parameters.

5.2.1 ∣. High-level summary of all simulation results

In general, performance was better for ${\widehat{P}}_{>q}(z)$ than for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$. Performance was typically better in larger meta-analyses (i.e., larger k), those with larger numbers of studies (i.e., larger E[N]), and those with normal, independent population effects and was typically worse in meta-analyses with other characteristics. Performance for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ declined when the covariate contrast involved an extreme quantile of one of the covariates. (In the Supplementary material, we more specifically describe results of regressing these performance metrics on main effects of the aforementioned six meta-analysis characteristics.)

In the case of ${\widehat{P}}_{>q}$, coverage was conservative (> 95%) for small values of k and declined somewhat as k increased. Coverage was slightly below nominal for k = 150 (93%; 10^th percentile: 88%); additional diagnostics regarding the bootstrap samples preliminarily suggested that this might have reflected infidelity of the bootstrap sampling distribution to the actual sampling distribution (Section 5.2.2). Below, we speculate based on statistical theory on possible mechanisms for this finding, though precisely testing these proposed mechanisms was beyond the scope of the present simulation study. This could be investigated in future work.

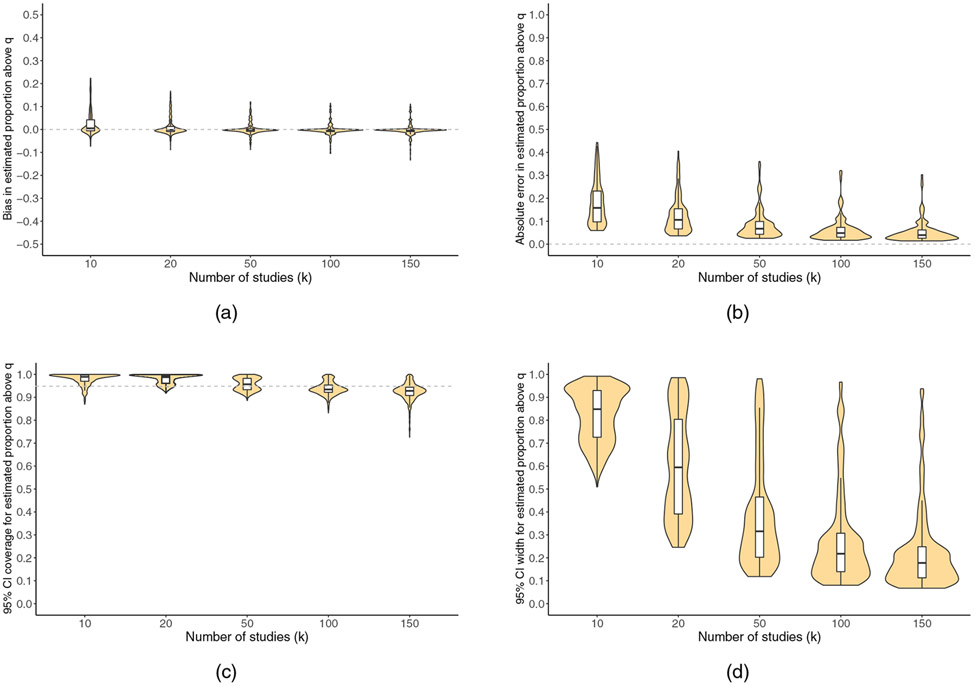
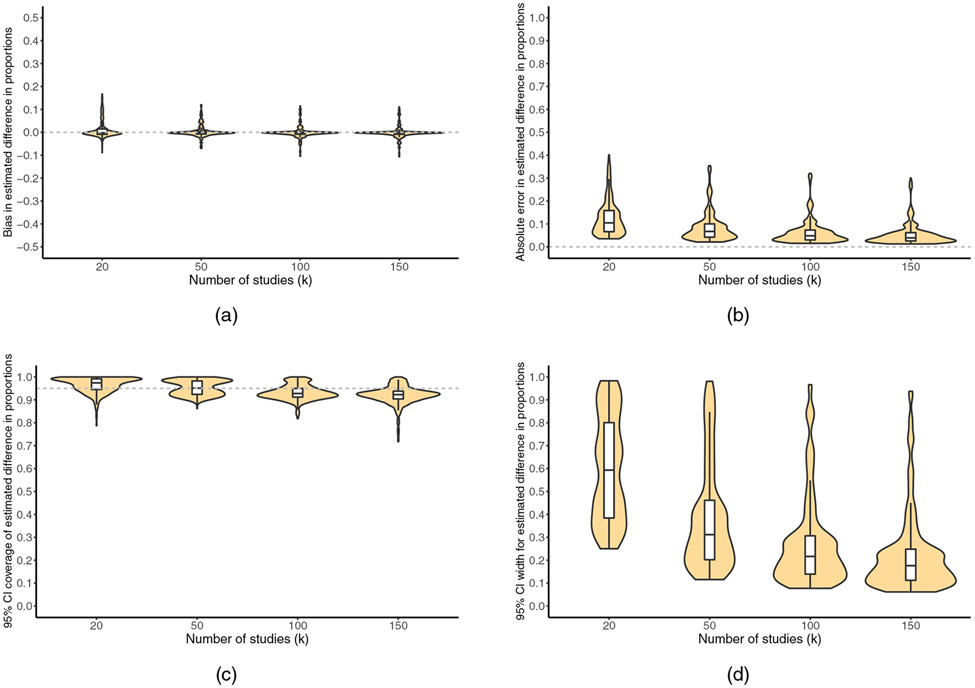
Figures 4 and 5 are violin plots (i.e., mirrored density plots) showing, for simulation scenarios fulfilling the guidelines given in Section 2.3, the distribution of each performance metric stratified by k. The Supplementary material contains similar violin plots showing the distribution of the performance metrics across all scenarios, as well as stratified by additional characteristics of the metaanalysis (k, E[N], the presence of clustering, the population effect distribution, the covariate contrast, and the true P _{> q}). The plots are provided to illustrate the extent of variability in performance metrics that might be expected across datasets (although some of the observed variability represents Monte-Carlo error).

FIGURE 4.

For ${\widehat{P}}_{>q}(z)$, violin plots showing the number of meta-analyzed studies (k) versus (a) bias, (b) absolute error, (c) 95% confidence interval coverage, and (d) 95% confidence interval width. White boxplots display the median, 25^th percentile, and 75^th percentile. Horizontal dashed reference lines represent perfect performance

FIGURE 5.

For ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$, violin plots showing the number of meta-analyzed studies (k) versus (a) bias, (b) absolute error, (c) 95% confidence interval coverage, and (d) 95% confidence interval width. White boxplots display the median, 25^th percentile, and 75^th percentile. Horizontal dashed reference lines represent perfect performance

5.2.2 ∣. Results for ${\widehat{P}}_{>q}(z)$

Point estimation.

Table 4 shows results for ${\widehat{P}}_{>q}(z)$. Across all scenarios, ${\widehat{P}}_{>q}(z)$ was approximately unbiased (bias = 0.00; 10^th percentile: −0.02, 90^th percentile: 0.08). However, because the estimator had substantial variability in some scenarios, it did have a non-negligible absolute error of 0.07 (90^th percentile: 0.23). The magnitude of the bias of ${\widehat{P}}_{>q}(z)$ did not seem to differ systematically by characteristics of the simulation scenarios that would be observable in practice (i.e., not unobservable parameters).

TABLE 4.

Main simulation results for ${\widehat{P}}_{>q}(z)$ in all scenarios, in scenarios with normally distributed population effects, and in scenarios fulfilling the reporting guidelines. Values are medians across scenarios with 10^th and 90^th percentiles given in parentheses. No. scenarios: the number of scenarios analyzed. Coverage: coverage of 95% confidence intervals. Cov. <85%: proportion of scenarios with coverage <85%. CI width: width of 95% confidence intervals. Width >0.90: proportion of scenarios with very large average CI width (>0.90). These results are discussed in Section 5.2.2

Scenarios	No. scenarios	${\widehat{\mathit{P}}}_{\mathit{z}}$ bias	${\widehat{\mathit{P}}}_{\mathit{z}}$ abs. error	${\widehat{\mathit{P}}}_{\mathit{z}}$ rel. bias	$\widehat{\mathit{E}}[\theta \mid \mathit{Z}=\mathit{z}]$ rel. bias	${\widehat{\tau }}_{ϵ}^2$ rel. bias	${\widehat{\mathit{P}}}_{\mathit{z}}$ coverage	${\widehat{\mathit{P}}}_{\mathit{z}}$ cov. < 85%	${\widehat{\mathit{P}}}_{\mathit{z}}$ CI width	${\widehat{\mathit{P}}}_{\mathit{z}}$ width >0.90
All	4679	0 (−0.02, 0.08)	0.07 (0.03, 0.23)	−0.01 (−0.18, 0.29)	0.05 (0.01, 0.17)	0.35 (0.14, 1.41)	0.95 (0.89, 1)	0.05	0.37 (0.12, 0.89)	0.10
Normal effects	2350	0 (−0.02, 0.02)	0.07 (0.03, 0.22)	−0.02 (−0.11, 0.20)	0.05 (0.01, 0.17)	0.32 (0.13, 1.41)	0.96 (0.91, 1)	0	0.37 (0.13, 0.90)	0.10
Not clustered exponential effects (i.e., scenarios fulfilling guidelines)	3522	0 (−0.02, 0.05)	0.07 (0.03, 0.22)	−0.02 (−0.13, 0.20)	0.05 (0.01, 0.17)	0.35 (0.14, 1.39)	0.96 (0.91, 1)	0.01	0.37 (0.12, 0.91)	0.11

Exploration of bootstrap bias corrections.

Bias-correcting ${\widehat{P}}_{>q}(z)$ via the bootstrap estimates did not improve and sometimes exacerbated bias, even when first taking the logit; we speculate this reflects the estimator's non-pivotality,⁴⁸ the non-existence of an Edgeworth expansion for sample quantiles,²¹ and potentially a failure to reach the appropriate asymptotics regarding the bootstrap sampling distribution in these datasets of 10 to 150 observations. For these reasons, the slightly below-nominal coverage seen at k = 150 might reflect what is essentially bias in the bootstrap sampling distribution. Future work could consider using a double bootstrap to correct such bias.²¹

Coverage.

Across all scenarios, coverage was nominal (95%) on average, though was less than 85% in 5% of scenarios. The distribution of population effects and the presence of clustering appeared to affect coverage, with normal effects and unclustered effects producing the best coverage. Among scenarios with normally distributed population effects, none (0%) had coverage less than 85% (Table 4). When considering the scenarios fulfilling the reporting guidelines in Section 2.3 (i.e., scenarios whose population effects were not both exponentially distributed and clustered), 1% of scenarios had coverage less than 85%. In these recommended scenarios, the average confidence interval width was 0.37, and the confidence interval was highly imprecise (width >0.90) in 11% of scenarios. Scenarios with k ≤ 20 often had average confidence interval widths greater than 0.60, particularly when the meta-analyzed studies had average sample sizes of 100 rather than 850. Specifically, with k ≤ 20, the average width was 0.74 (90^th percentile: 0.95), and the confidence intervals were highly imprecise in 24% of scenarios.

Diagnostics regarding bootstrapped inference.

The standard deviation of the bootstrap sampling distribution typically underestimated the empirical standard error of ${\widehat{P}}_{>q}(z)$, suggesting that when poor coverage occurred, it likely reflected, at least in part, infidelity of the bootstrap sampling distribution to the true sampling distribution. We also investigated whether characteristics of the bootstrap sampling distribution could be used as diagnostics for the confidence interval to perform poorly. However, characteristics such as the bootstrap distribution's skewness and the percentage of iterates for which the meta-regression or ${\widehat{P}}_{>q}(z)$ were not estimable were not associated with the performance of the confidence interval.

5.2.3 ∣. Results for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$

Point estimation.

Table 5 shows results for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$. Across all scenarios, ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ was approximately unbiased (bias = 0.00; 10^th percentile: −0.02; 90^th percentile: 0.08). Like ${\widehat{P}}_{>q}$, this estimator also had considerable sampling variability in some scenarios, resulting in an absolute error of 0.08 (90^th percentile: 0.24). The performance of the point estimate ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ did appear somewhat related to observable characteristics of the simulation scenarios: as was the case for ${\widehat{P}}_{>q}(z)$, considering only scenarios with normal population effects somewhat improved the absolute error to 0.07 (vs. 0.08 in all scenarios). Additionally, avoiding very rare covariate values when defining the contrast of interest seemed to improve point estimation: excluding scenarios in which the z₀ level involved the 98^th quantile of the continuous covariate (termed “BC-rare scenarios”; Table 1) improved the absolute error to 0.07. Including only scenarios fulfilling the reporting guidelines given in Section 2.3 (i.e., scenarios with k ≥ 20 that did not use the BC-rare contrast and did not have clustered exponential effects) slightly improved the absolute error to 0.06 (90^th percentile: 0.17). As with ${\widehat{P}}_{>q}(z)$, bias-correcting ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ via the bootstrap estimates was not effective.

TABLE 5.

Main simulation results for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ in all scenarios, in scenarios with normally distributed population effects, when excluding scenarios whose covariate contrast used an extreme quantile of the continuous covariate (“not BC-rare”), and in scenarios fulfilling the reporting guidelines. Values are medians across scenarios with 10^th and 90^th percentiles given in parentheses. No. scenarios: the number of scenarios analyzed. Coverage: coverage of 95% confidence intervals. Cov. <85%: proportion of scenarios with coverage <85%. CI width: width of 95% confidence intervals. Width >0.90: proportion of scenarios with very large average CI width (>0.90). These results are discussed in Section 5.2.3

Scenarios	No. scenarios	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ bias	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ abs. error	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ rel. bias	$\widehat{\mathit{E}}[\theta \mid \mathit{Z}=\mathit{z}]$ rel. bias	${\widehat{\tau }}_{ϵ}^2$ rel. bias	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ coverage	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ cov. < 85%	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ CI width	${\widehat{\mathit{P}}}_{\mathit{z}}$ width >0.90
All	4679	0 (−0.02, 0.08)	0.08 (0.03, 0.24)	−0.02 (−0.26, 0.33)	0.05 (0.01, 0.17)	0.35 (0.14, 1.41)	0.92 (0.67, 0.99)	0.24	0.39 (0.12, 0.90)	0.10
Normal effects	2350	0 (−0.03, 0.01)	0.07 (0.03, 0.23)	−0.03 (−0.18, 0.16)	0.05 (0.01, 0.17)	0.32 (0.13, 1.41)	0.92 (0.72, 0.99)	0.18	0.39 (0.13, 0.90)	0.10
Not BC-rare	3098	0 (−0.02, 0.09)	0.07 (0.03, 0.23)	−0.01 (−0.17, 0.33)	0.05 (0.01, 0.17)	0.35 (0.14, 1.39)	0.93 (0.84, 0.99)	0.11	0.37 (0.12, 0.89)	0.09
Not BC-rare nor clustered exponential effects; k ≥ 20 (i.e., scenarios fulfilling guidelines)	1908	0 (−0.02, 0.03)	0.06 (0.02, 0.17)	−0.02 (−0.14, 0.15)	0.04 (0.01, 0.13)	0.29 (0.13, 1.25)	0.94 (0.9, 0.99)	0.02	0.29 (0.11, 0.81)	0.05

Coverage.

Across all scenarios, coverage was somewhat below nominal (92%) on average and was less than 85% in 24% of scenarios. When restricting attention to scenarios fulfilling the guidelines, coverage was close to nominal (94%; 10^th percentile: 90%), and 2% of scenarios had coverage less than 85% (Table 5). As described above, this set of restrictions also produced the most improvement in the absolute error. In these scenarios, the average confidence interval width was 0.29, and the confidence interval was highly imprecise (width > 0.90) in 5% of scenarios. As with ${\widehat{P}}_{>q}(z)$, and characteristics of the bootstrap sampling distribution did not predict confidence interval coverage.

5.3 ∣. Exploratory investigations of other point estimation methods

As noted above, applying a bootstrap bias correction directly to ${\widehat{P}}_{>q}(z)$ or ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ was not effective. Given the bias seen in ${\widehat{\tau }}_{ϵ}^2$ (Tables 4 and 5), we also experimented with using bootstrapping to bias-correct the meta-regression estimates ${\widehat{\tau }}_{ϵ}^2$ as well as ${\widehat{\beta }}_0$, ${\widehat{\beta }}_{1c}$, and ${\widehat{\beta }}_{1b}$ before using them to calculate the calibrated estimates via Equation (2.4). (The bias in the latter three coefficient estimates was, however, typically small and was an order of magnitude smaller than that seen in ${\widehat{\tau }}_{ϵ}^2$.) That is, we bootstrapped the meta-regression model (again with 1000 iterates) and bias-corrected each of these meta-regression estimates by subtracting the bootstrapped estimate of its bias. We then calculated our proposed estimators using these bias-corrected estimates. As a benchmark representing the best possible bias reduction in ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ that could be achieved if, hypothetically, all bias in the meta-regression estimates were eliminated, we also calculated calibrated estimates using the actual parameters of the meta-regression rather than estimates.

We applied these approaches in the 32 “worst” scenarios from the main simulation, defined as the unique scenarios for which the relative bias of ${\widehat{P}}_{>q}(z)$, the relative bias of ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$, the coverage of the confidence interval for ${\widehat{P}}_{>q}(z)$, or the coverage of the confidence interval for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ were among the 10 worst for that performance metric across all scenarios analyzed with the one-stage method and in BC-rare scenarios. We focused on BC-rare scenarios because, as noted above, these scenarios seemed to particularly affect estimation of ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$; we focused on the one-stage method because it performed comparably to the two-stage method. To avoid reversion to the mean⁴⁹ that could arise from comparing results in the worst scenarios to those in the main simulations, we analyzed these scenarios via the usual one-stage method again in the newly generated datasets (a replication of the main simulation results).

Like the bootstrapped bias corrections applied directly to our proposed estimators in the main simulations, bias corrections on the meta-regression estimates did not improve and sometimes exacerbated bias in the proposed estimators (Table 6). However, using the meta-regression parameters rather than estimates improved bias by at least twofold. This suggests that for scenarios in which ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ performed poorly, a substantial portion, though not all, of their bias was attributable to bias in the standard meta-regression estimates that propagated to ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ via the calibrated estimates. We return to this point in the Discussion. Because these methods did not improve bias, we did not assess their impact on inference.

TABLE 6.

Secondary simulation results for ${\widehat{P}}_{>q}$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ in the 32 worst BC-rare scenarios when applying the basic one-stage method used in the main simulations, when bias-correcting the meta-regression estimates, and when using the true meta-regression parameters rather than estimates. Abs. bias: absolute error. Rel. bias: relative absolute error. These results are discussed in Section 5.3

Method	${\widehat{\mathit{P}}}_{\mathit{z}}$ bias	${\widehat{\mathit{P}}}_{\mathit{z}}$ abs. error	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ bias	${\widehat{\mathit{P}}}_{\mathit{z}}-{\widehat{\mathit{P}}}_{{\mathit{z}}_0}$ abs. error
One-stage	0.07	0.12	0.03	0.11
One-stage with bias-corrected meta-regression estimates	0.08	0.13	0.04	0.11
One-stage with meta-regression parameters (benchmark)	0.01	0.06	0.00	0.04

6 ∣. DISCUSSION

We have proposed straightforward, easily interpreted statistical metrics for meta-regression that characterize the percentage of meaningfully strong population effects for a specified level of the covariates and that further enable comparison of these percentages between two different levels of the covariates. As such, we believe the proposed metrics could usefully supplement standard reporting, which focuses only on average differences between levels of each covariate in turn. We provided simple R code to estimate the proposed metrics (Supplementary material or https://osf.io/gs7fp/).

These methods have limitations, including those inherent to meta-regression.⁵⁰ For example, even when the meta-analyzed studies are randomized, the covariates are not randomized across studies, so their effects on the outcome may be confounded.^50,51 That is, it might not be the covariate itself that causally affects the study's primary exposure effect size, but rather another variable associated with it. The difference ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ therefore represents an average difference between studies with covariates z versus those with z₀, not the causal effect of “changing” a study's covariates from z₀ to z. Similar considerations apply if using the proposed metrics to consider effect sizes in a hypothetical target population.⁵² Meta-regression and our proposed metrics allow consideration of combinations of covariates that do not occur in the data, but one should not extrapolate unreasonably beyond the observed data. Our proposed methods could validly be used to estimate which levels of the covariates have the largest ${\widehat{P}}_{>q}(z)$; but if doing so, ${\widehat{P}}_{>q}(z)$ for the apparently “best” levels may then be biased upward due to statistical reversion to the mean,⁴⁹ as is the case more generally with point estimation after conditioning on the size of the estimate. In relatively small meta-regressions, the BCa bootstrap (particularly for ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$) may fail to converge or may yield wide confidence intervals spanning most or all of the possible range [0, 1], which should instill appropriate circumspection about what can be learned from a relatively small meta-regression. Finally, as in meta-analysis more broadly, limitations in the statistics reported in the meta-analyzed papers often hampers extracting effect sizes on a scale that is comparable across studies and is substantively meaningful (Section 3.2); this problem would be mitigated if authors of original research were to publicly release deidentified datasets at the individual participant level.

The simulation results suggested that ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ were approximately unbiased on average. However, it is important to note that due to the estimators' variability, they did show non-negligible absolute errors of 0.07 and 0.06. When we specifically investigated the scenarios in which the estimators showed the most bias, almost all of the bias in ${\widehat{P}}_{>q}(z)$ and ${\widehat{P}}_{>q}(z)-{\widehat{P}}_{>q}(z_0)$ appeared to propagate to the estimators from the standard meta-regression estimate ${\widehat{\tau }}_{ϵ}^2$, which itself showed non-negligible bias (e.g., relative bias = 0.35) and perhaps to a lesser extent from the meta-regression coefficient estimates (Table 6). We used a moment-type estimator that accommodates clustering;^14,15 future work could investigate whether other heterogeneity estimators, such as the restricted maximum likelihood estimator, would perform better in this context.⁵³ Heterogeneity estimation is indeed a longstanding challenge in meta-analysis,^16,53 and developing methods to allow robust and more efficient heterogeneity estimation is an active research area. As methods continue to improve, we expect that their use will also naturally propagate to the performance of the proposed estimators. When using current heterogeneity estimation methods,¹⁴ we provided practical guidelines informed by the simulation results regarding performance across numerous scenarios with varying characteristics.

The simulation study itself was limited in scope for computational reasons: the 4800 scenarios we considered certainly do not represent the entire range of population effect distributions, sample sizes, and other characteristics that could potentially affect the estimators' performance. It would be useful to conduct more extensive simulation studies, for example assessing many more distributions of population effects, types of covariates (including clustered or correlated covariates), and choices of contrast.

As we have noted, our proposed methods are semiparametric in that, when the meta-regression is itself fit using semiparametric methods,¹⁴ the mean model must be correctly specified. If the mean model is misspecified, the meta-regression estimates themselves may be biased,¹⁴ and this bias may also propagate to our proposed estimators. In particular, meta-regression specifications usually include only main effects of the covariates; estimating interactions among the covariates with reasonable precision would typically be infeasible without quite large numbers of studies.²⁶ By omitting potential interactions from the mean model, for example, any covariates representing risks of bias are assumed to operate additively on the effect size scale on which the meta-analysis is conducted. Similarly to the applied example regarding dietary interventions, we might meta-regress studies' log-RR estimates on main effects of external generalizability and of susceptibility to social desirability bias, without including an interaction between the two covariates. This model assumes that the average biases produced by a lack of generalizability and by the susceptibility to social desirability bias are additive on the log-RR scale and multiplicative on the RR scale. However, in principle, the biases might in fact interact: subjects who were recruited because they were already highly motivated to change their behavior (representing poor generalizability) might be more likely to lie about their behavior to reduce cognitive dissonance or to conform to perceived pressure from the experimenters (representing a particularly pronounced social desirability bias effect), whereas a general sample of subjects who were not already motivated to change their behavior may report their behavior with less regard to perceived social desirability. Such effects would not be captured by a model with only main effects. However, with these caveats in mind, we hope that these methods will help investigators better understand how results from meta-analyses might vary across study characteristics.

Highlights.

What is already known

• Meta-regression analyses usually focus on differences in average effects between levels of each covariate.

• While useful, these metrics have limitations: they consider each covariate individually, rather than in combination, and they characterize only the mean of a potentially heterogeneous distribution of effects.

What is new

• We propose new metrics that address the questions: “For a given joint level of the meta-regression covariates, what percentage of the population effects are meaningfully strong?” and “For any two joint levels of the covariates, what is the difference between these percentages of meaningfully strong effects?”

• These metrics characterize the heterogeneous distribution of effects conditional on the covariates (not just the distribution's mean), and they enable direct comparison of joint levels of covariates.

• The first and second metrics above can be applied to meta-regressions with at least 10 and at least 20 studies, respectively. The metrics should be reported along with confidence intervals. Caution is warranted if the point estimates are both clustered and skewed. When using the second metric, the specified contrast should not use extreme covariate values.

Potential impact for RSM readers outside the authors' field

• These metrics could facilitate assessing and communicating how evidence strength differs for studies with different sets of characteristics.

DATA AVAILABILITY STATEMENT

All code and data required to reproduce the simulation study and applied examples are publicly available and documented, along with a simple code example (https://osf.io/gs7fp/).