Abstract
To elucidate the molecular mechanisms underlying genetic variants identified from genome-wide association studies (GWAS) for a variety of phenotypic traits encompassing binary, continuous, count, and survival outcomes, we propose a novel and flexible method to test for mediation that can simultaneously accommodate multiple genetic variants and different types of outcome variables. Specifically, we employ the Intersection-union test approach combined with likelihood ratio test to detect mediation effect of multiple genetic variants via some mediator (for example, the expression of a neighboring gene) on outcome. We fit high-dimensional generalized linear mixed models under the mediation framework, separately under the null and alternative hypothesis. We leverage Laplace approximation to compute the marginal likelihood of outcome and use coordinate descent algorithm to estimate corresponding parameters. Our extensive simulations demonstrate the validity of our proposed methods and substantial, up to 97%, power gains over alternative methods. Applications to real data for the study of Chlamydia trachomatis infection further showcase advantages of our method. We believe our proposed methods will be of value and general interest in this post-GWAS era to disentangle the potential causal mechanism from DNA to phenotype for new drug discovery and personalized medicine.
1. Introduction
Dissection of mediation pathways underlying genetic association will enhance understanding of disease mechanisms and biomarker development. An example is Chlamydia trachomatis infection. Chlamydia is the leading bacterial sexually transmitted infection in the United States (Centers for Disease Control and Prevention, 2019). Infection is often asymptomatic and after ascending to the upper genital tract may cause severe reproductive morbidities in women. Repeated infection leads to worse disease. Host genetics shapes susceptibility to chlamydia disease and/or reinfection (Bailey et al., 2009; Taylor et al., 2017; Zheng et al., 2018). DNA biomarkers for susceptibility to ascension or risk of reinfection are critically needed for targeted screening for women at high risk of disease and vaccine development. Genome-wide association studies (GWAS) provide candidate loci, but lack mechanistic interpretations. Although expression quantitative trait loci (eQTL) mapping can provide mechanistic hypotheses, GWAS and eQTL both only analyze two sources of data. There is a significant unmet need for simultaneously modeling all three sources of data (namely, genetic variants, gene expression and final outcome) by directly testing the mediation effects of multiple correlated single nucleotide polymorphisms (SNPs) via the expression of some gene (e.g., eGene associated with the eQTL SNP) on chlamydia ascension (binary outcome) and reinfection (time-to-event outcome).
Mediation analysis was firstly proposed by Baron and Kenny to study the association between an independent variable and an outcome by adding an intermediate variable, which is called the mediator (Baron and Kenny, 1986). In genetics and genomics studies, researchers are interested in testing mediation effects of the genetic variant(s), on the outcome through a certain mediator (e.g., the expression level of a neighboring gene). Non-Gaussian outcomes, such as binary, count and time-to-event outcomes (e.g. disease status, time until death), are commonly present in mediation analyses but have been under-studied. Huang et al developed mixed model based methods that can handle binary and time-to-event outcomes, but assume a priori that the genetic variants under testing are eQTLs (Huang et al., 2015; Huang, Cai and Kim, 2016).
We have previously proposed a method, SMUT, to assess mediation effect of high-dimensional genetic variants on any continuous outcome (Zhong et al., 2019). To the best of our knowledge, none of the existing methods can jointly test mediation effects of multiple correlated SNPs (not necessarily all eQTLs) on a non-Gaussian outcome. Here, we propose a generalized multi-SNP mediation intersection-union test to evaluate mediation effects of multiple correlated SNPs on a non-Gaussian outcome without prior knowledge of eQTLs. Both SMUT and methods proposed in this work are extensions of Baron and Kenny’s framework and leverage intersection-union test (IUT) (Berger and Hsu, 1996) to decompose mediation into two separate regression models. While our earlier SMUT method handles only Gaussian outcome, methods proposed here allow non-Gaussian outcomes by adopting the generalized linear mixed model (GLMM) (McCulloch, Searle and Neuhaus, 2008) or the mixed effects Cox proportional hazards (PH) model (Vaida and Xu, 2000; Pankratz, De Andrade and Therneau, 2005). More details germane to the differences between SMUT and methods proposed here are in Supporting Information Section 1. For presentation brevity, we hereafter refer to our method for a binary or count outcome as SMUT_GLM; while that for a time-to-event outcome as SMUT_PH.
The rest of this article is organized as follows. In Section 2, we present details of our proposed methods SMUT_GLM and SMUT_PH, followed by simulation studies and real data application in Section 3 and Section 4, respectively. Finally, Section 5 concludes the article with some discussions.
2. Methods
2.1. Notation
Without loss of generality, we assume that we have four types of data, namely, genotypes (as the potential causal variables), gene expression measurements (as the mediator, which can be other types of molecular measures such as metabolite levels or protein abundances), phenotypic trait (as the final outcome) and other covariates (e.g. age, gender). Let G be the n by q genotype matrix, where n is the sample size, q is the number of SNPs and Gij is the number of copies of the minor allele for the ith individual at the jth SNP. Let X be the n by p covariate matrix and Xij denote the jth covariate variable for the ith individual. Let M = (M1, M2,…,Mn)T and Y = (Y1, Y2,…,Yn)T where Mi and Yi denote the mediator and the outcome for the ith individual, respectively. If Yi is a binary or count outcome, Yi is related to the model in (2); if Yi is a time-to-event outcome, Mi is related to the model in (3) and Mi = (Zi, δi) where Zi = min(Ti,Ci) is the observation time, Ti is the failure time and Ci is the censoring time, and δi = I(Ti≤Ci) is the failure indicator; δi = 1 indicates that the failure is observed and δi = 0 indicates that the response is censored. We apologize for abusing notations. Basically, we want to use the same notation Yi to denote different types of outcomes.
2.2. SMUT_GLM and SMUT_PH model
SMUT_GLM and SMUT_PH model the effects of SNPs on the outcome mediated by the expression level of a single gene via two models, namely a mediator model and an outcome model. We assume the expression level is continuous and consider a linear model for the mediator model (1). As for the outcome model, we fit GLMM if the outcome conditional on SNPs’ effects follows an exponential family distribution (2); we fit mixed effects Cox PH model if the outcome is a time-to-event variable (3).
| (1) |
| (2) |
| (3) |
Where α1, α2 are fixed intercepts; fixed effects and ι = (ι1, ι2,…,ιp)T are vectors of covariates’ effects on the mediator and outcome, respectively; random effects β = (β1, β2,…,βq)T is a vector of SNPs’ effects on the mediator; fixed effect θ is the mediator’s effect on the outcome. The random effects γ = (γ1, γ2,…,γq)T is a vector of SNPs’ effects on the outcome; error terms is the link function; λ(ti) is the hazard function; λ0(ti) is an unspecified baseline hazard function.
We have showed that the hypotheses H0:βθ = 0 versus H1:βθ = 0 are valid for testing mediation effect in Supporting Information Section 8, where βθ ≠ 0 implies that SNPs exert mediation effects on the outcome. Following our previous work (Zhong et al., 2019), we employ IUT to decompose the hypothesis testing H0:βθ = 0 versus H1:βθ ≠ 0 into two sub-hypotheses versus and versus , such that and . Suppose the p values for testing β and θ being zero are p1 and p2, respectively. Then the p value for testing βθ being zero, using IUT, is the maximum of p1 and p2. In the following sections, we provide details regarding how to separately test β and θ to obtain p1 and p2
2.3. Testing β in the mediator model and θ in the outcome model
As in (Zhong et al., 2019), we adopt the widely used SKAT method (Wu et al., 2011) to test β in the mediator model to accommodate a potentially large number of correlated SNPs.
Our strategy for testing θ in the outcome model consists of four steps: (1) formulation of the likelihood function based on the nature of the outcome random variable Y, and (2) Laplace approximation of the likelihood function, and (3) application of the coordinate descent algorithm (Fu, 1998; Daubechies, Defrise and De Mol, 2004) to estimate parameters by maximizing the approximated likelihood function, and (4) calculation of the likelihood ratio statistic. These four steps allow us to test the mediator effect θ in the outcome model.
2.3.1. Likelihood function for the outcome model
To reduce the dimensionality of parameters in the outcome model, we adopted a linear mixed model for continuous outcome in our previous work (Zhong et al., 2019). We assume Y1,Y2,…,Yn are independent and identically distributed. When the outcome Yi (i = 1,2,…,n) conditional on γ follows an exponential family distribution, we adopt the GLMM in equation (2).
| (4) |
where τi is the canonical parameter; ϕ is the dispersion parameter; (y|γ) is the likelihood function of the outcome Y conditional on γ. When the outcome Yi (i = 1,2,…,n) is a time-to-event variable, we adopt the mixed effects Cox PH model in equation (3).
| (5) |
where Ri = {k:Zk ≥ Zi} is the risk set and PL is the partial likelihood function conditional on γ. For the GLMM in (4), ℓ(y|γ) denotes log L(y|γ) and L(y) denotes the likelihood function of the outcome unconditional on γ; for the mixed effects Cox PH model in (5), ℓ (y|γ) denotes log PL and L(y) denotes the partial likelihood of the outcome unconditional on γ. We again apologize for abusing notations. Our basic rationale is to employ the same notation ℓ(y|γ) and L(y) to denote different log-likelihood and likelihood functions, respectively, for different types of outcomes. Let fγ(γ) be the probability density function of γ, and . Then we have the following.
| (6) |
where . Technical details are in Supporting Information Section 2.1.
2.3.2. Laplace approximation
Laplace’s method is widely adopted to approximate the likelihood function (Breslow and Clayton, 1993; Raudenbush, Yang and Yosef, 2000; Pankratz et al., 2005). The integral in equation (6) can be approximated via Laplace’s method by taking Taylor expansion to the second order of h(γ) around its maximum point . After inserting the Taylor expansion into the integral, and taking logarithm, we have the approximated log-likelihood f.
| (7) |
For the GLMM in (4), we have
| (8) |
where Iq is a q by q identity matrix, W = diag(w1,w2,…,wn, and wi is recognizable as GLM (generalized linear model) iterative weight. For the mixed effects Cox PH model in (5), we have
| (9) |
where . More details of Laplace approximation are in Supporting Information Section 2.2.
2.3.3. Coordinate descent algorithm
We apply the coordinate descent algorithm to maximize the approximated log-likelihood in equation (9). Note that in equation (9) is a function of other parameters Instead of taking implicit differentiation of (Raudenbush et al., 2000), we use the approximation strategy proposed in (Schelldorfer, Meier and Bühlmann, 2014), which regards as fixed when updating ξ. This strategy is computationally convenient and efficient, at little cost of reduced accuracy. In addition, we take further approximation when taking derivatives of the approximated log-likelihood function f. Specifically, for the GLMM in (4), we assume W in equation (10) varies slowly as a function of (μ1, μ2,…μn)T (Breslow and Clayton, 1993). For the mixed effects Cox PH model in (5), we similarly assume that U in equation (11) varies slowly as a function of (η1, η2,…ηn)T. Under the assumption, the term in equation (9) is ignored when taking derivatives of the approximated log-likelihood function over (α2, ϕ, θ, ι1, ι2,…,ιp). Details of the coordinate descent algorithm are in Supporting Information Section 2.3. Finally, we employ the Newton-Raphson algorithm to sequentially update each parameter.
2.3.4. Likelihood ratio test
We obtain approximated likelihood under the null and the alternative hypothesis separately, denoted by L0 and L2 respectively. For GLMM, the likelihood ratio statistic 2(log L1 − logL0) asymptotically follows a chi-square distribution with one degree of freedom, and similarly for the partial likelihood ratio statistics for the survival outcome.
3. Simulation studies
3.1. Simulation settings
To evaluate the performance of SMUT_GLM and SMUT_PH in comparison with alternative methods, we conducted extensive simulations to investigate power and type-I error. Following our previous work (Zhong et al., 2019), we simulated a dataset of 10,000 pseudo-individuals measured at 2,891 SNPs with minor allele frequency (MAF) ≥ 1% in a 1Mb region using the COSI coalescent model (Schaffner et al., 2005) to generate realistic genetic data. The 10,000 pseudo-individuals were constructed by randomly pairing up 20,000 simulated chromosomes without replacement. To evaluate power and type-I error, we generated 500 datasets with 1,000 samples each by sampling without replacement from the entire pool of 10,000 samples simulated above. We randomly selected a set of causal SNPs, which is shared across the 500 simulated datasets, from these 2,891 SNPs. We then classified them into three categories: shared SNPs (sSNPs), mediator specific SNPs (mSNPs) and outcome specific SNPs (oSNPs). The sSNPs influence both the mediator and the outcome, while the mSNPs and oSNPs only contribute to the mediator and outcome, respectively.
We considered two scenarios in terms of causal SNP density: sparse and dense (Table 1). For binary or count outcome, sample size is 1,000 and there are 10 and 500 causal SNPs for sparse and dense scenarios, respectively. For time-to-event outcome, sample size is 200 and there are 10 and 150 causal SNPs for sparse and dense scenarios, respectively. When we fit the model, both the causal and non-causal SNPs (Table 1) are included in the model. Thus, the distribution of coefficients of genetic variants is effectively mis-specified for all the simulations. Covariates matrix X consists of a continuous variable generated from N(0,1) and a binary variable generated from Bernoulli(0.5). We generated the mediator via , where denotes the vector of genotype data for the ith individual from sSNPs and mSNPs, Xi denotes the vector of the covariates for the ith individual, α1 = 1, ιM = (0.5, − 0.5)Y, β ~ cβN(0, Iq) and cβ is a scalar to scale the SNPs’ effects; ϵi ~ N(0,1). We generated the binary or count outcome via , where denotes the vector of genotype data for the ith individual from sSNPs and oSNPs, α2 = 0,, ι = 0.5, − 0.5)T, γ ~ cγN (0, Iq) and cγ = 0.2. The link function g was specific to the type of the outcome (Supporting Information Section 2.1). We generated the time-to-event outcome based on Weibull baseline hazard via and ci ~ Exp (0.001), where ti is failure time and ci is censoring time, v ~ Unif (0,1), shape ρ = 1, scale parameter λ = 0.01. Note that across the 500 datasets, error terms ϵ were separately simulated for each dataset, but β and γ were fixed.
Table 1.
Causal SNP composition in the two simulated scenarios.
| Type of outcome | Sample size | Sparse or dense | # causal SNPs | # sSNPs | # mSNPs | # oSNPs | # non-causal SNPs |
|---|---|---|---|---|---|---|---|
| Binary or Count | 1000 | Sparse | 10 | 4 | 3 | 3 | 890 |
| Dense | 500 | 300 | 100 | 100 | 400 | ||
| Time-to-event | 200 | Sparse | 10 | 4 | 3 | 3 | 190 |
| Dense | 150 | 90 | 30 | 30 | 50 |
In the simulations, we tested the mediation effects of these SNPs on the binary, count or time-to-event outcome using SMUT_GLM and SMUT_PH, as well as other methods including SMUT, adapted LASSO (Tibshirani, 1996) and adapted Huang et al.’s method. In order to compare the performance of approximations that we adopted, we considered two versions of our method, both treating as fixed: (1) based on exact derivatives; (2) based on approximated derivatives. For a binary or count outcome, we refer to these two versions as SMUT_GLM exact and SMUT_GLM approxi. For a time-to-event outcome, we refer to the approximated version as SMUT_PH approxi. The exact version of SMUT_PH is not employed because it is hard to derive analytically. SMUT is naively applied to binary and count outcomes by treating them as continuous variables. The adapted LASSO approach adopts SKAT to consider all the genetic variant in the mediator model, while in the outcome model, employs LASSO for variable selection on all genetic variants as well as mediator and covariates, then refits GLM on the selected genetic variants together with mediator and covariates (latter two will be included regardless of LASSO variable selection results), and finally combines p values from the mediator and the refitted outcome model via IUT. The adapted Huang et al.’s method employs SKAT in the mediator model, adopts the original Huang et al.’s method in the outcome model, and then combines p values from the two models via IUT. We use adapted LASSO and SKAT + LASSO exchangeably. Similarly, we use adapted Huang et al. and SKAT + Huang et al. exchangeably. Details of the adapted LASSO and adapted Huang et al.’s method are in Supporting Information Section 3.
To test the robustness and generalizability of the methods, we considered two alternative situations where some assumption is violated. The first situation is the violation of the assumption that coefficients of genetic variants follow a Gaussian distribution. The second situation is when there is an unobserved mediator that is not adjusted in the analysis. Details and results of these two simulation studies are in Supporting Information Section 4.
3.2. Type-I error in simulations
We evaluated the validity of SMUT_GLM and SMUT_PH along with alternative methods in simulations. SMUT_GLM and SMUT_PH exhibited controlled type-I error rates, at α = 0.05 level, regardless of causal SNP density and types of outcome, as shown in Figures 1 and 2 for binary outcome in sparse and dense scenarios respectively, Figures 3 and 4 for time-to-event outcome in sparse and dense scenarios respectively, Web Figures S1 and S2 for count outcome in sparse and dense scenarios respectively. In each figure, the first panel (cβ = 0) and the leftmost point (θ = 0) in other panels (cβ ≠ 0) all correspond to the null of no mediation of the SNPs through the mediator. SMUT, adapted LASSO and adapted Huang et al.’s method also showed protected type-I error.
Figure 1.
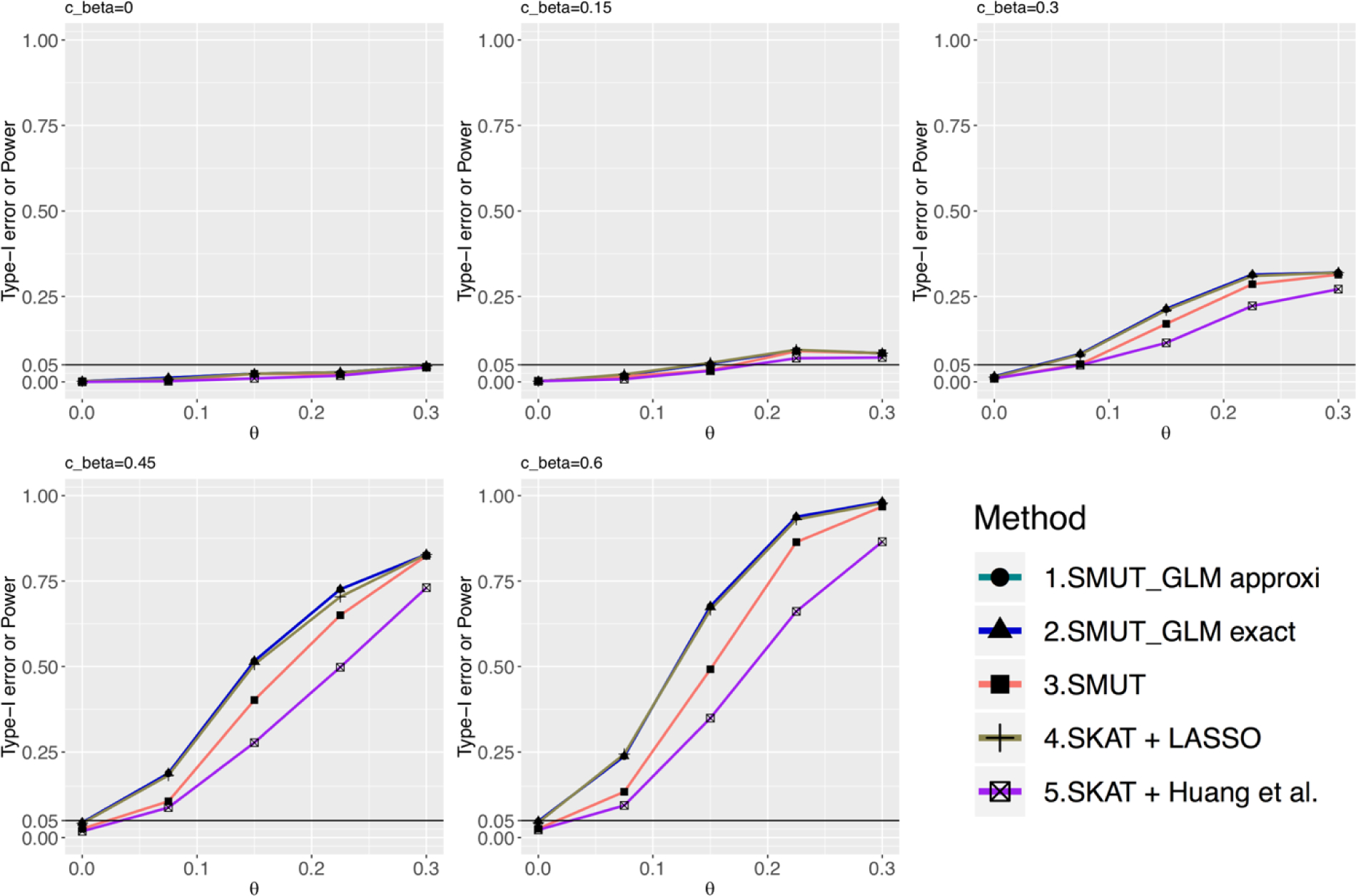
For binary outcome, power and type-I error under sparse causal SNPs scenario. The x-axis is the true mediator effect (θ) on the outcome. The y-axis is the power or type-I error. Sub-figures vary in cβ value. cβ = 0 (top-left sub-figure) or θ = 0 (left-most points in each sub-figure) are null settings where y-axis represents the corresponding type-I error. When cβ ≠ 0 and θ ≠ 0, it is under alternative hypothesis and y-axis represents the corresponding power. Line for the approximated version of SMUT_GLM is overlapped with the exact version.
Figure 2.
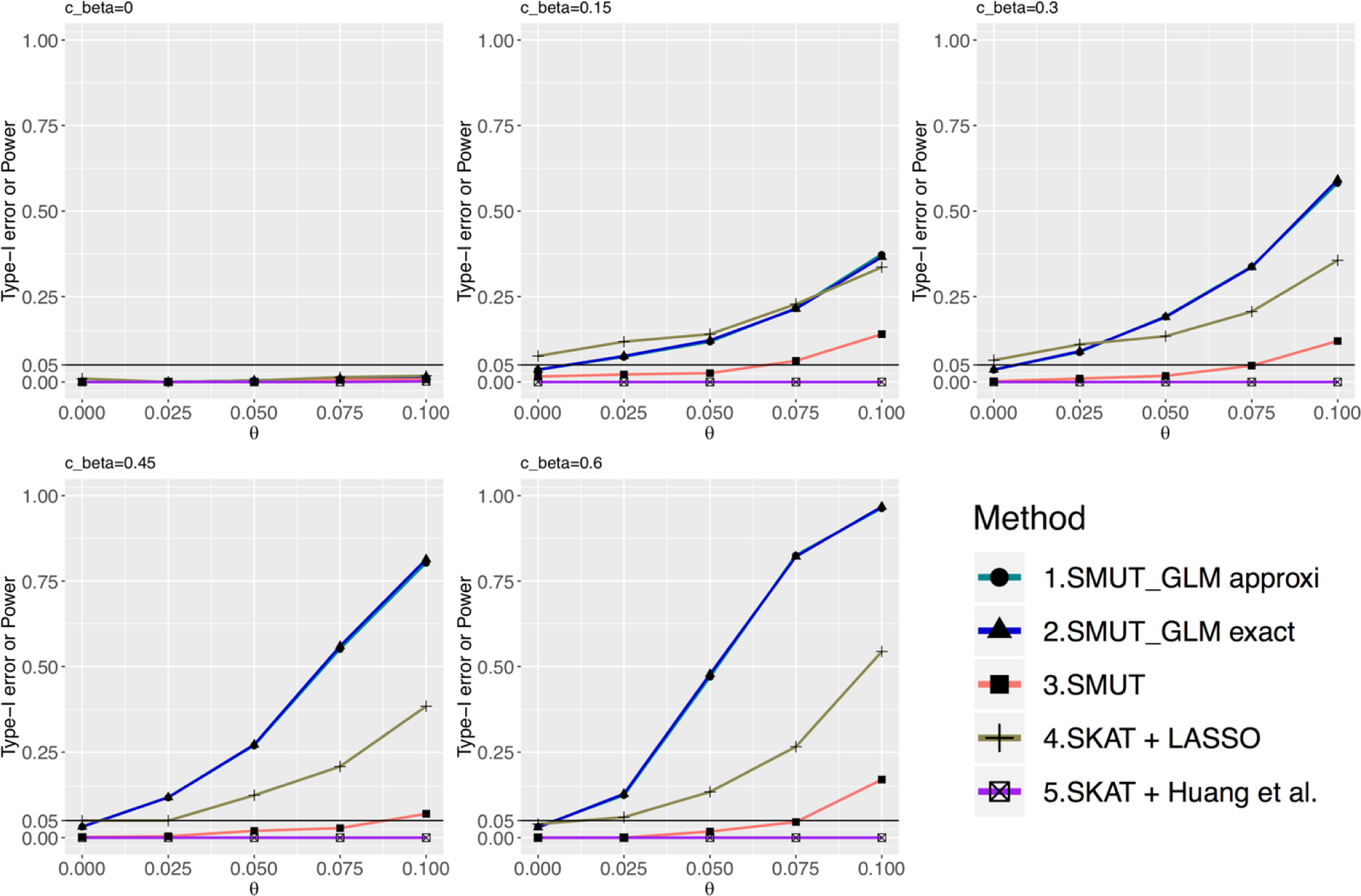
For binary outcome, power and type-I error under dense causal SNPs scenario. X-axis and y-axis are the same as in Figure 1. Line for the approximated version of SMUT_GLM is overlapped with the exact version.
Figure 3.
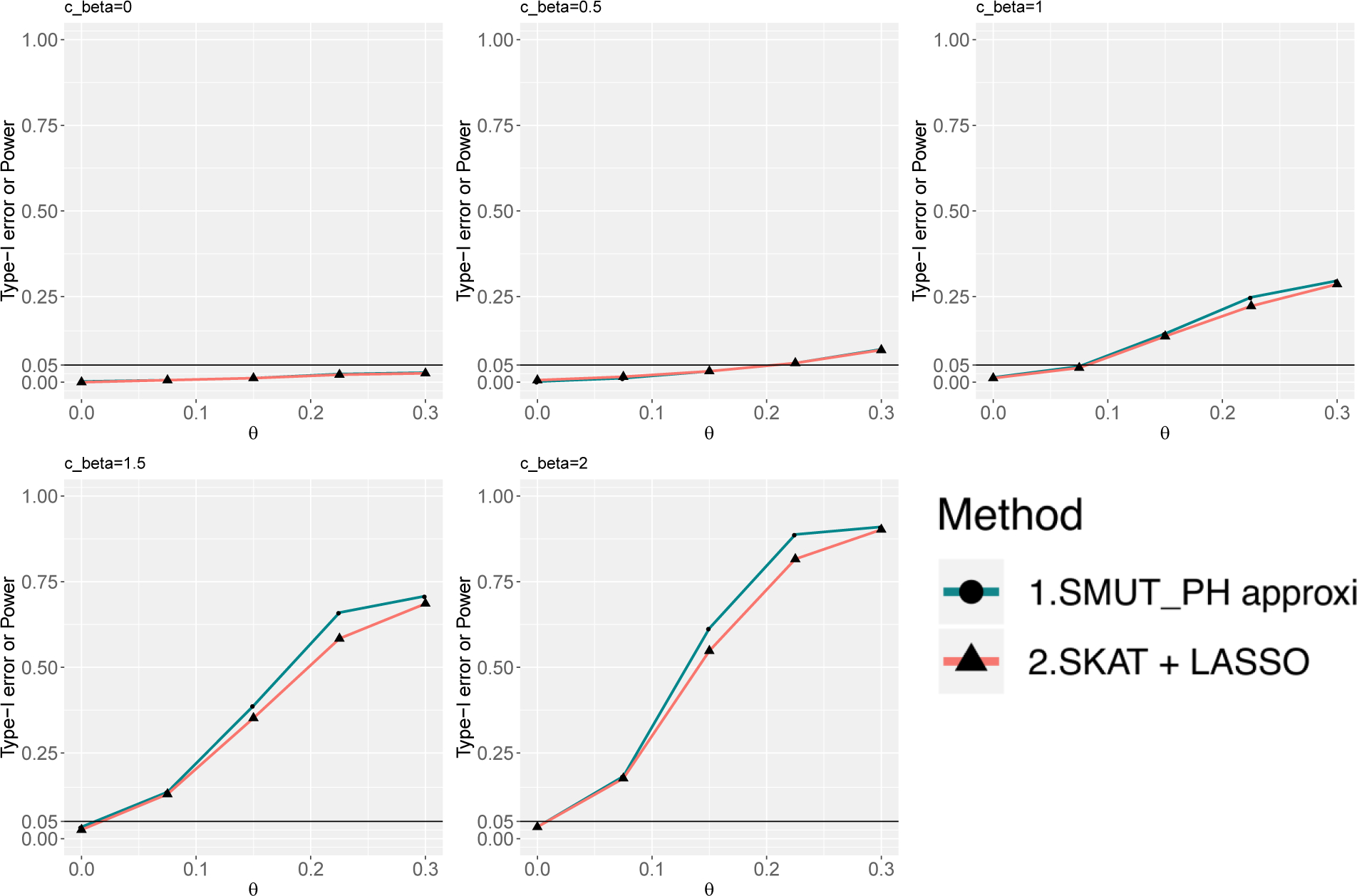
For time-to-event outcome, power and type-I error under sparse causal SNPs scenario. X-axis and y-axis are the same as in Figure 1.
Figure 4.
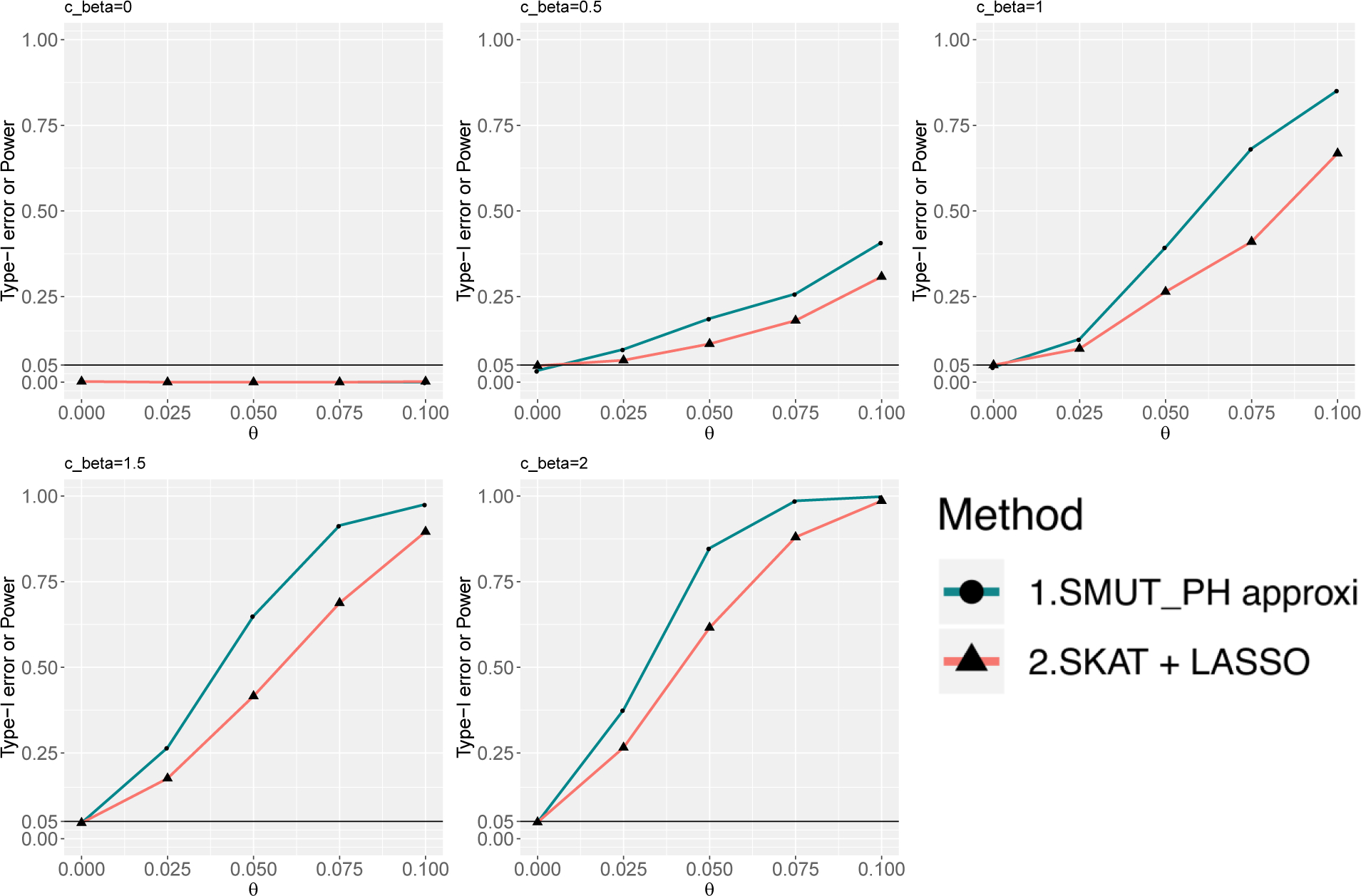
For time-to-event outcome, power and type-I error under dense causal SNPs scenario. X-axis and y-axis are the same as in Figure 1.
3.3. Power in simulations
SMUT_GLM and SMUT_PH demonstrated substantial power gains under both the sparse and dense scenarios. We also observed that the approximated version of SMUT_GLM demonstrated very similar performance when compared with its exact counterpart. For example, for binary outcome and under the scenario of dense causal SNPs when cβ = 0.6, θ = 0.1, exact SMUT_GLM, approximated SMUT_GLM, SMUT, adapted LASSO and adapted Huang et al. had 97%, 96%, 17%, 54% and 0% power, respectively. Thus, the power gain from the exact SMUT_GLM was 80%, 43% and 97% compared with SMUT, adapted LASSO and adapted Huang et al., respectively. The approximated SMUT_GLM had similar power gains. For time-to-event outcome, under the scenario of dense causal SNPs when cβ = 1, θ = 0.075, approximated SMUT_PH and adapted LASSO had 69% and 41% power, respectively, leading to a power gain of 28%. In addition, power gains appeared more profound with increasing cβ, likely because adapted LASSO and adapted Huang et al. becomes more conservative as the pleiotropy effect of SNPs on mediator and outcome (measured by cβ) increases.
4. Real data application
We assessed our methods and alternatives in real data from two clinical cohorts, which were designed for the study of chlamydia infection. Chlamydia trachomatis can ascend from the cervix to the uterus and fallopian tubes in some women, potentially resulting in pelvic inflammatory disease (PID) and severe reproductive morbidities, including infertility and ectopic pregnancy. Recurrent infection leads to worse disease. We analyzed genotype, gene expression and phenotype data of 200 participants combined from two cohorts, the Anaerobes and Clearance of Endometritis (ACE) cohort and the T cell Response Against Chlamydia (TRAC) cohort (Russell et al., 2015). The Institutional Review Boards for Human Subject Research at the University of Pittsburgh and the University of North Carolina approved the study and all participants provided written informed consent prior to inclusion. Descriptions of the ACE and TRAC cohorts, processing and quality control of genotype and gene expression data, and details of eQTL analysis and mediation analysis of other genes are in Supporting Information Section 6.
4.1. Binary outcome
The outcome of interest is ascending chlamydia infection, among participants who had chlamydia infection at enrollment. The control group is the 71 participants who had chlamydia infection restricted to the cervix, and the case group is the 72 participants with both cervical and endometrial chlamydia infection at enrollment. We analyzed genotype, gene expression and phenotype data from these 143 participants.
Here we presented SOS1 and CD151 genes, which were biologically related to the outcome, to illustrate the application of our proposed methods to a binary outcome. Son of sevenless homolog 1 (SOS1) is a guanine nucleotide exchange factor that in humans is encoded by the SOS1 gene. The importance of SOS1 for chlamydia invasion of host cells has been indicated by multiple biomedical studies (Carabeo et al., 2007; Lane et al., 2008; Hackstadt, 2012; Bastidas et al., 2013; Mehlitz and Rudel, 2013; Elwell, Mirrashidi and Engel, 2016). The CD151 gene encodes a protein that is known to complex with integrins. It promotes cell adhesion and may regulate integrin trafficking and/or function. It is a member of the tetraspanin family, which are considered as the gateways for infection (Hauck and Meyer, 2003; Hemler, 2008; Hassuna et al., 2009; Join-Lambert et al., 2010; N Monk and J Partridge, 2012; Seu et al., 2017). In addition, SNPs annotation database, RegulomeDB (Boyle et al., 2012), demonstrates that some SNPs in these two genes are eQTLs with experimental evidence. Thus, the presence of mediation effect via the expression of each gene is expected.
For the first gene, SOS1, mediation testing encompassed 83 SNPs with MAF ≥ 10% and significant eQTL association (with SOS1) at a FDR threshold of 10%, using SMUT_GLM, adapted LASSO and adapted Huang et al.’s method. Both SMUT_GLM and adapted Huang et al.’s method detected significant mediation effects, while adapted LASSO did not (Table 2). For the second gene CD151, our mediation (via expression of CD151) testing involved 40 SNPs with MAF ≥ 10% and significant eQTL (with CD151) at FDR 10%. Only SMUT_GLM showed significant mediation effects of these SNPs through the expression of CD151 on ascending chlamydia infection (Table 2). Marginal effects of selected SNPs on SOS1 and CD151 gene expression and ascending chlamydia infection were visually illustrated in Web Figures S19 and S20 respectively.
Table 2.
Real data application
| P values | ||||||
|---|---|---|---|---|---|---|
| Type of outcome | Gene | Probesets | #SNPs | SMUT_GLM | LASSO | Huang et al. |
| Binary | SOS1 | 2140519 | 83 | 0.0235 | 0.0691 | 0.0229 |
| Binary | CD151 | 1940132 | 40 | 0.0245 | 0.1192 | 0.2289 |
| SMUT_PH | LASSO | Huang et al. | ||||
| Time-to-event | BIRC3 | 7210154 | 4 | 0.001 | 0.001 | 0.002 |
4.2. Time-to-event outcome
TRAC participants returned for follow-up visits at 1, 4, 8, and 12 months after enrollment.
The outcome of interest we evaluated here is time to the first incident chlamydia infection. We analyzed genotype, gene expression and time-to-event data from all 181 participants in the TRAC cohort who had both genotype and gene expression data available.
Here we selected BIRC3 gene, which was biologically related to the outcome, to illustrate the application of our proposed methods to a time-to-event outcome. The gene BIRC3 encodes for Baculoviral IAP Repeat Containing 3, a E3 ubiquitin-protein ligase regulating NF-kappa-B signaling (Blankenship et al., 2009; Kim et al., 2010; Tan et al., 2013). It acts as an important regulator of pathogen recognition receptor signaling (Bertrand et al., 2009), which can have profound effects on the development of downstream adaptive immune responses (Takeda, Kaisho and Akira, 2003; Palm and Medzhitov, 2009; Kumar, Kawai and Akira, 2011). In addition, biological studies suggested that BIRC3 may protect mammalian host cells against apoptosis, leading to accommodate chlamydial growth (Bryant et al., 2004; Park, Yoon and Lee, 2004; Paland et al., 2006; Ying et al., 2008). Therefore, mediation effect via the expression of BIRC3 gene is logical. Our mediation testing involved 4 SNPs with MAF ≥ 10% and eQTL (with BIRC3) at FDR 10%, using SMUT_PH, adapted LASSO and adapted Huang et al.’s method. All the methods showed significant mediation effects through BIRC3 on incident chlamydia infection (Table 2). Marginal effects of selected SNPs on BIRC3 gene expression and time to the first incident chlamydia infection were visually illustrated in Web Figures S21.
5. Discussion
Our proposed methods, SMUT_GLM and SMUT_PH, extend our previous work (Zhong et al., 2019) to test mediation effect of multiple correlated genetic variants on a non-Gaussian outcome through a mediator. We adopt a mixed model based approach to handle high dimension of genetic variants and do not apply any variable selection of genetic variants. Our proposed methods are statistically more powerful than alternative methods including SMUT, adapted LASSO and adapted Huang et al.’s method. Analysis and discussions of possible reasons underlying alternative methods’ power loss are in Supporting Information Section 5. The approximated version of SMUT_GLM and SMUT_PH are also computationally efficient (Supporting Information Section 7.2).
One limitation of our proposed methods is that we assume the effects of genetic variants follow a Gaussian distribution. This may not be correct when there are non-causal SNPs in the model and in this case, a mixture distribution might be more appropriate. It is reassuring to observe protected type-I error from our simulation studies, which included a large number of non-causal SNPs in all scenarios considered. In addition, supplementary simulation studies (Supporting Information Section 4) further demonstrate controlled type-I error when the effects of genetic variants follow a mixture of two Gaussian distributions. More properly modeling the effects of genetic variants may further increase the statistical power under the alternative hypotheses but due to modeling complexity and subsequently inevitable computational costs, we decide not to further pursue this in our current work.
Our proposed methods can be further extended to handle multiple correlated outcomes for additional power gains as well as to accommodate multiple potentially correlated mediators to jointly assess their mediation effects. Besides, we could adopt nonparametric methods to handle the mediator model and outcome model with more flexibility. Details germane to possible methodological extensions are in Supporting Information Section 7.1. We anticipate our proposed methods will become a powerful tool to bridge the gap in terms of molecular mechanisms between various types of phenotypes and the corresponding associated genetic variant(s) identified in recent literature.
Supplementary Material
Acknowledgements
This work was supported by the National Institutes of Health U19 AI084024, U19 AI144181 and R01 AI119164 to TD; U19 AI144181 to XZ; R01 HL129132, R01 HL146500, and U544 HD079124 to YL. YL is also partially supported by U01 DA052713 and R01 GM105785. We thank all participants in ACE and TRAC for agreeing to take part in the studies, and all investigators in these two studies for sharing the data. We thank the editor, the associate editor and three anonymous referees for their helpful comments and suggestions, which significantly improved the manuscript.
Data Availability Statement
The data used in this paper to support our findings are available from the corresponding authors upon reasonable request.
References
- Bailey RL, Natividad-Sancho A, Fowler A, Peeling RW, Mabey DC, Whittle HC, et al. (2009) Host genetic contribution to the cellular immune response to Chlamydia trachomatis: Heritability estimate from a Gambian twin study. Drugs of today (Barcelona, Spain: 1998), 45, 45–50. [PubMed] [Google Scholar]
- Baron RM and Kenny DA (1986) The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. Journal of personality and social psychology, 51, 1173–1182. [DOI] [PubMed] [Google Scholar]
- Bastidas RJ, Elwell CA, Engel JN and Valdivia RH (2013) Chlamydial intracellular survival strategies. Cold Spring Harbor perspectives in medicine, 3, a010256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger RL and Hsu JC (1996) Bioequivalence trials, intersection-union tests and equivalence confidence sets. Statistical Science, 11, 283–319. [Google Scholar]
- Bertrand MJM, Doiron K, Labbé K, Korneluk RG, Barker PA and Saleh M (2009) Cellular inhibitors of apoptosis cIAP1 and cIAP2 are required for innate immunity signaling by the pattern recognition receptors NOD1 and NOD2. Immunity, 30, 789–801. [DOI] [PubMed] [Google Scholar]
- Blankenship JW, Varfolomeev E, Goncharov T, Fedorova AV, Kirkpatrick DS, Izrael-Tomasevic A, et al. (2009) Ubiquitin binding modulates IAP antagonist-stimulated proteasomal degradation of c-IAP1 and c-IAP2 1. Biochemical Journal, 417, 149–165. [DOI] [PubMed] [Google Scholar]
- Boyle AP, Hong EL, Hariharan M, Cheng Y, Schaub MA, Kasowski M, et al. (2012) Annotation of functional variation in personal genomes using RegulomeDB. Genome research, 22, 1790–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslow NE and Clayton DG (1993) Approximate Inference in Generalized Linear Mixed Models. Journal of the American Statistical Association, 88, 9. [Google Scholar]
- Bryant PA, Venter D, Robins-Browne R and Curtis N (2004) Chips with everything: DNA microarrays in infectious diseases. The Lancet infectious diseases, 4, 100–111. [DOI] [PubMed] [Google Scholar]
- Carabeo RA, Dooley CA, Grieshaber SS and Hackstadt T (2007) Rac interacts with Abi-1 and WAVE2 to promote an Arp2/3-dependent actin recruitment during chlamydial invasion. Cellular microbiology, 9, 2278–2288. [DOI] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention. (2019) Sexually Transmitted Disease Surveillance 2018. Atlanta: U.S. Department of Health and Human Services. [Google Scholar]
- Daubechies I, Defrise M and De Mol C (2004) An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences, 57, 1413–1457. [Google Scholar]
- Elwell C, Mirrashidi K and Engel J (2016) Chlamydia cell biology and pathogenesis. Nature Reviews Microbiology, 14, 385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu WJ (1998) Penalized regressions: the bridge versus the lasso. Journal of computational and graphical statistics, 7, 397–416. [Google Scholar]
- Hackstadt T (2012) In: Intracellular Pathogens I: Chlamydiales (eds Tan M and Bavoil P). American Society for Microbiology Press. [Google Scholar]
- Hassuna N, Monk PN, Moseley GW and Partridge LJ (2009) Strategies for targeting tetraspanin proteins. BioDrugs, 23, 341–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauck CR and Meyer TF (2003) ‘Small’talk: Opa proteins as mediators of Neisseria--host-cell communication. Current opinion in microbiology, 6, 43–49. [DOI] [PubMed] [Google Scholar]
- Hemler ME (2008) Targeting of tetraspanin proteins—potential benefits and strategies. Nature reviews Drug discovery, 7, 747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y-T, Cai T and Kim E (2016) Integrative genomic testing of cancer survival using semiparametric linear transformation models. Statistics in medicine, 35, 2831–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y-T, Liang L, Moffatt MF, Cookson WOCM and Lin X (2015) iGWAS: Integrative Genome-Wide Association Studies of Genetic and Genomic Data for Disease Susceptibility Using Mediation Analysis. Genetic Epidemiology, 39, 347–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Join-Lambert O, Morand PC, Carbonnelle E, Coureuil M, Bille E, Bourdoulous S, et al. (2010) Mechanisms of meningeal invasion by a bacterial extracellular pathogen, the example of Neisseria meningitidis. Progress in neurobiology, 91, 130–139. [DOI] [PubMed] [Google Scholar]
- Kim CW, Kim HK, Vo M-T, Lee HH, Kim HJ, Min YJ, et al. (2010) Tristetraprolin controls the stability of cIAP2 mRNA through binding to the 3′ UTR of cIAP2 mRNA. Biochemical and biophysical research communications, 400, 46–52. [DOI] [PubMed] [Google Scholar]
- Kumar H, Kawai T and Akira S (2011) Pathogen recognition by the innate immune system. International reviews of immunology, 30, 16–34. [DOI] [PubMed] [Google Scholar]
- Lane BJ, Mutchler C, Al Khodor S, Grieshaber SS and Carabeo RA (2008) Chlamydial entry involves TARP binding of guanine nucleotide exchange factors. PLoS pathogens, 4, e1000014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCulloch CE, Searle SR and Neuhaus JM (2008) Generalized, Linear, and Mixed Models, 2nd Edition., 424.
- Mehlitz A and Rudel T (2013) Modulation of host signaling and cellular responses by Chlamydia. Cell Communication and Signaling, 11, 90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- N Monk P and J Partridge L (2012) Tetraspanins-gateways for infection. Infectious Disorders-Drug Targets (Formerly Current Drug Targets-Infectious Disorders), 12, 4–17. [DOI] [PubMed] [Google Scholar]
- Paland N, Rajalingam K, Machuy N, Szczepek A, Wehrl W and Rudel T (2006) NF-$κ$B and inhibitor of apoptosis proteins are required for apoptosis resistance of epithelial cells persistently infected with Chlamydophila pneumoniae. Cellular microbiology, 8, 1643–1655. [DOI] [PubMed] [Google Scholar]
- Palm NW and Medzhitov R (2009) Pattern recognition receptors and control of adaptive immunity. Immunological reviews, 227, 221–233. [DOI] [PubMed] [Google Scholar]
- Pankratz VS, De Andrade M and Therneau TM (2005) Random-effects cox proportional hazards model: General variance components methods for time-to-event data. Genetic Epidemiology, 28, 97–109. [DOI] [PubMed] [Google Scholar]
- Park S-M, Yoon J-B and Lee TH (2004) Receptor interacting protein is ubiquitinated by cellular inhibitor of apoptosis proteins (c-IAP1 and c-IAP2) in vitro. FEBS letters, 566, 151–156. [DOI] [PubMed] [Google Scholar]
- Raudenbush SW, Yang ML and Yosef M (2000) Maximum Likelihood for Generalized Linear Models with Nested Random Effects via High-Order, Multivariate Laplace Approximation. Journal of Computational and Graphical Statistics, 9, 141–157. [Google Scholar]
- Russell AN, Zheng X, O’connell CM, Taylor BD, Wiesenfeld HC, Hillier SL, et al. (2015) Analysis of factors driving incident and ascending infection and the role of serum antibody in Chlamydia trachomatis genital tract infection. The Journal of infectious diseases, 213, 523–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ and Altshuler D (2005) Calibrating a coalescent simulation of human genome sequence variation. Genome Research, 15, 1576–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schelldorfer J, Meier L and Bühlmann P (2014) GLMMLasso: An Algorithm for High-Dimensional Generalized Linear Mixed Models Using ℓ 1 -Penalization. Journal of Computational and Graphical Statistics, 23, 460–477. [Google Scholar]
- Seu L, Tidwell C, Timares L, Duverger A, Wagner FH, Goepfert PA, et al. (2017) CD151 expression is associated with a hyperproliferative T cell phenotype. The Journal of Immunology, 199, 3336–3347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeda K, Kaisho T and Akira S (2003) Toll-like receptors. Annual review of immunology, 21, 335–376. [DOI] [PubMed] [Google Scholar]
- Tan BM, Zammit NW, Yam AO, Slattery R, Walters SN, Malle E, et al. (2013) Baculoviral inhibitors of apoptosis repeat containing (BIRC) proteins fine-tune TNF-induced nuclear factor $κ$B and c-Jun N-terminal kinase signalling in mouse pancreatic beta cells. Diabetologia, 56, 520–532. [DOI] [PubMed] [Google Scholar]
- Taylor BD, Zheng X, Darville T, Zhong W, Konganti K, Abiodun-Ojo O, et al. (2017) Whole-exome sequencing to identify novel biological pathways associated with infertility following pelvic inflammatory disease. Sexually transmitted diseases, 44, 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 267–288. [Google Scholar]
- Vaida F and Xu R (2000) Proportional hazards model with random effects. Statistics in medicine, 19, 3309–3324. [DOI] [PubMed] [Google Scholar]
- Wu MC, Lee S, Cai T, Li Y, Boehnke M and Lin X (2011) Rare-variant association testing for sequencing data with the sequence kernel association test. American Journal of Human Genetics, 89, 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ying S, Christian JG, Paschen SA and Häcker G (2008) Chlamydia trachomatis can protect host cells against apoptosis in the absence of cellular Inhibitor of Apoptosis Proteins and Mcl-1. Microbes and infection, 10, 97–101. [DOI] [PubMed] [Google Scholar]
- Zheng X, O’Connell CM, Zhong W, Nagarajan UM, Tripathy M, Russell AN, et al. (2018) Discovery of blood transcriptional endotypes in women with pelvic inflammatory disease. The Journal of Immunology, 200, 2941–2956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong W, Spracklen CN, Mohlke KL, Zheng X, Fine J and Li Y (2019) Multi-SNP mediation intersection-union test. Bioinformatics. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data used in this paper to support our findings are available from the corresponding authors upon reasonable request.


