Handling death as an intercurrent event in time to recovery analysis in COVID-19 treatment clinical trials

Abstract

In clinical trials with the objective to evaluate the treatment effect on time to recovery, such as investigational trials on therapies for COVID-19 hospitalized patients, the patients may face a mortality risk that competes with the opportunity to recover (e.g., be discharged from the hospital). Therefore, an appropriate analytical strategy to account for death is particularly important due to its potential impact on the estimation of the treatment effect. To address this challenge, we conducted a thorough evaluation and comparison of nine survival analysis methods with different strategies to account for death, including standard survival analysis methods with different censoring strategies and competing risk analysis methods. We report results of a comprehensive simulation study that employed design parameters commonly seen in COVID-19 trials and case studies using reconstructed data from a published COVID-19 clinical trial. Our research results demonstrate that, when there is a moderate to large proportion of patients who died before observing their recovery, competing risk analyses and survival analyses with the strategy to censor death at the maximum follow-up timepoint would be able to better detect a treatment effect on recovery than the standard survival analysis that treat death as a non-informative censoring event. The aim of this research is to raise awareness of the importance of handling death appropriately in the time-to-recovery analysis when planning current and future COVID-19 treatment trials.

1. Introduction

With the ongoing pandemic of coronavirus disease 2019 (COVID-19), investigating treatments for COVID-19 has remained a major task in drug development. In COVID-19 trials in hospitalized patients, key study objectives typically include investigating whether a treatment helps patients recover more quickly than standard of care, as measured by time to hospital discharge over a short duration (e.g., 28 days after randomization). In this type of trial, hospitalized patients also face a mortality risk competing with the opportunity to recover from the disease and be discharged from hospital. In other words, the event of death prevents the opportunity to observe hospital discharge because a deceased patient would never be able to recover and be discharged. Therefore, the competing risk of death must be properly accounted for in the analysis of recovery-based endpoints. Failure to appropriately account for death in the analysis could potentially underestimate a real treatment effect (risking an effective drug being withheld from patients) or overestimate the treatment effect (risking an ineffective drug becoming recommended treatment).

Recognizing the important impact of death on recovery-based endpoints, the US Food and Drug Administration (FDA) recommended in their published guidance on COVID-19 drug and biological products development that “death should not be considered a form of missing data” and should be handled via a composite variable strategy “with death taking a sufficiently unfavourable value” [1]. Prior to publication of this guidance, however, not all clinical trials had employed analysis strategies in compliance with this recommendation. Time-to-recovery was typically analyzed with standard survival analysis methods such as Kaplan-Meier (K-M) survival plots [2], log-rank test [3], Cox proportional hazards (PH) model [4], and restricted mean survival analysis [5,6], with death either treated as a non-informative censoring event [7] or imputed to be censored at the maximum follow-up timepoint (hereafter, “maximum time censoring” approach) [8]. Several works [[9], [10], [11], [12], [13], [14], [15], [16]] have recommended applying competing risk models to address the impact of death on the recovery-like event, including cumulative incidence function [9] [16,17], subdistribution hazard model [18], and cause-specific hazard model [19]. On the topic of COVID-19 clinical trials, one paper criticized that standard survival analysis methods like K-M methods and Cox PH models may lead to biased estimates and conclusions [11]. Ghosh (2021) [13] compared three competing risk regression approaches with application to COVID-19 survival data. However, no previous research has comprehensively investigated the performance of both parametric and non-parametric survival analysis methods with different censoring strategies versus parametric and non-parametric competing risk analysis approaches in the setting of COVID-19 trials.

Our research examined tests of the treatment effect for a time-to-recovery endpoint using nine survival analysis methods with different censoring schemes and modelling approaches through a simulation study and case studies using reconstructed data from a published clinical trial. Given the rapidly shifting landscape of COVID-19 treatment research, our work will increase awareness of the importance of appropriately handling death in the time-to-recovery analysis for current and future COVID-19 trials. Our research will be particularly helpful to address some key questions during study design and analysis planning, including whether standard survival analysis incorporating an appropriate censoring strategy is acceptable in trials of different settings (e.g., severely ill hospitalized patients vs. less ill patients with lower death rates), how different mortality risks between treatment groups may impact the opportunity of claiming a significant treatment effect on recovery, and how to construct a robust survival analysis in such settings.

2. Methods

2.1. Cumulative incidence function

The cumulative incidence function (CIF) of recovery, denoted as CIF _e(t), is defined as the marginal probability of occurrence of recovery up to time t, while accounting for competing risks (such as death) which may occur in the same observation period. For the sake of simplicity, we consider a recovery-based endpoint as the event of interest, and death as the only competing risk event, although one may extend the competing risk to multiple events. The event of interest, recovery or hospital discharge, may be referenced interchangeably.

In the presence of competing risk of death, the incidence function is formulated as the product of the hazard function of the event of interest and the overall survival. It is worth noting that overall survival represents the probability of patients surviving from both the event of interest (i.e., recovery) and the competing event (i.e., death). Thus, overall survival incorporates the effects of the hazard function of the event of interest and the hazard function of the competing risk. In other words, in our motivating example, overall survival acknowledges that a patient must have remained alive in order to experience recovery.

Standard survival analysis approaches, such as Kaplan-Meier and Cox PH model, generally result in upward bias in the estimation of the incidence function in the presence of competing risk(s) [[20], [21], [22]]. The problem is that, in standard approaches, overall survival does not account for the contribution of the hazard function from the competing risk and is simply attributed to the hazard function of the event of interest only. Thus, it leads to an upward biased overall survival, which in turn leads to an upward biased CIF _e. For this reason, careful forethought should be given to employ an appropriate analysis method to analyze event onset in the presence of a competing risk.

2.2. Non-parametric test of cumulative incidence functions in two treatment groups

The overall survival probability of being ‘event-free’ can be estimated using the Kaplan-Meier method, where an event refers to the onset of either recovery or competing death. The cumulative incidences in different treatment groups can then be compared using a modified log-rank Chi-square test [17].

An alternative summary of the cumulative recovery cases over time is the area under the cumulative incidence curve (CIF AUC) up to a specified timepoint post-baseline [9], such as the end of a 28-day treatment or observation period in a COVID-19 trial. It has an intuitive clinical interpretation that the CIF AUC is the average post-recovery time that patients spent across the 28 days of follow-up. Therefore, a greater CIF AUC implies better treatment efficacy. The between-treatment group comparison can be quantified by assessing the difference or ratio of the CIF AUCs.

2.3. Semi-parametric subdistribution hazard model

The subdistribution hazard function is defined as an instantaneous risk of recovery in the risk set of patients who have not yet experienced recovery. The risk set includes the patients who are not yet recovered as well as patients who died. The subdistribution hazard model is one of the most popular approaches to analyze time-to-event data in the context of competing risks as it explicitly bridges the subdistribution hazard function of the event to the CIF. Fine and Gray (1999) developed a Cox regression (semi-parametric) approach for handling the subdistribution hazards, assuming proportional subdistribution hazard rates [18]. The subdistribution hazard model allows one to directly estimate the effect of covariates on the CIF of the event of interest. In our case, the ratio of subdistribution hazards between the treatment groups can be interpreted as the treatment effect on the cumulative incidence of recovery. In prognostic research, the subdistribution hazard model is generally recommended over another competing risk method, the cause-specific hazard model, due to its feature of a direct relationship to the CIF [23]. As a side note, the Cox PH model censoring death at death time (further discussed in the Section 2.4) will provide an estimate of the cause-specific hazard ratio of recovery.

2.4. Standard survival analysis methods with different censoring strategies

The log-rank test [3], Cox PH model [4], and restricted mean survival time (RMST) approach [5,6] are widely used to analyze time-to-event data without incorporating the competing risk. If using a default censoring mechanism, patients who died would be censored at the time of death (which, for the Cox PH model, will provide an estimate of the cause-specific hazard ratio as briefly mentioned in Section 2.3). Alternatively, one could modify the censoring rules to account for the potential impact of competing death to the event of recovery such that death takes a sufficiently unfavourable value. For example, in the ACTT-1 trial [8], patients who died were censored at the end of the efficacy evaluation period. In our simulations in the next section, all three standard survival analysis methods with both censoring strategies (i.e., non-informatively censoring death at death time, or informatively imputing censoring time to the maximum follow up) are examined in comparison with the competing risk analysis methods.

2.5. Simulation

To evaluate the performance of competing risk survival analysis and standard survival analysis methods with different censoring strategies, a simulation study was conducted using settings from COVID-19 clinical trials so that the findings could be easily generalized to real trials and enlighten planning of robust statistical analyses. Note that the statistics in each of the examined analysis methods are different. Therefore, it is not possible to make a direct comparison of all these methods based on a common effect size or treatment effect estimate. Furthermore, for composite endpoints, certain operating characteristics (like bias) are challenging to compute directly. In this simulation study, the probability of observing a significant treatment effect was used to compare different analysis approaches with different statistics. This criterion is also easily interpretable to the research community since it straightforwardly evaluates which methods best demonstrate treatment efficacy when there is indeed a treatment benefit. Details are further described in Section 3.1, Claim of significance of treatment effects.

Simulation settings and analysis R/SAS packages are described in Supplementary Methods.

3. Results

3.1. Simulation study results

3.1.1. Claim of significance of treatment effects

In a typical randomized clinical trial, the primary objective is to test the hypothesis of treatment effect for an experimental treatment compared to control. In this simulation study, we analyzed the endpoint of time-to-recovery (e.g., hospital discharge) with various statistical analysis approaches. We estimated the empirical probability of declaring a “statistically significant” treatment effect, Pr(significance), in each setting to evaluate performance. For the significance criterion, we used one-sided alpha of 0.025.

The simulation study evaluated 9 statistical analysis approaches, denoted as: Method 1a and 1b: Cox PH hazard model; Method 2a and 2b: Log rank test; Method 3a and 3b: Test of the RMST ratio between treatment groups; in Methods 1a, 2a, and 3a, patients who died would be censored at the time of death; in Methods 1b, 2b, and 3b, patients who died were censored at the end of the study evaluation period (Study Day 28); Method 4: Subdistribution hazard model; Method 5: Test of CIF difference between treatment groups using a modified log-rank Chi-square test [17]; Method 6: Test of the ratio of the CIF AUC up to 28 days post-baseline [9].

In sections 3.1.2 and 3.1.3, we evaluated Pr(significance) for each of the 9 statistical analysis approaches in 135 settings from combinations of recovery and death rates (see Supplementary Methods for details), when latent times-to-event for recovery and death were simulated from independent or correlated exponential distributions and independent Weibull distributions. For clarity, we use the term “scenario” to describe the distributional forms within each section and “setting” to refer to a unique combination of the four parameters which vary within the scenario.

3.1.2. Scenario 1: independent exponential distributions

In the first scenario, latent times-to-event for recovery and death were simulated from independent exponential distributions. The hazards for both events (recovery and death) are constant in both treatment arms.

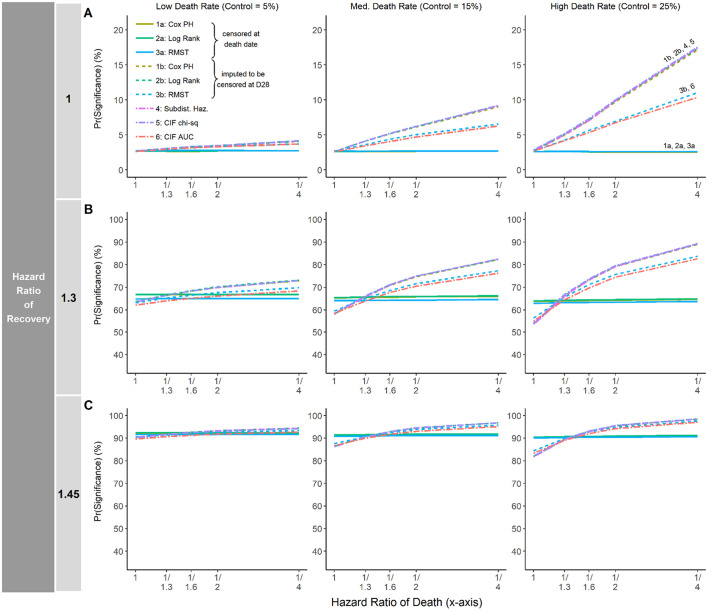
Fig. 1 plots the empirical probability of a study declaring a statistically significant treatment effect. The y-axis is the Pr(Significance) as measured by the proportion of simulations claiming the significant treatment effect with one-sided alpha <0.025. The x-axis plots the hazard ratio for death, with values ranging from 1 to 1/4. As shown in Fig. 1A, when the HR of recovery equals 1 (i.e., no difference between groups to directly improve recovery) and the death rate in the control arm is low (5%; left panel), there is almost no difference between approaches in detecting a treatment effect on recovery, regardless of the magnitude of the treatment effect on mortality (HR of death on the x-axis). On the other hand, when the HR of recovery equals 1 and the death rate is moderate (15%) to large (25%) (Fig. 1A, middle and right panels), there may be a substantial difference between statistical analysis approaches in Pr(significance) when the treatment effect has the benefit to reduce mortality (HR of death <1). For instance, when the HR of death =1/4 and HR of recovery = 1, the difference in Pr(significance) was as large as 18% vs. 2.5% if the death rate was 25% in the control group. Specifically, the competing risk methods (Methods 4, 5, 6) and standard methods using the maximum time censoring approach (Method 1b, 2b, 3b) have notably larger Pr(significance) (i.e., greater chance to claim treatment efficacy) than the standard methods that censor death at the time of death (Methods 1a, 2a, 3a). Note that, for the composite endpoint that incorporates both recovery and death, a true treatment effect exists when there is a treatment effect on either recovery itself or on death. And thus, only the setting furthest to the left in each panel of Fig. 1A (HR of recovery = 1 and HR of death = 1) reflects the null hypothesis of no treatment, and the Pr(significance) at that specific setting represents Type I error rates.

Fig. 1.

Pr(significance) for each analysis approach in settings where the median time-to-recovery in the control arm is 8 days.

The empirical probability of declaring statistical significance, Pr(Significance), when the median time to discharge in the control arm is 8 days. In each panel, the y-axis is the Pr(Significance) as measured by the proportion of simulations claiming the significant treatment effect with one-sided alpha <0.025. The x-axis plots the hazard ratio for death, with increasing magnitude of effect size from left to right. The death rate in the control arm is 5%, 15% and 25% for the first, second and third column, respectively. A) the hazard ratio of discharge equals 1. B) the hazard ratio of discharge equals 1.3. C) the hazard ratio of discharge equals 1.45.

Fig. 1B and C show Pr(significance) by analysis approach when the HR of recovery equals 1.3 and 1.45, respectively. In both cases, there is little difference between the analysis approaches in Pr(significance) for the recovery endpoint when the death rate is low (left panels in Fig. 1B and C), with the difference never more than 10 percentage points. However, when the death rate is moderate to large (15% or 25%; middle and right panels of Fig. 1B and C), the Pr(significance) can vary substantially between the analysis approaches. When there is no reduction in mortality under experimental treatment (HR of death = 1 in the middle and right panels of Fig. 1B and C), the competing risk methods and the maximum time censoring approaches (Methods 4, 5, 6, 1b, 2b, 3b) actually have slightly lower Pr(significance) than standard methods treating death as non-informative censoring (Methods 1a, 2a, 3a). This phenomenon occurs because deceased patients are placed into the risk set with an immortal time using the competing risk methods (Methods 4, 5, 6) and the maximum time censoring approaches (Method 1b, 2b, 3b). When there is little to no difference in mortality rates between the treatment groups, the larger risk set in these methods will attenuate hazard estimates, resulting in slower separation in the survival curves and less power to detect treatment difference for these approaches compared to the standard methods censoring death at the time of death. On the other hand, when there is a moderate to large treatment effect in reducing mortality (HR of death <1), the competing risk methods and maximum timepoint censoring approaches have considerably larger Pr(significance) than the standard methods censoring deaths at the time of death. In these settings, the smaller number of deceased patients in the treatment group will compensate for the ‘inflated’ risk set caused by a high death rate. This explains why the competing risk methods and the maximum time censoring approaches have considerably larger Pr(significance) than the standard methods beyond a crossing point in the middle and right panels of Fig. 1B and C.

The median time-to-recovery in the control group is 8 days in Fig. 1, and 12 days and 16 days in Supplementary Materials Fig. S1. Similar findings were observed across settings.

3.1.3. Scenarios 2 and 3: correlated exponential distributions and independent weibull distributions

In the second and third scenarios, latent times-to-event for recovery and death were simulated from correlated exponential distributions and independent Weibull distributions, respectively. Largely, similar results to Scenario 1 were observed. Another important observation is that when latent times-to-event for recovery and death were simulated from negatively correlated distributions, the standard methods that censor death at the time of death actually showed deflation in Pr(significance) as the treatment effect on reducing mortality increases in magnitude (Fig. S2). This is likely due to violating the assumption of non-informative censoring, since in this setting patients with a propensity to experience early death also have a propensity to experience longer times-to-recovery.

Results for these settings (including when hazards were non-proportional) are presented in Supplementary Results.

3.2. Case studies

Two case studies are presented using time-to-event data reconstructed from the RECOVERY trial comparing dexamethasone with usual care in hospitalized COVID-19 patients [24]. The primary outcome of the trial, 28-day mortality, was significantly lower in the dexamethasone group (22.9%) than in the usual care group (25.7%) (rate ratio = 0.83, P < 0.001), with a smaller benefit for the secondary outcome of time-to-hospital discharge still favouring dexamethasone (rate ratio = 1.10; 95% CI = 1.03–1.17). It provides a representative real study example to reflect the scenario that the treatment has relatively small benefit to improve hospital discharge with a larger effect in reducing mortality. Dexamethasone also demonstrated a significant benefit in reducing time-to-removal of mechanical ventilation (MV) for the subset of patients on MV at baseline (rate ratio = 1.47; 95% CI = 1.20–1.78).

4. Case Study 1: time-to-discharge

For the first case study, we evaluated the 9 approaches in analyzing the time-to-hospital discharge, with statistics and p-values presented in Table 1 . Although the statistics from these different methods are not directly comparable as previously described, the competing risk methods and the maximum time censoring approaches both yield lower p-values than the standard survival analysis methods that censor death at the time of death. Notably, the subdistribution hazards model, CIF-based chi-square test and the maximum time censoring approaches using Cox PH model and log-rank test (Methods 4, 5, 1b, 2b) all have p < 0.05. The AUC-based CIF test and maximum time censoring RMST test (Methods 6, 3b) have p-value <0.10. P-values from the standard methods (Methods 1a, 2a, 3a) are all non-significant. The results demonstrate the critical importance of the appropriate method selection for analyzing time-to-recovery in the presence of competing death: given the slight treatment benefit on hospital discharge, ignoring the reduced death rate in the treatment group may fail to claim a treatment effect.

Table 1.

Comparison of statistics and p-values obtained by different analysis approaches (Case Study 1).

Methods			Statistics		P value
Standard Survival Analysis	Censor death at the time of death	1a: Cox PH Model	Hazard ratio	1.035	0.289
		2a: Log Rank Test	N/A		0.287
		3a: RMST	Ratio of RMST	0.986	0.479
	Censor death at Day 28	1b: Cox PH Model	Hazard ratio	1.082	0.016
		2b: Log Rank Test	N/A		0.015
		3b: RMST	Ratio of RMST	0.968	0.067
Competing Risk Analysis		4: Subdistribution Hazard Model	Subdistribution hazard ratio	1.080	0.014
		5: CIF Chi-square	N/A		0.014
		6: CIF AUC	Ratio of CIF AUC	1.042	0.068

Method 1a: Cox PH model, censor death at the time of death;

Method 2a: Log rank test, censor death at the time of death;

Method 3a: Test the Restricted Mean Survival Time (RMST) difference, censor death at the time of death;

Method 1b: Cox PH model, censor death at Day 28;

Method 2b: Log rank test, censor death at Day 28;

Method 3b: Test the Restricted Mean Survival Time (RMST) difference, censor death at Day 28;

Method 4: Subdistribution hazard model;

Method 5: Test cumulative incidence function (CIF) difference using a modified log-rank Chi-square test;

Method 6: Test the difference of the area under the cumulative incidence function (CIF) curve.

Note: Hazard ratio > 1 in Methods 1a and 2a, Ratio of RMST<1 in Methods 2a and 2b, Subdistribution hazard ratio > 1 in Method 4, and Ratio of CIF AUC >1 in Method 6 indicate treatment benefit.

5. Case study 2: time-to-successful-removal of invasive mechanical ventilation

For the second case study, we evaluated the 9 statistical analysis approaches in analyzing the time-to- removal of MV among the subset of patients on MV at baseline using repeated samples from the reconstructed data to mimic a small to moderate sized trial setting (see Supplementary Methods for details). Table 2 summarizes for each method the empirical probability of detecting significant treatment effect with one-sided p-value <0.025 (and the average values of the statistics, which are not directly comparable). The competing risk methods and the maximum time censoring approaches (Methods 4, 5, 6, 1b, 2b, 3b) detected a treatment effect with a greater frequency than the standard methods (Methods 1a, 2a, 3a). The AUC-based CIF test (Method 6) and maximum time censoring RMST test (Method 3b) showed the largest chances to claim efficacy (each >95%). Thus, in a scenario with treatment efficacy in both improving the hospital discharge and reducing mortality, methods ignoring competing death would lead to a lower chance to claim a significant treatment effect than the ones that incorporate the competing death.

Table 2.

Comparison of average statistics and proportion of claiming significant treatment effect by different analysis approach (Case Study 2).

Methods			Statistics⁎		Pr(Significance)
Standard Survival Analysis	Censor death at the time of death	1a: Cox PH Model	Hazard ratio	1.344	63.0%
		2a: Log Rank Test	N/A		63.8%
		3a: RMST	Ratio of RMST	0.884	76.0%
	Censor death at Day 28	1b: Cox PH Model	Hazard ratio	1.446	86.4%
		2b: Log Rank Test	N/A		86.5%
		3b: RMST	Ratio of RMST	0.875	95.7%
Competing Risk Analysis		4: Subdistribution Hazard Model	Subdistribution hazard ratio	1.440	85.7%
		5: CIF Chi-square		N/A	86.6%
		6: CIF AUC	Ratio of CIF AUC	1.464	95.6%

Method 1a: Cox PH model, censor death at the time of death;

Method 1b: Log rank test, censor death at the time of death;

Method 1c: Test the Restricted Mean Survival Time (RMST) difference, censor death at the time of death;

Method 2a: Cox PH model, censor death at Day 28;

Method 2b: Log rank test, censor death at Day 28;

Method 2c: Test the Restricted Mean Survival Time (RMST) difference, censor death at Day 28;

Method 4: Subdistribution hazard model;

Method 5: Test cumulative incidence function (CIF) difference using a modified log-rank Chi-square test;

Method 6: Test the difference of the area under the cumulative incidence function (CIF) curve.

Note: Hazard ratio > 1 in Methods 1a and 2a, Ratio of RMST<1 in Methods 2a and 2b, Subdistribution hazard ratio > 1 in Method 4, and Ratio of CIF AUC >1 in Method 6 indicate treatment benefit.

^⁎Statistics calculated by taking the mean of statistics (on the log-scale) from 10,000 random samples.

A summary of conclusions from comparative evaluation of the 9 methods is provided in Table 3 .

Table 3.

Summary of high-level results and conclusions comparing the 9 methods.

Methods			Summary
Standard Survival Analysis	Censor death at the time of death	1a: Cox PH Model	Low death Rate (≤ 5%) No substantial impact on the statistical inference. Moderate to severe death rate (15%–25%) In general, lower chance to detect the treatment efficacy in the scenario that treatment reduces the death rate.
		2a: Log Rank Test
		3a: RMST
	Censor death at Day 28	1b: Cox PH Model	Analogous to competing risk analysis methods for the respective simulation settings.
		2b: Log Rank Test
		3b: RMST
Competing Risk Analysis		4: Subdistribution Hazard Model	Well established survival analysis methods to handle competing risk data. Incorporating the death effect into consideration for the claim of treatment efficacy on recovery.
		5: CIF Chi-square
		6: CIF AUC

Method 1a: Cox PH model, censor death at the time of death;

Method 1b: Log rank test, censor death at the time of death;

Method 1c: Test the Restricted Mean Survival Time (RMST) difference, censor death at the time of death;

Method 2a: Cox PH model, censor death at Day 28;

Method 2b: Log rank test, censor death at Day 28;

Method 2c: Test the Restricted Mean Survival Time (RMST) difference, censor death at Day 28;

Method 4: Subdistribution hazard model;

Method 5: Test cumulative incidence function (CIF) difference using a modified log-rank Chi-square test;

Method 6: Test the difference of the area under the cumulative incidence function (CIF) curve.

6. Discussion and conclusion

This research work focused on a comprehensive evaluation of the performance of nine survival analysis approaches, including popular competing risk analysis methods and standard survival analysis methods with multiple censoring strategies for death (time of death vs. maximum follow-up timepoint). Failure to appropriately account for death in analysis could potentially underestimate or overestimate the treatment effect. A key focus of this research was to evaluate the impact of the death rate and the hazard ratio of death on the performance of commonly used parametric and non-parametric survival analysis methods. Our simulations showed that, when the death rate is low, neglecting the unfavourable value associated with death in a non-informatively censoring manner may not have a substantial impact on the estimation or statistical inference. However, in the case of a moderate to high death rate, competing risk analyses and survival analyses with the maximum time censoring approach may better detect a treatment effect on recovery than the standard survival analysis that treat death as non-informative censoring if treatment also helps reduce mortality. The non-informative censoring in the paradigm of standard survival analysis methods may often yield ‘biased’ estimation of treatment effects. Thus, our research suggests that both the event of death and event of recovery are important to the estimation of the treatment effect since disease recovery is innately coupled with survival in COVID-19 trials. Accordingly, treating death as a non-informative censoring event in the time-to-recovery analysis would ignore the negative impact of death to the modification of the probability of recovery. Furthermore, as shown by simulations where the latent times-to-event for death and recovery were negatively correlated (reflecting the scenario where certain characteristics that increase the likelihood of death are also associated with longer times-to-recovery), standard survival analysis methods treating death as non-informative censoring may even lose power to detect a true treatment effect on recovery.

With the implementation of the ICH E9 (R1) addendum [25], strategies for handling intercurrent events have received an unprecedented amount of attention from researchers and regulatory agencies for their substantial impact on the definition of the clinical question of interest. In the setting of a time-to-recovery analysis, our evaluations have demonstrated that a composite variable strategy would be more appropriate than other strategies to allow the impact of the intercurrent death to be incorporated into the estimation of the treatment effect on recovery. In both the simulations and case studies we explored, we consistently observed similar results between the standard methods with maximum time censoring approach and their analogous competing risk counterparts for semi-parametric (Cox PH vs. Subdistribution PH), non-parametric (log-rank vs. CIF chi-square test), and non-parametric area-based (RMST vs. CIF AUC) methods. Intuitively they should be similar, since patients who die experience “immortal time” for the event of recovery in the competing risk methods, while the maximum time censoring approaches assume that these patients have an indefinitely long time to achieve the endpoint of recovery. Our findings suggest that standard survival analysis methods with alternative censoring rules can serve as an alternative to more sophisticated competing risk approaches in a setting with a well-defined and restricted follow-up period. Our simulations and case studies also show that the strength of evidence for inference may differ between ‘area’-based methods (CIF AUC, RMST) and ‘slope’-based methods (subdistribution hazard, Cox PH, log rank) depending on the setting (e.g. short duration of follow-up, whether the proportional hazards assumption is met, etc.).

In this work, the evaluation criteria for both simulations and case studies focused on the probability of (statistical) significance since the distinct statistics of different methods are not directly comparable. However, probability of significance should not be the sole criteria for selection of an appropriate statistical method, nor should researchers rely on a single analysis in evaluating treatment efficacy. Our comprehensive evaluation also did not suggest that any one method was superior to the others across all scenarios. Therefore, selection of the appropriate analysis method should consider model assumptions (e.g., the proportionality assumption for use of Cox PH or Subdistribution Hazard models), the scientific objective being studied, and the clinical relevance of the interpretation of results. It is also recommended to examine supplementary survival analysis methods and censoring strategies to further evaluate robustness of results and the totality of evidence.

This research was guided by the unique settings of COVID-19 clinical trials. In our simulations we have examined settings where the hazard ratio of death in the experimental group is less than or equal to 1 in reference to control. Settings with a hazard ratio of death greater than 1 were not examined since a treatment effect on recovery loses clinical meaningfulness for an experimental treatment that increases mortality. Our simulations also assumed one competing risk event of death. This is motivated by COVID-19 trials where death is the major event that competes with the endpoint of recovery. However, the research can be easily generalized to multiple competing risk events.

Our research demonstrated the importance of appropriate handling of death in time-to-recovery analysis and will be particularly beneficial to the researchers when planning current and future COVID-19 treatment trials. This research framework can be applied to evaluate the impact of censoring strategies in other populations, endpoints, settings, or even in non-COVID-19 indications with appropriate adjustment of the parameters to reflect the study settings.

Acknowlegements

This manuscript was sponsored by AbbVie Inc. AbbVie contributed to the design, research, and interpretation of data, writing, reviewing, and approving the content. Hong Li, Kevin Gleason, Yiran Hu, Sandra Lovell, Saurabh Mukhopadhyay, Li Wang, and Bidan Huang are employees of AbbVie Inc. and may own AbbVie stock. We are very thankful to Lois M. Larsen who provided expertise that greatly assisted this research.

Appendix A. Supplementary data

Supplementary material