Methods for the Analysis of 26 Million VOC Area Measurements during the Deepwater Horizon Oil Spill Clean-up

Abstract

The NIEHS GuLF STUDY is an epidemiologic study of the health of workers who participated in the 2010 Deepwater Horizon oil spill response and clean-up effort. Even with a large database of approximately 28 000 personal samples that were analyzed for total hydrocarbons (THCs) and other oil-related chemicals, resulting in nearly 160 000 full-shift personal measurements, there were still exposure scenarios where the number of measurements was too limited to rigorously assess exposures. Also available were over 26 million volatile organic compounds (VOCs) area air measurements of approximately 1-min duration, collected from direct-reading instruments on 38 large vessels generally located near the leaking well. This paper presents a strategy for converting the VOC database into hourly average air concentrations by vessel as the first step of a larger process designed to use these data to supplement full-shift THC personal exposure measurements. We applied a Bayesian method to account for measurements with values below the analytic instrument’s limit of detection while processing the large database into average instrument-hour concentrations and then hourly concentrations across instruments on each day of measurement on each of the vessels. To illustrate this process, we present results on the drilling rig ship, the Discoverer Enterprise. The methods reduced the 26 million measurements to 21 900 hourly averages, which later contributed to the development of additional full-shift THC observations. The approach used here can be applied by occupational health professionals with large datasets of direct-reading instruments to better understand workplace exposures.

Introduction

The Deepwater Horizon oil drilling rig exploded on 20 April 2010 and sank 2 days later (DWH disaster). Nearly 5 million barrels (779 million L) of oil were released in the ensuing 3 months following the explosion. Tens of thousands of workers were involved in the oil spill response and clean-up (OSRC). Volatile components of crude oil, along with other compounds associated with the OSRC effort, were released into the air. Oil clean-up work has been associated with detrimental health outcomes in previous oil spills (Laffon et al., 2016). Using surveys and health evaluations of the DWH disaster workers, the National Institute of Environmental Health Sciences’ GuLF Long-term Follow-up Study (GuLF STUDY) is investigating the relationship between OSRC work and potential health outcomes, in part by evaluating exposure–response relationships in epidemiologic analyses (Kwok et al., 2017).

Among the oil-related exposures of interest are total hydrocarbons (measured as total petroleum hydrocarbons, THCs) and some of its volatile components, i.e. benzene, toluene, ethylbenzene, xylene (o-, m-, and p-isomers combined), and n-hexane (BTEX-H). For each of these exposures, we developed quantitative estimates for exposure groups (EGs), unique combinations of job/activity, location, and time period, that were linked to study participants through their reported work histories (Stenzel et al., 2021a; Stewart et al., 2021a).

The DWH disaster was characterized by the collection of a large number of full-shift personal samples analyzed for THC and related crude oil chemicals over a short period of time (28 000 personal samples over 14 months). Nearly 26 200 samples met the study inclusion criteria, resulting in ~134 000 THC and BTEX-H measurements (Stenzel et al., 2021b). Despite this large number of samples, sufficient (in the number or in coverage of activities worked) personal exposure measurements were not available for some EGs worked by the study participants due to the large area of the Gulf impacted, scope of the OSRC work performed, number of workers involved in the effort, and limits in the number of professionals with appropriate exposure sampling expertise. In particular, measurements of workers on some of the large vessels supporting the on-water response efforts located primarily within a 5 nautical mile (nmi; 9.26 km) radius of the wellhead, had in some cases, large gaps in the days monitored. In addition, because different methods were tried to stop the leaking oil until the well was mechanically capped on 15 July 2010, the work, and as a result, the exposures were likely to be unusually dynamic and variable beyond what would be expected with ‘similar EGs’ discussed by Mulhausen and Damiano (2015). That is, whereas geometric standard deviations (GSDs) of measurement datasets at typical work environments range from 2 to 3, the GSDs for our datasets were typically on the order of 6 to 8. In such cases, a limited number of measurements may not be representative of the actual distribution of exposures from all tasks being performed over a period of time (in our case, months) and thus, may not be representative of average exposures experienced by the workers over this period of time. In addition, because these vessels were in the wellhead area, workers on these vessels potentially had some of the highest exposure levels in the study. Inaccurate exposure estimates could bias the exposure–response relationship and therefore adversely affect the interpretation of disease etiology.

To supplement the personal measurements, we used a second dataset of measurements containing more than 26 million direct-reading area measurements of approximately 1-min duration for volatile organic compounds (VOCs) (the VOC database). These measurements were collected on 38 vessels [drilling rigs, marine vessels (MVs) piloting underwater remotely operated vehicles (ROV vessels), and other large MVs] involved in the OSRC efforts at the wellhead. Many of these measurements were below the analytical instruments’ limit of detection (LOD; known as censored measurements). In the occupational health field, this VOC database represented a high volume data scenario, i.e. a scenario where the database is so massive that it cannot be analyzed using normally available computational resources.

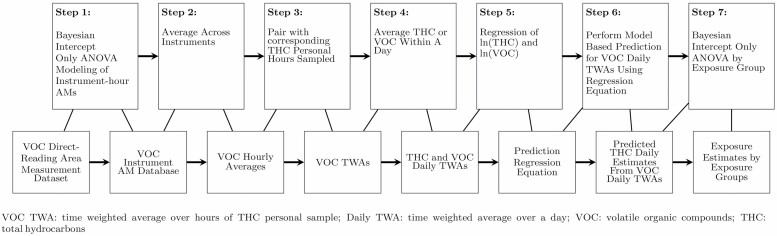
The overall goal of this component of the epidemiologic study was to develop daily estimates of full-shift personal exposures to THCs by vessel using these VOC data to supplement the limited number of THC full-shift personal measurements on these vessels (Fig. 1). The process described was to make the VOC database comprising short-duration area measurements, comparable to the THC database, comprising full-shift personal measurements. The purpose of this paper is to present the first two steps of the methods, which processed the 26 million VOC measurements into a manageable dataset (Steps 1 and 2 of Fig. 1). Through the use of Bayesian modeling, we initially developed hourly averages of each instrument’s measurements on each vessel-day, and then we calculated for each hour on a vessel-day an average across all instruments to create a vessel-level hourly VOC average. We provide summaries of the processed data across all vessel days and illustrate the method specifically by showing results from the Discoverer Enterprise (Enterprise). Using these hourly VOC averages, Ramachandran et al. (2021) describe the development of full-shift estimates of THC personal exposures using the VOC hourly concentrations to supplement the THC personal measurements, which likely developed more stable and representative exposure statistics for the workers on these vessels.

Figure 1.

Steps to developing the THC:VOC relationship for prediction of THC from VOC direct-reading area measurements. This paper presents Steps 1 and 2. VOC TWA: time weighted average over hours of THC personal sample; Daily TWA: time weighted average over a day.

An overview of the exposure assessment is found in Stewart et al. (2021a) and the development of EGs is in Stenzel et al. (2021a). Estimation of exposures to THC and benzene, toluene, ethylbenzene, xylene, and n-hexane are in Huynh et al. (2021a,b,c), Groth et al. (2017, 2021), and Ramachandran et al. (2021); to PM_2.5 in Pratt et al. (2021); to dispersant aerosols in Arnold et al. (2021); to dispersant vapors in Stenzel et al. (2021c); and to oil mist in Stewart et al. (2021a). Dermal exposures were also estimated (Gorman Ng et al., 2021; Stewart et al., 2021b).

Sampling background

The VOC database consisted of measurements collected from 30 April 2010 through 29 August 2010. The responsible party (RP) of the DWH disaster (BP Gulf Science Data, 2016) (as designated by the US government) collected these to (i) monitor the air around the operations activities to protect potential downwind receptors; (ii) monitor air in the vicinity of operations activities to protect worker health; and (iii) monitor specific activities to support safe operations. Levels in excess of 50 ppm for 15 min were used by the RP to support decisions that had to be made on short-term bases, such as providing respiratory protection or initiating efforts to suppress the oil vapors emanating from the leaking oil rising to the water surface. Area VOC measurements were collected with real-time direct-reading instruments on 4 drilling rig vessels, 13 ROV vessels, and 21 MVs involved in the OSRC effort. These vessels were located within a 5 nautical miles (nmi, 9.26 km) radius of the well and were generally stationary throughout their entire deployment during the OSRC effort.

Data from two of the MVs were removed from this database because all the VOC measurements collected on those vessels represented instrument testing (calibration or bump testing using a gas standard of known concentration) or the instrument indicated (via a warning message) that it was not operating within the instrumentation performance criteria specification. The RP indicated the VOC samples were collected using real-time multi-gas detectors (AreaRAE and MultiRAE at that time manufactured by RAE Corporation) equipped with a photoionization detector (PID) lamp (10.6 eV). The instrument manufacturer recommends that the instrument be calibrated using isobutylene at three concentrations: zero, ~10 and ~100 ppm. It is not clear from the available documentation what the RP used for their specific method of calibration. The response and decay times of the instrument are expressed as a bell-shaped curve of 10 s. The response time represents the time to reach 90% of the actual concentration. For example, if the actual concentration was 1 ppm, within 10–15 s the detector would indicate at least 90% of that concentration, or 0.9 ppm. Similarly, the decay time represents the time it takes to indicate 10% of the peak concentration. These response times suggest that measurements collected at least 30 s apart were likely independent of each other. The sensitivities relative to isobutylene for benzene, toluene, ethylbenzene, xylene, and n-hexane are 0.53, 0.50, 0.52, ~0.43 (depending on the makeup of the xylene isomers), and 4.3, respectively. For example, if the air concentration actually measured was 100 ppm benzene, the instrument would display 100 ppm/0.53 or 189 ppm. The BTEX chemicals are all more sensitive than isobutylene, while n-hexane is less sensitive (100 ppm n-hexane would result in an instrument display of 100/4.3 or 23 ppm).

The instruments stored measurements to one decimal place, and in most cases the sample was collected at a frequency of about one measurement a minute. The VOC database contained many measurements below the direct-reading instrument’s LOD (0.1 ppm). However, the limit of reporting (LOR) was 0.05 ppm. The instrument rounded off all measurements to the nearest 0.1 ppm. That is, if the concentration measured was between 0.05 and 0.14 ppm, it was recorded in the database as 0.1 ppm. If the value was between 0 and <0.05 ppm (actual concentrations can only be positive), it was recorded as 0.0 ppm.

The measurements were collected on one or more instruments at locations on each vessel determined by the industrial hygiene/safety staff on the vessel. The RP indicated in their offshore air monitoring plan that the area monitors were to be located in the common work areas and inside crew quarters, resulting in the instruments being located anywhere on the vessel, from inside, in the living quarters or offices to the operations area of the vessel, such as inside the ship’s engine room or outside on the open deck. Additional monitors could have been placed near the edge of the vessel or in other areas of interest. Unfortunately, the locations for the instruments on each vessel were not recorded. The monitoring plan indicated that handheld monitors were also available, but it implied that these data were not part of the VOC area measurement database because these data were to be logged on approved field forms.

The basic assumption of our using these data was that an instrument at a particular location generally should provide a reasonable estimate of the air concentrations experienced by individuals at that location, based on the RP’s stated purpose for conducting the area monitoring (‘monitor the air in the vicinity of operations activities to protect worker health’). Thus, we assumed that the instruments were often strategically located to reflect where individuals worked. Moreover, because the response effort was a temporary, but time-critical event, using the direct-reading results for an investigation of engineering controls (which is one use of direct-reading instrumentation in industry) was unlikely. We also assumed that a significant portion of most workers’ exposures was generated from the general environment, the major source of which was likely the vapor from the oil spill, although engine combustion products and other chemicals may have made a minor contribution to the overall VOC general environment air concentration. We also assumed, if there were other emission sources, that workers probably did not receive exposures from a single specific emission source associated with a task, such as taking an oil sample from a tank, but rather from multiple sources, some of which may have been monitored by nearby instruments.

With sufficient numbers of instruments and personal measurements, therefore, we hypothesized that there may have been a relationship between the personal sampling and the area monitoring data. We believed this to be reasonable for two reasons. First, we expected that the oil was the primary source of THC vapors in the general environment due to the leaking well, at least during the time the oil was being released, and that all workers would have received at least some, if not much, of their exposure from this source. Second, since attempting to stop the oil leakage was a dynamic situation, it is unlikely that most workers’ exposures would have had a single source all day, every day. This assumption would mean that exposures more likely reflected the more general, ambient air concentration rather than reflecting a single more concentrated source of exposure. Because a number of factors (possibly unknown) could impact any potential relationship between full-shift VOC time weighted averages (TWAs) and THC personal full-shift measurements, we used empirical data to determine the relationship, i.e. the correlation between the two substances by vessel over time.

There are additional complicating factors that impacted the correlation of VOC concentrations and THC personal measurements. First, whereas, the VOC instruments used a PID detector, the THC method used a hydrogen flame ionization detector (HFID). While both detectors have a comparable sensitivity to aromatics such as the BTEX chemicals, the PID detector has a very low sensitivity to saturated alkanes such as n-hexane (as noted above, benzene’s sensitivity factor is 0.53 and n-hexane’s is 4.3). Thus, with the PID detector, n-hexane is eight times less sensitive than benzene. In contrast, with HFID, n-hexane is only about 20% less sensitive than benzene. A second complication is that the composition of the crude oil was changing due to weathering, as described in the online supplementary material of Stenzel et al. (2021a). Weathering here resulted in the contribution of alkanes in the THC value changing more over time compared with that of the aromatics, which resulted in the relative correlation between VOC concentrations and THC measurements changing with weathering. For these reasons, in addition to the reasons mentioned above, we felt empirical observations rather than chemical properties and laws to derive the VOC:THC correlation was scientifically appropriate.

Methods

End goal of work

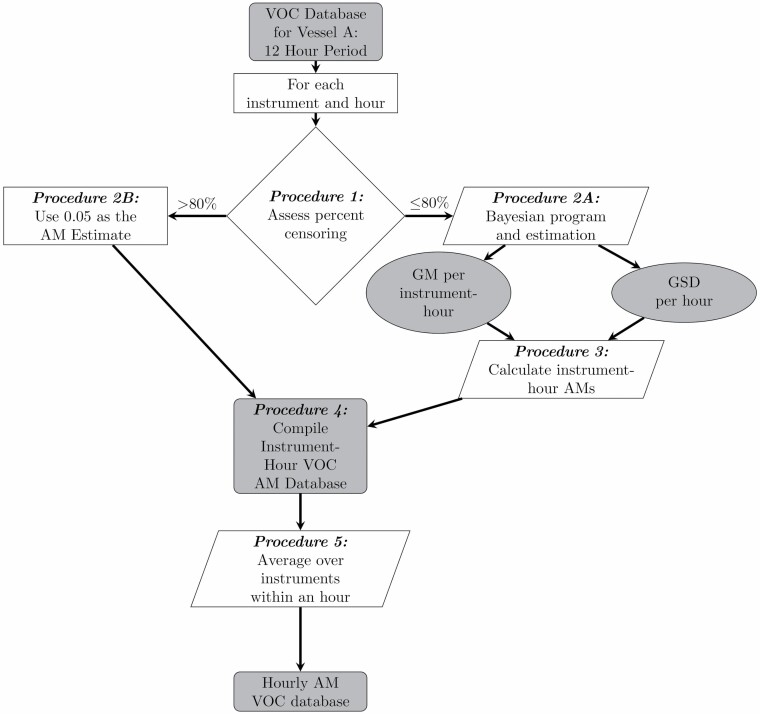
Our primary objective was to develop hourly averages across all instruments by vessel-day from the short-duration area VOC samples. The process of creating these hourly averages is described in Fig. 2. Ramachandran et al. (2021) then go on to describe how these hourly averages were further processed to develop full-shift averages for comparison with the THC full-shift personal measurements on the same vessels (Fig. 1, Steps 3–7). Those authors found a significant relationship between VOC daily TWAs and non-censored THC daily TWAs on the ROV vessels in time periods (TPs) 1a–1b, (i.e. 22 April–15 July 2010, the period of oil release; R-squared 0.61, N = 131). For more information on time periods, see Stewart et al. (2021a). Rationale for the use of this relationship can be found in Ramachandran et al. (2021). Using that relationship, Ramachandran et al. (2021) predicted ‘THC’ TWA estimates from full-shift VOC TWA measurements on vessel days without THC measurements. Descriptive exposure statistics using both the measured and the predicted THC values were then developed for each vessel. All estimation was done at the spatial level of the vessel.

Figure 2.

Flowchart of procedures in estimating VOC exposure of hourly averages on a vessel. Gray squares are databases that were analyzed. We ran 12-h datasets through this algorithm using parallel computing.

Procedure 1: assess percent censoring

We first determined the percentage of censored values (i.e. below the LOD) from the results for each instrument for each hour on each vessel (Fig. 2). We retained the same criteria to meet our performance goals as for our THC estimates, that is average relative bias [where relative bias is the absolute difference between the truth (value set in simulation to generate the data) and the estimate divided by the mean], designated as ≤15%, and an average root mean squared error [i.e. the square root of the sum of squared deviations between the real and estimated values (here the mean) divided by the square root of the number of observations; this whole quantity is then further divided by the mean to obtain the relative root mean squared error], designated by <65% (Huynh et al., 2016). To achieve these goals, Huynh et al. (2021a,b,c) use the threshold of N ≥ 5 measurements for ≤80% censoring. Here for the VOC data, we use a similar criterion. If the percent censoring was ≤80%, we proceeded with the Bayesian modeling described in Procedure 2A. If the percent censoring was >80%, we proceeded to Procedure 2B. If N < 5, the measurements were dropped, and no estimate was developed for that instrument-hour.

Procedures 2A and 3: Bayesian modeling (censoring ≤80%) of instrument-hour arithmetic means

When censoring was ≤80% and N ≥ 5, we used a Bayesian analysis of variance (ANOVA; intercept only regression) approach to account for the censored information and to model each instrument’s hourly geometric mean (GM) and an overall hourly GSD (i.e. a GSD for each hour across all instruments on a vessel-day), from which the arithmetic mean (AM) was calculated (Fig. 2, Procedure 2A).

Specifically, we assumed the mean of the natural log of the VOC measurements for each instrument-hour could be modeled using only an intercept term (i.e. each instrument-hour had its own intercept, which represented the mean of the measurements for the instrument-hour). Empirical analysis of air concentration variances within the same hour on different instruments on the same vessel suggested that variability was similar. Therefore, in our Bayesian ANOVA model, a common variance for each hour (i.e. the same variance across instruments) was assumed.

Let Y_ijk be the natural log of VOC for measurement k on instrument i at hour j where i = 1, …, Ninstr, j = 1, …, Nhours (or number of hours in the model), and k = 1, …, n_ij. The exact number of measurements k within an hour varied from instrument to instrument. This measurement is the average concentration over the measurement time of seconds to minutes. To account for censored data, we expand a standard Bayesian ANOVA model by considering censored and non-censored sets separately. Let C_y = {k: Y_k ≤ LOR_k(Y)} be the set for which Ys were censored (at or below the LOR), and let O_Y denote the observed measurements. Here, the LOR_k(Y) was ln(0.05) and was our censoring value. We assume common notation for probability density functions evaluated at q_i for normal distributions (N(q_i|μ,σ²)) with mean μ and variance σ² and uniform distributions (Unif(q_i|a,b)) with parameters a and b as written in common Bayesian textbooks such as Gelman et al. (2013). Then the joint posterior distribution had the following form:

$${\displaystyle \begin{array}{l}{\displaystyle {\displaystyle \prod _j^{\mathrm{N}\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{s}}}\mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}({\sigma }_j|a,b){\displaystyle \prod _i^{\mathrm{N}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}}}N({\mu }_{ij}|c,d)}\\ {\displaystyle \prod _{i,j,k\in O_y}}N(Y_{ijk}|{\mu }_{ij},{\sigma }_j^2){\displaystyle \prod _{i,j,k\in C_y}}\mathrm{\Phi }\left(\frac{\mathrm{l}\mathrm{n}(0.05)-{\mu }_{ij}}{{\sigma }_j}\right)\end{array}}$$ (1)

where Φ(Z) represents the standard normal cumulative density function of Z, μ_ij, is the intercept (i.e. the estimated mean on the log scale) for instrument i in hour j, and ${\sigma }_j^2$ is the variance of the logged measurements in hour j. We set a vague (i.e. providing limited information) proper (i.e. based on a formal statistical distribution) prior of N(μ_ij|c,d) [where we set the mean to be 0 (c = 0), and the variance to be 100 000 (d = 100 000)] on μ_ij to allow the inference on the mean to be drawn primarily from the data. We assumed μ_ijs were independent and identically distributed. We used an informative prior on the standard deviation, namely Unif(σ_j|a,b) where a = ln(1.01) and b = ln(12), to restrict GSDs to between 1.01 and 12, as was commonly observed in the GuLF STUDY full-shift personal THC measurements over the same time period (Huynh et al., 2021a,b,c).

This model uses an overarching Gibbs sampling strategy where left-censored values were sampled first, followed by the sampling of means and standard deviations at each Markov chain Monte Carlo iteration. We implemented this model in R using RJAGS (Plummer, 2003, 2016; R Core Team, 2017). This model can be thought of as a simplified version of the bivariate left-censored Bayesian model proposed by Groth et al. (2017), but instead of a regression expression with two chemicals described there, we consider a single μ_ij term (i.e. 1 chemical).

Bayesian models use Markov chain Monte Carlo methods to generate a posterior distribution of each parameter of interest. This model yielded posterior distributions of a GM per instrument-hour and a GSD per hour (across instruments). In Bayesian modeling we assess convergence of the model to better understand if the model has agreed on a solution. Convergence, as assessed by Gelman Rubin diagnostics and trace plots, indicated convergence well within the first 5000 iterations. To allow for optimal convergence, for every hour on each vessel in which an instrument had at least 5 measurements and had ≤80% censoring, we obtained 10 000 iterations after 5000 iterations of burn-in. This resulted in a distribution of 10 000 GMs for each instrument-hour and 10 000 GSDs for each hour. These posterior samples were saved.

In Procedure 3, we used those GMs and GSDs to calculate the posterior distribution of the corresponding AMs for each instrument-hour using the following formula:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{A}{\mathrm{M}}_{ij}=\mathrm{G}{\mathrm{M}}_{ij}\times \mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{1}{2}{(\ln (\mathrm{G}\mathrm{S}{\mathrm{D}}_j))}^2\right).}\end{array}}$$ (2)

Procedure 2B: instrument-hour AM calculations

In Procedure 2B (Fig. 2) we assigned all instrument-hours with censoring >80% and N ≥ 5, an AM of 0.05 ppm. Rationale for this decision is reported in Supplementary Material (available at Annals of Work Exposures and Health online).

Procedures 4–5: instrument-hour AM database and hourly AM database

Some of the AMs developed in Procedure 2A (<1%) were <0.05 ppm. Because for sets with >80% censoring, we assigned the value of 0.05 ppm, to have comparable data, we replaced any Bayesian AM estimate <0.05 ppm with 0.05 ppm (procedure is not shown in Fig. 2).

The results developed in Procedures 2B and 3 were then compiled into a single database of instrument-hour AMs. For each instrument-hour on each vessel, we retained the median estimate of the 10 000 instrument-hour AMs from Procedure 2A (to reflect the true center of the distribution of each instrument-hour AM) and the AM estimates of 0.05 ppm from Procedure 2B (Fig. 2, Procedure 4). We called these instrument-hour averages.

Finally, we averaged the instrument-hour averages across all instruments for each hour of each day on each vessel (Fig. 2, Procedure 5). This procedure across instruments provided the average concentration across all measured locations on a vessel for that hour (called hourly averages).

Procedures 1–4 were computationally intensive due to the size of the dataset. As a result, we used Minnesota’s Supercomputing Institute (MSI) at the University of Minnesota to perform these analyses. To make it feasible to calculate instrument-hour AMs, we performed the analysis on 12-h sets (0–12:59; 13:00–23:59) of VOC data on each vessel. We considered the measurements in an hour on each vessel to be independent for running the program. Therefore, we were able to set up multiple computers to run different 12-h periods of data simultaneously, saving valuable computing time (also known as parallel computing).

Results

ROV vessel and MV VOC data

As part of this work, we developed instrument-hour averages and hourly averages for 13 ROV vessels and 17 MVs (2 vessels not shown here are due to their lacking THC data that was needed by Ramachandran et al., 2021).

Table 1 describes the number of VOC measurements available, the number of instrument-hour averages, and the number of hourly averages developed for each of the ROV vessels and MVs. Although the number of instruments operational in a day did not vary substantially (N = 3–7), the number of measurements per instrument-hour did vary (N = 50–1678), likely due to differences in sampling frequency between instruments. On the Adriatic and Strongline, samples were taken every few seconds on average, while on many other vessels, measurements occurred roughly every minute on average. Days with VOC measurements also varied greatly by vessel, ranging from 2 to 109 (exact deployment dates for the DWH differed by vessel but were unavailable). Although over 100 000 instrument-hour averages were developed in this process, the number of hourly averages was much smaller (N < 22 000), which led to a more manageable dataset.

Table 1.

Description of VOC data available on vessels operating ROVs vessels and MVs. Rig data were not used to impute additional days of THC information. This table presents these statistics across the entire period of measurements (30 April–29 August 2010).

Vessel type	Vessel name	N Days with VOC	Total N instruments	N Average Instruments per Hour	N Average Measurements per Instrument-Hour	N Instrument- Hour Averages	N Hourly Averages
ROV Vessels	Boa Deep C	77	8	5	232	7667	1697
	Boa Sub C	51	20	5	195	4560	1008
	Casey Chouest	14	6	6	54	1706	286
	Chouest Holiday	30	8	4	19	2781	665
	Helix Express	52	6	5	58	5610	1119
	HOS Achiever	46	9	4	826	4312	1011
	Iron Horse	12	6	6	888	1511	259
	Normand Fortress	15	4	4	58	1273	347
	Ocean Intervention I	19	5	3	881	956	274
	Ocean Intervention III	109	16	6	73	16098	2521
	Olympic Challenger	49	9	5	52	5408	1075
	REM Forza	67	9	7	123	10550	1486
	Skandi Neptune	93	20	5	90	10761	2025
MVs	Adriatic	40	4	2	1165	2145	869
	Blue Dolphin	31	16	6	372	3810	609
	Helix Producer	30	7	4	57	2279	645
	Loch Rannoch	19	6	3	596	413	138
	Massachusetts	31	8	4	56	2511	616
	Monica Ann	44	7	5	50	5200	1001
	Normand Commander	48	10	5	57	5353	1048
	Odyssea Diamond	35	5	4	88	2866	721
	Overseas Cascade	18	9	7	53	1514	215
	Seacor Pride	6	3	3	59	297	99
	Seacor Reliant	2	4	4	70	32	9
	Seacor Vanguard	11	6	4	219	490	133
	Seacor Venture	17	2	2	51	589	331
	Stim Star III	15	13	6	142	1537	272
	Strongline	10	3	3	1678	546	182
	Tyler Stephen	53	9	4	57	4488	1185
	War Admiral	5	3	2	54	123	54

ROV Vessels: vessels operating remotely operated vehicles; N Days with VOC: number of days with at least 1 h of VOC information available; N Instruments: number of instruments that were operational on that vessel; N Average Instruments per Hour: the average number of instruments operating in each hour across all hours with measurements; N Average Measurements per Instrument-Hour: the average number of measurements in an instrument-hour across all instrument-hours on that vessel; N Instrument-Hour Averages: total number of instrument-hour AMs developed; N Hourly Averages: total number of hourly averages developed across all instruments.

Table 2 displays characteristics of the instrument-hour averages, hourly GSDs, and hourly averages. We present the median and maximum of all instrument-hour averages (from Procedure 4, Fig. 2) for each vessel (Instrument-hour Averages, Overall). We then calculated for illustration purposes an average for each day of measurements on each vessel from all available instrument-hours on the day and then averaged all daily values on the vessel (Instrument-hour Averages, Daily Averages). Similarly, we present the median and maximum of the GSD daily averages calculated by averaging all available GSDs in each day and then averaging across all measured days (Hourly GSD, Daily Averages). Finally, again for illustration, we present the median and maximum of all hourly averages calculated in Procedure 5, Fig. 2 across all measured instrument-hours for the vessel (Hourly Averages, Overall). The actual hourly averages that were the input for this final set of columns were used by Ramachandran et al. (2021) for further processing.

Table 2.

Statistics by vessel for instrument-hour averages (ppm), hourly GSDs, and hourly averages (ppm). The median, minimum (min), and maximum (max) are provided for each type of statistic. The minimum instrument-hour average was consistently 0.05 ppm and is therefore not shown.

Vessel type	Vessel name	Instrument-Hour Averages					Hourly GSD			Hourly Averages
		Overall		Daily Averages			Daily Averages			Overall
		Median	Max	Median	Min	Max	Median	Min	Max	Median	Min	Max
ROV Vessels	Boa Deep C	0.05	515.57	0.39	0.05	26.30	1.50	1.08	8.17	0.35	0.05	163.20
	Boa Sub C	0.05	3261.41	0.24	0.05	83.37	2.31	1.09	8.84	0.09	0.05	1269.47
	Casey Chouest	0.05	14.55	0.18	0.05	1.13	2.71	1.55	5.36	0.17	0.05	5.48
	Chouest Holiday	0.05	10.58	0.13	0.05	0.81	7.14	2.58	9.61	0.05	0.05	4.33
	Helix Express	0.05	76.75	0.11	0.05	4.10	2.54	1.09	7.01	0.05	0.05	35.12
	HOS Achiever	0.05	178.11	0.25	0.05	3.99	2.82	1.20	10.03	0.12	0.05	64.61
	Iron Horse	0.05	44.30	0.61	0.11	6.39	1.67	1.15	3.50	0.44	0.06	26.05
	Normand Fortress	0.05	36.92	0.05	0.05	1.38	3.14	1.12	3.63	0.05	0.05	11.45
	Ocean Intervention I	0.05	2.76	0.05	0.05	0.81	1.59	1.16	6.11	0.05	0.05	1.03
	Ocean Intervention III	0.05	5497.71	0.48	0.05	110.48	3.18	1.45	8.08	0.26	0.05	1104.76
	Olympic Challenger	0.05	90.00	0.14	0.05	1.42	3.41	1.27	10.60	0.06	0.05	18.10
	REM Forza	0.05	1118.21	1.04	0.05	14.67	2.53	1.22	7.00	0.28	0.05	244.56
	Skandi Neptune	0.10	1242.96	1.17	0.05	34.37	1.72	1.21	8.87	0.99	0.05	448.02
MVs	Adriatic	0.05	1.96	0.05	0.05	0.27	1.73	1.46	4.83	0.05	0.05	1.83
	Blue Dolphin	0.05	44.07	0.26	0.06	6.07	2.69	1.08	6.72	0.17	0.05	9.41
	Helix Producer	0.05	18.33	0.38	0.05	3.57	1.59	1.14	3.78	0.25	0.05	11.38
	Loch Rannoch	0.05	92.22	0.21	0.05	11.36	1.92	1.11	11.19	0.08	0.05	46.47
	Massachusetts	0.05	91.11	0.29	0.05	19.38	3.17	1.37	10.87	0.10	0.05	48.76
	Monica Ann	0.05	67.31	0.30	0.07	5.81	1.92	1.26	8.15	0.16	0.05	23.72
	Normand Commander	0.05	150.29	0.18	0.05	4.47	1.98	1.16	10.47	0.13	0.05	32.22
	Odyssea Diamond	0.05	70.32	0.36	0.06	3.38	2.42	1.37	9.10	0.21	0.05	30.68
	Overseas Cascade	0.05	298.52	0.25	0.05	6.64	2.38	1.21	11.50	0.13	0.05	58.81
	Seacor Pride	0.05	2.39	0.19	0.08	0.47	4.56	2.21	5.88	0.09	0.05	0.99
	Seacor Reliant	0.05	14.11	0.53	0.05	1.02	1.45	1.45	1.45	0.33	0.05	3.57
	Seacor Vanguard	0.29	7.78	0.61	0.15	1.58	1.58	1.34	2.17	0.64	0.05	3.83
	Seacor Venture	0.05	7.01	0.28	0.05	2.04	8.90	1.25	10.83	0.05	0.05	7.01
	Stim Star III	0.05	36.97	0.53	0.09	1.96	3.83	1.53	10.78	0.14	0.05	6.26
	Strongline	0.05	1.29	0.05	0.05	0.46	3.63	2.38	4.88	0.05	0.05	0.46
	Tyler Stephen	0.05	69.48	0.24	0.05	4.20	4.44	1.20	11.27	0.13	0.05	15.27
	War Admiral	0.05	7.27	0.52	0.28	1.96	2.20	1.07	2.73	0.34	0.05	3.11

Instrument-Hour Averages Overall: statistics using all instrument-hour averages (weighted equally); Instrument-Hour Daily Averages: the daily instrument-hour average was calculated and statistics were performed on the daily average instrument-hour averages; Hourly GSD Daily Averages: the hourly GSDs were averaged within a day and statistics were performed on the daily average hourly GSDs; Hourly Average Overall: we took the statistics of all hourly averages (weighted equally).

In all but two cases (Skandi Neptune and Seacor Vanguard, which had higher medians) the median instrument-hour average over all instrument-hour averages on a vessel was 0.05 ppm (the lowest possible value based on this method), reflecting generally low concentrations measured in any given hour by the instruments. However, the maximums of the individual instrument-hours were much higher: ranging from 1.29 ppm on the Strongline to 5497.71 ppm on the Ocean Intervention III.

When these instrument-hours were averaged within each day, similar patterns in the instrument-hour averages were observed, with the median daily average generally being low (<0.50 ppm), but with some individual days on some vessels exceeding 10 ppm.

The median hourly GSDs by vessel ranged from 1.45 on the Seacor Reliant to 8.90 on the Seacor Venture (Table 2), with minimums generally close to 1 (ranging from 1.07 on the War Admiral to 2.58 on the Chouest Holiday). Maximum daily average hourly GSDs ranged from 1.45 on the Seacor Reliant to 11.50 on the Overseas Cascade.

The median of all hourly averages by vessel remained below 1 ppm for all vessels (Table 2). The lowest hourly average for all vessels was 0.05 ppm and the maximum reported hourly average ranged from 0.46 ppm on the Strongline to 1269.47 ppm on the Boa Sub C.

Data example: Discoverer Enterprise

To illustrate our method, we describe the results for the Enterprise, the drilling rig ship positioned directly over the well. Approximately 2.5 million VOC direct-reading measurements were taken between 14 May and 3 July 2010 on this vessel. In total, 31 instruments operated for at least 1 h over this period, with an average of 20 instruments operational each day.

In this illustration, we analyzed VOC measurement results from 28 June 2010, which was a typical day in the GuLF STUDY’s time period 1b (15 May–15 July), when the crude oil was still being released and dispersant was being injected into the crude oil plume at the source of the leak, prior to the mechanical capping of the well. Although the instruments’ start and end times varied, several operated continuously on this particular day. Thus, this example allows us to view air concentrations during a continuous functioning period over an entire 24-h period.

Within-instrument and hour variability (prior to Procedure 1)

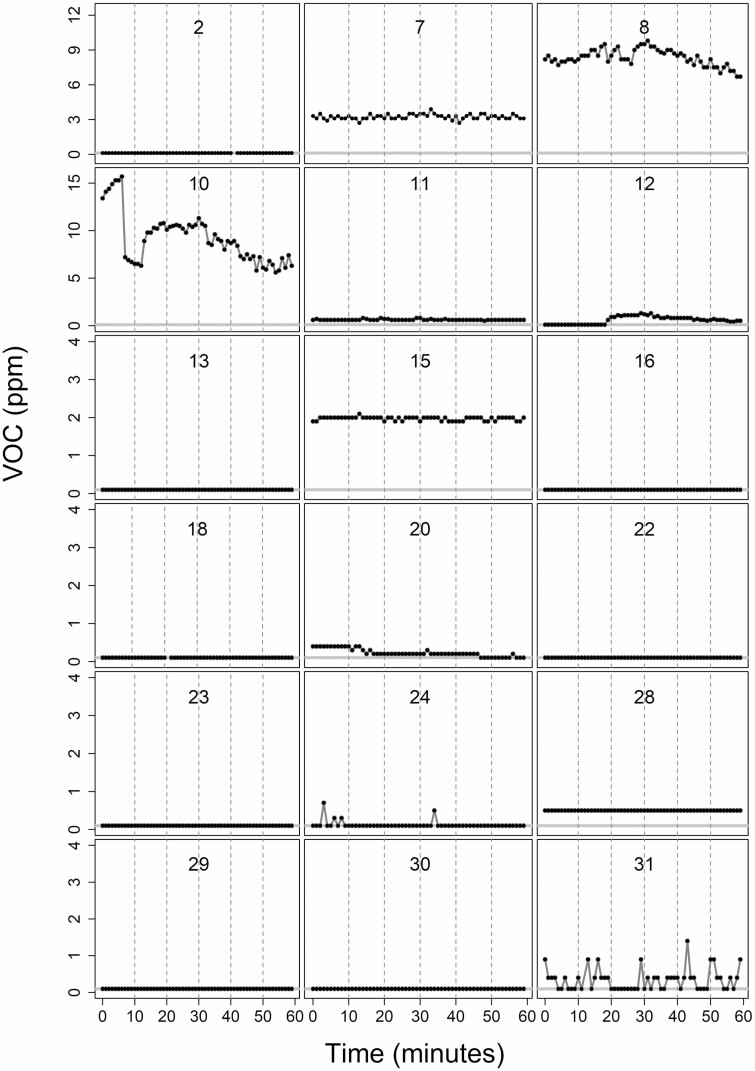
Prior to Procedure 1, we explored the raw air concentration data to display how the instrument measurements varied. Specifically, we plotted VOC measurement results from each instrument that operated between 12:00 and 13:00 on 6/28/2010 (Fig. 3), a time of higher concentrations on this day (e.g. instruments 8 and 10). Censored values were assigned 0.05 ppm for these plots.

Figure 3.

VOC concentrations within the 12:00–13:00 h on 6/28/2010 for selected instruments. The horizontal gray band represents the limit of reporting (LOR = 0.05 ppm). Each instrument that operated on this vessel on any day was given a number, 1–31. Only operational instruments (out of 35 total instruments) are presented. No modeling was performed, and censored values were imputed for these plots as the LOR. The VOC ppm scales for instruments 2, 7, and 8 are 0–12 ppm. Instruments 10–12 have a scale of 0–16 ppm. The remaining instruments have a scale of 0–4 ppm.

We notice that several instruments measured relatively constant levels of VOC at the LOR (instruments 2, 13, 16, 18, 22, 23, 29, and 30). Other instruments generally measured constant levels above the LOR (7, 11, 12, 15, 10, and 28), while others showed greater variation in concentrations reported (instruments 8, 10, 24, and 31).

Procedures 1, 2A–B, and 3: calculation of AMs

For all instrument-hours with ≥5 measurements, we assessed censoring (Fig. 2, Procedure 1) for each instrument-hour and applied Procedure 2A or 2B based on the censoring level present (≤80 or >80%). First, in Procedure 2A through the Bayesian modeling approach, we developed 10 000 GMs (for each instrument) and 10 000 GSDs (across all instruments) for each hour when censoring was ≤80%. Supplementary Table S1 (available at Annals of Work Exposures and Health online) displays the number of measurements and the median and 95% credible interval of the hourly GSD estimates for each hour on 28 June 2010. If all GSDs were averaged on this day (in Supplementary Table S1, available at Annals of Work Exposures and Health online), the average would represent one of the daily average values summarized in the GSD (daily average) columns in Table 2. The number of measurements per hour reported ranged from 441 to 660. The median posterior GSD estimates ranged from 1.5 to 2.2, the highest being in hour 21. Using the 10 000 posterior estimates of the GMs of the instrument-hour concentrations and the 10 000 posterior GSD estimates across all instruments from Procedure 2A, we calculated the posterior distribution of the 10 000 AMs (Fig. 2, Procedure 3). Next, we assigned 0.05 ppm to all instrument-hours with censoring >80% (Procedure 2B).

Procedures 4–5: instrument-hour AM and hourly AM analyses

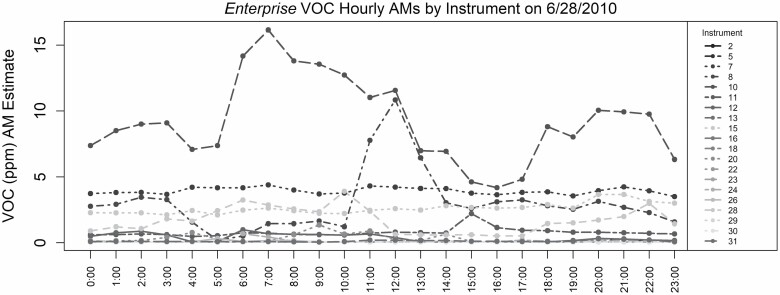
For the estimated Bayesian AMs that were <0.05 ppm, we assigned 0.05 ppm. Then, from the 10 000 Bayesian AMs for each instrument-hour on each vessel, we retained for the dataset only the median of the 10 000 posterior estimates of each instrument-hour AM from Procedure 2A and combined them with the imputed value for the instrument-hour AM with >80% censoring (0.05 ppm) into a single database (Fig. 2, Procedure 4). Supplementary Table S2 (available at Annals of Work Exposures and Health online) presents the variation in the instrument-hour AMs. The minimum instrument-hour AM was estimated to be 0.05 ppm, and the maximum instrument-hour AM reported on this day was in hour 7 (about 16 ppm). These 1-day values are equivalent to the input values used to calculate our ‘Overall’ instrument-hour averages across all measured hours in Table 2. From this instrument-hour AM database, we show the instrument-hour AMs by hour on 6/28/2010 (Fig. 4). Some instruments (e.g. instrument 26) measured lower concentrations (around 0.05 ppm), whereas other instruments measured concentrations that rose and fell throughout the day. Instrument 10 measured peak VOC concentrations (around 15 ppm) at 7:00. Instrument 8 measured relatively low concentrations early in the day that peaked to about 10 ppm around 12:00.

Figure 4.

VOCs AM estimates by instrument and hour on the Enterprise on 6/28/2010. Some instruments had higher levels of VOC while others had low levels of VOC likely due to the instruments’ locations on the vessel (i.e. inside in the living quarters versus the open deck).

The GSD of the instrument-hour AM statistics ranged by hour from 5.76 to 7.67. The GSDs were higher during hours 11 (11:00–12:00) and 12 (12:00–13:00).

Finally, we averaged the instrument-hour averages over instruments to obtain hourly averages across the vessel (Fig. 2, Procedure 5). These hourly averages were relatively constant around 1 ppm (Supplementary Table S2, available at Annals of Work Exposures and Health online). A slight peak in concentrations (1.7 ppm) occurred in hour 12 (12:00–13:00 h). These averages are equivalent to the input data we used to generate the statistics for ‘Hourly Averages: Overall’ in Table 2.

Discussion

We describe here a method to convert a big dataset of direct-reading area VOC measurements collected across multiple instruments on various vessels into a smaller, more manageable set of hourly vessel VOC concentration summaries of AMs (hourly averages). In an accompanying paper, Ramachandran et al. (2021) describe calculating full-shift VOC TWA exposure estimates from these hourly averages to be comparable to the hours of corresponding full-shift THC measurements on the same day. This procedure allowed us to identify the relationship between the two contaminants to eventually supplement the THC measurements for those days lacking THC measurements on vessels on which workers experienced some of the highest concentrations in the study, as shown by the maximums in the column ‘Instrument-hour Daily Averages’.

In our Bayesian modeling strategy, we elected to use an hourly GSD across all instruments rather than an instrument GSD (across all hours), or a GSD for each instrument-hour based on empirical data and practical reasons. As demonstrated in our data example on the Enterprise, the hourlyAM estimates on a particular instrument could vary greatly from one hour to another. For example, as displayed in Fig. 4, instruments 8 and 10 had variable AMs throughout the day on 6/28/2010. This implies that the concentrations could vary greatly for one instrument from one hour to the next, which would have resulted in high instrument-level GSDs (had we chosen this approach). The high variance in some of these instruments (over the instrument’s operation across the 4-month period), suggests that a common variance across all measured hours within the same instrument would not have been supported by the observed data. Thus, although in general, exposure estimates remained constant or similar across time and across most instruments, there were some exceptions. Computationally, introducing an instrument-hour variability estimate led to instability in the estimates particularly at high censoring levels. With higher censoring, the GSDs would have inflated to the upper bound allowed by our prior (GSD of 12), which seemed unreasonable. The practical reason for using an hourly GSD was that the work being performed on the vessels with VOC data was generally dynamic because varying approaches to stop the oil leakage were tried, and the workers on these vessels likely performed tasks associated with different areas of the vessel. These different tasks and locations would have resulted in somewhat varying exposures because air concentrations changed over time and by location. Specifically, evidence for this is provided in Table 2 in the range of the daily average instrument-hour VOC averages.

Ideally, if instrument location information had been available, spatial–temporal analysis strategies could have been employed, along with averaging approaches similar to the averaging approach described here, but to exploit as much information as possible, we also would have needed estimates for the time each study participant spent at each location. No data have been identified, nor are they likely to exist, as to how long individuals worked at various locations on the vessel. Thus, we assumed that the instruments were placed around the ship in such a way that an hourly average across all instruments was a reasonable approximation of vessel-level air concentrations for that hour. Although measuring workers’ personal exposures was not the RP’s first stated reason for using the direct-reading instrumentation, Ramachandran et al. (2021) found through empirical analyses that the area measurements actually tracked workers’ personal exposures well (R² = 0.61).

These analyses described above for estimating VOC hourly averages do not account for autocorrelation that may be present between some of these observations. However, the primary purpose of this paper was not to characterize VOC exposure, but rather to use the VOC measurements to estimate THC exposure as described further in Ramachandran et al. (2021). The exact values of the VOC estimates should be treated with some caution because ignoring autocorrelation may have influenced some of the estimates, particularly for the instruments with measurement duration of <15 to 20 s. However, there was likely greater uncertainty in using all instruments to represent exposures for all workers (in addition to linear regression uncertainty), so that the impact of autocorrelation on our estimates may be negligible. Future work should be done to formally estimate VOC exposures while accounting for autocorrelation.

There appeared to be a large number of medians of 0.05 ppm, the LOR for the instrumentation, for the instrument-hour averages. This suggests that most vessels had very low levels reported for most of the time, leading to medians to be 0.05 ppm. It has been shown, however, that it is not unusual for exposures to be generally low throughout the day but to have high peaks that substantially contribute to a full-shift exposure level (the AM estimate), particularly when high GSDs occur. The GSDs were generally higher in the GuLF STUDY than is typically seen under stable industrial processes (but less so under outdoor conditions), with GSDs of 6–8, which indicates the occurrence of both these lower exposures and peak exposures.

The process of supplementing the THC measurements with the VOC measurements was important for three reasons. First, the number of THC measurements on some of the vessels was limited. In the highly variable environment on these vessels, an AM based on a small number of measurements in a dynamic situation, such as in our study, may not accurately reflect the true distribution of exposures. Second, the sampling strategy for personal measurements did not appear to cover all activities, in that on many of these vessels, no measurements were available for several weeks (Ramachandran et al., 2021). Third, workers on some of these vessels experienced some of the highest exposure levels in the study. Inaccurate exposure estimates among the highest exposed group could affect the exposure–response relationships in the epidemiologic analyses and attenuate the observed disease risks in the highest exposure category.

Combining measurements from all instruments across an entire vessel to develop a single descriptive statistic is akin to what we have done with the workers on these vessels in the epidemiologic study. Conceptually, the hourly value assigned to the vessel for all instruments could be thought of as the average of all workers’ exposures for that hour on that vessel. This concept can be extended to the workers in the study. Because we have no job titles for the study participants on the ROV vessels and MVs, we had assigned all study participants who worked on a single vessel to a single EG for estimation purposes. Thus, the average of all the measurements on the vessel was assigned to all workers on the vessel. Further, the main source of the VOCs, at least before the well was capped (TPs 1a–1b), was expected to have been the volatized crude oil, which also was expected to be the main source of workers’ exposure. For some study participants on these vessels, we may have underestimated exposures [if one or more instruments were located indoors (in the living and office areas) and the participants only worked outdoors] and overestimated exposures for other participants (if they worked indoors, leading to lower estimated exposures than those that would have been observed if most of the instruments were located outdoors). We think few workers’ exposures were likely substantially overestimated because, based on external data available to us, few study participants likely worked indoors for their entire shift. In addition, outdoor workers spent time indoors (lunch, breaks), so that underestimation of exposure may not be severe if only a few instruments operated indoors. The assumption of little bias, therefore, seems reasonable.

The VOC data were used to supplement THC personal measurements on the MVs operating the ROVs, as well as the other MVs in the study that had VOC data, as described in Tables 1 and 2 (Ramachandran et al., 2021). In contrast, the VOC measurements from the Enterprise and the three other drilling rig vessels were not used to supplement the THC personal measurements taken on those vessels. We had extensive monitoring on the rig vessels (Huynh et al., 2021a), so that the VOC exposure estimates would have provided limited additional information over the THC personal measurements collected, as most days with VOC measurements also had THC measurements. Moreover, it is unclear how we would have assigned area measurements from unknown locations to the various and specific job EGs that we developed for the study participants (in contrast to the vessel-level EGs of the ROV vessel and MV participants) who either worked in a single primary area or who moved from location to location over time. Therefore, we display the results of the Enterprise in this paper only as an example of the methodology.

In the analysis on the Enterprise, we showed that the Bayesian method described here may be useful to estimate workers’ personal exposure levels from direct-reading instruments in situations where there are limitations to the sampling strategy, e.g. when personal measurements are lacking or insufficient, at least under certain circumstances. Industrial hygienists in chemical plants often use direct-reading instruments, such as fixed point monitoring systems, to facilitate the control of exposures. When used for controlling exposures (e.g. at an emission source), direct-reading instrumentation may not be appropriate for characterizing worker exposures. If, however, instruments are located throughout a workplace at locations frequented by workers, the measurement results may be useful. It has been recognized that while extensive area measurements may be easier to collect than personal exposures, these data are much more difficult to summarize and relate to (particularly full-shift) personal exposure levels. As a result, very few statistical strategies have been proposed to transform these often large datasets of short-duration concentrations into meaningful exposure statistics. We described a systematic and statistically valid method to develop summary statistics to more easily evaluate workplace exposures. This approach can be used by others in workplaces with high volume datasets to increase the usefulness of such information. It is important, however, to empirically analyze the relationship between the personal and area measurements to ensure that the latter can, in fact, be used to estimate worker exposures.

Future work could include expanding this strategy and investigating other analytical strategies for high volume datasets in occupational health. For example, this work assumed that the VOC measurements were normally distributed on a naturally logged scale. We also assumed that, on the same vessel, the measurements were independent of one another and the hours were independent of each other. Other distributions were not investigated. To better meet the equal variance assumptions of ANOVA, we assumed equal variances among the VOC observations on the same vessel in the same hour (i.e. one GSD assigned to all instruments). The Enterprise data support this assumption. Future work could investigate other variance assumptions.

We also assumed that the median posterior estimate of the instrument-hour AM was a representative estimate of the average VOC concentration in that hour. Due to the large sample size (26 million) of VOC measurements and the number of instrument-hour averages calculated, it was not feasible to save all posterior samples of the AMs or analyze these data together. Future work could consider investigating how results would differ based on differently chosen metrics (such as the 2.5 quantile, 97.5 quantile, or mean posterior estimate). Other work could include investigation of strategies for maintaining uncertainty throughout the VOC hourly average calculations, such as by saving the entire distribution of AM estimates, accounting for autocorrelation, and accounting for the variability of the instruments’ measurements within an hour.

Conclusion

A large, high volume dataset of over 26 million short duration, direct-reading VOC measurements on vessels responding to the Deepwater Horizon disaster was available from multiple instrument records across each vessel, but the instrument locations were not identified. After accounting for censoring, Bayesian methods were used to calculate instrument-hour means and from these, hourly means across all instruments on each vessel. These data were developed to supplement THC personal air measurements on those same vessels, as described elsewhere. This approach can be used by other health professionals in the workplace with big datasets that are generated from direct-reading instruments to measure air concentrations. This paper presents methodology to use the direct-reading data to predict actual exposures either prospectively or retrospectively, when personal measurement data may not be available or are limited.

Funding

This study was funded by the NIH Common Fund and the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences (ZO1 ES 102945). Dr Sudipto Banerjee would like to acknowledge funding from the following grants: NIH/NIEHSR01ES027027-01, NIH/NIEHS R01ES030210-01, NSF DMS-1513654, NSF IIS-1562303, and NSF DMS-1916349.

Conflict of interest

The authors declare no conflict of interest relating to the material presented in this article. Its contents, including any opinions and/or conclusions expressed, are solely those of the authors.

Data availability

The data underlying this article will be shared on reasonable request, consistent with protections for the privacy of study participants and existing multi-party agreements. Requests should be made following instructions on the study website https://gulfstudy.nih.gov.