Can agent-based simulation be used as a tool to support polypharmacy prescribing practice?

Abstract

Objective

We sought to develop a simulation modelling method to help better understand the complex interplay of factors that lead to people with type 2 diabetes and asthma not taking all of their medication as prescribed when faced with multiple medications (polypharmacy).

Research design and methods

In collaboration with polypharmacy patients, general practitioners, pharmacists and polypharmacy researchers, we developed a map of factors that directly and indirectly affect somebody’s decision to take their medication as prescribed when faced with multiple type 2 diabetes and asthma medications. We then translated these behavioural influences into logical rules using data from the literature and developed a proof-of-concept agent-based simulation model that captures the medicine-taking behaviours of those with type 2 diabetes and asthma taking multiple medications and which predicts both the clinical effectiveness and rates of adherence for different combinations of medications.

Conclusions

The model we have developed could be used as a prescription support tool or a way of estimating medicine-taking behaviour in cost-effectiveness analyses.

Introduction

Polypharmacy, in which people are prescribed multiple medications (commonly for multiple comorbidities),¹ is growing,^2–4 particularly as we face an ageing population developing multiple conditions.⁵ Polypharmacy can be problematic because of the consequent treatment burden, safety issues and because a significant number of people who are prescribed multiple medications do not take all of their medication.⁶ This can lead to wasted costs from unused medication⁷ and the resource and cost burden of patients accessing health services that might result from suboptimal control of their conditions.⁸ However, in some situations, non-adherence can lead to fewer adverse drug reactions.⁹

For many years, there has been a focus on increasing ‘adherence’ (formerly termed ‘compliance’) within such populations.¹⁰ Many studies have examined the potential factors that might lead to people not adhering to their prescription,¹¹ although often such studies have focused on single factors or small subsets. Other studies have been concerned with understanding how people manage their medicines in the context of their everyday lives.¹² In a synthesis of qualitative research, Pound et al ¹³ found considerable reluctance to take medicine and a preference to take as little as possible. Recognising the problem of treatment burden, May and colleagues¹⁴ have coined the term ‘minimally disruptive medicine’ to guide the search for less burdensome clinical practice.

Agent-based simulation (ABS) is a simulation modelling method that allows for the modelling of behavioural and motivational aspects within a system and uses such individual-level behaviours as the building blocks for the model, allowing population-level dynamics to emerge as properties of individual behaviours and interactions.¹⁵ ABS has a rich heritage of being used in this way in ecology,¹⁶ but has less often been applied to human systems.¹⁷ However, there is a developing interest in applying ABS to model health and social care systems in which the behaviours of individuals within that system are the focus or an integral component.^17–22

In this article, we present a novel and innovative proof-of-concept model, developed in collaboration with people experiencing polypharmacy, health professionals and polypharmacy researchers, to demonstrate the potential of agent-based modelling to better understand medicine-taking behaviour in the context of polypharmacy for those with both type 2 diabetes and asthma. We describe the development of the model, how the model works and its potential further development to be used as a tool for supporting polypharmacy prescribing policy.

Research design and methods

The software

The model described in this article was built using AnyLogic University 6.7.1 (The Anylogic Company, http://www.anylogic.com/).

The working group

The project working group included two operational researchers, two polypharmacy researchers, two patients taking multiple medications from the local patient involvement group (PenPIG), two pharmacists (one of whom is also a representative for the local Academic Health Science Network) and a general practitioner.

Population of interest

People with both type 2 diabetes and asthma represent a growing subpopulation,²³ who have to manage two very different conditions where treatment burden may be high because of potential conflicts between medications.²⁴ Therefore, we selected our population of interest in this model as those with both (and only) type 2 diabetes and asthma, although the modelling approach used here could be applied to other subpopulations.

Mapping the behavioural system

A key step when designing and developing any model is to gain an understanding of the system to be modelled.²⁵ In this project, we sought to understand the behavioural logic associated with the taking of prescribed medications. Therefore, we developed a map of potential factors that might directly or indirectly affect the medicine-taking behaviour of someone with type 2 diabetes and asthma. This map was developed collaboratively within the working group, drawing on the expertise of people taking multiple medications, researchers and prescribers and exploring the significant body of literature in this area. Literature search strategies were strategic and looked for combinations of terms for the conditions of interest and literature concerning medication that included broad terms of ‘burden of treatment’, ‘patient experiences’ and ‘adherence’. Specific searches were also undertaken that looked for special factors of interest, such as ‘needle anxiety’, ‘supply of medication’ and ‘storage of medication’. We also included studies of multimorbidity that featured one or more of the conditions of interest and included both qualitative and quantitative studies. A total of 164 relationships were identified using an iterative process.

Identifying relationships to model

We assume that our population of interest does not include pregnant women or children, as medicine taking among these subpopulations is more complex.^{26 27} For this initial prototype, we assume that the prescribed combination of medications represents the complete set of medications available to patients in that simulation, and therefore we did not need to consider the impact of someone’s willingness to try new medications or how that might be affected by their desire to be in control of their condition, their personal goals or their desire to feel better. Also, we did not need to model the impact of the patient having conditions other than type 2 diabetes and asthma, as we assume our population has both and only these two conditions. As diabetes and asthma medications are not considered to be either addictive or analgesic in nature (local pharmacist opinion), we did not need to consider how the addictive properties of medication or whether or not the medication provides pain relief would impact medicine taking. Our pharmacists considered that such medications were less likely to lose effectiveness over time (although obviously the severity of the conditions could worsen over time). We also assumed that medication supply problems were unlikely for common conditions such as diabetes and asthma. Finally, in order to ensure we were modelling individual behaviours associated with medicine taking, we assumed that our population was able to make their own decisions about their medications, and therefore we did not consider the impact of cognitive impairment or the need for assistance taking medications. After eliminating these factors, we were left with 142 influencing relationships to model (online supplementary appendix A).

Once we had identified those influencing factors that were not relevant to our modelled population, we explored the literature to identify potential quantitative and qualitative data that could be used to represent the remaining factors within the model. Principally, we were looking for data that could be translated into behavioural ‘rules of thumb’, either via quantitative data from which probabilities of behaviour could be inferred or qualitative data from which we could infer categorical data and relationships. As part of this process, for some relationships we found evidence that they were untrue, and for others we were unable to find usable data. In all, we were left with 70 relationships to be included in the model.

Due to the time frame of the project, we were unable to include real medication data in the prototype model and instead opted to develop the tool such that users could input such drug data by specifying the probability of condition progression and improvement for each medication. Consequently, some of the medication and condition severity-related factors are not explicitly captured in the prototype. This left us with a final total of 59 relationships that were modelled. Full details of the relationships that were included and excluded, and the reasons for exclusion, are detailed in online supplementary appendix A.

Translating the behavioural system into behavioural rules

For the 59 relationships to be included in the model, we needed to translate the quantitative and qualitative data found in the literature into behavioural rules that could be implemented in the model. Typically, these rules translated the data into ‘IF THEN’ statements that would determine the ‘state’ of certain influencing factors. For example, we found evidence to show that if someone’s perception of the severity of their condition is low, there is a 22% increased probability of non-adherence.²⁸ In the model, we translated this into a rule that states that if an agent’s perception of their state of health is less than or equal to 50%, the ‘proposed action’ from this influencing relationship would be to adhere only 78% of the time. Online supplementary appendix B details the full set of behavioural rules for each influencing factor modelled.

Evidence shows that the impact of perceived state of health has twice the impact on adherence as any other factor that might influence medicine-taking behaviour.²⁹ Therefore, in the model, we split the behavioural influences into two categories: ‘wellness factors’ which represent the influence of someone’s state of health, how well they feel and the effects of the drugs they are taking and ‘general factors’ which represent everything else. We configured the model so that the ‘wellness factors’ influenced behaviour twice as often as the ‘general factors’.

The influence of someone’s state of health on their medicine taking can be thought to be composed of two central components—how well they actually are/the effects of their medication and their perception of how well they are/the effects of their medication.²⁸ Such concepts can also be found in the health belief model.³⁰ Perceptions of state of health will change over time. To capture these elements, we used a linear operator learning rule within a reinforcement learning framework,³¹ which is a commonly used approach to describe reinforcement behaviours in ecological modelling.³² Reinforcement learning describes a learning in which actions that are more rewarding are increasingly taken, whereas actions that offer less reward (or punishment) are gradually avoided. In the context of medicine taking, this represents the way in which people will tend to take medications based on their beliefs about the effects the medication is having and their experience taking the medication.³³

Specifically, each person in the model maintains a perception of how well each combination of drugs makes them feel. If they have yet to experience a drug combination, we assume that they perceive that combination of drugs to be no better or worse than any other combination they have yet to try. For each simulated day in the model, each person updates their perception of the combination of drugs they are currently taking using the following linear operator learning rule:

${\displaystyle w^t=W^{t}s\alpha +(1-\alpha )w^{t-1}}$ ,

where w^t is the person’s perception of their state of health at time t, W^t is the person’s actual state of health at time t, s is their sensitivity to their true state of health (ranging from 0 representing complete insensitivity to 1 representing full awareness of true state of health), α represents how much their medicine taking is weighted in favour of how they currently feel compared with how they felt previously (ranging from 0 for people who do not update their perceptions based on new information to 1 for people who only consider new information) and w^t−1 is the person’s previous perception of their state of health taking this drug combination.

After a person in the model has updated their perception of their health state, they will compare it to their perceptions about how well they felt taking the other drug combinations. A threshold T is given by the ‘perceived wellness’ value of previously sampled medication combinations. If the person’s perception of their current health falls a given percentage below the threshold T, the proposed action from the ‘wellness factors’ will be to not take their medication. The person may then switch to the combination of medications that they perceive to make them feel most ‘well’. However, this may not be the action that is taken, as people are not just influenced by ‘wellness factors’.

In addition, each ‘general factor’ resolves to a binary value of ‘take’ or ‘don’t take’ via the behavioural rules translated from the data, which represents the ‘proposed action’ from that influencing factor. At the end of each simulated day, a proposed action will be selected at random from each person’s set of factors (both ‘general factors’ and ‘wellness factors’). The probability of selecting any action is determined by its weighting. In the prototype model, the probability of choosing the proposed action from the ‘wellness factors’ is 67%, compared with 33% for the ‘general factors’.²⁹ In the absence of data, we assume that all ‘general factors’ have equal weighting.

If the selected proposed action is ‘take’, then no action will be taken. Otherwise, if the selected proposed action is from the ‘wellness factors’, then the person in the model will switch to the proposed alternative drug combination that they perceive to make them feel most ‘well’. If the selected proposed action is from a ‘general factor’, then the person will either switch to their perceived best alternative or select a drug combination at random if the influence from how well they feel says they should take their medication.

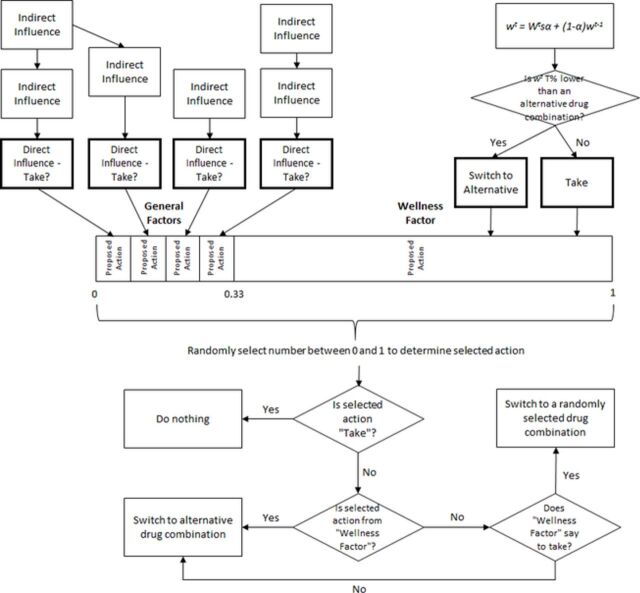
Figure 1 provides an overview of how the behaviour in the model works.

Figure 1.

Overview of the behavioural logic of the model for each person at each time step. Indirect general factors influence direct general factors, which resolve to a binary proposed action to take the medicine or not to take it. The wellness factor also resolves to a proposed action, depending on the person’s perception of their state of health with their current drug combination. Proposed actions are selected at random according to the weighting attributed to them, and the person will either switch their medication or continue as they are depending on the selected action.

States of health

Each person in the model is in two states at any one time—one representing their type 2 diabetes state of health and the other representing their asthma state of health. These represent the true states of health for each person in the model. For simplicity, we use three states of health for each condition in the prototype model, emulating the three most common stages of treatment for each condition.^{34 35} The true state of health value is calculated as the sum of the health values assigned to each state from each condition, with a Stage 1 (least severe) state of health assigned a value of 50%, a Stage 2 state of health assigned a value of 25% and a Stage 3 state of health (most severe) assigned a value of 0%. Therefore, the true overall state of health of any person in the model can range between 0% (most severe state of health for both conditions) and 100% (least severe state of health for both conditions).

Medication effects

Medication effects are specified in the model for each possible combination of medication. In the prototype, there are four prescribed medications—two for asthma and two for diabetes. People with both type 2 diabetes and asthma may take up to three to four different medications, depending on the stages of their conditions.^{34 35} The effects of the drugs for each combination are specified by the user of the model in terms of the probability per day of a transition between health states for each condition. This allows users to specify the effectiveness of each combination of medications for each condition.

Outputs

While running, the model reports adherence and wellness levels within the population over time. Users of the model are also able to access the details of any given person within the population. These details include their current state of health and perceived state of health, the severity of their conditions, the medicine-taking decision they are currently making and the factors that influenced that decision and parameter values relevant to the various factors that influence medicine taking.

Conclusions

The intention of building this model was for it to serve as a proof-of-concept to demonstrate how the medicine-taking behaviours of those taking multiple medications for both type 2 diabetes and asthma could be simulated, and how such a model could be used to provide evidence to inform prescribing practice. We have shown how such behaviours can be translated from qualitative and quantitative data in the literature into behavioural rules that can be used in an ABS, and how the effect of state of health and medication effectiveness on medicine-taking decisions can be simulated using reinforcement learning and a linear operator learning rule. We have also shown how adherence rates and states of health across the simulated population can be calculated and reported, which, along with the level of treatment burden, are likely to be key outcome measures when comparing medication combinations to inform prescribing practice.

The principal way in which this model could be used is to compare combinations of medication prescribed for those with type 2 diabetes and asthma, not only in terms of their clinical effectiveness but also the likely treatment burden and adherence to this prescription within a given population. However, the modelling method could be applied to any combination of conditions where people are taking multiple and perhaps conflicting medications. The evidence generated by a model such as we have described would allow trade-off decisions to be made—for example, a particular combination of medications may have a slightly lower clinical effectiveness but result in fewer side effects or a much higher level of adherence, helping to inform a decision about whether to accept a trade-off in clinical effectiveness in return for more people taking more of their medication as prescribed. These decisions could be made by the prescriber (such as a general practitioner) with individual patients using a simulation ‘population’ reflecting the patient in question, or on a larger scale in terms of informing prescribing policy locally or nationally. Comparisons in terms of treatment burden (how burdensome a treatment or combination of treatments is to follow) could be made externally to the model using expert judgement or internally if the model were extended to incorporate influencing factors such as complexity, frequency and flexibility of the treatment regimen, adverse drug reactions, complexity and portability of the format of delivery of the medications and total number of medications prescribed. We already include the influence of the level of interference with daily life, which is likely an important aspect of treatment burden,³⁶ and this could be extended to reflect specific medication regimens.

There is also potential for this model to be used to enhance traditional cost-effectiveness analyses. Such analyses seek to determine the cost-effectiveness of an intervention (often a new treatment) in terms of its incremental benefits and costs compared with an existing intervention for a given subpopulation.³⁷ Some cost-effectiveness studies have started to incorporate simple estimates of adherence,³⁸ acknowledging the potential impact of adherence on the cost-effectiveness of an intervention.³⁹ However, such studies typically use poor or invalid methods to incorporate concepts of adherence.⁴⁰ Our model could be used as a means of better estimating adherence rates for the studied population, either directly if the population was those with type 2 diabetes and asthma or with extension to the model for other subpopulations. Alternatively, the model could be extended to incorporate the cost-effectiveness elements, as we already allow the user to specify transition probabilities between health states with different drug combinations, and we assign quantifications of ‘wellness’ to each combination of drug states which could easily be used to represent quality adjusted life years (QALYs).⁴¹ If the model were extended to also assign costs to each combination of states, the cost-effectiveness analysis could be conducted solely using this simulation model, with the added benefit of a more sophisticated intrinsic means of considering medicine-taking behaviours.

To our knowledge, the method of simulating medicine-taking behaviours that we have outlined in this article has not been developed before, and therefore presents an innovative and exciting opportunity to model systems in health and social care where the medicine-taking behaviours of people within those systems is a non-trivial component. Furthermore, beyond medicine taking in polypharmacy, there is an increasing acknowledgement that many healthcare systems are significantly dependent on the behaviour of the ‘actors’ within that system. Clearly, the model would need to be validated against relevant data sets before being applied in any of the ways we have proposed in this article, but we feel strongly that the modelling approach we have outlined could be a vital tool to help to better understand the complex interplay of factors that lead to people who are prescribed multiple medications not taking all of their medication as prescribed.