A data-driven health index for neonatal morbidities

Summary

Whereas prematurity is a major cause of neonatal mortality, morbidity, and lifelong impairment, the degree of prematurity is usually defined by the gestational age (GA) at delivery rather than by neonatal morbidity. Here we propose a multi-task deep neural network model that simultaneously predicts twelve neonatal morbidities, as the basis for a new data-driven approach to define prematurity. Maternal demographics, medical history, obstetrical complications, and prenatal fetal findings were obtained from linked birth certificates and maternal/infant hospitalization records for 11,594,786 livebirths in California from 1991 to 2012. Overall, our model outperformed traditional models to assess prematurity which are based on GA and/or birthweight (area under the precision-recall curve was 0.326 for our model, 0.229 for GA, and 0.156 for small for GA). These findings highlight the potential of using machine learning techniques to predict multiple prematurity phenotypes and inform clinical decisions to prevent, diagnose and treat neonatal morbidities.

Graphical abstract

Highlights

• •Traditional definitions of prematurity based on gestational age need to be updated
• •Deep learning of maternal clinical data improves predictions of neonatal morbidity
• •Data-driven model leverages birthweight, type of delivery and maternal race
• •Accurate risk prediction can inform clinical decisions

Biological sciences; Cell biology; Molecular biology

Introduction

Prematurity or preterm birth (PTB) is the main cause of mortality in children under 5 years old and acute and chronic complications in surviving infants (Blencowe et al., 2013; Cheong and Doyle, 2012). In pregnancies at risk for PTB, such as those with preterm labor, preterm premature membrane rupture (PPROM), preeclampsia or fetal growth restriction, decisions around timing, and mode of delivery or therapeutic interventions are driven largely by risk predictions of neonatal morbidities based on the gestational age (GA) alone. In addition, the severity of prematurity is often defined using specific GA thresholds such as <28 weeks or <32 completed weeks (Who: Recommended Definiti, 1977). However, the evidence supporting the use of such thresholds is sparse (Higgins et al., 2005; Tyson et al., 2008), and difficulties in accurately estimating GA may lead to inaccurate risk predictions (Lynch and Zhang, 2007). Whereas birth before 37 weeks of gestation is associated with poor neonatal outcomes and mortality (Blencowe et al., 2012), prematurity and prematurity-related outcomes are likely to result from multiple etiologic pathways including genetic, demographic, psychosocial, and environmental factors (Ge et al., 2013; Melamed et al., 2009; Shapiro-Mendoza et al., 2006; Yancey et al., 1996; Yeo et al., 2017) that are unlikely to be adequately represented by GA at delivery alone.

Several prediction models have been proposed to combine clinical data for the prediction of neonatal mortality (Mcleod et al., 2020), overall illness severity (Dorling et al., 2005), or PTB (Ge et al., 2013; Neal et al., 2020; Yeo et al., 2017), but there is a lack of tools to reliably identify infants at risk of prematurity-associated morbidities beyond GA. The complexity of mechanisms involved and the relatively low prevalence of some neonatal morbidities pose significant challenges that machine learning methods have the potential to address, thus improving risk delineation to support clinical decisions and better prevent, diagnose, and treat neonatal morbidities. Previous studies demonstrated the feasibility and potential of using machine learning to build models for the prediction of adverse neonatal outcomes, such as mortality (Jaskari et al., 2020), sepsis (Mani et al., 2014), intraventricular hemorrhage (IVH) (Zhu et al., 2021), and jaundice (Daunhawer et al., 2019), or for monitoring relevant fetal vital signs such as heart rate and heart rate variability (Ponsiglione et al., 2021; Romano et al., 2013, 2016). However, a more holistic approach that targets multiple prematurity-associated morbidities would provide a more comprehensive assessment of infants’ risk and set the basis for precision medicine in the neonatal period.

The aim of this study was to develop and validate a multi-task deep neural network model to simultaneously predict a comprehensive range of neonatal morbidities while leveraging a population-based cohort of approximately 12 million livebirths in California from 1991 to 2012. Our ultimate goal is to derive a one-dimensional data-driven index of prematurity, compressing information contained in hospitalization records, to inform prenatal clinical decisions better than standard GA-based methods.

Results

Descriptive statistics of the study population

The 11,594,786 million livebirths were randomly split into training, validation, and test datasets, each consisting of 2,000,000, 2,000,000, and 7,594,786 livebirths, respectively (Table 1). The prevalence of neonatal morbidities in the two datasets ranged from 13.5% (jaundice) to 0.002% (CP) with 14.9% of newborns in both training and test datasets reporting more than one morbidity.

Table 1.

Descriptive statistics of study population

	Training dataset (n = 2,000,000)	Validation dataset (n = 2,000,000)	Test dataset (n = 7,594,786)
Maternal characteristics
Age [years]	28 (23, 32)	28 (23, 32)	28 (23, 32)
Race/Ethnicity
Non-Hispanic White	630,210 (31.5%)	630,985 (31.5%)	2,400,043 (31.6%)
Non-Hispanic Black	125,883 (6.3%)	125,628 (6.3%)	478,152 (6.3%)
Asian	222,181 (11.1%)	222,553 (11.1%)	841,332 (11.1%)
Pacific Islander	10,293 (0.5%)	10,438 (0.5%)	38,983 (0.5%)
Hispanic	982,397 (49.1%)	981,378 (49.1%)	3,726,848 (49.1%)
American Indian/Alaskan	9,092 (0.5%)	9,027 (0.5%)	33,622 (0.4%)
Other	1,323 (0.1%)	1,361 (0.1%)	5,085 (0.1%)
Missing/unknown	18,621 (0.9%)	18,630 (0.9%)	70,721 (0.9%)
Education
Some high school or less	595,377 (29.8%)	595,814 (29.8%)	2,257,225 (29.7%)
High school diploma/GED	542,869 (27.1%)	541,316 (27.1%)	2,062,298 (27.2%)
Some college	402,080 (20.1%)	402,262 (20.1%)	1,529,583 (20.1%)
College graduate or more	417,984 (20.9%)	419,258 (20.9%)	1,587,390 (20.9%)
Missing/unknown	41,690 (2.1%)	41,350 (2.1%)	158,290 (2.1%)
Parity
0	778,620 (38.9%)	776,915 (38.8%)	2,955,981 (38.9%)
1	628,421 (31.4%)	628,523 (31.4%)	2,386,792 (31.4%)
2	340,841 (17.0%)	342,372 (17.1%)	1,296,547 (17.1%)
3+	250,513 (12.5%)	250,684 (12.5%)	949,593 (12.5%)
Missing/unknown	1,605 (0.1%)	1,577 (0.1%)	5,873 (0.1%)
Prenatal fetal findings
Gender
Male	1,022,913 (51.1%)	1,023,808 (51.2%)	3,882,528 (51.1%)
Female	977,075 (48.9%)	976,172 (48.8%)	3,712,177 (48.9%)
Missing/unknown	12 (0.0%)	20 (0.0%)	81 (0.0%)
Birthweight [Kg]	3.37 (3.03, 3.69)	3.34 (3.03, 3.69)	3.37 (3.03, 3.69)
Obstetrical complications
GA [days]	276 (268, 282)	276 (268, 283)	276 (268, 282)
GA ≤32 weeks	24,793 (1.2%)	25,008 (1.2%)	93,371 (1.2%)
GA >32 and ≤37 weeks	170,446 (8.5%)	170,023 (8.5%)	644,986 (8.5%)
GA >37 and <40 weeks	965,946 (48.3%)	964,362 (48.2%)	3,664,423 (48.3%)
GA ≥40 weeks	661,724 (33.1%)	663,515 (33.2%)	2,516,606 (33.1%)
Unknown GA	177,091 (8.9%)	177,092 (8.9%)	675,400 (8.9%)
SGA	189,532 (10.0%)	188,741 (10.0%)	719,093 (10.0%)
PTB	213,426 (11.7%)	213,385 (11.7%)	808,043 (11.7%)
Neonatal outcomes
RDS	30,621 (1.5%)	30,645 (1.5%)	116,644 (1.5%)
IVH	3,883 (0.2%)	3,877 (0.2%)	14,729 (0.2%)
NEC	1,527 (0.1%)	1,522 (0.1%)	5,839 (0.1%)
ROP	4,232 (0.2%)	4,237 (0.2%)	15,923 (0.2%)
BPD	2,737 (0.1%)	2,750 (0.1%)	10,401 (0.1%)
PDA	17,056 (0.9%)	17,097 (0.9%)	64,545 (0.9%)
PVL	138 (0.01%)	141 (0.01%)	562 (0.01%)
Sepsis	18,969 (0.9%)	18,994 (0.9%)	71,827 (0.9%)
Pulmonary hemorrhage	585 (0.03%)	629 (0.03%)	2,323 (0.03%)
CP	36 (0.002%)	29 (0.001%)	141 (0.002%)
Pulmonary HTN	410 (0.02%)	421 (0.02%)	1,562 (0.02%)
Jaundice	269,534 (13.5%)	269,767 (13.5%)	1,023,709 (13.5%)
≥1 outcome	297,988 (14.9%)	298,065 (14.9%)	1,131,381 (14.9%)

Summary of maternal and newborn characteristics, including neonatal morbidities, in the training and validation datasets.

Correlation networks, obtained using Pearson’s, polychoric, or tetrachoric correlation coefficients, as appropriate, showed strong associations between RDS, IVH, NEC, ROP, BPD, PDA, sepsis, and jaundice (Figure S8A). supporting the multi-task approach used. Among clinical data, GA, birthweight, and spontaneous and medically indicated PTB showed the strongest correlations with these outcomes (Figures 1B and S8B).

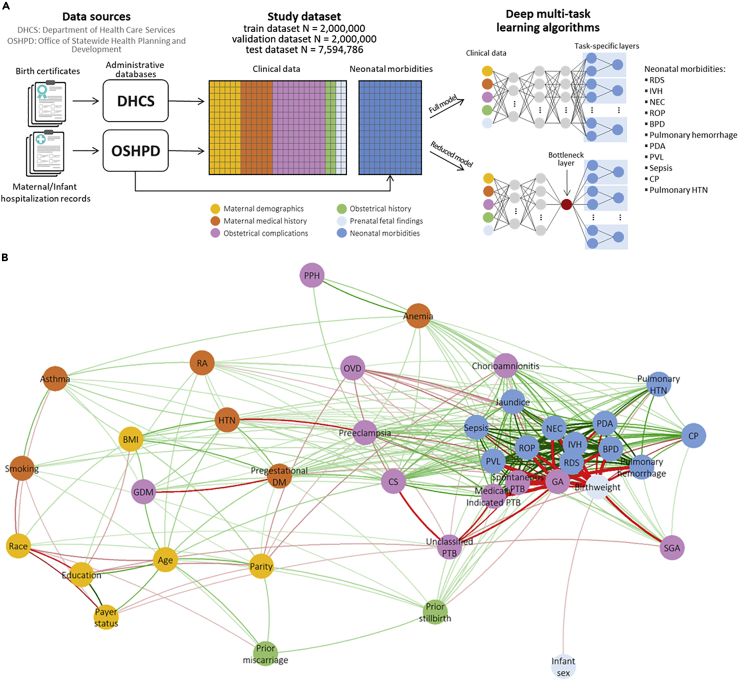
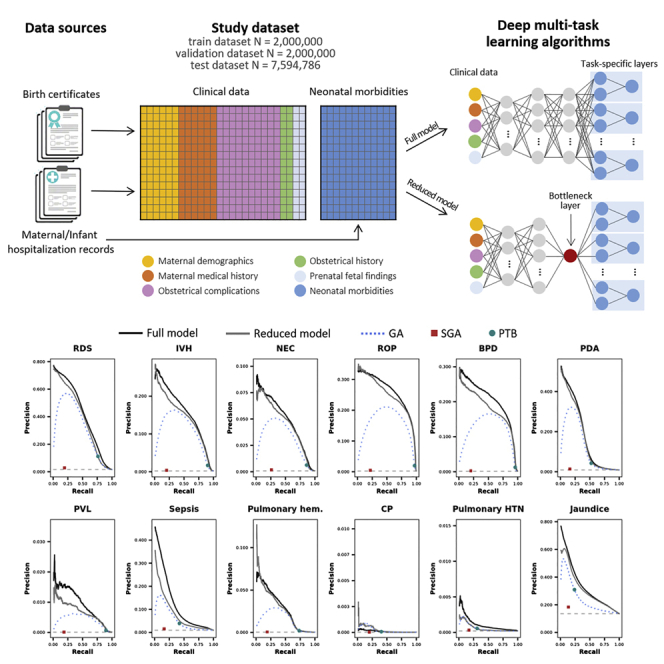
Figure 1.

Schematic of the study design and correlations between neonatal morbidities

(A) Schematic of the study design.

(B) Correlation network between neonatal morbidities and clinical variables: edges are drawn between pairs of neonatal morbidities/clinical variables that are correlated with the absolute value of the correlation coefficient exceeding 0.1; green (red) edges indicate positive (negative) correlations, AND the width of the edges is proportional to the correlation coefficient.

The deep NN models outperform traditional methods

The full and reduced models outperformed the traditional models in the prediction of each individual outcome, always exceeding the AUPRC of a random classifier by at least an order of magnitude (Figures 2 and S10; Tables S5 and S6). Only when predicting CP the GA-based model showed a greater AUPRC compared with the full model (2.2 E-04 vs. 1.0 E-04), not the reduced model (2.9 E-04).

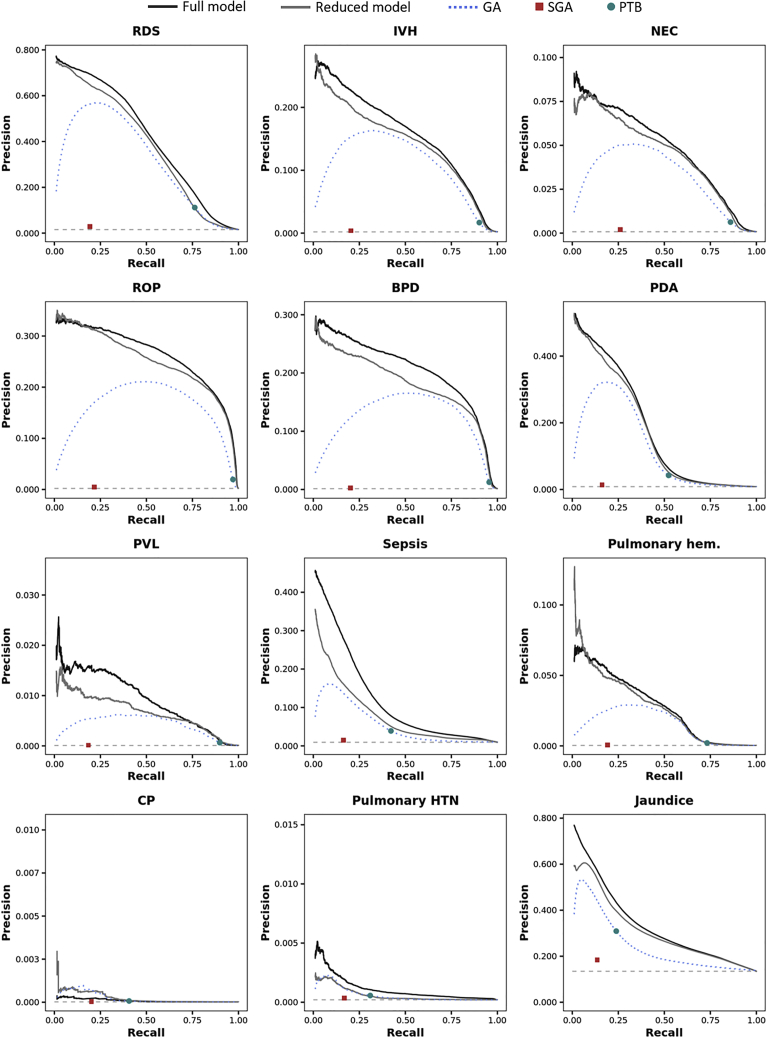
Figure 2.

Model performance in terms of precision and recall

Precision-recall curves (AUPRCs) in the test data set for the full model (black solid line), the reduced model (grey solid line), and the logistic regression models considering gestational age (blue dotted line), SGA (red square) and PTB (green dot). The horizontal light grey dashed line represents the expected precision-recall curve for a random classifier and depends on the prevalence of the morbidity.

The overall test AUPRC was 0.326 (±1.7 E-04) for the full model, 0.300 (±1.7 E-04) for the reduced model, and 0.229 (±1.5 E-04), 0.156 (±1.3 E-04), and 0.212 (±1.5 E-04) for GA, SGA, and PTB, respectively (the AUPRC of a random classifier would be 0.135; Figure S9). The overall test AUC was also higher for the full [0.963 (±5.0 E-05)] and reduced [0.960 (±5.4 E-05)] models compared with traditional models [GA: 0.950 (±6.3 E-05); SGA: 0.922 (±9.5 E-05); PTB: 0.942 (±6.5 E-05)].

Variable importance

Furthermore, we investigated the importance of each variable in the prediction of morbidities. Among the 26 clinical variables, birthweight, spontaneous, and medically indicated PTB showed the highest overall test AUPRC across morbidities: 0.251, 0.230, and 0.205, respectively. On the other hand, maternal age (overall test AUPRC: 0.140), prior miscarriage (0.142), and infant sex (0.143) showed the lowest univariable prediction performances (Figure S1).

The overall test AUPRC and AUC of the full model (i.e., the one including all the 26 clinical variables) were 0.325 and 0.963, respectively. After removal of the seven clinical variables with the lowest average AUPRC (maternal age, prior miscarriage, infant sex, maternal education, parity, payer status, and smoking), performances were still similar to those of the full model with an overall test AUPRC of 0.322 and AUC of 0.966 (Figure S2). By further excluding maternal race, the overall test AUPRC dropped to 0.315. The model based on the 10 features with the highest univariable overall test AUPRC (i.e., birthweight, spontaneous, and medically indicated PTB, CS, preeclampsia, chorioamnionitis, pre-gestational DM, SGA, gestational DM, and OVD) yielded an overall test AUPRC of 0.315 and an average AUC of 0.962. A progressive decrease in both AUPRC and AUC was observed when the number of clinical variables left in the model further decreased. According to the feature permutation experiment, birthweight (AUPRC and AUC decreased by 10.8% and 0.43%, respectively), CS (4.7% and 0.26%), OVD (1.5% and 0.12%), and maternal race (1.6% and 0.06%) were the clinical variables appearing to have the strongest importance in the prediction of morbidities returned by the model (Figure S3).

The reduced model as a one-dimensional score of neonatal health

As a one-dimensional score, the reduced model achieved good predictive performances for each morbidity of interest. Whereas AUPRCs and AUCs were generally lower than those of the full model (excluding CP, for which the reduced model performed better than the full model), the reduced model showed greater AUPRCs and AUCs compared with models based on GA, SGA, and PTB (Figure S4, and Tables S4 and S5). The score significantly correlated with the number of neonatal morbidities [Spearman’s rho (95% confidence interval) = −0.273 (−0.273, −0.272)], as it progressively decreases with the increase in the number of neonatal morbidities observed (Figures S6). For each neonatal morbidity, the score was lower in livebirths with the given morbidity compared with those without (Figure S7).

Moreover, the score obtained by the reduced model appeared to correlate with birthweight, CS, GA, SGA, preeclampsia, spontaneous and medically indicated PTB, and, to a less extent, pre-gestational DM and chorioamnionitis (Figure S5).

Discussion

Our model, trained on a large administrative dataset of more than 11 million livebirths, simultaneously predicted the risk of several neonatal morbidities, some of which are relatively rare, with good accuracy and precision. The benefits of using machine learning were further enhanced by the multi-task approach that exploits the pathological mechanisms that may be shared across multiple neonatal phenotypes. This led to significant improvements in terms of both discriminative ability and precision-recall compared with traditional risk models based on GA and/or birthweight and whose predictions of morbidities are obtained from separate independent models.

Whereas GA plays a central role in fetal development, the fetal development rate may vary from fetus to fetus and may be affected by genetic, clinical, and environmental factors (Wen et al., 2004). Our findings suggest that incorporating GA and phenotypical/clinical data into prematurity risk predictions using state-of-the-art machine learning approaches would result in more accurate characterizations of multiple neonatal morbidities. According to our model, established factors such as birthweight and caesarian delivery, but also operative vaginal delivery and maternal race appeared to contribute significantly to risk predictions, independently of GA, highlighting the potential role of obstetrical procedures and socio-cultural aspects in the development of neonatal morbidities.

We also explored the utility of a one-dimensional data-driven index obtained as the output of an intermediate layer of the deep NN, which compresses the information contained in the clinical variables that is considered to be useful in the prediction of all neonatal morbidities. Interestingly, this one-dimensional score appeared to outperform traditional one-dimensional scores based on GA and/or birthweight, and corelated with the number of morbidities that an infant eventually develops (Figure S6). This finding suggests that a new data-driven index that combines several clinical factors and goes beyond GA and/or birthweight can improve the identification of infants at high risk of prematurity-associated morbidities.

Our model showed the potential to accurately predict most of the morbidities considered, with AUCs exceeding 0.90 and AUPRCs more than 10 times those of the respective random classifier. Nevertheless, other morbidities such as CP, jaundice, pulmonary HTN, and PDA remain difficult to predict as indicated by AUCs between 0.66 and 0.79. The clinical variables used may not fully capture the etiological mechanisms underlying these morbidities. Therefore, further investigations incorporating information complementary to that provided by clinical data, such as biological information contained in genetic, genomic, and proteomic data, into similar data-driven approaches ensure a better understanding of biological mechanisms and improve risk predictions.

In conclusion, our data-driven index of prematurity has the promise to improve the prediction of neonatal morbidities and identify high-risk infants who may not otherwise be identified based on the GA alone. This would be an important step toward the optimization of neonatal care, especially in high-risk pregnancy, and the reduction of the burden of severe and potentially life-impacting neonatal morbidities.

Limitations of the study

Study limitations include the lack of more recent data (after 2012) and that the data were only available for one US state. These may limit generalizability of our findings to other culturally and socially different US states and countries, and more recent changes in prenatal and neonatal care.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Administrative data from the California Office of Statewide Health Planning and Development	Open Data Datasets Archive - HCAI
Birth certificates from the California Department of Health Care Services	Accessing Protected DHCS Data for Research (ca.gov)
Software and Algorithms
R	The Comprehensive R Archive Network (r-project.org)	version 3.6.3

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Nima Aghaeepour (naghaeep@stanford.edu).

Materials availability

This study did not generate new unique reagents. Pre-existing data access policies outlined by the the California Office of Statewide Health Planning and Development (OSHPD), and the California Perinatal Quality Care Collaborative (CPQCC) govern data access requests. Requests will be reviewed by the steering committees from each organization prior to providing access. Code is available at the following link https://nalab.stanford.edu/a-data-driven-health-index-for-neonatal-morbidities/. Further information and requests for resources should be directed to and will be fulfilled by the Lead contact, Nima Aghaeepour, PhD (naghaeep@stanford.edu)

Method details

Study population

The study’s source population from the Office of Statewide Health Planning and Development (OSHPD) consisted of 11,594,786 million livebirths in the state of California (US) from 1991 to 2012. These data contain linked birth certificates from California Vital Statistics records along with maternal and infant hospitalization records for nearly all inpatient deliveries(Herrchen et al., 1997). Livebirths with an implausible birthweight for the corresponding GA(Alexander et al., 1996) were excluded and those included in the analytical sample were randomly split into training, validation and test datasets.

Clinical data and neonatal morbidities

The deep neural network model described here aimed at predicting the following neonatal morbidities selected for being associated with prematurity: respiratory distress syndrome (RDS), intraventricular hemorrhage (IVH), necrotizing enterocolitis (NEC), retinopathy of prematurity (ROP), bronchopulmonary dysplasia (BPD), patent ductus arteriosus (PDA), periventricular leukomalacia (PVL), sepsis, pulmonary hemorrhage, cerebral palsy (CP), pulmonary hypertension (HTN), and jaundice. Data on the twelve neonatal morbidities considered were obtained from the 2015 International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) codes recorded on maternal and infant hospitalization clinical notes. The validity and accuracy diagnosis and procedures extracted from maternal discharge notes and birth certificates has been extensively studied and reported to be moderate to high across Californian hospitals . ICD-9-CM codes used to identify each neonatal morbidity are shown in Table S1.

ICD-9-CM diagnostic and procedure codes from maternal and infant hospitalization records along with complication and procedure codes recorded on the birth certificate were used to define the 26 clinical variables, plus gestational age (GA) at delivery that was used to stratify the training, validation and test datasets to develop GA-specific neural networks (NNs), used to develop predictions of the twelve neonatal morbidities. The complete list of clinical variables, information on how each variable was defined and descriptive statistics (including number and proportion of missing values) in the final analytical sample (i.e. training, validation and test datasets combined) are reported in Table S2.

Model development and training

Our model consisted of GA-stratified multi-task deep neural networks (NNs). NNs are a family of computing systems based on a collection of connected units or nodes, which receive a signal (input data or the signal returned by previous units), process it and then transmit it to the following units. Units are aggregated into layers, and each layer may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer containing the object of the prediction). NNs were chosen to obtain risk-prediction of the twelve neonatal morbidities given their ability to process vast amount of data, to learn and model complex non-linear relationships that can be generalized to unseen data, and because they do not require strict assumptions regarding the distribution of input variables and their associations (Subasi, 2020). In the presence of multiple outcomes, multi-task learning allows to predict multiple outcomes at the same time (Caruana, 1997). By leveraging the underlying mechanisms that are common among morbidities, the knowledge learned in predicting one morbidity is shared when predicting other morbidities. In order to obtain risk predictions independent from GA and to allow the model to predict neonatal morbidities with similar accuracy regardless of the GA, learn mechanisms linking input features and neonatal morbidities that go beyond GA, and predict morbidities with similar accuracy regardless of the GA, the training, validation and test datasets were each split into five subsets according to GA: GA ≤32 weeks, GA >32 and ≤37 weeks, GA >37 and <40 weeks, GA ≥40 weeks, and unknown GA. Then, five multi-task deep neural networks (NNs) were trained using each of these five subsets of the training dataset separately. Each NN consisted of a set of sequential layers shared across all the morbidities followed by one independent set of sequential layers for each of the twelve neonatal morbidities considered. The following layers characterize the set of shared layers:

• ▪a masking layer to inform the model what values should be skipped when processing the data because missing.
• ▪a batch normalization to transform the input data so that the mean is close to 0 and the standard deviation is close to 1.
• ▪a 16-unit densely-connected layer with ‘tanh’ activation.
• ▪a 32-unit densely-connected layer with ‘relu’ activation.
• ▪a 32-unit densely-connected layer with ‘tanh’ activation (bottleneck layer).
• ▪dropout layer to randomly set 30% of the input units to 0 to help prevent overfitting.

The output of the last layer in the set of shared layers is fed as input of twelve independent sets of layers (one for each neonatal morbidity). The following layers characterized these morbidity-specific sets of layers:

• ▪a 16-unit densely-connected layer.
• ▪dropout layer to randomly set 30% of the input units to 0.
• ▪a 16-unit densely-connected layer.
• ▪dropout layer to randomly set 30% of the input units to 0.
• ▪A one-unit layer with ‘sigmoid’ activation, containing the prediction for that morbidity.

Each multi-task deep NN was trained on the respective subset of the training dataset defined by GA, using a batch size of 512, Adam optimization, binary cross-entropy loss with early stopping (training was stopped after 10 consecutive epochs with no improvement in validation loss) or stop after 100 epochs. Validation loss was calculated on the corresponding subset of the validation dataset defined by GA. The model with the lowest validation loss across all epochs was retained. Each NN was trained on the respective subset of the training dataset defined by GA with early stopping when validation loss stopped improving.

Moreover, as hypothetical data-driven index of prematurity, a one-dimensional score (‘reduced model’) was derived from a multi-task NN with a similar architecture to that of the full model, as output of a single-unit bottleneck layer (Figure 1A). We trained a multi-task deep NN with the same architecture described previously without GA-stratification and including GA as input feature, and replacing the 32-unit bottleneck layer with a single-unit layer, to investigate the extent to which the information contained in the clinical variables could be compressed into a single score to then evaluate how this score would predict all the neonatal morbidities of interest. Associations of clinical variables and neonatal morbidities with the single-unit output of the bottleneck layer were then investigated using correlation networks. Test AUPRC and AUC to predict neonatal morbidities of the bottleneck output (hereafter called ‘reduced model’) were also calculated and compared to those of the full model and the traditional models based on GA, SGA and PTB.

For comparison purposes, three separate logistic regression models were trained using the training dataset, considering GA, small for GA (SGA: birthweight <10th percentile for GA and sex22) and PTB (GA<37 weeks), respectively. These models resemble algorithms traditionally used to estimate the risk of prematurity-associated morbidities and quantify the severity of PTB.

Ensemble methods to combine predictions from the five GA-specific NNs

The five multi-task deep NNs were used to predict the risk of each of the twelve neonatal morbidities in all livebirths in the test dataset, regardless of GA. Therefore, for each livebirth in the test dataset, five risk predictions for each morbidity were obtained. Several methods to combine these five risk predictions and obtain a single final risk prediction for each of the twelve morbidities were investigated

• 1.Average: the simple average across the five risk predictions.
• 2.Weighted average: a weighted average of the five risk predictions with a 40% weight to the risk prediction obtained from the GA-specific NN corresponding to the GA of the livebirth, a 20% weight to risk predictions obtained from the adjacent GA-specific NNs, and a 10% weight to risk predictions obtained from the other GA-specific NNs. For livebirths in the unknown GA group, a 50% weight was assigned to risk prediction obtained from the NN trained on livebirths with unknown GA and a 12.5% weight was assigned to each risk prediction obtained from the other GA-specific NNs.
• 3.Stacked prediction: for each livebirth, the risk prediction obtained from the GA-specific NN corresponding to the GA of that livebirth was used.
• 4.Logistic regression: using the training dataset, a series of logistic regression models (one for each neonatal morbidity) was trained to predict each morbidity using the five risk predictions. These models were then used to obtain the final risk predictions for the livebirths in the test dataset.
• 5.NN: using the training dataset, a series of deep NNs (one for each neonatal morbidity) was trained to predict each morbidity. Each of the twelve NNs took the five risk predictions for that morbidity as input before a 3-unit densely-connected layer with ‘relu’ activation and a single-unit output with ‘sigmoid’ activation. A batch size of 512, Adam optimization, binary cross-entropy loss, up to 100 epochs with early stopping after 10 consecutive epochs with no improvement in validation loss were used. The model with the lowest validation loss across all epochs was retained.

The area under the precision-recall curve (AUPRC) and area under the receiver operating characteristic curve (AUC) were used to evaluate the performance of these five ensemble methods in predicting each neonatal morbidity. In addition, an overall AUPRC and AUC were calculated to evaluate performances across all the twelve morbidities. The risk predictions of the twelve neonatal morbidities obtained from the ensemble methods were stacked to form a unique vector of risk predictions. Similarly, the twelve morbidity variables were stacked to form a unique morbidity vector. Overall AUPRC and AUC were calculated using these two stacked vectors. These AUPRCs and AUCs are shown in Table S3. Stacked prediction showed the highest overall AUPRC and AUC as well as for several individual morbidities; therefore, it was selected as our final model.

Comparison of the deep NN to standard approaches

In order to demonstrate the ability of NNs to learn complex non-linear relationships compared to standard regression techniques, we compared the predictive ability of our model to that of similarly-trained models that predict the neonatal morbidities using the same input features: standard multivariable logistic regression, multi-task logistic regression and multivariate random forest. Multi-task logistic regression was performed using the R package ‘RMTL’ with default hyperparameters (i.e. L21 regularization with λ1 = 0.1 and λ2=0) and extends the multi-task approach to linear regression (Cao et al., 2019). Multivariate random forest was implemented using the ‘IntegratedMRF’ R package with default hyperparameters. Multivariate random forest allows to incorporate the correlations between neonatal outcomes into traditional random forest approaches and has been shown to perform better than traditional random forest when outcomes are correlated (Rahman et al., 2017).

Briefly, for each of the twelve neonatal morbidities, GA-stratified models (standard logistic regression, multi-task logistic regression and multivariate random forest) were built with the neonatal morbidities as outcomes and all the demographic and clinical variables as predictors. Predictions were then stacked using the risk prediction obtained from the GA-specific model corresponding to the GA of each livebirth. Missing data were replaced with the mode or the mean, as appropriate. Models were trained on the training dataset and performances were evaluated on the test dataset.

Our model outperformed the other approaches in the prediction of all the twelve neonatal morbidities (Table S4). Overall AUPRC and AUC of our model were greater than those of standard logistic regression (AUPRC: 0.326 vs 0.310, AUC: 0.963 vs 0.961), multi-task logistic regression (AUPRC: 0.130, AUC: 0.935), and multivariate random forest (AUPRC: 0.266, AUC: 0.878).

All the analyses were performed using R v3.6.3 and the multi-task deep NNs were implemented using Keras through the R package ‘keras’.

Feature importance experiment

To evaluate the importance of clinical variables (features) towards the prediction of morbidities, a feature removal experiment was conducted. For each of the 26 clinical variables used as input in the training of NNs, a univariable logistic regression model was trained, using the training dataset, to predict each of the twelve neonatal morbidities. Test AUPRCs and AUCs to predict each morbidity were calculated along with an overall AUPRC and AUC obtained by stacking risk predictions and morbidity variables for the twelve morbidities into two unique vectors of risk prediction and neonatal morbidities, respectively. The clinical variables were then ranked on the basis of their overall test AUPRC. Subsequently, a series of multi-task deep NNs was trained, as previously described, progressively removing all the features, one at the time. Features were removed, one at the time, starting from the one with the lowest overall test AUPRC until only the feature with the highest overall test AUPRC remained. At each step, the overall test AUPRC and AUC were calculated as described above.

Similarly, we conducted a feature permutation experiment (Molnar, 2020). For each of the 26 clinical variables used as input, one at the time, the original variable in the training, validation and test datasets was replaced by randomly permuted values of that variable across all observations. The model was then re-trained using these modified versions of the training and validation datasets and the overall AUPRC and AUC were calculated on the modified test dataset. The permutation feature importance was then calculated as the percentage reduction in the overall test AUPRC (or AUC) compared to that of the original model. The higher the decrease in the model performance due to the permutation of a variable, the more important is that variable in obtaining predictions of the morbidities. Bootstrapping was used to calculate 95% confidence intervals; 1,000 independent samples, each of 1,000,000 livebirths, were drawn from the test data and AUPRCs and AUCs were calculated to estimate their distribution. 2.5% and 97.5% quantiles of the obtained distributions were used as limits of the 95% confidence intervals.

Correlation networks

Correlations between clinical variables and morbidities were calculated using Pearson’s, polychoric, or tetrachoric correlation coefficients, as appropriate, to define correlation networks. In these graphs, each clinical variable or output was represented by a node and all nodes were arranged into a two-dimensional space using the Fruchterman-Reingold force-directed graph drawing algorithm (Fruchterman and Reingold, 1991). Nodes correlated with a correlation coefficient exceeding 0.1 in absolute value were connected by edges whose width is directly proportional to the strength of the correlation between the nodes.

Quantification and statistical analysis

Model performances were evaluated on the test dataset using the area under the precision-recall curve (AUPRC), which focuses on the presence of the outcome and is more appropriate in imbalanced prediction tasks involving rare outcomes; and the area under the receiver operating characteristics curve (AUC). Standard errors for AUPRCs and AUCs were obtained using the first order delta method with logistic transformation and the deLong method, respectively. In addition, risk predictions and observed values across the 12 morbidities were each stacked into a unique vector of predictions and observed outcomes, respectively, in order to calculate the overall AUPRC and AUC across all the 12 morbidities.

Published: April 15, 2022

Data and code availability

• •De-identified human data can be requested to the California State Biobank, the California Office of Statewide Health Planning and Development (OSHPD), and the California Perinatal Quality Care Collaborative (CPQCC).
• •All original code is available at the following link: https://nalab.stanford.edu/a-data-driven-health-index-for-neonatal-morbidities/.