HIT web server: A hybrid method to improve electrostatic calculations for biomolecules

Abstract

The electrostatic features of highly charged biomolecules are crucial and challenging tasks in computational biophysics. The electrostatic calculations by traditional implicit solvent methods are efficient but have difficulties on highly charged biomolecules. We have developed a Hybridizing Ion Treatment (HIT) tool, which successfully hybridizes the explicit ions and implicit solvation model to accurately calculate the electrostatic potential for highly charged biomolecules. Here we implemented the HIT tool into a web server. In this study, a training set was prepared to optimize the number of frames for the HIT web server. The results on tubulins, DNAs, and RNAs, reveal the mechanisms for the motor proteins, DNA of HIV, and tRNA. This HIT web server can be widely used to study highly charged biomolecules, including DNAs, RNAs, molecular motors, and other highly charged biomolecules.

1. Introduction

The electrostatic calculations of biomolecules are fundamental in protein folding [1], protein stability [2], protein–protein interactions [3], protein-DNA/RNA interactions, and many other fields. Nevertheless, in cells, small biomolecules and ions make the environment of protein extremely intricate for electrostatic calculations. The highly-charged biomolecules always attract and utilize the bound ions to balances net charges. These bound ions directly changed the electrostatic surfaces, strongly affecting the interactions among biomolecules. So far, there are two types of methods to handle ions and water around biomolecules: explicit model and implicit model. The explicit model includes explicit ions and water (such as TIP3P [4] and TIP4P) [5], making the results more accurate. Thus it is widely used in molecular dynamics simulations [6], [7]. However, the high accuracy is accompanied by high computational complexity, making it difficult to be applied to electrostatic calculations. By comparison, the implicit model treats the ions and water around biomolecules as a homogeneous solution, saving massive calculation time. By the virtue of efficiency, it has been widely applied in the calculations of electrostatic potential. In the implicit model, Poisson-Boltzmann (PB) [8] model and Generalized Born (GB) [9] model are two of the most popular models. A traditional method like Delphi [10], based on the PB model, worked well in neutral system [11], [12] but cannot neutralize the net charges for the systems of highly charged biomolecules [13], [14], [15]. In this case, the whole system is unbalanced in charge, which is unrealistic and unreliable. In nature, the highly charged biomolecules are surrounded by oppositely charged ions, neaturalizing the system. These bound ions cannot be simulated by the current implicit models. Recently, we have developed a Hybridizing Ions Treatment (HIT) method [16] and applied it to a web server, which hybridizes the implicit solvent method with explicit ions to realistically calculate the electrostatic potential for highly charged biomolecules. It was proved that the hybrid method is more natural, accurate and reliable. In this work, the development of the HIT web server is reported. The electrostatic characters of highly charged biomolecules were calculated by HIT web server. The web server provides the target bound ions in PDB format for users.

2. Method

2.1. HIT algorithm

HIT uses the position information from explicit solvation simulations to calculate the ions occurrences to predict the binding sites. The process includes the preparation, initial, clustering, and optimal steps [16]. The preparation is to merge the frames of ions from the explicit MD simulation trajectory for analysis. The initial, clustering and optimal steps are three core steps to achieve the divisions, clustering, and optimizations (Fig. 1). The whole solvation box with ionic cloud was split into several cubes, then the ions in each cube were counted and sorted. After sorting, the clustering step clustered adjacent cubes into a binding area, where the selection of core cube followed the rank of cubes. If the core cube in the rank was clustered into the previous binding area, it will be skipped into the next one. The clustering was ceased when the number of ions in a cube is lower than the average number. Then, the optimization calculated the mass center of the binding area and place-bound ions there. More details are shown in our previous software paper about hybridizing ions treatment method [16].

Fig. 1.

The diagram of the HIT-webserver algorithm.

2.2. Web server technique

The Hybridizing Ion Treatment algorithm is integrated by two main components. They are the front end and the backend. The front end was developed using React web framework and it is embedded in the Django app backend. The React app uses HTML, CSS, and JavaScript to create a website where the user needs to input some information (Ion Name, Ions Number, cube size(Å)) and upload an ionic cloud file (merge.pdb). The merge.pdb file can be generated following the instructions found on the “Input file preparation” button. Once the user submitted the required information, it is sent to an endpoint on the Django app backend.

The Django app backend is coded using python, and it is being served using Niginx and Gunicorn on a server provided by the University of Texas at El Paso. The Hybrid Ion Treatment endpoint receives a POST request from the front-end with all the parameters required to run the Hybrid Ion Treatment script. A process is created using subprocess.popopen() to run the Hybridizing Ion Treatment shell script. Once the process is done, the generated output is compressed into a.zip file and sent back as an HTTP response to the front end. The front-end process the response and the users get the.zip file into the local computer Downloads folder. The tutorial is available at https://www.youtube.com/watch?v=WjY8BznPs10.

2.3. Training and testing

2.3.1. The training set

Training set used in this work is a 100 Å × 100 Å × 100 Å solvation box with 8 restrained potassium ions in a 150 mM KCl solution. The simulation was performed for 1 ns, from which 9 data sets (combined of 1000, 500, 333, 250, 200, 100, 50, 20, 10 frames) were prepared to analyze the relationship between the accuracy and the number of frames.

2.3.2. The testing set

Testing sets used in the work are the reversely transcripted DNA of HIV ((PDB: 5J2M) [17], tRNA (PDB: 4TNA) [18], alpha, and beta tubulins (PDB: 6AT4) [19]. The solvation model was built by CHARMM-GUI [20]. 10 ns simulations for each biomolecule were performed via NAMD [6] to acquire the ionic cloud (Fig. 1 first column). The bound ions were assembled with biomolecules while the charge and VDW radius were assigned by pdb2pqr [21] from CHARMM36 [20]. Then the surface of electrostatic potential was calculated by Delphi [10]. The surface was colored from red to blue by Chimera, representing −1 kT/e to 1 kT/e [22].

2.3.3. Simulation

Each simulation was in the NVT ensembles and performed by NAMD 2.12 [6]. The CHARMM36 [20] was applied as the force field. The temperature was set as 310 K (controlled with a Langevin thermostat with the damping constant as 1.0) and the harmonic restraints were applied to protein or the nucleic acid (no restraints on hydrogens). The time step was set as 2 fs/step. The PME (full-system periodic electrostatics) was applied in the simulation. The minimization was 10,000 steps and was followed by 10 ns simulation.

3. Results and discussion

3.1. The benchmarks of accuracy and running time based on the number of frames

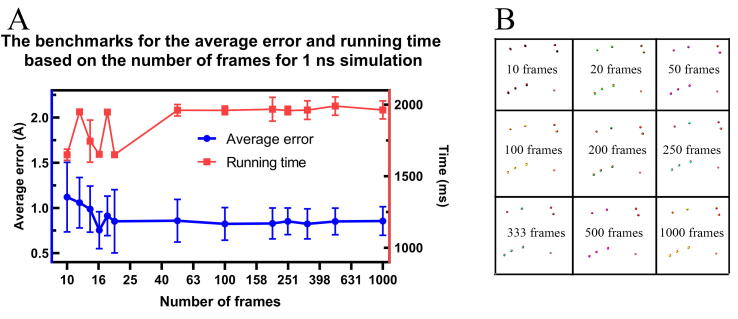
In Fig. 2A, the average error was calculated by the average of the distances between calculated bound ions and real bound ions (Fig. 2B). The average error reached stable when the number of frames is over 50. The 50 frames per nanosecond is corresponding to 10,000 steps per frame for 2 fs/steps in molecular dynamic simulation, which is a well-accepted frequency for MD simulations. Indeed, the results are more accurate with the longer simulations and more frames; so we strongly recommend users to run simulations as long as possible. Besides, the number of frames has no significant effect on running time. Generally, the 1 ns of simulation will take 2 s for users to get accurate results.

Fig. 2.

The benchmarks of average error, and running time (A) as well as the comparison between calculated bound ions with real bound ions with the different number of frames in 1 ns simulation. The real bound ions are colored red while the calculated bound ions are calculated in other colors according to the corresponding number of frames. (B).

3.2. The electrostatic potential surface of Proteins, DNA, and RNA

In Fig. 3, we provide the electrostatic potential surface of the electrostatic potential for alpha and beta tubulins, DNA of HIV as well as the tRNA. The first column shows the ionic cloud from the simulations. The cyan balls in the second and third columns are the calculated bound potassium ions. The third column shows the electrostatic surface. The alpha and beta tubulins (Fig. 3C and F) are always negatively charged, helping the binding with kinesin for cargo transfers. Compared with previous work [23], the bound ions on the surface did a modification on the charge distribution. The changed electrostatic surface [24] then changed force directions and intensity. The major groove of DNA bound more potassium ions than minor grooves, which could be due to the steric bulk (Fig. 3I). The density of bound potassium ions may be difficult for binding between DNA repairing proteins [25] (such as BER). This phenomenon may lead to new findings of the repelling of surrounding ions. In the tRNA, the T-arm is positively charged due to the bound potassium ions. In previous research, the molecular replacement with ions happened in the tRNA complex [26], [27]. The study of potassium is related to amino acid binding and transporting (Fig. 3L).

Fig. 3.

The ionic cloud, structures with bound potassium ions and the surface of the electrostatic surface of alpha-tubulin (A, B and C), beta-tubulin (D, E, and F), DNA of HIV (G, H and I), and tRNA (J, K, and L).

4. Conclusion

The HIT-webserver provides an efficient way to calculate bound ions via the trajectories from simulations. The webserver based on the High-Performance Computer (HPC) cluster accelerates the calculations by 10 times. HIT web server can be used for any biomolecules including protein and nucleic acids. The tool can also be downloaded from https://compbio.utep.edu/software/.

Author Contributions

The software is develoleped by Shengjie and implemented into a webserver by Juan. The simulation and testing is finished by Shengjie, Yixin, and Wenhan. Shengjie, Juan, Dongfang, and Lin contribute to the manuscript writing.

Availability

The HIT web server is available at: http://compbio.utep.edu/webservers/#/hit.

Significance

We developed a Hybrid Ion Treatment (HIT) method to calculate positions of bound ions for biomolecules. The HIT method significantly improves electrostatic calculations with bound ions. The web server was developed to provide efficient calculations via a high-performance computer cluster.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.