A multiple-testing procedure for high-dimensional mediation hypotheses

Abstract

Mediation analysis is of rising interest in epidemiology and clinical trials. Among existing methods, the joint significance (JS) test yields an overly conservative type I error rate and low power, particularly for high-dimensional mediation hypotheses. In this article we develop a multiple-testing procedure that accurately controls the family-wise error rate (FWER) and the false discovery rate (FDR) when testing high-dimensional mediation hypotheses. The core of our procedure is based on estimating the proportions of component null hypotheses and the underlying mixture null distribution of p-values. Theoretical developments and simulation experiments prove that the proposed procedure effectively controls FWER and FDR. Two mediation analyses on DNA methylation and cancer research are presented: assessing the mediation role of DNA methylation in genLetic regulation of gene expression in primary prostate cancer samples; exploring the possibility of DNA methylation mediating the effect of exercise on prostate cancer progression. Results of data examples include wellL-behaved quantile-quantile plots and improved power to detect novel mediation relationships. An R package HDMT implementing the proposed procedure is freely accessible in CRAN.

1. Introduction

Mediation analysis is of rising interest in clinical trials and epidemiology. The advance of high-throughput technologies has made it possible to interrogate molecular intermediate phenotypes such as gene expression and DNA methylation in a genome-wide fashion, some of which may mediate effects of treatments, external exposures and life-style risk factors on disease risk. For example, the SWOG Clinical Trials Network, as part of NCI National Clinical Trials Network is conducting multiple large randomized phase III trials for immunotherapies (e.g. Phase III trials SWOG S1404, SWOG S1418). Sequential specimens post treatment have been collected to interrogate whether molecular markers such as gene expressions mediate treatment effect. In epidemiology, an emerging topic is epigenetic modifications of DNA and histones, which may be an interface between environmental exposures and the genome for complex diseases such as cancers(Petronis, 2010; Kulis and Esteller, 2010; Relton and Davey Smith, 2010, 2012).

This paper is motivated by, but not limited to, studying the role of DNA methylation, one of the most studied epigenetic marks, in cancer etiology. We present two mediation analyses in the prostate cancer research. First, over 150 single nucleotide polymorphisms (SNPs) have been identified to be associated with the risk of prostate cancer in genome-wide association studies. Many of these SNPs influence expression of putative cancer genes as expression quantitative trait loci (eQTLs), as well as levels of CpG methylation in these genes as methylation quantitative trait loci (meQTLs). It is of interest to determine whether DNA methylation mediates genetic regulation of gene expression among these well-established risk loci. We analyze data for 69,602 triplets in genotypes, gene expression (measured by RNA-seq) and DNA methylation (measured by Infinium®HumanMethylation450 BeadChip array) among approximately 500 prostate cancer patients in The Cancer Genome Atlas (TCGA)(The Cancer Genome Atlas Research Network, 2015). Second, DNA methylation has been reported to be associated with vigorous physical activity and may mediate the beneficial effect of physical activity lowering risk of metastatic progression. We analyze data with frequency of exercise, half a million CpG methylation sites, and cancer outcomes from approximately 350 patients in a Seattle-based prostate cancer cohort.

Statistically, mediation analysis entails dissecting a mechanistical relationship between an exposure (denoted by X, e.g., in our examples cancer risk SNPs or exercise), a candidate mediator (denoted by M, e.g., DNA methylation), and an outcome (denoted by Y, e.g., gene expression or cancer progression). As originally formulated in the psychological literature(Baron and Kenny, 1986; MacKinnon, 2008), assuming there is no unmeasured confounding, the exposure X shall have a causal effect on the mediator M and, and the mediator shall have a causal effect on the outcome Y. Let the causal effect X → M be parameterized by α, and the causal effect M → Y be parameterized by β. This constitutes a composite null hypothesis, namely H₀: α = 0 or β = 0, in that two parameters have to be both non-zero in order to reject the null hypothesis. Much of recent methodological work for mediation analysis has been motivated by the potential outcomes framework in the causal inference(Rubin, 1978), providing a rigorous definition of mediation and direct effect and indirect effect(Robins and Greenland, 1992; Pearl, 2001). With suitable identifiability assumptions(VanderWeele and Vansteelandt, 2009; Imai et al., 2010), e.g., no unmeasured confounding, estimation of causal mediation parameters has been extended from linear models to generalized linear models and survival models(VanderWeele and Vansteelandt, 2010; VanderWeele, 2011; Tchetgen Tchetgen, 2011; Huang and Cai, 2016). A rigorous definition of mediation using the potential outcomes framework is described in web-based Supplementary Materials and also can be found in VanderWeele and Vansteelandt (2009, 2010); VanderWeele (2011).

When testing for mediation, properly controlling the type I error rate remains a challenge due to the composite null hypothesis. When evaluated in the recent literature(MacKinnon et al., 2002; Barfield et al., 2017), current procedures for testing mediation generally yield overly conservative p-values if both α = 0 and β = 0. The Sobel’s test performs a z-score test for the product of the two parameters(Sobel, 1982), though the distribution of the product of two normally distributed estimators is no longer normal when the parameters are both zero. The classical intersection-union test for mediation uses the maximum of the two p-values (denoted by p_max), one for testing α = 0 and the other for testing β = 0, though a naïve significance rule for the maximum p-value results in a valid but overly conservative test(Huang, 2018, 2019). In a genome-wide study with high-dimensional mediation hypotheses, the majority of null hypotheses may have both α = 0 and β = 0. The over-conservativeness issue is further exacerbated, as examplified recently in an epigenetic study(Barfield et al., 2017). We observed a similar problem in our exercise and prostate cancer outcome analysis, shown in Figure 1. The red triangles are the quantile-quantile plot for p_max of the joint significance test for mediation of the effect of exercise on prostate cancer progression by approximately half a million CpG probes on the Illumina HM450 array. If the expected quantiles are computed by a uniform distribution, the q-q plot is substantially below the diagonal line, suggesting that the naïve joint significance test procedure can be grossly conservative and lose power. Notably, this problem stems from the maximum p-value procedure being used for the intersection-union test(Berger, 1982), therefore is general and not limited to the scope of the mediation inference.

Figure 1:

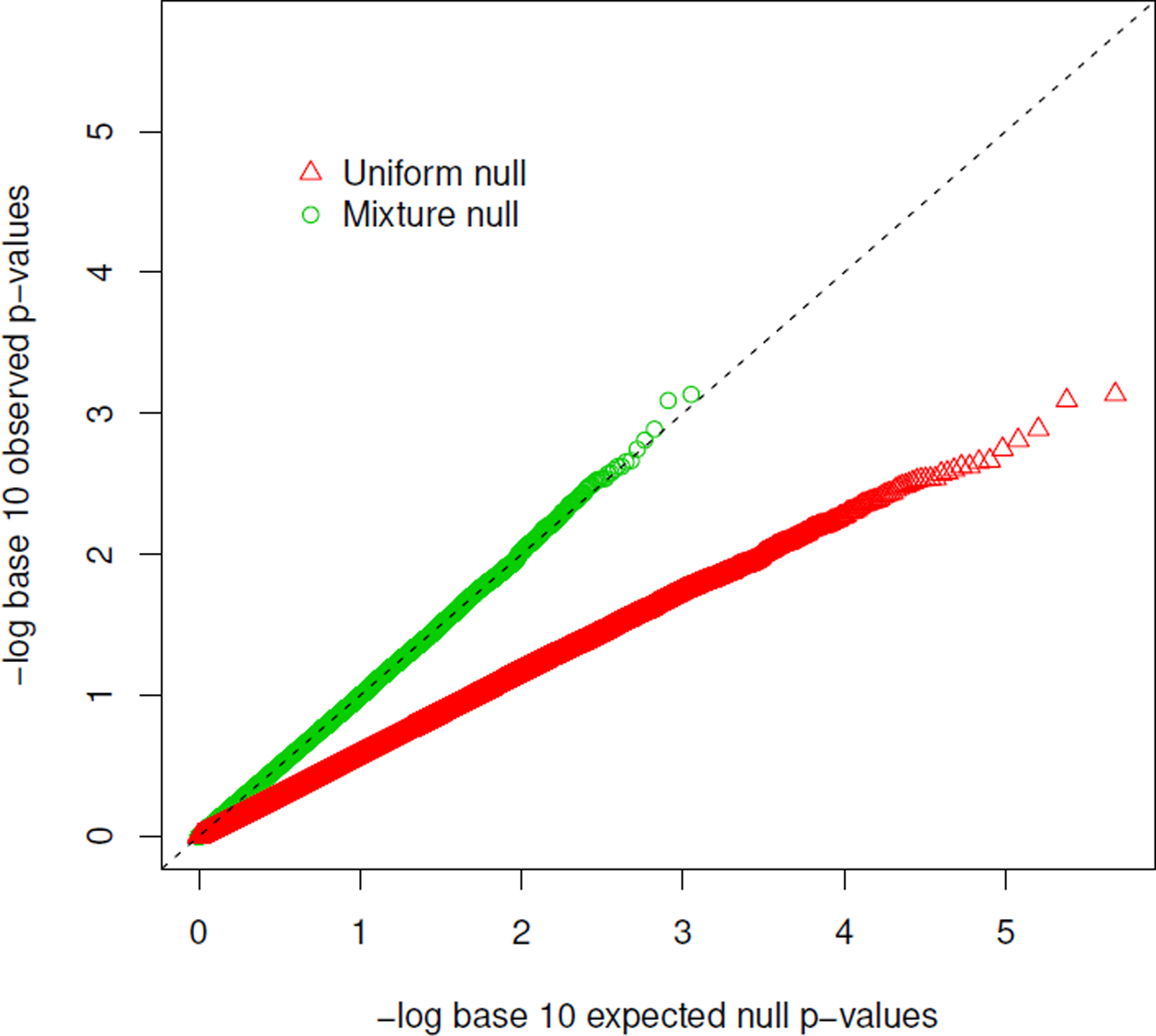
The q-q plot for a genome-wide mediation analysis for physical activity, DNA methylation and prostate cancer outcome among patients with localized diseases. The observed p-max values were compared to the expected quantiles generated by the uniform null distribution (red triangles) and the estimated mixture null distribution (green dots).

To correct the type I error rate for the Sobel’s test in high-dimensional mediation hypotheses, a recent proposal derived an approximation p-value from a composite normal product distribution under certain parametric assumptions(Huang, 2019). The advantage of this proposed method is that, because of approximation, it does not require estimating the proportions of component null hypotheses. However its applicability is limited to genome-wide testing with very sparse alternatives in both α and β parameters. If sample size increases, the approximation becomes less effective in controlling the type I error rate(Huang, 2019). This is rather restrictive to mediation analyses in epidemiology and genomics, for example in DNA methylation studies maternal smoking can cause large-scale DNA methylation alterations in blood of newborns(Joubert et al., 2016).

In this article, we propose a multiple testing procedure for assessing the significance of p_max derived from the intersection-union test, when there are high-dimensional mediation hypotheses. The core of the proposed algorithm is, in contrast to Huang (2019), estimation of the proportions of the three types of component null hypotheses: H₀₀: α = 0, β = 0; H₀₁: α = 0, β ≠ 06; H₁₀: α ≠ 0, β = 0, and then obtain the corresponding mixture null distribution for p_max. We call the proposed procedure “JS-mixture” to distinguish from the naïve JS procedure using the uniform null distribution, referred to as “JS-uniform”. Motivated by the asymptotic mixture null distribution, a simple multiple testing procedure is developed to control the family-wise error rate (FWER) and the false discovery rate (FDR). Finite-sample correction is also considered to improve the performance in low power settings. We show that our procedure provides much more accurate control of the family-wise error rate (FWER) and the false discovery rate (FDR) compared to the naïve joint significance test. As a proof of concept, the corrected quantile-quantile plot generated by JS-mixture, where the null p_maxs fall in the diagonal line, is shown in Figure 1 (green dots). We conduct extensive simulations to evaluate the performance of the proposed procedure. We apply the proposed procedure to the two prostate cancer studies, identifying candidate mediation relationships in SNP → CpG methylation → gene expression, and assessing evidence for mediation of exercise and cancer progression via CpG methylation.

2. Methods

Suppose data are collected for an exposure X, a vector of J candidate mediators (M₁, …, M_j, …, M_J), and an outcome Y among n independent and identically distributed (i.i.d.) subjects randomly drawn from a population. This is the standard setting for a DNA methylation study, e.g., the exercise and DNA methylation study example for prostate cancer. The notation can be more general. For example, there could be a vector of exposures X_j, such as SNPs, or there could be a vector of outcomes Y_j, such as gene expressions. Suppose, for simplicity of notation, both Y and X are continuous variables, though the proposed procedure works for dichotomized outcomes. The goal is to perform mediation analysis among triplets (X,M_j,Y) and identify some M_js that mediate the effect of X on Y, provided that the hypothesized direction of mediation is unequivocally X → M_j → Y. To proceed with causal mediation analysis, assume that there is no confounding in assessing the associations below, or confounding can be effectively accounted for by covariate adjustment. For ease of notation we omit covariate adjustment in the following models. The classical mediation test entails the following two linear regression models for (X,M_j,Y)(Baron and Kenny, 1986; MacKinnon, 2008),

$$\mathbb{E}\left(M_j|X\right)={\alpha }_{0j}+{\alpha }_{j}X,$$ (1)

$$\mathbb{E}\left(Y|M_j,X\right)={\beta }_{0j}+{\beta }_j{M}_j+{\beta }_{1j}X.$$ (2)

A mediation relationship stipulates that two conditions have to be met simultaneously: first, the exposure has a causal effect on the mediator (α_j ≠ 0); second, the mediator has a causal effect on the outcome conditional on the exposure (β_j ≠ 0). This constitutes a composite null hypothesis

$${\text{H}}_{0j}:{\alpha }_j=0\text{or}{\beta }_j=0,$$ (3)

which can be equivalently expressed as the union of the three disjoint component null hypotheses, namely

$$\begin{gathered} {\text{H}}_{01,j}:{\alpha }_j=0\text{and }{\beta }_j\ne 0, \\ {\text{H}}_{10,j}:{\alpha }_j\ne 0\text{and}{\beta }_j=0, \\ {\text{H}}_{00,j}:{\alpha }_j=0\text{and }{\beta }_j=0. \end{gathered}$$

Among existing tests for the mediation null hypothesis (3), the joint significant test (hereafter referred to as the “JS-uniform” procedure) performs best, balancing the type I error rate and power(MacKinnon et al., 2002; Barfield et al., 2017). This is an intersection-union test, first obtaining the p-values for testing α_j = 0 and β_j = 0, denoted by p_1j and p_2j respectively, then defining the overall p-value for mediation as

$$p_{\mathit{\text{max}},j}=p_{1j}\vee p_{2j},$$

where ∨ denotes the maximum of the two p-values. The usual uniform distribution for a null p-value is used to declare significance. While JS-uniform is a valid test, as we show next, the null distribution of p_max,j is generally not the uniform distribution, but a 3-component mixture distribution. Consequently, the JS-uniform procedure tends to be overly conservative, especially when the majority of hypotheses are H_00,js.

Let π₀₁, π₁₀, and π₀₀ denote the proportions corresponding to the three types of component null hypotheses among J mediation hypotheses. Because the probabilistic models (1) and (2) allow the factorization of the likelihood for α_j and the likelihood for β_j, p_1j and p_2j derived from likelihood maximization are independent. It follows that the distribution of p_max,j among null hypotheses H_0j is a 3-component mixture, whose cumulative distribution function is expressed as

$$\begin{gathered} \text{Pr}\left(p_{\mathit{\text{max}},j}\le t,{\text{H}}_{0j}\right)=\text{Pr}\left(p_{\mathit{\text{max}},j}\le t|{\text{H}}_{01,j}\right)\text{Pr}\left({\text{H}}_{01,j}\right)+ \\ \text{Pr}\left(p_{\mathit{\text{max}},j}\le t|{\text{H}}_{10,j}\right)\text{Pr}\left({\text{H}}_{10,j}\right)+ \\ \text{Pr}\left(p_{\mathit{\text{max}},j}\le t|{\text{H}}_{00,j}\right)\text{Pr}\left({\text{H}}_{00,j}\right) \\ ={\pi }_{01}\text{Pr}\left(p_{1j}\le t|{\text{H}}_{01,j}\right)\text{Pr}\left(p_{2j}\le t|{\text{H}}_{01,j}\right)+ \\ {\pi }_{10}\text{Pr}\left(p_{1j}\le t|{\text{H}}_{10,j}\right)\text{Pr}\left(p_{2j}\le t|{\text{H}}_{10,j}\right)+ \\ {\pi }_{00}\text{Pr}\left(p_{1j}\le t|{\text{H}}_{00,j}\right)\text{Pr}\left(p_{2j}\le t|{\text{H}}_{00,j}\right) \\ ={\pi }_{01}t\text{Pr}\left(p_{2j}\le t|{\text{H}}_{01,j}\right)+{\pi }_{10}t\text{Pr}\left(p_{1j}\le t|{\text{H}}_{10,j}\right)+{\pi }_{00}{t}^2. \end{gathered}$$ (4)

The derivation above uses the uniform distribution for null p_1j and null p_2j, as well as the independence between p_1j and p_2j. Note that Pr(p_2j ≤ t|H_01,j) and Pr(p_1j ≤ t|H_10,j) are the power function of rejecting β_j = 0 under H_01,j and the power function of rejecting α_j = 0 under H_10,j. When n is large, Pr(p_1j ≤ t|H_10,j) → 1 and Pr(p_2j ≤ t|H_01,j) → 1. The asymptotic mixture cumulative distribution (4) reduces to π₀₁t + π₁₀t + π₀₀t². The asymptotic null distribution of p_max,j can therefore be represented by

$$\left({\pi }_{01}+{\pi }_{10}\right)\mathcal{U}+{\pi }_{00}\mathcal{F}$$ (5)

where $\mathcal{U}$ is the standard uniform distribution between 0 and 1, $\mathcal{F}$ is the right-skewed distribution for the maximum of two independent p-values from the uniform distribution, with its cumulative distribution function (CDF) expressed as Pr(p_max,j ≤ t) = t². Regardless of finite samples or large samples, it is clear from (4) and (5) that the null distribution of p_max,j is a 3-component mixture, whose density is skewed toward 1. Using the uniform distribution as the null distribution as in the JS-uniform procedure will produce a conservative type I error rate. The forms of (4) and (5) also inform that the degree of conservativeness increases with π₀₀.

Derivation of the null distributions in finite samples (4) and in large samples (5) leads to a multiple testing procedure to correct the conservativeness of the JS-uniform procedure. When there are a large number of hypotheses being interrogated (J ≫ 0), one can estimate the proportions of H_01,j, H_10,j, and H_00,j from the observed distribution of p_1j and p_2j, j = 1, …, J, adapting the methods for estimating the proportion of nulls in the multiple testing literature(Storey et al., 2004; Langaas et al., 2005; Wang et al., 2011). The classical error measures such as FWER and FDR can be adjusted accordingly.

Table 1 describes the mediation testing outcomes when a multiple-testing significance rule is applied to J p_max,j values, so that those hypotheses with p_max,j less than or equal to some cut-off value t are rejected. Corresponding to t, we define the following empirical processes:

$$\begin{gathered} V_{00}(t)=\#\left\{p_{\mathit{\text{max}},j}\le t|{\text{H}}_{00}\right\}, \\ {V}_{01}(t)=\#\left\{p_{\mathit{\text{max}},j}\le t|{\text{H}}_{01}\right\}, \\ {V}_{10}(t)=\#\left\{p_{\mathit{\text{max}},j}\le t|{\text{H}}_{10}\right\}, \\ {V}_{11}(t)=\#\left\{p_{\mathit{\text{max}},j}\le t|{\text{H}}_{11}\right\}, \end{gathered}$$

$$R(t)=V_{11}(t)+V_{00}(t)+V_{01}(t)+V_{10}(t).$$

The key processes are V₀₁(t),V₁₀(t),V₀₀(t), denoting the numbers of the three types of false positives. Correspondingly, FWER for testing mediation is defined to be

$$\text{FWER}(t)=\text{Pr}\left[\left\{V_{00}(t)+V_{01}(t)+V_{10}(t)\right\}\ge 1\right],$$

and FDR for testing mediation is defined to be

$$\text{FDR}(t)=\mathbb{E}\left[\frac{V_{00}(t)+V_{01}(t)+V_{10}(t)}{R(t)\vee 1}\right],$$ (6)

where R(t) ∨ 1 = max(R(t), 1). We present in Section 2.1 – 2.3 a simple multiple-testing procedure that properly controls both FWER and FDR via estimating the proportions of component nulls and using the asymptotic mixture null distribution (5). While motivated by the large-sample mixture null distribution of p_max,j, we show that this procedure yields conservative estimates of the true FWER and FDR in finite samples, and it largely resolves the over-conservativeness issue of the JS-uniform procedure. In Section 2.4, we further improve the procedure by incorporating the finite-sample mixture null distribution of p_max,j (4), which provides more accurate control of FWER and FDR, especially for low power settings with a sizable π₀₁ or π₁₀.

Table 1:

Possible outcomes from J hypotheses for mediation.

		Accept null	Reject null	Total
Null is true	H01	U 01	V 01	J 01
	H10	U 10	V 10	J 10
	H00	U 00	V 00	J 00
Alternative is true	H11	U 11	V 11	J 11
Total		W	R	J

2.1. Estimation of π₀₀, π₀₁, π₁₀

Estimation of the proportion of null hypotheses has been studied extensively in the literature for FDR(Storey, 2002; Storey et al., 2004; Langaas et al., 2005; Wang et al., 2011). We propose an adaptation of an existing procedure first used in q-value estimation(Storey, 2002; Storey et al., 2004). Briefly, the proportion of null p_1js corresponding to α_j = 0, denoted by π₀₊(λ), and the proportion of null p_2js corresponding to β_j = 0, denoted by π₊₀(λ), can be estimated conservatively (greater than the true value) by the existing procedure:

$$\begin{gathered} {\widehat{\pi }}_{0+}(\lambda )=\frac{\frac{1}{J}\sum I\left(p_{1j}>\lambda \right)}{1-\lambda }, \\ {\widehat{\pi }}_{+0}(\lambda )=\frac{\frac{1}{J}\sum I\left(p_{2j}>\lambda \right)}{1-\lambda }, \end{gathered}$$

where I(·) is an indicator function, λ is a tuning parameter between 0 and 1, preferably close to 1. The rationale has been eloquently put previously(Storey, 2002; Storey et al., 2004): as along as each test has reasonable power, the p-values closer to 1 are more likely to be null p-values. Assuming p-values from null hypotheses are distributed as a uniform distribution, the number of null p_1j greater than λ can be approximated by $J{\widehat{\pi }}_{0+}(1-\lambda )$ as λ approaches 1, and the number of null p_2j greater than λ can be approximated by $J{\widehat{\pi }}_{+0}(1-\lambda )$ as λ approaches 1. Note that ${\widehat{\pi }}_{0+}$ and ${\widehat{\pi }}_{+0}$ are conservatively biased estimates of π₀₊ and π₊₀ (the estimators are greater than the parameters). One may simply pick a fixed λ close to 1. Alternatively, because there is a bias-variance trade-off when λ approaches 1, a smooth curve or a linear fitting line can be used to leverage estimators in a ladder of cutpoints λ = 0.05, …, 0.95. See previous developments on this topic(Storey, 2002; Storey et al., 2004; Wang et al., 2011).

Next, since π₀₊ = π₀₁ + π₀₀ and π₊₀ = π₁₀ + π₀₀, one can estimate the proportions of the three component nulls if π₀₀ can be estimated along with ${\widehat{\pi }}_{0+}(\lambda )$ and ${\widehat{\pi }}_{+0}(\lambda )$. The estimation method for one-dimensional p-values is applied to the two-dimensional p-values (p_1j, p_2j), which also leads to a biased estimator π₀₀,

$${\widehat{\pi }}_{00}(\lambda )=\frac{\frac{1}{J}\sum I\left(p_{1j}>\lambda ,p_{2j}>\lambda \right)}{{(1-\lambda )}^2},$$ (7)

under the similar rationale: as p_1j and p_2j both approach 1, the hypothesis is more likely from H₀₀. The denominator of (7) uses the independence of p_1j and p_2j. It follows that

$${\widehat{\pi }}_{01}(\lambda )={\widehat{\pi }}_{0+}(\lambda )-{\widehat{\pi }}_{00}(\lambda ),$$ (8)

$${\widehat{\pi }}_{10}(\lambda )={\widehat{\pi }}_{+0}(\lambda )-{\widehat{\pi }}_{00}(\lambda ),$$ (9)

$${\widehat{\pi }}_{11}(\lambda )=1-{\widehat{\pi }}_{00}(\lambda )-{\widehat{\pi }}_{01}(\lambda )-{\widehat{\pi }}_{10}(\lambda ).$$ (10)

With the estimates ${\widehat{\pi }}_{00}(\lambda )$, ${\widehat{\pi }}_{01}(\lambda )$, and ${\widehat{\pi }}_{01}(\lambda )$, the mixture null distribution (5) can be estimated to control FWER and FDR.

Remark.

We make one remark on estimation of the three null proportions, compared to estimation of the null proportion in the FDR literature(Storey, 2002; Storey et al., 2004). ${\widehat{\pi }}_{00}(\lambda )$, ${\widehat{\pi }}_{01}(\lambda )$, and ${\widehat{\pi }}_{10}(\lambda )$ are biased estimates for finite samples, and the degree of the bias depends on n, J and λ. For a fixed J and λ, the biases of ${\widehat{\pi }}_{00}(\lambda )$, ${\widehat{\pi }}_{01}(\lambda )$, and ${\widehat{\pi }}_{10}(\lambda )$ go to zero as n → ∞, since a larger sample size delivers greater power and therefore better separation between null p-values and alternative p-values. Different from estimation of the null proportion when there are only one-dimension p-values(Storey, 2002; Storey et al., 2004; Langaas et al., 2005; Wang et al., 2011), while ${\widehat{\pi }}_{00}(\lambda )$ is usually greater than π₀₀, ${\widehat{\pi }}_{01}(\lambda )$ and ${\widehat{\pi }}_{10}(\lambda )$ can be less than their corresponding parameter values. The influence of these null proportion estimators on properties of the proposed procedure will be examined when we tackle the theoretical properties in Section 2.2 and Section 2.3.

2.2. Family-wise error rate and q-q plot

To motivate a significance rule for controlling FWER, we assume that p_max,j under the null hypothesis is distributed as the large-sample mixture distribution (5) with the three types of component null hypotheses (H₀₀,H₀₁,H₁₀). This simplifies the estimation of the significance rule. While derived from the asymptotic mixture null distribution, we show that this rule indeed controls FWER in finite samples.

To control FWER(t_a) = Pr[{V₀₀(t_a) + V₀₁(t_a) + V₁₀(t_a)} ≥ 1] at a desired level a, where t_a is the corresponding cut-off for p_max,j, the Bonferroni method requires that the type I error rate for each individual test of the J tests should be controlled at $\frac{a}{J}$. The probability that a p_max,j is from the asymptotic mixture null distribution (5) and declared to be statistically significant given the p-value cut-off t_a is

$$\text{Pr}\left(p_{\mathit{\text{max}},j}\le t_a,{\text{H}}_j\in {\text{H}}_{00}\cup {\text{H}}_{01}\cup {\text{H}}_{10}\right)={\pi }_{01}{t}_a+{\pi }_{10}{t}_a+{\pi }_{00}{t}_a^2.$$ (11)

An estimator of the significance rule, denoted by ${\widehat{t}}_a$, for controlling the type I error rate of an individual mediation test at level $\frac{a}{J}$ is defined as the solution of the following quadratic equation

$${\widehat{\pi }}_{01}(\lambda )t_a+{\widehat{\pi }}_{10}(\lambda )t_a+{\widehat{\pi }}_{00}(\lambda )t_a^2=\frac{a}{J},$$ (12)

where estimators ${\widehat{\pi }}_{01}(\lambda )$, ${\widehat{\pi }}_{10}(\lambda )$, ${\widehat{\pi }}_{00}(\lambda )$ are expressed in (7), (8), and (9) in Section 2.1. Hereafter we omit (λ) in the estimators of the null proportions for simplicity of notation.

Two factors affect the performance of the proposed significance rule in finite samples. First, derivation of this rule uses the asymptotic mixture null distribution (5) for p_max,j, which essentially assumes that the two power functions Pr(p_2j ≤ t_a|H₀₁) and Pr(p_1j ≤ t_a|H₁₀) are 1. In finite samples, these two power functions may be less than 1. This may not matter when π₀₁ and π₁₀ are close to zero. However, if π₀₁ and π₁₀ are sizable, assuming Pr(p_2j ≤ t_a|H₀₁) = 1 and Pr(p_1j ≤ t_a|H₁₀) = 1 in the mixture null distribution will result in a more stringent rule than ${\widehat{t}}_a$. So using the asymptotic null distribution (5) in place of (4) will only result in a conservative rule. Second, while ${\widehat{\pi }}_{00}(\lambda )$ will tend to over-estimate π₀₀ when J is large, ${\widehat{\pi }}_{01}(\lambda )$ and ${\widehat{\pi }}_{10}(\lambda )$ may under-estimate their respective true values. The collective impact of these two factors on the performance of the derived FWER rule ${\widehat{t}}_a$ shall be examined.

We show in the following theorem that under mild regularity conditions that include weak dependence between p-values, the proposed JS-mixture procedure indeed controls FWER at level a in finite samples when J is large. In simulation experiments in Section 3, we show that the proposed procedure controls FWER in moderately high-dimensional settings, e.g., thousands of hypotheses.

Theorem 1. Among J hypotheses in Table 1, suppose the numbers and the fractions of the four types of hypotheses H₀₀, H₀₁, H₁₀, H₁₁ are (J₀₀, J₀₁, J₁₀, J₁₁) and (π₀₀, π₀₁, π₁₀, π₁₁), respectively, so that ${\text{lim}}_{J\to \infty }\frac{J_{l{l}^{\prime }}}{J}$ for ll′ ∈ (00, 01, 10, 11). Suppose the distributions of p_1j and p_2j are uniform between 0 and 1 under their respective null hypotheses and stochastically less than the uniform distribution under their respective alternative hypotheses. Assume for j ≠ j′, (p_1j, p_2j) and (p_1j′, p_2j′) are either independent or have weak dependence, so that the following processes converge almost surely to their respective limits for any t between 0 and 1,

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}\frac{\sum H_j\in H_{10}I\left(p_{1j}>t\right)}{J_{10}}\equiv G_{10}(t), \\ \underset{J\to \infty }{\text{lim}}\frac{\sum _{H_j\in H_{01}}I\left(p_{2j}>t\right)}{J_{01}}\equiv G_{01}(t), \\ \underset{J\to \infty }{\text{lim}}\frac{\sum _{H_j\in H_{11}}I\left(p_{2j}>t\right)}{J_{11}}\equiv G_{11,p_2}(t), \\ \underset{J\to \infty }{\text{lim}}\frac{\sum _{H_j\in H_{11}}I\left(p_{1j}>t\right)}{J_{11}}\equiv G_{11,p_1}(t), \\ \underset{J\to \infty }{\text{lim}}\frac{\sum _{H_j\in H_{11}}I\left(p_{1j}>t,p_{2j}>t\right)}{J_{11}}\equiv G_{11}(t), \end{gathered}$$

where G₁₀(t), G₀₁(t), G_11,p2(t),G_11,p1(t), and G₁₁(t) denote the limits when J → ∞. To control FWER at level a, the significance rule ${\widehat{t}}_a$ for p_max,j solves the quadratic equation (12), using the estimated proportions of component null hypotheses in (7),(8),(9). With these conditions, ${\widehat{t}}_a$ controls FWER at the level a when J → ∞, that is,

$$\underset{J\to \infty }{\text{lim}\text{sup}}\mathit{\text{Pr}}\left[\left\{V_{00}\left({\widehat{t}}_a\right)+V_{01}\left({\widehat{t}}_a\right)+V_{10}\left({\widehat{t}}_a\right)\right\}\ge 1\right]\le a.$$

The proof of Theorem 1 is left to Appendix. While for the same j, p_1j and p_2j are independent because of likelihood factorization, weak dependence between (p_1j, p_2j) and (p_1j′, p_2j′) for j ≠ j′ are allowed as long as the processes in Theorem 1 converge. This includes the block correlation structure typically encountered in genomic applications such as SNPs, CpG methylation, and gene expression.

Following the same derivation, the quantiles of p_max,j at the $\frac{j}{J}$ percentile can be obtained, accounting for the asymptotic mixture null distribution (5). Specifically, let t_j denote the quantile at $\frac{j}{J}$, j = 1, …, J. This vector of quantiles are derived as the solutions of the following set of J quadratic equations,

$$\left({\widehat{\pi }}_{01}+{\widehat{\pi }}_{10}\right)\cdot t_j+{\widehat{\pi }}_{00}{t}_j^2=\frac{j}{J}.$$

A q-q plot accounting for the asymptotic mixture null distribution can be drawn for visually assessing global significance using the estimated t_js.

2.3. False discovery rate

As expressed in (6), FDR(t) is defined to be the expected proportion of rejected hypotheses being null when the significance rule p_max,j ≤ t is applied, t ∈ [0, 1]. In testing for mediation, false positives may be composed of three types of null hypotheses, namely H₀₁, H₁₀, and H₀₀. An estimator of FDR(t) can be motivated heuristically using the mixture null distribution in large samples. When J is large, observe that

$$\text{FDR}(t)\approx \frac{\mathbb{E}\left\{V_{00}(t)+V_{01}(t)+V_{10}(t)\right\}/J}{\mathbb{E}\left\{R(t)\vee 1\right\}/J}.$$ (13)

Because of the independence between p_1j and p_2j, it follows that

$$\begin{gathered} \mathbb{E}\left\{\frac{V_{00}(t)}{J}\right\}={\pi }_{00}{t}^2, \\ \mathbb{E}\left\{\frac{V_{01}(t)}{J}\right\}={\pi }_{01}t\frac{\sum _{{\text{H}}_j\in {\text{H}}_{01}}\text{Pr}\left(p_{2j}\le t\right)}{J_{01}} \\ \le {\pi }_{01}t, \\ \mathbb{E}\left\{\frac{V_{10}(t)}{J}\right\}={\pi }_{10}t\frac{\sum _{{\text{H}}_j\in {\text{H}}_{10}}\text{Pr}\left(p_{1j}\le t\right)}{J_{10}} \\ \le {\pi }_{10}t. \end{gathered}$$

The inequalities above are based on Pr(p_1j ≤ t|H₁₀) ≤ 1 and Pr(p_2j ≤ t|H₀₁) ≤ 1. The equality holds for the asymptotic mixture null distribution. Therefore, using the estimated proportions ${\widehat{\pi }}_{00}$, ${\widehat{\pi }}_{01}$, and ${\widehat{\pi }}_{10}$ in (7), (8) and (9), a simple estimator for FDR(t) is obtained as

$${\widehat{\text{FDR}}}_{\lambda }(t)=\frac{{\widehat{\pi }}_{01}t+{\widehat{\pi }}_{10}t+{\widehat{\pi }}_{00}{t}^2}{\left\{R(t)\vee 1\right\}/J}.$$ (14)

To control FDR at level b, we define the significance threshold for p_max,j as

$${\widehat{t}}_b=\text{sup}\left\{t:{\widehat{\text{FDR}}}_{\lambda }(t)\le b\right\}.$$ (15)

Similar to the significance rule for controlling FWER in Section 2.2, this FDR estimator and significance rule assume the asymptotic mixture null distribution (5) for p_max. The accuracy of ${\widehat{\text{FDR}}}_{\lambda }(t)$ in finite samples is affected by two factors in the estimation: how close Pr(p_1j ≤ t|H₁₀) and Pr(p_2j ≤ t|H₀₁) can be approximated by 1, and how accurate ${\widehat{\pi }}_{00}(\lambda )$, ${\widehat{\pi }}_{01}(\lambda )$, and ${\widehat{\pi }}_{10}(\lambda )$ estimate the null proportions. For a fixed J, ${\widehat{\text{FDR}}}_{\lambda }(t)$ converges to FDR_λ(t) when sample size increases, as the power to reject the null hypotheses for p_1j and p_2j increases to 1, and the three estimates of null proportions converge to their respective true values. In finite samples, as noted before, ${\widehat{\pi }}_{00}(\lambda )$ over-estimates π₀₀, ${\widehat{\pi }}_{01}(\lambda )$ and ${\widehat{\pi }}_{10}(\lambda )$ may under-estimate π₀₁ and π₁₀ respectively. We prove in the following theorem that, in finite samples and when J is large, ${\widehat{\text{FDR}}}_{\lambda }(t)$ provides a conservative estimate of FDR(t) for a small t, and ${\widehat{t}}_b$ provides the control of the FDR at level b.

Theorem 2. Follow the notation and the assumptions in Theorem 1, and denote ${\widehat{\mathit{\text{FDR}}}}_{\lambda }(t)$ as in (14), which uses the estimated proportions of the component null hypotheses in (7),(8),(9). When J goes to ∞, ${\widehat{\mathit{\text{FDR}}}}_{\lambda }(t)$ is a conservative estimate of FDR(t) for all t ∈ (0, 1) that satisfies $G_{01}(t)\ge \frac{G_{01}(\lambda )}{1-\lambda }$ and $G_{10}(t)\ge \frac{G_{01}(\lambda )}{1-\lambda }$, so that

$$\underset{J\to \infty }{\text{lim}\text{sup}}\left\{{\widehat{FDR}}_{\lambda }(t)-FDR(t)\right\}\ge 0.$$

Moreover, the significance threshold ${\widehat{t}}_b$ expressed in (15) indeed controls the FDR at level b, so that

$$\underset{J\to \infty }{\text{lim}\text{sup}}FDR\left({\widehat{t}}_b\right)\le b.$$

The proof of Theorem 2 closely follows the proof of Theorem 1 with nearly identical assumptions, except that ${\widehat{\text{FDR}}}_{\lambda }(t)$ does not have simultaneously point-wise conservativeness for all t between 0 and 1, but only for t satisfying $G_{01}(t)\ge \frac{G_{01}(\lambda )}{1-\lambda }$ and $G_{10}(t)\ge \frac{G_{01}(\lambda )}{1-\lambda }$. Because λ is typically chosen to be close to 1, and the distribution of p-values under alternative hypotheses is stochastically less than the uniform distribution, the two conditions should hold for a small t, for example the significance cut-off to control FDR at level 0.05.

2.4. Finite-sample adjustment

When deriving the proposed multiple-testing procedure in Section 2.2 and 2.3, we used the asymptotic mixture null distribution (5) and assumed in (12) and (14) that the power to reject α_j = 0 and β_j = 0 under the hypotheses H₁₀ and H₀₁ are sufficiently high, so that

$$\text{Pr}\left(p_{1j}\le t|{\text{H}}_{10}\right)\to 1$$ (16)

$$\text{Pr}\left(p_{2j}\le t|{\text{H}}_{01}\right)\to 1,$$ (17)

where t is a significance threshold value for p_max,j. In low power settings, e.g., a ultra-high dimensional study where there are half a million CpG probes being interrogated, the p-value cut-off t to control FWER at 0.05 can be in the very far left tail of the p-value distribution, rending the conditions (16) and (17) difficult to hold. The impact of using the asymptotic mixture null distribution on the significance rule is not ignorable particulary when there are large proportions of H₀₁ or H₁₀. See, for example, the q-q plot for the exercise and prostate cancer outcome study using the approximations (16) and (17) in Supplementary Figure 1. While maintaining the control of FDR and the FWER, the significance rule can be conservative and the q-q plot may not be satisfactory in the tail of small p_max values.

Indeed, the performance of the proposed procedure in these scenarios can be further improved by utilizing the finite-sample mixture null distribution, essentially obtaining good finite-sample estimates of the two power functions, namely $\widehat{\text{Pr}}\left(p_{1j}\le t|{\text{H}}_{10}\right)$ and $\widehat{\text{Pr}}\left(p_{2j}\le t|{\text{H}}_{01}\right)$. We describe in Appendix the nonparametric estimates based on the Grenander estimator of a p-value density(Langaas et al., 2005), requiring that the density of p-value under the alternative hypothesis is stochastically less than the uniform distribution and decreasing in [0,1]. With the estimates $\widehat{\text{Pr}}\left(p_{1j}\le t|{\text{H}}_{10}\right)$ and $\widehat{\text{Pr}}\left(p_{2j}\le t|{\text{H}}_{01}\right)$, we show next how to adjust the proposed procedure to better control for FWER and FDR, as well as drawing a q-q plot.

Suppose we wish to determine the p_max cut-off value t_0.05 that control FWER at 0.05. We now solve the equation

$${\widehat{\pi }}_{01}{t}_{0.05}\widehat{\text{Pr}}\left(p_{2j}\le t_{0.05}|{\text{H}}_{01}\right)+{\widehat{\pi }}_{10}{t}_{0.05}\widehat{\text{Pr}}\left(p_{1j}\le t_{0.05}|{\text{H}}_{10}\right)+{\widehat{\pi }}_{00}{t}_{0.05}^2=\frac{0.05}{J}.$$ (18)

Let ${\tilde{t}}_{0.05}$ denote the solution of (18). Because the approximations (16) and (17) are no longer used, ${\tilde{t}}_{0.05}$ delivers a better performance in controlling FWER, as we show next in simulation studies. Note that (18) is not a quadratic equation. Solving (18) can be accomplished by an iterative algorithm: evaluate the two power functions $\widehat{\text{Pr}}\left(p_{2j}\le t_{0.05}|{\text{H}}_{01}\right)$ and $\widehat{\text{Pr}}\left(p_{1j}\le t_{0.05}|{\text{H}}_{10}\right)$ given the current estimate ${\tilde{t}}_{0.05}$, then treat these two probabilities as fixed quantities, and solve the quadratic equation (18) for the next estimate of ${\tilde{t}}_{0.05}$; iterate this algorithm until the estimate ${\tilde{t}}_{0.05}$ converges. The initial estimate to start the algorithm can be set to ${\tilde{t}}_{0.05}$. In our simulations the algorithm typically converges in 5~10 iterations. Similarly, the estimation of the quantiles of the mixture null distribution can be adjusted by this iterative algorithm. No iteration is needed for obtaining a more precise estimate of FDR(t) for a given t, expressed as

$$\widetilde{\text{FDR}}(t)=\frac{\left\{{\widehat{\pi }}_{01}\widehat{\text{Pr}}\left(p_{2j}\le t|{\text{H}}_{01}\right)+{\widehat{\pi }}_{10}\widehat{\text{Pr}}\left(p_{1j}\le t|{\text{H}}_{10}\right)\right\}t+{\widehat{\pi }}_{00}{t}^2}{\widehat{\text{Pr}}\left(p_{\mathit{\text{max}},j}\le t\right)}.$$

Remark.

In practice, finite-sample adjustment and the estimated power functions are only needed when π₁₀ ≫ 0 and π₀₁ ≫ 0, and they can be estimated with sufficient accuracy only when there are many p-values smaller than t. In high-dimensional testing, it is common that the null hypotheses dominate. Therefore, we implement two checking steps in our algorithm before estimating the power functions. First, we apply the Kolmogrove-Smirnov test to p_1j and p_2j, comparing them to a uniform distribution. If the Kolmogrove-Smirnov test fails to reject the null, we will assign π₀₊ = 1 or π₊₀ = 1. This will force π₀₁ = 0 or π₁₀ = 0, and eliminate the necessity of estimating the corresponding power functions. Second, for a particular small t, for example in searching for the FWER cut-off t_0.05, if there are few observed p_1js or p_2js that are less than t, we will use the approximation instead, avoiding use of a poor estimate of Pr(p_1j ≤ t|H₁₀) or Pr(p_2j ≤ t|H₀₁).

The proposed method is implemented in the R package HDMT (High-Dimensional Multiple Testing) which is freely accessible in CRAN. HDMT takes two vectors of p-values p_1j and p_2j as the input, and produces the estimators of null proportions, the q-q plot, FWER and FDR estimates. See Figure 1 for an example of the corrected q-q plot for genome-wide DNA methylation sites in the prostate cancer study. As a cautionary note, the estimators of null proportions for the two-dimensional p-values is merely for adjusting the significance rule - they can be substantially biased in a moderate level of sample sizes.

3. Simulation study

Simulated datasets were generated to evaluate the performance of the proposed multiple testing procedure. Specifically, a random sample was drawn from a population with n subjects (n=250 or 1000). The goal is to assess mediation of an exposure (denoted by X) effect on J quantitative traits (denoted by Y₁, …, Y_J) by J independent molecular markers (denoted by M₁, …, M_J, J = 5000 or 20000). Data for (X, M_j, Y_j) were generated sequentially as follows: X ~ Ber(0.2), M_j = α_jX + ϵ_j, Y_j = β_jM_j + ε_j, where ϵ_j and ε_j were independent random errors drawn from a standard normal distribution, α_j and β_j were set to generate null and alternative hypotheses. Five scenarios were designed to comprehensively evaluate error measures and power:

1. Dense nulls: π₀₀ = 0.60, π₀₁ = π₁₀ = 0.20, π₁₁ = 0. Under H₁₀, α_j=0.2 and β_j=0; Under H₀₁, α_j=0 and β_j=0.3; Under H₀₀, α_j=0 and β_j=0.

2. Sparse nulls: π₀₀ = 0.90, π₀₁ = π₁₀ = 0.05, π₁₁ = 0. Under H₁₀, α_j=0.2 and β_j=0; Under H₀₁, α_j=0 and β_j=0.3; Under H₀₀, α_j=0 and β_j=0.

3. Complete nulls: π₀₀ = 1, π₀₁ = π₁₀ = 0, π₁₁ = 0. So all α_j and β_j are zero.

4. Sparse alternatives: π₀₀ = 0.88, π₀₁ = π₁₀ = 0.05, π₁₁ = 0.02. Under H₁₀, α_j=0.2 τ and β_j=0; Under H₀₁, α_j=0 and β_j=0.3 τ; Under H₀₀, α_j=0 and β_j=0; Under H₁₁, α_j=0.2τ and β_j=0.3 τ. By changing the mediation effect size parameter τ from 0.5 to 2.5, α_j increases from 0.1 to 0.5, and β_j increases from 0.15 to 0.75.

5. Dense alternatives: π₀₀ = 0.40, π₀₁ = π₁₀ = 0.2, π₁₁ = 0.2. Under H₁₀, α_j=0.2τ and β_j=0; Under H₀₁, α_j=0 and β_j=0.3τ; Under H₀₀, α_j=0 and β_j=0; Under H₁₁, α_j=0.2τ and β_j=0.3 τ. By changing the mediation effect size parameter τ from 0.5 to 2.5, α_j increases from 0.1 to 0.5, and β_j increases from 0.15 to 0.75.

Table 2 shows means and variances of the estimated null proportions under the five scenarios among 5,000 simulated datasets. Under the fourth and (sparse alternatives) the fifth scenario (dense alternatives) with alternative mediation hypotheses, the estimators are shown for the parameter setting with τ = 1, α_j = 0.2 and β_j = 0.3. Nearly in all scenarios, ${\widehat{\pi }}_{00}$ over-estimated π₀₀, more so when sample size is 250 than sample size 1000. This is because there are a sizable portion of p_1j and p_2j from hypotheses H₀₁, H₁₀, and H₁₁ both falling into [λ,1], inflating the estimate for π₀₀. With a greater sample size, the chance of these p-values falling in the region [λ,1] gets smaller, and so the estimate of π₀₀ becomes more accurate. On the other hand, π₁₀ is consistently under-estimated when sample size is 250, while ${\widehat{\pi }}_{01}$ is much closer to its true value. This is because the power of testing α_j = 0 is much less than the power for testing β_j=0, since X is a binary variable and M_j are a continuous variable. Based on their probabilistic limits (19) and (20) derived in Appendix, this difference in power results in a better estimate for π₀₁. Increasing sample size reduces the bias of the proportion estimators in all scenarios, as expected. In scenarios with either sparse or dense alternatives, π₁₁ is estimated to be smaller than the true value, reflecting the typically low power for testing mediation. For a fixed sample size, increasing the number of tests from 5,000 to 20,000 does not affect the bias of estimators, but improves their precision.

Table 2:

Performance of the estimated proportions of the three null hypotheses (mean and standard deviation) under the four scenarios and different sample sizes and different numbers of tests in 10,000 simulated datasets.

	J=5000				J=20000
Dense null	π00 = 0.6	π10 = 0.2	π01 = 0.2	π11 = 0	π00 = 0.6	π10 = 0.2	π01 = 0.2	π11 = 0
n=250	0.701(0.022)	0.093(0.016)	0.194(0.014)	0.011(0.008)	0.701(0.012)	0.096(0.010)	0.197(0.007)	0.006(0.004)
n=1000	0.613(0.019)	0.182(0.014)	0.194(0.014)	0.011(0.008)	0.613(0.010)	0.185(0.007)	0.197(0.007)	0.006(0.004)
Sparse null	π00 = 0.9	π10 = 0.05	π01 = 0.05	π11 = 0	π00 = 0.9	π10 = 0.05	π01 = 0.05	π11 = 0
n=250	0.929(0.025)	0.018(0.016)	0.045(0.016)	0.008(0.008)	0.925(0.012)	0.022(0.008)	0.047(0.008)	0.006(0.004)
n=1000	0.903(0.023)	0.041(0.016)	0.044(0.016)	0.011(0.008)	0.903(0.012)	0.044(0.008)	0.047(0.008)	0.006(0.004)
Complete null	π00 = 1	π10 = 0	π01 = 0	π11 = 0	π00 = 1	π10 = 0	π01 = 0	π11 = 0
n=250	0.998(0.007)	0.001(0.005)	0.001(0.005)	0(0.001)	0.999(0.003)	0(0.002)	0(0.002)	0(0)
n=1000	0.998(0.007)	0.001(0.005)	0.001(0.005)	0(0.001)	0.999(0.003)	0(0.002)	0(0.002)	0(0)
Dense alternative	π00 = 0.4	π10 = 0.2	π01 = 0.2	π11 = 0.2	π00 = 0.4	π10 = 0.2	π01 = 0.2	π11 = 0.2
n=250	0.502(0.019)	0.098(0.017)	0.301(0.017)	0.099(0.015)	0.501(0.011)	0.099(0.010)	0.301(0.011)	0.099(0.010)
n=1000	0.413(0.016)	0.187(0.015)	0.212(0.014)	0.188(0.013)	0.413(0.008)	0.187(0.007)	0.213(0.007)	0.187(0.007)
Sparse alternative	π00 = 0.88	π10 = 0.05	π01 = 0.05	π11 = 0.02	π00 = 0.88	π10 = 0.05	π01 = 0.05	π11 = 0.02
n=250	0.907(0.024)	0.023(0.016)	0.058(0.017)	0.013(0.01)	0.905(0.012)	0.024(0.009)	0.060(0.009)	0.010(0.006)
n=1000	0.883(0.023)	0.046(0.018)	0.051(0.018)	0.020(0.012)	0.883(0.012)	0.047(0.009)	0.051(0.009)	0.019(0.007)

Table 3 shows the empirical FWER of the proposed procedures (JS-mixture) when the targeted FWER is 0.05, using either the asymptotic mixture null distribution (Section 2.2) or the procedure using the finite-sample mixture null distribution (Section 2.4). The standard JS procedure using the uniform null distribution (JS-uniform) was presented as the benchmark. In the first (dense null) and the second null scenario (sparse null), when using the proposed procedures, the empirical FWERs based on 5,000 simulated datasets are much closer to 0.05 than the JS-uniform procedure. The latter is confirmed to be overly conservative. As anticipated, the proposed procedure based on the finite sample correction (Section 2.4) performs better than the procedure based on the asymptotic null distribution (Section 2.2), bringing the empirical FWER further toward 0.05. In the sparse null and complete null scenario, because of the dominance of H₀₀, the over conservativeness of JS-uniform is worsen when compared to the dense null scenario. On the contrary, the performance of the JS-mixture procedure is less affected by the proportion of H₀₀, although there is a trend that the observed FWER for the JS-mixture using the asymptotic null distribution gets more accurate when the proportion of H₀₀ increases to 1. This is because of the approximation that the two power functions approach to 1 has less impact when the proportions of H₀₁ and H₁₀ decrease to zero. When π₀₀ = 1, there is no difference between the two developments of JS-mixture when π₀₀ = 1, because of ${\widehat{\pi }}_{01}={\widehat{\pi }}_{10}=0$ nearly in every simulated dataset.

Table 3:

The empirical FWER of the procedures (the proposed procedure and JS-uniform) in 5000 simulated datasets when the target FWER is 0.05.

		J=5000	J=20000
Dense nulls	π01 = π10 = 0.2
n=250	JS-uniform	0.0042	0.0034
	JS-mixture (asymptotic null)	0.0222	0.0158
	JS-mixture (finite-sample null)	0.0282	0.0298
n=1000	JS-uniform	0.0112	0.0122
	JS-mixture (asymptotic null)	0.0274	0.0302
	JS-mixture (finite-sample null)	0.0504	0.0536
Sparse nulls	π01 = π10 = 0.05
n=250	JS-uniform	0.0008	0.0006
	JS-mixture (asymptotic null)	0.0384	0.0192
	JS-mixture (finite-sample null)	0.0456	0.0292
n=1000	JS-uniform	0.0032	0.0022
	JS-mixture (asymptotic null)	0.0320	0.0298
	JS-mixture (finite-sample null)	0.0628	0.0564
Complete nulls	π01 = π10 = 0
n=250	JS-uniform	0.0000	0.0000
	JS-mixture (asymptotic null)	0.0488	0.0424
	JS-mixture (finite-sample null)	0.0494	0.0434
n=1000	JS-uniform	0.0000	0.0000
	JS-mixture (asymptotic null)	0.0466	0.0448
	JS-mixture (finite-sample null)	0.0476	0.0466

In Supplementary Table 1, the performance of the p-value approximation method in Huang (2019) (referred to as “p-comp” hereafter) is compared in an array of simulation settings including the aforementioned three null scenarios. Notably, the p-comp method did not control the FWER at 0.05 under the first (dense null) and the second null scenario (sparse null), producing excessively high error rates. This is because the p-comp method is only applicable to scenarios with very sparse signals for both α and β. Neither of our dense null and sparse null scenarios meets the sparsity criteria required by Huang (2019), that is, the standard deviations of the z-scores for testing α and β have to be less than 1.5.

The appropriate control of the type I error rate is also demonstrated by the q-q plots in Figure 2 (dense null) and Figure 3 (sparse null) and Supplementary Figure 2 (complete null). Each panel is comparing q-q plots for the proposed JS-mixture procedure using the finite-sample mixture null distribution and for the JS-uniform procedure in one simulated dataset. The proposed procedure yielded q-q plots that are mostly aligned with the diagonal line, while JS-uniform resulted in q-q plots much lower than the diagonal line. In Supplementary Figure 3–5, we also show the q-q plots for the p-comp method in these three null scenarios. Consistent with the results in Supplementary Table 1, the p-comp method does not yield diagonal q-q plots for first two null scenarios.

Figure 2:

The q-q plots for p-max when the uniform null distribution and the mixture null distribution were used in the scenario with dense nulls. The underlying mixture null distribution is generated by π₀₁ = π₁₀ = 0.2, and π₀₀ = 0.6. (a) 250 subjects and 5,000 candidate mediators. (b) 250 subjects and 20,000 candidate mediators. (c) 1,000 subjects and 5,000 candidate mediators. (d) 1,000 subjects and 20,000 candidate mediators.

Figure 3:

The q-q plots for p-max when the uniform null distribution and the mixture null distribution were used in the scenario with sparse nulls. The underlying mixture null distribution is generated by π₀₁ = π₁₀ = 0.05, and π₀₀ = 0.9. (a) 250 subjects and 5,000 candidate mediators. (b) 250 subjects and 20,000 candidate mediators. (c) 1,000 subjects and 5,000 candidate mediators. (d) 1,000 subjects and 20,000 candidate mediators.

Figure 4 shows the true FDR and the estimated FDR using the proposed procedure with the finite-sample mixture null distribution when there are dense alternative hypotheses (Scenario 5, 20% H₁₁). The FDRs were evaluated in one simulated dataset for different sample sizes and different numbers of tests. In all 4 parameter settings shown in Figure 4, the true FDR is smaller than the estimated FDR across the full range of p_max cut-off values. When sample size increases, power increases and the estimated FDRs get closer to the true FDRs, as the bias of estimating the null proportions decreases with sample size. Varying the number of hypotheses in this set of simulations from 5,000 to 20,000 slightly improves the performance of the estimated FDRs.

Figure 4:

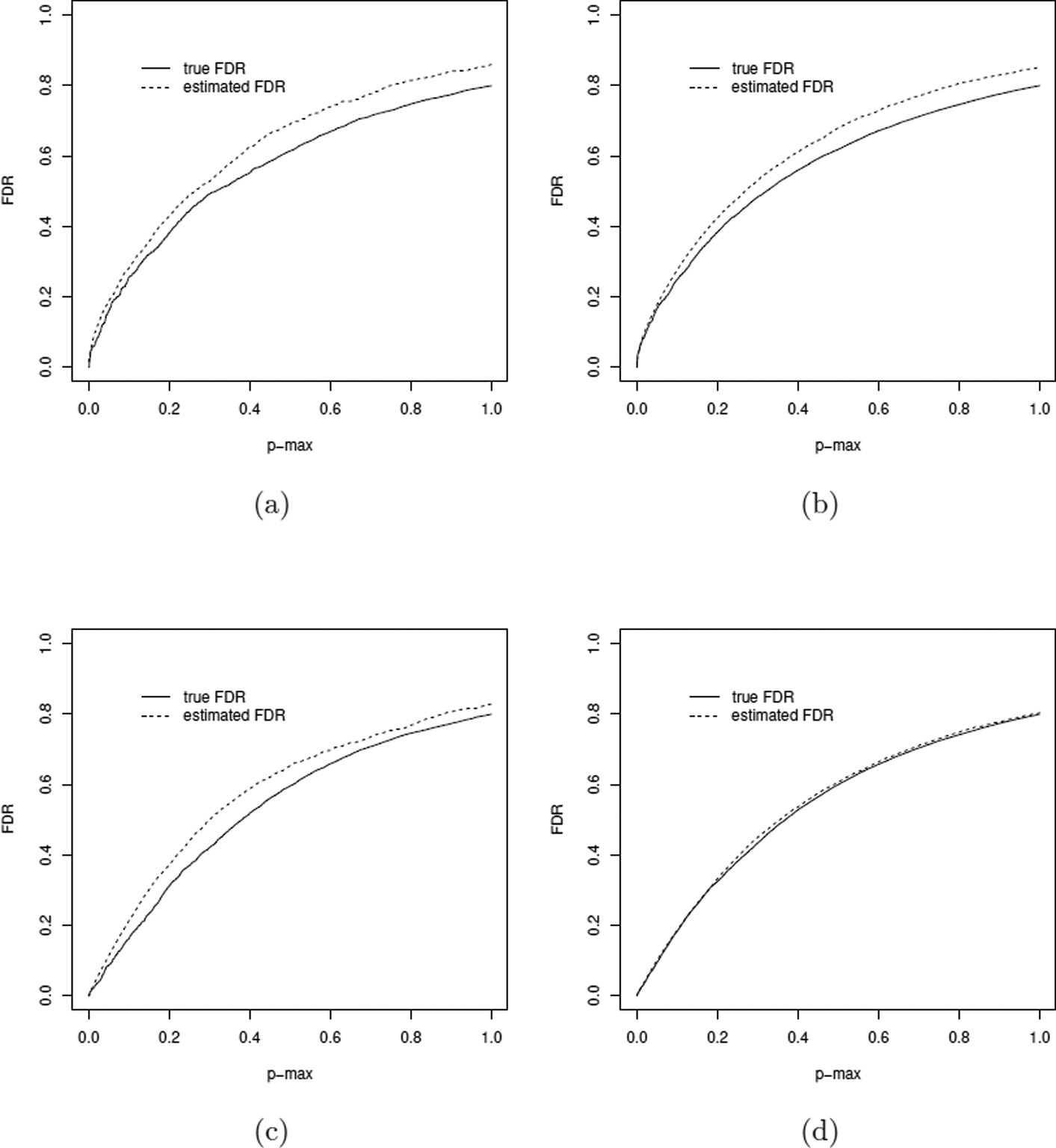
Controlling FDR with increasing p-value cut-off when there are dense alternative hypotheses. The underlying mixture distribution is generated by π₀₁ = π₁₀ = 0.2, π₀₀ = 0.4, π₁₁ = 0.2. The solid line is the true FDR and the dotted line is the estimated FDR using the proposed procedure with finite-sample mixture null distribution. (a) 250 subjects and 5,000 candidate mediators. (b) 250 subjects and 20,000 candidate mediators. (c) 1,000 subjects and 5,000 candidate mediators. (d) 1,000 subjects and 20,000 candidate mediators.

Figure 5 shows the power performance when the effect size of mediation increases (α_j increases from 0.1 to 0.5 and β_j increases from 0.15 to 0.75) under the fourth scenario (sparse alternative) and the fifth scenario (dense alternative). The sample size is set to be 1000 and the number of tests is set to 5000. The power was averaged over all markers under the alternative hypothesis H₁₁. Both FDR ≤ 0.05 and FWER ≤ 0.05 were examined as significance rules. Because the proposed procedure accounts for the finite-sample mixture null distribution, and is much less conservative than JS-uniform, the power gain can be as high as 20~40% when there is sparse alternative and when the majority of nulls are from H₀₀ (Figure 5b). Even when there are dense alternatives and a substantial proportion of nulls from H₀₁ and H₁₀, the power improvement of the proposed procedure is still clearly seen (Figure 5a).

Figure 5:

The average power curve when the mediation strength parameter τ increases, as α_j and β_j increase with τ. The sample size is 1,000 and the number of markers is 5,000. (a) Dense alternative where there are 20% H₁₁. (b) Sparse alternative when there are 2% H₁₁.

4. Data analysis

4.1. DNA methylation in genetic regulation of gene expression among 147 prostate cancer risk SNPs

Tremendous progress has been made by genome-wide association studies (GWAS) to identify genetic loci predisposing to prostate cancer. The most recent and the largest GWAS assembled 79,194 cases and 61,112 controls of European ancestry from 59 studies, and identified 62 novel loci associated with the overall prostate cancer risk(Schumacher et al., 2018). The polygenic risk score using the more commonly occurring 147 prostate cancer risk SNPs (minor allele frequency greater than 1%) captured 28.8% of the familial relative risk(Schumacher et al., 2018). Despite the remarkable progress in identifying prostate cancer risk SNPs, functional interpretation of these risk SNPs presents a huge challenge.

A common strategy to interpret functional activities of GWAS-identified risk SNPs is to investigate whether they affect gene expression. Such genetic determinants mostly influence genes in nearby genomic region, loosely defined as cis-eQTLs(Albert and Kruglyak, 2015; GTEx Consortium, 2018). Relatedly, SNPs have also been shown to contribute to variations of DNA methylation in several tissue types including blood, brain, and adipose tissue and are referred to as meQTL (Banovich et al., 2014; Smith et al., 2014). We have shown recently that the majority of 147 prostate cancer risk SNPs are either eQTL or meQTL. In this analysis, we perform a mediation analysis for 147 prostate cancer risk SNPs using DNA methylation and gene expression data from a large set of primary prostate tumor samples in TCGA (n=495). The details of TCGA study participants and data processing have been described previously(The Cancer Genome Atlas Research Network, 2015). Our goal is to test whether CpG methylation mediates genetic regulation of gene expression for these prostate cancer risk SNPs. For each risk SNPs, CpG methylation probes within 500 kb distance were first identified, and then the expressions of the corresponding genes associated with the CpG methylation probes, resulting in a total of 69,602 triplets for mediation testing.

Two sets of p-values were first computed. The association of prostate cancer risk SNPs with CpG methylation within 500 kb distance (loosely defined as cis-meQTLs), as in (1) of the mediation analysis, were assessed in the linear model regressing CpG methylation on the SNP, top 3 principal components of genotypes, top 15 principal components of CpG methylation data, age at diagnosis, and pathologic stage. The histogram of p-values for SNP-methylation associations is shown in Figure 6(a). The estimated proportion of null hypotheses H₀₊ is 0.93, confirming that some risk SNPs can influence local DNA methylation levels.

Figure 6:

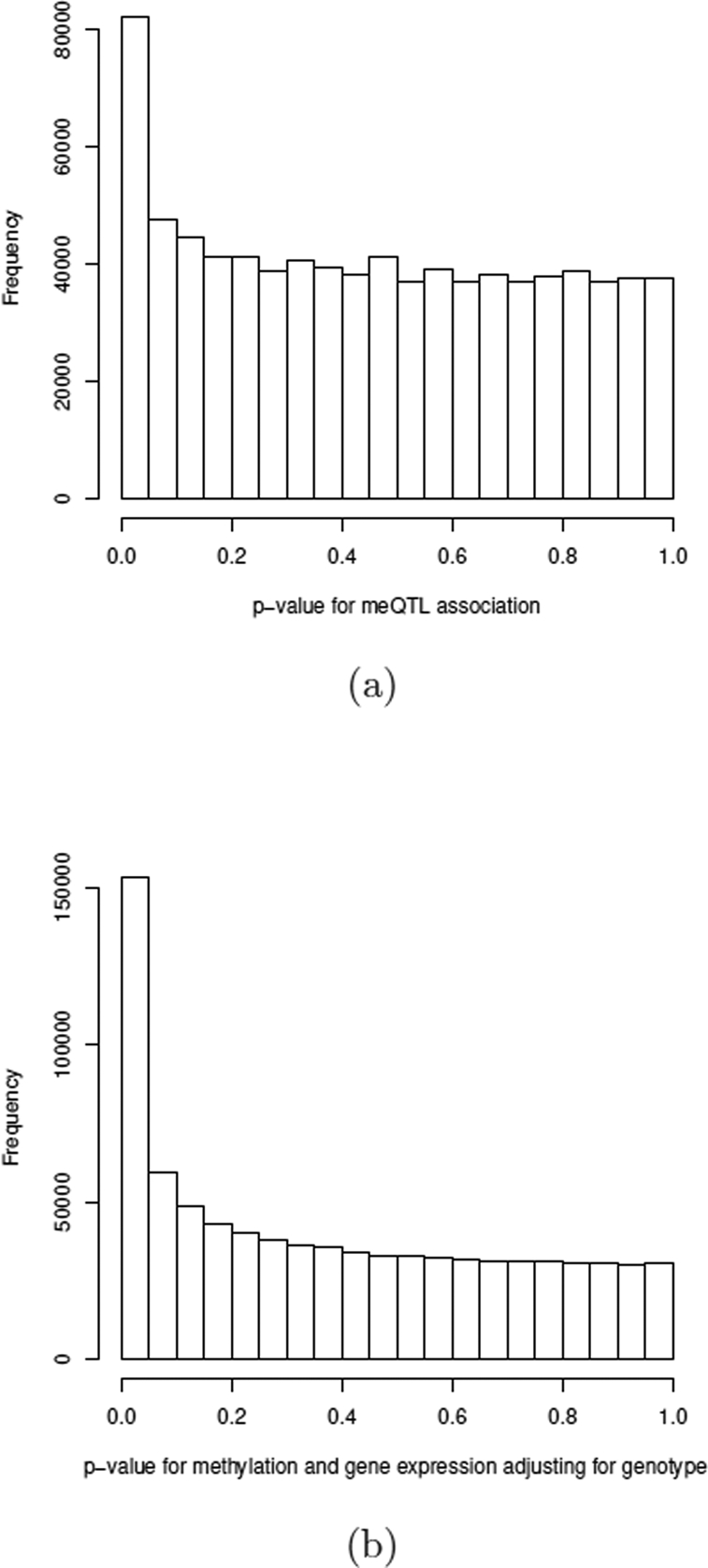
Characteristics of the two sets of p-values in testing mediation of CpG methylation in genetic regulation of gene expression. (a) Histogram of p-values for testing meQTL association with CpG methylation. (b) Histogram of p-values for testing CpG association with gene expression adjusting for genotype.

The association of CpG methylation and gene expression (measured by RNA-seq) conditional on the genotype, as in (2) of the mediation analysis, was assessed for each pair of gene expression and CpG methylation in the gene. All analyses were adjusted for the same set of covariates. The histogram of p-values for adjusted methylation-gene expression associations is shown in Figure 6(b). The estimated proportion of null hypotheses H₊₀ is 0.55, reinforcing that DNA methylation is a major determinant of gene expression.

We applied the JS-mixture procedure and obtained the null proportions ${\widehat{\pi }}_{00}=0.52$, ${\widehat{\pi }}_{10}=0.03$, and ${\widehat{\pi }}_{01}=0.42$. Figure 7 shows the q-q plots for p_max, using either the mixture null distribution or the uniform null distribution. Interestingly, the lower part of the q-q line when using the uniform null distribution does not exhibit much deviation from the diagonal line, likely because there are a substantial proportion of hypotheses in H₀₁ and H₁₀, under which the distribution of p_max is still close to a uniform distribution. The over-conservativeness is driven by the proportion of H₀₀. Nonetheless, at the FWER level 0.05 (the p_max cut-off 8.19×10⁻⁶, 81 triplets show evidence of mediation by the JS-mixture procedure, while a naïve Bonferroni correction to p_max using the uniform null distribution yields only 57 significant triplets, representing 42% more discoveries and showcasing the power advantage of the proposed JS-mixture procedure. Similarly, when using FDR 0.05 as a significance rule, the JS-mixture procedure yielded 241 significant triplets, while the naïve FDR procedure resulted in 123 significant triplets, representing nearly ~50% more discoveries.

Figure 7:

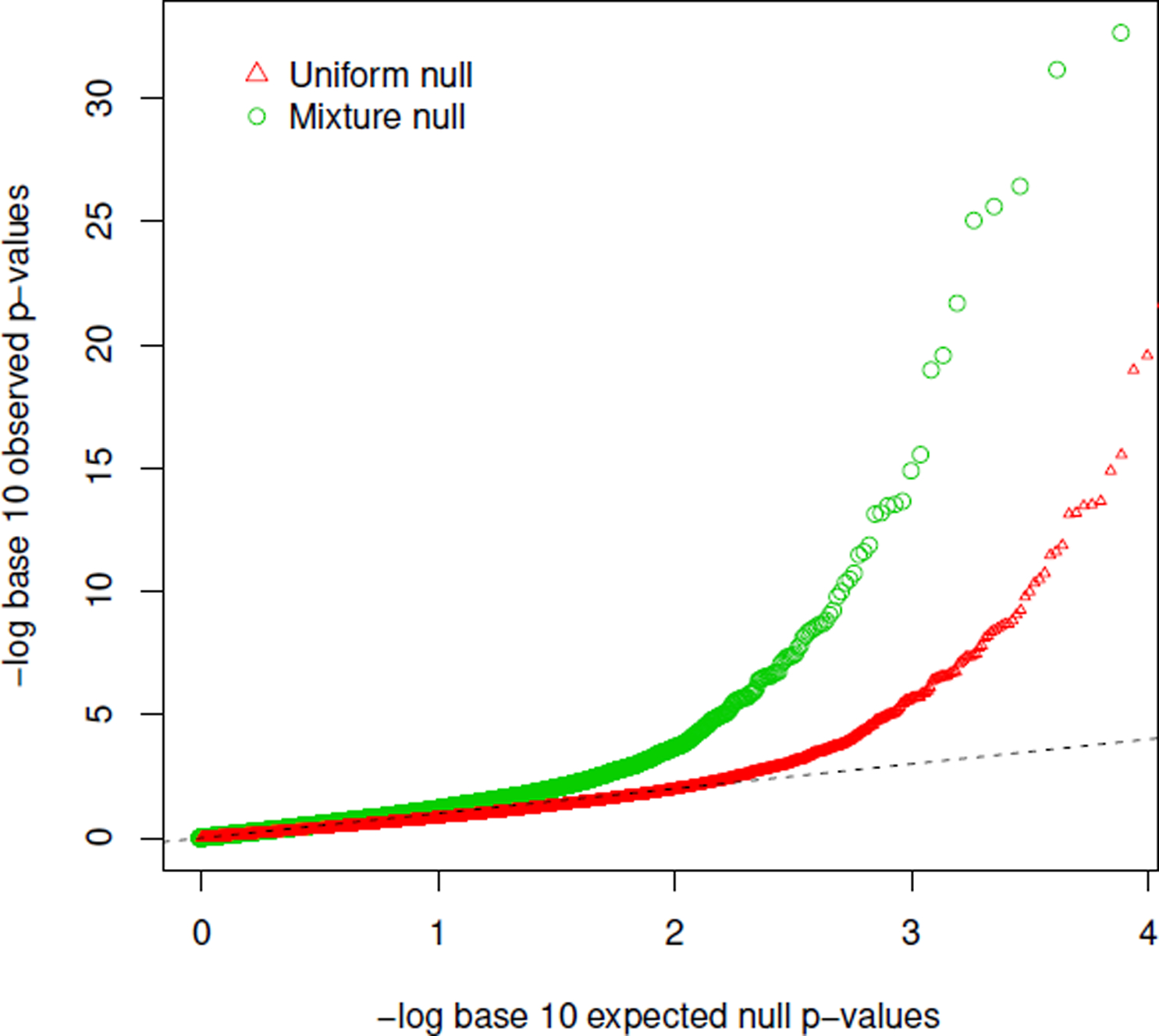
Comparison of q-q plots for p_max using the mixture null distribution and the uniform null distribution.

Table 4 shows the top ten triplets (SNP-CpG-Gene) ranked by p_max. All three SNPs involved in these triplets have been shown previously to be associated with respective genes. The contribution of our analysis is identification of CpG sites that may mediate genetic regulation of gene expression in each case. Among the top ten findings, eight triplets involve rs12653946, a SNP that is located in the upstream sequence of IRX4 and a known eQTL regulating gene expression of IRX4(Nguyen et al., 2012; Xu et al., 2014). This gene is a putative tumor suppressor gene that has been studied in prostate cancer cell lines(Nguyen et al., 2012). These CpG sites in Table 4 are located in a CpG island close to the transcription starting site. The CpG methylation levels are strongly associated with rs12653946 (p₁) and gene expression (p₂, adjusted for the genotype), and the estimated FDR for mediation using the proposed procedure is as small as 8.5e–31. The second triplet is rs5945619-cg16065628-NUDT11. This SNP has been reported to be eQTL for NUDT11, which is a diphosphoinositol polyphosphate phosphohydrolase involved in a variety of biologic functions, including vesicle trafficking, maintenance of cell wall integrity, and has been linked to prostate cancer previously(Grisanzio et al., 2012). Finally, the ninth triplet is related to RGS17, an overexpressed gene in human prostate cancer, which induces tumor cell proliferation through the cyclic AMP-PKA-CREB pathway(James et al., 2009).

Table 4:

Top 10 triplets (SNP-CpG-Gene) ranked by p_max and $\widetilde{\text{FDR}}$ for testing mediation.

SNP	CpG	Gene	Chr	p 1	p 2	p max	$\widetilde{\text{FDR}}$
rs12653946	cg09672187	IRX4	5	4.01e-65	2.13e-33	2.13e-33	8.50e-31
rs5945619	cg16065628	NUDT11	X	6.75e-32	2.79e-42	6.75e-32	1.49e-29
rs12653946	cg11279838	IRX 4	5	3.97e-64	3.61e-27	3.62e-27	7.10e-25
rs12653946	cg26195178	IRX4	5	2.52e-61	2.43e-26	2.43e-26	3.87e-24
rs12653946	cg14051264	IRX4	5	7.62e-67	8.86e-26	8.86e-26	1.16e-23
rs12653946	cg06161964	IRX4	5	1.99e-53	2.02e-22	2.02e-22	2.94e-20
rs12653946	cg00626856	IRX4	5	6.60e-56	2.66e-20	2.66e-20	3.91e-18
rs12653946	cg03587843	IRX4	5	1.95e-51	1.03e-19	1.03e-19	1.40e-17
rs1933488	cg23651356	RGS17	6	7.25e-20	2.81e-16	2.81e-16	4.52e-14
rs12653946	cg14823763	IRX4	5	8.13e-47	1.27e-15	1.27e-15	1.97e-13

4.2. DNA methylation and the association of vigorous physical activity with lower risk of metastatic progression

In a Seattle-based cohort of patients diagnosed with clinically localized prostate cancer (n=1354), we investigated the association between self-reported vigorous physical activity and prostate cancer progression to a metastatic-lethal phenotype. After adjusting extensively for covariates, patients who had vigorous physical activity at least once per week during the year before diagnosis were significantly less likely to progress to metastatic-lethal prostate cancer compared to those who had vigorous physical activity less frequently (hazard ratio 0.63, p-value=0.029). A subset of patients had prostate cancer tissue samples available for investigating DNA methylation (Infinium®HumanMethylation450 BeadChip array) and exercise (n=524). In this subset, the potential mediation of CpG methylation in the effect of physical activity on cancer progression is assessed using the proposed JS-mixture procedure.

Supplementary Figure 6 shows the histogram of p-values for the association of physical activity and half a million CpG sites on the HumanMethylation450 BeadChip array, suggesting there is little evidence of association between DNA methylation and physical activity after correcting for multiple-testing. Consistently, the estimated π₀₊ = 1. On the other hand, there are substantial CpG sites associated with cancer progression after adjusting for physical activity, as shown in Supplementary Figure 6(b). The estimated π₊₀ = 0.8. The three null proportions were estimated to be ${\widehat{\pi }}_{00}=0.8$, ${\widehat{\pi }}_{10}=0$ and ${\widehat{\pi }}_{01}=0.2$. The q-q plots for p_max under the uniform null and under the mixture null are shown in Figure 1, demonstrating that the proposed JS-mixture procedure is able to correct the over-conservativeness of the JS-uniform procedure. Though no mediation signal was identified, this pedagogical data example shows the utility of the proposed JS-mixture procedure in ultra-high dimensional mediation testing.

5. Discussion

We presented a novel multiple-testing procedure that addresses the over-conservativeness issue of the JS-uniform procedure that is widely used for testing high-dimensional mediation hypotheses. The proposed procedure, referred to as JS-mixture, estimates the proportions of three types of component null hypotheses and derives the FWER or FDR significance rule. With the theoretical proof and extensive simulation experiments and two data examples, we demonstrated that the proposed JS-mixture procedure is robust, broadly applicable to sparse and dense alternatives, and delivers much more satisfactory control of FWER and FDR than the JS-uniform procedure. The contributions of our work also include the R package HDMT, which implements the proposed procedure in a user-friendly fashion, and is freely accessible in CRAN to the statistical and epidemiologic research community. With increasing interest in causal mediation by molecular intermediaries such as gene expressions and epigenetics, the proposed method addresses an unmet methodological challenge. It is noteworthy that the proposed method is designed for, but not limited to, high-dimensional mediation hypotheses. It works for controlling type I errors of high-dimensional intersection-union tests that use the maximum of two independent p-values.

The main innovation of the proposed procedure is estimating the three-component mixture null distribution for multiple-testing adjustment. We adapted an existing procedure for estimating the proportion of null hypotheses, noting that these estimates are likely biased in finite samples. However, we proved that when the number of hypotheses is large, the significance rules developed based on the large-sample mixture null distribution in Section 2.2 and 2.3 provide valid control of FDR and FWER. The performance of this simple procedure is generally satisfactory for moderate to high-dimensional settings, for example, approximately 20,000 genes in a genome-wide gene expression study. We note that the accuracy of error control diminishes when there are a large portion of hypotheses from either H₀₁ or H₁₀ or both, yet the corresponding α_js and β_js have small effect sizes. This is exemplified by our data example (Supplementary Figure 1). For the latter scenario, the significance rule can be significantly improved using the finite-sample correction we developed in Section 2.4. One potential future work is to investigate whether parametric likelihood-based approaches for modeling the two-dimensional p-values will yield even more precise estimates, further improving the performance of the proposed procedure in small-to-moderate sample sizes. For example, a beta distribution can be used to model the distribution of p-values under alternative hypotheses.

The data examples we presented are pedagogical, illustrating the utilities of the proposed method. In both applications, the weak dependence condition in Theorem 1 and 2 holds because spatial correlation of CpG probes decays over chromosomal distance. The first example examined the mediation of genetic regulation of gene expression by DNA methylation among 147 established prostate cancer risk SNPs. While there are a significant number of triplets with evidence of mediation, we cannot rule out the possibility of reverse causation: because gene expression and DNA methylation were measured at the same time, DNA methylation could be a downstream event of active gene expression, reflecting the chromosomal state of active transcription. The classical mediation testing method using the JS procedure cannot distinguish causation from reverse causation. Therefore care needs to be exercised in interpreting these findings. The second example assessed the role of DNA methylation in mediating the effect of physical activity on prostate cancer metastatic progression. Though the q-q plot in Figure 1 demonstrates the validity the accuracy of the proposed procedure, the goal to discover any mediator is somewhat doomed by the low power to detect association among half a million CpG methylation sites and physical activity (Supplementary Figure 6b).

We anticipate an important area of application of our new method for assessing mediation is in cancer clinical trials testing new immunotherapy related treatments (e.g. PD-1/PD-L1 and CTLA-4 therapies, T-cell therapy, and cancer vaccines). Concurrently, new immuno-oncology assays are increasingly high-throughput and can be used to assess a large number of RNA transcripts simultaneously from patient samples after initiation of treatment. Assessment of these mediating factors, especially if conducted in multiple clinically defined subgroups, involves a high-dimensional strategy and may be a powerful tool for understanding the activity of existing immunotherapy treatments as well as developing new treatments. One example of high-throughput technologies for assessing candidate mediators is HTG EdgeSeq Immuno-Oncology assay (www.htgmolecular.com).

Appendix

A1: Proof Theorem 1: control of FWER by the proposed JS-mixture procedure

We first examine the asymptotic behavior of ${\widehat{\pi }}_{00}$, ${\widehat{\pi }}_{10}$, and ${\widehat{\pi }}_{10}$ when J → ∞. Denote by ${\pi }_{l{l}^{\prime }}^{*}$ the limits of the estimated fractions of the four component hypotheses, ll′ ∈ (00, 01, 10, 11). Because of the independence between p_1j and p_2j for the j^th hypothesis, and because of the uniform distribution for p_1j and p_2j under their respective null hypotheses, we obtain

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{00}\equiv {\pi }_{00}^{*}={\pi }_{00}+{\pi }_{01}\frac{G_{01}(\lambda )}{(1-\lambda )}+{\pi }_{10}\frac{G_{10}(\lambda )}{(1-\lambda )}+{\pi }_{11}\frac{G_{11}(\lambda )}{{(1-\lambda )}^2}, \\ \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{0+}\equiv {\pi }_{0+}^{*}={\pi }_{0+}+{\pi }_{10}\frac{G_{10}(\lambda )}{(1-\lambda )}+{\pi }_{11}\frac{G_{11,p_1}(\lambda )}{(1-\lambda )}, \\ \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{+0}\equiv {\pi }_{+0}^{*}={\pi }_{+0}+{\pi }_{01}\frac{G_{01}(\lambda )}{(1-\lambda )}+{\pi }_{11}\frac{G_{11,p_2}(\lambda )}{(1-\lambda )}, \\ \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{01}\equiv {\pi }_{01}^{*}={\pi }_{01}-{\pi }_{01}\frac{G_{01}(\lambda )}{(1-\lambda )}+\frac{{\pi }_{11}}{(1-\lambda )}\left\{G_{11,p_1}(\lambda )-\frac{G_{11}(\lambda )}{1-\lambda }\right\}, \end{gathered}$$ (19)

$$\underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{10}\equiv {\pi }_{10}^{*}={\pi }_{10}-{\pi }_{10}\frac{G_{10}(\lambda )}{(1-\lambda )}+\frac{{\pi }_{11}}{(1-\lambda )}\left\{G_{11,p_2}(\lambda )-\frac{G_{11}(\lambda )}{1-\lambda }\right\}.$$ (20)

Suppose ${\widehat{t}}_a$ is the p-value threshold applied to each of J tests to control the FWER at level a, which is determined by solving the quadratic equation ${\widehat{\pi }}_{01}{t}_a+{\widehat{\pi }}_{10}{t}_a+{\widehat{\pi }}_{00}{t}_a^2=\frac{a}{J}$. Let $t_a^{*}$ be the solution of the corresponding quadratic equation when ${\widehat{\pi }}_{01}$, ${\widehat{\pi }}_{10}$ and ${\widehat{\pi }}_{00}$ are replaced by their limits, namely ${\pi }_{01}^{*}{t}_a+{\pi }_{10}^{*}{t}_a+{\pi }_{00}^{*}{t}_a^2=\frac{a}{J}$. It follows that ${\text{lim}}_{J\to \infty }\left({\widehat{t}}_a-t_a^{*}\right)=0$.

When applying the estimated significance rule ${\widehat{t}}_a$ to all J mediation tests, the limit of the FWER when J goes to infinity can be examined as follows:

$$\begin{gathered} \underset{J\to \infty }{\text{lim}\text{sup}}\left\{\text{FWER}\left({\widehat{t}}_a\right)-a\right\} \\ =\underset{J\to \infty }{\text{lim}\text{sup}}\mathrm{Pr}\left\{\left(V_{00}\left({\widehat{t}}_a\right)+V_{01}\left({\widehat{t}}_a\right)+V_{10}\left({\widehat{t}}_a\right)\right)\ge 1\right\}-a \\ =\underset{J\to \infty }{\text{lim}\text{sup}}\mathrm{Pr}\left\{\left(\sum _{{\text{H}}_j\in \left\{{\text{H}}_{00},{\text{H}}_{01},{\text{H}}_{10}\right\}}I\left(p_{1j}\le {\widehat{t}}_a,p_{2j}\le {\widehat{t}}_a\right)\right)\ge 1\right\}-a \\ \le \underset{J\to \infty }{\text{lim}\text{sup}}\sum _{l{l}^{\prime }\in \{00,10,10\}}\mathrm{Pr}\left\{\left(\sum _{{\text{H}}_{j\in \left\{{\text{H}}_u\text{'}\right\}}}I\left(p_{1j}\le {\widehat{t}}_a\right)I\left(p_{2j}\le {\widehat{t}}_a\right)\right)\right\}-a \\ =\underset{J\to \infty }{\text{lim}\text{sup}}\left[J\left\{{\pi }_{00}{t}_a^{*2}+{\pi }_{01}{t}_a^{*}\left(1-G_{01}\left(t_a^{*}\right)\right)+{\pi }_{10}{t}_a^{*}\left(1-G_{10}\left(t_a^{*}\right)\right)\right\}-J\left({\pi }_{01}^{*}{t}_a^{*}+{\pi }_{10}^{*}{t}_a^{*}+{\pi }_{00}^{*}{t}_a^{*2}\right)\right] \\ =\underset{J\to \infty }{\text{lim}\text{sup}}\left(J{\pi }_{00}{t}_a^{*2}-J{\pi }_{00}^{*}{t}_a^{*2}\right) \end{gathered}$$ (21)

$$+\underset{J\to \infty }{\text{lim}\text{sup}}\left\{J{\pi }_{01}{t}_a^{*}\left(1-G_{01}\left(t_a^{*}\right)\right)-J{\pi }_{01}^{*}{t}_a^{*}\right\}$$ (22)

$$+\underset{I\to \infty }{\text{lim}\text{sup}}\left\{J{\pi }_{10}{t}_a^{*}\left(1-G_{10}\left(t_a^{*}\right)\right)-J{\pi }_{10}^{*}{t}_a^{*}\right\}$$ (23)

We show next that all three terms (21–23) are less than or equal to 0. Based on the expression for the limit ${\pi }_{01}^{*}$ in (19), we have

$${\pi }_{01}=\frac{{\pi }_{01}^{*}-\frac{{\pi }_{11}}{(1-\lambda )}\left\{G_{11,p_1}(\lambda )-\frac{G_{11}(\lambda )}{1-\lambda }\right\}}{1-\frac{G_{01}(\lambda )}{(1-\lambda )}}$$

Using this expression of π₀₁, for any given J we have

$$\begin{gathered} J{\pi }_{01}{t}_a^{*}\left(1-G_{01}\left(t_a^{*}\right)\right) \\ =J\left[{\pi }_{01}^{*}-\frac{{\pi }_{11}}{(1-\lambda )}\left\{G_{11,p_1}(\lambda )-\frac{G_{11}(\lambda )}{1-\lambda }\right\}\right]\frac{1-G_{01}\left(t_a^{*}\right)}{1-\frac{G_{01}(\lambda )}{(1-\lambda )}}{t}_a^{*} \\ \le J{\pi }_{01}^{*}{t}_a^{*}. \end{gathered}$$

Derivation of the above inequality uses the following observations: first, $G_{11,p_1}(\lambda )>\frac{G_{11}(\lambda )}{1-\lambda }$ because Pr(p_2j > λ|H₁₁) < 1 − λ, since p-values under alternative hypothesis is stochastically less than the uniform distribution; second, $G_{01}\left(t_a^{*}\right)>G_{01}(\lambda )/(1-\lambda )$. The latter is true because for a typical level a of interest, for example 0.05, $t_a^{*}$ has to be very small when there are a large number of hypotheses, and therefore should be much smaller than λ, the tuning parameter typically chosen to be between 0.5 and 1. This proves that (22) is less than 0. Note the equality holds when π₀₁ = π₁₀ = π₁₁ = 0.

Similarly, based on the expression for the limit ${\pi }_{10}^{*}$ in (20), we have

$${\pi }_{10}=\frac{{\pi }_{10}^{*}-\frac{{\pi }_{11}}{(1-\lambda )}\left\{G_{11,p_2}(\lambda )-\frac{G_{11}(\lambda )}{1-\lambda }\right\}}{1-\frac{G_{10}(\lambda )}{(1-\lambda )}}.$$

It follows that (23) is less than or equal to 0, because for any given J,

$$\begin{gathered} J{\pi }_{10}{t}_a^{*}\left(1-G_{10}\left(t_a^{*}\right)\right) \\ =J\left[{\pi }_{10}^{*}-\frac{{\pi }_{11}}{(1-\lambda )}\left\{G_{11,p2}(\lambda )-\frac{G_{11}(\lambda )}{1-\lambda }\right\}\right]\frac{1-G_{10}\left(t_a^{*}\right)}{1-\frac{G_{10}(\lambda )}{(1-\lambda )}}{t}_a^{*} \\ \le J{\pi }_{10}^{*}{t}_a^{*}. \end{gathered}$$

Finally, (21) is less than or equal to 0 because

$$\begin{gathered} J{\pi }_{00}{t}_a^{*2} \\ =J\left({\pi }_{00}^{*}-{\pi }_{01}\frac{G_{01}(\lambda )}{(1-\lambda )}-{\pi }_{10}\frac{G_{10}(\lambda )}{(1-\lambda )}-{\pi }_{11}\frac{G_{11}(\lambda )}{{(1-\lambda )}^2}\right)t_a^{*2} \\ \le J{\pi }_{00}^{*}{t}_a^{*2} \end{gathered}$$

Therefore combining (21)–(23), it follows that

$$\underset{J\to \infty }{\text{lim}\text{sup}}\left\{\text{FWER}\left({\widehat{t}}_a\right)-a\right\}\le 0,$$

i.e., when applying the significance cut-off $t_a^{*}$ FWER is controlled at level a when J → ∞.

A2: Proof of Theorem 2: control of FDR by the proposed JS-mixture procedure

Assuming p_1j and p_2j are independent, each of which under their respective null hypotheses takes the uniform distribution between 0 and 1. By the Glivenco-Cantelli theorem,

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}{\text{sup}}_{0\le t\le 1}\left|\frac{V_{10}(t)}{J}-{\pi }_{10}t\left(1-G_{10}(t)\right)\right|=0 \\ \underset{J\to \infty }{\text{lim}}{\text{sup}}_{0\le t\le 1}\left|\frac{V_{01}(t)}{J}-{\pi }_{01}t\left(1-G_{01}(t)\right)\right|=0 \\ \underset{J\to \infty }{\text{lim}}{\text{sup}}_{0\le t\le 1}\left|\frac{V_{00}(t)}{J}-{\pi }_{00}{t}^2\right|=0 \end{gathered}$$

Following the same derivation as in A1, let $c_1=G_{01}^{-1}\left\{G_{01}(\lambda )/(1-\lambda )\right\}$, $c_1=G_{10}^{-1}\left\{(\lambda )/(1-\lambda )\right\}$, and c = c₁ ∧ c₂. For any δ > 0 and δ ≤ t ≤ c,

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{01}t\equiv {\pi }_{01}^{*}t\ge {\pi }_{01}t\left(1-G_{01}(t)\right), \\ \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{10}t\equiv {\pi }_{10}^{*}t\ge {\pi }_{10}t\left(1-G_{10}(t)\right), \\ \underset{J\to \infty }{\text{lim}}{\widehat{\pi }}_{00}{t}^2\equiv {\pi }_{00}^{*}{t}^2\ge {\pi }_{00}{t}^2. \end{gathered}$$

Summation of the three terms above yields

$$\underset{J\to \infty }{\text{lim}}{\text{inf}}_{\delta \le t\le c}\left\{\frac{{\widehat{\pi }}_{01}t+{\widehat{\pi }}_{10}t+{\widehat{\pi }}_{00}{t}^2}{\left\{R(t)\vee 1\right\}/J}-\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{\left\{R(t)\vee 1\right\}/J}\right\}\ge 0.$$ (24)

Observe that

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}{\text{sup}}_{\delta \le t\le c}\left|\frac{V_{01}(t)+V_{10}(t)+V_{00}(t)}{R(t)\vee 1}-\frac{J\left\{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2\right\}}{R(t)\vee 1}\right| \\ \le \underset{J\to \infty }{\text{lim}}\left|\frac{J}{R(\delta )\vee 1}\right|{\text{sup}}_{\delta \le t\le c}\left|\frac{V_{01}(t)+V_{10}(t)+V_{00}(t)}{J}-\left\{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2\right\}\right| \\ =0. \end{gathered}$$ (25)

Therefore

$$\underset{J\to \infty }{\text{lim}}{\inf }_{\delta \le t\le c}\left\{\frac{{\widehat{\pi }}_{01}t+{\widehat{\pi }}_{10}t+{\widehat{\pi }}_{00}{t}^2}{\left\{R(t)\vee 1\right\}/J}-\frac{V_{01}(t)+V_{10}(t)+V_{00}(t)}{R(t)\vee 1}\right\}\ge 0,$$ (26)

i.e., $\underset{J\to \infty }{\text{lim}}{\inf }_{\delta \le t\le c}\left\{{\widehat{\text{FDR}}}_{\lambda }(t)-\frac{V_{01}(t)+V_{10}(t)+V_{00}(t)}{R(t)\vee 1}\right\}\ge 0.$

Because

$$\underset{J\to \infty }{\text{lim}}{\text{sup}}_{0\le t\le 1}|\frac{R(t)\vee 1}{J}-\left\{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2+{\pi }_{11}\left(1-G_{11}(t)\right)\right\}|=0,$$

we have

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}{\text{sup}}_{0\le t\le 1}|\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{(R(t)\vee 1)/J} \\ -\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2+{\pi }_{11}\left(1-G_{11}(t)\right)}|=0. \end{gathered}$$ (27)

Apply the triangle inequality to (25) and (27), we obtain

$$\begin{gathered} \underset{J\to \infty }{\text{lim}}{\text{sup}}_{\delta \le t\le c}|\frac{V_{01}(t)+V_{10}(t)+V_{00}(t)}{R(t)\vee 1} \\ -\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2+{\pi }_{11}\left(1-G_{11}(t)\right)}|=0 \end{gathered}$$ (28)

It follows that

$$\begin{gathered} 0=\mathbb{E}[\underset{J\to \infty }{\text{lim}}{\text{sup}}_{\delta \le t\le c}|\frac{V_{10}(t)+V_{01}(t)+V_{00}(t)}{R(t)\vee 1} \\ -\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2+{\pi }_{11}\left(1-G_{11}(t)\right)}|] \\ \ge \underset{J\to \infty }{\text{lim}}{\text{sup}}_{\delta \le t\le c}|\mathbb{E}\left[\frac{V_{10}(t)+V_{01}(t)+V_{00}(t)}{R(t)\vee 1}\right] \\ -\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2+{\pi }_{11}\left(1-G_{11}(t)\right)}|. \end{gathered}$$

This leads to

$$\underset{J\to \infty }{\text{lim}}{\text{sup}}_{\delta \le t\le c}\left|\text{FDR}(t)-\frac{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2}{{\pi }_{10}t\left(1-G_{10}(t)\right)+{\pi }_{01}t\left(1-G_{01}(t)\right)+{\pi }_{00}{t}^2+{\pi }_{11}\left(1-G_{11}(t)\right)}\right|=0.$$ (29)

Apply the triangle inequality theorem to (28) and (29), we have

$$\underset{J\to \infty }{\text{lim}}{\text{sup}}_{\delta \le t\le c}\left|\frac{V_{01}(t)+V_{10}(t)+V_{00}(t)}{R(t)\vee 1}-\text{FDR}(t)\right|=0.$$

Combining this result with (26), we conclude that

$$\underset{J\to \infty }{\text{lim}}{\inf }_{\delta \le t\le c}\left\{{\widehat{\text{FDR}}}_{\lambda }(t)-\text{FDR}(t)\right\}\ge 0.$$

Suppose ${\widehat{t}}_b=\text{sup}\left\{t:{\widehat{\text{FDR}}}_{\lambda }(t)\le b\right\}$. For a typical level b of interest for FDR, e.g., 0.05, ${\widehat{t}}_b$ will be on the left end of the p-value distribution, likely very close to 0 and less than c. Therefore based on (26) we have

$$\underset{J\to \infty }{\text{lim}\inf }\left\{{\widehat{\text{FDR}}}_{\lambda }\left({\widehat{t}}_b\right)-\frac{V_{01}\left({\widehat{t}}_b\right)+V_{10}\left({\widehat{t}}_b\right)+V_{00}\left({\widehat{t}}_b\right)}{R\left({\widehat{t}}_b\right)\vee 1}\right\}\ge 0.$$

Since ${\widehat{\text{FDR}}}_{\lambda }\left({\widehat{t}}_b\right)\le b$, it follows that

$$\underset{J\to \infty }{\text{limsup}}\left\{\frac{V_{01}\left({\widehat{t}}_b\right)+V_{10}\left({\widehat{t}}_b\right)+V_{00}\left({\widehat{t}}_b\right)}{R\left({\widehat{t}}_b\right)\vee 1}\right\}\le b.$$

By Fatou’s lemma,

$$\underset{J\to \infty }{\text{lim}\text{sup}}\left[\mathbb{E}\left\{\frac{V_{01}\left({\widehat{t}}_b\right)+V_{10}\left({\widehat{t}}_b\right)+V_{00}\left({\widehat{t}}_b\right)}{R\left({\widehat{t}}_b\right)\vee 1}\right\}\right]\le \mathbb{E}\left[\underset{J\to \infty }{\text{lim}\text{sup}}\left\{\frac{V_{01}\left({\widehat{t}}_b\right)+V_{10}\left({\widehat{t}}_b\right)+V_{00}\left({\widehat{t}}_b\right)}{R\left({\widehat{t}}_b\right)\vee 1}\right\}\right]\le b,$$

and so $\underset{J\to \infty }{\text{lim}\text{sup}}\text{FDR}\left({\widehat{t}}_b\right)\le b$.

A3: Grenander estimator of the density for p_2j under H₀₁ and p_1j under H₁₀

We show the Grenander estimator of the density for p_2j under H₀₁, denoted by ${\widehat{f}}_j\left(p_{2j}|{\text{H}}_{01}\right)$. The estimator ${\widehat{f}}_j\left(p_{1j}|{\text{H}}_{10}\right)$ can be similarly derived. The observed set of J p_2js is a mixture of p-values from four types of unobservable hypotheses: H₀₁, H₁₀, H₁₁ and H₀₀. First, we remove the set of p_2j that are likely from H₁₁, defined as FDR for testing α_j and FDR for testing β_j are both less than or equal to 0.2. The FDR cut-off is set to be 0.2 to be conservative, removing any candidate mediator with some evidence of mediation. Second, among the rest set of p_2j, we apply the grenander estimator of the decreasing density in [0,1]. See Section 4.1 of Langaas et al. (2005) for the expression of the grenander estimator for the density at p_2j, denoted by ${\widehat{f}}_j\left(p_{2j}\right)$. Because this subset of p_2js are restricted to a mixture distribution composed of H₀₁, H₁₀, and H₀₀, and the distribution of p_2j under H₁₀ and H₀₀ is uniform,

$${\widehat{f}}_j\left(p_{2j}\right)=\frac{{\widehat{\pi }}_{10}}{{\widehat{\pi }}_{10}+{\widehat{\pi }}_{01}+{\widehat{\pi }}_{00}}{\widehat{f}}_j\left(p_{2j}|{\text{H}}_{01}\right)+\frac{{\widehat{\pi }}_{00}+{\widehat{\pi }}_{01}}{{\widehat{\pi }}_{10}+{\widehat{\pi }}_{01}+{\widehat{\pi }}_{00}}$$

where ${\widehat{\pi }}_{10}$, ${\widehat{\pi }}_{01}$, ${\widehat{\pi }}_{00}$ are the estimated proportions. This leads to ${\widehat{f}}_j\left(p_{2j}|{\text{H}}_{01}\right)$.