Interval type-2 fuzzy computational model for real time Kalman filtering and forecasting of the dynamic spreading behavior of novel Coronavirus 2019

Abstract

This paper presents a computational model based on interval type-2 fuzzy systems for analysis and forecasting of COVID-19 dynamic spreading behavior. The proposed methodology is related to interval type-2 fuzzy Kalman filters design from experimental data of daily deaths reports. Initially, a recursive spectral decomposition is performed on the experimental dataset to extract relevant unobservable components for parametric estimation of the interval type-2 fuzzy Kalman filter. The antecedent propositions of fuzzy rules are obtained by formulating a type-2 fuzzy clustering algorithm. The state space submodels and the interval Kalman gains in consequent propositions of fuzzy rules are recursively updated by a proposed interval type-2 fuzzy Observer/Kalman Filter Identification (OKID) algorithm, taking into account the unobservable components obtained by recursive spectral decomposition of epidemiological experimental data of COVID-19. For validation purposes, through a comparative analysis with relevant references of literature, the proposed methodology is evaluated from the adaptive tracking and forecasting of COVID-19 dynamic spreading behavior, in Brazil, with the better results for RMSE of $1.24\times 10^{-5}$, MAE of $2.62\times 10^{-6}$, $R^2$ of 0.99976, and MAPE of $6.33\times 10^{-6}$.

1. Introduction

The increasing in complexity of real-world applications has motivated the development of computational intelligence techniques based on artificial neural networks [1], fuzzy logic [2], evolutionary computation [3], [4], and others, as useful tools for solution of practical problems [5], [6], [7], [8], [9]. Recently, the combination of different intelligent systems with traditional computational approaches has been proposed in different fields of research in order to develop more efficient tools [10], [11], [12], [13]. In the context of computational modeling of experimental data, type-2 fuzzy systems have attracted considerable attention by researches due to its interpretable rule-based structure with capability to treat nonlinearity and uncertainty [14], [15], [16].

Several researchers have proposed approaches for modeling experimental epidemiological data applied to novel Coronavirus 2019, in order to contribute in prevention [17], [18], [19]. However, associated to the epidemiological data analysis, the adopted model structures presents limitations related to the processing of uncertainties inherent to epidemiological datasets, such as underreporting, virus incubation period, lack of information, time to seek care and diagnosis, among other factors. Although some studies involving the application of fuzzy systems in modeling the propagation dynamics of Covid-19 have already been developed, this is a research field that is still open [20].

Differently of approaches from literature, the methodology in this paper is capable to process the uncertain spreading behavior of novel Coronavirus 2019 by using an interval type-2 fuzzy system into the Kalman filters design. The Kalman filter is a traditional mathematical tool widely used in data processing since its proposition in 1960 [21]. The proposed methodology was applied to the problem of tracking and forecasting the Covid-19 spreading behavior in Brazil and compared with others approaches from the literature in order to demonstrate its efficiency and applicability.

1.1. Related works

In recent years, the integration of Kalman filtering and fuzzy systems has received increasing interest from the scientific community in several application domains [22], [23], [24], [25]. In [26], an eight-layered neuro-fuzzy model is proposed to approximate nonaffine nonlinear dynamics with a state feedback quadratic stabilizing controller. In this approach, a constrained unscented Kalman filter is used for updating the parameters of both neuro-fuzzy model and the controller. In [27], a fuzzy adaptive error-state Kalman filter (FAESKF) is proposed and applied to attitude estimation problem of a small unmanned aerial vehicle (UAV). The efficiency is illustrated from experimental flight results for situations with high disturbance and absence of Global Positioning System (GPS) measurements. In [28], an active fault-tolerant control (FTC) scheme for robotic manipulators, subject to actuator faults, is proposed. The approach combines an interval type-2 fuzzy satin bowerbird algorithm for parameters optimization and adaptive state-augmented extended Kalman filter as a real time fault detection and diagnosis module. In [29], a strategy for optimizing the membership function parameters of an interval type-2 fuzzy system using Kalman filter is presented. The performance of methodology was validated from its application to different benchmark functions, presenting better results when compared to other approaches from the literature.

Recently, several researchers have dedicated themselves for developing methodologies of modeling and forecasting using experimental epidemiological data with applications to the novel Coronavirus 2019 [30], [31], [32], [33], [34]. In this context, a mathematical model for forecasting the future values of daily new cases of COVID-19 in India, USA, and Brazil, is proposed in [20]. The forecasting model is based on eigenvalue decomposition technique of Hankel matrix (EVDHM) and autoregressive integrated moving average (ARIMA) model. The EVDHM method is applied over a time series to decompose it into subcomponents in the sense to reduce its nonstationarity, and the ARIMA-based model is designed to forecast the future values of each subcomponent such that the final output value is obtained by adding the forecasts values of each subcomponent. In [35], the refined instrumental variable method is applied for estimating hybrid Box–Jenkins models of linear dynamic systems (RIVC). The mathematical model is applied to relate the daily death reports in the Italian and UK epidemics, and then provide 15-day-ahead forecasts of the UK daily death reports. The approach is also used for modeling and forecasting the epidemic using daily reports of COVID-19 patients in UK hospitals. In [36], a Bayesian structural time series (BSTS) model is applied for investigating the temporal dynamics of COVID-19 in top five affected countries around the world (United States, Brazil, Russia, India and United Kingdom), within the horizon of 30 days.

1.2. Motivation and contributions of the proposed methodology

The spread of novel Coronavirus 2019 has motivated the analysis of epidemiological data in order to contribute with the political/health authorities in decision-making and resource allocation [37], [38]. Thus, a large number of approaches have already been proposed in this context of forecasting the propagation dynamics of COVID-19 [39], [40], [41], [42]. However, the performance of these methodologies is compromised by the presence of uncertainties in experimental epidemiological data, which has opened a new field of research, in which the proposed methodology belongs to. The main contributions of the proposed methodology are the following:

• •A new computational tool based on the successful integration of Kalman filters and type-2 fuzzy systems for forecasting the experimental epidemiological data, which is useful for COVID-19 propagation analysis;
• •The formulation of a type-2 fuzzy version of Gustafson–Kessel clustering algorithm capable of defining specific operating regions on the epidemiological experimental data related to the dynamic propagation of COVID-19;
• •The formulation of type-2 fuzzy version of Observer/Kalman Filter Identification (OKID) algorithm, for parametric estimation of consequent proposition, from the specific operation regions defined on the epidemiological data.

The paper is organized as follows. In Section 2, the description of the proposed methodology for design of interval type-2 fuzzy Kalman filters is presented. In Section 3, experimental results for forecasting analysis of COVID-19 dynamic spread behavior is presented, as well as a comparative analysis between the proposed methodology and similar recent references from the literature. In Section 4, the final remarks and indications for further works are presented.

2. Methodology for type-2 Fuzzy Kalman filter

In this section, the mathematical formulation for development of the computational model based on interval type-2 fuzzy systems and Kalman filtering from experimental data, is presented. The recursive singular spectral analysis of epidemiological experimental data and adaptive parametric estimation of interval type-2 fuzzy Kalman filter, are addressed.

2.1. Pre-processing of experimental data

The Singular Spectral Analysis is a technique for extracting explainable unobservable components within the original data of time series [43].

2.1.1. Training step

Considering the initial experimental dataset referring to $p$ time series under analysis, given by:

$$\mathbf{y}=[{\mathbf{y}}_1{\mathbf{y}}_2\dots {\mathbf{y}}_{N_b}],\mathbf{y}\in {\mathbb{R}}^{p\times N_b}$$ (1)

where ${\mathbf{y}}_k\in {\mathbb{R}}^p$, such that $k=1,\dots ,N_b$. A set of $\rho$ delayed vectors with dimension $\delta$ is defined, where $\delta$ is an integer number defined by user with $2\le \delta \le N_b-1$ and $\rho =N_b-\delta +1$, to construct a trajectory matrix $\mathbf{H}$ given by:

$$\mathbf{H}=\left[\begin{array}{ccccc}\hfill y_1\hfill & \hfill y_2\hfill & \hfill y_3\hfill & \hfill \cdots \hfill & \hfill y_{\rho }\hfill \\ \hfill y_2\hfill & \hfill y_3\hfill & \hfill y_4\hfill & \hfill \cdots \hfill & \hfill y_{\rho +1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill y_{\delta }\hfill & \hfill y_{\delta +1}\hfill & \hfill y_{\delta +2}\hfill & \hfill \cdots \hfill & \hfill y_{N_b}\hfill \end{array}\right],\mathbf{H}\in {\mathbb{R}}^{\delta \times \rho }$$ (2)

Then, a covariance matrix $\mathbf{S}$ is computed by:

$$\mathbf{S}=\mathbf{H}{\mathbf{H}}^T,\mathbf{S}\in {\mathbb{R}}^{\delta \times \delta }$$ (3)

The Singular Value Decomposition (SVD) procedure is applied to matrix $\mathbf{S}$ and a set of eigenvalues (${\sigma }^1\ge {\sigma }^2\ge \cdots \ge {\sigma }^{\delta }\ge 0$) and eigenvector (${\mathit{\varphi }}^1,{\mathit{\varphi }}^2,\dots ,{\mathit{\varphi }}^{\delta }$) is obtained. Assuming $d=max\left(\varsigma \right)$, and ${\mathbf{V}}^{\varsigma }={\mathbf{H}}^T{\mathit{\varphi }}^{\varsigma }/\sqrt{{\sigma }^{\varsigma }}$ such that $\varsigma =1,\dots ,d$, the SVD of $\mathbf{H}$, is rewritten as follows:

$$\mathbf{H}={\mathbf{\Delta }}^1+{\mathbf{\Delta }}^2+\cdots +{\mathbf{\Delta }}^d$$ (4)

where ${\mathbf{\Delta }}^{\varsigma }{|}^{\varsigma =1,\dots ,d}$ is defined as:

$${\mathbf{\Delta }}^{\varsigma }=\sqrt{{\sigma }^{\varsigma }}{\mathit{\varphi }}^{\varsigma }{{\mathbf{V}}^{\varsigma }}^T,{\mathbf{\Delta }}^{\varsigma }\in {\mathbb{R}}^{\delta \times \rho }$$ (5)

The matrices ${\mathbf{\Delta }}^{\varsigma }{|}^{\varsigma =1,\dots ,d}$ are regrouped into $\xi$ independent matrices terms ${\mathbf{I}}^j{|}^{j=1,\dots ,\xi }$, where $\xi \le d$, as follows:

$${\mathbf{\Delta }}^{\varsigma }={\mathbf{I}}^1+{\mathbf{I}}^2+\cdots +{\mathbf{I}}^{\xi },\varsigma =1,\dots ,d$$ (6)

where $\xi$ is the number of unobservable components extracted from experimental dataset. The unobservable spectral components ${\alpha }^j{|}^{j=1,\dots ,\xi }$ are given by:

$${\alpha }_k^j=\left\{\begin{array}{c}\frac{1}{k}\sum _{\nu =1}^{k+1}{I}_{\nu ,k-\nu +1}^{j}1\le k\le {\delta }^{\ast }\hfill \\ \frac{1}{{\delta }^{\ast }}\sum _{\nu =1}^{{\delta }^{\ast }}{I}_{\nu ,k-\nu +1}^j{\delta }^{\ast }\le k\le {\rho }^{\ast }\hfill \\ \frac{1}{N_b-k+1}\sum _{\nu =k-{\rho }^{\ast }+1}^{N_b-{\rho }^{\ast }+1}{I}_{\nu ,k-\nu +1}^j{\rho }^{\ast }<k\le N_b\hfill \end{array}\right)$$ (7)

where ${\delta }^{\ast }=\text{min}(\delta ,\rho )$, ${\rho }^{\ast }=\text{max}(\delta ,\rho )$ and $N_b=\delta +\rho -1$ is the number of samples of initial experimental dataset.

2.1.2. Recursive step

After the training step of spectral analysis algorithm, the next steps are repeated for $k=N_b+1,N_b+2,\dots$, as described in sequel. The values of $\rho$ and ${\mathbf{S}}_k$ are updated, respectively, as follows:

$$\rho =k-\delta +1$$ (8)

$${\mathbf{S}}_k={\mathbf{S}}_{k-1}+{\mathbf{\Upsilon }}_k,{\mathbf{S}}_k\in {\mathbb{R}}^{\delta \times \delta }$$ (9)

where ${\mathbf{\Upsilon }}_k={\mathit{\psi }}_k{\mathit{\psi }}_k^T\in {\mathbb{R}}^{\delta \times \delta }$ with ${\mathit{\psi }}_k={\left[y_{\rho },y_{\rho +1},\dots ,y_k\right]}^T\in {\mathbb{R}}^{\delta \times 1}$. The SVD method is applied to covariance matrix ${\mathbf{S}}_k$ and the set of eigenvalues ${\sigma }_k^1,{\sigma }_k^2,\dots ,{\sigma }_k^{\delta }$ and eigenvectors ${\mathit{\varphi }}_k^1,{\mathit{\varphi }}_k^2,\dots ,{\mathit{\varphi }}_k^{\delta }$ are updated at $k$ so that $y_k$ is rewritten as follows:

$$y_k=h_k^1+h_k^2+\cdots +h_k^d$$ (10)

where $h_k^{\varsigma }={\kappa }_k^{\varsigma }{\mathit{\psi }}_k^T{\mathit{\varphi }}_k^{\varsigma }$, with $\varsigma =1,\dots ,d$, where ${\kappa }_k^{\varsigma }$ is the last element of the eigenvector ${\mathit{\varphi }}_k^{\varsigma }$. The regrouping of the terms $h_k^{\varsigma }{|}^{\varsigma =1,\dots ,d}$ in $\xi$ disjoint terms $I_k^j{|}^{j=1,\dots ,\xi }$, results in

$$y_k=I_k^1+I_k^2+\cdots +I_k^{\xi }$$ (11)

where $I_k^j={\alpha }_k^j,\text{with }j=1,\dots ,\xi$ and $k=N_b+1,N_b+2,\dots$, corresponds to the extracted unobservable components at instant of time $k$. The Algorithm 1 presents the computational steps related to the pre-processing of experimental data.

2.2. Interval type-2 fuzzy Kalman filter: Parametric estimation

The rule-based structure of the interval type-2 fuzzy Kalman filter presents the $i{|}^{[i=1,2,\dots ,c]}$-th fuzzy rule, with $n$th order, $m$ inputs, $p$ outputs, given by:

$$R^{\left(i\right)}:\text{ IF }{\mathbf{Z}}_k\text{ IS }{\tilde{W}}^i\text{ THEN }\left\{\begin{array}{c}{\widetilde{\hat{\mathbf{x}}}}_{k+1}^i={\tilde{\mathbf{A}}}_k^i{\widetilde{\hat{\mathbf{x}}}}_k^i+{\tilde{\mathbf{B}}}_k^i{\mathbf{u}}_k+{\tilde{\mathbf{K}}}_k^i{\tilde{\mathit{\epsilon }}}_k^i\hfill \\ {\widetilde{\hat{\mathbf{y}}}}_k^i={\tilde{\mathbf{C}}}_k^i{\widetilde{\hat{\mathbf{x}}}}_k^i+{\tilde{\mathbf{D}}}_k^i{\mathbf{u}}_k\hfill \end{array}\right)$$ (12)

where ${\mathbf{Z}}_k$ is the antecedent input variable; ${\tilde{W}}^i$ is the interval type-2 fuzzy set; ${\widetilde{\hat{\mathbf{x}}}}_k^i\in {\mathbb{R}}^n$ is the estimated state vector; ${\widetilde{\hat{\mathbf{y}}}}_k^i\in {\mathbb{R}}^p$ is the estimated output vector, ${\mathbf{u}}_k\in {\mathbb{R}}^m$ is the input signal vector, ${\tilde{\mathbf{A}}}_k^i\in {\mathbb{R}}^{n\times n}$, ${\tilde{\mathbf{B}}}_k^i\in {\mathbb{R}}^{n\times m}$, ${\tilde{\mathbf{C}}}_k^i\in {\mathbb{R}}^{p\times n}$, ${\tilde{\mathbf{D}}}_k^i\in {\mathbb{R}}^{p\times m}$ are the state space matrices of the local submodel and ${\tilde{\mathbf{K}}}_k^i\in {\mathbb{R}}^{n\times p}$ is the Kalman gain matrix. The residual error ${\tilde{\mathit{\epsilon }}}_k^i$ for $i$th rule is defined as ${\tilde{\mathit{\epsilon }}}_k^i={\mathbf{y}}_k-{\widetilde{\hat{\mathbf{y}}}}_k^i$.

The dynamics described by experimental dataset is approximated by the weighted sum of Kalman filters defined in the consequent proposition of interval type-2 fuzzy Kalman filter, considering the interval activation degrees ${\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)$, of each $i$th rule, as follows:

$${\widetilde{\hat{\mathbf{x}}}}_{k+1}=\sum _{i=1}^c{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\tilde{\mathbf{A}}}_k^i{\widetilde{\hat{\mathbf{x}}}}_k+\sum _{i=1}^c{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\tilde{\mathbf{B}}}_k^i{\mathbf{u}}_k+\sum _{i=1}^c{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\tilde{\mathbf{K}}}_k^i{\tilde{\mathit{\epsilon }}}_k^i$$

$${\widetilde{\hat{\mathbf{y}}}}_k=\sum _{i=1}^c{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\tilde{\mathbf{C}}}_k^i{\widetilde{\hat{\mathbf{x}}}}_k+\sum _{i=1}^c{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\tilde{\mathbf{D}}}_k^i{\mathbf{u}}_k$$ (13)

where ${\underset{\_}{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)$ and ${\overline{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)$ are, respectively, the lower and upper activation degrees of $i$th fuzzy rule, such that ${\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)=\left[{\underset{\_}{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right),{\overline{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)\right]$, and $c$ is the number of fuzzy rules defined for interval type-2 fuzzy Kalman filter.

$$\sum _{i=1}^c{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)=1,{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)\ge 0$$ (14)

2.2.1. Antecedent proposition: Parametric estimation

For the partitioning of experimental dataset in operation regions, an interval type-2 fuzzy Gustafson–Kessel clustering algorithm was developed, as formulated in sequel.

The initial estimation of interval type-2 fuzzy Kalman filter takes into account an experimental dataset initially collected $\mathbf{Z}\in {\mathbb{R}}^{p\times N_b}$ and the following arguments: the clusters number $c$, such that $1<c<N_b$, the termination tolerance $\mathcal{E}>0$, the randomly initial partition matrix ${\tilde{\mathbf{U}}}^{\left(0\right)}$, and the interval weighting exponent $\tilde{m}=\left[\underset{\_}{m},\overline{m}\right]$, such that $\overline{m}>\underset{\_}{m}>1$.

The first step of interval type-2 fuzzy clustering algorithm is to compute the centers of initial clusters defined by a random partition matrix ${\tilde{\mathbf{U}}}^{\left(0\right)}$ as follows:

$${\tilde{\mathbf{v}}}^{i^{\left(l\right)}}=\frac{\sum _{k=1}^{N_b}{\left({\tilde{\mu }}_{{\tilde{W}}^i}^i{\left({\mathbf{Z}}_k\right)}^{i^{(l-1)}}\right)}^{\tilde{m}}{\mathbf{Z}}_k}{\sum _{k=1}^{N_b}{\left({\tilde{\mu }}_{{\tilde{W}}^i}^i{\left({\mathbf{Z}}_k\right)}^{(l-1)}\right)}^{\tilde{m}}},1\le i\le c$$ (15)

where ${\mathbf{Z}}_k$ is the experimental dataset at instant $k$. After that, a covariance matrix ${\tilde{\mathbf{F}}}^i$ is computed for each cluster, given by:

$${\tilde{\mathbf{F}}}^i=\frac{\sum _{k=1}^{N_b}{\left({\tilde{\mu }}_{{\tilde{W}}^i}^i{\left({\mathbf{Z}}_k\right)}^{(l-1)}\right)}^{\tilde{m}}\left({\mathbf{Z}}_k-{\tilde{\mathbf{v}}}^{i^{\left(l\right)}}\right){\left({\mathbf{Z}}_k-{\tilde{\mathbf{v}}}^{i^{\left(l\right)}}\right)}^T}{\sum _{k=1}^N{\left({\tilde{\mu }}_{{\tilde{W}}^i}^i{\left({\mathbf{Z}}_k\right)}^{(l-1)}\right)}^{\tilde{m}}},1\le i\le c,1\le k\le N_b$$ (16)

The covariance matrix is used to calculate the distances ${{\tilde{D}}^i}_{k{\tilde{\mathbf{F}}}^i}$ between the sample ${\mathbf{Z}}_k$ and the center ${\tilde{\mathbf{v}}}^{i^{\left(l\right)}}$ of the $i$th cluster computed in the first step, as follows:

$${{\tilde{D}}^i}_{k{\tilde{\mathbf{F}}}^i}=\sqrt{{\left({\mathbf{Z}}_k-{\tilde{\mathbf{v}}}^{i^{\left(l\right)}}\right)}^T\left[\text{det}{\left({\tilde{\mathbf{F}}}^i\right)}^{1/n}{\left({\tilde{\mathbf{F}}}^i\right)}^{-1}\right]\left({\mathbf{Z}}_k-{\tilde{\mathbf{v}}}^{i^{\left(l\right)}}\right)}$$ (17)

The term $\left[\text{det}{\left({\tilde{\mathbf{F}}}^i\right)}^{1/n}{\left({\tilde{\mathbf{F}}}^i\right)}^{-1}\right]$ in Eq. (17) corresponds to the norm-inducing matrix ${\mathbf{A}}_i$ of $i$th cluster, which are used as optimization parameters, allowing each cluster to adapt the distance norm to the local topological structure of the dataset [44]. The interval partition matrix ${\tilde{\mathbf{U}}}^{\left(l\right)}$, is updated as follows:

If ${{\tilde{D}}^i}_{k{\tilde{\mathbf{F}}}^i}>0$ for $1\le i\le c$, $1\le k\le N_b$

$${\tilde{\mu }}_{{\tilde{W}}^i}^{i^{\left(l\right)}}\left({\mathbf{Z}}_k\right)=\left[{\underset{\_}{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right),{\overline{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)\right]$$ (18)

where

$${\underset{\_}{\mu }}_{{\tilde{W}}^i}^{i^{\left(l\right)}}\left({\mathbf{Z}}_k\right)=\text{min}\left[\frac{1}{\sum _{j=1}^c{\left({\underset{\_}{D}}_{k{\underset{\_}{\mathbf{F}}}^i}^i/{\underset{\_}{D}}_{k{\underset{\_}{\mathbf{F}}}^i}^i\right)}^{2/(\underset{\_}{m}-1)}},\frac{1}{\sum _{j=1}^c{\left({\overline{D}}_{k{\overline{\mathbf{F}}}^i}^i/{\overline{D}}_{k{\overline{\mathbf{F}}}^i}^i\right)}^{2/(\overline{m}-1)}}\right]$$ (19)

$${\overline{\mu }}_{{\tilde{W}}^i}^{i^{\left(l\right)}}\left({\mathbf{Z}}_k\right)=\text{max}\left[\frac{1}{\sum _{j=1}^c{\left({\underset{\_}{D}}_{k{\underset{\_}{\mathbf{F}}}^i}^i/{\underset{\_}{D}}_{k{\underset{\_}{\mathbf{F}}}^i}^i\right)}^{2/(\underset{\_}{m}-1)}},\frac{1}{\sum _{j=1}^c{\left({\overline{D}}_{k{\overline{\mathbf{F}}}^i}^i/{\overline{D}}_{k{\overline{\mathbf{F}}}^i}^i\right)}^{2/(\overline{m}-1)}}\right]$$ (20)

otherwise ${\tilde{\mu }}_{{\tilde{W}}^i}^{i^{\left(l\right)}}\left({\mathbf{Z}}_k\right)=\left[0,0\right]$ with ${\underset{\_}{\mu }}_{{\tilde{W}}^i}^{i^{\left(l\right)}}\left({\mathbf{Z}}_k\right)\in [0,1]$ e ${\overline{\mu }}_{{\tilde{W}}^i}^{i^{\left(l\right)}}\left({\mathbf{Z}}_k\right)\in [0,1]$. These steps are repeated iteratively for $l=1,2,\dots$, until $\Vert {\tilde{\mathbf{U}}}^{\left(l\right)}-{\tilde{\mathbf{U}}}^{(l-1)}\Vert <\mathcal{E}$. The Algorithm 2 presents the computational steps related to the proposed type-2 clustering algorithm.

2.2.2. Consequent proposition: Parametric estimation

For estimating the matrices that compose the state space submodels, defined in consequent proposition of interval type-2 fuzzy Kalman filter inference system, an interval type-2 fuzzy version of OKID (Observer/Kalman Filter Identification) algorithm [45], was developed. This algorithm considers the spectral components extracted from the experimental dataset and membership values estimated by interval type-2 Gustafson–Kessel clustering algorithm as weighting criteria for parametric estimation of consequent proposition. From the initial experimental dataset $\mathbf{Z}$, with ${\mathbf{Z}}_k={\left[{\mathbf{u}}_k{\mathit{\alpha }}_k^{\ast }\right]}^T$, where ${\mathit{\alpha }}_k^{\ast }$ is the spectral components that presents higher eigenvalue and are more significant to represent the dynamics of experimental dataset. Initially, the appropriate number of Markov parameters $q$ is chosen and a matrix of regressors is computed by:

$$\mathbf{\Lambda }=\left[\begin{array}{cccc}\hfill {\mathbf{u}}_q\hfill & \hfill {\mathbf{u}}_{q+1}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{u}}_{N_b-1}\hfill \\ \hfill {\mathbf{Z}}_{q-1}\hfill & \hfill {\mathbf{Z}}_q\hfill & \hfill \cdots \hfill & \hfill {\mathbf{Z}}_{N_b-2}\hfill \\ \hfill {\mathbf{Z}}_{q-2}\hfill & \hfill {\mathbf{Z}}_{q-1}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{Z}}_{N_b-3}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{Z}}_0\hfill & \hfill {\mathbf{Z}}_1\hfill & \hfill \cdots \hfill & \hfill {\mathbf{Z}}_{N_b-q-1}\hfill \end{array}\right]$$ (21)

The observer Markov parameters ${\widetilde{\overline{\mathbf{Y}}}}^i$ are calculated as follows:

$${\widetilde{\hat{\mathbf{y}}}}^T=\sum _{i=1}^c{\tilde{\mathbf{\Gamma }}}^i{\mathbf{\Lambda }}^T{\widetilde{\overline{\mathbf{Y}}}}^{i^T}$$ (22)

where

$${\tilde{\mathbf{\Gamma }}}^i=\left[\begin{array}{cccc}\hfill {\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_q\right)\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_{q+1}\right)\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill {\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_{N_b-1}\right)\hfill \end{array}\right]$$ (23)

corresponds to the diagonal weighting matrix related to the $i$th fuzzy rule obtained by interval type-2 fuzzy clustering algorithm described in Section 2.2.1,

$${\widetilde{\overline{\mathbf{Y}}}}^i=\left[\begin{array}{ccc}\hfill {\tilde{\mathbf{D}}}_k^i\hfill & \hfill {\tilde{\mathbf{C}}}_k^i{\widetilde{\overline{\mathbf{B}}}}_k^i\hfill & \hfill {\tilde{\mathbf{C}}}_k^i{\widetilde{\overline{\mathbf{A}}}}_k^i{\widetilde{\overline{\mathbf{B}}}}_k^i\cdots {\tilde{\mathbf{C}}}_k^i{\widetilde{\overline{\mathbf{A}}}}_k^{i^{\left(q-1\right)}}{\widetilde{\overline{\mathbf{B}}}}_k^i\hfill \end{array}\right]=\left[{\widetilde{\overline{\mathbf{Y}}}}_0^i{\widetilde{\overline{\mathbf{Y}}}}_1^i{\widetilde{\overline{\mathbf{Y}}}}_2^i\cdots {\widetilde{\overline{\mathbf{Y}}}}_q^i\right]$$ (24)

are the interval observer Markov parameters of $i$th rule and

$${\widetilde{\overline{\mathbf{A}}}}_k^i=\left[{\tilde{\mathbf{A}}}_k^i+{\tilde{\mathbf{K}}}_k^i{\tilde{\mathbf{C}}}_k^i\right]$$ (25)

$${\widetilde{\overline{\mathbf{B}}}}_k^i=\left[{\tilde{\mathbf{B}}}_k^i+{\tilde{\mathbf{K}}}_k^i{\tilde{\mathbf{D}}}_k^i,-{\tilde{\mathbf{K}}}_k^i\right]$$ (26)

corresponds to the coupled state matrix and coupled input matrix, since it has information about both the dynamics of experimental dataset and interval Kalman gain. From Eq. (22):

$$\mathbf{\Lambda }{\tilde{\mathbf{\Gamma }}}^i{\mathbf{y}}^T=\mathbf{\Lambda }{\tilde{\mathbf{\Gamma }}}^i{\mathbf{\Lambda }}^T{\widetilde{\overline{\mathbf{Y}}}}^{i^T}$$ (27)

where $\mathbf{y}=\left[{\mathbf{y}}_1{\mathbf{y}}_2\dots {\mathbf{y}}_{N_b}\right]\in {\mathbb{R}}^{p\times N_b}$ corresponds to real experimental dataset. Considering ${\tilde{\mathfrak{U}}}^i=\mathbf{\Lambda }{\tilde{\mathbf{\Gamma }}}^i{\mathbf{\Lambda }}^T$ and ${\tilde{\mathit{\aleph }}}^i=\mathbf{\Lambda }{\tilde{\mathbf{\Gamma }}}^i{\mathbf{y}}^T$, Eq. (27) is rewritten as:

$${\tilde{\mathfrak{U}}}^i{\widetilde{\overline{\mathbf{Y}}}}^{i^T}={\tilde{\mathit{\aleph }}}^i$$ (28)

Solving the Eq. (28) by QR factorization procedure [46], it has:

$${\tilde{\mathbf{Q}}}^i{\tilde{\mathbf{R}}}^i{\widetilde{\overline{\mathbf{Y}}}}^{i^T}={\tilde{\mathit{\aleph }}}^i$$ (29)

where ${\tilde{\mathbf{Q}}}^i$ is an orthogonal matrix, such that ${\left({\tilde{\mathbf{Q}}}^i\right)}^{-1}={\left({\tilde{\mathbf{Q}}}^i\right)}^T$ (its inverse is equal to its transpose) and ${\tilde{\mathbf{R}}}^i$ is an upper triangular matrix. The following expressions are considered:

$${\widetilde{\overline{\mathbf{Y}}}}_0^i={\tilde{\mathbf{D}}}_k^i$$ (30)

$${\widetilde{\overline{\mathbf{Y}}}}_j^i={\tilde{\mathbf{C}}}_k^i{\widetilde{\overline{\mathbf{A}}}}^{i^{\left(j-1\right)}}{\widetilde{\overline{\mathbf{B}}}}_k^i$$ (31)

$$=\left[{\tilde{\mathbf{C}}}_k^i{\left({\tilde{\mathbf{A}}}_k^i+{\tilde{\mathbf{K}}}_k^i{\tilde{\mathbf{C}}}_k^i\right)}^{\left(j-1\right)}\left({\tilde{\mathbf{B}}}_k^i+{\tilde{\mathbf{K}}}_k^i{\tilde{\mathbf{D}}}_k^i\right),\right)\left(-{\tilde{\mathbf{C}}}_k^i{\left({\tilde{\mathbf{A}}}_k^i+{\tilde{\mathbf{K}}}_k^i{\tilde{\mathbf{C}}}_k^i\right)}^{\left(j-1\right)}{\tilde{\mathbf{K}}}_k^i\right]$$ (32)

$$=\left[{\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(1\right)}},-{\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(2\right)}}\right],j=1,2,3,\dots$$ (33)

where ${\widetilde{\overline{\mathbf{Y}}}}_j^i$ corresponds to the interval observer Markov parameters obtained from Eq. (29). Thus, the system Markov parameters vector ${\tilde{\mathbf{Y}}}_j^i$, is given by:

$${\tilde{\mathbf{Y}}}_0^i={\widetilde{\overline{\mathbf{Y}}}}_0^i={\tilde{\mathbf{D}}}_k^i$$ (34)

$${\tilde{\mathbf{Y}}}_j^i={\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(1\right)}}-\sum _{\iota =1}^j{\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(2\right)}}{\tilde{\mathbf{Y}}}_{j-\iota }^i,\text{ for }j=1,\dots ,q$$ (35)

$${\tilde{\mathbf{Y}}}_j^i=-\sum _{\iota =1}^q{\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(2\right)}}{\tilde{\mathbf{Y}}}_{j-\iota }^i,\text{ for }j=q+1,\dots ,\infty$$ (36)

and the observer gain Markov parameters ${\tilde{\mathbf{Y}}}_j^{i^o}$ are obtained, as follows:

$${\tilde{\mathbf{Y}}}_1^{i^o}={\widetilde{\overline{\mathbf{Y}}}}_1^{i^{\left(2\right)}}={\tilde{\mathbf{C}}}_k^i{\tilde{\mathbf{K}}}_k^i$$ (37)

$${\tilde{\mathbf{Y}}}_j^{i^o}={\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(2\right)}}-\sum _{\iota =1}^{j-1}{\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(2\right)}}{\tilde{\mathbf{Y}}}_{j-\iota }^{i^o},\text{ for }j=2,\dots ,q$$ (38)

$${\tilde{\mathbf{Y}}}_j^{i^o}=-\sum _{\iota =1}^q{\widetilde{\overline{\mathbf{Y}}}}_j^{i^{\left(2\right)}}{\tilde{\mathbf{Y}}}_{j-\iota }^{i^o},\text{ for }j=q+1,\dots ,\infty$$ (39)

A Hankel matrix ${\tilde{\mathbf{H}}}^i\left(j-1\right)\in {\mathbb{R}}^{\gamma p\times \beta m}$ is constructed from system Markov parameters, as follows:

$${\tilde{\mathbf{H}}}^i\left(j-1\right)=\left[\begin{array}{cccc}\hfill {\tilde{\mathbf{Y}}}_j^i\hfill & \hfill {\tilde{\mathbf{Y}}}_{j+1}^i\hfill & \hfill \dots \hfill & \hfill {\tilde{\mathbf{Y}}}_{j+\beta -1}^i\hfill \\ \hfill {\tilde{\mathbf{Y}}}_{j+1}^i\hfill & \hfill {\tilde{\mathbf{Y}}}_{j+2}^i\hfill & \hfill \dots \hfill & \hfill {\tilde{\mathbf{Y}}}_{j+\beta }^i\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\tilde{\mathbf{Y}}}_{j+\gamma -1}^i\hfill & \hfill {\tilde{\mathbf{Y}}}_{j+\gamma }^i\hfill & \hfill \dots \hfill & \hfill {\tilde{\mathbf{Y}}}_{j+\gamma +\beta -2}^i\hfill \end{array}\right]$$ (40)

where $\gamma$ and $\beta$ are arbitrary integers defined by user. Considering $j=1$, the Hankel matrix ${\tilde{\mathbf{H}}}^i\left(0\right)$ is decomposed using Singular Value Decomposition procedure:

$${\tilde{\mathbf{H}}}^i\left(0\right)={\tilde{\mathbf{\Xi }}}^i{\tilde{\mathbf{\Sigma }}}^i{\tilde{\mathbf{\Psi }}}^{i^T}$$ (41)

where ${\tilde{\mathbf{\Xi }}}^i\in {\mathbb{R}}^{\gamma p\times \gamma p}$ and ${\tilde{\mathbf{\Psi }}}^i\in {\mathbb{R}}^{\beta m\times \beta m}$ are orthogonal matrices and ${\tilde{\mathbf{\Sigma }}}^i\in {\mathbb{R}}^{\gamma p\times \beta m}$ is the diagonal matrix of singular values. From this result, the observability matrix ${\tilde{\mathcal{P}}}_{\gamma }^i$ and controllability matrix ${\tilde{\mathcal{Q}}}_{\beta }^i$ are computed, as described below:

$${\tilde{\mathcal{P}}}_{\gamma }^i={\tilde{\mathbf{\Xi }}}_n^i{\left({\tilde{\mathbf{\Sigma }}}_n^i\right)}^{1/2}$$ (42)

$${\tilde{\mathcal{Q}}}_{\beta }^i={\left({\tilde{\mathbf{\Sigma }}}_n^i\right)}^{1/2}{\tilde{\mathbf{\Psi }}}_n^{i^T}$$ (43)

where

$${\tilde{\mathcal{P}}}_{\gamma }^i=\left[\begin{array}{c}\hfill {\tilde{\mathbf{C}}}_k^i\hfill \\ \hfill {\tilde{\mathbf{C}}}_k^i{\tilde{\mathbf{A}}}_k^i\hfill \\ \hfill {\tilde{\mathbf{C}}}_k^i{\tilde{\mathbf{A}}}_k^{i^2}\hfill \\ \hfill ⋮\hfill \\ \hfill {\tilde{\mathbf{C}}}_k^i{\tilde{\mathbf{A}}}_k^{i^{\gamma -1}}\hfill \end{array}\right]$$ (44)

$${\tilde{\mathcal{Q}}}_{\beta }^i=\left[{\tilde{\mathbf{B}}}_k^i{\tilde{\mathbf{A}}}_k^i{\tilde{\mathbf{B}}}_k^i{\tilde{\mathbf{A}}}_k^{i^2}{\tilde{\mathbf{B}}}_k^i\cdots {\tilde{\mathbf{A}}}_k^{i^{\beta -1}}{\tilde{\mathbf{B}}}_k^i\right]$$ (45)

Finally, the matrices that make up the consequent proposition of interval type-2 fuzzy Kalman filter inference system is computed, as follows:

$${\tilde{\mathbf{A}}}_k^i={\left({\tilde{\mathbf{\Sigma }}}_n^i\right)}^{-1/2}{\tilde{\mathbf{\Xi }}}_n^{i^T}{\tilde{\mathbf{H}}}_n^i\left(1\right){\tilde{\mathbf{\Psi }}}_n^{i^T}{\left({\tilde{\mathbf{\Sigma }}}_n^i\right)}^{-1/2}$$ (46)

$${\tilde{\mathbf{B}}}_k^i=\text{first }m\text{ columns of }{\tilde{\mathcal{Q}}}_{\beta }^i$$ (47)

$${\tilde{\mathbf{C}}}_k^i=\text{first }p\text{ rows of }{\tilde{\mathcal{P}}}_{\gamma }^i$$ (48)

$${\tilde{\mathbf{D}}}_k^i={\tilde{\mathbf{Y}}}_0^i$$ (49)

The interval Kalman gain matrix ${\tilde{\mathbf{K}}}_k^i$ is calculated from the observer gain Markov parameters vector ${\tilde{\mathbf{Y}}}_j^{i^o}$, as follows:

$${\tilde{\mathbf{Y}}}_j^{i^o}=-{\tilde{\mathcal{P}}}_{\gamma }^i{\tilde{\mathbf{K}}}_k^i$$ (50)

where ${\tilde{\mathcal{P}}}_{\gamma }^i$ is the observability matrix computed from Eq. (42) and ${\tilde{\mathbf{K}}}_k^i$ is the interval Kalman gain matrix. From Eq. (50):

$${\tilde{\mathcal{P}}}_{\gamma }^{i^T}{\tilde{\mathbf{\Gamma }}}^i{\tilde{\mathbf{Y}}}_j^{i^o}=-{\tilde{\mathcal{P}}}_{\gamma }^{i^T}{\tilde{\mathbf{\Gamma }}}^i{\tilde{\mathcal{P}}}_{\gamma }^i{\tilde{\mathbf{K}}}_k^i$$ (51)

From Eq. (51) and considering ${\tilde{\mathfrak{A}}}^i=-{\tilde{\mathcal{P}}}_{\gamma }^{i^T}{\tilde{\mathbf{\Gamma }}}^i{\tilde{\mathcal{P}}}_{\gamma }^i$ and ${\tilde{\mathfrak{N}}}^i={\tilde{\mathcal{P}}}_{\gamma }^{i^T}{\tilde{\mathbf{\Gamma }}}^i{\tilde{\mathbf{Y}}}_j^{i^o}$, it has:

$${\tilde{\mathfrak{A}}}^i{\tilde{\mathbf{K}}}_k^i={\tilde{\mathfrak{N}}}^i$$ (52)

The Eq. (52) is solved by QR factorization procedure to obtain the interval Kalman gain matrix ${\tilde{\mathbf{K}}}_k^i$.

Mechanism for Updating the Consequent Proposition

After the initial estimation of the consequent proposition of interval type-2 fuzzy Kalman filter, the state space submodels are updated recursively at instants $k=N_b+1,k=N_b+2,\dots$, considering the new samples of experimental dataset. For this, a regressors vector ${\mathit{\lambda }}_k$ is construct, at instant $k$, as follows:

$${\mathit{\lambda }}_k=\left[\begin{array}{c}\hfill {\mathbf{u}}_{k+1}\hfill \\ \hfill {\mathbf{Z}}_k\hfill \\ \hfill {\mathbf{Z}}_{k-1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{Z}}_{k-q}\hfill \end{array}\right]$$ (53)

According to regressors vector defined in Eq. (53), the interval observer Markov parameters ${\widetilde{\overline{\mathbf{Y}}}}_k^i$ are updated at the instant of time $k=N_b+1,k=N_b+2,\dots$, by the following:

$${\tilde{\mathfrak{U}}}_k^i={\tilde{\mathfrak{U}}}_{k-1}^i+{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\mathit{\lambda }}_k{\mathit{\lambda }}_k^T$$ (54)

$${\tilde{\mathit{\aleph }}}_k^i={\tilde{\mathit{\aleph }}}_{k-1}^i+{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\mathit{\lambda }}_k{\mathbf{y}}_k^T$$ (55)

The QR factorization procedure is applied to the term ${\tilde{\mathfrak{U}}}_k^i$ in updated Eq. (28), the observer Markov parameters for $i$th rule at sample $k$, ${\widetilde{\overline{\mathbf{Y}}}}_k^i$, are updated. Repeating the Steps 3 to 7, the consequent proposition of the interval type-2 fuzzy Kalman filter is updated recursively for each instant $k$. Similarly, updating the Eq. (52), it has:

$${\tilde{\mathfrak{A}}}_k^i={\tilde{\mathfrak{A}}}_{k-1}^i+{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\mathit{\lambda }}_k{\mathit{\lambda }}_k^T$$ (56)

$${\tilde{\mathfrak{N}}}_k^i={\tilde{\mathfrak{N}}}_{k-1}^i+{\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right){\mathit{\lambda }}_k{\mathit{\lambda }}_k^T$$ (57)

The Kalman gain matrices are updated through application of QR factorization to ${\tilde{\mathfrak{A}}}_k^i$. The Algorithm 3 presents the computational steps related to the parametric estimation and updating of consequent proposition.

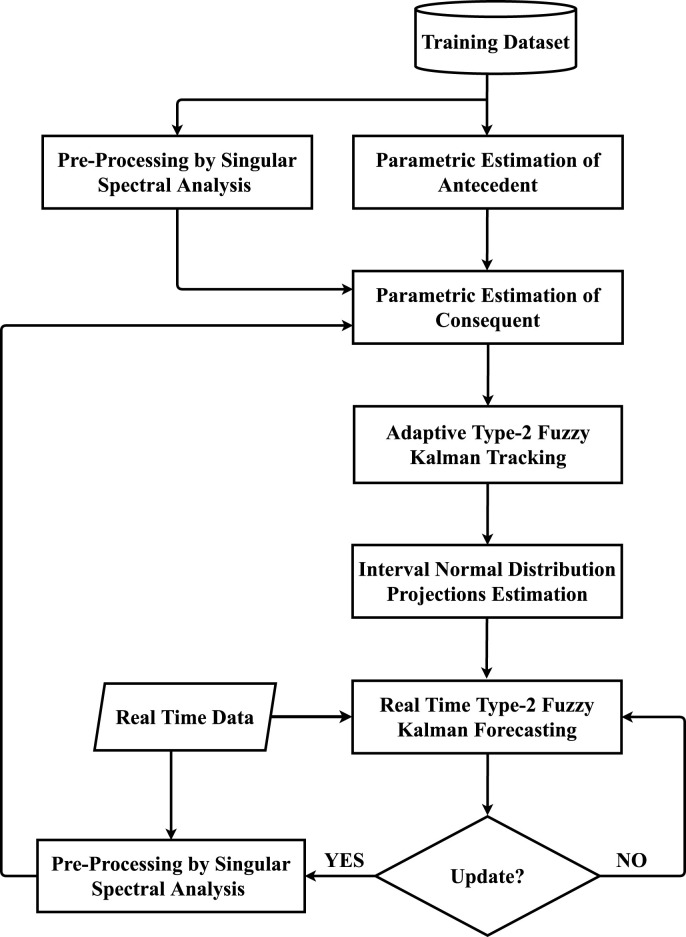
A flowchart of the proposed methodology, is shown in Fig. 1. The supplementary methods and materials related to the proposed interval type-2 fuzzy Kalman filter algorithm are in open access and provided from the link $<$ https://drive.google.com/drive/folders/1BvzMnaZZhtleJ1dVggJJGWISpNfwdvqD?usp=sharing $>$.

Fig. 1.

The flowchart of the proposed methodology corresponding to computational steps for designing the interval type-2 fuzzy Kalman filter.

3. Experimental results

In this section, the efficiency and applicability of the proposed methodology are illustrated by experimental results for forecasting the COVID-19 dynamic spread behavior and comparative analysis, considering the epidemiological experimental dataset of daily deaths reports by COVID-19 in Brazil.

3.1. Forecasting of COVID-19 in Brazil

The experimental dataset related to daily death reports, in Brazil, within the period ranging from 29 of February 2020 to 20 of July 2020, were used by the proposed methodology for solving the problem of forecasting the propagation dynamics of COVID-19, which were obtained from official report1 and is shown in Fig. 2. The input variable ${\mathbf{u}}_k$ is considered as white noise signal according to the proposed methodology. The first step for designing of interval type-2 fuzzy Kalman filter is the pre-processing of experimental dataset by singular spectral analysis. The appropriate number of unobservable components was determined from the Variance Accounted For (VAF), within a range from 2 to 15 ones, for best representation of experimental dataset, as shown in Fig. 3. From Fig. 3, considering the cost–benefit balance for practical application of proposed methodology, the appropriate number of unobservable components was $\xi =10$, with VAF value of 99.98% in efficiency to represent the experimental dataset and, at same time, reducing the computational load of interval type-2 fuzzy Kalman filter algorithm. The spectral unobservable components, extracted from the experimental dataset, are shown in Fig. 4.

Fig. 2.

The epidemiological data of daily deaths by Covid-19 in Brazil used for the implementation of proposed methodology.

Fig. 3.

The efficiency of unobservable components for representing the experimental dataset of the daily deaths reports in Brazil, according to VAF criterion.

Fig. 4.

The temporal behavior of spectral unobservable components ${\alpha }^j{|}^{j=1,\dots ,10}$, which were extracted from epidemiological experimental dataset of daily deaths, in Brazil.

The partitioning of discourse universe of experimental dataset related to daily deaths reports was performed considering $c=3$, $\mathcal{E}=10^{-5}$, and $\tilde{m}=[1.5,2.3]$. The interval type-2 fuzzy sets estimated by type-2 fuzzy Gustafson–Kessel clustering algorithm are shown in Fig. 5.

Fig. 5.

The upper (solid line) and lower (dashed line) fuzzy membership functions estimated from the interval type-2 fuzzy clustering of daily deaths reports, in Brazil.

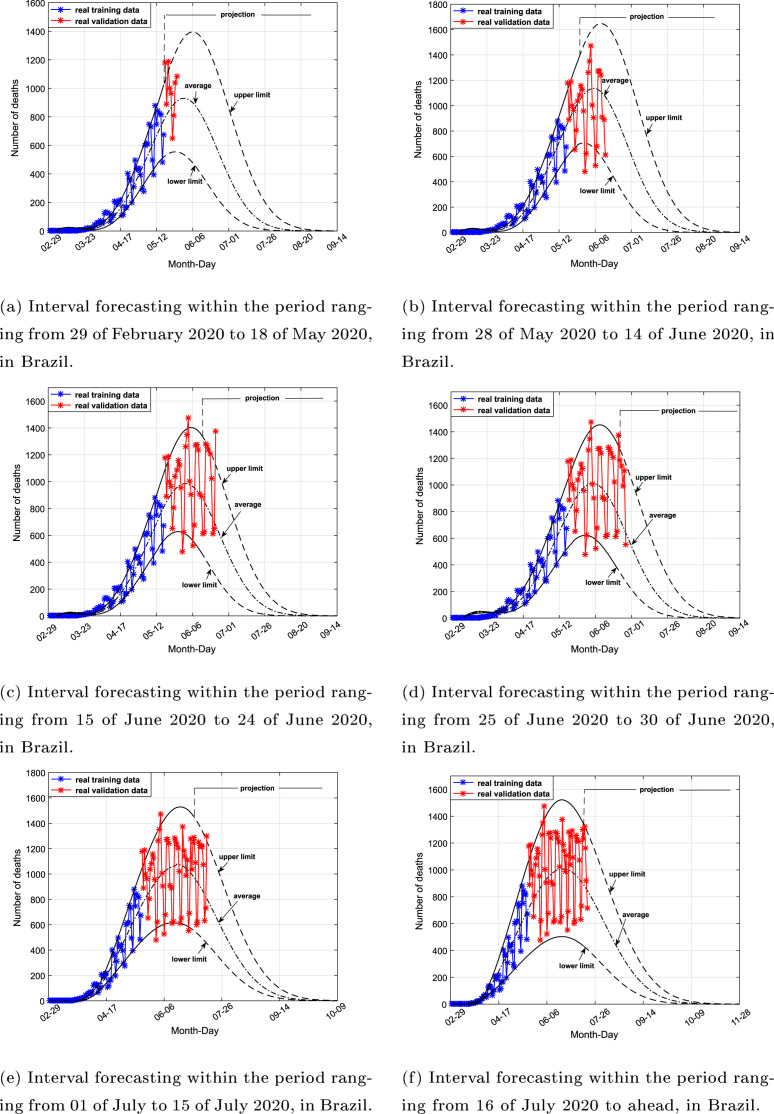
The daily deaths reports are partitioned as shown in Fig. 5. It was used as weighting criterion for estimation of state space models in consequent proposition of interval type-2 fuzzy Kalman filter by interval type-2 fuzzy OKID algorithm, formulated in Section 2.2.2. For this, the following parameters values was defined: $q=1$ (number of Markov parameters), $\gamma =15$ (number of rows of Hankel matrix) e $\beta =15$ (number of columns of Hankel matrix). Considering the epidemiological experimental dataset of daily deaths reports in Brazil, the unobservable components extracted by singular spectral analysis shown in Fig. 4, the interval type-2 fuzzy sets shown in Fig. 5, the training step was performed in order to obtain the initial estimation of interval type-2 fuzzy Kalman filter. The confidence region estimated by initial tracking of experimental dataset related to daily deaths reports in Brazil, resulting from the training step of interval type-2 fuzzy Kalman filter, is shown in Fig. 6. From this confidence region, shown in Fig. 6, interval normal projections were obtained, in order to define a confidence region for forecasting the further daily deaths reports in Brazil. The results for forecasting the Covid-19 spread behavior, considering the training step, is shown in Fig. 7(a). The results of updating of interval type-2 fuzzy Kalman filter for forecasting the COVID-19 spreading behavior, are shown in Fig. 7, Fig. 7. It can be seen an efficiency in the adaptability of estimated projections defined by interval type-2 fuzzy Kalman filter, which illustrates its applicability for adaptive tracking and real time forecasting the COVID-19 dynamic propagation. The estimated temporal behavior of the interval type-2 fuzzy Kalman gain matrices ${\tilde{\mathbf{K}}}^i{|}^{i=1,\dots ,3}$, during recursive updating of interval type-2 fuzzy Kalman filter inference system, is shown in Fig. 8.

Fig. 6.

The confidence region obtained by interval type-2 fuzzy Kalman filter for tracking the experimental dataset of daily deaths reports, in Brazil.

Fig. 7.

The interval response of interval type-2 fuzzy Kalman filter for tracking and forecasting of COVID-19 spreading behavior, in Brazil: (a) results based on training dataset ranging from 29 of February 2020 to 18 of May 2020; (b) update performed on 27 of May 2020; (c) update performed on 14 of June 2020; (d) update performed on 24 of June 2020; (e) update performed on 30 of June 2020; (f) update performed on 15 of July 2020.

Fig. 8.

Estimation of Kalman gains, for tracking and forecasting the COVID-19 spread behavior, in Brazil: (a) Rule 1, (b) Rule 2, (c) Rule 3.

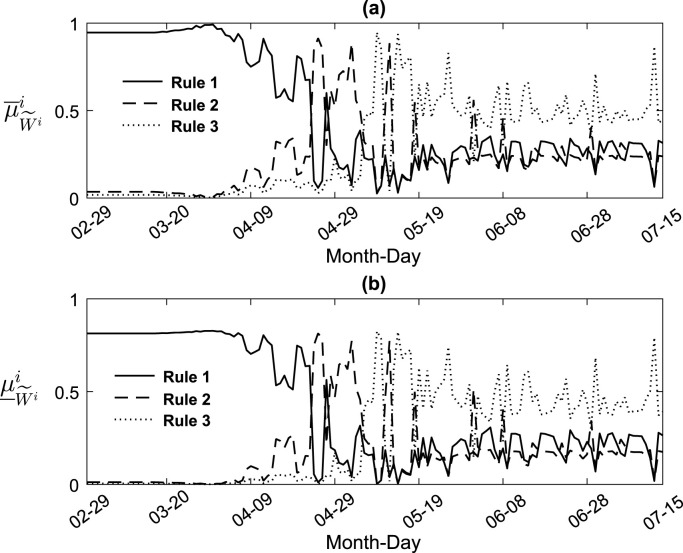
The normalized activation degrees of the rules of interval type-2 fuzzy Kalman filter, are shown in Fig. 9. The Variance Accounted For (VAF) criterion was used to verify the efficiency of interval type-2 fuzzy Kalman filter for forecasting the COVID-19 dynamic spread behavior, as shown in Fig. 10.

Fig. 9.

The instantaneous behavior of normalized activation degrees of the fuzzy rules: (a) Upper activation degrees, (b) Lower activation degrees.

Fig. 10.

Efficiency of interval type-2 fuzzy Kalman filter, in tracking and forecasting the COVID-19 dynamic spreading behavior, in Brazil.

3.2. The main impressions of the comparative analysis

In this section, a more detailed discussion on the results shown in Section 3.1 and a comparative analysis of proposed methodology with the approaches in [47], [48], [49], considering the metrics RMSE (Root Mean Square Error), MAE (Mean Absolute Error), R${}^2$ (coefficient of determination), and MAPE (Mean Absolute Percentage Error), is presented.

The initial forecasting of the dynamic spread behavior of COVID-19 shown in Fig. 7(a), in Brazil, is based on the training step of interval type-2 fuzzy Kalman filter considering the first experimental epidemiological data made available by the Ministry of Health of Brazil, corresponding to the period from March/2020 to May/2020. According to proposed methodology, the new experimental epidemiological data are recursively processed for parametric updating of the interval type-2 fuzzy Kalman filter, so that a new forecasting can be accurately achieved taking into account the variations of the recent epidemiological data, as illustrated in Figs. 7(b)–7(e).

The approach [47] is based on new short term forecasting model using an enhanced version of the adaptive neuro-fuzzy inference system (ANFIS) for forecasting the COVID-19 propagation dynamics in Brazil, within the horizon of 12 days. In Table 1 are shown the results for comparative analysis between the interval type-2 fuzzy Kalman filter and the approach in [47]. Once the approach in [47] consider the uncertainties inherent to COVID-19 propagation dynamics by using of fuzzy systems theory, it presents competitive results compared to interval type-2 fuzzy Kalman filter, but its performance is inferior due to its type-1 fuzzy structure for forecasting the uncertain dynamics of experimental epidemiological data. On the other hand, the uncertainties are processed by the interval type-2 fuzzy Kalman filter in approximating the dynamic behavior inherent to experimental dataset in interval fuzzy operating regions defined on fluctuations of propagation of the COVID-19, minimizing the errors of tracking and forecasting.

Table 1.

Results of the comparative analysis between the interval type-2 fuzzy Kalman filter and approach present in [47].

Methodology	RMSE	MAE	R${}^2$	MAPE(%)
Approach in [47]	19.432	14.273	0.904	0.3117
Interval type-2 fuzzy Kalman filter	11.547	3.330	0.999	6.33$\times 10^{-6}$

The approach in [48] is based on a firefly algorithm for ensemble neural network optimization applied to COVID-19 time series prediction in Brazil using type-2 fuzzy logic, within the horizon of 30 days. In Table 2 are shown the results for comparative analysis between the interval type-2 fuzzy Kalman filter and the approach in [48]. The approach in [48], although uses a type-2 fuzzy structure for modeling the epidemiological experimental data, it presents slightly inferior results compared to interval type-2 fuzzy Kalman filter once it does not consider the variability in the dynamics of the experimental dataset to update the propagation forecasts of COVID-19 [50]. On the other hand, the interval type-2 fuzzy Kalman filter presents greater efficiency due to its recursive parameterizing mechanism for adaptive tracking and real time forecasting of experimental dataset.

Table 2.

Results of the comparative analysis between the interval type-2 fuzzy Kalman filter and approach present in [48].

Methodology	RMSE	MAE	R${}^2$	MAPE(%)
Approach in [48]	2.53$\times 10^{-5}$	5.48$\times 10^{-6}$	0.99942	1.52$\times 10^{-1}$
interval type-2 fuzzy Kalman filter	1.24$\times 10^{-5}$	2.62$\times 10^{-6}$	0.99976	1.43$\times 10^{-1}$

The approach in [49] is based on a novel Deep Interval Type-2 Fuzzy LSTM (Long Short-Term Memory) model for prediction of the COVID-19 incidence, including new cases, recovery cases, and mortality rate in Brazil, within the horizon of 15 days. In Table 3 are shown the results for comparative analysis between the interval type-2 fuzzy Kalman filter and the approach in [49]. As it can be seen, although the approach in [49] presents satisfactory results once the LSTM model has the capability to learn higher-level features inherent to dataset, its performance is inferior than the interval type-2 fuzzy Kalman filter due to its computing limitation from tuning the hyper-parameter model and determining the number of layers, the number of neural units by layer, the activation function, the learning rate, the loss function, and other parameters.

Table 3.

Results of the comparative analysis between the interval type-2 fuzzy Kalman filter and approach present in [49].

Methodology	RMSE	MAE	R${}^2$	MAPE(%)
Approach in [49]	0.1021	0.0862	0.99913	1.23$\times 10^{-1}$
Interval type-2 fuzzy Kalman filter	0.1005	0.625	0.99954	1.54$\times 10^{-1}$

4. Final remarks

In this paper, an approach for designing of interval type-2 fuzzy Kalman filters, was proposed. Experimental results and comparative analysis shown the efficiency of the proposed methodology for adaptive forecasting the COVID-19 spreading dynamics, due to its recursive updating mechanism. For further works, the use of evolving interval type-2 fuzzy systems and multiobjective optimization techniques are of particular interest.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix. Notations

A.1. Symbols and variables

Symbol	Description
$n$	Minimum order of the interval type-2 fuzzy Kalman filter
$p$	Number of outputs
$m$	Number of inputs
$c$	Number of fuzzy rules
$q$	Number of Markov parameters
${\widetilde{\hat{\mathbf{x}}}}_{k+1}^i$	Estimated interval states vector
${\mathbf{y}}_k$	Real experimental data
${\widetilde{\hat{\mathbf{y}}}}_k^i$	Interval estimated output
${\mathbf{u}}_k$	Input signal
${\tilde{\mathbf{A}}}^i$	Interval state matrix of $i$th fuzzy rule
${\tilde{\mathbf{B}}}^i$	Interval input matrix of $i$th fuzzy rule
${\tilde{\mathbf{C}}}^i$	Interval output matrix of $i$th fuzzy rule
${\tilde{\mathbf{D}}}^i$	Interval direct transmission matrix of $i$th fuzzy rule
${\tilde{\mathbf{K}}}^i$	Interval Kalman gain matrix of $i$th fuzzy rule
${\widetilde{\overline{\mathbf{Y}}}}^i$	Interval observer gain Markov parameters vector of $i$th fuzzy rule
${\tilde{\mathcal{P}}}_{\gamma }^i$	Observability matrix
${\tilde{\mathcal{Q}}}_{\gamma }^i$	Controllability matrix
${\tilde{W}}^i$	Interval type-2 fuzzy set
${\mathbf{Z}}_k$	Experimental dataset of inputs and outputs
${\tilde{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)$	Type-2 membership value of $i$th fuzzy rule
${\underset{\_}{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)$	Lower membership value of $i$th fuzzy rule
${\overline{\mu }}_{{\tilde{W}}^i}^i\left({\mathbf{Z}}_k\right)$	Upper membership value of $i$th fuzzy rule
$\alpha$	Unobservable spectral components
$\xi$	Number of extracted unobservable spectral components
$\mathbf{H}$	Trajectory matrix
$\mathbf{S}$	Covariance matrix in Singular Spectral Analysis Algorithm
${\tilde{\mathit{\epsilon }}}_k^i$	Residual error
$\mathcal{E}>0$	Termination tolerance
$\tilde{m}$	Interval weighting exponent
${\tilde{\mathbf{v}}}^{i^{\left(l\right)}}$	Centers of the clusters
${\tilde{\mathbf{F}}}^i$	Covariance matrix of $i$th cluster
${{\tilde{D}}^i}_{k{\tilde{\mathbf{F}}}^i}$	Distance between the sample ${\mathbf{Z}}_k$ and ${\tilde{\mathbf{v}}}^{i^{\left(l\right)}}$
${\tilde{\mathbf{U}}}^{\left(l\right)}$	Partition matrix
$\mathbf{\Lambda }$	Matrix of Regressors
${\tilde{\mathbf{\Gamma }}}^i$	Diagonal weighting matrix
${\tilde{\mathbf{Q}}}^i$	Orthogonal matrix resulting of QR factorization
${\tilde{\mathbf{R}}}^i$	Upper triangular matrix resulting of QR factorization
${\tilde{\mathbf{H}}}^i$	Hankel matrix
${\tilde{\mathbf{\Sigma }}}^i$	Diagonal matrix of singular values
${\mathit{\lambda }}_k$	Regressors vector
$\gamma$,  $\beta$	Parameters related to dimension and hank of Hankel matrix ${\tilde{\mathbf{H}}}^i$
$\mathcal{R}$	Effective reproduction number

A.2. Abbreviations

Abbreviation	Description
COVID-19	Corona Virus Disease 2019
ES	Exponential Smoothing
FKF	Fuzzy Kalman Filter
KF	Kalman Filter
LASSO	Least Absolute Shrinkage and Selection Operator
LR	Linear Regression
LSTM	Long Short-Term Memory
MAE	Mean Absolute Error
MAD	Median Absolute Deviation
MAPE	Mean Absolute Percentage Error
MSE	Mean Square Error
OKID	Observer/Kalman Filter Identification
$R^2$	Coefficient of Determination
RMSE	Root Mean Square Error
RMSPE	Root Mean Square Percentage Error
SEIR	Susceptible–Exposed–Infectious–Recovered
SIR	Susceptible–Infectious–Recovered
SVD	Singular Value Decomposition
SVM	Support Vector Machine
VAF	Variance Accounted For
WCRVFL	Wavelet-Coupled Random Vector Functional Link