Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Mar 21;7(13):11240–11251. doi: 10.1021/acsomega.2c00142

Effective Approach with Extra Desorption Time to Estimate the Gas Content of Deep-Buried Coalbed Methane Reservoirs: A Case Study from the Panji Deep Area in Huainan Coalfield, China

Qiang Wei †,‡,§,*, Baolin Hu ∥,*, Huihuang Fang ‡, Chunshan Zheng ‡, Xiaowei Hou ⊥, Deyi Gao #, Hongjie Xu ∥, Huihu Liu ∥, Congqiu Shi †, Jiaying Tong †
PMCID: PMC8992273  PMID: 35415329

Abstract

graphic file with name ao2c00142_0012.jpg

In this study, 11 core coal samples were collected from deep-buried coalbed methane (CBM) reservoirs with burial depth intervals of 900–1500 m for gas estimation content by a direct method. In desorption experiments, the cumulative gas desorption data were recorded within 2 h in the field on the basis of the China National Standard method. For accuracy, two improved methods were proposed. The results show that the gas contents of deep-buried coal samples based on the China National Standard and mud methods are 3.58–9.89 m3/t (average of 6.03 m3/t) and 3.74–10.05 m3/t (average of 6.20 m3/t), respectively. The proposed Langmuir equation and logarithmic equation methods exhibited nonlinear relationships between the cumulative desorption volume and desorption time, which yield values of 6.33–13.34 m3/t (average of 9.36 m3/t) and 6.15–13.86 m3/t (average of 10.37 m3/t), respectively. In addition, the two proposed methods combine the raw data within 2 h by the China National Standard method and additional desorption points during extra time, which are helpful for the ability of the hypothetical methods to calculate the gas content. The Langmuir equation method is a relatively more accurate method to estimate the gas content in comparison with the proposed logarithmic method, which is based on the relative error and comparison plots of actual data and simulated results. From the perspective of numerical value, the Langmuir equation method gives values 1.06–3.39 times (average of 1.86 times) those of the China National Standard method. These analyses show that the proposed Langmuir equation method with extra desorption points is an effective method to determine the gas content of deep-buried CBM reservoirs.

1. Introduction

By 2050, energy consumption in the world will increase if current policy and technology trends continue, due to population and economic growth.1,2 In addition to petroleum and other liquids, natural gas will surpass coal and become the second largest source of primary energy.1,3 As a kind of natural gas, the coalbed methane (CBM) resource is abundant worldwide and has become a realistic and reliable supplementary resource of conventional natural gas.4 In addition, the development and utilization of CBM can effectively make up for the shortage of the natural gas supply and regional distribution and reduce emissions of greenhouse gases.4,5 Gas content is one of the essential parameters in CBM exploration and development, favorable area evaluation, and reservoir research.6,7 Gas content estimation methods include direct and indirect methods.8−10 The former uses a canister desorption measurement from core coal samples by measuring desorbed, lost, and residual gas contents, respectively.11 For this method, the lost gas content is obtained using graphic and analytical methods based on plots of the desorption times versus initial desorption points.12−14 The latter provides an means to determine the gas-bearing characteristics of coal seams in untapped blocks.7,15 Usually, the direct method is a more reliable and common method in the fields of CBM exploration and resource estimation because of the faster speed of data acquisition and higher accuracy of gas content calculations.17,18

The direct method was first proposed in 1970,19 and later the United States Bureau of Mines (USBM) adopted this method in an accelerated methane emission project.15,20 The basic principle of this method is that CBM has three occurrence states, namely adsorption, free, and water-soluble states, among which the adsorbed state is the main occurrence state of CBM.21−23 In addition, the coal seam has a triple structure of coal matrix, pores, and fractures.24−26 The adsorbed gas dissociates from the coal matrix to fracture through a desorption–diffusion process and escapes outward under the action of differential pressure.12,23,27 The gas desorption process is regarded as gas diffusion from a collection of spherical coal particles with a zero surface concentration and a constant initial gas concentration.23,28−30 On the basis of related research and guidelines,29,30 the cumulative desorption gas volume at the initial time is directly proportional to the square root of time, which is used to calculate the lost gas content. With a long exposure time, the lost gas content and relative error exhibit great numerical values.16 If the lost gas content accounts for more than 20% of the total gas content, it can be regarded as an inaccurate calculation.31

On the basis of these considerations, accurate direct methods have been used to estimate the lost gas content in the field, such as the USBM method, curve fit method (including linear regression, polynomial, and Amoco methods) and the Smith–Williams method.32−39 At present, because the in situ sealed sampling apparatus has already been optimized, it is widely used, as it reduces the errors of gas content calculations.16 However, various methods have different degrees of errors in gas content estimation due to their applicability and analytical principles.8,16,40,41 For instance, in the USBM method, the lost gas content is acquired on the basis of the desorbed data, and the total gas content is the sum of desorbed, lost, and residual gas contents.40 Comparably, the curve fit and Smith–Williams method are numerical analysis methods and the residual gas content is not within the scope of the calculations.8 In the former method, the gas content is fitted on the basis of a plot of cumulative desorption data and desorption time. However, the relative errors of the curve fit method (particularly the polynomial method) increase with an extension of the core recovery time.16 For the Smith–Williams method, the gas content is a function of the desorbed gas multiplied by a coefficient.33 Of note, the lost gas contents calculated by the USBM method and Smith–Williams method have been regularly underestimated.42

Commonly, the gas contents in deep-buried CBM reservoirs (burial depth >800 m) are an extrapolation of shallow reservoirs with similar behaviors and trends.43 The accurate gas content of deep-buried CBM reservoirs should be carefully estimated, rather than using an analogy method based on shallow reservoirs. With increased in the buried depth (burial depth 900–1500 m), the adsorbed methane molecules in the coal matrix tend to be saturated and are compactly arranged, and the increases in the gas content of deep-buried CBM reservoirs is mainly contributed by free gas.6,7 Additionally, due to the rapid drop of pressure during the retrieval process, the time for the conversion of adsorbed gas into free gas may be increased .16 Therefore, the amount of gas released in deep-buried CBM reservoirs is greater than that in shallow reservoirs, and the actual lost gas content is possibly higher than that of the USBM method.16

In terms of the advantages and drawbacks of above three approaches and the geological characteristics, 11 core coal samples were collected from deep-buried CBM reservoirs in the Panji Deep Area of the Huainan Coalfield. The geological background is omitted, because it has been described in detail in our previous reports.6,7,22,26 In this study, the gas desorption experiments were conducted exceeding 2 h on all coal samples in the field, and experiments on some samples were carried out for more than 40 h. The raw data of each experiment were recorded, including mud density, retrieval time, cumulative gas volume, and sample weight. On the basis of the above works, the gas content was calculated by following the China National Standard method, which is similar to the USBM method. For accuracy, the lost gas content was corrected on the basis of modified and updated multiple parameters, such as density of drilling medium (mud), burial depth, gas pressure, and actual exposure time of coal core sample in borehole: that is, the mud method. Afterward, we estimated the lost gas content based on the China National Standard method and differential retrieval times, which is not suitable for cumulative desorption data with extra desorption time. Therefore, two curve fit approaches (logarithmic equation method and Langmuir equation method) are proposed for gas content correction. By a comparison, the proposed Langmuir equation method was confirmed to be an effective method to investigate the gas content of deep-buried CBM reservoirs. This approach can estimate the lost and total gas contents from the cumulative desorption data, which serves as a new idea for the calculation of gas content in deep-buried CBM reservoirs. Furthermore, this study can provide guidance for the exploration of deep-buried CBM resources.

2. Samples and Methods

2.1. Sample Collection

Figure 1 shows the sampling sites of fresh coal core samples from the Panji Deep Area. According to the well distribution, a total of 11 samples were collected from the aforementioned sample sites to estimating the gas content using canister desorption measurements. Especially, seven coal samples were taken by the wireline core drilling technique and are marked in Table 1. All of the samples were cored under mud medium. The mud density was approximately 1.10 × 103 t/m3, which was obtained through tests during the sampling process. For accuracy, the exposure time in air of each coal sample was set within 8 min. Before this step, the canister was cleaned and flushed with argon, and the airtightness was tested with a pressure of 0.30–0.40 MPa.44 Meanwhile, the exposure times in the borehole and air of each coal sample are given in Table 1. In addition, the sample weight, gas pressure, and reservoir temperature were calculated, and the flowchart of the study is presented in Figure 2.

Figure 1.

Figure 1

Open in a new tab

Location map (a) and sampling sites (b) of coals from the Panji Deep Area in the Huainan Coalfield.

Table 1. Basic Information on the Collected Deep-Buried Coal Samples from the Panji Deep Areaa.

sample no. H (m) Gdaf (g) Pw (MPa) t1 (min) t2 (min) t3 (min) T (°C) sampling method
2-3 1415.20 228.48 14.43 63.5 8 29.41 58 traditional
4-3 1363.85 197.39 12.77 56 9 23.83 56 traditional
6-2 1228.40 383.40 11.15 48.5 3 20.00 52 traditional
17-1 913.90 204.20 6.38 25 6 7.92 42 wireline
20-4 1267.75 383.48 12.04 25 6 10.78 53 wireline
20-5 1369.30 220.84 13.36 22.5 7 9.97 55 wireline
21-4 1320.70 349.21 12.18 10 2 4.19 55 wireline
22-6 1367.20 142.90 13.16 20 3 8.74 55 wireline
26-4 1215.10 183.79 10.55 52.5 8 20.70 51 traditional
13-2 1171.6 302.12 10.21 11 3 4.36 48 wireline
13-3 1368.8 187.46 13.35 12.5 5 5.78 55 wireline
Open in a new tab
a

Definitions: H, burial depth; Gdaf, weight of each coal sample; Pw, gas pressure; t1, exposure time in the borehole based on China national standard, that is, half of the retrieval time; t2, exposure time before the sample is asealed in a canister of each coal sample; t3, exposure time in the borehole based on the mud pressure; T, reservoir temperature.

Figure 2.

Figure 2

Open in a new tab

Research flowchart of this study.

2.2. Estimation Methods of Gas Content

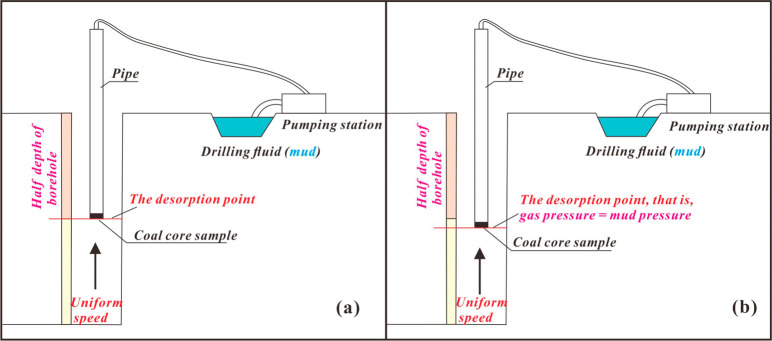
Canister desorption measurements of each coal sample were conducted byfollowing the China National Standard GB/T 23249-2009.31 Prior to measurement, the desorbed gas content was tested after each sample was heated to the reservoir temperature in a bath. During desorption measurement within 2 h, the desorbed volumes were recorded at time ranges of 1, 2, 3, 5, 10, 30, and 60 min (Table 2). When the desorption time exceeded 2 h, the desorption data were recorded at 60 min intervals. Afterward, the residual gas content was obtained using a portion of the crushed coal sample.45 Before calculation, the raw data of each coal sample were corrected on the basis of standard temperature and pressure conditions (STP); the detailed expressions are given in a report by Xu et al.16 Significantly, the desorption point is the half-depth of the borehole when the coal sample was raised.31 This method assumes that the desorption time of a coal core sample is half of the retrieval time: that is, the exposure time of sample in the borehole (t1). In addition, the exposure time before a core coal sample was sealed in a canister (t2) plus t1 is the total exposure time. Actually, the relationship between the gas pressure in the coal core and the surrounding mud pressure has undergone three changes during the retrieval process: (1) in the early stage of retrieval, the gas pressure of the coal core is less than that of the mud pressure; (2) as the process continues, the gas pressure of the coal core is equal to the mud pressure; (3) afterward the gas pressure of the coal core is greater than the mud pressure. Therefore, the gas desorption process was carried out under nonisobaric conditions in the mud medium;12,46 the exposure time based on the China National Standard is inconsistent with the actual situation. Detailed information is given in Figure 3.

Table 2. Raw Data of Sample 26-4 in Desorption Measurement within 2 h.

          desorption data
          ambient conditions
 STP conditions
time (min) time interval (min) ambient pressure (kPa) ambient temp (°C) bath temperature (°C) desorbed gas (cm3) accumulated volume (cm3) desorbed gas (cm3) accumulated volume (cm3)
19:25 0 101.3 11.5 42 0 0 0.00 0.00
19:26 1 101.3 11.5 42 7 7 6.04 6.04
19:28 2 101.3 11.5 42 3 10 2.59 8.63
19:31 3 101.3 11.5 42 3 13 2.59 11.23
19:35 4 101.3 11.5 42 4 17 3.46 14.68
19:40 5 101.3 11.5 42 8 25 6.92 21.60
19:45 5 101.3 11.5 42 7 32 6.06 27.66
19:50 5 101.3 11.5 42 6 38 5.20 32.86
19:55 5 101.3 11.5 42 4 42 3.47 36.33
20:00 5 101.3 11.5 42 4 46 3.47 39.79
20:05 5 101.3 11.5 42 5 51 4.34 44.13
20:10 5 101.3 11.5 42 5 56 4.34 48.47
20:15 5 101.3 11.5 42 6 62 5.21 53.68
20:20 5 101.3 11.5 42 2 64 1.74 55.42
20:25 5 101.3 11.5 42 5 69 4.34 59.76
20:35 10 101.3 11.5 42 6 75 5.22 64.98
20:45 10 101.3 11.5 42 7 82 6.09 71.07
20:55 10 101.3 10 42 3 85 2.61 73.68
21:05 10 101.3 10 42 4 89 3.48 77.16
20:15 10 101.3 10 42 2 91 1.74 78.90
20:25 10 101.3 10 42 3 94 2.61 81.52
Open in a new tab

Figure 3.

Figure 3

Open in a new tab

Determination of desorption points of the China National Standard method (a) and the mud method (b).

To correct the exposure time, the gas pressure is converted to the depth at which the mud pressure is equal, and then the time of a coal core arriving at the borehole from the depth can be calculated: that is, the exposure time of the coal core in the borehole (t3). The method can be expressed as46

2.2. 1

where t3 is the exposure time of coal core in borehole based on mud pressure (min), hed is the gas pressure that converted to the depth at which the mud pressure is equals (m), vs is the drilling speed (m/s), Pw is the gas pressure (MPa), t is the drilling time (min), h is the buried depth of the coal core (m), and ρm is the mud density with a value of 1.10 × 103 kg/m3. Notably, the vertical variation of gas pressure was obtained from the fitting results of neighboring coal mines in the Panxie Coal Mining Area, which was explained in our previous study.6

Consequently, the lost gas content can be acquired by the accumulated gas desorption volume and desorbed time, and the equation is31

2.2. 2

or

2.2. 3

where Vd is the desorbed volume in the desorption experiment (cm3), K is a constant to be determined; Vi is the desorbed volume at t2 (cm3), and t4 is the desorption time of the coal sample in the canister.

After desorption experiments, all of the coal samples were placed in thermostats to obtain the residual gas content. The total gas content of each coal sample was calculated by the summation of desorbed, lost, and residual gas contents, which can be expressed as31

2.2. 4

where Vt is the total gas content, Vd is the desorbed gas content, Vl is the desorbed gas, and Vr is the residual gas content. Due to the drawbacks of the above methods, the corrected estimation methods are shown in a later discussion.

3. Results

3.1. Basic Information on Deep-Buried Coal Samples

As shown in Table 1, all of the coal samples were collected at depths of 900–1500 m, more than half of which were obtained using the wireline coring method. The weights of each sample have different values of 142.90–383.48 g (average of 253.02 g); this is mainly due to the different thicknesses of coal seams drilled in the boreholes. On the basis of tests, the gas pressures (Pw) of coal seams were acquired and values obtained were in the range of 6.38–14.43 MPa (average of 11.60 MPa). Moreover, the temperature of the coal seam was obtained by a least-squares fitting calculation on the basis of neighboring coalmines from the Panxie Coal Ming Area, and the values are in the range of 42–58 °C (average of 52.73 °C). The detailed analysis process and related basic data of coal seams have been shown in our previous reports.6,7,22,26

3.2. Total Gas Content Based on the Direct Method

According to raw data of desorption measurements, the cumulative desorption data show a linear correlation with desorption time (sqrt) at the initial stage. The desorption volume has various values at given interval times from samples 2-3 to 26-4 in Figure 4, and this also appeared in the maximum volume (Figure 4). It should be noted that the released gas volume is correlated with the desorption time in the early process of desorption experiment, but the increase was slower at the remaining time. This finding suggests that deep-buried CBM reservoirs in this region contained high gas contents with a large proportion of free gas, which escaped during the retrieval stage, but the absorbed gas was still preserved in the coal matrix.

Figure 4.

Figure 4

Open in a new tab

Cumulative desorption data and fitting line based on mud and China national standard methods within 2 h of desorption experiments in the field: (a) sample 2-3; (b) sample 4-3; (c) sample 6-2; (d) sample 17-1; (e) sample 20-5; (f) sample 26-4.

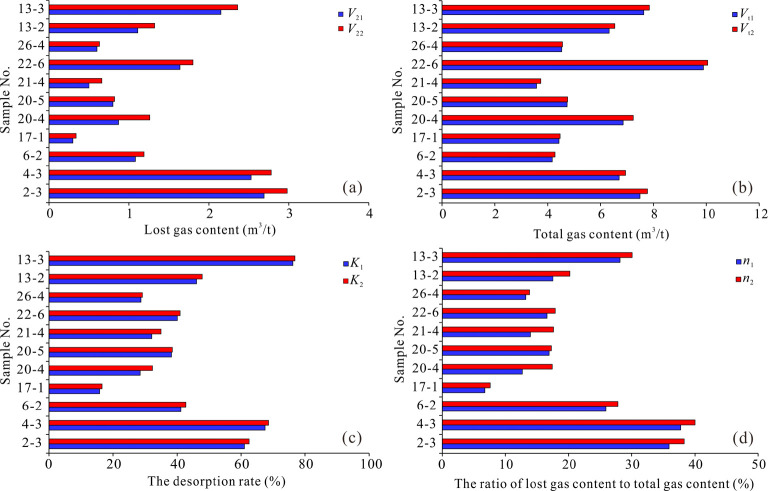
The desorbed gas content (V1) is in the range of 0.40–2.32 m3/t with an average of 1.47 m3/t. The simulated lost gas content (V21) based on the China national standard method of coal samples is shown in Table 3, and the value ranges from 0.30 to 2.69 m3/t with a mean value of 1.30 m3/t. The total gas content (Vt1) is 3.58–9.89 m3/t with an average of 6.03 m3/t. The K1 and n1 values are 15.80–76.18% (average of 43.22%) and 6.77–37.76% (average of 20.49%), respectively. For the mud method, the simulated lost gas content (V22) is 0.34–2.98 m3/t with an average of 1.47 m3/t, and the total gas content (Vt2) is 3.74–10.05 m3/t with an average of 6.20 m3/t. Moreover, the desorption rate (K2) is 16.55–76.82% with an average of 44.65%, and the n2 ranges from 7.61 to 40.00% with an average of 22.55%. Of note, the obvious difference in gas content of deep-buried CBM reservoirs is mainly reflected by the lost and residual gas contents. The results from the above two methods in Figure 5 indicate that the values of the China national standard method are lower than that of mud method, and the difference in lost gas content can be attributed to the desorption point in the borehole (Figure 4).

Table 3. Gas Content Estimation Based on China National Standard Method and Mud Method within 2 h of Desorption Experiments in the Fielda.

sample site burial depth (m) V1 (m3/t) V21 (m3/t) V22 (m3/t) V3 (m3/t) Vt1 (m3/t) Vt2 (m3/t) K1 (%) K2 (%) n1 (%) n2 (%)
2-3 1415 1.88 2.69 2.98 2.92 7.49 7.78 61.01 62.47 35.91 38.30
4-3 1363 1.99 2.53 2.78 2.18 6.7 6.95 67.46 68.63 37.76 40.00
6-2 1228 0.64 1.08 1.19 2.45 4.17 4.28 41.25 42.76 25.90 27.80
17-1 914 0.4 0.3 0.34 3.73 4.43 4.47 15.80 16.55 6.77 7.61
20-4 1268 1.08 0.87 1.26 4.9 6.85 7.24 28.47 32.32 12.70 17.40
20-5 1369 1.01 0.8 0.82 2.92 4.73 4.75 38.27 38.53 16.91 17.26
21-4 1320 0.65 0.5 0.66 2.43 3.58 3.74 32.12 35.03 13.97 17.65
22-6 1368 2.32 1.64 1.8 5.93 9.89 10.05 40.04 41.00 16.58 17.91
26-4 1215 0.7 0.6 0.63 3.23 4.53 4.56 28.70 29.17 13.25 13.82
13-2 1171.6 1.81 1.11 1.32 3.41 6.33 6.54 46.13 47.86 17.54 20.18
13-3 1368.8 3.67 2.15 2.36 1.82 7.64 7.85 76.18 76.82 28.14 30.06
Open in a new tab
a

Definitions: V1, desorbed gas content in the canister; V21, lost gas content based on the China national standard method; V22, lost gas content based on the mud method; V3, residual gas content in the laboratory; Vt1, total gas content based on the China national standard method; Vt2 = total gas content based on the mud method; K1, desorption rate based on the China national standard method; K2, desorption rate based on the mud method (%); n1, ratio of V21 to Vt1; n2, ratio of V22 to Vt2.

Figure 5.

Figure 5

Open in a new tab

Lost gas content (a), total gas content (b), K1 (c), and n1 (d) of deep-buried CBM reservoirs.

4. Discussion

4.1. Variations of Gas Contents Calculated by Traditional Methods

In the results given in Section 3, the total gas contents of deep-buried CBM reservoirs were calculated by the China national standard method and the mud method. Figure 6 gives clear evidence that the total gas contents obtained by different methods have obvious differences in the value of each sample, and the order is Vt2 > Vt1. The China national standard and mud methods used a desorption instrument to measure the variation law of gas content within the given desorption time intervals and estimated the lost gas content on the basis of the exposure time and desorption data of all coal samples. Afterward, the sealed tank was sent to a laboratory to determine the residual gas content. Therefore, the total gas content measured by these two methods consists of three parts: namely, lost, desorbed and residual gas contents. As shown in Tables 1 and 3, the total gas contents from the China national standard and mud methods are 3.58–9.89 m3/t (average of 6.03 m3/t) and 3.74–10.05 m3/t (average of 6.20 m3/t), respectively. Comparably, the gas contents obtained by the China national standard and mud methods are merely 19.81–45.70% and 20.70–46.44% of the value by an indirect method, respectively. The difference between the first two methods is mainly reflected in the lost gas content, and the mud medium and desorption points are the two parameters causing the difference in the numerical value of the total gas content.46 In fact, the differences in the first two methods and associated mechanisms are apparent, and more details are presented in Figure 3.

Figure 6.

Figure 6

Open in a new tab

Total gas content by various methods.

Generally, various methods have different degrees of error in the calculation of gas content. With the traditional method, the retrieval time is long and the reservoir temperature is different from that of the in situ desorption environment. As a result, the error increases with the increased buried depth of the coal seam. The China National Standard GB/T 23249-2009 stipulates that, when the buried depth is greater than 500 m, the actual gas content equals the estimated gas content multiplied by a correction factor (value of 1.2), which is similar to the Smith–Williams method.31 However, when the burial depth is >800m, the corrected gas content has difficulty in meeting the production needs of CBM.

The gas content of coal seams increases with burial depth, but it is affected by the positive effect of stratum pressure and the negative effect of reservoir temperature.7 After a certain depth is reached, the effect of reservoir temperature is greater than that of stratum pressure, thus resulting in more free gas and water-soluble gas in the deep-buried CBM reservoir.6 In comparison with conventional shallow coal seams, the time lapse is increased during the retrieval process in deep-buried CBM reservoirs. Due to the faster drop of pressure, the time when the adsorbed gas in the coal seam transforms into free gas may also be increased. The conventional method only considers the amount of free desorption gas in the retrieval process, thus underestimating the gas content.16 Additionally, the conventional mathematical model used in shallow coal seams may not be suitable for the calculation of lost gas content of deep-buried CBM reservoirs; thus, the results need to be corrected.

4.2. Gas Content Estimation Based on Multiple Function Fitting

4.2.1. Selection of Fitting Formula

On the basis of desorption characteristics of the China national standard and mud methods in section 4.1, a consensus came down to the fact that both the desorbed gas content and residual gas content are actual test data and the lost gas content is a simulated result. In order to obtain the accurate gas content, the proportion of lost gas content or the unnecessary error should be reduced to a certain extent. From the practical results of field application in this study, the lost gas content accounted for 6.77–37.76% of the total gas content on the basis of the China national standard method and this value in the range of 7.61–40.00% on the basis of the mud method. In the sampling process, the gas content and the degree of coal fragmentation are objective factors.40 However, the retrieval time has a significant effect on the lost gas content among the subjective factors.37 In other words, the shorter the retrieval time, the less lost gas content.8,16,38,39

The simulated lost gas contents of the selected samples with different desorption times are shown in Figure 7. For sample 2-3 as an example, when the exposure times (the sum of t1 and t2) are 71.5, 50, 30, and 100 min, the corresponding lost gas contents are 682.30, 484.41, 299.25, and 943.92 cm3, respectively. The result suggests that the simulated lost gas content is far from the data of actual desorption time (Table 3). As shown in Figure 7, the cumulative desorption volume is proportional to the square root of time in the early process of the desorption experiment. The slope of the initial linear portion of the desorption curve is decreased with an increase in simulated desorption time, and the estimated lost gas content is generally increased. The plots reveal that the estimated lost gas content is different from the actual results; the errors possibly increase with an increase in simulated buried depth. In a deep-buried exploration area, the coal sample is exposed in the borehole for a long time using the traditional drilling technology and more gas is lost. With an increase in drilling depth, the error obtained by a linear equation is difficult to guarantee. Therefore, adequate preparations should be made before sampling to avoid the factor of prolonging the sampling process due to operation errors. To a certain extent, the lost gas content estimated by traditional methods with desorption data of 2 h is uncertain, because the volume fitted by the linear relationship between cumulative points and desorption time (sqrt) increases significantly with an increase in exposure time. This result shows the urgency of finding a suitable method to solve the above problem.

Figure 7.

Figure 7

Open in a new tab

Lost gas contents of selected samples based on the China national standard method with different desorption times: (a) sample 2-3; (b) sample 4-3; (c) sample 6-2; (d) sample 17-1; (e) sample 20-5; (f) sample 26-4. The red symbols represent the actual desorption times.

On the basis of the above analyses, sample 13-2 was selected for a desorption experiment with a desorption time of >40 h in the field. As shown in Figure 8, the actual data suggest that the cumulative desorption volume in the canister is linearly related to the desorption time at the initial stage. As the desorption time increases, the increasing rate of cumulative volume shows a decreasing tendency and even tends to move to a certain value. In general, gas migration in coal occurs on three scales:47 (1) bulk flow through the cleat system, (2) diffusion through the coal matrix pore system, and (3) migration outside along the cleat system. In the field, the balance between gas pressure and mud pressure is broken until the pipe reaches the desorption point (Figure 3), and a large amount of adsorbed coalbed methane is converted into the free state through the multiple migration channels of coal. When the temperature remains unchanged, the gas will no longer desorb under the situation of pressure or concentration balance. During this process, the cumulative desorption volume showed the characteristics of large–small–stable. There was no linear correlation between desorption volume and desorption time, which was limited by pressure, temperature, and gas-bearing property. With this focus and the actual data in Figure 8, two hypotheses were made as follows.

Figure 8.

Figure 8

Open in a new tab

Cumulative desorption volumes of sample 13-2 with different methods and exposure times: (a) simulated results by eq 7; (b) simulated results by eq 9.

Hypothesis i. We assumed that there is a logarithmic relationship between the cumulative desorption volume and desorption time, which is the proposed logarithmic equation

4.2.1. 5

where V is the accumulative desorption volume from the desorption point in the borehole to the end of desorption process (cm3/g), t is the desorption time (min), which is the sum of t1 + t2 + t4 or t1 + t3 + t4, and A is a coefficient.

Given the assumption that the coal core sample was placed in a canister from the point when it started out of the borehole, the lost gas content can be considered as a portion of accumulative desorption volume. This relationship can be expressed as

4.2.1. 6

where V′ is the accumulated desorption in the canister (cm3/g) and C is the lost gas content (cm3/g). On the basis of eqs 5 and 6, the proposed method can be transformed as

4.2.1. 7

Hypothesis ii. We assumed that the relationship between the cumulative desorption volume and the desorption time conforms to the curve characteristics of a Langmuir equation, which is the proposed Langmuir equation

4.2.1. 8

where A is the desorbed gas in canister; B is the function of desorption rate and adsorption heat.

On the basis of eqs 6 and 8, the proposed method can be transformed as

4.2.1. 9

4.2.2. Comparison of Calculation Results of Different Functions

On the basis of actual data, the data points between cumulative desorption volumes and exposure times of sample 13-2 are plotted in Figure 8. As shown in Figure 8, a section of data is missing in the actual data, which may be related to the characteristics of the coal sample during the field test. In this study, firstOpt software was used to simulate the lost gas content and total gas content. With this software, let Inline graphic and y = V′. Then make x and y variables and A, B, and C parameters. Afterward, input the transformed equation and actual data into the software. On the basis of iterative analyses, the values of parameters A, B, and C can be obtained (Table 4). For comparison, the above two methods and four groups with different exposure times were fitted on sample 13-2; the results are shown in Figure 8 and Table 4.

Table 4. Simulation Results of Two Methods with Different Exposure Times of Sample 13-2a.
  simulation params
            
exposure time (min) A B C RMSE RSS CC (R2) CD (R2) F-test rel error (%)
Proposed Logarithmic Equation
17 641.14   1046.4 40.04 117045.21 0.9963 0.9926 9652.05 –2.72
20 651.62   1118.2 32.20 72578.14 0.9973 0.9948 12901.32 –4.74
42 669.1   1293.2 24.04 38139.55 0.9983 0.9966 18772.08 –13.19
67 684.67   1469.7 18.91 21823.71 0.9987 0.9974 22944 –24.05
av 661.63   1231.88 28.80 62396.65 0.9977 0.9954 16067.36 –11.18
Proposed Langmuir Equation
17 2939.88 29.60 349.51 11.85 6484.4 0.9996 0.9996 110869.68 –0.11
20 2946.62 30.12 340.79 11.73 6403.82 0.9996 0.9996 102759.45 –0.04
42 2965.28 31.68 314.35 11.57 5698.83 0.9998 0.9996 81203.49 0.13
67 3011.36 36.52 287.16 11.57 5448.95 0.9997 0.9994 61459.01 –3.16
av 2965.79 31.98 322.95 11.68 6009 0.9997 0.9996 89072.91 –0.79
Open in a new tab
a

Definitions: RMSE, root mean squared error; RSS, residual sum of squares; CC, correlation coefficient; CD = coefficient of determination; F-test, joint hypotheses test; rel error, 100 × (V′ (maximum desorption volume of actual data))/V′.

The simulation parameters are given in Table 4, including the simulation parameters (A, B, and C), RMSE (root mean squared error), RSS (residual sum of squares), CC (correlation coefficient), CD (coefficient of determination), F-test (joint hypotheses test), and RE (relative error). The results simulated by the proposed logarithmic equation indicate that the CC is in the range of 0.9963–0.9987, and the RMSE is in the range 18.91–40.04 (average of 28.80). In addition, the ranges of values of the F-test and RE are 9652.05–22944 (average of 16067.36) and −24.05% to 2.72% (average of −11.18%), respectively. Moreover, the corresponding lost gas contents at 17, 20, 42, and 67 min are 1046.4, 1118.2, 1293.2, and 1469.7 cm3, respectively. The simulation results by the proposed Langmuir equation suggest that the CC is in the range 0.9996–0.9998 and the RMSE is in the range 11.57–11.85 (average of 11.68). The ranges of values of the F-test and RE are 61459.01–110869.68 (average of 89072.91) and −3.16% to 0.11% (average of −0.79%), respectively. Moreover, the corresponding lost gas contents at 17, 20, 42, and 67 min are 349.51, 340.79, 314.35, and 287.16 cm3, respectively. It should be noted that the lost gas contents simulated by eq 7 increase with an increase in the exposure time, whereas the lost gas contents simulated by eq 9 exhibit lower values with longer exposure time; this opposite phenomenon may be caused by the different iterative method of proposed Langmuir equation method.

The values of RMSE and RSS of the simulation results by the proposed logarithmic equation are higher than those of results by the proposed Langmuir equation, but the value of F-test is lower than that of the proposed Langmuir equation. This analysis indicates that the dispersion degree of the data fitted by the proposed logarithmic equation is higher than that of the proposed Langmuir equation, which shows that the deviation between the simulated value and the true value of the former is greater than that of the latter. As the exposure time increases, the values of RMSE and RSS display a decreasing trend but there is an increasing value of F-test. In contrast, the first two values of the proposed Langmuir equation show irregular characteristics, but the F-test value decreases as the exposure time increases.

Additional information is given by the values of relative error. The relative error of the proposed logarithmic equation is −24.05% to −2.72% (average of −11.18%), and that of the proposed Langmuir equation is −3.16% to 0.13% (average of −0.79%). Notably, the proposed Langmuir equation shows satisfactory accuracy with smaller errors. Figure 9 shows that, as the exposure time increases, the difference between the simulated desorption maximum value (V′) and the real data increases. Significantly, the result simulated by the proposed logarithmic equation shows a significant reduction in comparison with the actual data, and the relative error between the proposed logarithmic and Langmuir equation methods also tends to increase. The above analysis indicates that shortening the time of coal in the borehole and the time the canister of each coal sample is sealed can effectively reduce the error between the maximum desorption volume and the lost gas content caused by the increases in exposure time.

Figure 9.

Figure 9

Open in a new tab

Relative errors of simulated gas contents of sample 13-2 by eqs 7 and 9. Definitions: relative error 1, (eq 7 – actual result) × 100%/eq 9; relative error 2, (eq 7 – actual result) × 100%/eq 7; relative error 3, (eq 7 – eq 9) × 100%/eq 7.

Figure 10 shows the comparison plots of actual data and simulated gas contents during the whole desorption process. As shown in Figure 10a, the simulated gas content of sample 13-2 by the proposed logarithmic equation method is significantly lower than that of the actual data at a desorption time (sqrt) interval of 40–52 min but is higher than that of the actual data at 20–32 min (Figure 10b). In contrast, the distribution of all available data of the proposed Langmuir equation method is basically consistent with the actual data of the above two samples. To sum up, the two proposed methods considered the regularity of gas desorption and obtained relevant parameters based on the desorption characteristics, which is obviously better than the linear fitting method (Figure 7). Furthermore, the proposed Langmuir equation method with extra desorption data is an effective method to determine the gas content in this study.

Figure 10.

Figure 10

Open in a new tab

Comparison plots of actual data and simulated gas contents at exposure times of 13 and 17.5 min of sample 13-2 (a) and sample 13-3 (b).

4.2.3. Gas Content Estimation of All Coal Samples

For the results of the China National Standard and mud methods shown in Table 3, V1 can be regarded as the whole part of the desorbed gas released from coal and that directly obtained within 2 h in the canister, and the V21 and V22 values were obtained by a least-squares method according to the values of the first several effective desorption points in the desorption experiment. Notably, the lost gas content is considered as a part of the cumulative desorption content during the whole process. In other words, the desorbed and lost gas contents are the desorbable parts under certain experimental conditions.6,16 In a previous section of this study, a series of desorption points was obtained through desorption experiments exceeding 2 h, and numerical parameters such as lost gas content and total gas content were obtained by the proposed logarithmic equation and Langmuir equation. On the basis of the above analyses, the simulated gas content by the latter equation has a relatively lower error in comparison with that of the former equation, which presents a more accurate result.

Therefore, the total gas contents of all the coal samples were measured by above two methods. As shown in Table 5 and Figure 11, the total gas contents are 6.33–13.34 m3/t (average of 9.36 m3/t) and 6.15–13.86 m3/t (average of 10.37 m3/t) for the proposed logarithmic equation and Langmuir equation methods, respectively. In comparison with the China National Standard method, the simulated data by the proposed logarithmic equation are 1.04–2.24 times those of the China National Standard method with an average of 1.66 times. Moreover, data for the proposed Langmuir equation are 1.06–3.39 times those of of China National Standard method with average of 1.86 times.

Table 5. Simulated Gas Contents of All Coal Samples.
  gas content (m3/t)
    
sample no. eq 7 eq 9 eq 7/China national standard method eq 9/China national standard method
2-3 10.72 13.86 1.43 1.85
4-3 7.46 9.79 1.11 1.46
6-2 9.36 12.18 2.24 2.92
17-1 9.65 10.56 2.18 2.38
20-4 9.66 9.33 1.41 1.36
20-5 13.34 16.02 2.82 3.39
21-4 6.33 6.94 1.77 1.94
22-6 10.31 10.46 1.04 1.06
26-4 6.32 6.15 1.40 1.36
13-2 11.44 9.35 1.81 1.48
13-3 8.37 9.39 1.10 1.23
Open in a new tab
Figure 11.

Figure 11

Open in a new tab

Comparison between the simulated gas contents by the proposed logarithmic equation and Langmuir equation methods of all coal samples.

5. Conclusions

In this study, the gas contents of deep-buried coal core samples were estimated by direct methods (China National Standard and mud methods). For accuracy, two improved methods were proposed. The conclusions are as follows.

  • (1)

    The gas contents of deep-buried coal samples based on China National Standard and mud methods is 3.58–9.89 m3/t (average of 6.03 m3/t) and 3.74–10.05 m3/t (average of 6.20 m3/t), respectively. Comparably, the simulated gas contents by the proposed Langmuir equation and logarithmic equation methods are 6.33–13.34 m3/t (average of 9.36 m3/t) and 6.15–13.86 m3/t (average of 10.37 m3/t), respectively.

  • (2)

    The two proposed simulation methods provide nonlinear relationships between the gas desorption volume and the desorption time and give means for accurately estimating the total gas content and lost gas content. On the basis of raw experimental data and the statistical methodology, the methods can be regarded as relative accurate estimation methods in comparison with traditional methods in the Panji Deep Area. Further work is needed to find a method that is applicable to a larger range with higher accuracy.

  • (3)

    For the field data within 2 h by the China National Standard method, additional desorption points during extra are is helpful for the ability of the hypothetical method to calculate the gas content. The estimated gas contents by eq 9 are 1.06–3.39 times those of the China National Standard method with an average of 1.86 times, which shows that this method is an effective method for determining the gas content of a deep-buried CBM reservoir.

Acknowledgments

This work was financially supported by the University Synergy Innovation Program of Anhui Province (No. GXXT-2021-018), the University Natural Science Research Project of Anhui Province (No. KJ2021A1113), and the Start-up Fund for Doctoral Research of Suzhou University (No. 2019jb20).

Author Contributions

The manuscript was written with contributions from all authors, and all authors have approved the final version of the manuscript.

The authors declare no competing financial interest.

References

  1. Energy Information Administration (EIA) , 2021. Data retrieved from https://www.eia.gov/outlooks/ieo/pdf/IEO2021_ChartLibrary_full.pdf.
  2. Azadeh A.; Tarverdian S. Integration of genetic algorithm, computer simulation and design of experiments for forecasting electrical energy consumption. Energy Policy 2007, 35, 5229–5241. 10.1016/j.enpol.2007.04.020. [DOI] [Google Scholar]
  3. Aydin G. The Modeling and Projection of Primary Energy Consumption by the Sources. Energy Source. Part B 2015, 10 (1), 67–74. 10.1080/15567249.2013.771716. [DOI] [Google Scholar]
  4. Energy Information Administration (EIA) , 2017. Data retrieved from https://www.eia.gov/dnav/ng/hist/rngr52nus_1a.htm.
  5. Aydin G.; Karakurt I.; Aydiner K. Analysis and mitigation opportunities of methane emissions from energy sector. Energy Source. Part A 2012, 34 (11), 967–982. 10.1080/15567031003716725. [DOI] [Google Scholar]
  6. Wei Q.; Hu B. L.; Li X. Q.; Feng S. B.; Xu H. J.; Zheng K. G.; Liu H. H. Implications of geological conditions on gas content and geochemistry of deep coalbed methane reservoirs from the Panji Deep Area in the Huainan Coalfield, China. J. Nat. Gas Sci. Eng. 2021, 85, 103712. 10.1016/j.jngse.2020.103712. [DOI] [Google Scholar]
  7. Wei Q.; Li X. Q.; Hu B. L.; Zhang X. Q.; Zhang J. Z.; He Y. K.; Zhang Y. C.; Zhu W. W. Reservoir characteristics and coalbed methane resource evaluation of deep-buried coals: A case study of the No.13–1 coal seam from the Panji Deep Area in Huainan Coalfield, Southern North China. J. Petro. Sci. Eng. 2019, 179, 867–884. 10.1016/j.petrol.2019.04.100. [DOI] [Google Scholar]
  8. Hou X. W.; Liu S. M.; Zhu Y. M.; Yang Y. Evaluation of gas contents for a multi-seam deep coalbed methane reservoir and their geological controls: in situ direct method versus indirect method. Fuel 2020, 265, 116917. 10.1016/j.fuel.2019.116917. [DOI] [Google Scholar]
  9. Diamond W. P.; Schatzel S. J. Measuring the gas content of coal: a review. Int. J. Coal Geol. 1998, 35, 311–331. 10.1016/S0166-5162(97)00040-2. [DOI] [Google Scholar]
  10. Moore T. A. Coalbed methane: a review. Int. J. Coal Geol. 2012, 101, 36–81. 10.1016/j.coal.2012.05.011. [DOI] [Google Scholar]
  11. Standard practice for determination of gas content of coal - direct desorption method, ASTM D7569-10; ASTM International: 2010. [Google Scholar]
  12. Yang Z. B.; Qin Y.; Wang Z. F.; Wang G. F.; Wu C. F. Desorption-diffusion model and lost gas quantity estimation of coalbed methane from coal core under drilling fluid medium. Sci. China (Earth Sciences) 2010, 53 (4), 626–632. 10.1007/s11430-010-0027-x. [DOI] [Google Scholar]
  13. Xu H. J.; Ahmad F.; Hu B. L.; Sun G.; Liu H. H.; Ding H.; Zhang M.; Fang H. H. Methodology for Lost Gas Determination from Exploratory Coal Cores and Comparative Evaluation of the Accuracy of the Direct Method. ACS Omega 2021, 6, 19695–19704. 10.1021/acsomega.1c02351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Sun J.; Xiao X. M.; Wei Q.; Chen P.; Tian H.; Wu Y. W. Gas in place and its controlling factors of the shallow Longmaxi shale in the Xishui area, Guizhou, China. J. Nat. Gas Sci. Eng. 2020, 77, 103272. 10.1016/j.jngse.2020.103272. [DOI] [Google Scholar]
  15. Li J. Q.; Lu S. F.; Zhang P. F.; Cai J. C.; Li W. B.; Wang S. Y.; Feng W. J. Estimation of gas-in-place content in coal and shale reservoirs: a process analysis method and its preliminary application. Fuel 2020, 259, 116266–116266. 10.1016/j.fuel.2019.116266. [DOI] [Google Scholar]
  16. Xu H. J.; Pan Z. J.; Hu B. L.; Liu H. H.; Sun G. A new approach to estimating coal gas content for deep core sample. Fuel 2020, 277, 118246. 10.1016/j.fuel.2020.118246. [DOI] [Google Scholar]
  17. Zhang J.; Liu D.; Cai Y.; Pan Z.; Yao Y.; Wang Y. Geological and hydrological controls on the accumulation of coalbed methane within the No. 3 coal seam of the southern Qinshui Basin. Int. J. Coal Geol. 2017, 182, 94–111. 10.1016/j.coal.2017.09.008. [DOI] [Google Scholar]
  18. Wang L.; Cheng L.; Cheng Y.; Liu S.; Guo P.; Jin K.; Jiang H. A new method for accurate and rapid measurement of underground coal seam gas content. J. Nat. Gas. Sci. Eng. 2015, 26, 1388–1398. 10.1016/j.jngse.2015.08.020. [DOI] [Google Scholar]
  19. Bertard C.; Bruyet B.; Gunther J. Determination of desorbable gas concentration of coal (direct method). Int. J. Rock Mech. Min. Sci. 1970, 7, 43–65. 10.1016/0148-9062(70)90027-6. [DOI] [Google Scholar]
  20. Yan J. W.; Fang X.; Guo Y.; Wang W.; Wu L.; Tan Z. H. Desorption Effects and Laws of Multiscale Gas-Bearing Coal with Different Degrees of Metamorphism. ACS Omega 2021, 6, 22114–22125. 10.1021/acsomega.1c02706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Smith D. M.; Williams F. L. Diffusion models for gas production from coals: Application to methane content determination. Fuel 1984, 63 (2), 251–255. 10.1016/0016-2361(84)90046-2. [DOI] [Google Scholar]
  22. Wei Q.; Zheng K. G.; Hu B. L.; Li X. Q.; Feng S. B.; Jiang W.; Zhu W. W.; Feng W. Q. Methane Adsorption Capacity of Deep-Buried Coals Based on Pore Structure in the Panji Deep Area of Huainan Coalfield, China[J]. Energy Fuels 2021, 35, 4775–4790. 10.1021/acs.energyfuels.0c03800. [DOI] [Google Scholar]
  23. Li M. M.; Liang W. M.; Lin H. X.; Yue G. W. Study on the Critical Value of Residual Gas Content Based on the Difference of Adsorption Structure between Soft and Hard Coal. ACS Omega 2021, 6, 16744–16754. 10.1021/acsomega.1c00533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Qu Z. H.; Wang G. G. X.; Jiang B.; Rudolph V.; Dou X.; Li M. Experimental study on the porous structure and compressibility of tectonized coals. Energy Fuels 2010, 24, 2964–2973. 10.1021/ef9015075. [DOI] [Google Scholar]
  25. Yang Y.; Liu S. Estimation and modeling of pressure-dependent gas diffusion coefficient for coal: a fractal theory-based approach. Fuel 2019, 253, 588–606. 10.1016/j.fuel.2019.05.009. [DOI] [Google Scholar]
  26. Wei Q.; Li X. Q.; Zhang J. Z.; Hu B. L.; Zhu W. W.; Liang W. L.; Sun K. X. Full-size pore structure characterization of deep-buried coals and its impact on methane adsorption capacity: A case study of the Shihezi Formation coals from the Panji Deep Area in Huainan Coalfield, Southern North China[J]. J. Petro. Sci. Eng. 2019, 173, 975–989. 10.1016/j.petrol.2018.10.100. [DOI] [Google Scholar]
  27. Hu B.; Cheng Y. P.; He X. X.; Wang Z. Y.; Jiang Z. N.; Wang C. H.; Li W.; Wang L. New insight into the CH4 adsorption capacity of coal based on microscopic pore properties. Fuel 2020, 262, 116675. 10.1016/j.fuel.2019.116675. [DOI] [Google Scholar]
  28. Huang Q.; Liu S.; Wang G.; Wu B.; Zhang Y. Coalbed methane reservoir stimulation using guar-based fracturing fluid: a review. J. Nat. Gas. Sci. Eng. 2019, 66, 107–125. 10.1016/j.jngse.2019.03.027. [DOI] [Google Scholar]
  29. Fu X. H.; Qin Y.; Wang G. G. X.; Rudolph V. Evaluation of gas content of coalbed methane reservoirs with the aid of geophysical logging technology. Fuel 2009, 88 (11), 2269–2277. 10.1016/j.fuel.2009.06.003. [DOI] [Google Scholar]
  30. Zhang R.; Liu S. Experimental and theoretical characterization of methane and CO2 sorption hysteresis in coals based on Langmuir desorption. Int. J. Coal Geol. 2017, 171, 49–60. 10.1016/j.coal.2016.12.007. [DOI] [Google Scholar]
  31. GB/T 23249-2009, Coalbed gas content measurement methods in geological exploration period; China Standards Press: 2009. [Google Scholar]
  32. GB/T 23250-2009, The direct method of determining coalbed gas content in the mine; China Standards Press: 2009. [Google Scholar]
  33. Smith D. M.; Williams F. L.. A new technique for determining the methane content of coal. In Proceedings of the 16th Intersociety Energy Conservation Engineering Conference, Atlanta, GA; 1981.
  34. Smith D. M.; Williams F. L. Diffusional effects in the recovery of methane from coalbeds. SPE J. 1984, 24, 529. 10.2118/10821-PA. [DOI] [Google Scholar]
  35. Liu D. M.; Yao Y. B.; Tang D. Z.; Tang S. H.; Che Y.; Huang W. H. Coal reservoir characteristics and coalbed methane resource assessment in Huainan and Huaibei coalfields, Southern North China. Int. J. Coal Geol. 2009, 79, 97–112. 10.1016/j.coal.2009.05.001. [DOI] [Google Scholar]
  36. Xu H.; Sang S.; Yang J.; Jin J.; Liu H.; Zhou X. Evaluation of coal and shale reservoir in Permian coal-bearing strata for development potential: A case study from well LC-1# in the northern Guizhou. China. Energy Explor. Exploit. 2019, 37 (1), 194–218. 10.1177/0144598718807553. [DOI] [Google Scholar]
  37. Saghafi A. Discussion on determination of gas content of coal and uncertainties of measurement. Int. J. Min. Sci. Techno. 2017, 27 (5), 741–748. 10.1016/j.ijmst.2017.07.024. [DOI] [Google Scholar]
  38. Lu M.; Pan Z.; Connell L. D.; Lu Y. A new method for the estimation of lost gas during the measurement of the gas content of coal. SPE Reserv. Eval. Eng. 2017, 20 (3), 627–638. 10.2118/176976-PA. [DOI] [Google Scholar]
  39. Wang F.; Zhao X.; Liang Y.; Li X.; Chen Y. Calculation model and rapid estimation method for coal seam gas content. Processes 2018, 6 (11), 223. 10.3390/pr6110223. [DOI] [Google Scholar]
  40. Chen Y. L.; Qin Y.; Li Z. P.; Shi Q. M.; Wei C. T.; Wu C. F.; Cao C. H.; Qu Z. H. Differences in desorption rate and composition of desorbed gases between undeformed and mylonitic coals in the Zhina Coalfield, Southwest China. Fuel 2019, 239 (1), 905–916. 10.1016/j.fuel.2018.11.085. [DOI] [Google Scholar]
  41. Liu H. H.; Sang S. X.; Wang G. G. X.; Li M. X.; Xu H. J.; Liu S. Q.; Li J. J.; Ren B.; Zhao Z. G.; Xie Y. Block scale investigation on gas content of coalbed methane reservoirs in southern Qinshui basin with statistical model and visual map. J. Petrol. Sci. Eng. 2014, 114, 1–14. 10.1016/j.petrol.2013.08.039. [DOI] [Google Scholar]
  42. Metcalfe R. S.; Yee D.; Seidle J. P.; Puri R.. Review of research efforts in coalbed methane recovery. In Society of Petroleum Engineers (SPE) Asia-Pacific Conference, Perth, Australia, 1991; pp 727–740.
  43. Li S.; Tang D. Z.; Pan Z. J.; Xu H.; Tao S.; Liu Y. F.; Ren P. F. Geological conditions of deep coalbed methane in the eastern margin of the Ordos Basin, China: implications for coalbed methane development. J. Nat. Gas Sci. Eng. 2018, 53, 394–402. 10.1016/j.jngse.2018.03.016. [DOI] [Google Scholar]
  44. Yee D.; Seidle J. P.; Hanson B W.. Gas sorption on coal and measurement of gas content In Hydrocarbons from Coal, AAPG. Studies in Geology; Law B. E., Rice D. D. , Eds.; Chapter 9, 1993; pp 203–218. [Google Scholar]
  45. Fu H.; Tang D.; Xu H.; Xu T.; Chen B.; Hu P. Geological characteristics and CBM exploration potential evaluation: A case study in the middle of the southern Junggar Basin, NW China. J. Nat. Gas Sci. Eng. 2016, 30, 557–570. 10.1016/j.jngse.2016.02.024. [DOI] [Google Scholar]
  46. Fan C. S.; Yang M. C. Discussion on the method of calculating gas loss by desorption method. J. Zhongzhou Coal 1994, 4, 24–26. (in Chinese). [Google Scholar]
  47. Clarkson C. R.; Bustin R. M. The effect of pore structure and gas pressure upon the transport properties of coal: a laboratory and modeling study. 2. Adsorption rate modeling. Fuel 1999, 78, 1345–1362. 10.1016/S0016-2361(99)00056-3. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES