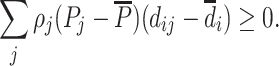Abstract
Physicians, judges, teachers, and agents in many other settings differ systematically in the decisions they make when faced with similar cases. Standard approaches to interpreting and exploiting such differences assume they arise solely from variation in preferences. We develop an alternative framework that allows variation in preferences and diagnostic skill and show that both dimensions may be partially identified in standard settings under quasi-random assignment. We apply this framework to study pneumonia diagnoses by radiologists. Diagnosis rates vary widely among radiologists, and descriptive evidence suggests that a large component of this variation is due to differences in diagnostic skill. Our estimated model suggests that radiologists view failing to diagnose a patient with pneumonia as more costly than incorrectly diagnosing one without, and that this leads less skilled radiologists to optimally choose lower diagnostic thresholds. Variation in skill can explain 39% of the variation in diagnostic decisions, and policies that improve skill perform better than uniform decision guidelines. Failing to account for skill variation can lead to highly misleading results in research designs that use agent assignments as instruments.
I. Introduction
In a wide range of settings, agents facing similar problems make systematically different choices. Physicians differ in their propensity to choose aggressive treatments or order expensive tests, even when facing observably similar patients (Chandra, Cutler, and Song 2011; Van Parys and Skinner 2016; Molitor 2017). Judges differ in their propensity to hand down strict or lenient sentences, even when facing observably similar defendants (Kleinberg et al. 2018). Similar patterns hold for teachers, managers, and police officers (Bertrand and Schoar 2003; Figlio and Lucas 2004; Anwar and Fang 2006). Such variation is of interest because it implies differences in resource allocation across similar cases and because it has increasingly been exploited in research designs using agent assignments as a source of quasi-random variation (e.g., Kling 2006).
In such settings, we can think of the decision process in two steps. First, there is an evaluation step in which decision makers assess the likely effects of the possible decisions given the case before them. Physicians seek to diagnose a patient’s underlying condition and assess the potential effects of treatment, judges seek to determine the facts of a crime and the likelihood of recidivism, and so on. We refer to the accuracy of these assessments as an agent’s diagnostic skill. Second, there is a selection step in which the decision maker decides what preference weights to apply to the various costs and benefits in determining the decision. We refer to these weights as an agent’s preferences. In a stylized case of a binary decision d ∈ {0, 1}, we can think of the first step as ranking cases in terms of their appropriateness for d = 1 and the second step as choosing a cutoff in this ranking.
Although systematic variation in decisions could in principle come from either skill or preferences, a large part of the prior literature we discuss below assumes that agents differ only in the latter. This matters for the welfare evaluation of practice variation, as variation in preferences would suggest inefficiency relative to a social planner’s preferred decision rule, whereas variation in skill need not. It matters for the types of policies that are most likely to improve welfare, as uniform decision guidelines may be effective in the face of varying preferences but counterproductive in the face of varying skill. As we show below, it matters for research designs that use agents’ decision rates as a source of identifying variation, as variation in skill will typically lead the key monotonicity assumption in such designs to be violated.
In this article, we introduce a framework to separate heterogeneity in skill and preferences when cases are quasi-randomly assigned, and we apply it to study heterogeneity in pneumonia diagnoses made by radiologists. Pneumonia affects 450 million people and causes 4 million deaths every year worldwide (Ruuskanen et al. 2011). Although it is more common and deadly in the developing world, it remains the eighth leading cause of death in the United States, despite the availability of antibiotic treatment (Kung et al. 2008; File and Marrie 2010).
Our framework starts with a classification problem in which both decisions and underlying states are binary. As in the standard one-sided selection model, the outcome only reveals the true state conditional on one of the two decisions. In our setting, the decision is whether to diagnose a patient and treat her with antibiotics, the state is whether the patient has pneumonia, and the state is observed only if the patient is not treated, because once a patient is given antibiotics it is often impossible to tell whether she actually had pneumonia. We refer to the share of a radiologist’s patients diagnosed with pneumonia as her diagnosis rate. We refer to the share of patients who leave with undiagnosed pneumonia—that is, the share of patients who are false negatives—as her miss rate. We draw close connections between two representations of agent decisions in this setting: (i) the reduced-form relationship between diagnosis and miss rates, which we observe directly in our data; and (ii) the relationship between true and false positive rates, commonly known as the receiver operating characteristic (ROC) curve. The ROC curve has a natural economic interpretation as a production possibilities frontier for “true positive” and “true negative” diagnoses. This framework thus maps skill and preferences to respective concepts of productive and allocative efficiency.
Using Veterans Health Administration (VHA) data on 5.5 million chest X-rays in the emergency department (ED), we examine variation in diagnostic decisions and outcomes related to pneumonia across radiologists who are assigned imaging cases in a quasi-random fashion. We measure miss rates by the share of a radiologist’s patients who are not diagnosed in the ED but return with a pneumonia diagnosis in the next 10 days. We begin by demonstrating significant variation in diagnosis and miss rates across radiologists. Reassigning patients from a radiologist in the 10th percentile of diagnosis rates to a radiologist in the 90th percentile would increase the probability of a diagnosis from 8.9% to 12.3%. Reassigning patients from a radiologist in the 10th percentile of miss rates to a radiologist in the 90th percentile would increase the probability of a false negative from 0.2% to 1.8%. These findings are consistent with prior evidence documenting variability in the diagnosis of pneumonia across and within radiologists based on the same chest X-rays (Abujudeh et al. 2010; Self et al. 2013).
We turn to the relationship between diagnosis and miss rates. At odds with the prediction of a standard model with no skill variation, we find that radiologists who diagnose at higher rates actually have higher rather than lower miss rates. A patient assigned to a radiologist with a higher diagnosis rate is more likely to go home with untreated pneumonia than one assigned to a radiologist with a lower diagnosis rate. This fact alone rejects the hypothesis that all radiologists operate on the same production possibilities frontier and suggests a large role for variation in skill. In addition, we find that there is substantial variation in the probability of false negatives conditional on diagnosis rate. For the same diagnosis rate, a radiologist in the 90th percentile of miss rates has a miss rate 0.7 percentage points higher than that of a radiologist in the 10th percentile.
This evidence suggests that interpreting our data through a standard model that ignores skill could be highly misleading. At a minimum, it means that policies focused on harmonizing diagnosis rates could miss important improvements in skill. Moreover, such policies could be counterproductive if skill variation makes varying diagnosis rates optimal. If missing a diagnosis (a false negative) is more costly than falsely diagnosing a healthy patient (a false positive), a radiologist with noisier diagnostic information (less skill) may optimally diagnose more patients; requiring her to do otherwise could reduce efficiency. Finally, a standard research design that uses the assignment of radiologists as an instrument for pneumonia diagnosis would fail badly in this setting. We show that our reduced-form facts strongly reject the monotonicity conditions necessary for such a design. Applying the standard approach would yield the nonsensical conclusion that diagnosing a patient with pneumonia (and thus giving her antibiotics) makes her more likely to return to the emergency room with pneumonia in the near future.
We show that, under quasi-random assignment of patients to radiologists, the joint distribution of diagnosis rates and miss rates can be used to identify partial orderings of skill among the radiologists. The intuition is simple: in any pair of radiologists, a radiologist that has both a higher diagnosis rate and a higher miss rate than the other radiologist must be lower-skilled. Similarly, a radiologist that has a lower or equal diagnosis rate but a higher miss rate, by a difference exceeding any difference in diagnosis rates, must also be lower-skilled.
In the final part of the article, we estimate a structural model of diagnostic decisions to permit a more precise characterization of these facts. Following our conceptual framework, radiologists first evaluate chest X-rays to form a signal of the underlying disease state and then select cases with signals above a certain threshold to diagnose with pneumonia. Undiagnosed patients who in fact have pneumonia will eventually develop clear symptoms, thus revealing false negative diagnoses. But among cases receiving a diagnosis, those who truly have pneumonia cannot be distinguished from those who do not. Radiologists may vary in their diagnostic accuracy, and each radiologist endogenously chooses a threshold selection rule to maximize utility. Radiologist utility depends on false negative and false positive diagnoses, and the relative utility weighting of these outcomes may vary across radiologists.
We find that the average radiologist receives a signal that has a correlation of 0.85 with the patient’s underlying latent state but that diagnostic accuracy varies widely, from a correlation with the latent state of 0.76 in the 10th percentile of radiologists to 0.93 in the 90th percentile. The disutility of missing diagnoses is, on average, 6.71 times higher than that of an unnecessary diagnosis; this ratio varies from 5.60 to 7.91 between the 10th and 90th radiologist percentiles. Overall, 39% of the variation in decisions and 78% of the variation in outcomes can be explained by variation in skill. We consider the welfare implications of counterfactual policies. While eliminating variation in diagnosis rates always improves welfare under the (incorrect) assumption of uniform diagnostic skill, we show that this policy may actually reduce welfare. In contrast, increasing diagnostic accuracy can yield much larger welfare gains.
Finally, we document how diagnostic skill varies across groups of radiologists. Older radiologists or radiologists with higher chest X-ray volume have higher diagnostic skill. Higher-skilled radiologists tend to issue shorter reports of their findings but spend more time generating those reports, suggesting that effort (rather than raw talent alone) may contribute to radiologist skill. Aversion to false negatives tends to be negatively related to radiologist skill.
Our strategy for identifying causal effects relies on quasi-random assignment of cases to radiologists. This assumption is particularly plausible in our ED setting because of idiosyncratic variation in the arrival of patients and the availability of radiologists conditional on time and location controls. To support this assumption, we show that a rich vector of patient characteristics that are strongly related to false negatives have limited predictive power for radiologist assignment. Comparing radiologists with high and low propensity to diagnose, we see statistically significant but economically small imbalance in patient characteristics in our full sample of stations, and negligible imbalance in a subset of stations selected for balanced assignment on a single characteristic (patient age). Further, we show that our main results are stable in this latter sample of stations and robust to adding or removing controls for patient characteristics.
Our findings relate most directly to a large and influential literature on practice variation in health care (Fisher et al. 2003a, 2003b; Institute of Medicine 2013). This literature has robustly documented variation in spending and treatment decisions that has little correlation with patient outcomes. The seeming implication of this finding is that spending in health care provides little benefit to patients (Garber and Skinner 2008), a provocative hypothesis that has spurred an active body of research seeking to use natural experiments to identify the causal effect of spending (e.g., Doyle et al. 2015). In this article, we build on Chandra and Staiger (2007) in investigating the possibility of heterogeneous productivity (e.g., physician skill) as an alternative explanation.1 By exploiting the joint distribution of decisions and outcomes, we find significant variation in productivity, which rationalizes a large share of the variation in diagnostic decisions. The same mechanism may explain the weak relationship between decision rates and outcomes observed in other settings.2
Perhaps most closely related to our article are evaluations by Abaluck et al. (2016) and Currie and MacLeod (2017), both of which examine diagnostic decision making in health care. Abaluck et al. (2016) assume that physicians have the same diagnostic skill (i.e., the same ranking of cases) but may differ in where they set their thresholds for diagnosis. Currie and MacLeod (2017) assume that physicians have the same preferences but may differ in skill. Also related to our work is a recent study of hospitals by Chandra and Staiger (2020), who allow for comparative advantage and different thresholds for treatment. In their model, the potential outcomes of treatment may differ across hospitals, but hospitals are equally skilled in ranking patients according to their potential outcomes.3 Relative to these papers, a key difference of our study is that we use quasi-random assignment of cases to providers.
More broadly, our work contributes to the health literature on diagnostic accuracy. While mostly descriptive, this literature suggests large welfare implications from diagnostic errors (Institute of Medicine 2015). Diagnostic errors account for 7%–17% of adverse events in hospitals (Leape et al. 1991; Thomas et al. 2000). Postmortem examination research suggests that diagnostic errors contribute to 9% of patient deaths (Shojania et al. 2003).
Finally, our article contributes to the “judges design” literature, which estimates treatment effects by exploiting quasi-random assignment to agents with different treatment propensities (e.g., Kling 2006). We show how variation in skill relates to the standard monotonicity assumption in the literature, which requires that all agents order cases in the same way but may draw different thresholds for treatment (Imbens and Angrist 1994; Vytlacil 2002). Monotonicity can thus only hold if all agents have the same skill. Our empirical insight that we can test and quantify violations of monotonicity (or variation in skill) relates to conceptual work that exploits bounds on potential outcome distributions (Kitagawa 2015; Mourifie and Wan 2017) as well as more recent work to test instrument validity in the judges design (Frandsen, Lefgren, and Leslie 2019) and to detect inconsistency in judicial decisions (Norris 2019).4 Our identification results and modeling framework are closely related to the contemporaneous work of Arnold, Dobbie, and Hull (2020), who study racial bias in bail decisions.
The remainder of this article proceeds as follows. Section II sets up a high-level empirical framework for our analysis. Section III describes the setting and data. Section IV presents our reduced-form analysis, with the key finding that radiologists who diagnose more cases also miss more cases of pneumonia. Section V presents our structural analysis, separating radiologist diagnostic skill from preferences. Section VI considers policy counterfactuals. Section VII concludes. All appendix material is in the Online Appendix.
II. Empirical Framework
II.A. Setup
We consider a population of agents j and cases i, with j(i) denoting the agent assigned case i. Agent j makes a binary decision dij ∈ {0, 1} for each assigned case (e.g., not treat or treat, acquit or convict). The goal is to align the decision with a binary state si ∈ {0, 1} (e.g., healthy or sick, innocent or guilty). The agent does not observe si directly but observes a realization 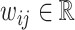 of a signal with distribution
of a signal with distribution 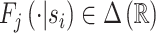 that may be informative about si and chooses dij based only on this signal.
that may be informative about si and chooses dij based only on this signal.
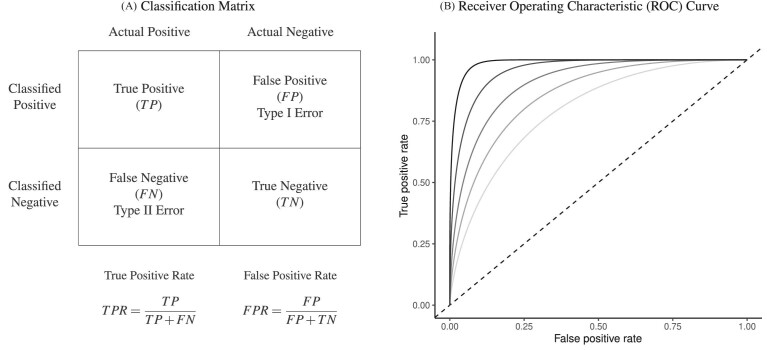
This setup is the well-known problem of statistical classification. For agent j, we can define the probabilities of four outcomes (Figure I, Panel A): true positives, or 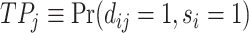 ; false positives (type I errors), or
; false positives (type I errors), or 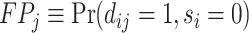 ; true negatives, or
; true negatives, or 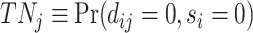 ; and false negatives (type II errors), or
; and false negatives (type II errors), or 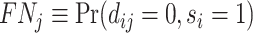 . Pj = TPj + FPj denotes the expected proportion of cases j classifies as positive, and Sj = TPj + FNj denotes the prevalence of si = 1 in j’s population of cases. We refer to Pj as j’s diagnosis rate, and we refer to FNj as her miss rate.
. Pj = TPj + FPj denotes the expected proportion of cases j classifies as positive, and Sj = TPj + FNj denotes the prevalence of si = 1 in j’s population of cases. We refer to Pj as j’s diagnosis rate, and we refer to FNj as her miss rate.
Figure I.
Visualizing the Classification Problem
Panel A shows the standard classification matrix representing four joint outcomes depending on decisions and states. Each row represents a decision and each column represents a state. Panel B plots examples of the receiver operating characteristic (ROC) curve. It shows the relationship between the true positive rate (TPR) and the false positive rate (FPR). The particular ROC curves shown in this figure are formed assuming the signal structure in equation (5), with more accurate ROC curves (higher αj) further from the 45-degree line.
Each agent maximizes a utility function uj(d, s) with uj(1, 1) > uj(0, 1) and uj(0, 0) > uj(1, 0). We assume without loss of generality that the posterior probability of si = 1 is increasing in wij, so that any optimal decision rule can be represented by a threshold τj with dij = 1 if and only if wij > τj.
We define agents’ skill based on the Blackwell (1953) informativeness of their signals. Agent j is (weakly) more skilled than j′ if and only if Fj is (weakly) more Blackwell-informative than 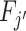 . By the definition of Blackwell informativeness, this will be true if either of two equivalent conditions hold: (i) for any arbitrary utility function u(d, s), ex ante expected utility from an optimal decision based on observing a draw from Fj is greater than from an optimal decision based on observing a draw from
. By the definition of Blackwell informativeness, this will be true if either of two equivalent conditions hold: (i) for any arbitrary utility function u(d, s), ex ante expected utility from an optimal decision based on observing a draw from Fj is greater than from an optimal decision based on observing a draw from 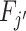 ; (ii)
; (ii) 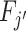 can be produced by combining a draw from Fj with random noise uncorrelated with si. We say that two agents have the same skill if their signals are equal in the Blackwell ordering, and we say that skill is uniform if all agents have equal skill.
can be produced by combining a draw from Fj with random noise uncorrelated with si. We say that two agents have the same skill if their signals are equal in the Blackwell ordering, and we say that skill is uniform if all agents have equal skill.
The Blackwell ordering is incomplete in general, and it is possible that agent j is neither more nor less skilled than j′. This could happen, for example, if Fj is relatively more accurate in state s = 0 while 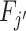 is relatively more accurate in state s = 1. In the case in which all agents can be ranked by skill, we can associate each agent with an index of skill
is relatively more accurate in state s = 1. In the case in which all agents can be ranked by skill, we can associate each agent with an index of skill  , where j is more skilled than j′ if and only if
, where j is more skilled than j′ if and only if 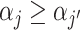 .
.
II.B. ROC Curves
A standard way to summarize the accuracy of classification is in terms of the receiver operating characteristic (ROC) curve. This plots the true positive rate, or 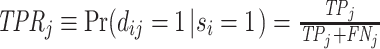 , against the false positive rate, or
, against the false positive rate, or 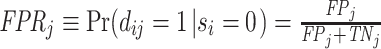 , with the curve for a particular signal Fj indicating the set of all (
, with the curve for a particular signal Fj indicating the set of all ( ,
,  ) that can be produced by a decision rule of the form
) that can be produced by a decision rule of the form 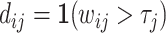 for some τj. Figure I, Panel B shows several possible ROC curves.
for some τj. Figure I, Panel B shows several possible ROC curves.
In the context of our model, the ROC curve of agent j represents the frontier of potential classification outcomes she can achieve as she varies the proportion of cases Pj she classifies as positive. If the agent diagnoses no cases (τj = ∞), she will have TPRj = 0 and FPRj = 0. If she diagnoses all cases (τj = −∞), she will have TPRj = 1 and FPRj = 1. As she increases Pj (decreases τj), both TPRj and FPRj must weakly increase. The ROC curve thus reveals a technological trade-off between the “sensitivity” (or TPRj) and “specificity” (or 1 − FPRj) of classification. It is straightforward to show that in our model, where the likelihood of si = 1 is monotonic in wij, the ROC curves give the maximum TPRj achievable for each FPRj, and they not only must be increasing but also must be concave and lie above the 45-degree line.5
If agent j is more skilled than agent j′, any (FPR, TPR) pair achievable by j′ is also achievable by j. This follows immediately from the definition of Blackwell informativeness, as j can always reproduce the signal of j′ by adding random noise.
Remark 1.
Agent j has higher skill than j′ if and only if the ROC curve of agent j lies everywhere weakly above the ROC curve of agent j′. Agents j and j′ have equal skill if and only if their ROC curves are identical.
The classification framework is closely linked with the standard economic framework of production. An ROC curve can be viewed as a production possibilities frontier of TPRj and 1 − FPRj. Agents on higher ROC curves are more productive (i.e., more skilled) in the evaluation stage. Where an agent chooses to locate on an ROC curve depends on her preferences, or the tangency between the ROC curve and an indifference curve. It is possible that agents differ in preferences but not skill, so that they lie along identical ROC curves, and we would observe a positive correlation between TPRj and FPRj across j. It is also possible that they differ in skill but not preferences, so that they lie at the tangency point on different ROC curves, and we could observe a negative correlation between TPRj and FPRj across j. Figure II illustrates these two cases with hypothetical data on the joint distribution of decisions and outcomes. This figure suggests some intuition, which we formalize later, for how skill and preferences may be separately identified.
Figure II.
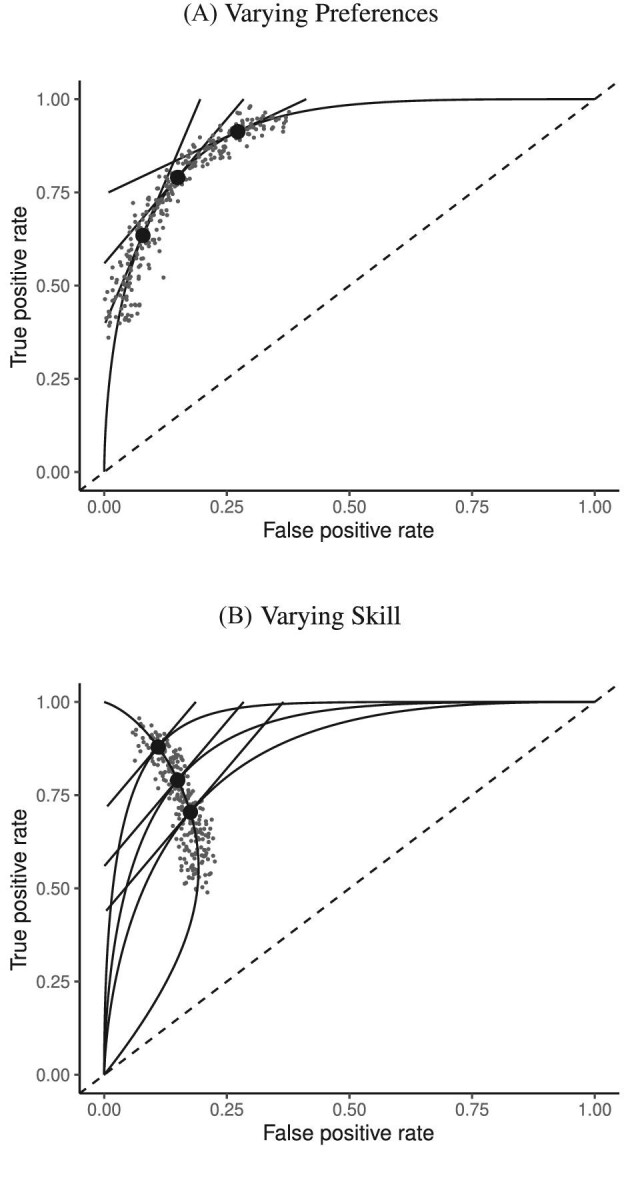
Hypothetical Data Generated by Variation in Preferences versus Skill
This figure shows two distributions of hypothetical data in ROC space. The top panel fixes skill and varies preferences. All agents are located on the same ROC curve and are faced with the trade-off between sensitivity (TPR) and specificity (1 − FPR). The bottom panel fixes the preference and varies evaluation skill. Agents are located on different ROC curves but have parallel indifference curves.
In the empirical analysis below, we visualize the data in two spaces. The first is the ROC space of Figure II. The second is a plot of miss rates FNj against diagnosis rates Pj, which we refer to as “reduced-form space.” When cases are randomly assigned, so that Sj is the same for all j, there exists a one-to-one correspondence between these two ways of looking at the data, and the slope relating FNj to Pj in reduced-form space provides a direct test of uniform skill.6
Remark 2.
Suppose
is equal to a constant S for all j. Then for any two agents j and j′,
 if and only if
if and only if 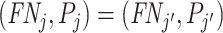 .
.If the agents have equal skill and
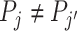 ,
, 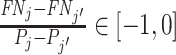 .
.
II.C. Potential Outcomes and the Judges Design
When there is an outcome of interest yij = yi(dij) that only depends on the agent’s decision dij, we can map our classification framework to the potential outcomes framework with heterogeneous treatment effects (Rubin 1974; Imbens and Angrist 1994). The object of interest is some average of the treatment effects yi(1) − yi(0) across individuals. We observe case i assigned to only one agent j, which we denote as j(i), so the identification challenge is that we only observe 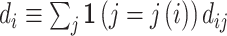 and
and 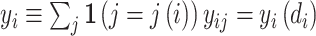 corresponding to j = j(i).
corresponding to j = j(i).
A growing literature starting with Kling (2006) has proposed using heterogeneous decision propensities of agents to identify these average treatment effects in settings where cases i are randomly assigned to agents j with different propensities of treatment. This empirical structure is popularly known as the “judges design,” referring to early applications in settings with judges as agents. The literature typically assumes conditions of instrumental variable (IV) validity from Imbens and Angrist (1994).7 This guarantees that an IV regression of yi on di instrumenting for the latter with indicators for the assigned agent recovers a consistent estimate of the local average treatment effect (LATE).
Condition 1
(IV Validity). Consider the potential outcome yij and the treatment response indicator dij ∈ {0, 1} for case i and agent j. For a set of two or more agents j and a random sample of cases i, the following conditions hold:
Exclusion: yij = yi(dij) with probability 1.
Independence: (yi(0), yi(1), dij) is independent of the assigned agent j(i).
Strict monotonicity: For any j and j′,
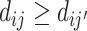 ∀i, or
∀i, or 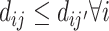 , with probability 1.
, with probability 1.
Vytlacil (2002) shows that Condition 1.iii is equivalent to all agents ordering cases by the same latent index wi and then choosing 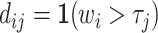 , where τj is an agent-specific cutoff. Note that this implies that the data must be consistent with all agents having the same signals and thus the same skill. An agent with a lower cutoff must have a weakly higher rate of both true and false positives. Condition 1 thus greatly restricts the pattern of outcomes in the classification framework.
, where τj is an agent-specific cutoff. Note that this implies that the data must be consistent with all agents having the same signals and thus the same skill. An agent with a lower cutoff must have a weakly higher rate of both true and false positives. Condition 1 thus greatly restricts the pattern of outcomes in the classification framework.
Remark 3.
Suppose Condition 1 holds. Then the observed data must be consistent with all agents having uniform skill. By Remark 2, for any two agents j and j′, we must have
.
This implication is consistent with prior work on IV validity (Balke and Pearl 1997; Heckman and Vytlacil 2005; Kitagawa 2015). If we define yi to be an indicator for a false negative and consider a binary instrument defined by assignment to either j or j′, equation (1.1) of Kitagawa (2015) directly implies Remark 3. An additional intuition is that under Condition 1, for any outcome yij, the Wald estimand comparing a population of cases assigned to agents j and j′ is 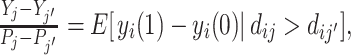 where Yj is the average of yij among cases treated by j (Imbens and Angrist 1994). If we define yi to be an indicator for a false negative, the Wald estimand lies in [−1, 0], since yi(1) − yi(0) ∈ {− 1, 0}.
where Yj is the average of yij among cases treated by j (Imbens and Angrist 1994). If we define yi to be an indicator for a false negative, the Wald estimand lies in [−1, 0], since yi(1) − yi(0) ∈ {− 1, 0}.
By Remark 3, strict monotonicity in Condition 1.iii of the judges design implies uniform skill. The converse is not true, however. Agents with uniform skill may yet violate strict monotonicity. For example, if their signals are drawn independently from the same distribution, they might order different cases differently by random chance. One might ask whether a condition weaker than strict monotonicity might be both consistent with our data and sufficient for the judges design to recover a well-defined LATE.
Frandsen, Lefgren, and Leslie (2019) introduce one such condition, which they call “average monotonicity.” This requires that the covariance between agents’ average treatment propensities and their potential treatment decisions for each case i be positive. To define the condition formally, let ρj be the share of cases assigned to agent j, let 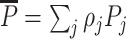 be the ρ-weighted average treatment propensity, and let
be the ρ-weighted average treatment propensity, and let 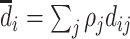 be the ρ-weighted average potential treatment of case i.
be the ρ-weighted average potential treatment of case i.
Condition 2
(Average Monotonicity). For all i,
Frandsen, Lefgren, and Leslie (2019) show that Condition 2, in place of Condition 1.iii, is sufficient for the judges design to recover a well-defined LATE. We note two more primitive conditions that are each sufficient for average monotonicity. One is that the probability that j diagnoses patient i is either higher or lower than the probability j′ diagnoses patient i for all i. The other is that variation in skill is orthogonal to the diagnosis rate in a large population of agents.
Condition 3
(Probabilistic Monotonicity). For any j and j′,
Condition 4
(Skill-Propensity Independence). (i) All agents can be ranked by skill and we associate each agent with an index αj such that j is (weakly) more skilled than j′ if and only if
; (ii) probabilistic monotonicity (Condition 3) holds for any pair of agents j and j′ with equal skill; (iii) the diagnosis rate Pj is independent of αj in the population of agents.
In Online Appendix A, we show that Condition 3 implies Condition 2. We also show that in the limit, as the number of agents grows large, Condition 4 implies Condition 2.
Under any assumption that implies that the judges design recovers a well-defined LATE, the coefficient estimand Δ from a regression of FNj on Pj must lie in the interval [−1, 0].8 The implication that Δ ∈ [−1, 0]—or, equivalently, 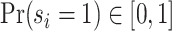 among compliers weighted by their contribution to the LATE—is our proposed test of monotonicity. While this test may fail to detect monotonicity violations, we show in Online Appendix D that it nevertheless may be stronger than the standard tests of monotonicity in the judges design literature because it relies on the key (unobserved) state for selection instead of on observable characteristics.
among compliers weighted by their contribution to the LATE—is our proposed test of monotonicity. While this test may fail to detect monotonicity violations, we show in Online Appendix D that it nevertheless may be stronger than the standard tests of monotonicity in the judges design literature because it relies on the key (unobserved) state for selection instead of on observable characteristics.
The results we show below imply Δ ∉ [−1, 0]. They thus imply violation not only of the strict monotonicity of Condition 1.iii but also of any of the weaker monotonicity Conditions 2, 3, and 4. They not only reject uniform skill but also imply that skill must be systematically correlated with diagnostic propensities. In Section V, we show why violations of even these weaker monotonicity conditions are natural: when radiologists differ in skill and are aware of these differences, the optimal diagnostic threshold will typically depend on radiologist skill, particularly when the costs of false negatives and false positives are asymmetric. We also show that this relationship between skill and radiologist-chosen diagnostic propensities raises the possibility that common diagnostic thresholds may reduce welfare.
III. Setting and Data
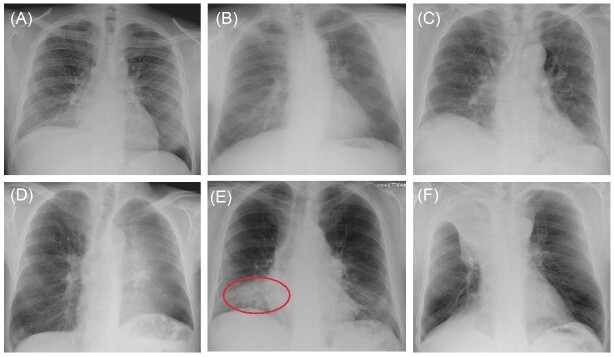
We apply our framework to study pneumonia diagnoses in the emergency department (ED). Pneumonia is a common and potentially deadly disease that is primarily diagnosed by chest X-rays. Reading chest X-rays requires skill, as illustrated in Figure III, which shows example chest X-ray images from the medical literature. We focus on outcomes related to chest X-rays performed in EDs in the Veterans Health Administration (VHA), the largest health care delivery system in the United States.
Figure III.
Example Chest X-rays
This figure shows example chest X-rays reproduced from figure 2 of Fabre et al. (2018), “Radiology Residents’ Skill Level in Chest X-Ray Reading”, Diagnostic and Interventional Imaging, 99, 361–370. Copyright ©2018 Société Française de Radiologie, published by Elsevier Masson SAS. All rights reserved. These chest X-rays represent cases on which there is expert consensus and which are used for training radiologists. Only Panel E represents a case of infectious pneumonia, and we add a red oval (color version available online) to denote where the pneumonia lies in the right lower lobe. Panel A shows miliary tuberculosis; Panel B shows a lung nodule (cancer) in the left upper lobe; Panel C shows usual interstitial pneumonitis; Panel D shows left upper lobe atelectasis; Panel F shows right upper lobe atelectasis.
In this setting, the diagnostic pathway for pneumonia is as follows:
A physician orders a radiology exam for a patient suspected to have the disease.
Once the radiology exam is performed, the image is assigned to a radiologist. Exams are typically assigned to radiologists based on whoever is on call at the time the exam needs to be read. We argue below that this assignment is quasi-random conditional on appropriate covariates.
The radiologist issues a report on her findings.
The patient may be diagnosed and treated by the ordering physician in consultation with the radiologist.
Pneumonia diagnosis is a joint decision by radiologists and physicians. Physician assignment to patients may be nonrandom, and physicians can affect diagnosis both via their selection of patients for X-rays in step i and their diagnostic propensities in step iv. However, so long as assignment of radiologists in step ii is as good as random, we can infer the causal effect of radiologists on the probability that the joint decision-making process leads to a diagnosis. While interactions between radiologists and ordering physicians are interesting, we abstract from them in this article and focus on a radiologist’s average effect, taking as given the set of physicians with whom she works.
VHA facilities are divided into local units called stations. A station typically has a single major tertiary care hospital and a single ED location, together with some medical centers and outpatient clinics. These locations share the same electronic health record and order entry system. We study the 104 VHA stations that have at least one ED.
Our primary sample consists of the roughly 5.5 million completed chest X-rays in these stations that were ordered in the ED and performed between October 1999 and September 2015.9 We refer to these observations as cases. Each case is associated with a patient and with a radiologist assigned to read it. In the rare cases where a patient received more than one X-ray on a single day, we assign the case to the radiologist associated with the first X-ray observed in the day.
To define our main analysis sample, we first omit the roughly 600,000 cases for which the patient had at least one chest X-ray ordered in the ED in the previous 30 days. We omit cases with missing radiologist identity, patient age, or patient gender, or with patient age greater than 100 or less than 20. Finally, we omit cases associated with a radiologist-month pair with fewer than five observations and cases associated with a radiologist with fewer than 100 observations in total. Online Appendix Table A.1 reports the number of observations dropped at each of these steps. The final sample contains 4,663,840 cases and 3,199 radiologists.10
We define the diagnosis indicator di for case i equal to 1 if the patient has a pneumonia diagnosis recorded in an outpatient or inpatient visit whose start time falls within a 24-hour window centered at the time stamp of the chest X-ray order.11 We confirm that 92.6% of patients who are recorded to have a diagnosis of pneumonia are also prescribed an antibiotic consistent with pneumonia treatment within five days after the chest X-ray.
We define a false negative indicator 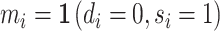 for case i equal to one if di = 0 and the patient has a subsequent pneumonia diagnosis recorded between 12 hours and 10 days after the initial chest X-ray. We include diagnoses in both ED and non-ED facilities, including outpatient, inpatient, and surgical encounters. In practice, mi is measured with error because it requires the patient to return to a VHA facility and for the second visit to correctly identify pneumonia. We show robustness of our results to endogenous second diagnoses by restricting analyses to veterans who solely use the VHA and who are sick enough to be admitted on the second visit in Section V.D.
for case i equal to one if di = 0 and the patient has a subsequent pneumonia diagnosis recorded between 12 hours and 10 days after the initial chest X-ray. We include diagnoses in both ED and non-ED facilities, including outpatient, inpatient, and surgical encounters. In practice, mi is measured with error because it requires the patient to return to a VHA facility and for the second visit to correctly identify pneumonia. We show robustness of our results to endogenous second diagnoses by restricting analyses to veterans who solely use the VHA and who are sick enough to be admitted on the second visit in Section V.D.
We define the following patient characteristics for each case i: demographics (age, gender, marital status, religion, race, veteran status, and distance from home to the VA facility where the X-ray is ordered), prior health care utilization (counts of outpatient visits, inpatient admissions, and ED visits in any VHA facility in the previous 365 days), prior medical comorbidities (indicators for prior diagnosis of pneumonia and 31 Elixhauser comorbidity indicators in the previous 365 days), vital signs (e.g., blood pressure, pulse, pain score, and temperature), and white blood cell (WBC) count as of ED encounter. For each case, we measure characteristics associated with the chest X-ray request. This contains an indicator for whether the request was marked as urgent, an indicator for whether the X-ray involved one or two views, and requesting physician characteristics that we define below. For each variable that contains missing values, we replace missing values with zero and add an indicator for whether the variable is missing. Altogether, this yields 77 variables of patient and order characteristics (hereafter, “patient characteristics”) in five categories, 11 of which are indicators for missing values. We detail these variables in Online Appendix Table A.2.
For each radiologist in the sample, we record gender, date of birth, VHA employment start date, medical school, and proportion of radiology exams that are chest X-rays. For each chest X-ray in the sample, we record the time a radiologist spent to generate the report in minutes and the length of the report in words. For each requesting physician in the sample, we record the number of X-rays ordered across all patients, above-/below-median indicators for their average patient predicted diagnosis or predicted false negative,12 the physician’s leave-out shares of pneumonia diagnoses and false negatives, and the physician’s leave-out share of orders marked as urgent.
In the analysis that follows, we extend our baseline model to address two limitations of our data. First, our sample includes all chest X-rays, not only those that were ordered for suspicion of pneumonia. If an X-ray was ordered for a different reason, such as a rib fracture, it is unlikely even a low-skilled radiologist would incorrectly issue a pneumonia diagnosis. We thus allow for a share κ of cases to have si = 0 and to be recognized as such by all radiologists. We calibrate κ using a random-forest algorithm that predicts pneumonia diagnosis based on all characteristics in Online Appendix Table A.2 and words or phrases extracted from the chest X-ray requisition. We set κ = 0.336, which is the proportion of patients with a random-forest predicted probability of pneumonia less than 0.01.13
Second, some cases that we code as false negatives due to a pneumonia diagnosis on the second visit may either have been at too early a stage to have been identified even by a highly skilled radiologist or have developed in the interval between the first and second visit. We therefore allow for a share λ of cases that do not have pneumonia detectable by X-ray at the time of their initial visit to develop it and be diagnosed subsequently. We estimate λ as part of our structural analysis below.
IV. Model-Free Analysis
IV.A. Identification
For each case i, we observe the assigned radiologist j(i), the diagnosis indicator di, and the false negative indicator mi. As the number of cases assigned to each radiologist grows large, these data identify the diagnosis rate Pj and the miss rate FNj for each j. The data exhibit one-sided selection in the sense that the true state is only observed conditional on di = 0.14
The first goal of our descriptive analysis is to flexibly identify the shares of the classification matrix in Figure I, Panel A, for each radiologist. This allows us to plot the actual data in ROC space as in Figure II. The values of Pj and FNj would be sufficient to identify the remaining elements of the classification matrix if we also knew the share 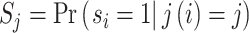 of j’s patients who had pneumonia since
of j’s patients who had pneumonia since
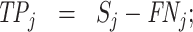 |
(1) |
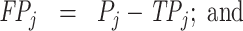 |
(2) |
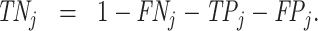 |
(3) |
Identification of the classification matrix therefore reduces to the problem of identifying the values of Sj.
Under random assignment of cases to agents, Sj will be equal to the overall population share 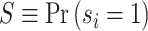 for all j. Thus, knowing S would be sufficient for identification. Moreover, the observed data also provide bounds on the possible values of S. If there exists a radiologist j such that Pj = 0, we would be able to learn S exactly, as S = Sj = FNj. Otherwise, letting
for all j. Thus, knowing S would be sufficient for identification. Moreover, the observed data also provide bounds on the possible values of S. If there exists a radiologist j such that Pj = 0, we would be able to learn S exactly, as S = Sj = FNj. Otherwise, letting 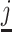 denote the radiologist with the lowest diagnosis rate (i.e.,
denote the radiologist with the lowest diagnosis rate (i.e., 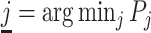 ) we must have
) we must have  .15 We show in Section V.B that S is point identified under the additional functional-form assumptions of our structural model. We use an estimate of S = 0.051 from our baseline structural model, and we also consider bounds for S; specifically, S ∈ [0.015, 0.073].16
.15 We show in Section V.B that S is point identified under the additional functional-form assumptions of our structural model. We use an estimate of S = 0.051 from our baseline structural model, and we also consider bounds for S; specifically, S ∈ [0.015, 0.073].16
The second goal of our descriptive analysis is to draw inferences about skill heterogeneity and the validity of standard monotonicity assumptions. Even without knowing the value of S, we may be able to reject the hypothesis of uniform skill using just the directly identified objects FNj and Pj. From Remark 2, we know that skill is not uniform if there exist j and j′ such that 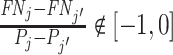 . This will be true in particular if j has both a higher diagnosis rate (
. This will be true in particular if j has both a higher diagnosis rate (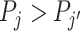 ) and a higher miss rate (
) and a higher miss rate (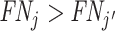 ). By the discussion in Section II.C, this rejects the standard monotonicity assumption (Condition 1.iii) as well as the weaker monotonicity assumptions we consider (Conditions 2–4).
). By the discussion in Section II.C, this rejects the standard monotonicity assumption (Condition 1.iii) as well as the weaker monotonicity assumptions we consider (Conditions 2–4).
With additional assumptions, the data may identify a partial or complete ordering of agent skill. Suppose, first, that we set aside the possibility that two agents’ signals may not be comparable in the Blackwell ordering and focus on the case where all agents can be ordered by skill. Then for any j and j′ with 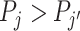 ,
, 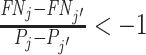 implies that agent j has strictly higher skill than agent j′ and
implies that agent j has strictly higher skill than agent j′ and 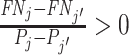 implies that agent j has strictly lower skill than agent j′. The ordering in this case is partial because if
implies that agent j has strictly lower skill than agent j′. The ordering in this case is partial because if 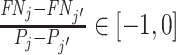 we can neither determine which agent is more skilled nor reject that their skill is the same. If we further assume (as in our structural model below) that agents’ signals come from a known family of distributions indexed by skill α, that all agents have Pj ∈ (0, 1), and that the signal distributions satisfy appropriate regularity conditions, the data are sufficient to identify each agent’s skill.17
we can neither determine which agent is more skilled nor reject that their skill is the same. If we further assume (as in our structural model below) that agents’ signals come from a known family of distributions indexed by skill α, that all agents have Pj ∈ (0, 1), and that the signal distributions satisfy appropriate regularity conditions, the data are sufficient to identify each agent’s skill.17
Looking at the data in ROC space provides additional intuition for how skill is identified. Although knowing the value of S is not necessary for the arguments in the previous two paragraphs, we suppose for illustration that this value is known so that the data identify a single point (FPRj, TPRj) in ROC space associated with each agent j.18 Agents j and j′ have equal skill if (FPRj, TPRj) and 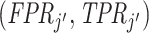 lie on a single ROC curve. Since ROC curves must be upward-sloping, we reject uniform skill if there exist j and j′ with
lie on a single ROC curve. Since ROC curves must be upward-sloping, we reject uniform skill if there exist j and j′ with 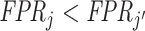 and
and 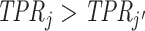 . Under the assumption that all agents are ordered by skill, this further implies that j must be strictly more skilled than j′. If signals are drawn from a known family of distributions indexed by α and satisfying appropriate regularity conditions, each value of α corresponds to a distinct nonoverlapping ROC curve, and observing the single point (FPRj, TPRj) is sufficient to identify the value of αj and the slope of the ROC curve at (FPRj, TPRj).
. Under the assumption that all agents are ordered by skill, this further implies that j must be strictly more skilled than j′. If signals are drawn from a known family of distributions indexed by α and satisfying appropriate regularity conditions, each value of α corresponds to a distinct nonoverlapping ROC curve, and observing the single point (FPRj, TPRj) is sufficient to identify the value of αj and the slope of the ROC curve at (FPRj, TPRj).
Agent preferences are also identified when agents are ordered by skill and signals are drawn from a known family of distributions. If the posterior probability of si = 1 is continuously increasing in wij for any signal, ROC curves must be smooth and concave (see Online Appendix B for proof). The implied slope of the ROC curve at (FPRj, TPRj) reveals the technological trade-off between false positives and false negatives, at which j is indifferent between d = 0 and d = 1. This trade-off identifies j’s cost of a false negative relative to a false positive, or 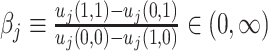 , which is, in turn, sufficient to identify the function uj(·,·) up to normalizations (see Online Appendix B for proof).
, which is, in turn, sufficient to identify the function uj(·,·) up to normalizations (see Online Appendix B for proof).
IV.B. Quasi-Random Assignment
A key assumption of our empirical analysis is quasi-random assignment of patients to radiologists. Our qualitative research suggests that the typical pattern is for patients to be assigned sequentially to available radiologists at the time their physician orders a chest X-ray. Such assignment will be plausibly quasi-random provided we control for the time and location factors that determine which radiologists are working at the time of each patient’s visit (e.g., Chan 2018).
Assumption 1
(Conditional Independence). Conditional on the hour of day, day of week, month, and location of patient i’s visit, the state si and potential diagnosis decisions
are independent of the assigned radiologist j(i).
In practice, we implement this conditioning by controlling for a vector 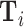 containing hour-of-day, day-of-week, and month-year indicators, each interacted with indicators for the station that i visits. Our results thus require that Assumption 1 holds and that this additively separable functional form for the controls is sufficient. We refer to
containing hour-of-day, day-of-week, and month-year indicators, each interacted with indicators for the station that i visits. Our results thus require that Assumption 1 holds and that this additively separable functional form for the controls is sufficient. We refer to 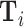 as our minimal controls.
as our minimal controls.
Although we expect assignment to be approximately random in all stations, organization and procedures differ across stations in ways that mean our time controls may do a better job of capturing confounding variation in some stations than in others.19 We therefore present our main model-free analyses for two sets of stations: the full set of 104 stations, and a subset of 44 of these stations for which we detect no statistically significant imbalance across radiologists in a single characteristic: patient age. Specifically, these 44 stations are all those for which the F-test for joint significance of radiologist dummies in a regression of patient age on those dummies and minimal controls, clustered by radiologist-day, fails to reject at the 10% level.
To provide evidence on the plausibility of quasi-random assignment, we look at the extent to which our vector of observable patient characteristics is balanced across radiologists conditional on the minimal controls. Paralleling the main regression analysis below, we first define a leave-out measure of the diagnosis propensity of each patient’s assigned radiologist,
 |
(4) |
where Ij is the set of patients assigned to radiologist j. We then ask whether Zi is predictable from our main vector 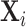 of patient i’s 77 observables after conditioning on the minimal controls.
of patient i’s 77 observables after conditioning on the minimal controls.
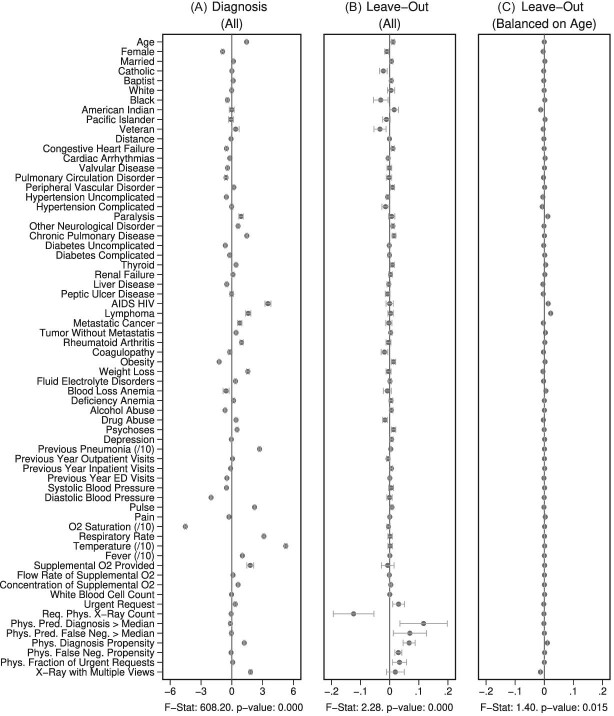
Figure IV presents the results. Panels A and B present individual coefficients from regressions of di (a patient’s own diagnosis status) and Zi (the leave-out propensity of the assigned radiologist), respectively, on the elements of 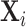 , controlling for
, controlling for 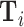 . Continuous elements of
. Continuous elements of 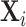 are standardized. At the bottom of each panel we report F-statistics and p-values for the null hypothesis that all coefficients on the elements of
are standardized. At the bottom of each panel we report F-statistics and p-values for the null hypothesis that all coefficients on the elements of 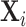 are equal to zero. Although
are equal to zero. Although 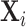 is highly predictive of a patient’s own diagnosis status, it has far less predictive power for Zi, with an F-statistic two orders of magnitude smaller and most coefficients close to zero. The small number of variables that are predictive of Zi—most notably characteristics of the requesting physician—are not predictive of di for the most part, and there is no obvious relationship between their respective coefficients in the regressions of di and Zi. Panel C presents the analogue of Panel B for the subset of 44 stations with balance on age.20 Here the F-statistic falls further and the ordering-physician characteristics that stand out in the middle panel are no longer individually significant. Thus, these stations that were selected for balance only on age also display balance on the other elements of
is highly predictive of a patient’s own diagnosis status, it has far less predictive power for Zi, with an F-statistic two orders of magnitude smaller and most coefficients close to zero. The small number of variables that are predictive of Zi—most notably characteristics of the requesting physician—are not predictive of di for the most part, and there is no obvious relationship between their respective coefficients in the regressions of di and Zi. Panel C presents the analogue of Panel B for the subset of 44 stations with balance on age.20 Here the F-statistic falls further and the ordering-physician characteristics that stand out in the middle panel are no longer individually significant. Thus, these stations that were selected for balance only on age also display balance on the other elements of  .
.
Figure IV.
Covariate Balance
This figure shows coefficients and 95% confidence intervals from regressions of diagnosis status di (left column) or the assigned radiologist’s leave-out diagnosis propensity Zi (middle and right columns, defined in equation (4)) on covariates 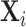 , controlling for time-station interactions
, controlling for time-station interactions 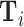 . The 66 covariates are the variables listed in Online Appendix A.2, without the 11 variables that are indicators for missing values. The left and middle panels use the full sample of stations. The right panel uses 44 stations with balance on age, defined in Section IV.B. The outcome variables are multiplied by 100. Continuous covariates are standardized so that they have standard deviations equal to 1. For readability, a few coefficients (and their standard errors) are divided by 10, as indicated by “/10” in the covariate labels. At the bottom of each panel, we report the F-statistic and p-value from the joint F-test of all covariates.
. The 66 covariates are the variables listed in Online Appendix A.2, without the 11 variables that are indicators for missing values. The left and middle panels use the full sample of stations. The right panel uses 44 stations with balance on age, defined in Section IV.B. The outcome variables are multiplied by 100. Continuous covariates are standardized so that they have standard deviations equal to 1. For readability, a few coefficients (and their standard errors) are divided by 10, as indicated by “/10” in the covariate labels. At the bottom of each panel, we report the F-statistic and p-value from the joint F-test of all covariates.
We present additional evidence of balance below and in the Online Appendix. As an input to this analysis, we form predicted values 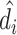 of the diagnosis indicator di, and
of the diagnosis indicator di, and 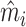 of the false negative indicator mi, based on respective regressions of di and mi on
of the false negative indicator mi, based on respective regressions of di and mi on 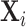 alone. This provides a low-dimensional projection of
alone. This provides a low-dimensional projection of 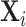 that isolates the most relevant variation.
that isolates the most relevant variation.
In Section IV.C, we provide graphical evidence on the magnitude of the relationship between predicted miss rates 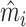 and radiologist diagnostic propensities Zi, paralleling our main analysis which focuses on the relationship between mi and Zi. This confirms that the relationship with
and radiologist diagnostic propensities Zi, paralleling our main analysis which focuses on the relationship between mi and Zi. This confirms that the relationship with 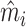 is economically small. We also show in Section IV.C that our key reduced-form regression coefficient is similar whether we control for none, all, or some of the variables in
is economically small. We also show in Section IV.C that our key reduced-form regression coefficient is similar whether we control for none, all, or some of the variables in 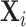 .
.
In Online Appendix Figure A.2, we show similar results to those in Figure IV using radiologists’ (leave-out) miss rates in place of the diagnosis propensities Zi. In Online Appendix Table A.3, we report F-statistics and p-values analogous to those in Figure IV and Online Appendix Figure A.2 for subsets of the characteristic vector 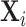 , showing that the main pattern remains consistent across these subsets.
, showing that the main pattern remains consistent across these subsets.
In Online Appendix Table A.4, we compare values of  and
and 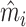 across radiologists with high and low diagnosis and miss rates, similar to a lower-dimensional analogue of the tests in Figure IV and Online Appendix Figure A.2. The results confirm the main conclusions we draw from Figure IV, showing small differences in the full sample of stations and negligible differences in the 44-station subsample.
across radiologists with high and low diagnosis and miss rates, similar to a lower-dimensional analogue of the tests in Figure IV and Online Appendix Figure A.2. The results confirm the main conclusions we draw from Figure IV, showing small differences in the full sample of stations and negligible differences in the 44-station subsample.
In Online Appendix Figure A.4, we present results from a permutation test in which we randomly reassign 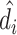 and
and 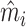 across patients within each station after partialing out minimal controls, estimate radiologist fixed effects from regressions of the reshuffled
across patients within each station after partialing out minimal controls, estimate radiologist fixed effects from regressions of the reshuffled 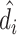 and
and 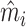 on radiologist dummies, and then compute the patient-weighted standard deviation of the estimated radiologist fixed effects within each station. Comparing these with the analogous standard deviation based on the real data provides a permutation-based p-value for balance in each station. We find that these p-values are roughly uniformly distributed in the 44 stations selected for balance on age, confirming that these stations exhibit balance on characteristics other than age. In Online Appendix Figure A.5, we present a complementary simulation exercise that suggests that we have the power to reject more than a small percentage of patients in these stations being systematically sorted to radiologists.
on radiologist dummies, and then compute the patient-weighted standard deviation of the estimated radiologist fixed effects within each station. Comparing these with the analogous standard deviation based on the real data provides a permutation-based p-value for balance in each station. We find that these p-values are roughly uniformly distributed in the 44 stations selected for balance on age, confirming that these stations exhibit balance on characteristics other than age. In Online Appendix Figure A.5, we present a complementary simulation exercise that suggests that we have the power to reject more than a small percentage of patients in these stations being systematically sorted to radiologists.
IV.C. Main Results
The first goal of our descriptive analysis is to flexibly identify the shares of the classification matrix in Figure I, Panel A, for each radiologist. This allows us to plot the data in ROC space, as in Figure II. We first form estimates 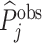 and
and 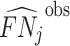 of each radiologist’s risk-adjusted diagnosis and miss rates.21 We further adjust these for the parameters κ and λ introduced in Section III to arrive at estimates
of each radiologist’s risk-adjusted diagnosis and miss rates.21 We further adjust these for the parameters κ and λ introduced in Section III to arrive at estimates 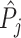 and
and 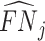 of underlying Pj and FNj. We fix the share κ of cases not at risk of pneumonia to the estimated value 0.336 discussed in Section III, and we fix the share λ of cases in which pneumonia manifests after the first visit at the value 0.026 estimated in the structural analysis.
of underlying Pj and FNj. We fix the share κ of cases not at risk of pneumonia to the estimated value 0.336 discussed in Section III, and we fix the share λ of cases in which pneumonia manifests after the first visit at the value 0.026 estimated in the structural analysis.
There is substantial variation in 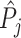 and
and 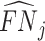 . Reassigning patients from a radiologist in the 10th percentile of diagnosis rates to a radiologist in the 90th percentile would increase the probability of a diagnosis from 8.9% to 12.3%. Reassigning patients from a radiologist in the 10th percentile of miss rates to a radiologist in the 90th percentile would increase the probability of a false negative from 0.2% to 1.8%. Online Appendix Table A.5 shows these and other moments of radiologist-level estimates.
. Reassigning patients from a radiologist in the 10th percentile of diagnosis rates to a radiologist in the 90th percentile would increase the probability of a diagnosis from 8.9% to 12.3%. Reassigning patients from a radiologist in the 10th percentile of miss rates to a radiologist in the 90th percentile would increase the probability of a false negative from 0.2% to 1.8%. Online Appendix Table A.5 shows these and other moments of radiologist-level estimates.
Finally, we solve for the remaining shares of the classification matrix by equations (1)–(3) and the prevalence rate S = 0.051 which we estimate in the structural analysis. We truncate the estimated values 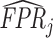 and
and 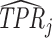 so that they lie in [0, 1] and so that
so that they lie in [0, 1] and so that 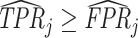 .22Online Appendix C provides further detail on these calculations. We present estimates of (FPRj, TPRj) in ROC space in Figure V. They show clearly that the data are inconsistent with the assumption that all radiologists lie along a single ROC curve, and instead suggest substantial heterogeneity in skill.23
.22Online Appendix C provides further detail on these calculations. We present estimates of (FPRj, TPRj) in ROC space in Figure V. They show clearly that the data are inconsistent with the assumption that all radiologists lie along a single ROC curve, and instead suggest substantial heterogeneity in skill.23
Figure V.

Projecting Data on ROC Space
This figure plots the true positive rate (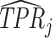 ) and false positive rate (
) and false positive rate ( ) for each radiologist across the 3,199 radiologists in our sample who have at least 100 chest X-rays. The figure is based on observed risk-adjusted diagnosis and miss rates
) for each radiologist across the 3,199 radiologists in our sample who have at least 100 chest X-rays. The figure is based on observed risk-adjusted diagnosis and miss rates  and
and  , then adjusted for the share of X-rays not at risk for pneumonia (
, then adjusted for the share of X-rays not at risk for pneumonia (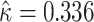 ) and the share of cases in which pneumonia first manifests after the initial visit (
) and the share of cases in which pneumonia first manifests after the initial visit (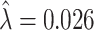 ). The values of
). The values of  and
and  are then computed using the estimated prevalence rate
are then computed using the estimated prevalence rate 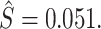 Values are truncated to impose
Values are truncated to impose 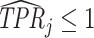 (affects 597 observations),
(affects 597 observations), 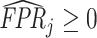 (affects 44 observations), and
(affects 44 observations), and 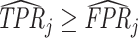 (affects 68 observations). See Section IV.C and Online Appendix C for more details.
(affects 68 observations). See Section IV.C and Online Appendix C for more details.
The second goal of our descriptive analysis is to estimate the relationship between radiologists’ diagnosis rates Pj and their miss rates FNj. We focus on the coefficient estimand Δ from a linear regression of FNj on Pj in the population of radiologists. As discussed in Section II.C, Δ ∈ [−1, 0] is an implication of the standard monotonicity of Condition 1.iii and the weaker versions of monotonicity we consider as well. Under our maintained assumptions, Δ ∉ [0, 1] implies that radiologists must not have uniform skill and skill must be systematically correlated with diagnostic propensities.
Exploiting quasi-experimental variation under Assumption 1, we can recover a consistent estimate of Δ from a 2SLS regression of mi on di instrumenting for the latter with the leave-out propensity Zi.24 In these regressions, we control for the vector of patient observables 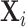 and the minimal time and station controls
and the minimal time and station controls 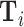 . Using the leave-out propensity is a standard approach that prevents overfitting the first stage in finite samples, which would bias the coefficient toward an OLS estimate of the relationship between mi and di (Angrist, Imbens, and Krueger 1999). We show in Online Appendix Figure A.7 that results are qualitatively similar if we use radiologist dummies as instruments.
. Using the leave-out propensity is a standard approach that prevents overfitting the first stage in finite samples, which would bias the coefficient toward an OLS estimate of the relationship between mi and di (Angrist, Imbens, and Krueger 1999). We show in Online Appendix Figure A.7 that results are qualitatively similar if we use radiologist dummies as instruments.
Figure VI presents the results. To visualize the IV relationship, we estimate the first-stage regression of di on Zi, controlling for 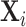 and
and 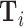 . We then plot a binned scatter of mi against the fitted values from the first stage, residualizing them with respect to
. We then plot a binned scatter of mi against the fitted values from the first stage, residualizing them with respect to 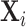 and
and 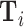 and recentering them to their respective sample means. The figure also shows the IV coefficient and standard error.
and recentering them to their respective sample means. The figure also shows the IV coefficient and standard error.
Figure VI.
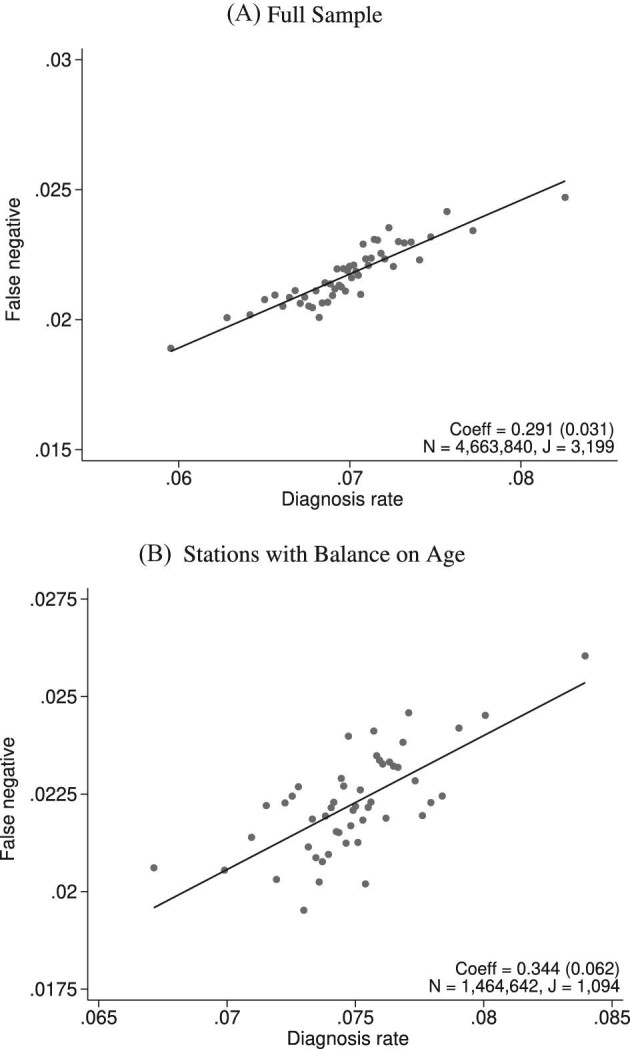
Diagnosis and Miss Rates
This figure plots the relationship between miss rates and diagnosis rates across radiologists using the leave-out diagnosis propensity instrument Zi, defined in equation (4). We first estimate the first-stage regression of diagnosis di on Zi controlling for covariates 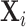 and minimal controls
and minimal controls 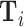 . We then plot a binned scatter of the indicator of a false negative mi against the fitted first-stage values, residualizing both with respect to
. We then plot a binned scatter of the indicator of a false negative mi against the fitted first-stage values, residualizing both with respect to 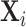 and
and 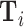 and recentering both to their respective sample means. Panel A shows results for the full sample. Panel B shows results in the subsample comprising 44 stations with balance on age, as defined in Section IV.B. The coefficient in each panel corresponds to the 2SLS estimate for the corresponding IV regression, as well as the number of cases (N) and the number of radiologists (J). The standard error is clustered at the radiologist level and is shown in parentheses.
and recentering both to their respective sample means. Panel A shows results for the full sample. Panel B shows results in the subsample comprising 44 stations with balance on age, as defined in Section IV.B. The coefficient in each panel corresponds to the 2SLS estimate for the corresponding IV regression, as well as the number of cases (N) and the number of radiologists (J). The standard error is clustered at the radiologist level and is shown in parentheses.
In the overall sample (Panel A) and in the sample selected for balance on age (Panel B), we show a strong positive relationship between diagnosis predicted by the instrument and false negatives, controlling for the full set of patient characteristics.25 This upward slope implies that the miss rate is higher for high-diagnosing radiologists not only conditionally (in the sense that the patients they do not diagnose are more likely to have pneumonia) but unconditionally as well. Thus, being assigned to a radiologist who diagnoses patients more aggressively increases the likelihood of leaving the hospital with undiagnosed pneumonia. Under Assumption 1, this implies violations in monotonicity. The only explanation for this under our framework is that high-diagnosing radiologists have less accurate signals, and that this is true to a large enough degree to offset the mechanical negative relationship between diagnosis and false negatives.
In Figure VII, we provide additional evidence on whether imbalances in patient characteristics may explain this relationship. This figure is analogous to Figure VI with the predicted false negative 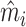 in place of the actual false negative mi and controls
in place of the actual false negative mi and controls 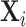 omitted. In the overall sample (Panel A), radiologists with higher diagnosis rates are assigned patients with characteristics that predict more false negatives. However, this relationship is small in magnitude in the full sample and negligible in the subsample of 44 stations with balance on age (Panel B). Notably, the positive IV coefficient in Figure VI is even larger in the latter subsample of stations.
omitted. In the overall sample (Panel A), radiologists with higher diagnosis rates are assigned patients with characteristics that predict more false negatives. However, this relationship is small in magnitude in the full sample and negligible in the subsample of 44 stations with balance on age (Panel B). Notably, the positive IV coefficient in Figure VI is even larger in the latter subsample of stations.
Figure VII.
Balance on Predicted False Negative
This figure plots the relationship between radiologist diagnosis rates and predicted false negatives of patients assigned to radiologists using the leave-out diagnosis propensity instrument Zi. Plots are generated analogously to those in Figure VI, except that the false negative indicator mi is replaced by the predicted value 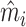 from a regression of mi on
from a regression of mi on 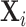 alone and controls
alone and controls 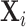 are omitted. Panel A shows results for the full sample. Panel B shows results in the subsample comprising 44 stations with balance on age, as defined in Section IV.B. The coefficient in each panel corresponds to the 2SLS estimate for the corresponding IV regression, as well as the number of cases (N) and the number of radiologists (J). The standard error is clustered at the radiologist level and is shown in parentheses.
are omitted. Panel A shows results for the full sample. Panel B shows results in the subsample comprising 44 stations with balance on age, as defined in Section IV.B. The coefficient in each panel corresponds to the 2SLS estimate for the corresponding IV regression, as well as the number of cases (N) and the number of radiologists (J). The standard error is clustered at the radiologist level and is shown in parentheses.
In Online Appendix Figure A.9, we show a scatterplot that collapses the underlying data points from Figure VI to the radiologist level. This plot reveals substantial heterogeneity in miss rates among radiologists with similar diagnosis rates: for the same diagnosis rate, a radiologist in the case-weighted 90th percentile of miss rates has a miss rate 0.7 percentage points higher than that of a radiologist in the case-weighted 10th percentile. This provides further evidence against the standard monotonicity assumption, which implies that all radiologists with a given diagnosis rate must also have the same miss rate.26
In Online Appendix D, we show that our data pass informal tests of monotonicity that are standard in the literature (Dobbie, Goldin, and Yang 2018; Bhuller et al. 2020), as shown in Online Appendix Table A.6. These tests require that diagnosis consistently increases in Pj in a range of patient subgroups.27 Thus, together with evidence of quasi-random assignment in Section IV.B, the standard empirical framework would suggest this as a plausible setting in which to use radiologist assignment as an instrument for the treatment variable dij.
However, were we to apply the standard approach and use radiologist assignment as an instrument to estimate an average effect of diagnosis dij on false negatives, we would reach the nonsensical conclusion that diagnosing a patient with pneumonia (and thus giving them antibiotics) makes them more likely to return with untreated pneumonia in the following days.28 Standard tests of monotonicity may pass while our test may strongly reject monotonicity by 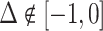 when monotonicity violations systematically occur along an underlying state si but not along observable characteristics. In Online Appendix D, we formally show that our test would be equivalent to a standard test if si were observable and were used as a characteristic to form subgroups within which to confirm a positive first stage.29
when monotonicity violations systematically occur along an underlying state si but not along observable characteristics. In Online Appendix D, we formally show that our test would be equivalent to a standard test if si were observable and were used as a characteristic to form subgroups within which to confirm a positive first stage.29
IV.D. Robustness
Given the small but significant imbalance that we detect in Section IV.B, we examine the robustness of our results to varying controls for patient characteristics and the set of stations we consider. We first divide our 77 patient characteristics into 10 groups.30 Next, we run separate regressions using each of the 210 = 1,024 possible combinations of these 10 groups as controls.
Figure VIII shows the range of the coefficients from IV regressions analogous to Figure VI across these specifications. The number of different specifications that corresponds to a given number of patient controls may differ. For example, controlling for either no patient characteristics or all patient characteristics each results in one specification. Controlling for n patient characteristics results in “10 choose n” specifications. For each number of characteristics on the x-axis, we plot the minimum, maximum, and mean IV estimate of Δ. The mean estimate actually increases with more controls, and no specification yields an estimate that is close to zero. Panel A displays results using observations from all stations, and Panel B displays results using observations from only the 44 stations in which we find balance on age. As expected, slope statistics are even more robust in Panel B.
Figure VIII.
Stability of Slope between Diagnosis and Miss Rates
This figure shows the stability of the IV estimate of Figure VI as we vary the set of patient characteristics we use as controls. We divide the 77 variables in 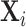 into 10 subsets as described in Section IV.D and rerun the IV regression of Figure VI using each of the 210 = 1,024 different combinations of the subsets in place of
into 10 subsets as described in Section IV.D and rerun the IV regression of Figure VI using each of the 210 = 1,024 different combinations of the subsets in place of 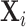 . The x-axis reports the number of subsets. The y-axis shows the average slope as a solid line and the minimum and maximum slopes as dashed lines. Panel A shows results in the full sample of stations; Panel B shows results in the subsample comprising 44 stations with balance on age, as defined in Section IV.B.
. The x-axis reports the number of subsets. The y-axis shows the average slope as a solid line and the minimum and maximum slopes as dashed lines. Panel A shows results in the full sample of stations; Panel B shows results in the subsample comprising 44 stations with balance on age, as defined in Section IV.B.
V. Structural Analysis
In this section, we specify and estimate a structural model with variation in skill and preferences. The model builds on the canonical selection framework by allowing radiologists to observe different signals of patients’ true conditions and rank cases differently by their appropriateness for diagnosis.
V.A. Model
Patient i’s true state si is determined by a latent index 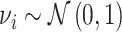 . If νi is greater than
. If νi is greater than 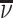 , then the patient has pneumonia:
, then the patient has pneumonia:
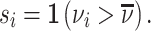 |
The radiologist j assigned to patient i observes a noisy signal 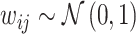 correlated with νi. The strength of the correlation between wij and vi characterizes the radiologist’s skill αj ∈ (0, 1]:31
correlated with νi. The strength of the correlation between wij and vi characterizes the radiologist’s skill αj ∈ (0, 1]:31
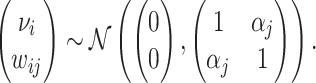 |
(5) |
We assume that radiologists know both the cutoff value 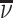 and their own skill αj. Note that normalizing the means and variances of νi and wij to zero and one respectively is without loss of generality.
and their own skill αj. Note that normalizing the means and variances of νi and wij to zero and one respectively is without loss of generality.
The radiologist’s utility is given by
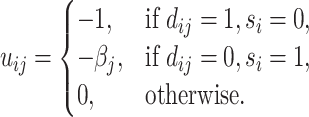 |
(6) |
The key preference parameter βj captures the disutility of a false negative relative to a false positive. Given that the health cost of undiagnosed pneumonia is potentially much greater than the cost of inadvertently giving antibiotics to a patient who does not need them, we expect βj > 1. We normalize the utility of correctly classifying patients to zero. Note that this parameterization of uj(d, s) with a single parameter βj is without loss of generality, in the sense that the ratio 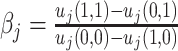 is sufficient to determine the agent’s optimal decision given the posterior
is sufficient to determine the agent’s optimal decision given the posterior 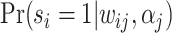 , as discussed in Section IV.A.
, as discussed in Section IV.A.
In Online Appendix E.1, we show that the radiologist’s optimal decision rule reduces to a cutoff value τj such that 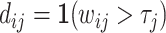 . The optimal cutoff τ* must be such that the agent’s posterior probability that si = 0 after observing wij = τ* is equal to
. The optimal cutoff τ* must be such that the agent’s posterior probability that si = 0 after observing wij = τ* is equal to 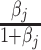 . The formula for the optimal threshold is
. The formula for the optimal threshold is
 |
(7) |
The cutoff value in turn implies FPj and FNj, which give expected utility
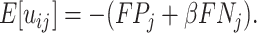 |
(8) |
The comparative statics of the threshold τ* with respect to  and βj are intuitive. The higher
and βj are intuitive. The higher  , and thus the smaller the share S of patients who in fact have pneumonia, the higher the threshold. The higher is βj, and thus the greater the cost of a missed diagnosis relative to a false positive, the lower the threshold.
, and thus the smaller the share S of patients who in fact have pneumonia, the higher the threshold. The higher is βj, and thus the greater the cost of a missed diagnosis relative to a false positive, the lower the threshold.
The effect of skill αj on the threshold can be ambiguous. This arises because αj has two distinct effects on the radiologist’s posterior on νi: (i) it shifts the posterior mean further from zero and closer to the observed signal wij; and (ii) it reduces the posterior variance. For αj ≈ 0, the radiologist’s posterior is close to the prior  regardless of the signal. If pneumonia is uncommon, in particular if
regardless of the signal. If pneumonia is uncommon, in particular if 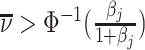 , she will prefer not to diagnose any patients, implying τ* ≈ ∞. As αj increases, effect (i) dominates. This makes any given wij more informative and so causes the optimal threshold to fall. As αj increases further, effect (ii) dominates. This makes the agent less concerned about the risk of false negatives and so causes the optimal threshold to rise. Given equation (7), we should expect thresholds to be correlated with skill when costs are highly asymmetric (i.e., βj is far from 1) or, for low skill, when the condition is rare (i.e.,
, she will prefer not to diagnose any patients, implying τ* ≈ ∞. As αj increases, effect (i) dominates. This makes any given wij more informative and so causes the optimal threshold to fall. As αj increases further, effect (ii) dominates. This makes the agent less concerned about the risk of false negatives and so causes the optimal threshold to rise. Given equation (7), we should expect thresholds to be correlated with skill when costs are highly asymmetric (i.e., βj is far from 1) or, for low skill, when the condition is rare (i.e., 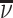 is high). Figure IX shows the relationship between αj and
is high). Figure IX shows the relationship between αj and 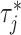 for different values of βj. Online Appendix E.1 discusses comparative statics of τ* further.
for different values of βj. Online Appendix E.1 discusses comparative statics of τ* further.
Figure IX.
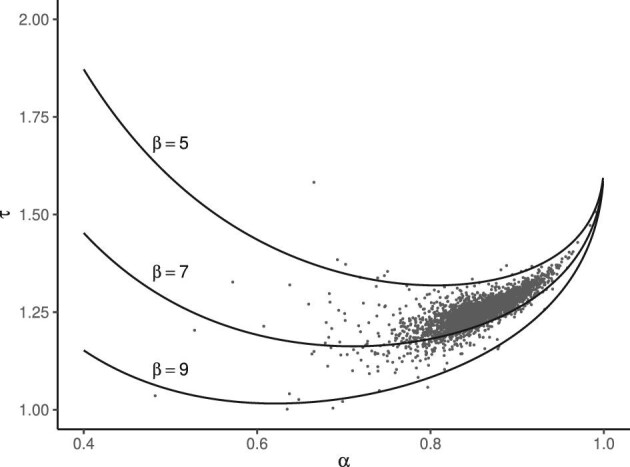
Optimal Diagnostic Threshold
This figure shows how the optimal diagnostic threshold varies as a function of skill α and preferences β with iso-preference curves for β ∈ {5, 7, 9}. Each iso-preference curve illustrates how the optimal diagnostic threshold varies with the evaluation skill for a fixed preference, given by equation (7), using 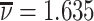 estimated from the model. Dots on the figure represent the empirical Bayes posterior mean of α (on the x-axis) and τ (on the y-axis) for each radiologist. The empirical Bayes posterior means are the same as those shown in Online Appendix Figure A.13. Details on the empirical Bayes procedure are given in Online Appendix E.3.
estimated from the model. Dots on the figure represent the empirical Bayes posterior mean of α (on the x-axis) and τ (on the y-axis) for each radiologist. The empirical Bayes posterior means are the same as those shown in Online Appendix Figure A.13. Details on the empirical Bayes procedure are given in Online Appendix E.3.
In Online Appendix G.1, we show that a richer model allowing pneumonia severity to impact both the probability of diagnosis and the disutility of a false negative yields a similar threshold-crossing model with equivalent empirical implications. In Online Appendix G.2, we explore an alternative formulation in which τj depends on a potentially misinformed belief about αj and an assumed fixed βj at some social welfare weight βs. From a social planner’s perspective, for a given skill αj, deviations from τ*(αj, βs) yield equivalent welfare losses regardless of whether they arise from deviations of βj from βs or from deviations of beliefs about αj from the truth.
If we know a radiologist’s FPRj and TPRj in ROC space, we can identify her skill αj by the shape of potential ROC curves, as discussed in Section IV.A, and her preference βj by her diagnosis rate and equation (7). Equation (5) determines the shape of potential ROC curves and implies that they are smooth and concave, consistent with utility maximization. It also guarantees that two ROC curves never intersect and that each (FPRj, TPRj) point lies on only one ROC curve.
The parameters κ and λ can be identified by the joint-normal signal structure implied by equation (5). With λ = 0, a radiologist with FPRj ≈ 0 must have a nearly perfectly informative signal and so should also have TPRj ≈ 1. We in fact observe that some radiologists with no false positives still have some false negatives, and the value of λ is determined by the size of this gap. Similarly, with κ = 0, a radiologist with TPRj ≈ 1 should either have perfect skill (implying FPRj ≈ 0) or simply diagnose everyone (implying FPRj ≈ 1). So the value of κ is identified if we observe a radiologist j with TPRj ≈ 1 and with FPRj far from 0 and 1, as the fraction of cases that j does not diagnose. In our estimation described below, we do not estimate κ but rather calibrate it from separate data as described in Section III.32
V.B. Estimation
We estimate the model using observed data on diagnoses di and false negatives mi. Recall that we observe mi = 0 for any i such that di = 1, and mi = 1 is possible only if di = 0. We define the following probabilities, conditional on 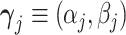 :
:
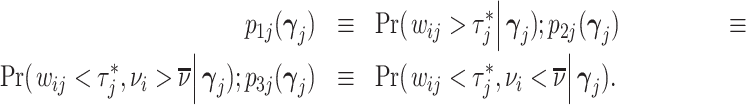 |
The likelihood of observing (di, mi) for a case i assigned to radiologist j(i) is
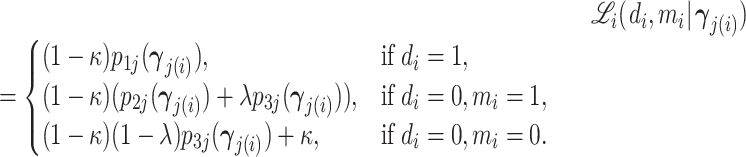 |
For the set of patients assigned to j, Ij ≡ {i: j(i) = j}, the likelihood of 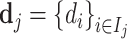 and
and 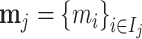 is
is
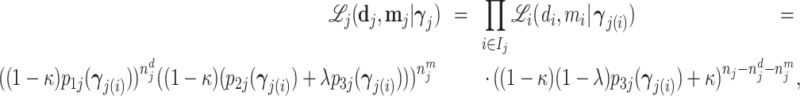 |
where 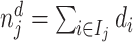 ,
, 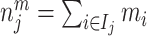 , and nj = |Ij|. From the above expression,
, and nj = |Ij|. From the above expression, 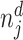 ,
, 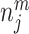 , and nj are sufficient statistics of the likelihood of
, and nj are sufficient statistics of the likelihood of 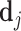 and
and  , and we can write the radiologist likelihood as
, and we can write the radiologist likelihood as 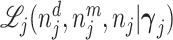 .
.
Given the finite number of cases per radiologist, we make an assumption on the population distribution of αj and βj across radiologists to improve power. Specifically, we assume
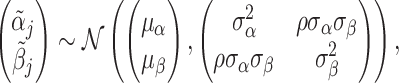 |
(9) |
where 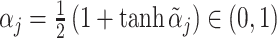 and
and 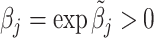 . We set ρ = 0 in our baseline specification but allow its estimation in Online Appendix F.
. We set ρ = 0 in our baseline specification but allow its estimation in Online Appendix F.
Finally, to allow for potential deviations from random assignment, we fit the model to counts of diagnoses and false negatives that are risk-adjusted to account for differences in patient characteristics 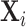 and minimal controls
and minimal controls 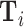 . We begin with the risk-adjusted radiologist diagnosis and miss rates
. We begin with the risk-adjusted radiologist diagnosis and miss rates 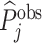 and
and 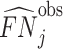 defined in Section IV.C. We then impute diagnosis and false negative counts
defined in Section IV.C. We then impute diagnosis and false negative counts 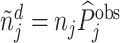 and
and 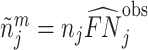 , where nj is the number of patients assigned to radiologist j; the imputed counts are not necessarily integers.
, where nj is the number of patients assigned to radiologist j; the imputed counts are not necessarily integers.
In a second step, we maximize the following log-likelihood to estimate the hyperparameter vector 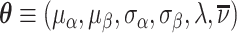 :
:
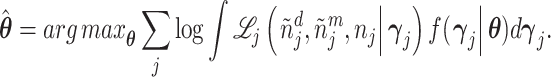 |
We compute the integral by simulation, described in further detail in Online Appendix E.2. Given our estimate of 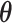 and each radiologist’s risk-adjusted data,
and each radiologist’s risk-adjusted data, 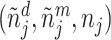 , we can also form an empirical Bayes posterior mean of each radiologist’s skill and preference (αj, βj), which we describe in Online Appendix E.3.
, we can also form an empirical Bayes posterior mean of each radiologist’s skill and preference (αj, βj), which we describe in Online Appendix E.3.
Our risk-adjustment approach can be seen as fitting the model to an “average” population of patients and radiologists whose distribution of diagnosis and miss rates are the same as the risk-adjusted values we characterize in our reduced-form analysis. An alternative would be to incorporate heterogeneity by station, time, and patient characteristics explicitly in the structural model; for example, allowing these to shift the distribution of patient health. Although this would be more coherent from a structural point of view, doing so with sufficient flexibility to guarantee quasi-random assignment would be computationally challenging. We show in Section V.D that our main results are qualitatively similar if we exclude  from risk adjustment or even omit the risk-adjustment step altogether. We show evidence from Monte Carlo simulations in Online Appendix G.3 that our linear risk adjustment is highly effective in addressing bias due to variation in risk across groups of observations, even when it is misspecified as additively separable.
from risk adjustment or even omit the risk-adjustment step altogether. We show evidence from Monte Carlo simulations in Online Appendix G.3 that our linear risk adjustment is highly effective in addressing bias due to variation in risk across groups of observations, even when it is misspecified as additively separable.
V.C. Results
Table I, Panel A shows estimates of the hyperparameter vector  in our baseline specification. Panel B shows moments in the distribution of posterior means of (αj, βj) implied by the model parameters. In the baseline specification, the mean radiologist skill is relatively high at 0.85. This implies that the average radiologist receives a signal that has a correlation of 0.85 with the patient’s underlying latent state νi. This correlation is 0.76 for a radiologist at the 10th percentile of this skill distribution and is 0.93 for a radiologist at the 90th percentile of the skill distribution. The average radiologist preference weights a false negative 6.71 times as high as a false positive. This relative weight is 5.60 at the 10th percentile of the preference distribution and is 7.91 at the 90th percentile of this distribution.
in our baseline specification. Panel B shows moments in the distribution of posterior means of (αj, βj) implied by the model parameters. In the baseline specification, the mean radiologist skill is relatively high at 0.85. This implies that the average radiologist receives a signal that has a correlation of 0.85 with the patient’s underlying latent state νi. This correlation is 0.76 for a radiologist at the 10th percentile of this skill distribution and is 0.93 for a radiologist at the 90th percentile of the skill distribution. The average radiologist preference weights a false negative 6.71 times as high as a false positive. This relative weight is 5.60 at the 10th percentile of the preference distribution and is 7.91 at the 90th percentile of this distribution.
TABLE I.
Structural Estimation Results
| Panel A: Model parameter estimates | |||||
|---|---|---|---|---|---|
| Estimate | Description | ||||
| μα | 0.945 | Mean of 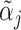 , , 
|
|||
| (0.219) | |||||
| σα | 0.296 | Standard deviation of 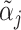
|
|||
| (0.029) | |||||
| μβ | 1.895 | Mean of 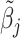 , , 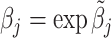
|
|||
| (0.249) | |||||
| σβ | 0.136 | Standard deviation of 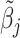
|
|||
| (0.044) | |||||
| λ | 0.026 | Share of at-risk negatives developing subsequent pneumonia | |||
| (0.001) | |||||
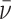
|
1.635 | Prevalence 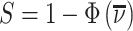
|
|||
| (0.091) | |||||
| κ | 0.336 | Share not at risk for pneumonia | |||
| Panel B: Radiologist posterior means | |||||
| Percentiles | |||||
| Mean | 10th | 25th | 75th | 90th | |
| α | 0.855 | 0.756 | 0.816 | 0.908 | 0.934 |
| (0.050) | (0.079) | (0.065) | (0.035) | (0.025) | |
| β | 6.713 | 5.596 | 6.071 | 7.284 | 7.909 |
| (1.694) | (1.608) | (1.659) | (1.750) | (1.780) | |
| τ | 1.252 | 1.165 | 1.208 | 1.298 | 1.336 |
| (0.006) | (0.009) | (0.006) | (0.008) | (0.012) | |
Notes. This table shows model parameter estimates (Panel A) and moments in the implied distribution of empirical Bayes posterior means across radiologists (Panel B). μα and σα determine the distribution of radiologist diagnostic skill α, and μβ and σβ determine the distribution of radiologist preferences β (the disutility of a false negative relative to a false positive). We assume that α and β are uncorrelated. λ is the proportion of at-risk chest X-rays with no radiographic pneumonia at the time of exam but subsequent development of pneumonia.  describes the prevalence of pneumonia at the time of the exam among at-risk chest X-rays. κ is the proportion of chest X-rays not at risk for pneumonia. It is calibrated as the proportion of patients with predicted probability of pneumonia less than 0.01 from a random forest model of pneumonia based on rich characteristics in the patient chart. Parameters are described in further detail in Sections V.A and V.B. The method to calculate empirical Bayes posterior means is described in Online Appendix E.3. Standard errors, shown in parentheses, are computed by block bootstrap, with replacement, at the radiologist level.
describes the prevalence of pneumonia at the time of the exam among at-risk chest X-rays. κ is the proportion of chest X-rays not at risk for pneumonia. It is calibrated as the proportion of patients with predicted probability of pneumonia less than 0.01 from a random forest model of pneumonia based on rich characteristics in the patient chart. Parameters are described in further detail in Sections V.A and V.B. The method to calculate empirical Bayes posterior means is described in Online Appendix E.3. Standard errors, shown in parentheses, are computed by block bootstrap, with replacement, at the radiologist level.
In Online Appendix Figure A.12, we compare the distributions of observed data moments of radiologist diagnosis and miss rates with those simulated from the model at the estimated parameter values.33 In all cases, the simulated data match the observed data closely.
In Figure IX, we display empirical Bayes posterior means for (αj, βj) in a space that represents optimal diagnostic thresholds. The relationship between skill and diagnostic thresholds is mostly positive. As radiologists become more accurate, they diagnose fewer people (their thresholds increase) because the costly possibility of making a false negative diagnosis decreases. In Online Appendix Figure A.13, we show the distributions of the empirical Bayes posterior means for αj, βj, and τj, and the joint distribution of αj and βj. Finally, in Online Appendix Figure A.14, we transform empirical Bayes posterior means for (αj, βj) into moments in ROC space. The relationship between TPRj and FPRj implied by the empirical Bayes posterior means is similar to that implied by the flexible projection shown earlier in Figure V.
V.D. Robustness
In Online Appendix F, we explore alternative samples, controls, and structural estimation approaches. To evaluate robustness to potential violations in quasi-random assignment, we estimate our model restricting to data from 44 stations with quasi-random assignment selected in Section IV.B. To assess robustness to our risk-adjustment procedure, we also estimate our model with moments that omit patient characteristics  from the risk-adjustment procedure, and we estimate the model omitting the risk-adjustment step altogether, plugging raw counts
from the risk-adjustment procedure, and we estimate the model omitting the risk-adjustment step altogether, plugging raw counts 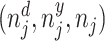 directly into the likelihood. To address potential endogenous return ED visits, we restrict our sample to only heavy VA users. To address potential endogenous second diagnoses, we restrict false negatives to cases of pneumonia that required inpatient admission.
directly into the likelihood. To address potential endogenous return ED visits, we restrict our sample to only heavy VA users. To address potential endogenous second diagnoses, we restrict false negatives to cases of pneumonia that required inpatient admission.
Finally, we consider sensitivity to alternative assumptions. First, we estimate an alternative model that allows for flexible correlation ρ. While λ and ρ are separately identified in the data, they are difficult to separately estimate, so we fix ρ = 0 in the baseline model.34 In the alternative approach, we fix λ = 0.026 and allow for flexible ρ. Second, we consider alternative values for κ and report results in Online Appendix Table A.10.
Our main qualitative findings are robust across all of these alternative approaches. Both reduced-form moments and estimated structural parameters are qualitatively unchanged. As a result, our decompositions of variation into skill and preferences, discussed in Section VI, are also unchanged.
V.E. Heterogeneity
To provide suggestive evidence of what may drive variation in skill and preferences, we project our empirical Bayes posterior means for (αj, βj) onto observed radiologist characteristics. Online Appendix Figure A.15 shows the distribution of observed characteristics across bins defined by empirical Bayes posterior means of skill αj. Online Appendix Figure A.16 shows analogous results for the preference parameter βj.
As shown in Online Appendix Figure A.15, higher-skilled radiologists are older and more experienced (Panel A).35 Higher-skilled radiologists also tend to read more chest X-rays as a share of the scans they read (Panel B). Interestingly, those who are more skilled spend more time generating their reports (Panel C), suggesting that skill may be a function of effort as well as characteristics like training or talent. Radiologists with more skill also issue shorter rather than longer reports (Panel D), possibly pointing to clarity and efficiency of communication as a marker of skill. There is little correlation between skill and the rank of the medical school a radiologist attended (Panel E). Finally, higher-skilled radiologists are more likely to be male, in part reflecting the fact that male radiologists are older and tend to be more specialized in reading chest X-rays (Panel F). The results for the preference parameter βj, in Online Appendix Figure A.16, tend to go in the opposite direction. This reflects the fact that our empirical Bayes estimates of αj and βj are slightly negatively correlated.
It is important to emphasize that large variation in characteristics remains, even conditional on skill or preference. This is broadly consistent with the physician practice style and teacher value-added literature, which demonstrate large variation in decisions and outcomes that appear uncorrelated with physician or teacher characteristics (Epstein and Nicholson 2009; Staiger and Rockoff 2010).
VI. Policy Implications
VI.A. Decomposing Observed Variation
To assess the relative importance of skill and preferences in driving observed decisions and outcomes, we simulate counterfactual distributions of decisions and outcomes in which we eliminate variation in skill or preferences separately. We first simulate model primitives (αj, βj) from the estimated parameters. Then we eliminate variation in skill by imposing 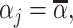 where
where 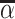 is the mean of αj, while keeping βj unchanged. Similarly, we eliminate variation in preferences by imposing
is the mean of αj, while keeping βj unchanged. Similarly, we eliminate variation in preferences by imposing 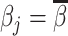 , where
, where 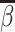 is the mean of βj, while keeping αj unchanged. For baseline and counterfactual distributions of underlying primitives—(αj, βj),
is the mean of βj, while keeping αj unchanged. For baseline and counterfactual distributions of underlying primitives—(αj, βj), 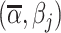 , and
, and 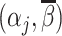 —we simulate a large number of observations per radiologist to approximate the shares Pj and FNj for each radiologist.
—we simulate a large number of observations per radiologist to approximate the shares Pj and FNj for each radiologist.
Eliminating variation in skill reduces variation in diagnosis rates by 39% and variation in miss rates by 78%. On the other hand, eliminating variation in preferences reduces variation in diagnosis rates by 29% and has no significant effect on variation in miss rates.36 These decomposition results suggest that variation in skill can have first-order effects on variation in decisions, something the standard model of preference-based selection rules out by assumption.
VI.B. Policy Counterfactuals
We evaluate the welfare implications of policies aimed at observed variation in decisions or at underlying skill. Welfare depends on the overall false positive FP and the overall false negative FN. We denote these objects under the status quo as FP0 and FN0, respectively. We then define an index of welfare relative to the status quo:
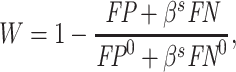 |
(10) |
where βs is the social planner’s relative welfare loss due to false negatives compared to false positives. This index ranges from W = 0 at the status quo to W = 1 at the first best of FP = FN = 0. It is also possible that W < 0 under a counterfactual policy that reduces welfare relative to the status quo.
We estimate FP0 and FN0 based on our model estimates as
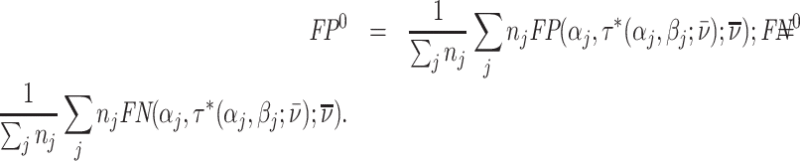 |
Here, 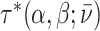 denotes the optimal threshold given the evaluation skill α, the preference β, and the disease prevalence
denotes the optimal threshold given the evaluation skill α, the preference β, and the disease prevalence 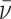 . We simulate a set of 10,000 radiologists, each characterized by (αj, βj), from the estimated hyperparameters. We then consider welfare under counterfactual policies that eliminate diagnostic variation by imposing diagnostic thresholds on radiologists.
. We simulate a set of 10,000 radiologists, each characterized by (αj, βj), from the estimated hyperparameters. We then consider welfare under counterfactual policies that eliminate diagnostic variation by imposing diagnostic thresholds on radiologists.
In Table II, we evaluate outcomes under two sets of counterfactual policies. Counterfactuals 1 and 2 focus on thresholds, and Counterfactuals 3–6 aim to improve skill.
TABLE II.
Counterfactual Policies
| Policy | Welfare | False negative | False positive | Diagnosed | Reclassified |
|---|---|---|---|---|---|
| 0. Status quo | 0 | 0.194 | 1.268 | 2.074 | 0 |
| (0.042) | (0.439) | (0.403) | |||
| 1. Fixed threshold | −0.002 | 0.200 | 1.232 | 2.033 | 0.193 |
| (0.015) | (0.075) | (0.177) | (0.113) | (0.224) | |
| 2. Threshold as function of skill | 0.004 | 0.192 | 1.271 | 2.080 | 0.126 |
| (0.020) | (0.080) | (0.157) | (0.101) | (0.246) | |
| 3. Improve skill to 25th percentile | 0.059 | 0.175 | 1.239 | 2.064 | 0.073 |
| (0.016) | (0.039) | (0.455) | (0.421) | (0.023) | |
| 4. Improve skill to 50th percentile | 0.144 | 0.153 | 1.169 | 2.016 | 0.184 |
| (0.027) | (0.033) | (0.445) | (0.417) | (0.059) | |
| 5. Improve skill to 75th percentile | 0.265 | 0.125 | 1.049 | 1.924 | 0.346 |
| (0.034) | (0.026) | (0.407) | (0.385) | (0.119) | |
| 6. Combine two signals | 0.348 | 0.108 | 0.947 | 1.839 | 0.470 |
| (0.024) | (0.024) | (0.379) | (0.359) | (0.144) | |
| 7. First best | 1 | 0 | 0 | 1 | 1.461 |
| (0.475) |
Notes. This table shows outcomes and welfare under the status quo and counterfactual policies further described in Section VI. Welfare is normalized to 0 for the status quo and 1 for the first best of no false negative or false positive outcomes. Numbers of cases that are false negatives, false positives, diagnosed, and reclassified are all divided by the prevalence of pneumonia. Reclassified cases are those with a classification (i.e., diagnosed or not) that is different under the counterfactual policy than under the status quo. The first row shows outcomes and welfare under the status quo. Subsequent rows show outcomes and welfare under counterfactual policies. Counterfactuals 1 and 2 impose diagnostic thresholds: Counterfactual 1 imposes a fixed diagnosis rate for all radiologists; Counterfactual 2 imposes diagnosis rates as a function of diagnostic skill. Counterfactuals 3 to 5 improve diagnostic skill to the 25th, 50th, and 75th percentiles, respectively. Counterfactual 6 allows two radiologists to diagnose a single patient and combine the (assumed) independent signals they receive. Standard errors, shown in parentheses, are computed by block bootstrap, with replacement, at the radiologist level.
Counterfactual 1 imposes a fixed diagnostic threshold to maximize welfare:
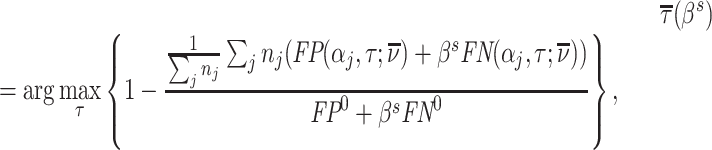 |
where 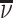 and the simulated set of αj are derived from our baseline model in Section V. Despite the objective to maximize welfare, a fixed diagnostic threshold may actually reduce welfare relative to the status quo by imposing this constraint. On the other hand, Counterfactual 2 allows diagnostic thresholds as a function of αj, implementing
and the simulated set of αj are derived from our baseline model in Section V. Despite the objective to maximize welfare, a fixed diagnostic threshold may actually reduce welfare relative to the status quo by imposing this constraint. On the other hand, Counterfactual 2 allows diagnostic thresholds as a function of αj, implementing 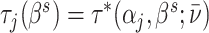 . This policy should weakly increase welfare and outperform Counterfactual 1.
. This policy should weakly increase welfare and outperform Counterfactual 1.
In Counterfactuals 3–6, we consider alternative policies that improve diagnostic skill—for example, by training radiologists, selecting radiologists with higher skill, or aggregating signals—so that decisions use better information. In Counterfactuals 3–5, we allow radiologists to choose their own diagnostic thresholds but improve the skill αj of all radiologists at the bottom of the distribution to a minimum level. For example, in Counterfactual 3, we improve skill to the 25th percentile α25, setting αj = α25 for any radiologist below this level. The optimal thresholds are then 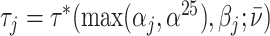 . Counterfactual 6 forms random two-radiologist teams and aggregates signals of each team member under the assumption that the two signals are drawn independently.37
. Counterfactual 6 forms random two-radiologist teams and aggregates signals of each team member under the assumption that the two signals are drawn independently.37
Table II shows outcomes and welfare under βs = 6.71, matching the mean radiologist preference βj. We find that imposing a fixed diagnostic threshold (Counterfactual 1) would actually reduce welfare. Although this policy reduces aggregate false positives, it increases aggregate false negatives, which are costlier. Imposing a threshold that varies optimally with skill (Counterfactual 2) must improve welfare, but we find that the magnitude of this gain is small. In contrast, improving diagnostic skill reduces false negatives and false positives and substantially outperforms threshold-based policies. Combining two radiologist signals (Counterfactual 6) improves welfare by 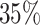 of the difference between status quo and first best. Counterfactual policies that improve radiologist skill naturally reclassify a much higher number of cases than policies that simply change diagnostic thresholds. This is because improving skill will reorder signals while changing thresholds leaves signals unchanged.
of the difference between status quo and first best. Counterfactual policies that improve radiologist skill naturally reclassify a much higher number of cases than policies that simply change diagnostic thresholds. This is because improving skill will reorder signals while changing thresholds leaves signals unchanged.
Table II also shows aggregate rates of diagnosis and “reclassification,” counting changes in classification (i.e., diagnosed or not) between the status quo and the counterfactual policy. Under all of the policies we consider, the numbers of reclassified cases are greater, sometimes dramatically so, than net changes in the numbers of diagnosed cases.
Online Appendix Figure A.18 shows welfare changes as a function of the social planner’s preferences βs. In this figure we consider Counterfactuals 1 and 3 from Table II. We also show the welfare gain a planner would expect if she set a fixed threshold under the incorrect assumption that radiologists have uniform diagnostic skill. In this calculation, we assume that the planner assumes a common diagnostic skill parameter 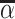 that rationalizes FP0 and FN0 with some estimate of disease prevalence
that rationalizes FP0 and FN0 with some estimate of disease prevalence 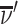 .
.
In this “mistaken policy counterfactual,” the planner would conclude that a fixed threshold would modestly increase welfare. In the range of βs spanning radiologist preferences from the 10th to 90th percentiles (Table I and Online Appendix Figure A.13), the skill policy outperforms the threshold policy, regardless of the policy maker’s belief on the heterogeneity of skill. The threshold policy only outperforms the skill policy when βs diverges significantly from radiologist preferences. For example, if βs = 0, the optimal policy is trivial: no patient should be diagnosed with pneumonia. In this case, there is no gain to improving skill, but there is a large gain to imposing a fixed threshold since radiologists’ preferences deviate widely from the social planner’s preferences.
VI.C. Discussion
We show that dimensions of “skill” and “preferences” have different implications for welfare and policy. Each of these dimensions likely captures a range of underlying factors. In our framework, “skill” captures the relationship between a patient’s underlying state and a radiologist’s signals about the state. We attribute this mapping to the radiologist because quasi-random assignment to radiologists implies that we are isolating the causal effect of radiologists. As suggested by the evidence in Section V.E, “skill” may reflect not only underlying ability but also effort. Furthermore, in this setting, radiologists may form their judgments with the aid of other clinicians (e.g., residents, fellows, nonradiologist clinicians) and must communicate their judgments to other physicians. Skill may reflect not only the quality of signals that the radiologist observes directly but also the quality of signals that she (or her team) passes on to other clinicians.
What we call “preferences” encompass any distortion from the optimal threshold implied by (i) the social planner’s relative disutility of false negatives, or βs, and (ii) each radiologist’s skill, or αj. These distortions may arise from intrinsic preferences or external incentives that cause radiologist βj to differ from βs. Alternatively, as we elaborate in Online Appendix G.2, equivalent distortions may arise from radiologists having incorrect beliefs about their own skill αj.
For purposes of welfare analysis, the mechanisms underlying “preferences” or “skill” do not matter insofar as they map to an optimal diagnostic threshold and deviations from it. However, practical policy implications (e.g., whether we train radiologists to read chest X-rays, collaborate with others, or communicate with others) will depend on institution-specific mechanisms.
VII. Conclusion
In this article, we decompose the roots of practice variation in decisions across radiologists into dimensions of skill and preferences. The standard view in much of the literature is to assume that such practice variation in many settings results from variation in preferences. We first show descriptive evidence that runs counter to this view: radiologists who diagnose more cases with a disease are also the ones who miss more cases that actually have the disease. We apply a framework of classification and a model of decisions that depend on diagnostic skill and preferences. Using this framework, we demonstrate that the source of variation in decisions can have important implications for how policy makers should view the efficiency of variation and for the ideal policies to address such variation. In our case, variation in skill accounts for 39% of the variation in diagnostic decisions, and policies that improve skill result in potentially large welfare improvements, whereas policies to impose uniform diagnosis rates may reduce welfare.
Our approach may be applied to settings with the following conditions: (i) quasi-random assignment of cases to decision makers, (ii) an objective to match decisions to underlying states, and (iii) signals of a case’s underlying state may be observable to the analyst under at least one of the decisions. Many settings of interest may meet these criteria. For example, physicians aim to match diagnostic and treatment decisions to each patient’s underlying disease state (Abaluck et al. 2016; Mullainathan and Obermeyer 2022). Judges aim to match bail decisions to whether a defendant will recidivate (Kleinberg et al. 2018). Under these conditions, this framework can be used to decompose observed variation in decisions and outcomes into policy-relevant measures of skill and preferences.
Our framework also contributes to an active and growing judges design literature that uses variation across decision makers to estimate the effect of a decision on outcomes (e.g., Kling 2006). In this setting, we demonstrate a practical test of monotonicity revealed by miss rates (i.e., Δ ∈ [−1, 0]), drawing on intuition delineated previously in the case of binary instruments (Balke and Pearl 1997; Kitagawa 2015). This generalizes to testing whether cases that suggest an underlying state relevant for classification—for example, subsequent diagnoses, appellate court decisions (Norris 2019), or discovery of contraband (Feigenberg and Miller 2022)—have proper density (i.e., 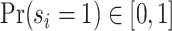 ) among compliers. We show that, although such tests may be stronger than those typically used in the judges design literature, they nevertheless correspond to a weaker monotonicity assumption that intuitively relates treatment propensities to skill and implies the “average monotonicity” concept of Frandsen, Lefgren, and Leslie (2019).
) among compliers. We show that, although such tests may be stronger than those typically used in the judges design literature, they nevertheless correspond to a weaker monotonicity assumption that intuitively relates treatment propensities to skill and implies the “average monotonicity” concept of Frandsen, Lefgren, and Leslie (2019).
The behavioral foundation of our empirical framework also provides a way to think about when the validity of the judges design may be at risk because of monotonicity violations. Diagnostic skill may be particularly important to account for when agents require expertise to match decisions to underlying states, when this expertise likely varies across agents, and when costs between false negatives and false positives are highly asymmetric. When all three of these conditions are met, we may have a priori reason to expect correlations between diagnostic skill and propensities, potentially casting doubt on the validity of the standard judges design. Our work suggests further testing to address this doubt. Finally, because the judges design relies on comparisons between agents of the same skill, our approach to measuring skill may provide a path for future research designs that correct for bias due to monotonicity violations by conditioning on skill. In Online Appendix G.4, we run a Monte Carlo simulation as a proof of concept for this possibility.
Supplementary Material
Footnotes
We thank Hanming Fang, Amy Finkelstein, Alex Frankel, Martin Hackmann, Nathan Hendren, Peter Hull, Karam Kang, Pat Kline, Jon Kolstad, Pierre-Thomas Leger, Jesse Shapiro, Gaurav Sood, Chris Walters, and numerous seminar and conference participants for helpful comments and suggestions. We also thank Zong Huang, Vidushi Jayathilak, Kevin Kloiber, Douglas Laporte, Uyseok Lee, Christopher Lim, Lisa Yi, and Saam Zahedian for excellent research assistance. The Stanford Institute for Economic Policy Research provided generous funding and support. Chan gratefully acknowledges support from NIH DP5OD019903-01.
Doyle, Ewer, and Wagner (2010) show a potential relationship between physician human capital and resource utilization decisions. Gowrisankaran, Joiner, and Leger (2017) and Ribers and Ullrich (2019) provide evidence of variation in diagnostic and treatment skill, and Silver (2021) examines returns to time spent on patients by ED physicians and variation in the physicians’ productivity. Mullainathan and Obermeyer (2022) show evidence of poor heart attack decisions (low skill) evaluated by a machine learning benchmark. Stern and Trajtenberg (1998) study variation in prescribing and suggest that some of it may relate to physicians’ diagnostic skill.
For example, Kleinberg et al. (2018) find that the increase in crime associated with judges who are more likely to release defendants on bail is about the same as if these more lenient judges randomly picked the extra defendants to release on bail. Arnold, Dobbie, and Yang (2018) find a similar relationship for black defendants being released on bail. Judges that are most likely to release defendants on bail in fact have slightly lower crime rates than judges that are less likely to grant bail. As in our setting, policy implications in these other settings will depend on the relationship between agent skill and preferences (see Hoffman, Kahn, and Li 2018; Frankel 2021).
Under this assumption, a sensible implication is that hospitals with comparative advantage for treatment should treat more patients. Interestingly, however, our work suggests that if comparative advantage (i.e., higher treatment effects on the treated) is microfounded on better diagnostic skill, then hospitals with such comparative advantage may instead optimally treat fewer patients.
Kitagawa (2015) and Mourifie and Wan (2017) develop tests of instrument validity based on an older insight in the literature noting that instrument validity implies nonnegative densities of compliers for any potential outcome (Imbens and Rubin 1997; Balke and Pearl 1997; Heckman and Vytlacil 2005). Recent work by Machado, Shaikh, and Vytlacil (2019) exploits bounds in a binary outcome to test instrument validity and sign average treatment effects. Similar to Frandsen, Lefgren, and Leslie (2019), we define a monotonicity condition in the judges design that is weaker than the standard one considered in these papers. However, we demonstrate a test that is stronger than the standard in the judges design literature.
Concavity follows from observing that if (FPR, TPR) and (FPR′, TPR′) are two points on an agent’s ROC curve generated by using thresholds τ and τ′, the agent can also achieve any convex combination of these points by randomizing between τ and τ′. That the ROC curve must lie weakly above the 45-degree line follows from noting that for any FPR an agent can achieve TPR = FPR by ignoring her signal and choosing d = 1 with probability equal to FPR. The maximum achievable TPR associated with this FPR must therefore be weakly larger.
The two facts in Remark 2 are immediate from the observation that FNj = Sj(1 − TPRj) and Pj = Sj · TPRj + (1 − Sj) · FPRj combined with the fact that ROC curves are increasing.
In addition to the assumption below, we require instrument relevance such that 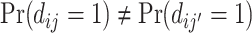 for some j and j′. This requirement can be assessed by a first-stage regression of di on judge indicators.
for some j and j′. This requirement can be assessed by a first-stage regression of di on judge indicators.
As noted, any LATE for the effect of di on 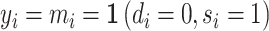 must lie in the interval [−1, 0]. This implies that the judges design IV coefficient estimand from a regression of mi on di instrumenting with radiologist indicators must lie in this interval. This corresponds to an OLS coefficient estimand from a regression of FNj on Pj.
must lie in the interval [−1, 0]. This implies that the judges design IV coefficient estimand from a regression of mi on di instrumenting with radiologist indicators must lie in this interval. This corresponds to an OLS coefficient estimand from a regression of FNj on Pj.
We define chest X-rays by the Current Procedural Terminology codes 71010 and 71020.
Online Appendix Figure A.1 presents distributions of cases across radiologists and radiologist-months and of radiologists across stations and station-months.
Diagnoses do not have time stamps per se but are linked to visits, with time stamps for when the visits begin. Therefore, the time associated with diagnoses is usually before the chest X-ray order; in a minority of cases, a secondary visit (e.g., an inpatient visit) occurs shortly after the initial ED visit, and we observe a diagnosis time after the chest X-ray order. We include International Classification of Diseases, Ninth Revision, (ICD-9) codes 480–487 for pneumonia diagnosis.
These predictions are fitted values from regressing di or mi on patient demographics.
We use an extreme gradient boosting algorithm first introduced in Friedman (2001) and use decision trees as the learner. We train a binary classification model and set the learning rate at 0.15, the maximum depth of a tree at 8, and the number of rounds at 450. We use all variables and all observations in each tree.
False negatives are observable by construction in our setting as we define si as cases of pneumonia that will not get better on their own and result in a subsequent observed diagnosis. We conservatively assume that false positives are unobservable, but in practice some cases can present with alternative explanations for a patient’s symptoms that would rule out pneumonia.
See Arnold, Dobbie, and Hull (2020) for a detailed discussion and implementation of identification using these boundary conditions.
To construct these bounds, instead of using the radiologist with the lowest diagnosis rate, we divide all radiologists into 10 bins based on their diagnosis rates, construct bounds for each bin using the group weighted-average diagnosis and miss rates, and take the intersection of all bounds. See Online Appendix C for more details.
For skill to be identified, the signal distributions need to satisfy regularity conditions guaranteeing that the miss rate FNj achievable for any given diagnosis rate Pj is strictly decreasing in skill. Then there is a unique mapping from (FNj, Pj) to skill.
Richer data could identify more points on a single agent’s ROC curve, for example, by exploiting variation in preferences (e.g., the cost of diagnosis) for the same agent while holding skill fixed.
In our qualitative research, we identify at least two types of conditioning sets that are unobserved to us. One is that the population of radiologists in some stations includes both “regular” radiologists who are assigned chest X-rays according to the normal sequential protocol and other radiologists who read chest X-rays only when the regular radiologists are not available or in other special circumstances. A second is that some stations consist of multiple sublocations, and patients and radiologists could sort systematically to sublocations. Because our fixed effects do not capture either radiologist “types” or sublocations, either of these could lead Assumption 1 to be violated.
For brevity, we omit the analogue of Panel A for these 44 stations. This is presented in Online Appendix Figure A.3 and confirms that the relationship between di and 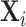 remains qualitatively similar.
remains qualitatively similar.
We form these as the fitted radiologist fixed effects from respective regressions of di and mi on radiologist fixed effects, patient characteristics 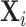 , and minimal controls
, and minimal controls 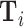 . We recenter
. We recenter 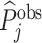 and
and 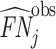 within each station so that the patient-weighted averages within each station are equal to the overall population rate and truncate these adjusted rates to be no less than zero. This truncation applies to 2 out of 3,199 radiologists in the case of
within each station so that the patient-weighted averages within each station are equal to the overall population rate and truncate these adjusted rates to be no less than zero. This truncation applies to 2 out of 3,199 radiologists in the case of 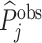 and 45 out of 3,199 radiologists in the case of
and 45 out of 3,199 radiologists in the case of 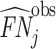 .
.
Imposing 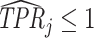 affects 597 observations (
affects 597 observations (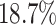 of the total). Imposing
of the total). Imposing 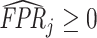 affects 44 observations. Imposing
affects 44 observations. Imposing 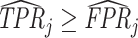 affects 68 observations.
affects 68 observations.
In Online Appendix Figure A.6, we show how the results change when we set S at the lower bound (S = 0.015) and upper bound (S = 0.073) derived in Section IV.A. The values of TPR and FPR change substantially, but the overall pattern of a negative slope in ROC space remains robust. As discussed in Section IV.A, the sign of the slope of the line connecting any two points in ROC space is in fact identified independently of the value of S, so this robustness is, in a sense, guaranteed. In the same figure, we show that varying the assumed values of λ and κ similarly affects the levels but not the qualitative pattern in ROC space.
Observed mi and di do not account for the parameters κ and λ, so we are estimating a coefficient Δobs from a regression of 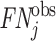 on
on 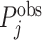 . In Online Appendix C, we show that Δ ∈ [−1, 0] is equivalent to Δobs ∈ [−1, −λ], which is an even smaller admissible range.
. In Online Appendix C, we show that Δ ∈ [−1, 0] is equivalent to Δobs ∈ [−1, −λ], which is an even smaller admissible range.
We show the first-stage relationship in Online Appendix Figure A.8.
In Online Appendix Figure A.10, we investigate the IV-implied relationship between diagnosis and false negatives in each station and show that in the vast majority of stations the station-specific estimate of Δ is outside of the bounds of [−1, 0].
In Online Appendix D, we show the relationship between these standard tests and our test. We discuss that these results suggest that (i) radiologists consider unobserved patient characteristics in their diagnostic decisions, (ii) these unobserved characteristics predict si, and (iii) their use distinguishes high-skilled radiologists from low-skilled radiologists.
As shown in Online Appendix Table A.7, in our sample of all stations, we also find that diagnosing and treating pneumonia implausibly increases mortality, repeat ED visits, patient-days in the hospital, and ICU admissions. However, in the sample of 44 stations with balance on age, these effects are statistically insignificant, reversed in sign, and smaller in magnitude.
We note in Section II.C a close connection between our test and tests of IV validity proposed by Kitagawa (2015) and Mourifie and Wan (2017). Our test maps more directly to monotonicity because we use an “outcome” 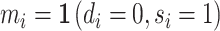 that is mechanically defined by di and si, so that “exclusion” in Condition 1.i is satisfied by construction.
that is mechanically defined by di and si, so that “exclusion” in Condition 1.i is satisfied by construction.
We divide all patient characteristics into five categories in Online Appendix Table A.2. We further divide the first category (demographics) into six groups: age and gender, marital status, race, religion, indicator for veteran status, and the distance between home and the VA station performing the X-ray. Combining these six groups with the other four categories gives us 10 groups.
The joint-normal distribution of vi and wij determines the set of potential shapes of radiologist ROC curves. This simple parameterization implies concave ROC curves above the 45-degree line, attractive features described in Section II.B. In Online Appendix Figure A.11, we map the correlation αj to the area under the curve (AUC), which is a common measure of performance in classification. The AUC measures the area under the ROC curve: an AUC value of 0.5 corresponds to classification no better than random chance (i.e., αj = 0) whereas an AUC value of 1 corresponds to perfect classification (e.g., αj = 1).
While κ is in principle identified, radiologists with the highest TPRj have FPRj ≈ 0 and do not have the highest diagnosis rate. These radiologists appear to have close to perfect skill, which is consistent with any κ. Thus, we cannot identify κ in practice. In Online Appendix Table A.10, we show that our results and their policy implications do not depend qualitatively on our choice of κ.
We construct simulated moments as follows. We first fix the number of patients each radiologist examines to the actual number. We then simulate patients at risk from a binomial distribution with the probability of being at risk of 1 − κ. For patients at risk, we simulate their underlying true signal and the radiologist-observed signal, νi and wij, respectively, using our posterior mean for αj. We determine which patients are diagnosed with pneumonia and which patients are false negatives based on τ*(αj, βj), νi, and  . We finally simulate patients who did not initially have pneumonia but later develop it with λ.
. We finally simulate patients who did not initially have pneumonia but later develop it with λ.
We do not have many points representing radiologists with many cases who exactly have FPRj = 0. Points in (FPRj, TPRj) space with FPRj ≈ 0 and TPRj < 1 can be rationalized by λ > 0, a very negative ρ, or some combination of both. With infinite data, we should be able to separately estimate λ and ρ, but with finite data, it is difficult to fit both λ and ρ.
These results are based on a model that allows underlying primitives to vary by radiologist j and age bin t (we group five years as an age bin), where within j, μα and μβ each change linearly with t. We estimate a positive linear trend for μα and a slightly negative trend for μβ. We find similar relationships when we assess radiologist tenure on the job and log number of prior chest X-rays.
Online Appendix Table A.8, Panel B shows these baseline results and standard errors, as well as corresponding results under alternative specifications described in Section V.D. Online Appendix Figure A.17 shows implications for variation in diagnosis rates and for variation in miss rates under a range of reductions in variation in skill or reductions in variation in preferences.
In practice, the signals of radiologists working in the same location may be subject to correlated noise. In this sense, we view this counterfactual as an upper bound of information from combining signals.
Contributor Information
David C Chan, Stanford University, Department of Veterans Affairs, and National Bureau of Economic Research, United States.
Matthew Gentzkow, Stanford University and National Bureau of Economic Research, United States.
Chuan Yu, Stanford University, United States.
Data Availability
Code replicating the tables and figures in this article can be found in Chan, Gentzkow, and Yu (2022) in the Harvard Dataverse, https://doi.org/10.7910/DVN/WKXOXC.
References
- Abaluck Jason, Agha Leila, Kabrhel Chris, Raja Ali, Venkatesh Arjun, “The Determinants of Productivity in Medical Testing: Intensity and Allocation of Care,” American Economic Review, 106 (2016), 3730–3764. [PubMed] [Google Scholar]
- Abujudeh Hani H., Boland Giles W., Kaewlai Rathachai, Rabiner Pavel, Halpern Elkarn F., Scott Gazelle G., Thrall James H., “Abdominal and Pelvic Computed Tomography (CT) Interpretation: Discrepancy Rates among Experienced Radiologists,” European Radiology, 20 (2010), 1952–1957. [DOI] [PubMed] [Google Scholar]
- Angrist J. D., Imbens G. W., Krueger A. B., “Jackknife Instrumental Variables Estimation,” Journal of Applied Econometrics, 14 (1999), 57–67. [Google Scholar]
- Anwar Shamena, Fang Hanming, “An Alternative Test of Racial Prejudice in Motor Vehicle Searches: Theory and Evidence,” American Economic Review, 96 (2006), 127–151. [Google Scholar]
- Arnold David, Dobbie Will S., Hull Peter, “Measuring Racial Discrimination in Bail Decisions,” NBER Working Paper no. 26999, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold David, Dobbie Will, Yang Crystal S., “Racial Bias in Bail Decisions,” Quarterly Journal of Economics, 133 (2018), 1885–1932. [Google Scholar]
- Balke Alexander, Pearl Judea, “Bounds on Treatment Effects from Studies with Imperfect Compliance,” Journal of the American Statistical Association, 92 (1997), 1171–1176. [Google Scholar]
- Bertrand Marianne, Schoar Antoinette, “Managing with Style: The Effect of Managers on Firm Policies,” Quarterly Journal of Economics, 118 (2003), 1169–1208. [Google Scholar]
- Bhuller Manudeep, Dahl Gordon B., Loken Katrine V., Mogstad Magne, “Incarceration, Recidivism, and Employment,” Journal of Political Economy, 128 (2020), 1269–1324. [Google Scholar]
- Blackwell David, “Equivalent Comparisons of Experiments,” Annals of Mathematical Statistics, 24 (1953), 265–272. [Google Scholar]
- Chan David C., “The Efficiency of Slacking Off: Evidence from the Emergency Department,” Econometrica, 86 (2018), 997–1030. [Google Scholar]
- Chan David C., Gentzkow Matthew, Yu Chuan, “Replication Data for: ‘Selection with Variation in Diagnostic Skill: Evidence from Radiologists’,” (2022), Harvard Dataverse, 10.7910/DVN/WKXOXC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandra Amitabh, Cutler David, Song Zirui, “Who Ordered That? The Economics of Treatment Choices in Medical Care,” in Handbook of Health Economics, vol. 2, Pauly Mark V., Mcguire Thomas G., and Barros Pedro P., eds. (Amsterdam: Elsevier, 2011), 397–432. [Google Scholar]
- Chandra Amitabh, Staiger Douglas O., “Productivity Spillovers in Healthcare: Evidence from the Treatment of Heart Attacks,” Journal of Political Economy, 115 (2007), 103–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandra Amitabh, Staiger Douglas O., “Identifying Sources of Inefficiency in Health Care,” Quarterly Journal of Economics, 135 (2020), 785–843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie Janet, Bentley MacLeod W., “Diagnosing Expertise: Human Capital, Decision Making, and Performance among Physicians,” Journal of Labor Economics, 35 (2017), 1–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobbie Will, Goldin Jacob, Yang Crystal S., “The Effects of Pretrial Detention on Conviction, Future Crime, and Employment: Evidence from Randomly Assigned Judges,” American Economic Review, 108 (2018), 201–240. [Google Scholar]
- Doyle Joseph J., Ewer S. M., Wagner T. H., “Returns to Physician Human Capital: Evidence from Patients Randomized to Physician Teams,” Journal of Health Economics, 29 (2010), 866–882. [DOI] [PubMed] [Google Scholar]
- Doyle Joseph J., Graves John A., Gruber Jonathan, Kleiner Samuel, “Measuring Returns to Hospital Care: Evidence from Ambulance Referral Patterns,” Journal of Political Economy, 123 (2015), 170–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein A. J., Nicholson S., “The Formation and Evolution of Physician Treatment Styles: An Application to Cesarean Sections,” Journal of Health Economics, 28 (2009), 1126–1140. [DOI] [PubMed] [Google Scholar]
- Fabre C., Proisy M., Chapuis C., Jouneau S., Lentz P. A., Meunier C., Mahe G., Lederlin M., “Radiology Residents’ Skill Level in Chest X-Ray Reading,” Diagnostic and Interventional Imaging, 99 (2018), 361–370. [DOI] [PubMed] [Google Scholar]
- Feigenberg Benjamin, Miller Conrad, “Would Eliminating Racial Disparities in Motor Vehicle Searches Have Efficiency Costs?,” Quarterly Journal of Economics, 137 (2022), 49–113. [Google Scholar]
- Figlio David N., Lucas Maurice E., “Do High Grading Standards Affect Student Performance?,” Journal of Public Economics, 88 (2004), 1815–1834. [Google Scholar]
- File Thomas M., Marrie Thomas J., “Burden of Community-Acquired Pneumonia in North American Adults,” Postgraduate Medicine, 122 (2010), 130–141. [DOI] [PubMed] [Google Scholar]
- Fisher Elliott S., Wennberg David E., Stukel Therese A., Gottlieb Daniel J., Lucas F. L., Pinder Etoile L., “The Implications of Regional Variations in Medicare Spending. Part 1: The Content, Quality, and Accessibility of Care,” Annals of Internal Medicine, 138 (2003a), 273–287. [DOI] [PubMed] [Google Scholar]
- Fisher Elliott S., Wennberg David E., Stukel Therese A., Gottlieb Daniel J., Lucas F. L., Pinder Etoile L., “The Implications of Regional Variations in Medicare Spending. Part 2: Health Outcomes and Satisfaction with Care,” Annals of Internal Medicine, 138 (2003b), 288–298. [DOI] [PubMed] [Google Scholar]
- Frandsen Brigham R., Lefgren Lars J., Leslie Emily C., “Judging Judge Fixed Effects,” NBER Working Paper no. 25528, 2019. [Google Scholar]
- Frankel Alex, “Selecting Applicants,” Econometrica, 89 (2021), 615–645. [Google Scholar]
- Friedman Jerome H., “Greedy Function Approximation: A Gradient Boosting Machine,” Annals of Statistics, 29 (2001), 1189–1232. [Google Scholar]
- Garber Alan M., Skinner Jonathan, “Is American Health Care Uniquely Inefficient?,” Journal of Economic Perspectives, 22 (2008), 27–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowrisankaran Gautam, Joiner Keith, Leger Pierre-Thomas, “Physician Practice Style and Healthcare Costs: Evidence from Emergency Departments,” NBER Working Paper no. 24155, 2017. [Google Scholar]
- Heckman James J., Vytlacil Edward, “Structural Equations, Treatment Effects, and Econometric Policy Evaluation,” Econometrica, 73 (2005), 669–738. [Google Scholar]
- Hoffman Mitchell, Kahn Lisa B., Li Danielle, “Discretion in Hiring,” Quarterly Journal of Economics, 133 (2018), 765–800. [Google Scholar]
- Imbens Guido W., Angrist Joshua D., “Identification and Estimation of Local Average Treatment Effects,” Econometrica, 62 (1994), 467–475. [Google Scholar]
- Imbens Guido W., Rubin Donald B., “Estimating Outcome Distributions for Compliers in Instrumental Variables Models,” Review of Economic Studies, 64 (1997), 555–574. [Google Scholar]
- Institute of Medicine , Variation in Health Care Spending: Target Decision Making, Not Geography (Washington, DC: National Academies Press, 2013). [PubMed] [Google Scholar]
- Institute of Medicine , Improving Diagnosis in Health Care (Washington, DC: National Academies Press, 2015). [PubMed] [Google Scholar]
- Kitagawa Toru, “A Test for Instrument Validity,” Econometrica, 83 (2015), 2043–2063. [Google Scholar]
- Kleinberg Jon, Lakkaraju Himabindu, Leskovec Jure, Ludwig Jens, Mullainathan Sendhil, “Human Decisions and Machine Predictions,” Quarterly Journal of Economics, 133 (2018), 237–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kling Jeffrey R., “Incarceration Length, Employment, and Earnings,” American Economic Review, 96 (2006), 863–876. [Google Scholar]
- Kung Hsiang-Ching, Hoyert Donna L., Xu Jiaquan, Murphy Sherry L., “Deaths: Final Data for 2005,” National Vital Statistics Reports, 56 (2008), 1–120. [PubMed] [Google Scholar]
- Leape Lucian L., Brennan Troyen A., Laird Nan, Lawthers Ann G., Russell Localio A., Barnes Benjamin A., Hebert Liesi, Newhouse Joseph P., Weiler Paul C., Hiatt Howard, “The Nature of Adverse Events in Hospitalized Patients,” New England Journal of Medicine, 324 (1991), 377–384. [DOI] [PubMed] [Google Scholar]
- Machado Cecilia, Shaikh Azeem M., Vytlacil Edward J., “Instrumental Variables and the Sign of the Average Treatment Effect,” Journal of Econometrics, 212 (2019), 522–555. [Google Scholar]
- Molitor David, “The Evolution of Physician Practice Styles: Evidence from Cardiologist Migration,” American Economic Journal: Economic Policy, 10 (2017), 326–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mourifie Ismael, Wan Yuanyuan, “Testing Local Average Treatment Effect Assumptions,” Review of Economics and Statistics, 99 (2017), 305–313. [Google Scholar]
- Mullainathan Sendhil, Obermeyer Ziad, “A Machine Learning Approach to Low-Value Health Care: Wasted Tests, Missed Heart Attacks and Mis-Predictions,” Quarterly Journal of Economics, 137 (2022), 679–727. [Google Scholar]
- Norris Samuel, “Examiner Inconsistency: Evidence from Refugee Appeals,” Becker Friedman Institute of Economics Working Paper 2018-75, 2019. [Google Scholar]
- Ribers Michael A., Ullrich Hannes, “Battling Antibiotic Resistance: Can Machine Learning Improve Prescribing?,” DIW Berlin Discussion Paper 1803, 2019. [Google Scholar]
- Rubin Donald B., “Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies,” Journal of Educational Psychology, 66 (1974), 688–701. [Google Scholar]
- Ruuskanen Olli, Lahti Elina, Jennings Lance C., Murdoch David R., “Viral Pneumonia,” Lancet, 377 (2011), 1264–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Self Wesley H., Mark Courtney D., McNaughton Candace D., Wunderink Richard G., Kline Jeffrey A., “High Discordance of Chest X-Ray and Computed Tomography for Detection of Pulmonary Opacities in ED Patients: Implications for Diagnosing Pneumonia,” American Journal of Emergency Medicine, 31 (2013), 401–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shojania Kaveh G., Burton Elizabeth C., McDonald Kathryn M., Goldman Lee, “Changes in Rates of Autopsy-Detected Diagnostic Errors Over Time: A Systematic Review,” Journal of the American Medical Association, 289 (2003), 2849–2856. [DOI] [PubMed] [Google Scholar]
- Silver David, “Haste or Waste? Peer Pressure and Productivity in the Emergency Department,” Review of Economic Studies, 88 (2021), 1385–1417. [Google Scholar]
- Staiger Douglas O., Rockoff Jonah E., “Searching for Effective Teachers with Imperfect Information,” Journal of Economic Perspectives, 24 (2010), 97–118. [Google Scholar]
- Stern Scott, Trajtenberg Manuel, “Empirical Implications of Physician Authority in Pharmaceutical Decisionmaking,” NBER Working Paper no. 6851, 1998. [Google Scholar]
- Thomas Eric J., Studdert David M., Burstin Helen R., John Orav E., Zeena Timothy, Williams Elliott J., Mason Howard K., Weiler Paul C., Brennan Troyen A., “Incidence and Types of Adverse Events and Negligent Care in Utah and Colorado,” Medical Care, 38 (2000), 261–271. [DOI] [PubMed] [Google Scholar]
- Van Parys Jessica, Skinner Jonathan, “Physician Practice Style Variation: Implications for Policy,” JAMA Internal Medicine, 176 (2016), 1549–1550. [DOI] [PubMed] [Google Scholar]
- Vytlacil Edward, “Independence, Monotonicity, and Latent Index Models: An Equivalence Result,” Econometrica, 70 (2002), 331–341. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code replicating the tables and figures in this article can be found in Chan, Gentzkow, and Yu (2022) in the Harvard Dataverse, https://doi.org/10.7910/DVN/WKXOXC.