BOUNDING THE LOCAL AVERAGE TREATMENT EFFECT IN AN INSTRUMENTAL VARIABLE ANALYSIS OF ENGAGEMENT WITH A MOBILE INTERVENTION

Abstract

Estimation of local average treatment effects in randomized trials typically relies upon the exclusion restriction assumption in cases where we are unwilling to rule out the possibility of unmeasured confounding. Under this assumption, treatment effects are mediated through the post-randomization variable being conditioned upon, and directly attributable to neither the randomization itself nor its latent descendants. Recently, there has been interest in mobile health interventions to provide healthcare support. Mobile health interventions such as the Rapid Encouragement/Education and Communications for Health (REACH), designed to support self-management for adults with type 2 diabetes, often involve both one-way and interactive messages. In practice, it is highly likely that any benefit from the intervention is achieved both through receipt of the intervention content and through engagement with/response to it. Application of an instrumental variable analysis in order to understand the role of engagement with REACH (or a similar intervention) requires the traditional exclusion restriction assumption to be relaxed. We propose a conceptually intuitive sensitivity analysis procedure for the REACH randomized trial that places bounds on local average treatment effects. Simulation studies reveal this approach to have desirable finite-sample behavior and to recover local average treatment effects under correct specification of sensitivity parameters.

1. Introduction.

There has been recent interest in studies of mobile (e.g., text message-based) interventions designed to improve health outcomes by targeting self-efficacy and self-care behaviors such as medication adherence (Greenwood et al., 2017; Marcolino et al., 2018). Rapid Encouragement/Education and Communications for Health (REACH), for instance, is a text message-delivered intervention designed to support medication adherence for patients with type 2 diabetes (Nelson et al., 2018, 2021). The REACH study was a randomized trial that sought to evaluate the effects of this intervention on hemoglobin A1c (HbA1c) as compared to a control condition. A key feature of the REACH study is that subjects in the intervention arm received both one-way text messages providing information and encouragement, and interactive (two-way) text messages requesting a response. Though subjects in the intervention arm received the same number of messages, there was variation in rate of response to interactive text messages across subjects within the intervention arm. The extent to which a subject responds to interactive messages serves as an objective measure of his or her engagement with the intervention. A natural study goal therefore includes determining the effect of the REACH intervention on HbA1c conditional on engagement. This goal is in some ways analogous to the goal of estimating local average treatment effects in a randomized trial with partial compliance.

The post-randomization nature of engagement obscures our ability to achieve the stated goal using standard regression techniques. Further, the almost certain presence of unmeasured common causes of engagement and HbA1c violates principles put forth by certain causal inference techniques such as inverse probability weighting and standardization (Rosenbaum and Rubin, 1983; Robins, 1986; Robins, Hernán and Brumback, 2000; Lunceford and Davidian, 2004; Funk et al., 2011). Defining and estimating causal effects in the setting of partial compliance has further complications as the number of possible treatment conditions is far beyond the number of treatment conditions prescribed by the study design. The principal stratification framework, developed by Frangakis and Rubin (2002), has been widely applied to estimation of local average treatment effects under treatment noncompliance (Greevy et al., 2004; Roy, Hogan and Marcus, 2008; Frangakis, Rubin and Zhou, 2002). One such application of this framework laid out a number of conditions under which each study subject’s principal stratum can be inferred based on observed data in the setting of partial treatment compliance (Jin and Rubin, 2008). Under such conditions, local average treatment effects of interest are identifiable. While such assumptions can be justified in certain drug trials, the major barrier to uncovering each subject’s principal stratum in the context of the REACH study, per the assumptions of Jin and Rubin (2008), is that subjects assigned to the control condition do not provide the necessary information to infer how they would engage with the REACH intervention had they hypothetically been assigned to it, specifically because they are given no intervention with which to engage.

Other applications of the principal stratification framework to settings of treatment noncompliance rely on an assumption known as the exclusion restriction (Imbens and Angrist, 1994; Angrist and Imbens, 1995; Angrist, Imbens and Rubin, 1996; Roy, Hogan and Marcus, 2008), under which it is not necessary to identify each subject’s principal stratum to identify causal effects. Stated within the context of the REACH study, the exclusion restriction requires any effect of the intervention on HbA1c to be mediated through engagement with the interactive text messages, and to be derived neither directly through randomization itself nor mediated through any of its latent descendants. Irrespective of a subject’s choice to respond to text message content, receipt of content may motivate or cue self-care behavior in a way that cannot be addressed through measured covariates; therefore the validity of the exclusion restriction assumption is tenuous at best in the case of REACH or other similar interventions.

The fact that subjects assigned to the control condition have a known engagement level of zero allows us to index local average treatment effects on the basis of a single variable (namely, engagement under assignment to the REACH intervention). In this work, we will make use of this simplification to derive and justify conditions suitable for a sensitivity analysis procedure under which local average treatment effects can be bounded. The importance of considering violations to the exclusion restriction assumption has been previously noted; in the setting of discrete principal strata applied to the setting of treatment compliance, Angrist, Imbens and Rubin (1996) are able to express the bias of an estimator based on instrumental variables in terms of the direct effect of the instrument on the outcome and the odds of being a non-complier. Since the focus of our work will involve continuous measures of engagement (e.g., proportion of messages receiving a response), we will also need to address matters of specifying non-identifiable functional forms that relate hypothetical levels of engagement to corresponding local average treatment effects.

The remainder of this manuscript is centered on the development of a sensitivity analysis procedure for the REACH study, and is organized as follows. In Section 2, we provide a description of our notation and assumptions, and define the local average treatment effects of interest in terms of an intuitive sensitivity parameter. In Section 3, we characterize the resulting bounds on such effects. In Section 4, we propose estimation and inferential procedures, as well as a framework for evaluating treatment effect heterogeneity. In Section 5, we conduct a simulation study in order to evaluate the finite-sample performance of our proposed procedure, and in Section 6, we apply our results to the REACH study. We conclude in Section 7 with a discussion of our findings and possible future directions for methodological research.

2. Definitions, assumptions, and weak identifiability.

In this section, we provide an outline of our notation, define a class of local average treatment effects of interest, and characterize assumptions for our sensitivity analysis procedure.

2.1. Notation.

Let i = 1, … ,N index independently sampled study subjects. We let (Z_i, A_i, Y_i) denote each subject’s observed binary randomization group (which serves as the instrument), engagement measure, and outcome, respectively. Let N₀ and N₁ denote the sample sizes in each of the respective randomization groups, with N₀ + N₁ = N. Without loss of generality, we assume higher values of A_i to signify higher levels of engagement (with A_i = 0 signifying no engagement). Following notation of the potential outcomes framework (Rubin, 1974), let $A_i^{z=0}$ and $A_i^{z=1}$ denote subject i’s potential engagement levels (e.g., text message response rate) under randomization to treatments z = 0 and z = 1; similarly, let $Y_i^{z=0}$ and $Y_i^{z=1}$ denote potential outcomes (e.g., HbA1c) under each respective treatment. For notational convenience, we will drop the subscript index i when referring to these random variables unless such subscripts are necessary to distinguish between subjects. Figure 1 depicts a directed acyclic graph (DAG) illustrating the temporal ordering of these observed variables. We will let L and U denote measured and unmeasured (respectively) common causes of A and Y; note that identifiability of target parameters relies on neither L nor U under the assumptions we will put forth, although we will later describe how information on observed covariates, L, may improve efficiency in estimation of target parameters. The intention-totreat (ITT) effect is defined as Δ_ITT = E[Y ^z=1] − E[Y ^z=0]; owing to randomization of Z, this quantity can be identified and is readily expressed as Δ_ITT = E[Y |Z = 1] − E[Y |Z = 0] under assumptions presented in Section 2.3 (to be discussed).

Fig 1.

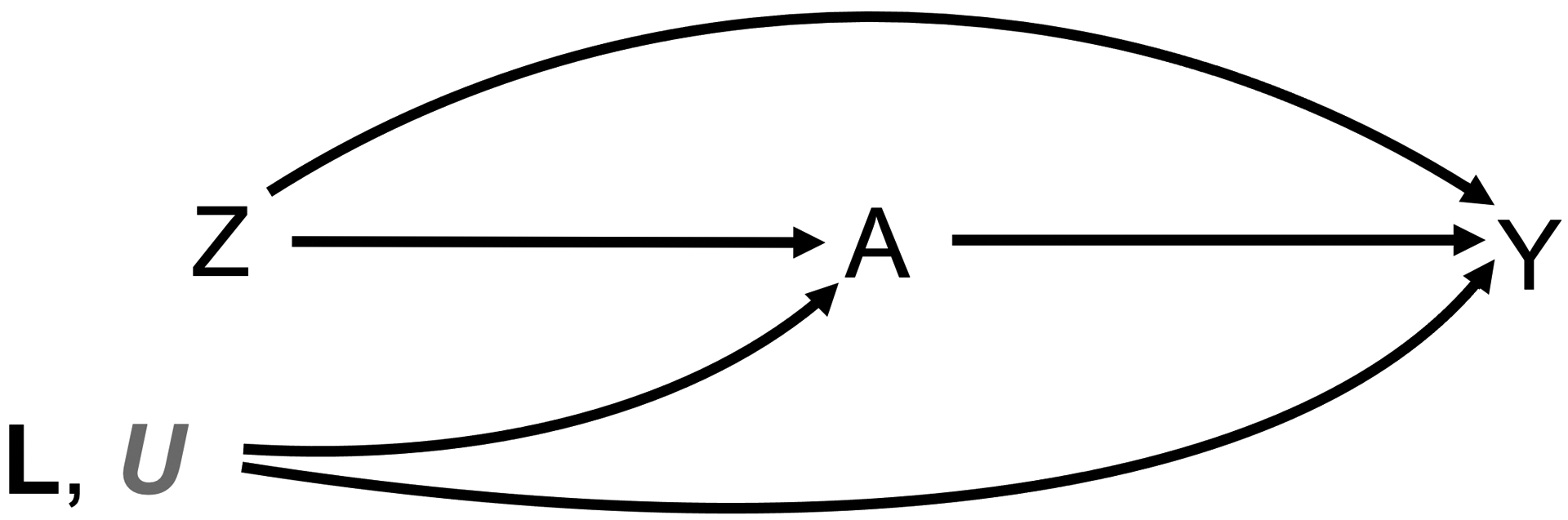
Directed acyclic graph depicting the temporal ordering and causal pathways between measured variables. Note that U (gray), is a collection of unobserved confounders impacting engagement and the outcome. Note that the direct path from Z to Y cannot reasonably be ruled out in the setting of a mobile health intervention such as REACH, and serves as a violation of the exclusion restriction assumption.

2.2. Engagement-compliance and local average treatment effects.

Although we will ultimately allow A to denote the (continuous) proportion of two-way text messages receiving a response in the context of the REACH study, we first consider A to be binary (for instance, the indicator of a text message response rate meeting or exceeding 80%) for simplicity of illustration. Under the principal stratification framework, we may use combinations of A^z=0 and A^z=1 to partition the population into four hypothetical engagement classes (Angrist, Imbens and Rubin, 1996; Frangakis and Rubin, 2002). The resulting classes are described in Table 1. A subject who would not engage under randomization to the control condition (Z = 0), but would engage under randomization to the intervention (Z = 1), could be referred to as engagement-compliant. In the setting of the REACH study, recall that it is impossible to engage with with the REACH intervention when assigned to control. Put another way, Z = 0 ⇒ A = 0 (or, A^z=0 = 0), such that neither engagement-defiant subjects nor always-engagers need consideration. Jin and Rubin (2008) refer to this as the treatment access monotonicity assumption, and it is trivially satisfied in the REACH study. We may therefore define principal strata on the basis of A^z=1 alone, terming those in the population with A^z=1 = 1 as engagement-compliant, and those for whom A^z=1 = 0 as never-engagers. Under our framework, compliance class is latent in the control group and observed in the intervention group, as A^z=1 is observed in subjects receiving the intervention and uniquely characterizes compliance class. This is in contrast with the usual setting of compliance, in which latency of A^z is not specific to z.

Table 1.

Characterization of engagement-compliance classes (principal strata) in the simple setting considering engagement as a binary variable. Note that only two such classes are applicable in our particular setting, uniquely defined by A^z=1.

A z=0	A z=1	Characterization	Applicable?
0	0	Never-engager	Yes
0	1	Engagement-compliant	Yes
1	0	Engagement-defiant	No
1	1	Always-engager	No

Now, we allow for the possibility that A^z=1 is continuous, with 0 ≤ A^z=1 ≤ 1. We define the following class of local average treatment effects, uniquely indexed by A^z=1:

$$\Delta (a)=\text{E}\left[Y^{z=1}-Y^{z=0}\mid A^{z=1}=a\right].$$

In plain language, Δ(a) denotes the average causal effect of randomization on the outcome of interest among a subpopulation having some specified hypothetical level of engagement, a, under treatment z = 1. We refer specifically to Δ(0) as the never-engager causal effect (NECE) and Δ(1) as the engagement-compliant causal effect (ECCE).

2.3. Assumptions.

We invoke the following assumptions in order to formulate bounds on the local average treatment effects characterized in Section 2.2.

1. No interference: $\left(A_i^z,Y_i^z\right)⫫Z_j$.

2. Consistency: A = A^Z and Y = Y ^Z.

3. Positivity: 0 < P(Z = 1) < 1.

4. Ignorability of randomization: Y ^z ⫫ Z and A^z ⫫ Z for each z = 0, 1.

5. Treatment access monotonicity: A^z=1 ≥ A^z=0 = 0.

6. Treatment-engagement dependence: $Z\cancel{⫫}A$.

In the context of the REACH study, each of these assumptions can be described as follows. The assumption of no interference implies that the randomized assignment of one individual to REACH or control influences neither the potential text message response rate (engagement) nor the potential HbA1c (outcome) of another individual. The assumption of consistency implies that the observed level of engagement and the observed HbA1c correspond to the potential engagement and potential HbA1c under the randomization actually received. In general, these first two assumptions are are often referred to as the stable unit treatment value assumption (SUTVA); when considered together, these assumptions ensure that the treatments being compared and the resulting potential outcomes are well defined; vaccine trials serve as a particularly well known area in which violations to SUTVA can pose challenges (Hudgens and Halloran, 2008). Positivity refers to a nonzero probability of assignment to each treatment group, and is trivially satisfied under randomization. Ignorability of randomization, also known as exchangeability, holds when the relationship between randomization group and each of the engagement and HbA1c measures is not subject to systematic confounding; this assumption can also be assumed under a valid randomization procedure. Importantly, neither measured or unmeasured confounding of the relationship between engagement and the outcome is precluded (Figure 1). Assumptions 1–4 together ensure identifiability of Δ_ITT.

As discussed in Section 2.2, treatment access monotonicity can reasonably be assumed in the context of the REACH study; specifically, engagement under assignment to the control condition is zero. The assumption of treatment-engagement dependence is satisfied so long as there exists a subject with an engagement level exceeding zero (i.e., responding to at least one text message) when assigned to the REACH intervention. Randomization is said to serve the role of a stronger instrument when it is more strongly associated with engagement; the mean level of engagement among subjects randomized to the treatment group, μ_A = E[A^z=1], serves as an identifiable quantity to characterize instrument strength. Specifically, μ_A = 0 implies no variation in A across the population (and renders randomization an invalid instrument); if μ_A = 1, then randomization is a “perfect instrument” such that A and Z are perfectly correlated and identically equal.

Notably absent from the list of assumptions we are willing to make in the REACH study is that of the exclusion restriction (namely, that Z ⫫ Y |A), under which it would follow that Δ(0) = E[Y ^z=1 − Y ^z=0|A^z=1 = 0] = 0. Expressed in terms of the DAG of Figure 1, the exclusion restriction does not permit a direct arrow from Z into Y. Although a conditional exclusion restriction assumption could serve as a possible solution to this challenge if sufficiently many variables on the pathway from Z into Y were measured, it is not feasible—and perhaps not even possible—to evaluate all potential self-care behaviors triggered by the text messages prior to outcome measurement in the context of the REACH study. We instead seek to allow the possibility that Δ(0) = γΔ(1) for some finite γ. Although γ is not identifiable, it will serve as a sensitivity parameter to be varied over a range of possible values. Specifying a range for γ will allow us to place bounds on Δ(a) for 0 < a < 1; these bounds will be the subject of Section 3.

2.4. Weak identifiability of Δ(a).

To underscore the role of γ, we can express the local average treatment effects of interest as Δ(a) = Δ(1)[γ + (1 − γ)h(a)] for 0 ≤ a ≤ 1 under some non-identifiable γ and h(·) with h(0) = 0 and h(1) = 1. By setting a = 0, it can be seen that γ = Δ(0)/Δ(1) possesses the conceptually intuitive interpretation as the ratio of the NECE to the ECCE. This parameterization relaxes the “through-the-origin” relationship presumed under the exclusion restriction, under which γ = 0. We will prove that Δ(a) can be identified if both γ and h(·) are chosen correctly.

Theorem 2.1.

Under Assumptions 1–6 of Section 2.3, Δ(a) is weakly identifiable in the sense that it can be identified under correct specification of γ and h(·).

Proof.

It is most straightforward to first derive an expression for Δ(1). Therefore, note the following:

$$\begin{array}{lll}{\Delta }_{\text{ITT}}\hfill & =\text{E}\left[Y^{z=1}-Y^{z=0}\right]\hfill & \hfill \text{(by definition)}\\ \hfill & ={\text{E}}_{A^{z=1},A^{z=0}}\left[\text{E}\left[Y^{z=1}-Y^{z=0}\mid A^{z=1},A^{z=0}\right]\right]\hfill & \hfill \text{(by iterated expectation)}\\ \hfill & ={\text{E}}_{A^{z=1}}\left[\text{E}\left[Y^{z=1}-Y^{z=0}\mid A^{z=1}\right]\right]\hfill & \hfill \text{(by treatment access monotonicity)}\\ \hfill & ={\text{E}}_{A^{z=1}}\left[\Delta \left(A^{z=1}\right)\right]\hfill & \hfill \text{(by definition)}\\ \hfill & ={\text{E}}_{A^{z=1}}\left[\Delta (1)\left\{\gamma +(1-\gamma )h\left(A^{z=1}\right)\right\}\right]\hfill & \hfill \text{(by parameterization)}\\ \hfill & =\Delta (1)\left\{\gamma +(1-\gamma )\text{E}\left[h\left(A^{z=1}\right)\right]\right\}\hfill & \hfill \text{(by linearity of expectation).}\end{array}$$

Together, treatment access monotonicity and treatment-engagement dependence imply that μ_h = E[h(A^z=1)] > 0; hence, rearranging the expression allows us to derive a well-defined expression for Δ(1) for all γ:

$$\Delta (1)=\frac{{\Delta }_{\text{ITT}}}{\gamma +(1-\gamma ){\mu }_h}.$$

Now, we may re-express Δ(a) based on its parameterization in terms of Δ(1):

$$\Delta (a)={\Delta }_{\text{ITT}}\times \frac{\gamma +(1-\gamma )h(a)}{\gamma +(1-\gamma ){\mu }_h}={\Delta }_{\text{ITT}}\times c_{\gamma ;h}(a),$$

Under Assumptions 1–4 in Section 2.3, Δ_ITT is identifiable and can be expressed, for instance, as E[Y |Z = 1] − E[Y |Z = 0]; similarly, μ_h is identifiable and can be expressed as E[h(A)|Z = 1]. □

2.5. Considerations regarding parameterizations of Δ(a).

While the exclusion restriction has been well described in many applications of traditional IV approaches, correct specification of h(·) is a key assumption that merits discussion and is therefore a focus if this work. Commonly, this assumption is implicitly expressed through dichotomization of a continuous A in order to characterize target parameters based on discrete principal strata. In the framework of Section 2.4, this is achieved by defining h(a) = 1(a > ζ) for some ζ, implying minimal treatment benefit to be derived among all for whom A^z=1 ≤ ζ, and maximal treatment benefit to be derived among all for whom A^z=1 > ζ.

Angrist and Imbens (1995) show that discretization of an A having a continuous doseresponse relationship tends to bias estimates of Δ(1) away from the null. At the same time, identification of h(·) under continuous A is not possible absent a continuous instrument, Z. In such settings, they propose characterizing local average treatment effects linearly across values of a continuous post-randomization variable A (in their work, via two-stage leastsquares). We will develop theory for general choices of h(·). Due to non-identifiability of h(·), however, it is still of interest to learn how different the most common choices of h(·) compare in this setting; therefore, in our simulation and application, we will compare both the linear case, in which h(a) = a is chosen to be the identity function, and the dichotomized case in which h(a) = 1(a > ζ). In practice, it is typically defensible to consider only monotone choices for h(·), for reasons we will discuss in Section 3.

3. Bounding local average treatment effects.

For ease of discussion, we assume without loss of generality that Δ_ITT is non-negative. Until now, we have placed quite minimal restrictions on the sensitivity parameter, γ and the function h(·). In any sensitivity analysis, however, the sensitivity parameter must be bounded in order to construct a range of resulting estimates for the target parameter. In the context of many mobile health interventions, it is reasonable to assume that γ = 0 is the smallest reasonable lower bound in the sense that receiving text messages should not provide a harmful effect relative to control among those who choose not to respond to any two-way text messages. The particular setting of γ = 0 is essentially equivalent to removing the direct arrow from Z into Y from the DAG of Figure 1, and corresponds to the classic instrumental variables technique under which the exclusion restriction is assumed true. Further, it is reasonable to assume that γ = 1 is the greatest reasonable upper bound in the sense that those choosing not to respond to any text messages should not receive greater benefit relative to control as compared to those who are fully engaged with the intervention. The particular setting of γ = 1 can be interpreted as implying that the ITT effect applies uniformly to the target population, irrespective of their level of engagement with the intervention. Along a similar line, for a fixed choice of γ between zero and one, it is sensible to consider only monotone choices for h(·) such that the intervention’s effect is greater in a subgroup with higher levels of engagement as compared to a subgroup with a lower level of engagement.

Note that although it may be reasonable to tighten the bounds on γ in the context of a particular study (e.g., REACH), we focus in this section on the geometry and the underlying theory for general choices of γ between 0 and 1. Note that these bounds are heuristic in nature, as sensitivity parameter bounds typically are; in Section 7, we will provide a further discussion of cases in which alternative bounds for γ may be more appropriate.

From Section 2.4, it follows that Δ(a) possesses a stationary property: Δ(μ_h) = Δ_ITT for all γ. Under a monotone choice for h(·), Δ(a) achieves global extrema at γ = 0 and γ = 1 for fixed values of a; these extrema are further unique if and only if Δ_ITT ≠ 0. Assuming without loss of generality that Δ_ITT is non-negative, the bounds for Δ(a) can be characterized as follows:

$$\begin{gathered} {\Delta }_{\text{ITT}}\times \frac{h(a)}{{\mu }_h}\le \Delta (a)\le {\Delta }_{\text{ITT}}\text{\hspace{1em}for }a\le {\mu }_h \\ \Delta (a)={\Delta }_{\text{ITT}}\text{\hspace{1em}for }a={\mu }_h \\ {\Delta }_{\text{ITT}}\le \Delta (a)\le {\Delta }_{\text{ITT}}\times \frac{h(a)}{{\mu }_h}\text{\hspace{1em}for }a>{\mu }_h. \end{gathered}$$

In the specific case of a = 0, the NECE is bounded by zero (below) and Δ_ITT (above); when a = 1, the ECCE is bounded by Δ_ITT (below) and the Wald formula (above):

$$0\le \Delta (0)\le {\Delta }_{\text{ITT}}\le \Delta (1)\le \frac{{\Delta }_{\text{ITT}}}{{\mu }_h}.$$

If Δ_ITT is non-positive, the directionality of each of these inequalities is reversed. These treatment effect bounds are illustrated in Figure 2 in the case where h(a) = a.

Fig 2.

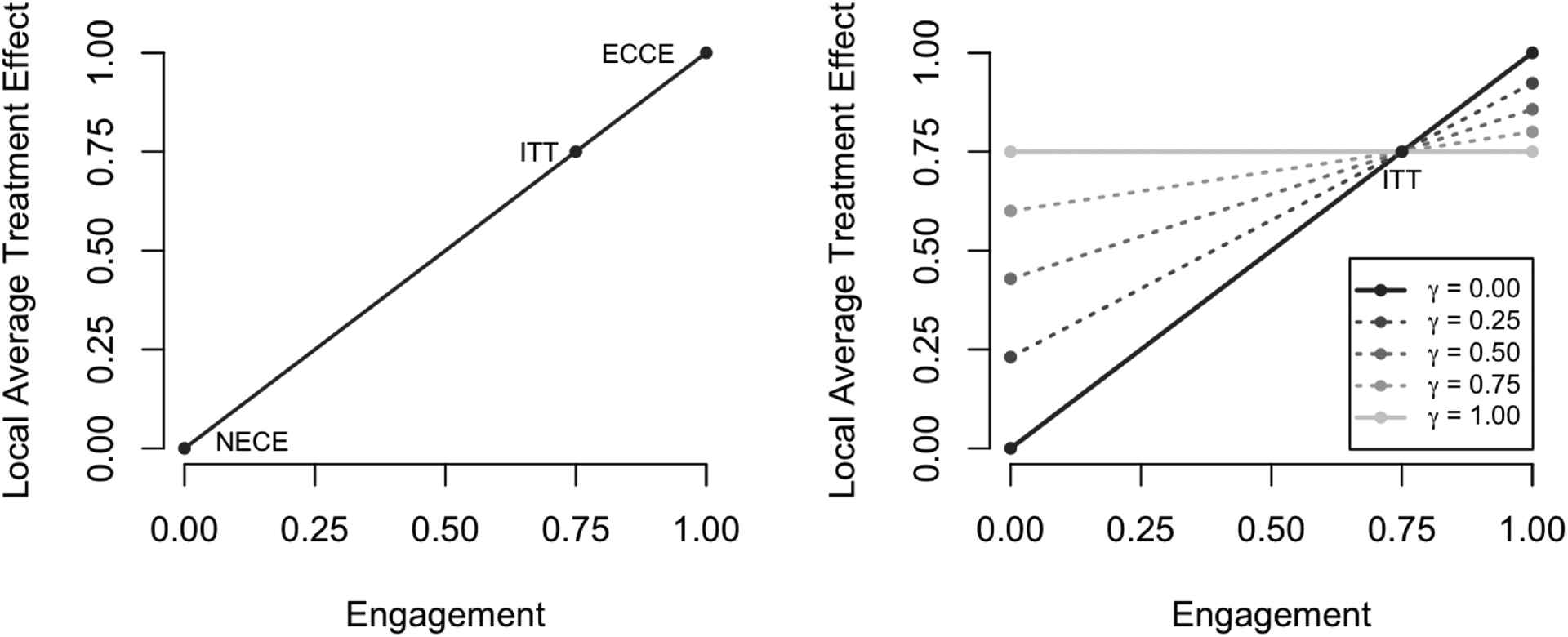
Illustration of treatment effect bounds in a simple setting. On the left, we highlight how the treatment effect would be characterized across different levels of engagement by a traditional IV analysis (γ =0). The presumed NECE, ECCE, and ITT are all shown in this case. On the right, we show how the treatment effect is characterized across different levels of engagement under various sensitivity parameters. Note at each level of engagement, the treatment is bounded by the ITT and a specified multiple thereof (solid lines); also depicted are the results for nontrivial values of γ (dotted lines).

Also of interest is to understand the behavior of local average treatment effects across γ for different instrument strengths (as defined by μ_h in this case). This behavior is illustrated in Figure 3, again considering the case where h(·) is the identity function. Linearity of Δ(a) in h(a) for fixed values of γ does not imply general linearity of Δ(a) in γ for fixed values of h(a). In fact, the latter condition only holds in the presence of a perfect instrument, which occurs if and only if μ_h = 1. This suggests that under a weak instrument (low engagement), a sensitivity analysis of Δ(0) and Δ(1) can be expected to produce greater fluctuations when varying values of γ closer to zero as compared to values closer to one; under a stronger instrument (higher engagement), sensitivity will be closer to constant across γ.

Fig 3.

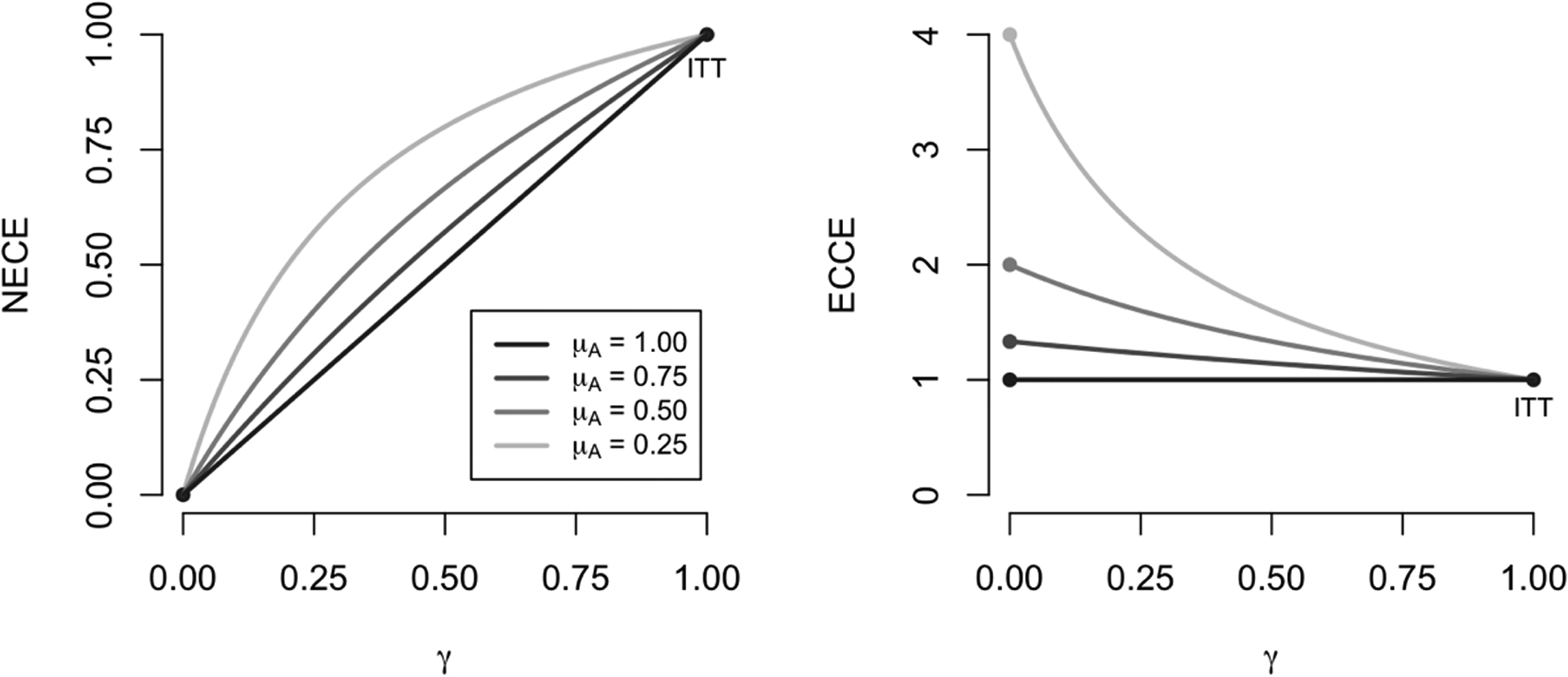
Illustration of treatment effect bounds in a simple setting. On the left, we highlight how the NECE, Δ(0), varies across the levels of γ for different values of μ_A, and on the right we similarly depict the ECCE, Δ(1). Note that μ_A characterizes instrument strength; weaker instruments are associated with higher curvature.

4. Estimation and inference.

The problem of estimating Δ(a) can be decomposed into the following steps: (1) specification of a value for γ, (2) specification of a form for h(·), (3) estimation of Δ_ITT and μ_h, and (4) plugging in estimates from the previous step into Equation (2) of Section 2.4. We must distinguish between the form of h(·) and value of γ that correspond to the unknowable data generating mechanism, and the values that are specified by the user. We will let h₀(·) and γ₀ correspond to the true underlying mechanism, and use the notation ${\widehat{\Delta }}_{h;\gamma }(a)$ to denote an estimator of Δ(a) under the user-specified sensitivity parameter, γ, and transformation, h. We will let Δ_h;γ(a) denote the value for which ${\widehat{\Delta }}_{h;\gamma }(a)$ is consistent—which may or may not be equal to Δ(a) = Δ_h0,γ0(a), depending on correctness of choices for h(·) and γ. A simple estimator utilizes the corresponding sample means in the obvious way:

$${\widehat{\Delta }}_{h;\gamma }(a)={\widehat{\Delta }}_{\text{ITT}}\times {\widehat{c}}_{\gamma ;h}(a)=\left({\overline{Y}}_{Z=1}-{\overline{Y}}_{Z=0}\right)\times \frac{\gamma +(1-\gamma )h(a)}{\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}}.$$

Owing to maximal efficiency associated with ${\overline{h(A)}}_{Z=1}$ as an estimator of μ_h, there is no obvious incentive to consider alternative estimators. On the other hand, greater efficiency for estimation of Δ_ITT intuitively corresponds to greater efficiency for estimation of Δ_h;γ(a). For instance, this could be achieved through adjustment for baseline covariates, L, in a linear regression model): E[Y |Z = z, L = ℓ] = β₀ + β₁z + f_θ(ℓ), where, f_θ(·) denotes a function of baseline covariates indexed by θ. Importantly, consistency of ${\widehat{\beta }}_1$ for Δ_ITT does not depend upon correct specification of f_θ (Tsiatis et al., 2008). Because Δ_ITT can be estimated in multiple ways, we discuss asymptotic theory generally rather than under a specific estimator.

Lemma 4.1.

Under treatment-engagement dependence (Assumption 6 of Section 2.3), ${\widehat{c}}_{\gamma ;h}(a)$ achieves $\sqrt{N_1}$-consistency and asymptotic normality for (γ, a) ≠ (0, 0).

Proof.

If the treatment-engagement dependence assumption is violated, then μ_A follows a degenerate distribution with a point mass at zero. In all other cases, this is a straightforward application of the Law of Large Numbers, the Lévy Central Limit Theorem, and δ-method with g_γ;a(μ_h) = c_γ;h(a), and so we do not provide this proof in detail. Letting ${\sigma }_h^2$ denote $\text{Var}\left(\sqrt{N_1}\left({\widehat{\mu }}_h-{\mu }_h\right)\right)$, the asymptotic variance associated with $\sqrt{N_1}\left({\widehat{c}}_{\gamma ;h}(a)-c_{\gamma ;h}(a)\right)$ is given by:

$${\sigma }_{c_{\gamma ;h}}^2(a)=\frac{{(1-\gamma )}^2{(\gamma +(1-\gamma )h(a))}^2}{{\left(\gamma +(1-\gamma ){\mu }_h\right)}^4}{\sigma }_h^2.$$

We do not require asymptotic theory under the condition that γ = a = 0, as ${\widehat{\Delta }}_0(0)=0$ identically by convention. □

Theorem 4.2.

Under both $\sqrt{N}$-consistency and asymptotic normality of ${\widehat{\Delta }}_{ITT}$, we have that $\sqrt{N}\left({\widehat{\Delta }}_{\gamma ;h}(a)-{\Delta }_{\gamma ;h}(a)\right){\to }_d\mathcal{N}\left(0,{\tau }_{\gamma ;h}^2(a)\right)$ for some ${\tau }_{\gamma ;h}^2(a)>0$.

Proof.

Let r denote the randomization fraction r ≡ lim N/N₁, and let ${\sigma }_{\text{ITT}}^2$ denote the asymptotic variance of $\sqrt{N}\left({\widehat{\Delta }}_{\text{ITT}}-{\Delta }_{\text{ITT}}\right)$. Invoking Slutsky’s theorem, we have that

$$\begin{gathered} \sqrt{N}\left({\widehat{\Delta }}_{\gamma ;h}(a)-{\Delta }_{\gamma ;h}(a)\right)=\sqrt{N}\left({\widehat{\Delta }}_{\text{ITT}}\times {\widehat{c}}_{\gamma ;h}(a)-{\Delta }_{\text{ITT}}\times c_{\gamma ;h}(a)\right) \\ =c_{\gamma ;h}(a)\left[\sqrt{N}\left({\widehat{\Delta }}_{\text{ITT}}-{\Delta }_{\text{ITT}}\right)\right]+{\widehat{\Delta }}_{\text{ITT}}\left[\sqrt{N}\left({\widehat{c}}_{\gamma ;h}(a)-c_{\gamma ;h}(a)\right)\right] \\ \approx c_{\gamma ;h}(a)\left[\sqrt{N}\left({\widehat{\Delta }}_{\text{ITT}}-{\Delta }_{\text{ITT}}\right)\right]+{\Delta }_{\text{ITT}}\left[\sqrt{r{N}_1}\left({\widehat{c}}_{\gamma ;h}(a)-c_{\gamma ;h}(a)\right)\right]. \end{gathered}$$

For which the variance can be expressed in the following general form:

$${\left[c_{\gamma ;h}(a)\right]}^2{\sigma }_{\text{ITT}}^2+r{\left({\Delta }_{\text{ITT}}\right)}^2{\sigma }_{c;h}^2(a)+2N{c}_{\gamma ;h}(a){\Delta }_{\text{ITT}}\text{Cov}\left({\widehat{c}}_{\gamma ;h}(a),{\widehat{\Delta }}_{\text{ITT}}\right).$$

□

The covariance term of Theorem 4.2 is estimator-specific. In the appendix, we provide an approximation in the special case in which ${\widehat{\Delta }}_{\text{ITT}}={\overline{Y}}_{Z=1}-{\overline{Y}}_{Z=0}$. For settings in which the a specific form for the asymptotic covariance cannot be neither analytically derived in closed-form nor approximated, we propose utilizing the nonparametric bootstrap procedure to estimate standard errors and forming either symmetric Wald-based or percentile-based confidence intervals (Efron and Tibshirani, 1986).

Note the following important corollaries; proofs of the first two are trivial and are hence not provided.

Corollary 1.

If the user-specified sensitivity parameter, γ, and transformation h(·) are each “chosen correctly” in the sense that γ = γ₀ = Δ(0)/Δ(1) and h(·) = h₀(·), then ${\widehat{\Delta }}_{\gamma ;h}(a){\to }_p\Delta (a)\equiv {\Delta }_{{\gamma }_0;h_0}(a)$ for 0 ≤ a ≤ 1.

Corollary 2.

If ${\widehat{\Delta }}_{\text{ITT}}$ and ${\widehat{\Delta }}_{\text{ITT}}^{\prime }$ are consistent estimators of Δ_ITT, each having the same asymptotic correlation with ${\widehat{c}}_{\gamma ,h}(a)$, and with ${\sigma }_{\text{ITT}}^2<{\left[{\sigma }_{\text{ITT}}^{\prime }\right]}^2$, then the estimator ${\widehat{\Delta }}_{\gamma ;h}(a)$ based on ${\widehat{\Delta }}_{\text{ITT}}$ achieves greater asymptotic efficiency as compared to that based on ${\widehat{\Delta }}_{\text{ITT}}^{\prime }$.

Corollary 3.

For all (γ, a) ≠ (0, 0), (1), ${\tau }_{\gamma ;h}^2(a)$ is decreasing in a, and (2) a Wald test of the null hypothesis H₀ : Δ_γ;h(a) = 0 is asymptotically equivalent to a Wald test of the null hypothesis H₀ : Δ_ITT = 0. That is, for sufficiently large N,

$$W_N^{\gamma ;h}=N{\left[\frac{{\widehat{\Delta }}_{\gamma ;h}(a)}{{\widehat{\tau }}_{\gamma ;h}(a)}\right]}^2\approx W_N^{\text{ITT}}=N{\left[\frac{{\widehat{\Delta }}_{\text{ITT}}}{{\widehat{\sigma }}_{\text{ITT}}}\right]}^2$$

Proof.

The first statement is trivial; the second follows by noting that Δ_γ;h(a) = 0 ⇔ Δ_ITT = 0 when (γ, a) ≠ (0, 0); and then invoking Slutsky’s theorem to note the asymptotic distribution of ${\widehat{\Delta }}_{\gamma ;h}(a)$ under the null:

$$\sqrt{N}\left({\widehat{\Delta }}_{\gamma ;h}(a)-{\Delta }_{\gamma ;h}(a)\right)\stackrel{H_0}{\approx }{c}_{\gamma ;h}(a)\left[\sqrt{N}\left({\widehat{\Delta }}_{\text{ITT}}-{\Delta }_{\text{ITT}}\right)\right],$$

with asymptotic variance ${\tau }_{\gamma ;h}^2(a)\approx c_{\gamma ;h}^2(a){\sigma }_{\text{ITT}}^2$. Therefore, Wald-based confidence intervals for both Δ_ITT and Δ_γ;h(a) will possess the same coverage properties, asymptotically. Note that $W_N^{\gamma ;h},W_N^{\text{ITT}}{\to }_d{\chi }_1^2$. □

5. Simulation studies.

In this section, we conduct a set of simulation studies in order to evaluate the finite-sample performance of the sensitivity analysis procedure. In each simulation scenario considered, we use K = 5,000 Monte Carlo iterations. We vary the sample size across two levels (N = 50 and N = 200); the true value of γ₀ = Δ(0)/Δ(1), across five different levels, evenly spaced between zero and one (inclusive); and the instrument strength (low, moderate, and high), as characterized by mean level of engagement. Treatment randomization was generated as Z ~ Bernoulli(0.5). A measured (L) and an unmeasured (U) confounder of engagement (A) and the outcome (Y ) were each generated as marginally independent standard normal covariates. Engagement under randomization to Z = 1 (i.e., A^z=1) was generated as a semi-continuous variable with inflation at zero and one as follows:

$$\begin{gathered} \text{P}\left(A^{z=1}=1\mid U=u,L=l\right)=\text{expit}\left({\alpha }_{01}+{\alpha }_{11}u+{\alpha }_{21}l\right)\text{,} \\ \text{P}\left(A^{z=1}=0\mid U=u,L=l,A^{z=1}\ne 1\right)=\text{expit}\left({\alpha }_{00}+{\alpha }_{10}u+{\alpha }_{20}l\right), \\ \text{logit}\left(A^{z=1}\right)~\mathcal{N}(\mu ={\alpha }_0+{\alpha }_{1}U+{\alpha }_{2}L,{\sigma }^2={\sigma }_A^2;A^{z=1}\notin \{0,1\}. \end{gathered}$$

In generating the engagement variable, we fixed certain parameters as follows, setting α₀₁ = α₀₀ = −2, α₁₀ = α₂₀ = −1, α₁₁ = α₂₁ = 1, α₁ = α₂ = 0.8, and σ_A = 0.2. Instrument strength, characterized by μ_A, is controlled by variations in the parameter α₀, which we set as α₀ = −2.50 for low instrument strength (μ_A ≈ 0.25), α₀ = −0.05 for moderate instrument strength (μ_A ≈ 0.50), and α₀ = 2.30 for high instrument strength (μ_A ≈ 0.75).

The outcome was generated as $Y~\mathcal{N}\left(\mu ={\beta }_0+{\beta }_{1}Z+{\beta }_{2}A+{\beta }_{3}U+{\beta }_{4}L,{\sigma }^2={\sigma }_Y^2\right)$. Note that for the purposes of these simulations, h(·) is chosen to be the identity function in the data generation, although we will consider violations to this in Section 5.3. We fixed β₀ = 9, β₃ = 0.2, β₄ = 0.3, and σ_Y = 0.8. The true (non-identifiable) value of γ₀, is governed by the pair (β₁, β₂), and is specifically given by γ₀ = β₁/(β₂ + β₂). We therefore select (β₁, β₂) under five cases in order to vary γ₀ between zero and one; the i^th case utilizes β₁ = (1 − i)/5 and β₂ = −(4/5+β₁) for i = 1, … ,5. Many aspects of this simulation is designed to approximately mirror our subsequent application to the REACH study in Section 6.

5.1. Operating characteristics under correct specification.

Our first goal was to evaluate performance of the methodology under correct specification of both γ and h(·) under the data generation mechanism described. For the purposes of these simulations, Δ(1) will be the target estimand, and is given by Δ(1) = β₁ + β₂ = −0.8.

We estimated the ITT effect in two ways: one based on a simple outcome mean difference (such that the asymptotic approximation to the variance appearing in the appendix would apply), and another based on a linear regression, adjusting linearly for the observed covariate, L (such that the bootstrap standard errors would be required). In either case, Δ(1) was estimated using the approach described in Section 4 under correct specification of γ and h(·), employing B = 500 bootstrap replicates for the regression-based estimation method. We extract the average point estimates and Monte Carlo empirical standard errors (ESE), along both the average standard error (large-sample theory based approximation for the first case, and the bootstrap standard error for the second case), coverage based on symmetric 95% Wald-based confidence intervals, and estimated power.

Key results from the first simulation case are summarized in Table 2. When the value of γ is correctly specified, the sensitivity analysis approach is able to correctly capture the ECCE, with low bias and with standard errors based on the large-sample approximation closely reflecting the true repeat-sample variability (as represented by the empirical Monte Carlo standard error). The level of bias associated with smaller sample sizes is consistent with prior insights regarding bias of the Wald estimator (Buse, 1992). Coverage appears to be adequate even in smaller sample sizes. Unsurprisingly, power increases with higher sample size, with higher instrument strength, and with larger magnitude of the ITT effect.

Table 2.

Results of the simulation study under correct selection of γ and h. Each simulation scenario is described by μ_A (instrument strength, given by average level of engagement) and γ₀ (extent of departure from exclusion restriction); further, results are shown under two different sample sizes (N =50 and N =200). Provided in the table for reference is the implied intention-to-treat effect, Δ_ITT. Depicted are the average point estimates, empirical standard error (ESE), the average large-sample-theory (LST) standard error for ${\widehat{\Delta }}_{\gamma }(1)$, the coverage probability, and power. Note that in all cases, Δγ (1) = −0.80.

			N = 50					N = 200
μ A	γ 0	ΔITT	Est.	ESE	$\widehat{\text{SE}}$	CP	Power	Est.	ESE	$\widehat{\text{SE}}$	CP	Power
0.25	0.00	−0.20	−0.858	1.223	1.155	0.968	0.063	−0.803	0.513	0.518	0.961	0.342
0.25	0.25	−0.35	−0.819	0.589	0.573	0.944	0.300	−0.803	0.286	0.285	0.946	0.815
0.25	0.50	−0.50	−0.803	0.411	0.390	0.933	0.536	−0.803	0.200	0.197	0.943	0.982
0.25	0.75	−0.65	−0.796	0.316	0.298	0.931	0.745	−0.798	0.154	0.151	0.945	1.000
0.25	1.00	−0.80	−0.806	0.252	0.245	0.939	0.900	−0.802	0.125	0.124	0.944	1.000
0.50	0.00	−0.40	−0.818	0.523	0.506	0.948	0.371	−0.802	0.252	0.249	0.95	0.899
0.50	0.25	−0.50	−0.808	0.397	0.390	0.944	0.545	−0.799	0.199	0.196	0.947	0.983
0.50	0.50	−0.60	−0.802	0.343	0.320	0.931	0.694	−0.801	0.167	0.162	0.943	0.998
0.50	0.75	−0.70	−0.803	0.288	0.275	0.937	0.817	−0.798	0.143	0.139	0.941	1.000
0.50	1.00	−0.80	−0.798	0.252	0.245	0.937	0.894	−0.801	0.124	0.124	0.948	1.000
0.75	0.00	−0.60	−0.800	0.344	0.338	0.943	0.663	−0.800	0.167	0.169	0.953	0.999
0.75	0.25	−0.65	−0.801	0.312	0.303	0.940	0.754	−0.801	0.154	0.153	0.95	1.000
0.75	0.50	−0.70	−0.804	0.288	0.276	0.936	0.822	−0.798	0.142	0.140	0.948	1.000
0.75	0.75	−0.75	−0.801	0.270	0.257	0.930	0.864	−0.796	0.132	0.130	0.949	1.000
0.75	1.00	−0.80	−0.800	0.252	0.244	0.941	0.898	−0.799	0.126	0.124	0.942	1.000

Analogous results from the second simulation case are summarized in Table 3. Overall patterns are similar to those shown in Table 2; we note the general improvement in efficiency associated with including the pre-treatment covariate in the model; further, the small-sample bias associated with the weaker instrument strength (μ_A = 0.25) appears to be uniformly reduced as compared to the unadjusted model.

Table 3.

Results of the simulation study under correct selection of γ and h. Each simulation scenario is described by μ_A (instrument strength, given by average level of engagement) and γ₀ (extent of departure from exclusion restriction); further, results are shown under two different sample sizes (N =50 and N =200). Provided in the table for reference is the implied intention-to-treat effect, Δ_ITT. Depicted are the average point estimates, empirical standard error (ESE), the average bootstrap standard error for ${\widehat{\Delta }}_{\gamma }(1)$, the coverage probability, and power. Note that in all cases, Δγ(1)=−0.80.

			N = 50					N = 200
μ A	γ 0	ΔITT	Est.	ESE	$\widehat{\text{SE}}$	CP	Power	Est.	ESE	$\widehat{\text{SE}}$	CP	Power
0.25	0.00	−0.20	−0.810	1.137	1.378	0.987	0.040	−0.794	0.486	0.503	0.966	0.370
0.25	0.25	−0.35	−0.794	0.556	0.563	0.956	0.293	−0.794	0.265	0.270	0.947	0.850
0.25	0.50	−0.50	−0.799	0.384	0.379	0.943	0.563	−0.798	0.187	0.187	0.951	0.990
0.25	0.75	−0.65	−0.809	0.293	0.290	0.946	0.796	−0.801	0.143	0.144	0.949	1.000
0.25	1.00	−0.80	−0.808	0.239	0.235	0.943	0.921	−0.801	0.120	0.117	0.942	1.000
0.50	0.00	−0.40	−0.806	0.494	0.507	0.958	0.371	−0.802	0.237	0.238	0.951	0.927
0.50	0.25	−0.50	−0.804	0.387	0.386	0.950	0.552	−0.800	0.187	0.188	0.954	0.989
0.50	0.50	−0.60	−0.802	0.320	0.317	0.942	0.717	−0.798	0.159	0.156	0.944	0.999
0.50	0.75	−0.70	−0.797	0.276	0.269	0.937	0.836	−0.798	0.134	0.134	0.951	1.000
0.50	1.00	−0.80	−0.799	0.240	0.235	0.938	0.917	−0.801	0.116	0.117	0.949	1.000
0.75	0.00	−0.60	−0.801	0.323	0.325	0.950	0.703	−0.803	0.158	0.157	0.948	0.999
0.75	0.25	−0.65	−0.801	0.295	0.295	0.948	0.770	−0.803	0.145	0.145	0.948	1.000
0.75	0.50	−0.70	−0.801	0.277	0.271	0.940	0.837	−0.801	0.135	0.134	0.947	1.000
0.75	0.75	−0.75	−0.804	0.253	0.250	0.943	0.891	−0.804	0.124	0.125	0.950	1.000
0.75	1.00	−0.80	−0.798	0.236	0.235	0.945	0.917	−0.800	0.117	0.117	0.951	1.000

5.2. Incorrect specification of γ.

In this set of simulations, we utilize the same data generating mechanism as described in the prior simulations, using the adjusted regression model for estimation of Δ_ITT as per the second case of Section 5.1, but this time varying the user-specified sensitivity parameter, γ. Note that the linearity of h(·) is still correctly specified in this case. Figure 4 demonstrates the properties of our estimation procedure under various specified levels of γ for the cases of both low and high instrument strength. Of note, specifying γ = γ₀ results in nearly unbiased estimation, as expected (and as demonstrated in Tables 2 and 3). Further, selections of γ that are closer to the correct value (γ₀) result in less bias than selections of γ that are further from γ₀. The curvilinear relationship between γ and Δ_γ(a) for fixed values of a is reflected in these figures, and is more pronounced for the lower engagement scenarios. Moreover, the figures also reflect the stationary property discussed in Section 3, whereby Δ_γ(μ_A) = Δ_ITT.

Fig 4.

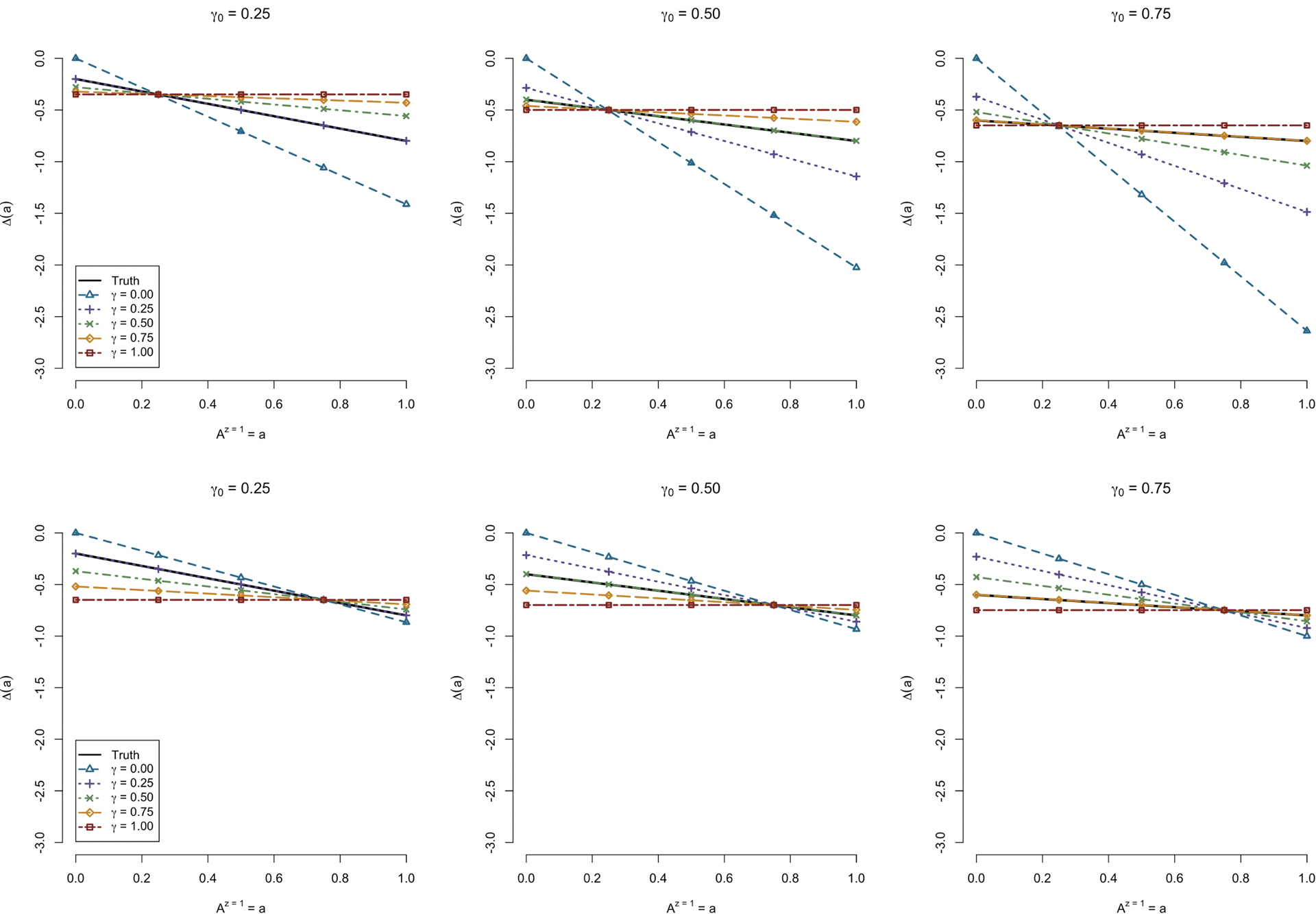
Simulation study results across different values of γ (possibly misspecified) under γ₀ =0 (left), γ₀ =0.50 (center), and γ₀ = 1 (right). Plotted are the average point estimates across different levels of a for various selections of γ. The upper panels depict the situation in which the mean level of engagement is lower; the upper panels depict the situation in which the mean level of engagement is higher

5.3. Incorrect specification of h(·).

In this set of simulations, we again utilize the same data generating mechanism as described in prior simulations, using the adjusted regression model for estimation of Δ_ITT as per the second case of Section 5.1, but this time utilizing a step function to model the relationship between A and Y (namely, h(a) = 1(a > ζ) for varying values of ζ around the mean level of continuous engagement). We depict this result for three choices of γ₀ (0.25, 0.50, and 0.75), all of which are correctly specified in this simulation; and for both the moderate and high instrument strength setup. Figure 5 demonstrates the properties of our estimation procedure under varying specified levels of ζ. Focusing on estimation of the ECCE, choosing ζ close to the average level of engagement results in comparably lower bias. Further, when γ is higher, results of dichotomization are understandably less sensitive to choices of ζ. Importantly, this result augments the findings of Angrist and Imbens (1995), in which dichotomization tended to bias estimates of Δ(1) away from the null. Here, that seems only to be the case when ζ is chosen to be higher than the mean level of engagement; notably, however, the levels of bias introduced by lower choices of ζ do not as severely attenuate the estimate of Δ(1).

Fig 5.

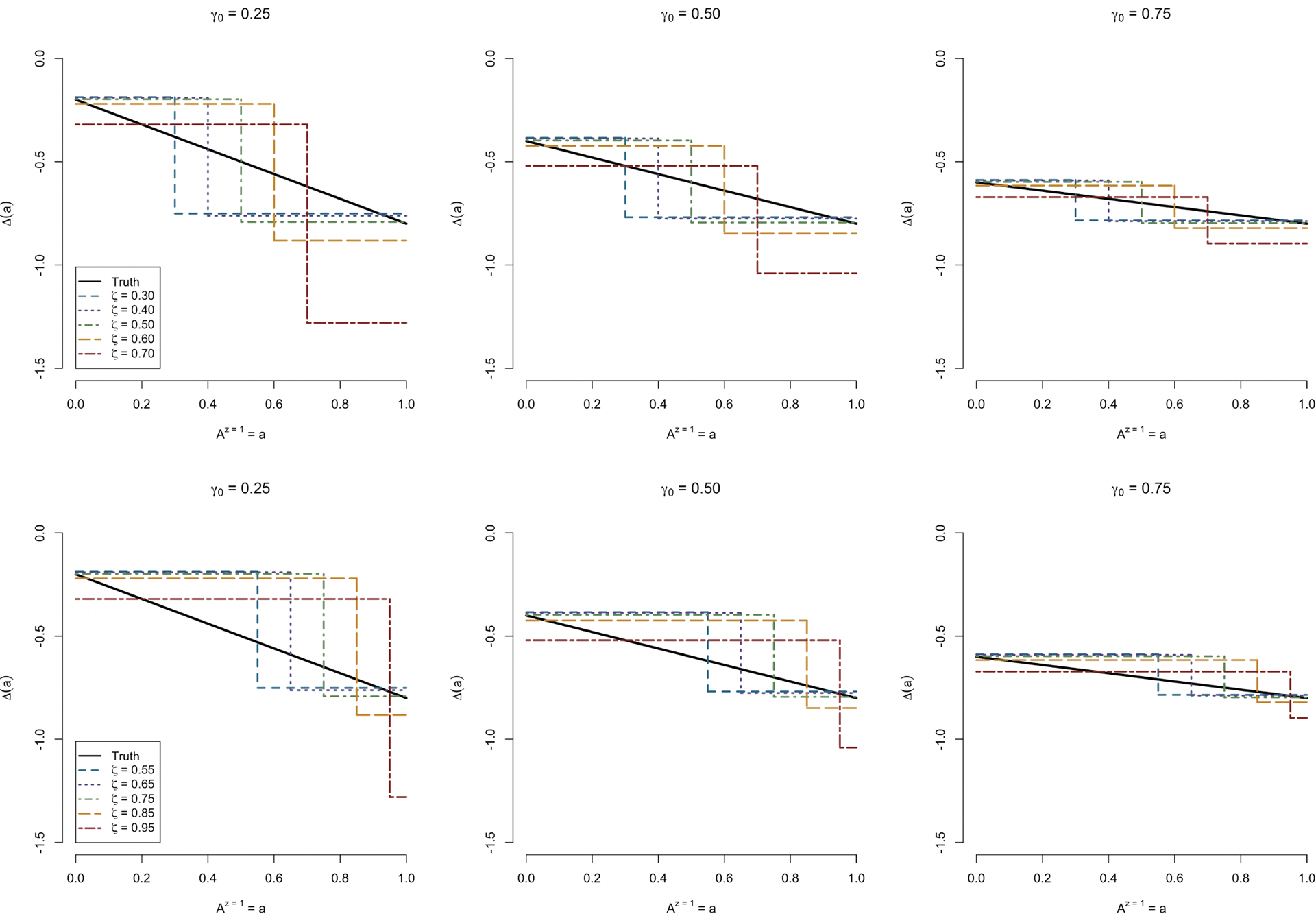
Simulation study results under incorrect dichotomization of A, shown for γ₀ =0.25 (left), γ₀ =0.50 (center), and γ₀ =0.75 (right). Plotted are the average point estimates across different levels of a for various selections of γ. The upper panels depict the situation in which the mean level of engagement is moderate; the upper panels depict the situation in which the mean level of engagement is higher.

6. Local average treatment effects in the REACH study.

6.1. Description of data.

We now apply our developed approach to the REACH study. The intervention, Z, is characterized by randomization to either a control condition (N₀ = 106), or to the REACH intervention (N₁ = 109). Subjects considered for this analysis all had uncontrolled HbA1c at baseline, characterized as either meeting or exceeding 8.5%. Subjects in the intervention arm received daily text messages over a period of six months including one-way messages that provided self-care information and encouragement and two-way messages that asked about medication adherence. At the end of each week, subjects in the intervention arm received adherence feedback based on his or her responses that week. Subject-specific engagement (A) was defined as the proportion of two-way text messages receiving a response.

Measured baseline covariates, L, were as follows: demographic and socioeconomic factors included age, gender, race/ethnicity (defined as non-Hispanic White, non-Hispanic Black, Hispanic, and other), and years of education. Clinical factors included duration of diabetes mellitus, insulin status, and baseline HbA1c. Measures of adherence, self-care, and self-efficacy included the Perceived Diabetes Self-Management scale (PDSMS-4), the Diabetes Adherence to Medications and Refills scale (ARMS-D), the Summary of Diabetes Self-Care Activities measure (SDSCA), and the Personal Diabetes Questionnaire (PDQ).

The outcome, Y, is given by HbA1c six-months post randomization; we consider an average causal effect of REACH on HbA1c of 0.50% to be clinically meaningful. Subject-specific engagement, A, was measured as the proportion of text messages responded to (applicable only to subjects assigned to the intervention arm). The engagement values for subjects withdrawing prior to the six-month period were considered pragmatically; such subjects were considered as having zero-engagement for the remainder of the six-month period post-withdrawal.

6.2. Addressing missing data.

Missingness rates were very low for baseline covariates (three subjects were missing information on education, two were missing information on diabetes mellitus duration, one was missing their PDSMS-4 score, and three were missing their SDSCA score). Twenty subjects (9.3%) were missing values on six-month HbA1c. Data on randomization group, age, gender, race/ethnicity, ARMS-D, PDQ, insulin status, response rate, and baseline HbA1c were complete.

Missing data were addressed using multiple imputation via chained equations and included all variables described thus far in Section 6 (Van Buuren et al., 2006). To formally characterize the assumptions made in addressing missing data in this fashion, let R_L denote the vector of missingness indicators for baseline covariates, and R_Y the indicator of missingness for six-month HbA1c. Further partition the data into the missing and observed components: (L_missing, Y_missing) and (L_observed, Y_observed). We presume the missing data mechanism to be at random, in the sense that (R_L, R_Y) ⫫ (L_missing, Y_missing)|L_observed, Y_observed, A, Z (Rubin, 1987). We believe this assumption to be reasonable based on the breadth of baseline variables collected.

6.3. Description of sensitivity analysis.

The multiple imputation procedure was aggregated with the bootstrap using the pooled-sample nested approach recommended by Schomaker and Heumann (2018). We report 95% confidence intervals based on the 0.025 and 0.975 quantiles of B = 500 nonparametric bootstrap replicates and M = 500 multiple-imputation iterations. We estimate the ITT using linear regression, adjusting for baseline HbA1c using a natural cubic spline with knots at the three inner quartiles (8.90%, 9.70%, and 11.1%), as recommended by Harrell (2001). We believe a range of γ spanning between 0.25 and 0.75 is reasonable for the context of the REACH study. This range reflects the belief that the total effect of the intervention can be explained by a combination of both effects mediated and not mediated by engagement with it, and also underscores our uncertainty regarding the relative proportions of each.

We model Δ_γ(a) in two ways: (1) linearly, with h(a) = a chosen as the identity function, and (2) dichotomously, with h(a) = 1(a ≥ 0.80). All analyses were performed using R, version 4.0.2 (R Core Team, 2020). The analytic data set is available as supplementary material, along with all documented code used for analysis (Spieker et al., 2021).

6.4. Results.

Figure 6 presents a histogram of the distribution of engagement across patients in the intervention arm. The mean subject-specific text message response rate was 81.4% (SD: 23.1%). The median response rate was 91.5%, with interquartiles given by 74.0% and 91.5%. Approximately 11% of subjects had a response rate no higher than 50%. The ITT was estimated to be −0.761% (95% CI: [−1.30%, −0.24%]; p = 0.0049).

Fig 6.

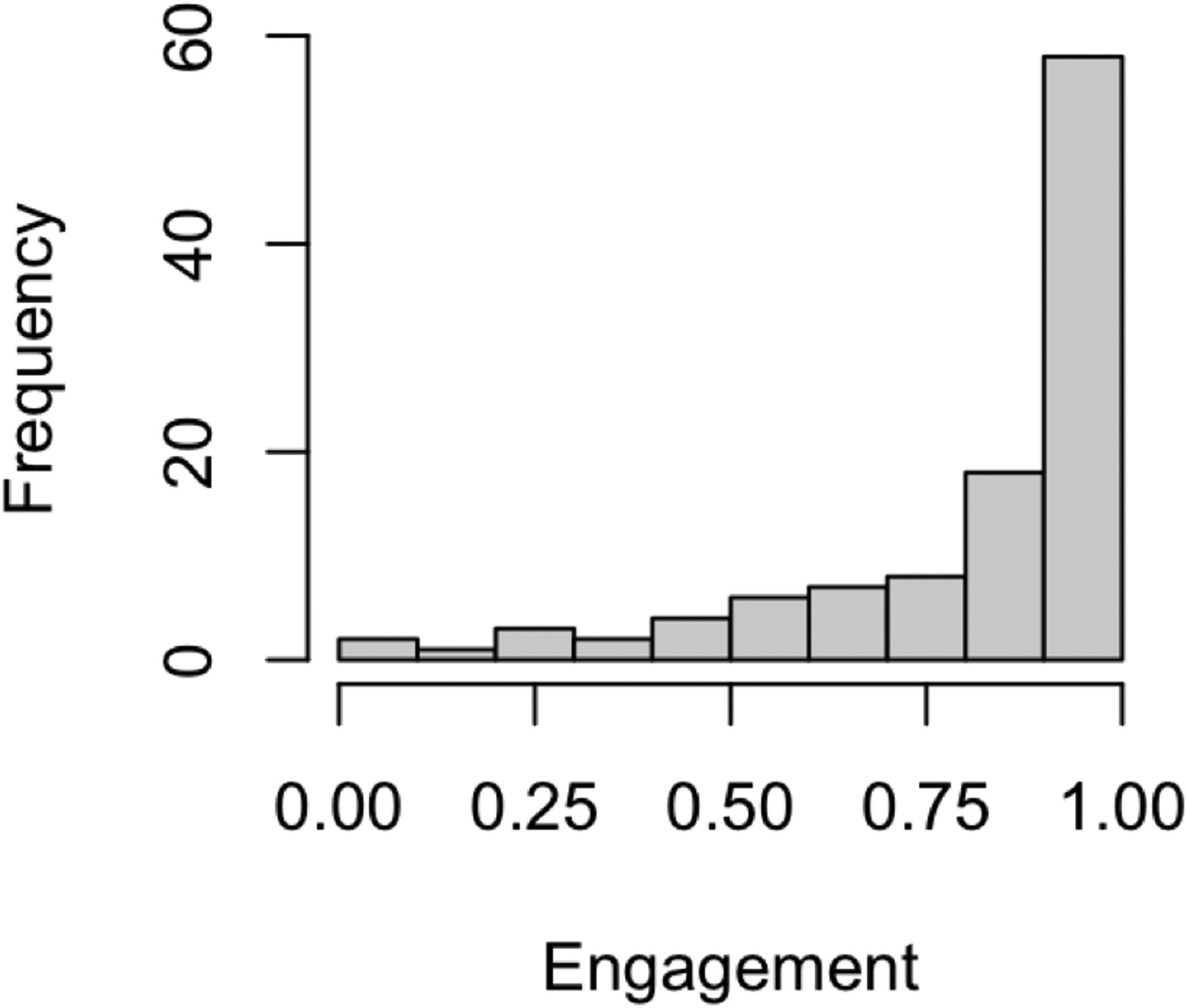
Histogram of subject-specific engagement within the REACH intervention group, defined as proportion of text messages responded to over the six-month period.

The results of the sensitivity analysis under different sensitivity parameters are shown in Table 4. Of note, the estimates of the NECE are comparable across γ between each of the linear and dichotomous parameterizations; for low values of γ, the dichotomization approach produces estimates of the ECCE that are further from the null as compared to the linear approach. These results are consistent with the results of the simulation study. If the linear parameterization is more closely satisfied, we would expect the estimates produced by the dichotomization approach to be biased.

Table 4.

Results from the REACH study. Presented are the estimated local average treatment effects and respective quantile-based bootstrap 95% confidence intervals for the NECE and the ECCE across different values of γ, each each characterization of engagement (linear and dichotomous).

	Linear: h(a) = a		Dichotomous: h(a) = 1 (a ≥ 0.80)
	${\widehat{\Delta }}_{\gamma }(0)$	${\widehat{\Delta }}_{\gamma }(1)$	${\widehat{\Delta }}_{\gamma }(0)$	${\widehat{\Delta }}_{\gamma }(1)$
γ	Est. (95% CI)	Est. (95% CI)	Est. (95% CI)	Est. (95% CI)
0.25	−0.22 [−0.38, −0.07]	−0.88 [−1.51, −0.27]	−0.25 [−0.42, −0.08]	−0.99 [−1.69, −0.30]
0.50	−0.42 [−0.72, −0.13]	−0.84 [−1.43, −0.26]	−0.45 [−0.77, −0.14]	−0.90 [−1.53, −0.28]
0.75	−0.60 [−1.02, −0.18]	−0.80 [−1.36, −0.25]	−0.62 [−1.05, −0.19]	−0.82 [−1.40, −0.25]

We focus now on interpreting results from the linear parameterization, in which there is an embedded range of local average treatment effects for each γ. We display these results in Figure 7, specifically emphasizing the choices of a = 0, 0.5, 0.814, and 1. The choice of a = 0.814 is designed to illustrate the stationary property described in Section 3. A number of insights can be gained based from this analysis. One can fix γ to learn about effects among subgroups defined by their engagement level. For instance, if γ = 0.50, engagement levels meeting or exceeding 19.2% are associated with treatment effect estimates exceeding the clinically meaningful threshold of 0.50%. On the other hand, if γ = 0.75, all levels of engagement are associated with treatment effect estimates exceeding that threshold. One can further derive insights regarding local average treatment effects on the basis of confidence interval endpoints instead of point estimates. For instance, if γ = 0.25, engagement levels under 10.8% rule out both a null effect and a clinically meaningful effect.

Fig 7.

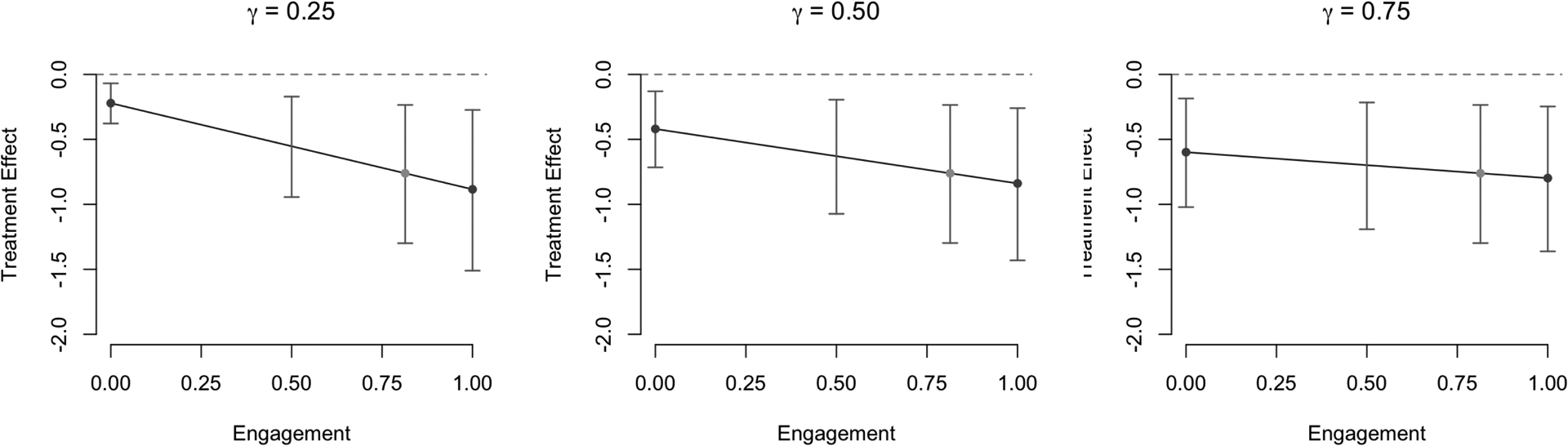
Local average treatment effects and corresponding confidence intervals across levels of A^z=1 = a for three different values of the sensitivity parameter, γ. Also depicted in each plot are the estimated NECE and ECCE (dark gray points) and ITT (light gray point), and quantile-based bootstrap 95% confidence intervals for local average treatment effects at specified levels of a.

In addition to characterizing information regarding local average treatment effects at fixed levels of γ, one can also search for the values of γ that meet a particular criteria. For instance, only for γ > 0.609 does the estimated effect of REACH among never-engagers exceed the clinically relevant threshold of 0.5%. This would imply that we estimate REACH to be uniformly effective across levels of engagement if we believe that the effect among never-engagers is at least 60.9% that of the engagement-compliant.

7. Discussion.

In this paper, we have derived and presented a sensitivity analysis approach to accommodate departures from the exclusion restriction when estimating local average treatment effects, with specific applications to engagement in mobile health interventions. In this setting, the principal stratification framework is simplified by the impossibility of engaging with an intervention not received. Hence, local average treatment effects can be characterized conditional on a single (partially latent, and possibly transformed) variable. Placing reasonable bounds on the sensitivity parameter in turn results in conceptually intuitive bounds on the average causal effect.

Our proposed approach is designed to aid insights regarding average causal effects of the intervention at various levels of engagement with the intervention, particularly when violations to the exclusion restriction assumption cannot be ruled out. We presented asymptotic theory that holds for invertible transformations of the post-randomization variable; our simulations and application focused on linear and dichotomous treatment of engagement, under which our sensitivity procedure appeared to have desirable finite-sample properties. Angrist and Imbens (1995) suggest the linear parameterization when further information can not be assumed. We acknowledge that there may be settings in which alternative continuous parameterizations may be defensible. Further study of different transformations and their possible advantages could be of interest for future studies; moreover, continuous randomization to different text message frequencies may allow the nature of the transformation to be uncovered using observed data rather than simply assumed by the researcher.

Our illustrative example demonstrates various ways that this approach can be used to glean insights regarding treatment effect heterogeneity across levels of engagement. As γ functions as a sensitivity parameter, bounds must be heuristically justified based on the study context. Naturally, the tighter the bounds on γ that can reasonably be considered in practice, the more robust and precise the conclusions that can be derived. Consideration of γ smaller than zero may be appropriate, for instance, in a study involving a psychological outcome, in which receipt of content with which to engage could be relatively harmful on a psychological outcome among the subgroup of subjects who would never engage with that intervention. In the context of REACH, this is not a concern. For similar interventions featuring mostly two-way content, it stands to reason that lower values of γ may be more reasonable as compared to interventions comprising mostly one-way content. We note that engagement with an intervention is more of an abstract concept than response to two-way text messages. For instance, a subject’s true engagement in the abstract sense is partially reflected by his or particular level of attention to text messages (length of time read). Proportion of text messages receiving a response is one of many possible objective measures of engagement, but does not necessarily serve as a perfect surrogate for intrinsic engagement in the most abstract sense. The results of a sensitivity analysis are driven in large part by the average level of the engagement metric in the study. In the particular case of the REACH study, text message response rates tended to be high, such that the ECCE was less sensitive to fluctuations in the sensitivity parameter as compared to the NECE. Had the average engagement rate been lower, the ECCE would have been more sensitive to fluctuations in γ.

Challenges associated with and methods to address missing data have been described in settings of noncompliance (Jo, 2002, 2007). In our unique setting, the identifying assumptions allow us to express local average treatment effects as specific multiples of ITT effects. Therefore, the challenges associated specifically with partial compliance have minimal impact on the approach used to address missing data. Fully conditional specification (i.e., multiple imputation by chained equations) is generally regarded as a gold-standard approach to address missing data in a way that allows us to assume missingness at random rather than the stronger assumption of missingness completely at random.

Specific procedures for sensitivity analyses have long been an area of interest in methodological causal inference research, many times in the context of violations to the assumption of ignorability/no unmeasured confounding (Lin, Psaty and Kronmal, 1998; Imai, Keele and Yamamoto, 2010; Jo and Vinokur, 2011; Stuart and Jo, 2015; Dorie et al., 2016). Prior work has investigated the sensitivity of non-IV based causal inference approaches when the exclusion restriction is not satisfied (Millimet and Tchernis, 2013). Many of the sensitivity analysis procedures developed for departures from the IV assumptions are applicable only to the case of four discrete principal strata (e.g, in the example of treatment compliance) such as the approach of Angrist, Imbens and Rubin (1996) as described in Section 1. Again in the case of four discrete principal strata, Baiocchi, Cheng and Small (2014) propose a number of sensitivity analysis procedures for departures to IV assumptions, and Stuart and Jo (2015) demonstrate how the exclusion restriction can be replaced with an alternative assumption referred to principal ignorability when predictors of stratum membership are thought to be well understood. The corresponding approach is analogous to propensity score methods in order to predict subgroup-specific stratum membership. Such approaches are best suited for settings in which predictors of principal stratum are known and measured, and not when substantive unmeasured confounding is suspected as in the case of continuous measures of engagement with an intervention (e.g., REACH). Generalizing the methodology of Stuart et al. to the setting in which strata are defined by a single continuous post-randomization variable, however, may serve as a potential topic of interest for future research.

In terms of other possible implementations of this framework, consider settings in which treatment is not randomized. In such a circumstance, it is possible—likely, even—that pre-intervention covariates would play a role beyond those described in the context of the REACH study. If such covariates are associated with the intervention received, the ignorability assumption would need to be updated to reflect possible confounding; adjustment for such variables would be necessary to identify local average treatment effects rather than simply desirable as a method to gain precision.

Appendix.

Here, we elaborate on an asymptotic approximation for the variance of $\sqrt{N}\left({\widehat{\Delta }}_{\text{ITT}}-{\Delta }_{\text{ITT}}\right)$ in the special case where ${\widehat{\Delta }}_{\text{ITT}}={\overline{Y}}_{Z=1}-{\overline{Y}}_{Z=0}$. Specifically, the task is to devise a form for $\text{Cov}\left({\widehat{c}}_{\gamma ;h}(a),{\widehat{\Delta }}_{\text{ITT}}\right)$. Since the randomization groups (Z = 0 and Z = 1) are independent, this reduces as follows:

$$\text{Cov}\left({\overline{Y}}_{Z=1}-{\overline{Y}}_{Z=0},\frac{\gamma +(1-\gamma )h(a)}{\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}}\right)=\text{Cov}\left({\overline{Y}}_{Z=1},\frac{\gamma +(1-\gamma )h(a)}{\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}}\right).$$

Now, we note the following general approximation to the following covariance based on the second-order Taylor expansion about (μ_X, μ_Y) for general random variables X and Y :

$$\begin{gathered} \text{Cov}\left(X,Y^{-1}\right)\equiv \text{E}\left[X{Y}^{-1}\right]-\text{E}[X]\text{E}\left[Y^{-1}\right] \\ \approx -\frac{\text{Cov}(X,Y)}{\text{E}{[Y]}^2}. \end{gathered}$$

Applying second-order approximation, we have that

$$\begin{gathered} \text{Cov}\left({\overline{Y}}_{Z=1},\frac{\gamma +(1-\gamma )h(a)}{\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}}\right)\approx \frac{\text{Cov}\left({\overline{Y}}_{Z=1},\frac{\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}}{\gamma +(1-\gamma )h(a)}\right)}{\text{E}{\left[\frac{\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}}{\gamma +(1-\gamma )h(a)}\right]}^2} \\ =(\gamma +(1-\gamma )h(a))\text{Cov}\left({\overline{Y}}_{Z=1},\gamma +(1-\gamma ){\overline{h(A)}}_{Z=1}\right) \\ =(1-\gamma )(\gamma +(1-\gamma )h(a))\text{Cov}\left({\overline{Y}}_{Z=1},{\overline{h(A)}}_{Z=1}\right) \\ =N_1^{-1}(1-\gamma )(\gamma +(1-\gamma )h(a))\text{Cov}\left(Y_1,h\left(A_1\right)\right). \end{gathered}$$

This expression takes a form that can be readily estimated based on the observed data. In this setting, the total asymptotic variance τ_γ;h(a) can be approximated as:

$${\left[c_{\gamma ;h}(a)\right]}^2{\sigma }_{\text{ITT}}^2+r{\left({\Delta }_{\text{ITT}}\right)}^2{\sigma }_{c;h}^2(a)+2r{c}_{\gamma ;h}(a){\Delta }_{\text{ITT}}(1-\gamma )(\gamma +(1-\gamma )h(a))\text{Cov}\left(Y_1,h\left(A_1\right)\right).$$