Ensemble machine learning model identifies patients with HFpEF from matrix-related plasma biomarkers

Abstract

Arterial hypertension can lead to structural changes within the heart including left ventricular hypertrophy (LVH) and eventually heart failure with preserved ejection fraction (HFpEF). The initial diagnosis of HFpEF is costly and generally based on later stage remodeling; thus, improved predictive diagnostic tools offer potential clinical benefit. Recent work has shown predictive value of multibiomarker plasma panels for the classification of patients with LVH and HFpEF. We hypothesized that machine learning algorithms could substantially improve the predictive value of circulating plasma biomarkers by leveraging more sophisticated statistical approaches. In this work, we developed an ensemble classification algorithm for the diagnosis of HFpEF within a population of 480 individuals including patients with HFpEF, patients with LVH, and referent control patients. Algorithms showed strong diagnostic performance with receiver-operating-characteristic curve (ROC) areas of 0.92 for identifying patients with LVH and 0.90 for identifying patients with HFpEF using demographic information, plasma biomarkers related to extracellular matrix remodeling, and echocardiogram data. More impressively, the ensemble algorithm produced an ROC area of 0.88 for HFpEF diagnosis using only demographic and plasma panel data. Our findings demonstrate that machine learning-based classification algorithms show promise as a noninvasive diagnostic tool for HFpEF, while also suggesting priority biomarkers for future mechanistic studies to elucidate more specific regulatory roles.

NEW & NOTEWORTHY Machine learning algorithms correctly classified patients with heart failure with preserved ejection fraction with over 90% area under receiver-operating-characteristic curves. Classifications using multidomain features (demographics and circulating biomarkers and echo-based ventricle metrics) proved more accurate than previous studies using single-domain features alone. Excitingly, HFpEF diagnoses were generally accurate even without echo-based measurements, demonstrating that such algorithms could provide an early screening tool using blood-based measurements before sophisticated imaging.

INTRODUCTION

Hypertension continues to be a major cardiovascular disease and, coupled with an aging society, often leads to an increase in left ventricular (LV) mass termed LV hypertrophy (LVH). The development of LVH is a risk factor for reduced diastolic function and chronic heart failure, wherein myocardial remodeling can lead to impaired LV filling, a stiffer LV, and increased diastolic pressure, which could lead to further abnormalities of the heart tissue (1, 2). Prolonged periods of LVH may lead to heart failure with a preserved ejection fraction (HFpEF) (3, 4). The progression from LVH to HFpEF can be difficult to detect and is usually recognized only when the patient presents with symptoms (1, 2, 5, 6). The complete mechanistic pathway from hypertrophy to heart failure is unknown, and its diagnosis within patients requires costly approaches and testing such as cardiac MRI or echocardiograms (7).

Previous studies attempting the prediction or risk stratification for HFpEF have each generally focused on information from just a single domain, for example, either demographics/clinical history, imaging-based approaches, or the use of blood-based measurements (i.e., biomarkers). However, strategies that use a multidomain approach to synthesize identified key variables in a predictive model remain to be established. Accordingly, we sought to apply machine learning approaches, which provide for a comprehensive and unbiased approach for evaluating variables from multiple domains, in patients with established LVH but no HFpEF and in patients with HFpEF to develop refined prediction models.

Hypertension has been shown to produce changes in both the structural and biochemical composition of heart tissue. One important component of the structural make-up of cardiac tissue is fibrillar collagen (type I and III). Thus, it has been shown that hypertension is correlated with an increase in extracellular matrix accumulation, which is regulated by changes in the relative ratio between collagen production and degradation (8–12). The maturation to a collagen fibril requires multiple processing steps, which leads to certain byproducts of these reactions. Specifically, the cleavage of the NH₂-terminal propeptide of procollagen type I and procollagen type III (PINP and PIIINP) produces fragments that can be detected in a blood sample, allowing for the quantification of collagen production. Alternatively, carboxyl-terminal telopeptide of collagen type I (CITP) is a product from the process of collagen degradation, and thus can be used as a biomarker for the quantification of collagen degradation (3). The group of interstitial proteases, known as the matrix metalloproteinases (MMPs), plays a critical role in the process of collagen degradation (13). The MMP family consists of 23 uniquely functional proteases that can be grouped in terms of their substrate. The MMPs focused herein are MMP-1 (collagenase), MMP-2 (gelatinase), MMP-3 (stromelysin), MMP-7 (stromelysin), MMP-8 (collagenase), and MMP-9 (gelatinase). The group of MMPs also has inhibitors, namely, the tissue inhibitors of metalloproteinases (TIMPs), which act upon both the mature proteases and the pro-proteases (12).

Recent studies into the application of machine learning techniques for the classification of numerous pathologies have shown predictive capabilities of many different data types and prediction tasks (13–17). In our present study, we look to expand on previous work that investigates the use of remodeling-related biomarkers for the classification of the myocardial hypertrophic disease states, left ventricular hypertrophy and diastolic heart failure. To improve the predictive power of these biomarkers for classification, we used multiple advanced machine learning frameworks.

METHODS

Patients and Data

Patient data were previously collected for 480 individuals as described by Zile et al. (2). The original study recruited volunteers between 2004 and 2006 from health fairs, physician referral, and echocardiographic studies. All patients provided written informed consent, and the research protocol was reviewed and approved by the Institutional Review Board at the Medical University of South Carolina. Patients were excluded if they had evidence of a clinical condition that might modulate circulating plasma profiles including pulmonary disease, end-stage renal disease, rheumatological disease, poorly controlled diabetes, a recent major surgical procedure, myocardial infarction, active infection, or other fibrotic and/or inflammatory conditions.

The patients were divided into three categories: referent control patients (n = 277), patients with LVH (n = 143), and patients with HFpEF (n = 60). The definitions for these categories were based on previous studies and Lahey Clinic and the Heart Failure and Echocardiography Associations of the European Society of Cardiology, and further discussed previously by Zile et al. (2). Briefly, LVH was defined as an increase in LV wall thickness of >1.2 cm and/or an increase in LV mass index >95 in women and >115 g/m² in men measured in echocardiograms; HFpEF diagnosis required 1) clinical signs of heart failure using Framingham Criteria, Boston Criteria, exercise testing, or quality-of-life survey; 2) preserved EF of >50%; 3) normal LVEDVi of <90 mL/m²; and 4) evidence of diastolic LV dysfunction.

The patient data array included patient demographics, biomarkers derived from plasma samples, and image features from echocardiography. A primary goal of our study was to test the predictive ability of data that could be acquired noninvasively and without sophisticated imaging, so we parsed the data into a “limited” feature set that included age, sex, race, height, weight, body surface area (BSA), heart rate, systolic blood pressure, diastolic blood pressure, pulse pressure, and a plasma biomarker panel including MMP-1, MMP-2, MMP-3, MMP-7, MMP-8, MMP-9, TIMP-1, TIMP-2, TIMP-3, TIMP-4, PINP, PIIINP, CITP, cardiotrophin (CT-1), NH₂-terminal propeptide of brain natriuretic peptide (NT-proBNP), soluble receptor for advanced glycation end products (sRAGE), and osteopontin. This specific list of biomarkers was chosen to include molecules that were 1) established to have some mechanistic link to tissue remodeling from previous studies and 2) previously validated to be detectable in patient plasma samples. The “expanded” feature set included all the variables included in the basic array, as well as mechanical biomarkers derived from echocardiogram data: left ventricular internal diameter end diastole (LVIDd), LV internal diameter end systole (LVIDs), LV end-diastolic volume (EDV), LV end-diastolic volume index (EDVi = EDV/BSA), LV end-systolic volume (ESV), LV end-systolic volume index (ESVi = ESV/BSA), stroke volume (SV), ejection fraction (EF), peak systolic stress (PSS), end systolic stress (ESS), and end diastolic stress (EDS). Feature averages and variability for each group are shown in Table 1, and baseline statistical comparisons across groups were previously reported (2).

Table 1.

Summary statistics for patient groups

Features	Control	LVH	HFpEF
Patients, n	277	143	60
Females, %	71.0	55.3	61.0
African American, %	19.8	40.1	36.8
Age, yr	55.97 (13.66)	60.32 (11.68)	66.30 (11.81)
Height, cm	167.03 (11.65)	169.82 (10.77)	168.67 (9.55)
Weight, kg	77.98 (19.13)	90.64 (22.09)	92.95 (24.07)
Body surface area, m2	1.89 (0.25)	2.06 (0.29)	2.07 (0.29)
Systolic BP, mmHg	127.44 (12.64)	134.75 (10.92)	139.63 (18.37)
Diastolic BP, mmHg	75.41 (7.26)	79.56 (8.13)	76.88 (9.32)
Pulse pressure, mmHg	68.78 (9.84)	67.25 (10.97)	68.80 (10.71)
Heart rate, beats/min	52.02 (10.70)	55.19 (10.67)	62.75 (16.19)
MMP1, ng/mL	0.76 (0.63)	0.86 (0.66)	0.89 (0.73)
MMP2, ng/mL	348.29 (143.61)	324.52 (144.43)	418.32 (170.64)
MMP3, ng/mL	10.16 (6.27)	9.35 (5.04)	11.38 (5.86)
MMP7, ng/mL	1.57 (1.19)	1.84 (1.17)	2.13 (1.38)
MMP8, ng/mL	2.60 (3.56)	3.29 (3.91)	1.95 (1.52)
MMP9, ng/mL	101.33 (87.39)	126.20 (87.32)	125.08 (67.60)
TIMP1, ng/mL	70.68 (23.32)	81.94 (25.25)	84.44 (24.89)
TIMP2, ng/mL	77.61 (14.41)	83.23 (14.38)	81.83 (12.95)
TIMP3, ng/mL	7.39 (7.89)	9.22 (9.54)	5.62 (6.67)
TIMP4, ng/mL	1.47 (0.65)	1.46 (0.62)	1.86 (0.76)
PINP, ng/mL	37.81 (20.04)	34.24 (22.96)	40.58 (24.82)
PIIINP, ng/mL	7.18 (1.86)	7.59 (2.05)	9.14 (3.19)
CITP, ng/mL	2.87 (1.78)	3.55 (2.02)	3.80 (3.19)
CT-1, ng/mL 10−3	0.05 (0.10)	0.04 (0.08)	0.02 (0.04)
pro-NT BNP, pg/mL	87.51 (90.22)	88.60 (99.51)	210.67 (253.91)
sRAGE, ng/mL	3.39 (2.47)	3.06 (2.74)	2.86 (1.97)
OSTEO, ng/mL	74.05 (31.20)	85.97 (56.91)	93.15 (42.15)
LVIDd, cm	4.65 (0.44)	4.84 (0.50)	4.80 (0.54)
LVIDs, cm	2.83 (0.38)	2.93 (0.46)	2.93 (0.45)
EDV, mL	99.42 (21.76)	107.13 (25.74)	110.03 (29.00)
EDVi, mL/m2	52.83 (10.45)	52.46 (12.03)	53.41 (13.46)
ESV, mL	31.85 (10.08)	34.40 (13.02)	35.02 (13.11)
ESVi, mL/m2	16.86 (4.89)	16.76 (5.96)	16.86 (6.31)
SV, mL	67.57 (15.13)	72.72 (18.63)	75.02 (20.52)
PSS, g/cm2	53.44 (14.42)	45.84 (11.97)	44.67 (12.48)
ESS, g/cm2	38.96 (10.52)	33.30 (8.61)	31.40 (8.98)
EDS, g/cm2	15.51 (3.91)	12.54 (3.56)	16.44 (6.27)
EF	0.68 (0.06)	0.68 (0.09)	0.68.(0.07)

Values are means (SD). BP, blood pressure; CITP, carboxyl-terminal telopeptide of collagen type I; CT-1, cardiotrophin; EDS, end diastolic stress; EDV, LV end-diastolic volume; EDVi, LV end-diastolic volume index; EF, ejection fraction; ESS, end systolic stress; ESV, LV end-systolic volume; ESVi, LV end-systolic volume index; HFpEF, heart failure with preserved ejection fraction; LVH, left ventricular hypertrophy; LVIDd, left ventricular internal diameter end diastole; LVIDs, LV internal diameter end systole; MMP, matrix metalloproteinase; NT-proBNP, NH₂-terminal propeptide of brain natriuretic peptide; OSTEO, osteopontin; TIMP, tissue inhibitors of metalloproteinases; PINP, NH₂-terminal propeptide of procollagen type I; PIIINP, NH₂-terminal propeptide of procollagen type III; PSS, peak systolic stress ; sRAGE, soluble receptor for advanced glycation end products; SV, stroke.

Across the full data set of 38 features × 480 patients, only 1.3% of data points were missing (average of 7 patients missing for each feature). For patients with missing data, we first normalized the data using a z-score approach to normalize the data with respect to the sample means and standard deviations (18). We then found the five nearest-neighbors for each patient that had minimal mean squared errors across all features, and we imputed each individual missing value with the average of that variable across the five nearest-neighbors for each patient.

To visualize the high-dimensional data set in an unbiased, unsupervised manner, we performed dimensionality reduction with t distributed Stochastic Neighbor Embedding (t-SNE). This nonlinear technique for dimensionality reduction creates a mapping of data set elements that seeks to minimize the divergence of a distribution of the pairwise similarities of the inputs and a distribution of the pairwise similarities of the subsequent embedded points (19). We used a standardized Euclidean distance metric and a perplexity of 50, where the perplexity is the number of the local nearest neighbors of each point.

Machine Learning Algorithms for Classification

The patient data used for classification were defined in two ways. In the first (“limited set”), the patient data were exclusively biochemical biomarkers from a blood plasma panel, patient demographic information, and blood pressures. In the second (“expanded set”), the patient data included all the information in the limited set as well as data gathered through more advanced echocardiography image processing. The complete patient matrix was then imported into the MATLAB Classification Learner within the Statistics and Machine Learning Toolbox, R2019B. Resulting algorithm codes are all freely accessible through the Richardson laboratory modeling GitHub repository: https://github.com/SysMechBioLab/HFpEF_diagnosis.

We used six different machine learning algorithms for patient classification: logistic regression, discriminate analysis, naïve Bayes, support vector machines, k-nearest neighbors, and an ensemble algorithm. These supervised algorithms are frequently used for binary classification problems, and they cover both probabilistic and deterministic models. The logistic regression approach looks to estimate parameters of a linear model that represents the log-odds of a particular class (20). Discriminate analysis assumes that the conditional probabilities of each class follow a Gaussian distribution and the model attempts to approximate these Gaussian parameters for class assignment (21). A naive Bayes classifier uses the naive Bayes probability model with a predetermined decision rule to create a classifier that minimizes the misclassification probability (22). A support vector machine model for classification seeks to find a hyperplane within the subspace that can best separate data from each class (23). The k-nearest neighbors approach finds an object’s k-nearest neighbors through a distance metric, and uses the neighbors’ classes for the object’s own classification (24). Ensemble approaches to classification use multiple machine learning algorithms with the goal of having improved performance over the individual components of the ensemble. Specifically, we used a voting ensemble that averaged the classification probabilities from each of the six individual algorithms, and then classified each patient according to the average.

Model Optimization

For fitting the algorithms, patients were randomly split into a training subset (80%) and a testing subset (20%), the hyperparameters were then optimized using the training subset only, and the performance metrics (accuracy, precision, receiver-operator-characteristic curves, etc.) were calculated on the testing subset. All reported performance indicators therefore represent validation performance with data that were not used for model fitting. To ensure that our conclusions were not an artifact of a single, particular, randomized 80/20 split, we repeated the process five times (i.e., 5 different testing-training splits) and calculated the same performance metrics each time using different training sets.

Each of the approaches, other than the simple logistic regression approach, was optimized using a Bayesian hyperparameter optimization approach over 100 iterations (25). Bayesian optimization uses a Gaussian process model of an objective function, a Bayesian update procedure for the modification of the model, and an acquisition function that is maximized according to the value of the expected improvement (26). The Gaussian process’s posterior distribution allows for efficient use of experimental data as a means for subsequent parameter selection. Accordingly, the optimizable hyperparameters for each machine learning approach are as follows: the discriminate type, including linear, diagonal linear, quadratic, and linear quadratic for the discriminate analysis approach; the distribution (Gaussian or Kernel) as well as the kernel type for the naive Bayes approach; the kernel function (Gaussian, linear, quadratic, and cubic), the box constraint level, and the kernel scale for the support vector machine approach; the number of neighbors, the distance metric (Euclidean, city block, Chebyshev, cubic, Mahalanobis, cosine, correlation, Spearman, Hamming, and Jaccard), and the distance weight (equal, inverse, and squared inverse) for the k-nearest neighbor approach (25).

Model Testing and Feature Selection

After training simulations, the accuracies of the testing groups were calculated, with true positive (TP), true negative (TN), false positive (FP), and false negative (FN) using the formula for accuracy of a binary classification model:

$$\text{A}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}=\frac{\text{T}\text{N}+\text{T}\text{P}}{\text{T}\text{N}+\text{T}\text{P}+\text{F}\text{N}+\text{F}\text{P}}.$$

In addition, precision, F₁ scores and Matthews Correlation Coefficients were calculated as follows:

$$\text{Pr}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}=1-\text{f}\text{a}\text{l}\text{s}\text{e}\text{d}\text{i}\text{s}\text{cov}\text{e}\text{r}\text{y}\text{r}\text{a}\text{t}\text{e}=\frac{\text{T}\text{P}}{\text{T}\text{P}+\text{F}\text{P}},$$

$${\text{F}}_1=\frac{\text{T}\text{P}}{\text{T}\text{P}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.(\text{F}\text{P}+\text{F}\text{N})},$$

$$\text{M}\text{C}\text{C}=\frac{\text{T}\text{P}\times \text{T}\text{N}-\text{F}\text{P}\times \text{F}\text{N}}{\sqrt{(\text{T}\text{P}+\text{F}\text{P})(\text{T}\text{P}+\text{F}\text{N})}(\text{T}\text{N}+\text{F}\text{P})(\text{T}\text{N}+\text{F}\text{N})}.$$

These statistical evaluations of the classifiers were used because the accuracy is not a complete measure of a classifier’s ability, especially when there exists a large difference in the number of samples of each class (27). In this case, accuracy is heavily weighted toward the class with the larger number of samples. The F₁ score is a frequently used statistic to evaluate the predictive power of a classifier; however, it also ignores the true negative group. Thus, an additional statistical evaluator was employed, the Matthews correlation coefficient, which is dependent on the correct prediction of both the positive and negative classes (28).

Feature selection was conducted using a minimum redundancy maximum relevancy (mRMR) algorithm (29). This algorithm seeks to find a set of features from the sample set that can effectively represent the response and minimize the redundancy of the feature set through the use of mutual information of the feature variables, or by how much the uncertainty of a variable in the set can be minimized by information of another variable. As a result, a higher weighting of a variable due to the algorithm is proportional to its confidence and so is the difference between a variable and the subsequent variable in the ranking.

RESULTS

The mapping of the high-dimensional data into a two-dimensional space through t-SNE displayed clear clustering patterns using either the limited feature set (Fig. 1A) or the expanded feature set (Fig. 1B). In both cases, the groups with control patients and patients with LVH were almost entirely self-contained with the HFpEF group clustered at the interface and boundaries (Fig. 1). This general group separability shown through t-SNE provided further motivation for machine learning-based classification models. After the selected classification simulations were completed, receiver-operating-characteristic (ROC) curves were recorded to assess predictive performance (Fig. 2). With the expanded feature set, most machine learning algorithms overperformed the previously reported LVH classification based on biomarkers alone by Zile et al. (2). But interestingly, HFpEF classification was equally accurate with the limited and expanded sets (Fig. 2F).

Figure 1.

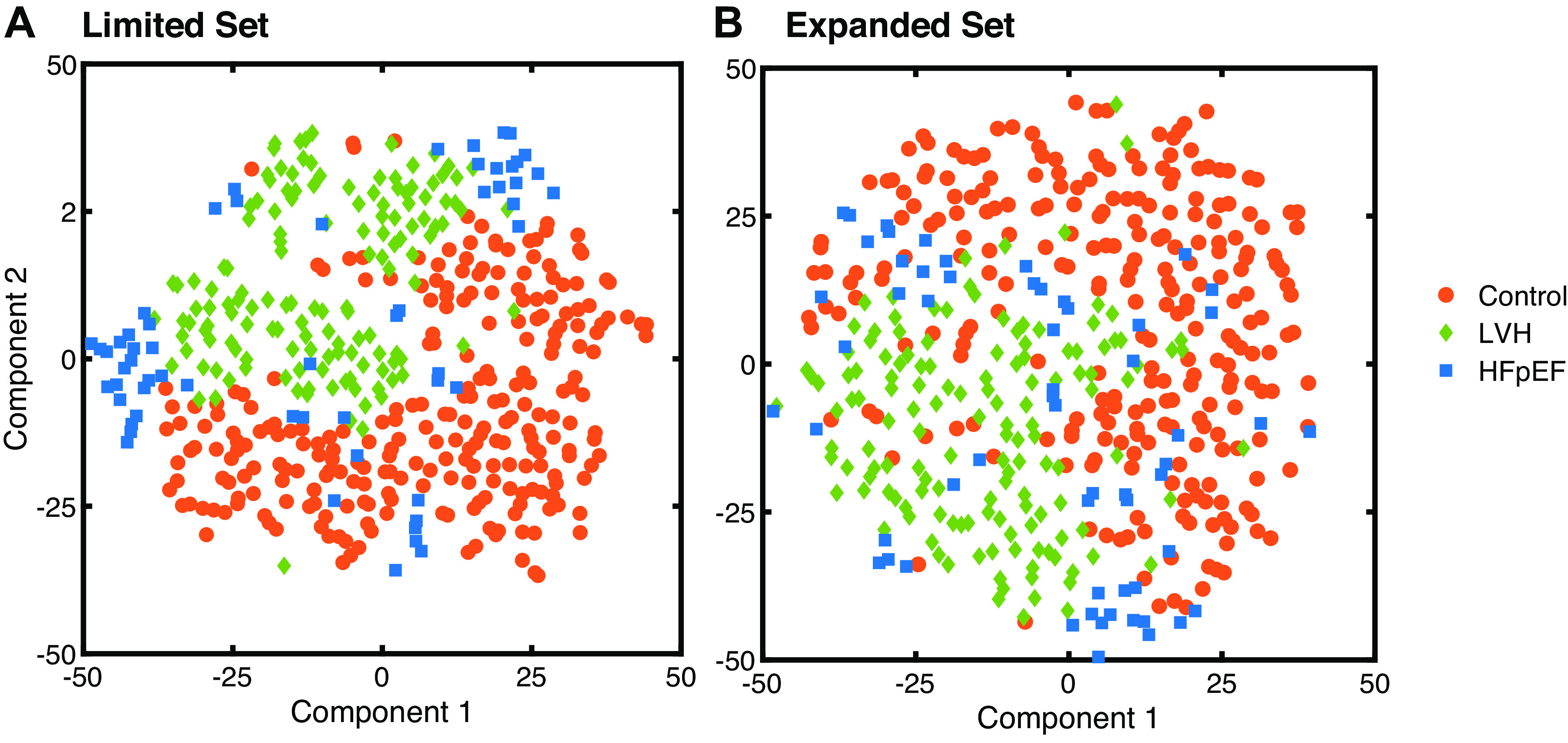
t-distributed stochastic neighbor embedding (t-SNE) dimensionality reduction of the limited set (A) and expanded set (B) of patient data demonstrated stark clustering of control vs. LVH vs. patients with HFpEF across the first 2 principal t-SNE components. HFpEF, heart failure with preserved ejection fraction; LVH, left ventricular hypertrophy.

Figure 2.

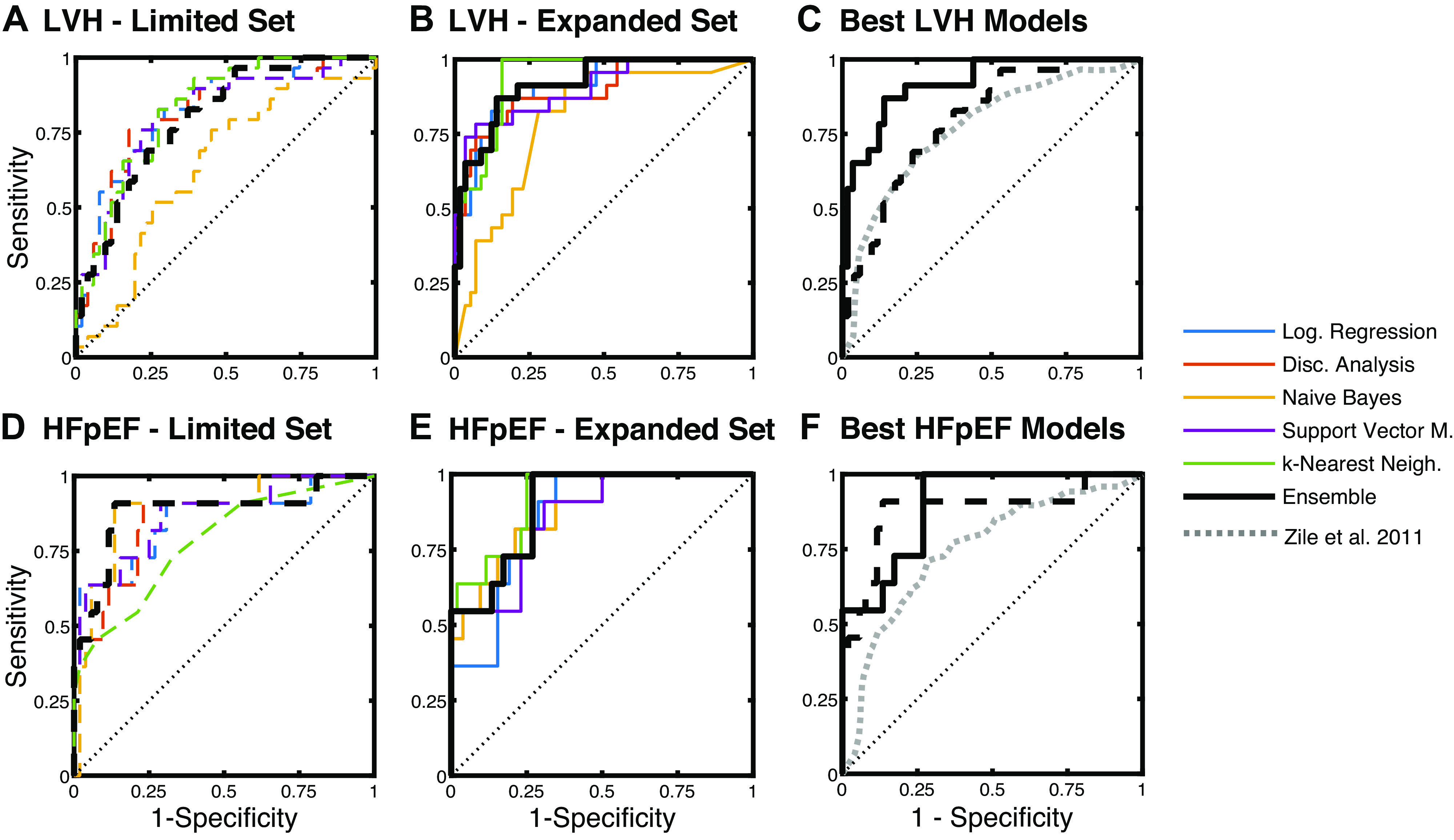
Receiver-operating-characteristic curves for classification of LVH (A–C) and HFpEF (D–F). Limited feature set included plasma biomarkers, as well as patient demographics and basic clinical measurements (blood pressure, heart rate, etc.). The expanded feature set included all variables in the limited set, as well as echo-based LV structure and functional measures. The voting ensemble approach had the most consistent performance. HFpEF, heart failure with preserved ejection fraction; LVH, left ventricular hypertrophy.

Overall performance of the various algorithms was compared across F₁ scores, MCCs, precision, AUCs, and accuracy levels, with various algorithms reaching as high as 94% AUC and 92% accuracy (Fig. 3). Not surprisingly, different methodologies worked better or worse depending on the classification task. For example, naive Bayes performed much better with the HFpEF limited task compared with other tasks, whereas discriminate analysis performed much better with the LVH expanded task. Across all classification tasks, the ensemble algorithm showed the most consistently high performance, reaching as high as 92% AUC in the case of the LVH expanded set. This is not surprising given the ensemble approach’s ability to combine the high-performing predictions from the individual algorithms while discounting the low-performing predictions. In general, prediction performance was expectedly improved by using the full expanded data set rather than just the limited data set, likely due to more detailed information provided by the echocardiograms. Interestingly, accuracies were generally higher for the HFpEF classification compared with the LVH classification. These results were largely consistent across five different randomized training-testing splits of the data set, which showed only minor variability in performance (standard deviations for the ensemble AUC was 3.5%). Algorithm performances were also consistent across sex and race categories with insignificant differences between female versus male AUC values (P = 0.39) and black versus white AUC values (P = 0.45).

Figure 3.

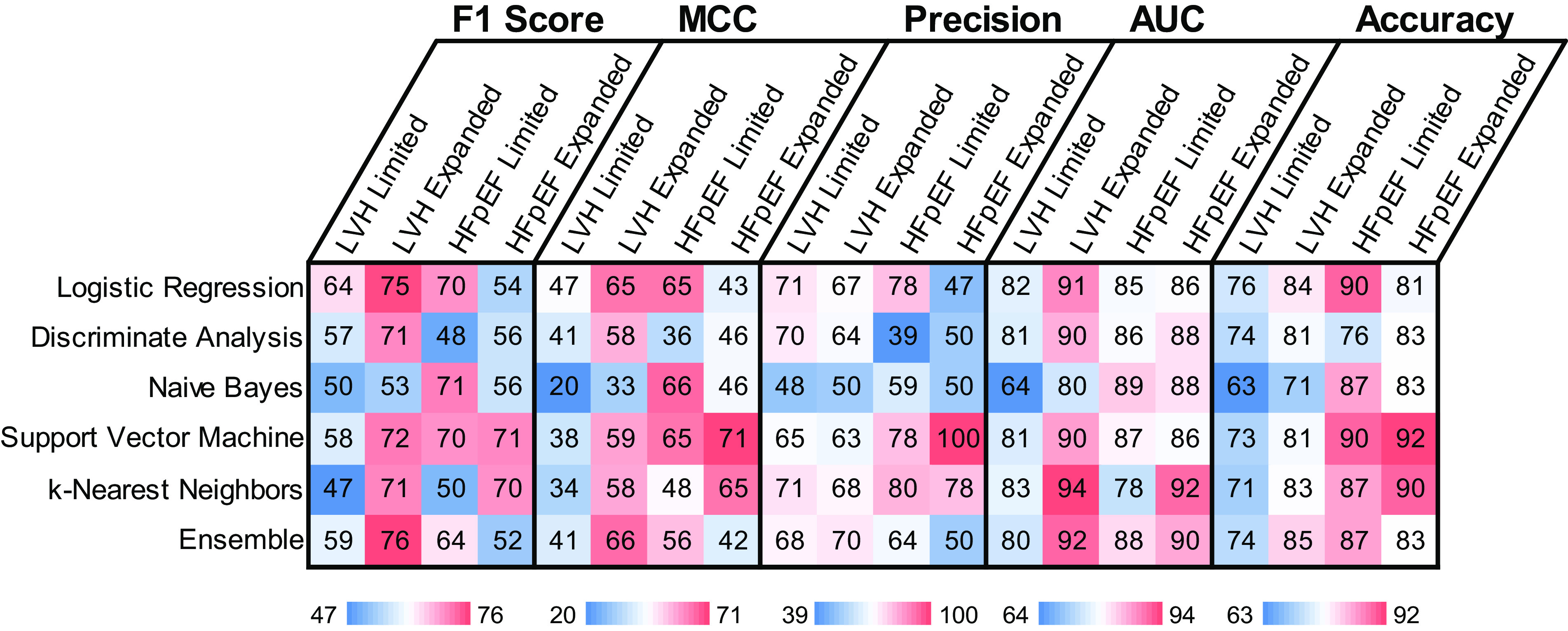
Performance metrics (in %) for each machine learning algorithm included F₁ scores, Matthews correlation coefficients (MCC), precision, ROC area under the curve (AUC), and overall accuracy for classification of patients with LVH and patients with HFpEF, including the limited and expanded feature sets. HFpEF, heart failure with preserved ejection fraction; LVH, left ventricular hypertrophy; ROC, receiver-operating-characteristic curve.

To better interpret our modeling predictions, we performed an mRMR feature selection approach for generating a ranked list of feature importance (Fig. 4). The most-heavily weighted features for the limited LVH classification included some basic features such as age, race, sex, BSA, and heart rate, as well as some plasma biomarkers such as TIMP3, MMP9, and MMP3. With the expanded feature set, several echo-based metrics emerged as important features including EDVi and ESV along with MMP8 and PINP. The most heavily weighted features for the limited HFpEF classification mostly included plasma biomarkers such as TIMP2, MMP1, MMP9 and MMP7, along with a few basic features such as heart rate and diastolic BP. With the expanded feature set, EDVi and LVIDd also emerged as helpful predictors for HFpEF. In general, the non-MMP and non-TIMP plasma biomarkers ranked very low across all four classification tasks. Interestingly, apart from a few volume measures, other echo-based variables ranked relatively poorly in the feature importance analysis.

Figure 4.

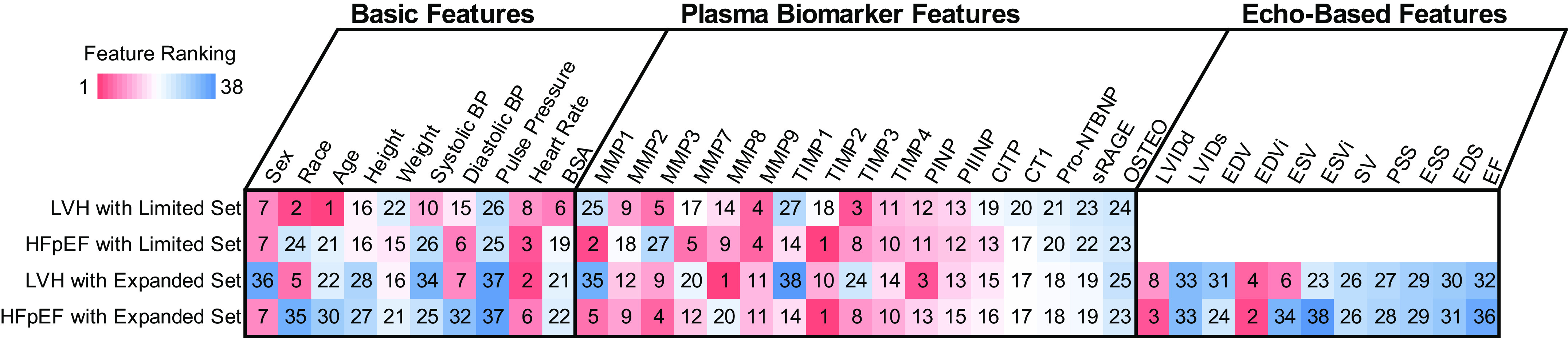
Feature selection by mRMR identified a ranked list of each feature’s importance to LVH or HFpEF classification tasks using the limited feature set (basic features + plasma biomarker features) or the expanded feature set (basic + plasma + echo-based features). Note the red colors denote higher-performance rankings while blue colors denote lower-performance ranking. BP, blood pressure; CITP, carboxyl-terminal telopeptide of collagen type I; CT-1, cardiotrophin; EDS, end diastolic stress; EDV, LV end-diastolic volume; EDVi, LV end-diastolic volume index; EF, ejection fraction; ESS, end systolic stress; ESV, LV end-systolic volume; ESVi, LV end-systolic volume index; HFpEF, heart failure with preserved ejection fraction; LVH, left ventricular hypertrophy; LVIDd, left ventricular internal diameter end diastole; LVIDs, LV internal diameter end systole; MMP, matrix metalloproteinase; mRMR, minimum redundancy maximum relevancy; NT-proBNP, NH₂-terminal propeptide of brain natriuretic peptide; OSTEO, osteopontin; TIMP, tissue inhibitors of metalloproteinases; PINP, NH₂-terminal propeptide of procollagen type I; PIIINP, NH₂-terminal propeptide of procollagen type III; PSS, peak systolic stress ; sRAGE, soluble receptor for advanced glycation end products; SV, stroke.

DISCUSSION

The progression of hypertension-induced LVH and HFpEF is complex and uses various mechanistic pathways. As a means of dealing with the difficulty of mapping the interactions that lead to these cardiac pathologies, machine learning approaches offer predictive power without fully understanding these mechanistic complexities. By using advanced machine learning techniques, we looked to minimize the need for more detailed kinetic studies involving cellular regulation of extracellular remodeling and the specific roles played by key factors of matrix turnover. After a survey of multiple approaches, a voting ensemble method was shown to have consistently high predictive power based upon accuracy and the AUC of the ROC curves. Other metrics of model performance showed mixed results for patient classification, which suggests that different models perform better on different sets of classes within the data. As a result of the complexities of the mechanisms that contribute toward diagnosis, it is expected that the boundaries within the various models are also complex.

The mRMR algorithm is a filter method of feature selection which statistically performs selection based on relationships to the outcome variable and was chosen because of its generalized use with multiple types of machine learning approaches and its documented use in biological applications, specifically in areas such as gene expression and protein site interactions (29–31). In this particular study, biomarkers used were strongly related to one another (such as the proteases and their tissue inhibitors, or various echo-based features calculated from other echo features). The mRMR algorithm seeks to alleviate these frequent concerns of feature selection by ensuring that the variables selected are maximally dissimilar. After feature analysis was conducted with the mRMR algorithm, MMPs 1, 3, 9 and TIMPs 2, 3, 4 were found as important features for HFpEF classification whereas MMP8 and PINP also helped with LVH classification. These findings are corroborated with the previous study by Zile et al. of HFpEF classification through logistic regression (2). Previous work has found that MMP3 and MMP9 were significant predictive biomarkers of HFpEF (2). TIMP2 and TIMP4 plasma levels are also increased in patients with HFpEF, and it has been shown that MMP2 and MMP7 are increased whereas MMP8 levels are decreased in patients with HFpEF when compared with patients with LVH (2, 8).

In LVH and patients with HFpEF compared with the control group, increased PINP and PIIINP are highly indicative of accelerated fibrillar production and increased TIMPs1–4 are indicative of collagen remodeling with high cardiovascular expression. Combined, these biomarkers are shown to be predictive in accordance with the known effects of fibrotic events in heart failure (32). Interestingly, NT-proBNP, the current gold-standard biomarker in hypertrophic disease states, ranking relatively low in the feature rankings for the classification tasks (33).

Notably, feature selection showed that only a few important features came from echocardiographic data relating to the structure of the heart. For the expanded set for HFpEF classification, ventricular volumes emerged as highly rated features, which is supported by previous evidence of ventricular mechanics being associated with pathologies related to diminished ventricular function, such as cardiomyopathy and arterial stenosis (34, 35). Of course, these echo features are computed using ventricular anatomies and therefore depend on advanced imaging and postprocessing after echocardiography or cardiac magnetic resonance. Excitingly, our algorithms were able to identify patients with HFpEF with 90% accuracy even without the echo-based measurements, instead using only the limited data set which can be obtained from basic demographic features, simple clinical measures, and plasma biomarkers. This limited data-based classification could therefore be applied broadly as an early patient screening panel.

It is important to note several key limitations in the current work that limit the model’s predictive power. First, the patient data used in this study consisted of 480 patients, many of whom were previously associated with cardiology clinics and studies. A larger, prospective study with more diverse patients would be needed to further validate the results found herein and expand these classification models with additional patients. Another limitation of the current study is the limited set of biomarkers that is specifically tuned toward extracellular remodeling. Although this focus allows for a more direct future investigation into the correlated mechanistic pathways, a more expansive array of biomarkers could provide the machine learning approaches with valuable features for classification. Biomarkers considered in the current study have multiple functions in addition to fibrotic turnover, and thus, a mechanistic model solely focusing on the process of fibrillar collagen synthesis and degradation may not sufficiently explain each of their individual roles in structural tissue change and diminished heart function. The creation of a more expansive systems network could also provide interesting insights into the mechanisms underlying these complex pathologies. Current studies into possible biomarkers for the classification of heart failure with preserved ejection fraction show the promise of MR-proANP, MR-proADM, troponins, sST2, GDF-15, and galectin-3 (36).

Our work shows promise of the use of advanced machine learning techniques for the classification of patients with heart pathologies. A more comprehensive study with a larger patient sampling pool and additional biomarkers in the panel could provide evidence for the clinical application of the ensemble algorithm for these classification problems before the use of expensive imaging or invasive measurements.

GRANTS

This work was funded by National Institutes of Health Grants HL144927 (to C. F. Baicu, A. Bradshaw, M. R. Zile, and W. J. Richardson) and GM121342 (to W. J. Richardson).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.W., M.R.Z., and W.J.R. conceived and designed research; M.W., A.Y., C.F.B., and W.J.R. analyzed data; M.W., A.Y., C.F.B., A.D.B., F.G.S., M.R.Z., and W.J.R. interpreted results of experiments; M.W., A.Y., and W.J.R. prepared figures; M.W. and W.J.R. drafted manuscript; M.W., A.Y., C.F.B., A.D.B., F.G.S., M.R.Z., and W.J.R. edited and revised manuscript; M.W., A.Y., C.F.B., A.D.B., F.G.S., M.R.Z., and W.J.R. approved final version of manuscript.