Backward bifurcation and optimal control in a co-infection model for SARS-CoV-2 and ZIKV

Abstract

In co-infection models for two diseases, it is mostly claimed that, the dynamical behavior of the sub-models usually predict or drive the behavior of the complete models. However, under a certain assumption such as, allowing incident co-infection with both diseases, we have a different observation. In this paper, a new mathematical model for SARS-CoV-2 and Zika co-dynamics is presented which incorporates incident co-infection by susceptible individuals. It is worth mentioning that the assumption is missing in many existing co-infection models. We shall discuss the impact of this assumption on the dynamics of a co-infection model. The model also captures sexual transmission of Zika virus. The positivity and boundedness of solution of the proposed model are studied, in addition to the local asymptotic stability analysis. The model is shown to exhibit backward bifurcation caused by the disease-induced death rates and parameters associated with susceptibility to a second infection by those singly infected. Using Lyapunov functions, the disease free and endemic equilibria are shown to be globally asymptotically stable for ${\mathcal{R}}_{0}1$, respectively. To manage the co-circulation of both infections effectively, under an endemic setting, time dependent controls in the form of SARS-CoV-2, Zika and co-infection prevention strategies are incorporated into the model. The simulations show that SARS-CoV-2 prevention could greatly reduce the burden of co-infections with Zika. Furthermore, it is also shown that prevention controls for Zika can significantly decrease the burden of co-infections with SARS-CoV-2.

Introduction

Arbovirus diseases (ARBOD) transmitted by Aedes aegypti, such as zika, dengue and chikungunya and the concurrent circulation of these diseases are of major public health concerns in tropical and subtropical regions. The Coronavirus pandemic caused by the “severe acute respiratory syndrome coronavirus 2” (SARS-CoV-2) has posed serious health challenges in countries with overlapping epidemics, consequently increasing the burden on public health system [1]. This is why, SARS-CoV-2 and arboviruses (ARBOD) epidemics co-occurrence has become a matter of great concern to government and health agencies in tropical regions of the world. Indeed, the resemblance in clinical symptoms of Zika and SARS-CoV-2, especially at the early stages of infection is a great challenge which makes appropriate diagnosis very difficult. Hence, the delay in the administration of an appropriate treatment leads to increase in the spread of infection. [2], [3]. Wrong diagnosis can result in lack of the proper care of the right disease and leads to worst health conditions [1], [4]. Rosario and Siqueira [5], in a recent study, also observed that arboviral infections could have life-threatening implications, such as Guillain-Barré syndrome (GBS), encephalitis, myelitis and others.

Mathematical modeling has become an important tool for studying the dynamics of infectious diseases [6], [7], [8], [9], [10], [11], [12]. Several models have been developed to study the dynamics of SARS-CoV-2 [13], [14], [15], [16], [17]. Atangana [13] developed and analyzed a fractal-fractional model for SARS-CoV-2 to assess the impact of lockdown prior to the advent of vaccination, and showed that effective lockdown strategy was very appropriate to contain the spread of the disease at the onset of the pandemic. Also, Khan and Atangana [14] modeled the dynamics of SARS-CoV-2 with quarantine and isolation. They analyzed the dynamical behavior of the disease by describing the interactions among the bats and unknown hosts. Kolebaje and co-authors [15] modeled the dynamics of COVID-19 in some African countries using a real data. They estimated the basic reproduction numbers for some countries and also presented how the disease could be controlled. In another study, Bonyah and co-workers [16] investigated a fractional optimal control model for COVID-19. They highlighted the importance of different control strategies in mitigating the spread of the disease. Moreover, the stability and optimal analysis for a COVID-19 model with quarantine and media awareness were discussed by the authors in [17].

Numerous mathematical studies have investigated the dynamics of SARS-CoV-2 and its co-infection with other diseases such as dengue [26], HIV [27], diabetes [28], [29], [30], [31], tuberculosis [32], [33] and malaria [34], [35], [36]. Most of the co-infection models in the literature do not include the assumption that susceptible individuals can get incident co-infection with the two diseases (an assumption which is possible for some diseases, and yet always ignored). Since there has not been any model yet to study the co-infection between SARS-CoV-2 and Zika virus, we therefore consider a robust novel mathematical model for the co-interactions between these two diseases, capturing incident co-infection by susceptible individuals. We shall also examine how this assumption could influence the dynamics of a co-infection model.

The major contributions of the paper are highlighted as follows:

• i.The positivity and boundedness of solution of the model are discussed.
• ii.The model presented herein is qualitatively analyzed for the occurrence of backward bifurcation.
• iiiUsing Lyapunov functions, the stability of both the disease free and endemic equilibria are examined, when ${\mathcal{R}}_0<1$ and ${\mathcal{R}}_0>1$, respectively.
• iv.Time dependent controls are incorporated into the model and analyzed via the Pontryagin’s principle.
• v.The entire model is simulated to examine the impact of various optimal control strategies on the dynamics of SARS-CoV-2, Zika virus and their co-infections.

Model formulation

At any time $t$, the total human population ${\mathcal{N}}_h\left(t\right)$ consists of the following epidemiological states: Susceptible humans ${\mathcal{S}}_h\left(t\right)$, infectious humans with SARS-CoV-2 ${\mathcal{K}}_{\text{C}}^h\left(t\right)$, infectious humans with Zika virus ${\mathcal{K}}_{\text{Z}}^h\left(t\right)$, humans co-infected with SARS-CoV-2 and zika virus ${\mathcal{K}}_{\text{CZ}}^h\left(t\right)$, with $\mathcal{R}\left(t\right),{\mathcal{K}}_{\text{Z}}^h\left(t\right)$ denotes infected population recovered from SARS-CoV-2 and zika virus, respectively. The total vector population, at any time $t$, ${\mathcal{N}}_v\left(t\right)$ consists of the following states: ${\mathcal{S}}_v\left(t\right),{\mathcal{K}}_{\text{Z}}^v\left(t\right)$, denoting susceptible vectors and vectors infected with Zika virus, respectively. Susceptible humans catch SARS-CoV-2 at the rate $\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}$. Individuals in this state may catch zika virus either from infected humans or vectors at the rate $\frac{{\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v}{{\mathcal{N}}_h}$, respectively. Furthermore, since concurrent infection with both diseases is possible, we have assumed that susceptible individuals can get co-infected with SARS-CoV-2 and zika virus at the rate $\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}$. Human–human-transmission of Zika has been investigated in the literature (see, for example [22]). It is also assumed that the natural death rate for each epidemiological group is ${\mu }_h$. Infected individuals with SARS-CoV-2 can get infected with zika virus at the rate, ${\alpha }_1\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}$. Likewise, those infected with zika virus can get infected with SARS-CoV-2 at the rate ${\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}$. The death rates due to SARS-CoV-2, zika or co-infection are given by ${\eta }_{\text{C}},{\eta }_{\text{Z}}$ and ${\eta }_{\text{CZ}}$, respectively. Moreover, recovery rates from SARS-CoV-2, zika virus or co-infection are denoted by ${\zeta }_{\text{C}},{\zeta }_{\text{Z}}$ and ${\zeta }_{\text{CZ}}$, respectively. In this model, we have assumed that no reversion or re-infection after recovery either from single or dual infections. Incorporating re-infection could be an extension to the proposed model. Parameters in the model are well defined in Table Table 1.

$$\frac{d{\mathcal{S}}_h}{dt}={\Lambda }_h-\left(\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}+\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}+\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}+{\mu }_h\right){\mathcal{S}}_h$$$$\frac{d{\mathcal{K}}_{\text{C}}^h}{dt}=\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h-{\alpha }_1\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{C}}^h$$$$\frac{d{\mathcal{K}}_{\text{Z}}^h}{dt}=\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h-{\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h$$$$\frac{d{\mathcal{K}}_{\text{CZ}}^h}{dt}=\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h+{\alpha }_1\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{C}}^h+{\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h$$$$-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h$$$$\frac{d\mathcal{R}}{dt}={\zeta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h-{\mu }_h\mathcal{R}$$$$\frac{d{\mathcal{S}}_v}{dt}={\Lambda }_v-\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}+{\mu }_v\right){\mathcal{S}}_v$$$$\frac{d{\mathcal{K}}_{\text{Z}}^v}{dt}=\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v$$ (1)

Table 1.

Description of parameters in the model (1).

Parameter	Description	Value	References
${\eta }_{\text{C}}$	SARS-CoV-2 disease-induced death rate	0.015/day	[18]
${\eta }_{\text{Z}}$	Zika disease-induced death rate, respectively	0.001	[19]
${\zeta }_{\text{C}}$	SARS-CoV-2 recovery rate	$\frac{1}{15}$/day	[20], [21]
${\zeta }_{\text{Z}}$	Zika recovery rates	$0.09-0.15$	[22]
${\eta }_{\text{CZ}}$	Co-infected disease-induced death rate	0.015/day	Assumed
${\zeta }_{\text{C}}$	Co-infected recovery rate	$\frac{1}{15}$/day	Assumed
${\Lambda }_h$	Human recruitment rate	$\frac{4,108,508}{74.9\times 365}$ per day	[23]
${\Lambda }_v$	Vector recruitment rate	20,000 per day	[19]
${\beta }_1$	Contact rate for SARS-CoV-2 infection	0.5944	[24]
${\beta }_2$	Contact rate for zika infection (human to human)	0.0100	[22]
${\beta }_2^h$	Contact rate for zika infection (vector to human)	0.43	[22]
${\beta }_2^v$	Contact rate for zika infection (human to vector)	$0.60-0.75$	[22]
${\beta }_3$	Co-infection contact rate (human to human)	0.200	Assumed
${\mu }_h$	Human natural death rate	$\frac{1}{74.9\times 365}$ per day	[25]
${\mu }_v$	Vector removal rate	$\frac{1}{21}$ per day	[19]
${\alpha }_1,{\alpha }_2$	Modification parameters	1.0	Assumed

Analysis of the model

We shall now analyze the model qualitatively (1) without considering the controls. We begin with the following:

Positivity of solutions

For the model (1) to be epidemiologically meaningful, it is appropriate to show that all its state variables are non- negative over time. We prove the results below:

Theorem 1

Let the initial data be ${\mathcal{S}}_h\left(0\right)\ge 0,{\mathcal{K}}_{\text{C}}^h\left(0\right)\ge 0,{\mathcal{K}}_{\text{Z}}^h\left(0\right)\ge 0,{\mathcal{K}}_{\text{CZ}}^h\left(0\right)\ge 0,\mathcal{R}\left(0\right)\ge 0,{\mathcal{S}}_v\left(0\right)\ge 0,{\mathcal{K}}_{\text{Z}}^v\left(0\right)\ge 0$ .

Then the solutions, $({\mathcal{S}}_h,{\mathcal{K}}_{\text{C}}^h,{\mathcal{K}}_{\text{Z}}^h,{\mathcal{K}}_{\text{CZ}}^h,\mathcal{R},{\mathcal{S}}_v,{\mathcal{K}}_{\text{Z}}^v)$ , of the model (1) are non-negative for all time $t>0$ .

Proof

See Appendix A “Proof of Theorem 1”.

Boundedness

We claim the following result:

Theorem 2

The closed set $\mathcal{Q}={\mathcal{Q}}^h\times {\mathcal{Q}}^v$ , with

$${\mathcal{Q}}^h=.\{({\mathcal{S}}_h,{\mathcal{K}}_{\text{C}}^h,{\mathcal{K}}_{\text{Z}}^h,{\mathcal{K}}_{\text{CZ}}^h,\mathcal{R})\in {\mathfrak{R}}_{+}^6:{\mathcal{S}}_h+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h$$

$$+\mathcal{R}\le \frac{{\Lambda }_h}{{\mu }_h}.\},$$

$${\mathcal{Q}}^v=.\left\{({\mathcal{S}}_v,{\mathcal{K}}_{\text{Z}}^v)\in {\mathfrak{R}}_{+}^2:{\mathcal{S}}_v+{\mathcal{K}}_{\text{Z}}^v\le \frac{{\Lambda }_v}{{\mu }_v}.\right\}.$$

is positively invariant with respect to the model (1) .

Proof

Adding all the equations corresponding to the human components of the system (1), we have

$$\frac{d{\mathcal{N}}_h}{dt}={\Lambda }_h-{\mu }_h{\mathcal{N}}_h\left(t\right)-[{\eta }_{\text{C}}{\mathcal{K}}_C^h+{\eta }_{\text{Z}}{\mathcal{K}}_Z^h+{\eta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h].$$ (2)

It follows from (2) that

$${\Lambda }_h-({\mu }_h+3\eta ){\mathcal{N}}_h\le \frac{d{\mathcal{N}}_h}{dt}\le {\Lambda }_h-{\mu }_h{\mathcal{N}}_h,$$

where $\eta =min\{{\eta }_{\text{C}},{\eta }_{\text{Z}},{\eta }_{\text{CZ}}\}$.

which can be re-written as

$$\frac{d{\mathcal{N}}_h}{dt}\le {\Lambda }_h-{\mu }_h{\mathcal{N}}_h.$$ (3)

By applying the comparison theorem [37] and simplifying, we obtain that

$$N_h\left(t\right)\le \frac{{\Lambda }_h}{{\mu }_h}.$$ (4)

Therefore, the total human population, ${\mathcal{N}}_h\left(t\right)\le \frac{{\Lambda }_h}{{\mu }_h}$ as $t\to \infty$. Following the arguments similar to those given above, the total vector population, ${\mathcal{N}}_v\left(t\right)\le \frac{{\Lambda }_v}{{\mu }_v}$. Hence, the system (1) has the solution in $\mathcal{Q}$. Thus, the given system is positively invariant.

The basic reproduction number of the model

By setting the right-hand sides of the equations in the model (1) to zero, we obtain the disease free equilibrium (DFE) as follows:

$${\psi }_0=\left({\mathcal{S}}_h^{\ast },{\mathcal{K}}_{\text{C}}^{h\ast },{\mathcal{K}}_{\text{Z}}^{h\ast },{\mathcal{K}}_{\text{CZ}}^{h\ast },{\mathcal{R}}^{\ast },{\mathcal{S}}_v^{\ast },{\mathcal{K}}_{\text{Z}}^{v\ast }\right)=\left(\frac{{\Lambda }_h}{{\mu }_h},0,0,0,0,\frac{{\Lambda }_v}{{\mu }_v},0\right).$$

The stability of the DFE is studied by applying the next generation operator method [38] to the system (1). The transfer matrices are given by

$$F=\left(\begin{array}{cccc}\hfill {\beta }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_2\hfill & \hfill 0\hfill & \hfill {\beta }_2^h\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\frac{{\beta }_2^v{S}^{v\ast }}{{\mathcal{N}}_h}}^{\ast }\hfill & \hfill {\frac{{\beta }_2^v{S}^{v\ast }}{{\mathcal{N}}_h}}^{\ast }\hfill & \hfill 0\hfill \end{array}\right),V=\left(\begin{array}{cccc}\hfill {\mathcal{G}}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathcal{G}}_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathcal{G}}_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mu }_v\hfill \end{array}\right)$$ (5)

where,

$${\mathcal{G}}_1={\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h,{\mathcal{G}}_2={\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h,{\mathcal{G}}_3={\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h.$$

The basic reproduction number of the model (1) is given by

${\mathcal{R}}_0=\rho \left(F{V}^{-1}\right)=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}$, where ${\mathcal{R}}_{0\text{C}}$, ${\mathcal{R}}_{0\text{Z}}$ and ${\mathcal{R}}_{0\text{CZ}}$ are the associated reproduction numbers for SARS-CoV-2, Zika and co-infection of both diseases, respectively and are given by

$${\mathcal{R}}_{0\text{C}}=\frac{{\beta }_1}{{\mathcal{G}}_1},{\mathcal{R}}_{0\text{Z}}=\frac{1}{2}\frac{{\beta }_2}{{\mathcal{G}}_2}+\frac{1}{2}\sqrt{{\left(\frac{{\beta }_2}{{\mathcal{G}}_2}\right)}^2+\frac{4{\beta }_2^h{\beta }_2^v{\Lambda }_v{\mu }_h}{{\Lambda }_h{\mu }_v^2{\mathcal{G}}_2}},{\mathcal{R}}_{0\text{CZ}}=\frac{{\beta }_3}{{\mathcal{G}}_3}.$$

For the sake of simplicity, reproduction number associated with the human-to-human Zika transmission is denoted by ${\mathcal{R}}_{0\text{Z}}^h=\frac{{\beta }_2}{{\mathcal{G}}_2}$, and the reproduction number associated with the vector-to-human-to-vector Zika transmission denotes ${\mathcal{R}}_{0\text{Z}}^{vh}=\sqrt{\frac{{\beta }_2^h{\beta }_2^v{\Lambda }_v{\mu }_h}{{\Lambda }_h{\mu }_v^2{\mathcal{G}}_2}}$. Thus, the Zika associated reproduction number can be re-written as

$${\mathcal{R}}_{0\text{Z}}=\frac{1}{2}{\mathcal{R}}_{0\text{Z}}^h+\frac{1}{2}\sqrt{{\mathcal{R}}_{0\text{Z}}^{h2}+4{\mathcal{R}}_{0\text{Z}}^{v2}}.$$

Local asymptotic stability of the disease free equilibrium (DFE) of the model

Theorem 3

The DFE, ${\mathcal{H}}_0$ , of the model (1) is locally asymptotically stable (LAS) if ${\mathcal{R}}_0<1$ , and unstable if ${\mathcal{R}}_0>1$ .

Proof

The local stability of the model (1) is analyzed by the Jacobian matrix of the system (1) evaluated at the disease-free equilibrium, ${\mathcal{H}}_0$ and is given by:

$$\left(\begin{array}{ccccccc}\hfill -{\mu }_h\hfill & \hfill -{\beta }_1\hfill & \hfill -{\beta }_2\hfill & \hfill -{\beta }_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\beta }_2^h\hfill \\ \hfill 0\hfill & \hfill {\beta }_1-{\mathcal{G}}_1\hfill & \hfill 0\hfill & \hfill {\zeta }_{\text{Z}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2-{\mathcal{G}}_2\hfill & \hfill {\zeta }_{\text{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2^h\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_3-{\mathcal{G}}_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\zeta }_{\text{C}}\hfill & \hfill {\zeta }_{\text{Z}}\hfill & \hfill {\zeta }_{\text{CZ}}\hfill & \hfill -{\mu }_h\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{{\beta }_2^v{\mathcal{S}}_v^{\ast }}{{\mathcal{N}}_h^{\ast }}\hfill & \hfill -\frac{{\beta }_2^v{\mathcal{S}}_v^{\ast }}{{\mathcal{N}}_h^{\ast }}\hfill & \hfill 0\hfill & \hfill -{\mu }_v\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\beta }_2^v{\mathcal{S}}_v^{\ast }}{{\mathcal{N}}_h^{\ast }}\hfill & \hfill \frac{{\beta }_2^v{\mathcal{S}}_v^{\ast }}{{\mathcal{N}}_h^{\ast }}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\mu }_v\hfill \end{array}\right).$$ (6)

The eigenvalues are given by

$$p_1=-{\mu }_v,p_2=-{\mu }_h\left(\text{with multiplicity of 2}\right),$$ (7)

whereas, the remaining eigenvalues are the solutions of the equations given by

$$(p+{\mathcal{G}}_1(1-{\mathcal{R}}_{0\text{C}}))=0,p^2+\left({\mathcal{G}}_2+{\mu }_v-\frac{{\beta }_2{\mathcal{S}}_v^{\ast }}{{\mathcal{N}}_h^{\ast }}\right)p+{\mu }_v{\mathcal{G}}_2(1-{\mathcal{R}}_{0\text{Z}}^h-{\mathcal{R}}_{0\text{Z}}^{vh2})=0,(p+{\mathcal{G}}_3(1-{\mathcal{R}}_{0\text{CZ}}))=0$$ (8)

Applying the Routh Hurwitz criterion, the roots of equations in (8) have negative real parts if and only if ${\mathcal{R}}_{0\text{C}}<1$ and ${\mathcal{R}}_{0\text{Z}}<1$. Thus, the DFE, ${\mathcal{H}}_0$ is locally asymptotically stable if ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}<1$.

Endemic equilibrium points of the model

Suppose the reproduction number ${\mathcal{R}}_0=max\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}>1$.

Also, let the factors playing a significant role in the disease transmission for the proposed model at steady state be denoted by:

$${\lambda }_{\text{C}}^{h\ast }=\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^{h\ast }}{{\mathcal{N}}_h^{\ast }},{\lambda }_{\text{Z}}^{h\ast }=\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^{h\ast }+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^{v\ast })}{{\mathcal{N}}_h^{\ast }},{\lambda }_{\text{CZ}}^{h\ast }=\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^{h\ast }}{{\mathcal{N}}_h^{\ast }},$$$${\lambda }_{\text{Z}}^{v\ast }=\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^{h\ast }+{\mathcal{K}}_{\text{CZ}}^{h\ast })}{{\mathcal{N}}_h^{\ast }}{\mathcal{S}}_v^{\ast },$$$${\lambda }_{\text{C2}}^{\ast }={\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^{h\ast }}{{\mathcal{N}}_h^{\ast }},{\lambda }_{\text{Z2}}^{\ast }={\alpha }_1\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^{h\ast }+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^{v\ast })}{{\mathcal{N}}_h^{\ast }}$$ (9)

Then the model (1) will have multiple endemic equilibria $E^{\ast }=({\mathcal{S}}_h^{\ast },{\mathcal{K}}_{\text{C}}^{h\ast },{\mathcal{K}}_{\text{Z}}^{h\ast },{\mathcal{K}}_{\text{CZ}}^{h\ast },{\mathcal{R}}^{\ast },{\mathcal{S}}_v^{\ast },{\mathcal{K}}_{\text{Z}}^{v\ast })$, where

$${\mathcal{S}}_h^{\ast }=\frac{{\Lambda }_h}{({\lambda }_{\text{C}}^{h\ast }+{\lambda }_{\text{Z}}^{h\ast }+{\lambda }_{\text{CZ}}^{h\ast }+{\mu }_h)},$$$${\mathcal{K}}_{\text{C}}^{h\ast }=\frac{{\Lambda }_h{\lambda }_{\text{C}}^{h\ast }}{({\mathcal{G}}_1+{\lambda }_{\text{C}2}^{h\ast })({\lambda }_{\text{C}}^{h\ast }+{\lambda }_{\text{Z}}^{h\ast }+{\lambda }_{\text{CZ}}^{h\ast }+{\mu }_h)},$$$${\mathcal{K}}_{\text{Z}}^{h\ast }=\frac{{\Lambda }_h{\lambda }_{\text{Z}}^{h\ast }}{({\mathcal{G}}_2+{\lambda }_{\text{C}2}^{h\ast })({\lambda }_{\text{C}}^{h\ast }+{\lambda }_{\text{Z}}^{h\ast }+{\lambda }_{\text{CZ}}^{h\ast }+{\mu }_h)}$$$${\mathcal{K}}_{\text{CZ}}^{h\ast }=\frac{{\lambda }_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{h\ast }+{\lambda }_{\text{C}2}^{h\ast }{\mathcal{K}}_{\text{C}}^{h\ast }+{\lambda }_{\text{C}2}^{h\ast }{\mathcal{K}}_{\text{Z}}^{h\ast }}{{\mathcal{G}}_3},$$$${\mathcal{R}}^{h\ast }=\frac{{\zeta }_C{\mathcal{K}}_{\text{C}}^{h\ast }+{\zeta }_Z{\mathcal{K}}_{\text{Z}}^{h\ast }+{\zeta }_{CZ}{\mathcal{K}}_{\text{CZ}}^{h\ast }}{{\mu }_h},$$$${\mathcal{S}}_v^{\ast }=\frac{{\Lambda }_v}{({\lambda }_{\text{Z}}^{v\ast }+{\mu }_v)}{\mathcal{K}}_{\text{Z}}^{v\ast }=\frac{{\Lambda }_v{\lambda }_{\text{Z}}^{v\ast }}{{\mu }_v({\lambda }_{\text{Z}}^{v\ast }+{\mu }_v)}$$ (10)

Backward bifurcation analysis of the model to assess the impact of incident co-infection

In this section, we shall examine the impact of the assumption of allowing incident co-infection with both diseases

$({\beta }_3\ne 0)$ with the help of backward bifurcation analysis. The phenomenon of backward bifurcation, which has been observed in several disease models, is usually characterized by the co-existence of a stable disease free equilibrium and a stable endemic equilibrium when the associated reproduction number of the model is less than unity. The public health implication of the backward bifurcation phenomenon of model (1) is that, the classical epidemiological requirement of having the reproduction number ${\mathcal{R}}_0$ less than unity, although necessary, is no longer sufficient for the effective control of the diseases. The following result is obtained using the approach in [39].

To carry out the analysis, we set the disease induced death rates equal to zero because the disease-induce death rates give rise to backward bifurcation in a vector-host model (see for example, [19]). Note that, the sub-model for SARS-CoV-2 does not undergo backward bifurcation, as already shown by the authors in [36]. Furthermore, some researchers on co-infection models (without the assumption of incident co-infection by susceptible individuals) [36], [40], [41] are of the view that the dynamical behavior of the sub-models usually predict the behavior of the complete co-infection models. This motivates the analysis in this paper, under the assumption of incident co-infection with both diseases.

Setting the disease induced death rates ${\eta }_{\text{C}}={\eta }_{\text{Z}}={\eta }_{\text{CZ}}=0$, results in a constant population model, where, ${\mathcal{N}}_h=\frac{{\Lambda }_h}{{\mu }_h}$ with ${\overline{\beta }}_1=\frac{{\mu }_h{\beta }_1}{{\Lambda }_h},{\overline{\beta }}_2=\frac{{\mu }_h{\beta }_2}{{\Lambda }_h},{\overline{\beta }}_3=\frac{{\mu }_h{\beta }_3}{{\Lambda }_h},{\overline{\beta }}_2^h=\frac{{\mu }_h{\beta }_2^h}{{\Lambda }_h},{\overline{\beta }}_2^v=\frac{{\mu }_h{\beta }_2^v}{{\Lambda }_h}$. The resulting model with bilinear incidence rates is thus presented in (11). We are interested to investigate the question that if backward bifurcation occurs or not under this situation. If it does not occur, then the disease induced death will be the actual cause and the dynamics of the sub-model surely influences the complete model. However, if it occurs, we need to determine the parameter(s) which cause(s) such occurrence in addition to disease induced death rate in the co-infection model.

Theorem 4

The model (1) with negligible induced death rates ${\eta }_{\text{C}}={\eta }_{\text{Z}}={\eta }_{\text{CZ}}=0$ , exhibits backward bifurcation if the coefficient $a$ given below

$$a=2({\overline{\beta }}_1{\phi }_1-{\alpha }_1{\overline{\beta }}_2{\phi }_3-{\alpha }_1{\overline{\beta }}_2^h{\phi }_7){\phi }_2{\delta }_2+2{\overline{\beta }}_2{\phi }_1{\phi }_3{\delta }_3+2{\overline{\beta }}_2^h{\phi }_1{\phi }_7{\delta }_3-2{\alpha }_2{\overline{\beta }}_1{\phi }_2{\phi }_3{\delta }_3+2{\overline{\beta }}_2{\phi }_1{\phi }_4{\delta }_4+2{\overline{\beta }}_2^v{\phi }_3{\phi }_6{\delta }_7+2{\overline{\beta }}_2^v{\phi }_4{\phi }_6{\delta }_7+2({\alpha }_1{\overline{\beta }}_2+{\alpha }_{2}2{\overline{\beta }}_1){\phi }_2{\phi }_3{\delta }_4+2{\alpha }_1{\overline{\beta }}_2^h{\phi }_2{\phi }_7{\delta }_4$$

is positive.

Proof

Suppose

$${\mathcal{H}}_e=({\mathcal{S}}^{h\ast \ast },{\mathcal{K}}_{\text{C}}^{h\ast \ast },{\mathcal{K}}_{\text{Z}}^{h\ast \ast },{\mathcal{K}}_{\text{CZ}}^{h\ast \ast },{\mathcal{R}}^{\ast \ast },{\mathcal{S}}^{v\ast \ast },{\mathcal{K}}_{\text{Z}}^{v\ast \ast })$$

denote an arbitrary endemic equilibrium of the model. By the following change of variables,

$$\mathcal{S}=x_1,{\mathcal{K}}_{\text{C}}=x_2,{\mathcal{K}}_{\text{Z}}=x_3,{\mathcal{K}}_{\text{CZ}}=x_4,\mathcal{R}=x_5,{\mathcal{S}}_v=x_6,{\mathcal{K}}_{\text{Z}}^v=x_7,$$

the model (1) can be re-presented in the following form

$$\frac{d{x}_1}{dt}={\Lambda }_h-\left({\overline{\beta }}_1{x}_2+({\overline{\beta }}_2{x}_3+{\overline{\beta }}_2^h{x}_7)+{\overline{\beta }}_3{x}_4+{\mu }_h\right)x_1$$$$\frac{x_2}{dt}={\overline{\beta }}_1{x}_2{x}_1-\left({\zeta }_{\text{C}}+{\mu }_h\right)-{\alpha }_1({\overline{\beta }}_2{x}_3+{\overline{\beta }}_2^h{x}_7)x_2$$$$\frac{d{x}_3}{dt}=({\overline{\beta }}_2{x}_3+{\overline{\beta }}_2^h{x}_7)x_1-\left({\zeta }_{\text{Z}}+{\mu }_h\right)x_3-{\alpha }_2{\overline{\beta }}_1{x}_2{x}_3$$$$\frac{d{x}_4}{dt}={\overline{\beta }}_3{x}_4{x}_1+{\alpha }_1({\overline{\beta }}_2{x}_3+{\overline{\beta }}_2^h{x}_7)x_2+{\alpha }_2{\overline{\beta }}_1{x}_2{x}_3-\left({\zeta }_{\text{CZ}}+{\mu }_h\right)x_4$$$$\frac{d{x}_5}{dt}={\zeta }_{\text{C}}{x}_2+{\zeta }_{\text{Z}}{x}_3+{\zeta }_{\text{CZ}}{x}_4-{\mu }_h{x}_5$$$$\frac{d{x}_6}{dt}={\Lambda }_v-\left({\overline{\beta }}_2^v(x_3+x_4)+{\mu }_v\right)x_6$$$$\frac{d{x}_7}{dt}={\overline{\beta }}_2^v(x_3+x_4)x_6-{\mu }_v{x}_7$$ (11)

Consider the case when ${\mathcal{R}}_0=max\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1$. If the contact rate ${\beta }_3$ (say) is chosen as a bifurcation parameter, then solving for ${\beta }_3={\beta }_3^{\ast }$ from ${\mathcal{R}}_0=1$ we have

$${\beta }_3={\beta }_3^{\ast }={\mathcal{G}}_3$$

Similarly, for ${\mathcal{R}}_0=max\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1$, we have ${\beta }_3={\mathcal{G}}_3$. Evaluating the Jacobian of the system (11) at the DFE, $J\left({\mathcal{H}}_0\right)$, we obtain:

$$J\left({\mathcal{H}}_0\right)=\left(\begin{array}{ccccccc}\hfill -{\mu }_h\hfill & \hfill -{\beta }_1{x}_1^{\ast }\hfill & \hfill -{\beta }_2{x}_1^{\ast }\hfill & \hfill -{\beta }_3{x}_1^{\ast }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\beta }_2^h{x}_1^{\ast }\hfill \\ \hfill 0\hfill & \hfill {\beta }_1{x}_1^{\ast }-{\mathcal{G}}_1\hfill & \hfill 0\hfill & \hfill {\zeta }_{\text{Z}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2{x}_1^{\ast }-{\mathcal{G}}_2\hfill & \hfill {\zeta }_{\text{C}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2^h{x}_1^{\ast }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_3{x}_1^{\ast }-{\mathcal{G}}_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\zeta }_{\text{C}}\hfill & \hfill {\zeta }_{\text{Z}}\hfill & \hfill {\zeta }_{\text{CZ}}\hfill & \hfill -{\mu }_h\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\beta }_2^v{x}_7^{\ast }\hfill & \hfill -{\beta }_2^v{x}_7^{\ast }\hfill & \hfill 0\hfill & \hfill -{\mu }_v\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_2^v{x}_7^{\ast }\hfill & \hfill {\beta }_2^v{x}_7^{\ast }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\mu }_v\hfill \end{array}\right)$$ (12)

Using the approach in [39], the matrix $J\left({\mathcal{H}}_0\right)$ has a right eigenvector associated with the zero eigenvalue of $J\left({\mathcal{H}}_0\right)$ given by $\mathbf{\phi }={\left[{\phi }_1,{\phi }_2,{\phi }_3,\dots ,{\phi }_7\right]}^T$, where the components are:

$${\phi }_1=-\frac{1}{\mu }\left[{\beta }_1{x}_1^{\ast }{\phi }_2-{\beta }_2{x}_1^{\ast }{\phi }_3+{\beta }_2^h{x}_1^{\ast }{\phi }_7+{\beta }_3{x}_1^{\ast }{\phi }_4\right]<0,$$

$${\phi }_2=\frac{{\beta }_1{x}_1^{\ast }}{{\mathcal{G}}_1}>0,{\phi }_3={\phi }_3>0,{\phi }_4=\frac{{\beta }_3{x}_1^{\ast }}{{\mathcal{G}}_3}>0,$$

$${\phi }_5=\frac{1}{\mu }({\zeta }_{\text{C}}{\phi }_2+{\zeta }_{\text{Z}}{\phi }_3+{\zeta }_{\text{CZ}}{\phi }_4)>0,$$

$${\phi }_6=-\frac{1}{{\mu }_v}\left({\beta }_2^v{x}_6^{\ast }({\phi }_3+{\phi }_4)\right)=-{\phi }_7<0,{\phi }_7=\frac{1}{{\mu }_v}\left({\beta }_2^v{x}_6^{\ast }({\phi }_3+{\phi }_4)\right)$$

The non-zero components of the left eigenvector of $J\left({\mathcal{H}}_0\right){|}_{{\beta }_3={\beta }_3}^{\ast }$, $\mathbf{\delta }=[{\delta }_1,{\delta }_2,\dots ,{\delta }_7]$ satisfying $\mathbf{\phi .\delta }=1$ are

$${\delta }_2=\frac{{\beta }_1{x}_1^{\ast }}{{\mathcal{G}}_1}>0,{\delta }_3={\delta }_3>0,{\delta }_4=\frac{{\beta }_3{x}_1^{\ast }}{{\mathcal{G}}_3}>0,{\delta }_7=\frac{{\beta }_2^h{x}_1^{\ast }{\delta }_3}{{\mu }_v}$$

Using Theorem 4.1 in [39] and computing the non-zero partial derivatives of $f\left(x\right)$ at the disease free equilibrium, (${\mathcal{H}}_0$)), the associated bifurcation coefficients are defined below

$$a=\sum _{k,i,j=1}^7{\delta }_k{\phi }_i{\phi }_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}(0,0)\text{and}b=\sum _{k,i=1}^7{\delta }_k{\phi }_i\frac{{\partial }^2{f}_k}{\partial x_i\partial {\beta }_3^{h\ast }}(0,0),$$

where,

$$a=2({\overline{\beta }}_1{\phi }_1-{\alpha }_1{\overline{\beta }}_2{\phi }_3-{\alpha }_1{\overline{\beta }}_2^h{\phi }_7){\phi }_2{\delta }_2+2{\overline{\beta }}_2{\phi }_1{\phi }_3{\delta }_3+2{\overline{\beta }}_2^h{\phi }_1{\phi }_7{\delta }_3-2{\alpha }_2{\overline{\beta }}_1{\phi }_2{\phi }_3{\delta }_3+2{\overline{\beta }}_2{\phi }_1{\phi }_4{\delta }_4+2{\overline{\beta }}_2^v{\phi }_3{\phi }_6{\delta }_7+2{\overline{\beta }}_2^v{\phi }_4{\phi }_6{\delta }_7+2({\alpha }_1{\overline{\beta }}_2+{\alpha }_{2}2{\overline{\beta }}_1){\phi }_2{\phi }_3{\delta }_4+2{\alpha }_1{\overline{\beta }}_2^h{\phi }_2{\phi }_7{\delta }_4$$ (13)

$$b=\sum _{k,i=1}^7{\delta }_k{\phi }_i\frac{{\partial }^2{f}_k}{\partial x_i\partial {\beta }^{\ast }}(0,0)={\phi }_4{\delta }_4{x}_1^{\ast }>0$$ (14)

It clearly shows that even under the assumption that the disease induced death rates are zero, the bifurcation coefficients $a$ and $b$ are positive which indicates the occurrence of backward bifurcation. However, if we set the parameters associated with the susceptibility to infection with a second disease by individuals infected with single infection ${\alpha }_1={\alpha }_2=0$, then the co-efficient satisfies

$$a=2({\overline{\beta }}_1{\phi }_2{\delta }_2+{\overline{\beta }}_2{\phi }_3{\delta }_3+{\overline{\beta }}_2^h{\phi }_7{\delta }_3+{\overline{\beta }}_2{\phi }_4{\delta }_4){\phi }_1+2{\overline{\beta }}_2^v({\phi }_3+{\phi }_4){\phi }_6{\delta }_7<0(\text{since}{\phi }_1<0,{\phi }_6<0),$$

which rules out the possibility of backward bifurcation in the co-infection model. Thus, it is concluded that, human disease-induced death rates and terms associated with susceptibility to additional infection by singly infected individuals can induce backward bifurcation in the co-infection model for two diseases. Therefore, it is observed that, in addition to disease induced death rates (which induced bifurcation in the sub-model), parameters associated with infection with a second disease cause backward bifurcation in the complete model. Hence, by allowing incident co-infection with both diseases, the dynamics of the sub-model does not always drive or influence the dynamics of the complete co-infection model.

Global asymptotic stability of the disease-free equilibrium of the model (1) for a special case

Theorem 5

In the absence of infection with a second disease by singly infected individuals (that is, ${\alpha }_1={\alpha }_2=0$ ), the DFE of the model (1) given by ${\mathcal{Q}}_0$ , is GAS in $\mathcal{Q}$ provided that ${\mathcal{R}}_0\le 1$ .

Proof

See Appendix B “Proof of Theorem 5”

The epidemiological implication of Theorem 5 is; if those already infected with a single disease do not get infected with a second disease, then both SARS-CoV-2 and Zika can be eliminated from the population provided that the threshold quantity, ${\mathcal{R}}_0<1$, regardless of the initial sizes of the sub-populations.

Global asymptotic stability of endemic equilibrium of the model (1) for a special case

Theorem 6

In the absence of infection with a second disease by singly infected individuals (that is, ${\alpha }_1={\alpha }_2=0$ ), the endemic equilibrium ${\mathcal{Q}}_e$ , of the model (1) with ${\eta }_{\text{C}}={\eta }_{\text{Z}}={\eta }_{\text{CZ}}=0$ is globally asymptotically stable (GAS) in $\mathcal{Q}⧵{\mathcal{Q}}_0$ with ${\mathcal{Q}}_0={\mathcal{Q}}_0^h\times {\mathcal{Q}}_0^v$ whenever ${\mathcal{R}}_0<1$ , where

$${\mathcal{Q}}_0^h=.\left\{({\mathcal{S}}_h,{\mathcal{K}}_{\text{C}}^h,{\mathcal{K}}_{\text{Z}}^h,{\mathcal{K}}_{\text{CZ}}^h,\mathcal{R})\in {\mathcal{Q}}^h:{\mathcal{K}}_{\text{C}}^h={\mathcal{K}}_{\text{Z}}^h={\mathcal{K}}_{\text{CZ}}=0.\right\}$$

$${\mathcal{Q}}_0^v=.\left\{({\mathcal{S}}_v,{\mathcal{K}}_{\text{Z}}^v)\in {\mathcal{Q}}^v:{\mathcal{K}}_{\text{Z}}^v=0.\right\}$$

Proof

See Appendix C “Proof of Theorem 6”

The epidemiological significance of Theorem 6 is; if those already infected with a single infection do not get infected with a second disease, and if diseases induced death is negligible, then both SARS-CoV-2 and HBV will persist in the population provided that the threshold quantity, ${\overline{\mathcal{R}}}_0>1$.

Optimal control analysis

It was observed in the preceding sections that the occurrence of backward bifurcation in the model (1) makes the effective control of both diseases difficult in the population. The aim of this section is to incorporate the time dependent controls into the model (1) to obtain the optimal interventions for the elimination of the co-infections. They are defined as follows: ${\theta }_1\left(t\right)$: SARS-CoV-2 prevention control, ${\theta }_2\left(t\right)$: Zika prevention control, ${\theta }_3\left(t\right)$: Control against incident co-infection, and ${\theta }_4\left(t\right)$: Control against infection with a second disease, and the optimal control model is given by:

$$\frac{d{\mathcal{S}}_h}{dt}={\Lambda }_h-\left((1-{\theta }_1)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}+(1-{\theta }_2)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}\right)$$$$\left(+(1-{\theta }_3)\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}+{\mu }_h\right){\mathcal{S}}_h$$$$\frac{d{\mathcal{K}}_{\text{C}}^h}{dt}=(1-{\theta }_1)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h$$$$-{\alpha }_1(1-{\theta }_4)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{C}}^h$$$$\frac{d{\mathcal{K}}_{\text{Z}}^h}{dt}=(1-{\theta }_2)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h$$$$-{\alpha }_2(1-{\theta }_4)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h$$$$\frac{d{\mathcal{K}}_{\text{CZ}}^h}{dt}=(1-{\theta }_3)\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h+{\alpha }_1(1-{\theta }_4)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{C}}^h$$$$+{\alpha }_2(1-{\theta }_4)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h$$$$\frac{d\mathcal{R}}{dt}={\zeta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h-{\mu }_h\mathcal{R}$$$$\frac{d{\mathcal{S}}_v}{dt}={\Lambda }_v-(1-{\theta }_2)\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}+{\mu }_v\right){\mathcal{S}}_v$$$$\frac{d{\mathcal{K}}_{\text{Z}}^v}{dt}=(1-{\theta }_2)\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v$$ (15)

subject to the initial conditions

$${\mathcal{S}}_{h0}={\mathcal{S}}_h\left(0\right),{\mathcal{K}}_{\text{C}0}^h={\mathcal{K}}_{\text{C}}^h\left(0\right),{\mathcal{K}}_{\text{Z}0}={\mathcal{K}}_{\text{Z}}\left(0\right),{\mathcal{K}}_{\text{CZ}0}^h={\mathcal{K}}_{\text{CZ}}^h\left(0\right),$$

$${\mathcal{R}}_0=\mathcal{R}\left(0\right),{\mathcal{S}}_{\text{V}0}={\mathcal{S}}_v\left(0\right),{\mathcal{K}}_{\text{Z}0}^v={\mathcal{K}}_{\text{Z}}^v\left(0\right).$$

Let us consider the following objective function

$$J\left[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4\right]={\int }_0^T[{\mathcal{K}}_{\text{C}}^h\left(t\right)+{\mathcal{K}}_{\text{Z}}^h\left(t\right)+{\mathcal{K}}_{\text{CZ}}^h\left(t\right)+{\mathcal{S}}_{\text{V}}\left(t\right)+{\mathcal{K}}_{\text{Z}}^v\left(t\right)+\frac{{\omega }_1}{2}{\theta }_1^2+\frac{{\omega }_2}{2}{\theta }_2^2+\frac{{\omega }_3}{2}{\theta }_3^2+\frac{{\omega }_4}{2}{\theta }_4^2]dt,$$ (16)

where $T$ is the final time. The total cost includes the cost of SARS-CoV-2 and arboviruses preventive measures. We need to find an optimal control ${\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast }$ such that

$$J({\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast })=min\left\{J({\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast })\right|{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4\in U\},$$ (17)

where $U=\left\{({\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast })\right\}$ is the control set such that ${\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast }$ are measurable with $0\le {\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast }\le 1$ for $t\in [0,T]$. The Hamiltonian is given by:

$$\mathcal{X}={\mathcal{K}}_{\text{C}}^h\left(t\right)+{\mathcal{K}}_{\text{Z}}^h\left(t\right)+{\mathcal{K}}_{\text{CZ}}^h\left(t\right)+{\mathcal{S}}_{\text{V}}\left(t\right)+{\mathcal{K}}_{\text{Z}}^v\left(t\right)+\frac{{\xi }_1}{2}{\theta }_1^2+\frac{{\xi }_2}{2}{\theta }_2^2+\frac{{\xi }_3}{2}{\theta }_3^2+\frac{{\xi }_4}{2}{\theta }_4^2+{\varrho }_1({\Lambda }_h-\left((1-{\theta }_1)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}+(1-{\theta }_2)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}\right)\left(+(1-{\theta }_3)\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}+{\mu }_h\right){\mathcal{S}}_h)+{\varrho }_2((1-{\theta }_1)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h-{\alpha }_1(1-{\theta }_4)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{C}}^h)+{\varrho }_3((1-{\theta }_2)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h$$ (18)

$$-{\alpha }_2(1-{\theta }_4)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h)+{\varrho }_4((1-{\theta }_3)\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h+{\alpha }_1(1-{\theta }_4)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{C}}^h+{\alpha }_2(1-{\theta }_4)\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h)+{\varrho }_5\left({\zeta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h-{\mu }_h\mathcal{R}\right)+{\varrho }_6\left({\Lambda }_v-(1-{\theta }_2)\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}+{\mu }_v\right){\mathcal{S}}_v\right)+{\varrho }_7\left((1-{\theta }_2)\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v\right)$$

Existence

We now establish the existence of solution for the optimal control that minimizes the objective functional $J$.

Theorem 7

Suppose$J$is defined on the control set$U$subject to system(15)with non-negative initial conditions at$t=0$, then there exists an optimal control$u^{\ast }=({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)$such that$J\left(u^{\ast }\right)=min\left\{J({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)|{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4\in U\right\}$, if the following conditions given in [42] hold:

• (i.) The admissible control set U is convex and closed.
• (ii.) The state system is bounded by a linear function in the state and control variables.
• (iii.) The integrand of the objective functional in (16) is convex with respect to the controls.
• (iv.) The Lagrangian is bounded below by ${\varpi }_1{\left|\theta \right|}^{{\varpi }_3}-{\varpi }_2$ , where, ${\varpi }_1>0,{\varpi }_2>0,{\varpi }_3>1$ .

Proof

Let $U={[0,1]}^4$ be the control set consisting of $\theta =({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)\in U$, $x=(\mathcal{S},{\mathcal{K}}_{\text{C}}^h,{\mathcal{K}}_{\text{Z}}^h,{\mathcal{K}}_{\text{CZ}}^h,\mathcal{R},{\mathcal{S}}_v,{\mathcal{K}}_{\text{Z}}^v)$ and $f(t,x,\theta )$ the right hand of (15), that is (Eq. (19) is given in Box I),

To prove Theorem 7, we proceed as follows:

• (i.)
  It is obvious to note that the $U={[0,{\theta }_{max}]}^4$ is closed. In addition, consider any two arbitrary elements $v,w\in U$, where $v=(v_1,v_2,v_3,v_4),w=(w_1,w_2,w_3,w_4)$. Then,

  $$\lambda v+(1-\lambda )w\in {[0,{\theta }_{max}]}^4,\forall \lambda \in [0,{\theta }_{max}].$$

  That is, $\lambda v+(1-\lambda )w\in U$, and hence $U$ is a convex set.
• (ii.)
  The control system (15) can be expressed as a linear function of control variables $({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)$ with the coefficients as functions of time and state variables:

  $$f(t,x,\theta )=\vartheta (t,x)+\varphi (t,x)\theta$$

  with ($\varphi (t,x)$ is given in Box II)

  $$\vartheta (t,x)=\left(\begin{array}{c}\hfill {\Lambda }_h-\left(\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}+\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}+\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}+{\mu }_h\right){\mathcal{S}}_h\hfill \\ \hfill \frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h-{\alpha }_1\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill \frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h-{\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill \frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h+{\alpha }_1\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h+{\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h\hfill \\ \hfill {\zeta }_{\text{C}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h-{\mu }_h{\mathcal{K}}_{\text{Z}}^v\hfill \\ \hfill {\Lambda }_v-\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}+{\mu }_v\right){\mathcal{S}}_v\hfill \\ \hfill \frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v\hfill \end{array}\right),$$

  As the parameters and variables of the model are positive, we have

  $$\Vert f(t,x,\theta )\Vert \le \Vert \vartheta (t,x)\Vert +\Vert \varphi (t,x)\Vert \Vert \theta \Vert \le a+b\Vert \theta \Vert ,wherea>0,b>0.$$
• (iii.)
  The optimal control problem’s Lagrangian is given by

  $$\mathcal{L}={\mathcal{K}}_{\text{C}}^h\left(t\right)+{\mathcal{K}}_{\text{Z}}^h\left(t\right)+{\mathcal{K}}_{\text{CZ}}^h\left(t\right)+{\mathcal{S}}_{\text{V}}\left(t\right)+{\mathcal{K}}_{\text{Z}}^v\left(t\right)+\frac{1}{2}\sum _{i=1}^4{\xi }_i{\theta }_i^2.$$ (20)

  Let us consider two arbitrary elements $v,w\in U$, with $v=(v_1,v_2,v_3,v_4),w=(w_1,w_2,w_3,w_4)$. and $\lambda \in [0,{\theta }_{max}]$. We now show that,

  $$\mathcal{L}[t,x,(1-\lambda )v+\lambda w]\le (1-\lambda )\mathcal{L}(t,x,v)+\lambda \mathcal{L}(t,x,w).$$

  it follows from (20) that,

  $$\mathcal{L}[t,x,(1-\lambda )v+\lambda w]={\mathcal{K}}_{\text{C}}^h\left(t\right)+{\mathcal{K}}_{\text{Z}}^h\left(t\right)+{\mathcal{K}}_{\text{CZ}}^h\left(t\right)+{\mathcal{S}}_{\text{V}}\left(t\right)+{\mathcal{K}}_{\text{Z}}^v\left(t\right)+\frac{1}{2}\sum _{i=1}^4{\xi }_i{[(1-\lambda ){\theta }_i+\lambda w_i]}^2,(1-\lambda )\mathcal{L}(t,x,v)+\lambda \mathcal{L}(t,x,w)={\mathcal{K}}_{\text{C}}^h\left(t\right)+{\mathcal{K}}_{\text{Z}}^h\left(t\right)+{\mathcal{K}}_{\text{CZ}}^h\left(t\right)+{\mathcal{S}}_{\text{V}}\left(t\right)+{\mathcal{K}}_{\text{Z}}^v\left(t\right)+\frac{1}{2}(1-\lambda )\sum _{i=1}^4{\xi }_i{v}_i^2+\frac{1}{2}\lambda \sum _{i=1}^4{\xi }_i{w}_i^2.$$ (21)

  Taking the difference of the two equations given above, we have

  $$\mathcal{L}[t,x,(1-\lambda )v+\lambda w]-[(1-\lambda )\mathcal{L}(t,x,v)+\lambda \mathcal{L}(t,x,w)]=\frac{1}{2}({\lambda }^2-\lambda )\sum _{i=1}^4{\xi }_i{(v_i-w_i)}^2\le 0,since\lambda \in [0,{\theta }_{max}].$$ (22)

  Thus,

  $$\mathcal{L}[t,x,(1-\lambda )v+\lambda w]\le [(1-\lambda )\mathcal{L}(t,x,v)+\lambda \mathcal{L}(t,x,w)],$$

  gives

  $$\mathcal{L}[t,x,(1-\lambda )v+\lambda w]-[(1-\lambda )\mathcal{L}(t,x,v)+\lambda \mathcal{L}(t,x,w)]\le 0,$$

  and hence convexity of $\mathcal{L}$.
• (iv.)
  There exists constants ${\varpi }_1,{\varpi }_2$ and ${\varpi }_3$ such that, $\mathcal{L}\ge {\varpi }_1{\left|\theta \right|}^{{\varpi }_3}-{\varpi }_2$, ${\varpi }_1>0$, ${\varpi }_2>0$, ${\varpi }_3>1$ We now establish the bound on $\mathcal{L}$. Note that ${\varsigma }_4{\theta }_4^2\le {\varsigma }_4$. As ${\theta }_4\in [0,1]$, $\frac{1}{2}{\varsigma }_4{\theta }_4^2\le \frac{1}{2}{\varsigma }_4$. Now,

  $$\mathcal{L}>\frac{{\xi }_1}{2}{\theta }_1^2+\frac{{\xi }_2}{2}{\theta }_2^2+\frac{{\xi }_3}{2}{\theta }_3^2+\frac{{\xi }_4}{2}{\theta }_4^2\ge \frac{{\xi }_1}{2}{\theta }_1^2+\frac{{\xi }_2}{2}{\theta }_2^2+\frac{{\xi }_3}{2}{\theta }_3^2+\frac{{\xi }_4}{2}{\theta }_4^2-\frac{{\xi }_4}{2}\ge min\left(\frac{{\xi }_1}{2},\frac{{\xi }_2}{2},\frac{{\xi }_3}{2},\frac{{\xi }_4}{2}\right)\left({\theta }_1^2+{\theta }_2^2+{\theta }_3^2+{\theta }_4^2\right)-\frac{{\xi }_4}{2}\ge min\left(\frac{{\xi }_1}{2},\frac{{\xi }_2}{2},\frac{{\xi }_3}{2},\frac{{\xi }_4}{2}\right){|{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4|}^2-\frac{{\xi }_4}{2}$$

  Hence,

  $$\mathcal{L}\ge {\varpi }_1{\left|\theta \right|}^{{\varpi }_3}-{\varpi }_2,\text{where},{\varpi }_1=min\left(\frac{{\xi }_1}{2},\frac{{\xi }_2}{2},\frac{{\xi }_3}{2},\frac{{\xi }_4}{2}\right)>0,$$

  $${\varpi }_2=\frac{{\xi }_4}{2}>0\text{and}{\varpi }_3=2>1.\square$$

Box I.

$$f(t,x,\theta )=\left(\begin{array}{c}\hfill {\Lambda }_h-\left((1-{\theta }_1)\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}+(1-{\theta }_2)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}+(1-{\theta }_3)\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}+{\mu }_h\right){\mathcal{S}}_h\hfill \\ \hfill (1-{\theta }_1)\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h-{\alpha }_1(1-{\theta }_4)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill (1-{\theta }_2)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h-{\alpha }_2(1-{\theta }_4)\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill (1-{\theta }_3)\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h+{\alpha }_1(1-{\theta }_4)\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h+{\alpha }_2(1-{\theta }_4)\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h\hfill \\ \hfill {\zeta }_{\text{C}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h-{\mu }_h{\mathcal{K}}_{\text{Z}}^v\hfill \\ \hfill {\Lambda }_v-(1-{\theta }_2)\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}+{\mu }_v\right){\mathcal{S}}_v\hfill \\ \hfill (1-{\theta }_2)\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v\hfill \end{array}\right)$$ (19)

Box II.

$$\varphi (t,x)=\left(\begin{array}{cccc}\hfill \frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h\hfill & \hfill \frac{{\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v}{{\mathcal{N}}_h}{\mathcal{S}}_h\hfill & \hfill \frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}}{{\mathcal{N}}^h}{\mathcal{S}}_h\hfill & \hfill 0\hfill \\ \hfill -\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_1\frac{{\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill 0\hfill & \hfill -\frac{{\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v}{{\mathcal{N}}_h}{\mathcal{S}}_h\hfill & \hfill 0\hfill & \hfill {\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}}{{\mathcal{N}}^h}{\mathcal{S}}_h\hfill & \hfill -{\alpha }_1\frac{{\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h-{\alpha }_2\frac{{\beta }_1{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{N}}_h}{\mathcal{K}}_{\text{Z}}^h\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$

Theorem 8

Suppose the set $\theta =\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4\}$ minimizes $J$ over $U$ , then adjoint variables ${\varrho }_1,{\varrho }_2,\dots ,{\varrho }_7$ , satisfy the adjoint equations

$$-\frac{\partial {\varrho }_i}{\partial t}=\frac{\partial \mathcal{X}}{\partial i},$$

with (where the adjoint functions given in the Appendix D “Adjoint functions”)

$${\varrho }_i\left(t_f\right)=0,\text{where},i=\mathcal{S},{\mathcal{K}}_{\text{C}}^h,{\mathcal{K}}_{\text{Z}}^h,{\mathcal{K}}_{\text{CZ}}^h,\mathcal{R},{\mathcal{S}}_v,{\mathcal{K}}_{\text{Z}}^v.$$ (23)

Furthermore,

$${\theta }_1^{\ast }=min\left\{1,max\left(0,\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h({\varrho }_2-{\varrho }_1)}{{\xi }_1{\mathcal{N}}_h}\right)\right\},$$$${\theta }_2^{\ast }=min\left\{1,max\right)\left(\times \left(0,\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h({\varrho }_3-{\varrho }_1)+{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v({\varrho }_7-{\varrho }_6)}{{\xi }_2{\mathcal{N}}_h}\right)\right\},$$$${\theta }_3^{\ast }=min\left\{1,max\left(0,\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h({\varrho }_4-{\varrho }_1)}{{\xi }_3{\mathcal{N}}_h}\right)\right\},$$$${\theta }_4^{\ast }=min\left\{1,max\right)\left(\times \left(0,\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\alpha }_1{\mathcal{K}}_{\text{C}}^h({\varrho }_4-{\varrho }_2)+{\beta }_1{\mathcal{K}}_{\text{C}}^h{\alpha }_2{\mathcal{K}}_{\text{Z}}^h({\varrho }_4-{\varrho }_2)}{{\xi }_4{\mathcal{N}}_h}\right)\right\},$$ (24)

Proof of Theorem 8

Considering $U^{\ast }=({\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast })$ and the associated solutions ${\mathcal{S}}_h^{\ast },{\mathcal{K}}_{\text{C}}^{h\ast },{\mathcal{K}}_{\text{Z}}^{h\ast },{\mathcal{K}}_{\text{CZ}}^{h\ast },{\mathcal{R}}^{\ast },{\mathcal{S}}_v^{\ast },{\mathcal{K}}_{\text{Z}}^{v\ast }$, Pontryagin’s Maximum Principle [43] is applied to obtain the following:

$$-\frac{d{\varrho }_1}{dt}=\frac{\partial \mathcal{X}}{\partial {\mathcal{S}}_h},{\varrho }_1\left(t_f\right)=0,-\frac{d{\varrho }_2}{dt}=\frac{\partial \mathcal{X}}{\partial {\mathcal{K}}_{\text{C}}^h},{\varrho }_2\left(t_f\right)=0,-\frac{d{\varrho }_3}{dt}=\frac{\partial \mathcal{X}}{\partial {\mathcal{K}}_{\text{Z}}^h},{\varrho }_3\left(t_f\right)=0,-\frac{d{\varrho }_4}{dt}=\frac{\partial \mathcal{X}}{\partial {\mathcal{K}}_{\text{CZ}}^h},{\varrho }_4\left(t_f\right)=0,-\frac{d{\varrho }_5}{dt}=\frac{\partial \mathcal{X}}{\partial \mathcal{R}},{\varrho }_5\left(t_f\right)=0,-\frac{d{\varrho }_6}{dt}=\frac{\partial \mathcal{X}}{\partial {\mathcal{S}}_v},{\varrho }_6\left(t_f\right)=0,-\frac{d{\varrho }_7}{dt}=\frac{\partial \mathcal{X}}{\partial {\mathcal{K}}_{\text{Z}}^v},{\varrho }_7\left(t_f\right)=0.$$ (25)

On the interior of the set, where $0<{\theta }_j<1$   $\forall$ ($j=1,\dots ,4$), we have

$$0=\frac{\partial \mathcal{X}}{\partial {\theta }_1}={\xi }_1\mathcal{N}{\theta }_1^{\ast }-{\beta }_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h({\varrho }_2-{\varrho }_1),$$$$0=\frac{\partial \mathcal{X}}{\partial {\theta }_2}={\xi }_2\mathcal{N}{\theta }_2^{\ast }-[({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h({\varrho }_3-{\varrho }_1)+{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v({\varrho }_7-{\varrho }_6)],$$$$0=\frac{\partial \mathcal{X}}{\partial {\theta }_3}={\xi }_3\mathcal{N}{\theta }_3^{\ast }-{\beta }_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h({\varrho }_4-{\varrho }_1),$$$$0=\frac{\partial \mathcal{X}}{\partial {\theta }_4}={\xi }_4\mathcal{N}{\theta }_4^{\ast }-\left[({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\alpha }_1{\mathcal{K}}_{\text{C}}^h({\varrho }_4-{\varrho }_2)+{\beta }_1{\mathcal{K}}_{\text{C}}^h{\alpha }_2{\mathcal{K}}_{\text{Z}}^h({\varrho }_4-{\varrho }_2)\right].$$ (26)

Therefore,

$${\theta }_1^{\ast }=\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h({\varrho }_2-{\varrho }_1)}{{\xi }_1{\mathcal{N}}_h},$$$${\theta }_2^{\ast }=\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h({\varrho }_3-{\varrho }_1)+{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v({\varrho }_7-{\varrho }_6)}{{\xi }_2{\mathcal{N}}_h},$$$${\theta }_3^{\ast }=\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h({\varrho }_4-{\varrho }_1)}{{\xi }_3{\mathcal{N}}_h},$$$${\theta }_4^{\ast }=\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\alpha }_1{\mathcal{K}}_{\text{C}}^h({\varrho }_4-{\varrho }_2)+{\beta }_1{\mathcal{K}}_{\text{C}}^h{\alpha }_2{\mathcal{K}}_{\text{Z}}^h({\varrho }_4-{\varrho }_2)}{{\xi }_4{\mathcal{N}}_h}.$$ (27)

$${\theta }_1^{\ast }=min\left\{1,max\left(0,\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h({\varrho }_2-{\varrho }_1)}{{\xi }_1{\mathcal{N}}_h}\right)\right\},$$

$${\theta }_2^{\ast }=min\left\{1,max\right)\times \left(\left(0,\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h({\varrho }_3-{\varrho }_1)+{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v({\varrho }_7-{\varrho }_6)}{{\xi }_2{\mathcal{N}}_h}\right)\right\},$$

$${\theta }_3^{\ast }=min\left\{1,max\left(0,\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h({\varrho }_4-{\varrho }_1)}{{\xi }_3{\mathcal{N}}_h}\right)\right\},$$

$${\theta }_4^{\ast }=min\left\{1,max\right)\left(\times \left(0,\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v){\alpha }_1{\mathcal{K}}_{\text{C}}^h({\varrho }_4-{\varrho }_2)+{\beta }_1{\mathcal{K}}_{\text{C}}^h{\alpha }_2{\mathcal{K}}_{\text{Z}}^h({\varrho }_4-{\varrho }_2)}{{\xi }_4{\mathcal{N}}_h}\right)\right\},$$ (28)

Numerical simulations

In this section, simulations of the control system (15) are carried out. This is done with MATLAB using the forward backward sweep by Runge Kutta method. The quadratic cost functions $\frac{1}{2}{\omega }_1{\theta }_1^2,\frac{1}{2}{\omega }_2{\theta }_2^2,\frac{1}{2}{\omega }_3{\theta }_3^2$ and $\frac{1}{2}{\omega }_4{\theta }_4^2$ are used. The weight constants are assumed as: ${\omega }_1=25,{\omega }_2=20,{\omega }_3=35$ and ${\omega }_4=45$.

In the subsequent sections, we investigate the impact of various control strategies on the co-dynamics of both diseases and their co-infection. For the demographic parameters, ${\Lambda }_h$ and ${\mu }_h$, we obtained their values based on the total population and life expectancy of Espirito Santo state, Brazil (a country with co-endemicity of both SARS-CoV-2 and zika virus), which are approximately given by 4,108,508 and 74.9 respectively [23], [25]. The initial conditions used for the simulations are set as follows: ${\mathcal{S}}_h\left(0\right)=3,600,000;{\mathcal{I}}_{\text{C}}^h\left(0\right)=800;{\mathcal{I}}_{\text{Z}}^h\left(0\right)=24;{\mathcal{I}}_{\text{CZ}}^h\left(0\right)=100;\mathcal{R}\left(0\right)=100;{\mathcal{S}}_v\left(0\right)=4000;{\mathcal{I}}_{\text{Z}}^v\left(0\right)=600$.

Strategy A: Impact of SARS-CoV-2 prevention control (${\theta }_1\ne 0$)

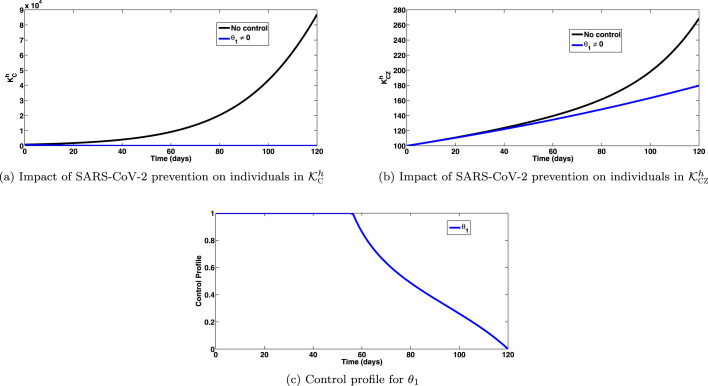
The simulations of the optimal control system (15) when the strategy that prevents SARS-CoV-2 (${\theta }_1\ne 0$) is implemented, are depicted in Fig. 1, Fig. 1, respectively. On implementation of this intervention strategy, for ${\beta }_1=0.2441,{\beta }_2=0.02441,{\beta }_2^h=0.200,{\beta }_3=0.18,{\beta }_2^v=0.501$, so that ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1.1938>1$, we observe a significant decrease in the total number of individuals infected with SARS-CoV-2, as expected (shown in Fig. 1(a)). Interestingly, this strategy has significant impact on co-infected cases. It is observed that, significant co-infected cases of SARS-CoV-2 and Zika are averted by this control strategy (as depicted in Fig. 1(b)). The control profile for this intervention strategy is depicted in Fig. 1(c), showing very high impact against incident infections either with SARS-CoV-2 or co-infections.

Fig. 1.

Impact of SARS-CoV-2 prevention (${\theta }_1$) on individuals in ${\mathcal{K}}_{\text{C}}^h$ and ${\mathcal{K}}_{\text{CZ}}^h$ epidemiological classes. Here, ${\beta }_1=0.2441,{\beta }_2=0.02441,{\beta }_2^h=0.200,{\beta }_3=0.18,{\beta }_2^v=0.501$, so that ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1.1938>1$.

Strategy B: Impact of Zika prevention controls (${\theta }_2\ne 0$)

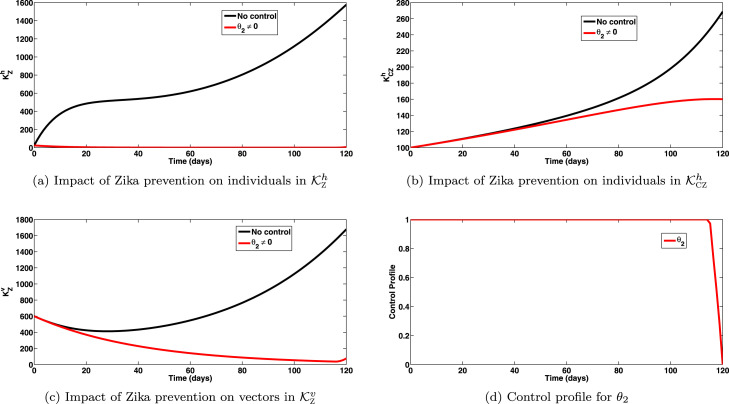
The simulations of the optimal control system (15) when the strategy that prevents Zika transmission (from both human and vectors) (${\theta }_2\ne 0$) is implemented, are depicted in Figs. 2(a), 2(b), 2(c), respectively. Implementation of this intervention strategy, for ${\beta }_1=0.2441,{\beta }_2=0.02441,{\beta }_2^h=0.200,{\beta }_3=0.18,{\beta }_2^v=0.501$, so that ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1.1938>1$ shows a significant decrease in the total number of individuals infected with Zika virus, as expected (shown in Fig. 2(a)). Also, this strategy has high positive population level impact on co-infected cases, as observed in Fig. 2(b). It is interesting to note that zika prevention strategy averts more co-infection cases than the SARS-prevention strategy. Equally, this strategy caused great reduction in infected vector populations as observed in Fig. 2(c). The control profiles for this strategy are depicted by Fig. 2(d). It is observed that the control has very high effect against Zika transmission.

Fig. 2.

Impact of Zika prevention (${\theta }_2$) on individuals in ${\mathcal{K}}_{\text{Z}}^h$ and ${\mathcal{K}}_{\text{CZ}}^h$, and vectors in ${\mathcal{K}}_{\text{Z}}^v$ epidemiological class. Here, ${\beta }_1=0.2441,{\beta }_2=0.02441,{\beta }_2^h=0.200,{\beta }_3=0.18,{\beta }_2^v=0.501$, so that ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1.1938>1$.

Strategy C: Impact of control against co-infections with both diseases (${\theta }_3\ne 0,{\theta }_4\ne 0$)

The simulations of system (15) when the strategy that prevents incident co-infection with SARS-CoV-2 and Zika virus (${\theta }_3\ne 0$) is implemented, are depicted in Fig. 3, Fig. 3. Implementation of this intervention strategy, for ${\beta }_1=0.2441,{\beta }_2=0.02441,{\beta }_2^h=0.200,{\beta }_3=0.18,{\beta }_2^v=0.501$, so that ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1.1938>1$ indicates a significant decrease in the total number of individuals co-infected with SARS-CoV-2 and Zika virus as depicted by Fig. 3(a). Thus, to avert co-infection cases in the population, it is not enough to prevent new single cases. Efforts must also be made to prevent individuals from getting infected with concurrent infections. This control strategy also caused a great reduction of infected vector population, as shown in Fig. 3(b). Also, the simulation of the system (15) when the strategy that prevents infection with a second disease by those already infected, is depicted by Fig. 3(c). It is observed that a good number of co-infected cases is averted when this strategy is strictly put in place. The control profiles for prevention of incident co-infections and prevention of an additional infection by singly infected individuals, are presented in Fig. 3, Fig. 3. It is observed that, the control strategy against incident co-infections attains its peak value nearly after 50 days into the simulation period and throughout maintains this value. Moreover, the control against infection with a second disease, was at its peak throughout the simulation period.

Fig. 3.

Impact of control against incident co-infections ${\theta }_3$ and ${\theta }_4$ on individuals in ${\mathcal{K}}_{\text{CZ}}^h$ and ${\mathcal{K}}_{\text{CZ}}^h$, and vectors in ${\mathcal{K}}_{\text{Z}}^v$ epidemiological class. Here, ${\beta }_1=0.2441,{\beta }_2=0.02441,{\beta }_2^h=0.200,{\beta }_3=0.18,{\beta }_2^v=0.501$, so that ${\mathcal{R}}_0=\text{max}\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}=1.1938>1$.

Conclusion

In this paper, a new mathematical model for SARS-CoV-2 and Zika co-dynamics was presented, incorporating incident co-infection by susceptible individuals which is not common in the existing models. We discussed the impact of this assumption on the dynamics of a co-infection model. The model also incorporated sexual transmission of Zika. The positivity and boundedness of solution of the developed model was investigated, in addition to local asymptotic stability analysis. The model was shown to exhibit backward bifurcation, caused by disease induced death rates and parameters associated with susceptibility to a second infection by those already infected. Employing the Lyapunov functions, the disease free and endemic equilibria were shown to be globally asymptotically stable for ${\mathcal{R}}_0<1$ and ${\mathcal{R}}_0>1$, respectively. To manage the co-circulation of both infections in an effective manner, under an endemic setting, time dependent controls in the form of SARS-CoV-2, Zika and co-infection prevention strategies were incorporated into the model. The simulations showed that SARS-CoV-2 prevention could greatly reduce the burden of co-infections with Zika. Furthermore, it was shown that prevention controls for Zika can significantly reduce the burden of co-infections with SARS-CoV-2. We expect that the findings of this paper will open new avenues of research in this direction.

The model proposed in this paper focused only on SARS-CoV-2 and Zika co-infection, without vaccination or re-infection either with single or both diseases. Incorporating vaccination for SARS-CoV-2 and re-infection for both diseases, one could obtain an extension of the model. Also, the emergence of different variants of SARS-CoV-2 attracts further studies on their co-infections with other diseases, such as Zika, dengue, TB, influenza, Malaria and others. One could therefore, consider multi-strains of SARS-CoV-2 and co-infection with zika virus. Also, more investigations could be carried out to the mathematical (stochastic, agent based modeling, within/intra-host) and epidemiological dynamics of SARS-CoV-2 and Zika co-infection. The current research was not a case study because of insufficient data and information about the co-infection of both diseases. For instance, little is known about infection acquired cross-immunity between both diseases. Not much information is available to answer the question: whether the current available vaccines against SARS-CoV-2 could have any impact on the dynamics of zika virus. Thus, further studies with more reliable data and detailed information about the co-infection of both diseases is viable.

CRediT authorship contribution statement

Andrew Omame: Conceptualization, Formal analysis, Methodology, Writing – original draft, Software. Mujahid Abbas: Writing – original draft, Validation, Writing – review & editing, Supervision. Chibueze P. Onyenegecha: Writing – original draft, Review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A: Proof of Theorem 1

Let

$t_1=sup\{t>0:{\mathcal{S}}_h\left(0\right)>0,{\mathcal{K}}_{\text{C}}^h\left(0\right)>0,{\mathcal{K}}_{\text{Z}}^h\left(0\right)>0,{\mathcal{K}}_{\text{CZ}}^h\left(0\right)>0,\mathcal{R}\left(0\right)>0,{\mathcal{S}}_v\left(0\right)>0,{\mathcal{K}}_{\text{Z}}^v\left(0\right)>0\in [0,t]\}$. Thus, $t_1>0$.

Suppose further, ${\lambda }_{\text{C}}=\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h},{\lambda }_{\text{Z}}=\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h},{\lambda }_{\text{CZ}}=\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}$, then the first model equation can be written as:

$$\frac{d{\mathcal{S}}_h}{dt}={\Lambda }_h-({\lambda }_{\text{C}}+{\lambda }_{\text{Z}}+{\lambda }_{\text{CZ}}+\mu ){\mathcal{S}}_h,$$ (29)

Applying the integrating factor method on (29), we obtain

$$\frac{d}{dt}\left\{{\mathcal{S}}_h\left(t\right)exp\left[{\int }_0^t({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du+\mu t\right]\right\}={\Lambda }_{h}exp\left[{\int }_0^t({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du+\mu t\right]$$

and

$${\mathcal{S}}_h\left(t_1\right)exp\left[{\int }_0^{t_1}({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du+\mu {\left(t\right)}_1\right]-{\mathcal{S}}_h\left(0\right)={\Lambda }_h{\int }_0^{t_1}exp\left[{\int }_0^x({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du+\mu x\right]dx,$$

with,

$${\mathcal{S}}_h\left(t_1\right)={\mathcal{S}}_h\left(0\right)exp\left[-{\int }_0^{t_1}({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du-\mu t_1\right]+exp\left[-{\int }_0^{t_1}({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du-\mu t_1\right]\times {\Lambda }_h{\int }_0^{t_1}exp\left[{\int }_0^x({\lambda }_{\text{C}}\left(u\right)+{\lambda }_{\text{Z}}\left(u\right)+{\lambda }_{\text{CZ}}\left(u\right))du+\mu x\right]dx>0.$$

Similarly, it can be shown that:

$${\mathcal{K}}_{\text{C}}^h\left(0\right)>0,{\mathcal{K}}_{\text{Z}}^h\left(0\right)>0,{\mathcal{K}}_{\text{CZ}}^h\left(0\right)>0,\mathcal{R}\left(0\right)>0,{\mathcal{S}}_v\left(0\right)>0,{\mathcal{K}}_{\text{Z}}^v\left(0\right)>0.$$

Appendix B: Proof of Theorem 5

Consider the Lyapunov function

$${\mathcal{L}}_1=ln\left[({\mathcal{S}}_h-{\mathcal{S}}_h^0)+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R}+({\mathcal{S}}_v-{\mathcal{S}}_v^0)+{\mathcal{K}}_{\text{Z}}^v\right]+\frac{1}{{\mathcal{G}}_1}{\mathcal{K}}_{\text{C}}^h+\frac{1}{{\mathcal{G}}_2}{\mathcal{K}}_{\text{Z}}^h+\frac{1}{{\mathcal{G}}_3}{\mathcal{K}}_{\text{CZ}}^h+\frac{{\beta }_2^h}{{\mu }_v{\mathcal{G}}_2}{\mathcal{K}}_{\text{Z}}^v,$$

with Lyapunov derivative

$${\dot{\mathcal{L}}}_1=\frac{1}{\left[({\mathcal{S}}_h-{\mathcal{S}}_h^0)+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R}+({\mathcal{S}}_v-{\mathcal{S}}_v^0)+{\mathcal{K}}_{\text{Z}}^v\right]}\times ({\Lambda }_h-\left(\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}+\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}+\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}+{\mu }_h\right){\mathcal{S}}_h+\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h+\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h+\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h+{\zeta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h-{\mu }_h\mathcal{R}+{\Lambda }_v-\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}+{\mu }_v\right){\mathcal{S}}_v+\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v)+\frac{1}{{\mathcal{G}}_1}\left(\frac{{\beta }_1{\mathcal{K}}_{\text{C}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h\right)+\frac{1}{{\mathcal{G}}_2}\left(\frac{({\beta }_2{\mathcal{K}}_{\text{Z}}^h+{\beta }_2^h{\mathcal{K}}_{\text{Z}}^v)}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h\right)+\frac{1}{{\mathcal{G}}_3}\left(\frac{{\beta }_3{\mathcal{K}}_{\text{CZ}}^h}{{\mathcal{N}}_h}{\mathcal{S}}_h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h\right)+\frac{{\beta }_2^h}{{\mu }_v{\mathcal{G}}_2}\left(\frac{{\beta }_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h)}{{\mathcal{N}}_h}{\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v\right)$$

which can be further simplified into

$${\dot{\mathcal{L}}}_1=\frac{1}{\left[({\mathcal{S}}_h-{\mathcal{S}}_h^0)+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R}+({\mathcal{S}}_v-{\mathcal{S}}_v^0)+{\mathcal{K}}_{\text{Z}}^v\right]}\times ({\Lambda }_h-{\mu }_h({\mathcal{S}}_h+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R})+{\Lambda }_v-{\mu }_v({\mathcal{S}}_v+{\mathcal{K}}_{\text{Z}}^v)-({\eta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\eta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\eta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h))+\left(\frac{{\beta }_1}{{\mathcal{G}}_1}-1\right){\mathcal{K}}_{\text{C}}^h+\left(\frac{{\beta }_2}{{\mathcal{G}}_2}+\frac{{\beta }_2^h{\beta }_2^v{\mathcal{S}}_v}{{\mu }_v{\mathcal{G}}_2{\mathcal{N}}_h}-1\right){\mathcal{K}}_{\text{Z}}^h+\left(\frac{{\beta }_3}{{\mathcal{G}}_3}+\frac{{\beta }_2^h{\beta }_2^v{\mathcal{S}}_v}{{\mu }_v{\mathcal{G}}_2{\mathcal{N}}_h}-1\right){\mathcal{K}}_{\text{CZ}}^h$$

Simplifying further (noting that ${\mathcal{S}}_h+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R}\le \frac{{\Lambda }_h}{{\mu }_h},{\mathcal{S}}_v+{\mathcal{K}}_{\text{Z}}^v\le \frac{{\Lambda }_v}{{\mu }_v}$, and $\frac{{\mathcal{S}}_v}{{\mathcal{N}}_h}<\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{N}}_h^{\ast }}$), we have

$${\dot{\mathcal{L}}}_1\le -\frac{({\eta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\eta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\eta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h)}{\left[({\mathcal{S}}_h-{\mathcal{S}}_h^0)+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R}+({\mathcal{S}}_v-{\mathcal{S}}_v^0)+{\mathcal{K}}_{\text{Z}}^v\right]}+\left(\frac{{\beta }_1}{{\mathcal{G}}_1}-1\right){\mathcal{K}}_{\text{C}}^h+\left(\frac{{\beta }_2}{{\mathcal{G}}_2}+\frac{{\beta }_2^h{\beta }_2^v{\mathcal{S}}_v^{\ast }}{{\mu }_v{\mathcal{G}}_2{\mathcal{N}}^{\ast }}-1\right){\mathcal{K}}_{\text{Z}}^h+\left(\frac{{\beta }_3}{{\mathcal{G}}_3}+\frac{{\beta }_2^h{\beta }_2^v{\mathcal{S}}_v^{\ast }}{{\mu }_v{\mathcal{G}}_2{\mathcal{N}}^{\ast }}-1\right){\mathcal{K}}_{\text{CZ}}^h=-\frac{({\eta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\eta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^h+{\eta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^h)}{\left[({\mathcal{S}}_h-{\mathcal{S}}_h^0)+{\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h+\mathcal{R}+({\mathcal{S}}_v-{\mathcal{S}}_v^0)+{\mathcal{K}}_{\text{Z}}^v\right]}+\left({\mathcal{R}}_{0\text{C}}-1\right){\mathcal{K}}_{\text{C}}^h+\left({\mathcal{R}}_{0\text{Z}}^h+{\mathcal{R}}_{0\text{Z}}^{vh2}-1\right){\mathcal{K}}_{\text{Z}}^h+\left({\mathcal{R}}_{0\text{CZ}}+{\mathcal{R}}_{0\text{Z}}^{vh2}-1\right){\mathcal{K}}_{\text{CZ}}$$

Since all the model parameters and variables are non-negative, it follows that ${\dot{\mathcal{L}}}_1<0$ for ${\mathcal{R}}_0=max\{{\mathcal{R}}_{0\text{C}},{\mathcal{R}}_{0\text{Z}},{\mathcal{R}}_{0\text{CZ}}\}\le 1$. Hence, ${\mathcal{L}}_1$ is a Lyapunov function on $\mathcal{Q}$. Thus, the DFE is globally asymptotically stable [44].

Appendix C: Proof of Theorem 6

Consider the model (1) with ${\eta }_{\text{C}}={\eta }_{\text{Z}}={\eta }_{\text{CZ}}=0(\text{with}{\mathcal{N}}_h=\frac{{\Lambda }_h}{{\mu }_h},{\overline{\beta }}_1=\frac{{\mu }_h{\beta }_1}{{\Lambda }_h},{\overline{\beta }}_2=\frac{{\mu }_h{\beta }_2}{{\Lambda }_h},{\overline{\beta }}_2^h=\frac{{\mu }_h{\beta }_2^h}{{\Lambda }_h},{\overline{\beta }}_3=\frac{{\mu }_h{\beta }_3}{{\Lambda }_h},{\overline{\beta }}_2^h=\frac{{\mu }_h{\beta }_2^h}{{\Lambda }_h},{\overline{\beta }}_2^v=\frac{{\mu }_h{\beta }_2^v}{{\Lambda }_h})$ and ${\mathcal{R}}_0>1$, so that the associated unique endemic equilibrium exists. Also, consider the non-linear Lyapunov function:

$${\mathcal{L}}_2={\mu }_v[{\mathcal{S}}_h-{\mathcal{S}}_h^{\ast }-{\mathcal{S}}_h^{\ast }ln\left(\frac{{\mathcal{S}}_h}{{\mathcal{S}}_h^{\ast }}\right)+{\mathcal{K}}_{\text{C}}^h-{\mathcal{K}}_{\text{C}}^{h\ast }-{\mathcal{K}}_{\text{C}}^{h\ast }ln\left(\frac{{\mathcal{K}}_{\text{C}}^h}{{\mathcal{K}}_{\text{C}}^{h\ast }}\right)+{\mathcal{K}}_{\text{Z}}^h-{\mathcal{K}}_{\text{Z}}^{h\ast }-{\mathcal{K}}_{\text{Z}}^{h\ast }ln\left(\frac{{\mathcal{K}}_{\text{Z}}^h}{{\mathcal{K}}_{\text{Z}}^{h\ast }}\right)+{\mathcal{K}}_{\text{CZ}}-{\mathcal{K}}_{\text{CZ}}^{h\ast }-{\mathcal{K}}_{\text{CZ}}^{h\ast }ln\left(\frac{{\mathcal{K}}_{\text{CZ}}}{{\mathcal{K}}_{\text{CZ}}^{h\ast }}\right)]+{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }\left[{\mathcal{S}}_v-{\mathcal{S}}_v^{\ast }-{\mathcal{S}}_v^{\ast }ln\left(\frac{{\mathcal{S}}_v}{{\mathcal{S}}_v^{\ast }}\right)+{\mathcal{K}}_{\text{Z}}^v-{\mathcal{K}}_{\text{Z}}^{v\ast }-{\mathcal{K}}_{\text{Z}}^{v\ast }ln\left(\frac{{\mathcal{K}}_{\text{Z}}^v}{{\mathcal{K}}_{\text{Z}}^{v\ast }}\right)\right]$$

with Lyapunov derivative,

$${\dot{\mathcal{L}}}_2={\mu }_v[\left(1-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}\right)\dot{{\mathcal{S}}_h}+\left(1-\frac{{\mathcal{K}}_{\text{C}}^{h\ast }}{{\mathcal{K}}_{\text{C}}^h}\right){\dot{\mathcal{K}}}_{\text{C}}^h+\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{h\ast }}{{\mathcal{K}}_{\text{Z}}^h}\right){\dot{\mathcal{K}}}_{\text{Z}}^h+\left(1-\frac{{\mathcal{K}}_{\text{CZ}}^{h\ast }}{{\mathcal{K}}_{\text{CZ}}}\right){\dot{\mathcal{K}}}_{\text{CZ}}^h]+{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }\left[\left(1-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}\right)\dot{{\mathcal{S}}_v}+\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{v\ast }}{{\mathcal{K}}_{\text{Z}}^v}\right){\dot{\mathcal{K}}}_{\text{Z}}^v\right]$$ (30)

Substituting the derivatives in (1) into ${\dot{\mathcal{L}}}_2$, we have

$${\dot{\mathcal{L}}}_2={\mu }_v\left(1-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}\right)\times \left[{\Lambda }_h-{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h-({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^h+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h-{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h-{\mu }_h{\mathcal{S}}_h\right]+{\mu }_v\left(1-\frac{{\mathcal{K}}_{\text{C}}^{h\ast }}{{\mathcal{K}}_{\text{C}}^h}\right)\left[{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h\right]+{\mu }_v\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{h\ast }}{{\mathcal{K}}_{\text{Z}}^h}\right)\left[({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^h+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h\right]$$ (31)

$$+{\mu }_v\left(1-\frac{{\mathcal{K}}_{\text{CZ}}^{h\ast }}{{\mathcal{K}}_{\text{CZ}}^h}\right)\left[{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h\right]+{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{v\ast }}{{\mathcal{K}}_{\text{Z}}^v}\right)\left[{\Lambda }_v-{\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v-{\mu }_v{\mathcal{S}}_v\right]+{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{v\ast }}{{\mathcal{K}}_{\text{Z}}^v}\right)\left[{\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v\right]$$

From model (1) at steady state, we have

$${\Lambda }_h={\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }{\mathcal{S}}_h^{\ast }+({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^{v\ast }){\mathcal{S}}_h^{\ast }+{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{\ast }+{\mu }_h{\mathcal{S}}_h^{\ast }$$$${\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }{\mathcal{S}}_h^{\ast }=\left({\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^{h\ast }({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^{v\ast }){\mathcal{S}}_h^{\ast }=\left({\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^{h\ast }$$$${\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{\ast }=\left({\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^{h\ast }$$$${\zeta }_{\text{C}}{\mathcal{K}}_{\text{C}}^h+{\zeta }_{\text{Z}}{\mathcal{K}}_{\text{Z}}^{h\ast }+{\zeta }_{\text{CZ}}{\mathcal{K}}_{\text{CZ}}^{h\ast }={\mu }_h{\mathcal{R}}^{\ast }$$$${\Lambda }_v={\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^{h\ast }+{\mathcal{K}}_{\text{CZ}}^{h\ast }){\mathcal{S}}_v^{\ast }+{\mu }_v{\mathcal{S}}_v^{\ast }$$$${\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^{h\ast }+{\mathcal{K}}_{\text{CZ}}^{h\ast }){\mathcal{S}}_v^{\ast }={\mu }_v{\mathcal{K}}_{\text{Z}}^{v\ast }$$ (32)

Substituting the expressions in (32) into (31) gives

$${\dot{\mathcal{L}}}_2={\mu }_v\left(1-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}\right)[{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }{\mathcal{S}}_h^{\ast }+({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^{v\ast }){\mathcal{S}}_h^{\ast }+{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{\ast }+{\mu }_h{\mathcal{S}}_h^{\ast }-{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h-({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^h+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h-{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h-{\mu }_h{\mathcal{S}}_h]+{\mu }_v\left(1-\frac{{\mathcal{K}}_{\text{C}}^{h\ast }}{{\mathcal{K}}_{\text{C}}^h}\right)\left[{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h-\left({\eta }_{\text{C}}+{\zeta }_{\text{C}}+{\mu }_h\right){\mathcal{K}}_{\text{C}}^h\right]+{\mu }_v\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{h\ast }}{{\mathcal{K}}_{\text{Z}}^h}\right)\left[({\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^h+{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^v){\mathcal{S}}_h-\left({\eta }_{\text{Z}}+{\zeta }_{\text{Z}}+{\mu }_h\right){\mathcal{K}}_{\text{Z}}^h\right]+{\mu }_v\left(1-\frac{{\mathcal{K}}_{\text{CZ}}^{h\ast }}{{\mathcal{K}}_{\text{CZ}}^h}\right)\left[{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h-\left({\eta }_{\text{CZ}}+{\zeta }_{\text{CZ}}+{\mu }_h\right){\mathcal{K}}_{\text{CZ}}^h\right]+{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{v\ast }}{{\mathcal{K}}_{\text{Z}}^v}\right)[{\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^{h\ast }+{\mathcal{K}}_{\text{CZ}}^{h\ast }){\mathcal{S}}_v^{\ast }+{\mu }_v{\mathcal{S}}_v^{\ast }-{\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v-{\mu }_v{\mathcal{S}}_v]+{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }\left(1-\frac{{\mathcal{K}}_{\text{Z}}^{v\ast }}{{\mathcal{K}}_{\text{Z}}^v}\right)\left[{\overline{\beta }}_2^v({\mathcal{K}}_{\text{Z}}^h+{\mathcal{K}}_{\text{CZ}}^h){\mathcal{S}}_v-{\mu }_v{\mathcal{K}}_{\text{Z}}^v\right]$$

which after some algebraic manipulations is reduced to

$${\dot{\mathcal{L}}}_2={\mu }_h{\mu }_v{\mathcal{S}}_h^{\ast }\left(2-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_h}{{\mathcal{S}}_h^{\ast }}\right)+{\mu }_v{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }{\mathcal{S}}_v^{\ast }\left(2-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-\frac{{\mathcal{S}}_v}{{\mathcal{S}}_v^{\ast }}\right)+{\mu }_v[2{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }{\mathcal{S}}_h^{\ast }+2{\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h^{\ast }+2{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_h^{\ast }+2{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{\ast }-\frac{{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }{\mathcal{S}}_h^{\ast 2}}{{\mathcal{S}}_h}-{\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }{\mathcal{S}}_h-\frac{{\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h^{\ast 2}}{{\mathcal{S}}_h}-{\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h-\frac{{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_h^{\ast 2}}{{\mathcal{S}}_h}-\frac{{\overline{\beta }}_2^h{\mathcal{K}}_{\text{Z}}^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h}{{\mathcal{K}}_{\text{Z}}^h}-\frac{{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{\ast 2}}{{\mathcal{S}}_h}-{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h]+{\beta }_2^h{\mathcal{S}}_h^{\ast }[{\overline{\beta }}_2^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_v^{\ast }+{\overline{\beta }}_2^v{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_v^{\ast }-\frac{{\overline{\beta }}_2^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_v^{\ast 2}}{{\mathcal{S}}_v}+{\overline{\beta }}_2^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_v^{\ast }+{\overline{\beta }}_2^v{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_v^{\ast }-\frac{{\overline{\beta }}_2^v{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_v^{\ast 2}}{{\mathcal{S}}_v}-\frac{{\overline{\beta }}_2^v{\mathcal{K}}_{\text{Z}}^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_v}{{\mathcal{K}}_{\text{Z}}^v}-\frac{{\overline{\beta }}_2^v{\mathcal{K}}_{\text{CZ}}^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_v}{{\mathcal{K}}_{\text{Z}}^v}]$$ (33)

The above can be simplified to

$${\dot{\mathcal{L}}}_2={\mu }_h{\mu }_v{\mathcal{S}}_h^{\ast }\left(2-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_h}{{\mathcal{S}}_h^{\ast }}\right)+{\mu }_v{\overline{\beta }}_2^h{\mathcal{S}}_h^{\ast }{\mathcal{S}}_v^{\ast }\left(2-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-\frac{{\mathcal{S}}_v}{{\mathcal{S}}_v^{\ast }}\right)+{\mu }_v{\mathcal{S}}_h^{\ast }{\mathcal{S}}_h^{\ast }\left({\overline{\beta }}_1{\mathcal{K}}_{\text{C}}^{h\ast }+{\overline{\beta }}_2{\mathcal{K}}_{\text{Z}}^{h\ast }+{\overline{\beta }}_3{\mathcal{K}}_{\text{CZ}}^{h\ast }\right)\left(2-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_h}{{\mathcal{S}}_h^{\ast }}\right)+{\overline{\beta }}_2^h{\overline{\beta }}_2^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h^{\ast }{\mathcal{S}}_v^{\ast }\left(4-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-{\frac{{\mathcal{K}}_{\text{Z}}^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h}{{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{K}}_{\text{Z}}^h{\mathcal{S}}_h}}^{\ast }-{\frac{{\mathcal{K}}_{\text{Z}}^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_v}{{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{K}}_{\text{Z}}^v{\mathcal{S}}_v}}^{\ast }\right)+{\overline{\beta }}_2^h{\overline{\beta }}_2^v{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h^{\ast }{\mathcal{S}}_v^{\ast }\left(4-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-{\frac{{\mathcal{K}}_{\text{Z}}^v{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h}{{\mathcal{K}}_{\text{CZ}}^{v\ast }{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h}}^{\ast }-{\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_v}{{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{K}}_{\text{Z}}^v{\mathcal{S}}_v}}^{\ast }\right).$$ (34)

As arithmetic mean is greater that geometric mean, the following inequalities from (34) hold:

$$\left(2-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_h}{{\mathcal{S}}_h^{\ast }}\right)\le 0,\left(2-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-\frac{{\mathcal{S}}_v}{{\mathcal{S}}_v^{\ast }}\right)\le 0,$$

$$\left(4-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-{\frac{{\mathcal{K}}_{\text{Z}}^v{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{S}}_h}{{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{K}}_{\text{Z}}^h{\mathcal{S}}_h}}^{\ast }-{\frac{{\mathcal{K}}_{\text{Z}}^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_v}{{\mathcal{K}}_{\text{Z}}^{h\ast }{\mathcal{K}}_{\text{Z}}^v{\mathcal{S}}_v}}^{\ast }\right)\le 0,$$

$$\left(4-\frac{{\mathcal{S}}_h^{\ast }}{{\mathcal{S}}_h}-\frac{{\mathcal{S}}_v^{\ast }}{{\mathcal{S}}_v}-{\frac{{\mathcal{K}}_{\text{Z}}^v{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{S}}_h}{{\mathcal{K}}_{\text{CZ}}^{v\ast }{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h}}^{\ast }-{\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{K}}_{\text{Z}}^{v\ast }{\mathcal{S}}_v}{{\mathcal{K}}_{\text{CZ}}^{h\ast }{\mathcal{K}}_{\text{Z}}^v{\mathcal{S}}_v}}^{\ast }\right)\le 0.$$

Thus, $\dot{{\mathcal{L}}_2}\le 0$ for ${\overline{\mathcal{R}}}_0>1$. Hence, ${\mathcal{L}}_2$ is a Lyapunov function in $\mathcal{D}⧵{\mathcal{D}}_0$ and we conclude that the GAS of EEP is globally asymptotically stable for ${\overline{\mathcal{R}}}_0>1$.

Appendix D: Adjoint functions

$${\varrho }_1^{\prime }={\varrho }_3\left(\frac{\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)-\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_4\left(\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\mathcal{K}}_{\text{CZ}}^h{\beta }_3\left({\theta }_3-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_2\left(\frac{{\mathcal{K}}_{\text{C}}^h{\beta }_1\left({\theta }_1-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_1\left({\mu }_h-\frac{\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)-\frac{{\mathcal{K}}_{\text{C}}^h{\beta }_1\left({\theta }_1-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}-\frac{{\mathcal{K}}_{\text{CZ}}^h{\beta }_3\left({\theta }_3-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+\frac{{\mathcal{S}}_v{\beta }_v^2{\varrho }_6\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}-\frac{{\mathcal{S}}_v{\beta }_v^2{\varrho }_7\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}$$

$${\varrho }_2^{\prime }={\varrho }_1\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_5{\zeta }_1-{\varrho }_3\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+\frac{{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_4\left(\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}-\frac{{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_2\left({\eta }_1+{\mu }_h+{\zeta }_1+\frac{{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)-\frac{{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+\frac{{\mathcal{S}}_v{\beta }_v^2{\varrho }_6\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}-\frac{{\mathcal{S}}_v{\beta }_v^2{\varrho }_7\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}-1$$

$${\varrho }_3^{\prime }={\varrho }_3\left({\eta }_2+{\mu }_h+{\zeta }_2+\frac{{\mathcal{S}}_h{\beta }_2\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)-\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_4\left(\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1{\beta }_2\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_5{\zeta }_2-{\varrho }_6\left(\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)\left(-\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_7\left(\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)\left(-\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_1\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\mathcal{S}}_h{\beta }_2\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(+\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_2\left(\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1{\beta }_2\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-1$$

$${\varrho }_4^{\prime }={\varrho }_7\left(\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)\left(-\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_3\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_5{\zeta }_3-{\varrho }_6\left(\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)\left(-\frac{{\mathcal{S}}_v{\beta }_v^2\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_2\left(\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_4\left({\eta }_3+{\mu }_h+{\zeta }_3+\frac{{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)\left(-\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_1\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-\frac{{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-1$$

$${\varrho }_5^{\prime }={\varrho }_5{\mu }_h-{\varrho }_3\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_2\left(\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+{\varrho }_1\left(\frac{{\mathcal{S}}_h\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_2-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{S}}_h{\beta }_1\left({\theta }_1-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)-{\varrho }_4\left(\frac{{\mathcal{K}}_{\text{CZ}}^h{\mathcal{S}}_h{\beta }_3\left({\theta }_3-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1\left({\mathcal{K}}_{\text{Z}}^h{\beta }_2+{\mathcal{K}}_{\text{Z}}^v{\beta }_h^2\right)\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)\left(+\frac{{\mathcal{K}}_{\text{C}}^h{\mathcal{K}}_{\text{Z}}^h{\alpha }_2{\beta }_1\left({\theta }_4-1\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}\right)+\frac{{\mathcal{S}}_v{\beta }_v^2{\varrho }_6\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}-\frac{{\mathcal{S}}_v{\beta }_v^2{\varrho }_7\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}^2}$$

$${\varrho }_6^{\prime }={\varrho }_6\left({\mu }_v-\frac{{\beta }_v^2\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}\right)+\frac{{\beta }_v^2{\varrho }_7\left({\theta }_2-1\right)\left({\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}-1$$

$${\varrho }_7^{\prime }={\varrho }_7{\mu }_v-\frac{{\mathcal{S}}_h{\beta }_h^2{\varrho }_1\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{S}}_h{\beta }_h^2{\varrho }_3\left({\theta }_2-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}-\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1{\beta }_h^2{\varrho }_2\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}+\frac{{\mathcal{K}}_{\text{C}}^h{\alpha }_1{\beta }_h^2{\varrho }_4\left({\theta }_4-1\right)}{\left({\mathcal{K}}_{\text{C}}^h+{\mathcal{K}}_{\text{CZ}}^h+{\mathcal{K}}_{\text{Z}}^h+\mathcal{R}+{\mathcal{S}}_h\right)}-1$$