Abstract
We perform path-integral molecular dynamics (PIMD), ring-polymer MD (RPMD), and classical MD simulations of HO and DO using the q-TIP4P/F water model over a wide range of temperatures and pressures. The density , isothermal compressibility , and self-diffusion coefficients D(T) of HO and DO are in excellent agreement with available experimental data; the isobaric heat capacity obtained from PIMD and MD simulations agree qualitatively well with the experiments. Some of these thermodynamic properties exhibit anomalous maxima upon isobaric cooling, consistent with recent experiments and with the possibility that HO and DO exhibit a liquid-liquid critical point (LLCP) at low temperatures and positive pressures. The data from PIMD/MD for HO and DO can be fitted remarkably well using the Two-State-Equation-of-State (TSEOS). Using the TSEOS, we estimate that the LLCP for q-TIP4P/F HO, from PIMD simulations, is located at MPa, K, and g/cm. Isotope substitution effects are important; the LLCP location in q-TIP4P/F DO is estimated to be MPa, K, and g/cm. Interestingly, for the water model studied, differences in the LLCP location from PIMD and MD simulations suggest that nuclear quantum effects (i.e., atoms delocalization) play an important role in the thermodynamics of water around the LLCP (from the MD simulations of q-TIP4P/F water, MPa, K, and g/cm). Overall, our results strongly support the LLPT scenario to explain water anomalous behavior, independently of the fundamental differences between classical MD and PIMD techniques. The reported values of for DO and, particularly, HO suggest that improved water models are needed for the study of supercooled water.
Subject terms: Chemistry, Physics
Introduction
Water is an anomalous liquid with thermodynamic and dynamical properties that behave unexpectedly upon cooling and/or pressurization; see, e.g., Ref.1. For example, experiments performed in the 1970’s by Angell et al.2–4 show that water isobaric heat capacity and isothermal compressiblity exhibit an apparent divergency at K and MPa. More recent experiments that extend Angell’s studies to lower temperatures identify a maxima in and at K ( MPa)5,6. Although many theoretical approaches have been proposed to explain water anomalous behavior, the so-called liquid–liquid phase transition (LLPT) scenario7,8 is currently the explanation best-supported by experiments5,9–13, computer simulations7,14–18, and theory14,19–23. In the LLPT scenario, water at low temperatures exists in two distinct liquid states, low-density and high-density liquid (LDL and HDL). In the P–T plane, LDL and HDL are separated by a first-order LLPT line that ends at a liquid–liquid critical point (LLCP) at higher temperatures. Importantly, the LLPT hypothesis explains naturally the maxima in and observed recently upon cooling water at MPa5,10. It also explains, naturally, the complex behavior of water in the glass state8,9,24–34 which, arguably, is not clearly explained by other approaches, such as the singularity free scenario35.
Available experimental data suggest that the LLCP in water is located at about = 50–100 MPa and K1,12. Unfortunately, due to water rapid crystallization at these conditions, the existence of the LLCP in water has not been confirmed in experiments. Strong evidence for the existence of a LLPT in water is available from recent sub-microsecond experiments at K9; additional evidence of the LLPT in water is available from experiments performed at 130–140 K, in the the so-called ultraviscous liquid state of water36,37. Many computer simulations validate the LLPT hypothesis. Specifically, a LLCP has been identified in classical computer simulations using popular models, such as ST2, TIP4P/2005, and TIP4P/ice7,14,18,38–44. A recent classical MD simulation using a water model developed from density functional theory combined with machine learning techniques also suggests that water exhibits a LLCP in the supercooled regime21. Not surprisingly, the location of the LLCP in computer simulations vary with the water model considered. For example, in the case of the ST2 water model, the LLCP temperature is overestimated ( K, MPa, g/cm)41; while in the TIP4P/2005 and TIP4P/Ice water models it is underestimated ( K, MPa, and g/cm for TIP4P/2005; K, MPa, g/cm for TIP4P/Ice)18. In all these cases, the LLCP pressure is overestimated by approximately 100 MPa6. The computer simulation studies that find a LLCP in water are based on classical models where the atoms delocalization due to nuclear quantum effects (NQE) are neglected. This can be troublesome because water is a light molecule and delocalization effects of its H atoms occur even at standard temperatures and pressures45,46. For example, the temperature of maximum density and the glass transition temperature (T) of HO and DO differ by 7–10 K, a clear sign of non-negligible NQE. Path-integral computer simulations of water-like models that have a LLCP clearly show that NQE can indeed shift the location of the LLCP as well as alter the shape and slope of the and maxima lines47,48. Interestingly, while experiments in glassy water have estimated differences in the location of the LLCP in HO and DO ( K, MPa)49,50, the issue of isotope effects on the location of the LLCP has not been explored in computational and theoretical studies.
In this work we perform extensive path-integral, ring-polymer, and classical molecular dynamics (PIMD, RPMD, MD) simulations of light and heavy water using the q-TIP4P/F model and explore the corresponding phase diagram and thermodynamic/dynamical anomalous properties. One goal of this work is to determine the NQE (due to atoms delocalization) on the location of the LLCP, LLPT, and supercritical anomalous lines (such as maxima lines in , , and ) in q-TIP4P/F water (HO). The second goal of this work is to study isotope substitution effects in water, i.e., whether PIMD simulations of HO and DO can reproduce the subtle differences in the phase diagram and anomalous properties of HO and DO observed in experiments. In a previous study, we performed PIMD simulations of q-TIP4P/F water at MPa and showed that this model reproduces some signatures of the LLPT scenario, specifically, a maximum in was found in HO and DO at 230–235 K () MPa46. Here, we extend our previous study to a wide range of temperatures and pressures in order to explore the possible existence of a LLCP in HO and DO. By combining the PIMD/MD results and the two-state equation of state (TSEOS)14,22,23, we are able to identify a LLCP in both HO and DO. The TSEOS is based on the assumption that liquid water is a mixture of two interconvertible (liquid) states. The TSEOS has been shown to fit remarkably well the computer simulations results obtained from classical MD simulations of ST2 and TIP4P/2005 water as well as a water model based on DFT and machine learning techniques14,19–21,23; it has also been applied to the case of real water20,51. While at low temperatures the TSEOS predicts that water separates into LDL and HDL, at high temperatures ( K), it predicts a rather homogeneous liquid (HDL) which is consistent with recent computer simulations52,53.
Our paper is organized as follows. In “Simulation method”, we present the computer simulation details. In “Results”, we discuss the results from our PIMD/RPMD and classical MD simulations of HO using the q-TIP4P/F water model. The phase diagram of DO is briefly discussed and compared with the phase diagram of HO. A summary and discussions are included in “Summary and discussion”.
Simulation method
Our results are based on PIMD/RPMD and classical MD simulations of a system composed of water molecules in a cubic box with periodic boundary conditions. HO and DO molecules are represented using the non-rigid q-TIP4P/F model54. This model is based on the TIP4P/2005 model for water55, commonly used in classical MD simulations. The q-TIP4P/F water model was optimized for path integral computer simulations and has been shown to be able to reproduce remarkably well the properties of liquid water at MPa46,54. Here, we perform PIMD and MD simulations at constant N, P, and T over a wide range of temperatures and pressures, K and 500 MPa; see Supplementary Fig. S1 of the Supplementary Information (SI). The temperature of the system is maintained constant using a stochastic (local) path integral Langevin equation (PILE) thermostat56 while the pressure of the system is controlled by using a Monte Carlo Barostat (additional computational details can be found in Ref.46). In the PIMD simulations, the time step dt is set to 0.25 fs and the number of beads per ring-polymer/atom was set to ; in Ref.46, it is shown that this value of is large enough to obtain well-converged dynamical, thermodynamic, and structural properties of q-TIP4P/F water at MPa and K. In order to ensure that the conclusions in Ref.46 applied to the pressures we considered in this work, we have also performed additional PIMD simulations using beads per ring-polymer (see SI). Consistent with Ref.46, we found that most of the thermodynamic and dynamical properties converged with , with the enthalpy being the only expected exception. Short-range (Lennard–Jones pair potential) interactions are calculated using a cutoff = 1.0 nm and long range electrostatic interactions are computed using the Particle Mesh Ewald (PME) method with the same cutoff . In the classical MD simulations, we employ a time step fs and set . All PIMD and classical MD simulations are performed using the OpenMM software package (version 7.4.0)57. The OpenMM software package is also used to perform the RPMD simulations which are used for the calculation of the diffusion coefficients of H2O and D2O. Details on the calculation of the diffusion coefficients can be found in Ref.46. We note that in the OpenMM software package, the RPMD application sets the mass of the ring-polymer beads to the physical mass of the corresponding atom. When used to calculate static equilibrium properties (energies, density, and RDF), the RPMD simulations reduce to PIMD simulations.
In all PIMD/RPMD and classical MD simulations, the system is equilibrated for a time interval followed by a production run of time length . The values of and depend on the state point simulated. Typical simulation times for PIMD/RPMD range from 2.5 ns to 100 ns. Simulation times for classical MD simulations range from 2.5 ns to 2–3 . To confirm that the system reaches equilibrium, we monitor the mean-square displacement (MSD) of the water molecules in the system as a function of time and confirm that the PIMD/RPMD and classical MD simulations satisfy the requirement that , , where is the time it takes for the MSD of water molecules to reach 1 nm.
Results
The results are presented as follows. In “Liquid–liquid phase transition”, we show that the phase diagrams of HO from MD and PIMD simulations are consistent with the existence of a LLPT and LLCP at low temperatures. Since a LLCP generates anomalous loci of maxima in and , the behavior of and are discussed in “Thermodynamic response functions: and ”. The self-diffusion coefficient of HO and DO are the topic of “Diffusion coefficient” where we identify the anomalous locus of diffusivity maxima. A complete phase diagram for HO is presented in “Phase diagram” where we also discuss similar results obtained for DO.
Liquid–liquid phase transition
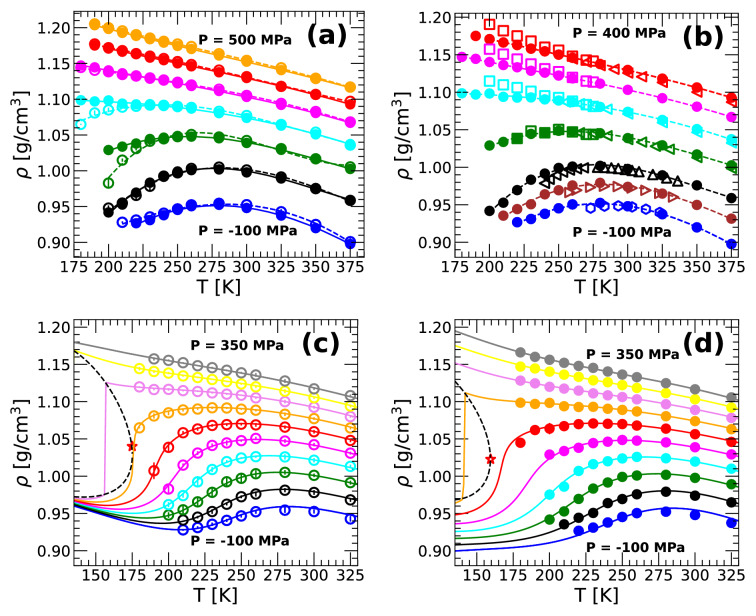
Figure 1a shows the density of HO from both classical MD (open circles) and PIMD simulations (solid circles) along the isobars MPa and at temperatures in the range 180–375 K. The densities from MD and PIMD simulations overlap practically throughout the entire temperature and pressure range considered with some deviations being noticeable only at 100–200 MPa and K. As we will show below, these T–P conditions are in the proximity of the LLCP. We note that the densities of q-TIP4P/F HO are in remarkable good agreement with the corresponding experimental values. To show this, we include in Fig. 1b the densities from experiments and PIMD simulations of q-TIP4P/F HO. Deviations between experiments and PIMD simulations are small, 0.02–0.03 g/cm, and are present only at MPa and K (similar values of hold for the case of MD simulations). It follows that both MD and PIMD simulations of q-TIP4P/F water predict the correct location (T and P) for the density maximum of water. In these and other cases, the computer simulation results can be fitted remarkably well using the TSEOS14,20–23,58. In Fig. 1c,d, we compare the isobars obtained from the MD and PIMD simulations of q-TIP4P/F water with the corresponding fit using the TSEOS (a brief explanation of the methodology used to obtain the TSEOS can be found in Refs.14,21). The TSEOS is fitted using only the PIMD and MD data for K and MPa. As shown in Fig. 1c,d, the TSEOS isobars are in excellent agreement with the simulation results over a majority of the state points simulated. Interestingly, the TSEOS also predicts a minimum in the isobars of q-TIP4P/F water. While at the studied temperatures we do not observe density minima in the classical MD and PIMD simulations, density minima were reported at different pressures in TIP4P/2005 and ST2 water15,42. The optimized parameters for the TSEOS are given in Table S1 of the SI.
Figure 1.
Density of q-TIP4P/F water as function of temperature along selected isobars. (a) Comparison of from classical MD (open circles) and PIMD simulations (solid circles). Pressures are (bottom to top) MPa. (b) Density of q-TIP4P/F water from PIMD simulations (solid circles) and experiments (open symbols; squares, left-triangles, up-triangles, right-triangles, and diamonds are, respectively, from Refs.12,16,59–61). Pressures are (bottom to top) MPa. Deviations between experiments and simulations are noticeable only at high pressures, MPa, and low temperatures, K. (c) Fit of the q-TIP4P/F water densities shown in (a) using the TSEOS (solid lines). (d) Fit of the q-TIP4P/F water densities shown in (b) using the TSEOS (solid lines). Pressures in (c) and (d) are (bottom to top) MPa. The liquid–liquid binodal line and LLCP predicted from the TSEOS are denoted by the black dashed line and red star.
The TSEOS also provides a good estimation of the LLCP location. For example, in the case of TIP4P/2005 water, the TSEOS predicts that K, MPa, and g/cm14, which is in good agreement with recent MD simulations that were able to access the LLCP, K, MPa, and g/cm18; similar results were found in an MD simulation study combined with the potential energy landscape theoretical approach43. Using the TSEOS, one can estimate the LLCP location (). The values of () for the case of q-TIP4P/F HO, based on classical MD and PIMD simulations, are given in Table 1 and are indicated in Fig. 1c,d by a red star. It follows that including NQE can shift the location of the LLCP. Specifically, relative to the classical case (MD simulations), adding NQE (PIMD simulations) lowers and by K, MPa, respectively; is not affected by the inclusion of NQE. Interestingly, recent studies based on water-like monoatomic model liquids that exhibit a LLCP, show that including NQE has the effects of lowering and increasing , while leaving unaffected47,48.
Table 1.
Estimated pressure , temperature , and density of the LLCP of q-TIP4P/F HO. Values of , , and are obtained by using the TSEOS in combination with data from classical MD and PIMD simulations at K. Numbers in parenthesis are standard deviations.
| PIMD | Classical MD | |
|---|---|---|
| 167 (9) | 203 (4) | |
| 159 (6) | 175 (1) | |
| 1.02 (0.01) | 1.03 (0.01) |
We also compare the volumes predicted by the TSEOS with the corresponding values obtained from our MD and PIMD simulations. Fig. 2a,b show P(V) along isotherms based on the classical MD and PIMD simulations, respectively. In both cases, MD and PIMD simulations, the values of P(V) obtained from the TSEOS are in excellent agreement with our simulations. This strongly indicates that the TSEOS is reliable in predicting the properties of q-TIP4P/F water from both MD and PIMD simulations. We note that the P(V) isotherms shown in Fig. 2a,b seem to develop an inflection point as the temperature decreases, consistent with the existence of a LLCP at K. Similarly, as shown in Fig. 2c, the potential energy PE(V) along isotherms is an increasing function of V at high temperatures but it develops a concave region (i.e., ) at low temperatures. The Helmholz free energy of the system is and hence, a concavity in PE can lead to a concavity in F(V) (at constant N and T) at very low temperatures. A concavity in F(V) implies that the system exhibits a first-order (liquid–liquid) phase transitions62, again, consistent with the presence of LLCP/LLPT at low temperatures.
Figure 2.
Pressure of q-TIP4P/F water as a function of volume along selected isotherms. Circles are results from (a) classical MD and (b) PIMD simulation. The solid lines are the results from the TSEOS. Isotherms correspond to (top to bottom) K and are shifted by MPa, respectively. An inflection point in P(V) seems to develop at K consistent with the existence of a LLPT in q-TIP4P/F water at lower temperatures. (c) Potential energy for selected isotherms at (bottom to top) K. Solid symbols are from PIMD simulations; lines are guides to the eye.
Thermodynamic response functions: and
We obtain the isothermal compressibility of q-TIP4P/F water by calculating the density fluctuations of the system63,
| 1 |
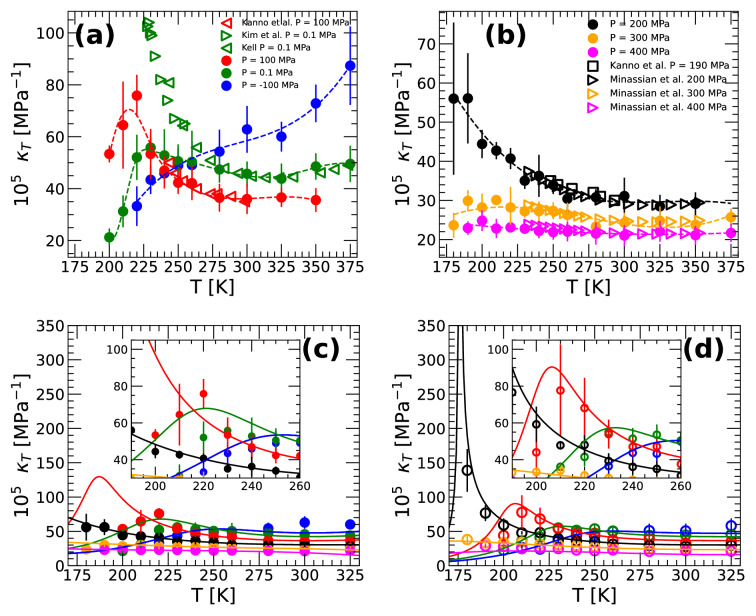
where indicates average over time and is the Boltzmann’s constant. Fig. 3a,b show the for HO obtained from PIMD simulations (solid circles) together with available experimental data (open symbols) at low and high pressures, respectively. At MPa (Fig. 3b), the experimental and PIMD simulation values of practically overlap; a similar agreement is found at MPa (Fig. 3a). However, at MPa, where more experimental data is available, the experimental increases more rapidly upon cooling than found in PIMD simulations. Hence, relative to real water, the density fluctuation in q-TIP4P/F water are underestimated at MPa and in the supercooled regime. We note that the values of obtained from classical MD and PIMD simulations overlap (within error bars) at K and hence, they were omitted in Fig. 3a,b; the obtained from MD simulations is shown in Fig. S2 of the SI.
Figure 3.
(a) Isothermal compressibility of q-TIP4P/F water from PIMD simulations at pressures MPa (solid circles; dashed lines are guides to the eye). Experimental data for are indicated by open symbols (red left-triangles, green left- and right-triangles are from Refs.5,65,66, respectively). (b) Same as (a) for pressures MPa; experimental values of are from Refs.65,67. (c) Comparison between the values of obtained from the PIMD simulations [solid circles; from (a) and (b)] and the TSEOS (solid lines). (d) Comparison between the values of obtained from the MD simulations (empty circles) and the TSEOS (solid lines). Insets are magnifications of the main panels. The predictions of the TSEOS are in very good agreement with the MD simulation results and semiquantitative agreement in the case of PIMD simulations.
An important result from Fig. 3a is the presence of maxima in at and 100 MPa. This is an anomalous property that was originally predicted by the LLPT hypothesis scenario and later confirmed by experiments5,17. The experimental data from Ref.5 is included in Fig. 3a; the experimental -maximum occurs at K ( MPa; open right triangles) and it is very sharp. While the -maximum in PIMD simulations occurs at a similar temperature ( K), this maximum is much smaller and wider relative to the experiments. Within the LLCP hypothesis scenario, the -maximum is expected to increase as one approaches the LLCP and it should diverge at the LLCP. This is fully consistent with the PIMD simulations results shown in Fig. 3a. Specifically, as the pressure increases from MPa to MPa, the -maximum shifts to lower temperatures and increases in height. The same behavior of is found in classical MD simulations of water models that exhibit a LLCP14,15,21,64.
We also calculate using the TSEOS. The TSEOS provides an expression for the Gibbs free energy of the system from which the isothermal compressibility can easily be obtained,
| 2 |
A comparison of the values of obtained from the TSEOS and our MD/PIMD simulations are presented in Fig. 3c,d. The predictions from the TSEOS agree rather well with the MD simulation results [inset of Fig. 3d]. In the case of PIMD simulations [inset of Fig. 3c], the TSEOS provides compressibility values that are in good agreement with the simulation results at high temperatures. However, at lower temperatures, the TSEOS predicts slightly larger maxima in that are shifted to lower temperatures relative to the simulations. This suggests that, the location of the LLCP in q-TIP4P/F water from PIMD may be located at slightly lower and/or higher relative to the corresponding estimated values resulting from the TSEOS.
Next, we discuss the isobaric heat capacity,
| 3 |
In our previous work (at MPa)46, the enthalpy was calculated directly from MD and PIMD simulations at selected temperatures and then, the values of H(T) were fitted using a fourth-order polynomial. The resulting analytic expression for H(T) was then used in Eq. (3) to calculate . The use of a fourth-order polynomial in the fitting procedure is rather arbitrary. It captures the qualitative increase of upon cooling at low pressures but it may play a relevant role in identifying a -maximum, which is known to occur in experiments10. Accordingly, in this work, we take advantage of the TSEOS and use it to calculate H(T) at selected pressures; after all, the TSEOS reproduces very well the behavior (and maxima) of (see Fig. 1) and (see Fig. 3). Specifically, for a given pressure, we use the polynomial expression of G(T) given by the TSEOS and obtain an analytical expression for H(T) using the Gibbs–Helmholtz equation,
| 4 |
The obtained H(T) is then used in Eq. (3) to calculate . Figure 4a,b show the H(T) of q-TIP4P/F water obtained from (i) the TSEOS (solid lines) and (ii) classical MD and PIMD simulations (empty/solid circles). The TSEOS predictions are in excellent agreement with our simulations throughout the entire temperature and pressure range considered in this work.
Figure 4.
Enthalpy H(T) of q-TIP4P/F water as a function of temperature for selected pressures. Results are from (a) PIMD simulations (solid circles) and (b) classical MD simulations (empty circles). Lines are the corresponding H(T) obtained from the TSEOS. In both cases, the TSEOS predictions are in excellent agreement with the MD/PIMD simulation results.
Figure 5a,b show, respectively, the of q-TIP4P/F water from PIMD and classical MD simulations at selected pressures, above and below the estimated LLCP pressure; open symbols are experimental values. The from classical MD and PIMD simulations are qualitatively similar. Specifically, at the temperature studied, exhibits a maximum at approximately MPa. This -maximum increases and shifts to lower temperatures as the pressure increases towards the LLCP pressure. At MPa , is a monotonic decreasing function of T. Note that classical MD simulations predict much larger values of than found in PIMD simulations (which is known to occur when NQE are omitted68).
Figure 5.
(a) Heat capacity of q-TIP4P/F water for P = -100, 0.1, 100, 200, 300, and 400 MPa. was calculated by using Eq. (3) and the H(T) expression obtained from the TSEOS and PIMD simulations (solid lines). Experimental data are indicated by empty triangles (left-triangles from Refs.4,69; right-triangles from Refs.59). (b) Same as (a) for the case of classical MD simulations. The experimental data from Pathak et al.10 (green up-triangles) show a maximum at K.
Differences between the experimental data and MD/PIMD simulations are noticeable. For example, as shown in Fig. 5a, at MPa, PIMD simulations predict that decreases upon heating while experiments show the opposite behavior. In particular, at MPa, the of q-TIP4P/F water is in semiquantitative agreement with experiments down to K. The maximum in , at MPa, occurs at 228 K and 216 K in experiments and q-TIP4P/F water, respectively. However, the maxima of in q-TIP4P/F water is much smaller and wider than found in the experiments of Pathak et al.10. This is consistent with the estimated location of the LLCP in experiments and in our simulations. The LLCP in real water is estimated to be located at 50–100 MPa and K, while in q-TIP4P/F water we find =159 K and = 167 MPa. Accordingly, at MPa, experiments are much closer to the corresponding LLCP than in the case of q-TIP4P/F water6. Our results for also imply that PIMD and MD simulations of q-TIP4P/F water cannot reproduce the entropy fluctuations observed in real water at low temperatures and pressures.
Diffusion coefficient
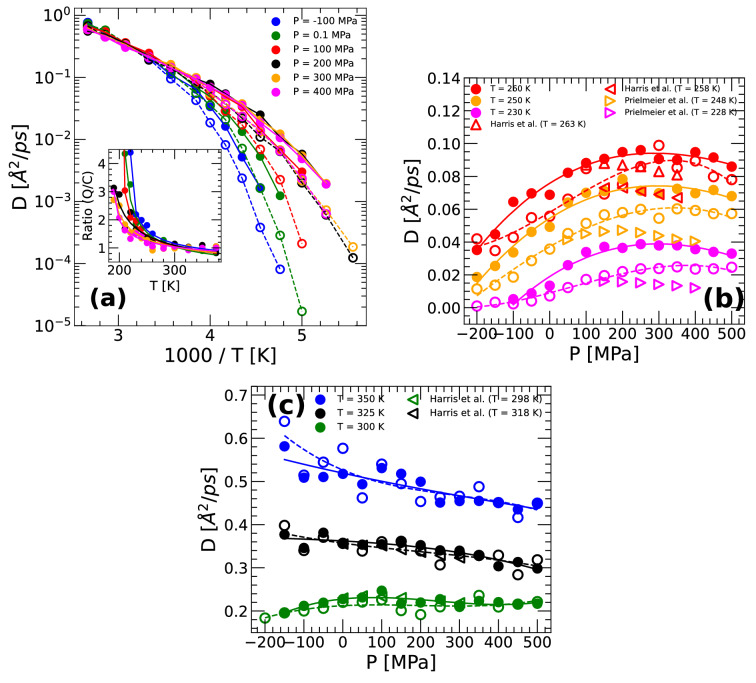
We also calculate the self-diffusion coefficient of q-TIP4P/F water D(T) as function of temperature at selected pressures. To obtain D(T), we employ the same methodology used in Ref.46. Briefly, using the RPMD simulation technique, we first calculate the mean-square displacement (MSD) of the oxygen atoms/ring-polymer centroids. D(T) is then evaluated from the slope of the MSD at long times, in the so-called diffusive regime. Figure 6a shows the D(T) of q-TIP4P/F water obtained from RPMD (solid circles) and classical MD (open circles) simulations. At high temperatures, D(T) is Arrhenius at all pressures studied, i.e.,
| 5 |
where , are constants; is the Boltzmann constant. At low temperatures, the behavior of D(T) depends on the pressure. Specifically, at high pressures, MPa, in the HDL domain, D(T) is non-Arrhenius and its behavior is well described by Mode Coupling Theory (MCT), i.e.,
| 6 |
where , , and the MCT temperature are constants. At low pressures (< 200 MPa), D(T) also obeys MCT but only down to approximately 200–220 K. Upon further cooling, D(T) seems to exhibit a crossover from non-Arrhenius ( 200–220 K) to Arrhenius ( K) behavior. An Arrhenius regime at low temperatures can be identified in Fig. 6a for the case MPa; the cases of MPa are less evident due to the limited available data at K.
Figure 6.
(a) Diffusion coefficient of q-TIP4P/F water as function of temperature at selected pressures. Results from RPMD simulations are indicated by solid circles; empty circles are results from classical MD simulations. Inset: ratio of the diffusion coefficients obtained from RPMD and MD simulations shown in the main panel. The inclusion of NQE increases water dynamics upon supercooling. (b,c) Diffusion coefficients of q-TIP4P/F water as function of pressure obtained from RPMD (solid circles) and classical MD simulations (empty circles); empty triangles correspond to experimental data (left-triangles and right-triangles from Refs.70,71, respectively). An anomalous diffusivity maximum exist in q-TIP4P/F water at approximately K.
The values of D from the MD/PIMD simulations are compared with the corresponding experimental values in Fig. 6b,c along different isotherms. At high temperatures, approximately K (Fig. 6c), the values of D(P) from classical MD and PIMD simulations practically overlap with the available experimental data at all pressures studied. Instead, at K (Fig. 6b), our simulation results predict values of D(P) that deviate by up to a factor of 4 from the corresponding experimental data, depending on pressure. Interestingly, overall, classical MD simulations are in slightly better agreement with experiments compared to the RPMD simulation results. Not surprising, as shown in the inset of Fig. 6a, the inclusion of NQE increases water diffusivities, particularly upon cooling within the supercooled regime.
One of the main points of Fig. 6b is the presence of an anomalous maximum in the diffusion coefficient of q-TIP4P/F water. Such a D-maximum is consistent with experiments and implies that there is a range of temperatures at which D increases (anomalously) with increasing P.
Phase diagram
Figure 7a,b show, respectively, the phase diagram of q-TIP4P/F water obtained from PIMD and classical MD simulations. These phase diagrams include the LLCP, coexistence line, -maxima, -maxima, and Widom line calculated from the TSEOS. Also included are the lines of -maxima, D-maxima, -maxima, -maxima, and -minima obtained from our MD/PIMD simulations. We also show the maxima/minima of these properties reported in experiments, where available. The liquid-vapor boundary lines shown in Fig. 7a,b correspond to the conditions at which spontaneous cavitation occurs during our computer simulation.
Figure 7.
Phase diagram of q-TIP4P/F HO obtained from (a) PIMD/RPMD and (b) classical MD simulations. The black solid and dashed lines are, respectively, the LLPT and Widom lines obtained from the TSEOS; the filled red star is the LLCP from the TSEOS. The red and blue solid lines are the -maxima and -maxima line from the TSEOS. The magenta crosses represent the vaporization line where the liquid spontaneously cavitates during the computer simulations. The green up-triangles are the density maxima. Blue up and down triangles represent, respectively, the maxima and minima in the isothermal compressibilities; red triangles indicate the maxima in . Brown up-triangles are the maxima in the diffusion coefficient; orange circles represent the MCT temperature (see Eq. 5). Experimental data are shown by empty triangles5,19,71,78–80; filled symbols are results from MD/PIMD simulations. The estimated location of the LLCP based on experiments is ( K, 50–100 MPa)12.
The phase diagrams of q-TIP4P/F water resulting from the classical MD and PIMD simulations are qualitatively similar. As found previously in ST242 and TIP4P/2005 water15, the and -maxima lines obtained from the TSEOS originate at the LLCP and deviate from each other at higher temperatures. The -maxima line (blue up-triangles) connects smoothly with the -minima line (blue down-triangles). In addition, as shown in Ref.35, the point in Figs. 7 and 8 where the -maxima line has infinite slope is located on the -extrema line, at which . The -maxima line has a nose shape. In particular, our simulations suggest that, at low pressures, the -maxima line is re-entrant and deviates from the liquid-vapor boundary line [see, in particular, Fig. 7b]. This implies that the ’re-entrant spinodal’ hypothesis scenario proposed to explain water anomalous behavior is not supported by MD/PIMD simulations of q-TIP4P/F water. Hence, our results are consistent with Refs.7,72, where computer simulations performed using the ST2 and TIP4P water model found that the spinodal line is also not re-entrant. We note that Fig. 7a,b also include available experimental data. When compared with experiments, both classical MD and PIMD reproduce correctly the location of the -maxima and minima lines; the PIMD simulation results reproduce slightly better the location of the -maxima line.
Figure 8.

Same as Fig. 7 for the case of DO. Results are from PIMD/RPMD simulations using the q-TIP4P/F water model. The empty green-up triangles are experimental maxima densities from Ref.81. The empty blue-up triangle is the isothermal compressibility maxima from Ref.5. The estimated location of the LLCP based on experiments is ( K, MPa)50.
Regarding the D-maxima line, both MD and RPMD simulations overestimate the corresponding pressures relative to the experiments, with the RPMD simulations performing slightly better. We also include in Fig. 7a,b the MCT temperatures extracted from Fig. 6a. The experimental MCT temperature at MPa is K73 and hence, this temperature is underestimated in both MD and RPMD simulations.
Overall, the results from classical MD simulations in Fig. 7b are consistent with the TSEOS. Accordingly, one may conclude that the reported location of the LLCP based on the TSEOS is robust in the case of classical MD simulations. For example, the -maxima from MD simulations and from the TSEOS (blue triangles and blue solid lines) overlap; similarly, the corresponding -maxima lines (red triangles and red solid lines) also overlap. In addition, we find that the line shows a sudden change in slope at the intersection with the Widom line. This is consistent with the view that the Widom line separates the LDL-like liquid at low pressures from the HDL-like liquid at high pressures. The sharp crossover in is reminiscent of the glass transition temperature of water as a function of pressure which shows a sudden change as the system evolves from LDL (low pressure) to HDL (high pressure)31,74,75.
In the case of PIMD simulations (Fig. 7a), the -maxima line obtained from the TSEOS (blue solid line) is located at slightly lower pressure relative to the PIMD simulation results (blue up-triangles). Similarly, the Widom line predicted by the TSEOS is located at a pressure slightly lower than the pressure at which the slope of suddenly changes. Hence, in the case of PIMD simulations for water, the reported location of the LLCP may shift slightly if additional data points at K are considered in the TSEOS calculation. Additional PIMD simulations are also needed to improve the determination of the -maxima line at low temperatures.
The similarities in the phase diagrams of Fig. 7a,b imply that, at least for the q-TIP4P/water model, the LLPT hypothesis scenario remains a solid, viable explanation of water anomalous behavior even if NQE (i.e., atoms delocalization) are included. This is important since (i) the LLCP scenario has been tested only in classical MD simulations and, mostly, rigid water models, and (ii) the location of the LLCP is extremely sensitive to small variations in the water model considered (e.g., small changes in the partial charges of the H and O atoms can easily shift the location of the LLCP to (P, T) conditions that are physically inaccessible to the liquid state; see, e.g., Refs.76,77). Overall, including NQE shifts the location of the LLCP, LLPT line, and maxima/minima lines towards lower temperatures (see also Ref.47,48).
So far, our discussion has been centered on HO. The same analysis presented here for HO was done for the case of DO by performing PIMD simulations using the q-TIP4P/F model. The analogous to Figs. 1, 2, 3, 4, 5 and 6 are included in Figs. S4–S8 of the SI. Here, we only discuss the phase diagram of q-TIP4P/F DO; see Fig. 8. The phase diagram of DO is qualitatively similar to the phase diagram of HO. The LLCP in q-TIP4P/F DO is located at ( g/cm, MPa, K). Relative to q-TIP4P/F HO, the LLCP in DO is shifted by ( g/cm, MPa, K). Accordingly, our results indicate that isotope substitution in water can play an important role in the phase behavior of low-temperature and supercooled water. These values of and are consistent with the locations of the LLCP in HO and DO estimated by Mishima and Stanley from decompression-induced experiments of ice IV49,50 where ( MPa, K).
Summary and discussion
We performed classical MD, PIMD, and RPMD simulations of HO using the q-TIP4P/F model over a wide range of temperatures and pressures. At supercritical temperatures, most properties studied are practically insensitive to whether one employs classical MD and PIMD simulations ( MPa). Specifically, the and obtained from classical MD or PIMD simulations overlap (within error bars) down to K and K, respectively (Fig. 1 and Fig. S2 of the SI). In the case of , the quantitative values vary for classical MD and PIMD results, but this is expected to occur due to NQE68. Nonetheless, the qualitative behavior of is independent on whether NQE are included or excluded. Similarly, the behavior of D(T) is not affected whether one employs classical MD or RPMD simulations down to K (Fig. 6a). Relative to the classical MD simulations, including NQE (RPMD simulations) increases the values of D(T) at K (inset of Fig. 6a). In both cases, the D(T) from computer simulations are in good agreement with experiments where data is available (Fig. 6b,c).
Deviations between MD and PIMD simulations become noticeable at approximately 100–200 MPa and K. Our results strongly indicate that at these thermodynamic conditions, q-TIP4P/F water exhibits a LLCP. Using a two-state equation of state, we estimate that the LLCP is located at g/cm, MPa, K) when NQE are not included (classical MD); including NQE (PIMD simulations) shifts the location of the LLCP to g/cm, MPa, K); see Fig. 1c,d. Consistent with the existence of a LLCP, our study shows the presence of loci of maxima in and in the P–T phase diagram of q-TIP4P/F water. These anomalous maxima lines, together with the loci of maxima in D and are included in Fig. 7. We stress that the location of the LLCPs reported in this work are estimations provided by the TSEOS. Our estimation of the LLCP for HO is based on PIMD simulations using beads per ring-polymer. While PIMD simulations with are computationally expensive, additional PIMD simulations employing beads per ring-polymer are desirable at low temperatures in order to obtain a more precise estimation of the LLCP location in HO (q-TIP4P/F water). While our results conclusively show that the LLCP in HO shifts to lower T when NQE are included, obtaining the exact values of () may require additional data at K (particularly for the case of PIMD simulations of HO where is low).
Overall, our results for HO (e.g., Fig. 7) are consistent with previous classical computer simulations of water using the (rigid) ST242 and TIP4P/200515 water models. It follows that the present study validates the LLPT hypothesis for water to the case where NQE are included. We note, however, that the LLCP in q-TIP4P/F water, as well as in ST2, TIP4P/2005, and TIP4P/Ice water, is located at pressures and temperatures that are off compared to the experimental predictions6,46. This provides a thermodynamic explanation of why these water models are unable to reproduce the sharp increase in and observed in experiments at MPa5,10. Specifically, these water models predict that MPa, while MPa estimated from experiments1,50. Accordingly, computer simulations show a mild increase in and , relative to experiments, upon isobaric cooling at P = 0.1 MPa. We note that the and quantify the fluctuations in entropy and volume, respectively. Hence, from a microscopic point of view, the weak increase of and upon isobaric cooling at P = 0.1 MPa is due to the inability of current water models (ST2, TIP4P/2005, TIP4P/Ice, etc) to reproduce the anomalously large fluctuations (in entropy and volume) of real water in the supercooled regime. At least for the q-TIP4P/F model studied, the inclusion of NQE (quantum fluctuations due to atoms delocalization) is not sufficient to reproduce the anomalously large fluctuations (in entropy and volume) of real water at low temperatures. Accordingly, additional sources of fluctuations may be missed in rigid (e.g., TIP4P/2005, ST2) as well as flexible water models, such as q-TIP4P/F model.
We also performed extensive PIMD simulations of heavy water using the q-TIP4P/F model. The results are summarized in the phase diagram of Fig. 8 (see also the SI). The PIMD simulations confirm that isotope substitution has minor effects on the properties of water. While the phase diagram of DO is qualitatively identical to the phase diagram of HO, the location of the corresponding LLCP differ. Specifically, calculations based on the TSEOS, applied to PIMD data at K, predict that in the case of DO, ( g/cm, MPa, K) which represents a non-negligible shift relative to HO ( g/cm, MPa, K). This is important since computer simulations of water-like models show that the introduction of NQE can indeed shift considerably the location of the LLCP47,48. In particular, the differences in the relative values of (, , ) between q-TIP4P/F HO and DO are somewhat consistent with the predictions from experiments in glassy water ( MPa, K)49,50 and with the relative location of the -maximum at 1 bar10. The present study shows that many questions previously addressed in computational studies of supercooled water at low temperatures, using classical water models, are accessible via PIMD simulations. For example, it would be interesting to explore the relationship between dynamics and structure of water at low temperatures and how the Stokes–Einstein and Stokes–Einstein–Debye relationships are affected by isotope substitution82–85.
Supplementary Information
Acknowledgements
This work was supported by the SCORE Program of the National Institutes of Health under award number 1SC3GM139673 and the NSF CREST Center for Interface Design and Engineered Assembly of Low Dimensional systems (IDEALS), NSF Grant number HRD-1547380. This work was supported, in part, by a grant of computer time from the City University of New York High Performance Computing Center under NSF Grants CNS-0855217, CNS-0958379 and ALI-1126113.
Author contributions
N.G. and G.E.L. designed research; A.E. performed research; A.E., G.E.L., and N.G. analyzed data; and A.E., G.E.L., and N.G. wrote the paper.
Data availibility
All study data are included in the article and/or SI.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-022-09525-x.
References
- 1.Gallo P, Amann-Winkel K, Angell CA, Anisimov MA, Caupin F, Chakravarty C, Lascaris E, Loerting T, Panagiotopoulos AZ, Russo J, et al. Water: A tale of two liquids. Chem. Rev. 2016;116:7463. doi: 10.1021/acs.chemrev.5b00750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Speedy R, Angell C. Isothermal compressibility of supercooled water and evidence for a thermodynamic singularity at - 45 C. J. Chem. Phys. 1976;65:851. doi: 10.1063/1.433153. [DOI] [Google Scholar]
- 3.Angell C, Shuppert J, Tucker J. Anomalous properties of supercooled water. Heat capacity, expansivity, and proton magnetic resonance chemical shift from 0 to-38%. J. Phys. Chem. 1973;77:3092. doi: 10.1021/j100644a014. [DOI] [Google Scholar]
- 4.Angell C, Sichina W, Oguni M. Heat capacity of water at extremes of supercooling and superheating. J. Phys. Chem. 1982;86:998. doi: 10.1021/j100395a032. [DOI] [Google Scholar]
- 5.Kim KH, Späh A, Pathak H, Perakis F, Mariedahl D, Amann-Winkel K, Sellberg JA, Lee JH, Kim S, Park J, et al. Maxima in the thermodynamic response and correlation functions of deeply supercooled water. Science. 2017;358:1589. doi: 10.1126/science.aap8269. [DOI] [PubMed] [Google Scholar]
- 6.Pathak H, Späh A, Amann-Winkel K, Perakis F, Kim KKH, Nilsson A. Temperature dependent anomalous fluctuations in water: Shift of 1 kbar between experiment and classical force field simulations. Mol. Phys. 2019;117:3232. doi: 10.1080/00268976.2019.1649486. [DOI] [Google Scholar]
- 7.Poole PH, Sciortino F, Essmann U, Stanley HE. Phase behaviour of metastable water. Nature (London) 1992;360:324. doi: 10.1038/360324a0. [DOI] [Google Scholar]
- 8.Mishima O, Stanley HE. The relationship between liquid, supercooled and glassy water. Nature (London) 1998;396:329. doi: 10.1038/24540. [DOI] [Google Scholar]
- 9.Kim KH, Amann-Winkel K, Giovambattista N, Späh A, Perakis F, Pathak H, Parada ML, Yang C, Mariedahl D, Eklund T, et al. Experimental observation of the liquid–liquid transition in bulk supercooled water under pressure. Science. 2020;370:978. doi: 10.1126/science.abb9385. [DOI] [PubMed] [Google Scholar]
- 10.Pathak H, Späh A, Esmaeildoost N, Sellberg JA, Kim KH, Perakis F, Amann-Winkel K, Ladd-Parada M, Koliyadu J, Lane TJ, et al. Enhancement and maximum in the isobaric specific-heat capacity measurements of deeply supercooled water using ultrafast calorimetry. Proc. Natl. Acad. Sci. 2021;118:6. doi: 10.1073/pnas.2018379118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Suzuki Y, Mishima O. Experimentally proven liquid–liquid critical point of dilute glycerol-water solution at 150 K. J. Chem. Phys. 2014;141:094505. doi: 10.1063/1.4894416. [DOI] [PubMed] [Google Scholar]
- 12.Mishima O. Volume of supercooled water under pressure and the liquid–liquid critical point. J. Chem. Phys. 2010;133:144503. doi: 10.1063/1.3487999. [DOI] [PubMed] [Google Scholar]
- 13.Späh A, Pathak H, Kim KH, Perakis F, Mariedahl D, Amann-Winkel K, Sellberg JA, Lee JH, Kim S, Park J, et al. Apparent power-law behavior of water’s isothermal compressibility and correlation length upon supercooling. Phys. Chem. Chem. Phys. 2019;21:26. doi: 10.1039/C8CP05862H. [DOI] [PubMed] [Google Scholar]
- 14.Singh RS, Biddle JW, Debenedetti PG, Anisimov MA. Two-state thermodynamics and the possibility of a liquid–liquid phase transition in supercooled TIP4P/2005 water. J. Chem. Phys. 2016;144:144504. doi: 10.1063/1.4944986. [DOI] [PubMed] [Google Scholar]
- 15.González MA, Valeriani C, Caupin F, Abascal JL. A comprehensive scenario of the thermodynamic anomalies of water using the TIP4P/2005 model. J. Chem. Phys. 2016;145:054505. doi: 10.1063/1.4960185. [DOI] [PubMed] [Google Scholar]
- 16.Pallares G, Gonzalez MA, Abascal JLF, Valeriani C, Caupin F. Equation of state for water and its line of density maxima down to - 120 MPa. Phys. Chem. Chem. Phys. 2016;18:5896. doi: 10.1039/C5CP07580G. [DOI] [PubMed] [Google Scholar]
- 17.Pallares G, Azouzi MEM, González MA, Aragones JL, Abascal JL, Valeriani C, Caupin F. Anomalies in bulk supercooled water at negative pressure. Proc. Natl. Acad. Sci. 2014;111:7936. doi: 10.1073/pnas.1323366111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Debenedetti PG, Sciortino F, Zerze GH. Second critical point in two realistic models of water. Science. 2020;369:289. doi: 10.1126/science.abb9796. [DOI] [PubMed] [Google Scholar]
- 19.Holten V, Bertrand C, Anisimov M, Sengers J. Thermodynamics of supercooled water. J. Chem. Phys. 2012;136:094507. doi: 10.1063/1.3690497. [DOI] [PubMed] [Google Scholar]
- 20.Holten V, Anisimov M. Entropy-driven liquid–liquid separation in supercooled water. Sci. Rep. 2012;2:1. doi: 10.1038/srep00713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gartner TE, Zhang L, Piaggi PM, Car R, Panagiotopoulos AZ, Debenedetti PG. Signatures of a liquid–liquid transition in an ab initio deep neural network model for water. Proc. Natl. Acad. Sci. 2020;117:26040. doi: 10.1073/pnas.2015440117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Biddle JW, Singh RS, Sparano EM, Ricci F, González MA, Valeriani C, Abascal JL, Debenedetti PG, Anisimov MA, Caupin F. Two-structure thermodynamics for the TIP4P/2005 model of water covering supercooled and deeply stretched regions. J. Chem. Phys. 2017;146:034502. doi: 10.1063/1.4973546. [DOI] [PubMed] [Google Scholar]
- 23.Holten V, Palmer JC, Poole PH, Debenedetti PG, Anisimov MA. Two-state thermodynamics of the ST2 model for supercooled water. J. Chem. Phys. 2014;140:104502. doi: 10.1063/1.4867287. [DOI] [PubMed] [Google Scholar]
- 24.Loerting T, Giovambattista N. Amorphous ices: Experiments and numerical simulations. J. Phys. Condens. Matter. 2006;18:R919. doi: 10.1088/0953-8984/18/50/R01. [DOI] [Google Scholar]
- 25.Mishima O, Calvert L, Whalley E. ‘Melting ice’ I at 77 K and 10 kbar: A new method of making amorphous solids. Nature (London) 1984;310:393. doi: 10.1038/310393a0. [DOI] [Google Scholar]
- 26.Mishima O, Calvert L, Whalley E. An apparently first-order transition between two amorphous phases of ice induced by pressure. Nature (London) 1985;314:76. doi: 10.1038/314076a0. [DOI] [Google Scholar]
- 27.Amann-Winkel K, Böhmer R, Fujara F, Gainaru C, Geil B, Loerting T. Colloquium: Water’s controversial glass transitions. Rev. Mod. Phys. 2016;88:011002. doi: 10.1103/RevModPhys.88.011002. [DOI] [Google Scholar]
- 28.Angell CA. Amorphous water. Annu. Rev. Phys. Chem. 2004;55:559. doi: 10.1146/annurev.physchem.55.091602.094156. [DOI] [PubMed] [Google Scholar]
- 29.Wong J, Jahn DA, Giovambattista N. Pressure-induced transformations in glassy water: A computer simulation study using the TIP4P/2005 model. J. Chem. Phys. 2015;143:074501. doi: 10.1063/1.4928435. [DOI] [PubMed] [Google Scholar]
- 30.Engstler J, Giovambattista N. Heating-and pressure-induced transformations in amorphous and hexagonal ice: A computer simulation study using the TIP4P/2005 model. J. Chem. Phys. 2017;147:074505. doi: 10.1063/1.4998747. [DOI] [PubMed] [Google Scholar]
- 31.Giovambattista N, Loerting T, Lukanov BR, Starr FW. Interplay of the glass transition and the liquid–liquid phase transition in water. Sci. Rep. 2012;2:1. doi: 10.1038/srep00390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Giovambattista N, Starr FW, Poole PH. State variables for glasses: The case of amorphous ice. J. Chem. Phys. 2019;150:224502. doi: 10.1063/1.5092586. [DOI] [PubMed] [Google Scholar]
- 33.Martelli F, Giovambattista N, Torquato S, Car R. Searching for crystal-ice domains in amorphous ices. Phys. Rev. Mater. 2018;2:075601. doi: 10.1103/PhysRevMaterials.2.075601. [DOI] [Google Scholar]
- 34.Handle PH, Sciortino F, Giovambattista N. Glass polymorphism in TIP4P/2005 water: A description based on the potential energy landscape formalism. J. Chem. Phys. 2019;150:244506. doi: 10.1063/1.5100346. [DOI] [PubMed] [Google Scholar]
- 35.Sastry S, Debenedetti PG, Sciortino F, Stanley HE. Singularity-free interpretation of the thermodynamics of supercooled water. Phys. Rev. E. 1996;53:6144. doi: 10.1103/PhysRevE.53.6144. [DOI] [PubMed] [Google Scholar]
- 36.Mishima O. Reversible first-order transition between two HO amorphs at 0.2 GPa and 135 K. J. Chem. Phys. 1994;100:5910. doi: 10.1063/1.467103. [DOI] [Google Scholar]
- 37.Amann-Winkel K, Gainaru C, Handle PH, Seidl M, Nelson H, Bohmer R, Loerting T. Water’s second glass transition. Proc. Natl. Acad. Sci. 2013;110:17720. doi: 10.1073/pnas.1311718110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Palmer JC, Martelli F, Liu Y, Car R, Panagiotopoulos AZ, Debenedetti PG. Metastable liquid–liquid transition in a molecular model of water. Nature (London) 2014;510:385. doi: 10.1038/nature13405. [DOI] [PubMed] [Google Scholar]
- 39.Palmer JC, Car R, Debenedetti PG. The liquid–liquid transition in supercooled ST2 water: A comparison between umbrella sampling and well-tempered metadynamics. Faraday Discuss. 2013;167:77. doi: 10.1039/c3fd00074e. [DOI] [PubMed] [Google Scholar]
- 40.Palmer JC, Poole PH, Sciortino F, Debenedetti PG. Advances in computational studies of the liquid–liquid transition in water and water-like models. Chem. Rev. 2018;118:9129. doi: 10.1021/acs.chemrev.8b00228. [DOI] [PubMed] [Google Scholar]
- 41.Liu Y, Palmer JC, Panagiotopoulos AZ, Debenedetti PG. Liquid–liquid transition in ST2 water. J. Chem. Phys. 2012;137:2140505. doi: 10.1063/1.4769126. [DOI] [PubMed] [Google Scholar]
- 42.Poole PH, Saika-Voivod I, Sciortino F. Density minimum and liquid–liquid phase transition. J. Phys. Condens. Matter. 2005;17:L431. doi: 10.1088/0953-8984/17/43/L01. [DOI] [Google Scholar]
- 43.Handle PH, Sciortino F. Potential energy landscape of TIP4P/2005 water. J. Chem. Phys. 2018;148:134505. doi: 10.1063/1.5023894. [DOI] [PubMed] [Google Scholar]
- 44.Poole PH, Bowles RK, Saika-Voivod I, Sciortino F. Free energy surface of ST2 water near the liquid–liquid phase transition. J. Chem. Phys. 2013;138:034505. doi: 10.1063/1.4775738. [DOI] [PubMed] [Google Scholar]
- 45.Ceriotti M, Fang W, Kusalik PG, McKenzie RH, Michaelides A, Morales MA, Markland TE. Nuclear quantum effects in water and aqueous systems: Experiment, theory, and current challenges. Chem. Rev. 2016;116:7529. doi: 10.1021/acs.chemrev.5b00674. [DOI] [PubMed] [Google Scholar]
- 46.Eltareb A, Lopez GE, Giovambattista N. Nuclear quantum effects on the thermodynamic, structural, and dynamical properties of water. Phys. Chem. Chem. Phys. 2021;23:6914. doi: 10.1039/D0CP04325G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu Y, Sun G, Eltareb A, Lopez GE, Giovambattista N, Xu L. Nuclear quantum effects on the thermodynamic response functions of a polymorphic waterlike monatomic liquid. Phys. Rev. Res. 2020;2:013153. doi: 10.1103/PhysRevResearch.2.013153. [DOI] [Google Scholar]
- 48.Nguyen B, Lopez GE, Giovambattista N. Nuclear quantum effects on the liquid–liquid phase transition of a water-like monatomic liquid. Phys. Chem. Chem. Phys. 2018;20:8210. doi: 10.1039/C7CP08505B. [DOI] [PubMed] [Google Scholar]
- 49.Mishima O, Stanley HE. Decompression-induced melting of ice IV and the liquid–liquid transition in water. Nature (London) 1998;392:164. doi: 10.1038/32386. [DOI] [Google Scholar]
- 50.Mishima O. Liquid–liquid critical point in heavy water. Phys. Rev. Lett. 2000;85:334. doi: 10.1103/PhysRevLett.85.334. [DOI] [PubMed] [Google Scholar]
- 51.Caupin F, Anisimov MA. Thermodynamics of supercooled and stretched water: Unifying two-structure description and liquid-vapor spinodal. J. Chem. Phys. 2019;151:034503. doi: 10.1063/1.5100228. [DOI] [PubMed] [Google Scholar]
- 52.Duboué-Dijon E, Laage D. Characterization of the local structure in liquid water by various order parameters. J. Phys. Chem. B. 2015;119:8406. doi: 10.1021/acs.jpcb.5b02936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ansari N, Dandekar R, Caravati S, Sosso G, Hassanali A. High and low density patches in simulated liquid water. J. Chem. Phys. 2018;149:204507. doi: 10.1063/1.5053559. [DOI] [PubMed] [Google Scholar]
- 54.Habershon S, Markland TE, Manolopoulos DE. Competing quantum effects in the dynamics of a flexible water model. J. Chem. Phys. 2009;131:024501. doi: 10.1063/1.3167790. [DOI] [PubMed] [Google Scholar]
- 55.Abascal JL, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005;123:234505. doi: 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- 56.Ceriotti M, Parrinello M, Markland TE, Manolopoulos DE. Efficient stochastic thermostatting of path integral molecular dynamics. J. Chem. Phys. 2010;133:124104. doi: 10.1063/1.3489925. [DOI] [PubMed] [Google Scholar]
- 57.Eastman P, Friedrichs MS, Chodera JD, Radmer RJ, Bruns CM, Ku JP, Beauchamp KA, Lane TJ, Wang L-P, Shukla D, et al. OpenMM 4: A reusable, extensible, hardware independent library for high performance molecular simulation. J. Chem. Theory Comput. 2013;9:461. doi: 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Holten V, Limmer DT, Molinero V, Anisimov MA. Nature of the anomalies in the supercooled liquid state of the mW model of water. J. Chem. Phys. 2013;138:174501. doi: 10.1063/1.4802992. [DOI] [PubMed] [Google Scholar]
- 59.Wagner W, Pruß A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data. 2002;31:387. doi: 10.1063/1.1461829. [DOI] [Google Scholar]
- 60.Kell G. Precise representation of volume properties of water at one atmosphere. J. Chem. Eng. Data. 1967;12:66. doi: 10.1021/je60032a018. [DOI] [Google Scholar]
- 61.Hare D, Sorensen C. Densities of supercooled HO and DO in 25 glass capillaries. J. Chem. Phys. 1986;84:5085. doi: 10.1063/1.450660. [DOI] [Google Scholar]
- 62.Callen HB. Thermodynamics and an Introduction to Thermostatistics. Wiley; 2006. [Google Scholar]
- 63.Pathria R, Beale PD. Statistical Mechanics. Elsevier; 2011. [Google Scholar]
- 64.Abascal JL, Vega C. Widom line and the liquid–liquid critical point for the TIP4P/2005 water model. J. Chem. Phys. 2010;133:234502. doi: 10.1063/1.3506860. [DOI] [PubMed] [Google Scholar]
- 65.Kanno H, Angell C. Water: Anomalous compressibilities to 1.9 kbar and correlation with supercooling limits. J. Chem. Phys. 1979;70:4008. doi: 10.1063/1.438021. [DOI] [Google Scholar]
- 66.Kell GS. Density, thermal expansivity, and compressibility of liquid water from 0. deg. to 150. deg. Correlations and tables for atmospheric pressure and saturation reviewed and expressed on 1968 temperature scale. J. Chem. Eng. Data. 1975;20:97. doi: 10.1021/je60064a005. [DOI] [Google Scholar]
- 67.Ter Minassian L, Pruzan P, Soulard A. Thermodynamic properties of water under pressure up to 5 kbar and between 28 and 120 C. Estimations in the supercooled region down to - 40 C. J. Chem. Phys. 1981;75:3064. doi: 10.1063/1.442402. [DOI] [Google Scholar]
- 68.Vega C, Conde MM, McBride C, Abascal JLF, Noya EG, Ramírez R, Sesé LM. Heat capacity of water: A signature of nuclear quantum effects. J. Chem. Phys. 2010;132:046101. doi: 10.1063/1.3298879. [DOI] [PubMed] [Google Scholar]
- 69.Troncoso J. The isobaric heat capacity of liquid water at low temperatures and high pressures. J. Chem. Phys. 2017;147:084501. doi: 10.1063/1.4990381. [DOI] [PubMed] [Google Scholar]
- 70.Harris KR, Woolf LA. Pressure and temperature dependence of the self diffusion coefficient of water and oxygen-18 water. J. Chem. Soc. Faraday Trans. 1980;76:377. doi: 10.1039/f19807600377. [DOI] [Google Scholar]
- 71.Prielmeier F, Lang E, Speedy R, Lüdemann H-D. Diffusion in supercooled water to 300 MPa. Phys. Rev. Lett. 1987;59:1128. doi: 10.1103/PhysRevLett.59.1128. [DOI] [PubMed] [Google Scholar]
- 72.Poole PH, Sciortino F, Essmann U, Stanley HE. Spinodal of liquid water. Phys. Rev. E. 1993;48:3799. doi: 10.1103/PhysRevE.48.3799. [DOI] [PubMed] [Google Scholar]
- 73.Torre R, Bartolini P, Righini R. Structural relaxation in supercooled water by time-resolved spectroscopy. Nature (London) 2004;428:296. doi: 10.1038/nature02409. [DOI] [PubMed] [Google Scholar]
- 74.Gordon A, Giovambattista N. Glass transitions in a monatomic liquid with two glassy states. Phys. Rev. Lett. 2014;112:145701. doi: 10.1103/PhysRevLett.112.145701. [DOI] [PubMed] [Google Scholar]
- 75.Gartner TE, Torquato S, Car R, Debenedetti PG. Manifestations of metastable criticality in the long-range structure of model water glasses. Nat. Commun. 2021;12:1. doi: 10.1038/s41467-021-23639-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Smallenburg F, Poole PH, Sciortino F. Phase diagram of the ST2 model of water. Mol. Phys. 2015;113:2791. doi: 10.1080/00268976.2015.1043966. [DOI] [Google Scholar]
- 77.Horstmann R, Vogel M. Relations between thermodynamics, structures, and dynamics for modified water models in their supercooled regimes. J. Chem. Phys. 2021;154:054502. doi: 10.1063/5.0037080. [DOI] [PubMed] [Google Scholar]
- 78.Henderson SJ, Speedy RJ. Temperature of maximum density in water at negative pressure. J. Phys. Chem. 1987;91:3062. doi: 10.1021/j100295a084. [DOI] [Google Scholar]
- 79.Vedamuthu M, Singh S, Robinson GW. Properties of liquid water. 4. The isothermal compressibility minimum near 50. degree. C. J. Phys. Chem. 1995;99:9263. doi: 10.1021/j100022a047. [DOI] [Google Scholar]
- 80.Holten V, Qiu C, Guillerm E, Wilke M, Ricka J, Frenz M, Caupin F. Compressibility anomalies in stretched water and their interplay with density anomalies. J. Phys. Chem. Lett. 2017;8:5519. doi: 10.1021/acs.jpclett.7b02563. [DOI] [PubMed] [Google Scholar]
- 81.Kanno H, Angell C. Volumetric and derived thermal characteristics of liquid DO at low temperatures and high pressures. J. Chem. Phys. 1980;73:1940. doi: 10.1063/1.440331. [DOI] [Google Scholar]
- 82.Zhang C, Galli G. Dipolar correlations in liquid water. J. Chem. Phys. 2014;141:084504. doi: 10.1063/1.4893638. [DOI] [PubMed] [Google Scholar]
- 83.Ansari N, Onat B, Sosso GC, Hassanali A. Insights into the emerging networks of voids in simulated supercooled water. J. Phys. Chem. B. 2020;124:2180. doi: 10.1021/acs.jpcb.9b10144. [DOI] [PubMed] [Google Scholar]
- 84.Mazza MG, Giovambattista N, Stanley HE, Starr FW. Connection of translational and rotational dynamical heterogeneities with the breakdown of the Stokes–Einstein and Stokes–Einstein–Debye relations in water. Phys. Rev. E. 2007;76:031203. doi: 10.1103/PhysRevE.76.031203. [DOI] [PubMed] [Google Scholar]
- 85.Ragueneau, P., Caupin, F., & Issenmann, B. Shear viscosity and Stokes–Einstein violation in supercooled light and heavy water. arXiv:2112.09024 (2021). [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI.