Abstract
Although free‐water diffusion reconstruction for diffusion‐weighted imaging (DWI) data can be applied to both single‐shell and multishell data, recent finding in synthetic data suggests that the free‐water indices from single‐shell acquisition should be interpreted with care, as they are heavily influenced by initialization parameters and cannot discriminate between free‐water and mean diffusivity modifications. However, whether using a longer multishell acquisition protocol significantly improve reconstruction for real human MRI data is still an open question. In this study, we compare canonical diffusion tensor imaging (DTI), single‐shell and multishell free‐water imaging (FW) indices derived from a short, clinical compatible diffusion protocol (b = 500 s/mm2, b = 1,000 s/mm2, 32 directions each) on their power to predict brain age. Age was chosen as it is well‐known to be related to widespread modification of the white matter and because brain‐age estimation has recently been found to be relevant to several neurodegenerative diseases. We used a previously developed and validated data‐driven whole‐brain machine learning pipeline to directly compare the precision of brain‐age estimates in a sample of 89 healthy males between 20 and 85 years old. We found that multishell FW outperform DTI indices in estimating brain age and that multishell FW, even when using low (500 ms2) b‐values secondary shell, outperform single‐shell FW. Single‐shell FW led to lower brain‐age estimation accuracy even of canonical DTI indices, suggesting that single‐shell FW indices should be used with caution. For all considered reconstruction algorithms, the most discriminant indices were those measuring free diffusion of water in the white matter.
Keywords: brain age, DTI, free‐water imaging, multishell DWI
Multishell but not single‐shell free‐water diffusion imaging predicts brain age better than canonical diffusion imaging. Multishell free‐water in isolation performs similarly to more complex models including FA, MD, RD and AD.
1. INTRODUCTION
Diffusion‐weighted imaging (DWI) is the tool of choice to inquire white matter microstructure in vivo. Since the inception of the diffusion tensor imaging model (Pierpaoli, Jezzard, Basser, Barnett, & Di Chiro, 1996), more complex modeling of diffusion data have become available to the scientific community, such as free‐water imaging (FW) (Pasternak et al., 2012; Pasternak, Sochen, Gur, Intrator, & Assaf, 2009). Diffusion tensor imaging (DTI) and FW differ in the way in which they reconstruct the diffusion signal in a voxel, and in their requirements in terms of acquisition parameters. DTI models each voxel as a single compartment and can be performed with a single‐shell acquisition (one “b‐value,” ~1,000 s/mm2), and with a low number of diffusion gradient directions (at least 6, but generally >16 are used). In FW reconstruction, the signal is supposed to have two contributions: one from the tissue, and another from free diffusing water. A free‐water map is calculated and can be used to correct DTI indices for the free‐water content at any given voxel as well as a microstructural index per se. Free‐water imaging has been shown to provide more sensitive estimate of DTI indices than classical DTI, thus being best suited as biomarker (Hoy, Koay, Kecskemeti, & Alexander, 2014; Pasternak et al., 2009; Pasternak et al., 2012).
The free‐water model can be solved for both single‐shell (i.e., only one b‐value, e.g., b = 1,000 s/mm2) (Pasternak et al., 2009) and multishell (i.e., more than one b‐value, e.g., b = 500 s/mm2 and b = 1,500 s/mm2) acquisitions (Henriques et al., 2017; Hoy et al., 2014). However, the problem is ill‐posed for single‐shell acquisition (Pasternak et al., 2009). Recently, it has been suggested that even if single‐shell acquisitions lead to plausible free‐water reconstruction, they are less accurate and more prone to errors than multishell acquisitions (Golub, Neto Henriques, & Gouveia Nunes, 2021): the accuracy of the indices derived from single‐shell free‐water reconstruction algorithm are extremely sensitive to the initialization parameters and single‐shell reconstruction cannot distinguish between free‐water and mean diffusivity alterations (Golub et al., 2021).
Although differences in the accuracy of single‐shell and multishell free‐water reconstruction have been shown both in synthetic (Golub et al., 2021; Hoy et al., 2014) and single‐subject real data (Hoy et al., 2014), there is a lack of study comparing these two methods in bigger sample. In particular, an open question is whether the added benefit of the increased accuracy granted by the multishell protocol for FW imaging is enough to offset the negative impact that a longer acquisition time (due to the need of using a multishell protocol) could have on subjects and patients compliance, especially in sensitive populations such as elderly subjects, or patient with neurodegenerative diseases.
In this study we compared DTI, and single‐shell and multishell FW indices derived from a multishell protocol comprising two shells (b = 500 s/mm2 and b = 1,000 s/mm2) with 32 directions each. The main aim of this study is two‐folded: on the one hand, we aimed to test the added value of including a short diffusion acquisition (b = 500 s/mm2) to calculate multishell FW indices, in the light of the recent reporting of suboptimal solution from single‐shell acquisition (Golub et al., 2021). On the other hand, we wanted to replicate previous finding that FW imaging lead to more accurate age predictions than canonical DTI model.
We chose to compare the different indices in terms of (a) the variance in age they explained in our sample and (b) their ability to predict the age of unseen subject. Although age prediction may seem a trivial task (as asking someone their age is easier then perform an MRI followed by complex multivariate analyses), age predicted using brain imaging (henceforth brain age) has been shown in previous studies to be a marker of pathology (Cole & Franke, 2017; Cole, Marioni, Harris, & Deary, 2019; Franke & Gaser, 2019) and age‐related neurodegeneration is a predictive marker of pathological aging and dementia (Fossel, 2020). Moreover, age is well known to be related to widespread microstructural modifications in the white matter (Moseley, 2002; Sala et al., 2012; Salat et al., 2005; Sullivan & Pfefferbaum, 2006). The different reconstruction models used to analyze data from DWI have given generally consistent results about white matter change over aging, with tract specific peak (Lebel et al., 2012) and greater longitudinal changes in associative tracts (Bender, Völkle, & Raz, 2016). Generally, these results hold when DTI indices are corrected for free‐water compartment, although association with age tends to become weaker and the proportion of free‐water in each voxel becomes the best predictor of aging (Chad, Pasternak, Salat, & Chen, 2018). A recent study comparing several diffusion reconstruction algorithms based on multishell acquisition (DTI, diffusion kurtosis imaging, neurite orientation dispersion and density imaging, restriction spectrum imaging, spherical mean technique multicompartment and white matter tract integrity) showed a general advantage of the multishell based indices over canonical DTI indices to track brain age, with the neurite orientation dispersion and density imaging being particularly predictive (Beck et al., 2021). This study also report global rather than regional specific associations among the indices and age (Beck et al., 2021). However, the study by Beck and colleagues did not include free‐water imaging among the reconstruction algorithms studies and used a region‐of‐interest rather than a voxel‐wise approach, which could hide possible regional‐specific association.
Here we will use general linear models to assess the variance explained by the different indices and a previously validated voxel‐wise machine‐learning approach that combines features selection and reduction steps with support vector regression (Nemmi et al., 2019; Nemmi et al., 2019) to predict brain age from DTI, and single‐shell and multishell FW indices. Our machine learning method can directly compare the predictive power of the different indices and can produce a multiparametric signature of age by selecting only the most discriminant parameters and brain regions.
2. MATERIALS AND METHODS
2.1. Subjects
Eighty‐nine males between 20 and 85 years of age (56 ± 18 years) were included in this study (a histogram of the age distribution is reported in Figure S1, Supporting Information). All subjects were right‐handed, without any history of neurological and psychiatric disease and with no history of alcohol abuse. Exclusion criteria were MMSE lower than 28 and the presence of any gross brain abnormality as revealed by T1 or FLAIR imaging by an expert radiologist. This study was approved by the local ethics committee, was in compliance with the Declaration of Helsinki and all participants gave their written informed consent.
2.2. MRI acquisition
All the subjects were scanned with a 3‐T MRI scanner (Philips Achieva, Inserm/UPS UMR1214 ToNIC Technical Platform, Toulouse, France) with a 32‐channel head antenna. An anatomical T1 was acquired using a 3D Turbo Field Echo (TFE) sequence, with the following parameters: echo time TE = 3.7 ms, repetition time TR = 8.1 ms, flip angle = 8°, FOV = 240 × 240 voxels, number of slices = 170, voxel size = 1 mm (isotropic). For the DWI, 1 the parameters were TE = 55 ms; TR = 12.36 s; flip angle = 90°; FOV = 112 × 112 voxels; number of slices = 65; voxels size = 2 mm (isotropic); EPI factor = 59; parallel factor = 2; phase encoding direction = postero‐anterior; b‐value (number of directions) = 0 (1), 500 (32), 1,000 (32) s/mm2; total acquisition time = 16 ms.
2.3. DWI preprocessing
All images were visually inspected for obvious artifact by one of the authors (FN) and all were deemed acceptable. To increase signal‐to‐noise ratio, usually low in DWI because of random noise, DWIs were first denoised using the local principal component analysis (LPCA) algorithm (Manjón, Coupé, Martí‐Bonmatí, Collins, & Robles, 2010); then the eddy current induced distortions and head movements were corrected using FMRIB Software Library (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012). We also calculated the framewise displacement (FD) from the realignment parameter as suggested in Power, Barnes, Snyder, Schlaggar, and Petersen (2012). For all subjects no volume showed a framewise displacement (FD) relative to the previous one of more than 1.5 mm. The mean average FD (i.e., the sample average of the average FD for each subject) was of 0.67 [0.63, 0.71] mm and no subjects had an average FD higher than 1 mm. Association between FD and age and between FD and model performances are reported in Data S1 (see In‐scanner movement, age and performances).
2.4. Diffusion metrics computation and normalization
The images acquired with the b‐value of 1,000 s/mm2 were used to calculate the DTI metrics (MD, FA, AD and RD) and the single‐shell FW images. The entire diffusion acquisition (i.e., b = 500 s/mm2 and b = 1,000 s/mm2) were used to calculate FW multishell. For each of the diffusion metrics computation, the unique b = 0 s/mm2 image was used. Thus, in the rest of the article, the references to acquisitions with b = 1,000 s/mm2 and/or b = 500 s/mm2 implicitly take into account the acquisition of this b = 0 s/mm2 image. The DIPY toolbox (Garyfallidis et al., 2014), available on python, was used to compute the DTI indices (Basser, Mattiello, & LeBihan, 1994) and the FW multishell indices (Henriques et al., 2017; Hoy et al., 2014). The single‐shell FW images were computed using the extension to the DIPY toolbox recently proposed by Golub and colleagues (Golub et al., 2021). We chose a hybrid initialization for the regularized gradient descent optimization, as suggested by Golub and colleagues (Figure 1a). For each subject, the FA map was normalized to the Montreal Neurological Institute (MNI) template of FA using a combination of linear and nonlinear registration (Jenkinson et al., 2012). The resulting warping field was used to normalize the other maps. We chose to use FA maps for normalization since we wanted to avoid using a different imaging modality such as T1‐weighted MRI, as our focus is on DWI. Moreover, FA maps are those with the highest contrast between gray and white matter and the most adapted to align white matter tracts across subjects (Smith et al., 2006).
FIGURE 1.
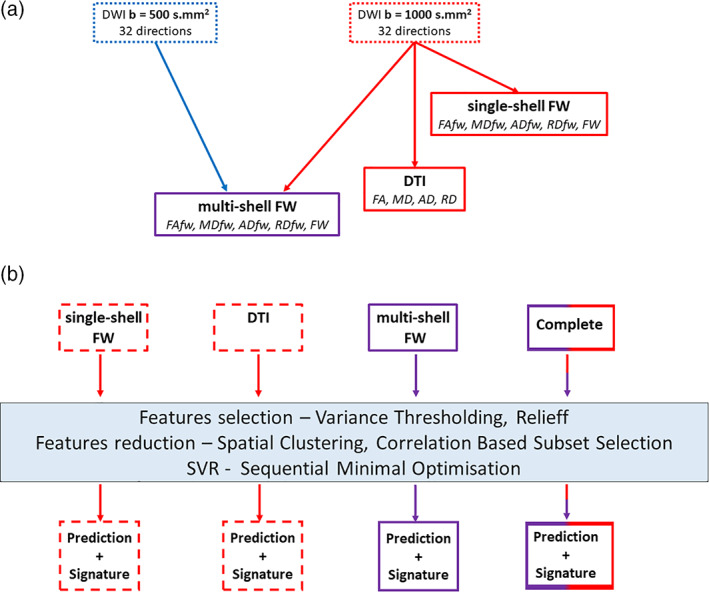
Methods summary. (a) Schematic representation of the DWI acquisitions and the derived indices. (b) Summary of the different models fitted and of the multivariate pipeline. Throughout the figure, blue refers to the b = 500 s/mm2 acquisition, red refers to the b = 1,000 s/mm2 acquisition and purple refers to multishell. DTI, diffusion tensor imaging; FW, free‐water; SVR, supporting vector regression
As a follow‐up analysis, to ascertain that our results were independent from the spatial normalization method used, we also performed TBSS‐style normalization and skeletonization of the different images following the methods detailed in Smith et al. (2006) using FSL (Jenkinson et al., 2012).
2.5. Variance explained approach
For each set of indices (i.e., DTI, multishell FW and single‐shell FW) and each voxel, we fitted a linear model with age as dependent variable and a polynomial expansion of third order (to account for possible nonlinear effect) of the imaging indices as independent variable. Then, for each voxel, we tested if at least one of the models was significant (as assessed by the overall F statistic associated with the model). If at least one of the models was significant, we compared the adjusted R 2 of the three models and assigned to the voxel a label related to the model with the highest adjusted R 2. Note that this procedure is meant to be more descriptive than inferential in nature, as no statistical significance is implied by these comparisons. The results of this analysis should only be interpreted in conjunction to the results of the machine learning approach. All analyses were performed using R.
2.6. Machine learning approach
For brain‐age estimation we used a previously published machine‐learning pipeline (Meng et al., 2017) that our group recently optimized (Nemmi, Cignetti, et al., 2019; Nemmi, Pavy‐Le Traon, et al., 2019). This pipeline takes as input 3D brain images and through a series of features selection and reduction steps coupled with a support vector machine (SVM) model output a prediction of the value of the observed variable, age in this study, together with a low dimensional set of the most predictive brain regions (see Nemmi, Pavy‐Le Traon, et al., 2019 and Nemmi, Cignetti, et al., 2019 for more details). In particular, the pipeline aims to select the smallest set of brain regions/modalities that maximize the predictive power and minimize redundancy of information. Within each modality, the voxels that survive features selection are spatially clustered and the resulting clusters from all modalities are further reduced using a correlation based set selection procedure. One important parameter of the pipeline is the minimum size of the clusters (henceforth “cluster extent”) that are allowed to enter the SVM model. In our previous studies, values around 100 voxels gave the best results. As such, we present the result obtained using a cluster size threshold of 100 voxels in the main body of the manuscript. Performances for different values of these parameters are reported in Table S1 and Figure S6.
2.7. Cross‐validation procedure
We adopted a 10‐times repeated 10‐folds cross‐validation scheme for independent testing. A single repetition looked as follows: we divided our sample in 10 subsamples of equal size, in turns, we used 9 subsample as training set and 1 subsample as testing set, until all subsample were used as testing set. The feature selection and reduction steps were carried out using only the training sample. Then we used the predictive clusters found in the training sample as features within the test sample and fitted the model using only the test sample, obtaining the brain age for the test sample. We summarized the results by stacking the brain age calculated in the 10 subsamples and using these brain ages to calculate the Pearson correlation between actual age and brain age as well as the mean absolute error (MAE) between brain age and actual age. This whole procedure was repeated 10 times (i.e., the 10 repetitions), using different subsampling for each repetition. Once the 10 repetitions complete, we calculated the average Pearson correlation and the average MAE for each model. In this manuscript, we report the average correlation and MAE over the 10 CV repetitions.
We used the variability between folds (i.e., different training samples) to assess the discriminant power of the features (i.e., clusters): for each cluster, we calculated a predictivity score (from 0 to 100) based on the number of folds that cluster was selected among the predictive ones. Throughout the figures in this paper, clusters are color‐coded according to the number of folds they have been chosen.
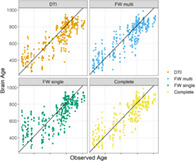
As a supplementary analysis, we also run a leave‐one‐out cross‐validation for each of the model. The results of the leave‐one‐out cross‐validations have been used to create the scatterplots showing the relationship between brain age and actual age for each of the model, while the complete set of scatterplots for the 10 repetitions of each 10‐folds cross‐validation are reported in Data S1.
2.7.1. Models
Henceforth, the models presented will be called “DTI,” comprising FA, MD, AD, RD; “single‐shell FW,” comprising the free‐water map and the free‐water‐corrected FA, MD AD and RD calculated using images acquired at b = 1,000 s/mm2; “multishell FW,” comprising the free‐water map and the free‐water‐corrected FA, MD, AD and RD calculated using the multishell protocol (i.e., images from both b = 500 s/mm2 and b = 1,000 s/mm2); “complete” model, comprising the DTI indices and the FW multishell indices (see Figure 1b). As a follow‐up to our results we also run models for FW (both multishell and single shell) in isolation. Moreover, the models whose results are presented in the main body of the manuscript (i.e., those with a cluster extent of 100 voxels) were repeated using TBSS‐style images. The results of these models are reported in Data S1.
2.7.2. Permutations
For each machine learning model (i.e., DTI, single/multishell FW, complete), we performed permutation analyses to assess that the performances of the models were significantly different from chance. Specifically, for each repetition (i.e., a specific subsampling of the subject) we repeated the fitting of the SMO model shuffling the ages of the training set. This operation was repeated 100 times (for computational reasons a higher number of permutations would be ill advised) in order to have an approximation of the null distribution of the performance (i.e., the expected size of the MAE and the correlation between predictions and ground truth if there was no relationship between features and outcome). We then measured the number of times that the shuffled ages led to a lower (higher) MAE (correlation), added the original performance and divided for the number of permutations (i.e., 100).
3. DISCRIMINANT FEATURES TESTING
In the light of the high correlation of the features used in the models and of the fact that age‐association of DTI indices has been shown to be relatively spatially homogeneous (Cox et al., 2016; Slater et al., 2019), we decided to perform a follow‐up test of the discriminant power of the regions deemed to be most discriminative by the machine learning models. To this aim, we created “low discriminative” index maps by removing from each maps all voxels that had been selected in more than 50% of the folds by the machine learning models. We then used these “low discriminative” maps as input to the same machine learning pipeline and compared the performances of these “low discriminative” models to those of the original ones. The idea is that if there is a real regional specificity, the “low discriminative” models should show a sizeable drop in performances. On the contrary, if no drop is observed, one can assume that there is not real spatial specificity, and the association of the different indices with age is more global.
4. RESULTS
4.1. Variance explained approach
Of all voxels for which at least one model was significant, 47% (35287) showed the highest adjusted R 2 for the multishell FW model, 29% (22173) showed the highest adjusted R 2 for the single‐shell FW model, and 24% (18211) voxels showed the highest adjusted R 2 for the DTI model. As for the spatial location of the voxels, the pattern is quite scattered, with no easily recognizable topological regularity (Figure 1). Figure S2 reports the actual adjusted R 2 values for the three models for the same slices shown in Figure 2.
FIGURE 2.
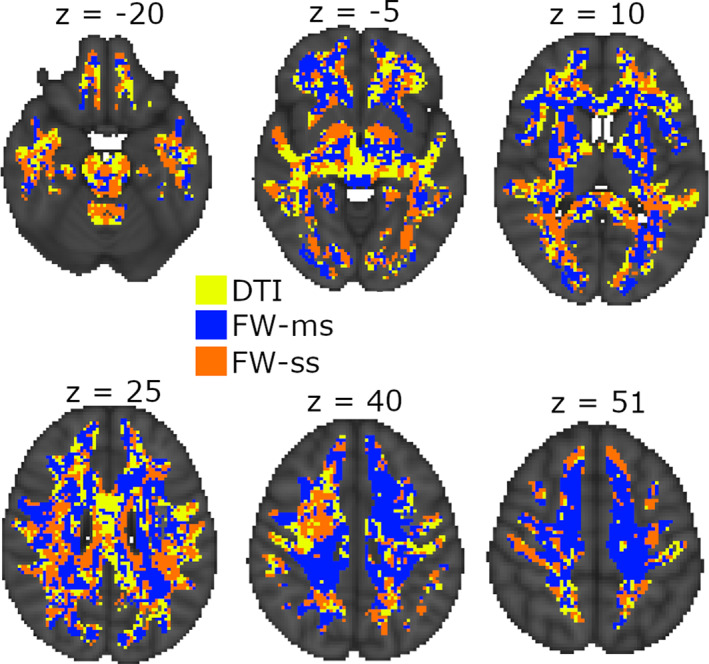
Most explicative model voxel‐wise. The figure shows the set of indices (color coded) that explained the most variance for age, as measured by the adjusted R 2 of the associated linear model. DTI, diffusion tensor imaging; FW‐ms, free‐water multishell; FW‐ss, free‐water single shell
4.2. DTI indices
When using the DTI indices (i.e., FA, MD, AD, RD) we obtained the following results (cluster extent threshold = 100 voxels, see Figure S12 and Table S1 for an overview of the performances of other cluster extent thresholds): MAE = 96 [89.3, 103], r = .82 [0.79, 0.85] (Figure 1). These performances were significantly different from chance level. The performance from leave‐one‐out cross validation were identical, with a MAE of 96 and an r of 82. Figure 4 reports the scatterplot illustrating the relationship between predicted and actual age. MD and RD were chosen for ~85% of the folds, being chosen together ~70% of the times (Figure S3). As for spatial distribution, the most frequently selected voxels were in the brainstem and in the superior longitudinal fasciculus (on the right) for MD, and in the superior longitudinal fasciculus and in the superior corona radiata for RD (Figure 3). The performance of the model and the most frequently selected indices was similar, albeit slightly worse, when using TBSS‐derived images (see Data S1, TBSS style models).
FIGURE 3.

Comparison of performance. This figure reports the performance for all the repetitions of the different models, measured as Pearson correlation between predicted and actual age and mean absolute error (MAE) between predicted and actual age in months on the Y axis
4.3. FW: Multishell
When using the FW‐corrected indices (i.e., FW, FA fw‐corrected, MD fw‐corrected, AD fw‐corrected and RD fw‐corrected) we obtained the following results (cluster extent = 100 voxels): MAE = 83.64 [81.5, 85.8], r = 0.87 [0.86, 0.89] (Figure 1). This performance was significantly different from chance. The results from the leave‐one‐out cross‐validation were slightly better, with a MAE of 80 and an r of .89. Figure 4 reports the scatterplot illustrating the relationship between predicted and actual age. FW was chosen 100% of the folds; for 64 folds FW was selected together with RD fw‐corrected (Figure S7). Interestingly, running a model using also the FW led to almost identical results (see supplementary results, FW in isolation). As for spatial distribution, the most frequently selected voxels were in the body of the corpus callosum, in the right superior longitudinal fasciculus, in the right inferior fronto‐occipital fasciculus, in the forceps minor and major and in the thalamic radiation bilaterally (Figure 5). RD fw‐corrected was mostly selected in the forceps and the body of the corpus callosum, with a similar spatial distribution as FW (Figure 6). The performance of the model and the most frequently selected indices were similar, albeit slightly worse, when using TBSS‐derived images (see Data S1, TBSS style models).
FIGURE 4.

Scatterplots of brain age and observed age. The figure reports the predictions obtained by the leave‐one‐out cross‐validations together with the observed age of the subjects. The black lines represent the identity line. The complete sets of scatterplots from the 10 repetitions of the 10‐folds cross‐validations is presented as Figure S5
FIGURE 5.
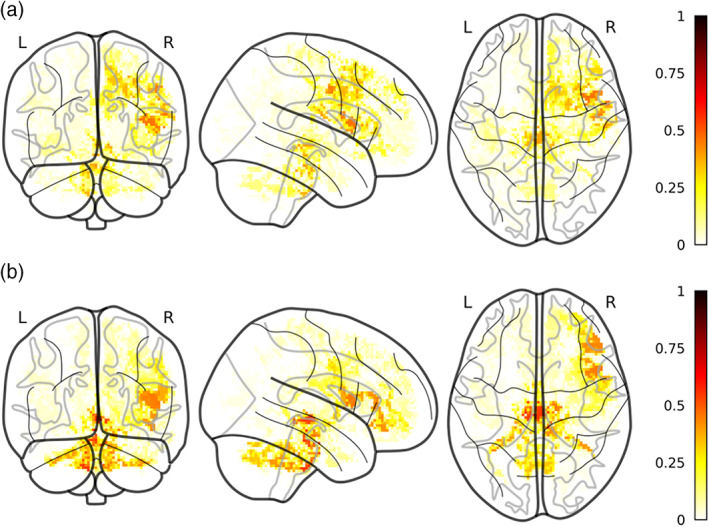
Most selected voxels for DTI model. The figure reports the most selected voxels for RD (a) and MD (b) for a cluster extent of 100. Color‐code is relative to the proportion of folds in which a certain voxel has been selected over the whole 100 folds
FIGURE 6.
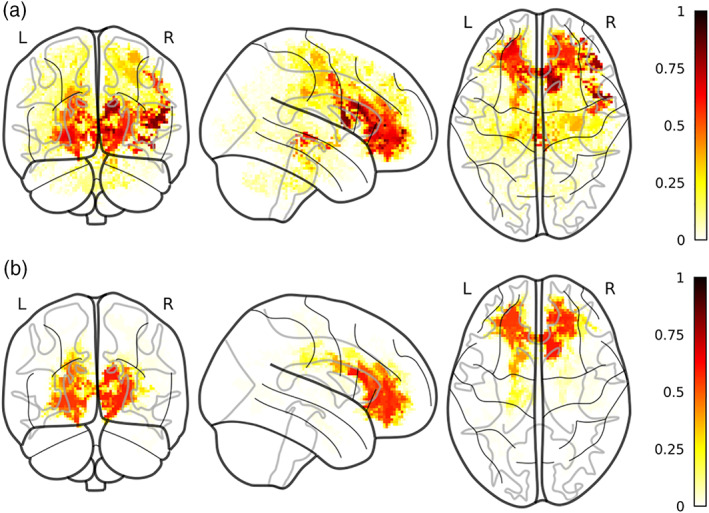
Most selected voxels for FW multishell model. The figure reports the most selected voxels for FW (a) and RD fw‐corrected (b). Color‐code is relative to the proportion of folds in which a certain voxel has been selected over the whole 100 folds
4.4. FW: Single shell
When using FW‐corrected indices derived from one shell only (b = 1,000 s/mm2), we obtained the following results (cluster extent threshold = 100). MAE = 106 [100.3, 111.7], r = 0.77 [0.74, 0.79]. These performances were significantly different from chance level. The results from the leave‐one‐out cross validation were similar, with a MAE of 108 and an r of 75. Figure 4 reports the scatterplot illustrating the relationship between predicted and actual age. The model fitted with single‐shell FW indices selected free‐water as the most discriminant index (selected 100 times). Interestingly, running a model using also the FW led to almost identical results (see supplementary results, FW in isolation). The most discriminant clusters for the single‐shell models broadly overlapped with those from the multishell model (Figure S8). The performance of the model and the most frequently selected indices were similar, albeit slightly worse, when using TBSS‐derived images (see Data S1).
4.5. Complete mode
When combining DTI and multishell FW indices, we obtained the following results (cluster extent threshold 100): MAE = 82.2 [79.6, 84.9], r = .88 [0.87, 0.89]. This performance was significantly different from chance level. The results from the leave‐one‐out cross‐validation were slightly worse, with a MAE of 91 and an r of 85. Figure 4 reports the scatterplot illustrating the relationship between predicted and actual age. FW was chosen in all folds, 75 times in association with MD and 55 times in association with RD (Figure S9). The spatial distribution of the most selected voxels for FW overlapped with those from the FW only models (both multishell and single‐shell), in the right superior longitudinal fasciculus, in the right corticospinal tract, in the forceps and in the right thalamic radiation. However, its distribution was unilateral on the right, at variance with the FW only models, which were more bilateral. The distribution of MD and RD roughly followed the same pattern, although the voxels were chosen with less consistency (Figure S10). The performance of the model and the most frequently selected indices were similar, albeit slightly worse, when using TBSS‐derived images (see Data S1, TBSS style models).
4.6. Free‐water in isolation
The models that included only the FW index from single‐shell and multishell acquisition reached almost identical performances than those including all indexes. In particular, the FW multishell model showed a mean MAE of 84.4 [80.5, 88.2] months and a mean correlation of 0.87 [0.85, 0.88]. The FW single‐shell model showed a mean MAE of 105 [99.1, 111] and a mean correlation of 0.77 [0.75, 0.80] (Figure 7).
FIGURE 7.
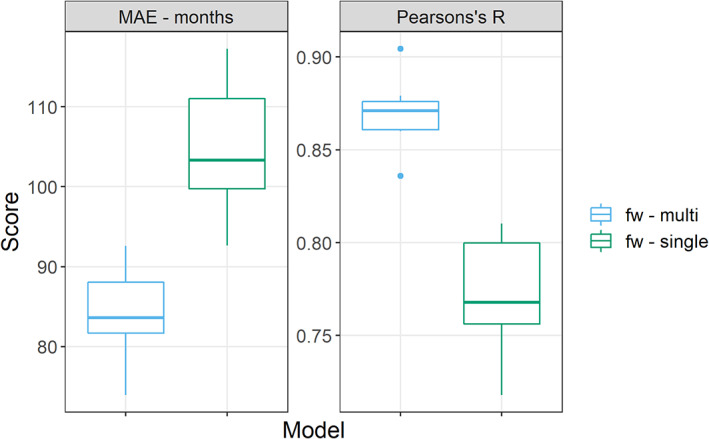
This figure reports the performance for all the repetitions of the FW models for a cluster extent of 100 voxels, measured as Pearson correlation between predicted and actual age and mean absolute error (MAE) between predicted and actual age in months on the Y axis
4.7. Discriminant features testing
The performances of the models trained using the “low discriminative” maps (cluster extent = 100) were similar to those of the original model in term of correlation with actual age, but were lower than the performances of the original models in term of MAE. Specifically, the “low discriminative” DTI models reached an average correlation of 0.76 [0.75, 0.76] and an average MAE of 109.5 [105.7, 113.2]. The “low discriminative” FW multishell model reached an average correlation of 0.75 [0.73, 0.76] and an average MAE of 110.8 [107.8, 113.9]. The “low discriminative” FW single‐shell model reached an average correlation of 0.76 [0.74, 0.77] and an average MAE of 109.4 [106.5, 112.3]. Finally, the complete model reached an average correlation of 0.8 [0.78, 0.81] and an average MAE of 104.2 [100.4, 108]. These results are graphically presented in Figure S10. Table 1 reports the average differences and their confidence intervals among the original and the “low discriminative” models.
TABLE 1.
Average differences and associated 95% confidence intervals between the original and the “low discriminative” models
| Model | Pearson's r | MAE |
|---|---|---|
| Complete | 0.08 [0.06, 0.10] | −21.95 [−26.81, −17.10] |
| DTI | 0.08 [0.06, 0.09] | −14.64 [−19.24, −10.03] |
| FW multishell | 0.13 [0.11, 0.15] | −27.18 [−31.39, −22.96] |
| FW single shell | 0.01 [−0.02, 0.04] | −3.43 [−9.52, 2.67] |
5. DISCUSSION
Our study showed that white matter microstructural indices derived from DTI, multishell and single‐shell free‐water imaging can all predict brain age above chance level and with accuracy broadly comparable to previous study using machine learning to calculate brain age (Cole et al., 2018; Cole et al., 2019; Cole, Leech, & Sharp, 2015; Corps & Rekik, 2019; Madan & Kensinger, 2018; Richard et al., 2018). Although several previous studies have shown statistical association between white matter microstructure and age (Cox et al., 2016; Lebel et al., 2012; Slater et al., 2019) and at least three previous studies (Beck et al., 2021; Cole, 2019; Richard et al., 2018) showed the predictive power of various diffusion reconstruction algorithms in regard to age, the present study is the first one to use a data‐driven voxel‐wise framework to compare DTI and single‐shell‐ and multishell‐derived FW parameters in their ability to predict brain age.
Between‐models comparisons showed that multishell free‐water indices led to the best absolute performance in terms of MAE and Pearson's correlation. Interestingly, using free‐water in isolation (i.e., without free‐water‐corrected AD, MD, FA and RD) led to performances similar to those obtained all free‐water indices, suggesting that the free‐water is indeed the most predictive feature. This is in line with previous studies comparing different diffusion reconstruction models that found FW indices to be better predictor of age relative to DTI (Chad et al., 2018; Cox et al., 2016). An interesting finding is that using multishell free‐water reconstruction substantially and significantly increases the prediction accuracy relative to the single‐shell reconstructions. This is in line with the fact that the free‐water reconstruction problem is ill‐defined for single‐shell acquisition and that this can lead to suboptimal reconstruction, even with careful selected initialization parameters for the optimization (Golub et al., 2021; Henriques et al., 2017; Hoy et al., 2014). These results show that the b500 acquisition, lasting between 3 and 5 min depending on the number of directions acquired, can be easily included in a diffusion MRI protocol in clinical routine or for sensitive population without great increase in the total acquisition time and can drastically improve the precision of the free‐water reconstruction. Somewhat surprisingly, the single‐shell FW model led to significantly worse performance than the DTI model. Interestingly, this pattern of performance (i.e., FW multishell = complete model > DTI > FW single shell) is observed also when using TBSS‐style normalization and skeletonization (Smith et al., 2006) of the different indices, albeit all models fair slightly worse than their non‐TBSS counterpart, suggesting that our results are not related to the pipeline chosen for spatial normalization. It should also be added that the well‐known age‐related bias in brain‐age calculation (i.e., a systematic overestimation of the age of the younger subjects and underestimation of the age of the older subjects) (Aycheh et al., 2018; Cole et al., 2017; Liang, Zhang, & Niu, 2019; Pardoe & Kuzniecky, 2018), although presents for all models, was more visible for the FW single‐shell model (see Figure S13). This result can be taken as a further evidence that single‐shell FW is sensitive to initialization and can lead to suboptimal reconstruction. Another competing explanation for the different performances of the single‐shell and multishell free‐water indices is that the latter have a higher signal‐to‐noise ratio, since they are reconstructed using 64 measures, unlike the single‐shell indices, reconstructed using 32 measures. Although one could possibly further inquire this hypothesis by using a “reduced” version of the multishell protocol (i.e., choosing 16 directions from b500 and 16 directions from the B1000), this would still rise some confounds. In fact, two different methods could be used to reduce the multishell protocol to only 32 directions: either one chooses the same 16 directions for both bs, or one chose to have the overall same 32 directions than in the single‐shell protocol, by having 16 directions from b = 500 and 16 directions from b = 1,000. In the first case, the single‐shell protocol and the reduced multishell protocol would still not be comparable, since the number of observations is the same but the number of directions is not. In the second case, one would have 16 directions with higher SNR (b = 500) than the other 16 (b = 1,000), and thus this protocol would still not be comparable to the single‐shell one. Thus, future study using protocols constructed ad hoc are needed to answer this hypothesis. In any case, it needs to be noticed that DTI and single‐shell FW were derived from exactly the same data, but the former showed higher performance than the latter, suggesting that a signal‐to‐noise ratio explanation cannot be the unique answer. The fact that the DTI model had performances higher than the single‐shell FW model also suggest that the better performance of the multishell FW model is not an artifact due to the higher number of features entered (i.e., the corrected DTI indices plus FW) entailing overfitting, as the single‐shell FW model included the same number of features, and still fared worse than the DTI model, which only included less features.
Within model comparisons of indices suggest that, for all models, the most informative indices are those reflecting increased free diffusion of water in the white matter: we found that RD and MD were the most informative indices for DTI and the amount of free‐water and free‐water‐corrected RD were the most predictive indices for the free‐water (both multishell and single shell). When combining all indices, free‐water was chosen 100% of times, but was frequently selected together with canonical MD and RD. This can be taken as a evidence that demyelination and axonal damage (Kronlage et al., 2017; Tu et al., 2016) or increase in interstitial space within the white matter (Chad et al., 2018; Meier‐Ruge, Ulrich, Brühlmann, & Meier, 1992) are the most noticeable phenomena in white matter aging (although interpretation of DTI indices based on underlying tissue should be taken with caution (Wheeler‐Kingshott & Cercignani, 2009). Note however that in the free‐water model, the free‐water was chosen 75% of the time in combination with free‐water‐corrected RD (in largely overlapping spatial cluster), suggesting that myelin microstructure and macrostructure (i.e., enlarged interstitial space) could both play an important role in age prediction. It should be noted that when running models using free‐water in isolation, the performances were almost identical to the one obtained by the full models both for single‐shell and multishell indices (see supplementary results, FW in isolation), highlighting that FW bring the vast majority of the relevant information for the prediction. The importance of the free diffusion of water in the white matter in predicting age is in line with previous finding specifically on free‐water models (Chad et al., 2018).
As for our topological finding, they are in line with those reported in previous studies focusing on the association between white matter microstructure and age, specifically for association fibers (Bender et al., 2016; Lebel et al., 2012; Slater et al., 2019). However, it should be noted that for the DTI model, we found that among the most discriminant indices were clusters of mean diffusivity in the brainstem. This structure has rarely been reported in studies about white matter aging, either because it was not within the included ROIs (Lebel et al., 2012; Slater et al., 2019) or because did not show strong association with age (Cox et al., 2016; Kodiweera, Alexander, Harezlak, McAllister, & Wu, 2016). The difference between previous studies and ours may be explained by the voxel‐wise approach we adopted that may be best suited to find spatial‐specific association with age in the brain‐stem that may be hidden by an ROI approach. It should however be noted that the clusters in the brainstem were only found for the DTI canonical model, which did not lead to the best performance. As such, the importance of these clusters should be taken with caution. More intriguing is the fact that the topological distribution of the most discriminant clusters differs among models. In particular, DTI highlighted clusters in the anterior thalamic radiation and the superior longitudinal fasciculus, for RD and MD. On the other hand, while the free‐water‐corrected model did lead to clusters in the abovementioned areas, it also included extended parts of the uncinated fasciculus, the fornix and the rostrum of the corpus callosum. These differences can be related to the tract‐specific trajectories for different microstructural indices, as reported in previous studies (Cox et al., 2016; Slater et al., 2019) or could be related to the fact that the effect of free‐diffusing water is eliminated in the FW model. Interestingly, while the models fitted without the most discriminant regions showed almost identical correlation between brain age and actual age, they showed, for the most part, worse MAE, with the “low discriminative” DTI model being on average 1 year further from the actual age than the original model, and the FW multishell and the complete model being on average almost 2 years further from the actual age than the original models. The single‐shell FW model stands out, being almost identical to the original model also in term of MAE. It should be noted that on the top of the worsening of the performances, the “low discriminative” model are also more similar to each other than the original one, with DTI, single‐shell and multishell models having almost identical performances. Taken together these results suggest than, even if part of the information about the brain age is still present outside the regions deemed to be the most discriminant by the original models, as shown by the overall still good performances of the “low discriminative” model, a certain degree of regional specificity is present, as attested by the drop in performance, measures with MAE, from the original to the “low discriminative” models. In turn, this suggests that claim of global rather than spatial specific association between diffusion indices and age (Cox et al., 2016; Slater et al., 2019) should be interpreted with caution.
This study has several limitations that should be taken into account. First of all, we acknowledge that the sample size is limited. We have adopted 10‐folds cross‐validation and avoided to fit hyperparameters to the model in order to limit the possible optimistic bias (Varoquaux et al., 2017), but the risk remains. On the other hand, the fact that the study is monocentric limits possible sources of confound related to different scanning hardware or sequence implementation. The sample included only male subjects: on one hand this is a limitation, in so much that this prevents the generalization of our finding to the general population. Finally, we did not include indices derived from other methods of analysis of diffusion data, such as NODDI (Zhang, Schneider, Wheeler‐Kingshott, & Alexander, 2012), HARDI (Tuch et al., 2002), QSI (Tuch, Reese, Wiegell, & Wedeen, 2003) or q‐ball (Tuch, 2004). These methods require ad hoc and longer MRI acquisition that were not compatible with our aim of performing a short clinical‐compatible diffusion protocol.
In conclusion, we showed that a short, clinical compatible multishell diffusion protocol can be used to derive multishell free‐water‐corrected DTI that outperform both canonical DTI indices and single‐shell‐derived FW indices in predicting subjects age. We also showed that single‐shell reconstruction led to worse performance than canonical DTI model, in line with recent work that draw attention on the draw‐back of this method, in term of sensitivity to initialization parameters and ability to separate mean‐diffusivity and free‐water related modification. Future studies are needed to apply our acquisition and analysis methods to bigger samples including both male and female subjects or within a pathological model such as Parkinson's disease in order to generalize our results.
CONFLICT OF INTEREST
The authors declare no potential conflict of interest.
AUTHOR CONTRIBUTIONS
Federico Nemmi: Conceptualization; methodology; software; formal analysis; writing – first draft. Mathilde Levardon: Software; formal analysis; writing – review and editing. Patrice Péran: Conceptualization; validation; supervision; writing – review and editing.
Supporting information
Appendix S1: Supporting Information
ACKNOWLEDGMENTS
We thank the Inserm/UPS UMR1214 Technical Platform for the MRI acquisitions. The authors would like to thank Marc Golub for sharing the DIPY extension code and assistance with its use. We thank also Abdel‐Kader Boulanouar and Perrine Bertrand for their contributions in the acquisition of data. For funding, we thank the Institut des sciences du cerveau de Toulouse (ISCT).
Nemmi, F. , Levardon, M. , & Péran, P. (2022). Brain‐age estimation accuracy is significantly increased using multishell free‐water reconstruction. Human Brain Mapping, 43(7), 2365–2376. 10.1002/hbm.25792
Funding information Institut des sciences du cerveau de Toulouse (ISCT)
ENDNOTE
These acquisitions date of 2011–2012 and were not especially optimized, explaining the long acquisition time, and also the very long repetition time. Nowadays, an acquisition of b‐values of 500 (32) and 1,000 (32) s/mm2, with two averages, would only take about 10 min.
DATA AVAILABILITY STATEMENT
Data sharing outside the study lab was not included in the informed consent and as such we cannot share the data used for this study. However, the code used for the machine learning analysis is available at https://github.com/fnemmi‐tonic/multimodal_MRI_pipeline_prediction.
REFERENCES
- Aycheh, H. M. , Seong, J.‐K. , Shin, J.‐H. , Na, D. L. , Kang, B. , Seo, S. W. , & Sohn, K.‐A. (2018). Biological brain age prediction using cortical thickness data: A large scale cohort study. Frontiers in Aging Neuroscience, 10, 252. 10.3389/FNAGI.2018.00252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser, P. J. , Mattiello, J. , & LeBihan, D. (1994). MR diffusion tensor spectroscopy and imaging. Biophysical Journal, 66(1), 259–267. 10.1016/S0006-3495(94)80775-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck, D. , de Lange, A. M. , Maximov, I. I. , Richard, G. , Andreassen, O. A. , Nordvik, J. E. , & Westlye, L. T. (2021). White matter microstructure across the adult lifespan: A mixed longitudinal and cross‐sectional study using advanced diffusion models and brain‐age prediction. NeuroImage, 224, 117441. 10.1016/J.NEUROIMAGE.2020.117441 [DOI] [PubMed] [Google Scholar]
- Bender, A. R. , Völkle, M. C. , & Raz, N. (2016). Differential aging of cerebral white matter in middle‐aged and older adults: A seven‐year follow‐up. NeuroImage, 125, 74–83. 10.1016/j.neuroimage.2015.10.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chad, J. A. , Pasternak, O. , Salat, D. H. , & Chen, J. J. (2018). Re‐examining age‐related differences in white matter microstructure with free‐water corrected diffusion tensor imaging. Neurobiology of Aging, 71, 161–170. 10.1016/j.neurobiolaging.2018.07.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, J. (2019). Multi‐modality neuroimaging brain‐age in UK biobank: Relationship to biomedical, lifestyle and cognitive factors. Neurobiology of Aging, 92, 34–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, J. H. , & Franke, K. (2017). Predicting age using neuroimaging: Innovative brain ageing biomarkers. Trends in Neurosciences, 40(12), 681–690. 10.1016/j.tins.2017.10.001 [DOI] [PubMed] [Google Scholar]
- Cole, J. H. , Leech, R. , & Sharp, D. J. (2015). Alzheimer's disease neuroimaging initiative. Prediction of brain age suggests accelerated atrophy after traumatic brain injury. Annals of Neurology, 77(4), 571–581. 10.1002/ana.24367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, J. H. , Marioni, R. E. , Harris, S. E. , & Deary, I. J. (2019). Brain age and other bodily “ages”: Implications for neuropsychiatry. Molecular Psychiatry, 24(2), 266–281. 10.1038/s41380-018-0098-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, J. H. , Poudel, R. P. K. , Tsagkrasoulis, D. , Caan, M. W. A. , Steves, C. , Spector, T. D. , & Montana, G. (2017). Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage, 163, 115–124. 10.1016/j.neuroimage.2017.07.059 [DOI] [PubMed] [Google Scholar]
- Cole, J. H. , Ritchie, S. J. , Bastin, M. E. , Valdés Hernández, M. C. , Muñoz Maniega, S. , Royle, N. , … Deary, I. J. (2018). Brain age predicts mortality. Molecular Psychiatry, 23(5), 1385–1392. 10.1038/mp.2017.62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corps, J. , & Rekik, I. (2019). Morphological brain age prediction using multi‐view brain networks derived from cortical morphology in healthy and disordered participants. Scientific Reports, 9(1), 9676. 10.1038/s41598-019-46145-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, S. R. , Ritchie, S. J. , Tucker‐Drob, E. M. , Liewald, D. C. , Hagenaars, S. P. , Davies, G. , … Deary, I. J. (2016). Ageing and brain white matter structure in 3,513 UK biobank participants. Nature Communications, 7(1), 1–13. 10.1038/ncomms13629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fossel, M. (2020). A unified model of dementias and age‐related neurodegeneration. Alzheimers Dementia, 16(2), 365–383. 10.1002/alz.12012 [DOI] [PubMed] [Google Scholar]
- Franke, K. , & Gaser, C. (2019). Ten years of BrainAGE as a neuroimaging biomarker of brain aging: What insights have we gained? Frontiers in Neurology, 10, 789. 10.3389/fneur.2019.00789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garyfallidis, E. , Brett, M. , Amirbekian, B. , Rokem, A. , van der Walt, S. , Descoteaux, M. , & Nimmo‐Smith, I. (2014). Dipy, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics, 8, 8. 10.3389/fninf.2014.00008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub, M. , Neto Henriques, R. , & Gouveia Nunes, R. (2021). Free‐water DTI estimates from single b‐value data might seem plausible but must be interpreted with care. Magnetic Resonance in Medicine, 85(5), 2537–2551. 10.1002/mrm.28599 [DOI] [PubMed] [Google Scholar]
- Henriques, R. N. , Rokem, A. , Garyfallidis, E. , St‐Jean, S. , Peterson, E. T. , & Correia, M. M. (2017). [Re] optimization of a free water elimination two‐compartment model for diffusion tensor imaging. ReScience, 3, 2. 10.1101/108795 [DOI] [Google Scholar]
- Hoy, A. R. , Koay, C. G. , Kecskemeti, S. R. , & Alexander, A. L. (2014). Optimization of a free water elimination two‐compartment model for diffusion tensor imaging. NeuroImage, 103, 323–333. 10.1016/j.neuroimage.2014.09.053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson, M. , Beckmann, C. F. , Behrens, T. E. J. , Woolrich, M. W. , & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
- Kodiweera, C. , Alexander, A. L. , Harezlak, J. , McAllister, T. W. , & Wu, Y. C. (2016). Age effects and sex differences in human brain white matter of young to middle‐aged adults: A DTI, NODDI, and q‐space study. NeuroImage, 128, 180–192. 10.1016/j.neuroimage.2015.12.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kronlage, M. , Pitarokoili, K. , Schwarz, D. , Godel, T. , Heiland, S. , Yoon, M. S. , … Bäumer, P. (2017). Diffusion tensor imaging in chronic inflammatory demyelinating polyneuropathy: Diagnostic accuracy and correlation with electrophysiology. Investigative Radiology, 52(11), 701–707. 10.1097/RLI.0000000000000394 [DOI] [PubMed] [Google Scholar]
- Lebel, C. , Gee, M. , Camicioli, R. , Wieler, M. , Martin, W. , & Beaulieu, C. (2012). Diffusion tensor imaging of white matter tract evolution over the lifespan. NeuroImage, 60(1), 340–352. 10.1016/j.neuroimage.2011.11.094 [DOI] [PubMed] [Google Scholar]
- Liang, H. , Zhang, F. , & Niu, X. (2019). Investigating systematic bias in brain age estimation with application to post‐traumatic stress disorders. Human Brain Mapping, 40(11), 3143–3152. 10.1002/HBM.24588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madan, C. R. , & Kensinger, E. A. (2018). Predicting age from cortical structure across the lifespan. European Journal of Neuroscience, 47(5), 399–416. 10.1111/ejn.13835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manjón, J. V. , Coupé, P. , Martí‐Bonmatí, L. , Collins, D. L. , & Robles, M. (2010). Adaptive non‐local means denoising of MR images with spatially varying noise levels. Journal of Magnetic Resonance Imaging, 31(1), 192–203. 10.1002/jmri.22003 [DOI] [PubMed] [Google Scholar]
- Meier‐Ruge, W. , Ulrich, J. , Brühlmann, M. , & Meier, E. (1992). Age‐related white matter atrophy in the human brain. Annals of the New York Academy of Sciences, 673(1), 260–269. 10.1111/j.1749-6632.1992.tb27462.x [DOI] [PubMed] [Google Scholar]
- Meng, X. , Jiang, R. , Lin, D. , Bustillo, J. , Jones, T. , Chen, J. , … Calhoun, V. D. (2017). Predicting individualized clinical measures by a generalized prediction framework and multimodal fusion of MRI data. Neuroimage, 145, 218–229. 10.1016/j.neuroimage.2016.05.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moseley, M. (2002). Diffusion tensor imaging and aging—A review. NMR in Biomedicine, 15(7–8), 553–560. 10.1002/nbm.785 [DOI] [PubMed] [Google Scholar]
- Nemmi, F. , Pavy‐Le Traon, A. , Phillips, O. R. , Galitzky, M. , Meissner, W. G. , Rascol, O. , & Péran, P. (2019). A totally data‐driven whole‐brain multimodal pipeline for the discrimination of Parkinson's disease, multiple system atrophy and healthy control. NeuroImage: Clinical, 23, 101585. 10.1016/j.nicl.2019.101858 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nemmi, F. , Cignetti, F. , Assaiante, C. , Maziero, S. , Audic, F. , Péran, P. , & Chaix, Y. (2019). Discriminating between neurofibromatosis‐1 and typically developing children by means of multimodal MRI and multivariate analyses. Human Brain Mapping, 40(12), 3508–3521. 10.1002/hbm.24612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardoe, H. , & Kuzniecky, R. (2018). NAPR: A cloud‐based framework for neuroanatomical age prediction. Neuroinformatics, 16(1), 43–49. 10.1007/S12021-017-9346-9 [DOI] [PubMed] [Google Scholar]
- Pasternak, O. , Sochen, N. , Gur, Y. , Intrator, N. , & Assaf, Y. (2009). Free water elimination and mapping from diffusion MRI. Magnetic Resonance in Medicine, 62(3), 717–730. 10.1002/mrm.22055 [DOI] [PubMed] [Google Scholar]
- Pasternak, O. , Westin, C. F. , Bouix, S. , Seidman, L. J. , Goldstein, J. M. , Woo, T. U. , … Kubicki, M. (2012). Excessive extracellular volume reveals a neurodegenerative pattern in schizophrenia onset. Journal of Neuroscience, 32(48), 17365–17372. 10.1523/JNEUROSCI.2904-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierpaoli, C. , Jezzard, P. , Basser, P. J. , Barnett, A. , & Di Chiro, G. (1996). Diffusion tensor MR imaging of the human brain. Radiology, 201, 637–648. 10.1148/radiology.201.3.8939209 [DOI] [PubMed] [Google Scholar]
- Power, J. D. , Barnes, K. A. , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage, 59(3), 2142–2154. 10.1016/j.neuroimage.2011.10.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard, G. , Kolskår, K. , Sanders, A. M. , Kaufmann, T. , Petersen, A. , Doan, N. T. , … Westlye, L. T. (2018). Assessing distinct patterns of cognitive aging using tissue‐specific brain age prediction based on diffusion tensor imaging and brain morphometry. PeerJ, 2018(11), e5908. 10.7717/peerj.5908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sala, S. , Agosta, F. , Pagani, E. , Copetti, M. , Comi, G. , & Filippi, M. (2012). Microstructural changes and atrophy in brain white matter tracts with aging. Neurobiology of Aging, 33(3), 488–498. 10.1016/j.neurobiolaging.2010.04.027 [DOI] [PubMed] [Google Scholar]
- Salat, D. H. , Tuch, D. S. , Greve, D. N. , van der Kouwe, A. J. , Hevelone, N. D. , Zaleta, A. K. , … Dale, A. M. (2005). Age‐related alterations in white matter microstructure measured by diffusion tensor imaging. Neurobiology of Aging, 26(8), 1215–1227. 10.1016/j.neurobiolaging.2004.09.017 [DOI] [PubMed] [Google Scholar]
- Slater, D. A. , Melie‐Garcia, L. , Preisig, M. , Kherif, F. , Lutti, A. , & Draganski, B. (2019). Evolution of white matter tract microstructure across the life span. Human Brain Mapping, 40(7), 2252–2268. 10.1002/hbm.24522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Jenkinson, M. , Johansen‐Berg, H. , Rueckert, D. , Nichols, T. E. , Mackay, C. E. , … Behrens, T. E. J. (2006). Tract‐based spatial statistics: Voxelwise analysis of multi‐subject diffusion data. NeuroImage, 31(4), 1487–1505. 10.1016/j.neuroimage.2006.02.024 [DOI] [PubMed] [Google Scholar]
- Sullivan, E. V. , & Pfefferbaum, A. (2006). Diffusion tensor imaging and aging. Neuroscience & Biobehavioral Reviews, 30(6), 749–761. 10.1016/j.neubiorev.2006.06.002 [DOI] [PubMed] [Google Scholar]
- Tu, T. W. , Williams, R. A. , Lescher, J. D. , Jikaria, N. , Turtzo, L. C. , & Frank, J. A. (2016). Radiological‐pathological correlation of diffusion tensor and magnetization transfer imaging in a closed head traumatic brain injury model. Annals of Neurology, 79(6), 907–920. 10.1002/ana.24641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch, D. S. (2004). Q‐ball imaging. Magnetic Resonance in Medicine, 52(6), 1358–1372. 10.1002/mrm.20279 [DOI] [PubMed] [Google Scholar]
- Tuch, D. S. , Reese, T. G. , Wiegell, M. R. , Makris, N. , Belliveau, J. W. , & Van Wedeen, J. (2002). High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic Resonance in Medicine, 48(4), 577–582. 10.1002/mrm.10268 [DOI] [PubMed] [Google Scholar]
- Tuch, D. S. , Reese, T. G. , Wiegell, M. R. , & Wedeen, V. J. (2003). Diffusion MRI of complex neural architecture. Neuron, 40(5), 885–895. 10.1016/S0896-6273(03)00758-X [DOI] [PubMed] [Google Scholar]
- Varoquaux, G. , Raamana, P. R. , Engemann, D. A. , Hoyos‐Idrobo, A. , Schwartz, Y. , & Thirion, B. (2017). Assessing and tuning brain decoders: Cross‐validation, caveats, and guidelines. NeuroImage, 145, 166–179. 10.1016/J.NEUROIMAGE.2016.10.038 [DOI] [PubMed] [Google Scholar]
- Wheeler‐Kingshott, C. A. M. , & Cercignani, M. (2009). About “axial” and “radial” diffusivities. Magnetic Resonance in Medicine, 61(5), 1255–1260. 10.1002/mrm.21965 [DOI] [PubMed] [Google Scholar]
- Zhang, H. , Schneider, T. , Wheeler‐Kingshott, C. A. , & Alexander, D. C. (2012). NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 61(4), 1000–1016. 10.1016/j.neuroimage.2012.03.072 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supporting Information
Data Availability Statement
Data sharing outside the study lab was not included in the informed consent and as such we cannot share the data used for this study. However, the code used for the machine learning analysis is available at https://github.com/fnemmi‐tonic/multimodal_MRI_pipeline_prediction.


