Spectral Photon Counting CT: Imaging Algorithms and Performance Assessment

Abstract

Photon counting x-ray detectors (PCDs) with spectral capabilities have the potential to revolutionize computed tomography (CT) for medical imaging. The ideal PCD provides accurate energy information for each incident x-ray, and at high spatial resolution. This information enables material-specific imaging, enhanced radiation dose efficiency, and improved spatial resolution in CT images. In practice, PCDs are affected by non-idealities, including limited energy resolution, pulse pileup, and cross talk due to charge sharing, K-fluorescence, and Compton scattering. In order to maximize their performance, PCDs must be carefully designed to reduce these effects and then later account for them during correction and post-acquisition steps. This review article examines algorithms for using PCDs in spectral CT applications, including how non-idealities impact image quality. Performance assessment metrics that account for spatial resolution and noise such as the detective quantum efficiency (DQE) can be used to compare different PCD designs, as well as compare PCDs with conventional energy integrating detectors (EIDs). These methods play an important role in enhancing spectral CT images and assessing the overall performance of PCDs.

I. Introduction

COMPUTED tomography (CT) is a workhorse for medical imaging, with an estimated 81 million exams performed annually in the United States alone [1]. Since the first CT scanner was introduced almost 50 years ago, image quality has vastly improved through technological advancements, further increasing its clinical utility. However, there is still room for improvement. Radiation dose is a growing concern, despite efforts to reduce the dose through better protocols, more efficient hardware, and advanced algorithms. Image contrast, particularly between soft tissues and from contrast agents, can be increased, while image noise can be further decreased. Many clinical applications could benefit from increased spatial resolution. Spectral x-ray information could be better lever-aged to obtain quantitative material-specific imaging. While many approaches and technologies are being developed to address one or more of these, a leading candidate is spectroscopic photon counting detectors (PCDs).

Conventional CT scanners utilize an indirect conversion process to detect x-rays: a scintillator converts x-ray photons into light photons, which are then converted to electric charge by a photodiode and integrated. Since the amount of light is proportional to the x-ray energy and signal is collected for many x-ray photons, such detectors are referred to as energy integrating detectors (EIDs). PCDs directly convert x-ray photons to charge carriers and are fast enough to count individual x-ray photons and bin them according to their energy (Fig. 1). As will be discussed, PCDs offer the potential to improve dose efficiency through a combination of higher geometric efficiency, lower sensitivity to electronic noise, and optimal weighting of the signal; improved spatial resolution; and better spectral imaging, enabling the quantification of two or more materials. Unique to PCDs is the ability to provide spectroscopic information, typically in the form of counts in energy bins or windows (Fig. 2). Spectral imaging is “always on”, without having to resort to special protocols (kV switching) or dedicated hardware (dual source, split filter).

Fig. 1.

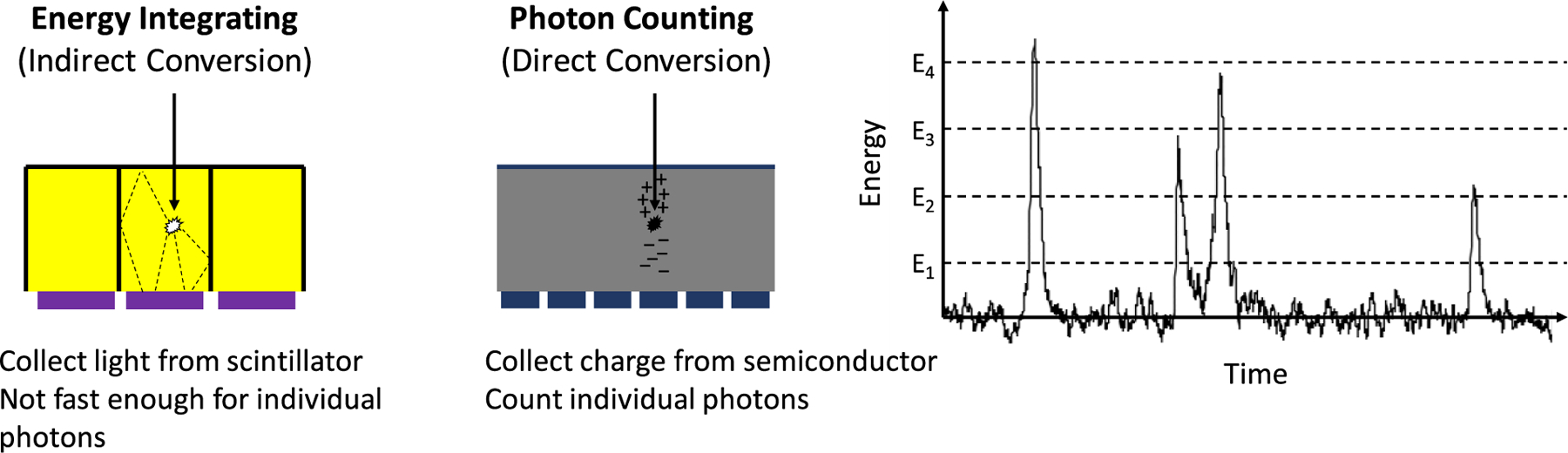
Energy integrating detectors use an indirect conversion process to detect x-rays. Multiple photons contribute to each measurement. Photon counting detectors use direct converters and fast electronics to count individual photons in energy bins.

Fig. 2.

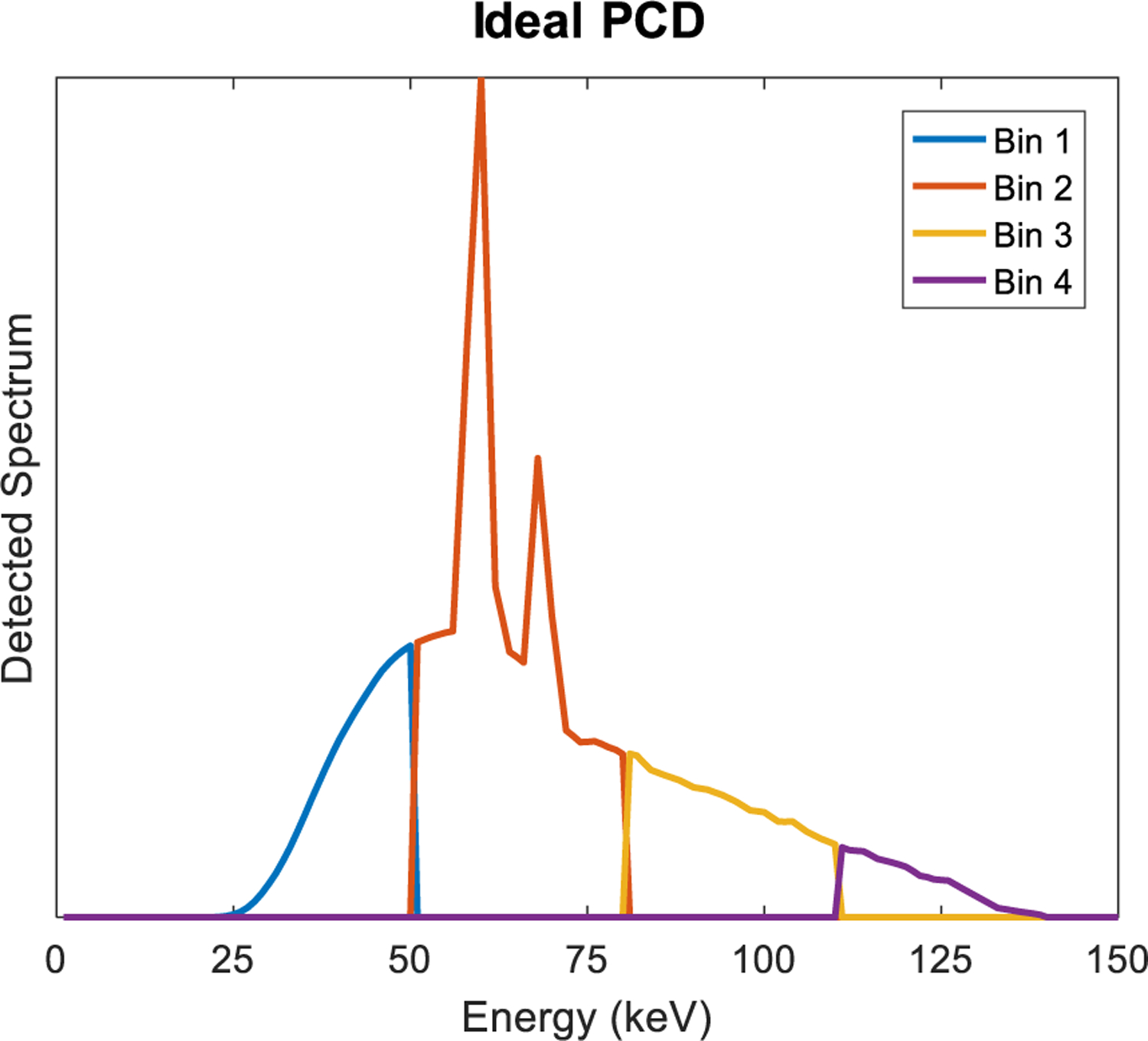
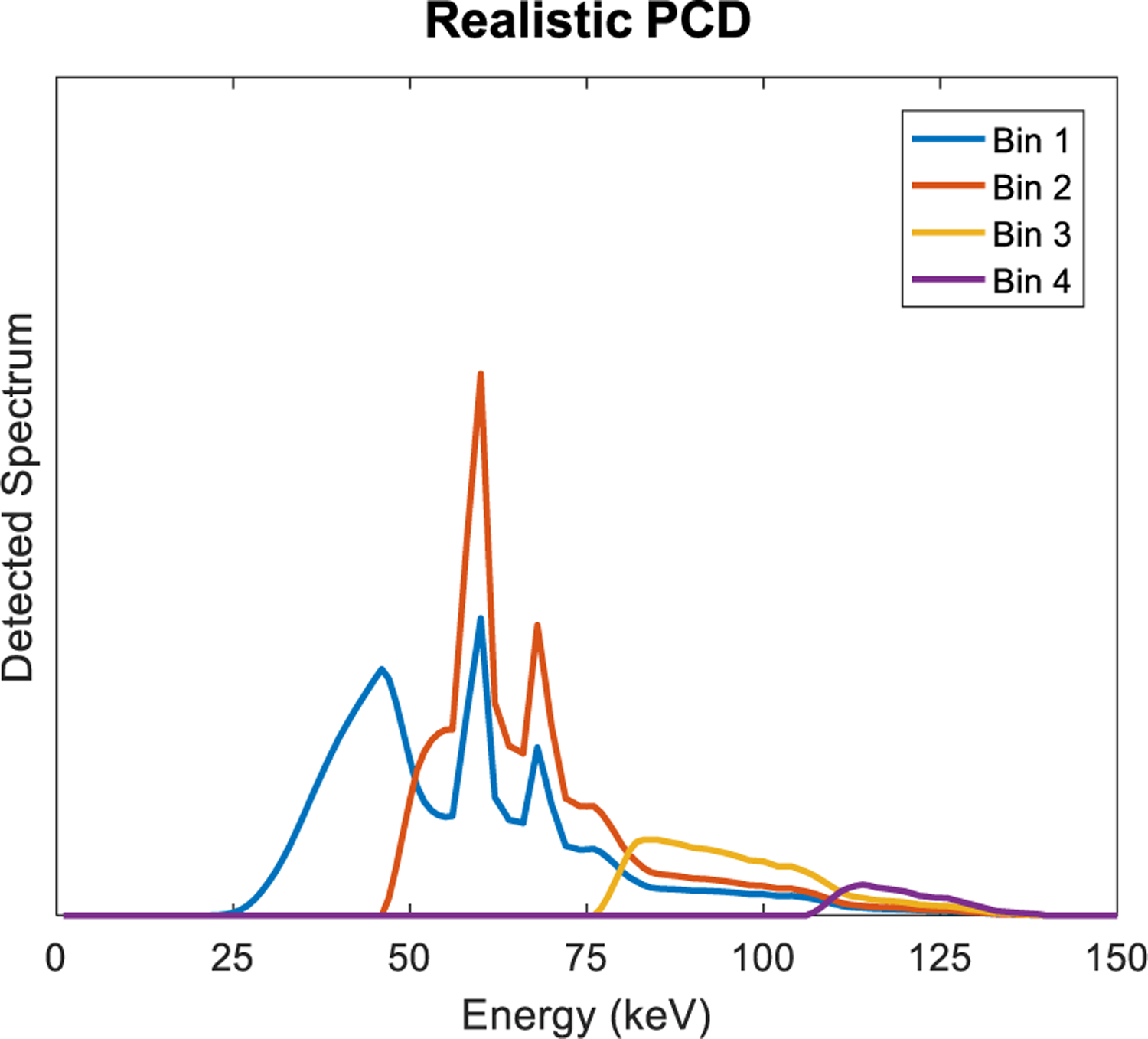
An ideal PCD counts photons in each energy bin. Here, the detected spectrum is divided into 4 bins.

Compared with the 40+ years of EID development, PCDs for CT applications are relatively new. In particular, the past decade has seen tremendous development of PCD technology. Early results showed increased contrast-to-noise ratio (CNR) of iodine and calcium for spectral photon counting CT (SPCCT) over conventional CT in phantom experiments [2]–[6]. Inspired by these early results, Taguchi and Iwanczyk published a visionary paper for what PCDs might bring [7]. Since then, prototype SPCCT scanners have been built and demonstrated with human imaging, including: head and neck scans [8]; clinical-scale SPCCT [9], [10]; increased iodine CNR in abdominal imaging compared to an EID system [11]; better reader-rated diagnostic quality, reduced noise, and higher CNR for lung nodule detection in chest CT [12]; vascular imaging of head and neck with lower noise and less image artifacts such as those due to beam hardening [13]; better gray matter-white matter differentiation in non-contrast head CT and increased CNR; and a dedicated breast SPCCT system [14], [15].

A number of topical reviews have been written recently on PCDs that give an overview of the technology and its potential applications, including by Taguchi [16], Fredenberg [17], Willemink et al [18], and Leng et al [19]. Yet other papers include a review with a focus on PCD electronics [20] or contrast agent development [21], [22]. This special issue also includes a review of PCD hardware [23] and clinical applications [24]. The focus of this review paper specifically examines algorithms and performance analysis for imaging, with a focus on clinical CT applications. The extra information provided by PCDs needs to be used efficiently, and its potential benefit in imaging applications needs to be assessed using rigorous, quantitative comparisons. There is no doubt in the advantages of an ideal PCD, and with an ideal energy response, no electronic noise, no pulse pileup, and perfect geometric efficiency, the algorithms for extracting relevant imaging information are straightforward. However, in the absence of an ideal PCD, we must understand how to use PCDs in the presence of imperfections and how they affect imaging tasks.

II. Algorithms

A. Energy Weighting

A simple way for PCDs to benefit image quality is through their ability to give photons of different energies different weights in their contribution to a conventional “grayscale” image. X-ray tubes produce photons with a broad spectrum of energies. Photon weighting (with weights w(E )) of the detected spectrum N (E ) happens at the detector, either inherently (as in energy integration or in photon counting) or during data processing (as can be done with spectroscopic PCDs). The detected signal is then S = ∫ w (E ) N (E ) dE. Tapiovaara and Wagner showed that to maximize the contrast-to-noise ratio (CNR) of an image, optimal weighting should give more weight to lower energy photons since they have higher CNR (per photon) than higher energy photons [25]. Energy integration inherently does the opposite, by weighting proportional to photon energy. Photon counting, where all photons have equal weight, is an improvement over energy integration (e.g., of about 10% in mammography [26]). Better yet, the optimal weighting was found to be approximately proportional to E ⁻³ for photoelectric contrast (Fig. 3), giving more weight to lower energy photons [27]. These optimal weights were found to give an improvement of about 30% over energy integration in mammography [26]. Such weighting can be applied if the PCD provides counts in energy bins or windows. Then, during processing of the data, a single image from the weighted sum of the binned counts can be formed, where weights are determined based on the energies represented by each bin.

Fig. 3.

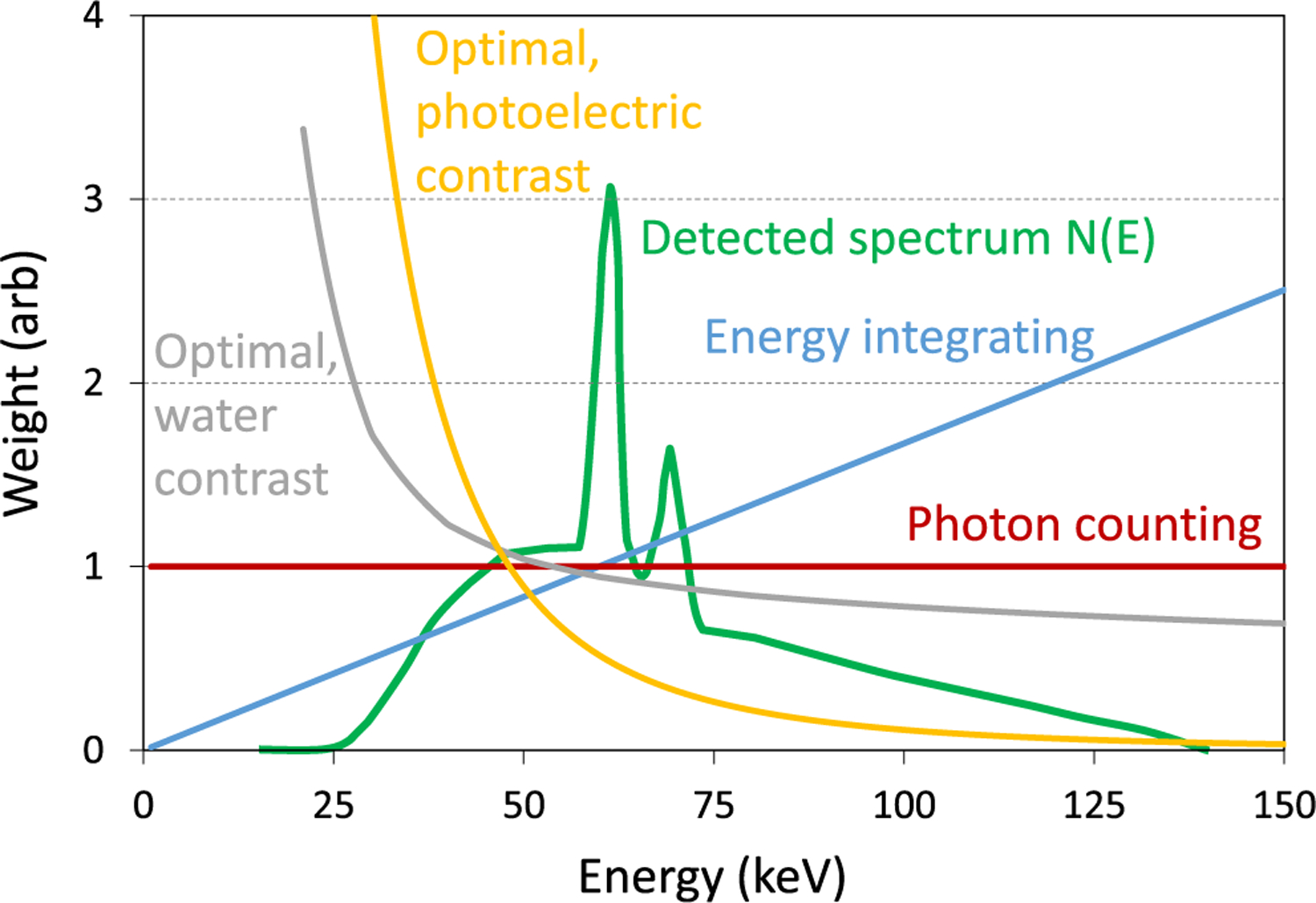
Different energy weighting schemes.

One disadvantage of increased weighting of lower energies in the projection domain is that it leads to increased beam hardening after CT reconstruction [28]. Another option is to reconstruct projections of the individual energy bins, then apply image-based weighting. Optimal image-based weighting was shown to improve CNR by 15% to 57% over energy integration, depending on the task [29]. Additionally, in the image domain, each bin has relatively little beam hardening, so the weighted sum of the reconstructed bin images has less beam hardening than a reconstruction of the weighted sum of all binned counts. However, in practice, object scatter and limited energy resolution of PCDs reduce such gains and should be accounted for. For example, a scatter-to-primary ratio of 0.5 can reduce iodine CNR by 24% without scatter correction, but this reduction is only 10% with scatter correction [30]. The concept of energy weighting can also be extended to preserving information content for material decomposition by weighting the bins by the attenuation of the basis functions as a function of energy [31].

B. Spectral Imaging

Beyond energy weighting, spectral information contained in the binned counts can be used for material-specific imaging. This simply extends the principles of dual-energy imaging to multi-energy imaging, with PCDs providing spectral information through two or more energy bins [32]. Using the same principles as dual-energy imaging, x-ray attenuation can be decomposed into basis functions that represent physical effects (photoelectric absorption and Compton scattering) or materials (e.g., bone and water) [33], [34]. When using materials as basis functions, the resulting line integrals or images are of the mass density of the basis materials. High-Z materials, as would be used in contrast agents, have K-edges in their attenuation curves that can be uniquely identified (Fig. 4). This opens up possibilities for novel contrast agents beyond iodine, especially higher atomic number materials such as gadolinium, tantalum, gold, and bismuth.

Fig. 4.

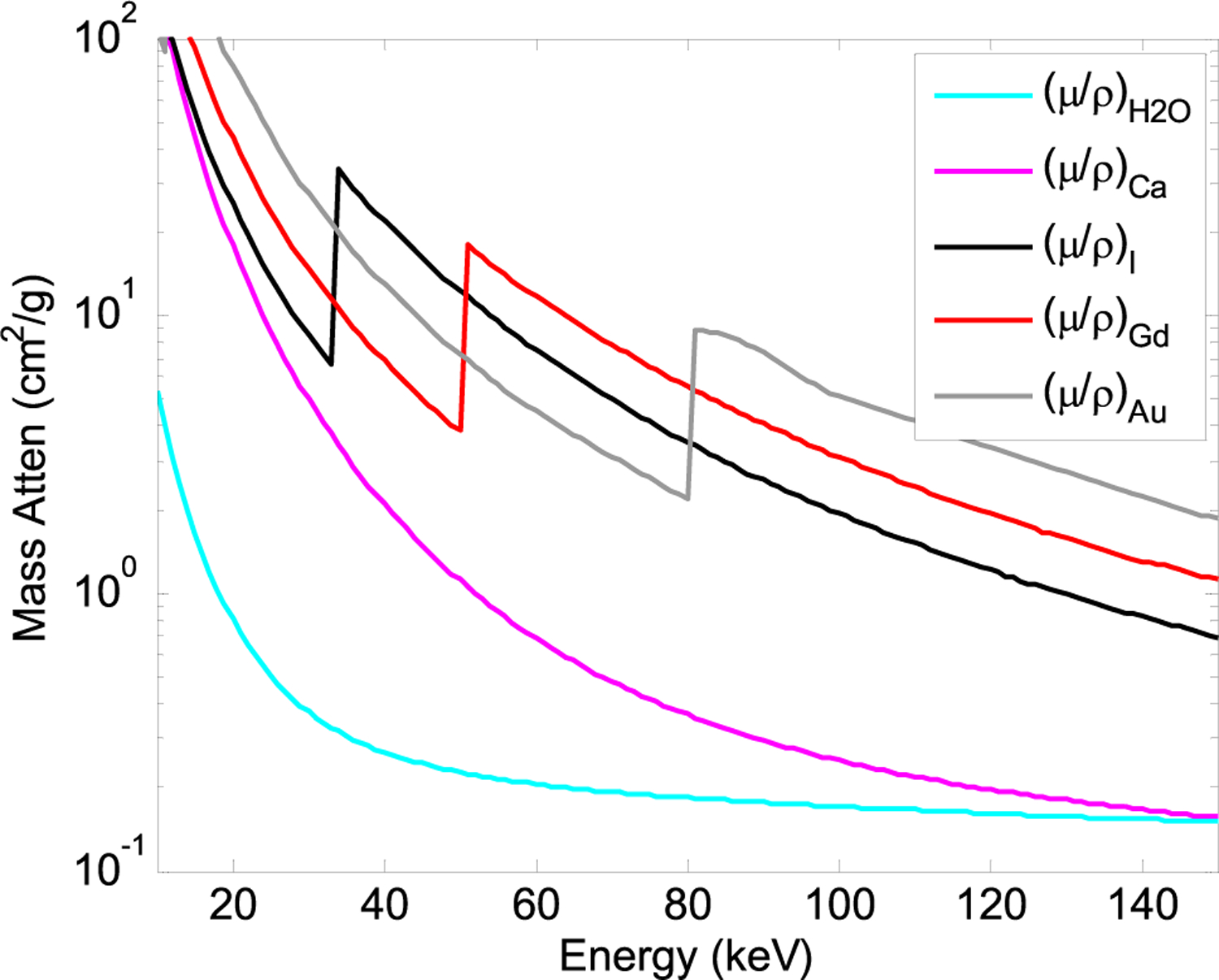
Mass attenuation curves for different materials.

A small-animal CT system was shown to be able to differentiate fat, muscle, and bone, despite the small difference in effective atomic number (Z) between fat (∼6.5) and muscle (∼7.5) [35]. Still, there are limitations in differential sensitivity to materials, for example in detecting small quantities of iron, which can be difficult to distinguish from calcium [36]. Materials with similar Z (and hence attenuation as a function of energy) form an ill-conditioned problem, resulting in high sensitivity to measurement noise or incorrect modeling assumptions. Even at high dose levels and large slice thickness, accurate decomposition and quantification of fat and muscle was found to be difficult [37].

Materials with K-edges have a unique difference in attenuation that an estimator can leverage. Although iodine is the most commonly used contrast agent in CT, its relatively low K-edge energy makes it difficult to uniquely quantify in many clinical applications (separating iodine and calcium because few if any photons with energy below the iodine K-edge can reach the detector), although it can still be suitable for imaging thinner objects, such as small animals, breasts, or extremities. For example, SPCCT was used to quantify iodine uptake in knee cartilage, potentially enabling assessment of cartilage health [38].

Other higher-Z contrast materials with higher K-edge energies are being investigated, such as gold that can be incorporated into nanoparticles [39]. Gadolinium was also used to quantify uptake in knee cartilage [40]. Additionally, more than one contrast agent can be quantified if their K-edges are sufficiently different. Early results demonstrated the feasibility of simultaneously quantifying iodine and gadolinium [2], which have K-edges at 33.2 keV and 50.2 keV, respectively, as well as iodine and gold (80.7 keV) simultaneously [41].

Multiple contrast agents can be used to study different processes simultaneously, with the contrast agents administered through different pathways or at different timepoints. Cormode et al used SPCCT to simultaneously image and quantify iodinated contrast and gold nanoparticles in a rabbit model [42], finding that the rapid scanning with SPCCT enabled measurement of contrast agent kinetics in different organs. More recently, the group demonstrated in-vivo single-acquisition multi-phase liver imaging with a dual contrast agent protocol of iodine and gadolinium [43]. Other dual contrast agent, dual-phase imaging was also performed of the heart [44] and kidneys [45] using iodine and gadolinium in a canine model. Iodine and gadolinium were also used to separate the colon lumen from polyps for CT colonography [46]. Simultaneous imaging of three contrast materials (iodine/gadolinium/bismuth) has also been investigated [45], [47].

1). Material Decomposition:

To perform material decomposition, there should be at least as many energy bins as desired basis materials, although additional constraints such as volume conservation [48], mass conservation [49], or both [50] may enable more basis materials than energy bins. Nonetheless, information from all the energy bins should be used in a dose-efficient way, such as with a statistical material decomposition algorithm like maximum likelihood [2], [51]. Thus, having more energy bins provides more information that reduces noise in the basis material images, although with diminishing returns as the number of bins increases [31]. For K-edge materials, a good strategy would be to have one energy bin just below and another just above the K-edge energy (i.e., one energy threshold is at the K-edge energy).

In practice, empirical measurements can help inform material decomposition algorithms, such as measuring step wedges of different basis materials and mapping the measured counts to the known thicknesses of these basis materials [52]. Some interpolation and bias corrections may be needed as well since the step wedges typically represent a small subset of possible basis material thicknesses, although they should span the expected range of thickness combinations for the imaged object [53].

2). Noise Reduction:

Ideal PCDs provide better spectral information than dual energy methods with EIDs. Compared to a dual-source EID system, ideal PCDs are able to reduce noise in virtual non-contrast images by 29% and in iodine images by 43% [54]. Still, as in dual energy imaging with EIDs, noise in basis material images is higher than in grayscale images, and there is a large increase in noise when decomposing more materials using conventional material decomposition methods [55].

The increased noise in basis material images can be compensated by suppressing the anti-correlated noise in the basis material images [56] or through more advanced reconstruction methods. Some methods operate in the projection domain and suppress noise through additional regularization [57], [58], while others do this in the image domain [59]–[62]. Others use the sum of all energy bins as a prior to improve the basis material or energy bin images [63], [64], or seek to exploit the structural redundancy between basis material images and energy bin images [65], [66]. Additional priors such as volume conservation can also help reduce noise [67]. Material decomposition and reconstruction can be viewed jointly, by using the spectral projections to reconstruct material decomposition images [68]–[70]. These typically have a forward model that maps material images to spectral projections and are solved by iterative reconstruction methods. Incorporation of regularization can help promote inter- and intra-image sparsity during reconstruction [71]. Model-based reconstruction can also incorporate the detector’s spectral response, polychromatic information, and a statistical model. The authors of [72] reported that together with image regularization, image noise was reduced up to 90% compared to conventional material decomposition followed by filtered backprojection.

C. Reduced Beam Hardening

After material decomposition, a weighted sum of the basis material images can be used to create virtual monoenergetic (VM) images. These general principles are used in DECT and carry over to SPCCT [73]. The weights are simply the attenuation coefficients of the basis materials at the specified energy, and the resulting VM image appears as if it were produced by a monoenergetic beam. Being monoenergetic, there should not be any beam hardening. While this requires using spectral information to create the basis material images, combining them in this way makes the VM image suitable largely for grayscale tasks, with the additional benefit of beam hardening correction. In addition, basis material images have anti-correlated noise. When combining them with a weighted sum (as in VM images), the noise tends to cancel out and be much lower to that in basis material images. Further, there is an energy for which noise is the lowest or for which CNR is maximized [74].

SPCCT can also be robust against metal artifact. For metals without K-edges in the diagnostic energy range such as aluminum, titanium, or steel, the benefit is a result of reduced beam hardening. Other metals with K-edges such as platinum or gold can be included as an additional basis material. The combination of spectral information and statistical reconstruction was shown to substantially improve image quality around metal, reducing streaks typical of metal artifact [75]. Another straightforward approach to reducing beam hardening or metal artifact is to simply use the high energy bins since higher energies are less susceptible to beam hardening and penetrate metal better [76], [77]. This said, if the metal is so attenuating that few photons penetrate the object and reach the detector, the SPCCT image will suffer from “photon starvation,” just like conventional images. Even so, PCDs have the advantage of not adding electronic noise to the photon-starved measurements, unlike EIDs.

D. Spatial Resolution

The direct conversion of x-ray photons to charge carriers in PCDs enables spatial separation of detector pixels using the electric field inside the detector, without the need for septa between pixels. This in turn enables higher intrinsic spatial resolution than EIDs. The smaller pixels of PCDs are also in part out of necessity, to reduce count rates per pixel.

High spatial resolution images have been shown with prototype SPCCT systems, including a high-resolution mode that leverages sub-pixels to achieve an effective pixel size of 0.25 mm at isocenter. The 10% MTF, as measured by a wire phantom, corresponded to 17.7 lp/cm (or 280 um) resolution [78]. Another benefit of acquiring data at higher resolution is its improved dose efficiency. This was shown by comparing the high-resolution detector mode combined with a softer kernel with use of binned pixels. At the same in-plane resolution, slice thickness, and dose, the high-resolution detector mode showed 19% less noise than a standard mode with binned pixels [79]. This phenomenon was explained by Baek et al [80], who showed that acquiring data with smaller pixels reduces image noise for image reconstructions at a given resolution.

The improved spatial resolution can potentially benefit many clinical applications, including temporal bone imaging, lung nodule volume quantification and shape differentiation [81] and bronchial walls [82], coronary artery and stent imaging [83], and characterization of renal stone morphology [84].

It should be noted that EIDs are also improving in spatial resolution [85]. A key challenge to overcome in EIDs is the septa between individual detector pixels that prevent the spread of light. The finite thickness of the septa reduces the geometric efficiency of the detector, particularly as the pixel size decreases. Thinner septa can avoid this problem. Other methods for increasing EID spatial resolution, such as a comb filter to decrease the effective detector size, are not dose efficient compared to PCDs [86]. Regardless of the detector type, as detector resolution increases, other aspects of the CT system need to match the increased resolution, otherwise they will limit the resolution. These include a smaller focal spot and increased angular sampling [87].

To summarize, the potential benefits of an ideal PCD are shown in Table 1, assuming that dose efficiency is proportional to the square of CNR and inversely proportional to the square of noise.

TABLE I.

Improved dose efficiency: Ideal PCD vs EID

	“Grayscale” imaging	“Spectral” imaging
Higher geometric efficiency	1.5	1.5
Better spectral information	Optimal weighting 1.3 ‒ 2.5 [29]	Basis material imaging 2.0 ‒ 3.1 (or more) [54]
No electronic noise	At very low flux	At very low flux
Noise aliasing	At high spatial freq.	At high spatial freq.
TOTAL	2.0 ‒ 3.7 or more	3.0 ‒ 4.6 or more

III. Accounting for Non-Idealities

A. Spatial-Spectral Degradation

An ideal PCD would measure the exact energy of each photon incident on each pixel. However, a number of physical effects degrade the spatial-spectral performance of PCDs, including charge trapping, charge sharing, K-fluorescence, Compton scattering, and electronic noise. Photons incident at pixel boundaries create charge clouds that can be collected by two or more pixels, with the signal in each pixel corresponding to less than the energy of the original photon. Secondary photons from Compton scattering and fluorescence in the detector can be detected in neighboring pixels (Fig. 5), again causing multiple events that share the total energy of the incident photon. K-fluorescence is more likely to occur in higher-Z detectors such as cadmium telluride (CdTe), while Compton scattering is more likely to occur in lower-Z detectors such as silicon (Si). Electronic noise can be thresholded out (see Fig. 1), but still adds uncertainty to the photon energy and can lead to uncounted event if the threshold exceeds the signal generated by the photon. These effects collectively lead to: incorrect energy assignment; incorrect counts, including undercount (signal is no longer above the lowest energy bin threshold) or overcount (multiple pixels have signal above the lowest energy bin threshold); reduced spatial resolution (counts in neighboring pixels); and spatial-spectral correlations between energy bins in different pixels.

Fig. 5.

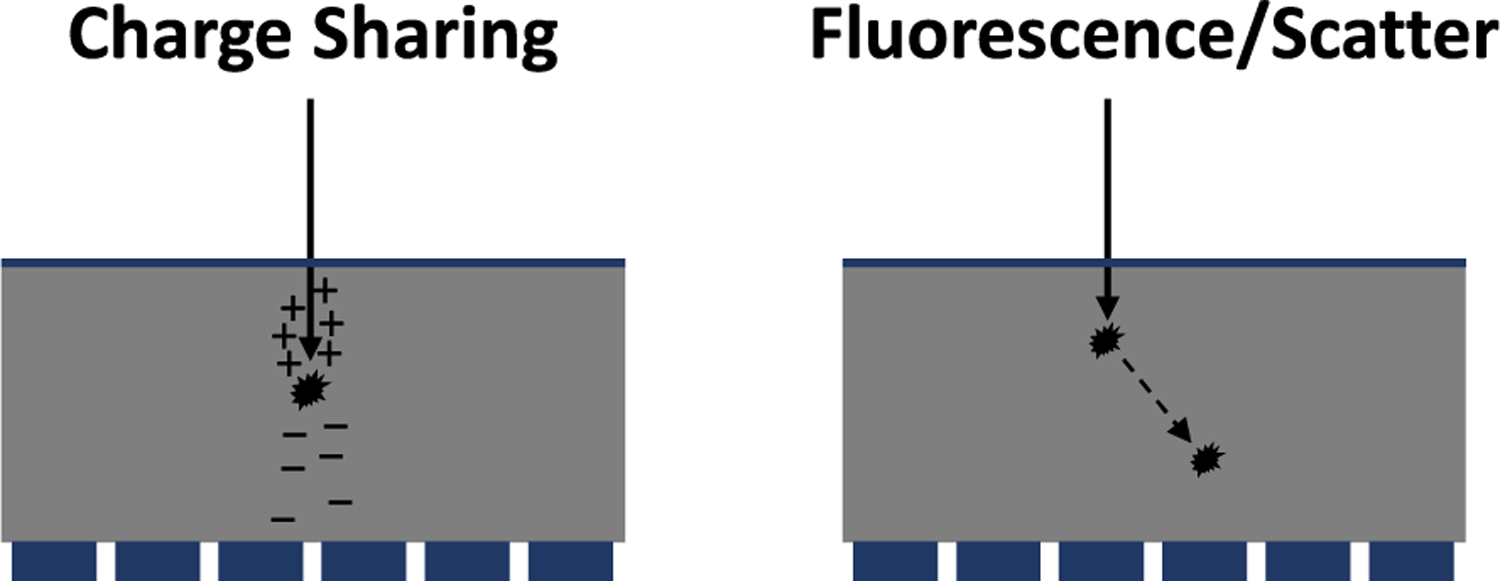
Illustration of charge sharing and K-fluorescence/Compton scattering, which lead to spatial-spectral degradation.

Spatial-spectral degradation depends on many detector design considerations, but perhaps none more than detector material and pixel size. As pixels become smaller, the likelihood of charge sharing and cross talk from secondary photons increases. In particular, Xu et al recommended that charge sharing effects should be taken into account for CdTe detectors when the pixel is smaller than 1 mm² [88]. K-fluorescence in CdTe detectors can lead to a large fraction of incident x-rays experiencing escaped photons (upwards of 20%, depending on pixel size) [89]. On the other hand, Si detectors have a high fraction of Compton scatter, which increases with increasing photon energy [90].

The impact on image quality can be substantial. K-edge contrast imaging is particularly sensitive since the most unique signature is in a narrow band of energies around the K-edge. Compared with an ideal detector, a realistic CdTe detector whose energy response contains significant tailing, may have an SNR reduction by a factor of 2–3 for such spectral tasks [91]. The penalty for grayscale imaging is less than in such spectral tasks since grayscale imaging relies less on energy information.

These effects should be accounted for by characterizing the spectral response of a detector. The energy response functions can be measured, for example with the monochromatic beam of a synchrotron [92] or with radionuclide sources [93]. Once characterized, they can be included in the forward model to more accurately solve the inverse problem of material decomposition. Conversely, spectral degradation can be compensated by empirical calibration, for example with measurements of a multi-material step wedge phantom [51]. In addition, anti-coincidence or charge summing logic in the detector electronics can be used to recover spectral information and spatial resolution [94], [95], but at the expense of count rate capability due to the increased processing time and increased pulse pileup due to the possible inadvertent summing of the signals from different photons. Other concepts, such as coincidence counters for charge sharing [96] and multi-energy inter-pixel variants [97], [98], may be helpful in correcting and compensating for charge sharing.

B. Pulse Pileup

The charge generated by an x-ray photon is collected and shaped to form a pulse. The pulse has a finite duration, and effectively triggers a dead time approximately the same duration as the pulse. If another photon arrives during this dead time, pileup is said to occur. Due to the overlap in signal, the second count may be lost. In addition, the recorded count may reflect a partial sum of the photon energies, which alters the detected spectrum (Fig. 6).

Fig. 6.

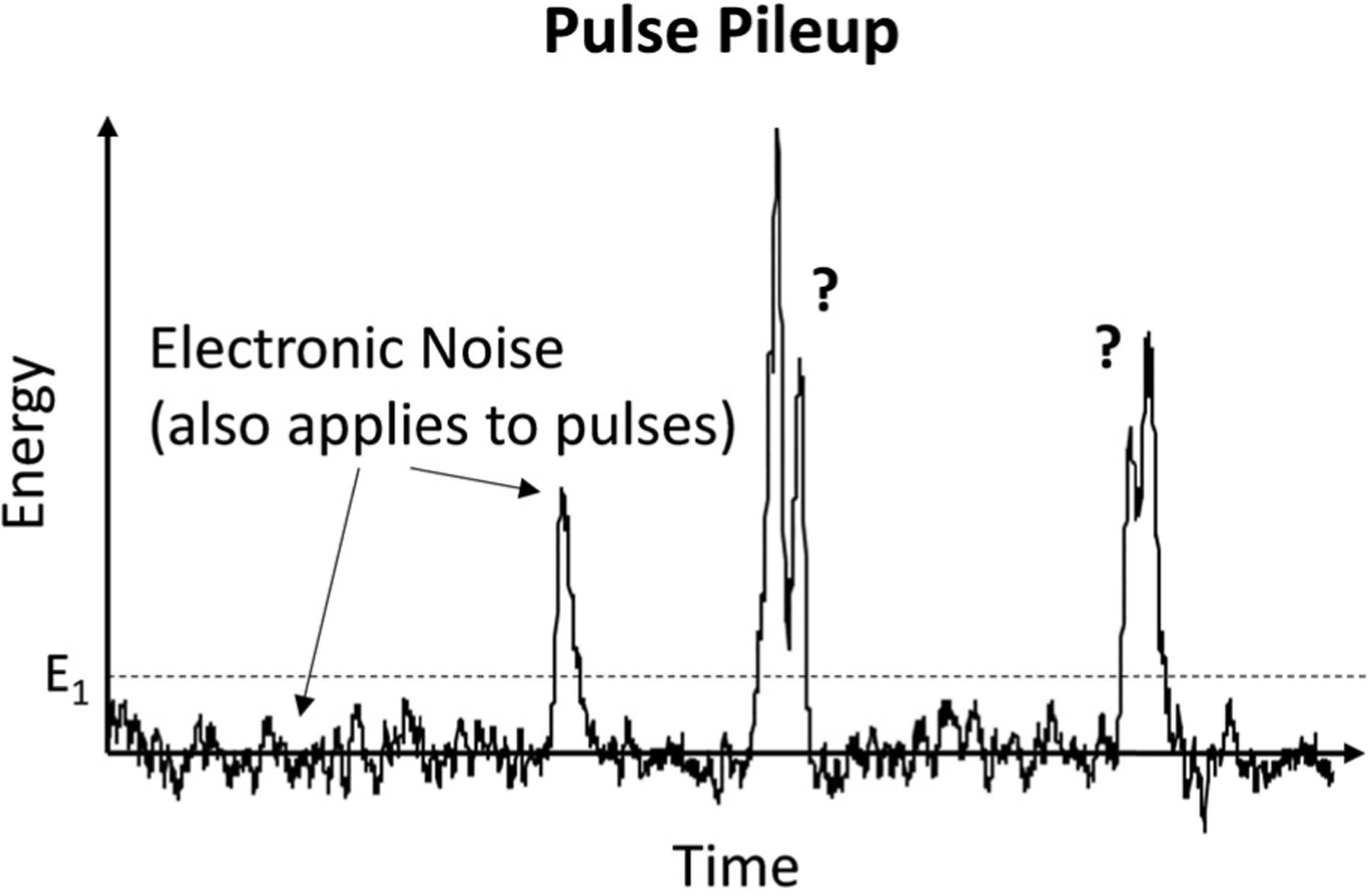
Pulse pileup leads to lost counts and spectral distortion.

Depending on the detector design, the behavior may be paralyzable or non-paralyzable. Paralyzable detectors require a full dead time without pileup to reset the detector into the active state. Non-paralyzable detectors reset into the active state at the end of a dead time, regardless of whether another pulse occurred during the dead time. While real detectors behave somewhere in between, these models are well-described and useful for understanding the impact on the total counts. For example, a non-paralyzable detector asymptotically approaches the maximum periodic count rate (equal to the inverse of the dead time, 1/τ) as the input count rate increases. By contrast, for paralyzable detectors, as the input count rate increases the output rate reaches a maximum (when the input rate is equal to 1/τ) and then decreases asymptotically to zero [99]. With both, when the input rate is high the measured counts are no longer Poisson distributed with equal mean and variance [100]. For non-paralyzable detectors, because the relationship between output and input count rates is monotonic a correction for lost counts is possible. For paralyzable detectors this is only possible for input rates below 1/τ. The lost counts lead to worse imaging performance, even after correction. As mentioned above, real detectors may not behave according to either model. A recent paper describes a semi-nonparalyzable model that better captures realistic pileup behavior [101]. In addition, high photon fluxes can cause saturation from polarization effects that further degrades the detector energy response and limit its count rate, particularly for CdTe/CZT detectors [20], [92], [102].

In addition to the errors in measured count rate, the detected spectrum under pileup can be substantially distorted, shifted to higher energies and can include counts at photon energies higher than those actually in the input spectrum. Although Monte Carlo simulation can predict how pileup will affect the detected spectrum under different input spectra and count rates, analytic methods are preferred for faster prediction of pileup spectra under different imaging conditions [103], [104]. The detected spectra and count statistics can then be applied to imaging tasks to predict performance, such as how pileup increases the noise in material decomposition estimates [105], [106].

Models of pileup distortions can also be used to correct for such distortions [107]. Ideally, the model only requires a small number of measurements or parameters to estimate, and is accurate enough to capture the spectral distortions of a real PCD [102]. With an accurate pileup spectrum model, material decompositions can be accurately performed; otherwise, errors in the model lead to biases in the material decomposition [108]. Non-spectral tasks, such as VM imaging, are less sensitive to spectral distortion [109]. As mentioned above, compared to an ideal detector, even with corrections one should expect higher noise levels due to pileup.

Care must be taken to avoid pileup or other high-flux effects when imaging at clinical dose levels [110]. The incident count rate per pixel can be reduced by decreasing the detector pixel size. As a result, many detectors have small pixel size, which comes with the benefit of increased spatial resolution, but at the expense of increased cross talk, as previously discussed. These effects, taken together, suggest that at very high x-ray flux, pileup limits image quality and smaller pixels are preferred. The detector can also be segmented in the depth direction, further decreasing the input rate per counter [111][5]. At low flux or for thick objects, cross talk becomes the limiting factor and larger pixels are preferred [109]. Detector count rates also depend on semiconductor properties (e.g., carrier mobility), design (e.g., detector thickness, depth segments), and pulse shaping time (e.g., shorter shaping time decreases dead time but increases electronic noise). Increasingly, detectors have been shown to support count rates in the range required by clinical CT systems (up to 100 Mcps/mm², million counts per second per mm²) [112]. The unattenuated beam can exceed 1000 Mcps/mm² [113], [114], although it is reduced by the patient and a bowtie filter. Other proposed solutions include methods to reduce the peak incident count rate, e.g., dynamic bowties that reduce flux where the scanned object is least attenuating [115], which improves both dose efficiency and image quality. Other concepts for pulse-detection logic, such as measuring the peak duration (width), may also provide useful information to overcome pileup [116].

C. Use of Artificial Intelligence

Artificial intelligence (AI) is increasingly being investigated for countless applications, including for PCD corrections. While such approaches generally require training data to fit models such as neural networks, they can often avoid explicit models. The training data could be in the form of empirical measurements of known objects and thicknesses (e.g., step wedges of basis materials) that include non-idealities such as spectral or pileup distortions. Then, neural networks can be trained to directly map binned counts corrupted by such distortions to basis material images. Such approaches have been demonstrated for handling spectral distortions [117] and pileup [118], [119]. In addition to neural networks, different machine learning methods are being investigated [120], [121]. The extensive amount of training data needed may pose a challenge to AI approaches, and methods such as transfer learning can incorporate simulation data to reduce the amount of empirical data needed [122].

D. Patient Scatter

While scattered x-rays from the patient are a problem in all x-ray systems, they do add some unique challenges to PCDs. Conventional CT scanners have substantially increased longitudinal coverage, enabling increased coverage in axial mode and faster helical scanning, but also leading to increased patient scatter [123]. Current SPCCT prototypes have limited longitudinal coverage, enabling narrower collimation with reduced scatter. However, as longitudinal coverage increases, so will scatter. The scatter signal distorts the measured spectrum toward lower energies and adds undesired bias and noise into the binned counts, which in turn affect imaging tasks such as material decomposition, as shown by Monte Carlo studies [124], [125]. Even a relatively low scatter-to-primary ratio of 3.5% can have a substantial impact on iodine quantification [126].

An anti-scatter grid can be effective at removing scatter, but it detracts from one of the main advantages of PCDs. EIDs already have septa that separate pixel scintillators to avoid cross talk, so a grid aligned with the septa has minimal, if any, effect on geometric efficiency and quantum detection efficiency (QDE). However, in PCDs, septa are not typically included, so overlaying a grid would reduce the geometric efficiency to the grid fill factor (Fig. 7). The tradeoff between geometric efficiency and scatter was investigated in [127]. Without a grid, scatter can reduce DQE by more than 50%, whereas a grid limits the DQE reduction to 19%, with approximately half the reduction from geometric efficiency and the other half from residual scatter. Aside from grid-based solutions, Sossin et al. developed an approach to estimate binned scatter counts using a partial attenuator in the beam [128], [129]. However, even if the average scatter signal can be removed, noise from the scatter will remain. Likely, some combination of hardware and software-based solutions is needed to physically reject scatter and correct for residual scatter, respectively.

Fig. 7.

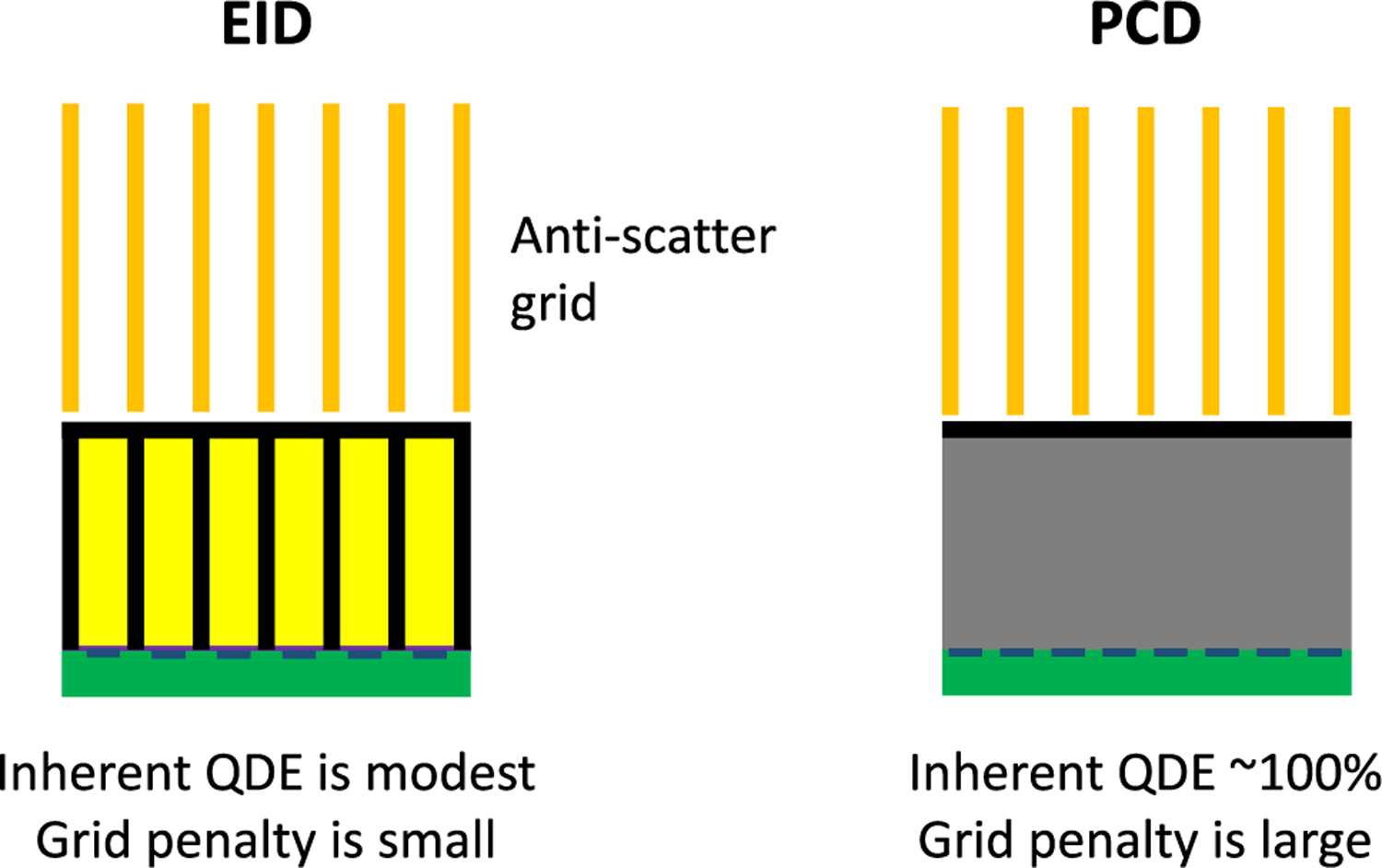
Effect of anti-scatter grids on quantum efficiency.

IV. Performance Assessment

A. Dose Efficiency

The question of dose efficiency is deeply intertwined with the discussion on grayscale and spectral imaging performance. In general, measurement noise (standard deviation) is inversely proportional to the square root of dose, so any reduction in noise can instead be used for dose reduction. Conversely, increased noise may have to be overcome with increased dose to maintain precision. Typically, dose efficiency is assessed by examining measurement noise for fixed dose, enabling the fairest comparison. Here, we assume the behavior is approximately linear and exclude noise reduction from non-linear denoising algorithms, which can affect spatial resolution, noise texture, and/or introduce bias. For grayscale imaging, dose efficiency is commensurate with increased CNR [29], [30], [110], as discussed in Section II. A and C.

Multi-material acquisition and decomposition from a single scan has the advantage of simultaneous acquisition, which limits motion and registration issues. However, the potential for dose reduction by using a single CT acquisition instead of multi-phase CT scans should be carefully considered. A recent study showed conventional dual-phase imaging at different time points following a single contrast injection (e.g., arterial, venous phases) is more dose efficient than a single scan with dual contrast agents. For the same total dose, simultaneous imaging of dual contrast agents may result in increased noise; conversely, for equal noise, the dose would need to be increased greatly [130]. In addition, dual contrast scans may require larger amounts of contrast agents in total, raising toxicity concerns.

Another important consideration for dose efficiency is to ensure the source spectrum (tube voltage, filtration) is optimized for the detector and imaging task, which can vary from non-contrast imaging to quantification of iodine or gadolinium [131]. For example, lower tube voltage for smaller objects (as low as 60 kVp for pediatric-sized phantoms) was shown to increase the detectability index per unit dose by up to 30% for adipose imaging and 70% for iodinated imaging, as compared to an EID [132]. Additionally, Shikhaliev showed that adding a K-edge filter to the source improves dose efficiency since it creates a pseudo bi-modal spectrum with greater energy separation between photons [133]. Perhaps counterintuitively, even discarding photons from certain energies can help spectral tasks [31].

For dual energy tasks, such as two-material decomposition or single contrast agent imaging, DECT can have competitive performance as compared to SPCCT. Such comparisons should allow for source spectrum optimization for both [134]. DECT performance largely depends on the separation between the two measured spectra, so, for example, an optimized dual source DECT with filtration can perform at the level of realistic PCDs [54]. Further improvements can be achieved by combining dual spectra with PCDs, for example in a hypothetical dual source SPCCT system, which would outperform both dual source DECT and single source SPCCT [135].

At very low doses, where EIDs suffer from electronic noise, the relative performance of PCDs is much higher. This is particularly evident in regions of photon starvation, such as the shoulders. Yu et al showed that at the same low dose, PCD images had noticeably less streak artifacts and less image degradation than EID images [136]. Conversely, at very high doses (and flux rates), the relative performance of PCDs falls when pileup becomes significant (Fig. 8).

Fig. 8.

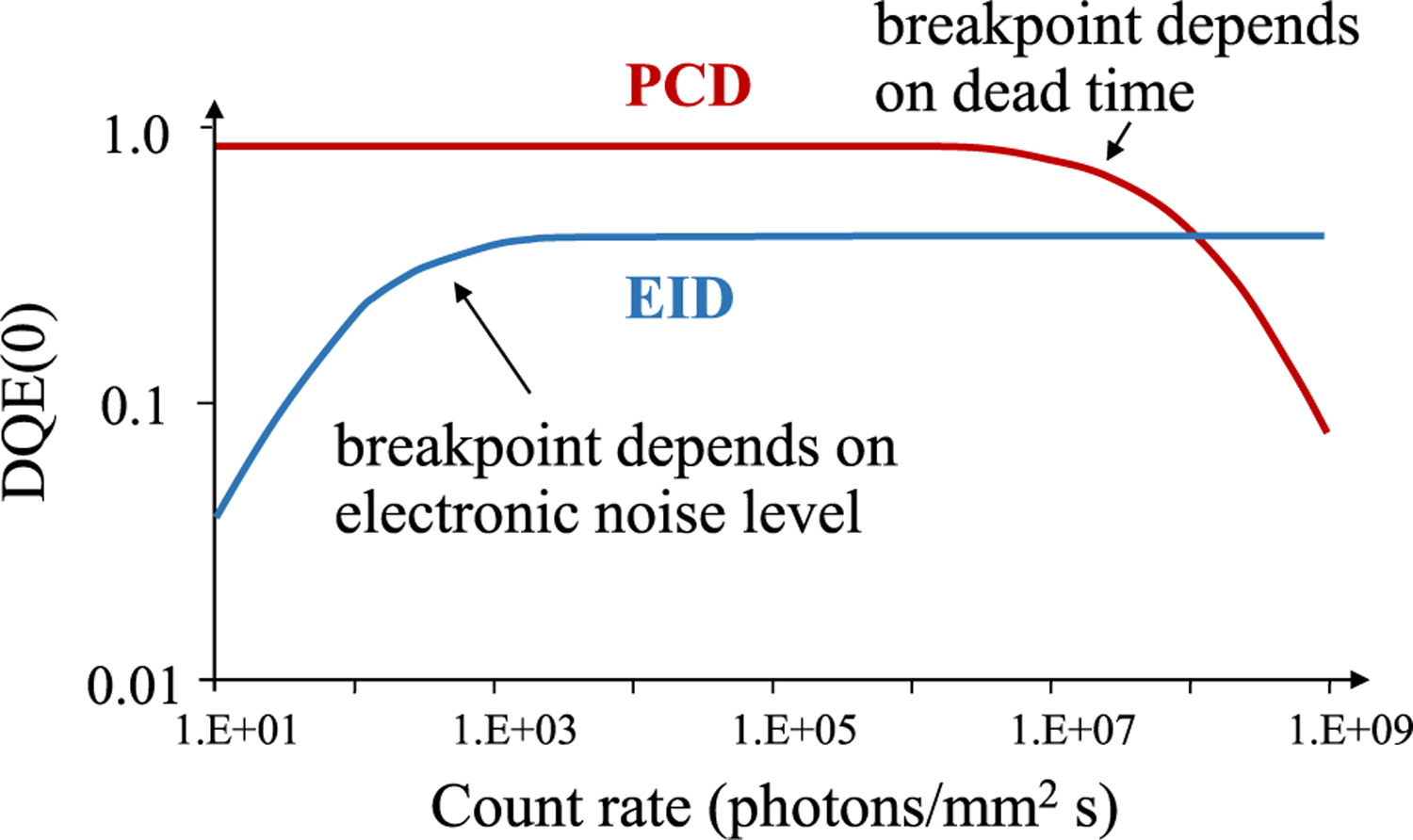
PCDs do not suffer from electronic noise but do have count rate limitations.

B. CRLB

Noise is a critical part of assessing measurement quality, particularly when examining CNR, dose efficiency, and material-specific imaging. Often, noise is understood in one domain (e.g., binned counts), and needs to be used to predict the noise in another domain (e.g., basis material line integrals). The Cramér-Rao lower bound (CRLB) is a useful tool in that regard since it propagates uncertainty from one domain to another. It gives the minimum variance (or covariance matrix) for an unbiased estimator. The CRLB therefore provides the performance of the best-case scenario for a maximally efficient unbiased estimator that makes use of all energy information in the binned counts. Calculating the CRLB can be useful for detector or system design, by understanding how design choices affect imaging performance. This approach was used in the original dual energy paper by Alvarez and Macovski [33] to analyze dual energy performance and has since been applied to assess PCD performance [137].

In the case of estimating basis material noise from binned counts, the CRLB requires the probability distribution of the binned counts. Because the true distribution is often intractable, a multivariate Gaussian approximation is assumed instead, using the first and second-order statistics of the true distribution (mean and covariance matrix, respectively).

In addition, the sensitivity of the binned counts (mean m, covariance Σ) to the material thicknesses (t) needs to be known or determined empirically. Then, for material indices i, j, the Fisher information matrix is:

$$F_{ij}\left(t\right)={\left(\frac{\partial m}{\partial t_i}\right)}^T{\Sigma }^{-1}\left(\frac{\partial m}{\partial t_j}\right)+\frac{1}{2}\text{tr}\left({\Sigma }^{-1}\left(\frac{\partial \Sigma }{\partial t_i}\right){\Sigma }^{-1}\left(\frac{\partial \Sigma }{\partial t_j}\right)\right).$$ (1)

The covariance sensitivity can be difficult to compute and has been shown to be negligible (constant covariance) when the number of photons is reasonably high [55]. The CRLB is then the matrix inverse of the Fisher information: C (t) = F⁻¹ (t).

C. DQE

The detective quantum efficiency (DQE) is a more comprehensive metric of a detector’s performance or overall imaging performance and can be used to compare PCDs and EIDs [138]. DQE is a function of spatial frequency and can be defined as the ratio of output to input SNR:

$$\text{DQE}\left(f\right)=\frac{{\text{SNR}}_{\text{out}}^2\left(f\right)}{{\text{SNR}}_{\text{in}}^2\left(f\right)}.$$ (2)

Despite the relatively simple definition, evaluating it must consider the effects that degrade SNR as a function of spatial frequency f. The zero-frequency DQE is often easier to evaluate, since this reflects large-area tasks (“large” compared with the length of spatial correlations caused by the mechanisms that lead to cross-talk across pixels). For example, it was shown that processes that lead to multiple counts in neighboring pixels inherently reduce DQE(0) [139]. For the frequency-dependent DQE( f ), cascaded systems analysis helps create theoretical models of DQE by identifying and analyzing individual physical processes that lead to signal creation [140]. The approach can include cross talk from characteristic/scatter photons, stochastic conversion of x-ray photons to secondary quanta, depth-dependent charge collection, and electronic noise [141]. Such models have been compared to measurements and showed good agreement in MTF and DQE [142].

Realistic models should further include spatial-spectral effects between neighboring detector pixels and energy bins (Fig. 9). This cross talk leads to correlations that can be captured by their signal statistics. Monte Carlo simulations of these effects can reveal the impact on DQE as a function of pixel size, photon energy, and detection threshold [143]. While Monte Carlo is the gold standard, computationally efficient methods have been developed as well [144]. A photon counting toolkit (PcTK) that models spatial-spectral cross-talk and correlation between PCD pixels has been developed and made available to academic researchers. It includes models for detection efficiency, charge sharing, K-fluorescence, and electronic noise [145]. The toolkit was used, for example, to examine the effect of sub-pixel binning and masking, e.g., due to an anti-scatter grid [146].

Fig. 9.

Spectral cross-talk of realistic PCDs, showing incident photons that contribute to each energy bin.

To understand the impact on spectral tasks such as material decomposition, the PCD statistics, including spatial-spectral correlations, need to be propagated through to the task. Using the CRLB, Rajbhandary et al found that such effects can increase basis material noise by 35% and virtual monoenergetic noise by 10% when using smaller CdTe pixels (4×4 binning of 0.25×0.25 mm² sub-pixels instead of a single 1 mm² pixel) [147]. As previously discussed, this disadvantage of smaller pixels can be mitigated through charge sharing compensation, and smaller pixels do have advantages in avoiding pileup. Rahbhandary et al then extended the model to calculate DQE( f ), by including a small-signal sinusoidal imaging task and determining the CRLB with realistic detector correlations. It was shown that these correlations degrade DQE( f ) beyond what is lost by the imperfect response in each detector pixel [148].

Recently, a comprehensive framework for DQE( f ) analysis for spectral (basis material) and grayscale (virtual monoenergetic) imaging was developed, taking into account the full spatial-frequency dependence of the available energy information [149]. The framework was used to compare two realistic PCDs made of different materials: CdTe and Si. CdTe has higher stopping power and little Compton scattering, while Si offers higher carrier mobility (count rate), low electronic noise, negligible K-fluorescence escape, wide availability, and potentially low cost [90]. Monte Carlo simulation was used to determine the extent of spatial-spectral correlations, and the detector DQE was propagated to detection and quantification imaging tasks. The two detectors were found to have different advantages, with CdTe having better water/iodine detection, and Si having better material quantification performance [150].

So far, all such models of spatial-spectral correlations have been in the low-count regime, to avoid needing to include the effects of pileup. A comprehensive DQE model is still needed to combine spatial-spectral effects with pileup. Such comprehensive models will provide a complete picture of PCD performance and could facilitate optimization of SPCCT systems.

D. Task-Based Performance

While DQE describes detector or system-level performance, it can be helpful to incorporate the imaging task into a performance metric such as detectability index. Depending on the spatial frequency dependence of detector performance and imaging task, it is possible to derive optimal frequency-dependent bin weights, which can improve the detectability index by 10% as compared to conventional bin weights that are constant across all spatial frequencies [151], [152]. Performance also depends on the observer, and has been investigated with ideal [153], Hotelling [154], channelized Hotelling [155], and human observers [156]. A complete assessment of the impact of PCDs may ultimately be determined by incorporating the detector performance, task, and observer model into a comprehensive performance metric.

V. Summary

In summary, PCDs offer vast potential, including unique spectral information, higher dose efficiency, and higher spatial resolution. Competing EID technologies have over 40 years of engineering refinement, while PCDs are still a rapidly evolving technology. Key technical problems still need to be solved, including count rate, spectral distortion, reproducibility, and cost. Selection of the detector material may be key, with CdTe and Si having different pros and cons. Scatter mitigation needs to be optimized, otherwise some of the intrinsic gains of PCDs will be lost. The potential for spectral tasks is greater than grayscale tasks, but spectral tasks tend to be more sensitive to non-idealities than grayscale tasks. The impact of such non-idealities on image quality needs to be considered carefully and thoroughly. With the right properties, PCDs can revolutionize medical x-ray imaging in general and CT imaging in particular.