Blood vessel-on-a-chip examines biomechanics of microvasculature

Abstract

We use a three-dimensional (3D) microvascular platform to measure the elasticity and membrane permeability of the endothelial cell layer.The microfluidic platform is connected with a pneumatic pressure controller to apply hydrostatic pressure. The deformation is measured by tracking the mean vessel diameter under varying pressures up to 300 Pa. We obtain a value for the Young’s modulus of the cell layer in low strain where a linear elastic response is observed and use a hyperelastic model that describes the strain hardening observed at larger strains (pressure). A fluorescent dye is used to track the flow through the cell layer to determine the membrane flow resistance as a function of applied pressure. Finally, we track the 3D positions of cell nuclei while the vessel is pressurized to observe local deformation and correlate inter-cell deformation with the local structure of the cell layer. This approach is able to probe the mechanical properties of blood vessels in vitro and provides a methodology for investigating microvascular related diseases.

1. Introduction

Organ microvasculature consists of an interwoven network of capillaries, arterioles, and venules, which provide the tissue with nutrients and oxygen essential for its own function ¹. They are constantly subjected to hemodynamic forces resulting from flow and pressure and their wall performs as an essential membrane by allowing nutrients and waste substances to pass across it ². Whenever hydrostatic pressure in oral mucosa or bone is high (e.g., (0.8 to 2) kPa), the microvascular membrane becomes more permeable to the movement of the molecules from the blood stream to the interstitium leading to edema, the accumulation of excess interstitial fluid and damage of the surrounding tissue ^3–7.

Although the mechanical stimulation environment plays such an important role in the vessel functionality, in vivo studies are limited due to the challenge of developing material probes or replicating physiological environments ⁸. To this end, an ideal in vitro 3D microvascular model must incorporate the hemodynamic components of the microvessels. The majority of in vitro studies have been limited to two-dimensional (2D) models by plating endothelial cells (ECs) on a flat surface such as a Petri dish ⁹, porous membrane ^10,11, or patterned hydrogel ¹² to form a confluent monolayer to mimic the blood vessel wall. However, these 2D models cannot replicate the proper physical structure of blood vessels in vivo, and of note is its circular shape and polarized surfaces. Thus, in vitro microfluidic systems must overcome these limitations by mimicking the 3D mechanical microenvironment of cells. By incorporating detailed in vitro measurements and computational models into these microfluidic systems, these platforms would be most informative – as diagnostics, prognostics, or as indicators of therapy effectiveness either before or after treatment ^13–15.

Blood vessel elasticity is an important feature of vascular functionality reflecting the extent of vascular injury owing to cardiovascular risk factors, and it provides risk stratification and determines prognostic value ^16–18. Previous measurements on elasticity have focused on large vessels such as arteries, where macroscale inflation and tensile strength have been measured ^19–21. The physical descriptions of these large vessels are based on the development of hyperelastic models of the multiple layers of arterial tissue, which are smooth muscle cells, adventitia layer, and endothelium ²².

In contrast, endothelial cells in capillaries form a single monolayer in vivo and are characterized by antithrombotic and anti-inflammatory activity, regulation of blood pressure, and barrier function in the tissue. Measurements of the elasticity of the isolated endothelium are less common and typically performed in vitro in a 2D substrate supported geometry. Atomic force microscopy (AFM) has been used in this geometry to probe mechanical properties at subcellular scale, and it is difficult to measure the integrity of the entire cell layer ^23–26. Measuring elasticity and integrity of the layer is critical for understanding how the structure and connections between cells change under influence of disease and therapies.

In this study, therefore, we use a 3D blood vessel model platform to recapitulate and measure the elasticity of the 3D microvasculature. Specifically, in this microfluidic platform, vessels comprising a single endothelial layer in a collagen matrix were connected to a pneumatic pressure controller to regulate the hydrostatic pressure without the induction of considerable flow through the vessel. By applying a range of sinusoidal and square wave pressures, we observed the radial deformation of the capillary vessel. We compared the stress strain response to quasilinear viscoelastic (QLV) equations using a hyperelastic model that describes the strain hardening observed at larger strains (pressure). Finally, we correlated the changes on the diffusion (permeability) across the endothelial cell layer under pressurized conditions using fluorescent labeling. Overall, the measurements on this platform may pave the way to determine the microvessel elasticity as a prognostic factor of microvascular diseases.

2. Materials and Methods

Cell culture

Human umbilical vein endothelial cells (HUVECs) (Lonza) were cultured in endothelial cell growth medium (EGM-2) (Lonza). All experiments were performed with HUVECs at passage 4 to 5.

Fabrication of microfluidic platform

Masters are used for replication by molding microfluidic devices created with a polyjet 3D printer (Connex 500; Stratasys.com). Computer-aided design (CAD) models designed in Autodesk Inventor are exported as .STL files, uploaded on 3D printer software, and printed by inkjet nozzle deposition of 30 μm thick layer of a Ultra-Violet (UV)-curing photopolymer (VeroWhite Connex 500; Stratasys.com). Once the liquid layer is deposited, it is cured by intense ultraviolet light (see Figure 1a and b). Secondly, the scaffolds are plasma treated for 5 min and silanized overnight in trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma). Polydimethylsiloxane (PDMS; Sylgard 184, Dow-Corning; Krayden) devices are fabricated from these scaffolds. The PDMS devices are treated with 0.01 by volume fraction poly-L-lysine (PLL; (Sigma) and 0.5 by volume fraction glutaraldehyde (Sigma) to promote collagen I adhesion. After washing overnight in water, steel acupuncture needles (diameter=160 μm Seirin, Kyoto, Japan) are introduced into the devices and a solution of 3 mg/mL type 1 collagen (Thermo Fisher Scientific), 1x M199 medium (Thermo Fisher Scientific), 1 mmol/L 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES), 0.1 mol/L NaOH and NaHCO3 (0.035 by mass fraction), is infused and allowed to polymerize for 40 min at 37 ◦C. The needles are removed to create 160 μm diameter channels with a length of approximately 2 cm within the collagen gel. A suspension of 1 million/mL HUVECs is introduced into devices followed by cell growth media (EGM2). The cells are given 2 min to adhere to the top surface of the channel and then flipped to allow cells to adhere to the bottom surface of the channel for another 2 min. This process causes the amount to cells adhering to the channel surface to be higher on the sides (coated twice) than on the top and bottom. The non-adherent cells were washed out and fresh media was replaced into the device. The final vessel diameters without applied pressure are typically in the range of (110 to 150) μm diameter. Two to four devices are made in a batch for a set of each experiments. In total, over 20 different devices are used in this study and representative results are shown for the different measurement methods.

Fig. 1.

Blood vessel-on-a-chip platform. (A-B) 3D printed scaffold (master) for PDMS microfluidic devices; Bar = 2 cm. (C) Photograph of PDMS device; Bar = 1 cm. (D) Schematic of the components of the pressurized blood on a chip system.

The ports of the devices are connected to the same pneumatic pressure source such that the same pressure is applied to each side. We assume that the cell growth media has the physical properties of water. An electronic pressure regulator (Enfield) is used to fill an air cylinder with a 2.5 kPa pressure sensor (Omega) connected for feedback to the regulator (see Figure 1d).

The microfluidic device is mounted on an inverted microscope with a holder sealing connections to pneumatic system. Bright-field imaging is performed on an Olympus IX71 with a digital camera (Andor Zyla). The pressure controller and camera are operated simultaneously with a python-based instrument-control package (Pythics) ²⁷.

Imaging

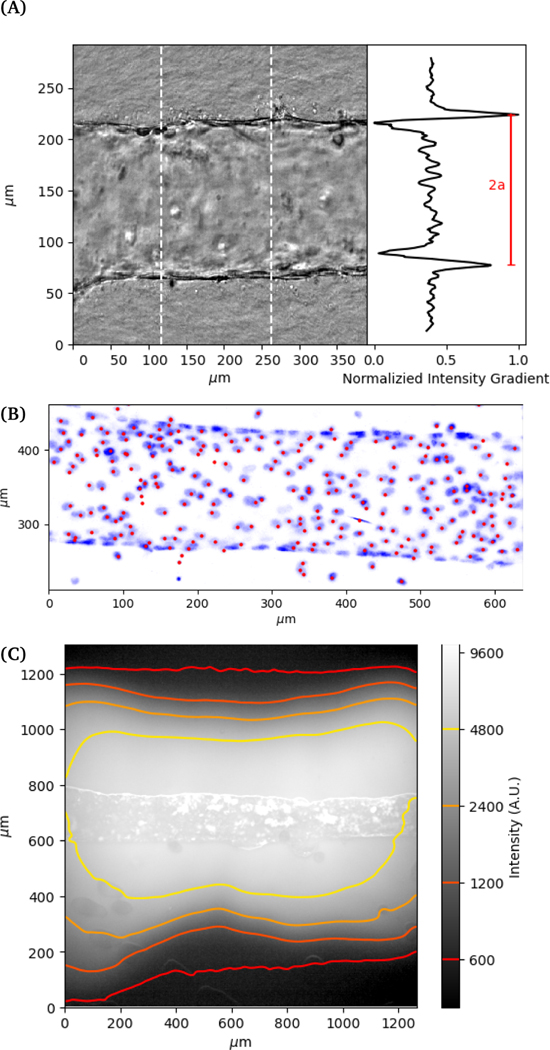
Images are recorded in a central region of the vessel, approximately 1 cm wide, where we not observe any variation in properties with position in this region. The deformation of the vessel under pressurization is imaged using phase contrast microscopy on an Olympus IX70 with a digital camera (Andor Zyla). Images are recorded simultaneously with the pressure readings from the pressure controller (see Figure 2a). Images of the channel are used to obtain its dimension by using the maximum gradient in intensity to determine the outer edge of the vessel. Gaussian fits to the peaks of the intensity gradient are used to determine the subpixel position of the walls. The distance between the two outer edges averaged over a section of the channel is used to determine the vessel diameter. Flow out of the membrane is imaged using fluorescence imaging with 70 kDa Dextran dye.

Fig. 2.

(A) Example of deformed vessel imaged with phase contrast. Vessel width is measured by tracking distance between interfaces. (B) Projection of 3D confocal image of nuclei stained blue and image-process identified locations red. (C) Flow of fluorescent dye Dextran out of vessel at 200 Pa. The image and contour plot show the fluorescence signal on a log scale.

For 3D imaging, we record confocal microscope (Zeiss LSM 800) images while applying a constant applied pressure to the vessel. The cell nuclei are labelled with DAPI (4,6-diamidino-2-phenylindole) fluorophore and single channel z-scan is performed. The 3D positions of cell nuclei are located from confocal images using feature finding algorithms ²⁸ (see Figure 2b).

Statistical analysis

For statistical purposes, the unit of measurement was the result obtained for each microfluidic device and each experiment carried out a minimum of three separate times on different devices. Relationships between measurements will be examined between the different groups by multi-variate analysis based upon their scientific relevance with significance set at p<0.05.

Model

The inflation of a finite thickness cylindrical shell is a common approach for measuring the elasticity in the microvasculature ^29–31.

We define the measured strain as $\lambda =\frac{a}{a_0}$. The size of the cell layer is approximately h ≈ 5 μm, much smaller than the initial radius of the vessel a₀ ≈ 75 μm. The cell layer extends to the PDMS channels, as shown in Figure 1, where axial deformation is constrained. In the thin layer limit, h << a, assuming fixed ends, the following equation relates the change in radius to the applied pressure across the cell layer for a linear elastic,

$$\epsilon =\lambda -1=\frac{\text{Δ}P{a}_0\left(1-v^2\right)}{Eh}$$ (1)

where E is the Young’s modulus, and ν is Poisson’s ratio. For our measurements, we assume incompressibility ν = 0.5.

We use a nonlinear equilibrium elastic model, originally proposed by Gent, which is commonly used to describe the response of the microvasculature and other soft materials with finite extensibility ^32,33.

The relationship between strain and pressure for the Gent model, assuming that the side walls constrain axial deformation and incompressibility of the cell layer, is given by:

$$\text{Δ}P=-\frac{h{J}_m\left({\lambda }^4-1\right)\mu }{a_0{\lambda }^2\left(1-\left(2+J_m\right){\lambda }^2+{\lambda }^4\right)}.$$ (2)

where μ is the shear elastic modulus, J_m is a parameter related to the maximum strain by, ${\lambda }_{max}=\sqrt{\left(2+J_m+\sqrt{J_m}\sqrt{4+J_m}\right)/2}$. These parameters characterize both the modulus of the cell layer and strain hardening behavior. We use the mean cell layer thickness measured using confocal imaging (see supplemental ??).

The deformation of the collagen matrix will result in a contribution to the stress at the interface. This exterior stress at the outer side of the cell interface will be nonzero compared to the reference ambient condition. To estimate this contribution to the pressure drop across the cell layer, we use the equation for a cylindrical vessel in an unbounded elastic material, the pressure at the interface is:

$$\text{Δ}{P}_c=\frac{E_{coll}\epsilon }{(1+v)}$$ (3)

The pressure drop across the cell layer, ΔP, defined above is the applied pressure minus the contribution of the pressure from the collagen matrix, $\text{Δ}P=\text{Δ}{P}_{app}-\text{Δ}{P}_c$. Due to the low modulus of the collagen material, measured in previous studies to be Ecoll ≈ 200 Pa, the resistance to deformation is estimated to be small compared to the cell layer, which is in the range of E ≈ 7 kPa ^34–38. For a linear elastic response of the cell layer the relative contribution of the collagen layer to the pressure drop is approximately $P_c/P_{app}\approx 10\%$. The contribution of collagen to the pressure drop is calculated using the measured strain to determine the pressure drop across the cell layer.

3. Deformation Results

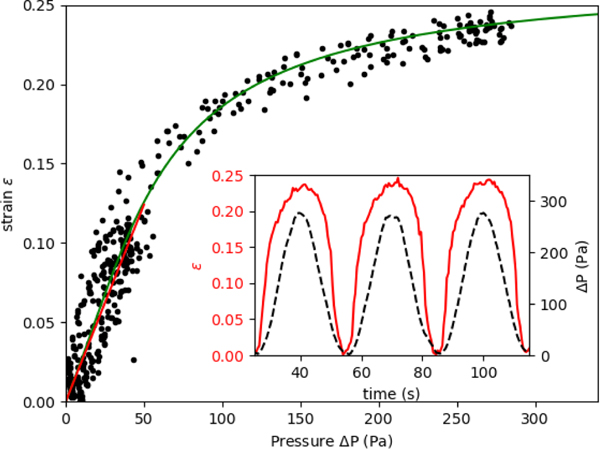
When the applied pressure is modulated in a sinusoidal waveform to sample the vessel deformation response over a range of applied pressures, Figure 3 (inset) shows both the strain and applied pressure as a function of time, within a period of 30 s. The strain response is also repeatable to multiple pressure cycles, indicating that there is no significant damage to the cells with increasing measurement statistics. Vessel strain is symmetric during increasing and decreasing pressure, which can also be seen in a single relationship between strain vs pressure data. This indicates that the system does not exhibit viscoelasticity or have any buildup of pressure that could occur in the collagen. The purely elastic response is verified by applying a step function in pressure (see supplemental material), where we observe that the vessel changes upon the change in pressure within the sampling time of the camera, 10 frames per second.

Fig. 3.

Measured strain of vessel compared to the applied pressure in sine wave function with period 60 s. Black circles show measured values on single vessel over multiple cycles for Sine waves with amplitude of 50 Pa and 300 Pa. The fitted response to Eq. 2 is shown in solid green. The fitted parameters are of membrane elasticity μ_m = μh = 7.5 kPa μm and the maximum strain ε_max=0.27. The linear elastic response is shown in red from (0 to 50) Pa with a membrane elasticity of 22.6 kPa μm. (Inset) Timeseries showing variation in applied pressure and measured vessel deformation.

The amplitude of the sine function is set to a value where nonlinear deformation is observed but does not damage the vessel so that subsequent experiments can be conducted. For the devices tested here, we restrict our applied pressure to a maximum value of 300 Pa. This is within the range of physiological hydrostatic pressure values in the brain and alveolar bone, (0.01 to 2) kPa ^3–5. Some devices did not deform similarly after being subjected to higher pressures, likely as a result of irreversible damage to the cell layer.

The pressure-strain curve, shown in Figure 3, shows the strain hardening behavior at higher applied pressures. At low pressures, below about 50 Pa, the strain response is approximately linear. A linear elasticity value can be obtained for the cell layer from this small amplitude deformation using Eq. 1. For the vessel shown in Figure 3, the membrane elasticity Eh is found to be 22.6 kPa μm. To estimate a value for the Young’s modulus we use the mean measured thickness value of h = 5.3μm (see Supplemental ??), which gives a value of Young’s modulus of E = 4.3 kPa . The mean linear response from other vessels produced in our microfluidic device give values within the range of (3.0 to 10.0) kPa. The maximum strain, ε_max, determined by fitting the parameter J_m, varies over the range of 0.27 to 0.57.

The measured linear elasticity value for the cell layer is much larger than the elastic modulus for the collagen matrix, as noted in the previous section. The measured value for the cell layer also agrees with theoretical estimates and measurements of the Young’s modulus of endothelial cells using AFM, which has been measured in the range of (5 to 30) kPa ^39–43. Although collagen itself strain hardens, it’s modulus remains below that of the cell layer at these strains ⁴⁴.

4. Membrane Permeability

Using applied pressure the flow per unit area through a porous membrane is given by:

$$Q/A=\text{Δ}P/K$$ (4)

where K is the resistance to flow through the membrane. In our experiment, we assume that the applied pressure is much larger than the osmotic pressure across the membrane. The osmotic pressure is estimated using $\text{Π}=cRT$, where c is the fluorophore concentration, R is the gas constant, T is the temperature. The 70 kDa Dextran at a concentration of 12 μg/mL at room temperature (293 K) yields a pressure of $\text{Π}\approx 0.5$ Pa, much lower than than smallest applied pressure of 50 Pa. The resistance can be related to the properties of the porous membrane by

$$K=\frac{32\mu h}{\epsilon d^2}$$ (5)

where ε is the porosity, d is the pore diameter, μ is the viscosity, and H is the layer thickness.

The flow out of the membrane is determined by tracking the increase in fluorescence. The radial flow out of the membrane follows the equation:

$$v(a)=\frac{r}{a}v(r)$$ (6)

The velocity field is integrated to find the position as a function of time $r(t)={\int }_{t=0}^{t}v(r)dt$. The position is compared to the change in position of a constant fluorescence intensity. This equation assumes that convection is dominant over diffusion in the transport of fluorophore. Defining a Peclet number as $Pe=VA/D_{dex}$, where V is the characteristic velocity over a distance A and D_dex is the diffusivity of Dextran. Typical values for flow velocity of 5 μm/s over the length of A ≈ 100 μm. The diffusion coefficient for the Dextran is approximately 2.6×10⁻¹¹ m²/s ⁴⁵. These values give a Peclet number of approximately 20, indicating that convective transport is much faster here than diffusion.

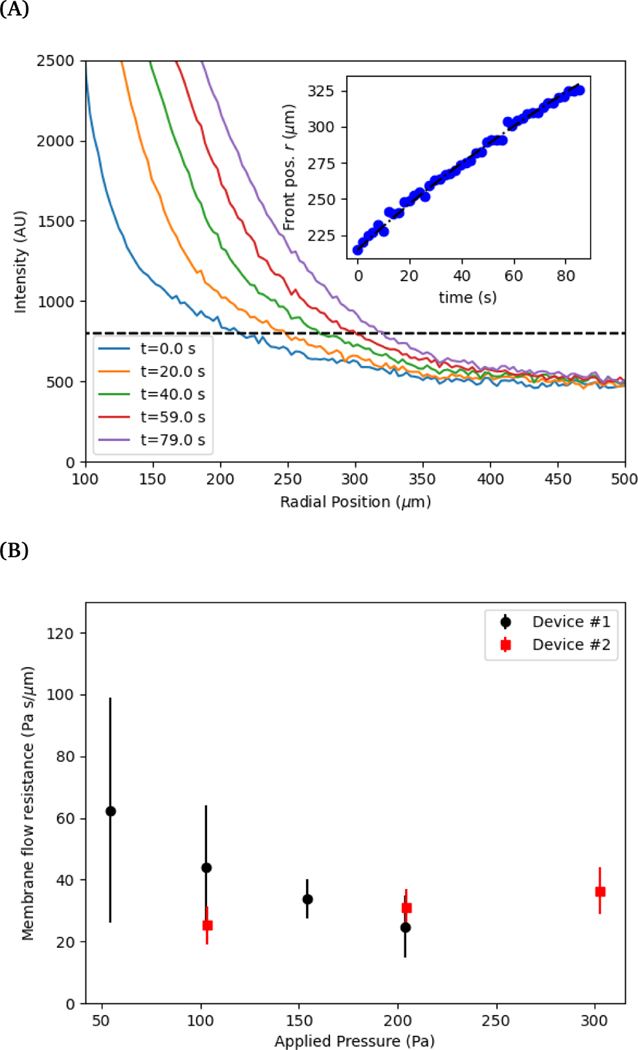
The velocity measured by tracking the fluorescent front gives a measurement of the fluid flux out of the membrane per area, see Figure 4 (A). Using this measured value and the applied pressure drop provides a measurement of the flow resistance of the membrane, see Figure 4 (B). The magnitude of the resistance shows a slight decrease for a set of measurements while almost no change is observed with another vessel. Recall from Eq 5, the membrane permeability depends on both the pore size and the porosity. An increase in pore size due to stretching of the cell layer is likely the cause for the decrease resistance with increasing applied pressure. The variability in the pore locations can lead to a large variation in resistance. We show in the following section that there can be significant variability in the spatial locations of pores.

Fig. 4.

(A) The radial position of the advancing fluorescent front as a function of time. The threshold intensity used to track the position of the front is shown in a dashed line. (Inset) The measured position is compared to the integrated radial flow field using Eq. 6. (B) Membrane resistance for two different devices (labeled 1 and 2) as a function of applied pressure. Error bars indicate the variation in measured resistance at different points along the vessel in axial direction.

For comparison, we estimate the membrane flow resistance using Eq. 5 and the following parameters: pore diameter d ≈ 1 μm, porosity ε ≈ 0.01, cell layer thickness H ≈ 5μm, and viscosity μ ≈ 1 mPa-s. This gives a resistance of approximately 10.6 Pa-s/μm, within the range of the measured values. In comparison, we estimate the resistance of flow of the same fluid through the surrounding collagen, where we estimate an effective pore size of d_col ≈ 80 μm, porosity of ε_col ≈ 0.9, and thickness of h_col ≈ 15 mm ^36,46. This gives a value of approximately 5.6×10⁵ Pa-s/m. The flow resistance of the porous cell layer is thus roughly 300 times greater than the flow resistance of the collagen.

The flow of liquid through the ports also adds to the resistance of the system. Using the maximum measured velocity of 1 μm/s and the area of the vessels as $A=2\pi a_0$, we estimate a flow rate of 0.02 μL/s. The resistance for the channel section is estimated by $K_{tube}=\frac{8\mu L}{\pi a_0^4}$, where L is the length of the channel section and a₀ is the radius as the vessel section. The pressure drop across this can be estimated by $\text{Δ}P=K_{tube}Q$. At the highest pressure measured, 300 Pa, the flow rate corresponds to approximately 1 Pa pressure drop, which contributes less than 1 percent of the total applied pressure drop. The experimental geometry thus is effective to measure the permeability property of the membrane comprising the endothelial cell layer.

The permeability of a cell layer is typically determined by tracking the diffusion of a fluorescent solute through the membrane. The change in fluorescence intensity, measured outside of the vessel and monitored over time, is related to the membrane permeability ^47,48. The solute permeability can be converted to membrane flow resistance by using the osmotic pressure differential,

$$Q/A=\frac{P_d}{cRT}\text{Π}$$ (7)

where P_d is the solute permeability. The term $\frac{P_d}{cRT}$ can be compared to the membrane resistance measured with applied pressure. The solute permeability for the same vessel system is approximately P_d ≈ 40 nm/s for 70 kDa Dextran at a concentration of 12 μg/mL ⁴⁷. This gives a value for the membrane flow resistance of approximately 10 Pa-s/μm, which is comparable to the values measured using an active or driving applied pressure in Figure 4.

Previous measurements of membrane flow resistance, often reported as conductance, vary depending on the methods and cell type. Measurements in a microfludic device show similar values in the range of 10 Pa-s/μm ⁴⁹. While other measurements of a cell layer cultured on a filter give values in the range of 10⁴ Pa-s/μm ⁵⁰. The higher resistance values are consistent with submicron pore sizes between cells while the lower values observed here and in other microfluidic devices are indications of larger micrometer scale pores in the cell layer.

5. Local strain

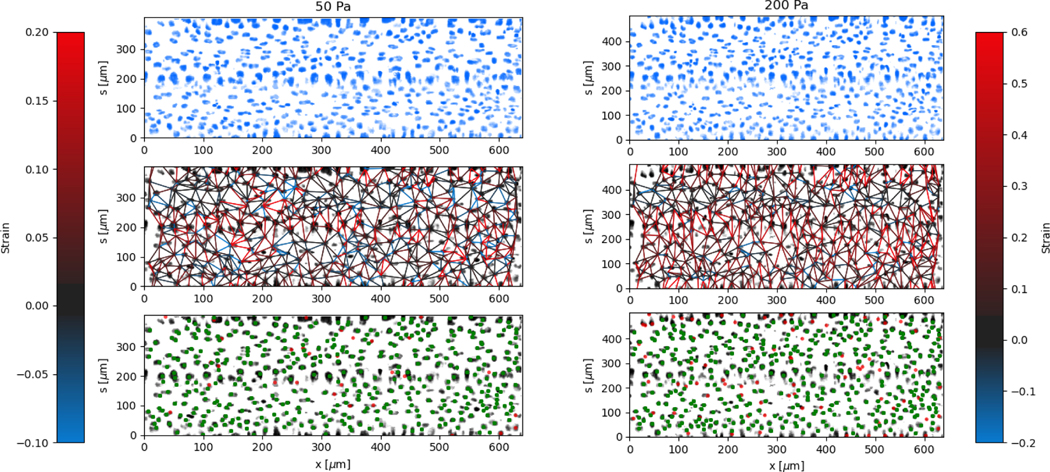
The local deformation of the vessel surface is measured by tracking the 3D positions of cell nuclei from 3D confocal images ²⁸. A mean surface of the vessel is determined by fitting to an elliptic cylindrical shell to the nuclei positions. We define an axis, s, on this surface in the circumferential direction. The projection of the nuclei positions onto the mean surface locates the cells on the x-s plane, in both the axial and circumferential directions. Two-dimensional images are also extracted from the three-dimensional image data by averaging pixel intensity normal to the mean surface. The positions are tracked for each applied pressure value in comparison to a reference image taken at zero pressure ²⁸. The mean circumferential strain is determined by the change in the arclength of the ellipse. This mean strain is used as an initial position estimate for linking the nuclei positions for different applied pressures. Nuclei that are located but not linked to the reference frame are excluded from the analysis, artificially lowering the cell density. This method typically results in over 85 percent of nuclei being linked from the reference frame, with the largest number of unlinked particles coming at highest strains and in locations of highest seeding density. After linking, neighboring nuclei are determined using Delauney triangulation and the distance between nuclei is measured. The change in distance between cells with applied pressure is used to calculate the local strain (ΔL/L). The results of the local strain, represented by the color of the line between the tracked cells, are shown at different applied pressures in Figure 5.

Fig. 5.

Local deformation determined from tracking nuclei on the vessel surface at different applied pressures, 50 Pa and 200 Pa. The lines between between neighboring cell nuclei show strain magnitude according to the colorbar. The strain increases with applied pressure, but has variations primarily in the circumferential s direction. The imposed images are of the mean fluorescent intensity of cell nuclei labeling (DAPI) on the surface of the vessel. In the bottom-row plots, tracked (linked, see text) nuclei from P = 0 Pa are identified green, and unlinked nuclei are identified red.

The stretching of the entire surface can be observed by the increase in the circumferential axis, s, for each of the applied pressures. This global strain follows a similar nonlinear elastic response observed with the measurement of the vessel width using phase contrast in Figure 3, although the circumferential strains are 0.06,0.14,0.19, and 0.28 and in this case represent the linear portion of the global strain response. We note that this vessel exhibited a maximum strain parameter on the higher end of the vessels tested, e.g. where ε_max ≈ 0.5.

The local strain between nuclei varies significantly along the circumferential direction. The local strain in the axial direction is small, which is expected due to the uniform cross section and fixed ends. Local rearrangements caused by irregularities of the structure of the layer may result in strain in the axial direction. Inaccuracies in tracking the center of the nuclei between different images may also result in some erroneous strain measurements, which will be more noticeable in the axial direction due to the lack of global stretching in this direction.

The regions of the largest strain at low pressures continue to be the regions of greatest strain at higher applied pressures. Similarly, the regions of lowest strain do not change significantly even at the highest applied pressures. This indicates that the primary contribution to the global strain comes from the most deformable parts of the cell layer, rather than various regions reaching a finite extensibility threshold at different applied pressures.

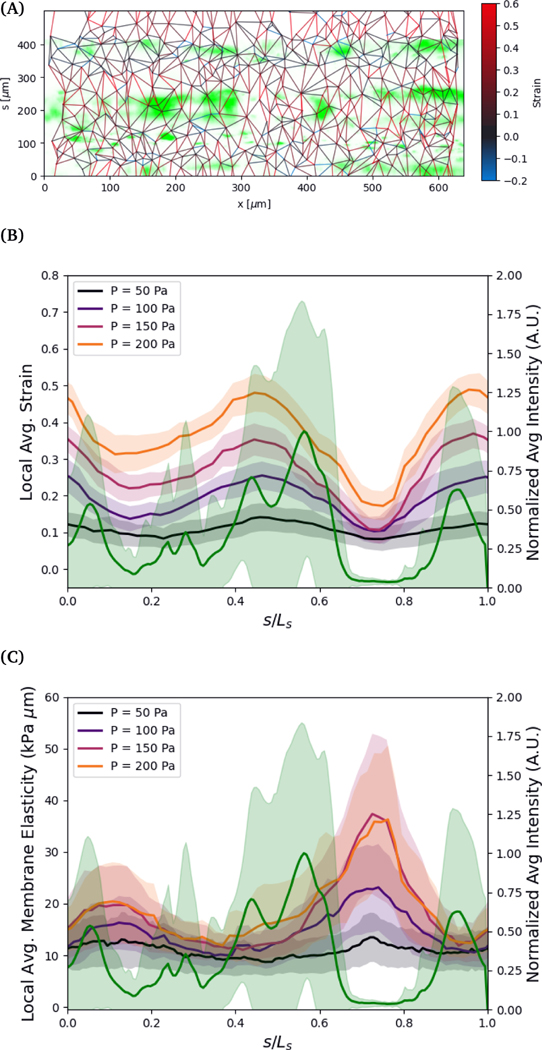
The variation in the circumferential local strain can be understood primarily by the density of voids in the cell structure. The voids are observed by flowing 0.75 μm particles through the vessel and observing where they flow out, see Figure 6. The particles can exit the vessel through larger voids, and then get trapped by the collagen network surrounding the vessel. The regions closer to where the seeded particles accumulate, indicative of voids in the vessel, tend to show greater deformation. This is more clearly visualized by comparing the axially averaged elasticity and fluorescence intensity as a function of the circumferential direction normalized by the arclength, see Figure 6 (B). The deformation is greatest in or adjacent to regions of higher fluoresence intensity, where the tracer particles have accumulated in the collagen outside of the cell layer.

Fig. 6.

A) Mean fluorescent intensity (shown in green) at the vessel wall surface of 0.75 μm polystyrene particles seeded into the vessel under applied pressure. Strain between tracked nuclei at applied pressure of 200 Pa. B,C) Axial mean of particle fluorescence intensity normalized by maximum mean compared to local strain and elasticity at different applied pressures as a function of normalized circumferential direction. The width of lines shows the standard deviation of the fluorescence intensity, strain, and elasticity along the axial direction.

To further understand the variations in structure, we estimate the effective local elasticity at each applied pressure. Assuming minimal leakage from the vessel, the pressure drop across the vessel wall can be approximated as uniform. We compute an estimate of local elasticity based on the the hoop stress in the vessel, computed as ${\sigma }_{\theta }=\text{Δ}Pa(s)/h$. Note that the relationship between strain and stress varies slightly due to the nonspherical cross section of the vessel. For the range of applied pressures, (50 to 200) Pa, and the geometry of the vessels, the applied hoop stresses are in the range of approximately (1000 to 4000) Pa. The strain in the circumferential s direction is defined by, ${\epsilon }_S=\text{Δ}{l}_s/l_s=\text{Δ}l/l\sin (\varphi )$, where l is the distance between nuclei, and l_s is the distance in the s direction. We exclude neighbors in the axial direction by angles less than $|\varphi |<\pi /4$.

The strains in the circumferential direction result in approximate values of elasticity in the range of (3 to 8) kPa, which agree with the range of linear elasticity measured by tracking the vessel width using phase contrast in the range of ΔP ≈ (0 to 50) Pa. The results, shown in Figure 6, show large variations in the elasticity in the circumferential direction, inverse in magnitude to the strain. The elliptical shape of the vessel cross section does not explain the variations in strain observed in Fig. 5. Rather, the variation in strain is a result of variations in local elasticity and are mostly closely related to the presence of voids as indicated by the expelled fluorescence tracers. In this particular vessel, the global linear elastic response continues to ΔP_app=200 Pa, thus no strain hardening is observed.

There are many factors that could lead to the variation in the local elasticity of the cell layer. As noted, the clearest indication of the local elasticity variation from our observations are voids in the cell layer. The decrease in elasticity in these regions likely result from weaker connections between neighboring cells. These voids may result from variations in seeding density, as discussed in the methods section, but some vessels with a low degree of seeding density variation have the same propensity for voids.

The density of voids and lower elasticity may also result from higher regions of curvature during seeding. The elliptical shape of the collagen scaffold creates regions of higher curvature, typically along the sides of the vessel, which are centered around s/max(s) ≈ 0,1 and s/max(s) ≈ 0.5.

6. Conclusions

In this study, we used a 3D microvascular model to observe mechanical properties of the cell layer under applied pressure. This is accomplished by using pneumatic controls that apply pressures in the 100 Pa range. The nonlinear elastic response of the cell layer is measured by observing the radial expansion of cylindrical vessel using phase contrast microscopy. The permeability of the cell layer is also be measured by monitoring the flux of fluorescent dye through the cell layer. Finally, the local structure is investigated by tracking the change in relative position of the cell nuclei under applied pressure, which allowed us to measure the local mechanical properties of the vessel. We observed significant variation in local deformation, where the largest deformations correlate with local porosity.

Our approach, focused on understanding the mechanical properties of a single endothelial monolayer, may be advantageous for understanding the role of endothelium mechanics in normal and disease states. Tissue injury inevitably disrupts the mechanical homeostasis of the microvasculature that underlies its normal architecture and function. Endothelial cell injury in the microvasculature of organs (i.e. bone, oral mucosa) may be triggered by bacteria infection, hypoxia, and shear stress ⁵¹. In addition, the extracellular matrix stiffness can affect endothelial cell migration, proliferation, and barrier integrity, and contributing to the emergence of vascular diseases ^52–54. Thus, understanding the inter-play between the microenvironmental mechanical determinants and endothelial behavior is pertinent to understanding the causes of microvascular related diseases and might have important therapeutic implications.

Pascal-scale pressure control using a pneumatic pump enables many possibilities for further study of bio-mimetic vascular devices. For instance, the variation in mechanical properties could be studied for different cell types, vessel diameters, and exposure to molecules introduced to the vessel. The effects of applied stress on the cell layer over time can be investigated in a cell culture chamber. Finally, the pressure controller can also be used to drive flow through the vessel, recreating a physiological flow environment.

These methods can be used to investigate the relationship between the structure and elasticity of the endothelial cell layer and surrounding extracellular matrix in a more detail. In particular, the measurement of local variation in elasticity could be used as a measure of spatial variable of the vessel integrity. This in turn can be related to factors such as the density of various cell layer components, including actin and vascular endothelial (VE)-cadherin, that may alter local mechanical properties. Finally, the system can be modified to include perivascular cells, such as pericytes, to identify their role in microvascular mechanics ⁴⁷.